Preprint
Article
Effects of Revenue-Sharing Contracts and Overconfidence on Innovation for Key Components
Altmetrics
Downloads
53
Views
15
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
04 October 2023
Posted:
06 October 2023
You are already at the latest version
Alerts
Abstract
Revenue-sharing (RS) contracts are a common approach to incentivize innovation of upstream suppliers by addressing the uneven profit distribution between upstream and downstream firms. Considering the possible overconfidence characterizing decision makers in the supply chain, we investigate the effect of the RS contract and the tendency of overconfidence of supply chain members on the investment in R&D of key components of products in the context of an upstream supplier that is the leader in the R&D and production of key components. We find that regardless of the bargaining power of either party, a RS contract can increase the R&D investment in key components. Regarding the effects of overconfidence of either downstream manufacturer or up-stream supplier, it can increase the R&D investment in key components. Supplier (manufacturer) overconfidence can harm their own profits but increase the profits of the manufacturer (supplier), and when the level of overconfidence is below a certain threshold, the damage to their own profits is less than the increase in each other's profits, thus benefiting the whole supply chain. In addition, we also find a joint effect of RS contracts and overconfidence: when the bargaining power of the supplier is low, the RS contract has a certain compensatory effect on the loss of their own profits caused by overconfidence.
Keywords:
Subject: Business, Economics and Management - Business and Management
1. Introduction
High-tech products such as industrial machines, biopharmaceuticals, high-performance medical devices, smart phones and electrical equipment often have many key components that have a significant impact on their performance. For example, development of computer numerical control (CNC) systems for industrial machine tools has greatly improved the accuracy, speed and efficiency of the parts processed on the machine tool. While the provision of high-tech key components contributes to sales of upstream suppliers, it also improves the quality of the end product, which in turn benefits downstream manufacturers (Fossas-Olalla et al., 2015). Studies have found that suppliers are less willing to invest in innovation if they need to bear the full cost of R&D and production (Laseter & Ramdas, 2002). At the same time, given the features of long R&D cycles, high R&D investment costs, and high R&D sophistication, innovations in key high-tech components require collaboration among supply chain members. On the other hand, downstream firms are often willing to help upstream suppliers to facilitate R&D. For example, Rundle Medical has invested in the industrial end of upstream R&D and production in the in-vitro diagnostics industry. RS contracts are one of the simple and effective collaboration approaches. Wang and Shin's (2015) study points out that RS contracts are a good way to promote collaborations with upstream key component suppliers on investment in innovation and product quality while wholesale pricing and investment-sharing contracts may lead to underinvestment in innovation upstream. In the biopharmaceutical sector, Alpha and Mega signed a RS contract in 2002 to support development of a new diabetes drug by the upstream firms. In the smartphone sector, Apple signed a RS contract with AT&T to guarantee Apple's revenues and incentivize innovation in R&D of component parts. In the area of mobile apps, the iOS and Android operating systems have incentivized app providers to offer more attractive products by allocating 70 per cent of sales revenue to app developers.
While the incentives from downstream to upstream in the supply chains can affect innovation decisions and performance, some characteristics (including cognitive limitations) of individual supply chain members can also have significant effects on industrial innovations. Overconfidence is one of these influential characteristics. For example, both Jack Welch of General Electric and Steve Jobs of Apple demonstrated overconfidence in their decision-making during their tenures as the CEO of their firms. Markovitch et al. (2015) suggest that overconfidence of decision makers is associated with high forecasts of new product sales. This means that overconfident decision makers tend to have a higher value recognition of their own R&D products, or of the core components that they choose to use, and adopt RS contract incentives to promote their R&D, relative to the market. Overconfident downstream manufacturers are more likely to enter RS contracts with upstream component suppliers to incentivize them to innovate so that the quality of the end-product can be improved. Overconfident suppliers are also often willing to invest more in maintaining the high technology content of their components. On the other hand, Plous (1993) indicates that overconfidence in judgement and decision-making can also potentially generate catastrophic results for the firm. For example, cellphone maker OPPO had to shut down its chip design subsidiary Zheku Technology, because OPPO was overconfident in its own R&D capabilities and potential market demand, but its own chip manufacturing eventually failed to meet the need for chips for mobile phone production. However, some scholars argue that overconfidence does not necessarily undermine performance of supply chain innovation (Kirshner & Shao, 2019; Li, 2019; Wang & Shin, 2015).
Prior research has analyzed the impact of the downstream manufacturers’ overconfidence on innovation in key components by the upstream suppliers (Du et al., 2021). However, no research has examined the impact of the level of overconfidence of both upstream and downstream members on innovation in key components under the RS contract. Therefore there is an urgent necessity to analyze the mechanism of their impact. Wang and Shin (2015) propose that RS contracts are the most effective approach for promoting R&D investment of upstream suppliers, but their study did not examine the role played by overconfidence in innovation of supply chain members. Therefore, there is a gap in the existing research on innovation collaboration between upstream and downstream supply chain members regarding how overconfidence and RS contracts affect the innovation decisions of upstream suppliers, and whether their joint impact on innovation is complementary or substitutive when both supply chain members are overconfident as well as having a RS contract between upstream and downstream firms.
The existing research gaps have motivated our study to examine the effects of RS contracts and overconfidence on innovation decision-making of supply chain members by addressing the following three research questions:
What is the impact of manufacturers’ or/and suppliers’ overconfidence on upstream key component innovation and respective profit outcomes?
How does the RS contract affect the profit level and distribution of overconfident supply chain members?
How do RS contracts and overconfidence interact with each other to affect decision-making on key component innovation?
We adopted a game-theoretic approach to construct a supply chain model consisting of a single supplier and a single manufacturer, both of which tend to be overconfident. The supplier is a Stackelberg leader responsible for the innovation and production of key components, and the fellow manufacturer uses RS contracts to incentivize the supplier to invest in R&D of key components. Through gaming modelling, we first compared the level of innovation and profits under four scenarios: neither side is overconfident, either the supplier or manufacturer side is overconfident, and both sides are overconfident under the RS contract. Secondly, we developed a sensitivity analysis of the RS proportion and the degree of overconfidence. Finally, we examined the determination of RS ratios by performing a bilateral bargaining model.
Our study contributes to the literature of collaborative innovation in supply chains in two aspects. First, while the existing studies have only analyzed the impact of overconfidence of one supply chain member on supply chain innovation, our study extends prior research by not only considering overconfidence of both supply chain members, but also analyzing the interactive effects of RS contracts and overconfidence on upstream supply chain innovation. Our research findings suggest that when the overconfidence level of an overconfident supply chain member is below a certain threshold, the absolute value of profit increase resulting from the overconfidence of the other supply chain member is greater than the absolute value of the profit decrease for the overconfident supply chain member. Moreover, the RS contract has a compensatory effect on the profit loss suffered from overconfidence when the supplier's bargaining power is low. Second, by analyzing the effects of both exogenous RS proportions and overconfidence on the optimal outcome, our study provides a theoretical basis for supply chain members to understand the effects of revenue-sharing contracts and overconfidence on innovation performance.
2. Literature review
2.1. Innovation incentive contracts in supply chains
Prior research on supply chain innovation incentive contracts has focused on incentivizing upstream green innovation (Yenipazarli, 2017; Liu et al., 2020), and incentive mechanism design between upstream and downstream supply chain members (Aydin & Parker, 2018; Yu et al., 2021). Among them, some studies have paid attention to innovation in upstream key components. In the context of upstream suppliers' innovation of key components that can improve performance of the final product, Wang and Shin (2015) analyze the impact of three types of contracts —wholesale price contract, quality-dependent wholesale price contract and RS contract — on coordination of the supply chain, and their findings suggest that RS contracts can play a role in coordinating the supply chain. After comparing RS and investment-sharing contracts in a supply chain consisting of a financially-constrained upstream start-up supplier that has invested in quality innovations and a downstream manufacturer that is facing demand uncertainty, Xing et al. (2022) provide a reference for the manufacturer on which contract to choose in which situation. Based on a supply chain setting between automobile manufacturers (marketers) and battery manufacturers (innovators), Yu et al. (2021) analyze four types of R&D co-operation contracts in the R&D and sales phases, including two vertical co-operation models of revenue-sharing contracts and fixed R&D payment fees, as well as two types of co-development contracts in which the marketer is in charge of the sales phase, or the innovator is in charge of the sales phase. Based on an analysis of the impact of demand uncertainty on supply chain innovation investment decisions, Liu et al. (2023) suggest that centralized decision-making has the highest investment efficiency and better value of investment choices, and that volume discount contracts are preferred when market volatility is high. Focusing on comparing the differences between various contracts in innovation promotion, these prior studies have provided valuable insights by showing that revenue-sharing contracts can indeed incentivize upstream suppliers to innovate in R&D. Building on these studies, our study focuses on revenue-sharing contracts and examines the effect of overconfidence as one of the common cognitive biases of decision makers on collaborative innovation of supply chain members.
2.2. Overconfidence in supply chains
The second stream of relevant research is the issue of overconfidence in supply chains. When making R&D decisions, or operational decisions such as production volume and wholesale price, supply chain members tend to have several behavioral characteristics, of which overconfidence is a common one and an important cause of biased decision-making. Based on a review of more than 600 papers (Moore & Healy, 2008; Moore & Schatz, 2017) on overconfidence, Moore and associates classified three types of overconfidence: over-precision — people believe that they are more accurate in making predictions about what is actually going on (Li, 2019), over-positioning — people believe that they have above-average abilities, and overestimation — people usually overestimate their actual abilities, behaviors, level of control and likelihood of success (Li, 2019). The existing literature in operations management research mainly focuses on over-precision and overestimation. Over-precision is usually portrayed as the expected distribution of market demand having the same mean as the actual value but lower variance (Kirshner & Shao, 2019, Li, 2019; Ren & Croson, 2013). Overestimation means that the mean of the expected market demand distribution is larger than the actual value (Ren & Croson, 2013). Corporate decision makers are more prone to overconfidence in overestimating the benefits generated from R&D and innovation investments in the supply chain. For example, Apple's founder Steve Jobs was happy to overestimate the expected benefits of uncertainty associated with new technologies.
A study by Hirshleifer et al. (2012) finds that decision makers who overestimate the benefits from an innovation project tend to invest more in the firm's innovation projects. In their study investigating how overconfidence with regard to overestimation of a firm's decision makers in a supply chain affects the decisions of other firms in the chain, Nelson and Schwartz (2019) find that overestimation of demand by downstream customer firms leads to increased investment by upstream suppliers. Through an empirical study in the context of durable goods manufacturing and high technology barrier industries, Phua et al. (2018) suggest that the overestimated overconfidence of decision makers of downstream manufacturers can attract more suppliers and encourage suppliers to make R&D investments. Tang et al. (2015) show that the tendency of decision makers to evaluate firms higher than the actual situation of the firms, i.e., to overestimate the expected firm performance, can positively influence the innovation activities of firms, but the strength of the influence is contingent on the external environment. In their research on overconfidence of the supply chain members, Xiao et al. (2020) have analyzed the implications of retailers' equity concerns and manufacturers' overconfidence for sustainable two-phase supply chains, and they suggest that RS contracts are the most lucrative of the three types of decentralized contract. Du et al. (2021) analyze which of the wholesale price contract and the cost-sharing contract is able to provide a better incentive for upstream suppliers to innovate when the manufacturer overestimates the ability of innovation to increase demand, and find that the wholesale price contract is not favorable to supplier innovation, and they also find that the cost-sharing contract is more favorable to supplier innovation than the centralized decision-making model. Wang et al. (2022) build a two-tier logistics service supply chain consisting of logistics service providers and logistics service integrators, analyzing the impact of logistics service integrators' overconfidence on the innovation of green logistics service products and proposing an incentive contract of "green subsidy and loss sharing". Hao et al. (2023) examine the effect of overconfidence in one or both partners on inventory responsibility allocation and profitability.
Among the above studies on overestimated overconfidence, the studies done by Xiao et al. (2020), Du et al. (2021), Wang et al. (2022), and Hao et al. (2023) are more relevant to the topic examined in this paper. Hao et al. (2023) examine the impact of overconfidence on the allocation of inventory responsibility on both sides of the supply chain, in contrast to this paper's focus on promoting innovation in upstream suppliers. Xiao et al. (2020), Du et al. (2021), and Wang et al. (2022) focus on overconfidence on one side of the supply chain, but do not explore the interactive effects of overconfidence on the decision-making of each member of the supply chain. In particular, given its focus on revenue-sharing contracts, the study by Xiao et al. (2020) is highly valuable to our study. Extending the study by Xiao et al., our paper further explores the situation where bilateral bargaining models determine revenue-sharing proportions. This unique focus of our study enables us to generate some new research findings. For example, our study suggests that overconfidence of a supplier (manufacturer) damages its own profits but increases the profits of the manufacturer (supplier), and that when the degree of overconfidence is under a certain threshold, the value of the damage to its own profits is smaller than the value of the increase to the other side's profits, resulting in pure benefits for the whole supply chain.
3. Model description and basic assumptions
The research setting for this study is a supply chain consisting of a single supplier and single manufacturer. The basic assumptions are stated as: both supply partners tend to be overconfident, the supplier is a Stackelberg leader responsible for the R&D and production of the key components, and the manufacturer is a follower responsible for the manufacturing and sales of products. After the supplier's R&D on key components, in addition to the one-off R&D costs invested upfront, it is assumed that the unit cost of production of key components increases as the level of R&D investment increases. In order to better co-ordinate the R&D inputs of key components from upstream and downstream of the supply chain, the supplier and the manufacturer share the sales revenue through a RS contract. The game sequence includes four steps, which are shown in Figure 1.
Step 1: Supplier and manufacturer negotiate to determine the percentage of RS to be received by the supplier (). In this paper, bargaining power is defined as the effect of the profits that each of the cooperative firms can make from the co-operation on the parties' bargaining objective function (Feng & Lu, 2013). The greater the bargaining power of a party, the greater the impact of its profits on the bargaining objective function. We denote the supplier's bargaining power by (), the manufacturer's bargaining power by , and the manufacturer's (supplier's) full bargaining power by (). indicates that the parties have equal bargaining power.
Step 2: The supplier determines the level of R&D inputs in key components ; in order to characterize the incremental marginal cost, the R&D investment is in the form of a quadratic; the amount of R&D investment is , where the R&D coefficient is (Chen et al., 2019). Let the production cost per unit of key components be , denoting the production cost per unit of key components when no R&D in-puts are made, and for simplicity of the model, it is set to 0, so that (Chen et al., 2019). denotes the effect of the level of R&D inputs on unit production costs.
Step 3: The supplier determines the wholesale price of key components based on previous inputs. It is worth noting that since Step 2 and Step 3 are consecutive decisions made by the supplier, simultaneous or sequential decisions in Step 2 and Step 3 do not affect the equilibrium outcome of the game.
Step 4: The manufacturer acts as a follower and determines the volume of product to be produced based on the overall decisions of the supplier (Li & Zhao, 2022; Lin et al., 2014; Niu et al., 2019). The manufacturer's unit assembly costs are not taken into account; when unit assembly costs are positive, this portion can be considered in the unit production costs of the supplier's components (Li & Zhao, 2022).
R&D investment in components can improve product performance, and customers are willing to pay a higher price for products with better performance: for example, the high-end industrial mother machine loaded with Huazhong 9, a new generation of intellectual CNC system developed by Huazhong CNC, has been received favorably customers. We let the manufacturer's inverse demand function be (Feng & Lu, 2013; Xie et al., 2021), where is the selling price of the product, is the maximum selling price of the product without R&D investment in key components, is the coefficient of influence of the level of R&D investment in key components on the selling price of the product, and in order to ensure economic feasibility, we have . In addition, market acceptance of technological performance improvements resulting from R&D investments is characteristically uncertain. Assuming a continuous random variable on the interval with mean , variance , cumulative distribution function and probability density function (Du et al., 2021), we have .
In this paper, overconfidence is defined as an overestimation of one's own ability or results (overestimation), which manifests in the form of an overestimation of the impact of the level of R&D investment in key components on the selling price of a product, with the mean value of (the investment) being higher than its actual mean value . Both the manufacturer and the supplier tend to be overconfident, and the decision objectives of both sup-ply chain partners are stated as:
In the above equations, () is the overconfidence coefficient of the supplier (manufacturer); in this case, the mean value of the supplier's (manufacturer's) perception is (), and the variance is . There can be four models: SM (both the supplier and manufacturer are overconfident, in this case, ), SN (only the supplier is overconfident, in this case, ), NM (only the manufacturer is overconfident, in this case, ), and NN (there is no overconfidence on both sides, in this case, ). and denote the expectations of the utility functions of the supplier and the manufacturer, respectively.
The profit functions for each side are formulated as:
In the above equations, and represent the expectation of the profit function of supplier and manufacturer, respectively, when or when , and when or when , . We denote the supply chain profit by ().
The supplier and the manufacturer differ in their level of overconfidence in the impact of the level of R&D investment in key components on the selling price of the product; they can be aware of the level of overconfidence of the other party, but they do not update their own level of overconfidence based on the level of overconfidence of the other party that they have learnt in the game. The descriptions of the notations appearing in this paper are shown in Table 1.
4. Model analysis
This section models the tendency of both the manufacturer and the supplier to be overconfident about the impact of the level of R&D inputs in key components on the selling price of the product. We focus on analyzing the impact of the model's main inputs (the revenue-sharing proportion and the coefficient of overconfidence) on the outcomes: the level of R&D inputs, the volume of production, the wholesale price, and the profit. The optimal solution is denoted by *.
Under the conditions , , , and when , , when , [see the proof following Lemma 4 for the above conditions] and when the income sharing ratio is exogenous, there are Lemmas 1-4.
Lemma 1: In model SM, the optimal wholesale price is , the optimal level of R&D is , the optimal production volume is , the optimal profits of the two firms are and , and the total profit of the supply chain is .
Lemma 2: In model SN, the optimal wholesale price is , the optimal level of R&D is , the optimal production volume is , the optimal profits of the two firms are ,, and the total profit of the supply chain is .
Lemma 3: In model NM, the optimal wholesale price is , the optimal level of R&D is , the optimal production volume is , the optimal profits of the two firms are ,, and the total profit of the supply chain is .
Lemma 4: In model NN, the optimal wholesale price is , the optimal level of R&D is , the optimal production volume is , the optimal profits of the two firms are , , and the total profit of the supply chain is .
In the above equation , , , there are , in model SM’ , there are ,,in model SN’ , there are , in model NM’ , and there are , in model NN’ .
Proof of Lemmas 1-4: The solution by inverse induction is obtained by taking the derivative of Eq. (2) with respect to and making it equal to zero:
The solution by inverse induction is obtained by taking the derivative of Eq. (2) with respect to zero and setting it equal to zero: , , therefore, is an extreme value solution. Substituting into Eq. (1) and taking the derivatives of Eq. (1) with respect to and to make them equal to 0, we obtain and . Hessian matrices , first-order leading minor is significantly less than 0; second-order leading minor is . To ensure that Eq. (1) is strictly concave with respect to and , it is necessary to ensure that is positive in all four models SM, SN, NM and NN. Therefore, , , and must be satisfied at the same time. Substituting and into , we obtain , and substituting , , and into equations (3) and (4), we obtain and . is constant. It is also necessary to ensure that , , , . After the constraints take the intersection, it is sufficient to ensure that , [ to ensure], [ to ensure], and when , [ to ensure], and when , [ to ensure].
Where , , , , and .
4.1. Comparative analysis
A comparison of Lemmas 1-4 leads to Corollary 1-4.
Corollary 1 , , ; when , , , when , , ; if and only if and , otherwise .
Proof , ,,,,,,
,,, when , , or (discard). When , or (discard). When , we have , . When , we have , , where , only if and 时,.
In order to observe the relationship with , with , and with more clearly, we have conducted a numerical analysis, and set . The boundary line between and , and is the same as . The relationship between and when we have , and under this condition, see Table 2. Under this numerical assumption, in order to ensure that the Lemmas 1-4 are established, there are , , , , .
From Corollary 1, among the four models, the optimal wholesale price , optimal level of R&D inputs , and optimal production volume are the highest when both the supplier and the manufacturer are overconfident (model SM); the optimal wholesale price , optimal level of R&D inputs , and optimal production volume are the lowest when neither the supplier nor the manufacturer is overconfident (model NN); and the optimal wholesale price , optimal level of R&D inputs , and optimal production volume are between models SM and NN for the supplier-only or manufacturer-only overconfidence (model SN or model NM). The optimal wholesale price , optimal level of R&D inputs , and optimal production volume for the case where only the supplier or only the manufacturer is overconfident (Model SN or Model NM) are set between Model SM and Model NN. This suggests that overestimation of the impact of the level of R&D inputs in key components on the selling price of the product by either the supplier or the manufacturer leads to an increase in the optimal wholesale price , optimal level of R&D inputs , and optimal production volume . When both overestimate the impact of the level of R&D inputs on the selling price of key components, the impacts are superimposed so that the optimal wholesale price , the optimal level of R&D inputs , and the optimal production volume are the highest.
From Corollary 1 and Table 2, it can be seen that when the overconfidence coefficient in Model SN satisfies the relationship with the one in Model NM, the level of R&D inputs and production volume of the formulation in Model SN will be higher than that in Model NM, and in the reverse case, it will be low. The overconfidence coefficient in Model SN satisfies the relationship (i.e. is smaller) with the one in Model NM, and when , the wholesale price of key components formulated in Model SN will be higher than that formulated in Model NM, and vice versa.
Corollary 2 , ; when , , when , .
Proof ,,,.Let , after multiplication cross, shifting to the left side of the equation gives , let be equal to the above equation. Since , when , so , and when , , so there must exist a point with respect to which makes .
In order to observe the relationship between with more clearly, we make a graph, see Figure 2(a), with the same parameter values as above .
Corollary 2 compares the profitability of the manufacturer in the four models, where supplier overconfidence alone must increase the manufacturer's profitability and manufacturer overconfidence alone must reduce the manufacturer's profitability compared to neither model (overestimating the impact of the level of R&D inputs in key components on the selling price of the product). The manufacturer's profits are higher when the supplier is overconfident than when only the manufacturer is overconfident. The manufacturer's profits will be higher when only the supplier is overconfident compared to when both are overconfident. Corollary 2 illustrates that manufacturer overconfidence decreases the manufacturer's profits because the manufacturer overestimates the impact of the level of R&D inputs in key components on the selling price of the product and makes decisions accordingly, but does not actually achieve this utility, thus harming its own profits. The supplier's overconfidence leads the supplier to set higher levels of R&D inputs for key components, which increases customer acceptance, which in turn leads the manufacturer to produce more products, and therefore increases the manufacturer's profits.
When manufacturer's and supplier's overconfidence act at the same time, the effects of both will be superimposed, see Corollary 2 and Figure 2(a). The relationship between manufacturer's and supplier's overconfidence satisfies the condition , and vice versa . This is because when the manufacturer's overconfidence is greater than the supplier's overconfidence, the manufacturer's overconfidence dominates the manufacturer's own profit reduction, resulting in a lower compared to . When the manufacturer's overconfidence is small compared to the supplier's overconfidence, the supplier's overconfidence plays a dominant role in increasing the manufacturer's profits, resulting in being higher compared to .
Corollary 3 , .When , ; when , .
Proof ,,,
. Let , after multiplication cross, shifting to the left side of the equation yields . Let be equal to the above equation, since , when , ; when , , so there must exist a point with respect to such that . In order to observe the relationship between and more clearly, we make a graph, see Figure 2(b), with the same parameter values as above .
Corollary 3 compares the profitability of the supplier in the four models, where overconfidence on the part of the manufacturer alone must increase the profitability of the supplier, and overconfidence on the part of the supplier alone must harm the profitability of the supplier, compared to neither model (overestimating the impact of the level of R&D investment in key components on the selling price of the product). Supplier profits are higher when the manufacturer is overconfident than when only the supplier is overconfident. Supplier profits will be higher when only the manufacturer is overconfident compared to when both are overconfident. Corollary 3 shows that supplier overconfidence damages supplier profits because the supplier overestimates the impact of the level of R&D inputs in key components on the selling price of the product and makes a decision accordingly; however, the manufacturer does not order as much as the supplier expects, thus damaging the supplier's profits. The manufacturer's overconfidence may cause the manufacturer to order more critical components, thus increasing the supplier's profitability.
When manufacturer's overconfidence and supplier's overconfidence act simultaneously, the effects of both will be superimposed, see Corollary 3 and Figure 2(b). The relationship between manufacturer's and supplier's overconfidence satisfies the condition , and vice versa . This is because when the manufacturer's overconfidence is larger than the supplier's overconfidence, the manufacturer's overconfidence plays a dominant role in increasing the supplier's profit, resulting in higher compared to . When the manufacturer's overconfidence is smaller than the supplier's overconfidence, the supplier's overconfidence plays a dominant role in the supplier's own damage, resulting in higher compared to .
Corollary 4 .
Proof , obviously increases with increasing , because , substituting in gives .
Corollary 4 demonstrates that the maximum level of overconfidence of the supplier in Model SN is higher than the maximum level of overconfidence of the manufacturer in Model NM. Corollary 4 shows that an upstream supplier who is in the supply chain leader position and develops and produces key components may choose aggressive managers to make decisions for the firm. A downstream manufacturer that is a follower in the supply chain and assembles the end product with key components should choose a conservative decision maker for the decision-making process.
4.2. Sensitivity analysis
To reveal more managerial insights, we analyze the effects of exogenous RS proportions and overconfidence on the optimal outcome and obtain the following proposition.
Proposition 1: When , , , ; when , , ; . .
Proof , , , under the constraints given in the text, is monotonically decreasing in and , so is constant.
, where , , ,, ; for the value of see the proof after Lemma 4. Thus, we only need to determine the positivity or negativity of . Under the restriction, , , , , there is one and only one root between , where . In the above equation, when , ; when , , ; when , , ; when , , ., , , , holds under the conditions that the values of , and are constant.
We graphically analyze the impact of changes in the proportion of revenue-sharing received by suppliers on and , as shown inFigure 3.
From Proposition 1, supplier profit , optimal level of R&D investment , and optimal production volume increase as the supplier's share of RS ; in all four models, the manufacturer's profit increases and then decreases as the supplier's share of RS .
Figure 3 verifies that increases and then decreases as . From Proposition 1 and Figure 3(a)(b)(c), it can be observed that in comparison to the absence of overconfidence in both, the manufacturer will be willing to share a larger proportion of profits with the supplier for its own profit considerations when the supplier alone is overconfident, and the proportion of profits that the manufacturer is willing to share a larger proportion of with the supplier for its own profit considerations when the manufacturer alone is overconfident will decrease. When both are overconfident [Figure 3(d)], the two effects will be superimposed, and the proportion of profit that the manufacturer is willing to share with the supplier for the sake of its own profitability will be in the range between models SN and NM.
Proposition 2., , , , , ,, .
Proof , ,, , , , , , .
, ,, , , , .
From Proposition 2, it can be seen that the optimal level of R&D investment, the optimal production volume, and the manufacturer's profit all increase with the supplier's overconfidence coefficient, but the supplier's profit decreases with the supplier's overconfidence coefficient, in both models SN and SM. Proposition 2 suggests that supplier overconfidence increases the supplier's R&D investment in key components, which improves the market acceptance of the product, which in turn motivates the manufacturer to produce more products and increases the manufacturer's profitability, but at the disadvantage of the supplier's profit.
Proposition 3: , , , , , , , .
Proof , ,, , , , ,.
It can be seen from Proposition 3 that the optimal level of R&D investment , the optimal production volume , and the manufacturer's profit increase with the manufacturer's coefficient of overconfidence, but the manufacturer's profit decreases with the manufacturer's coefficient of overconfidence, in both models NM and SM. Propositions 1-3 provide another explanation as to why the optimal level of R&D input and optimal production volume are largest in model SM among the four models, and why the supplier's (manufacturer's) profit is largest when only the manufacturer (supplier) is overconfident, and smallest when only the supplier (manufacturer) is overconfident. This is because the optimal level of R&D investment and the optimal production volume increase with both the manufacturer's overconfidence coefficient and the supplier's overconfidence coefficient. In addition, both manufacturer/supplier profits are smaller than their own overconfidence and larger than the other's overconfidence.
Proposition 4: When , , when , ; when , , when , .
Proof , is a cubic function with respect to and the coefficients of the cubic and quadratic terms of the primary term are negative, expression omitted, when , , when , , when , , when , , thus, there must exist a point such that in the interval .
, is a cubic function with respect to and the coefficients of the cubic and quadratic terms of the primary term are negative, expression omitted, when , , when , , when , , thus, there must exist a point such that in the interval .
To better observe Proposition 4 and Corollary 5, see Figure 4.
From Proposition 4 and Figure 4(a)(b), it is clear that in a supply chain consisting of two parties, the upstream supplier who develops and produces the key components and the downstream manufacturer who assembles the end-products using the key components, when overconfidence exists in only one party (model SN or model NM), as long as the degree of this overconfidence is small (, ), the supply chain profit will increase with the degree of overconfidence, allowing the supply chain to gain more profit.
Combining Propositions 2 and 3, it can be inferred that when overconfidence exists in only one party (model SN or model NM), the value of the increase in the other party's profit from the overconfidence is greater than the value of the damage to one's own profit. There exists an optimal degree of overconfidence (, ) for both model SN and model NM that maximizes supply chain profit, and once this value is exceeded, supply chain profit decreases with the degree of overconfidence.
Corollary 5
(a) When , , when , . When , , when , .
(b) When , if , ; if , . When , if , ; if , .
Proof
(a) Let , after cross-multiplication, move to the left side of the equation, the left side is , is a cubic function on , the expression is omitted, when , ; when , , there must exist a point so that in the interval .
Let , after cross-multiplication, move to the left side of the equation, the left side is , is a cubic function on , the expression is omitted, when , ; when , ; when , ; there must exist a point so that in the interval .
(b) Let , after cross-multiplication, move to the left side of the equation, the left side is , is a cubic function on , and also a cubic function with respect to . The expression is omitted.
When , if , , if , , , there must exist a point in , such that in the interval .
When , if , , , if , , , there must exist a point in with respect to , such that in the interval .
Corollary 5(a) and Figure 4(a)(b) demonstrate that when overconfidence exists on only one side (model SN or model NM), as long as the degree of that overconfidence is relatively small ( , ), it can lead to an increase in supply chain profitability compared to model NN. However, once the degree of overconfidence is large, it can harm supply chain profits.
Corollary 5(b) and Figure 4(c)(d) indicate that when both the supplier and the manufacturer are overconfident (model SM), a relatively small degree of overconfidence in both of them, when , or when , , can lead to higher supply chain profitability in the SM model as compared to that in the NN model. The opposite would be detrimental to supply chain profitability.
These findings also corroborate the view of some scholars that overconfidence is potentially disastrous (Plous, 1993). Regardless of whether the model is SN, NM or SM, when the level of overconfidence is large it can damage the profitability of the whole supply chain.
4.3. Bargaining Model for Bilateral Negotiations
Next, we analyze the situation where the RS proportion is negotiated between the supplier and the manufacturer.
In the first stage of the game, the two players negotiate to determine the optimal revenue-sharing proportion to be enjoyed by the supplier, where the GNB mechanism is used to solve the optimization problem of the two firms:
i=SM, SN, NM and NN (5)
Lemma 5. , , , . When , , .
Proof
Derivation of equation (5) is sufficient to make it 0. For i=NN, the derivation is easy to obtain and is omitted. Now for i=SN to explain. i=SN when the , , is a quadratic function on . It is sufficient to decide that is positive or negative, when , when , and there must exist a point (where is a function on ) such that . and are proved in the same way as , omitted. When the manufacturer has full bargaining power , then the revenue-sharing proportion is entirely determined by the manufacturer, i.e., the manufacturer will choose in Proposition 1 and the relation is satisfied Since is a continuous function with respect to , when there is .
In Figure 5(a), when , ; when , ; when , ; when , ; when , ; it is constant that is greater than .
In other words, when , ; when , ; when , ; when , ; when , ; when , .
In Figure 5(b), when , ; when , ; when , ; when , ; when , ; it is constant that is greater than .
In other words, when , ; when , ; when , ; when , ; when , ; when , .
When the supplier's bargaining power , the revenue-sharing proportion is entirely determined by the manufacturer, and the value of in each model when is shown in In Figure 3(a)(b)(c)(d), when the downstream and upstream firms decide on revenue sharing, the optimal decision of the downstream firm is to share a certain proportion of the revenue with the upstream firm instead of exclusively capturing all of the revenue by itself.
In conjunction with Proposition 1, since supplier profits increase with the RS proportion, it can be inferred that as the supplier's bargaining power gradually increases, the RS proportion obtained by the supplier, as determined by the two parties through negotiations, will gradually increase. Therefore, the greater the bargaining power of the supplier, the higher the level of R&D investment in key components will be when the revenue-sharing proportion is set through negotiation between the two parties. in each model when , so the level of R&D inputs in key components must be higher than in the case where there is no revenue-sharing contract, regardless of the value of the supplier's bargaining power. When the supplier's bargaining power , the upstream firm will have exclusive access to all revenues. This is similar to the findings in the literature (Xiao et al., 2020).
From Lemma 5 and Figure 5(a)(b), we can see that when the supplier's bargaining power is low, among the four models, the supplier receives the highest percentage of RS in Model SN. This is because the supplier makes more R&D inputs for its overconfidence compared to the other models but without the concurrent concerted effort from the manufacturer, so that the manufacturer is willing to share a slightly larger percentage of revenue with the supplier in this model; of the four models, model NM has the lowest percentage of revenue-sharing for the supplier, because the manufacturer makes decisions under its own overconfidence utility, yet does not actually achieve this utility, but increases the supplier's profit. When the bargaining power of the supplier is relatively low, the proportion of RS to the supplier will be lower compared to other models. It can be seen that in this case the RS contract has a compensatory effect on the loss of profit due to overconfidence.
5. Conclusions
This paper introduces the overestimation of overconfidence in the context of downstream manufacturer incentives for upstream suppliers of key components to invest in R&D through revenue-sharing contracts, and further analyzes the use of bilateral negotiation and bargaining models for determining revenue-sharing proportions to investigate the impact of overconfidence and revenue-sharing proportions and bargaining power of one or both parties on the level of R&D inputs, wholesale prices, production volumes and profits of key components of products.
The study shows that: (1) overconfidence (or a RS contract) on either side increases the level of R&D inputs into key components, and that the level of R&D inputs into key components increases with the degree of overconfidence (the supplier's share of RS); furthermore that the level of R&D inputs into key components is higher when both parties are overconfident than when only one of the parties is overconfident. (2) In all three models — manufacturer-only, supplier-only, and both overconfident — the greater the degree of overconfidence, the greater the loss of profits for the self, but the greater the increase in profits for the other. (3) When a bilateral negotiation bargaining model is used to determine the RS proportion, if the supplier's bargaining power is low, the supplier receives the highest revenue-sharing proportion when only the supplier is overconfident, and the supplier receives the lowest revenue-sharing proportion when only the manufacturer is overconfident. It can be observed that the RS contract has a compensatory effect on the loss of profit due to overconfidence when using a bilateral negotiation bargaining model and the supplier's bargaining power is low.
This study enriches the theory of supply chain overconfidence by providing recommendations on whether to use overestimated overconfident decision makers when downstream adopts RS contracts to incentivize upstream production of key components for R&D innovations of products with high R&D difficulties.
Author Contributions
Conceptualization, C.W., H.C. and Y.K.; methodology, C.W.; software, C.W.; validation, C.W., H.C. and Y.K.; formal analysis, C.W., H.C.; investigation, C.W., and H.C.; data curation, C.W.; writing—original draft preparation, C.W.; writing—review and editing, H.C. and Y.K.; supervision, H.C. and Y.K.; project administration, H.C.. All authors have read and agreed to the published version of the manuscript.”
Funding
This research is supported by the National Natural Science Foundation of China (No. 71774072, 72072080); National Social Science Foundation of China (No. 19BJY094); Nanjing University of Aeronautics and Astronautics Postgraduate Education Teaching Reform Research Project (No. 2020YJXGG29); Educational Humanities and Social Sciences Foundation (No. 18YJA630008). The first author Chengli Wei was funded by the China Scholarship Council (File No.202206830112)
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aydin, A., & Parker, R. P. (2018). Innovation and technology diffusion in competitive supply chains. European Journal of Operational Research, 265(3), 1102–1114. [CrossRef]
- Chen, J. Y., Dimitrov, S., & Pun, H. (2019). The impact of government subsidy on supply Chains’ sustainability innovation. Omega, 86(7), 42–58. [CrossRef]
- Du, X., Zhan, H., Zhu, X., & He, X. (2021a). The upstream innovation with an overconfident manufacturer in a supply chain. Omega, 105(12), 1–14. [CrossRef]
- Du, X., Zhan, H., Zhu, X., & He, X. (2021b). The upstream innovation with an overconfident manufacturer in a supply chain. Omega (United Kingdom), 105. [CrossRef]
- Feng, Q., & Lu, L. X. (2013). Supply chain contracting under competition: Bilateral bargaining vs. stackelberg. Production and Operations Management, 22(3), 661–675. [CrossRef]
- Fossas-Olalla, M., Minguela-Rata, B., López-Sánchez, J.-I., & Fernández-Menéndez, J. (2015). Product innovation: When should suppliers begin to collaborate? Journal of Business Research, 68(7), 1404–1406. [CrossRef]
- Hao, Z., Li, J., & Cai, J. (2023). Allocation of inventory responsibilities in overconfident supply chains. European Journal of Operational Research, 305(1), 207–221. [CrossRef]
- Hirshleifer, D., Low, A., & Teoh, S. H. (2012). Are Overconfident CEOs Better Innovators? Journal of Finance, 67(4), 1457–1498. [CrossRef]
- Kirshner, S. N., & Shao, L. (2019). The overconfident and optimistic price-setting newsvendor. European Journal of Operational Research, 277(1), 166–173. [CrossRef]
- Laseter, T. M., & Ramdas, K. (2002). Product types and supplier roles in product development: An exploratory analysis. IEEE Transactions on Engineering Management, 49(2), 107–118. [CrossRef]
- Li, M. (2019). Overconfident Distribution Channels. Production and Operations Management, 28(6), 1347–1365. [CrossRef]
- Li, W., & Zhao, X. (2022). Competition or coopetition? Equilibrium analysis in the presence of process improvement. European Journal of Operational Research, 297(1), 180–202. [CrossRef]
- Lin, Y. T., Parlaktürk, A. K., & Swaminathan, J. M. (2014). Vertical integration under competition: Forward, backward, or no Integration? Production and Operations Management, 23(1), 19–35. [CrossRef]
- Liu, G., Yang, H., & Dai, R. (2020). Which contract is more effective in improving product greenness under different power structures: Revenue sharing or cost sharing? Computers and Industrial Engineering, 148. [CrossRef]
- Markovitch, D. G., Steckel, J. H., Michaut, A., Philip, D., & Tracy, W. M. (2015). Behavioral Reasons for New Product Failure: Does Overconfidence Induce Overforecasts? Journal of Product Innovation Management, 32(5), 825–841. [CrossRef]
- Moore, D. A., & Healy, P. J. (2008). The Trouble With Overconfidence. Psychological Review, 115(2), 502–517. [CrossRef]
- Moore, D. A., & Schatz, D. (2017). The three faces of overconfidence. In Social and Personality Psychology Compass (Vol. 11, Issue 8, p. 12331). [CrossRef]
- Nelson, A., & Schwartz, A. (2019). Trickle-Down Overconfidence: The Impact of Customer Overconfidence on Supplier Firms. SSRN Electronic Journal. [CrossRef]
- Niu, B., Li, J., Zhang, J., Cheng, H. K., & Tan, Y. (Ricky). (2019). Strategic Analysis of Dual Sourcing and Dual Channel with an Unreliable Alternative Supplier. Production and Operations Management, 28(3), 570–587. [CrossRef]
- Phua, K., Tham, T. M., & Wei, C. (2018). Are overconfident CEOs better leaders? Evidence from stakeholder commitments. Journal of Financial Economics, 127(3), 519–545. [CrossRef]
- Plous, S. (1993). The psychology of judgment and decision making. In Mcgraw-Hill Book Company. [CrossRef]
- Ren, Y., & Croson, R. (2013). Overconfidence in newsvendor orders: An experimental study. Management Science, 59(11), 2502–2517. [CrossRef]
- Tang, Y., Li, J., & Yang, H. (2015). What I See, What I Do: How Executive Hubris Affects Firm Innovation. Journal of Management, 41(6), 1698–1723. [CrossRef]
- Wang, D., Liu, W., & Liang, Y. (2022). Green innovation in logistics service supply chain: the impacts of relationship strength and overconfidence. Annals of Operations Research. [CrossRef]
- Wang, J., & Shin, H. (2015). The impact of contracts and competition on upstream innovation in a supply chain. Production and Operations Management, 24(1), 134–146. [CrossRef]
- Xiao, Q., Chen, L., Xie, M., & Wang, C. (2020). Optimal contract design in sustainable supply chain: Interactive impacts of fairness concern and overconfidence. Journal of the Operational Research Society, 72(7), 1–20. [CrossRef]
- Xie, L., Hou, P., & Han, H. (2021). Implications of government subsidy on the vaccine product R&D when the buyer is risk averse. Transportation Research Part E: Logistics and Transportation Review, 146(2), 1–34. [CrossRef]
- Xing, G., Xia, B., & Guo, J. (2022). Contract choice for upstream innovation in a finance-constrained supply chain. International Transactions in Operational Research, 29(3), 1897–1914. [CrossRef]
- Yenipazarli, A. (2017). To collaborate or not to collaborate: Prompting upstream eco-efficient innovation in a supply chain. European Journal of Operational Research, 260(2), 571–587. [CrossRef]
- Yu, X., Lan, Y., & Zhao, R. (2021). Strategic green technology innovation in a two-stage alliance: Vertical collaboration or co-development? Omega (United Kingdom), 98. [CrossRef]
Figure 1.
Sequence of the game.
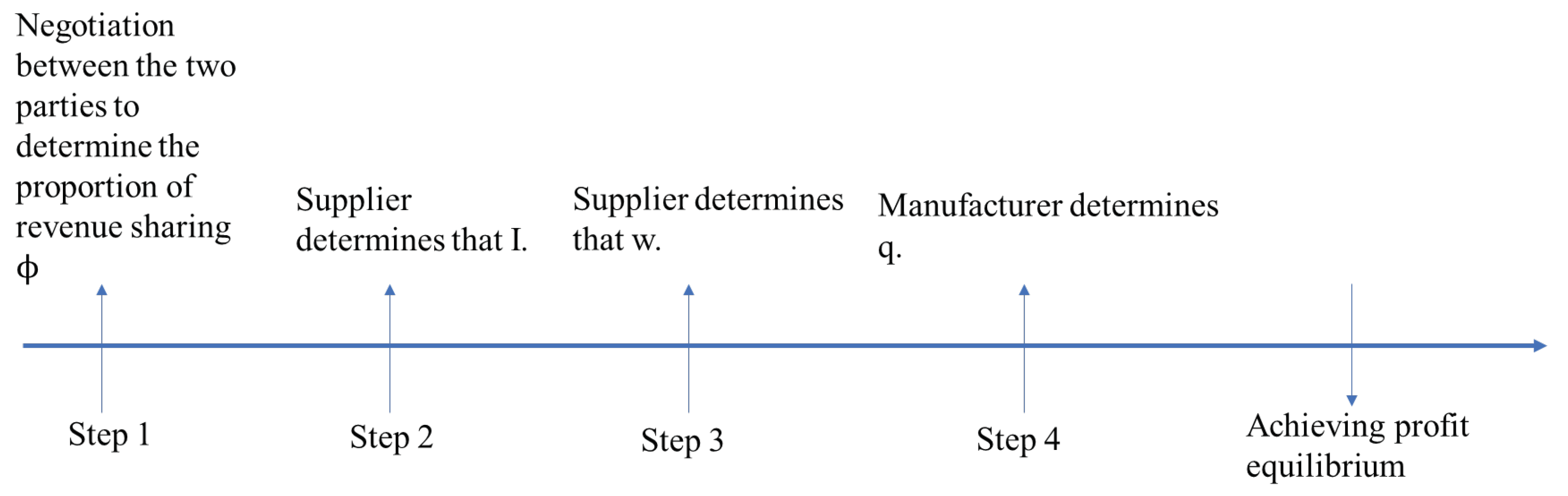
Figure 2.
Effect of changes in and on the relationship between profit size in models NN and SM. (a) The effect of changes in and on the relationship between and size (b) The effect of changes in and on the relationship between and size.
Figure 2.
Effect of changes in and on the relationship between profit size in models NN and SM. (a) The effect of changes in and on the relationship between and size (b) The effect of changes in and on the relationship between and size.
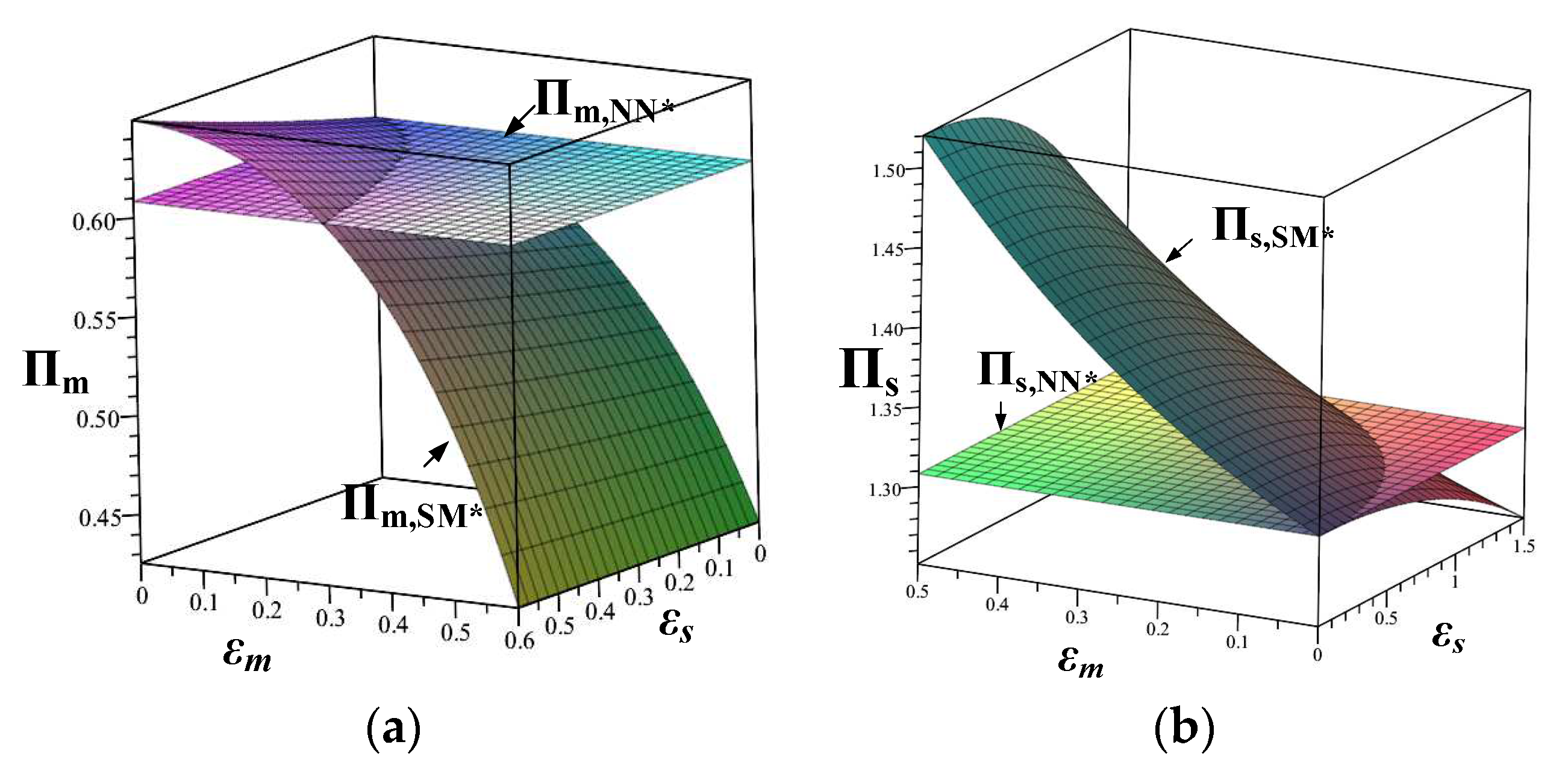
Figure 3.
Impact of changes on and in each model (). (a) Impact of changes on and (b) Impact of changes on and () (c) Impact of changes on and () (d) Impact of changes on and ()
Figure 3.
Impact of changes on and in each model (). (a) Impact of changes on and (b) Impact of changes on and () (c) Impact of changes on and () (d) Impact of changes on and ()

Figure 4.
The relationship between and , and (). (a) The relationship between and (b) The relationship between and . (c) 1 of the relationship between and (d) 2 of the relationship between and .
Figure 4.
The relationship between and , and (). (a) The relationship between and (b) The relationship between and . (c) 1 of the relationship between and (d) 2 of the relationship between and .
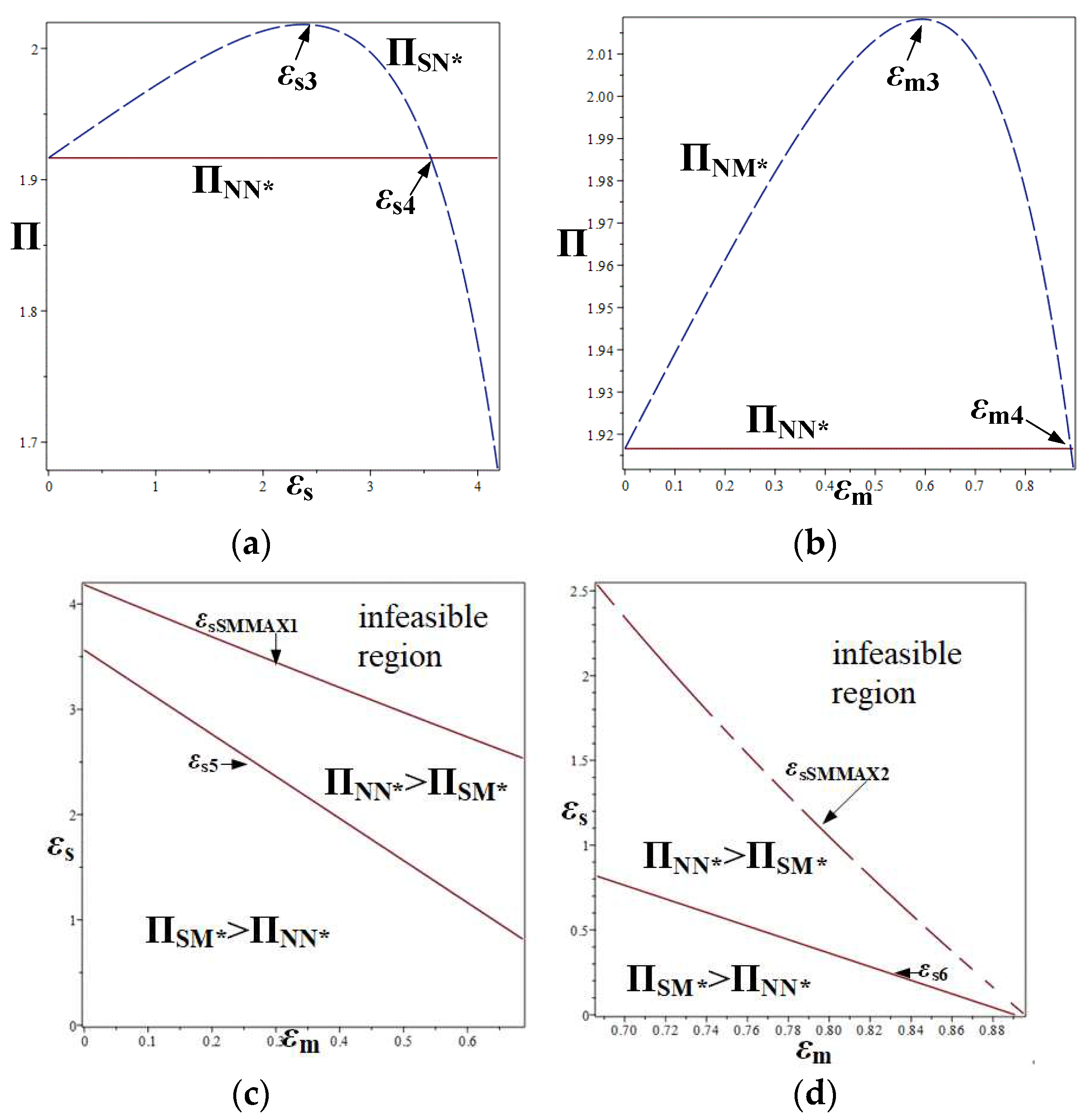
Figure 5.
Impact of supplier's bargaining power on supplier's share of optimal revenue-sharing (); (a) (b) .
Figure 5.
Impact of supplier's bargaining power on supplier's share of optimal revenue-sharing (); (a) (b) .
Table 1.
Notations.
| Notations | Description |
|---|---|
| Sales volume = Production volume | |
| Level of R&D inputs in key components | |
| Unit component wholesale price of supplier | |
| Selling price of the product | |
| The percentage of RS to be received by the supplier | |
| Supplier's bargaining power | |
| Maximum selling price of the product without R&D investment | |
| Overconfidence coefficient of the supplier | |
| Overconfidence coefficient of the manufacturer | |
| Production cost per unit of key components | |
| Coefficient of influence of the level of R&D inputs on the selling price | |
| R&D coefficient | |
| Profit in the supplier under model i | |
| Profit in the manufacturer under model i | |
| Profit in the supply chain under model i | |
| Decision objectives | |
| Superscript | |
| The ). |
Table 2.
Effects of changes in and on the size relationships of , and in models SN and NM.
| Variable | ||||
| (At this point ) | ||||
| (At this point ) | ||||
| (At this point ) | ||||
| (At this point ) | ||||
| (At this point ) | ||||
| (At this point ) | ||||
| (At this point There is no ) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







