I. INTRODUCTION

II. THE IRREVERSIBILITY OF INDIVIDUAL PARTICLE’S MOTION

A. Distinguishing equation of motion and specific motion

As mentioned in Introduction, people imply that the time reversibility of the equations of motion necessarily leads to the time reversibility of the motion of individual micro particles. That is to say, the motion of each particle can be carried out anticlockwise, since the form of the equation of motion that the particle obeys remain unchanged under time inversion.

An equation of motion expresses a physical law that the movement of particles must follow. The physical laws determine how the physical quantities of a particle, such as the coordinates, momentum, etc., vary with time. Equations of motion usually appear as differential equations. In classical mechanics, the most fundamental one is Newton’s second law. It takes the form of

$$\frac{\mathrm{d}}{\mathrm{d}t}p-F=0.$$

(4)

This equation determines how a particle’s moment should vary with time when it is subject to a force F. Equation (4) is also the first equation in (1).

We assume that there is no friction in the force F. This equation of motion is considered to be reversible in time or symmetrical with respect to time [7,9,16], i.e., under the transformation of (2) and (3), the form of (4) remains unchanged.

When we talk about the motion of a particle, we mean its specific motion process, or simply referred to as motion. In classical mechanics, it refers to the specific expression that shows that with time going, how a particle’s physical quantities such as spatial coordinates, velocity, momentum, and energy, actually vary.

Suppose that the variation of a particle’s momentum with time is known as

$$p=p(t).$$

(5)

At any moment, the magnitude and direction of the momentum are explicitly known. Let time be inversed, $t\to -t$. Then, if the momentum expressed by Equation (5) satisfies $-p(-t)=p(t)$, we say that this motion is of time-reversal invariance, otherwise it is not.

Thus, we distinguish between the equation of motion and specific motion. Regarding the change in momentum of classical particles, the mathematical expression of the equation of motion is (4), while that of a specific motion is (5). A specific motion process can be illustrated by a picture. For instance, with the specific expression (5), a schematic diagram of momentum over time can be drawn. Figure 1 below is a schematic diagram for two-particle oscillations. The differential equation (4) cannot be represented graphically. What we actually see is the specific motion of the particle, the process represented by (5). Although the specific expression (5) certainly follows the laws of physics, it cannot be directly seen from (4) itself.

Figure 1. The sketches of the collisions of two free particles. (i) In classical mechanics, a particle with a momentum is represented by a line segment with an arrow. (a) The momenta of the particles before the collision are $(p_1,p_2)$ and after the collision are $({p^{\prime }}_1,{p^{\prime }}_2)$, respectively. The original collision process is denoted as $(p_1,p_2)\to ({p^{\prime }}_1,{p^{\prime }}_2)$. (b) The time-inverse collision of (a), $(-{p^{\prime }}_1,-{p^{\prime }}_2)\to (-p_1,-p_2)$. (c) The reverse collision of (a), $(-{p^{\prime }}_1,-{p^{\prime }}_2)\to (-p_1,-p_2)$. (d) The reciprocal collision of (a), $({p^{\prime }}_1,{p^{\prime }}_2)\to (p_1,p_2)$. (ii) In QM, a plane wave with a momentum is represented by a line segment with an arrow. (a) The scattering of two free particles having plane waves with momenta $(p_1,p_2)$. After the scattering, the two particles transit to the two plane waves with momenta $({p^{\prime }}_1,{p^{\prime }}_2)$. The original transition process is denoted as $(p_1,p_2)\to ({p^{\prime }}_1,{p^{\prime }}_2)$. (b), (c), and (d) are respectively the time-inverse, reverse, and reciprocal transition processes of (a). The denotations of the (b), (c), and (d) are the same as those in the case of classical mechanics. Processes (b) and (c) look the same but the former is anticlockwise and the latter is clockwise. (a) and (d) are clockwise processes.

Figure 1. The sketches of the collisions of two free particles. (i) In classical mechanics, a particle with a momentum is represented by a line segment with an arrow. (a) The momenta of the particles before the collision are $(p_1,p_2)$ and after the collision are $({p^{\prime }}_1,{p^{\prime }}_2)$, respectively. The original collision process is denoted as $(p_1,p_2)\to ({p^{\prime }}_1,{p^{\prime }}_2)$. (b) The time-inverse collision of (a), $(-{p^{\prime }}_1,-{p^{\prime }}_2)\to (-p_1,-p_2)$. (c) The reverse collision of (a), $(-{p^{\prime }}_1,-{p^{\prime }}_2)\to (-p_1,-p_2)$. (d) The reciprocal collision of (a), $({p^{\prime }}_1,{p^{\prime }}_2)\to (p_1,p_2)$. (ii) In QM, a plane wave with a momentum is represented by a line segment with an arrow. (a) The scattering of two free particles having plane waves with momenta $(p_1,p_2)$. After the scattering, the two particles transit to the two plane waves with momenta $({p^{\prime }}_1,{p^{\prime }}_2)$. The original transition process is denoted as $(p_1,p_2)\to ({p^{\prime }}_1,{p^{\prime }}_2)$. (b), (c), and (d) are respectively the time-inverse, reverse, and reciprocal transition processes of (a). The denotations of the (b), (c), and (d) are the same as those in the case of classical mechanics. Processes (b) and (c) look the same but the former is anticlockwise and the latter is clockwise. (a) and (d) are clockwise processes.

It is generally implicitly assumed that if the equation of motion (4) is time-reversible, then necessarily (5) is also temporally reversible. “The equations of classical mechanics are invariant under time reversal. Intuitively, this says that if a film of a sequence of events is run backward, what is seen on the screen appears to be physically possible.”[9] This is equating (4) and (5), which reflects that the two concepts, the equation of motion and the motion of particles, are confused.

The irreversibility of movement is occasionally mentioned. It was mentioned [1,2] that the irreversibility of single particle motion in an infinitely large system was trivial irreversibility. However, there was no conceptual distinction between motion and equations of motion.

Let a differential equation be integrated in some way so as to obtain the expression of the physical quantity with time. Such a relation is called the general solution of a differential equation. For example, the indefinite integral solution of Equation (4) results in a general solution:

$$p(t)={\displaystyle \int \mathrm{d}{t}^{\prime }}F(t^{\prime })+C.$$

(6)

The process of finding a general solution is a purely mathematical operation without adding any physical factors.

So, does Equation (6) describe the specific motion of the particle? Or, is it equivalent to Equation (5)? The answer is no. this is because there is a pending constant in Equation (6), the value of which can only be determined by initial conditions. To set this constant is to add physical factors.

Physically, any specific motion of any particle has a starting point in time. From the Big Bang model, we know that our universe has a time beginning. Therefore, any movement that actually occurs in the universe has a starting point in time. Movement without a starting point of time does not exist. Few literature notices that specific motion should have initial conditions [6].

Hereafter, the initial time is denoted as $t_0$. When we mentioned time inversion above, we took $t\to -t$, which defaulted $t_0=0$. As $t_0\ne 0$, time inversion should expressed as $t-t_0\to -(t-t_0)$.

Mathematically, differential equations with derivative with respect to time are always solved under certain initial conditions. For example, the initial condition required to solve Equation (4) is

$$p(t=t_0^{+})=p_0,t_0^{+}=t_0+0^{+}.$$

(7)

A solution of the equation of motion that meets certain initial conditions is what describes the specific motion, so that is called a specific solution. For example, the specific solution of Equation (4) satisfying the initial condition (7) is

$$p(t)={\displaystyle {\int }_{t_0}^t\mathrm{d}{t}^{\prime }}F(t^{\prime })+p_0.$$

(8)

In Equation (8), the initial condition has already been used, i.e., the pending constant has been determined. Thus, Equation (8) clearly describes the specific process of movement, which is just Equation (5) that is required.

Above, we have tacitly assumed that time evolves clockwise from the initial moment $t_0$. So, we talk about the movement in the time range

$$t>t_0.$$

(9)

The possible characteristics of the motion can be analyzed from the general solution of the equation of motion (6). For example, for a celestial body subject to gravitational action, there is a relationship between its radial and angular coordinates. The relationship may be elliptical, parabolic, or hyperbolic. When making such a qualitative analysis, the initial condition is not necessary, so that is usually ignored. But the qualitative analysis does not provide a specific orbit, because there is a coefficient called eccentricity to be determined by the initial condition. Therefore, analyzing the specific movement process needs the initial condition.

It is seen there are actually two elements for describing the motion of a particle: the differential equation (4) and the initial conditions and (7). The physical law (4) itself has only differential equations with no initial conditions.

Under different initial conditions, a differential equation may have different specific solutions, i.e., the details of the motion under different conditions may be different, reflecting different specific movement processes. These processes obey the same physical law. For example, imagine an object moving closer to the Earth from a distance. When approaching the Earth to a certain extent, it may fall to, may rotate around, and may move away from, the Earth. These three movements are different, and which one is achieved depends on the initial conditions of the motion of this object. However, these three possible specific motions follow the same physical law: objects move according to Newton’s second law (4) under the gravitational pull of the Earth.

Therefore, we make it clear that equations of motion (4) cannot be equated with specific motion (5). The temporal inversion of Equation (4) does not determine the temporal inversion of the specific motion (5).

Only a specific solution (8) that meets the initial conditions describes a specific motion. So, is equation (8) temporally inverted or reversible? It seems not easy to give the answer directly from (8) itself. We do a further analysis below.

III. THE IRREVERSIBILITY OF TWO-PARTICLE COLLISION PROCESSES

B. Detailed balance

From Boltzmann’s H theorem [51], it can be shown that detailed balance is the sufficient and necessary conditions for a gas to reach equilibrium [15,52,72,74]. Here, we review the principle of detailed balance.

For the two-molecule collision in Figure 1a, the mathematical expression of the detailed balance is

$$f(p_1)f(p_2)=f({p^{\prime }}_1)f({p^{\prime }}_2).$$

(60)

The $f(p)$ is the momentum distribution function of the gas. In equilibrium, it is the Maxwell-Boltzmann distribution.

We inspect the physical meaning of Equation (60). It reveals that for the two particles participating the collision, the product of the distribution of the initial state is equal to that of the final state. In Equation (60), the left hand side equals to the right hand side. On the other hand, the right hand side also equals to the left hand side. That is, not only the collision $(p_1,p_2)\to ({p^{\prime }}_1,{p^{\prime }}_2)$in Figure 1a, but also its reciprocal collision $({p^{\prime }}_1,{p^{\prime }}_2)\to (p_1,p_2)$ shown by Figure 1d, satisfies Equation (60).

The detailed balance tells us that a pair of collisions reciprocal to each other retains the distribution function unchanged. Suppose that in an equilibrium gas there are four molecules. The momenta of molecules 1 and 2 are $p_1$ and $p_2$, and those of 3 and 4 are ${p^{\prime }}_1$ and ${p^{\prime }}_2$, respectively. Let molecules 1 and 2 collide as in Figure 1a, $(p_1,p_2)\to ({p^{\prime }}_1,{p^{\prime }}_2)$. After the collision, two extra ${p^{\prime }}_1$ and ${p^{\prime }}_2$ molecules are generated and two $p_1$ and $p_2$ molecules are reduced. As a result, the distribution function of the gas may deviate from the equilibrium one. If, meanwhile, another collision between molecules 3 and 4 takes place as in Figure 1d, $({p^{\prime }}_1,{p^{\prime }}_2)\to (p_1,p_2)$, then, the extra ${p^{\prime }}_1$ and ${p^{\prime }}_2$ are reduced and the reduced $p_1$ and $p_2$ are restored. This retrieves the equilibrium distribution.

It is seen that the occurrence of a pair of reciprocal collisions can keep the distribution function unchanged and this unchanged distribution is an equilibrium one. Conversely, if a gas is in equilibrium, when a collision of Figure 1a takes place, there must also a reciprocal collision of Figure 1d, although this pair of reciprocal collisions changes the microscopic state of the gas. Someone [50] thought that the detailed balance was a sufficient but not necessary condition for equilibrium, but it has been proved that the detailed balance was a sufficient and necessary condition [7,52].

As a comparison, we consider a pair of reverse collisions Figure 1a,c. Assume that there are four molecules. The momenta of molecules 1 and 2 are $p_1$ and $p_2$, and those of 3 and 4 are $-{p^{\prime }}_1$ and $-{p^{\prime }}_2$, respectively. Let molecules 1 and 2 collide as in Figure 1(a), $(p_1,p_2)\to ({p^{\prime }}_1,{p^{\prime }}_2)$, and 1 and 2 collide as in Figure 1c, $(-{p^{\prime }}_1,-{p^{\prime }}_2)\to (-p_1,-p_2)$. After this pair of collisions, four molecules, ${p^{\prime }}_1$, ${p^{\prime }}_2$, $-p_1$, and $-p_2$ are produced, and other four, $p_1$, $p_2$, $-{p^{\prime }}_1$, and $-{p^{\prime }}_2$ are reduced. Apparently, the momentum distribution function changes. Therefore, a pair of reverse collisions cannot retain the distribution unchanged.

For the detailed balance, we address the following points. Before doing so, we remind the distinguish between macro and micro infinitesimals in time and space [46]. The macro (micro) infinitesimal in time is called macro-instant (micro-instant). Macroscopic instruments can do measurements during macro-instant. Spatially, a macro subregion is a very small region but it still belongs to a macro one. A micro region can contain merely a small number of molecules.

(i) Detailed balance is achieved within a macro-instant.

When a gas is in equilibrium, a pair of reciprocal collisions Figure 1a,d occur within the same macro-instant but not the same micro-instant. Macroscopically, the pair of $(p_1,p_2)\to ({p^{\prime }}_1,{p^{\prime }}_2)$ and $({p^{\prime }}_1,{p^{\prime }}_2)\to (p_1,p_2)$ occur simultaneously, but microscopically, they occur sequentially. The system is in equilibrium at every macro-instant.

(ii) Detailed balance is achieved in a macro region.

A pair of reciprocal collisions occurs within a macro subsystem but not in a micro region. This is also what equilibrium requires. “If a closed macroscopic system is in a state such that in any macroscopic subsystem the macroscopic physical quantities are to a high degree of accuracy equal to their mean values, the system is said to be in a state of statistical equilibrium (or thermodynamic or thermal equilibrium).” [14] Equilibrium is reached in any macro subsystem, while in a micros region, detailed balance cannot be reached.

Based on the discussion of (i) and (ii) above, detailed balance is achieved statistically in macro subsystems. The equilibrium refers to that in macro subregions and at macro-instant. Microscopically, the gas is nonequilibrium everywhere and every time. Micro states cannot be distinguished by instruments that measure macro parameters.

(iii) Detailed balance is independent of reverse collisions.

Detailed balance (60) ensures that in equilibrium, the pair of reciprocal collisions occurs, with no requirement of the reverse collision Figure 1c. The pair of reciprocal collisions takes place clockwise, irrespective to any anticlockwise process [72]. On the other hand, as mentioned above, a pair of reverse collisions does not guarantee the invariance of the momentum distribution function. Therefore, the discussing whether a macro process is reversible is not based on whether two-particle collisions are reversible.

Detailed balance itself also contains

$$f(-p_1)f(-p_2)=f(-{p^{\prime }}_1)f(-{p^{\prime }}_2).$$

(61)

That is to say, the collision process Figure 1c and its reciprocal process also keep the momentum distribution unchanged in the case of equilibrium.

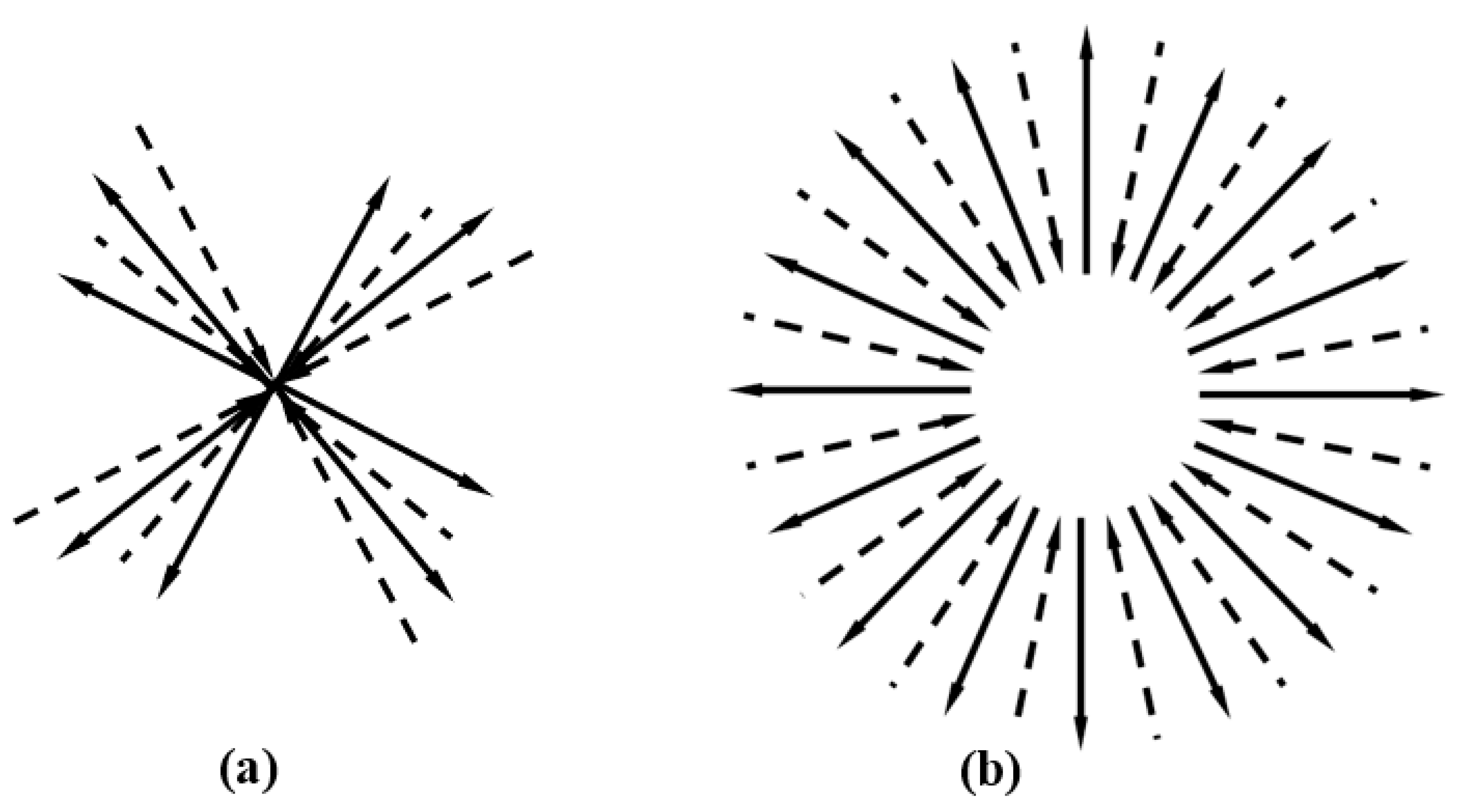
We imagine a picture of the angular distribution of molecular momentum in a gas in equilibrium. Since the number of molecules in the gas is sufficiently large, by detailed balanced, there must be many reciprocal collisions, all of which have the same values of the incident and outgoing momenta, but in different directions. We superimpose events in one figure. Figure 2a is a superposition of four events of Figure 1d, where the incident and outgoing particles are represented by dashed and solid lines, respectively. Figure 2b roughly illustrates the superposition of a large number of collision events. The angle between the momenta of the two incident particles evenly distributes within solid angle 0~4π, and that of the outgoing particles also does so. Since the number of particles is large enough, both are dense enough and the angular distribution is uniform.

Reversing the directions of the arrows for both the solid and dashed lines in Figure 2b leads to the schematic diagram of Equation (61). This is a superposition of schematic diagram of Figure 1c in all directions. This shows that for reciprocal collisions, as well as for reverse collisions, the momentum of the incoming and outgoing particles are uniformly distributed in all directions. This means that if there is a collision of Figure 1a, then there will be a reverse collision Figure 1c.

Therefore, although the detailed balance itself does not require the reverse process of a collision to appear, we believe that once the detailed balance is reached, then, in the equilibrium state, the reverse collision process of any collision also inevitably occur. That a pair of reverse collisions, Figures 1a,c occur in a macro-instant should be a by-product when an equilibrium state is reached.

Figure 2. (a) The superposition of four Figure 1d in different directions. Incident and outgoing particles are represented by dashed and solid lines, respectively. (b) The superposition of a large number of similar collisions, which shows that in equilibrium, the momentum distribution is isotropic.

Figure 2. (a) The superposition of four Figure 1d in different directions. Incident and outgoing particles are represented by dashed and solid lines, respectively. (b) The superposition of a large number of similar collisions, which shows that in equilibrium, the momentum distribution is isotropic.

We conceive a situation that slightly deviates from detailed balance.

When Boltzmann derived the H theorem, he obtained the following inequality [13].

$$\ln \frac{f(p_1)f(p_2)}{f({p^{\prime }}_1)f({p^{\prime }}_2)}[f(p_1)f(p_2)-f({p^{\prime }}_1)f({p^{\prime }}_2)]\ge 0.$$

(62)

The equal sign holds only when the detailed balance (60) is reached. Suppose that the gas is very close to equilibrium, such that the momentum distribution of the two particles before the collision belongs to the equilibrium distribution with temperature T.

$$f(p_1)\propto \exp (-\frac{\epsilon (p_1)}{k_{\mathrm{B}}T}),f(p_2)\propto \exp (-\frac{\epsilon (p_2)}{k_{\mathrm{B}}T}).$$

(63)

After the collision, the distribution belongs to that with temperature $T+\Delta T$.

$$f({p^{\prime }}_1)\propto \exp (-\frac{\epsilon ({p^{\prime }}_1)}{k_{\mathrm{B}}(T+\Delta T)}),f({p^{\prime }}_2)\propto \exp (-\frac{\epsilon ({p^{\prime }}_2)}{k_{\mathrm{B}}(T+\Delta T)}),$$

(64)

where

$$\Delta T\ll T.$$

(65)

For an elastic collision (59), the total energy before and after the collision is denoted by ε, $\epsilon =\epsilon (p_1)+\epsilon (p_2)=\epsilon ({p^{\prime }}_1)+\epsilon ({p^{\prime }}_2)$. We derive from Equation (62) that

$$-\frac{\epsilon }{k_{\mathrm{B}}}(\frac{1}{T}-\frac{1}{T+\Delta T})(1-\exp [\frac{\epsilon }{k_{\mathrm{B}}}(\frac{1}{T}-\frac{1}{T+\Delta T}{\left)\right])\mathrm{e}}^{-\epsilon /k_{\mathrm{B}}T}\ge 0.$$

(66)

No matter whether the two molecules become a hotter or cooler distribution after the collision, this expression is not less than zero. It is equal to zero only if $\Delta T=0$. This means that areas with slightly lower (higher) temperatures will increase (decrease) temperatures. Heat always flows from the hotter to the cooler area, making the temperature approach the same everywhere.

The isotropic distribution shown in Figure 2b is ideal only when the number of molecules in the gas approached infinity. In this equilibrium state the momentum distribution remains unchanged.

Therefore, a necessary condition for achieving detailed balance is that the number of molecules in the gas is sufficiently large. Although the molecule number in the actual gas is as high as the order of magnitude of Avogadro constant, it is not really infinity after all. So, even in every macro-instant, it is not guaranteed that for every two-particle collision, there always occur a corresponding reciprocal process. As a result, the momentum distribution of the molecule may deviate from the equilibrium distribution. This deviation is the fluctuation. Macro physical quantities are averages calculated by means of the distribution function. Therefore, they fluctuate around their average values. Obviously, the larger the molecule number, the smaller the fluctuation.

Now, consider a region in the gas which is macroscopically small enough, say, a submillimeter-scale region, the particle number in this region is much smaller than that of the whole gas. If in 1 m³ there are $N~{10}^{23}$ particles, then in ${10}^{-16}$ m³ there are $N_1~{10}^7$ particles, such that $N_1\ll N$. In such a small region fluctuation will be comparatively large. It is possible that the number of particles with momentum in a certain direction in a macro-instant is much greater than that with opposite momentum. If a pollen granule is positioned in this region, the molecular impact it receives is not isotropic, so that it suffers a net force. The pollen is subject to this force to move. This is the reason of Brownian motion, which reflects that in such a small area, detailed balance cannot be achieved.

Brownian motion also indicates that at a macro-instant, the number of particles entering and leaving the region is not always equal. That is to say, the density of particle numbers in this region is variable with times. The molecular number density in different small regions at a micro-instant are not the same. The density varies around its average value. The fluctuation in a gas actually embodies the non-equilibrium at micro-instant.

When the detailed balance is not achieved, the left and right side of Equation (60) are not equal. This mean that at least a collision of Figure 1a does not have its reciprocal collision at a macro-instant. Consequently, the momentum distribution function will change. The gas cannot tend to equilibrium. Rather, it is in a non-equilibrium state. As a result, the macroscopic state may change.

Now consider a case that an ideal gas expands into a vacuum, shown in Figure 3. Figure 3a shows that the gas is confined in the left half of a box by a partition. At the initial moment, the partition is removed and the gas begins to expand. The border line between the gas and vacuum is called frontline.

Figure 3. Schematic diagram of a gas expansion into vacuum. The dotted line indicates the border line between gas and vacuum, called frontline. (a) The gas is confine inside the left half box by a partition. At the initial moment, the partition is drawn and the gas starts expansion. (b) the gas expands to 3/4 box. (c) The gas is evenly distributed in the whole box, i.e., the equilibrium state is reached.

Figure 3. Schematic diagram of a gas expansion into vacuum. The dotted line indicates the border line between gas and vacuum, called frontline. (a) The gas is confine inside the left half box by a partition. At the initial moment, the partition is drawn and the gas starts expansion. (b) the gas expands to 3/4 box. (c) The gas is evenly distributed in the whole box, i.e., the equilibrium state is reached.

At the moment that the partition is just drawn, there is no particles on the right side of the frontline. Suppose that on the left side of the frontline, two particles moving rightward collide, as in Figure 1a, and after the collision, they enter the vacuum on the right side of the frontline. If a corresponding reciprocal collision of another two particle occurs as in Figure 1d, they also enter the vacuum. At this moment, since there are no particles on the right side of the frontline, there is no reverse collision in Figure 1c. Therefore, the molecules always enter the vacuum from the left side of the frontline. There is no mechanism for particles to immediately return to the left side of the frontline. The frontline moves rightward.

Assuming that at the moment in Figure 3b, the momenta of all molecules in the gas are reversed, will the frontline move leftward? The analysis is actually the same as that for Figure 3a. Since the right side of the frontline is a vacuum, the molecules on the left side of the frontline still enter the vacuum, and there is no a mechanism for particles return to the left of the frontline. The frontline continues moving rightward. This shows that Loschmidt’s reasoning does not apply.

We next see the equilibrium state in Figure 3c. At every micro-instant, it is in a micro state. Every micro state in a macro state is equiprobable to appear. For a micro state in the macro state, when all the molecules’ momentum directions are reversed, the resultant is still a micro state in this macro state. When a gas evolves from a non-equilibrium state to the equilibrium state of Figure 3c, it can be any of these micro states. Conversely, any micro state in Figure 3c can be the one, denoted as A, that is achieved by reversing all the molecule momentum directions of a micro state, denoted as B, the latter being achieved from a non-equilibrium state. Following Loschmidt’s reasoning, we assume reversing all the molecular momentum in A to obtain state B, and with time going, the B will undergo a reverse process to go back to the original non-equilibrium state, such as Figure 1b. However, we know that such a process has never happened and we do not expect so. This again shows that Loschmidt's reasoning does not again.

On account of that the molecule number in the gas considered is not infinite, when there is a collision Figure 1a, the probability that its reverse collision Figure 1c is not zero. It seems that there is a nonzero probability for the reverse process of the gas to happen, say, from Figure 3c to Figure 3b. Nevertheless, this probability is so small that it is equivalent to impossibility. In Boltzmann’s language, although the evolution from Figure 3b to Figure 3a or from Figure 3c to Figure3d “has a definite calculable (though inconceivably small) probability, which approaches zero only in the limiting case when the number of molecules is infinite.” The time needed is so remote that “One may recognize that this is practically equivalent to never. …… If a much smaller probability than this is not practically equivalent to impossibility, then no one can be sure that today will be followed by a night and then a day.” [58]

A frictionless quasi-static process is the exhibition of a series of equilibrium states. Therefore, such a process is reversible. However, this reversibility does not come from the reversibility of the motion of individual particles, nor from the reversibility of the two-particle collision. Rather, it is the statistical average effect of a large number of molecules colliding each other when the detailed balance is reached.

It is seen that macroscopic reversibility requires a large number of molecules in the gas. Usually, a gas contains molecules in the order of magnitude of the Avogadro constant, is very close to meeting this requirement.

In summary, the motion of microscopic particles is irreversible. Nevertheless, when the number of molecules that make up the gas is very large, the macro state of the gas can be in equilibrium when detailed balance is reached. The equilibrium state is the statistical average effect of the motion of a large number of microscopic molecules. Frictionless quasi-static processes are reversible.

IV. CONCLUSION

References

1. Swendsen, R.H. Questions and answers. J. Stat. Phys. 1974, 10, 175–177. [Google Scholar] [CrossRef]
2. Swendsen, R.H. Explaining irreversibility. Am. J. Phys. 2008, 76, 643–648. [Google Scholar] [CrossRef]
3. Lebowitz, J.L. Boltzmann's Entropy and Time's Arrow. Phys. Today 1993, 46, 32–38. [Google Scholar] [CrossRef]
4. J. L. Lebowitz, Macroscopic laws, microscopic dynamics, time’s arrow and Boltzmann’s entropy. Physica A 194, 1-27 (1993). [CrossRef]
5. Lebowitz, J.L. Statistical mechanics: A selective review of two central issues. Rev. Mod. Phys. 1999, 71, S346–S357. [Google Scholar] [CrossRef]
6. Lebowitz, J.L. Microscopic origins of irreversible macroscopic behavior. Phys. A: Stat. Mech. its Appl. 1999, 263, 516–527. [Google Scholar] [CrossRef]
7. R. L. Liboff, Introduction to the Theory of Kinetic Equations (John Wiley & Sons, Inc., New York, 1969).
8. Evans, D.J.; Searles, D.J. The Fluctuation Theorem. Adv. Phys. 2002, 51, 1529–1585. [Google Scholar] [CrossRef]
9. M. L. Bellac, F. Mortessagne, and G. G. Batroun, Equilibrium and Non-Equilibirum Statistical Thermodynamics (Cambridge University Press, Cambridge, 2004).
10. F. Schwable, Statistical Mechanics 2nd ed. (Springer-Verlag, Berlin, Heidelberg, 2006). Chapter 10.
11. C. M. Van Vliet, Equilibrium and Non-equilibrium Statistical Mechanics (World Scientific Pub. Singapore, Hackensack, NJ, 2008).
12. P. L. Krapivsky, S. Redner, E. Ben-Naim, A Kinetic View of Statistical Physics (Cambridge University Press, Cambridge, New York, 2010).
13. R. C. Tolman, The Principles of Statistical Mechanics (Dover Publications, New York, 1979).
14. L. D. Landau and E. M. Lifshitz, Statistical Physics Part 1 Vol. 5 of Course of Theoretical Physics (Pergmon Press, New York, 1980). Chapter 1.
15. Ter Haar, D. Foundations of Statistical Mechanics. Rev. Mod. Phys. 1955, 27, 289–338. [Google Scholar] [CrossRef]
16. D. J. Evans, D. J. Searles, and S. R. Williams, Fundamentals of Classical Statistical Thermodynamics Dissipation, Relaxation and Fluctuation Theorem (Wiley-VCH Verlag GmbH & Co. KGaA, Boschstr. 12, 69469 Weinheim, Germany, 2016).
17. Tanimura, Y. Numerically “exact” approach to open quantum dynamics: The hierarchical equations of motion (HEOM). J. Chem. Phys. 2020, 153, 020901. [Google Scholar] [CrossRef]
18. Barbier, M.; Gaspard, P. Microreversibility and the statistics of currents in quantum transport. Phys. Rev. E 2020, 102, 022141. [Google Scholar] [CrossRef]
19. Platini, T. Measure of the violation of the detailed balance criterion: A possible definition of a “distance” from equilibrium. Phys. Rev. E 2011, 83, 011119. [Google Scholar] [CrossRef]
20. Prigogine, Non-equilibrium statistical mechanics (Dover Publications, Inc., Mineola, New York, 2017). 255.
21. Evans, D.J.; Cohen, E.G.D.; Morriss, G.P. Probability of second law violations in shearing steady states. Phys. Rev. Lett. 1993, 71, 2401–2404. [Google Scholar] [CrossRef] [PubMed]
22. Evans, D.J.; Searles, D.J. Equilibrium microstates which generate second law violating steady states. Phys. Rev. E 1994, 50, 1645–1648. [Google Scholar] [CrossRef] [PubMed]
23. Dorosz, S.; Pleimling, M. Fluctuation ratios in the absence of microscopic time reversibility. Phys. Rev. E 2009, 79, 030102. [Google Scholar] [CrossRef] [PubMed]
24. Peres, Quantum Theory: Concepts and Methods (KLUWER ACADEMIC PUBLISHERS, NEW YORK, 2002). 347.
25. Langmuir, I. The constitution and fundamental properties of solids and liquids. Part I. Solids. J. Am. Chem. Soc. 1916, 38, 2221–2295. [Google Scholar] [CrossRef]
26. Frisch, H.L. Poincaré Recurrences. Phys. Rev. 1956, 104, 1–5. [Google Scholar] [CrossRef]
27. R. L. Liboff, Kinetic Theory, Classical, Quantum, and Relativistic Descriptions 3rd ed. (Spinger-Verlag New York, Inc., Berlin, 2003).
28. Hahn, E.L. Spin Echoes. Phys. Rev. 1950, 80, 580–594. [Google Scholar] [CrossRef]
29. Hahn, E.L. Free nuclear induction. Phys. Today 1953, 6, 4–9. [Google Scholar] [CrossRef]
30. Rothstein, J. Nuclear Spin Echo Experiments and the Foundations of Statistical Mechanics. Am. J. Phys. 1957, 25, 510–518. [Google Scholar] [CrossRef]
31. Blatt, J.M. An Alternative Approach to the Ergodic Problem. Prog. Theor. Phys. 1959, 22, 745–756. [Google Scholar] [CrossRef]
32. R. Reif, Statistical Physics Berkeley Physics Course Volume 4 (McGraw-Hill, Inc., 1965).
33. Orban, J.; Bellemans, A. Velocity-inversion and irreversibility in a dilute gas of hard disks. Phys. Lett. A 1967, 24, 620–621. [Google Scholar] [CrossRef]
34. N. V. Brilliantov and Thorsten Poschel, Kinetic theory of granular gases (Oxford University Press, Oxford, 2004). 128.
35. E. Fermi, J. Pasta, E. Ulam. M. Tsinghou, Studies of Nonlinear Systems. Report LA-1940, Los Alamos Scientific Laboratory of the University of California (55). https://people.math.umass.edu/~kevrekid/math697wa/ACC0041.
36. Zabusky, N.J.; Kruskal, M.D. Interaction of "Solitons" in a Collisionless Plasma and the Recurrence of Initial States. Phys. Rev. Lett. 1965, 15, 240–243. [Google Scholar] [CrossRef]
37. Tuck, J.; Menzel, M. The superperiod of the nonlinear weighted string (FPU) problem. Adv. Math. 1972, 9, 399–407. [Google Scholar] [CrossRef]
38. Walker, G.H.; Ford, J. Amplitude Instability and Ergodic Behavior for Conservative Nonlinear Oscillator Systems. Phys. Rev. B 1969, 188, 416–432. [Google Scholar] [CrossRef]
39. Lunsford, G.H.; Ford, J. On the Stability of Periodic Orbits for Nonlinear Oscillator Systems in Regions Exhibiting Stochastic Behavior. J. Math. Phys. 1972, 13, 700–705. [Google Scholar] [CrossRef]
40. Lebowitz, J.L.; Penrose, O. Modern ergodic theory. Phys. Today 1973, 26, 23–29. [Google Scholar] [CrossRef]
41. Hasegawa, H. Responses to applied forces and the Jarzynski equality in classical oscillator systems coupled to finite baths: An exactly solvable nondissipative nonergodic model. Phys. Rev. E 2011, 84, 011145. [Google Scholar] [CrossRef] [PubMed]
42. Li, J.; He, D. Finite-time fluctuation theorem for oscillatory lattices driven by a temperature gradient. Phys. Rev. E 2021, 103, 062122. [Google Scholar] [CrossRef]
43. Palmer, R. Broken ergodicity. Adv. Phys. 1982, 31, 669–735. [Google Scholar] [CrossRef]
44. Jack, R.L.; Garrahan, J.P. Metastable states and space-time phase transitions in a spin-glass model. Phys. Rev. E 2010, 81, 011111. [Google Scholar] [CrossRef] [PubMed]
45. Frisch, H.L. An Approach to Equilibrium. Phys. Rev. 1958, 109, 22–29. [Google Scholar] [CrossRef]
46. Wang, H.-Y. Liouville equation in statistical mechanics is not applicable to gases composed of colliding molecules. Phys. Essays 2023, 36, 13–21. [Google Scholar] [CrossRef]
47. M. Born and H. S. Green, A General Kinetic Theory of Liquids. I. The Molecular Distribution Functions. Proceedings of the Royal Society of London. Series A Mathematical and Physical Sciences 188(1012), 10-18 (1946). https://www.jstor.org/stable/97937.
48. Kirkwood, J.G. The Statistical Mechanical Theory of Transport Processes I. General Theory. J. Chem. Phys. 1946, 14, 180–201. [Google Scholar] [CrossRef]
49. Kirkwood, J.G. The Statistical Mechanical Theory of Transport Processes II. Transport in Gases. J. Chem. Phys. 1947, 15, 72–76. [Google Scholar] [CrossRef]
50. de Boer, J. Molecular distribution and equation of state of gases. Rep. Prog. Phys. 1949, 12, 305–374. [Google Scholar] [CrossRef]
51. E. M. Lifshitz and L. P. Pitaevskii, Physical Kinetics, Vol. 10 of Course of Theoretical Physics (Pergamon Press, Oxford, 1981). Chapter 1.
52. Kerson Huang, Statistical Mechanics 2nd ed. (John Wiley & Sons. New York, 1987).
53. L. E. Reichl, A modern course in statistical physics 2nd ed. (John Welei & Sons, Inc. New York, 1998).
54. Tessarotto, M.; Cremaschini, C. First-principle proof of the modified collision boundary conditions for the hard-sphere system. Phys. Lett. A 2014, 378, 1760–1766. [Google Scholar] [CrossRef]
55. Tessarotto, M.; Cremaschini, C. Modified BBGKY hierarchy for the hard-sphere system. Eur. Phys. J. Plus 2014, 129, 1–23. [Google Scholar] [CrossRef]
56. Abramov, R.V. The Random Gas of Hard Spheres. J 2019, 2, 162–205. [Google Scholar] [CrossRef]
57. Abramov, R.V. Correction: Abramov, R. The Random Gas of Hard Spheres. J 2019, 2, 162–205. J 2020, 3, 324–328. [Google Scholar] [CrossRef]
58. L. Boltzmann, Lectures on gas theory. Courier Corporation (Dover Publications, Inc. New York (2012). Chap. 1.
59. Evans, D.J.; Searles, D.J. Causality, response theory, and the second law of thermodynamics. Phys. Rev. E 1996, 53, 5808–5815. [Google Scholar] [CrossRef]
60. J. D. Bjorken and S. S. Drell, Relativistic quantum mechanics (McGraw-Hill Book Co., New York, 1964).
61. H. Kleinert, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets 5th ed. (World Scientific Publishing Co. Pte. Ltd., Singapore, 2009). Chap. 1.
62. W. Greiner and J. Reinhardt, Quantum Electrodynamics 4th ed. (Springer-Verlag Berlin, Heidelberg, 2009).
63. Wachter, A. Relativistic Quantum Mechanics; Springer Science and Business Media LLC: Dordrecht, GX, Netherlands, 2011; ISBN 3540255028. [Google Scholar]
64. Huai-Yu Wang, The mathematical physical equations that the retarded and advanced Green’s functions satisfy. Physics Essays 35(4), 380-391 (2022). [CrossRef]
65. Wang, H.-Y. A generalized scattering theory in quantum mechanics. J. Phys. Commun. 2023, 7, 075001. [Google Scholar] [CrossRef]
66. Huai-Yu Wang, Green’s Function in Condensed Matter Physics (Alpha Science International ltd. and Science Press, Beijing, 2012).
67. Huai-Yu Wang, Mathematics for Physicists (World Scientific Publishing Company and Science Press, Singapore and Beijing 2017).
68. J. J. Sakurai, Modern Quantum Mechanics (Addison-Wesley Publishing Company, Inc., 1994).
69. J. Kestin and J. R. Dorfman, A Course in Statistical Thermodynamics (Academic Press, Inc., New York, 1971).
70. S. Chapman and T. G. Cowling, The Mathematical Theory of Non-uniform Gases An Account of The Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases 3rd ed. (Cambridge University Press, Cambridge, 1970).
71. C. L. Tien and J. H. Lienhard, Statistical thermodynamics (Hemisphere Pub. Corp., Washington, New York, 1979).
72. Isihara, Statistical Physics (Academic Press, Inc., New York, 1971).
73. L. D. Landau and E. M. Lifshitz, Mechanics Vol. 1 of Course of Theoretical Physics 3rd ed. (Pergmon Press, New York, 1976).
74. M. Toda, R. Kubo, and N. Saito, Statistical Physics I Equilibrium Statistical Mechanics (Springer-Verlag, Berlin, Hedelberg, 1983).
75. R. Hakim, Introduction to Relativistic Statistical Mechanics Classical and Quantum (World Scientific Publishing Co. Pte. Ltd. Singapore, 2011).
76. L. D. Landau and E. M. Lifshitz, Quantum Mechanics Non-relativistic Theory Vol. 3 of Course of Theoretical Physics 3rd ed. (New York: Pergmon Press 1977). Chap. 18.
77. Messiah, Quantum Mechanics II 2nd ed. (John Wiley & Sons, Inc., Mineloa, New York, 1962). Chap. 19.
78. D. C. Mattis and R. H. Swendsen, Statistical mechanics made simple 2dn ed. (World Scientific, Singapore, 2008).