Prerpints.org logo
Preprint
Article

Prediction of Oxygen Distribution in Silos and Chambers Filled with Various Agricultural Commodities

Altmetrics

Downloads

89

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

04 October 2023

Posted:

09 October 2023

You are already at the latest version

Alerts
Abstract
In the context of post-harvest pest management in agricultural products, the adoption of modified atmospheres presents an eco-friendly alternative to conventional pesticides. This study focuses on nitrogen gas as a potential agent for insect control in stored commodities, utilizing computational simulations to investigate its penetration and distribution within two common storage configurations: chamber-contained pallets and silos. By employing the convection-diffusion equation, the simulations reveal insights into nitrogen distribution dynamics and duration required for oxygen reduction. The results highlight the influence of boundary conditions, commodity porosity, and convection effects on nitrogen dispersion. In chamber scenarios, boundary condition type significantly affects oxygen reduction time, while in silos, convection and diffusion interact to establish a consistent diffusion layer thickness. This research enhances the understanding of modified atmosphere techniques and their potential for sustainable pest management. It provides practitioners with valuable quantitative insights, paving the way for optimized modified atmosphere strategies in real-world agricultural contexts.
Keywords: 
Subject: Biology and Life Sciences  -   Agricultural Science and Agronomy

1. Introduction

Modified atmospheres offer a promising approach for effectively managing insects in post-harvest stages of agricultural products, serving as a viable alternative to conventional pesticides. With growing concerns among consumers about the hazards associated with residual insecticides in food and their detrimental impact on the environment, adopting modified atmospheres on an industrial scale presents a feasible and eco-friendly strategy for pest control across various commodities [1,2,3].
The term ’modified atmospheres’ encompasses a range of techniques aimed at altering gas proportions within a designated space, such as a chamber. This adjustment involves introducing specific gases, like nitrogen or carbon dioxide, to significantly reduce oxygen levels or elevate carbon dioxide concentrations. This deliberate atmospheric manipulation capitalizes on the fact that insects and many microorganisms rely on oxygen for their aerobic processes. Consequently, modifying the atmosphere can severely impede their development and ultimately jeopardize their survival [3].
The employment of modified atmospheres offers a multitude of advantages. It stands as a chemical-free, environmentally conscious methodology that leaves no residues on treated products. Furthermore, its mechanism of action disrupts respiration physiology, significantly minimizing the likelihood of target organisms developing resistance [4].
At present, the saturation of the atmosphere with nitrogen holds greater potential when contrasted with the infusion of carbon dioxide. Nitrogen infusion into the intended space can be achieved using atmospheric air generators. Prior investigations into nitrogen utilization have exhibited encouraging outcomes against numerous insect species prevalent in stored products. Earlier research has demonstrated the survival capabilities of stored-product insects under exceedingly low oxygen concentrations, persisting for extended periods, spanning days or even weeks. This has led to the proposal that the necessary oxygen levels for achieving a desirable degree of insect control should remain below 2% [5].
There remains inadequate information concerning nitrogen penetration into packaged goods like pallets or vertical structures such as silos. Numerical modeling has been partially applied in similar contexts. [6] published pertinent research, developing a computational model to assess nitrogen concentration within chamber-contained pallets holding currants or herbs, targeting stored product insect populations resistant to phosphine. Beyond this study, no relevant investigations matching the parameters of our current work (chambers and silos, diverse agricultural commodities) were found. [7] study presents numerical simulation findings involving liquid nitrogen injection into a container, indicating the efficacy and applicability of controlled atmosphere treatments for preserving mature pepino fruit quality. [8] also explored nitrogen gas concentration for refrigeration and atmosphere adjustment in corn storage. Similarly, [9] conducted Computational Fluid Dynamics (CFD) simulations using ozone gas to combat the maize weevil, Sitophilus zeamais (Motschulsky) (Coleoptera: Curculionidae), in rice grains. Furthermore, [10] employed numerical simulations to predict ozone concentration and flow characteristics in bulked paddy rice. [11] utilized CFD to model phosphine gas distribution within grain silos and metal containers, successfully validating this model in a real-world scenario.
In this study, we utilize computer simulation to investigate the penetration and distribution of Nitrogen and Oxygen in two commonly employed configurations for storing agricultural products: palletized systems and silos. Our numerical model solves relevant equations, offering practitioners valuable insights into these applications.

2. Materials and Methods

2.1. Computational model description

The convection-diffusion, or advection-diffusion, equation serves as a fundamental tool for elucidating transport phenomena involving the transfer of heat, mass, and other physical properties through diffusion and advection mechanisms [12]. In the context of a one-dimensional spatial domain devoid of sources or sinks, and with constant diffusivity ( D e f f ) and velocity (u), the convection-diffusion equation is succinctly expressed as follows:
∂ C ∂ t + u ∂ C ∂ x = D e f f ∂ 2 C ∂ x 2
In the preceding equation, the variable C represents the concentration of nitrogen gas, while t denotes the temporal parameter in seconds. The symbol D e f f corresponds to the effective diffusion coefficient with units of m 2 / s − 1 , which accommodates porous effects inherent to gas flow within the product matrix.
The solution to Equation (1) provide predictions regarding nitrogen (and consequently, oxygen) concentration during controlled atmosphere treatments, be it within silos or chambers with palletized commodities. For the latter scenario, we posit a uniform nitrogen concentration encompassing the pallets (in adherence to a Dirichlet boundary condition), where gas diffusion ( u = 0 ) predominates as the chief modality for nitrogen gas dispersion within the pallet structure.
The numerical simulations are executed upon a one-dimensional mesh framework, thereby yielding predictions concerning the spatial separation between the chamber’s concentration domain (exterior surface of the pallet) and the pallet’s core. In the context of silos, these simulations extend to the vertical gap spanning from the silo’s base to its apex (as depicted in Figure 1).
According to [13] in order to represent the role of porosity on ordinary molecular diffusion, the diffusion coefficient must be scaled with tortuosity. Specifically, an effective diffusivity coefficient could be set as:
D e f f = D m τ 2
[13] in their review article, they studied numerous formulations of porosity in a system of porous media. A relation between tortuosity and porosity for random homogeneous isotropic sphere packings [14] is provided by the equation :
τ 2 = 3 − ϕ 2
The temperature-depended binary diffusion coefficient ( D m [ m 2 / s ] ) for Nitrogen and Oxygen is calculated based on the equations provided by [12]:
D m = A T 3 2 p σ 12 2 Ω 1 M W 1 + 1 M W 2
where A is approximately 1.859 × 10 − 3 atm · Å 2 · cm 2 K 3 / 2 · s g mol (with Boltzmann constant k b , and Avogadro constant N A ), 1 and 2 index the two kinds of molecules present in the gaseous mixture, T is the absolute temperature [K], M W is the molar mass [g/mol], p is the pressure [atm], σ 12 = 1 2 ( σ 1 + σ 2 ) is the average collision diameter, Ω is a temperature-dependent collision integral (dimensionless).
Indicatively, D m is equal to 1.944 · 10 − 5 and 2.064 · 10 − 5 at temperatures 20 [ o C ] and 30 [ o C ] respectively.
In summary, given the availability of porosity values, the complete set of parameters is established, enabling the utilization of Equation (1) for predictive purposes. The pertinent porosity values for a selection of prevalent commodities that undergo nitrogen treatments are tabulated in Table 1.

2.2. Validation

To evaluate the precision of the computational code, the authors validated the model predictions against both the numerical solution presented by [27] and experimental data available in the scientific literature [28]. As previously mentioned, [27] provided the numerical solution for Equation (1),
C ( x , t ) = C o 2 e r f c x − u t 2 D e f f t + C o 2 e x p u x D e f f e r f c x + u t 2 D e f f t
Authors compared the model results with solution provided by [27] (Equation (5)) when u = 1 , D e f f = 0.02 , C o = 100 at t = 2 . Results are shown in Figure 2. It is evident that the model accurately solves the equation, aligning closely with the numerical solution. Notably, the Mean Absolute Error was calculated to be 0.02987
To access further the accuracy of the model, we run simulations for a nitrogen application as described by [28]. [28] reported a Nitrogen application to a concrete silo containing 2400 tonnes of wheat at the Cyprus Grain Commission’s Limassol port silo. The silo was made of concrete (bin diameter 10.5 m, height to eaves 33.4 m, total storage capacity 3,046 m 3 ). Structural sealing was carried out and air tight valves were installed to improve the air tightness of the bins. The bin was loaded with grain up to about 1 m below bin roof holding 2400 tonnes of wheat (m.c. 11.8 % wet basis, 19 o C ). The oxygen ( O 2 ) concentration was monitored by taking gas samples at 1 m above and 3 m below grain surface and analyzing them using a portable meter. After reaching O 2 concentration below 0.9 % in bins A, B and C, this concentration was continuously maintained by the E c O 2 system below 0.9 %. Purge time was 56 hours until 0.9 % O 2 concentration was reached and the nitrogen volume used to reach this concentration was 3571 m 3 . Based on the above data, the model predicts that the 0.9 % O 2 concentration will be reached after 53.97 hours. Which is very accurate since it differs 3.62 % from the duration (56 hours) reported by [28].

3. Results

The results section has been divided according to the two configurations under examination: chamber and silo. In the chamber, diffusion is the primary factor influencing the penetration of nitrogen into the pellet core, whereas in the silo, both diffusion and convection effects need to be taken into account.

3.1. Chamber

The goal of this section is to provide an approximate (rule of thumb) duration that 1.0 % O 2 concentration is reached at the center of a pallet during a nitrogen treatment for a wide range of agricultural products. While no single dimensional pallet standard exist, a few different sizes are widely used. Based on [29] standard, the largest dimension of a pallete is 1.219 [m] (48 inches).
For the purposes of this section, two different boundary conditions were considered (Figure 3). The first one (Case A) considers that pallets are placed inside a chamber with uniform (99.5 %) nitrogen concentration whereas the second one (Case B) the nitrogen concentration gradually increases from 78 % to 99.5 % [6]. Thus, the first scenario represents the shortest duration for low (1%) oxygen concentration to be reached at the pallet core, whereas the second one represents a realistic scenario (as already reported by [6]).

3.1.1. Constant boundary condition (Case A)

The results for this scenario are displayed in Table 2 (under the column ’Case A’). The average duration required for O 2 concentration to reach 1%, is approximately 10.7 hours. Among the individual items, walnuts (kernels) exhibit the shortest duration, predicted at 9.7 hours, while prunes require the longest time at 11.5 hours. This outcome aligns with expectations given the differing porosity levels, with prunes possessing the highest and lowest porosity values.

3.1.2. Time variable boundary condition (Case B)

The comprehensive time required for a 99% N 2 concentration, for the second boundary condition, to reach the center of the pallet is presented in Table 2 under the column "Case B (total)". Additionally, the table indicates the time necessary to attain the desired concentration levels at the center of the pallet after the boundary condition has reached 99% N 2 (column "Case B"). On average, Case B (total) demands around 133.3 hours (with a minimum of 133.0 hours and a maximum of 133.6 hours). For column "Case B" specifically, the average duration is 2.7 hours (ranging from a minimum of 2.3 hours to a maximum of 2.9 hours). Notably, similar to Case A, the extremities are attributed to the same products (walnuts and prunes respectively). With the "Case B" column displaying relatively low values, it is evident that the primary factor influencing the duration is the shape of the boundary condition (the time taken to achieve 99% N 2 concentration), rather than the specific agricultural commodity being treated.

3.2. Silo

In this section, we examine a standard silo with a height of 30 meters and a diameter of 10 meters. A typical nitrogen generator has a flow capacity of 72 m 3 /hour, as cited in [30]. The generator produces nitrogen with a purity of 99.5%. For this scenario, the simulation model predicts the vertical concentration profile of N 2 taking into account both the diffusion effects but also the forced N 2 flow (convection). Table 3 displays the time required for the N 2 concentration to reach 99% at three different heights: 10 meters, 20 meters, and the silo’s top at 30 meters. It is evident that most agricultural products exhibit similar behavior, with average times of 13.5 hours, 25.4 hours, and 37.0 hours for the respective locations.
Table 3 shows the required time for N 2 to reach 99% at 10 m, 20 m, and 30 m (top of the silo). It’s clear that most of the agricultural products present the same behavior, i.e. 13.5 hours, 25.4 hours, and 37.0 hours for the three locations. In contrast to the chamber scenario, the range of hours for each location is more constrained despite the greater distance. This phenomenon is due to the prevailing convection effects (induced flow from the generator) to a certain degree over diffusion effects, which are influenced by the commodity’s porosity.
The study of nitrogen distribution draws parallels to the analysis of thermoclines in hot water storage tanks during charging, as observed in [31] and [32]. Although the physical phenomena involve distinct fluid viscosities (nitrogen gas vs. water), the similarities in convection and diffusion make certain parameters applicable. For our study, the term "thermocline thickness" δ [32] is adapted to represent the diffusion layer’s thickness. Figure 4 illustrates that at 12 hours, the diffusion layer’s thickness was δ ( 12 h ) = 4.49 m , while at 24 hours, δ ( 24 h ) = 6.35 m , consistent with the observations of [31]. This alignment signifies the anticipated increase in the diffusion layer’s thickness over time.

4. Discussion

Modified atmospheres have emerged as a promising and eco-friendly approach for pest management in post-harvest agricultural products, offering an alternative to traditional insecticides. This study focused on the use of modified atmospheres, particularly nitrogen gas, to control insect infestations in stored commodities. The research aimed to investigate the penetration and distribution of nitrogen and oxygen in two common storage configurations: chamber-contained pallets and silos.
The utilization of computer simulations enabled a comprehensive exploration of the effects of modified atmospheres on insect control. The results presented insights into the dynamics of nitrogen distribution within various agricultural commodities, shedding light on the time required for oxygen concentration to decrease to desirable levels for pest suppression.
In the case of chamber-contained pallets, the simulations provided valuable information regarding the duration needed for oxygen concentration to reach 1% within the core of the pallets. The study considered both constant and time-variable boundary conditions, reflecting uniform nitrogen concentration and gradual nitrogen infusion, respectively. It was observed that the type of boundary condition significantly influenced the time required for achieving the desired oxygen levels, with boundary shape playing a pivotal role. Moreover, variations in porosity among different commodities were found to impact the duration of oxygen reduction, corroborating the link between porous structure and gas diffusion.
In the context of silos, the investigation delved into nitrogen distribution across varying heights within the silo. Convection effects, induced by nitrogen flow from generators, played a substantial role in addition to diffusion. The study demonstrated that, unlike the chamber scenario, the range of hours required for nitrogen concentration to reach specific levels in different heights of the silo was relatively constrained. This observation emphasized the dominance of convection effects, which contributed to a more consistent diffusion layer thickness over time.

5. Conclusions

This study contributes to the understanding of modified atmosphere techniques for insect control in stored agricultural commodities. By employing computational simulations, the research provides practitioners and stakeholders with quantitative insights into the temporal and spatial dynamics of nitrogen distribution. The findings underscore the importance of boundary conditions, commodity porosity, and convection effects in shaping the efficacy of modified atmosphere treatments.
Moving forward, this research can serve as a foundation for optimizing modified atmosphere strategies in real-world scenarios. Further investigations could explore additional factors that might influence gas distribution, such as temperature, humidity, and pressure variations. Moreover, experimental validation of the simulation results would enhance the accuracy of the predictions and strengthen the applicability of the proposed models to diverse agricultural settings. Overall, the study advances the knowledge surrounding modified atmospheres as a sustainable pest management strategy and offers a basis for refining and implementing these techniques in the agricultural industry.

Author Contributions

Conceptualization, E.K. and P.A.; methodology, E.K., P.A.; software, E.K.; investigation, P.A.; writing—original draft preparation, E.K., P.A., C.A..; writing—review and editing, E.K., P.A., C.A.. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Banks, H.; Annis, P.; Calderon, M.; Barkai-Golan, R. Food preservation by modified atmospheres, 1990.
  2. Calderon, M.; Barkai-Golan, R. Food preservation by modified atmospheres; CRC Press, 1990.
  3. Navarro, S. The use of modified and controlled atmospheres for the disinfestation of stored products. Journal of Pest Science 2012, 85, 301–322. [Google Scholar] [CrossRef]
  4. Athanassiou, C.G.; Arthur, F.H. Recent advances in stored product protection; Springer, 2018.
  5. Athanassiou, C.G.; Chiou, A.; Rumbos, C.I.; Sotiroudas, V.; Sakka, M.; Nikolidaki, E.K.; Panagopoulou, E.A.; Kouvelas, A.; Katechaki, E.; Karathanos, V.T. Effect of nitrogen in combination with elevated temperatures on insects, microbes and organoleptic characteristics of stored currants. Journal of Pest Science 2016, 90, 557–567. [Google Scholar] [CrossRef]
  6. Agrafioti, P.; Kaloudis, E.; Athanassiou, C.G. Utilizing low oxygen to mitigate resistance of stored product insects to phosphine. Journal of the Science of Food and Agriculture 2022, 102, 6080–6087. [Google Scholar] [CrossRef] [PubMed]
  7. Guo, J.; Wei, X.; Du, X.; Ren, J.; Lü, E. Numerical simulation of liquid nitrogen injection in a container with controlled atmosphere. Biosystems Engineering 2019, 187, 53–68. [Google Scholar] [CrossRef]
  8. Carvalho, D.; Santos, I.; Vargas, G.; Martins, M.; Ferreira, A. Utilization of nitrogen gas for refrigeration and atmosphere modification in grain storage: a simulation study. Ist International Symposium on CFD Applications in Agriculture 1008, 2012, pp. 127–132. [Google Scholar] [CrossRef]
  9. Silva, M.; Faroni, L.; Martins, M.; Sousa, A.; Bustos-Vanegas, J. CFD simulation of ozone gas flow for controlling Sitophilus zeamais in rice grains. Journal of Stored Products Research 2020, 88, 101675. [Google Scholar] [CrossRef]
  10. Pandiselvam, R.; Chandrasekar, V.; Thirupathi, V. Numerical simulation of ozone concentration profile and flow characteristics in paddy bulks. Pest Management Science 2017, 73, 1698–1702. [Google Scholar] [CrossRef]
  11. Agrafioti, P.; Kaloudis, E.; Bantas, S.; Sotiroudas, V.; Athanassiou, C.G. Modeling the distribution of phosphine and insect mortality in cylindrical grain silos with Computational Fluid Dynamics: Validation with field trials. Computers and Electronics in Agriculture 2020, 173, 105383. [Google Scholar] [CrossRef]
  12. Bird, R.; Stewart, W.; Lightfoot, E. Transport phenomena, 2 ed.; Wiley, 2002.
  13. Shen, L.; Chen, Z. Critical review of the impact of tortuosity on diffusion. Chemical Engineering Science 2007, 62, 3748–3755. [Google Scholar] [CrossRef]
  14. Neale, G.H.; Nader, W.K. Prediction of transport processes within porous media: Diffusive flow processes within an homogeneous swarm of spherical particles. AIChE Journal 1973, 19, 112–119. [Google Scholar] [CrossRef]
  15. Dingke, Z.; Fielke, J. Some physical properties of Australian Nonpareil almonds related to bulk storage. International Journal of Agricultural and Biological Engineering 2014, 7, 116–122. [Google Scholar] [CrossRef]
  16. Tavakoli, M.; Tavakoli, H.; Rajabipour, A.; Ahmadi, H.; Gharib-Zahedi, S.M.T. Moisture-dependent physical properties of barley grains. International Journal of Agricultural and Biological Engineering 2010, 2, 84–91. [Google Scholar] [CrossRef]
  17. Balasubramanian, D. PH—Postharvest Technology. Journal of Agricultural Engineering Research 2001, 78, 291–297. [Google Scholar] [CrossRef]
  18. Seifi, M.R.; Alimardani, R. The Moisture Content Effect on Some Physical and Mechanical Properties of Corn (Sc 704). Journal of Agricultural Science 2010, 2. [Google Scholar] [CrossRef]
  19. Aydin, C. PH—Postharvest Technology. Biosystems Engineering 2002, 82, 297–303. [Google Scholar] [CrossRef]
  20. Kashaninejad, M.; Mortazavi, A.; Safekordi, A.; Tabil, L. Some physical properties of Pistachio (Pistacia vera L.) nut and its kernel. Journal of Food Engineering 2006, 72, 30–38. [Google Scholar] [CrossRef]
  21. Tsami, E.; Katsioti, M. Drying kinetics for some fruits: predicting of porosity and color during dehydration. Drying Technology 2000, 18, 1559–1581. [Google Scholar] [CrossRef]
  22. Karimi, N. Moisture-dependent physical properties of seedless and seeded raisin (Vitis vinifera L.) varieties. Agronom Res. Moldavia 2015, 161, 5–16. [Google Scholar] [CrossRef]
  23. Varnamkhasti, M.G.; Mobli, H.; Jafari, A.; Keyhani, A.; Soltanabadi, M.H.; Rafiee, S.; Kheiralipour, K. Some physical properties of rough rice (Oryza Sativa L.) grain. Journal of Cereal Science 2008, 47, 496–501. [Google Scholar] [CrossRef]
  24. Deshpande, S.; Bal, S.; Ojha, T. Physical Properties of Soybean. Journal of Agricultural Engineering Research 1993, 56, 89–98. [Google Scholar] [CrossRef]
  25. Altuntaş, E.; Erkol, M.H. Physical properties of shelled and kernel walnuts as affected by the moisture content. Czech Journal of Food Sciences 2018, 28, 547–556. [Google Scholar] [CrossRef]
  26. Karimi, M.; Kheiralipo, K.; Tabatabaee, A.; Khoubakht, G.; Naderi, M.; Heidarbeig, K. The Effect of Moisture Content on Physical Properties of Wheat. Pakistan Journal of Nutrition 2008, 8, 90–95. [Google Scholar] [CrossRef]
  27. Zoppou, C.; Knight, J.H. Analytical Solutions for Advection and Advection-Diffusion Equations with Spatially Variable Coefficients. Journal of Hydraulic Engineering 1997, 123, 144–148. [Google Scholar] [CrossRef]
  28. Navarro, S.; Athanassiou, C.; Varnava, A.; Vroom, N.; Yiassoumis, D.; Leandrou, I.; Hadjioannou, S. Control of stored grain insects by using nitrogen in large concrete silos in Cyprus. Proceedings of the 9th international conference of controlled atmospheres and fumigation in stored products, Antalya, Turkey, 2012, pp. 15–19.
  29. Flat pallets for intercontinental materials handling — Principal dimensions and tolerances. Standard, International Organization for Standardization, Geneva, CH, 2004.
  30. Athanassiou, C.G.; Sakka, M.K. Using Nitrogen for the Control of Stored Product Insects: One Single Application for Multiple Purposes. Agrochemicals 2022, 1, 22–28. [Google Scholar] [CrossRef]
  31. Kaloudis, E.; Grigoriadis, D.; Papanicolaou, E.; Panidis, T. Large eddy simulations of turbulent mixed convection in the charging of a rectangular thermal storage tank. International Journal of Heat and Fluid Flow 2013, 44, 776–791. [Google Scholar] [CrossRef]
  32. Kaloudis, E.; Grigoriadis, D.; Papanicolaou, E. Numerical simulations of constant-influx gravity currents in confined spaces: Application to thermal storage tanks. International Journal of Thermal Sciences 2016, 108, 1–16. [Google Scholar] [CrossRef]
Preprints 86935 g001
Figure 1. A pallet (on the left) and a silo (on the right) are illustrated. The black line indicates the position corresponding to the numerical solution.
Figure 1. A pallet (on the left) and a silo (on the right) are illustrated. The black line indicates the position corresponding to the numerical solution.
Preprints 86935 g001
Preprints 86935 g002
Figure 2. Comparison of the model results to the analytical solution.
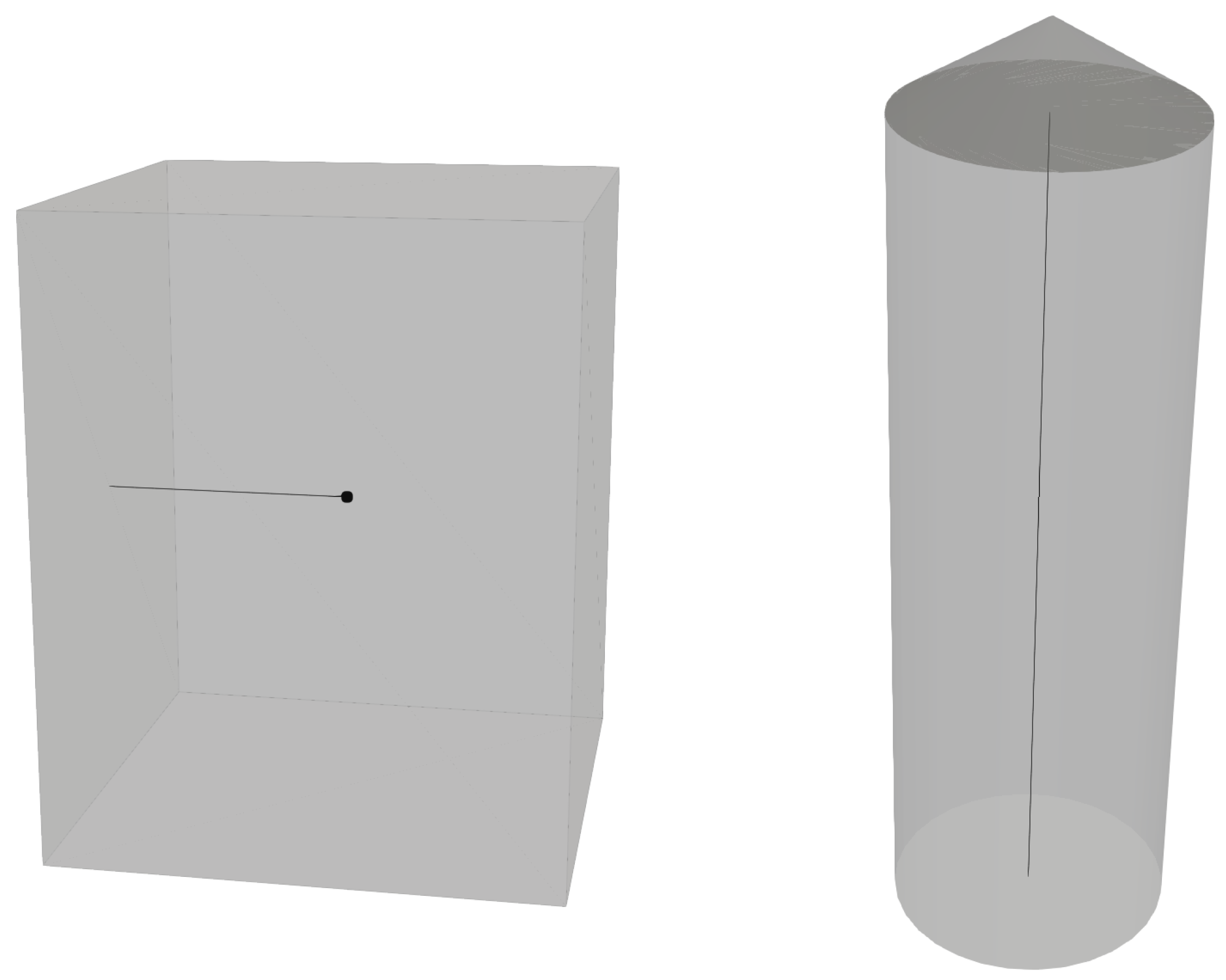
Figure 2. Comparison of the model results to the analytical solution.
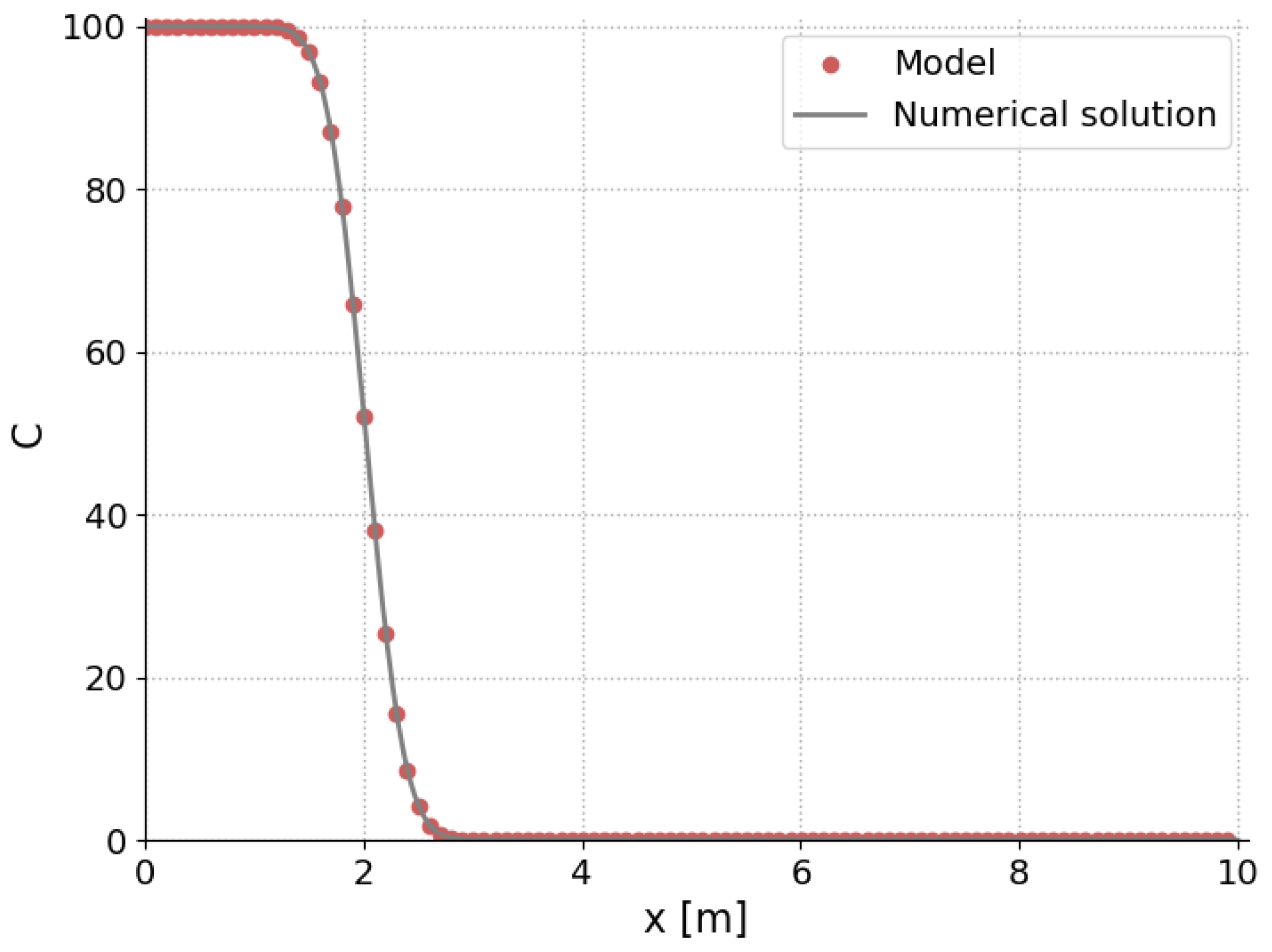
Preprints 86935 g002
Preprints 86935 g003
Figure 3. The two boundary conditions considered for this study for the chamber/pallette simulations.
Figure 3. The two boundary conditions considered for this study for the chamber/pallette simulations.
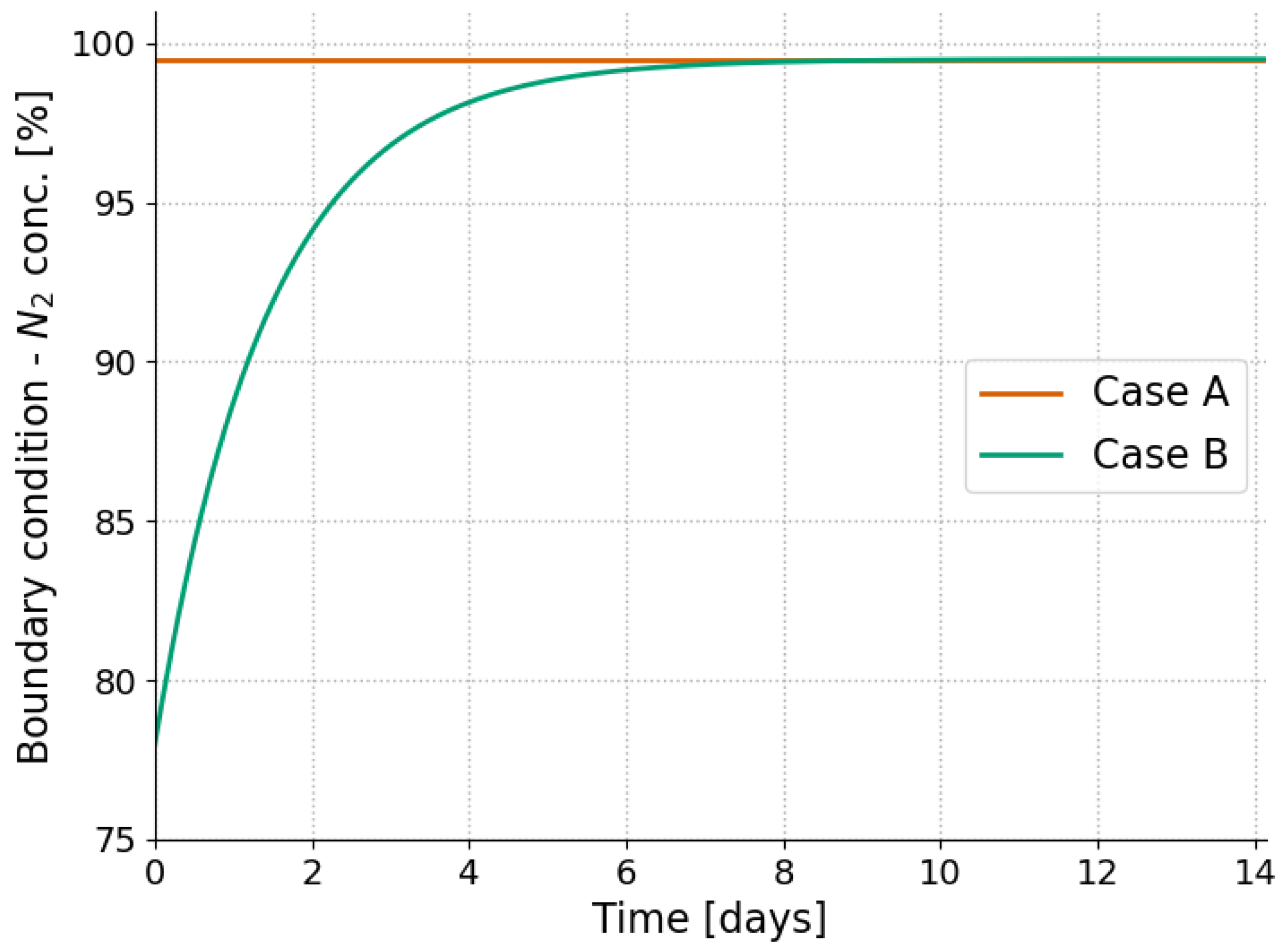
Preprints 86935 g003
Preprints 86935 g004
Figure 4. The distribution of Nitrogen at two time instances.
Figure 4. The distribution of Nitrogen at two time instances.
Preprints 86935 g004
Table 1. Porosity values per commodity.
Table 1. Porosity values per commodity.
Product Porosity Source
almonds (in-hull) 0.67 [15]
almonds (in-shell) 0.58 [15]
barley 0.45 [16]
cashew 0.49 [17]
corn 0.48 [18]
hazelnut (kernel) 0.43 [19]
pistachio (nut) 0.57 [20]
pistachio (kernel) 0.50 [20]
prunes 0.33 [21]
raisins 0.40 [22]
rice 0.57 [23]
soy bean 0.38 [24]
walnut (shelled) 0.61 [25]
walnut (kernel) 0.75 [25]
wheat 0.44 [26]
Table 2. Simulation results (time to reach 1 % O 2 ) at the center of the pallette.
Table 2. Simulation results (time to reach 1 % O 2 ) at the center of the pallette.
Product Case A [h] Case B (total) [h] Case B [h]
almonds (in-hull) 10.0 133.1 2.4
almonds (in-shell) 10.4 133.2 2.6
barley 11.0 133.4 2.7
cashew 10.8 133.4 2.7
corn 10.9 133.4 2.7
hazelnut (kernel) 11.1 133.4 2.8
pistachio (nut) 10.5 133.2 2.6
pistachio (kernel) 10.8 133.3 2.7
prunes 11.5 133.6 2.9
raisins 11.2 133.5 2.8
rice 10.5 133.2 2.6
soybean 11.3 133.5 2.8
walnut (shelled) 10.3 133.2 2.5
walnut (kernel) 9.7 133.0 2.3
wheat 11.0 133.4 2.8
Table 3. Simulation results (time to reach 1 % O 2 ) at three positions in the silo. height 30 m corresponds to the top of the silo.
Table 3. Simulation results (time to reach 1 % O 2 ) at three positions in the silo. height 30 m corresponds to the top of the silo.
Product height 10 m [h] height 20 m [h] height 30 m [h]
almonds (in-hull) 13.6 25.5 37.1
almonds (in-shell) 13.5 25.4 37.0
barley 13.5 25.3 36.9
cashew 13.5 25.4 36.9
corn 13.5 25.4 36.9
hazelnut (kernel) 13.5 25.3 36.9
pistachio (nut) 13.5 25.4 37.0
pistachio (kernel) 13.5 25.4 36.9
prunes 13.4 25.2 36.8
raisins 13.4 25.3 36.9
rice 13.5 25.4 37.0
soybean 13.4 25.3 36.8
walnut (shelled) 13.6 25.5 37.0
walnut (kernel) 13.6 25.6 37.2
wheat 13.5 25.3 36.9
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated