Preprint
Article
The Multi-Objective Model of the Hub Covering Location-Routing Problem with Simultaneous Delivery and Pickup Under Uncertainty
Altmetrics
Downloads
134
Views
51
Comments
0
This version is not peer-reviewed
Submitted:
06 October 2023
Posted:
09 October 2023
You are already at the latest version
Alerts
Abstract
In this paper, a model of the hub covering the location-routing problem with simultaneous delivery and pickup should be designed in order to minimize the total costs, minimize the maximum vehicles travel time and minimize the amount of CO_2 gas emissions. Two-stage stochastic programming is used in this paper to control the uncertainty parameters of the problem. The mathematical model aims to decide the appropriate location of hubs and vehicle routing for simultaneous delivery and pickup of products. In this regard, the results obtained from the LP-Metric method show that there is a conflict between the objective functions, and with the reduction of the amount of CO_2 gas emissions and the reduction of the maximum vehicles travel time, the total costs have increased. On the other hand, by examining the economical factor, it was observed that by reducing this factor, the robustness factors are changed and the total costs of the network are reduced. MOIWO and MOALO were used to solve the problem in large scale, the result of which was the existence of a significant difference between the calculation time averages. Also, the efficiency of these methods was very high compared to the LP-Metric method and the maximum relative difference was less than 2.83%. The results of numerical examples show a higher efficiency of the MOALO than the MOIWO.
Keywords:
Subject: Engineering - Industrial and Manufacturing Engineering
1. Introduction
The optimal design of the supply chain network plays a vital role in reducing transportation costs and improving system performance (Nozari et al., 2022). Transportation of goods in the supply chain is an important activity that has a great impact on the overall performance of manufacturing companies and the final cost of products by sending and delivering raw materials and finished products on time. For this reason, companies are constantly under pressure to reduce costs as well as increase their service levels (Szmelter-Jarosz et al., 2021). Among other things that companies should continuously monitor is the collection of products distributed by their company. Therefore, in addition to meeting customer demand, companies are also responsible for collecting products. This issue has been announced by governments due to the harmful environmental effects. In order to overcome these pressures, they must regularly redesign their service network and improve logistics processes with better coordination of decisions at strategic and operational levels (Ghahremani-Nahr et al., 2022). Hub location problems have been widely used in recent decades due to their high applications in modern transportation and communication systems. Hubs in the transportation networks of goods and passengers, etc., are places that receive the flow from different sources and direct it to the destination nodes or other hubs; Therefore, the goal of hub location-routing problems is to meet demands by moving people, goods, and information through special facilities called "hubs" that are known as distribution intermediaries between source nodes and destination nodes (Alumur et al., 2021). In a location-routing network, due to the large volume of goods transported from origin to destination, effective design of a network can ensure high-quality services (Li & Wang, 2023). In this network, by reducing the number of links in the source and destination nodes, hubs prevent any direct connection of all nodes, which in turn leads to a reduction in costs, a reduction in gas emissions, and a reduction in the time of goods transfer compared to networks with complete graph connections. (Ghaffarinasab et al., 2022). Also, using the economical factor (0 < α < 1) for communication between hubs also leads to a large reduction in the total network cost (Taherkhani & Alumur, 2019).
In recent years, various types of hub location problems have been studied, one of the most important of which is the hub covering location-routing problem. In these networks, each hub can only transfer goods and services to other nodes within a predefined radius and collect the returned goods. Hub Covering location-routing networks have attracted the attention of many researchers due to various application fields in long-distance communication networks, air transportation, goods transportation, postal services, public and urban transportation, rail transportation, and emergency services (Mokhtarzadeh et al., 2021). As the demand for freight increases with population growth, the importance of the proper design of transportation networks in uncertain conditions becomes apparent (Davari et al., 2013). The use of hubs in transportation networks not only significantly reduces operating costs and network structure preparation costs and delivery time, but also causes better services to customers and reduces the harmful effects of environmental pollution (Hasanzadeh et al., 2018). Therefore, the main concept of hub covering location-routing in the design of a transportation network is that a number of decisions must be made, including the location of hub facilities and non-hub nodes, the allocation of all source and destination nodes (non-hub) directly to the hub, and flow routing. These decisions are aimed at reducing the costs of the total network, reducing the amount of gas emissions and reducing the maximum travel time of vehicles. In addition, considering whether there is a limit to transfer the amount of products through the transportation network or there is no limit, hub location problems are classified into two sub-problems with limited capacity and unlimited capacity. Capacity limitations may be related to network links or hub nodes (Rahmati et al., 2022). These decisions are aimed at reducing the costs of the total network, reducing the amount of gas emissions and reducing the maximum travel time of vehicles. In addition, considering whether there is a limit to transfer the amount of products through the transportation network or there is no limit, hub location problems are classified into two sub-problems with limited capacity and unlimited capacity. Capacity limitations may be related to network links or hub nodes (Rahmati et al., 2022). There is also another type of capacity limitation, which is related to the number of non-hub nodes that can be assigned to a specific hub; Therefore, decision makers can include these considerations during their planning (Zahedi and Nahar, 2020).
According to the stated content, the aim of this research is to design the hub covering location-routing model with delivery and pick-up under uncertainty. To deal with the uncertainty parameters of the model, the two-stage stochastic programming (TSSP) method was used and different scenarios were proposed for each of the uncertainty parameters. Also, the combination of location and routing problems in the hub covering model has led to the use of LP-Metric, MOIWO and MOALO methods to solve the problem. The results of the multi-objective model will be analyzed in order to minimize the total costs, minimize the maximum vehicle travel time and minimize the amount of gas emissions.
The structure of the paper is such that in the second part, the research literature is reviewed and the research gap is identified. In the third part, the modeling of the hub covering location-routing problem with delivery and pick-up under uncertainty is discussed. In the fourth part, various solution methods including LP-Metrics, MOIWO and MOALO methods have been investigated. In the fifth section, the analysis of the mathematical model and the sensitivity analysis of the problem are discussed, and in the sixth section, the conclusions and future suggestions of the research are discussed.
2. Literature review
In recent years, hub location problems have attracted the attention of many researchers, and various models have been developed, such as covering hub problems, median hubs, P-hubs, etc. According to the focus of this paper on the hub covering location-routing problem, the research conducted has been reviewed in the following.
Lopes et al. (2016) solved the hub location-routing model using GA with random search. They also used the branch and cut algorithm to check the efficiency of their solution method. Computational experiments on several benchmark examples of routing problems showed that the proposed algorithm is effective on medium-to-large-sized examples, while the branch and cut algorithm solves small to medium-sized problems optimally. Karimi (2018) presented a model of a hub covering location-routing with simultaneous delivery and pickup. In this paper, the main goal was to minimize the costs of hub location and vehicle routing considering the limited hubs capacity. The results showed that the Tabu search method is more effective than other methods in finding good-quality solutions. Karimi and Setak (2018) developed a transportation scheduling and hub location problem where the hub network is not fully interconnected. The objective of the proposed model was to maximize the total amount of flow delivered by the last predetermined time and also to minimize the total costs. Wang and Qin (2020) presented a model for the hub covering location problem under uncertainty. The primary goal of this model was to minimize the costs of setting up hubs. To solve this model, a hybrid algorithm named GA-VNS was used and by analyzing several numerical examples, the high efficiency of this method was shown. Rajabi and Darestani (2020) presented a bi-objective optimization model to reduce the time and costs of the hub covering location problem. In this model, the cost, time and capacity of the central hub were considered as fuzzy parameters. NSGA II and NRGA were used to solve the bi-objective model. The results show that there is no significant difference between the CPU. Also, by ranking the solution methods with TOPSIS, the NSGA II has shown its efficiency in solving large numerical examples. Pourmohammadi et al. (2021) presented a multi-objective mathematical model for hub location and routing problem under uncertainty in flow, cost, time and number of job opportunities. The objective of this model is to minimize the total cost of transportation including routing and fixed cost and to maximize employment and regional development as a social responsibility. FIWO algorithm, variable neighborhood search and game theory were used to solve the model. Ghiasi and Vahdani (2021) presented a model for the hub location-routing problem considering balance and capacity decisions. To reduce the total cost of location and routing, GA and ICA have been used. The comparative results of the problem examples show that the GA has a better performance compared to the colonial competition algorithm and considering the capacity and balance considerations can be effective in reducing the costs of the investigated network. Ratli et al. (2022) designed a heuristics method to solve the hub location-routing problem. Their improved algorithm used a sequential variable neighborhood descent with multiple neighborhoods required to match the complex nature of the problem. The calculation results on 912 samples showed that the presented innovative method has the ability to solve 691 problems. Fallah- Tafti et al. (2022) developed a mathematical model for rapid transit networks based on the hub location model, which includes stops (stations) in hub and non-hub levels. In this model, which aimed to minimize the costs of locating the hub and routing the means of transportation, a local search algorithm was used. Hajipour et al. (2022) presented a mathematical model for locating the fire station and facilities assigned to the stations in different periods and emergency situations (wars and natural disasters). This model is designed dynamically according to the demand and covering radius of the facilities, based on traffic and the type of area and phase in different periods. Due to the NP-hardness of the problem, PSO and ABC were used to solve the problem, and the results showed that the provided PSO is better than ABC in terms of the quality of solutions and computing time. Ghaffarinasab and Kara (2022) modeled the multi-allocation hub location problem in which risk is measured using the conditional mean criterion. In this paper, the classic multiple allocation hub location problem, i.e. bladder hub, maximum hub covering and central hub, was investigated. Benders decomposition algorithm was used to solve the mathematical model. Rahmati et al. (2023) modeled a hub location problem with two-stage stochastic profit maximization with uncertain demand. In this model, the advanced sample mean approximation method was used to achieve the appropriate number of scenarios. Also, k-means clustering and self-organizing map clustering algorithms were used for clustering similar samples. Finally, the proposed models were analyzed using the famous Australia Post dataset. Motamedi et al. (2023) used six new techniques in prioritizing customers in the hub optimization problem. In these techniques, each strategy assigns a value to each customer based on distance and demand parameters, where customers are prioritized based on this value. Comparing the no-priority strategy with the best customer prioritization strategy shows that the no-priority strategy has an adverse effect on delivery time. Li et al. (2023) designed a multimodal transportation network based on hub location for emergency relief operations. The nonlinear model presented by them was a bi-objective model with minimization of transportation time and transportation costs. They used the MOGWO to solve this problem. The results showed that the presented model can provide practical management insights for departments and transport companies.
The literature review shows that there is a research gap in objective functions, constraints and solution methods. Since the minimization of network costs has been discussed in most of the papers. This paper tries to reduce the minimum vehicle traffic time by developing a mathematical model, in addition to reducing costs, and minimizing the amount of gas emissions caused by vehicle traffic. On the other hand, there is no hub covering location model that integrates with the vehicle routing problem. Using the TSSP method can easily control the uncertainty parameters. In addition to delivering goods, the presented model also pick-up returned products at the same time. The literature review shows that the use of meta-heuristic methods is common, but new algorithms have not been used on the hub covering location-routing model. This problem made MOALO and MOIWO to be used in this paper in addition to the LP-Metrics method.
3. Definition of the problem
In this section, the hub covering location and routing problem with simultaneous delivery and pick-up uncer uncertainty is discussed. For example, Figure (1) can be considered as an example of the investigated problem.
Figure 1.
The problem of hub covering locating and routing.
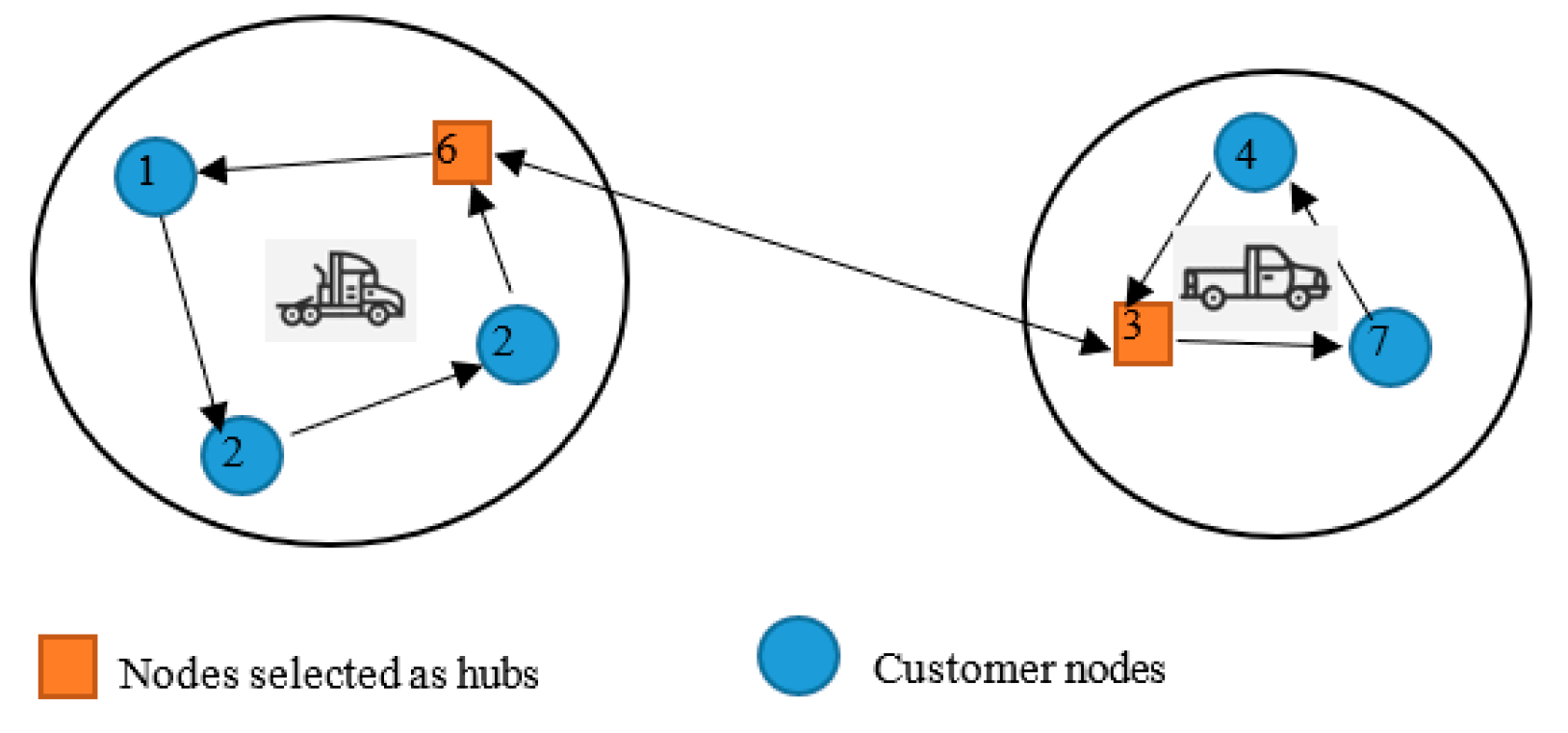
The main goal in the investigated problem is to determine the optimal number and location of nodes from the network as hubs, assign non-hub nodes to hubs, determine the optimal transportation route to meet uncertainty simultaneous delivery and pickup, and determine the optimal number of vehicles to distribute products. Therefore, to explain the problem better, 7 nodes are considered according to Figure (1). It can be seen that nodes 3 and 6 are selected as hubs in this problem, nodes 1-2-5 are assigned to hub number 6 and nodes 7 are assigned to hub number 3. The way of assigning these nodes to the hubs is based on the covering radius considered for each hub. That is, to distribute the products to the nodes assigned to each hub, vehicles related to that hub are used. In this case, the customers who are within the transportation radius of each vehicle (selected hub) can be allocated to that hub. Also, another goal of this problem is the optimal routing of vehicles, which can be seen according to Figure (1), the optimal route of the 1st vehicle from hub number 6 includes going through nodes 1, 5 and 3 and the optimal route of the 2nd vehicle from hub number 3 as well. It includes going through nodes 7 and 4.
In this paper, parameters such as delivery and pick-up demand, transportation time and transportation cost are taken into consideration in an uncertainty manner, which take on different values in different scenarios, the result of which can be a change in the optimal location of the facility as well as the optimal routing of vehicles. Therefore, the modeling of a hub covering location and routing problem with delivery and pickup under uncertainty can be done according to the following assumptions and scope of the study:
- Delivery and pick-up demand, transportation time and transportation cost are taken into account in an uncertain manner.
- Modeling the uncertainty problem with the probabilistic method will be based on the scenario.
- The covering radius of each hub is variable and has a direct relationship with the quality of its service.
- All capacities of the hub and vehicles are known and specified.
- Transportation between hubs has a discount (economical factor).
Based on the above assumptions, the mathematical model seeks to minimize the total costs, minimize the maximum vehicles travel time and minimize the amount of gas emissions caused by the traffic of vehicles at the same time. Considering the assumptions of the above model, the number of nodes and vehicles are considered. Other parameters and variables for decision making in uncertain conditions can be presented as follows.
Parameters
| Uncertainty transportation cost between node and node | |
| Uncertainty transport time between node and node | |
| The distance between node and node | |
| The emission rate of gas from the traffic of vehicle between node and node | |
| The fixed cost of determining node k as a hub based on the quality of service | |
| The initial fixed cost of using the vehicle | |
| The amount of uncertainty delivery and withdrawal demand between node and node | |
| The number of nodes that should be selected as hubs. | |
| Number of vehicles in each hub | |
| The maximum covering radius of the vehicle in the distribution of products based on the quality of service | |
| Vehicle capacity in product distribution | |
| Maximum hub capacity | |
| Coefficient of economical factor | |
| The total amount of output flow from node |
Variables
| Maximum travel time by vehicles from hub centers | |
| The amount of flow that starts from node and passes through hub and hub | |
| The amount of flow that starts from node and passes through node and hub | |
| 1; if vehicle v passes through node and node 0; otherwise. |
|
| 1; if hub is selected 0; otherwise |
|
| 1; if node is assigned to vehicle 0; otherwise. |
Modeling the problem
| (1) | |
| (2) | |
| (3) | |
| (4) | |
| (5) | |
| (6) | |
| (7) | |
| (8) | |
| (9) | |
| (10) | |
| (11) | |
| (12) | |
| (13) | |
| (14) | |
| (15) | |
| (16) | |
| (17) | |
| (18) | |
| (19) |
Equation (1) reduces the total costs. These costs include the cost of transporting products between nodes, the cost of locating nodes as hubs, and the fixed costs of using vehicles. Equation (2) shows the second objective function of the problem and includes minimizing the maximum travel time between nodes. Equation (3) deals with the minimization of CO2 gas emissions caused by vehicle traffic. Equation (4) calculates the total output current from each node. Equation (5) provides flow balance between nodes and ensures that the amount of pickup and delivery occurs simultaneously at each node. Equation (6) guarantees that the total output flow from each node can be carried by only one of the available vehicles. Equation (7) guarantees that each vehicle visits each node (customer) only once. Equation (11) guarantees that the vehicles must pass through the selected hubs. Equations (12) and (13) guarantee that each route should be assigned to only one vehicle. Equation (14) shows the maximum travel time between nodes. Equation (15) calculates the covering radius resulting from the traffic of each vehicle. The relation (16) guarantees that each vehicle cannot move more than its capacity. The relation (17) ensures that only the hubs that have the ability to exchange products between their nodes as much as less than their capacity are selected. The relation (18) and (19) shows the type of the decision variables.
Due to the uncertainty of the parameters of delivery and pick-up demand, transportation time and transportation cost, the TSSP method has been used to control the model. Therefore, by defining as the number of scenarios, parameters and decision variables need to be redefined and modified as follows.
Sets
| The number of scenarios |
parameters
| Transportation cost between node and node in scenario | |
| Transportation time between node and node in scenario | |
| The amount of delivery and pick-up demand between node and node in scenario | |
| The probability of occurrence of scenario |
Also, the amount of the total output flow from node can be defined as follows.
| (20) |
Decision making variables
| The amount of flow that starts from node in scenario and passes through hub and hub | |
| The amount of flow that starts from node and passes through node and hub in scenario | |
| 1; if, in scenario , vehicle passes through node and node 0; otherwise. | |
| 1; if node is assigned to vehicle in scenario s0; otherwise. |
4. Solution methods
Three different methods have been used to solve the mathematical model. These methods include LP-Metrics, MOALO and MOIWO. For this purpose, a brief description of the solution methods has been given below.
4.1. LP-Metrics
To analyze numerical examples in small scale, one of the multi-objective decision-making methods called LP-Metrics has been used. To use this method to convert the multi-objective model into a single-objective model, the three-objective model must first be solved through the individual optimization method and the most optimal value of each objective function must be determined.
Therefore, the optimal value of each objective function with the individual optimization method without considering other objective functions with , where represents the number of objective functions. Then, by using the equation (40) and the optimal value of the obtained objective functions , the problem can be solved:
In relation is the weight assigned to each objective function.
4.2. MOALO
As with other population-based algorithms, the MOALO approximates optimal solutions to optimization problems by applying a random set of solutions. This collection is based on science inspired by the interaction between ants and ant lion. There are two populations in the ant-lion algorithm: the set of ants and the set of ant-lion. The general steps of the ant lion algorithm to change these sets and finally to estimate the global optimality for the desired optimization problem are as follows:
- The ant set is initialized with random values and the main search factors in the ant lion algorithm.
- The fitness value of each ant is evaluated using the objective function in each iteration.
- Ants move around the anthill using random steps in the search space.
- The ant lion population is never assessed. In fact, the ant lion assumes the location of the ants in the first iteration and moves to the new location of the ants in the remaining iterations, if the ants get better.
- An ant valve is assigned to each ant and its position is revealed when the ant becomes more suitable.
- There is a selective ant lion that affects the movement of ants regardless of its distance.
- If any ant lion is better than the chosen ant, it takes its place as the chosen ant.
- Steps 2 to 7 are repeated until the final criterion is met satisfactorily.
- The position and fit value of the selected ant lion is returned as the best estimate for the global optimum.
The main responsibility of ants is to explore the search space. They should move through the search space using a random walk. Ant lions retain the best position obtained by ants and direct the search of ants to promising regions of the search space. In order to solve the optimization problems, the anthill algorithm simulates the random walk of ants, diving into the anthill hole, constructing the hole, moving the ant to the anthill, catching the prey and reconstructing the hole, and choosing the chosen one.
4.3. MOIWO
This algorithm has taken advantage of the weed propagation pattern and today it is used in various users such as designing supply chain networks, vehicle routing and other optimization problems. In this algorithm, the goal is to find the best point of a certain environment for seeds to live. Parent grasses search by seed dispersal. In the first stage, the parts of the environment that are candidates for the best area to live are determined, and in the next stages, the search is carried out in areas with better living conditions. Therefore, the main idea of the method is to increase focus and search power with the passage of time in a range with the possibility of a better answer. The implementation steps of this algorithm are expressed as a mixture:
- 1-
- Generating the initial population: a certain number of answers are selected with a uniform distribution in the problem search space.
- 2-
- Calculating the degree of qualification: The degree of qualification of grasses is measured by the qualification function
- 3-
- Determining the number of new grasses: According to the qualification level of each parent grass, the number of new seeds around each grass is determined.
- 4-
- Distribution of new seeds: the seeds of new grasses are distributed for each parent (old) grass, with Gaussian distribution around the parent half.
- 5-
- Struggle to maintain survival: At each stage, the qualification level of all grasses is determined and both old and new grasses are ranked in order. If the final population exceeds the maximum population limit, additional responses with lower eligibility are eliminated.
- 6-
- Repetition of steps: return to the fifth step and repeat the steps until we reach the maximum number of repetition steps.
5. Analysis of the results
In this section, the solution of the multi-objective model of the hub covering location and routing problem with simultaneous delivery and pickup has been discussed. For this purpose and to show the output of the above model, a small numerical example has been designed and the multi-objective problem has been solved using the LP-Metrics method. In the following, in order to solve the problem in large scale, MOALO and MOIWO are used and statistical and non-statistical comparisons are shown on the results of this problem. Finally, the most efficient algorithm has been shown in terms of computational indicators and its performance compared to other algorithms.
5.1. Solving the problem in a small scale
To show the output of the model, a small scale problem with 5 nodes and 2 vehicles in 3 different scenarios is considered. Other parameters obtained from the model are described in Table (1).
Table 1.
The lower and upper limits of the deterministic parameters used in the model based on uniform distribution.
Table 1.
The lower and upper limits of the deterministic parameters used in the model based on uniform distribution.
| parameter | Interval boundaries | parameter | Interval boundaries |
| parameter | The first scenario | The second scenario | The third scenario |
As stated in the LP-Metrics method, first the best value of each objective function should be calculated from the individual optimization method and based on these values, the effective solutions of the three-objective problem should be shown. Therefore, Table (2) shows the best value of each objective function as well as the calculated efficient solutions for each objective function.
Table 2.
The best value of each objective function obtained from the individual optimization method and efficient solutions.
Table 2.
The best value of each objective function obtained from the individual optimization method and efficient solutions.
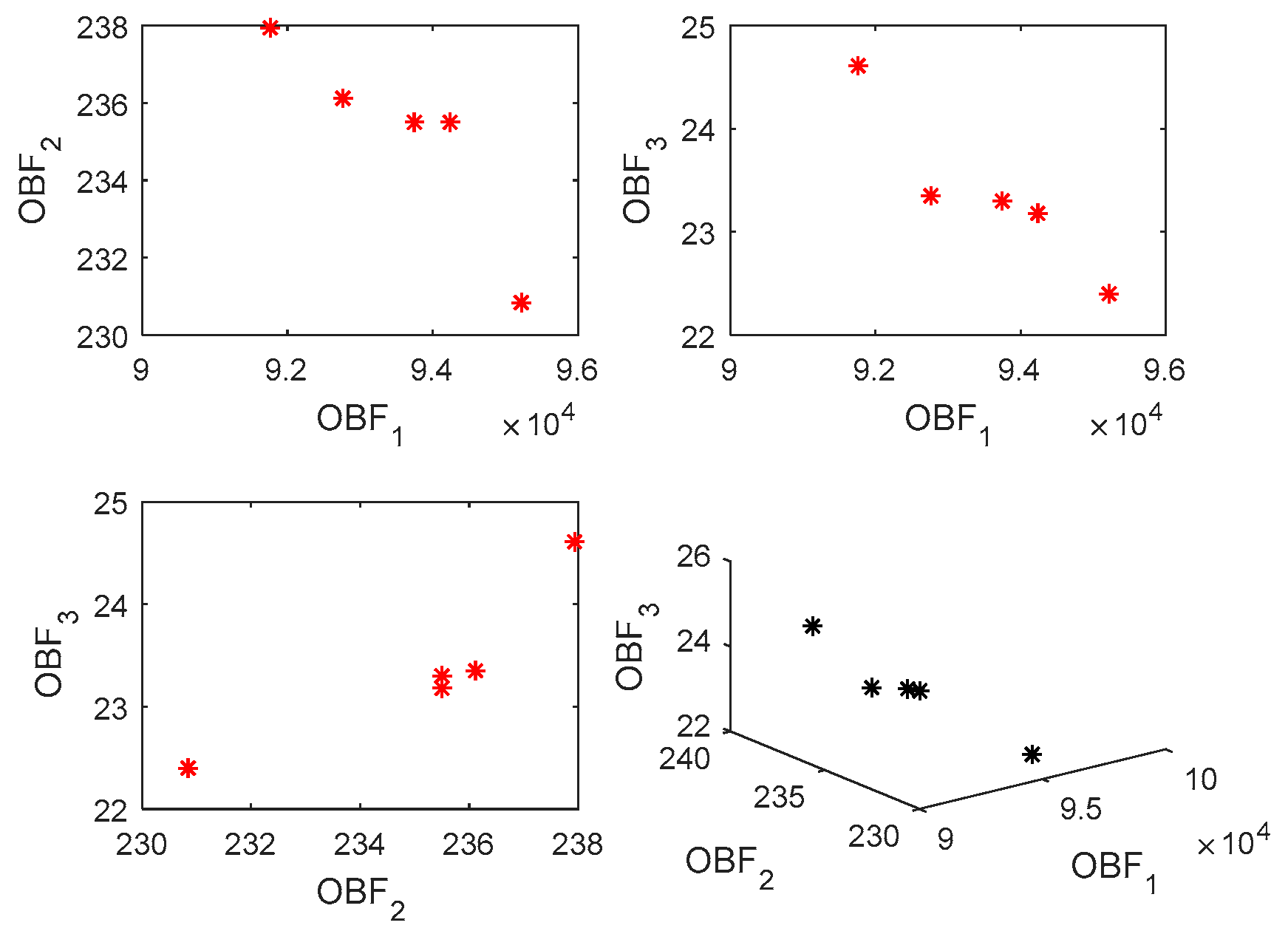
| The best solution | 91433.03 | 224.78 | 22.4 |
| Solution 1 | 91761.66 | 237.94 | 24.61 |
| Solution 2 | 92763.37 | 236.12 | 23.35 |
| Solution 3 | 93746.42 | 235.50 | 23.30 |
| Solution 4 | 94236.82 | 235.50 | 23.18 |
| Solution 5 | 95219.13 | 230.84 | 22.40 |
According to the results of Table (2), it can be seen that with the reduction of the amount of pollution as well as the maximum travel time between the nodes, the total costs of the network have increased due to different location and routing between the nodes. Figure (2) shows the Pareto front resulting from solving the sample problem.
Figure 2.
Pareto front obtained from solving the sample problem.
To show the results of solving the problem, Figures (3) and (4) show the best location and routing problem of the covering hub for the objective functions and the first efficient solution, respectively.
Figure 3.
Locating the hub and the optimal path assigned by the individual optimization method.
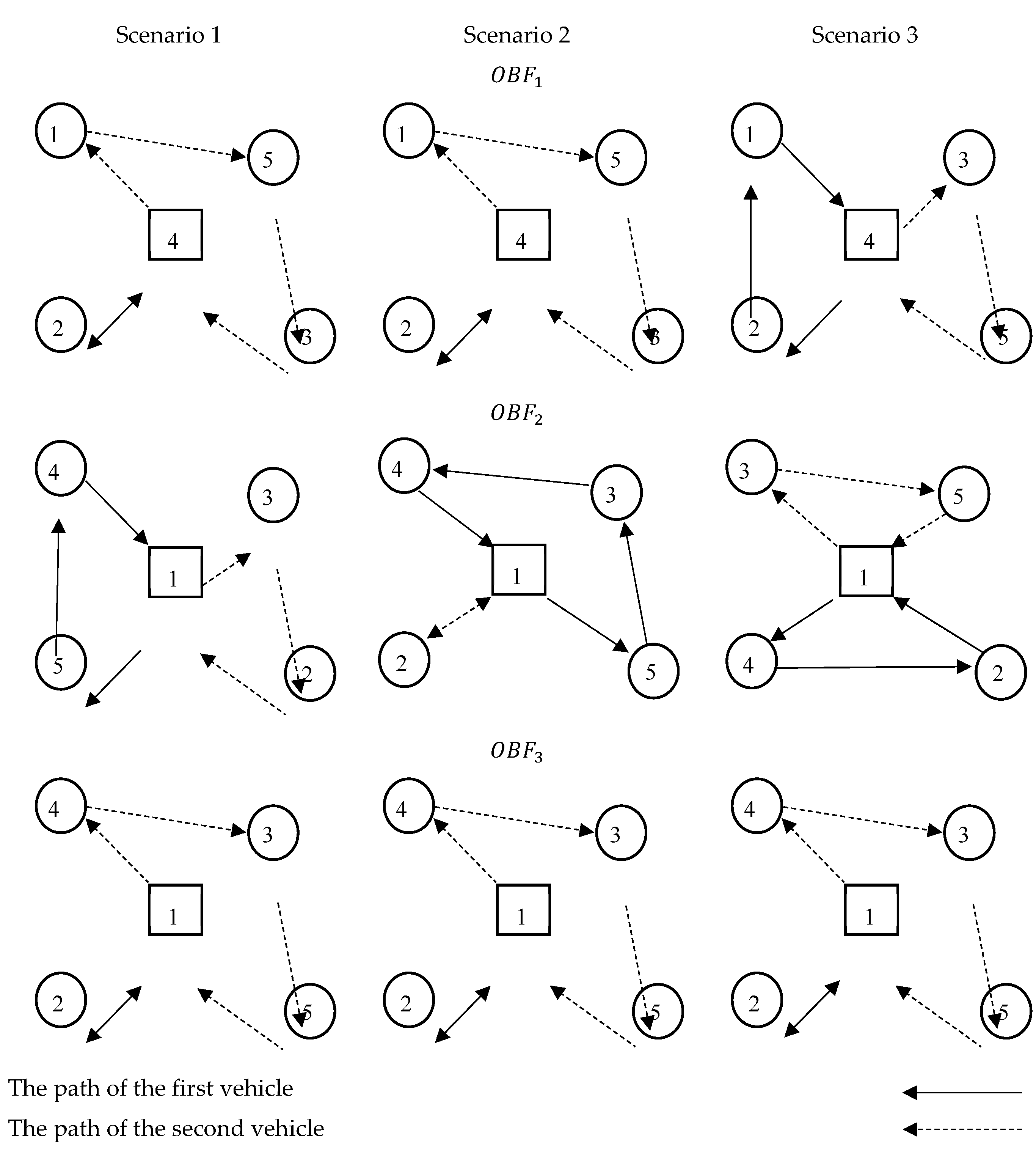
According to Figure (3) for the first objective function, it can be seen that node No. 4 is selected as a hub and two vehicles No. 1 and 2 have traveled different routes in different scenarios to meet customer demand. In Figure (3), for the second objective function, unlike the first objective function, node No. 1 is selected as the hub, and also the vehicle routing has undergone changes. This is due to considering the second objective function separately. Also, based on Figure (3), for the third objective function, it can be stated that in order to reduce the amount of pollution in the most optimal state, node number 1 should be selected as a hub, with the difference that vehicle routing will not be the same as the problem of the second objective function. In this figure, it can be seen that the location and routing of the vehicle has been fixed in all scenarios.
If the goal of simultaneous optimization is the goal, the optimal path and optimal routing will change. This problem has been obtained for the first effective solution by the LP-Metrics method in the form of (4).
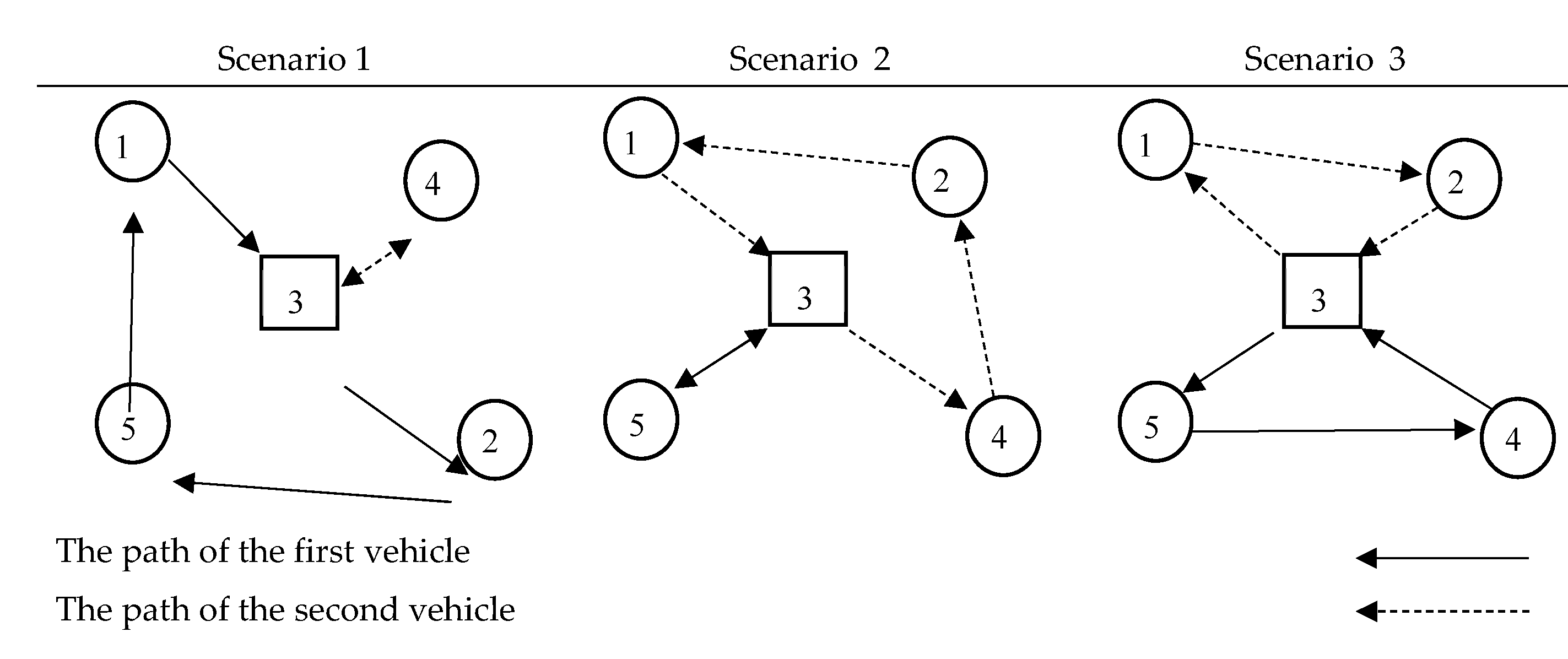
Unlike Figure (3), in order to solve the multi-objective model and consider three objective functions at the same time, it can be seen that in Figure (4), node number 3 is selected as a hub. While node number 4 was chosen as the most optimal place to reduce costs and node number 1 was chosen as the most optimal place to reduce time and the amount of gas emissions.
Table (4) shows the values of the variables related to simultaneous pickup and delivery by vehicles, and Figure (5) shows the optimal amount of delivery and pick-up for efficient solution 1 in the first scenario. Also, the demand between different nodes in the first scenario is shown in Table (3).
Table 3.
Amount of flow demand between the problem nodes in the first scenario.
| Flow | Node 1 | Node 2 | Node 3 | Node 4 | Node 5 |
| Node 1 | 0 | 19 | 16 | 13 | 13 |
| Node 2 | 19 | 0 | 19 | 10 | 15 |
| Node 3 | 16 | 19 | 0 | 18 | 11 |
| Node 4 | 13 | 10 | 18 | 0 | 14 |
| Node 5 | 13 | 15 | 11 | 14 | 0 |
Table 4.
The optimal amount of pickup and delivery by vehicles in the first scenario.
| Vehicle 1 | Vehicle 2 | |||||
| Flow | 23 | 52 | 15 | 31 | 43 | 34 |
| Node 1 | [19,32] | [13,13] | - | [16,61] | [13,13] | - |
| Node 2 | - | [15,63] | [19,48] | [19,29] | [10,10] | - |
| Node 3 | [19,46] | [11,27] | [16,16] | - | [18,18] | - |
| Node 4 | [10,37] | [14,27] | [13,13] | - | - | [18,55] |
| Node 5 | [15,15] | - | [13,53] | [11,40] | [14,14] | - |
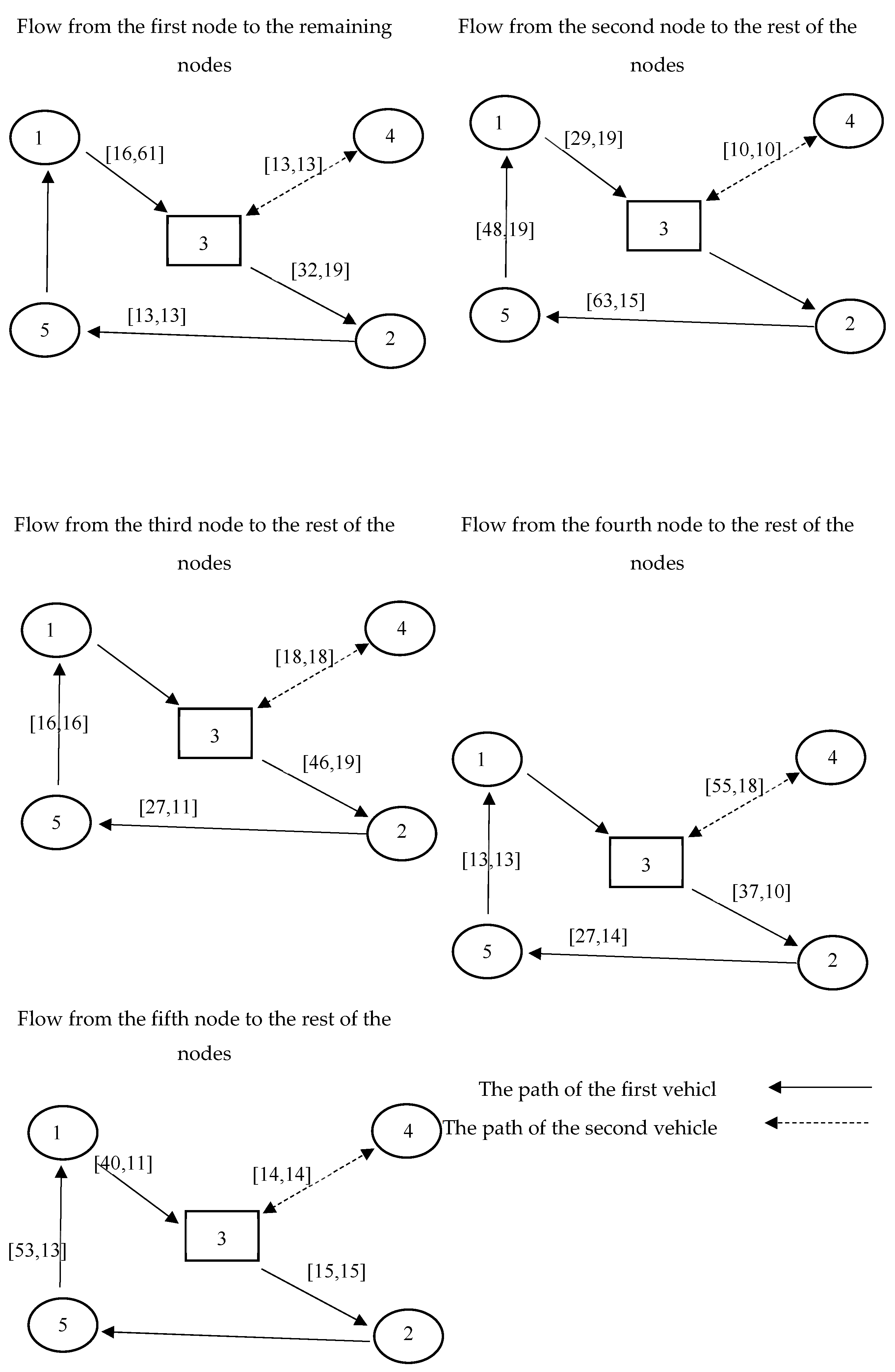
For example, the interpretation of Table (4) for node number 1 is that the amount of demand between node number 1 and other nodes is calculated by vehicles and the delivery and pick-up amount is shown in the Table as [delivery amount, pick-up amount]. For the flow of node number 1, 61 units of goods were picked up and in node number 3, 13 units of goods were delivered by the first vehicle. Then 19 units of goods were delivered to node number 2 and 13 units of goods were delivered to node number 5. On the way of the second vehicle, it can be seen that only 13 units of goods were picked up and it was also delivered to node number 4. For an easier understanding of the problem, Figure (5) is drawn.
Figure 5.
The flow of goods between nodes by different vehicles.
There are various parameters in the problem that affect the value of the objective functions. One of the most important parameters of the problem is the coefficient of economical factor (). According to the changes of this parameter in the problem, the values of the objective functions for the effective solution number 1 have been obtained in the form of Table (5).
Table 5.
Changes in the values of the objective functions in different coefficients of economical factor.
Table 5.
Changes in the values of the objective functions in different coefficients of economical factor.
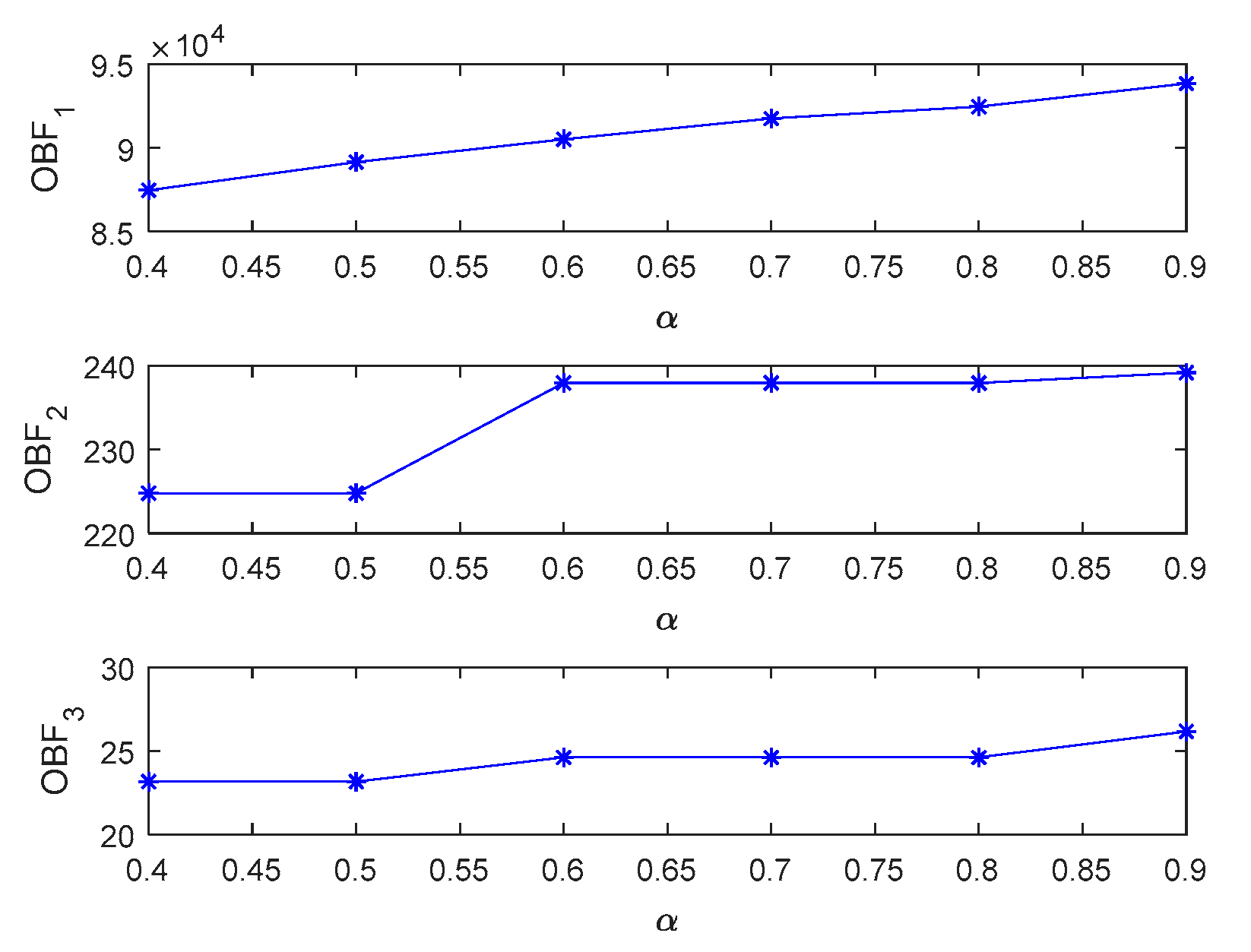
| 0.9 | 93846.2 | 239.18 | 26.17 |
| 0.8 | 92468.66 | 237.94 | 24.61 |
| 0.7 | 91761.66 | 237.94 | 24.61 |
| 0.6 | 90524.36 | 237.94 | 24.61 |
| 0.5 | 89165.67 | 224.78 | 23.17 |
| 0.4 | 87485.68 | 224.78 | 23.17 |
The results of the above table show that the cost of the total network has decreased with the increase and decrease coefficient of economical factor. The more the reduction of the economical factor increases, due to the change in routing, the maximum travel time and also the amount of gas emissions will be relatively reduced. Figure (5) shows the changes in the values of the objective functions in different coefficients of economy of scale.
Figure 5.
Changes in the values of the objective functions in different coefficients of economical factor.
Figure 5.
Changes in the values of the objective functions in different coefficients of economical factor.
After examining the mathematical model in small scale, numerical examples in large scale with different solution methods have been analyzed.
5.2. Analysis of numerical examples of large scale
In this section, 16 numerical examples in large scale have been designed according to Table (6) and various methods such as LP-Metrics, MOIWO and MOALO have been used to solve the problem. The data used in the modeling are in accordance with the data in Table (1).
Table 6.
Size of sample problems in different scale.
| Sample problem | N | V | S | Sample problem | N | V | S |
| 1 | 10 | 5 | 3 | 9 | 80 | 28 | 5 |
| 2 | 15 | 8 | 3 | 10 | 100 | 32 | 6 |
| 3 | 20 | 10 | 3 | 11 | 120 | 35 | 6 |
| 4 | 25 | 12 | 4 | 12 | 140 | 40 | 6 |
| 5 | 30 | 15 | 4 | 13 | 160 | 45 | 7 |
| 6 | 40 | 18 | 4 | 14 | 180 | 50 | 7 |
| 7 | 50 | 20 | 5 | 15 | 200 | 55 | 7 |
| 8 | 60 | 23 | 5 | 16 | 220 | 60 | 8 |
After solving sample problems with different solution methods; The outputs obtained from the multi-objective model including NPF, MSI, SM and computing time indicators are shown in Table (7).
Table 7.
Indices obtained from solving numerical examples in a large scale.
| LP-Metrics | MOIWO | MOALO | ||||||||||
| numerical examples | ||||||||||||
| 1 | 8 | 3687.02 | 0.725 | 526.48 | 16 | 4996.41 | 0.4 | 135.93 | 20 | 3751.62 | 0.781 | 143.61 |
| 2 | 12 | 3084.16 | 0.598 | 1266.48 | 30 | 3733.86 | 0.59 | 199.34 | 29 | 6157.36 | 0.766 | 217.83 |
| 3 | 13 | 5587.8 | 0.56 | 2974.64 | 28 | 4691.99 | 0.314 | 275.18 | 11 | 3220.97 | 0.376 | 299.36 |
| 4 | - | - | - | - | 11 | 3193.2 | 0.533 | 360.84 | 17 | 5678.24 | 0.617 | 392.17 |
| 5 | - | - | - | - | 16 | 6205.2 | 0.593 | 470.55 | 33 | 5523.75 | 0.535 | 509.52 |
| 6 | - | - | - | - | 33 | 3516.3 | 0.358 | 597.05 | 15 | 4017.45 | 0.324 | 643.07 |
| 7 | - | - | - | - | 19 | 3972.64 | 0.335 | 712.15 | 16 | 5462.81 | 0.473 | 768.19 |
| 8 | - | - | - | - | 17 | 6034.05 | 0.438 | 859.66 | 17 | 6380.34 | 0.73 | 923.63 |
| 9 | - | - | - | - | 28 | 5292.4 | 0.716 | 1037.55 | 31 | 3092.83 | 0.728 | 1108.88 |
| 10 | - | - | - | - | 31 | 6332.98 | 0.341 | 1257.48 | 31 | 3019.36 | 0.644 | 1330.42 |
| 11 | - | - | - | - | 27 | 3656.88 | 0.785 | 1499.75 | 26 | 5633.4 | 0.318 | 1581.77 |
| 12 | - | - | - | - | 30 | 5239.53 | 0.65 | 1796.3 | 19 | 5252.94 | 0.439 | 1878.48 |
| 13 | - | - | - | - | 29 | 3678.97 | 0.519 | 2089.54 | 32 | 5089.2 | 0.361 | 2201.75 |
| 14 | - | - | - | - | 10 | 3673.31 | 0.533 | 2493.1 | 32 | 5503.57 | 0.584 | 2604.12 |
| 15 | - | - | - | - | 12 | 5450.35 | 0.783 | 2967.18 | 18 | 4806.01 | 0.643 | 3103.62 |
| 16 | - | - | - | - | 29 | 5450.74 | 0.315 | 3715.48 | 26 | 3390.67 | 0.55 | 3899.14 |
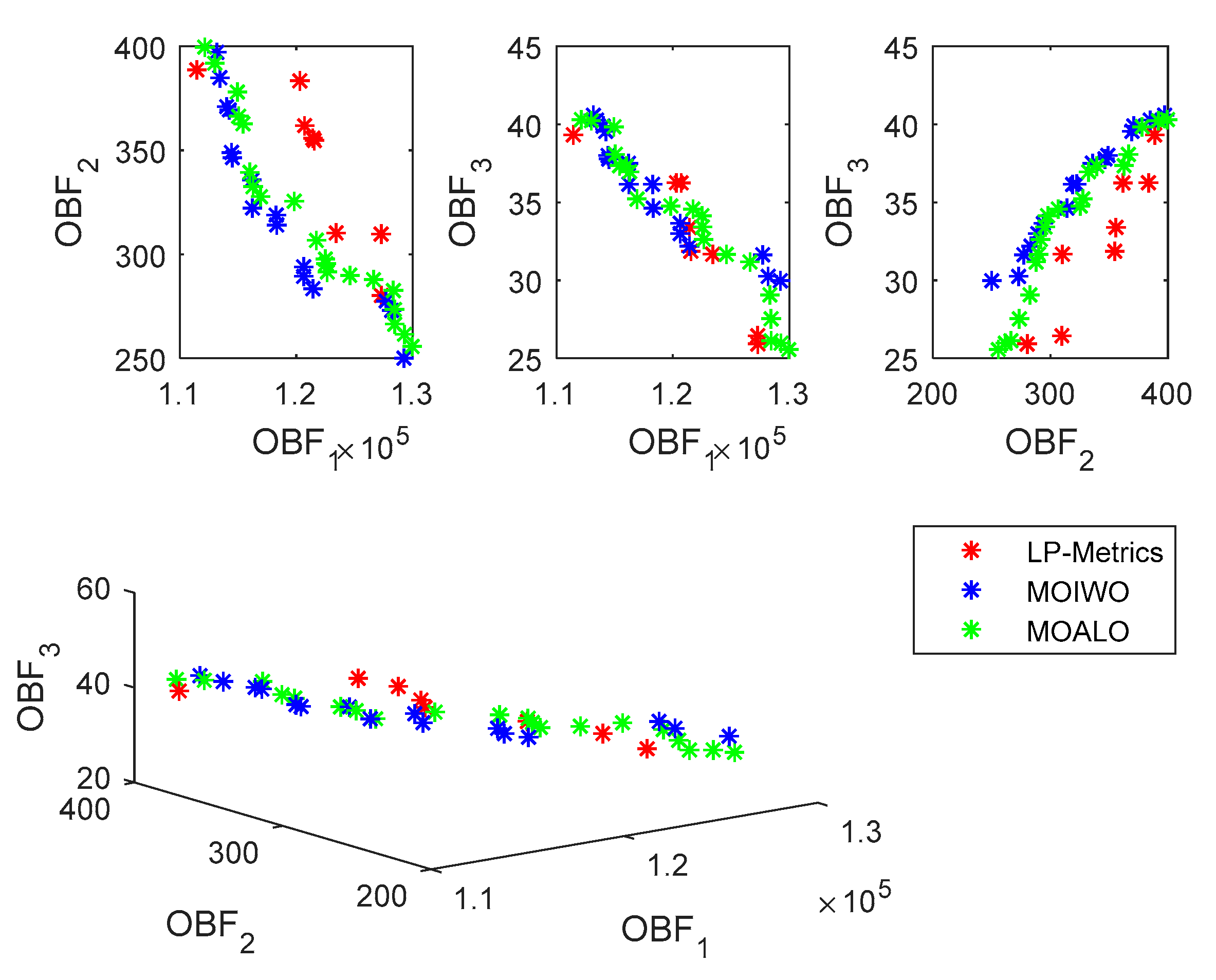
Based on the results of Table (7), it can be seen that the LP-Metrics method was only able to solve sample problems number 1 to 3. This method has the highest problem solving time among different solution methods. While meta-heuristic algorithms with results close to the LP-Metrics method have solved all the numerical examples. In these analyses, the maximum percentage of relative difference between the results of meta-heuristic algorithms and the LP-Metrics method was less than 2.83%. Also, on average, MOALO has the highest NPF and the lowest SM and CPU-time. While MOIWO has won the most MSI.
Figure (6) shows the Pareto front obtained from different solution methods for the first numerical example of large scale.
Figure 6.
Pareto front comparison between different solution methods in the first sample problem.
Based on the fact that different solution methods, including meta-heuristic algorithms, have obtained different values of comparison indices, the significant difference of these indices between the two solution methods has been investigated at the 95% confidence level. The analyzes carried out are shown in Table (8).
Table 8.
The results of the T-test at the 95% confidence level.
| Indicator | mean difference | 95% confidence interval | T-Value | P-Value |
| NPF | 0.44 | (-5.12 5.99) | 0.17 | 0.869 |
| MSI | 54 | (-904 1012) | 0.12 | 0.906 |
| SM | 0.0416 | (-0.0755 0.01588) | 0.76 | 0.461 |
| CPU-time | 71.2 | (46.2 96.1) | 6.07 | 0.000 |
The results of table (8) show that there is a significant difference only among the indicators of computing time. Therefore, due to the short solution time of the MOALO, this algorithm is selected as an efficient algorithm. Figure (7) also shows the boxplot comparing the averages of indicators at the 95% confidence level.
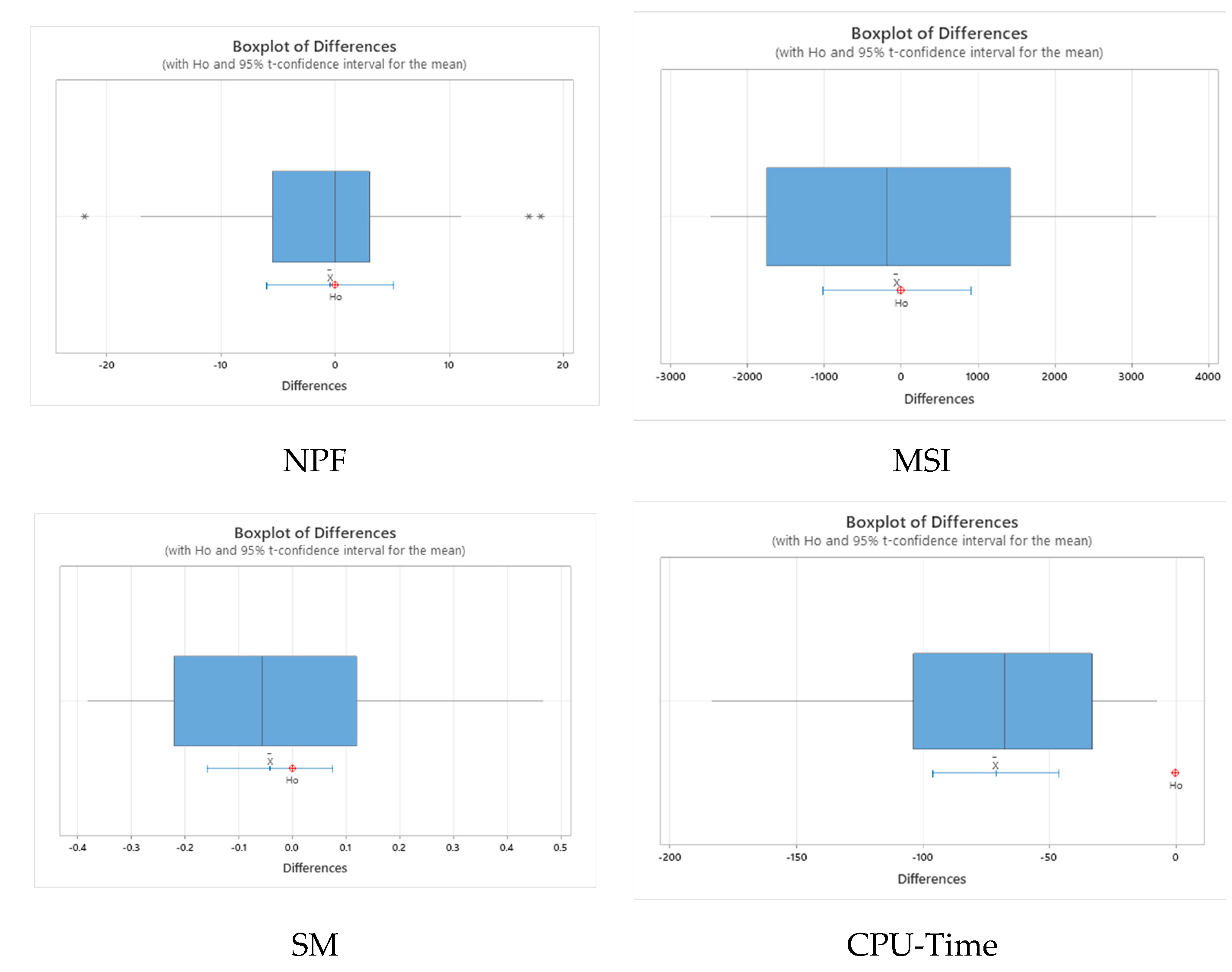
Figure 7.
Boxplot comparing the average indicators at the 95% confidence level.

6. Conclusion
In this paper, the modeling and solving of a new problem of covering hub location-routing with simultaneous delivery and pick-up under uncertainty was discussed. The non-determinism of the problem data led to the use of the TSSP method to control the uncertainty parameters. The designed model took different strategic decisions such as hub location and tactical decisions such as vehicle routing at the same time. Examining the results of solving the model with the LP-Metrics method showed that the costs related to the network have increased with the reduction of gas emissions and the maximum time of vehicle traffic. Also, by examining the economical factor, it was observed that the more this value decreases, the more vehicles tend to move through the hubs and it leads to the reduction of the total network costs. This change in the route of vehicles leads to a reduction in the amount of gas emissions, as well as a reduction in the amount of gas emissions.
MOIWO and MOALO were used to analyze numerical examples in large scale and evaluate different solution methods. Investigations of these solution methods on different numerical examples also showed that there was a conflict between the objective functions, and with the decrease of the second and third objective functions, the first objective function increased. Also, the solution time of these solution methods has been much less compared to the LP-Metrics method. The LP-Metrics method has not been able to solve numerical examples of very large scale. Based on the results, it was observed that the LP-Metrics method was only able to solve sample problems number 1 to 3. While meta-heuristic algorithms with results close to the LP-Metrics method have solved all the numerical examples. In these analyses, the maximum percentage of relative difference between the results of meta-heuristic algorithms and the LP-Metrics method was less than 2.83%. Also, on average, MOALO has the highest NPF and the lowest SM and CPU-time. While MOIWO has won the most MSI. On the other hand, by examining the significant relationship between the averages of the indicators, it was also observed that there is a significant difference between the averages of the computing time.
The results obtained from this model help the managers in the design of the fleet network to manage the costs of the total network, the delivery time of the goods and reduce the harmful environmental effects. Also, on the other hand, the existence of the two-stage stochastic programming method also helps managers in analyzing different scenarios and their impact on strategic and tactical decisions. Due to the high efficiency of the solution methods proposed in this paper, managers can use MOIWO and MOALO to achieve the desired results in case studies with larger sizes. The limitations in this research, such as not considering the queuing system in the distribution and collection of products, can be suggested as one of the future researches. Also, the use of uncertainty control methods such as fuzzy robust can also increase the richness of the mathematical model.
Funding
The authors received no financial support for the research, authorship and/or publication of this paper.
Conflicting Interests
The authors declared no potential conflicts of interest with respect to the research, authorship and/or publication of this paper.
Ethical approval
This paper does not contain any studies with human participants performed by any of the authors.
References
- Alumur, S. A., Campbell, J. F., Contreras, I., Kara, B. Y., Marianov, V., & O’Kelly, M. E. (2021). Perspectives on modeling hub location problems. European Journal of Operational Research, 291(1), 1-17. [CrossRef]
- Davari, S., Zarandi, M. F., & Turksen, I. B. (2013). The incomplete hub-covering location problem considering imprecise location of demands. Scientia Iranica, 20(3), 983-991.
- Eghbali, M., Abedzadeh, M., & Setak, M. (2014). Multi-objective reliable hub covering location considering customer convenience using NSGA-II. International Journal of System Assurance Engineering and Management, 5, 450-460. [CrossRef]
- Fallah-Tafti, M., Honarvar, M., Tavakkoli-Moghaddam, R., & Sadegheih, A. (2022). Mathematical modeling of a bi-objective hub location-routing problem for rapid transit networks. RAIRO-Operations Research, 56(5), 3733-3763. [CrossRef]
- Ghaffarinasab, N., & Kara, B. Y. (2022). A conditional β-mean approach to risk-averse stochastic multiple allocation hub location problems. Transportation Research Part E: Logistics and Transportation Review, 158, 102602.
- Ghaffarinasab, N., Kara, B. Y., & Campbell, J. F. (2022). The stratified p-hub center and p-hub maximal covering problems. Transportation Research Part B: Methodological, 157, 120-148.
- Ghahremani-Nahr, J., Kian, R., Sabet, E., & Akbari, V. (2022). A bi-objective blood supply chain model under uncertain donation, demand, capacity and cost: a robust possibilistic-necessity approach. Operational Research, 22(5), 4685-4723. [CrossRef]
- Ghiasi, M. S., & Vahdani, B. (2021). A Meta-Heuristic Approach for Hub Location-Routing Problem with Capacity and Balancing Decisions. Journal of Industrial Management Perspective, 11(3, Autumn 2021), 69-106. [CrossRef]
- Hajipour, V., Fattahi, P., Bagheri, H., & Babaei Morad, S. (2022). Dynamic maximal covering location problem for fire stations under uncertainty: Soft-computing approaches. International Journal of System Assurance Engineering and Management, 13(1), 90-112. [CrossRef]
- Hasanzadeh, H., Bashiri, M., & Amiri, A. (2018). A new approach to optimize a hub covering location problem with a queue estimation component using genetic programming. Soft Computing, 22, 949-961. [CrossRef]
- Karimi, H. (2018). The capacitated hub covering location-routing problem for simultaneous pickup and delivery systems. Computers & Industrial Engineering, 116, 47-58. [CrossRef]
- Karimi, H., & Setak, M. (2018). A bi-objective incomplete hub location-routing problem with flow shipment scheduling. Applied Mathematical Modelling, 57, 406-431. [CrossRef]
- Li, C., Han, P., Zhou, M., & Gu, M. (2023). Design of multimodal hub-and-spoke transportation network for emergency relief under COVID-19 pandemic: A meta-heuristic approach. Applied Soft Computing, 133, 109925. [CrossRef]
- Li, H., & Wang, Y. (2023). Hierarchical Multimodal Hub Location Problem with Carbon Emissions. Sustainability, 15(3), 1945. [CrossRef]
- Lopes, M. C., de Andrade, C. E., de Queiroz, T. A., Resende, M. G., & Miyazawa, F. K. (2016). Heuristics for a hub location-routing problem. Networks, 68(1), 54-90. [CrossRef]
- Mokhtarzadeh, M., Tavakkoli-Moghaddam, R., Triki, C., & Rahimi, Y. (2021). A hybrid of clustering and meta-heuristic algorithms to solve a p-mobile hub location–allocation problem with the depreciation cost of hub facilities. Engineering Applications of Artificial Intelligence, 98, 104121. [CrossRef]
- Motamedi, Z., Ghodratnama, A., Pasandideh, S. H. R., & Tavakkoli-Moghaddam, R. (2023). Scheduling of transportation fleet based on the customer’s priority in a hub location problem. Scientia Iranica. [CrossRef]
- Nozari, H., Ghahremani-Nahr, J., & Szmelter-Jarosz, A. (2022). A multi-stage stochastic inventory management model for transport companies including several different transport modes. International Journal of Management Science and Engineering Management, 1-11. [CrossRef]
- Pourmohammadi, P., Tavakkoli-Moghaddam, R., Rahimi, Y., & Triki, C. (2021). Solving a hub location-routing problem with a queue system under social responsibility by a fuzzy meta-heuristic algorithm. Annals of Operations Research, 1-30. [CrossRef]
- Rahmati, R., Bashiri, M., Nikzad, E., & Siadat, A. (2022). A two-stage robust hub location problem with accelerated Benders decomposition algorithm. International Journal of Production Research, 60(17), 5235-5257. [CrossRef]
- Rahmati, R., Neghabi, H., Bashiri, M., & Salari, M. (2023). Stochastic green profit-maximizing hub location problem. Journal of the Operational Research Society, 1-23. [CrossRef]
- Rajabi, Z., & Avakh Darestani, S. (2020). Bi-objective Optimization of a Multi-product multi-period Fuzzy Possibilistic Capacitated Hub Covering Problem: NSGA-II and NRGA Solutions. Journal of Optimization in Industrial Engineering, 13(2), 73-87.
- Ratli, M., Urošević, D., El Cadi, A. A., Brimberg, J., Mladenović, N., & Todosijević, R. (2022). An efficient heuristic for a hub location routing problem. Optimization Letters, 1-20. [CrossRef]
- Szmelter-Jarosz, A., Ghahremani-Nahr, J., & Nozari, H. (2021). A neutrosophic fuzzy optimisation model for optimal sustainable closed-loop supply chain network during COVID-19. Journal of Risk and Financial Management, 14(11), 519. [CrossRef]
- Taherkhani, G., & Alumur, S. A. (2019). Profit maximizing hub location problems. Omega, 86, 1-15. [CrossRef]
- Wang, J., & Qin, Z. (2020). Chance constrained programming models for uncertain hub covering location problems. Soft Computing, 24(4), 2781-2791. [CrossRef]
- Zahedi, M., & Nahr, J. (2020). Designing a hub covering location problem under uncertainty conditions. Management science letters, 9(3), 477-500. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







