Prerpints.org logo
Preprint
Article

Black Holes in Starobinsky-Bel-Robinson Gravity and the Breakdown of Quasinormal Modes/Null Geodesics Correspondence

Altmetrics

Downloads

94

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 October 2023

Posted:

09 October 2023

You are already at the latest version

Alerts
Abstract
We show that perturbations of a scalar field in the background of the black hole obtained with the Starobinsky-Bel-Robinson Gravity is unstable unless the dimensionless coupling $\beta$ describing the compactification of M-theory is small enough. In the sector of stability quasinormal spectrum show peculiar behavior both in the frequency and time domains: the ringing consists of two stages where two different modes dominate. The WKB method does not reproduce part of the spectrum including the fundamental mode, which is responsible for the first stage of the ringing. Consequently, the correspondence between the eikonal quasinormal modes and null geodesics allows to reproduce only part of the eikonal spectrum. The frequencies are obtained with the help of three methods (Frobenius, WKB and time-domain integration) with excellent agreement among them.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

1. Introduction

Quasinormal modes (QNMs) of black holes are proper oscillation frequencies which depend on the parameters of the black hole and not on the way of perturbations [1,2,3,4]. The data from gravitational waves together with observations in the electromagnetic spectra [5,6,7] in principle should allow in the future to determine the black hole’s mass, angular momentum, and charge and thereby to test gravitational theory in the strong field limit. Nevertheless, by now the uncertainty in the mass and angular momentum of a black is large, what allows for big room for alternative theories of gravity [8,9].
Among various alternative/modified theories of gravity the Starobinsky inflation model plays an important role. It uses the idea that the early universe went through an inflationary de Sitter era [10] and was conceived by Alexei A. Starobinsky in [11]. The model incorporates modifications to General Relativity by introducing a quadratic curvature term. This framework allows for an inflationary phase driven by a scalar field, addressing cosmological issues like the horizon and flatness problems. It generates a scale-invariant density perturbation spectrum, consistent with cosmic microwave background and large-scale structure observations, making it a significant inflationary model in modern cosmology.
Recently a new gravitational theory in four dimensions has been proposed in the form of a sum of the modified R + α R 2 Starobinsky inflation allowing for the leading Bel–Robinson-tensor-squared term. These corrections are inspired by the gravitational effective action of superstrings/M-theory compactified to four dimensions [12,13,14,15]. The Starobinsky–Bel–Robinson Lagrangian possesses only two free parameters, which makes it attractive for studying various physical phenomena which could potentially be observed and, thereby, the theory could be tested. Consequently, the corrected Schwarzschild-like spacetime was perturbatively obtained in [14], while cosmological applications were considered in [15,16,17]. Various effects around such black holes have been recently considered in [18,19]
Here we propose the first study of the quasinormal frequencies in the background of black holes in the Starobinsky–Bel–Robinson gravity. We will consider a test scalar field, which is the simplest case frequently sharing the properties of other spin fields. Apparently the most important aspect of the quasinormal spectrum is its (in)stability [20,21,22,23,24,25,26,27], because usually to prove the stability analytically is difficult, and the thorough analysis of quasinormal modes allows to judge about (in)stability. The onset of instability in the scalar sector may indicate the possible instability in the gravitational one. The neutral test scalar field in the Schwarzschild, Kerr and Kerr-Newman spacetimes are known to be stable under the quasinormal mode boundary conditions, because the corresponding quasinormal frequencies are damped [28,29,30].
Here we will consider the evolution of perturbations of the scalar field in the black hole background in the Starobinsky–Bel–Robinson gravity. We will show that the scalar field is unstable unless the higher curvature correction parameter β is small enough. We find the critical value of the parameter β at the threshold of instability and analyze the quasinormal spectrum in the stable sector.
The paper is organized as follows. In sec. II we briefly describe the black hole spacetime and wave-like equation. Sec. III summarize the methods used for the analysis of the quasinormal spectrum, while in sec. IV we present the obtained results for the instability threshold and quasinormal modes in the range of parameters corresponding to the stability. In the Conclusions we review the obtained results and mention some points for future investigation.

2. The metric

Using the compactification coupled with the presence of stringy fluxes, the appropriate 4 D gravity models may be described by the following action:
S = M p l 2 ∫ d 4 x − g R + R 2 6 m 2 − β 32 m 6 P 4 2 − E 4 2 .
Here g is the metric determinant, R is the Ricci scalar. m is a free mass parameter, β > 0 is a dimensionless coupling describing the compactification of M-theory, P 4 2 and E 4 2 are the Pontryagin and Euler topological densities which are related to the Bel-Robinson tensor T μ ν λ ρ in four dimensions as follows:
T μ ν δ ρ T μ ν δ ρ = 1 4 P 4 2 − E 4 2 .
The Bel-Robinson tensor has the following form:
T μ ν δ σ = R μ ρ γ δ R ρ γ ν σ + R μ ρ γ σ R ρ γ ν δ − 1 2 g μ ν R ρ γ α δ R ρ γ α σ .
It can be seen from Eq.(1) that the gravity action depends only on the two parameters, m and β . This allows for various applications such as Hawking radiation, entropy, inflation, optical phenomena etc. [12,13,14,15,19] The black hole solution in SBR gravity depends on the value of β corrected to first order perturbations.
The line element of the spherically symmetric metric is
d s 2 = − f ( r ) d t 2 + 1 f ( r ) d r 2 + r 2 d Ω 2 .
where the metric function has the form [14]:
f ( r ) = 1 − 2 M r + β M 6 8 2 π M r 3 3 108 r − 194 M 5 r .
Here r s = 2 M is the Schwarzschild radius and M is the mass parameter. The tidal force effects and shadows for this metric were considered in [19].
Coefficient ( 8 2 π ) 3 ≈ 44901.9 which means that β ∼ 3 · 10 − 5 (at M = 1 ) must already be considered as large deformation of the Schwarzschild spacetime. As we are interested here also in the testing of the null geodesics/eikonal quasinormal modes correspondence correspondence for generic black-hole spacetimes, we will not be limited by the regime of tiny β only and include consideration of relatively large deformations of the Schwarzschild spacetime which already cannot be described as a small correction.

3. The methods

3.1. Wave-like equation and boundary conditions

We will consider the test neutral massless scalar field Φ which obeys the general covariant Klein-Gordon equation,
1 − g ∂ μ g μ ν − g ∂ ν Φ = 0 .
After the separation of variable,
Φ = ψ ℓ ( r ) r Y ℓ m ( θ , ϕ ) e − i ω t ,
the equation for the scalar field can be reduced to the wave-like form:
d 2 ψ l d r * 2 + ω 2 − U ( x ) ψ ℓ = 0 .
The effective potential is
U ( r ) = f ( r ) ℓ ( ℓ + 1 ) r 2 + f ′ ( r ) r ,
where the tortoise coordinate x can be expressed as follows:
d r * d r = 1 f ( r ) .
The effective potential is shown on fig Figure 1. There one can see that the when β is increasing, the additional gap appears, which at sufficiently large values of β becomes negative. This is an indication that a bound state with negative energy may be formed, which means the onset of instability. Therefore, thorough analysis of quasinormal modes is necessary.
The quasinormal modes are eigenvalues of the above second order differential equation under the requirements of purely ingoing waves at the event horizon and purely outgoing waves at infinity.

3.2. Higher order WKB method

For an additional check of accurate results obtained by the Frobenius method in the range of stability we will also use the WKB method. It was applied for the first time to the problem of finding of quasinormal modes and grey-body factors of black holes by B. Schutz and C. Will [31]. The first order WKB formula was afterwords generalized to higher orders up to the 13-th order [32,33,34]. Recently it shas been further improved by using the Padé approximants [34], so that the relative error of the WKB formula with Padé approximants is usually from quite few times to a few orders smaller than without them. The WKB formula can be expressed in the following general form [35]:
ω 2 = U 0 + A 2 ( K 2 ) + A 4 ( K 2 ) + A 6 ( K 2 ) + … − i K − 2 V 2 1 + A 3 ( K 2 ) + A 5 ( K 2 ) + A 7 ( K 2 ) … ,
where for the quasinormal frequencies we have
K = n + 1 2 , n = 0 , 1 , 2 , …
Here n is the overtone number, U 0 is the value of the effective potential in its maximum, U 2 is the value of the second derivative of the potential in this point, and A 2 , A 3 , A 4 , … depend on higher derivatives of the potential in its maximum. We will use the sixth order WKB method obtained in [33] with Padé approximants m ˜ = 4 and 5, where the definition of m ˜ and further details on this method can be found in [34,35]. The higher order WKB method has been used for finding quasinormal modes and grey-body factors in numerous works, showing very good concordance with the result obtained by other methods (see, for example [36,37,38,39] and references therein).

3.3. Time-domain integration

The integration in the time domain that we employ as the main method is founded on the wavelike equation expressed using the light-cone variables u = t − r * and v = t + r * . We implement the discretization approach introduced by Gundlach-Price-Pullin [40] as follows:
Ψ N = Ψ W + Ψ E − Ψ S −
Δ 2 V S Ψ W + Ψ E 4 + O Δ 4 ,
Here, the notations for the points are the following: N ≡ u + Δ , v + Δ , W ≡ u + Δ , v , E ≡ u , v + Δ , and S ≡ u , v . We impose the initial Gaussian wave package on the null surfaces u = u 0 and v = v 0 . The quasinormal frequencies can then be extracted from the time-domain profiles reasonably accurately using the Prony method, as detailed in, for instance, [3]. Although the time-domain integration method is indeed an accurate and convergent technique for generating time-domain profiles, the extraction of frequencies with high precision can be challenging. Generally, achieving a convergence with the exact results from the Leaver method, with a discrepancy of less than one percent, is attainable for the first and higher multipoles [41,42]. The challenging point of the method is the construction of the effective potential as a function of the tortoise coordinate r * which can be done in the following way. One can numerically integrate the equation d r * = d r / f ( r ) and find r * ( r ) then using its connection with the coordinates u , v to built U ( r * ) . An important feature of the time-domain integration which we will use here is that it includes contributions of all overtones and, is, thereby, efficient for detecting the instability.

3.4. Frobenius method

The Frobenius or Leaver method is based on the convergent procedure and is therefore allows us to find quasinormal frequencies with great accuracy [43,44]. As it is also broadly discussed in the literature, here we will only briefly mention the key points of the method. The differential master wave-like equation has a regular singular point at the event horizon r = r g and the irregular singular point at r = ∞ . Using the new function of the radial coordinate P ( r ) ,
Ψ ( r ) = P ( r , ω ) 1 − r g r − i ω / F ′ ( r g ) y ( r ) ,
we then choose the factor P such that it provides regularity if y ( r ) in the range r 0 ≤ r < ∞ , for the outgoing wave at infinity and ingoing wave at the horizon. Therefore, we can write down the Frobenius series in the following way:
y ( r ) = ∑ k = 0 ∞ a k 1 − r g r k .
Then, the Guassian eliminations reduce the problem to an algebraic equation. In addition, for further increasing of the convergence we will use the Nollert improvement [45], which was generalized to an arbitrary number of terms recurrence relations by A. Zhidenko in [46]. The Frobenius method, however, requires an initial guess for the value of quasinormal frequency, when finding the roots of the corresponding algebraic equations and if the corresponding zeros are highly localized in the parametric space, it might be difficult to find such an initial guess for every mode, so that there is a risk of missing some modes. Therefore the WKB and time-domain integration methods are useful for getting such an initial guess.

4. The threshold of instability

From the form of the effective potentials it is evident that once β is increased, the negative gap outside the black hole becomes deeper (Figure 1), so that one should check whether the scalar field is stable. Time-domain integration at various values of β and ℓ = 0 shows that, indeed, the instability occurs at some critical value:
β c r ≈ 0.1364 .
Although usually perturbations at higher multipole numbers are more stable, because the effective potential get higher, there are examples of instability developing at high ℓ as well [25,47], so that higher multipoles must be investigated for possible (in)stability as well. The modes with ℓ = 1 , 2 and higher multipoles (see, for example, table II) are stable at least for those values of β for which the stability of the ℓ = 0 perturbations is guaranteed. The unstable mode has non-oscillatory exponential form as can be seen from Figure 2. This non-oscillatory character of the unstable mode was rigorously proved in [48] for spherically symmetric black holes.
Because of the large numerical pre-factor, the threshold of instability corresponds to a very large deformation of the Schwarzschild spacetime, so that, obviously, the regime of small β -corrections is safe as to the possible development of instability.

5. Quasinormal frequencies in the stable sector

Table 1. Quasinormal modes obtained by the time-domain integration and subsequent extraction of frequencies with the Prony method for various values of β , ℓ = 0 , M = 1 . The higher order WKB data with Padé approximants are evidently diverge from the correct time-domain integration results when β grows.
Table 1. Quasinormal modes obtained by the time-domain integration and subsequent extraction of frequencies with the Prony method for various values of β , ℓ = 0 , M = 1 . The higher order WKB data with Padé approximants are evidently diverge from the correct time-domain integration results when β grows.
β Time-domain WKB
10 − 6 0.110022 - 0.105870 i 0.109460 - 0.103417 i
5 · 10 − 6 0.110119- 0.105857 i 0.109426 - 0.103701 i
10 − 5 0.110244 - 0.105843 i 0.109436 - 0.103135 i
3 · 10 − 5 0.110766 - 0.105798 i 0.083291 - 0.094837 i
5 · 10 − 5 0.111322 - 0.105778 i 0.091824 - 0.129149 i
7 · 10 − 5 0.111892 - 0.105784 i 0.086486 - 0.138424 i
10 − 4 0.112733 - 0.105896 i 0.032663 - 0.143389 i
10 − 3 0.121337 - 0.115261 i –
Table 2. Quasinormal modes obtained by the time-domain integration and subsequent extraction of frequencies with the Prony method for various values of β , ℓ = 1 , M = 1 . The higher order WKB data with Padé approximants are evidently diverge from the correct time-domain integration results when β grows.
Table 2. Quasinormal modes obtained by the time-domain integration and subsequent extraction of frequencies with the Prony method for various values of β , ℓ = 1 , M = 1 . The higher order WKB data with Padé approximants are evidently diverge from the correct time-domain integration results when β grows.
β Time-domain WKB
10 − 6 0.293003 - 0.097665 i 0.292990 - 0.097690 i
5 · 10 − 6 0.293090 - 0.097568 i 0.293246 - 0.097705 i
10 − 5 0.293202- 0.097447 i 0.293569 - 0.097658 i
2 · 10 − 5 0.293430- 0.097203 i 0.294184 - 0.097428 i
3 · 10 − 5 0.293667- 0.096956 i 0.294743 - 0.097104 i
4 · 10 − 5 0.293912 - 0.096706 i 0.295266 - 0.096741 i
5 · 10 − 5 0.294166 - 0.096453 i 0.295776 - 0.096360 i
10 − 4 0.295543 - 0.095136 i 0.299002 - 0.094337 i
3 · 10 − 4 0.304555 - 0.091160 i 0.279144 - 0.059728 i
5 · 10 − 4 0.315643 - 0.093030 i 0.278248 - 0.138408 i
7 · 10 − 4 0.323746 - 0.099017 i 0.006171 - 0.042030 i
10 − 3 0.330159 - 0.109229 i 0.082300 - 0.106786 i
When the multipole number ℓ is large, one can find quasinormal frequencies in the analytic form. It is convenient to use κ = ℓ + 1 / 2 instead of ℓ. We find the location of the peak of the effective potential expanded in powers of κ and, afterwards, to use the higher order WKB technique as prescribed in [49] in order to obtain an analytic expression for the quasinormal modes in the eikonal approximation and at the first order beyond it in the regime of small β and 1 / ℓ :
r m a x = 3 M − M 3 κ 2 + β 2502656 2 π 3 295245 M 5 κ 2 − 210944 2 π 3 32805 M 5 + O 1 κ 4 , β 2
Finally, applying the above expansion for r m a x and using higher order WKB formula we obtain
ω = κ 3 3 M − i K 3 3 M + 29 − 60 K 2 1296 3 M κ + 13312 2 3 π 3 κ 59049 M 7 + 115712 i 2 3 π 3 K 59049 M 7 + 64 2 3 π 3 91860 K 2 − 11783 7971615 M 7 κ β + O 1 κ 2 , β 2 .
Neglecting orders ∼ 1 / κ in the above equation, we obtain the eikonal formula which is exact in the regime ℓ → ∞ . The eikonal formula is interesting, because, as was stated in [50], parameters connected to unstable circular null geodesics around a spherically symmetric, and asymptotically flat or de Sitter black hole are dual to the quasinormal modes in the ℓ ≫ n limit. Thus, real and imaginary parts of the ℓ ≫ n quasinormal mode are proportional to the frequency and instability timescale of the circular null geodesics, respectively:
ω n = Ω ℓ − i ( n + 1 / 2 ) | λ | , ℓ ≫ n .
Here Ω is the angular velocity at the unstable null geodesics, and λ is the Lyapunov exponent.
An intricate aspect of this correspondence lies in its applicability, which extends to the Schwarzschild black hole and several other scenarios. However, in [51], it was demonstrated that this correspondence falters when the wave-like equation’s dominant eikonal centrifugal term deviates from f ( r ) ℓ ( ℓ + 1 ) / r 2 . This divergence occurs, for instance, in the context of gravitational perturbations within the Einstein-Gauss-Bonnet [51,52] or Einstein-dilaton-Gauss-Bonnet theories [53]. Broadly speaking, the aforementioned correspondence holds true when the first-order WKB formula [31] is applicable, signifying the presence of an effective potential with a singular maximum and two turning points.
Furthermore, even within these scenarios, the WKB formula might prove inadequate in reproducing the complete spectrum of the eikonal regime. This limitation becomes evident in the Schwarzschild-de Sitter spacetime, where two categories of modes emerge: Schwarzschild modes that are influenced by the Λ -term [54,55], and de Sitter modes that are modified by the presence of a black hole [56,57]. Consequently, as elucidated in [58], although the correspondence suggested by equation (19) holds formally, the parameter n no longer accurately represents the overtone number.
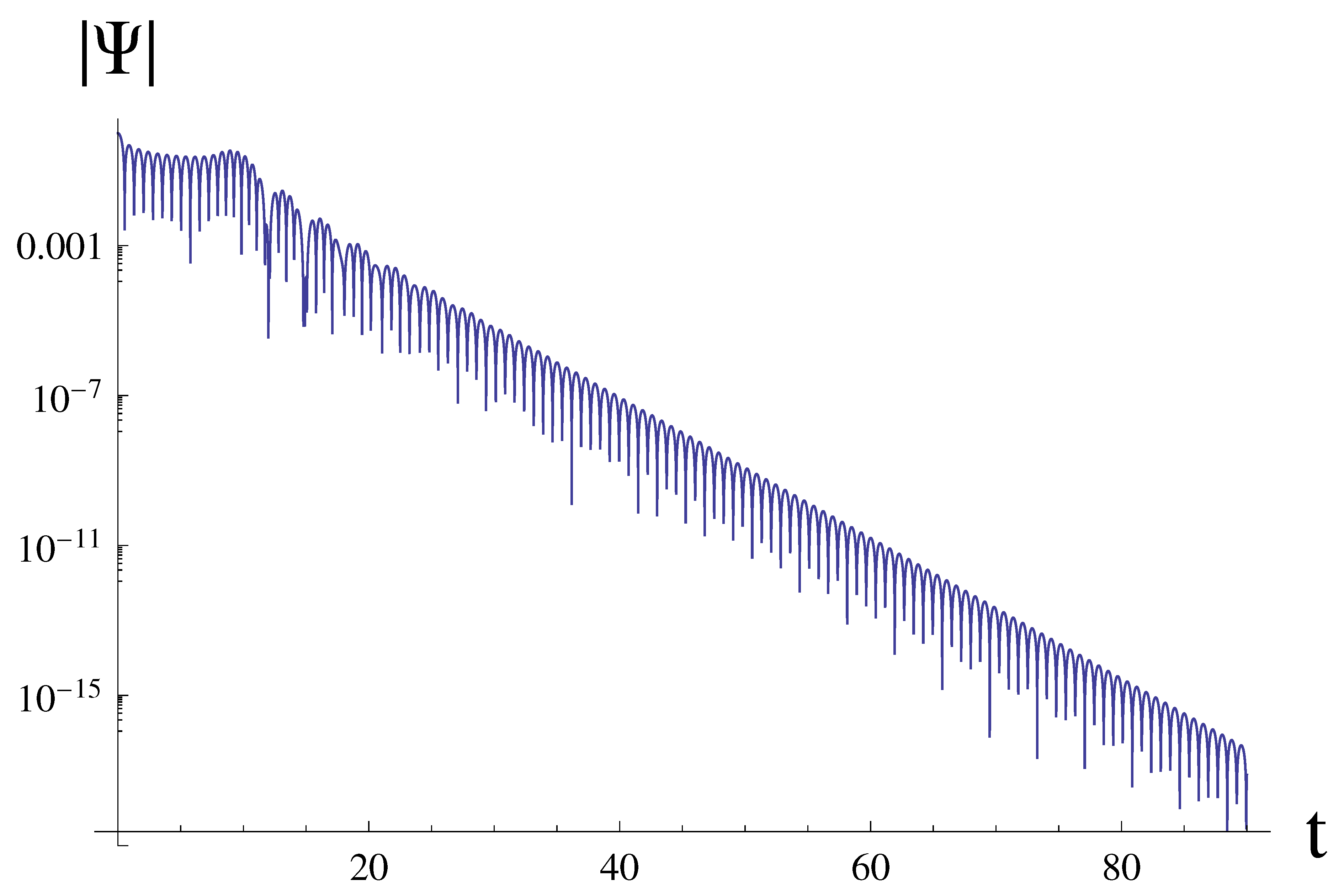
Here we observe, in a sense, similar situation: as can be seen from Figure 3, there are two stages of the ringing on which two different modes dominate. The mode at the first stage is slower decaying and, formally, is the fundamental one, while the first overtone dominates at the second longer stage. However, the fundamental mode which is reproduced with the time-domain integration and Frobenius method with very good concordance between them, cannot be found by the WKB method which gives only the first overtone. Thus, while the correspondence works for the part of the eikonal spectrum, it does not allow one to reproduce the whole spectrum in the eikonal regime. It is essential that the effective potential at such small values of β appears as a WKB-good single peak barrier. It is worth mentioning that consequently the break-down of the null geodesics/eikonal quasinormal modes correspondence for our case must also violate the correspondence between the quasinormal modes and radius of the shadow considered in [59,60].
Lower modes are shown in tables I and II, where we can see that the WKB approach cannot be trusted unless the parameter β is tiny. At the same time, the time-domain integration always provides relatively good accuracy for the fundamental mode with relative error less than one percent at least for ℓ = 1 when there are sufficient number of oscillations in the profile. Nevertheless, it is difficult to achieve great accuracy with the time-domain integration, because of arbitrariness of the fitting of the profile with a sum of exponents within the Prony method.

6. Conclusions

This work is the first analysis of quasinormal modes of the black hole in the Starobinsky-Bel Robinson gravity suggested recently in [14]. It proved out that the black hole possesses a rich quasinormal spectrum with the following features:
  • At unphysically large values of the parameter of compactification β it produces instability, while the regime of small β is free from instability
  • In the eikonal limit ℓ → ∞ the correspondence breaks down, because it reproduces only part of the eikonal spectrum, but, unlike [58], this breakdown is for an asymptotically flat space.
  • The ringing consists of the two stages at each of which different modes dominate. This could be well seen in the regime of large ℓ.
Our work could be extended to fields of other spin and considerations of higher overtones, which could be done with the help of the Frobenius method.

Acknowledgments

The author would like to acknowledge R. A. Konoplya for careful reading of the manuscript and most useful discussions. This work was supported by RUDN University research project FSSF-2023-0003.

References

  1. Kokkotas, K.D.; Schmidt, B.G. Quasinormal modes of stars and black holes. Living Rev. Rel. 1999, 2, 2. [Google Scholar] [CrossRef]
  2. Nollert, H.P. TOPICAL REVIEW: Quasinormal modes: the characteristic `sound’ of black holes and neutron stars. Class. Quant. Grav. 1999, 16, R159–R216. [Google Scholar] [CrossRef]
  3. Konoplya, R.A.; Zhidenko, A. Quasinormal modes of black holes: From astrophysics to string theory. Rev. Mod. Phys. 2011, arXiv:gr-qc/1102.4014]83, 793–836. [Google Scholar] [CrossRef]
  4. Berti, E.; Cardoso, V.; Starinets, A.O. Quasinormal modes of black holes and black branes. Class. Quant. Grav. 2009, arXiv:gr-qc/0905.2975]26, 163001. [Google Scholar] [CrossRef]
  5. Barack, L.; others. Black holes, gravitational waves and fundamental physics: a roadmap. Class. Quant. Grav. 2019, arXiv:gr-qc/1806.05195]36, 143001. [Google Scholar] [CrossRef]
  6. Akiyama, K.; others. First Sagittarius A* Event Horizon Telescope Results. VI. Testing the Black Hole Metric. Astrophys. J. Lett. 2022, 930, L17. [Google Scholar] [CrossRef]
  7. Goddi, C.; others. BlackHoleCam: Fundamental physics of the galactic center. Int. J. Mod. Phys. D 2016, arXiv:astro-ph.HE/1606.08879]26, 1730001. [Google Scholar] [CrossRef]
  8. Konoplya, R.; Zhidenko, A. Detection of gravitational waves from black holes: Is there a window for alternative theories? Phys. Lett. B 2016, arXiv:gr-qc/1602.04738]756, 350–353. [Google Scholar] [CrossRef]
  9. Yunes, N.; Yagi, K.; Pretorius, F. Theoretical Physics Implications of the Binary Black-Hole Mergers GW150914 and GW151226. Phys. Rev. D 2016, arXiv:gr-qc/1603.08955]94, 084002. [Google Scholar] [CrossRef]
  10. Starobinsky, A.A. Spectrum of relict gravitational radiation and the early state of the universe. JETP Lett. 1979, 30, 682–685. [Google Scholar]
  11. Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
  12. Ivanov, V.R.; Ketov, S.V.; Pozdeeva, E.O.; Vernov, S.Y. Analytic extensions of Starobinsky model of inflation. JCAP 2022, arXiv:gr-qc/2111.09058]03, 058. [Google Scholar] [CrossRef]
  13. Ketov, S.V. Starobinsky–Bel–Robinson Gravity. Universe 2022, arXiv:gr-qc/2205.13172]8, 351. [Google Scholar] [CrossRef]
  14. Campos Delgado, R.; Ketov, S.V. Schwarzschild-type black holes in Starobinsky-Bel-Robinson gravity. Phys. Lett. B 2023, arXiv:gr-qc/2209.01574]838, 137690. [Google Scholar] [CrossRef]
  15. Ketov, S.V.; Pozdeeva, E.O.; Vernov, S.Y. On the superstring-inspired quantum correction to the Starobinsky model of inflation. JCAP 2022, arXiv:gr-qc/2211.01546]12, 032. [Google Scholar] [CrossRef]
  16. Do, T.Q.; Nguyen, D.H.; Pham, T.M. Stability investigations of isotropic and anisotropic exponential inflation in the Starobinsky-Bel-Robinson gravity 2023. arXiv:gr-qc/2303.17283.
  17. Pozdeeva, E.; Ketov, S.; Vernov, S. String-Inspired Correction to R2 Inflation. Phys. Sci. Forum 2023, 7, 2. [Google Scholar] [CrossRef]
  18. Belhaj, A.; Belmahi, H.; Benali, M.; Hassouni, Y.; Sedra, M.B. Deflection angle and Shadows by Black Holes in Starobinsky-Bel-Robinson Gravity from M-theory 2023. arXiv:hep-th/2304.03883.
  19. Arora, D.; Molla, N.U.; Chaudhary, H.; Debnath, U.; Atamurotov, F.; Mustafa, G. Exploring Tidal Force Effects and Shadow Constraints for Schwarzschild-like Black Hole in Starobinsky-Bel-Robinson Gravity 2023. arXiv:gr-qc/2308.13901.
  20. Whiting, B.F. Mode Stability of the Kerr Black Hole. J. Math. Phys. 1989, 30, 1301. [Google Scholar] [CrossRef]
  21. Dias, O.J.C.; Santos, J.E. Origin of the Reissner-Nordström–de Sitter instability. Phys. Rev. D 2020, arXiv:hep-th/2005.03673]102, 124039. [Google Scholar] [CrossRef]
  22. Ishihara, H.; Kimura, M.; Konoplya, R.A.; Murata, K.; Soda, J.; Zhidenko, A. Evolution of perturbations of squashed Kaluza-Klein black holes: escape from instability. Phys. Rev. D 2008, arXiv:hep-th/0802.0655]77, 084019. [Google Scholar] [CrossRef]
  23. Kodama, H.; Konoplya, R.A.; Zhidenko, A. Gravitational stability of simply rotating Myers-Perry black holes: Tensorial perturbations. Phys. Rev. D 2010, arXiv:gr-qc/0904.2154]81, 044007. [Google Scholar] [CrossRef]
  24. Cardoso, V.; Lemos, M.; Marques, M. On the instability of Reissner-Nordstrom black holes in de Sitter backgrounds. Phys. Rev. D 2009, arXiv:gr-qc/1001.0019]80, 127502. [Google Scholar] [CrossRef]
  25. Takahashi, T.; Soda, J. Catastrophic Instability of Small Lovelock Black Holes. Prog. Theor. Phys. 2010, arXiv:gr-qc/1008.1618]124, 711–729. [Google Scholar] [CrossRef]
  26. Cuyubamba, M.A.; Konoplya, R.A.; Zhidenko, A. Quasinormal modes and a new instability of Einstein-Gauss-Bonnet black holes in the de Sitter world. Phys. Rev. D 2016, arXiv:gr-qc/1604.03604]93, 104053. [Google Scholar] [CrossRef]
  27. Zhu, Z.; Zhang, S.J.; Pellicer, C.E.; Wang, B.; Abdalla, E. Stability of Reissner-Nordström black hole in de Sitter background under charged scalar perturbation. Phys. Rev. D 2014, arXiv:hep-th/1405.4931]. [Addendum: Phys.Rev90, 044042. [Google Scholar] [CrossRef]
  28. Ohashi, A.; Sakagami, M.a. Massive quasi-normal mode. Class. Quant. Grav. 2004, 21, 3973–3984. [Google Scholar] [CrossRef]
  29. Konoplya, R.A.; Zhidenko, A. Stability and quasinormal modes of the massive scalar field around Kerr black holes. Phys. Rev. D 2006, 73, 124040. [Google Scholar] [CrossRef]
  30. Konoplya, R.A.; Zhidenko, A. Massive charged scalar field in the Kerr-Newman background I: quasinormal modes, late-time tails and stability. Phys. Rev. D 2013, arXiv:gr-qc/1307.1812]88, 024054. [Google Scholar] [CrossRef]
  31. Schutz, B.F.; Will, C.M. Black Hole Normal Modes: A semianalytic approach. Astrophys. J. Lett. 1985, 291, L33–L36. [Google Scholar] [CrossRef]
  32. Iyer, S.; Will, C.M. Black Hole Normal Modes: A WKB Approach. 1. Foundations and Application of a Higher Order WKB Analysis of Potential Barrier Scattering. Phys. Rev. D 1987, 35, 3621. [Google Scholar] [CrossRef] [PubMed]
  33. Konoplya, R.A. Quasinormal behavior of the d-dimensional Schwarzschild black hole and higher order WKB approach. Phys. Rev. D 2003, 68, 024018. [Google Scholar] [CrossRef]
  34. Matyjasek, J.; Opala, M. Quasinormal modes of black holes. The improved semianalytic approach. Phys. Rev. D 2017, arXiv:gr-qc/1704.00361]96, 024011. [Google Scholar] [CrossRef]
  35. Konoplya, R.A.; Zhidenko, A.; Zinhailo, A.F. Higher order WKB formula for quasinormal modes and grey-body factors: recipes for quick and accurate calculations. Class. Quant. Grav. 2019, arXiv:gr-qc/1904.10333]36, 155002. [Google Scholar] [CrossRef]
  36. Matyjasek, J. Accurate quasinormal modes of the five-dimensional Schwarzschild-Tangherlini black holes. Phys. Rev. D 2021, arXiv:gr-qc/2107.04815]104, 084066. [Google Scholar] [CrossRef]
  37. Guo, G.; Wang, P.; Wu, H.; Yang, H. Superradiance instabilities of charged black holes in Einstein-Maxwell-scalar theory. JHEP 2023, arXiv:gr-qc/2301.06483]07, 070. [Google Scholar] [CrossRef]
  38. Matyjasek, J. Quasinormal modes of dirty black holes in the effective theory of gravity with a third order curvature term. Phys. Rev. D 2020, arXiv:gr-qc/2009.10793]102, 124046. [Google Scholar] [CrossRef]
  39. Konoplya, R.A. Quantum corrected black holes: quasinormal modes, scattering, shadows. Phys. Lett. B 2020, arXiv:gr-qc/1912.10582]804, 135363. [Google Scholar] [CrossRef]
  40. Gundlach, C.; Price, R.H.; Pullin, J. Late time behavior of stellar collapse and explosions: 1. Linearized perturbations. Phys. Rev. D 1994, 49, 883–889. [Google Scholar] [CrossRef]
  41. Bronnikov, K.A.; Konoplya, R.A. Echoes in brane worlds: ringing at a black hole–wormhole transition. Phys. Rev. D 2020, arXiv:gr-qc/1912.05315]101, 064004. [Google Scholar] [CrossRef]
  42. Konoplya, R.A.; Zinhailo, A.F.; Stuchlik, Z. Quasinormal modes and Hawking radiation of black holes in cubic gravity. Phys. Rev. D 2020, arXiv:gr-qc/2006.10462]102, 044023. [Google Scholar] [CrossRef]
  43. Leaver, E.W. An Analytic representation for the quasi normal modes of Kerr black holes. Proc. Roy. Soc. Lond. A 1985, 402, 285–298. [Google Scholar] [CrossRef]
  44. Leaver, E.W. Spectral decomposition of the perturbation response of the Schwarzschild geometry. Phys. Rev. D 1986, 34, 384–408. [Google Scholar] [CrossRef] [PubMed]
  45. Nollert, H.P. Quasinormal modes of Schwarzschild black holes: The determination of quasinormal frequencies with very large imaginary parts. Phys. Rev. D 1993, 47, 5253–5258. [Google Scholar] [CrossRef]
  46. Zhidenko, A. Massive scalar field quasi-normal modes of higher dimensional black holes. Phys. Rev. D 2006, 74, 064017. [Google Scholar] [CrossRef]
  47. Konoplya, R.A.; Zhidenko, A. The portrait of eikonal instability in Lovelock theories. JCAP 2017, arXiv:hep-th/1705.01656]05, 050. [Google Scholar] [CrossRef]
  48. Konoplya, R.A.; Murata, K.; Soda, J.; Zhidenko, A. Looking at the Gregory-Laflamme instability through quasi-normal modes. Phys. Rev. D 2008, arXiv:hep-th/0807.1897]78, 084012. [Google Scholar] [CrossRef]
  49. Konoplya, R.A.; Zhidenko, A. Analytic expressions for quasinormal modes and grey-body factors in the eikonal limit and beyond, arXiv: 2309.02560. 2023, arXiv:gr-qc/2309.02560. [Google Scholar]
  50. Cardoso, V.; Miranda, A.S.; Berti, E.; Witek, H.; Zanchin, V.T. Geodesic stability, Lyapunov exponents and quasinormal modes. Phys. Rev. D 2009, arXiv:hep-th/0812.1806]79, 064016. [Google Scholar] [CrossRef]
  51. Konoplya, R.A.; Stuchlík, Z. Are eikonal quasinormal modes linked to the unstable circular null geodesics? Phys. Lett. B 2017, arXiv:gr-qc/1705.05928]771, 597–602. [Google Scholar] [CrossRef]
  52. Konoplya, R.A.; Zinhailo, A.F. Quasinormal modes, stability and shadows of a black hole in the 4D Einstein–Gauss–Bonnet gravity. Eur. Phys. J. C 2020, arXiv:gr-qc/2003.01188]80, 1049. [Google Scholar] [CrossRef]
  53. Konoplya, R.A.; Zinhailo, A.F.; Stuchlík, Z. Quasinormal modes, scattering, and Hawking radiation in the vicinity of an Einstein-dilaton-Gauss-Bonnet black hole. Phys. Rev. D 2019, arXiv:gr-qc/1903.03483]99, 124042. [Google Scholar] [CrossRef]
  54. Zhidenko, A. Quasinormal modes of Schwarzschild de Sitter black holes. Class. Quant. Grav. 2004, 21, 273–280. [Google Scholar] [CrossRef]
  55. Konoplya, R.A.; Zhidenko, A. High overtones of Schwarzschild-de Sitter quasinormal spectrum. JHEP 2004, 06, 037. [Google Scholar] [CrossRef]
  56. Konoplya, R.A.; Zhidenko, A. Nonoscillatory gravitational quasinormal modes and telling tails for Schwarzschild–de Sitter black holes. Phys. Rev. D 2022, arXiv:gr-qc/2209.12058]106, 124004. [Google Scholar] [CrossRef]
  57. Cardoso, V.; Costa, J.a.L.; Destounis, K.; Hintz, P.; Jansen, A. Quasinormal modes and Strong Cosmic Censorship. Phys. Rev. Lett. 2018, arXiv:gr-qc/1711.10502]120, 031103. [Google Scholar] [CrossRef]
  58. Konoplya, R.A. Further clarification on quasinormal modes/circular null geodesics correspondence. Phys. Lett. B 2023, arXiv:gr-qc/2210.08373]838, 137674. [Google Scholar] [CrossRef]
  59. Jusufi, K. Quasinormal Modes of Black Holes Surrounded by Dark Matter and Their Connection with the Shadow Radius. Phys. Rev. D 2020, arXiv:gr-qc/1912.13320]101, 084055. [Google Scholar] [CrossRef]
  60. Jafarzade, K.; Kord Zangeneh, M.; Lobo, F.S.N. Shadow, deflection angle and quasinormal modes of Born-Infeld charged black holes. JCAP 2021, arXiv:gr-qc/2010.05755]04, 008. [Google Scholar] [CrossRef]
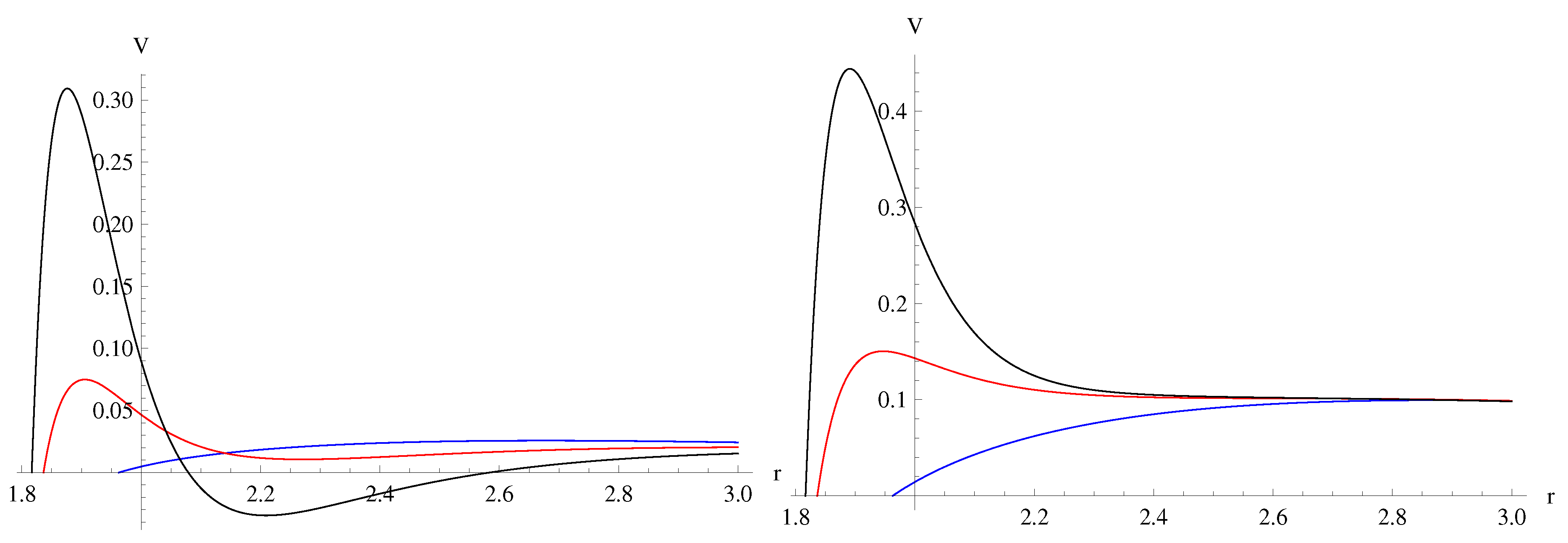
Preprints 87261 g001
Figure 1. Effective potentials for ℓ = 0 (left) and ℓ = 1 (right) at β = 10 − 4 (blue), β = 10 − 3 (red), β = 0.002 (black); M = 1 .
Figure 1. Effective potentials for ℓ = 0 (left) and ℓ = 1 (right) at β = 10 − 4 (blue), β = 10 − 3 (red), β = 0.002 (black); M = 1 .
Preprints 87261 g001
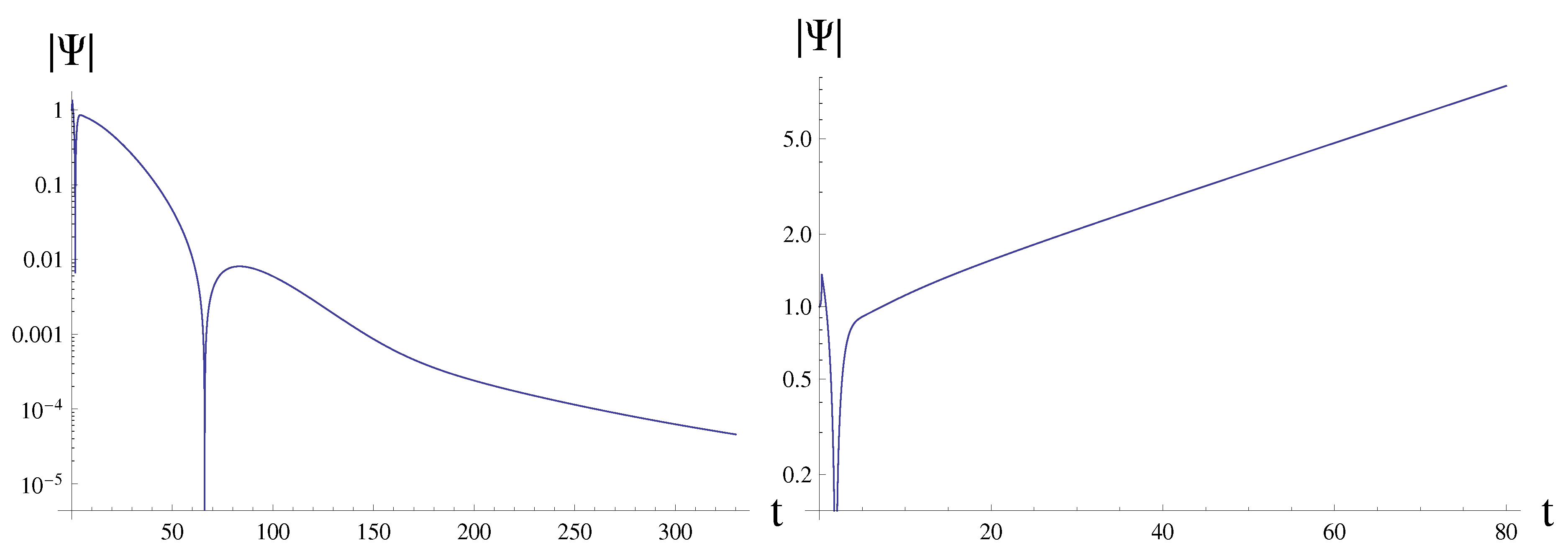
Preprints 87261 g002
Figure 2. Time domain profiles for the stable decayed oscillations β = 0.13635 (left) and at the instability β = 0.13640 (right); M = 1 , ℓ = 0 .
Figure 2. Time domain profiles for the stable decayed oscillations β = 0.13635 (left) and at the instability β = 0.13640 (right); M = 1 , ℓ = 0 .
Preprints 87261 g002
Preprints 87261 g003
Figure 3. Time domain profile for the stable decayed oscillations β = 0.002 , M = 1 , ℓ = 20 . The fitting in the range formally gives 30 < t < 85 gives two modes ω 0 = 4.14628 − 0.431359 i and ω 1 = 6.29882 − 0.629939 i which is the reflection of the two stages of oscillations, the Frobenius method gives ω 0 = 4.147393 − 0.431639 i and ω 1 = 6.296855 − 0.627813 i while the WKB formula produces only the second of the two modes ω 1 = 6.29683 − 0.62783 i .
Figure 3. Time domain profile for the stable decayed oscillations β = 0.002 , M = 1 , ℓ = 20 . The fitting in the range formally gives 30 < t < 85 gives two modes ω 0 = 4.14628 − 0.431359 i and ω 1 = 6.29882 − 0.629939 i which is the reflection of the two stages of oscillations, the Frobenius method gives ω 0 = 4.147393 − 0.431639 i and ω 1 = 6.296855 − 0.627813 i while the WKB formula produces only the second of the two modes ω 1 = 6.29683 − 0.62783 i .
Preprints 87261 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated