Preprint
Article
A Self-Calibration of Capacitor Mismatch Error for Pipeline ADCs
Altmetrics
Downloads
125
Views
29
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
08 October 2023
Posted:
09 October 2023
You are already at the latest version
Alerts
Abstract
This study proposes self-calibration of capacitor mismatch errors for high-resolution pipeline analog-to-digital converters (ADCs). The proposed calibration circuit recursively amplifies the capacitor mismatch error by re-utilizing a multiplying digital-to-analog converter in a pipeline stage without increasing the circuit complexity, and the amplified error voltage is converted into digital code by utilizing the remaining pipeline stages. Error correction is performed by subtracting the digital code from the ADC output during normal operation. A prototype of a 12-bit pipeline ADC is fabricated in a 0.18 µm standard CMOS process. The ADC comprises eight 1.5-bit stages, followed by a 4-bit flash ADC as the final stage; the capacitor mismatch errors in the first two pipeline stages are corrected by utilizing the proposed self-calibration technique. At a sampling rate of 30 MS/s, the measured differential and integral nonlinearities improve from +0.82/-0.75 and +1.12/-1.79 to +0.45/-0.41 and +0.47/-0.91 after calibration, respectively. Further, the measured dynamic performances improve significantly with calibration. For an input frequency of 2.09 MHz, the ADC achieves a spurious-free dynamic range (SFDR) and signal-to-noise and distortion ratios (SNDR) of 69.3dB and 63.9dB before calibration, respectively. After calibration, the SFDR and SNDR increase to 84.1dB and 68.9dB, respectively, and the effective number of bits is approximately 11.1bit. The power consumption of the ADC is 35mW under 1.8V supply, and the resulting figure of merit is 514fJ/conversion step.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
The pipeline analog-to-digital converter ADC architecture is the most suitable for high-speed operations with medium-to-high resolution among various ADC architectures. However, because the analog-to-digital conversion of the pipeline ADC is performed in the analog domain, various errors generated from analog circuits, such as charge injection, finite gain error of an operational amplifier (op-amp), and capacitor mismatch error, must be suppressed to achieve high resolution. Most errors, except the capacitor mismatch error, can be addressed owing to advances in circuit techniques and CMOS technologies [1–5]. However, capacitor mismatch significantly depends on the CMOS technology and requires special calibration circuitry to minimize the linearity degradation of the ADC output.
The calibration of capacitor mismatch has been investigated for several decades, and numerous techniques have been reported [3,6–21]. Calibration techniques can be categorized into two types: analog and digital. Digital calibration techniques [6,7,8,9,10,11,12] move analog errors to the digital domain by utilizing different methods and digitally correcting them. However, they increase circuit complexity and power consumption. In contrast, analog calibration has a simpler circuit design compared with digital calibration [3,13–21]. The capacitor error averaging technique proposed in [3,16,17] is an effective analog calibration technique. In this technique, calibration can be performed in the background, meaning normal operation is not hindered by calibration. However, additional clock phases are required to average the capacitor mismatch errors, thereby decreasing the operation speed of the ADC. Self-calibration is another effective analog calibration technique [18–21]. As suggested by the name self-calibration utilizes the remaining pipeline stages to correct capacitor mismatch errors in the early pipeline stages, thereby eliminating the need for calibration circuitry and simplifying circuit implementation. Unlike the error-averaging technique, although the calibration is performed in the foreground, the capacitance does not drift or age over time, and the foreground calibration still functions effectively.
This study proposes another method to implement self-calibration. Without increasing the circuit complexity, the proposed calibration circuit re-utilizes the multiplying digital-to-analog converter (MDAC) in a pipeline stage to recursively amplify the capacitor mismatch error and then converts it into a digital code by the remaining pipeline stages. The digital error is subtracted from the ADC output.
A 12-bit pipeline ADC that employs self-calibration is fabricated by utilizing a 0.18 µm standard CMOS process. After calibration, the measured differential nonlinearity (DNL) and integral nonlinearity (INL) increase from +0.82/-0.75 and +1.12/-1.79 to +0.45/-0.41 and +0.47/-0.91, respectively. The dynamic performance also improves significantly after calibration. At a sampling rate of 30 MS/s, the ADC achieves a spurious-free dynamic range (SFDR) and a signal-to-noise and distortion ratio (SNDR) of 84.1dB and 68.9dB for an input frequency of 2.09 MHz, respectively. The power consumption of the ADC is 35mW under a 1.8 V supply and the figure of merit (FOM) is 512 fJ/conversion step.
The remainder of this paper is organized as follows: Section 2 presents the proposed MDAC for self-calibration and its operating principles. Section 3 explains the implementation of the ADC that employs the proposed self-calibration technique. Finally, the measurement results and conclusions are presented in Section 4 and Section 5, respectively.
2. Proposed self-calibration technique
A switched-capacitor amplifier (SCA) with a gain of two is a key building block of the MDAC in a 1.5-bit pipeline stage. The conventional SCA and proposed self-calibrating SCA for gain-of-two amplification are shown in Figure 1. Compared with the conventional SCA, only two additional switches, which are placed in the dashed box, are added to self-calibrate the capacitor mismatch error.
The SCA operates in two modes: calibration and normal. In the calibration mode, the error voltage caused by the capacitor mismatch is converted into a digital signal, saved in memory, and subtracted from the ADC output. In normal operation, the two additional switches remain OFF and the SCA functions as a conventional MDAC for a 1.5-bit pipeline stage. The operation of the SCA during capacitor mismatch calibration is shown in Figure 2. The SCA operates with a two-phase non-overlapping clock, sampling, and amplification phases, similar to the conventional SCA. In the sampling phase, the reference voltage VREF is applied to the feedback capacitor (CF) and a common-mode voltage or 0 is applied to the sampling capacitor (CS), as shown in Figure 2 (a). The total charge sampled on the capacitors is expressed as follows:
In the amplification phase, the bottom plate of CF is flipped around and connected to the op-amp output, whereas the bottom plate of CS is connected to VREF, as shown in Figure 2 (b). From the principle of charge conservation, the total charge Q at the end of the amplification phase is as follows
Suppose CF =C and CS=(1+ε)C. In that case, the op-amp output voltage becomes VREF multiplied by the mismatch factor, which is called the error voltage (VE), expressed as follows:
In sampling phase 2, as shown in Figure 2 (c), VOUT is sampled on CS by turning S4 and S6 ON. The charge on CS is then transferred to CF in amplification phase 2) and VOUT becomes
Because VREF is known, the mismatch factor ε can be derived from the digitized value of VE converted by the remaining pipeline stages.
The proposed SCA is particularly advantageous in that VE can be accurately amplified by a power of two with no additional circuits by repeating the processes of sampling phase 2 and amplification phase 2.
Furthermore, amplification by a gain of two can be considered as a 1.5-bit pipeline stage operation when the amplitude input is relatively small. A block diagram of the 1.5-bit pipeline stage and its transfer curve for the stage’s analog input and output voltages are shown in Figure 3, according to which, the digital output is “01” and the MDAC output is twice the input when the input amplitude is within ±VREF/4. Generally, the capacitor mismatch is small and VE remains within ±VREF/4 even after several amplifications. Therefore, suppose the digital output is “01” even with no sub-ADC. In that case, the 1.5-bit stage operation is performed whenever VE is amplified by a fact of two.
For self-calibration, redundant stages are required to accurately measure the mismatch errors generated by the front pipeline stages. For example, suppose the capacitor mismatch error that occurs in the first stage is converted to the remaining stages in a 12-bit pipeline ADC that performs a 1-bit or 1.5-bit conversion per stage. In that case, the converted error voltage has only 11-bit accuracy, which is insufficient for correction. At least two redundant stages must be added to increase the accuracy by more than two bits. As previously explained, amplification of the small-error voltage by a factor of two corresponds to the addition of one redundant stage. In other words, the accuracy of the error voltage is increased to 13 bits by amplifying the error voltage twice before it is converted by the remaining stages, which allows self-calibration with no additional circuitry. Calibration must only be performed for a few MSB stages according to the capacitor-matching characteristics provided in the CMOS process, and proceeds in the reverse direction from the rear stage.
A comparison of the dynamic performance of a 12-bit pipeline ADC before and after calibration is shown in Figure 4. In the simulations, only capacitor mismatch was considered, and calibration was performed for the first two stages. The mismatch between CS and CF was assumed to be 0.5% (ε is 0.005) based on the technology information. As shown in the simulation results, the mismatch calibration effectively improved the ADC performance. SNDR and SFDR increased from 59.9 dB to 73.9 dB and 62.3 dB to 93.6 dB, respectively. The dynamic performances were also compared according to the number of redundant bits or stages. As shown in Figure 5, the performance improved with the number of redundant bits and saturated at 2 or more bits. Therefore, in this study, the number of redundant bits was determined to be two.
3. ADC implementation
A 12-bit pipeline ADC was designed as the readout circuit in a CMOS image sensor. A block diagram of the ADC is shown in Figure 6. The ADC was composed of eight 1.5-bit stages followed by a 4-bit flash ADC as the final stage, a reference generation circuit, and distributed clock drivers. A simplified circuit for the first stage is shown in Figure 7. Because the ADC did not have a dedicated front-end sample or hold amplifier, the sub-ADC of the first stage had its own input sampling network that held the input signal while the comparator made its decision. The second stage was similar to the first and was a scaled-down version of the first stage, except that the sub-ADC did not have a sampling network. Capacitor mismatch calibration was performed only for the first and second stages. Therefore, from the 3rd stage, the circuit configurations were similar to that of the conventional 1.5-bit pipeline stage. An op-amp of the MDAC was shared between two adjacent stages to reduce power consumption [22]. During calibration, the mismatch error between each CS and CF was amplified and converted into a digital signal, as explained in the previous section. During normal operation, the ADC output code was corrected by adding or subtracting the converted error voltage whenever the digital output value of the calibrated stage was either “00” or “10.”
A simplified circuit of the op-amp with a gain-boosting amplifier is shown in Figure 8. A folded-cascode architecture with PMOS input transistors was employed to set the input common-mode (CM) voltage lower than the output CM voltage, and the output cascade transistors were gain-boosted to increase the DC gain of the op-amp without reducing the output signal swing. The switched-capacitor CM feedback circuit proposed in [23] was utilized to determine the output CM voltage of the op-amp. As shown in Figure 7, a simple differential pair was utilized as the gain-boosting amplifier. A PMOS transistor (M3) was added between the input transistors for CM control of the amplifier. The simulated DC gain of the op-amp was higher than 90 dB for all the corners. The op-amp for the first and second stages consumed approximately 4 mA from the 2.8 V supply. The second, third, and fourth op-amps consumed approximately 1 mA, 0.5 mA, and 0.5 mA, respectively.
4. Measurement results
A 30 MS/s 12-bit pipeline ADC that employed the proposed self-calibrating technique was implemented in 0.18 µm CMOS technology and the ADC occupied a die area of 0.35 mm2. The die micrograph and the printed circuit board for the chip measurement are shown in Figure 9. The measured static performances of the ADC before and after calibration are shown in Figure 10. Before the calibration, the measured DNL and INL were less than +0.82/-0.75 and +1.12/-1.79 LSB, respectively. After calibration, the DNL and INL improved to +0.45/-0.41 and +0.47/-0.91 LSB, respectively. The measured power spectra for input frequencies of 2.09 MHz and 14.1 MHz are also shown in Figure 11, respectively. At an input frequency of 2.09 MHz, the measured SNDR and SFDR improved from 63.9dB and 69.3dB to 68.9dB and 84.1dB, respectively, and the resulting ENOB was 11.1 bit after calibration. After calibration, the measured dynamic performances versus the input frequency are shown in Figure 12. The measured SNDR and SFDR varied from 67.9 to 69.1 dB, 82.4 to 84.2 dB, respectively, for input frequencies up to the Nyquist frequency. The total ADC power consumption was 35 mW, including the reference generation and all peripheral circuits. The FOM, which is calculated as power/(2ENOB·sampling frequency), was 512 fJ/conversion. The ADC performance is summarized in Table 1.
5. Conclusion
A self-calibration technique that can be implemented without increasing the circuit complexity was proposed and validated through fabrication. The calibration circuit required only two switches to be added to the SCA, which comprised the MDAC of the pipeline stage and recursively amplified the capacitor mismatch errors. The amplified mismatch error was converted into digital code by utilizing the remaining pipeline stages, and error correction was performed by subtracting the error code from the ADC output during normal operation. A 12-bit 30 MS/s pipeline ADC comprising eight 1.5-bit stages, followed by a 4-bit flash ADC, was fabricated in a 180 nm CMOS process. The effectiveness of the calibration technique was validated through the measurement results. After calibration, the measured DNL and INL improved from +0.82/-0.75 and +1.12/-1.79 to +0.45/-0.41 and +0.47/-0.91, respectively. Further, calibration significantly improved the dynamic performance. For an input frequency of 2.09 MHz, the measured SFDR and SNDR improved from 69.3dB and 63.9dB to 84.1dB and 68.9dB, respectively, resulting in an ENOB of 11.1 bits. The ADC consumed 35 mW from an 1.8 V supply, and the resulting FOM was 512 fJ/conversion stage.
Author Contributions
Conceptualization, D. S; methodology, D. S. and J. K.; validation, D. S.; formal analysis, D. S. and S. C.; writing—original draft preparation, D. S. and S. C.; writing—review and editing, B. L.; supervision, B. L. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
This work was supported in part by the National Research Foundation of Korea (NRF) Grant through the Korean Government (MSIT) under Grant 2021R1A2C22013480, and in part by the National Research and Development Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT under Grant NRF-2022M3H4A1A01009658.
Conflicts of Interest
The authors declare no conflict of interest.
References
- K. Bult and G. Geelen, “A fast-settling CMOS opamp for SC circuits with 90-dB DC gain”, IEEE J. Solid-State Circuits, vol. 25, pp.1379–1384, Dec. 1990. [CrossRef]
- S. H. Lewis and P.R. Gray, “A pipelined 5-Msample/s 9-bit analog-to-digital converter”, IEEE J. Solid-State Circuits, vol. 22, pp. 954-961, Dec. 1987. [CrossRef]
- T.-C. Hung, and T.-H. Kuo, “A 75.3-dB SNDR 24-MS/s Ring Amplifier-Based Pipelined ADC Using Averaging Correlated Level Shifting and Reference Swapping for Reducing Errors From Finite Opamp Gain and Capacitor Mismatch”, IEEE J. Solid-State Circuits, vol. 54, pp. 1425–1435, May. 2019. [CrossRef]
- Stoeble, V. Dias and C. Schwoerer, “An 80 MHz 10 b pipeline ADC with dynamic range doubling and dynamic reference selection”, ISSCC Dig. Tech. Papers, pp. 462–539, Feb. 2004. [CrossRef]
- B-G. Lee et al., “A 14-b 100-MS/s Pipelined ADC With a Merged SHA and First MDAC”, IEEE J. Solid-State Circuits, vol. 43, pp. 2613–2619, Dec. 2008. [CrossRef]
- U.-K. Moon and B.-S. Song, “Background Digital Calibration Techniques for Pipelined ADC’s ”, IEEE J. Solid-State Circuits, vol. 44, pp. 102–109, Feb. 1997. [CrossRef]
- J. Guo, W. Law, W. J. Helms, and D. J. Allstot, “Digital Calibration for Monotonic Pipelined A/D Converters”, IEEE Trans. Instrum.Meas., vol. 53, pp. 1485-1492, Dec. 2004. [CrossRef]
- M. Furuta, S. Kawahito and D. Miyazaki, “A Digital-Calibration Technique for Redundant Radix-4 Pipelined Analog-to-Digital Converters”, IEEE Trans. Instrum. Meas., vol. 56, pp. 2301-2311, Dec. 2007. [CrossRef]
- M. Taherzadeh-Sani and A. Hamoui, “Digital Background Calibration of Capacitor-Mismatch Errors in Pipelined ADCs”, IEEE Trans. Circuits Syst. II, vol. 53, pp. 966-970, Sept. 2006. [CrossRef]
- K. Ragab, L. Chen, A. Sanyal, and N. Sun, “Digital Background Calibration for Pipelined ADCs Based on Comparator Decision Time Quantization”, IEEE Trans. Circuits Syst. II, vol. 62, pp. 456-460, May 2015. 20 May. [CrossRef]
- Y. Yang, Y. Lyu and Y. Hu, "A Mismatch Compensation Scheme for Cyclic-pipelined ADC via Dynamic Element Matching Technique," 2022 IEEE International Symposium on Circuits and Systems (ISCAS), Austin, TX, USA, 2022, pp. 3229-3233. [CrossRef]
- J. Wei, C. Zhang and M. Liu, "A 11-Bit 1-GS/s 14.9mW Hybrid Voltage-Time Pipelined ADC With Gain Error Calibration," in IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 69, no. 3, pp. 799-803, March 2022. 20 March. [CrossRef]
- Y. Zhang et al., “A 20 MHz Bandwidth 79 dB SNDR SAR-Assisted Noise-Shaping Pipeline ADC With Gain and Offset Calibrations”, IEEE J. Solid-State Circuits, vol. 57, pp. 745–756, March. 2022. [CrossRef]
- P.W. Li, M.J. chin, P.R. Gray, and R. Castello, “A Ratio–Independent Algorithmic Analog-to-Digital Conversion Technique”, IEEE J. Solid-State Circuits, vol. 19, pp. 828–836, Dec. 1984. [CrossRef]
- H. Liu, J. Sun, H. Xu and L. Zhang, "A 16b 120MS/s Pipelined ADC Using an Auxiliary-Capacitor-Based Calibration Technique Achieving 90.5dB SFDR in 0.18 μm CMOS," IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 69, no. 3, pp. 809-813, March 2022. [CrossRef]
- B.-S. Song, M.F. Tompsett and K.R. Lakshmikumar, “A 12-bit 1-Msample/s capacitor error-averaging pipelined A/D converter”, IEEE J. Solid-State Circuits, vol. 23, pp. 1324–1333, Dec. 1988. [CrossRef]
- H.-S. Chen, B.-S. Song, and K. Bacrania, “A 14-bit 20-Msample/s CMOS pipelined ADC”, IEEE J. Solid-State Circuits, vol. 36, pp. 997–1001, June. 2001. [CrossRef]
- H.-S. Lee, D. Hodges and P.R. Gray, “A self-calibrating 12b 12s CMOS ADC”, ISSCC Dig. Tech. Papers, pp. 64–66, Feb. 1984.
- Y.M. Lin, B. Kim and P.R. Gray, “A 13-b 2.5-MHz self-calibrated pipelined A/D converter in 3-m CMOS”, IEEE J. Solid-State Circuits, vol. 26, pp. 628–636, April. 1991.
- P.C. Yu, and H.-S. Lee, “A 2.5-V, 12-b, 5-MSample/s Pipelined CMOS ADC”, IEEE J. Solid-State Circuits, vol. 31, pp. 1854–1861, Dec. 1996. [CrossRef]
- S. Chatterjee and S. Roy, “A Self-Calibration Method of a Pipeline ADC Based on Dynamic Capacitance Allotment”, IEEE Trans. VLSI Syst., vol. 30, pp. 666-670, May. 2022. [CrossRef]
- B-G. Lee et al., “A 14-b 100-MS/s Pipelined ADC With a Merged SHA and First MDAC”, IEEE J. Solid-State Circuits, vol. 43, pp. 2613–2619, Dec. 2008. [CrossRef]
- Choksi and L.R. Carley, “Analysis of switched-capacitor common-mode feedback circuit”, IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 50, pp. 906-917, Dec. 2003. [CrossRef]
Figure 1.
Simplified circuit diagram of an SCA for gain-of-two amplification: (a) Conventional SCA. (b) Proposed self-calibrating SCA.
Figure 1.
Simplified circuit diagram of an SCA for gain-of-two amplification: (a) Conventional SCA. (b) Proposed self-calibrating SCA.
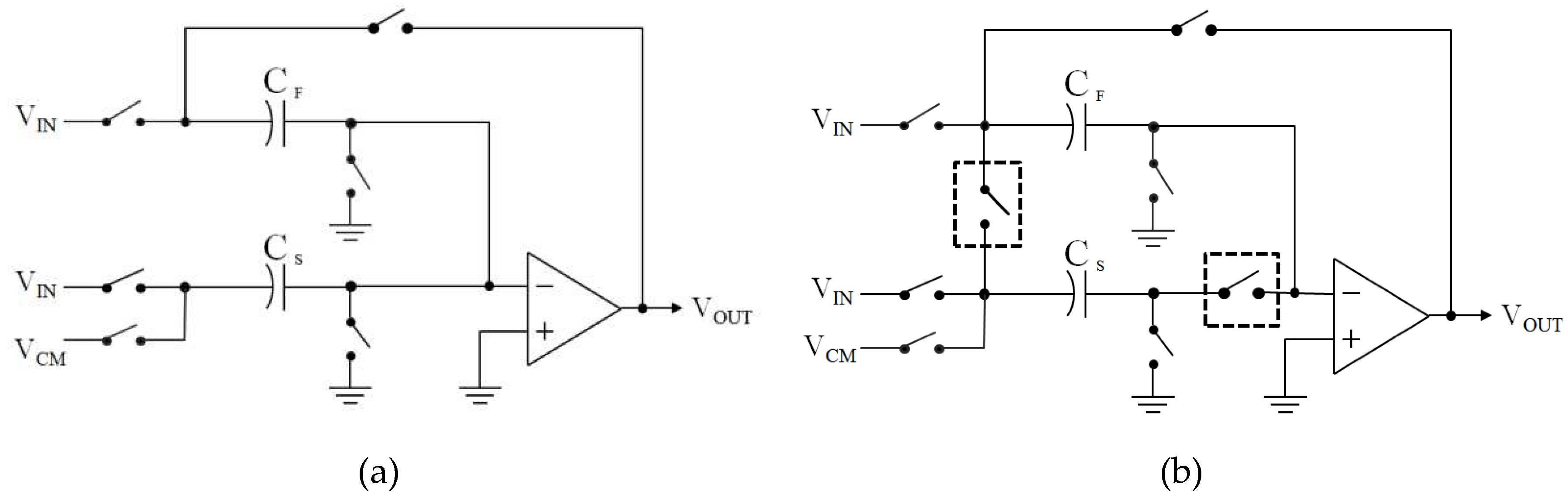
Figure 2.
Operation of the self-calibrating SCA at each clock phase: (a) Sampling Phase 1. (b) Amplification Phase 1. (c) Sampling Phase 2. (d) Amplification Phase 2.
Figure 2.
Operation of the self-calibrating SCA at each clock phase: (a) Sampling Phase 1. (b) Amplification Phase 1. (c) Sampling Phase 2. (d) Amplification Phase 2.
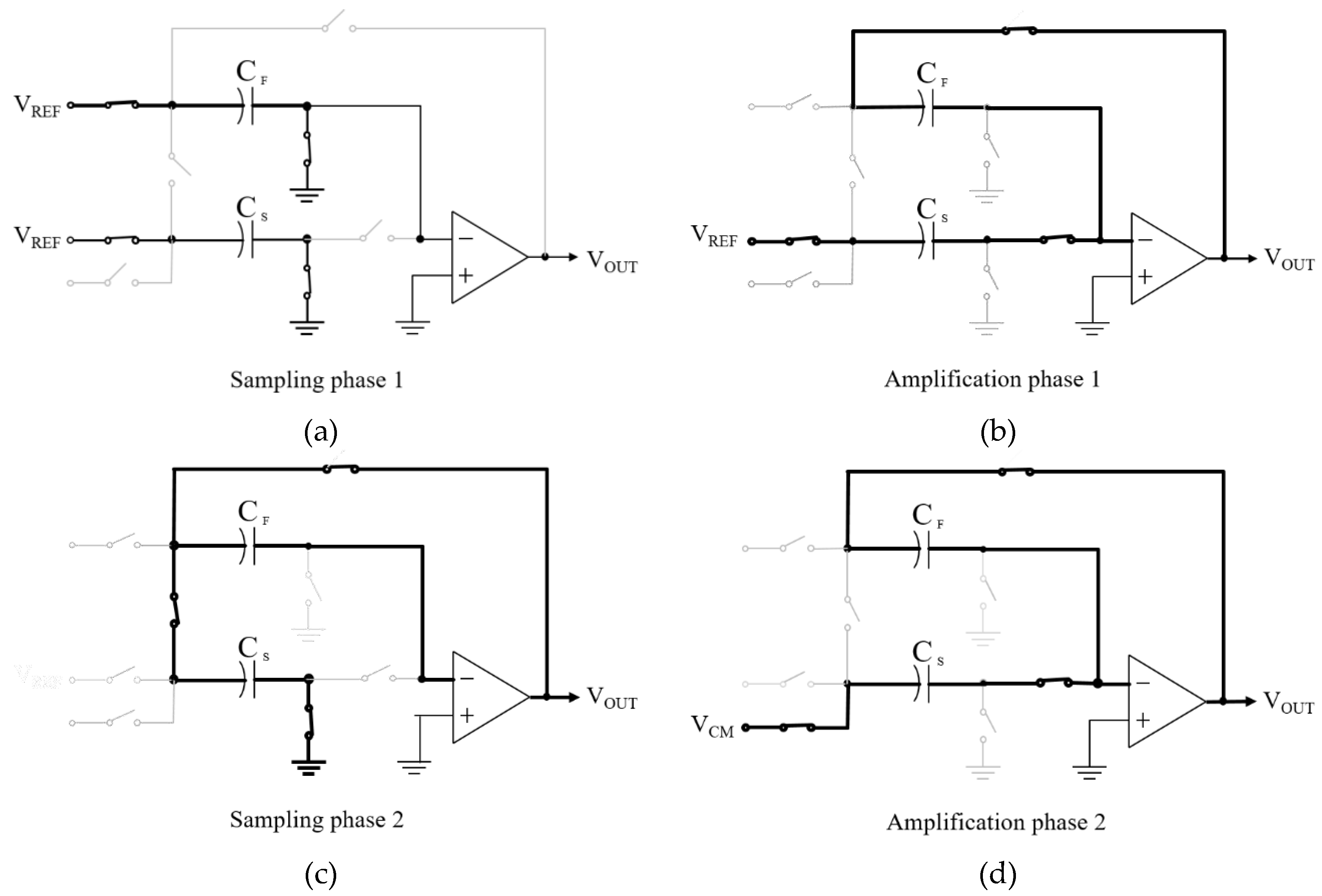
Figure 3.
Block diagram of a 1.5-bit pipeline stage (a) and its transfer curve (b).
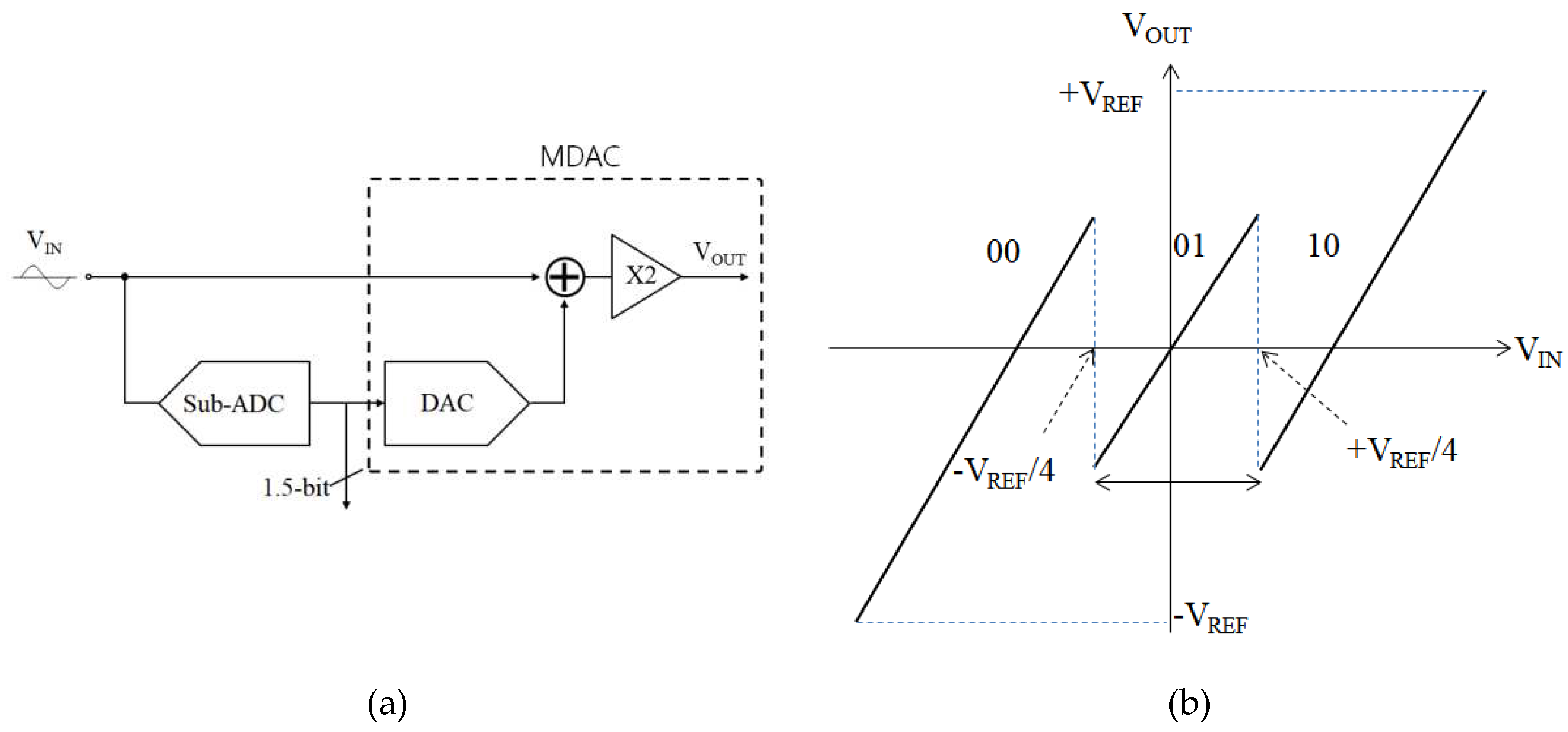
Figure 4.
Simulated dynamic performances of a 12-bit pipeline ADC: (a) Before calibration. (b) After calibration.
Figure 4.
Simulated dynamic performances of a 12-bit pipeline ADC: (a) Before calibration. (b) After calibration.
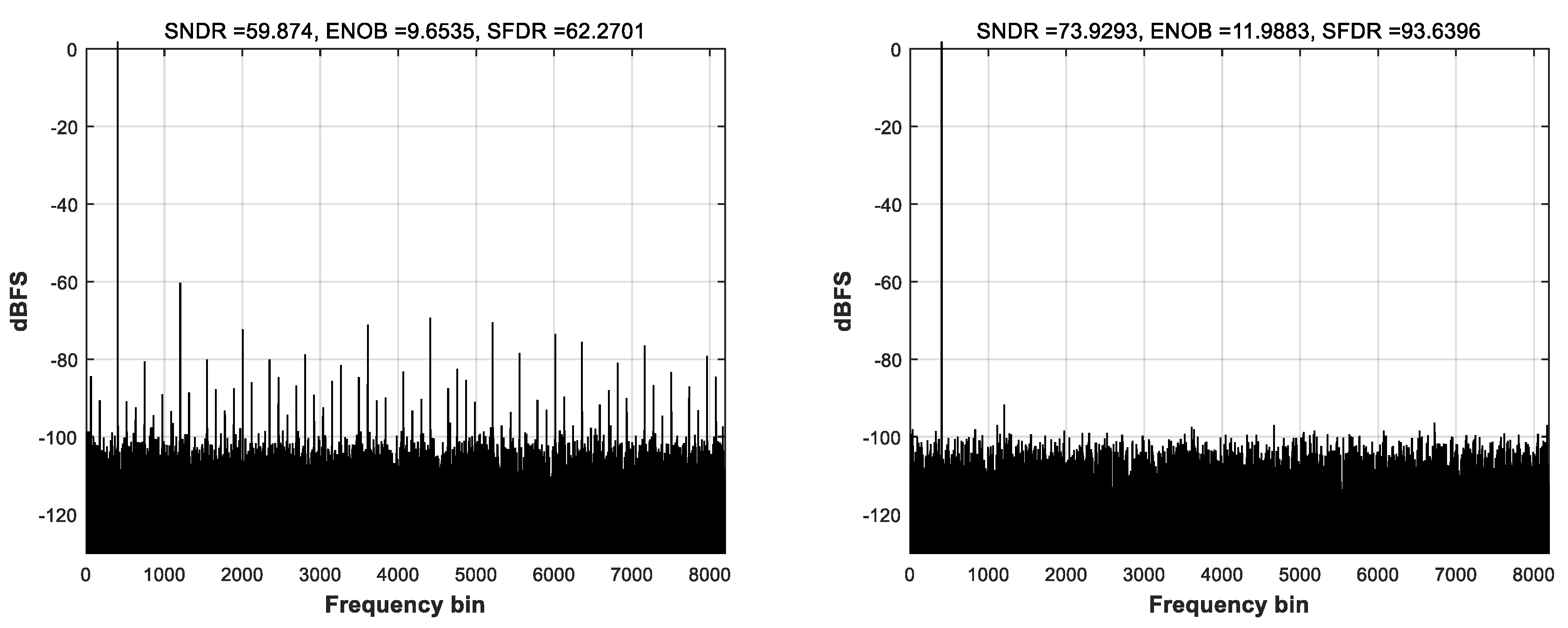
Figure 5.
Comparison of the dynamic performance according to the number of redundant bits: (a) No calibration. (b) No redundancy. (c) 1-bit redundancy. (d) 2-bit redundancy.
Figure 5.
Comparison of the dynamic performance according to the number of redundant bits: (a) No calibration. (b) No redundancy. (c) 1-bit redundancy. (d) 2-bit redundancy.
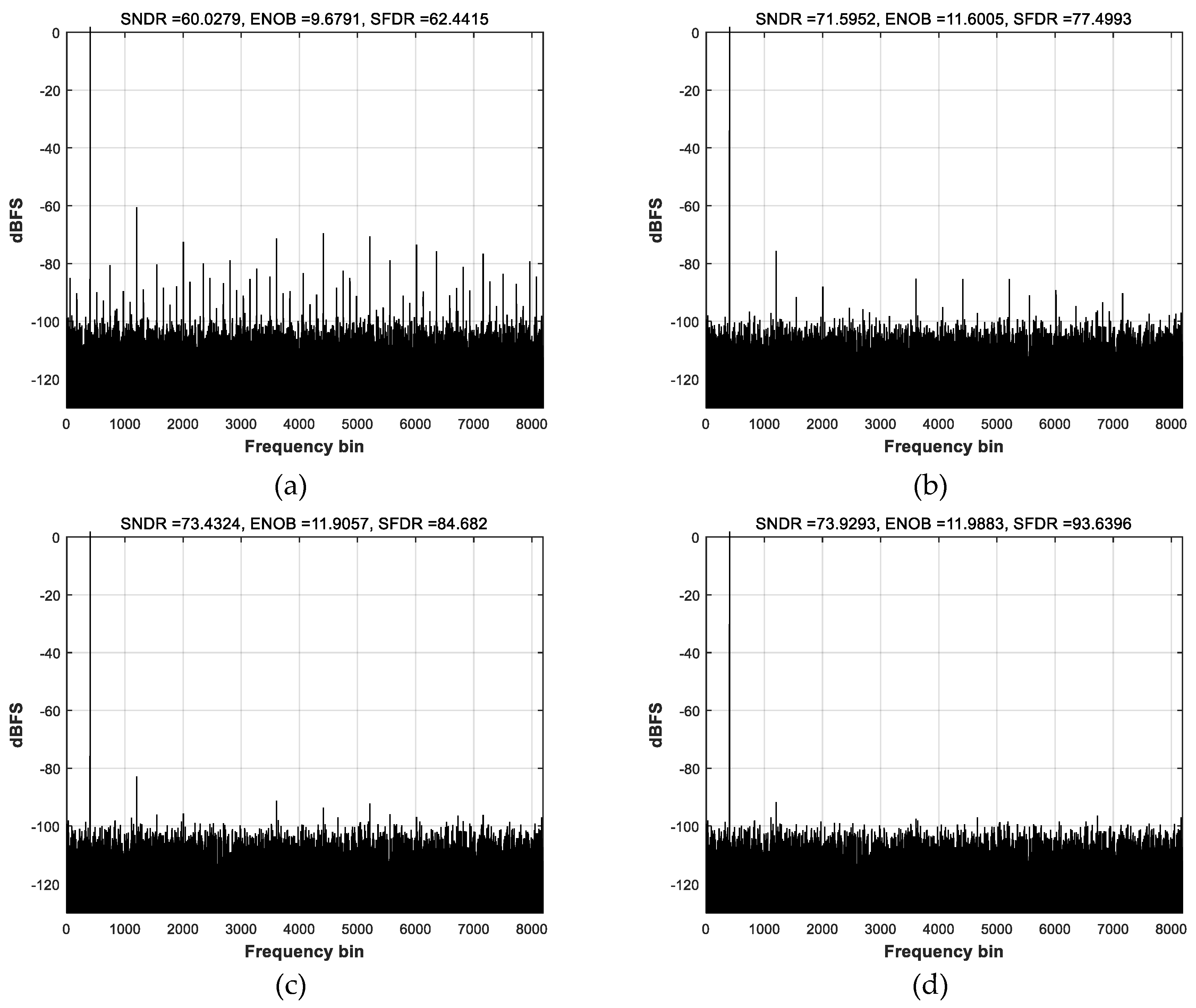
Figure 6.
Block diagram of the ADC.
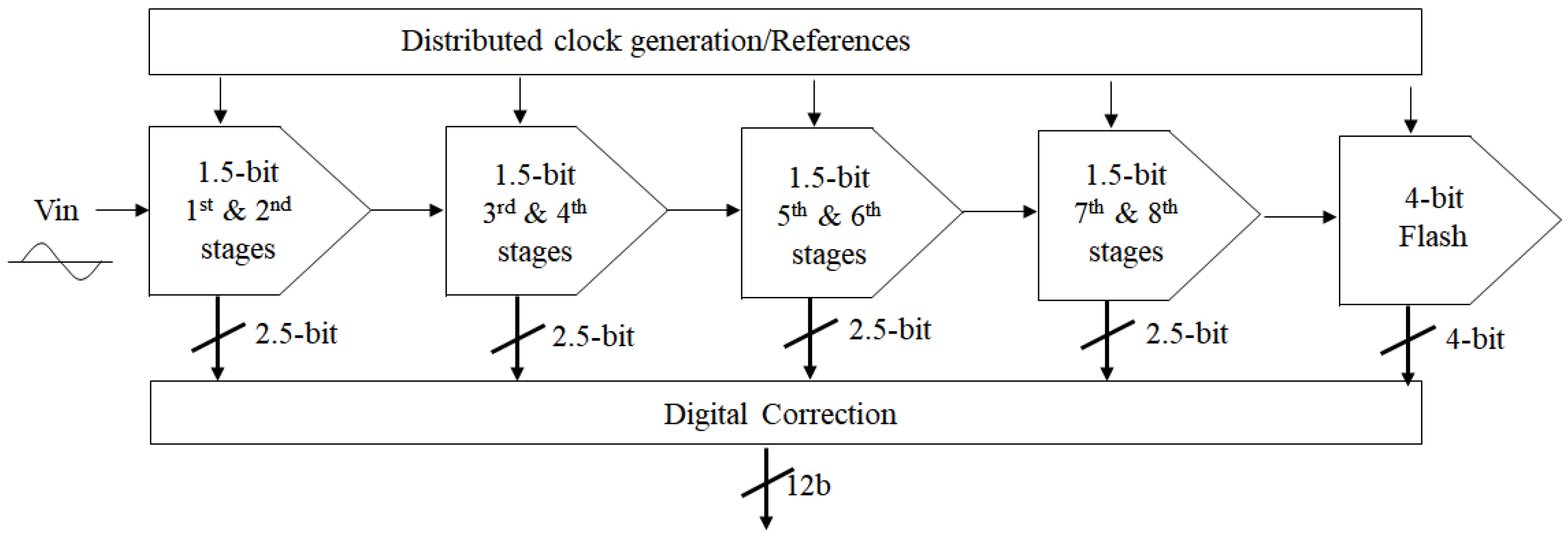
Figure 7.
Simplified circuit of the 1st stage of the ADC.
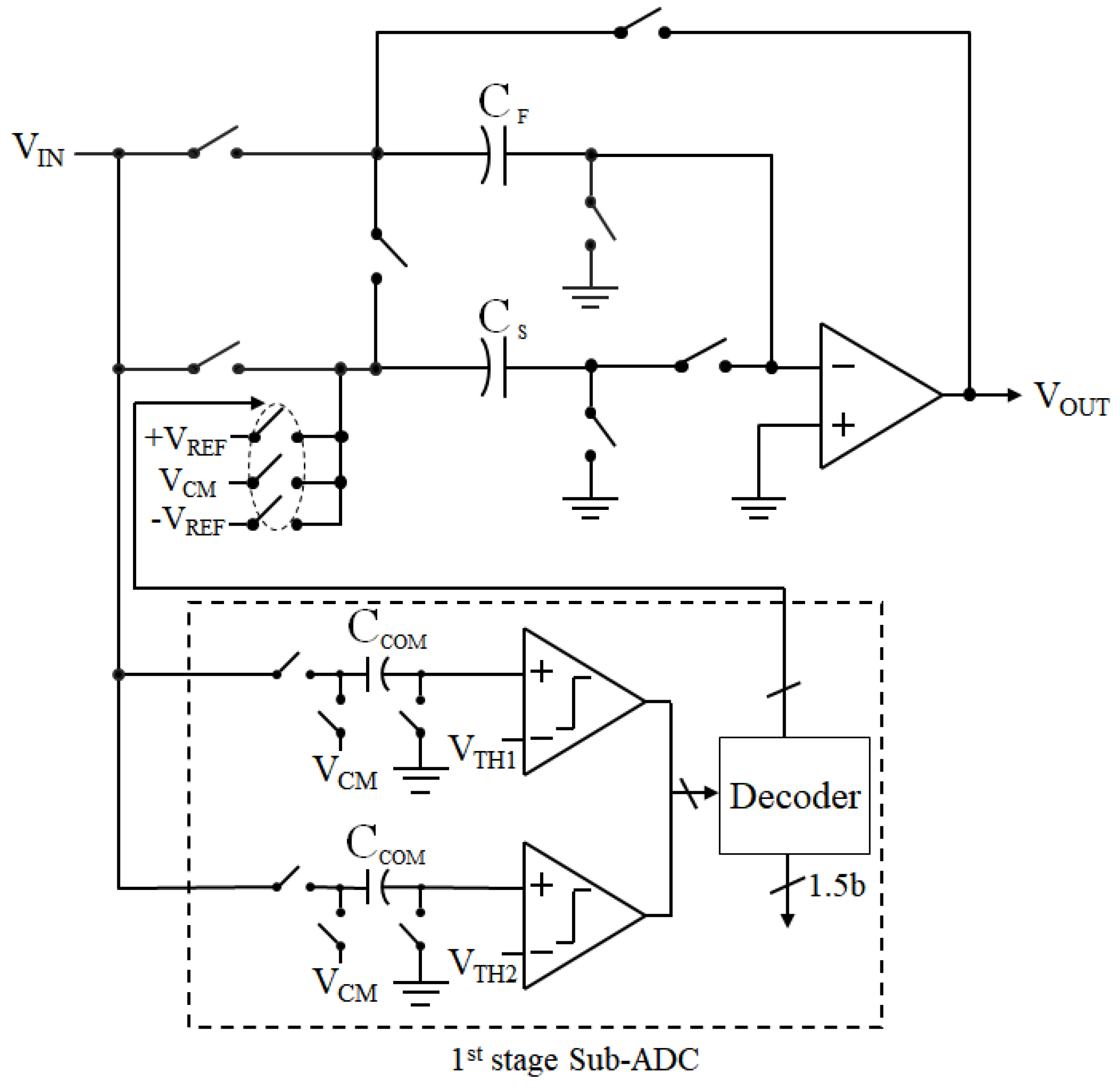
Figure 8.
Circuit diagram of the main op-amp and gain-boosting amplifier.
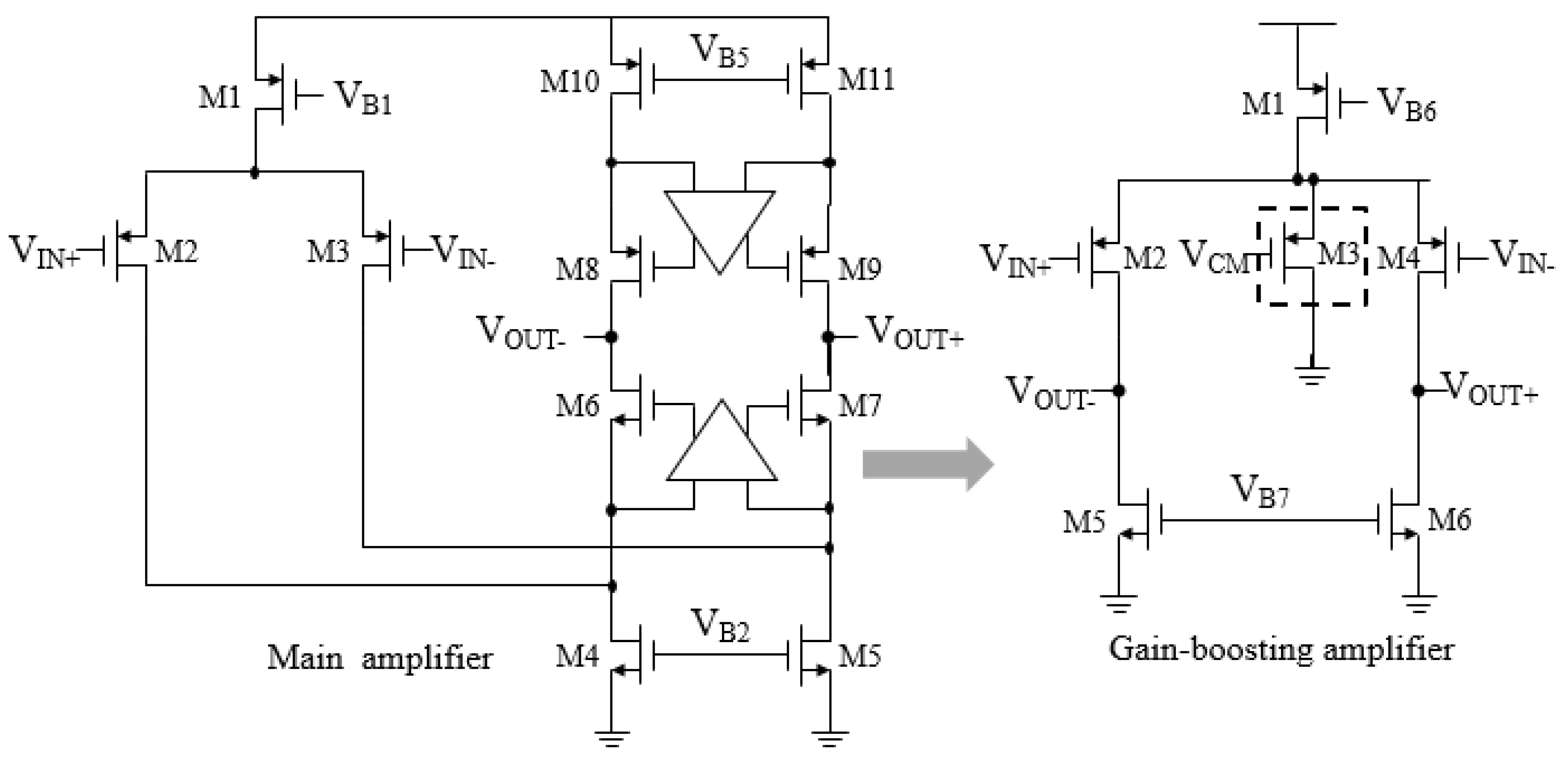
Figure 9.
Chip micrograph (a) and measurement board (b).

Figure 10.
Measured static performances before and after calibration: (a) Before calibration. (b) After calibration.
Figure 10.
Measured static performances before and after calibration: (a) Before calibration. (b) After calibration.
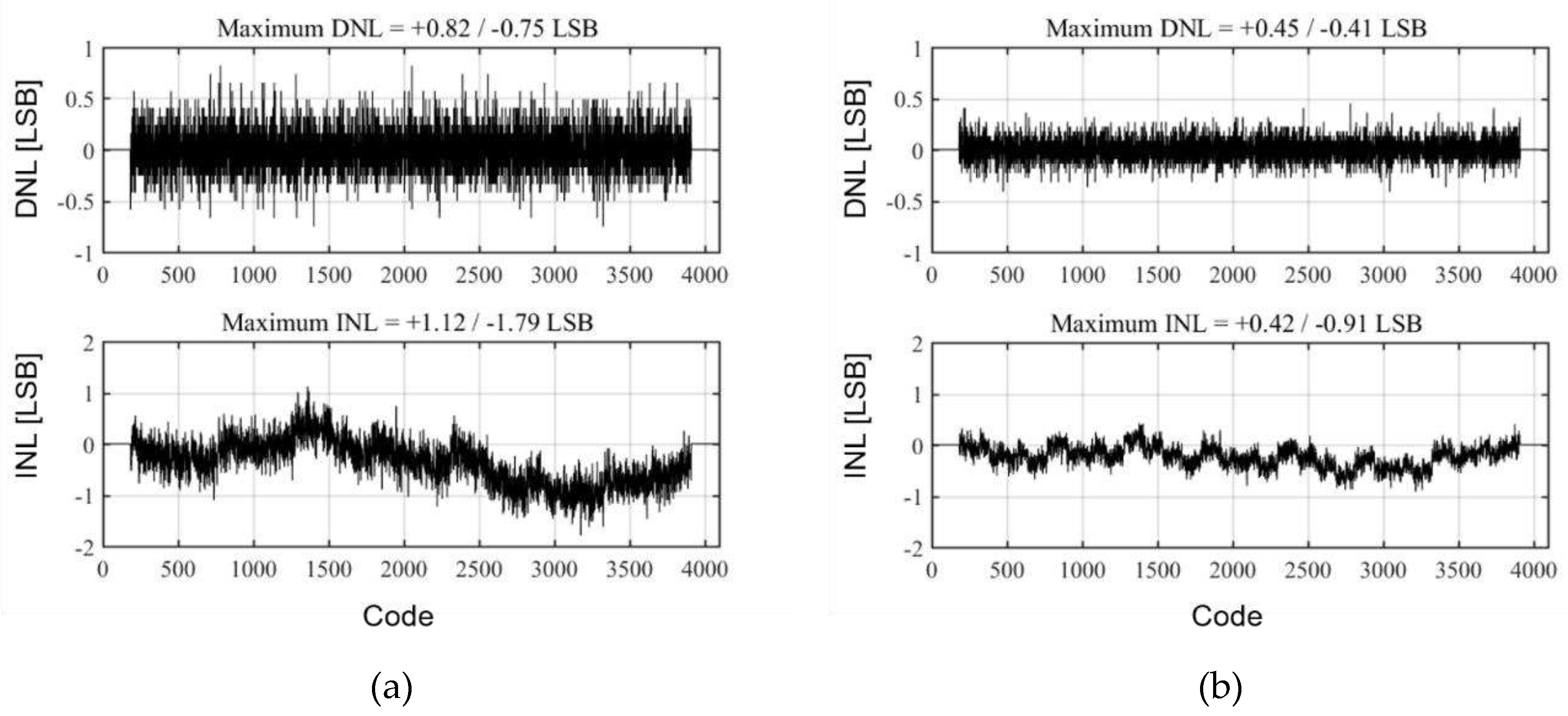
Figure 11.
Measured dynamic performances for input frequencies of 2.09 MHz and 14.1MHz before and after calibration: (a) Before calibration with 2.09 MHz input (b) After calibration with 2.09 MHz input (c) Before calibration with 14.1MHz input (d) After calibration with 14.1MHz input.
Figure 11.
Measured dynamic performances for input frequencies of 2.09 MHz and 14.1MHz before and after calibration: (a) Before calibration with 2.09 MHz input (b) After calibration with 2.09 MHz input (c) Before calibration with 14.1MHz input (d) After calibration with 14.1MHz input.
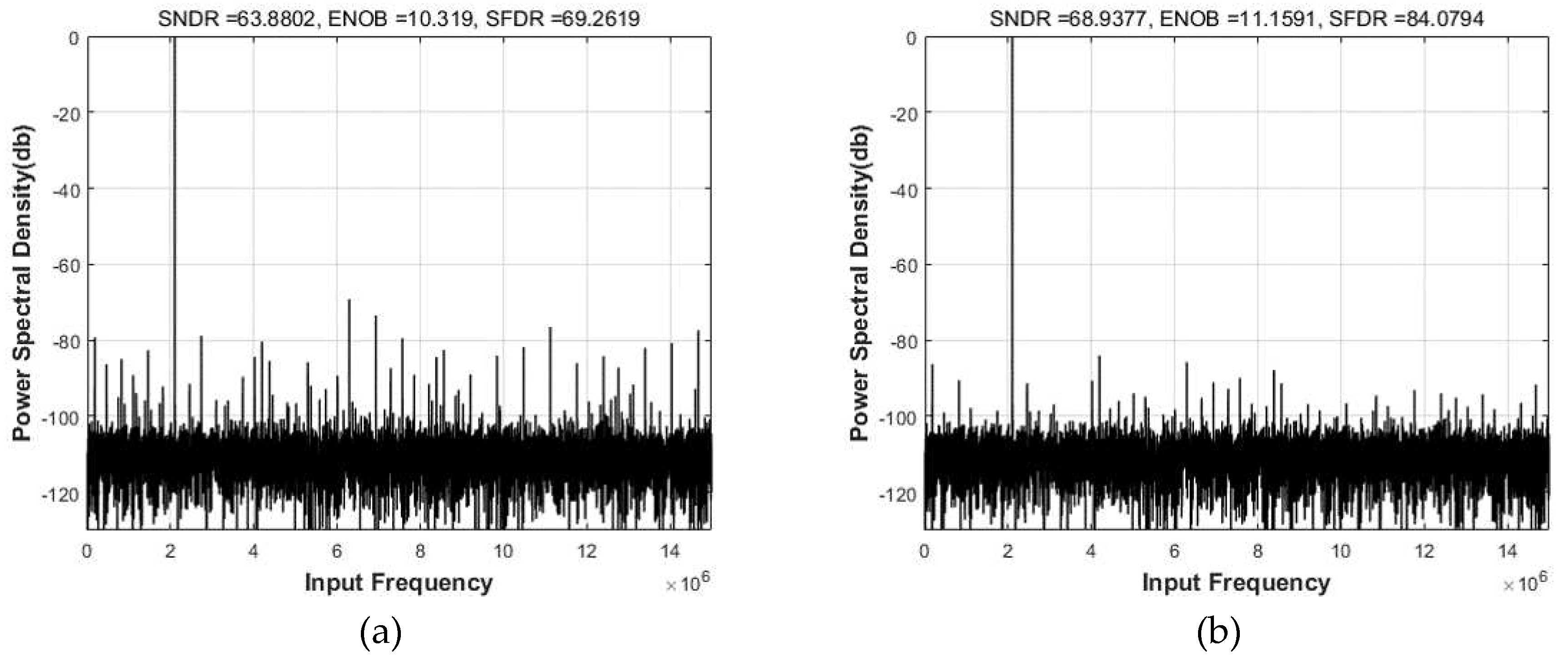
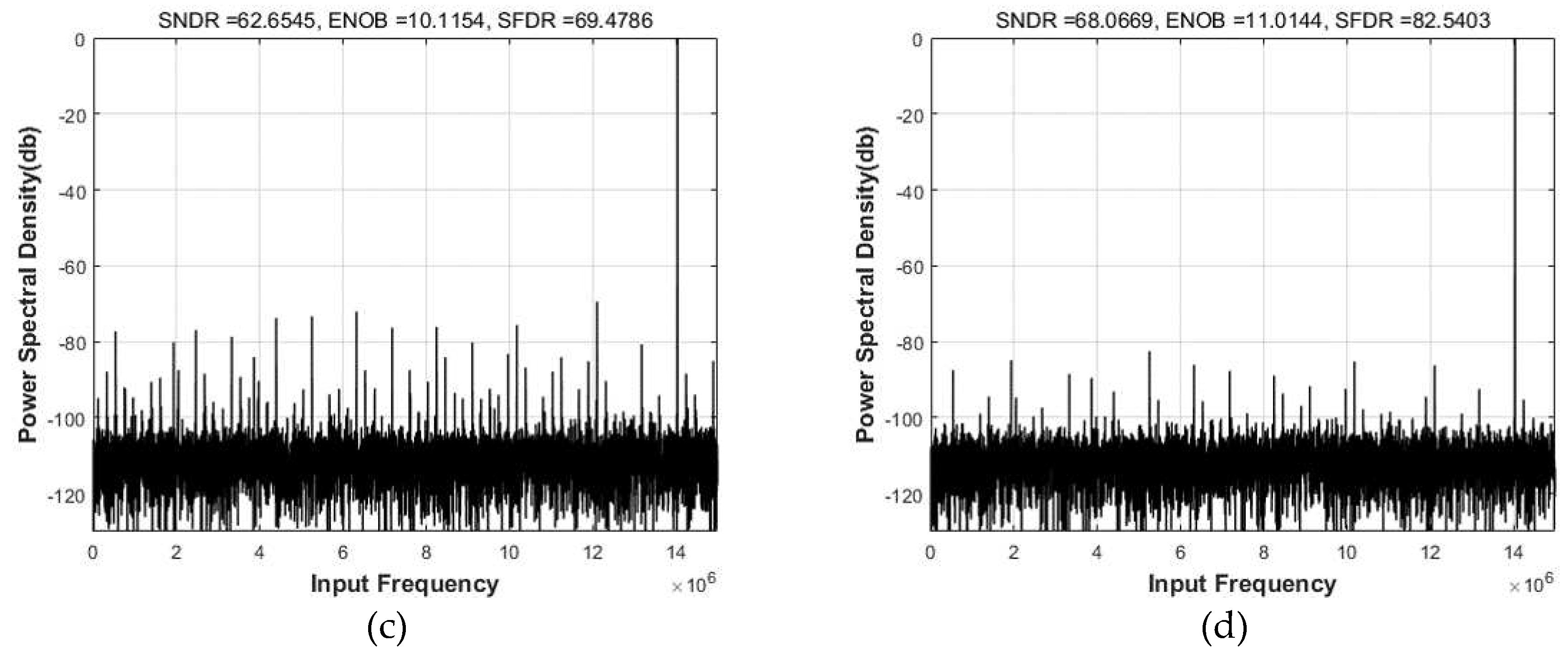
Figure 12.
Measured dynamic performances versus input frequency.
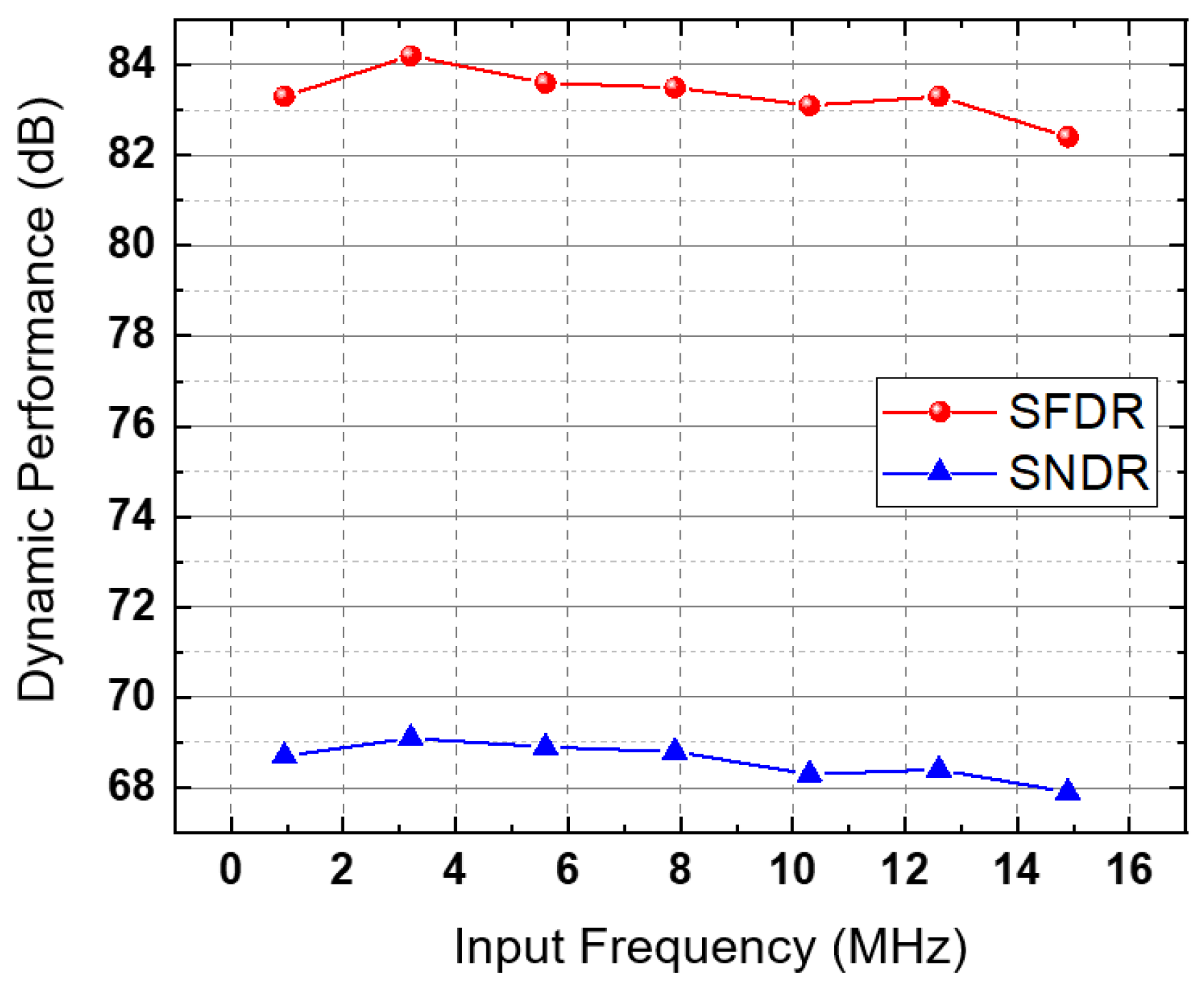
Table 1.
Performance summary.
| Process [um] | 0.18 | |
| Supply [V] | 1.8 | |
| Resolution [bit] | 12 | |
| Sampling Frequency [MHz] | 30 | |
| ADC Area [mm2] | 0.351 | |
| Before Calibration | After Calibration | |
| SFDR [dB] @ Fin=2.09 MHz | 69.2 | 84.1 |
| SNDR [dB] @ Fin=2.09 MHz | 63.9 | 68.9 |
| ENOB [bit] | 10.3 | 11.1 |
| DNL [LSB] INL [LSB] |
+0.82/-0.75 +1.12/-1.79 |
+0.45/-0.41 +0.47/-0.91 |
| Power Consumption [mW] | 35 | 35 |
| FoMw [fj/conv-step] | 911 | 512 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






