Interpretable Geometry Problem Solving Using Improved RetinaNet and Graph Convolutional Network

This paper proposes an interpretable geometry solution based on the formal language set of text and diagram. Geometry problems are solved by machines, which still poses challenges in natural language processing and computer vision. Significant progress promotes existing methods in the extraction of geometric formal languages. However, the neglect of the graph structure information in the formal language and the lack of further refinement of the extracted language set can lead to the poor effect of the theorem prediction and affect the accuracy in problem solving. In this paper, the formal language graph is constructed by the extracted formal language set and used to theorem prediction by graph convolutional network. So as to better extract the relationship set of diagram elements, an improved diagram parser was proposed. The test results indicate that the improved method has good results in solving the problem with interpretability geometry.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Geometry problems are usually described by texts and diagram. The texts represent the known geometric information and the solving objective, while geometric diagram further supplement and formalize the relevant information. Geometry problem solver is asked to take the geometry problem as input and generate solving results. The solver understands the problem by transforming words and diagram into vector representation or formal language set. Then, through logical reasoning solve problem based on extracted information. Math word problem (MWP) solving task is similar with geometry problem and provides many approaches to consider. Wang et al. [1] use the recurrent neural network (RNN) model to transform MWP into equation formworks without sophisticated feature engineering, and use Seq2seq [2] training to maximize the conditional probability of the target solving sequenceuse. An equation normalization method called Ensemble [3] normalizes the duplicated equations with the uniqueness of expression tree and improves the accuracy of target solving sequence prediction. Many additional methods such as generating expression recursively with a goal-driven manner [4], combining knowledge graph to solve problems [5], contrastive learning approach [6], and though general tree to reduce predicted expression [7] etc. are used to improve problem solving ability. Comparing to MWP, geometry problem has an additional diagram which makes geometry problem solving more difficult. Now available approaches such as GeoS parse texts and graph into formal language sets [8], GeoQA [9] uses text encoder and diagram encoder and assists tasks and Inter-GPS [10] through theorems reasoning final results by formal language set. These techniques serve as a foundation for future research.

Despite the promising results demonstrated by prior methods, there are still several issues that require attention and resolution: 1) The interpretability of geometry problem solving is not fully reflected. Similar to the human brain, unknown information is obtained by calculation or theorem based on question description until the corresponding answer is solved. Existing methods rarely demonstrate reasoning processes similar to the human brain, resulting in insufficient interpretability of problem solving. 2) The relationship set obtained in formal language from the problem description is underutilized totally. Although the relationship set extracted by text and chart diagram analyzers parser helps with theorem prediction, the diagram structure present in the relationship set is neglected. Consequently, we posit that there is still potential for enhancing theorem prediction. 3) The current method for detecting geometry diagram symbols is susceptible to gradient disappearance or explosion, which results in a decrease in the fitting speed of the model and a reduction in the effectiveness of object detection. Additionally, the object detection model dataset is considerably distinct from that of the geometry diagram, leading to substandard transfer learning performance. 4) There is still scope for modified in the interpretability of available methods in solving problems. While some methods can provide interpretable solutions , they may not be able to identify the reason for errors once a solution is incorrect, thereby hindering further research.

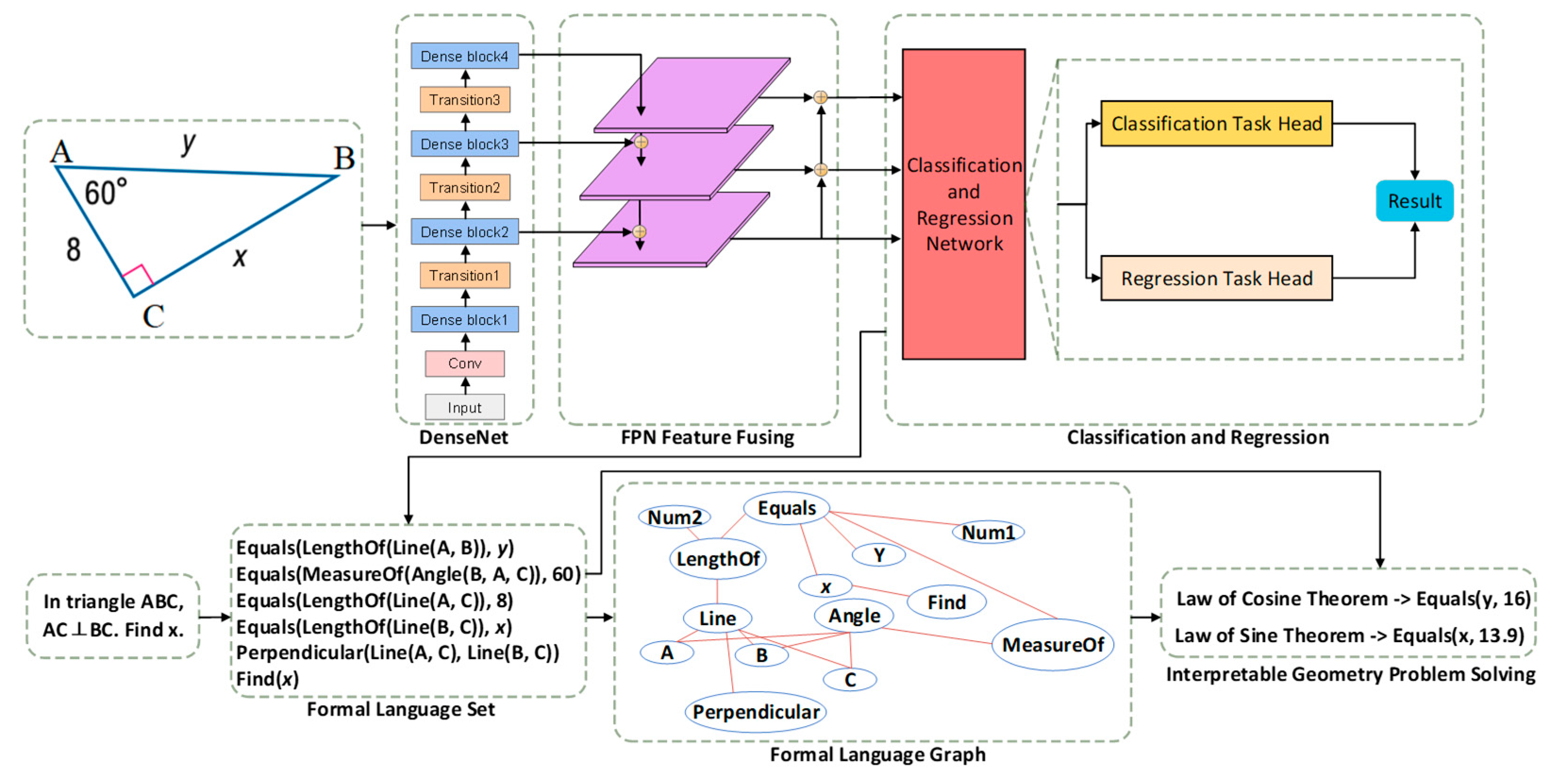
Consequently, we presents a framework for geometry problem solving with interpretablity. First, the text parser and diagram parser extract formal language set from problem description. text parser identifies geometric elements by regular matching to convert the problem text into text logic forms. For geometric diagram understanding, we utilize diagram parser by improved RetinaNet [11] which is efficiently improve the diagram parsing results. For better diagram feature extraction, two auxiliary tasks which fine-tune the DenseNet [12] model were designed. Then, the extracted formal language set is encoded by a graph convolutional neural network. The node representations of abstracted formal language set preserve the graph structure information within it. Finally, the node representations are used to predict theorems of reasoning process, and the solving result is obtained based on the predicted theorems and the extracted formal language set. The proposed framework facilitates future research by providing an interpretable problem solving procedure that can accurately identify the reason for errors if the solving fails.

To sum up, our contribution has the following three points :

The text parser and diagram parser are proposed to extract formal language set from problem description. For text parsing, we use a rule-based text parser to convert the problem text into a text logical form and identify the graph elements in the text through regular expressions. For diagram parsing, we propose an enhanced RetinaNet for detecting diagram symbols. This improved method increases the accuracy of diagram symbol detection and the accuracy of diagram formal language set extraction. Moreover, it leads to a boost in the improved RetinaNet model fitting speed and a reduction of parameters. Two auxiliary tasks also designed to improve parsing procedure.
Using the extracted relationship set for theorem prediction. Through diagram framework in the relationship set, the formal language graph is constructed. We utilize graphic convolution neural network that encodes structural information in the relationship set. The node embedding of formal language set is used to predict theorems.
Explainable problem problem solving has been achieved by predicted theorems and formal language set. The problem solving procedure is in a step by step way to reason by theorems. In the experiment, our geometric solver achieves better results and we also formally show the interpretable solution process.

2. Related Work

2.1. Methods for Math Problem Solving

Mathematical problem solving is mainly done in two regions: mathematical word problems (MWPs) and geometry problems. Compared with MWPs, geometric problems are ordinarily described by joint text and diagram, making the resolution of geometric problems more complicated.

Designing an automatic solver for a long-standing mathematical word problem is a challenging task. The development of MWPs can be roughly divided into three periods. The first stage is rule-based matching and manual definition of templates and rules. Bakman [13] shows a shift from an ocular comprehending of word problems to a process of conscious control by developing an understanding of free-form multi-step arithmetic problems with additional information. Huang [14] aggregates problem information with the same template, aligning the numbers in MWPs to the template generated by the equation. Roy [15] proposed a framework for translating natural language descriptions of concepts into mathematical expressions. MWPs mainly use the strategies of semantic parsing, feature engineering, and statistical learning in the second stage. D. Goldwasser and D. Roth [16] no longer focus on traditional machine learning methods that focus on learning to provide information, but introduce a learning algorithm to explain the problems, getting feedback in the early task before starting learning. The third stage of the solver uses a deep-learning approach. Chiang [17] proposed a neural network method to automatically solve the MWPS according to the semantic operation symbols in the text. Huang [18] proposed for the combination of replication and contrast mechanisms into the sequence to sequence model solves the problem of generating pseudo numbers and generating pseudo numbers at the wrong positions. Although there are many MWPs methods, the current situation is not optimistic, the accuracy of many methods is not guaranteed, and there is much room for improvement in this field.

Due to the structural diversity and layout complexity of geometric pictures, the solution of geometric problems is not explored. However, several large datasets for solving geometric problems have also been published in recent years. Chen et al. [9] proposed the GeoQA dataset, containing 4998 different geometric problems in Chinese middle school examinations, which is solved by comprehensively analyzing multi-modal information and generating interpretability programs. Zhang [19] constructs a new large-scale geometric diagram dataset PGDP5K, proposes an improved instance segmentation method, and combines geometric features and prior knowledge to achieve relationship classification and analysis. Jian et al. [20,21] use feature learning and contrastive learning to solve geometry problems. Lu [10] constructed a dataset Geometry3K consisting of 3002 geometric problems and annotated with formal language. This geometric solution method utilizes formal language and symbolic reasoning, while also designing a theorem predictor to infer theorem applications, resulting in more reasonable and accurate solution results. However, the diagram parser has room for improvement in relation parsing, and the resulting formal language set has not been fully utilized.

2.2. Graph Neural Network

Graphs are being widely used as data information. Semantic description of entities and their relationships through diagrams, including well-defined types and attributes [22], and constructing a graph based on connections in the image, refining the representation of each region on the object through the graph structure [23]. Using GNN maximizes the preservation of graph structure information and attributes [24]. Kipf [25] proposed an effective variant of convolutional neural networks operating on graphs, known as GCN, which has achieved good results in tasks such as intelligent recommendation [26] and text classification [27].

In the field of solving mathematical problems, it is also widely used. Tsai et al. [7] transform the information into a certain vector space and embedded the information in the geometric domain to express the physical meaning of a formula parameter in the decoding process. Wu [5] utilizes graph attention networks and embeds background knowledge to model entities and relationships in the problem into entity graphs, thus proposing a new knowledge perception sequence to solve mathematical problems in tree networks. To our knowledge, there are not many ways to recode the extracted relationship set, and we believe this can increase the utilization of the relationship set [28]. Therefore, we use GCN-based feature extraction methods to encode the extracted formal language set, in order to facilitate solution improvement and preserve the structural information of the graph in the set.

2.3. Methods for Diagram Processing

In geometric problems, graph processing has two categories: feature learning and extracting relationship sets. Feature learning converts graph information into vectors and serves as input to predict the solution result [9,20]. Although the tedious feature engineering can be eliminated in diagram processing, the symbolic information in the image may be lost and lack of interpretability of feature learning results. In the second way, diagram parsing task is considered as relation set extraction with formal language description. Lu et al. [10] use Hough transform to extract geometry primitives then using deep learning method to identify diagram symbols. Zhang et al. proposed PGDPNet [19] using special scene graph generation and graph neural network to get better geometry diagram parsing results. Gan et al. [29,30] identifies visualization primitives from the graph and obtain the relationships between them, and extract text entities and geometric relationships from the problem text using the S² model matching method. However, the necessary information omitted in the question text is included in the figure. This is a complex relationship that cannot be expressed by traditional methods.

Geometry relation extraction such as introducing a submodular optimization formulation and a greedy but accurate approximation procedure for diagram understanding [31], applying rule-based parsing method with regular expressions to perform text parsing and diagrams parsing based on feature encoding [10], which are all used distance and pre-defined rules. However, there is still room for improvement in extracting complex original relationships. Therefore, an automatic graph parser that can extract relationship sets by detecting different graph symbols without intervention has been proposed.

3. Methodology

In this section, interpretable geometry problem solver will be introduced in detail. Firstly, texts and diagram are processed by text parser and diagram parser. Processing results are relation set which is described by formal language. Following Inter-GPS [10], the rule-based text parser is used to extract relation set in texts. For diagram analyzing, the diagram parser is based on improved RetinaNet [11] with DenseNet feature learning and Hough Transformation [32]. The improved RetinaNet detects symbols and texts in the diagram. The detected results combine Hough Transformation to generate diagram relation set following [10]. For better diagram processing, two auxiliary tasks are used to fine-tuning pretrained DenseNet. Secondly, the extracted formal language set builds a formal language graph and is embedded by two-layer graph convolutional network. The embedding results are used for theorem prediction by Seq2Seq [33] network. Finally, the problem is solved interpretably by relation set and theorems. The overall structure of the model is as Figure 1 shown.

3.1. Text Parser

The text parser transforms the text description of the problem into a set of text relations through a rule-based method. The text relationship set is represented in regular language, including formalization of geometric shapes, unary geometric properties, other geometric attributes, binary geometric properties, and numerical attribute information. The geometric information rule representation used in this chapter is shown in Table 1.

The text parser transforms problem texts into text logic forms. Firstly, the regular expression used to identify diagram elements in the texts and use formal language to replace. For example, a string “triangle ABC” matches triangle and is replaced by “Triangle(A,B,C)”. Secondly, unary geometric attributes have been matched, such as a string “Triangle(A,B,C) is equilateral”. The equilateral is found and string is replaced by “Equilateral(Triangle(A,B,C))”. Thirdly, other geometry attributes have been found and replaced, such as a string “area of Triangle(A,B,C)” replaced by “AreaOf(Triangle(A,B,C))”. Fourthly, the binary geometry relations are recognized such as “Line(A,B) is perpendicular to Line(B,C)” replaced by “Perpendicular(Line(A,B), Line(B,C))”. Finally, match the numerical attributes and relations. For example, “Angle(A) and Angle(B) are complementary” can be transformed into: “Equals(SumOf(MeasureOf(Angle(A)),MeasureOf(Angle(B))),90)”. Figure 2 shows the case of text parser extracts formal language set of relations.

Introduce the text parsing process in detail next. The model takes the extracted text features as input, if text contains the “Find” and is the last one, the analytical result is used as the target solution result, parses the text resolution form into a tree structure, and performs a depth-first search. As shown in Algorithm 1, input the extracted text features and output text formal language logic forms.

Algorithm 1 : Parse text logic forms

Input: Extracted text features stored in text_logic_forms_annot T^A
Output: Encoded text formal language logic forms T^F

1：Assign the text logic form to text_logic_forms
2：for each text logic form：
if debug_mode()：Outputs the text logic form
if text contains the “Find” and is the last one：the analytical result is used as the target solution result
else：text is parsed into res for DFS

3：return T^F

3.2. Diagram Parser

The graph parser is used to abstract formal language aggregation from diagram. Traditionally, the diagram is embedded by convolutional networks which need to make more layer of convolutional networks to get deeper representations and global information. The expansion of network layers, however, can render the network vulnerable to issues such as gradient disappearance or explosion, resulting in sluggish or even unfeasible network fitting. Therefore, we proposed improved RetinaNet by replacing backbone of RetinaNet using DenseNet [12] to embed diagram features. Comparing with ResNet [34], in different layers DenseNet also adds connections. The added connections alleviate the gradient disappearance and gradient explosion. Moreover, the improved RetinaNet has fewer parameters which makes diagram parser extracting speed faster.

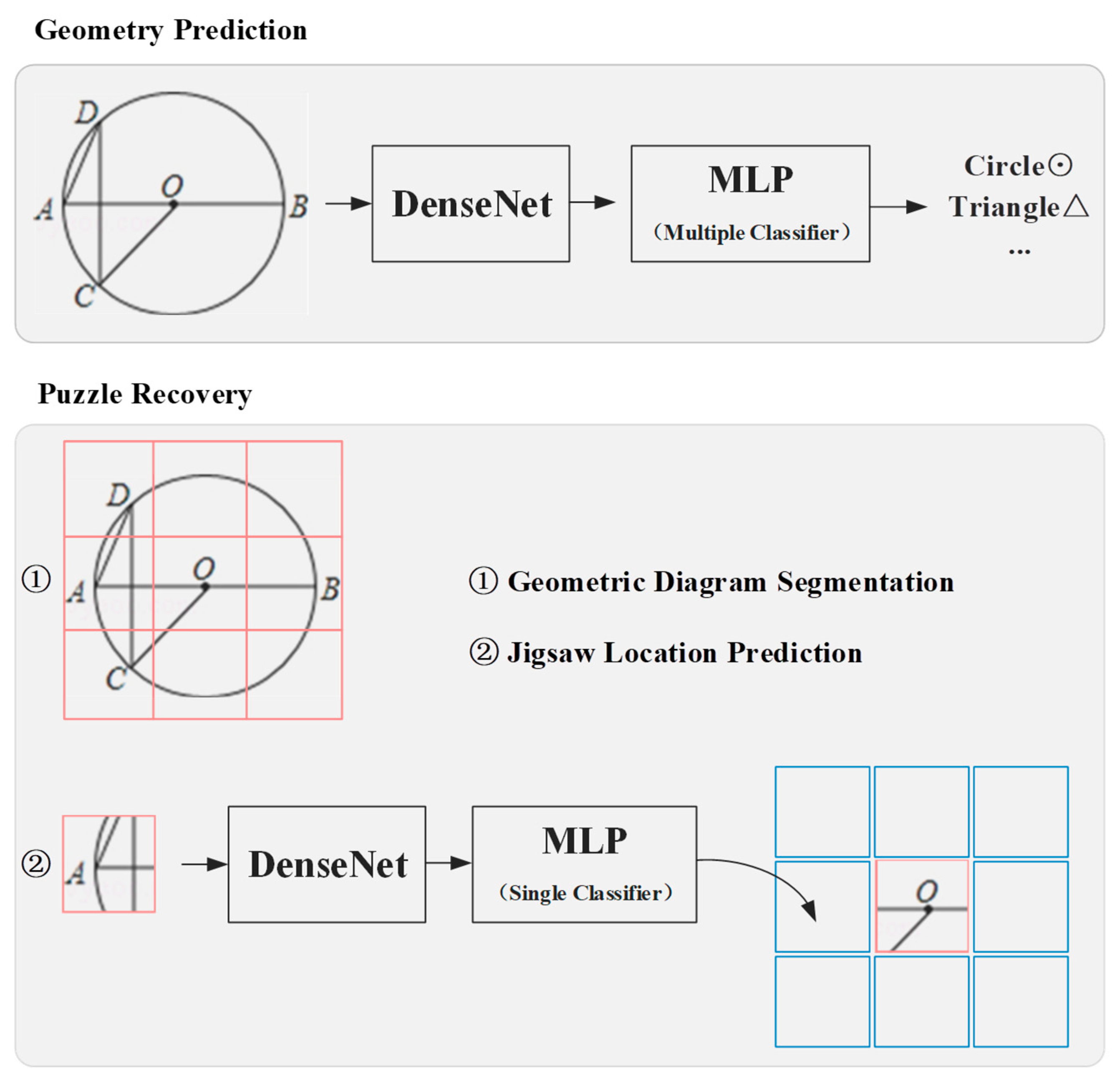
However, using a beforehand DenseNet pattern, which is exercised on real-life pictures, for geometric image feature extraction may result in poor performance due to the significant differences between the two types of images. To overcome this issue, we developed two auxiliary tasks, namely geometry prediction and puzzle restoration, to adjust slightly the DenseNet model for geometric image feature extraction, as illustrated in Figure 3. For the geometry prediction task, we established a direct connection between DenseNet and a multilayer perceptron classifier. The pattern was then trained to perform classifications with geometric shapes, for example, rectangle and round. Regarding the puzzle restoration task, the image is delimited in a 3x3 manner, with the intermediate image slice kept constant and the other eight slices placed randomly. We then trained DenseNet to predict the correct position.

In [31], the problem of diagram understanding is revisited through a novel approach. Do primitive, corners initialization, and initialize mentions for graphs in geometric problems, iteratively add the primitives that maximize gain to recognize primitives and alignments preseted the chart and text. Use the Hough transform for a given graph during initialization primitive. However, the outcome of the Hough transform only provides message regarding the parametric representation of the primitive, and not regarding the zero and end points of the straight lines or circle

Therefore, post-processing is necessary to determine endpoints.

Consequently, based on the function of the Hough transform detecting the visual elements, we extracted the symbols and text areas in the geometric picture through the improved RetinaNet, and then the geometric elements (such as points, lines and circles in the picture) are extracted through the Hough transformation. Optical characters are then identified using the API to identify characters in the text area. After obtaining the element aggregation P and the symbol aggregation S, you require to associate the symbols with the relevant elements. Inspired by Lu et al. [10], this chapter uses an optimization algorithm to complete the association task, as shown in Equation(1):

\begin{matrix} \begin{matrix} m i n \sum_{s} dist (s_{i}, p_{j}) \times 1 \{s_{i} assi gns to p_{j}\} \\ s . t . (s_{i}, p_{j}) \in F e a s i b i l i t y s e t F, \end{matrix} # \end{matrix} (1)

(1)

which the

d i s t

equation determines the Euclidean distance among the sign

s_{i}

and the element

p_{j}

;

F

delimits the signs of geometric constraints, such as the vertical symbols that are only valid for two orthogonal lines.

Next, detail the diagram resolution process. The model takes the stored diagram features as input, first defines the dots and lines in the chart, Sort each form in the diagram logic forms, and place the perpendicular condition to the last one, parsing the chart resolution form into a tree structure, and conducts depth-first search. As shown in Algorithm 2, input the stored graph features and output diagram formal language logic forms.

Algorithm 2 : Parse diagram logic forms

Input: Extracted image features stored in diagram_logic_forms_annot D^A
Output: Encoded diagram formal language logic forms D^F

1：Set up the logical parser L^P according to the debug_mode of the data storage address
2：if diagram_parser() then
3： Defines point in diagram_parser D^P
Using the lambda(), the variable ch is defined as the points in the graph
Travel the point in D^P, the value of debug_mode is true, and output this point
4： Defines line in D^P
for the line segments Ls in the chart：Remove the header-tail space
if Ls has a length of 2 and both the first and second ones are letters：The head-end letters are defined as Ls
5： Defines circle in D^P
for the points in the circle：Take points as a circle definition
6： Assign the graph logic form to logic_forms
7： Sort each form in D^F, and place the perpendicular condition to the last one
8： for each logic form:
if logic form():
if debug_mode()：Outputs this logic form
try：parse the above forms to tree, DFS the parsing tree
except：output error
9： return D^F

3.3. GCN-based Theorem Predictor

Graph convolutional networks (GCNs), the traditional convolution algorithm for processing graph structure data has been adapted to to handle the information of diagram structure. Upon observation, it has been determined that the relation set extracted from between the issue text and graph exhibit a graph structure. Following the approach presented in reference [25], we have employed a graph convolutional network to encode the relation set message into vectors. To begin, we define several constants, such as 90 and 180, among others. We then replace non-constant numbers with the term ‘NumX’, where X represents the ordering of the variables. The node number present in the formal language chart, denoted by |V|, which includes predicates, primitives, marks, and other relevant symbols. To construct the graph, we build undirected edges between predicates.

In form, take into account a graph

G = (V, E)

,wherein

E

and

V (| V | = n)

are collects of edges and nodes, respectively. Let

A

represent the adjacency matrix of the chart, and it refers to the matrix used to indicate the connection of the nodes. For an undirected graph with

N

nodes, the adjacency matrix is a real symmetric matrix of

N * N

. In addition, we introduce the degree matrix

D

of the chart which is used as a matric describing the degrees of each node in the graph, where the degree of the hybrid represents the number of edges attached to that node. Given one-hot embedding of each node

x_{i}

in relation set, each node is embedded by

x_{i} = M x_{i}

. Preset the feature matrix of formal language graph

X = (x_{1}, \dots, x_{n})

, each is a feature vector of

V

. The GCN can only catch the nearest neighbor message via one layer of convolution. When GCN layers are stacked multiple times, the message regarding the larger neighborhood will be consolidated, consequently, we employ a two-layer GCN to encode whole relation set diagram as below the Equation(2):

Z = GCN (X, A)

(2)

where

Z = (z_{1}, \dots, z_{n})

are the node embedding generating by GCN. Then, the embedding of the nodes can be used to predict theorems.

Once the parsing is completed, the extracted aggregate includes all the necessary message. In order to streamline the problem-solving process and improve its accuracy, we utilize a typical Seq2Seq [33] framework to generate theorems. In the encoder section of the model, a bidirectional LSTM having two layers network is used to encode the node succession of the abstract formal language set. Every node inserting is generated using the GCN output. The theorem sequences are then generated by a single-layer Gate Recurrent Unit (GRU), based on the encoder outputs.

Next, the geometric problem solving process is introduced in detail. The model takes the diagram parsing and text parsing results as input, initialization defines the theorem used in the solution process, first try to get the answer without using the theorem, success is return, otherwise continue. As shown in Algorithm 3, enter the diagram parse forms and text logic forms and output target.

Algorithm 3 : Set up, initialize and run the logic solver

Input: diagram_logic_forms D^F and text_logic_forms T^F
Output: target problem solving T

1：Initialization defines the theorem used in the solution process
2：Search initialization：
remove no-use points
initialize the Ls
find all the triangles, quads
solve the relationship between angles, line segments, and arcs3
3：Solutions algorithm：
if round_or_step is false：
try to get the answer before using theorems
else：
check order_lst

4：return target T

3.4. Solving for the Interpretability Geometry Problem

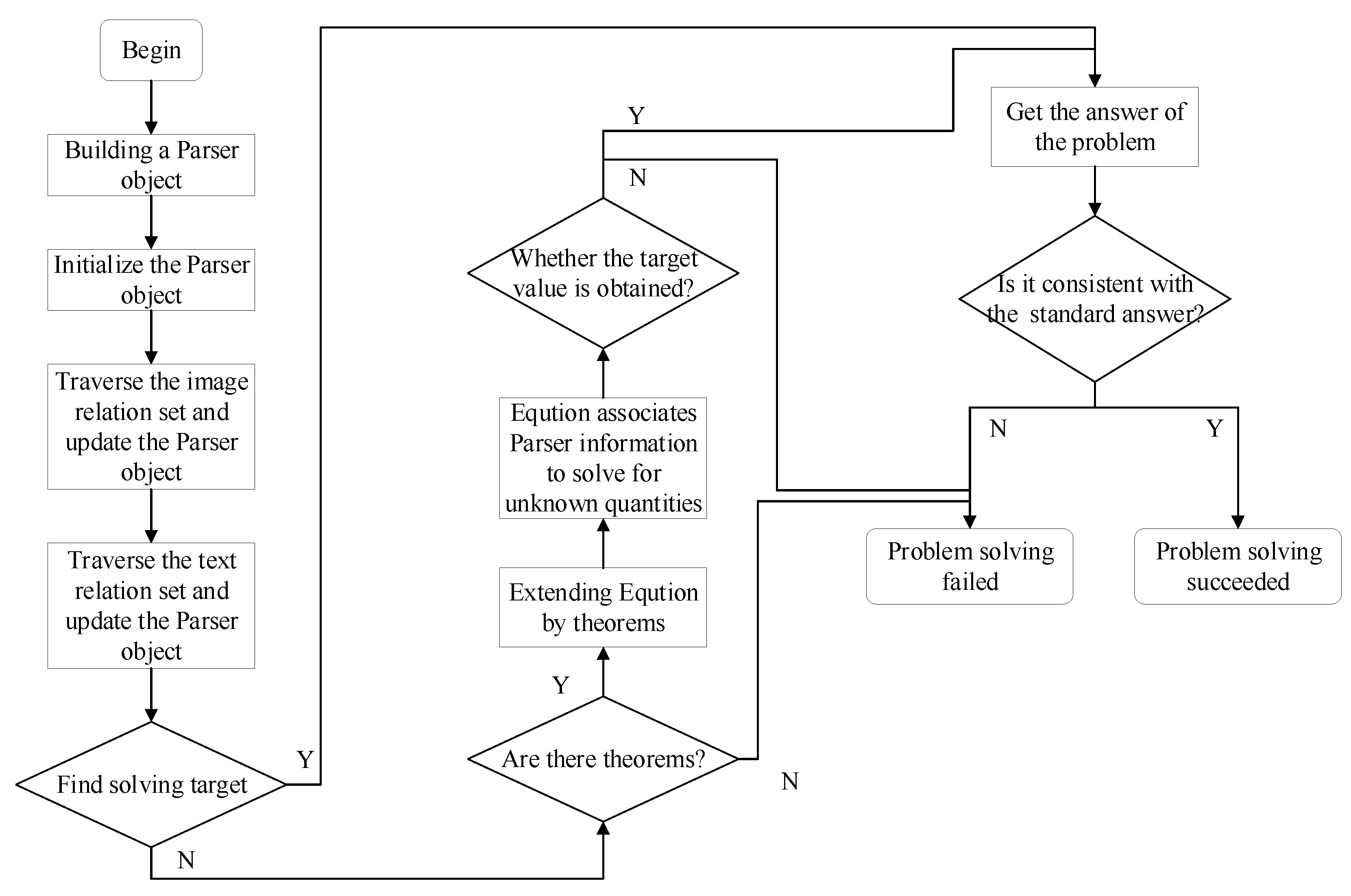
Figure 4 shows the flowchart of interpretable geometry problem solving. In the process of solving, the relationship set is used to update the Parser object. The Parser object contains all the information related to the problem solving, including known points, lines, circles, segment length and angles, etc. After updating the Parser object, we first try to search for the value of the solved target in the Parser object. If not, further reasoning is conducted through the theorem predicted by the graph convolutional neural network. When using theorem reasoning, the equality set Equation, which is an equation with unary or multivariate unknown variables. Connect the equality set Equation with all the information contained in the Parser object in order to try to solve the unknown variables within the equality set Equation. Finally, try to search whether to get the value of the solved target. If the search is successful, the problem is successful. Interpretability is reflected in the process of solving the problem. You can see the internal information of Parser objects in real time, as well as the Equation set generated after the use of the theorem. The solution process is shown in detail, and you can see which theorems make the solution of the unknown quantity successful. If the problem solution fails, we can locate the problem from the text relationship set, the picture relation set and the theorem, which is beneficial to the improvement of the geometric problem solver.

4. Experiment

4.1. Experimental Setup and Implementation Details

4.1.1. Experimental Setup

To estimate the ability of graph element parsing and the problem-solving performance, we use the Geometry3K dataset proposed in Inter-GPS [10]. It includes 3,002 geometric problems annotated in a formal language, and 11 beforehand defined geometric signs. We removed the signs that appeared under 100 times during the course of the experiment. For geometric symbol detection, we used the defined six geometric symbols in Table 2.

We used mAP (mean Average Precision) to estimate the capability of the modified RetinaNet. The mAP is the average of the average accuracy across all symbolic classes. The calculation formula for AP and mAP is as follows, Equation (3) and (4):

A P = \int_{0}^{1} P (R) d R

(3)

m A P = \frac{1}{n} \sum_{i = 1}^{n} A P_{i}

(4)

among, P represents accuracy, which expresses the proportion of forecasted active samples that are actually positive. R represents Recall, which expresses the proportion of actual active samples that are forecasted correctly. The variable n is the number of sign classes, which is 6.

To estimate the ability of our pattern on geometry problem solving, we select the alternative that is near to the output value and has a difference of under 1. If there is no option that satisfies this condition, we randomly select an alternative as the answer. At last, we survey the precision of the model’s answers.

4.1.2. Implementation Details

In the diagram parsing process, we implement the model suggested improvement through the Pytorch framework. DenseNet-121 is used as the backbone of graph analysis, and the method is fine-tuned through two auxiliary tasks, where the maximum count of epoch is 50 and the batch size is 8.In symbol detection, the batch extent is interpose to 2, and the rest hyperparameters and internal settings are the same. Every node in the formal language diagram is inserted in a 256-dimensional vector to implement the prediction of the GCN theorem. The Seq2Seq model is trained by using a batch extent of 16, a maximum epoch of 100 and an Adam optimizer. We eliminated the random error by taking the average of the indicators and trained the model 5 times for each experiment.

4.2. Experimental Results

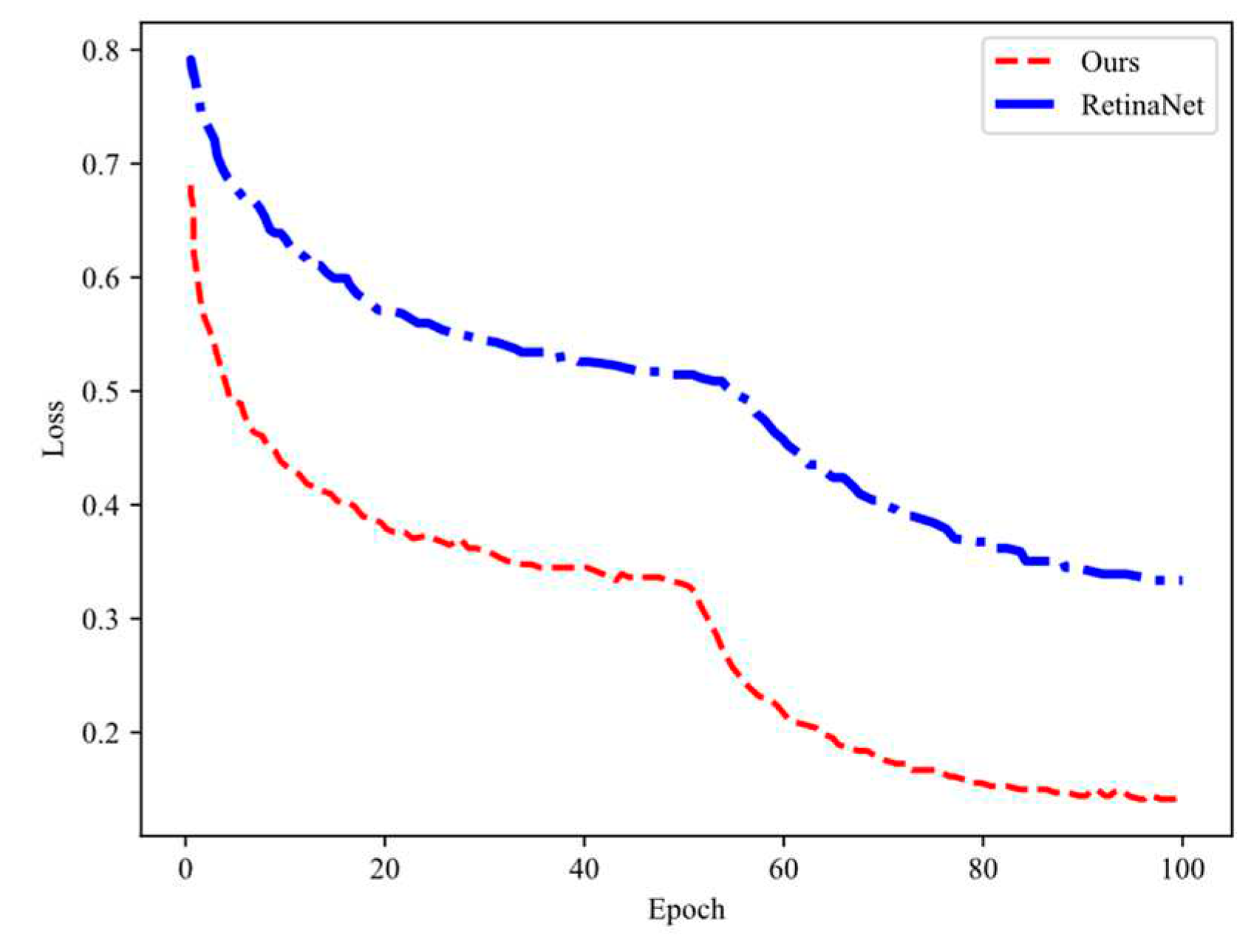
Figure 5 illustrates the tendency of loss change for the progressed algorithm and RetinaNet, which we measured in our research. Upon replacing the RetinaNet backbone network with DenseNet-121, we observed a rapidly decline in the reverse value, indicating a better fit. The follow decline rate existede relatively steady and steadied through 90 exercise epochs. Our findings support the effectiveness of replacing the backbone network and demonstrate an improvement in the detection model convergence speed and effectiveness.

To validate the capability of the progressed graph-resolved sign detection method, we compared SSD, RetinaNet, and our own model by the same dataset, resulting in experimental effects as in Table 3.

Our improved method achieved an mAP of 83.83%, which is a 7.37% improvement over SSD and a 4.27% improvement over RetinaNet. So that, the algorithm progressed in this text under the same dataset outperforms other algorithms in terms of mAP. This indicates that the improved graph parser has efficacious feature definition performance, and the subsequent two auxiliary tasks can effectively improve the detection ability of graph elements.

We evaluated the geometry problem-solving capability using the Geometry3K dataset, as shown in Table 4. We compared our proposed method with RelNet [35], FiLM-BART, Inter-GPS, and our progressed graph parser with GCN theorem predictor. The bolded scores indicate the highest performance, and the “‡” labels the outcome reported by Lu et al. [10]. Our pattern achieves excellent expression on various problem-solving goals. To solve the problem ratio and the goal of the difficult line, compared to Inter-GPS, our method improved performance by 8.3% and 3.7%, respectively. In addition, be similar to RelNet and FiLM-BART, our approach has achieved significant improvements.

The performance of our model in solving geometric problems indicates the effectiveness of GCN theorem predictor and improved graph parser is proved.

4.3. Interpretable Geometry Solution

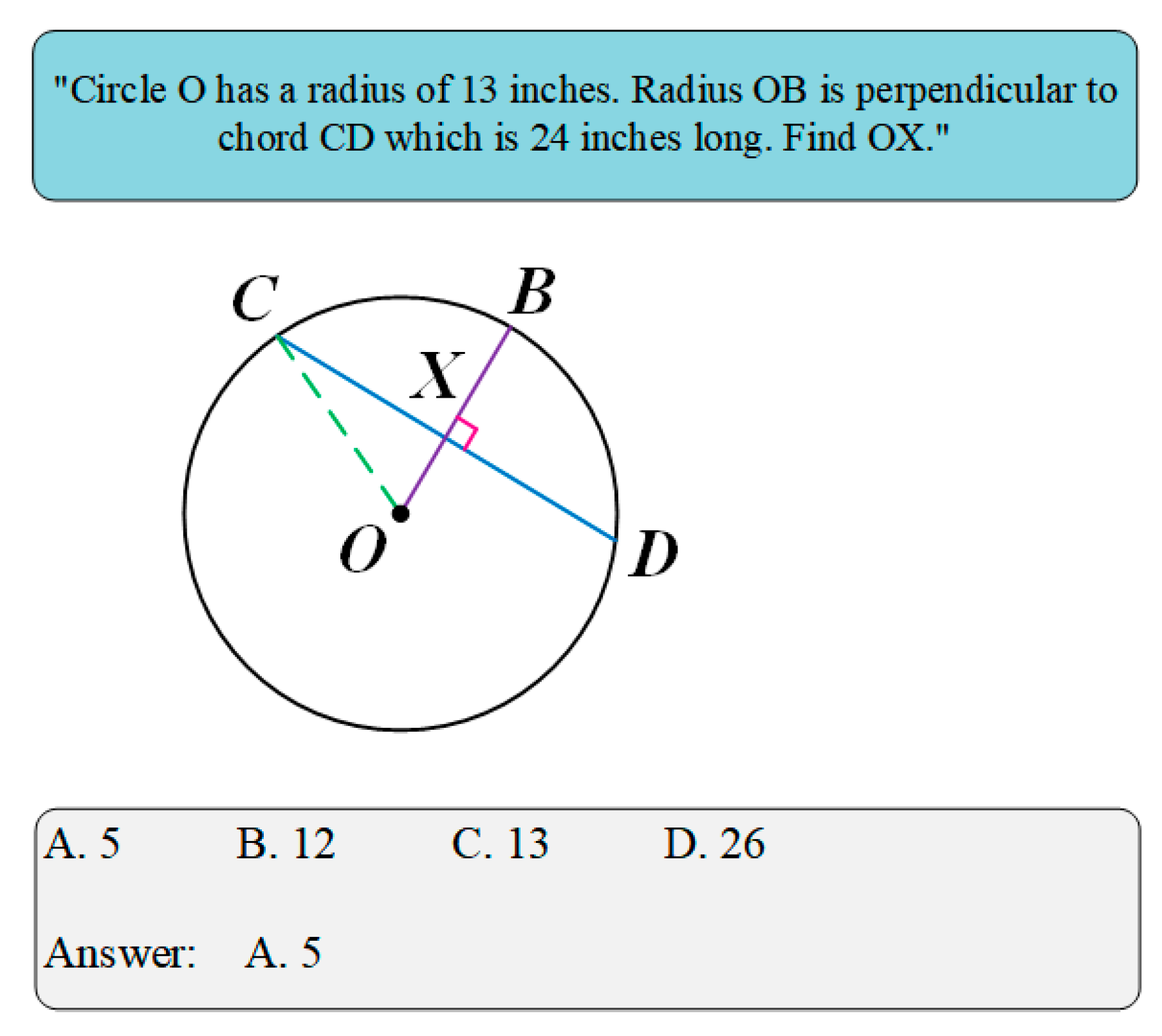
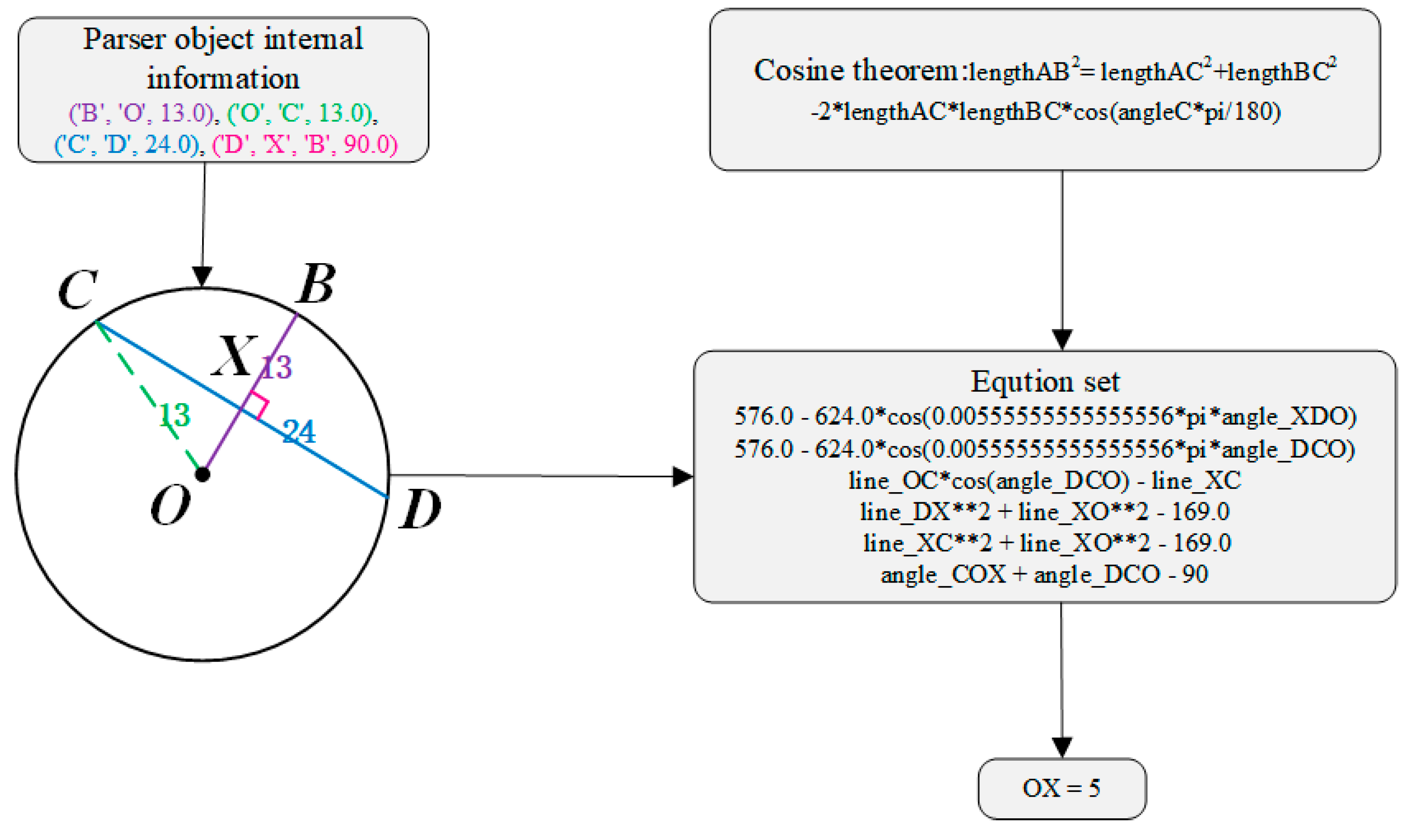
Next the procedure of solving geometric problem interpretably is demonstrated. Taking the example of geometry problem as shown in Figure 6, the steps of our model solving the problem are given in detail.

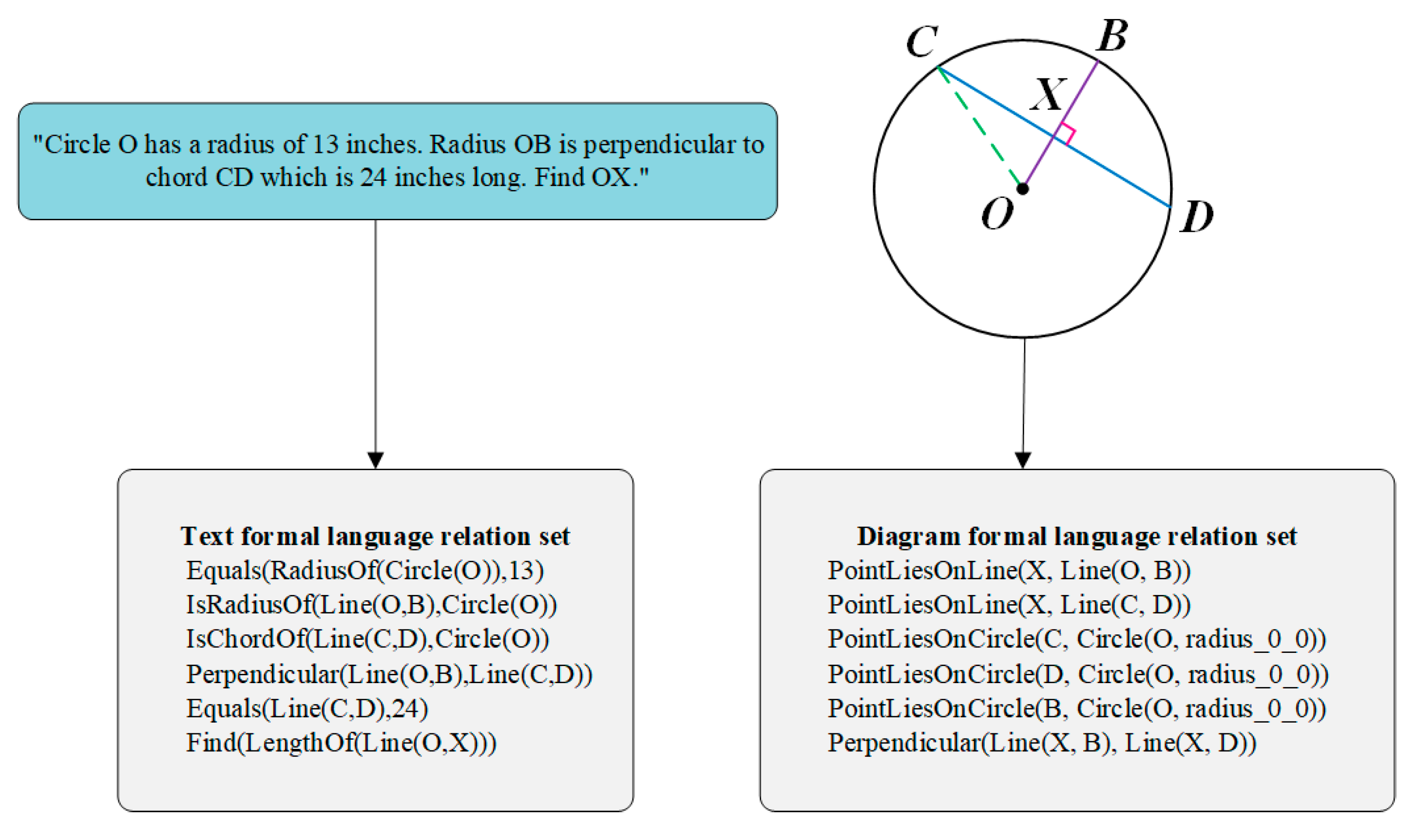
The text and diagram are parsed by text parser and diagram parser. The parsing results are relation set descripted by formal language as shown in Figure 7.

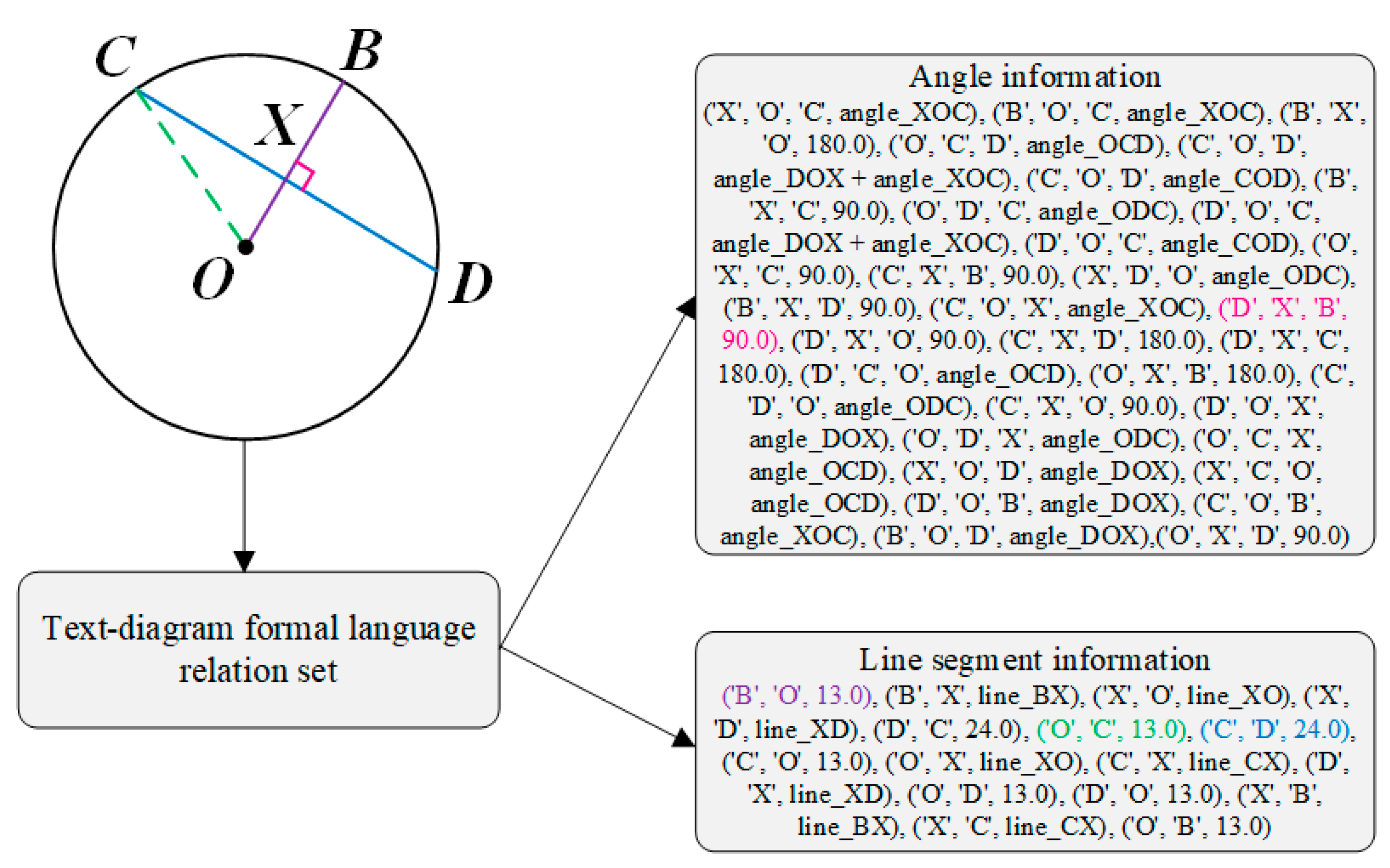
Integrate the text and diagram relation set to update Parser object. Parser object update by walking through every relation in the relation set. After that, the angle information and line segment information within the Parser object are shown in Figure 8.

After going through the internal information of the Parser object, the length of the line segment OX is not found which is solving target. The graph convolution network is used for coding and theorem prediction, the predicted theorem is cosine theorem. The equation set is generated through the cosine theorem, and then the OX length is 5 through the joint vertical equation, as shown in Figure 9. The pattern yields the positive answer and has good interpretability.

4.4. Typical Case Analyzing

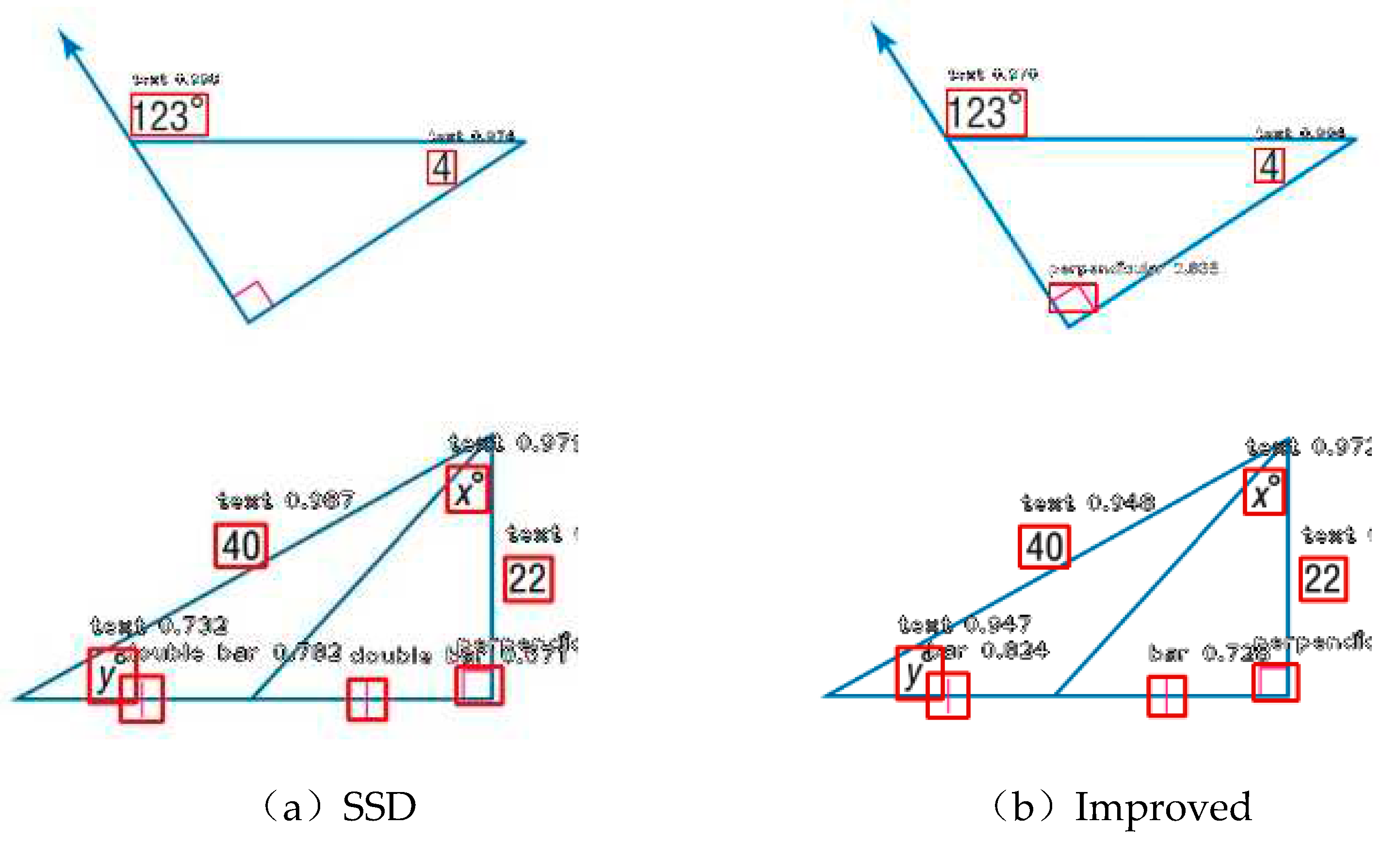
Comparing with conventional SSD, our model illustrates the results of graph aggregation symbol detection. Compared with the vertical symbols that cannot be detected in the first graph, the improved algorithm improves the detection accuracy of the system for smaller set symbols. At the same time, the detected symbols were misclassified due to the misidentification of short bars as double bars. In contrast, the errors of traditional SSD algorithms, the improved algorithm greatly progress the precision of sign detection and classification.

Figure 10. Comparison of SSD and the improved algorithm on symbol detection.

We showed two typical geometry problem solving cases in our task, as shown in Figure 11. By solving the analytical problem of interpretability and obtaining the correct results, the model shows the accuracy of graph geometric symbol detection and the correctness of theorem prediction.

As shown in Figure 12, the symbol ‘A’ not shown in the figure is incorrectly identified, resulting the set of relationships error, so that the problem cannot be correctly inferred. This shows the problem of the geometry solver in the inference.Meanwhile, this highlights the fact that incorrect extraction of the relationship set can seriously affect the solution.

5. Conclusion

In this paper, we solve the geometric solving problem of interpretability by GCN based theorem prediction and progressed sign detection of graph geometry. So as to better abstract the graph element features, we designed two deputy director Wu to fine-tune the graph symbol detector. Secondly, by transforming the extracted formal language set into a formal language graph, we fully utilize the structural message and train the nodes with two layers of GCN. The apply of graph convolutional networks in encoding every node in the relation set proved to be more efficacious. The accuracy of the predictions is improved by taking the embedding of the relational nodes as an input to the prediction. Meanwhile, the test results evidence the effectiveness of the measure and show good performance in the geometric solving problem of interpretability. For future work, we programme to explore methods for self-correcting the extracted relation set, as incorrect extraction can lead to contradictions and failure in problem solving.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No. 62107014) and the Science Foundation of Henan Province (No. 232102320155, 2022ZSZ008, 2023HYTP046). The authors gratefully acknowledge the helpful comments and suggestions of the reviewers, which have improved the presentation.

References

Y. Wang, X. Liu, and S. Shi, “Deep neural solver for math word problems,” in Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, 2017, pp. 845–854. [CrossRef]
K. Cho et al., “Learning phrase representations using RNN encoder-decoder for statistical machine translation,” EMNLP 2014—2014 Conf. Empir. Methods Nat. Lang. Process. Proc. Conf., pp. 1724–1734, 2014. [CrossRef]
L. Wang, Y. Wang, D. Cai, D. Zhang, and X. Liu, “Translating a math word problem to a expression tree,” Proc. 2018 Conf. Empir. Methods Nat. Lang. Process. EMNLP 2018, pp. 1064–1069, 2020. [CrossRef]
Z. Xie and S. Sun, “A goal-driven tree-structured neural model for math word problems,” IJCAI Int. Jt. Conf. Artif. Intell., vol. 2019-Augus, pp. 5299–5305, 2019.
Q. Wu, Q. Zhang, J. Fu, and X. Huang, “A knowledge-aware sequence-to-tree network for math word problem solving,” EMNLP 2020—2020 Conf. Empir. Methods Nat. Lang. Process. Proc. Conf., no. 2019, pp. 7137–7146, 2020. [CrossRef]
Z. Li et al., “Seeking Patterns, Not just Memorizing Procedures: Contrastive Learning for Solving Math Word Problems,” pp. 2486–2496, 2021. [CrossRef]
S. H. Tsai, C. C. Liang, H. M. Wang, and K. Y. Su, “Sequence to General Tree: Knowledge-Guided GeometryWord Problem Solving,” ACL-IJCNLP 2021—59th Annu. Meet. Assoc. Comput. Linguist. 11th Int. Jt. Conf. Nat. Lang. Process. Proc. Conf., vol. 2, pp. 964–972, 2021. [CrossRef]
M. Seo, H. Hajishirzi, A. Farhadi, O. Etzioni, and C. Malcolm, “Solving geometry problems: Combining text and diagram interpretation,” Conf. Proc. - EMNLP 2015 Conf. Empir. Methods Nat. Lang. Process., no. September, pp. 1466–1476, 2015. [CrossRef]
J. Chen et al., “GeoQA: A Geometric Question Answering Benchmark Towards Multimodal Numerical Reasoning,” pp. 513–523, 2021. [CrossRef]
P. Lu et al., “Inter-GPS: Interpretable geometry problem solving with formal language and symbolic reasoning,” ACL-IJCNLP 2021 - 59th Annu. Meet. Assoc. Comput. Linguist. 11th Int. Jt. Conf. Nat. Lang. Process. Proc. Conf., pp. 6774–6786, 2021. [CrossRef]
T. Y. Lin, P. Goyal, R. Girshick, K. He, and P. Dollar, “Focal Loss for Dense Object Detection,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 42, no. 2, pp. 318–327, 2020. [CrossRef]
G. Huang, Z. Liu, L. Van Der Maaten, and K. Q. Weinberger, “Densely connected convolutional networks,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 4700–4708. [CrossRef]
Y. Bakman, “Robust understanding of word problems with extraneous information,” arXiv Prepr. math/0701393, 2007. [CrossRef]
D. Huang, S. Shi, C.-Y. Lin, and J. Yin, “Learning fine-grained expressions to solve math word problems,” in Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, 2017, pp. 805–814. [CrossRef]
S. Roy and D. Roth, “Mapping to declarative knowledge for word problem solving,” Trans. Assoc. Comput. Linguist., vol. 6, pp. 159–172, 2018. [CrossRef]
D. Goldwasser and D. Roth, “Learning from natural instructions,” Mach. Learn., vol. 94, no. 2, pp. 205–232, 2014. [CrossRef]
T. R. Chiang and Y. N. Chen, “Semantically-aligned equation generation for solving and reasoning math word problems,” NAACL HLT 2019 - 2019 Conf. North Am. Chapter Assoc. Comput. Linguist. Hum. Lang. Technol. - Proc. Conf., vol. 1, pp. 2656–2668, 2019. [CrossRef]
D. Huang, J. Liu, C. Y. Lin, and J. Yin, “Neural math word problem solver with reinforcement learning,” COLING 2018 - 27th Int. Conf. Comput. Linguist. Proc., pp. 213–223, 2018.
M. L. Zhang, F. Yin, Y. H. Hao, and C. L. Liu, “Plane Geometry Diagram Parsing,” IJCAI Int. Jt. Conf. Artif. Intell., pp. 1636–1643, 2022. [CrossRef]
F. Guo, P. Jian, Y. Wang, and Q. Wang, “A Framework of Cross-Modal Learning for Solving Geometry Problems,” TALE 2021 - IEEE Int. Conf. Eng. Technol. Educ. Proc., pp. 506–512, 2021. [CrossRef]
P. Jian, F. Guo, Y. Wang, and Y. Li, “Solving Geometry Problems via Feature Learning and Contrastive Learning of Multi-Modal Data,” Comput. Model. Eng. \& Sci., vol. 136, pp. 1707--1728, 2023. [CrossRef]
S. Ji, S. Pan, E. Cambria, P. Marttinen, and P. S. Yu, “A Survey on Knowledge Graphs: Representation, Acquisition, and Applications,” IEEE Trans. Neural Networks Learn. Syst., pp. 1–27, 2021. [CrossRef]
T. Yao, Y. Pan, Y. Li, and T. Mei, “Exploring visual relationship for image captioning,” in Proceedings of the European conference on computer vision (ECCV), 2018, pp. 684–699. [CrossRef]
H. Cai, V. W. Zheng, and K. C. C. Chang, “A Comprehensive Survey of Graph Embedding: Problems, Techniques, and Applications,” IEEE Trans. Knowl. Data Eng., vol. 30, no. 9, pp. 1616–1637, 2018. [CrossRef]
T. N. Kipf and M. Welling, “Semi-supervised classification with graph convolutional networks,” 5th Int. Conf. Learn. Represent. ICLR 2017 - Conf. Track Proc., pp. 1–14, 2017. [CrossRef]
Y. Yang, C. Huang, L. Xia, and C. Li, Knowledge Graph Contrastive Learning for Recommendation, vol. 1, no. 1. Association for Computing Machinery, 2022. [CrossRef]
L. Yao, C. Mao, and Y. Luo, “Graph convolutional networks for text classification,” 33rd AAAI Conf. Artif. Intell. AAAI 2019, 31st Innov. Appl. Artif. Intell. Conf. IAAI 2019 9th AAAI Symp. Educ. Adv. Artif. Intell. EAAI 2019, pp. 7370–7377, 2019. [CrossRef]
F. Guo and P. Jian, “A Graph Convolutional Network Feature Learning Framework for Interpretable Geometry Problem Solving,” in 2022 International Conference on Intelligent Education and Intelligent Research (IEIR), 2022, pp. 59–64. [CrossRef]
W. Gan, X. Yu, C. Sun, B. He, and M. Wang, “Understanding plane geometry problems by integrating relations extracted from text and diagram,” in Pacific-Rim Symposium on Image and Video Technology, 2017, pp. 366–381. [CrossRef]
W. Gan, X. Yu, T. Zhang, and M. Wang, “Automatically Proving Plane Geometry Theorems Stated by Text and Diagram,” Int. J. Pattern Recognit. Artif. Intell., vol. 33, no. 7, 2019. [CrossRef]
M. J. Seo, H. Hajishirzi, A. Farhadi, and O. Etzioni, “Diagram understanding in geometry questions,” Proc. Natl. Conf. Artif. Intell., vol. 4, pp. 2831–2838, 2014. [CrossRef]
M. Seo, H. Hajishirzi, A. Farhadi, O. Etzioni, and C. Malcolm, “Solving Geometry Problems : Combining Text and Diagram Interpretation,” no. September, pp. 1466–1476, 2015. [CrossRef]
Sutskever, O. Vinyals, and Q. V. Le, “Sequence to sequence learning with neural networks,” Adv. Neural Inf. Process. Syst., vol. 4, no. January, pp. 3104–3112, 2014. [CrossRef]
K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., vol. 2016-Decem, pp. 770–778, 2016. [CrossRef]
T. Bansal, A. Neelakantan, and A. McCallum, “Relnet: End-to-end modeling of entities \& relations,” arXiv Prepr. arXiv1706.07179, 2017. [CrossRef]
M. Lewis et al., “BART: Denoising Sequence-to-Sequence Pre-training for Natural Language Generation, Translation, and Comprehension,” pp. 7871–7880, 2020. [CrossRef]
E. Perez, F. Strub, H. De Vries, V. Dumoulin, and A. Courville, “Film: Visual reasoning with a general conditioning layer,” in Proceedings of the AAAI Conference on Artificial Intelligence, 2018, vol. 32, no. 1. [CrossRef]

Figure 1. The general architecture of proposed construct.

Figure 2. Case of text parser extracts relations.

Figure 3. Diagrammatic sketch of two auxiliary tasks.

Figure 4. Flow chart of interpretable geometry problem solving.

Figure 5. Curve of loss value change.

Figure 6. Geometry topic display.

Figure 7. Text-diagram formal language relation set.

Figure 8. Parser object internal information display.

Figure 9. Generating and solving equation sets.

Table 1. Rule based geometric information representation

Geometry	Unary geometric attribute	Other geometric attributes	Binary geometric relationship	Numeric Properties
Point	Isosceles	AreaOf	PointLiesOnLine	HalfOf
Line	Equilateral	PerimeterOf	PointLiesOnCircle	RatioOf
Angle	Reguar	RadiusOf	Parallel	SumOf
Triangle		DiameterOf	Perpendicular	AverageOf
Quadrilateral		CircumferenceOf	IsMidpointOf	Add
Polygon		AltitudeOf	IsRadiusOf	Mul
Pentagon		HypotenuseOf	IsChordOf	Sub
Circle		MeasureOf		Div
Arc		LengthOf		Pow
				Equals
				Find

Table 2. Symbols with occurrence times more than 100 in Geometry3K

	0	1	2	3	4	5
Name	Text	Perpendicular	Bar	Parallel	Angle	Double bar
Number	12365	1165	529	397	196	138

Table 3. Comparison of the results for mAP among the three methods.

Method	SSD	RetinaNet	Ours
mAP(%)	76.46	79.56	83.83

Table 4. Comparison results of different methods on Geometry3K

	All	Angle	Length	Area	Ratio	Line	Triangle	Quad	Circle	Other
RelNet‡	29.6	26.2	34.0	20.8	41.7	29.6	33.7	25.2	28.0	25.9
FiLM-BART‡	33.0	32.1	33.0	35.8	50.0	34.6	32.6	37.1	30.1	37.0
Inter-GPS‡	57.5	59.1	61.7	30.2	50.0	59.3	66.0	52.4	45.5	48.1
Ours	56.1	61.2	57.0	32.1	58.3	63.0	62.2	48.3	47.6	44.4

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer