A Portable Three-Layer Compton Camera for Wide-Energy Range Gamma-Ray Imaging: Design, Simulation and Preliminary Testing

(1) Background: The imaging energy range of a typical Compton camera is limited due to the fact that scattered gamma photons are seldom fully absorbed when the incident energies are above 3 MeV. Further improving the upper energy limit of gamma-ray imaging has important application significance in active interrogation of special nuclear materials and chemical warfare agents, as well as range verification of proton therapy; (2) Methods: To realize gamma-ray imag-ing in a wide energy range of 0.3~7 MeV, a principle prototype, named a portable three-layer Compton camera, was developed using the scintillation detector that consist of an silicon photo-multiplier array coupled with a Gd3Al2Ga3O12:Ce pixelated scintillator array. Implemented in a list-mode maximum likelihood expectation maximization algorithm, a far-field energy-domain imaging method based on two-interaction and three-interaction events was applied to estimate the initial energy and spatial distribution of gamma-ray sources. The simulation model of detec-tors was established based on Monte Carlo simulation toolkit Geant4. The reconstructed images of a 133Ba, a 137Cs and a 60Co point-like sources were successfully obtained with our prototype in laboratory tests and compared with simulation studies; (3) Results: The proportion of effective imaging events accounted for about 2%, which made our prototype realize reconstructing the distribution of a 0.05 μSv/h 137Cs source in 10 seconds. The angular resolution for resolving two 137Cs point-like sources was 15°. Additional simulated imaging of the 6.13 MeV gamma-rays from 14.1 MeV neutron scattering with water preliminarily demonstrated the imaging capability for high incident energy; (4) Conclusions: We concluded that the prototype had good imaging per-formance in a wide energy range (0.3~7 MeV), which showed potential in several MeV gam-ma-ray imaging applications.

Keywords:

Subject: Physical Sciences - Radiation and Radiography

1. Introduction

The Compton camera [1], which reconstructs images to visually display the spatial distribution of radioactive materials, has found extensive applications in astronomical observation [2], nuclear medicine [3], proton therapy [4,5], neutron activation imaging [6,7], and environmental measurement [8,9]. These applications benefit from the Compton camera's advantages of a wider field of view (2π or 4π) and a wider energy range (from several hundreds of keV to a few MeV). In a Compton camera, the single scattering events occurring at two pixels of the detector are the main effective imaging events, that is, the incident gamma photon scatters at the first interaction position, and the scattered photon deposits all of its energy at the second interaction position. However, with the increase of energy, the probability of a scattered gamma photon being fully absorbed will decrease, and the probability of continuing scattering or escaping the detector will increase. In addition, the pair-production events that occur in high energy gamma-ray imaging will cause the image artifacts to contaminate the image [10]. Therefore, the imaging energy range of a typical Compton camera usually ranges from 0.3 to 3 MeV.

Further improving the upper energy limit of traditional gamma-ray imaging has important application significance in many fields. In active interrogation of special nuclear materials (SNM), the energy range of interest is between 2.5 and 6 MeV [11]. In detection of chemical warfare (CW) agents using fast 14 MeV neutrons, measuring the ratios of chemical elements abundances: C/Cl, C/N, C/S, C/F, C/P, C/O requires collecting gamma-rays within 8 MeV [12]. In the range verification in proton therapy, prompt gammas (PGs) are emitted from nuclear de-excitation in a characteristic spectrum, with a broad continuum ranging from 1 to 7 MeV [13], the frequently-used among them are 4.44 and 6.13 MeV gamma-rays, from the de-excitation of ¹²C* and ¹⁶O*, respectively.

To realize Compton imaging above 3 MeV, some improved methods on the basis of scattering-absorption structure are adopted, such as adding scatterer layers and increasing the absorber volume [3,4,5,14]. A different approach is to consider more than two interaction events based on three parallel detector layers, which is called three-Compton telescope [6,15]. In this method, incident gamma photons are scattered at two interaction positions in the first two layers of detectors, and the second scattered photons do not need to be fully absorbed at the third interaction position in the third layer of detectors. In recent years, the IRIS group of IFIC-Valencia has developed and improved the prototype using this method for proton therapy treatment monitoring, which is called MACACO (Medical Applications CompAct COmpton camera) [16,17,18]. The prototype is composed of three detector layers, each made of a LaBr₃ monolithic scintillator crystal coupled to a silicon photomultiplier (SiPM) array.

This article aims to realize gamma-ray imaging in a wide energy range of 0.3~7 MeV using three position-sensitive detector planes. Considering the small size and easy handing of SiPM, as well as the advantages of low cost and high detection efficiency of scintillator, each detector plane is composed of a pixelated scintillator array coupled to a SiPM array. Ce-doped Gadolinium Aluminum Gallium Garnet (Gd₃Al₂Ga₃O₁₂:Ce, GAGG:Ce) is selected as the scintillator material due to the characteristics of high light yield, good energy resolution, non-hygroscopic and no natural radioactivity [19]. The position-sensitive detector of GAGG:Ce array coupled to SiPM array has been widely applied in Compton imaging system and achieved good imaging results [3,4,7,8,9,20,21]. In our previous work, two types of GAGG-SiPM detector modules with varying thicknesses have been designed to achieve three-Compton imaging in the energy range of 0.3~7 MeV [22]. Experimental testing and evaluation were done on the position resolution and pixel energy resolution of detector modules.

In this paper, the distance between three detector modules was further analyzed from the perspective of the effective event ratio based on Geant4 Monte Carlo simulation toolkit. To obtain the energy and direction of gamma-ray sources with a wide energy-domain, in addition to using three-interaction (3-interaction) events, the space and spectral reconstruction were carried out for two-interaction (2-interaction) events according to the information of interaction position and deposited energy. The principle prototype, named a portable three-layer Compton camera (TLCC), was developed on the basis of detector module, data acquisition system and image reconstruction algorithm. The imaging performance of the prototype was evaluated by using single point-like sources and multiple point-like sources under simulation and experimental conditions. Based on the emitted gamma-ray data coming from 14.1 MeV neutron scattering with water, the imaging ability of the system to a 6.13 MeV source was demonstrated by simulation. This work will provide a reference for the research of Compton imaging technology under several MeV energies.

2. Materials and Methods

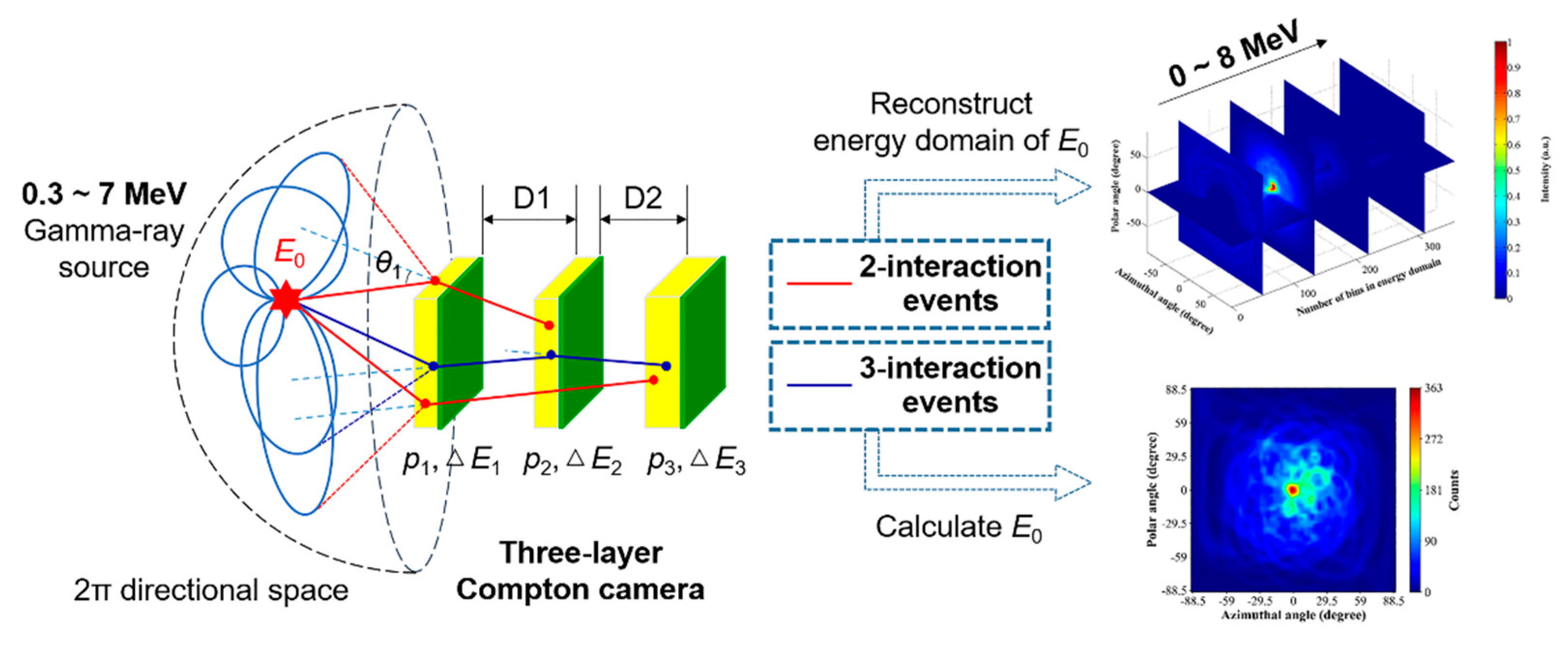
2.1. Wide-energy range gamma-ray imaging

To reconstruct the incident direction of 0.3~7 MeV gamma-rays, the far-field energy-domain imaging method based on 2-interaction and 3-interaciton events of TLCC is proposed, as shown in Figure 1. A 2-interaction event is that a gamma-ray only interacts with the pixels of two detectors (Det1-Det2, Det1-Det3, or Det2-Det3) and a 3-interaction event is that a gamma-ray interacts with the pixels of three detectors sequentially (Det1-Det2-Det3). Here, in the three-layer detector structure, the sequence of events is determined according to the physical order of the detectors. However, it is noteworthy that events with deposited energy greater than 256 keV at the scattering position should be excluded to eliminate back scattering [22].

In Compton imaging, each event will create a cone with an opening apex angle derived from the Compton scattering formula, known as a Compton cone. The cone's axis is given by the vector connecting the first two interaction positions. The surface of a Compton cone represents the possible original directions of the incident gamma photon. If the incident energy E₀ and the energy loss at the first interaction △E₁ are known, then the opening angle (the Compton scattering angle at the first interaction, θ₁) is represented by:

c o s θ_{1} = 1 - m_{e} c^{2} (\frac{1}{E_{0} - Δ E_{1}} - \frac{1}{E_{0}}),

(1)

where m_ec² is the rest mass of the electron.

Actually, there is no priori knowledge of the incident gamma-ray energy in some applications. Therefore, how to estimate the initial energy becomes the key to realize Compton imaging. For a 3-interaciton event which a gamma photon undergoes two successive Compton scatter interactions followed by a third interaction, the energy of incident gamma photon can be calculated. If the interaction positions at the 3-interaction sites are p₁, p₂, and p₃, the energy losses at each detector layers are △E₁, △E₂, and △E₃, and the scattering angle at the first two interaction sites are θ₁, θ₂, then the incident energy E₀ can be calculated as:

E_{0} = Δ E_{1} + \frac{1}{2} (Δ E_{2} + \sqrt{Δ E_{2}^{2} + \frac{4 m_{e} c^{2} Δ E_{2}}{1 - c o s θ_{2}}}),

(2)

c o s θ_{2} = \frac{p_{1} p_{2} \cdot p_{2} p_{3}}{| p_{1} p_{2} | | p_{2} p_{3} |} .

(3)

However, the efficiency of collecting 3-interaction events is significantly lower. It is necessary to estimate the possible incident energy according to the summation of the observed 2-interaction events. In this paper, the spectral dimension is added to the emission distribution, and it is extended over both spatial domain and energy domain. Thus, each event can obtain the emission energy from any value in the spectral range. Considering that the gamma-ray emission follows a Poisson distribution, the list-mode maximum likelihood expectation maximization (LM-MLEM) [23] is appropriate for reconstructing the initial energy and spatial distribution of gamma-ray sources through the iterative calculation. Here, the system matrix t_ij_,E0, presents the probability of an emission from the jth pixel under incident energy E₀ to be detected as the ith event. The LM-MLEM algorithm is described as follows:

λ_{j, E_{0}}^{n} = \frac{λ_{j, E_{0}}^{n - 1}}{s_{j, E_{0}}} \sum_{i} \frac{t_{i j, E_{0}}}{\sum_{k} t_{i k, E_{0}} λ_{k, E_{0}}^{n - 1}},

(4)

where λ_j_,E0ⁿ denotes the image value of pixel j after n iterations, s_j_,E0 is the sensitivity of the detector for pixel j. In this paper, the Compton cone of each event is expressed in spherical coordinate system, and the imaging space for Formula (4) is the 2π directional space. Therefore, s_j_,E0 is assumed to be uniform in this work. When the source-to-detector distance is large comparing with the detector size, the vertex of each Compton cone is approximately considered to be at the coordinate origin. Under the far-field approximation, the system matrix t_ij_,E0 is formulated as:

t_{i j, E_{0}} = \frac{p_{i} (E_{0})}{ω (θ_{i, E_{0}}) \sqrt{2 π} σ} e x p [- \frac{{(θ_{i, E_{0}} - α_{i j, E_{0}})}^{2}}{2 σ^{2}}],

(5)

where p_i(E₀) is the probability of the event origins from incident energy E₀, θ_i_,E0 is the scattering angle calculated from Formula (1), ω(θ_i_,E0) is the error weight coefficient related to the scattering angle θ_i_,E0, α_ij_,E0 is the angle between the spherical coordinate vector and the Compton cone axis vector, σ is the Gaussian width of the cone (a constant small value correspond to the uncertainty of the cone angle). The reconstructed result of gamma-ray direction is expressed by polar angle and azimuthal angle (θ, φ). In Formula (5), ω(θ_i_,E0) and p_i(E₀) are described in detail as:

ω (θ_{i, E_{0}}) = π (θ_{i, E_{0}} + \frac{\sqrt{π} σ}{2} e x p [- \frac{θ_{i, E_{0}}^{2}}{2 σ^{2}}] + θ_{i, E_{0}} \cdot e r f (\frac{θ_{i, E_{0}}}{\sqrt{2} σ})),

(6)

p_{i} (E_{0}) = {\begin{cases} \frac{1}{\sqrt{2 π σ_{E_{1, i}}^{2} + σ_{E_{2, i}}^{2}}} e x p [- \frac{{(E_{0} - E_{1, i} - E_{2, i})}^{2}}{2 (σ_{E_{1, i}}^{2} + σ_{E_{2, i}}^{2})}], i f E_{0} \in [E_{1, i} + E_{2, i} \pm 3 (σ_{E_{1, i}} + σ_{E_{2, i}})] \\ {\frac{2 π m_{e} c^{2}}{{(E_{0} - E_{1, i} - E_{2, i})}^{2}} \frac{d σ_{C} (E_{0} - E_{1, i})}{d Ω} |}_{E_{2, i}}, i f E_{0} > E_{1, i} + E_{2, i} + 3 (σ_{E_{1, i}} + σ_{E_{2, i}}) \end{cases},

(7)

E_{0}_{b i n} [i] = {\begin{cases} (0.5 + i) \times 5,_{} i f_{} i < 200 \\ 1000 + (0.5 + (i - 200)) \times 10,_{} i f_{} 200 \leq i < 300 \\ 2000 + (0.5 + (i - 300)) \times 100,_{} i f_{} i > 300 \end{cases},

(8)

where E_1,i, E_2,i, σ_E_1,i, and σ_E_2,i are the deposited energy and Gaussian standard deviation of the first two interactions, respectively. From Formula (7), the system matrix is divided into photoelectric absorption and Compton scattering according to the second interaction. If the scattered gamma photon from the first interaction is fully absorbed at the second interaction, a Gaussian function is used to describe the situation (E₀∈[(E₁+E₂)±3(σ_E₁+σ_E₂)]). If the second interaction is a Compton scattering and the scattered photon escapes the detector, thus only partial energy of the incident gamma-ray is deposited (E₀>(E₁+E₂)+3(σ_E₁+σ_E₂)). The term dσ_C(E₀-E_1,i)/dΩ|_E_2,i presents the probability that the gamma photon with energy (E₀-E₁) deposits E₂ in the second interaction by Compton scattering, which is predicted by the Klein-Nishina formula.

In the far-field energy-domain imaging method, the spatial reconstruction part is similar to that proposed by Kishimoto A [3] and Omata A [21], and the energy domain part is similar to that proposed by Xu D [24] and Muñoz E [25]. In order to reduce the burden of matrix calculation in iterative reconstruction, the spatial and spectral imaging space are simplified appropriately. The number of bins in (θ, φ) spatial domain is set to 60×60, which means the angle accuracy of each bin is 3°. The number of bins in E₀ energy domain is set to 360, which is an inter-partition distribution covering the energy range of 0 to 8 MeV, as shown in Formula (8).

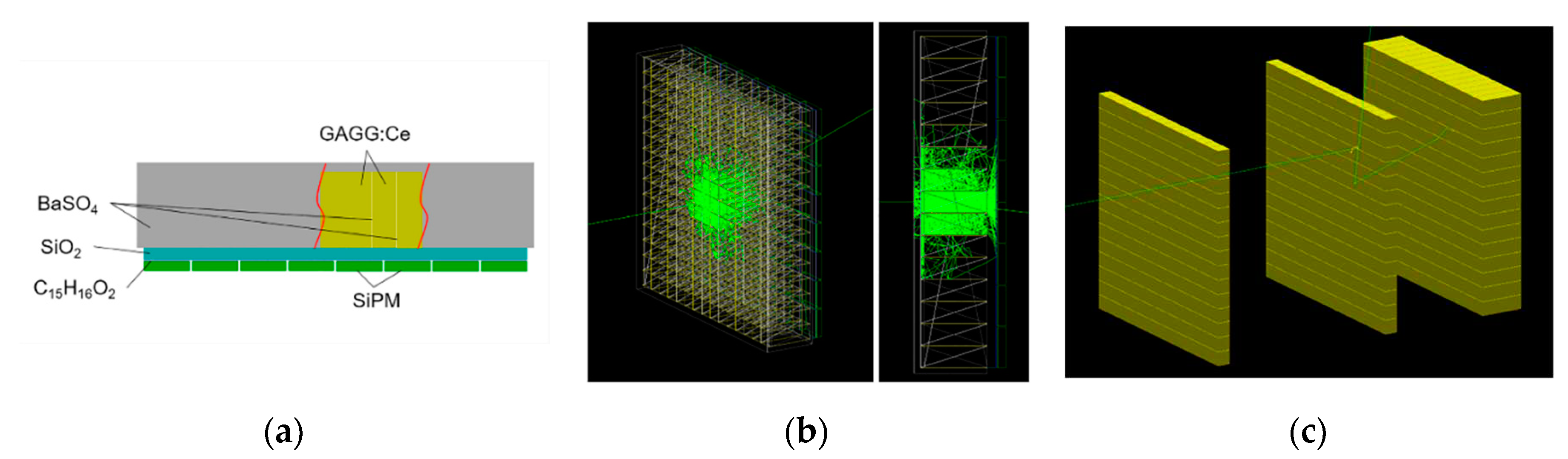
2.2. Materials and Monte Carlo simulation

In the prototype of TLCC, each layer is a position-sensitive detector composed of GAGG:Ce scintillator array and SiPM array. In order to improve the position resolution accuracy of the detector while taking into account the complexity of readout electronics, the pixel number of scintillator array is usually larger than that of SiPM array. An optical light guide with a certain thickness should be placed between scintillator array and SiPM array, so that the scintillation light generated by the interacting crystal pixel can be shared by neighboring SiPM pixels to avoid saturation of a single SiPM pixel. Based on Geant4 Monte Carlo simulation toolkit [26], a detector simulation model including optical parameters of materials was constructed in our previous work [22], as shown in Figure 2.

In the simulation, the number of pixels of SiPM array is set as 8×8=64, in which the effective area of a single pixel is 6×6 mm² and the pixel gap is 0.2 mm. At this time, the area of SiPM array is 49.4×49.4 mm². The thickness of BaSO₄ reflective layer between pixels of scintillator array is fixed at 0.1 mm. The spatial resolution and interaction event types of the detector are studied by changing the geometric parameters such as GAGG pixel size, pixel thickness and light guide thickness. The physical process is defined by PhysicsList class of Geant4, in which G4DecayPhysics class and BiasedRDPhysics class are selected to contain radioactive decay process, G4EmStandardPhysics class is selected to contain electromagnetic interaction process, and G4OpticalPhysics class is selected to contain optical process. Following simulation study, the GAGG pixel number and pixel size were designed to be 15×15 and 3.2×3.2 mm². The pixel thickness was designed to be 3 mm or 10 mm, which corresponded to the first two detectors and the third detector respectively. The thickness of the light guide was expected to be 1.25 mm.

In this work, the distance between the three-layer detectors (D1, D2) is further studied to maximize effective detection efficiency for a wide range of gamma-ray energy. In Geant4, the initial gamma-ray is generated by PrimaryGeneratorAction class. The point-like source with mono energy of 364.4, 2614.5, and 6130 keV is defined for ¹³¹I, ²³²Th and high energy gamma-ray emitter as an example, respectively, with a 1 m distance away from the centre of the detector. Here, the mono energy sources are used to better calculate the percentage of events that are fully-absorbed through two or three interactions under different incident energies. The results are shown in Figure 3. It can be seen that whether there are two or three interactions, the probability of full-absorbed decreases with the increase of D1 and D2. Among them, the distance between the second and third layers (D2) has a more significant influence. In addition, with the increase of incident energy, the proportion of 2-interaction full-absorbed decreases sharply, while the proportion of 3-interaction full-absorbed increases gradually. In order to collect more effective imaging events in the energy range of 0.3 to 7 MeV, according to the simulation results and the actual physical volume of the detector module, the distance between the three-layer detectors is set to D1=40 mm and D2=22 mm.

Based on the detector simulation model, the imaging performance of the prototype, such as detection efficiency, field-of-view (FOV) and angular resolution, can be evaluated and compared with experimental results. To match the real radionuclide testing conditions, the gamma photon will be emitted according to the probabilities per decay, i.e., for a ⁶⁰Co nuclide, the energy of 1173.2 keV is emitted with 0.9985 probability, and the energy of 1332.5 keV is emitted with 0.999826 probability. The total emission gamma photon number N of a nuclide is obtained by multiplying the emission probability of each energy branch by the base number of 10⁷. The source-to-detector distance is set to 1 m. The emission direction of gamma-ray source is defined within a fixed solid angle instead of 4π to improve the calculation efficiency. In this work, the solid angle Ω is set to the angle corresponding to a circle with a radius of 10 cm at 1 m, which is enough to cover the area of the detector. At this time, Ω is calculated to be 0.031 sr.

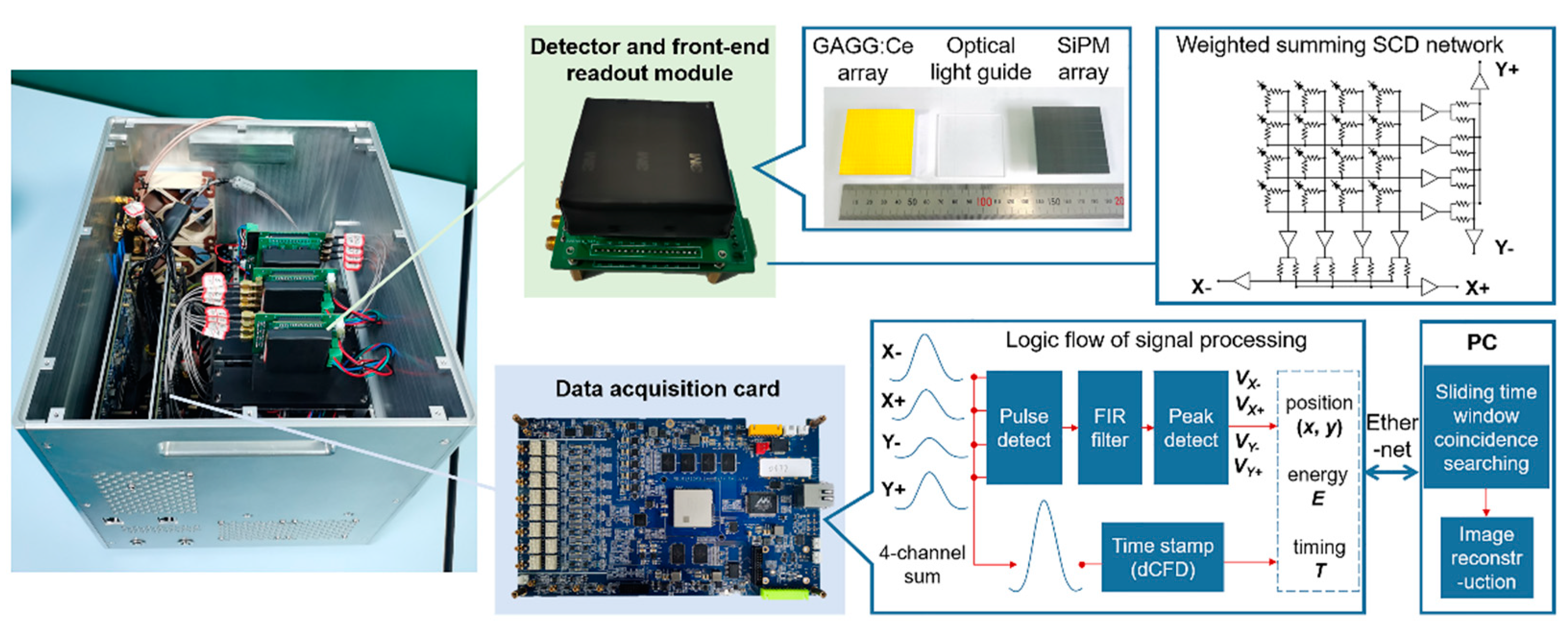
2.3. The principle prototype and data acquisition

The TLCC prototype, shown in Figure 4, is mainly composed of detector and front-end readout modules, data acquisition system and image reconstruction software. The system has three position-sensitive detectors: two scatterers and an absorber of GAGG:Ce scintillator (Epic Crystal Co., Ltd) with a density of 6.63 g/cm³. All the GAGG:Ce array blocks consist of 15×15 pixels separated by a 0.1 mm BaSO₄ spacer. The GAGG:Ce array is coupled to a 8×8 SiPM array ArrayJ-60035-64P (Semiconductor Components Industries, LLC), in which the sensitive area of a pixel is 6.07×6.07 mm². The size of each GAGG:Ce element in the array is 3.2×3.2×3 mm³ for the scatterer and 3.2×3.2×10 mm³ for the absorber respectively. There is a 1.25 mm thick SiO₂ light guide coupled between GAGG:Ce array and SiPM array. The periphery of the detector module is wrapped with Teflon and treated by light-shielding.

The weighted summing symmetric charge division (SCD) network [27] is used as the front-end readout circuit connected to the SiPM array, which achieves transferring 64-channel signals of 8×8 array SiPM to 4-channel quasi-Gaussian signals. A total of 12 output signals from three detector modules are fed to the data acquisition card. After digital sampling by analog-to-digital converters (ADCs), the pulse detection, FIR filtering and peak detection are completed in field-programmable gate array (FPGA) to get the amplitude of the signal. The gamma-ray interaction position (x, y) and deposited energy E in a detector can be calculated by the amplitude of 4-channel signals [22]. The analogue pulses are sampled at 25 ns intervals (40 MHz).

To get coincidence events of the system, it is necessary to obtain the time stamp of the signal by using the method of digital constant fraction discriminator (dCFD) in FPGA. In this method, the original 4-channel sum signal will be divided into two signals. One is delayed and another is inverted and attenuated by a factor. The sum of these two signals is a bipolar pulse with a zero-crossing point. The time stamp at zero-crossing is estimated by linear interpolation. The advantage of this method is that the trigger is independent on the signal peak height. Finally, the packaged data (position, energy, and timing) of interaction events are transmitted to a personal computer (PC) for coincidence event selection and image reconstruction via Ethernet. The sliding time window coincidence searching method is used to select coincidence events. The received event information is stored in three queues in a list mode according to the serial numbers of the three detectors. When the search starts, the time window is set to 2 clock ticks (50 ns), and each queue dequeues one event. Taking the minimum time stamp of the dequeued three events as the starting time, it is judged whether the time stamps of the other two events are within the time window, if so, it is recorded as a coincidence event, otherwise recorded as a single interaction event. Then the next event in the queue continues to dequeue, and the above process is repeated. This method can simultaneously select 2-interaction and 3-interaction events in real time. The sequence of each selected event is rearranged according to the physical order of detectors.

In order to realize image reconstruction, the detector characterization should be carried out first to obtain the calibration value of deposited energy on each pixel. All the measurements were done inside an air-conditioning room. The bias voltage of SiPM was fixed to 28.5 V and the temperature maintained a 22°C constant to avoid variations in the SiPM's response. Considering that the maximum number of photons that can be received by the photosensitive elements of a SiPM per unit time is limited, the linearity of the detector will become worse in the high energy region. Therefore, the logarithmic function was used to fit the energy and SiPM's pulse amplitude. The fitting function is:

E = a - \frac{1}{b} l n (1 - \frac{P A}{c}),

(9)

where PA is the digital pulse amplitude of SiPM, E is the energy with keV unit. Taking No.29 pixel and No.112 pixel as the representatives of the edge region and the central region respectively, the relationships between the pulse amplitudes and photopeak energies of 59.5 keV, 81 keV, 122 keV, 511 keV, 661.7 keV, 834.8 keV, 1274.5 keV, and 1332.5 keV in the three detectors were shown in Figure 5a. After the energy calibration of pixels in the three detectors was completed, the energy resolution of pixels was calculated as the ratio of the full width half maximum (FWHM) to the photopeak energies. The FWHM is defined as 2.35σ of the Gaussian distribution obtained by Gaussian fitting. As shown in Figure 5b, the measured FWHMs of the photopeak energies can be fitted as:

F W H M = a + b \sqrt{E + c E^{2}}

(10)

The averaged energy resolution of the pixels was measured as (7.47±0.58)%, (7.43±0.61)%, and (8.37±0.87)% at 661.7 keV, for the three detectors, respectively. The data of pixel energy resolution in the three detectors was also used in G4UserEventAction class of the Geant4 simulation model to reproduce the experimental behavior of the prototype.

3. Results

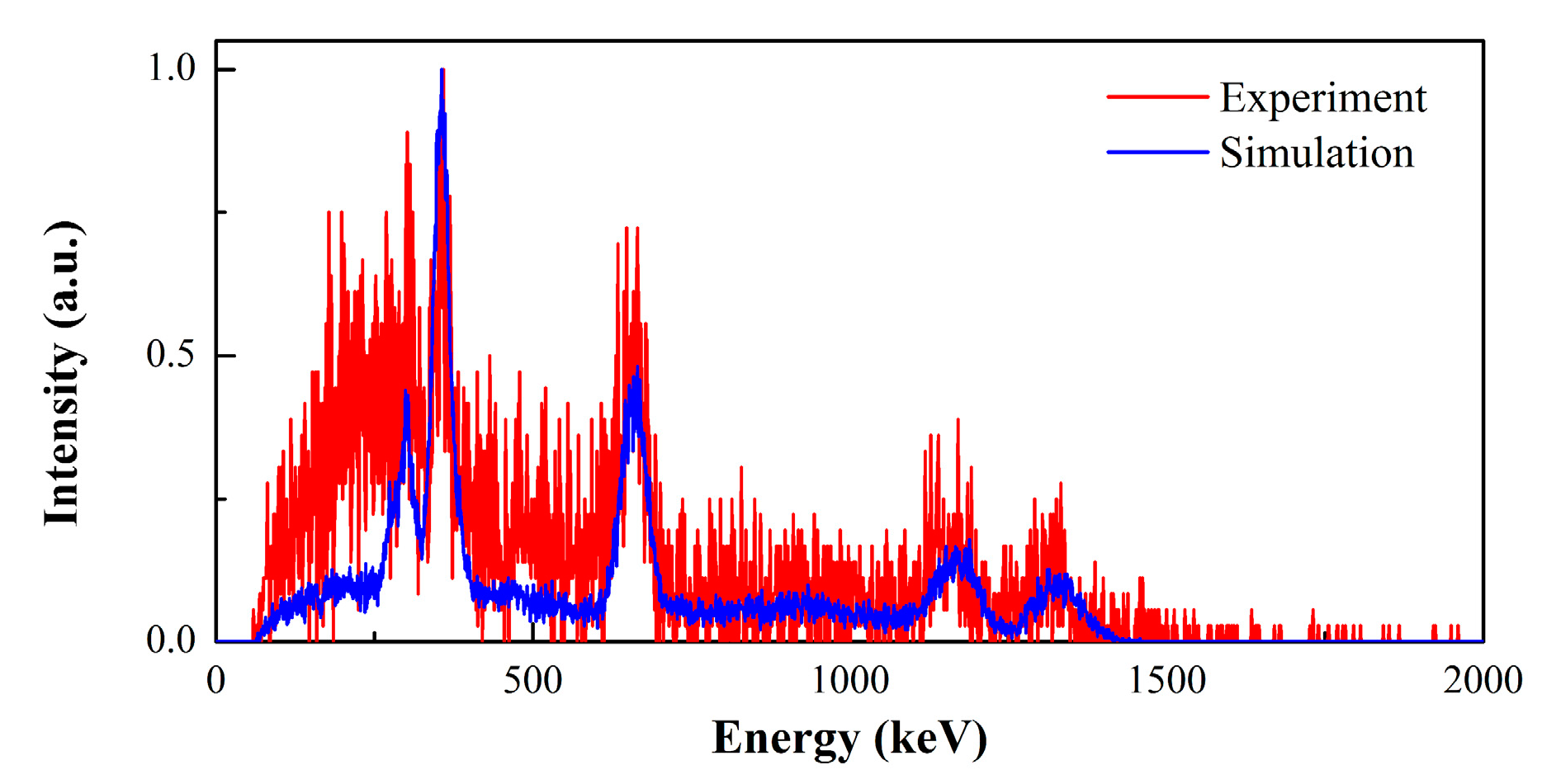
3.1. Single source imaging and performance evaluation

In this paragraph, we presented the results of experimental measurements and simulated data for several single point-like sources (¹³³Ba, ¹³⁷Cs, ⁶⁰Co) to validate the imaging performance of the prototype, such as detection efficiency, field of view (FOV), and imaging sensitivity. The activities of them are 0.262 MBq, 1.88 MBq, and 1.92 MBq, respectively. The coincidence summed energy spectra of the 2-interaction and 3-interaction events in the prototype was shown in Figure 6, in which both the experimental and simulation results were displayed. The natural background spectra in the same acquisition time were deducted from the experimental spectra of coincidence events. The vertical axis in the figure is represented by normalized intensity. For all the radionuclides, the photopeaks can be clearly observed, and the intensity distribution of photopeaks is in good agreement with the simulation. In the low energy range of less than 500 keV, more coincidence events were obtained in the experiment than in the simulation due to the influence of the scattering from the room environment around the detector.

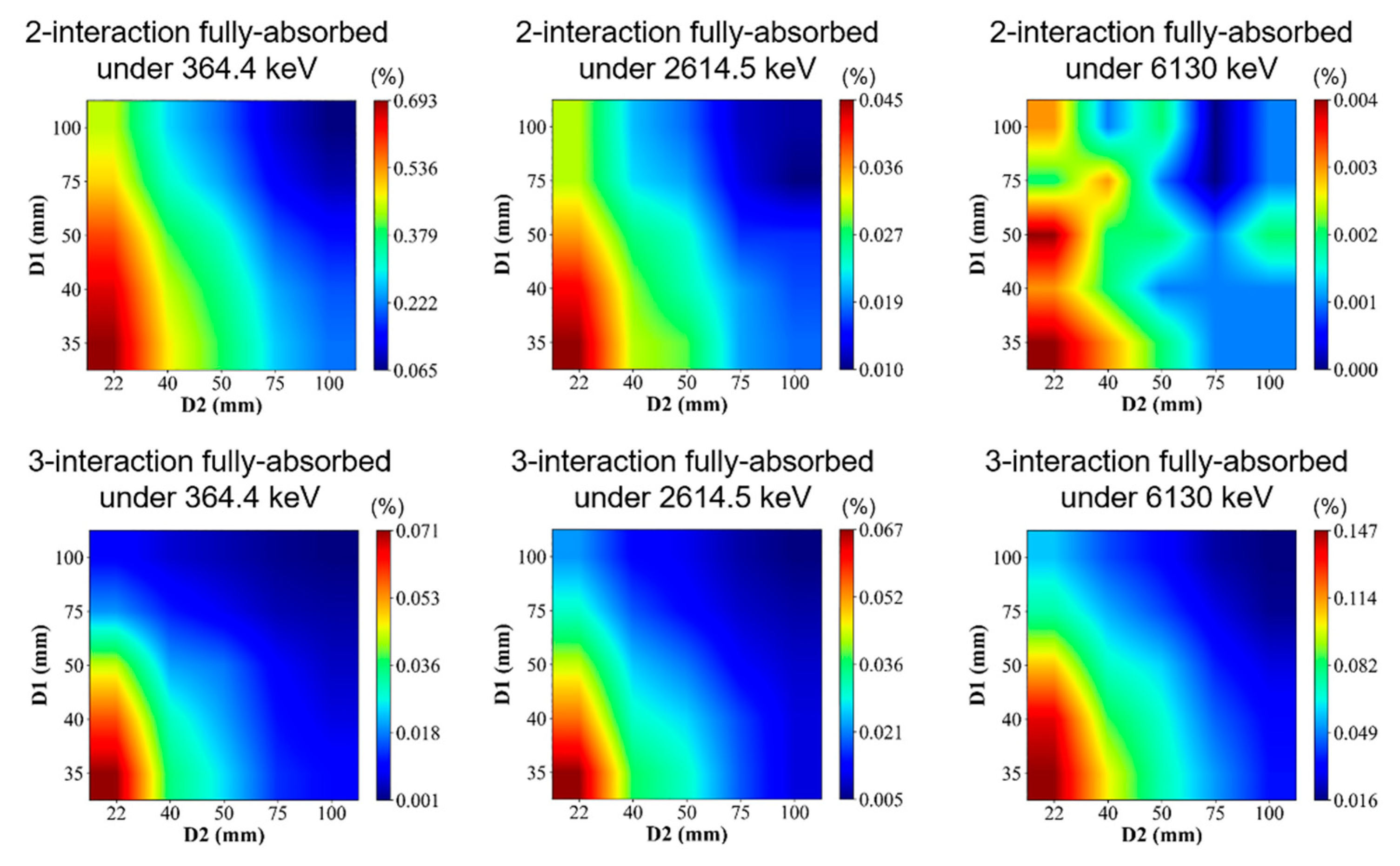
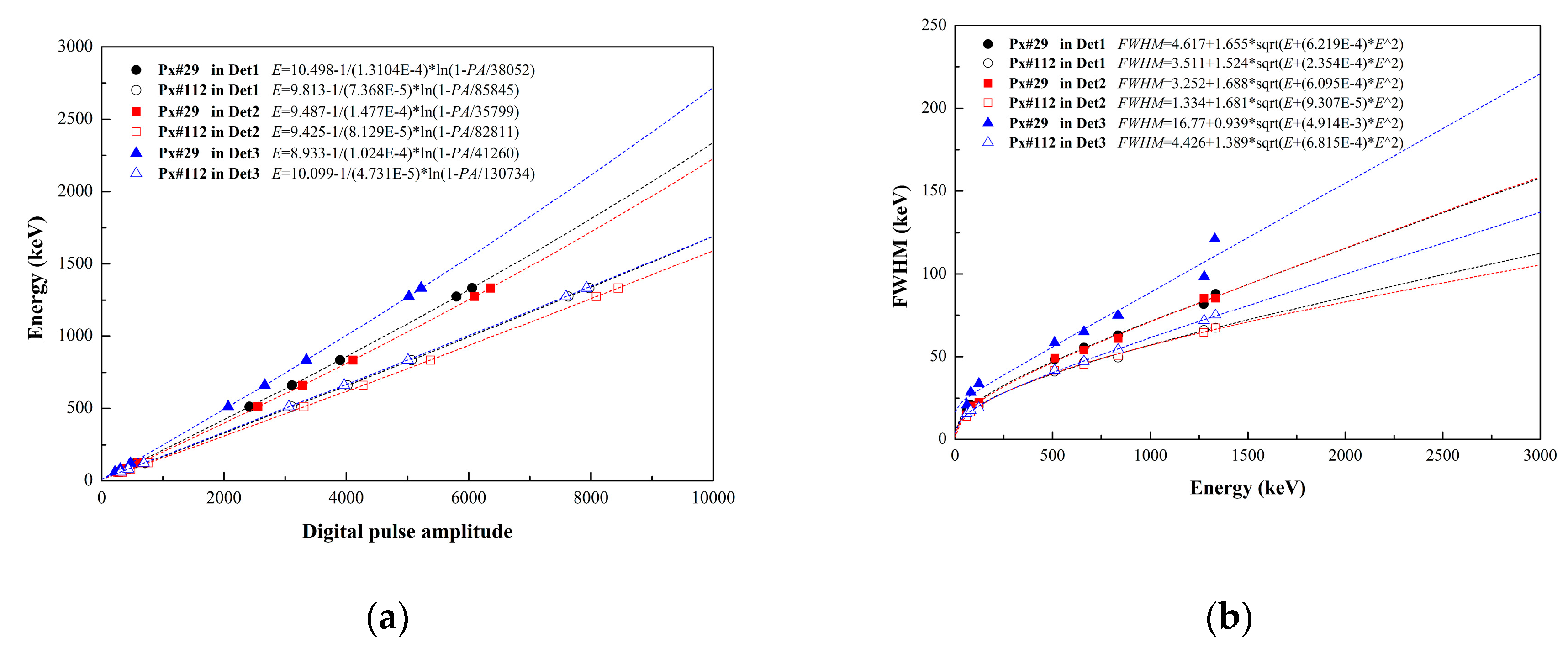
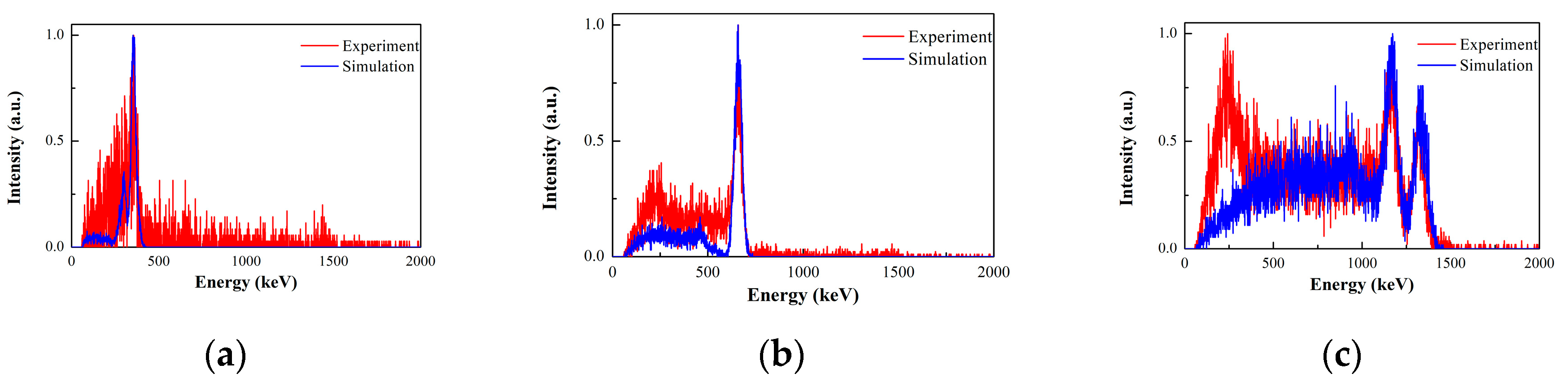
3.1.1. Detection efficiency and image resolution

The detection efficiency in Compton imaging system is defined as the proportion of effective imaging events in the measured events. The number of measured events is equal to the total count recorded by detector minus the count of natural background. During the experimental tests in this paper, the count rate of natural background was 198 cps (57.5 cps, 49 cps, and 91.5 cps for Det1, Det2, and Det3, respectively).

Table 1 summarized the detection efficiency evaluation results by three point-like sources (¹³³Ba, ¹³⁷Cs, ⁶⁰Co) positioned at the centre of FOV under the conditions of simulation and experiment. For the simulation, the gamma-ray emitter with a solid angle Ω=0.031 sr was placed 1 m away from the front of the detector. The emission number was given by the sum of the emission probability of each energy branch multiplied by the base number 10⁷. For the experiments, the detail testing conditions (radioactivity, source-to-detector distance and acquisition time) were listed in the table. The natural background of the same acquisition time has been subtracted to get the total count from the source. Both 2-interaction and 3-interaction events were counted as the effective imaging events. The events that deposit energy higher than 256 keV at scattering position were excluded. As shown in Table 1, for the sources with different energies, the proportion of effective imaging events accounted for about 2%. The difference between simulation and experiment results mainly comes from the scattering of environment. Compared with selecting imaging events by setting energy window in Compton camera with two-layer structure [28], the proportion of effective imaging events in this prototype is increased by an order of magnitude.

The reconstructed images obtained under the test conditions in Table 1 were shown in Figure 7. The 3-interaction images and 2-interaction images with 1 and 10 iterations of MLEM were all displayed. It is difficult to indicate the distribution of point source in the 3-interaction images because of the small number of events. For the 2-interaction images, the image resolution can be evaluated by the FWHM value, which is calculated from the profile plots taken through the maximum value on polar angle direction and azimuthal angle direction. The Gaussian fitting was used to obtain the FWHM value of reconstructed hotspot. The simulated imaging resolutions of ¹³³Ba, ¹³⁷Cs and ⁶⁰Co source after 10 iterations were 5.1°, 3.7°, and 3.7° FWHM, respectively. And the experimental imaging resolutions of ¹³³Ba, ¹³⁷Cs and ⁶⁰Co source after 10 iterations were 8.7°, 6.0°, and 7.3° FWHM, respectively.

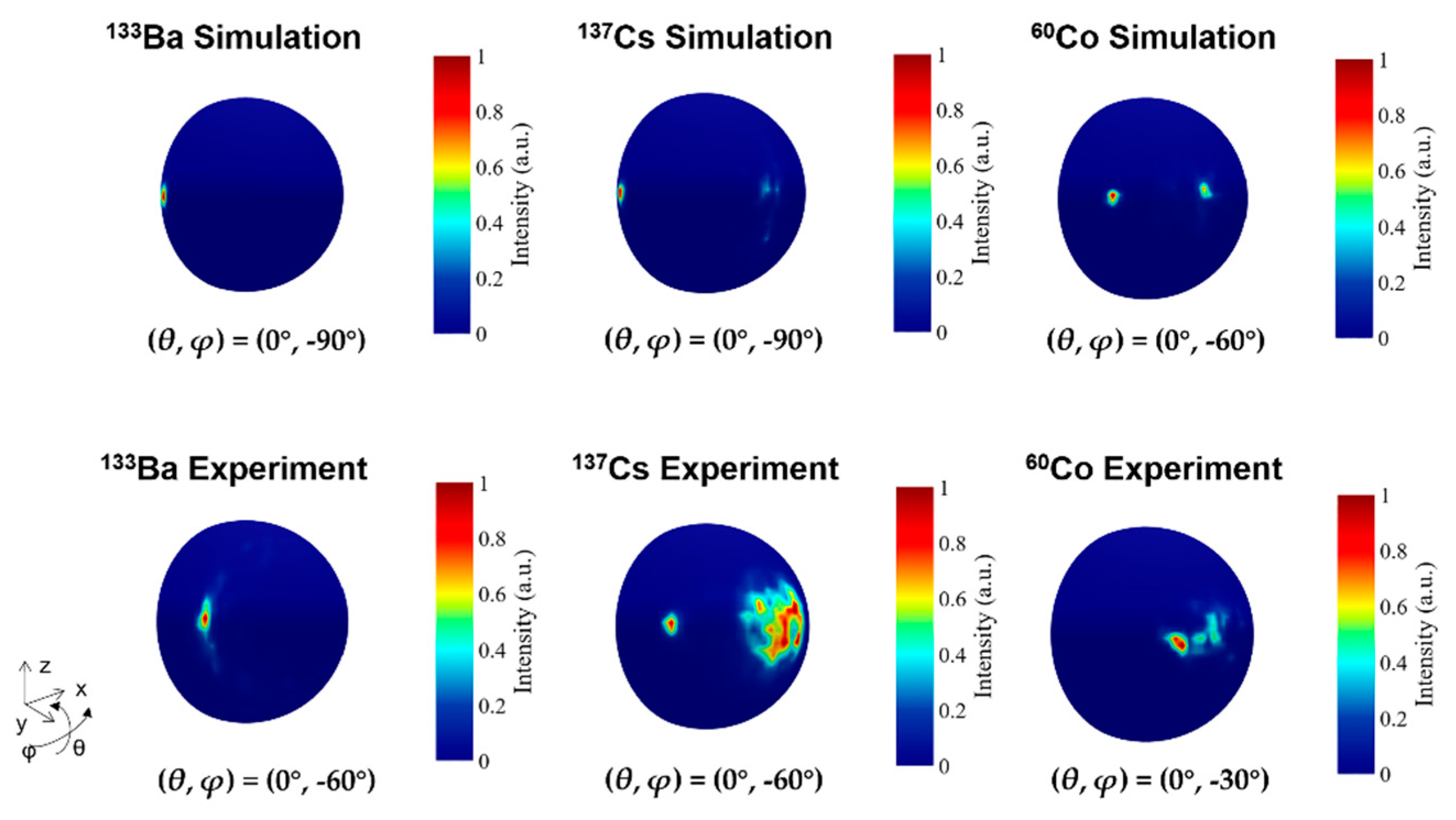
3.1.2. Field of view

The ideal FOV of the prototype is 2π, that is, the polar angle θ ranges from -90° to 90° and the azimuthal angle φ ranges from -90° to 90°. However, the reconstructed hotspot is formed by the accumulation of Compton cone. When the radioactive source is positioned at the boundary of FOV, it will inevitably produce hotspot artifacts in the middle area opposite. On the other hand, in image reconstruction, the deposited energy at the scatterer will be limited as E₁<E/(1+2E/m_ec²), where E is the initial energy of the incident gamma-ray. The energy limitation of scatterer is manifested in the size of the Compton ring formed for each event. Obviously, the higher the initial energy, the smaller the radius of the ring. Therefore, the FOV of high incident energy gamma-ray source is smaller than that of low incident energy.

Figure 8 showed the 2-interaction reconstructed images for the ¹³³Ba, ¹³⁷Cs, and ⁶⁰Co source positioned at the boundary of FOV after 10 iterations. The simulation results showed that the imaging FOV of the prototype can be described as -90° to 90°, -90° to 90°, and -60° to 60° for ¹³³Ba, ¹³⁷Cs, and ⁶⁰Co point-like sources, respectively. The experimental results showed that the imaging FOV of the prototype can be described as -60° to 60°, -60° to 60°, and -30° to 30° for ¹³³Ba, ¹³⁷Cs, and ⁶⁰Co point-like sources, respectively.

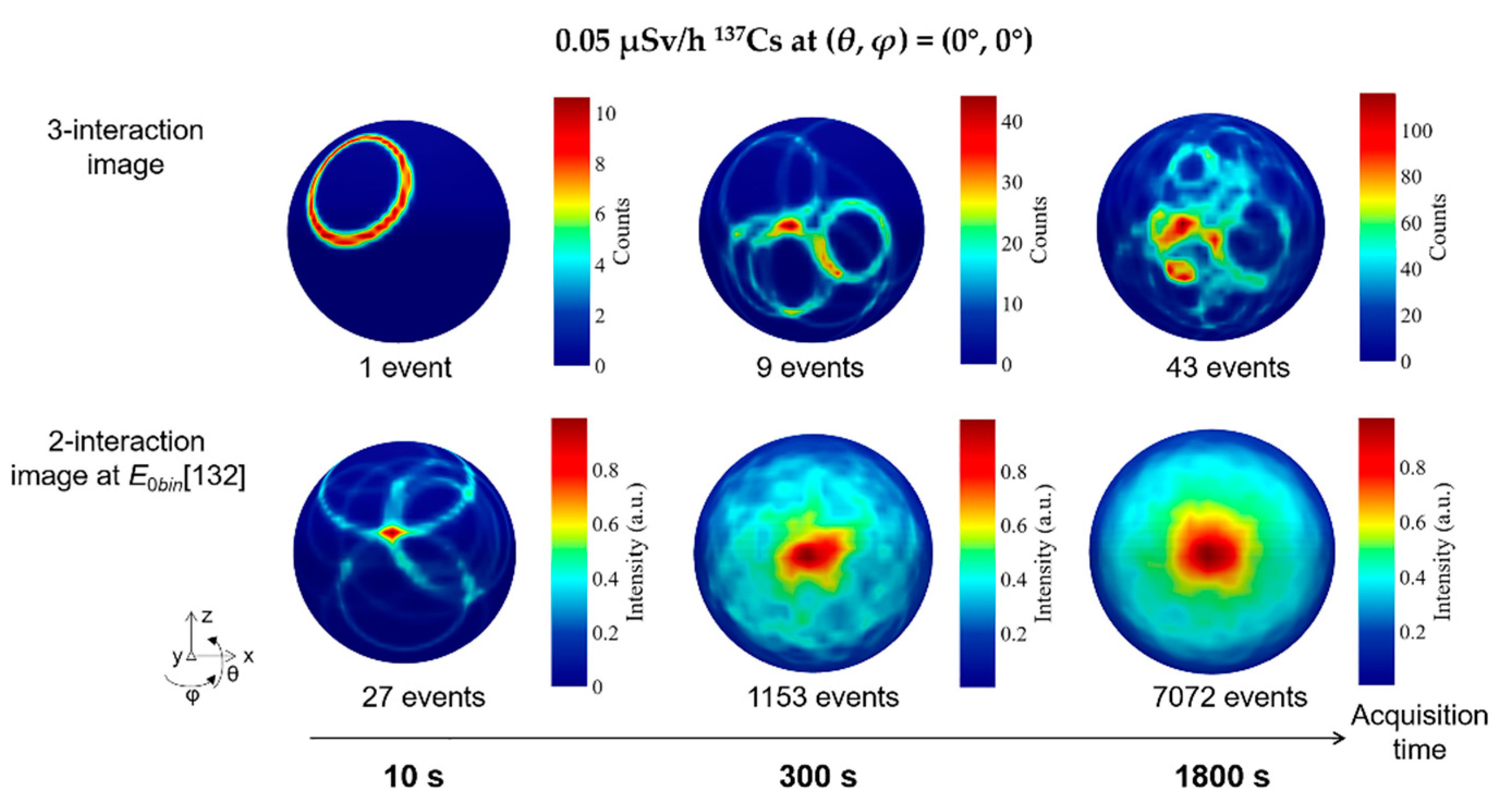
3.1.3. Imaging sensitivity

The imaging sensitivity indicator is defined as the minimum exposure time necessary to correctly locate a single point source. In the experimental measurement, we placed a ¹³⁷Cs point-like source with an activity of 1.88 MBq at a distance of 1.6 m in front of the detector. At this time, the produced dose rate from source at the detector position was about 0.05 μSv/h. The reconstruction process using 3-interaction and 2-interaction events was shown in Figure 9. The number of MLEM iterations of the 2-interaction images was 1 here. The reconstructed images of 3-interaction events could not show the correct hotspot due to the small number of events. However, the hotspot was preliminarily identified within 10 seconds when 27 events were recorded as 2-interaction events. With the increase of acquisition time, the confidence of the reconstructed hotspot was gradually improved. When 1153 two-interaction events were collected within 300 seconds, the maximum value position of reconstructed hotspot was stable at (θ, φ)=(0°, 0°).

3.2. Multiple point-like source imaging

This section presented the imaging tests performed with multiple point-like sources in the simulation and experiments. The radioactive sources are the same as those mentioned above.

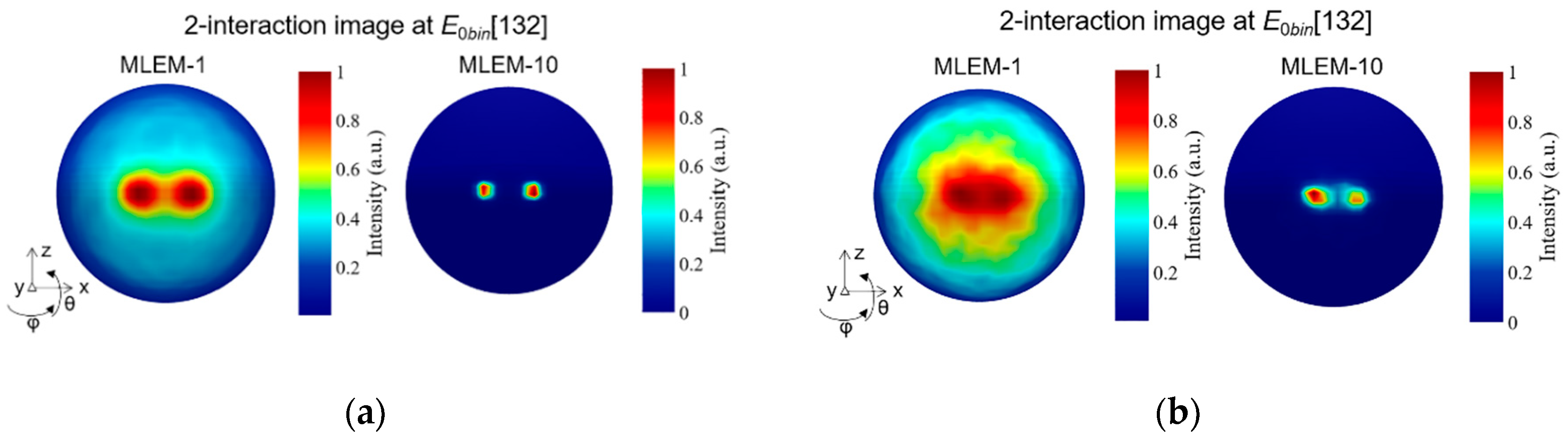
3.2.1. Angular resolution

In Compton camera, the angular resolution measure (ARM) is the distribution of the minimum angular distance between the known source position and Compton cones. In the experimental evaluation, the angular resolution is estimated as the minimum angle for identifying two separate sources.

Figure 10 showed the measurement results of angular resolution in the simulation and experiment. Two ¹³⁷Cs point-like sources were positioned at (θ, φ)=(0°, -7.5°) and (θ, φ)=(0°, 7.5°). The iteration of MLEM was set to 1 and 10. Two of the sources with the angular distance of 15° were roughly separated in the reconstructed image when using 1 iteration, whereas they were completely discriminated when using 10 iterations in both simulation and experimental measurement.

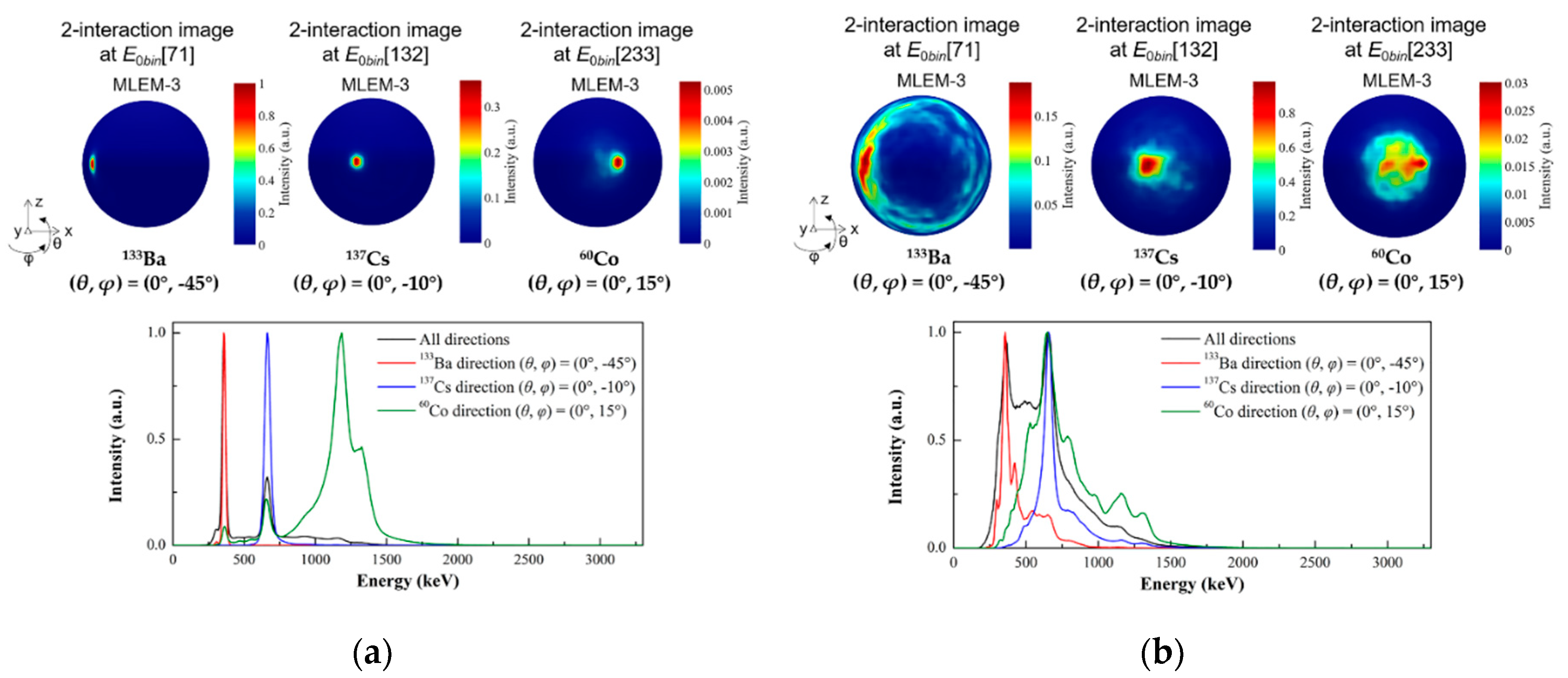
3.2.2. Simultaneous imaging of three point-like sources

The TLCC prototype can provide the image for each energy slice as well as the spectra for each direction. Thus, the capability of simultaneous separating radionuclides with various energies was evaluated. In the simulation and experimental measurements, we placed three point-like sources ¹³³Ba, ¹³⁷Cs, and ⁶⁰Co at the emission directions of (θ, φ)=(0°, -45°), (0°, -10°), and (0°, 15°), respectively. The coincidence summed energy spectra of 2-interaction and 3-interaction events for the simultaneous measurement of the three sources were shown in Figure 11. The experimental results of the distribution and relative intensity of photopeaks of the three radionuclides were in good agreement with the simulation results.

The 2-interaction reconstructed images at the corresponding energy slices and the reconstructed initial energy spectra after 3 iterations were shown in Figure 12. The energy slice of E_0bin[71], E_0bin[132], E_0bin[233] represented the initial energy around 356 keV, 661.7 keV, and 1332.5 keV, respectively. The results demonstrated that the prototype correctly distinguished the incident direction of each radionuclide. From the normalized intensity distribution of the reconstructed initial energy spectra, the photopeaks corresponding to the three nuclides can be distinguished. However, in the experimental results, the reconstruction of high energy nuclides (⁶⁰Co) was significantly influenced by low energy nuclides (¹³⁷Cs), which led to the low photopeak intensity of high energy nuclide and the relatively poor quality of reconstructed image. Nevertheless, the incident direction of the high energy nuclide can be correctly indicated when the corresponding energy slice was selected.

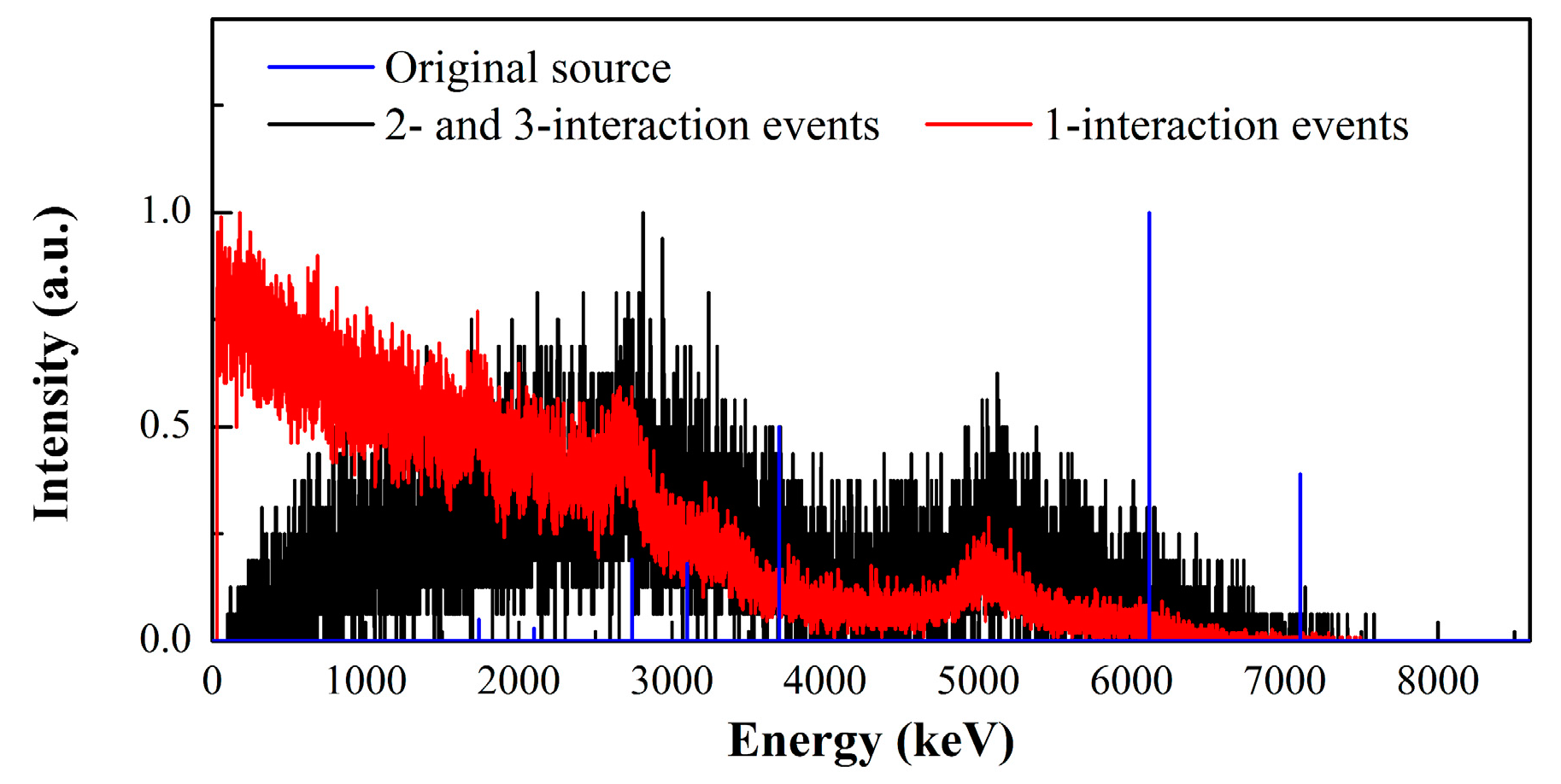
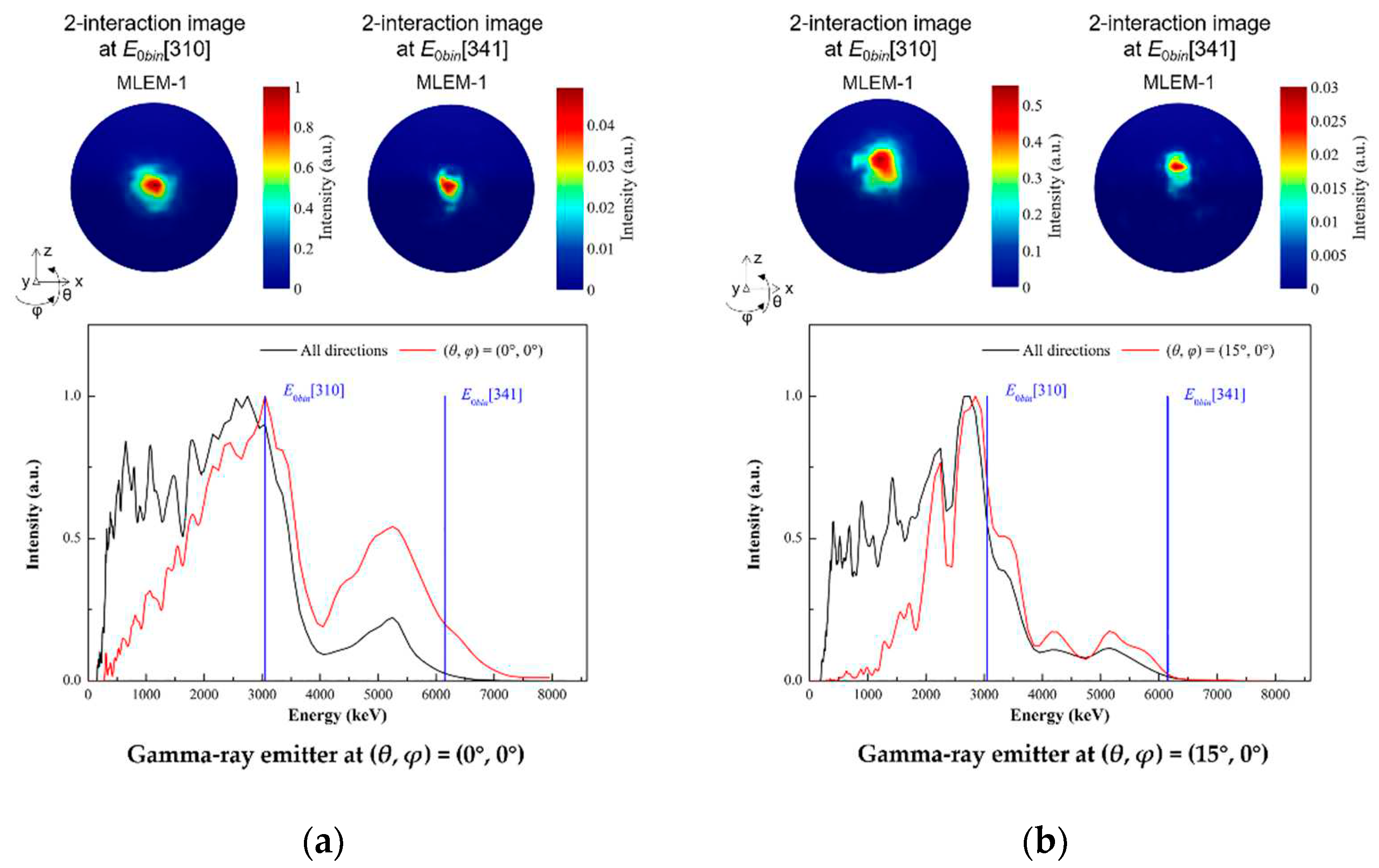
3.3. High energy gamma-rays imaging evaluation

In order to further evaluate the imaging ability of the prototype for higher energy gamma-rays, we used the relative yield data of gamma-rays from the water target under 14.1 MeV neutron bombardment at 90° to the incident neutron beam [29] as original sources in the simulation, as shown by the blue line in Figure 13. Among them, 6.13 and 7.12 MeV gamma-rays are from excitation of levels in ¹⁶O, 3.1 and 3.7 MeV gamma-rays are generated by de-excitation of the first two levels in ¹³C following the ¹⁶O(n, α)¹³C reaction.

In the simulation, a gamma-ray emitter with the above original energy was positioned at a distance of 1 m in front of the detector. The measured single interaction spectra and coincidence summed energy spectra of 2-interaction and 3-interaction events were shown in Figure 13. As can be seen, it is challenging to fully deposit incident energy through either a single interaction point or a number of interaction points for incident gamma-rays with energies higher than 3 MeV. At this time, using the traditional energy window method to select imaging events makes it difficult to correctly reconstruct the incident direction of a high energy gamma-ray source. However, the energy-domain imaging method can resolve this conundrum by calculating the likelihood of incident energy in the energy-domain corresponding to each coincidence interaction event.

We placed the gamma-ray emitter at two different incident direction of (θ, φ)=(0°, 0°) and (15°, 0°) to evaluate the imaging capability of the prototype. Figure 14 showed the reconstructed initial energy spectra and the 2-interaction reconstructed images with 1 iteration of MLEM in the Geant4 simulation. The energy slice of E_0bin[310] and E_0bin[341] represented the initial energy around 3.1 MeV and 6.13 MeV, respectively. Although 6.13 MeV energy had a low relative intensity in the reconstructed initial energy spectra, its reconstructed direction was consistent with 3.1 MeV. The simulation results demonstrated the prototype can correctly indicate the 6.13 MeV source with various incident directions.

4. Discussion

The objective of this work was to develop a prototype three-layer Compton camera (TLCC), consist of three GAGG-SiPM position-sensitive detectors, dedicated to applications in gamma-ray imaging with a wide energy range of 0.3~7 MeV. All detectors can distinguish the interaction positions in the 15×15 scintillator array. The averaged energy resolution of the pixels was measured as (7.47±0.58)%, (7.43±0.61)%, and (8.37±0.87)% at 661.7 keV, for the three detectors, respectively.

The far-field energy-domain imaging method based on two-interaction and three-interaction events was adopted, in which the three-Compton reconstruction was used for three-interaction events, as well as the space and spectral reconstruction was used for two-interaction events. This method realized simultaneously estimating the initial energy and spatial distribution of gamma-ray sources.

The simulation model of detectors was established based on Geant4 Monte Carlo simulation toolkit. The distance between three-layer detectors was optimized to maximize effective detection efficiency for a wide range of gamma-ray energy. The imaging tests using ¹³³Ba, ³⁷Cs and ⁶⁰Co radionuclides under the conditions of single point-like source and multiple point-like sources were carried out with our prototype in laboratory measurements and compared with simulation studies.

The proportion of effective imaging events of TLCC accounted for about 2%, which was much higher than using traditional energy window method to choose imaging events. A 0.05 μSv/h ¹³⁷Cs source at the centre of FOV was correctly identified in 10 seconds with our prototype. The imaging resolution of ¹³³Ba, ¹³⁷Cs and ⁶⁰Co source at the centre of FOV after 10 iterations were 8.7°, 6.0°, and 7.3° FWHM, respectively. The angular resolution for resolving two ¹³⁷Cs point-like sources was measured as 15°. It was also investigated in the simulation that TLCC can obtain the reconstructed images of a 6.13 MeV source from different directions, in which the emitted gamma-ray data came from 14.1 MeV neutron scattering with water.

The simulation and experimental results showed that the TLCC prototype has good imaging performance in a wide energy range. Future work will further test the imaging ability of the prototype under the experimental conditions of the higher energy gamma-ray source.

Author Contributions

Conceptualization, J.Z. and J.L.; methodology, J.Z. and X.A.; software, J.Z., X.X. and Y.C.; validation, B.Z. and X.M.; writing—original draft preparation, J.Z.; writing—review and editing, J.L.; supervision, X.A.; funding acquisition, J.Z., B.Z. and J.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China, grant number 12205372, and Science Foundation of State Key Laboratory of NBC Projection for Civilian, grant number SKLNBC2021-05.

Conflicts of Interest

The authors declare no conflict of interest.

References

Parajuli, R.K.; Sakai, M.; Parajuli, R.; Tashiro, M. Development and Applications of Compton Camera—A Review. Sens. 2022, 22, 7374. [Google Scholar] [CrossRef]
De Angelis, A.; Tatischeff, V.; Argan, A.; Brandt, S.; Bulgarelli, A.; Bykov, A.; Costantini, E.; Curadoda Silva, R.; A. Grenier, I.; Hanlon, L.; et al. Gamma-ray astrophysics in the MeV range: The ASTROGAM concept and beyond. Exp. Astron. 2021, 51, 1225–1254.
Kishimoto, A.; Kataoka, J.; Taya, T.; Tagawa, L.; Mochizuki, S.; Ohsuka, S.; Nagao, Y.; Kurita, K.; Yamaguchi, M.; Kawachi, N.; et al. First demonstration of multi-color 3-D in vivo imaging using ultra-compact Compton camera. Sci. Rep. 2017, 7, 1–7. [Google Scholar] [CrossRef]
Mochizuki, S.; Kataoka, J.; Koide, A.; Fujieda, K.; Maruhashi, T.; Kurihara, T.; Sueoka, K.; Tagawa, L.; Yoneyama, M.; Inaniwa, T. High-precision compton imaging of 4.4 MeV prompt gamma-ray toward an on-line monitor for proton therapy. Nucl. Instruments Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect. Assoc. Equip. 2018, 936, 43–45. [Google Scholar] [CrossRef]
Fontana, M.; Ley, J.L.; Dauvergne, D.; Freud, N.; Krimmer, J.; Létang, J.M.; Maxim, V.; Richard, M.-H.; Rinaldi, I.; Testa, É. Monitoring ion beam therapy with a Compton camera: Simulation studies of the clinical feasibility. IEEE Trans. Radiat. Plasma Med. Sci. 2020, 4, 218–232. [Google Scholar] [CrossRef]
Lee, T.; Lee, W. Multiple scattering Compton camera with neutron activation for material inspection. Nucl. Instruments Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect. Assoc. Equip. 2015, 784, 423–429. [Google Scholar] [CrossRef]
Koshikawa, N.; Omata, A.; Masubuchi, M.; Kataoka, J.; Kadonaga, Y.; Tokoi, K.; Nakagawa, S.; Imada, A.; Toyoshima, A.; Matsunaga, K.; et al. Activation imaging: New concept of visualizing drug distribution with wide-band X-ray and gamma-ray imager. Nucl. Instruments Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect. Assoc. Equip. 2023, 1045. [Google Scholar] [CrossRef]
Shikaze, Y.; Nishizawa, Y.; Sanada, Y.; Torii, T.; Jiang, J.; Shimazoe, K.; Takahashi, H.; Yoshino, M.; Ito, S.; Endo, T.; Tsutsumi, K.; Kato, S.; Sato, H.; Usuki, Y.; Kurosawa, S.; Kamada, K.; Yoshikawa, A. Field test around Fukushima Daiichi nuclear power plant site using improved Ce:Gd3(Al,Ga)5O12 scintillator Compton camera mounted on an unmanned helicopter. J. Nucl. Sci. Technol. 2016, 53, 1907–1918. [Google Scholar] [CrossRef]
Sato, Y.; Terasaka, Y.; Utsugi, W.; Kikuchi, H.; Kiyooka, H.; Torii, T. Radiation imaging using a compact Compton camera mounted on a crawler robot inside reactor buildings of Fukushima Daiichi Nuclear Power Station. J. Nucl. Sci. Technol. 2019, 56, 801–808. [Google Scholar] [CrossRef]
Shy, D.; Xia, J.; He, Z. Artifacts in High-Energy Compton Imaging With 3-D Position-Sensitive CdZnTe. IEEE Trans. Nucl. Sci. 2020, 67, 1920–1928. [Google Scholar] [CrossRef]
Runkle, R.C.; Chichester, D.L.; Thompson, S.J. Rattling nucleons: New developments in active interrogation of special nuclear material. Nucl. Instruments Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect. Assoc. Equip. 2012, 663, 75–95. [Google Scholar] [CrossRef]
Sudac, D.; Pavlovic, M.; Obhodas, J.; Nad, K.; Orlic, Z.; Uroic, M.; M. Korolija; Rendic, D.; Meric, I.; Pettersen, H.; et al. Detection of Chemical Warfare (CW) agents and the other hazardous substances by using fast 14 MeV neutrons. Nucl. Instruments Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect. Assoc. Equip. 2020, 971, 164066. [Google Scholar] [CrossRef]
Verburg, J.M.; Riley, K.; Bortfeld, T.; Seco, J. Energy- and time-resolved detection of prompt gamma-rays for proton range verification. Phys. Med. Biol. 2013, 58, L37–L49. [Google Scholar] [CrossRef] [PubMed]
Caffrey, A.; Harkness-Brennan, L.; Alshammari, H.; Boston, A.; Boston, H.; Griffiths, O.; Judson, D.; Kalantan, S.; Le Crom, B.; Nolan, P.; et al. Gamma-ray imaging performance of the GRI+ Compton camera. J. Instrum. 2021, 16, P09015. [Google Scholar] [CrossRef]
Kroeger, R.; Johnson, W.; Kurfess, J.; Phlips, B.; Wulf, E. Three-Compton telescope: theory, simulations, and performance. IEEE Trans. Nucl. Sci. 2002, 49, 1887–1892. [Google Scholar] [CrossRef]
Muñoz, E.; Barrio, J.; Etxebeste, A.; Ortega, P.G.; Lacasta, C.; Oliver, J.F.; Solaz, C.; Llosá, G. Performance evaluation of MACACO: a multilayer Compton camera. Phys. Med. Biol. 2017, 62, 7321–7341. [Google Scholar] [CrossRef] [PubMed]
García, A.R.; Barrio, J.; Etxebeste, A.; López, J.G.; Jiménez-Ramos, M.C.; Lacasta, C.; Muñoz, E.; Oliver, J.F.; Roser, J.; Llosá, G. MACACO II test-beam with high energy photons. Phys. Med. Biol. 2020, 65, 245027. [Google Scholar] [CrossRef]
Barrientos, L.; Borja-Lloret, M.; Casaña, J.; Hueso-González, F.; Ros, A.; Roser, J.; Senra, C.; Solaz, C.; Viegas, R.; Llosá, G. System characterization and performance studies with MACACO III Compton camera. Radiat. Phys. Chem. 2023, 208, 110922. [Google Scholar] [CrossRef]
Iwanowska, J.; Swiderski, L.; Szczesniak, T.; Sibczynski, P.; Moszynski, M.; Grodzicka, M.; Kamada, K.; Tsutsumi, K.; Usuki, Y.; Yanagida, T.; et al. Performance of cerium-doped Gd3Al2Ga3O12 (GAGG:Ce) scintillator in gamma-ray spectrometry. Nucl. Instruments Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect. Assoc. Equip. 2013, 712, 34–40. [Google Scholar] [CrossRef]
Yan, X.S. Prototypes of SiPM-GAGG Scintillator Compton Cameras. Adv. X-Ray Radiat. Detect.; Springer: Cham, Switzerland, 2023; pp. 239–258. [Google Scholar]
Omata, A.; Masubuchi, M.; Koshikawa, N.; Kataoka, J.; Kato, H.; Toyoshima, A.; Teramoto, T.; Ooe, K.; Liu, Y.; Matsunaga, K.; et al. Multi-modal 3D imaging of radionuclides using multiple hybrid Compton cameras. Sci. Rep. 2022, 12, 1–9. [Google Scholar] [CrossRef]
ZHANG, J.; MA, X.; Zhang, B.; Xiao, X.; LI, J.; LEI, W.; Zhao, W.; AI, X. Simulation design and performance evaluation of the wide-energy range gamma-ray imaging detectors. Sci. Sin. Technol. 2023. [Google Scholar] [CrossRef]
Wilderman, S.J.; Clinthorne, N.H.; Fessler, J.A.; Rogers, W.L. List-mode maximum likelihood reconstruction of Compton scatter camera images in nuclear medicine. In Proceedings of the 1998, https://doiEEE Nuclear Science Symposium Conference Rec.ord, ON, ssmicanada, 8–14 November.1998, Torog/10.1109/nto; pp. 17738716–1720. [Google Scholar]
Xu, D.; He, Z. Gamma-ray energy-imaging integrated spectral deconvolution. Nucl. Instruments Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect. Assoc. Equip. 2007, 574, 98–109. [Google Scholar] [CrossRef]
Muñoz, E.; Barrientos, L.; Bernabéu, J.; Borja-Lloret, M.; Llosá, G.; Ros, A.; Roser, J.; Oliver, J.F. A spectral reconstruction algorithm for two-plane Compton cameras. Phys. Med. Biol. 2020, 65, 025011. [Google Scholar] [CrossRef] [PubMed]
Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. GEANT4—a simulation toolkit. Nucl. Instrum. Methods Phys. Res., Sect. A. 2003, 506, 250–303. [Google Scholar] [CrossRef]
Park, H.; Yi, M.; Lee, J.S. Silicon photomultiplier signal readout and multiplexing techniques for positron emission tomography: a review. Biomed. Eng. Lett. 2022, 12, 263–283. [Google Scholar] [CrossRef]
Zhang, J.P.; Liang, X.Z.; Cai, J.L.; Liu, Y.; Huang, X.C.; Li, D.W.; Xiao, X.; Pang, X.Y.; Zhang, Z.M.; Wei, L.; Shuai, L. Prototype of an array SiPM-based scintillator Compton camera for radioactive materials detection. Radiat. Detect. Technol. Methods 2019, 3, 17. [Google Scholar] [CrossRef]
McDonald, W.; Robson, J.; Malcolm, R. Scattered neutrons and gamma rays from the 16O(n, n′γ)16O reaction at En=14.1 MeV. Nucl. Phys. 1966, 75, 353–370. [Google Scholar] [CrossRef]

Figure 1. The principle diagram of far-field energy-domain imaging method for wide-energy range gamma-ray imaging.

Figure 2. The detector simulation model constructed in Geant4. (a) The schematic of materials and placement; (b) The schematic of optical photon transportation in a single detector module; (c) The schematic of three-layer detectors.

Figure 3. Percentage of events that are fully-absorbed through two or three interactions under different incident energies.

Figure 4. Photograph and signal processing flow of the three-layer Compton camera prototype.

Figure 5. The spectral performance of No.29 pixel and No.112 pixel in the three detectors at eight energies (59.5 keV, 81 keV, 122 keV, 511 keV, 661.7 keV, 834.8 keV, 1274.5 keV, 1332.5 keV). (a) The photopeak energies (keV) as functions of digital pulse amplitude; (b) The measured FWHMs of the photopeak energies and fitting curves.

Figure 6. Comparison between the experimental measurements and simulated data for the coincidence summed energy spectra of 2-interaction and 3-interaction events. (a) ¹³³Ba source; (b) ¹³⁷Cs source; (c) ⁶⁰Co source.

Figure 7. The reconstructed images of single point-like source (¹³³Ba, ¹³⁷Cs, ⁶⁰Co) at the centre of FOV using 3-interaction and 2-interaction events with the conditions of simulations and experiments in Table 1. The iteration numbers of 1 and 10 were used to reconstruct the 2-interaction image. The profile plots taken through the maximum value of the 2-interaction image on polar angle direction and azimuthal angle direction were shown.

Figure 8. The simulation and experimental results of the 2-interaction reconstructed images after 10 iterations for a source (¹³³Ba, ¹³⁷Cs, ⁶⁰Co) positioned at the boundary of field of view.

Figure 9. The 3-interaction images and 2-interaction images with 1 iteration of MLEM for a 0.05 μSv/h ¹³⁷Cs source at (θ, φ)=(0°, 0°). The hotspot can be preliminarily identified within 10 seconds.

Figure 10. The 2-interaction image of two ¹³⁷Cs point-like sources separated by 15° for the measurement of angular resolution. (a) The simulation result; (b) The experimental result.

Figure 11. The coincidence summed energy spectra of 2-interaction and 3-interaction events for the simultaneous measurement of 3 point-like sources (¹³³Ba, ¹³⁷Cs, and ⁶⁰Co). Both the simulation and experimental results were shown.

Figure 12. Multiple source localization with the prototype under the following test conditions: a ¹³³Ba source positioned at (θ, φ)=(0°, -45°), a ¹³⁷Cs source positioned at (θ, φ)=(0°, -10°) and a ⁶⁰Co source positioned at (θ, φ)=(0°, 15°). The 2-interaction reconstructed images at the corresponding energy slices and reconstructed initial energy spectra after 3 iterations were shown. The vertical axis of the reconstructed energy spectra was represented by normalized intensity. (a) The simulation results; (b) The experimental results.

Figure 13. The measured single interaction spectra and coincidence summed energy spectra of 2-interaction and 3-interaction events, in which the data was generated from a water target under 14.1 MeV neutron bombardment in the Geant4 simulation. The relative intensity of original gamma-ray energies was indicated by the blue line.

Figure 14. The reconstructed initial energy spectra and the 2-interaction reconstructed images with 1 iteration of MLEM for the water target under 14.1 MeV neutron bombardment in the Geant4 simulation. The energy slice of E_0bin[310] and E_0bin[341] represented the initial energy around 3100 keV and 6130 keV, respectively. (a) The gamma-ray emitter of water target was positioned at (θ, φ)=(0°, 0°); (b) The gamma-ray emitter of water target was positioned at (θ, φ)=(15°, 0°).

Table 1. The detection efficiency of TLCC for a point-like source at the centre of FOV under the conditions of simulation and experiment.

Settings of gamma emission$conditions		Nuclide	Representative$energy (keV)	Total count from source	Count of 2-interaction events	Count of 3-interaction events	Proportion of effective events (%)
Simulation$(N gammas emit within Ω=0.031 sr at d=1 m, N is equal to the sum of the emission probability of each energy branch multiplied by the base number 10⁷)	N = 13418000	¹³³Ba	356	760871	11266	65	1.49
	N = 8499000	¹³⁷Cs	661.7	317619	10029	129	3.20
	N = 19983260	⁶⁰Co	1173.2/1332.5	585709	13415	141	2.31
Experiment$(Point-like source with radioactivity A, distance d and acquisition time t)	A = 0.262 MBq$d = 0.25 m$t = 3600 s	¹³³Ba	356	376788	8253	43	2.20
	A = 1.88 MBq$d = 1 m$t = 1800 s	¹³⁷Cs	661.7	628321	13186	87	2.11
	A = 1.92 MBq$d = 1 m$ t = 1800 s	⁶⁰Co	1173.2/1332.5	1129416	20176	148	1.80

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer