Preprint
Article
A GPU Accelerated Method for 3-D Nonlinear Kelvin Ship Wave Patterns Simulation
Altmetrics
Downloads
77
Views
20
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.zip (5.78MB )
This version is not peer-reviewed
Submitted:
09 October 2023
Posted:
10 October 2023
You are already at the latest version
Alerts
Abstract
Ship wave is of great interest for wave drag, coastal erosion and ship detection. In this paper, a highly-paralleled numerical scheme is proposed for simulating three-dimensional (3-D) nonlinear Kelvin ship waves effectively. First, a numerical model for nonlinear ship waves is established based on potential flow theory, boundary integral method and Jacobian-free Newton-Krylov (JFNK) method. In order to improve computational efficiency and reduce data storage of JFNK method, a banded preconditioner method is then developed by formulating the optimal bandwidth selection rule. After that, a Graphics Process Unit (GPU) based parallel computing framework is designed, and a GPU solver is developed by using Compute Unified Device Architecture (CUDA) language. Finally, numerical simulations of 3-D nonlinear ship waves under multiple scales are performed by using the GPU and CPU solvers. Simulation results show that the proposed GPU solver is more efficient than the CPU solver with the same accuracy. More than 66% GPU memory can be saved and the computational speed can be accelerated up to 20 times. Hence, the computation time for Kelvin ship waves simulation can be significantly reduced by applying the GPU parallel numerical scheme, which lays a solid foundation for practical ocean engineering.
Keywords:
Subject: Engineering - Marine Engineering
1. Introduction
The focus of this research is on innovation of highly parallel algorithms to simulate the contours of a three-dimensional free surface that appears to be stationary at the stern of a moving vessel, known as “Kelvin ship waves” [1]. Research on the kelvin wave shape has been continuously put to practical use in hull design, ship detection and environmentally friendly shipping policies [2].
Froude [3], a famous naval architect, first comprehensively described the morphology and main characteristics of ship waves. Under the assumption of infinite water depth, Kelvin [4] replaced a moving ship with a pressure disturbance point moving in a constant velocity straight line on the water surface, proposed the famous Kelvin angle of . In recent years, with the further study of ship wave characteristics, Rabaud [5] noted that the wake angle will be less than the well-known Kelvin angle if the vessel speed is sufficiently large. Subsequently, various effect factors for the Kelvin wake form were discussed in plenty of papers, e.g., Froude number [6], non-axisymmetric and interference effects, shear current,surface tension, the bottom topography, submergence depth, finite water depth and viscosity [7], etc. Accordingly, the research method of ship waves has gradually shifted from the previous analytical algorithms to numerical simulation.
The overwhelming majority of analytical algorithms of ship wave patterns concerns linear theories. Havelock [8] provided a linear solution for the problem of flow under a pressure distribution. Such ideal perturbations can also be replaced by a single submerged point source singularity [8] and submerged bodies [2]. Moreover, thin ship theory was alse used in the study of the ship wave pattern [9]. As the development of computer technology, numerical simulation methods are becoming increasing popular, the research focus shifted from linear problems to nonlinear problems. Nowadays, there are three numerical methods widely used to solve surface wave problems: boundary integral method, finite-difference method and finite-element method. In particular, Forbes [10] apply boundary integral method to build a series of integro-differential equation, the full nonlinear free surface flow problem was solved with moderate efficiencies. In more recent times, according to this method, many papers solve fully 3-D nonlinear ship waves with meshes between and [11,12]. And Pethiyagoda [6] noted that the points used along the direction should be more than 100 to make a sufficient standard about grid-independence.
With increasing mesh size, however, the computation time increases exponentially using only Central Processing Unit (CPU) computation power. As the rapid improvement of the electronics industry, the Graphics Processing Unit (GPU) has become another method of acceleration for optimizing the execution of large numbers of threads. Currently, the powerful GPU parallel computing ability has been used to improve the studies on ocean engineering. Hori [13] simulated 2-D dam-break flow by developing a GPU-based MPS code and achieved 7 times speedup. As for 3-D nonlinear free surface problem, Pethiyagoda [6] combined the GPU acceleration technique with the boundary integral method and LU [14] developed a GPU-accelerated high-order spectral solver. Xie [15] developed the MPSGPU-SJTU solver with GPU acceleration technique for the liquid sloshing simulation.
This paper presents a parallel solution framework based on GPU for nonlinear ship wave problem, in which almost all operations are performed in GPU device. Since the nonlinear boundary integral equation on each node is independent of the synchronous equations on other nodes, plenty of threads on GPU can be used to complete the integration operation for each node simultaneously. In addition, the parallel computing method can be used for the calculation of the large-scale linear sparse system, the complex inversion process is quickly finished by using Compute Unified Architecture (CUDA) language. According to this framework, a highly-paralleled GPU solver is proposed to simulate 3-D nonlinear Kelvin ship waves. The computation speed for the 3-D nonlinear ship waves simulation can be significantly increased, it is convenient to study the larger scale problems. On the other hand, the size of Random-Access Memory limits grid growth, the application of the banded preconditioner method can greatly save running memory to break through this limitation. The banded preconditioner method helps to achieve the standard for the grid-independence.
The rest of the paper is as follows. A brief introduction of the problem formulation is given in Section 2. In Section 3, the banded preconditioner JFNK algorithm is described. In Section 4, the theory and implementation of the GPU acceleration technique are presented. The accuracy, efficiency and capability of the GPU solver are verified in Section 5, and a summary in Section 6 concludes the paper.
2. Numerical Model
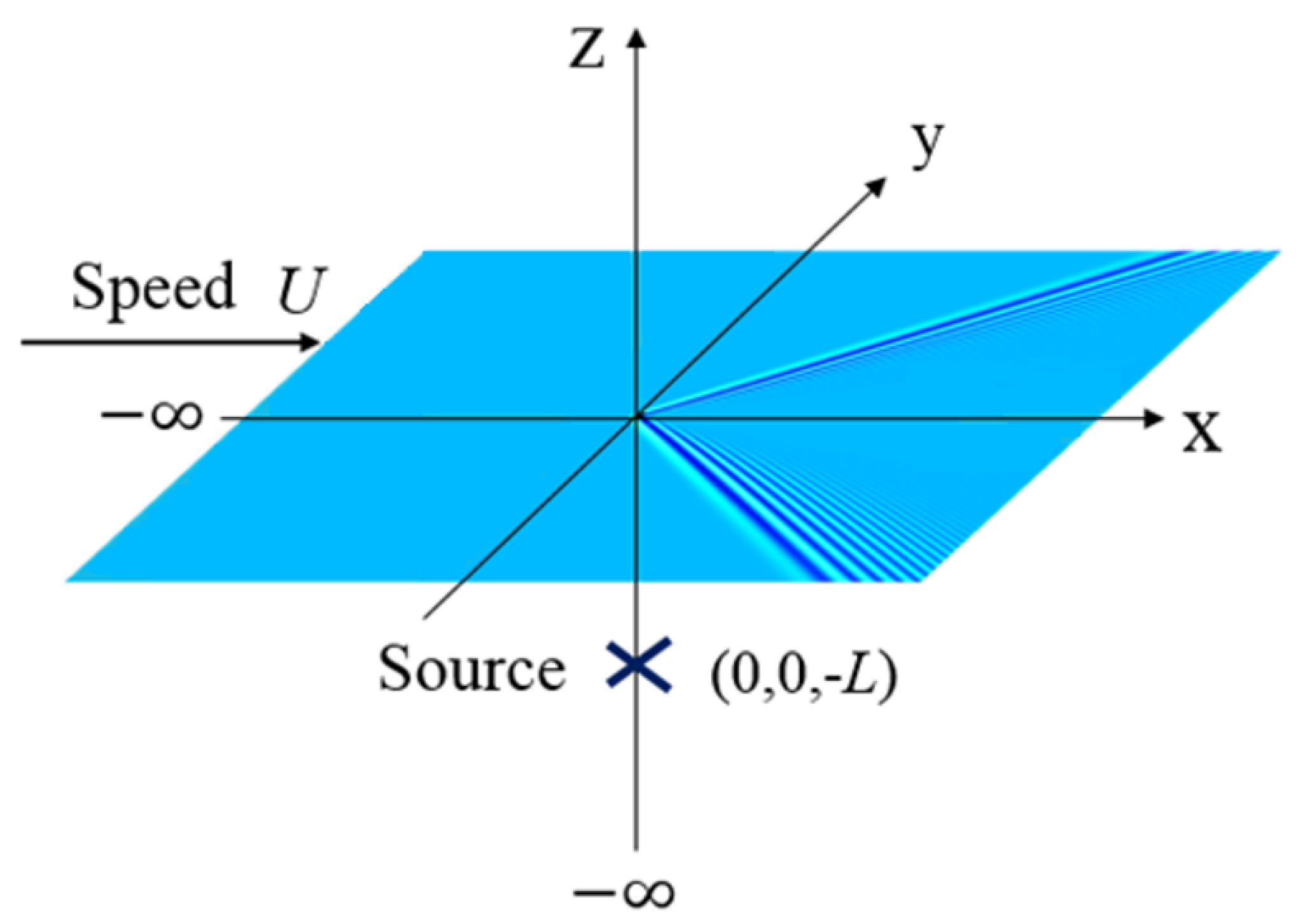
This paper supposes that a flow is moving at a uniform speed U along the positive x-axis direction. Considering the inviscid incompressible fluid of infinite depth without rotational flow, ignoring the influence of surface tension, the potential flow theory is applied. Therefore, a source singularity of strength m is introduced at a distance L below the surface, as illustrated in Figure 1. The transient waves can be generated with the disturbance of source. Free surface wave height and flow field velocity potential can be expressed as and .
Dimensionless analysis is performed with fluid velocity U and distance L. The velocity potential satisfies Laplace’s equation, the free surface kinematic and dynamic boundary condition, the radiation condition and the limiting behavior of source singularity. With , the boundary integral equation is written:
where the and are kernel functions [12].
Figure 1.
Flow field diagram.
Moreover, the free surface conditions can be simplified by the symbol . Then the kinematic and dynamic boundary conditions of the free surface are combined to be
To solve the above nonlinear problem numerically, the mesh is established on the free surface (N and M represent the number of longitude and latitude lines of the mesh, respectively). The x-coordinates and y-coordinates of nodes are and with regular intervals in the coordinate system, thus the vector of unknowns is
With more equations provided by applying the radiation condition as follows:
where is the decay coefficient.
Furthermore, more details about the governing equations, the boundary integral method and numerical discretization are provided by Sun[12].
3. Banded Proconditioner JFNK Algorithm
3.1. Jacobian-free Newton-Krylov method
JFNK method combines inexact Newton iteration method with Krylov subspace method. Its core content is the Generalized Minimum Residual (GMRES) algorithm, according to the matrix free idea, uses the finite difference form to approximate the product of coefficient matrix and vector, avoiding the Jacobian matrix calculation and storage alone. JFNK method mainly has two processes, namely external and internal iterations. The external iteration is the inexact Newton iteration method, and the damping parameter is used to ensure that the nonlinear residual decreases significantly in each iteration for , as follows:
Its internal iteration is GMRES algorithm [16], which efficiently solves the correction in inexact Newton iteration, that is, computes large-scale linear equations as follows:
where is the Jacobian matrix [17].
Firstly, the approximate solution of is found by projecting obliquely onto the Krylov subspace
where m is the value of the subspace dimension.
An initial linear residual is defined, given an initial guess , for the Newton correction,
Subsequently, is minimized to a suitable value by the GMRES iteration. Wherein Jacobian-vector products are approximated with finite difference:
where v represents an arbitrary vector used in building the Krylov subspace [18], and the h is a small perturbation
Finally, the initial guess can be defined as below:
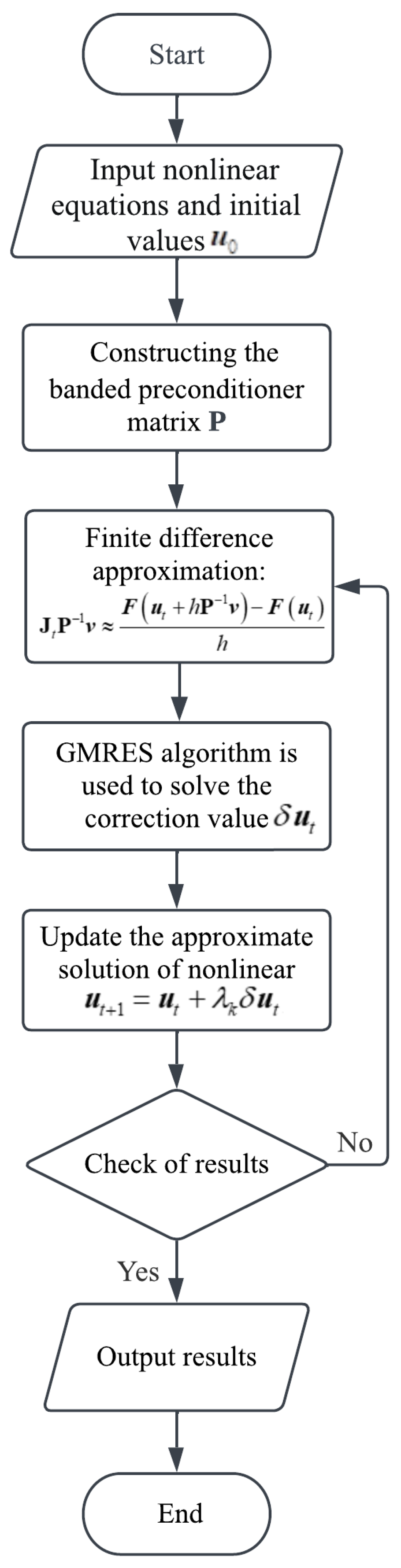
The nonlinear equations are solved according to the calculation flow of baned preconditioner JFNK method, as shown in Figure 2. Note that in the figure is a unit orthogonal vector in the orthonormal basis of Krylov subspace.
Figure 2.
Calculation flow chart of the banded preconditioner JFNK method.
3.2. Banded preconditioner method
Iterative methods, e.g. GMRES method etc., are currently most popular choices for solving large sparse linear systems of equations. However, this process of prcconditioning is essential to most successful application of iterative methods, since the convergence of a matrix iteration depends on the properties of the matrix, e.g. the eigenvalue, etc., [19]. Generally, the methods for choosing the appropriate preconditioner are different for the specific problems. In this section, a banded preconditioner method for solving the nonlinear ship wave problem is proposed.
3.2.1. Building preconditioner matrix
For a good preconditioner , it should be cheap to form and to factorizeis. Meanwhile, the preconditioned Jacobian should be easier to solve, which means the eigenvalues are more concentrated. In general, it is feasible to consider a matrix constructed from the same problem under simplified physics. This paper applies the numerical scheme to the linearized governing equations which apply formally in the limit
According to the linear free surface boundary condition, the boundary integral equation is described:
After numerical discretization, the linear system can be described, as follows:
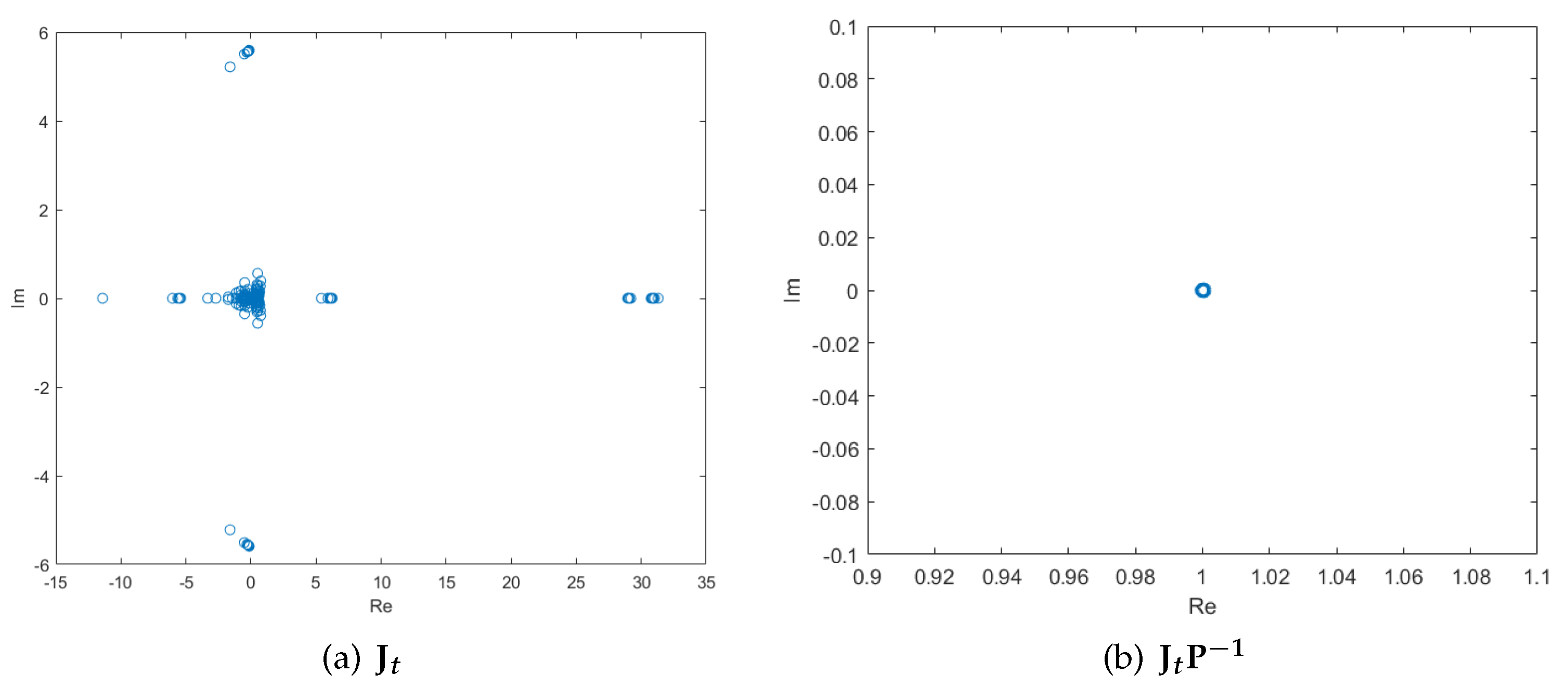
where is the weighting function for numerical integration, for Then the linear Jacobian can be calculated directly, by differentiating the linear system with respect to . Therefore, the preconditioner matrix can be formed cheaply, and the eigenvalues of obviously cluster as shown in Figure 3.
Figure 3.
The distribution of eigenvalues of and on a mesh.
3.2.2. Preconditioner factorisation and storage
The JFNK method requires the result of the product of the inverse preconditioner matrix and vector, . In general, the operation of inverting a matrix should be converted to solving a system of linear equations, . Find the solution , the result of will be got. In order to calculate this linear system rapidly, the following block matrix method is used to process the preprocessing matrix, where and are the unit matrix and the four submatrices.
Accordingly, the vector can be divided into upper and lower parts , and then the solution can be got after three cheap steps, as follows:
The calculation of in the Eq. (12) can be facilitated according to the progressive order from Eqs. (20) - (22).
3.2.3. The banded preconditioner
After the factorisation operation, the calculation and storage of preconditioner matrix are optimized. However, the size of submatrix is , it will increase dramatically as the size of mesh increases. Consequently, there will be two problems when the preconditioner matrix size is large. One is a memory problem, the running memory of this computer cannot accommodate this preconditioner matrix; the other is an efficiency problem, inverting the preconditioner matrix will take much time.
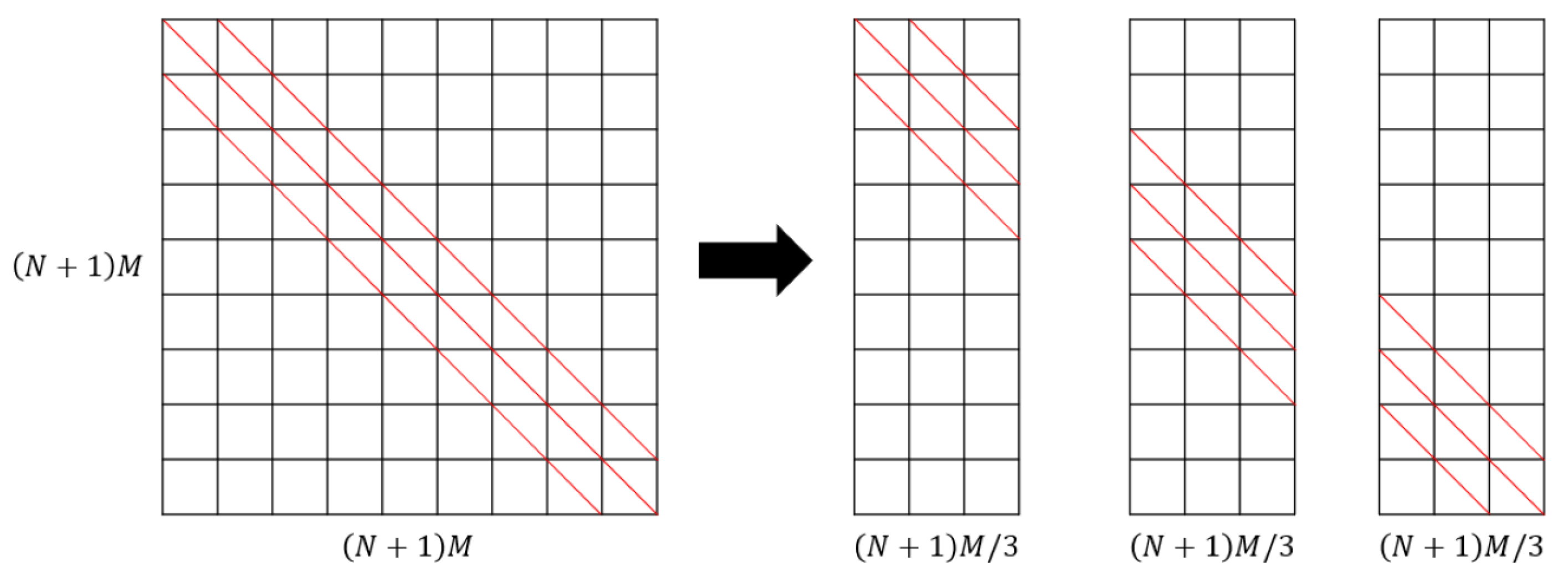
By observing the preconditioner matrix, it can be found that the values decay with distance from the main block diagonal. This observation suggests using a banded approximation to the matrix for our preconditioner, as shown in Figure 4. Moreover, batch construction avoids the problem of insufficient running memory due to the large size of the submatrix . The compressed sparse row (CSR) data format is used to save this matrix. Hence, a lot of memory can be saved.
Figure 4.
Construction of the banded preconditioner.
The feasibility of the banded preconditioner matrix method is verified, as shown in Figure 5. The tightness of clustering can be further improved by increasing the bandwidth. When the , the eigenvalues of have been clustered, satisfying the requirement of the GMRES method.
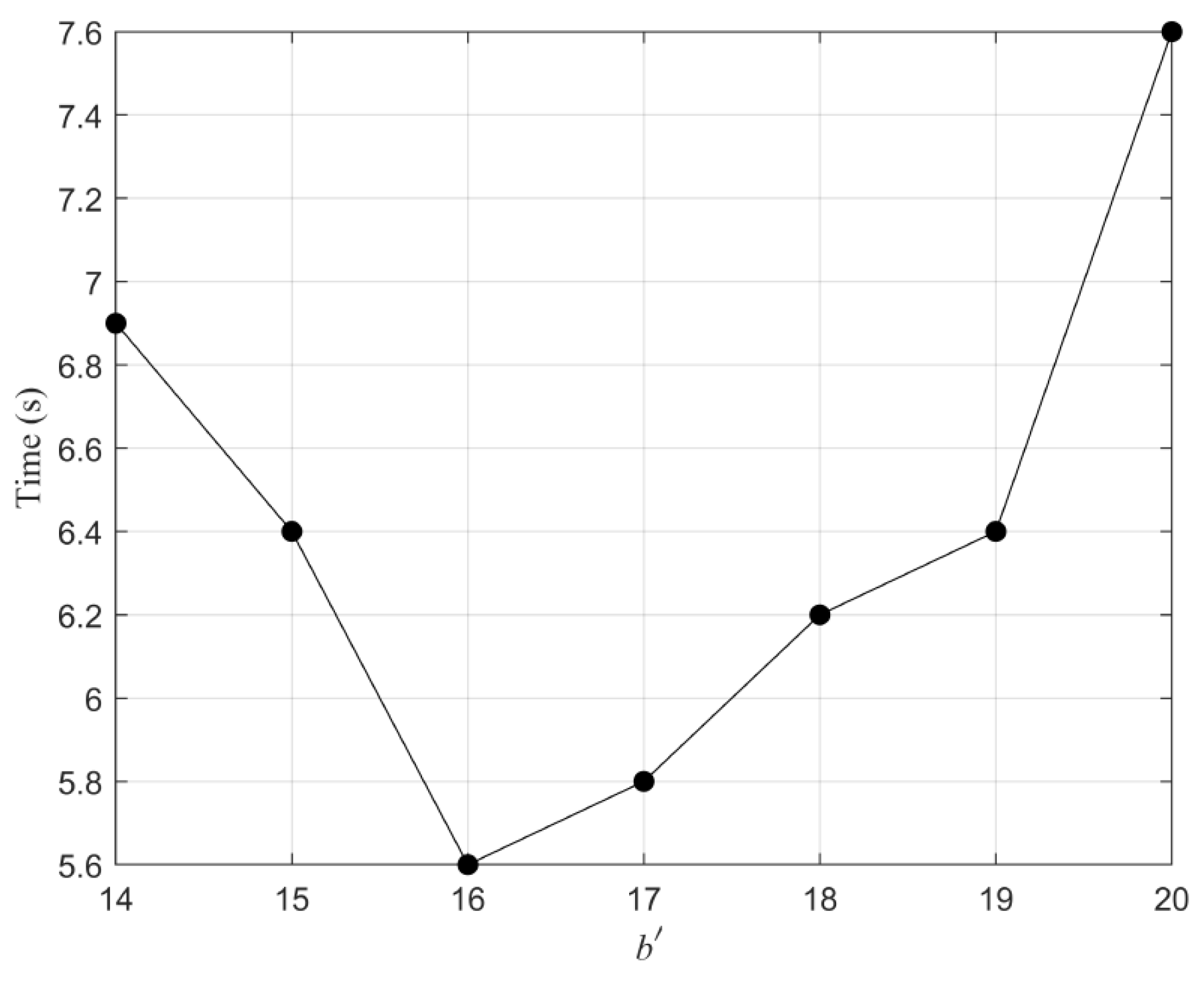
For certain bandwidth values, the computing speed of GMRES will not be significantly improved by increasing the bandwidth further. However, the time required for inverse operation will increase in these cases as the banded preconditioner matrix size increases. The bandwidth regulates the runtime of inverting banded preconditioner matrix and the number of the inner iterations of the GMRES method. The runtime of inverting banded preconditioner matrix increases with the bandwidth, while the inner iterations decrease with the bandwidth. Therefore, the total runtime will decrease first and then increase with the bandwidth, as shown in Figure 6. The case is , mesh and , when (bandwidth ) is less than 14, an ill-conditioned coefficient matrix is formed, the accuracy of the solution is low. The runtime decreases with ranges from 14 to 16, then the runtime increases monotonically with ranges from 16 to 20. For the case of mesh, the shortest running time is 5.6s with the optimal bandwidth . Therefore, provided that the appropriate bandwidth is selected, not only can save memory, but also can improve the computational efficiency.
Figure 5.
The distribution of eigenvalues of and on a mesh for: .
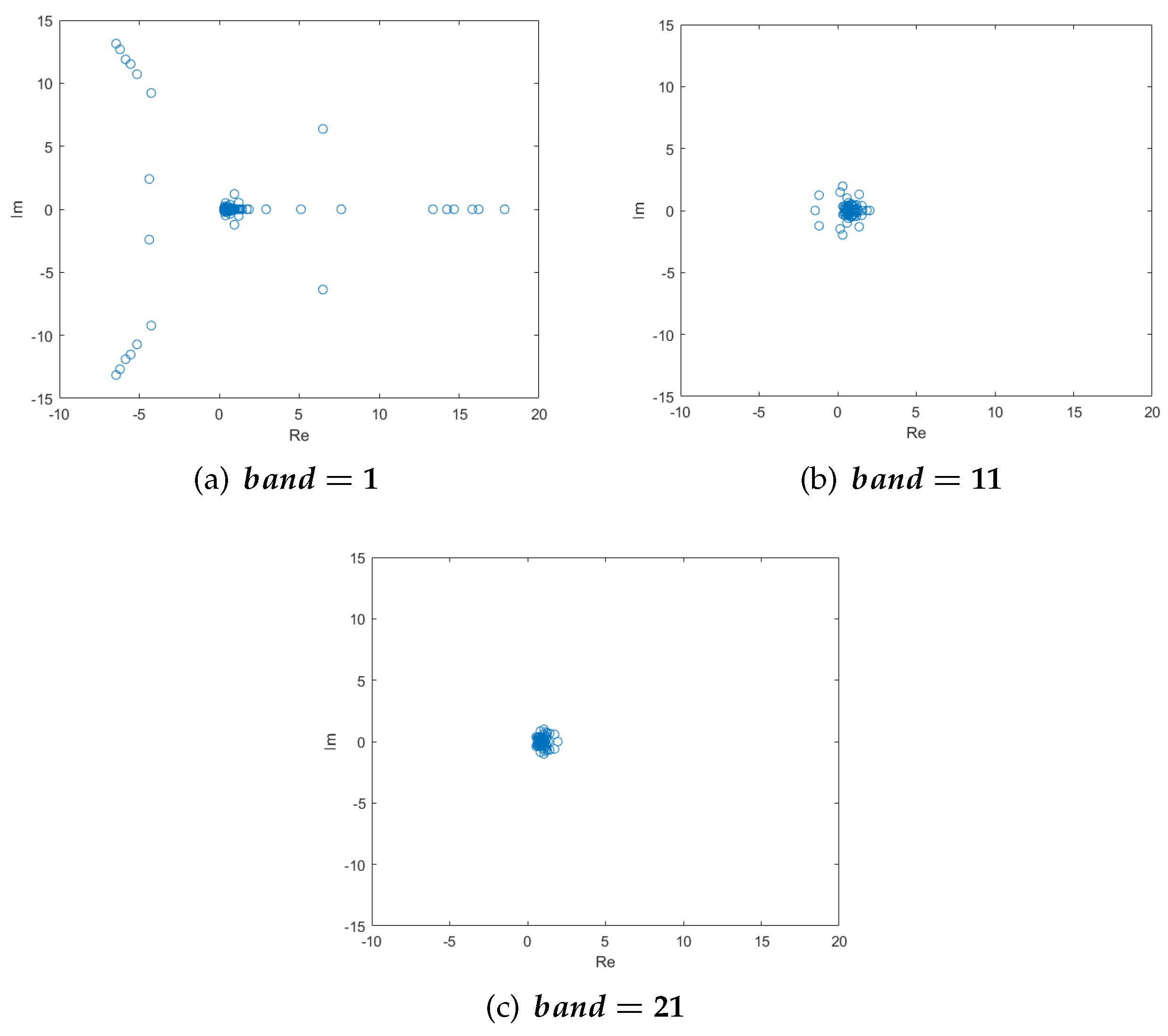
Figure 6.
The plot of runtime against the bandwidth, computed on a mesh, .
4. GPU Parallel Computing Framework
Although the banded preconditioner JFNK algorithm can improve the computational efficiency of nonlinear ship wave problem, the running time of the program will increase significantly with the increase of the mesh size, which is very unfavorable to the further study of nonlinear ship wave. The reason is that the CPU is not good at handling such large-scale nonlinear equations. Compared with CPU, GPU possesses more arithmetic logic units in the same chip area [21]. The computational efficiency of nonlinear ship wave can be greatly improved by utilizing the GPU acceleration technique.
4.1. Parallel computing framework design
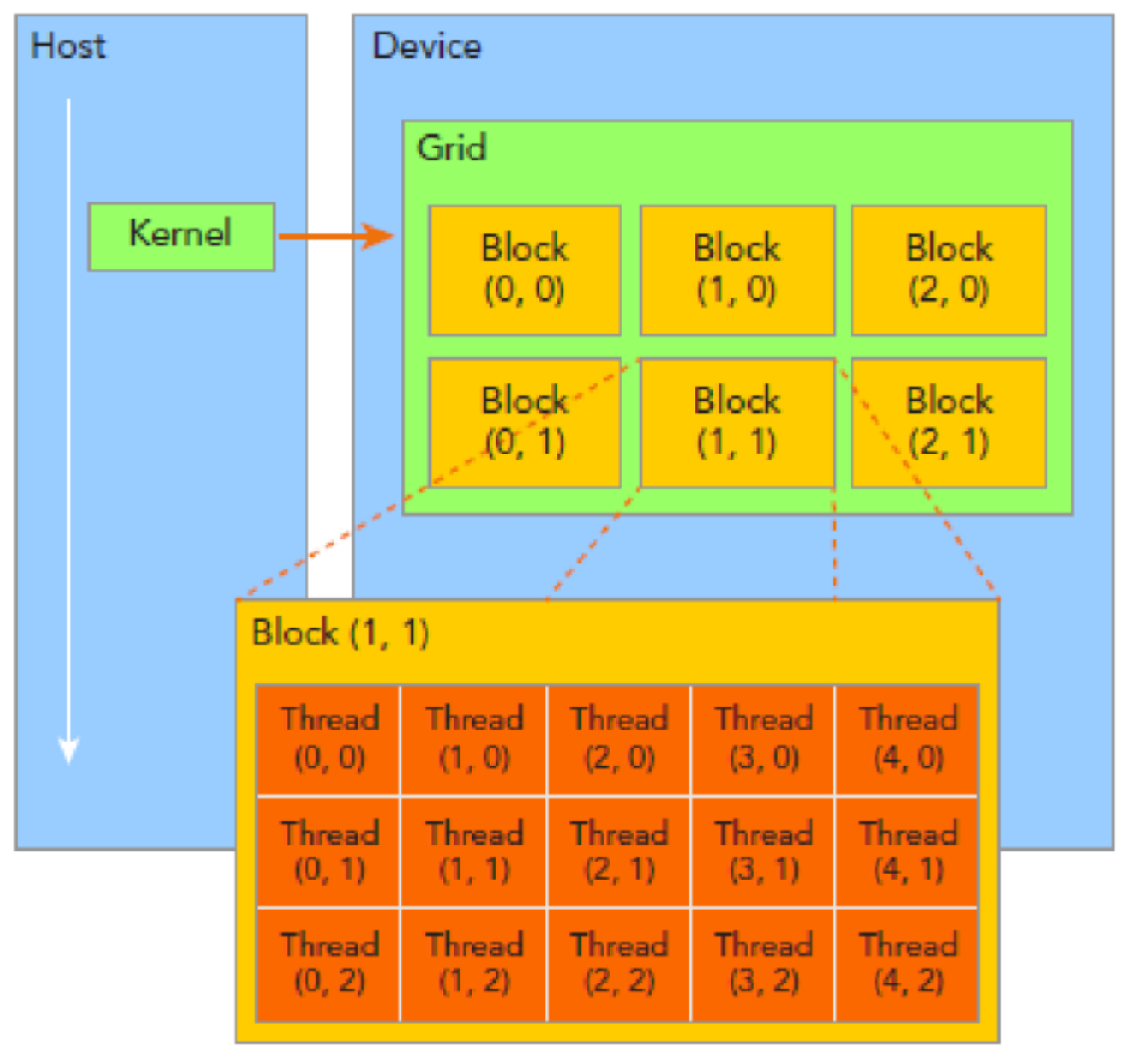
Compute Unified Device Architecture (CUDA) language is used to develop the numerical scheme for computing ship wave patterns. CUDA is a parallel computer platform and programming model developed by NVIDIA, powered by the GPU [21]. CUDA toolkit includes abundant GPU accelerated libraries, tools and runtime library, which can be compiled in C language, C++ language and Fortran language. In addition, CUDA source program can be executed on multiple GPUs. By applying the hybrid programming model, the parallel computing process consists of kernel function on device and serial code on host CPU. Figure 7 shows the CUDA execution mode and thread hierarchy.
Figure 7.
Illustration of CUDA execution mode and thread organization hierarchy [21].
Figure 7.
Illustration of CUDA execution mode and thread organization hierarchy [21].
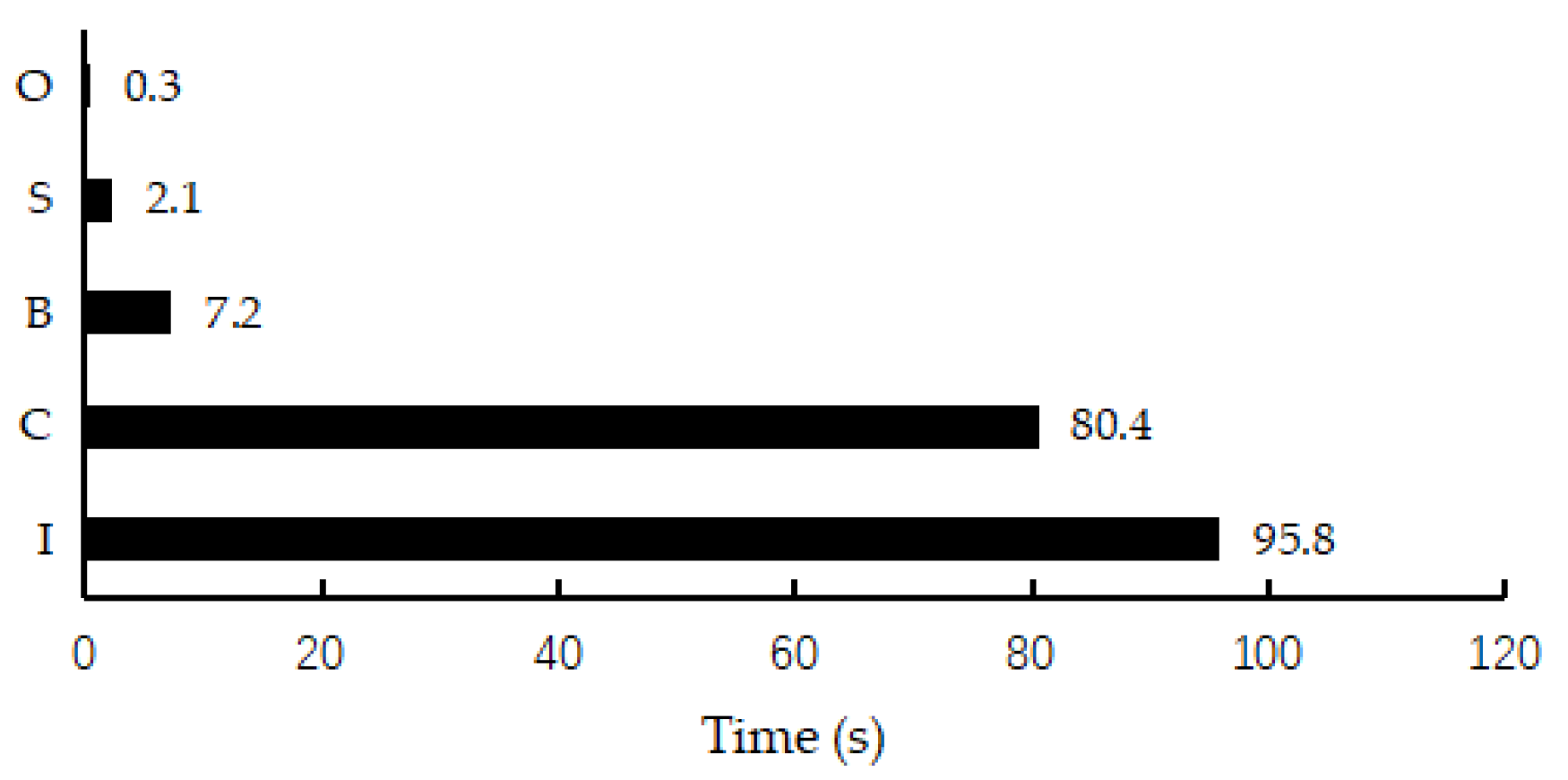
As for the solver of ship wave pattern, as described above, there are four main parts: building preconditioner matrix, creating nonlinear system, inverting preconditioner matrix and solving linear equations by GMRES algorithm. Simulation results of the CPU solver proposed by Sun[12] show that the parts of creating nonlinear system and inverting preconditioner matrix take up most of the time, as shown in Figure 8. This figure shows the computation time distribution of the CPU solver on a mesh case. The total runtime is 185.8 seconds, in which the runtime of inverting preconditioner matrix and creating nonlinear system is 95.8 and 80.4 seconds respectively. Each of them takes up nearly half the total runtime. Therefore, calculations on these two parts parallelly are vital for improving computational efficiency. And the part of building preconditioner matrix and solving linear equations will also be executed in GPU to further shorten the program running time.
Figure 8.
The computation time distribution of ship wave solver. The alphabet I represents the part of inverting preconditioner matrix, the alphabet C represents the part of creating nonlinear system, the alphabet B represents the part of building preconditioner matrix, the alphabet S represents the part of solving linear equations by GMRES algorithm and the alphabet O represents the part of other code in the solver.
Figure 8.
The computation time distribution of ship wave solver. The alphabet I represents the part of inverting preconditioner matrix, the alphabet C represents the part of creating nonlinear system, the alphabet B represents the part of building preconditioner matrix, the alphabet S represents the part of solving linear equations by GMRES algorithm and the alphabet O represents the part of other code in the solver.
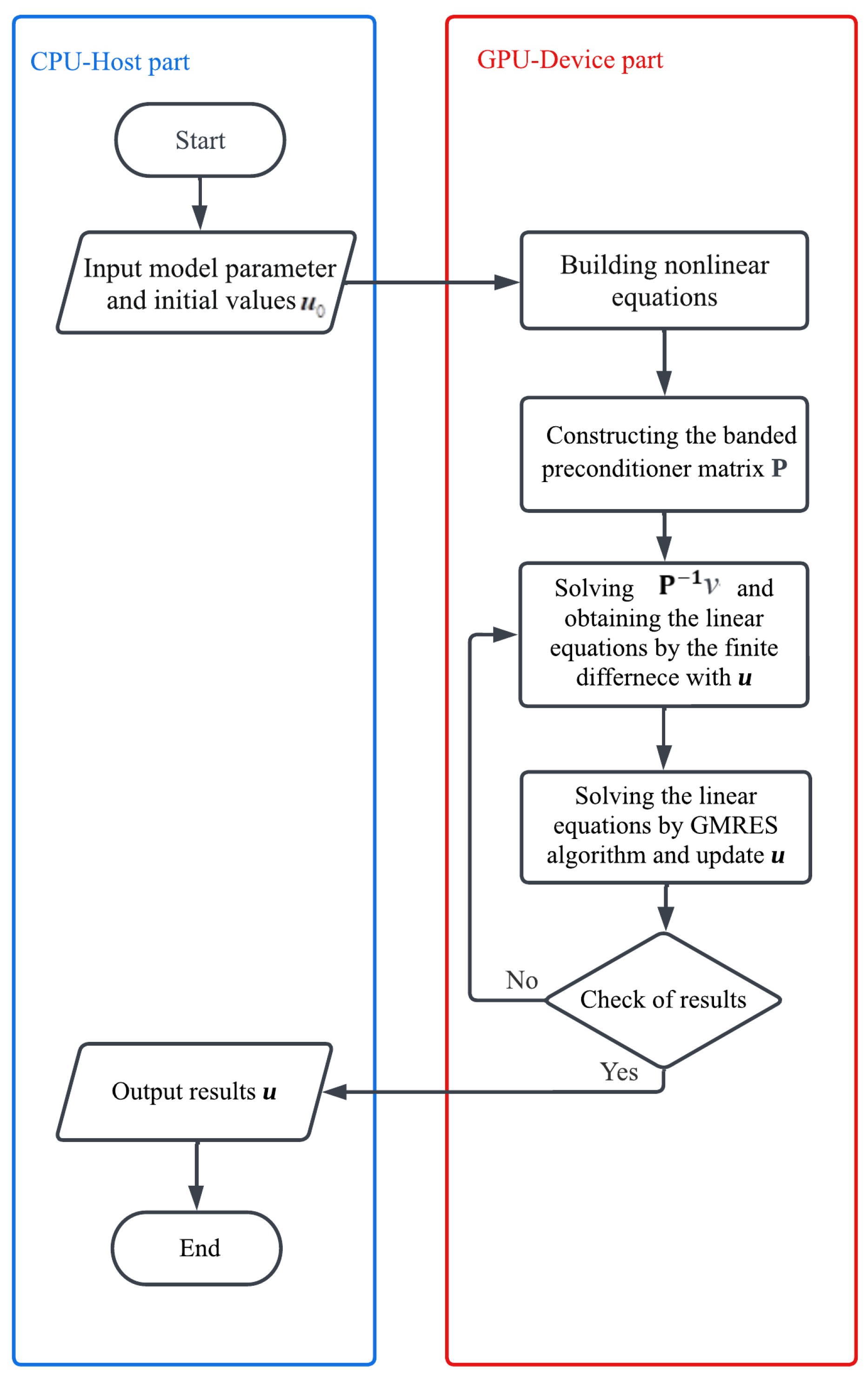
Based on the above analysis, the GPU solver of Kelvin ship waves adopts a hybrid programming model. The entire parallel computing procedure is shown as follows :
Step 1: Input calculation parameters including the initial guess, the data is transferred from CPU to GPU;
Step 2: According to the calculation parameters, the nonlinear equations are created in the GPU device;
Step 3: The banded preconditioner method is applied to build the banded preconditioner matrix in GPU;
Step 4: QR decomposition algorithm is used to invert the preconditioner matrix, and saving the decomposition results outside the loop body to avoid repeated QR decomposition of preprocessing;
Step 5: The result of is calculated directly using the QR decomposition results, by combining the result of with the approximate solution of the nonlinear equations, the finite difference approximation is carried out to obtain the linear equations;
Step 6: The GMRES algorithm is used to calculate the linear equations, obtain the correction values and update the approximate solutions ;
Step 7: Check of the approximate solutions of the nonlinear equations: If the accuracy requirement is not met, back to Step 5; if the accuracy requirement is met, the result is transferred from the GPU to the CPU.
The corresponding calculation flow chart is shown in Figure 9 which shows the calculation procedure more clearly.
Figure 9.
The computational flow chart of GPU implementation.
4.2. GPU solver implementation
4.2.1. Creating nonlinear system
The programming for creating nonlinear system on GPU by using CUDA language is briefly shown in Table 1. On the whole, the dimension of the GPU grid is the equivalent of the size of mesh, which means that one block can complete the relevant equations of one node in mesh. One block has 1024 threads, these plenty of threads can calculate Eq. (1), Eq. (2) and Eqs. (4)-(7) simultaneously.
Table 1.
The programming on GPU.
| Device Part | |
|---|---|
| Device function 1 | |
| 1 | devicedouble Integral(double a,double b,double c,double d,double e) |
| 2 | { |
| 3 | double val= b/sqrt(c)*log(2*c*a + d*b+ 2*sqrt(c*(c*a*a+ d*b*b +e*b*b))); |
| 4 | return val; |
| 5 | } |
| Device function 2 | |
| 1 | devicedouble Integrall(double a,double b,double c,double d,double e) |
| 2 | { |
| 3 | double val = a/sqrt(e)*log(2*d*b + d*s+ 2*sqrt(e*(c*a*a+ d*a*b +e*b*b))); |
| 4 | return val; |
| 5 | } |
| Kernel function | |
| 1 | globalvoid nonlinear(const long int N, const long int M, … ) |
| 2 | { |
| 3 | shareddouble A, B, C, … ; |
| 4 | sharedlong int K, l, blockpos, … ; |
| 5 | long int i, j, threadPos, … ; |
| 6 | threadPos = threadIdx.x; k = blockIdx.x; l = blockIdx.y ; |
| 7 | // Calculate necessary values |
| 8 | while(threadPos<(M*N)) { … } |
| 9 | // Calculation of the 16 parts to the closed integral |
| 10 | if(threadIdx.x==blockDim.x-1) { … } |
| 11 | … |
| 12 | if(threadIdx.x==blockDim.x-16) { … } |
| 13 | // Sum up all thread contributions |
| 14 | for(i=blocDim/2;i>0;i=i/2){ … } |
| 15 | //Split the free surface condition and radiation conditions between 5 blocks |
| 16 | if(k==0&&l==0) { … } … if(k==0&&l==5) { … } |
| 17 | } |
| Host Part | |
| 1 | int main |
| 2 | { |
| 3 | // Initialize data on CPU |
| 4 | InitialData(double* cpuData, double* gpuData); |
| 5 | long int i, j, threadPos, … ; |
| 6 | // Copy data from CPU to GPU |
| 7 | cudaMemcpy(cpuData, gpuData, Datasize, cudaMemcpyHostToDevice); |
| 8 | // Set dimensions of the grid and thread |
| 9 | dim3 block(1024, 1); dim3 grid(M, N - 1); |
| 10 | // Start Kernel function |
| 11 | Nonlinear≪ grid, block≪(gpuData); |
| 12 | // Copy data from GPU to CPU |
| 13 | cudaMemcpy(gpuData, cpuData, Datasize, cudaMemcpyDeviceToHost); |
| 14 | return 0; |
| 15 | } |
In the device part, there are two device functions which are called by the kernel function multiple times. These two device functions are formed to solve the singularity in the second integral of the boundary integral equation. The 16 special threads are set separately for fast computation. Other threads with the same CUDA code are used to complete the calculation of the remaining parts of the boundary integral equation. After threads have finished computing, all thread contributions are summed up, and nonlinear equations are built. Then arbitrarily choose 5 blocks to calculate the free surface condition and the radiation condition, nonlinear equations can be obtained. Therefore, these equations are formed by using the threads on GPU.
In the host part, the environment variables are configurated firstly. Then the data is transferred from CPU to GPU and the parallel instruction is sent to GPU. Finally, CPU gets the computation results from GPU.
4.2.2. Building preconditioner matrix
The building preconditioner matrix is decomposed to several tasks that can be operated in parallel by corresponding kernel functions in GPU blocks. The parallel idea and program structure are roughly similar to the part of creating nonlinear equations.
In the device part, in order to avoid data storage conflicts in GPU, three kernel functions are used to construct the preconditioner matrix in turn. As mentioned above, the preconditioner matrix size is , and four submatrices are formed by block decomposition method and banded preconditioner method: Submatrix is a tridiagonal matrix of size ; the submatrix and only differ between coefficients, and the base matrix can be constructed to represent them respectively with a size of , and ; the submatrix is a sparse matrix with a size of . Firstly, thread blocks are called in the GPU to fulfill the parallel construction of the four submatrices by the kernel function precondition(), and the two device functions mentioned above are also used to eliminate the singularity of the linear boundary integral equation. Then the kernel function matrix() is written to call thread blocks for parallel computation of , which involves solving multiple right-handed linear systems and matrix multiplication. Finally, the subtraction operation between matrices is completed by kernel function Schur(), and thread blocks are called to perform parallel operation of . The programming for building preconditioner matrix on GPU by using CUDA language is briefly shown in Table 2.
In the host part, the variables are first defined according to calculation parameters, then data is transferred from the CPU to the GPU, then the dimension of the thread blocks and thread grid is specified, and finally the kernel functions precondition(), matrix(), and Schur() are successively released. This part of the host side code is similar to the establishment of nonlinear equations and will not be repeated here.
Table 2.
The programming on GPU.
| Device Part | |
|---|---|
| Kernel functions | |
| 1 | globalvoid precondition(const long int N, const long int M, … ) |
| 2 | { |
| 3 | // Calculate submatrix |
| 4 | while(threadPos<N+3) { … }; |
| 5 | if(blockIdx.x==0) { … }; |
| 6 | // Calculate basis matrix |
| 7 | if(blockIdx.x==0) { while(threadPos<N+1) { … } }; |
| 8 | // Calculate submatrix |
| 9 | while(threadPos<N*M) { … }; |
| 10 | // Sum up all thread contributions |
| 11 | for(i=blocDim/2;i>0;i=i/2){ … } |
| 12 | } |
| 13 | globalvoid matrix(const long int N, const long int M, … ) |
| 14 | { |
| 15 | // Calculate |
| 16 | double Bcoef = 1/(); |
| 17 | double Ccoef = 2*3.1415; |
| 18 | if(blockIdx.x==0) { while(threadPos<N+1) { … } }; |
| 19 | } |
| 20 | globalvoid Schur(const long int N, const long int M,double*_b,double*D ) |
| 21 | { |
| 22 | // Calculate |
| 23 | int l=blockIdx.x; |
| 24 | int k=blockIdx.y; |
| 25 | int pos=1*(N+1)+k; |
| 26 | while(threadPos<N+1) |
| 27 | { |
| 27 | D[(1*(1+N)+threadPos)*M*(1+N)+pos]=D[(1*(1+N)+ |
| 28 | threadPos)*M*(1+N)+pos]-_b[threadPos*(1+N)+k]; |
| 29 | threadPos+=blockDim.x; |
| 30 | } |
| 31 | } |
4.2.3. Inverting preconditioner matrix
Comparing the Math Kernel Library which is famous for the computation of sparse linear algebra, the cuSolverSP library is generally faster for solving sparse linear systems [22]. In this paper, the cuSolverSP library is adopted to invert preconditioner matrix. The present sparse linear system is special, the right-hand term of the system changes continuously in the iteration whereas the left-hand term does not. The characteristic of the sparse linear system suggests using QR factorization to calculate [19]. By QR factorization, the sparse matrix is decomposed into an orthogonal matrix and an upper triangular matrix, which are saved in GPU memory and are directly used to solve linear equations in each iteration. Finally, the preconditioner-vector products can be obtained.
Step1: Using CSR data format to save preconditioner matrix with an appropriate bandwidth;
Step2: In the analysis stage, cusolverSpXcsrqrAnalysis() function is used to analyze the sparsity of orthogonal matrix and upper triangular matrix in QR decomposition. This process may consume a large amount of memory. If the memory is insufficient to complete the analysis, the program will stop running and return the corresponding error message;
Step3: In the preparation stage, cusolverSpXcsrqrAnalysis() function is used to select the appropriate computing space to prepare for QR decomposition. Here, two memory blocks are prepared in the GPU, one to store the orthogonal matrix and the upper triangular matrix, and the other to perform QR decomposition;
Step4: The cusolverSpDcsrqrSetup() function is called to allocate storage space for the orthogonal and upper triangular matrices based on the results of the preparation stage. Then, cusolverSpDcsrqrFactor() function is used to complete the QR decomposition of coefficient matrix outside the cycle;
Step5: Using cusolverSpDcsrqrZeroPivot() function checks the singularity of the decomposition results, if the nearly singular the program terminates operation and error is given, return to step 1 to choose the bandwidth again;
Step6: In the loop body, the cusolverSpDcsrqrSolve() function is repeatedly called, and the solution of linear equations can be obtained directly by using the decomposition results stored in GPU;
The main CUDA functions are shown in Table 3.
Table 3.
The list of CUDA functions for QR factorization.
| No. | Function name | Goal |
|---|---|---|
| 1 | cusolverSpXcsrqrAnalysisHost(); | Analyze structure |
| 2 | cusolverSpDcsrqrBufferInfoHost(); | Set up workspace |
| 3 | cusolverSpDcsrqrSetupHost(); | QR factorization |
| 4 | cusolverSpDcsrqrFactorHost(); | QR factorization |
| 5 | cusolverSpDcsrqrZeroPivotHost(); | Check singular |
| 6 | cusolverSpDcsrqrSolveHost(); | Solve system |
4.2.4. Solving linear equations by GMRES algorithm
In the process of solving linear equations, because the matrix free idea is adopted to avoid the storage of coefficient matrix, there is no product operation of coefficient matrix and vector in GMRES algorithm, so the operations that can be parallel in this part are operations between vectors. Therefore, this paper mainly uses cuBLAS library to complete the CUDA programming of GMRES algorithm to solve linear equations.
The cuBlasDdot() function is used to realize the inner product of vectors in the GMRES algorithm; the vector subtraction is calculated using cublasDaxpy() function; cublasDnrm2() function is used to calculate the Euclidean norm of the vector; cublasDscal() function is used to divide vector and scalar. After obtaining the orthonormal basis of Krylov subspace and the upper Hessnberg matrix, cublasDrotg() function is used to perform Givens rotation transformation on the upper Hessnberg matrix in GPU device to obtain the upper triangular matrix. Then the solution of linear least squares problem in GMRES algorithm is obtained, and cublasDspmv() function is used to achieve orthonormal basis and vector multiplication to get the solution of linear equations.
5. Numerical Simulations and Discussion
In this section, numerical simualtion of ship wave in multiple cases are carried out using the CPU and GPU solvers, and the simulation results are discussed. The effectiveness of the developed banded preconditioner JFNK method is first verified. Then, comparisons between the proposed GPU solver and the CPU solver on accuracy and efficiency are performed. Finally, verifying the capability of GPU solver by comparing simulation results with real ship wakes. The parameters of the computing environment are listed in Table 4.
Table 4.
The computing environment of high-performance computing cluster.
| CPU | GPU | |
|---|---|---|
| Card | Intel Xeon Bronze 3204 | NVIDIA Tesla A100 |
| Memory | 64 GB | 40 GB |
| Max Cores | 6 per node | 6912 |
| Programming language | C++ | CUDA, C++ |
5.1. Verification of the banded preconditioner JFNK method
To reveal the effectiveness of the banded preconditioner method, numerical simulations on different mesh sizes,i.e.,, , and with are carried out.
The overall runtimes against bandwidth on these four mesh sizes are illustrated in Figure 10. An optimal value of bandwidth exists for a certain mesh size. Furthermore, the optimal value of increases with the mesh size and approximately equals , in which means the number of latitude lines of the mesh. Therefore, the optimal bandwidth can be set to to get an optimal efficiency.
According to the optimal bandwidth selection rule, the running memories against the bandwidth are shown in Table 5. Correspondingly, the required running memory is drastically reduced by applying the banded preconditioner JFNK method. The mean reduction ratio is about 3.2, this means that the banded preconditioner JFNK method can save running memory by at least two-thirds.
Figure 10.
Optimal values of bandwidth for different mesh sizes.
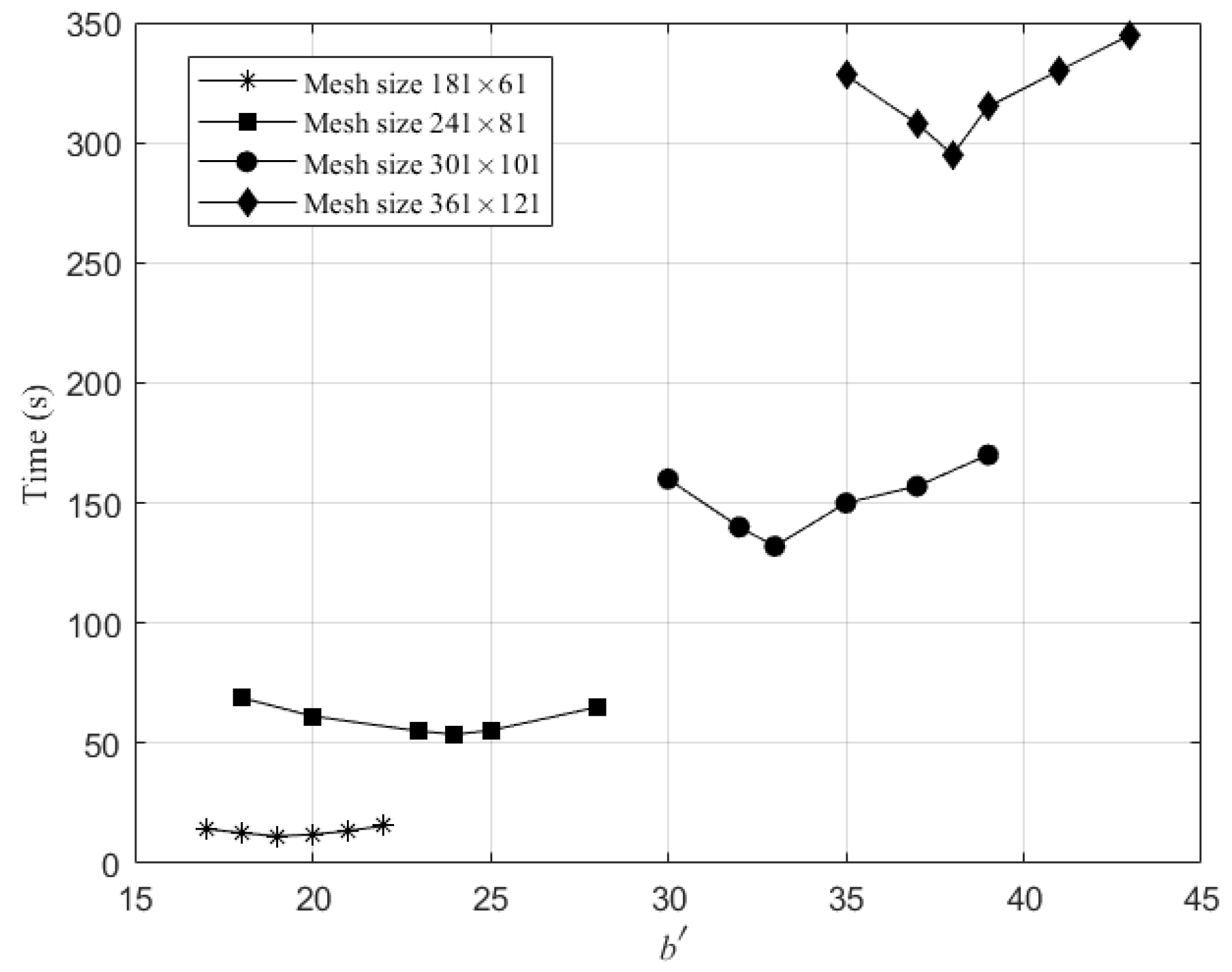
Table 5.
The running memory usage before and after applying the banded preconditioner method.
| Mesh size | Before | After | Reduction ratio | |
|---|---|---|---|---|
| 0.91GB | 19 | 0.28GB | 3.2 | |
| 2.9GB | 24 | 0.88GB | 3.3 | |
| 6.9GB | 33 | 2.3GB | 3.0 | |
| 15GB | 38 | 4.6GB | 3.3 |
5.2. Verification of the GPU solver
5.2.1. Accuracy
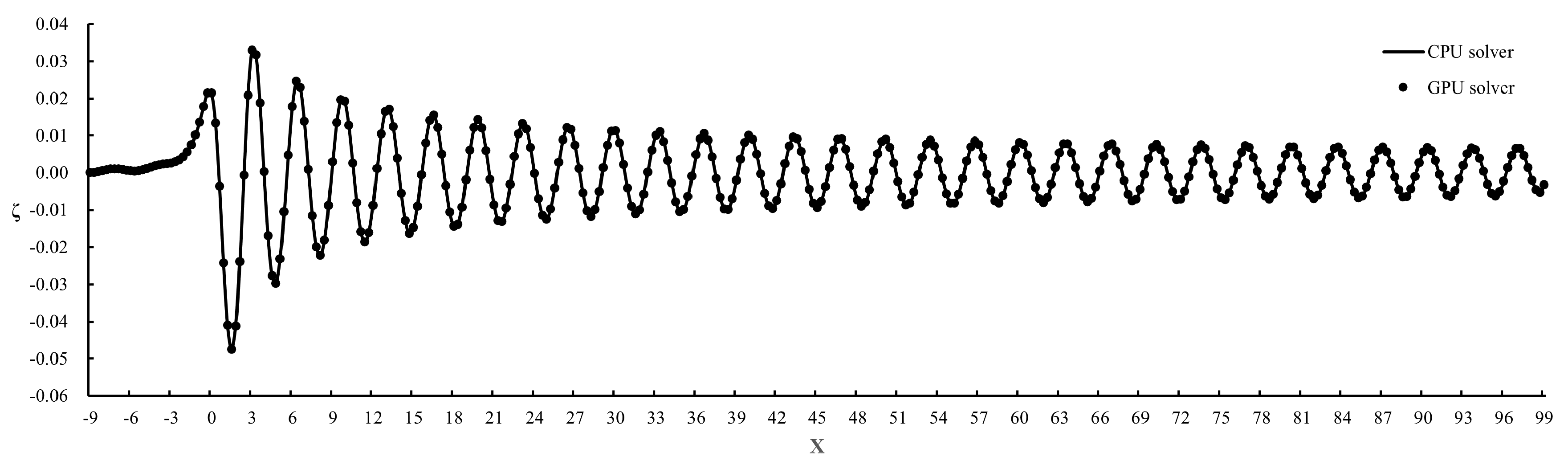
To verify the accuracy of the GPU solver, numerical simulations are conducted on and with a mesh and . The simulated wave heights on the centerline are compared with that of the CPU solver proposed by Sun [12], which is shown in Figure 11. The almost all points in the figure are traversed through the center by line, indicating that the calculation results of the GPU solver are very consistent with those of the CPU solver.
Furthermore, the MSE is used to further explain the error between them, as follows:
where is the amount of data, and represent CPU results and GPU results respectively. According to Eqs.(23), the calculated MSE is 9.37E-8, indicating that the calculation error between the GPU and CPU solver is minimal. Since the CPU solver has been verified by Sun [12], the accuracy of the proposed GPU solver can also be acceptable.
Figure 11.
A comparison of the centerline profiles for the simulation results of CPU solver and GPU solver, computed on a mesh with and . The solid line represents the simulation result of the GPU solver, the solid circles represent the simulation result of the CPU solver.
Figure 11.
A comparison of the centerline profiles for the simulation results of CPU solver and GPU solver, computed on a mesh with and . The solid line represents the simulation result of the GPU solver, the solid circles represent the simulation result of the CPU solver.
5.2.2. Efficiency
To verify the efficiency of the GPU solver, numerical simulation are conducted on and with five mesh sizes, namely , , , , and . The overall runtimes of GPU solver are compared with that of the CPU solver proposed by Sun [12], as shown in Figure 12. It clearly shows that the overall runtimes of the GPU solver are much shorter than that of the CPU solver. The clear accelerated-up ratios between the GPU solver and the CPU solver are shown in Table 6. The accelerated-up ratio on all cases are around 20.0. Therefore, the computaion efficiency of the proposed GPU solver is much higher than the CPU solver.
Figure 12.
The runtime of the GPU solver and CPU solver at different mesh sizes, red bars represent the GPU solver results and blue bars represent the CPU solver results.
Figure 12.
The runtime of the GPU solver and CPU solver at different mesh sizes, red bars represent the GPU solver results and blue bars represent the CPU solver results.
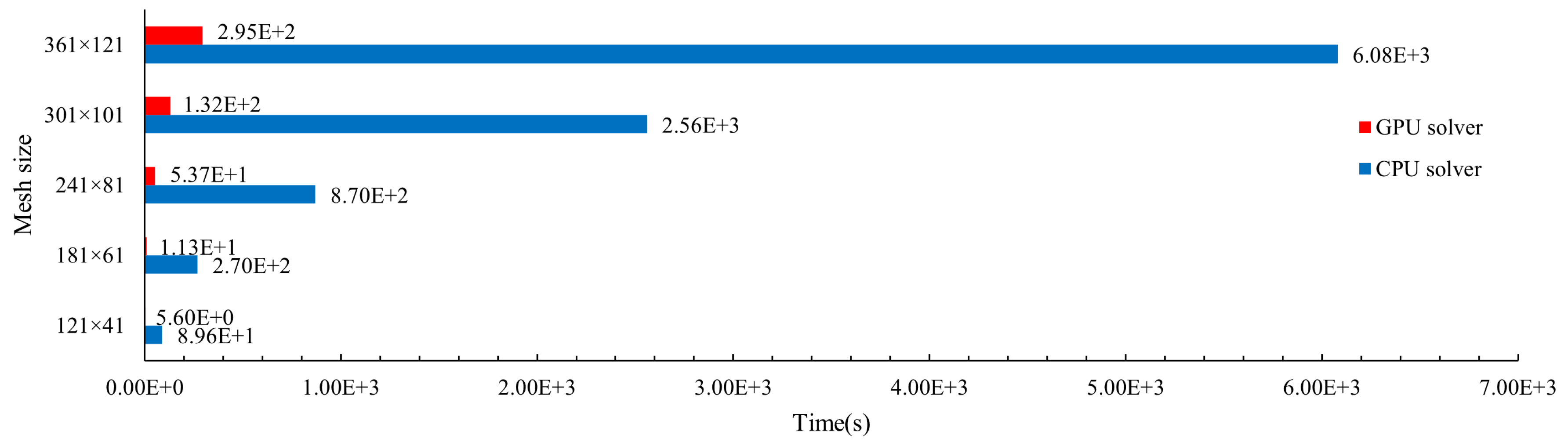
The proposed GPU solver has also been compared with another GPU solver proposed by Pethiyagoda [6] on these cases. The comparison of computation time between them is shown in Table 6. Obviously, the efficiency of the GPU solver proposed in this paper is higher than the GPU solver proposed by Pethiyagod [6], and the advantage is more significant with the increase of the mesh size. The reason is that Pethiyagoda [6] only introduced the GPU acceleration technique in the boundary integral method not the whole processs, whereas this paper proposes a complete parallel computing framework including the parallel process for inverting preconditioner matrix. In the process of inverting, the larger mesh size the heavier computational load, hence the advantage of the GPU solver proposed in this paper can be more significant.
Table 6.
The comparisons of runtime between CPU solver and GPU solvers on different mesh sizes, the CPU solver is proposed by Sun [12], one GPU solver is proposed in this paper, the other GPU solver is proposed by Pethiyagoda [6](results of Exp. ).
| Mesh size | CPU solver | Exp. | GPU solver | Accelerated-up ratio |
|---|---|---|---|---|
| 8.96E+1 s | 1.61E+1 s | 5.60E+0 s | 16.1 | |
| 2.70E+2 s | 1.22E+2 s | 1.13E+1 s | 23.9 | |
| 8.70E+2 s | 5.51E+2 s | 5.37E+1 s | 16.0 | |
| 2.56E+3 s | 1.78E+3 s | 1.32E+2 s | 19.3 | |
| 6.08E+3 s | 5.04E+3 s | 2.95E+2 s | 20.6 |
5.2.3. Capability
In the proposed GPU solver, like the CPU solver [12], three parameters can be used to regulate simulation results, namely source strength, source type and Froude number. The wake characteristics can be regulated by adjusting these parameters. For example, the wake waves of vessels of high speed and small overall length can be generated by using Rankine source, lower source strength and larger Froude number; oppositely, it is appropriate to choose small Froude number and a higher strength Kelvin source. As shown in Figure 13, the simulation patterns of GPU solver are compared with the real ship wave patterns. It is found that the simulation patterns are consistent with the real ship waves, the proposed GPU solver can also generate high quality simulation patterns for 3-D nonlinear ship wave.
Figure 13.
Wake pattern of real ship waves and the GPU solver computational results. The picture of real speedboat wake pattern comes from internet https://www.quanjing.com, accessed on 1 september 2023; the picture of real fishing ship wake comes from https://www.shutterstock.com, accessed on 1 september 2023; the picture of real large vessel wake comes from internet https://blogs.worldbank.org, accessed on 6 september 2023.
Figure 13.
Wake pattern of real ship waves and the GPU solver computational results. The picture of real speedboat wake pattern comes from internet https://www.quanjing.com, accessed on 1 september 2023; the picture of real fishing ship wake comes from https://www.shutterstock.com, accessed on 1 september 2023; the picture of real large vessel wake comes from internet https://blogs.worldbank.org, accessed on 6 september 2023.


6. Conclusions
The numerical simulation of ship wave is important for practical ocean engineering. This paper proposes a highly-paralleled numerical scheme for simulating three-dimensional (3-D) nonlinear Kelvin ship waves effectively, including a numerical model for nonlinear ship waves, a banded preconditioner JFNK method and a GPU based parallel computing framework. Numerical simulations show that the proposed GPU solver can save GPU memory and obtain high efficiency significantly. This highly-paralleled numerical scheme provides an opportunity for the further study of the nonlinear Kelvin ship waves on a large scale.
- (1)
- The bandwidth has an effect on the running memory and runtime of the GPU solver. Based on the mesh size, the value of the most appropriate bandwidth is around , with more than 66% GPU memory can be saved.
- (2)
- The GPU solver can obtain an accurate numerical solution. The mean square error of GPU solver results and CPU solver results is =9.37E-8, which is acceptable.
- (3)
- By designing the GPU parallel computing framework, the computation of ship wave simulation is accelerated up to 20 times.
Although an highly-paralleled numerical scheme for nonlinear ship wave is proposed in this paper, some assumptions are still made in the construction of the numerical model, such as infinite water depth and the steady motion of ship on calm water. It is of great significance to improve simulation results by further exploring the influence of finite water depth, tangential flow and unsteady ship motion on nonlinear ship waves.
Author Contributions
Validation, X.S., M.C. and J.D.; investigation, X.S.; writing—original draft preparation, X.S. and M.C.; writing—review and editing,X.S. and M.C.; supervision, X.S. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the National Key R&D Program of China (No.2022YFB4300803, 2022YFB4301402), the Ministry of Industry and Information Technology of the People’s Republic of China(No. CBG3N21-3-3), and the National Science Foundation of Liaoning Province, China(No.2022-MS-159).The authors would like to express sincere thanks for their support.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| JFNK | Jacobian-free Newton-Krylov |
| GMRES | Generalized Minimum Residual |
| CUDA | Compute Unified Device Architecture |
| GPU | Graphics Process Unit |
| CPU | Central Processing Unit |
| MSE | Mean Square Error |
References
- Dias, F. Ship Waves and Kelvin. j.Fluid Mech. 2014, 746, 1–4. [Google Scholar] [CrossRef]
- Tuck, E.; Scullen, D. A comparison of linear and nonlinear computations of waves made by slender submerged bodies. J Eng Math 2002, 42, 255–264. [Google Scholar] [CrossRef]
- Froude, w. Experiments upon the effect produced on the wave-making resistance of ships by length of parallel middle body; Institution of Naval Architects, 1877.
- Kelvin, L. On Ship Waves. Proc. Inst. Mech. Engrs. 1887, 38, 409–434. [Google Scholar] [CrossRef]
- Rabaud, M.; Moisy, F. Ship Wakes: Kelvin or Mach Angle? Phys. Rev. Lett 2013, 110, 214503.1–214503.5. [Google Scholar] [CrossRef] [PubMed]
- Pethiyagoda, R.; Moroney, T.; Lustri, C.; McCue, S. Kelvin Wake Pattern at Small Froude Numbers. J. Fluid Mech. 2021, 915, A126. [Google Scholar] [CrossRef]
- Ma, C.; Zhu, Y.; Wu, H.; He, J.; Zhang, C.; Li, W.; Noblesse, F. Wavelengths of the Highest Waves Created by Fast Monohull Ships or Catamarans. Ocean Eng. 2016, 113, 208–214. [Google Scholar] [CrossRef]
- Havelock, T. Wave resistance: Some cases of three-dimensional fluid motion. Proc. R. Soc. London. Ser. A, Contain. Pap. a Math. Phys. 1919, 95, 354–365. [Google Scholar] [CrossRef]
- J.H., M. The wave resistance of a ship. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1898, 45, 106–123. [Google Scholar] [CrossRef]
- Forbes, L. An algorithm for 3-dimensional free-surface problems in hydrodynamics. J. Comput. Phys. 1989, 82, 330–347. [Google Scholar] [CrossRef]
- Parau, E.; Vanden-Broeck, J. Three-dimensional waves beneath an ice sheet due to a steadily moving pressure. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 2011, 369, 2973–2988. [Google Scholar] [CrossRef]
- Sun, X.; Cai, M.; Wang, J.; Liu, C. Numerical Simulation of the Kelvin Wake Patterns. Appl. Sci. 2022, 12, 6265. [Google Scholar] [CrossRef]
- Hori, C.; Gotoh, H.; Ikari, H.; Khayyer, A. GPU-Acceleration for Moving Particle Semi-Implicit Method. Comput. Fluids. 2011, 51, 174–183. [Google Scholar] [CrossRef]
- Lu, X.; Dao, M.H.; Le, Q.T. A GPU-accelerated domain decomposition method for numerical analysis of nonlinear waves-current-structure interactions. Ocean Eng. 2022, 259, 111901. [Google Scholar] [CrossRef]
- Xie, F.; Zhao, W.; Wan, D. CFD Simulations of Three-Dimensional Violent Sloshing Flows in Tanks Based on MPS and GPU. J. Hydrodyn. 2020, 32, 672–683. [Google Scholar] [CrossRef]
- Saad, Y.; Schultz, M. GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
- Brown, P.; Saad, Y. Hybrid Krylov Methods for Nonlinear Systems of Equations. SIAM J. Sci. Stat. Comput. 1990, 11, 450–481. [Google Scholar] [CrossRef]
- Dembo, R.; Eisenstat, S.; Steihaug, T. Inexact Newton Methods. SIAM J. Numer. Anal. 1982, 19, 400–408. [Google Scholar] [CrossRef]
- Trefethen, L.; Bau, D. Numerical linear algebra; Siam, 1997.
- Lustri, C.J.; Chapman, S.J. Steady Gravity Waves Due to a Submerged Source. J. Fluid Mech. 2013, 732, 400–408. [Google Scholar] [CrossRef]
- NVIDIA. CUDA Toolkit Documentation v11.7.1., 2022.
- Grossman, M.; Mckercher, T. Professional CUDA C programming; China Machine Press: Beijing, China, 2017. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





