Prerpints.org logo
Preprint
Case Report

Experimental Study on Heat and Mass Transfer Characteristics of an Evaporative Cooler for Supercritical CO2 Cooling

Altmetrics

Downloads

77

Views

10

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 October 2023

Posted:

09 October 2023

You are already at the latest version

Alerts
Abstract
To study the heat and mass transfer characteristics of an evaporative cooler for cooling high-temperature working fluids such as supercritical carbon dioxide, an experimental device of the evaporative cooler was built, and a corresponding test system was constructed. Then, the experimental study was carried out based on the orthogonal test method, and the law and extent of the influence of water flow in the tube, spray water flow rate, inlet water temperature in the tube, and air flow rate on heat dissipation, cooling efficiency, and heat and mass transfer coefficients have been obtained. The correlation equations of the heat and mass transfer coefficients were obtained by fitting the orthogonal experimental data, and the validity of the correlation equations was confirmed by the verification experiment.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Evaporative coolers have the advantages of water saving[1], energy saving[2], and compact structure, and have been widely used in industrial cooling[2,3,4], heat pump systems[5], refrigeration systems[6], data centers[7], and other fields. To design evaporative coolers reasonably, extensive research has been carried out on the heat and mass transfer of evaporative coolers.
In terms of experimental research, Facão, and Oliveira[8] studied the evaporative cooler used for building heat dissipation and gave the correlation equation of heat and mass transfer coefficient. Hasan and Sirén [9] conducted a comparative study on two evaporative coolers and found that the heat and mass transfer coefficient of finned tubes is lower than that of bare tubes. Yoo et al. [10] studied the influence of spray water flow rate on the cooling efficiency and heat dissipation of evaporative coolers gave the correlation equation of the mass transfer coefficient and carried out experimental verification. Heyns and Kröger[11] found that the heat transfer coefficient of an evaporative cooler is a function of airflow velocity, spray water velocity, and spray water temperature, and the mass transfer coefficient is a function of airflow velocity and spray water velocity. According to the experimental results, the correlation equations of the heat transfer coefficient and mass transfer coefficient were established. Zheng et al. [12,13,14] studied the evaporative cooler using elliptical tubes, analyzed the influence of the parameters of water in the tube, spray water, and airflow on the performance of the evaporative cooler, and obtained the correlation equation of the heat and mass transfer coefficient. Jiang et al.[15] studied the evaporative cooler using plate-finned tubes and obtained the correlation equation of heat and mass transfer coefficients.
In terms of numerical simulation and algorithm optimization, Stabat and Marchio[16] proposed a simplified model based on the heat transfer unit number method and analyzed the characteristics of the heat and mass transfer process of the evaporative cooler. Papaefthimiou et al. [17] evaluated the sensitivity of the thermal performance characteristics of the evaporative cooler to the inlet air condition based on a thermodynamic model. The study found that the lower the wet bulb temperature of the inlet air, the higher the water temperature drop in the pipe and the evaporation of spray water. Zheng et al. [18] established a mathematical model of the evaporative cooler based on Matlab software and analyzed the heat and mass transfer mechanism of the circular tube evaporative cooler. Nasr et al. developed a rapid design algorithm for evaporative coolers with plain tubes [19] and twisted tubes[20], giving the relationship between heat transfer coefficient, pressure drop, heat transfer area, and mass transfer coefficient. Mahdi and Jaffal [21,22] carried out an exergy analysis on the evaporative cooler and found that the exergy loss is directly proportional to the air flow rate, the water flow rate in the pipe, the water inlet temperature in the pipe, and wet bulb temperature at the air inlet, and inversely proportional to the spray water flow. The correlation equation of the heat and mass transfer coefficients was established. Wei et al. [23] proposed a simplified calculation method to analyze the performance of two types of evaporative coolers and found that heat dissipation is mainly determined by the air flow rate and the water flow rate in the tube. Xie et al.[24,25,26] carried out numerical simulations on evaporative coolers using plain tubes, elliptical tubes, and finned tubes, and found that the influences of air flow rate, air inlet temperature, and spray water temperature on the heat transfer coefficient decreased in turn, and the spray mixing nanoparticles in water can improve the heat and mass transfer coefficient, and the influence of air flow rate on heat and mass transfer is higher than that of spray water flow rate. Lee et al. [27] simulated and experimented with an evaporative cooler using an elliptical tube, mainly studying the influence of the nozzle angle on the heat transfer coefficient. Based on CFD simulation, Zhu et al. [28] analyzed the influence of the uncertainty of environmental conditions on the performance of evaporative coolers and proposed a multi-scale model for optimizing evaporative coolers and their cooling water systems. Zhao et al. [29] carried out a numerical simulation on the evaporative cooler using elliptical finned tubes and analyzed the influence of wind speed and spray density on the performance of evaporative coolers under different structures and found that elliptical finned tubes can significantly improve the performance of evaporative coolers.
Table 1. Summary of the temperature conditions in the literature.
Table 1. Summary of the temperature conditions in the literature.
Authors Year Water temperature
in the tube/℃		 Spray water
temperature/℃		 Dry bulb air temperature /℃ Wet bulb air temperature /℃
Facão and Oliveira[8] 2000 15 - 28 - - 10 - 20
Hasan and Sirén[9] 2002 21 17 - 18 19 -2 0 16
Stabat and Marchio[16] 2004 23 - 42 - - 16 - 24
Nasr and Behfar[19] 2010 15.6 - 10 8.5
Yoo et al.[10] 2010 32 - 42 - - 27
Heyns and Kröger[11] 2010 - 35 - 53 16 - 22 14 - 18
Zheng et al.[12] 2011 13.7 - 36 11 - 28 4 - 15 2.1 - 9.6
Zheng et al.[13] 2012 13.7 - 36 11 - 28 4 - 15 2.1 - 9.6
Zheng et al.[18] 2012 15 - 24 15.1 - 25.4 13.1 - 32.5 10.5 - 19.8
Papaefthimiou et al.[17] 2012 35 20 10 - 45 8.1 - 30.3
Jiang et al.[15] 2013 30.1 - 36.6 25 - 26 27.2 20 - 25
Zheng et al. [14] 2013 13.7 - 55 11 - 28 - 18 - 28
Nasr and Jafarifar[20] 2015 45 13 - -
Mahdi and Jaffal[21] 2016 35 - 55 - - 7 - 24
Wei et al.[23] 2017 16 - 37 13.6 - 18.1 - 10 - 23
Xie et al.[24] 2017 37 10 - 35 10 - 34 -
Lee et al.[27] 2019 - 25 25 19.5
Zhu et al.[28] 2020 40 - 57 - - -
Zhao et al.[29] 2021 - 35 - 41 25 - 37 28
However, the temperature of the medium in the pipe involved in the above research is relatively lower (temperature range: around 15-60°C), so it is necessary to carry out further research on the working condition of the medium in the tube with a high temperature. Therefore, this study focused on the heat and mass transfer characteristics of the evaporative cooler under the condition of high temperature of the medium in the tube (temperature range: 70-110°C). First, the experimental device and test system were constructed, and the performance of the evaporative cooler was experimentally studied based on the orthogonal experimental scheme. Secondly, through the analysis of the experimental results, the sensitive factors of the heat transfer coefficient and the heat transfer coefficient are clarified, and the correlation equations of the heat and mass transfer coefficients are obtained by fitting the experimental data. Finally, the predictive abilities of the correlation equations are verified by verification experiments.

2. Experimental Study

2.1. Experimental device

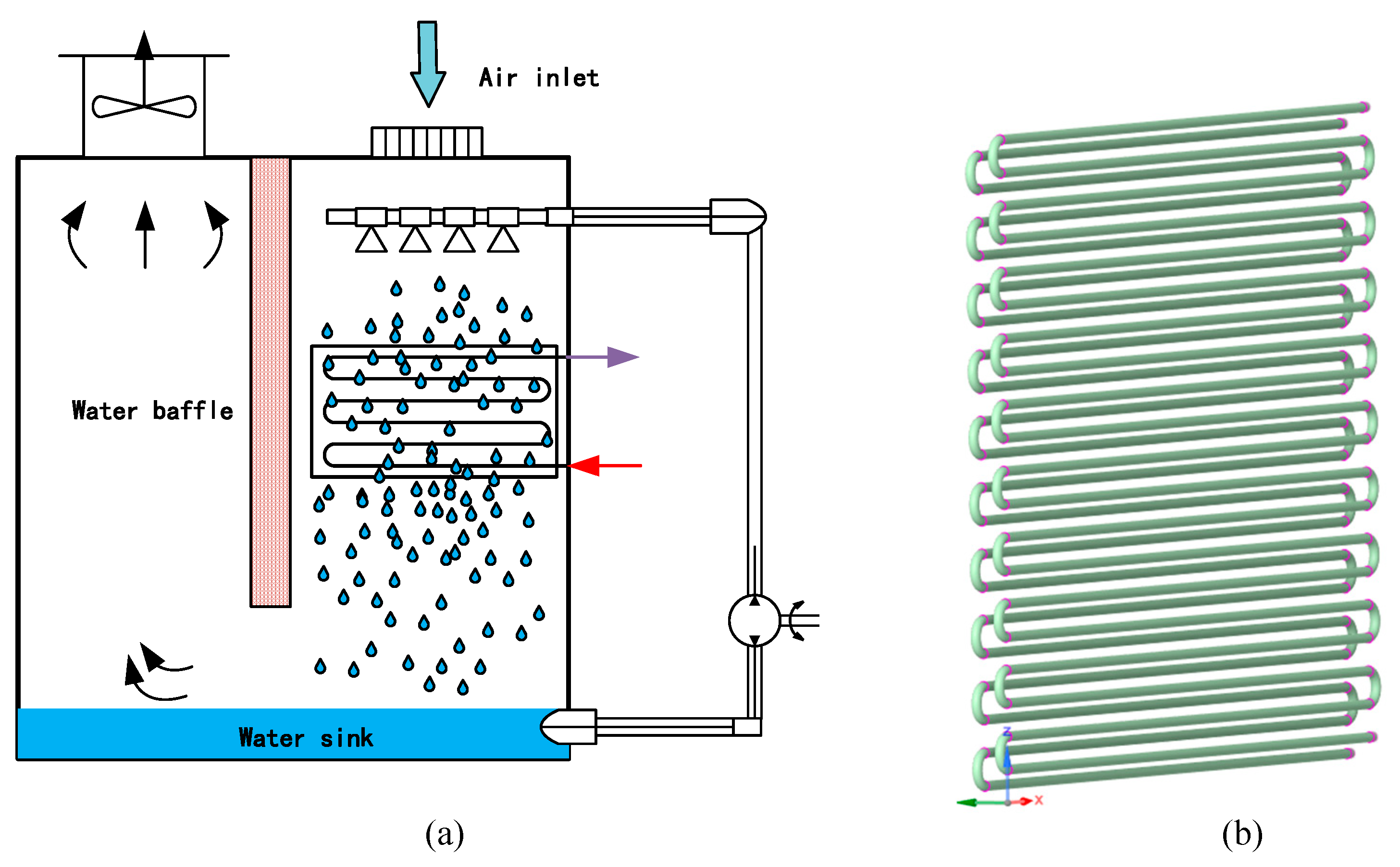
Figure 1(a) and (b) show the schematic diagram of the experimental setup and the tube bundle diagram of the cooling coil, respectively. The cooling coil bundle has a length of 1020 mm, a width of 610 mm, and a height of 1850 mm. There are two rows of coiled tubes in the tube bundle, each row of coiled tubes contains twenty copper tubes, and the transverse and longitudinal tube spacings are 60 mm and 20 mm, respectively. The material of the coil is copper, and its specification is ϕ12.0 mm×1.2 mm. The shell of the experimental device adopts a transparent acrylic plate, to observe the spraying condition and the distribution of the water film outside the tube.

2.2. Test system

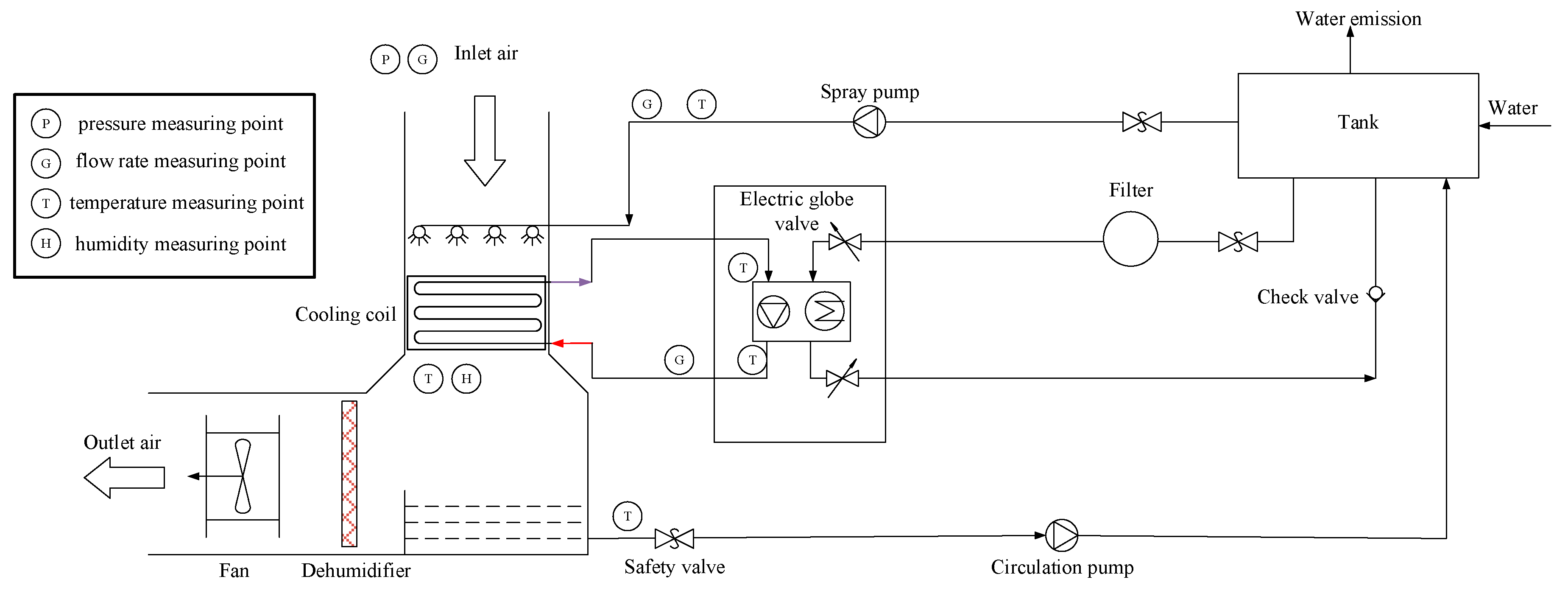
Based on the test system shown in Figure 2, the experiment was carried out and completed in an environment with a dry bulb air temperature of 17.0°C and a wet bulb air temperature of 10.7°C. In this system, the air flow rate, the spray water flow rate, and the flow rate and the inlet temperature of the water in the tube can be adjusted. The air flow rate is controlled by a fan speed controller. The spray water flow rate is regulated by a valve. The flow rate and the inlet temperature of water in the tube are controlled by a valve and a temperature control unit control, respectively. The temperature control unit has a maximum heating power of 20 kW. In addition, the test system also monitors the air outlet temperature and humidity, the outlet temperature of water in the tube, and the inlet and outlet temperatures of spray water. Table 2 lists the relevant measuring instruments and their parameters.

2.3. Experimental design

The orthogonal experiment method is used to design the experiment scheme, and the heat dissipation, cooling efficiency, heat transfer coefficient, and mass transfer coefficient are used as the investigation indicators. As shown by Table 3, the L25(56) orthogonal table is used to conduct the orthogonal experiment and to analyze the impact of the four factors of (A) the flow rate of water in the tube, (B) the spray water flow rate, (C) the inlet temperature of water in the tube and (D) the air flow rate on each inspection index. Thereby, the primary and secondary influencing factors affecting each index are screened and obtained. This experiment does not examine the interaction, and the four influencing factors are arranged in the 2nd, 3rd, 4th, and 5th columns of the L25(56) orthogonal table in turn, and the 1st and 6th columns are empty columns for error analysis.

3. Results and Discussion

This chapter analyzes the influence law and influence degree of various influencing factors on heat dissipation, cooling efficiency, heat transfer coefficient, and mass transfer coefficient. Furthermore, according to the analysis results, the main influencing factors of the heat transfer coefficient and mass transfer coefficient are clarified, and the correlation equations of the heat transfer coefficient and mass transfer coefficient are obtained by fitting the experimental data.

3.1. Effects of various influencing factors on heat dissipation

The heat dissipation of the evaporative cooler directly reflects its cooling capacity, and the calculation equation is:
Q t = m t c p T ti − T to
where   Q t ,   m t ,   c p ,   T ti , and T to are heat dissipation (kW), the mass flow rate of water in the tube (kg·s-1), the heat capacity of water (kJ·kg-1·℃-1), the inlet temperature of water in the tube (℃), and the outlet temperature of water in the tube (℃), respectively.
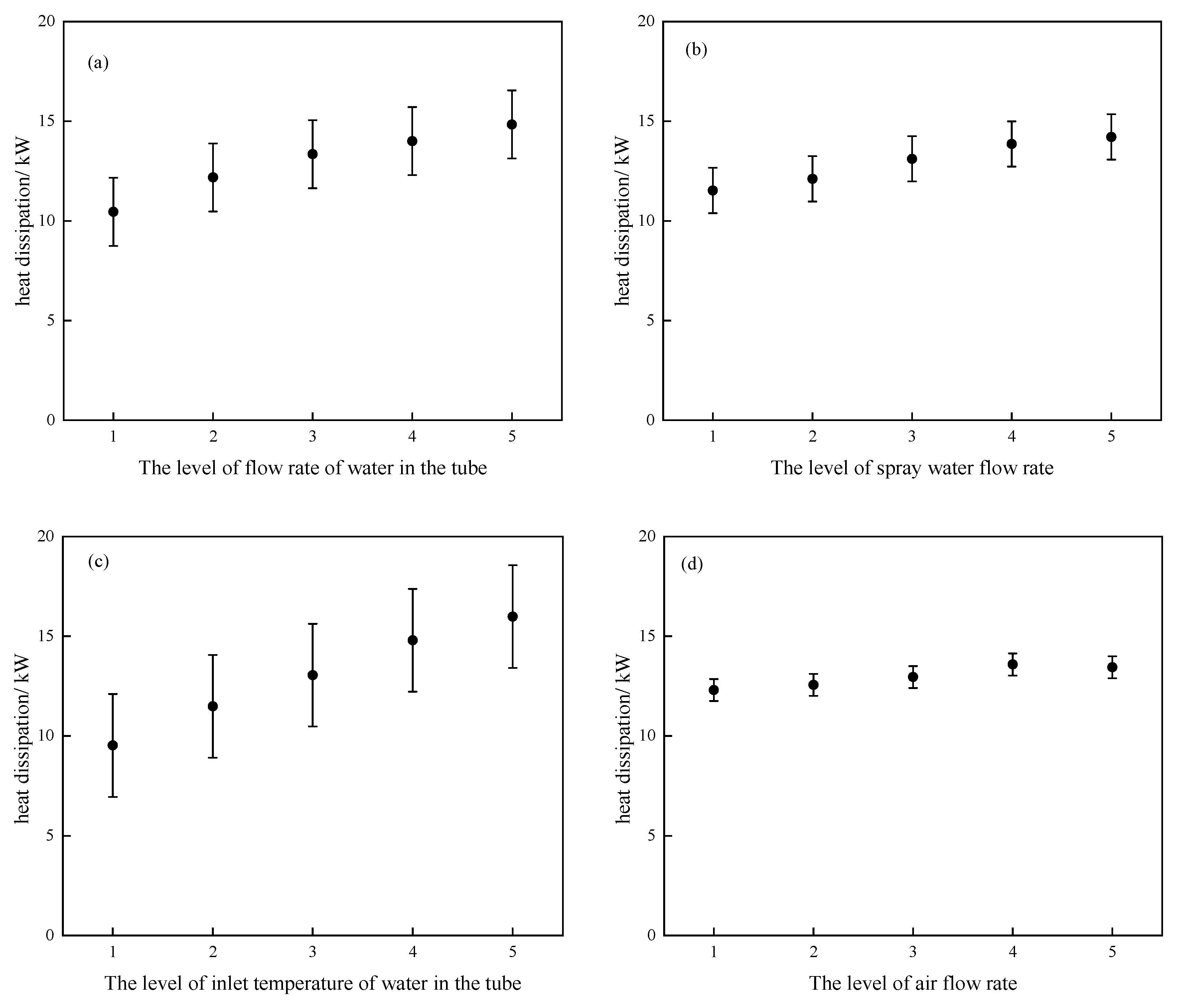
Figure 3 shows the relationship between the heat dissipation of the evaporative cooler and various influencing factors. As shown in Figure 3, with the increase of the levels of various influencing factors, heat dissipation is on the rise, that is, heat dissipation is positively correlated with the flow rate of water in the tube, the inlet temperature of water in the tube, the spray water flow rate, and the air flow rate. To quantitatively analyze the influence of each influencing factor on heat dissipation, this paper conducts variance analysis on the experimental data, and the results of variance analysis based on the F test are shown in Table 4. Statistics usually judge the significance of factors based on a significant level equal to 0.05, so this paper selects a significant level of 0.05 to distinguish whether the influencing factors are significant.
Table 4 shows that the flow rate and the inlet temperature of water in the tube have the most significant influence on the heat dissipation, followed by the spray water flow rate, and the air flow rate has no obvious effect. Therefore, to increase the heat dissipation of an evaporative cooler, one can first consider increasing the flow rate and the inlet temperature of water in the tube and then consider increasing the spray water flow rate.

3.2. Effects of various influencing factors on cooling efficiency

The limit of the outlet temperature of water in the tube is the ambient wet bulb temperature, and the cooling efficiency can be used to evaluate the difference between the outlet temperature of water in the tube and the ambient wet bulb temperature. The formula for calculating the cooling efficiency is:
ε = T ti − T to T ti − T a , wb × 100 %
where ε is the cooling efficiency and T a , wb is the ambient wet bulb temperature (℃).
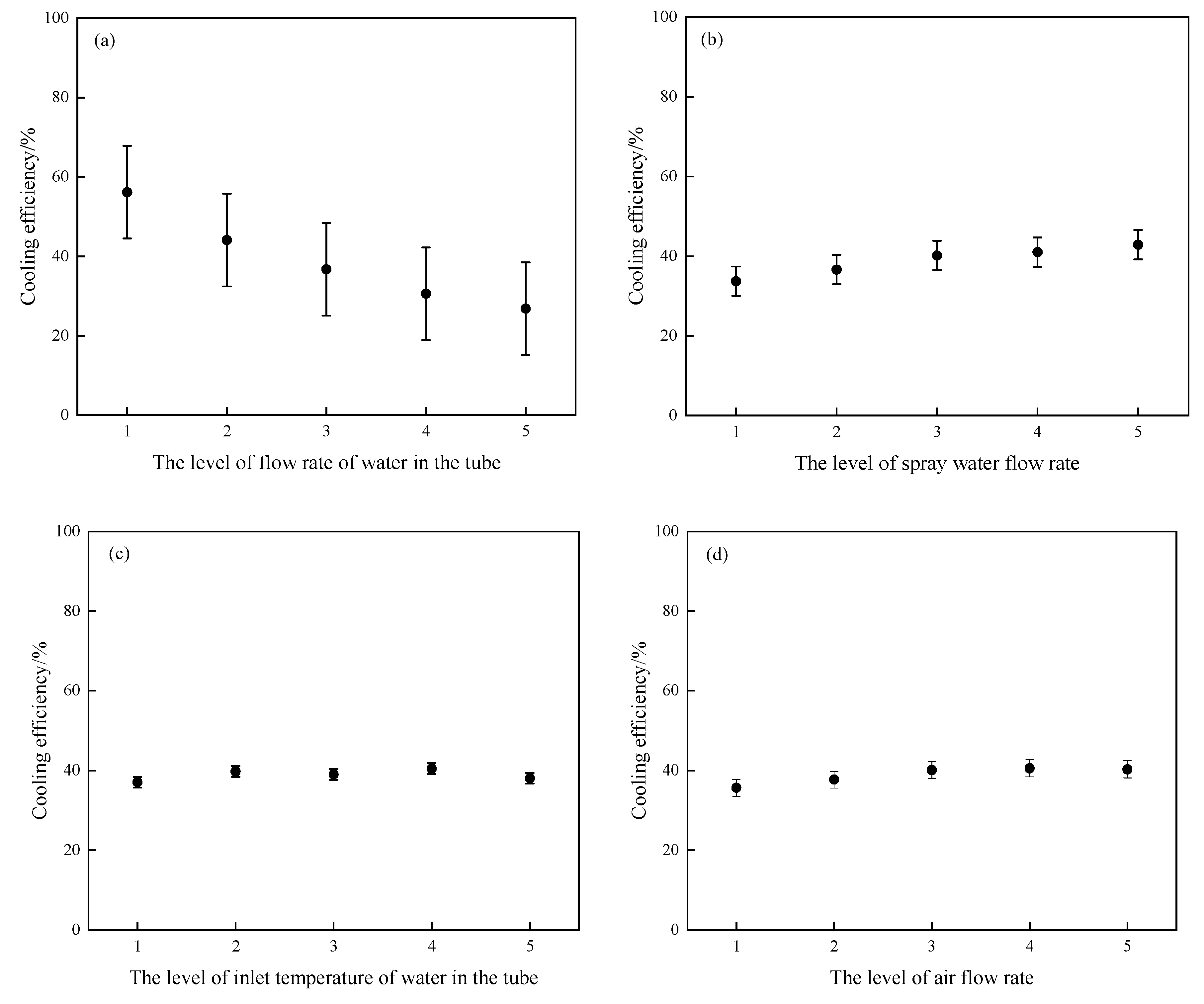
Figure 4 shows the influence of various influencing factors on cooling efficiency. As shown in Figure 4(a), the cooling efficiency decreases as the flow rate of water in the tube increases. Figure 4(b) shows that the cooling efficiency increases with the increase of the spray water flow rate. As shown in Figure 4(c) and (d), there is no significant change in the cooling efficiency by changing the inlet temperature of water in the tube and the air flow rate. To quantitatively analyze the influence of various influencing factors on cooling efficiency, the variance analysis of the experimental data was conducted. The results of variance analysis based on the F test are shown in Table 5. According to Table 5, it can be seen that the flow rate of water in the tube has the most significant influence on the cooling efficiency, followed by the spray water flow rate, while both the inlet temperature of water in the tube and the air flow rate have no obvious influence on the cooling efficiency.

3.3. Effects of various influencing factors on the heat transfer coefficient

The heat transfer coefficient is calculated by:
K = c p m t T ti − T to A o Δ T m
where K is the heat transfer coefficient (W·m-2·℃-1), A o is the external surface area of the tube (m2), and Δ T m is the logarithmic mean temperature difference (℃). Δ T m is calculated by:
Δ T m = T ti − T w − T to − T w l n T ti − T w T to − T w
where T w is the water film temperature outside the tube (℃), which is generally taken as the average value of the inlet and outlet temperatures of the spray water.
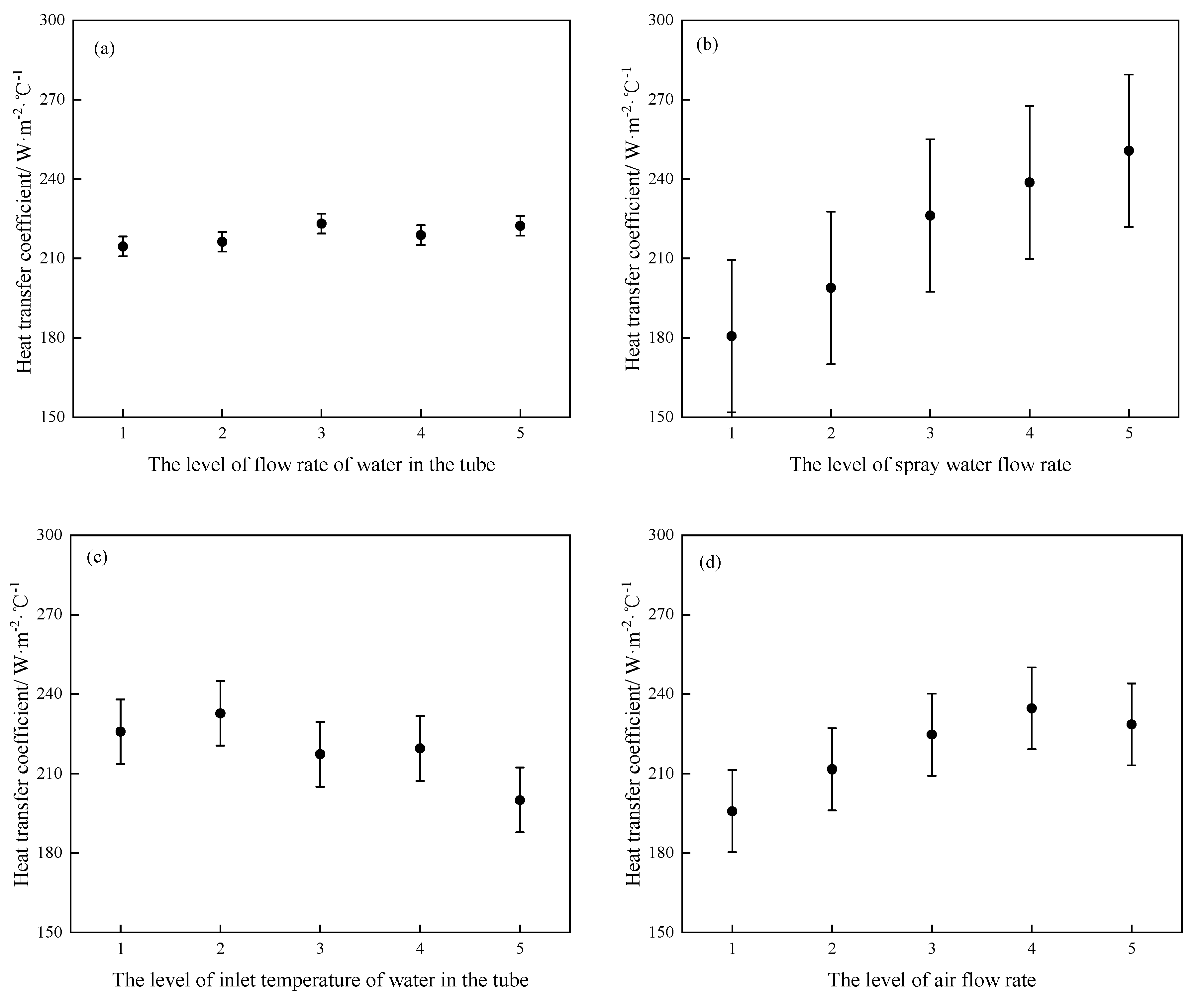
Figure 5 shows the relationship between the heat transfer coefficient of the evaporative cooler and various influencing factors. Figure 5(a) shows that changing the flow rate of water in the tube has no significant effect on the heat transfer coefficient. As shown in Figure 5(b) and (d), the heat transfer coefficient increases with the increase of the spray water flow rate and the air flow rate, indicating that the heat transfer outside the tube is the dominant factor in the heat transfer of the evaporative cooler. As shown in Figure 5(c), as the inlet temperature of water in the tube increases, the heat transfer coefficient decreases. To quantitatively analyze the influence of various influencing factors on cooling efficiency, the variance analysis of the experimental data was conducted. The results of variance analysis based on the F test are shown in Table 6. It can be seen from Table 6 that the spray water flow rate has the most significant effect on the heat transfer coefficient, followed by the inlet temperature of water in the tube and the air flow rate, and the flow rate of water in the tube has no obvious effect on the heat transfer coefficient.

3.4. Effects of various influencing factors on the heat transfer coefficient

The mass transfer coefficient is used to evaluate the mass transfer effect between the air and the liquid film outside the tube. Based on Merkel’s theory [15,30], the mass transfer coefficient is calculated by:
h d = m a A o l n i wm − i ao i wm − i ai
where h d is the mass transfer coefficient (kg·m-2·s-1), m a is the air flow rate (kg·s-1), i mw is the enthalpy of saturated humid air at the spray water temperature (kJ·kg-1), i ai and i ao are the enthalpy of the air inlet and outlet (kJ·kg-1), respectively.
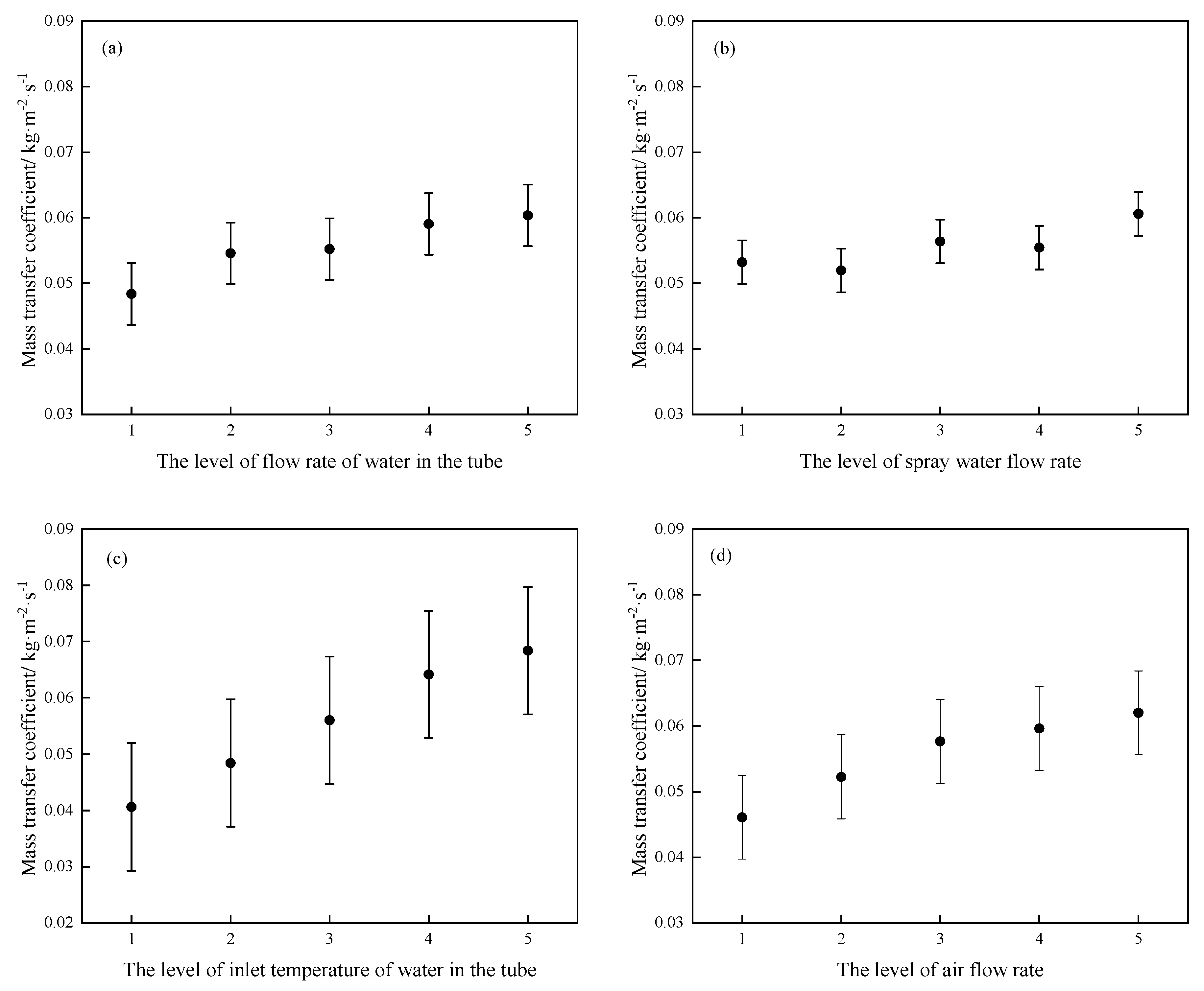
Figure 6 shows the relationship between the mass transfer coefficient and various influencing factors. As shown in Figure 6(a) and (b), the mass transfer coefficient does not change significantly with the change of the flow rate of water in the tube and the spray water flow rate. As shown in Figure 6(c) and (d), the greater the inlet temperature of water in the tube and the air flow rate, the greater the mass transfer coefficient. To quantitatively analyze the influence of various influencing factors on cooling efficiency, the variance analysis of the experimental data was conducted. The results of variance analysis based on the F test are shown in Table 7. It can be seen from Table 7 that the inlet temperature of water in the tube has the most significant effect on the mass transfer coefficient, followed by the flow rate of water in the tube and the air flow rate on the mass transfer coefficient, and the spray water flow rate has no obvious effect on the mass transfer coefficient.

3.5. Correlation equations of the heat and mass coefficients

From the analysis of the above experimental results, the significant influencing factors of the heat transfer coefficient are the spray water flow rate, the air flow rate, and the inlet temperature of water in the tube, and the influence of the flow rate of water in the tube is not significant. The significant influencing factors of the mass transfer coefficient are the inlet temperature of water in the tube, the air flow rate, and the flow rate of water in the tube, but the influence of the spray water flow rate is not significant. Correlation analysis can be carried out on the heat and mass transfer coefficients based on significant factors.
To facilitate the correlation analysis, the three influencing factors of the spray water flow rate, the air flow rate, and the flow rate of water in the tube needs to be fluxed, and the spray water flux, the air flux, and the flux of water in the tube are obtained, respectively.
The spray water flux is calculated by:
G w = m w 2 N ⋅ 2 L t ⋅ d o
where Gw is the spray water flux (kg·s-1·m-2), N the number of tubes in each row, d o the outer diameter of the tube (m), and L t the single tube length (m).
The flux of water in the tube is calculated by:
G t = m t 2 N ⋅ 2 L t ⋅ d i
where Gt is the flux of water in the tube (kg·s-1 m-2), and d i is the inner diameter of the tube (m).
The air flux is calculated by:
G a = m a [ ( N + 1 / 2 ) S T − ( N + 1 ) d o ] L t
where Ga is air flux (kg·s-1 m-2), and ST is the tube spacing (m).
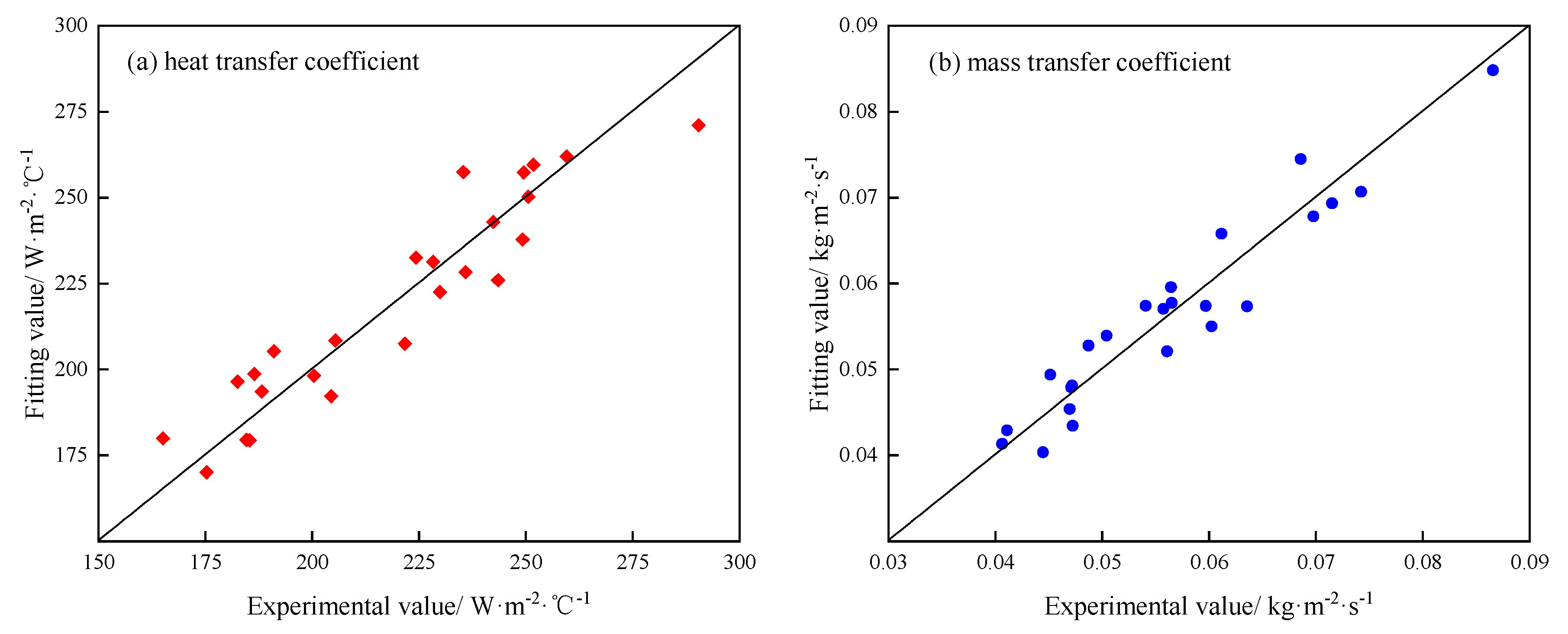
Referring to the suggestions of Heyns and Kröger[11] and Jiang et al. [15] on the correlation equations of the heat and mass transfer coefficients, the correlation equations in this paper are in the form of power functions. Thus, the correlation equation (9) of the heat transfer coefficient and the correlation equation (10) of the mass transfer coefficient were obtained based on the above-mentioned orthogonal experimental data fitting, and the fitting situation of the correlation equations to the orthogonal experimental data are shown in Figure 7.
K = 1799.577 G a 0.283 G w 0.803 T ti − 0.272
h d = 0.000332 G a 0.509 G t 0.173 T ti 1.116  
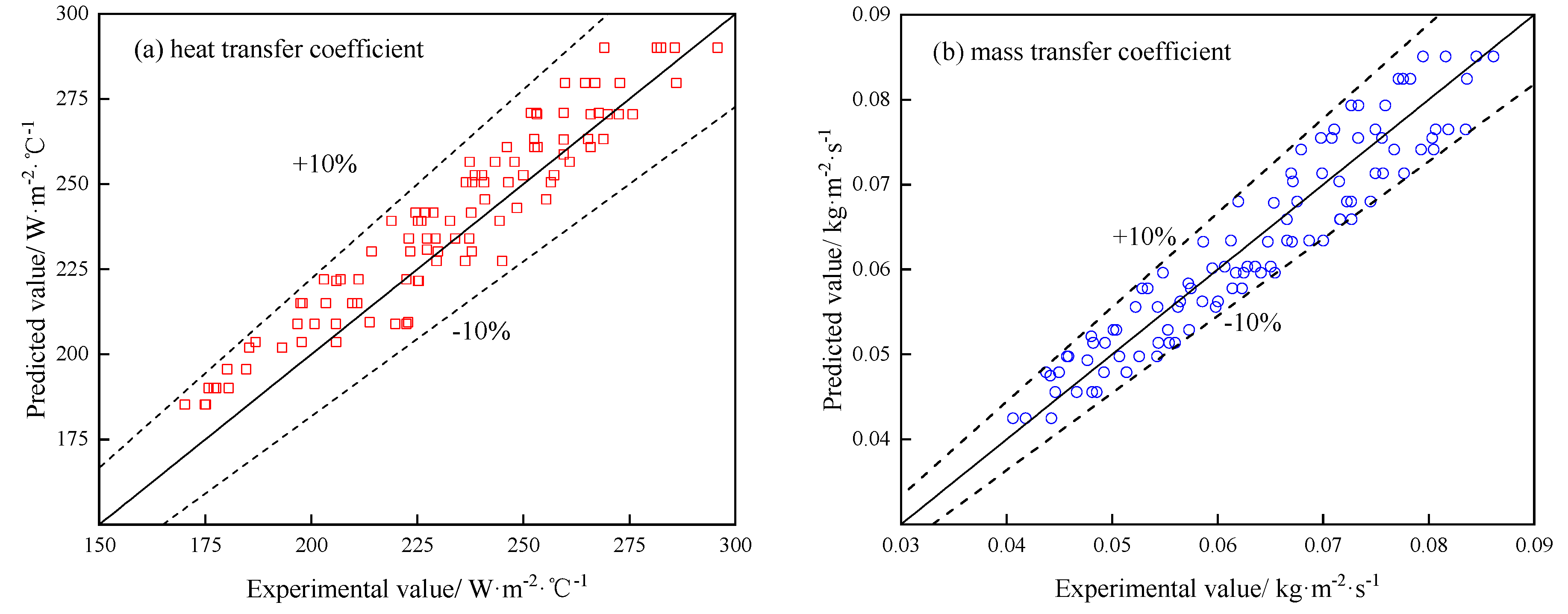
To verify the validity of the orthogonal experiment and the correlation equations obtained, 100 sets of verification experiments were further carried out, and the relative errors between the experimental data and the predicted values of the correlation equations were calculated using Eq. (11).
δ = x e x p − x pre x e x p
where δ is a relative error, x e x p is experimental value, and x pre is the predicted value of the correlation equation.
Figure 8 shows the comparisons between the verification experimental value and the predicted value of the correlation equations, and the relative errors of all data are less than 10%. Among them, the average relative error of the heat transfer coefficient is 4.25%, and the average relative error of the mass transfer coefficient is 5.42%. The above verification experiment results show that the correlation equation can effectively predict the heat and mass transfer coefficients and verify the validity of the orthogonal experiment.

4. Conclusions

To study the heat and mass transfer characteristics of the evaporative cooler in the cooling process of high-temperature water, an experimental device for evaporative cooling and a test system were constructed, and the experimental research was carried out based on the orthogonal experimental method. The main conclusions are as follows:
(1) The flow rate and the inlet temperature of water in the tube have the most significant influence on the heat dissipation of the evaporative cooler, followed by the spray water flow rate, and the air flow rate has a weaker effect. If it is necessary to increase the heat dissipation of the evaporative cooler, the flow rate and the inlet temperature of water in the tube, and the spray water flow rate can be increased.
(2) The spray water flow rate has the most significant effect on the heat transfer coefficient of the evaporative cooler, followed by the inlet temperature of water in the tube and the air flow rate, and the flow rate of water in the tube has no obvious effect on the heat transfer coefficient.
(3) The inlet temperature of water in the tube has the most significant effect on the mass transfer coefficient of the evaporative cooler, followed by the flow rate of water in the tube and the air flow rate, and the spray water flow rate has no obvious effect on the mass transfer coefficient.
(4) Under the working conditions of this study, the correlation equations of the heat and mass transfer coefficients for the evaporative cooler are K = 1799.577 G a 0.283 G w 0.803 T ti − 0.272 and h d = 0.000332 G a 0.509 G t 0.173 T ti 1.116 , respectively.

Acknowledgments

Support from the National Key R&D Program of China (Grant No. 2022YFE0120900) is gratefully acknowledged.

References

  1. Zhou Y, Zhang P, Zhao J, et al. Experimental study on performance of a closed wet cooling tower for air wet-bulb temperature near 0°C[J]. Journal of Thermal Science, 2019,28(5): 1015-1023.
  2. Alhamid M I, Bismo S, Nainggolan F, et al. Analysis of the effectiveness of ozonation on corrosion and bacteria on closed system cooling towers[J]. AIP Conference Proceedings, 2019, 2062(1): 020046.
  3. Liu J, Zhang L, Lin Z, et al. Research of technical and economic performance of plastic capillary mats used as the heat exchanger of a closed-circuit cooling tower[J]. Applied Thermal Engineering, 2019, 153: 800-807.
  4. Wagner T V, Parsons J R, Rijnaarts H H M, et al. A review on the removal of conditioning chemicals from cooling tower water in constructed wetlands[J]. Critical Reviews in Environmental Science and Technology, 2018, 48(19-21): 1094-1125.
  5. Zhou Y, Zhu X, Ding X. Theoretical investigation on thermal performance of new structure closed wet cooling tower[J]. Heat Transfer Engineering, 2018, 39(5): 460-472.
  6. Bhuva J, H. Improvement in the performance of cooling tower of thermal power plant: a review[J]. International Journal for Research in Applied Science and Engineering Technology, 2018, 6(3): 3043-3046.
  7. Nadjahi C, Louahlia H, Lemasson S. A review of thermal management and innovative cooling strategies for data center[J]. Sustainable Computing: Informatics and Systems, 2018, 19: 14-28.
  8. Facão J, Oliveira A C. Thermal behaviour of closed wet cooling towers for use with chilled ceilings[J]. Applied Thermal Engineering, 2000, 20(13): 1225-1236.
  9. Hasan A, Sirén K. Performance investigation of plain and finned tube evaporatively cooled heat exchangers[J]. Applied Thermal Engineering, 2003, 23(3): 325-340.
  10. Yoo S, Kim J, Han K. Thermal performance analysis of heat exchanger for closed wet cooling tower using heat and mass transfer analogy[J]. Journal of Mechanical Science and Technology, 2010, 24(4): 893-898.
  11. Heyns J A, Kröger D G. Experimental investigation into the thermal-flow performance characteristics of an evaporative cooler[J]. Applied Thermal Engineering, 2010, 30(5): 492-498.
  12. Zheng W Y, Zhu D S, Song J, et al. Experimental investigation of heat and mass transfer of novel closed circuit cooling tower[J]. Chemical Engineering (China), 2011, 39(09): 34-37.
  13. Zheng W Y, Zhu D S, Song J, et al. Experimental and computational analysis of thermal performance of the oval tube closed wet cooling tower[J]. Applied Thermal Engineering, 2012, 35: 233-239.
  14. Zheng W, Y. Experimental investigation and numerical simulation of the heat and mass transfer in evaporative cooler[D]. Shanghai: East China University of Science and Technology, 2013.
  15. Jiang J, Liu X, Jiang Y. Experimental and numerical analysis of a cross-flow closed wet cooling tower[J]. Applied Thermal Engineering, 2013, 61(2): 678-689.
  16. Stabat P, Marchio D. Simplified model for indirect-contact evaporative cooling-tower behaviour[J]. Applied Energy, 2004, 78(4): 433-451.
  17. Papaefthimiou V D, Rogdakis E D, Koronaki I P, et al. Thermodynamic study of the effects of ambient air conditions on the thermal performance characteristics of a closed wet cooling tower[J]. Applied Thermal Engineering, 2012, 33: 199-207.
  18. Zheng W Y, Zhu D S, Song J, et al. Simulation of closed wet cooling towers[J]. Journal of Chemical Engineering of Chinese Universities, 2012, 26(02): 216-221.
  19. Jafari Nasr M R, Behfar R. A novel design for evaporative fluid coolers[J]. Applied Thermal Engineering, 2010, 30(17-18): 2746-2752.
  20. Nasr M R J, Jafarifar S. Extension of the rapid design algorithm for twisted-tube evaporative fluid coolers[J]. Chemical Engineering & Technology, 2015, 38(5): 787-796.
  21. Qasim S M, Hayder M J. Investigation of the effect of packing location on performance of closed wet cooling tower based on exergy analysis[J]. IOP Conference Series. Materials Science and Engineering, 2016, 145(3): 32009-32014.
  22. Mahdi Q S, Jaffal H M. Energy and exergy analysis on modified closed wet cooling tower in Iraq[J]. Ai-Khawarizmi Engineering Journal, 2016, 12(2): 45-49.
  23. Wei X, Li N, Peng J, et al. Performance analyses of counter-flow closed wet cooling towers based on a simplified calculation method[J]. Energies, 2017, 10(3): 282.
  24. Xie X, He C, Xu T, et al. Deciphering the thermal and hydraulic performances of closed wet cooling towers with plain, oval, and longitudinal fin tubes[J]. Applied Thermal Engineering, 2017, 120: 203-218.
  25. Xie X, Zhang Y, He C, et al. Bench-scale experimental study on the heat transfer intensification of a closed wet cooling tower using aluminum oxide nanofluids[J]. Industrial & Engineering Chemistry Research, 2017, 56(20): 6022-6034.
  26. Xie X, Liu H, He C, et al. Deciphering the heat and mass transfer behaviors of staggered tube bundles in a closed wet cooling tower using a 3-d vof model[J]. Applied Thermal Engineering, 2019, 161: 114202.
  27. Lee Y, Hong S, Dang C, et al. Effect of counter current airflow on film dispersion and heat transfer of evaporative falling film over a horizontal elliptical tube[J]. International Journal of Heat and Mass Transfer, 2019, 141: 964-973.
  28. Zhu Q, Zhang B, Chen Q, et al. Model reductions for multiscale stochastic optimization of cooling water system equipped with closed wet cooling towers[J]. Chemical Engineering Science, 2020, 224: 115773.
  29. Zhao R, Bu S, Zhao X, et al. Study on thermal performance of new finned heat exchange tube bundles in cooling tower[J]. International Journal of Thermal Sciences, 2021, 168: 107064.
  30. Zhu X, Chen S, Shen S, et al. Experimental study on the heat and mass transfer characteristics of air-water two-phase flow in an evaporative condenser with a horizontal elliptical tube bundle[J]. Applied Thermal Engineering, 2020, 168: 114825.
Preprints 87172 g001
Figure 1. Evaporative cooler experimental device: (a) the schematic diagram, and (b) the bundle diagram.
Figure 1. Evaporative cooler experimental device: (a) the schematic diagram, and (b) the bundle diagram.
Preprints 87172 g001
Preprints 87172 g002
Figure 2. The schematic diagram of the test system.
Figure 2. The schematic diagram of the test system.
Preprints 87172 g002
Preprints 87172 g003
Figure 3. Influence of various factors on the heat dissipation: (a) flow rate of water in the tube; (b) spray water flow rate; (c) inlet temperature of water in the tube; and (d) air flow rate.
Figure 3. Influence of various factors on the heat dissipation: (a) flow rate of water in the tube; (b) spray water flow rate; (c) inlet temperature of water in the tube; and (d) air flow rate.
Preprints 87172 g003
Preprints 87172 g004
Figure 4. Influence of various factors on the cooling efficiency: (a) flow rate of water in the tube; (b) spray water flow rate; (c) inlet temperature of water in the tube; and (d) air flow rate.
Figure 4. Influence of various factors on the cooling efficiency: (a) flow rate of water in the tube; (b) spray water flow rate; (c) inlet temperature of water in the tube; and (d) air flow rate.
Preprints 87172 g004
Preprints 87172 g005
Figure 5. Influence of various factors on the heat transfer coefficient: (a) flow rate of water in the tube; (b) spray water flow rate; (c) inlet temperature of water in the tube; and (d) air flow rate.
Figure 5. Influence of various factors on the heat transfer coefficient: (a) flow rate of water in the tube; (b) spray water flow rate; (c) inlet temperature of water in the tube; and (d) air flow rate.
Preprints 87172 g005
Preprints 87172 g006
Figure 6. Influence of various factors on the mass transfer coefficient: (a) flow rate of water in the tube; (b) spray water flow rate; (c) inlet temperature of water in the tube; and (d) air flow rate.
Figure 6. Influence of various factors on the mass transfer coefficient: (a) flow rate of water in the tube; (b) spray water flow rate; (c) inlet temperature of water in the tube; and (d) air flow rate.
Preprints 87172 g006
Preprints 87172 g007
Figure 7. Comparisons between the orthogonal experimental data and the fitting values of the correlation equation: (a) heat transfer coefficient, and (b) mass transfer coefficient.
Figure 7. Comparisons between the orthogonal experimental data and the fitting values of the correlation equation: (a) heat transfer coefficient, and (b) mass transfer coefficient.
Preprints 87172 g007
Preprints 87172 g008
Figure 8. Comparisons between the verification experimental data and the predicted values of the correlation equation: (a) heat transfer coefficient, and (b) mass transfer coefficient.
Figure 8. Comparisons between the verification experimental data and the predicted values of the correlation equation: (a) heat transfer coefficient, and (b) mass transfer coefficient.
Preprints 87172 g008
Table 2. Measurement instruments and parameters.
Table 2. Measurement instruments and parameters.
Parameter Sensor Accuracy
The spray water flow rate Rotameter (DK800-6) ±2 L/h
The air flow rate Vane anemometer (GT8907) ±0.01 m/s
Ambient temperature and humidity thermometer (VICTOR 231) ±0.1℃/±0.1%RH
Outlet air temperature K type thermocouple ±0.75% t
Outlet air humidity Humidity Sensor (TH10S-B-IP67) ±0.1%RH
The inlet temperature of water in the tube The temperature control unit (MAIPT) ±0.1℃
The outlet temperature of water in the tube The temperature control unit (MAIPT) ±1℃
The flow rate of water in the tube Rotameter (LZB-25) ±10 L/h
Table 3. Values corresponding to the levels of different influencing factors.
Table 3. Values corresponding to the levels of different influencing factors.
Level Factor A:
The flow rate of water in the tube (kg·h-1)		 Factor B:
The spray water flow rate (kg·h-1)		 Factor C:
The inlet temperature of water in the tube (℃)		 Factor D:
The air flow rate (m3·h-1)
1 200 40 70.0 83.25
2 300 45 80.0 99.90
3 400 50 90.0 124.65
4 500 55 100.0 132.30
5 600 60 110.0 146.70
Table 4. Variance analysis of heat dissipation.
Table 4. Variance analysis of heat dissipation.
Factor Average deviation sum of squares F0.05(4,8) F value Significance of difference
Factor A 14.57 3.84 17.43 Significant
Factor B 6.47 3.84 7.74 Significant
Factor C 33.17 3.84 39.68 Significant
Factor D 1.53 3.84 1.82 Not significant
Table 5. Variance analysis of the cooling efficiency.
Table 5. Variance analysis of the cooling efficiency.
Factor Average deviation sum of squares F0.05(4,8) F value Significance of difference
Factor A 0.0681 3.84 114.81 Significant
Factor B 0.0068 3.84 11.38 Significant
Factor C 0.0009 3.84 1.51 Not significant
Factor D 0.0022 3.84 3.75 Not significant
Table 6. Variance analysis of heat transfer coefficient.
Table 6. Variance analysis of heat transfer coefficient.
Factor Average deviation sum of squares F0.05(4,8) F value Significance of difference
Factor A 69.45 3.84 0.51 Not significant
Factor B 4151.75 3.84 30.61 Significant
Factor C 745.17 3.84 5.49 Significant
Factor D 1197.63 3.84 8.83 Significant
Table 7. Variance analysis of the mass transfer coefficient.
Table 7. Variance analysis of the mass transfer coefficient.
Factor Average deviation sum of squares F0.05(4,8) F value Significance of difference
Factor A 0.00011 3.84 4.19 Significant
Factor B 0.00006 3.84 2.12 Not significant
Factor C 0.00064 3.84 24.49 Significant
Factor D 0.00020 3.84 7.78 Significant
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated