Prerpints.org logo
Preprint
Article

Increasing the Dynamic Range of Magnetorheological Fluid Gradient Pinch Mode Valves

Altmetrics

Downloads

99

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

10 October 2023

Posted:

10 October 2023

You are already at the latest version

Alerts
Abstract
Magnetorheological (MR) fluids have been known to react to magnetic fields of sufficient magnitudes. While in the presence of the field the material develops a yield stress. The tunable property has made it attractive in e.g. semi-active damper applications in vibration control domain in particular. Within the context of a given application the fluids can be exploited in at least one of the fundamental operating modes of which the so-called gradient pinch mode has been least explored. Contrary to the other operating modes, the MR fluid volume in the flow channel is exposed to a non-uniform magnetic field in such a way that the Venturi-like contraction is developed in a flow channel solely by means of a solidified material in the regions near the walls rather than mechanically driven changes of the channel’s geometry. The pinch mode rheology of the material has made it a potential candidate in developing on a new category of MR valves. By convention, a pinch mode valve features a single flow channel with poles over which non-uniform magnetic field is induced. In this study the authors examine ways of extending the dynamic range of pinch mode valves by employing a number of such arrangements (stages) in series. To accomplish this, the authors developed a prototype of a multi-stage (three-stage) valve, and then compared its performance against that of a single-stage valve across a wide range of hydraulic and magnetic stimuli. To summarize, improvements in the pinch mode valve dynamic range are evident, however, at the same time it is hampered by the presence of serial air gaps in the flow channel.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Magnetorheological (MR) fluids are known representatives of smart materials which react to magnetic fields. The material itself is a suspension of fine, micron-size soft magnetic particles. It is known to exhibit Newtonian fluid like properties while in the absence of magnetic field. However, as soon as it is magnetized, the particles in the material form chain structures resulting in a resistance-to-flow build-up or a yield stress increase in the material. In comparison to the off-state (zero field) behaviour, the material exhibits typical Bingham plastic or pseudo-solid characteristics; the material’s field-induced yield stress has to be overcome to initiate flow.
Since the discovery in the mid-20th century the technology has been commercialized primarily in semi-active vehicle suspension systems (in the form of continuously variable MR fluid based dampers)[1,2,3,4] or MR powertrain mounts [5,6]. The technology is valveless; contrary to conventional semi-active valve-based dampers. In MR dampers pistons have no moving components; the adjustments of the output are solely by means of magnetic field and modifications of the fluid rheology. The core element of the MR damper is a simple fixed solenoid with at least one radial or an annular flow channel. With the fluid’s energized by the magnetic flux induced by the solenoid the changes in the rheology of the material can be utilized in real-time [7,8] to follow the changing conditions while driving the car.
The MR fluid devices are known to operate in one of the so-called fundamental operating modes: flow [2], shear [9], squeeze [10], pinch [11,12,13,14,15,16] of which the latter has been researched and explored to a little extent. Prototype pinch mode valve designs are few and little modelling has been published so far in this regard in comparison to the other operating modes. Contrary to the other operating modes, the fluid volume in the flow channel is exposed to a non-uniform magnetic field in such a way that the flux density is highest in the areas adjacent to the channel surface(s) (walls) and smallest in the center of the flow path. This results in a Venturi-like contraction but accomplished solely through material means and not by manipulating the channel’s geometry (size, cross-section area). For comparison, in flow mode, the fluid flow is driven by pressure gradient across the flow channel, and magnetic flux crosses it in the direction perpendicular to the flow. Similar orientation of magnetic flux relative to the fluid flow can be observed in shear mode prototypes (rotary brakes or clutches) [9] or small-stroke squeeze mode vibration mounts [17]. Based on the prior art and own research it is expected that implementing pinch mode MR valves may widen the MR fluid application scope and deliver performance benefits that is difficult to be achieved with MR devices based on the other operating principles. For instance, experimental works of the pinch mode inventors [14] with such MR valves have showed the relationship between the pressure drop and the flow rate cannot be captured by the conventional Bingham plastic type behaviour. Instead, the pressure-flow rate plots are to reveal field dependent changes in the pressure-flow rate curve slope [11,12,14]. It is a feat that can only be achieved with flow-mode valves at the cost of employing expensive electronics or complex designs of MR valves [18]. It is, therefore, speculated that this may contribute to a new category of controlled MR valves.
So far, prior art by the authors in the field have involved magnetostatic sizing studies of a prototype flow bench [15], computational fluid dynamics (CFD) analyses [19] as well as extensive experimental studies [12,14] involving a single-stage pinch mode valve assembly. Generally, the obtained results have proved the pinch mode principle, however, at the same time the outcome of the experiments showed the need for increasing the dynamic range of the examined valves. In this paper the authors propose to realize this improvement by employing a serial multi-stage pinch mode valve. Our work is an extension of the research carried out by Lee et al. [12], however, the flow characterization work is to be carried out within a far lower flow rate range (below 1 l/min) where the foreseen performance benefits are likely to be optimal (e.g. in the form of a magnetic field activated hydraulic bypass). Moreover, the fluid in the Lee’s valve is energized asymmetrically in the annulus, whereas in our configuration the valve’s principle is that of a long restrictive orifice which, in our opinion, is more inline with the original pinch mode valve patent application [11] and where most performance benefits are foreseen.
To summarize, we commence the study by highlighting the pinch mode operating principles, and the key details of the developed test rig, experimental procedure and the MR pinch mode valves structures. That is followed by revealing crucial elements of the finite-element (FE) analyses involving the developed prototypes and fundamental aspects of the competitive experimental study on the single-stage valve and the three-stage valve assemblies, respectively. Finally, the performance of both valves is compared and conclusions are drawn.

2. Pinch mode fundamentals

As already mentioned, MR fluids can be operated in at least one of the four fundamental operating modes of which the so-called pinch mode is the least explored. Figure 1 reveals the pinch mode principle. As shown, the main difference is in the distribution of the magnetic field. In comparison to the other operating modes, the magnetic poles are orientated in the direction parallel to the fluid flow which results in a non-uniform distribution of magnetic field. The field’s concentration is the largest in the near-wall zones, and, ideally, zero at the center of the gap. Effectively, it traps the particles in the high flux density zones, and at the same time it allows them to pass freely through the central region. The effective diameter deff of the flow channel is magnetic field dependent, and it would vary from deff=D (off-state), where D – diameter of the flow channel, to deff=0 (max. magnetic field strength).
As a remainder, in flow mode the flux travels the flow gap in the direction perpendicular to the fluid flow. When magnetized, the particles form chain structures which need to be broken to initiate flow through the gap. On the macro-scale, the flux energizes the fluid, thus inducing a yield stress. The yield stress must be overcome to initiate flow. The behaviour of the fluid in this mode can be best described with the pressure drop vs flow rate relationships in Figure 1. In comparison with the gradient pinch mode, only the threshold pressure varies with magnetic field; the curve’s slope is invariant of the magnetic field strength H (or the magnetic flux density B).

3. Experimental procedure

3.1. Test rig

To carry out the research, an in-house rig for testing MR valves at Brno University of Technology was modified and developed – see Figure 2. It incorporates the hydraulic dynamometer (3), the rheometer (4) and the rigid frame (2). The Inova hydraulic dynamometer AH 40-150 (arrow A) forces the fluid through the valve (arrow B). The fluid in the gap is exposed to the magnetic field characterized by the field strength H and the flux density B (5). The MR pinch valve (4) is located between the floating pistons (1) and is stationary. The pressure drop across the valve was monitored with two pressure sensors (8) HBM P8AP (10 bar). The MR fluid temperature was measured using the sensor PT100 located near the entrance to the MR pinch valve (9). The position of the floating piston (7) was monitored by the resistance position sensor RC13 supplied by Megatron. The fluxmeter Bell 5180 with the ultra-thin transverse probe STB1X-0201 was used for monitoring magnetic flux in the magnetic circuit. The probe was located in the air gap located in the solenoid’s core (11). Also, the Fluke i30 current clamp was used to monitor the electric current supplied to the coil. All signals were recorded at the sampling frequency of 1 kHz with the data analyzer Dewe-800.

3.2. Test plan, material description and data postprocessing method

To carry out the valve experiments the MR fluid MRF-122EG manufactured by Lord Corp. was used in the tests. The experimentally determined viscosity of this fluid is 0.056 Pa.s (at the ambient temperature T=30 °C). The MR fluid contains CIP (carbonyl iron powder) spherical particles (average diameter of the particles – 2.1 µm). The MR fluid was homogenized for 1 hour before filling into the rheometer. The input displacement waveform was designed to be a linearly increasing function of the floating piston velocity- see Figure 3. It is a constant acceleration input (A=2 mm/s2). The measurements were performed within the coil excitation range from I=0 A to I=3 A (900 A.t) in the single-stage case and within the current range from 0 to 3.4 A (1190 A.t) in the case of the three-stage valve. Data post-processing involved filtering the signals by means of a moving average filter only (50 samples, time increment – 50 ms).
To determine the relationship between the input flow rate Q through the valve and the resulting pressure drop, the simple linear regression model was applied as follows
Δp(B,Q) = k(B).Q + ΔpOFF(B)
where Δp(B,Q) is valve pressure drop, k(B) refers to the pressure-flow rate curve slope at a given magnetic flux density level B (or the coil current I), ΔpOFF is the pressure offset. The coefficients k(B) and ΔpOFF were determined using the least squares curve fit approach. To normalize the slope k change with the magnetic field, the dimensionless slope factor K was introduced
K(B) = k(B) / k(B=0)
Similarly, the turn-up ratio (valve gain) F can be calculated as
F(B,Q) = Δp(B,Q) / Δp(0,Q)

4. MR pinch mode valves

4.1. Single-stage prototype

To study the behaviour of MR fluid in pinch mode, the authors developed a single-stage MR pinch valve concept (see Figure 4). The MR pinch valve incorporates the thru-hole circular channel (diameter D=3 mm) (4), the magnetic core assembly (1) and the electromagnetic coil with N=300 wire turns (3). The magnetic core assembly reveals the two magnetic pole pieces (1), the bronze non-magnetic spacer (2) and the air gap (5). The air gap (size − 0.8mm) is for monitoring the magnetic flux (6) in the circuit by means of the transverse Hall probe. The magnetic core was manufactured using a low carbon steel alloy (grade 11SMn30). The key dimensions incl. the prototype valve’s photo can be seen in the illustration below.

4.2. Three-stage prototype

The three-stage prototype in Figure 5 is likely to deliver a larger dynamic range in comparison with the single-stage valve by employing a series of three pinch gaps in the flow channel. The components (1, 5, 6) in Figure 5 are shared with the single-stage valve. Moreover, the number of coil wire turns (4) was increased for the 3-stage valve; the coil’s wire turns number is N=350. The purpose of the increased wire turns number is to compensate for the additional air gaps in between the spacers (2). The flow channel’s diameter is also equal to D=3 mm. In this configuration the active zone is composed of the three pinch gaps formed by the three bronze non-magnetic spacers (2) and the two low-carbon magnetic poles (3). Again, the key dimensions can be seen in the figure below.

4.3. FE magnetostatic analysis and experimental validation

Carrying out a magnetostatic analysis was crucial for estimating the flux in the flow channel as well as the comparison between the two valve assemblies. The magnetostatic 2D-axisymmetric analysis was performed in Ansys Electronics Desktop 2023 R1. Figure 6 reveals the simplified geometry of the FE (finite-element) models. The following material properties were assumed for the specific components in the circuit: orange – low-carbon alloy steel 11SMn30, green – MR fluid MRF-122EG, gray – bronze or aluminum. The gap in the upper section of the core is for monitoring the flux induced in the structure (see Figure 4, ref. 6).
The mesh size in the active zone (flow channel and pinch gaps) was set to be equal to 0.2 mm and in the remaining portion of the solenoid it was set to 0.5 mm.
As already mentioned, the verification of the numerical results was carried out by the authors via measurements of the magnetic flux density in the air gap. The magnetic flux density was measured using the fluxmeter (F.W. Bell 5180) and by means of the transverse probe (STB1X-0201). The supplied current was measured with the Fluke i30 current clamps. Figure 7 shows the comparison of the obtained results from the model against the experimental data. To accomplish the measurements, the flux probe was inserted into the air gap (See Figure 2). It is evident that agreement between the experiment and the model is good. The relative error does not exceed 15%. It can also be argued that both valves reveal nearly identical electric current vs magnetic flux characteristics. At lower electric currents, the single-stage valve’s output (magnetic flux density B) slightly exceeds the output of the three-stage valve, and it is inferior at the currents higher than 2 A.

5. Magnetostatic analysis and laboratory test results

5.1. FE calculations

Figure 8 shows the magnetic flux density map in the single-stage pinch valve at I=3 A and in more detail at the current levels I= 3 A (a), I=2 A (b) and I=1 A (c). In this prototype, the MR fluid magnetization is higher compared to the three-stage pinch valve (see Figure 9). The maximum magnetic flux density B in the single-stage valve is roughly B=900 mT compared to the output flux density B=550 mT of the three-stage pinch valve. The magnetic flux density maps of the single-stage valve are similar to those of the three-stage pinch valve (side pinch gaps only).
Next, Figure 9 (left) shows the magnetic flux density map for the three-stage valve at the electric current level of I=3.4 A. In more detail the flux density map in the active zone can be seen in Figure 9 (right) at I=3.4 A (a), I=3 A (b), I=2 A (c) I=1 A (d). It can be seen that the magnetic flux density maps distribution over the middle pinch gap is different when compared to the neighbours. It likely due to the flux leakage between the neighbouring poles. As seen in Figure 9, there is a significant flux leakage between the neighboring poles. Instead of traveling into the flow channel only, a portion of the flux bypasses it, thus degrading the magnetic circuit performance. This is, however, an inherent feature of the multi-stage configuration, and challenged in future works.
It is crucial to notice to the limitations of the magnetic model. The MRF fluid properties are assumed to be time-invariant. Also, it is assumed that the MR fluid is homogenous in the control volume. However, it can be expected that the magnetophoretic force [20] causes the migration of particles in the fluid due to the magnetic flux density gradient. Therefore, the concentration of ferromagnetic particles (density) in the active zone is not constant and the magnetic properties (relative permeability, magnetic saturation, etc.) are position (volume) dependent. This has a direct impact on the magnetic flux density map in the active zones. The presented magnetic model does not account for that behaviour. For this reason, the performance of the prototypes was compared at the same magnetic flux that roughly corresponds with the electric current excitation.

5.2. Flow bench testing

5.2.1. Single-stage valve

Figure 10 shows the plot of MR valve pressure drop versus flow rate data set collected during the velocity increase stage. The illustration shows the data at various levels of the magnetic flux density (or up to I=3 A). In Figure 10 the increase in the slope of the flow curve K and the pressure drop offset change with the increase in the magnetic field B are evident. Based on the calculations from the measured data, the estimated pressure-flow rate curve slope varies by a factor of K=6.6 at the maximum electric current excitation I=3 A compared to the off-state condition (I=0 A). The measured curves are not smooth and reveal unexpected pressure drop twitches. A more detailed description of this phenomenon can be found in [14].
The turn-up ratio F of this valve reaches 10.3 at the flow rate of 10 000 mm3/s. It is evident that as the flow rate decreases, the turn-up ratio F increases (contrary to conventional pinch mode valves) at least within the examined flow rate range.

5.2.2. Three-stage valve

Next, Figure 11 shows the plot of MR valve pressure drop versus flow rate data set collected during the velocity increase stage with the three-stage pinch MR valve prototype. It can be observed that at higher magnetic fields (corresponding to the current levels I=3 A and I=3.4 A) the curves exhibit a bi-linear character. At low flow rates (up to Q=3500 mm3/s), the slope is significantly steeper than at the higher flow rates. The estimated pressure drop-flow rate curve’s slope varies by a factor of K=28 at the maximum electric current excitation I=3.4 A compared to the off-state condition (I=0 A) at low flow rates Q. Above Q=3500 mm3/s, the slope factor significantly decreases down to K=9.1. The valve’s turn-up ratio F reaches 15.5 at a Q=10 000 mm3/s. Again, as the flow rate Q decreases, the valve’s turn-up increases.
Next, repeatability of the valve’s output was examined. Figure 12 shows the outcome of the experiment at I=3.4 A. It can be seen that the data at low flow rates are relatively well repeatable. However, above the flow rate Q=3500 mm3/s the variations between the consecutive runs become evident; the curve slope varies from K=9 (Run 1) to K=17 (Run 4). We hypotheses that this behaviour is caused by increasing the concentration of particles in the active zone in time. A similar phenomenon was also observed with the single-stage pinch valve. To comprehend this behaviour, it will probably be necessary to observe the active zone and particle clusters visually. The computed tomography method [21,22] or the fluorescence method with a confocal microscope [23] can be used for providing in insight into this behaviour.
We expected that the flow rate would be linearly increasing during the experiment. Unfortunately, in some cases is not like this. For example, in Figure 11 at the electric current of 1.5 A and the flow rate of appr. 7500 mm3/s this behaviour is evident.

5.3. Valve performance comparison

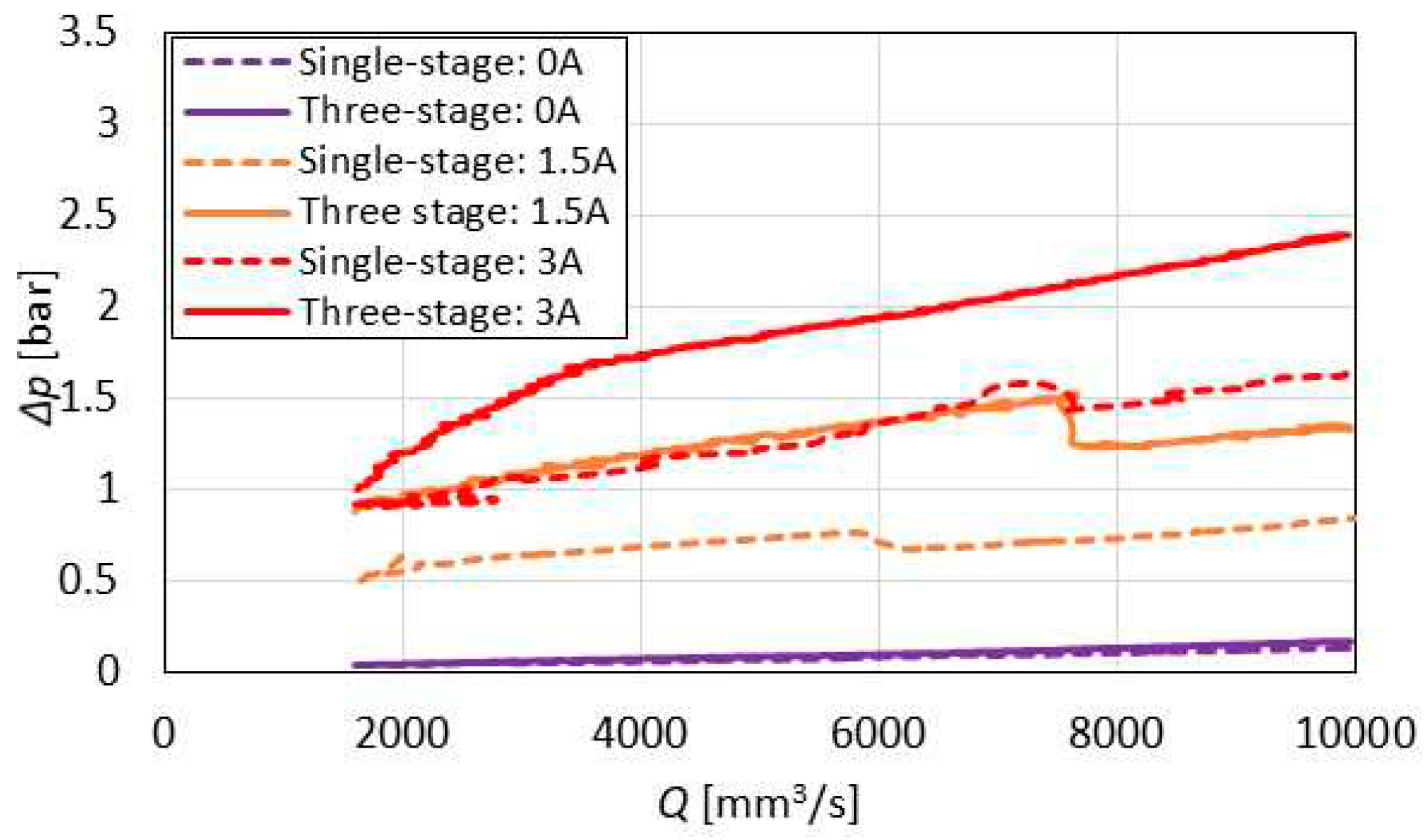
Except for the presence of multiple pinch stages in the latter prototype, both valves are identical and were examined under the same test conditions. The three-stage pinch MR valve’s maximum output exceeds the performance of the single-stage valve by a factor of 1.55. The off-state performance of the two valves is nearly identical – the pressure drop difference at 10 000 mm3/s does not exceed 0.02 bar. This was likely caused by minor discrepancies in the temperature during the tests as seen in Figure 13 – the MR fluid’s temperature was 0.8 °C lower while testing the three-stage pinch MR valve compared to the single-stage pinch MR valve.
In comparison with the single-stage valve, the three-stage pinch MR valve reaches the significantly higher turn-up F of 17 as opposed to 11.5 for the single-stage prototype. Another significant difference is in the three-stage pinch MR valve’s bilinear behaviour as illustrated in Figure 13. At low flow rates the curve’s slope factor K reaches the value of 28 only to drop down to 9.1 at higher flow rates. It seems that the observed behaviour in pinch mode at low flow rates may be an interesting loading mode for microfluidic systems working with MR fluid [20,24].
The pressure drop measurements at flow rates below 1500 mm3/s were not presented due to the significant influence of the hydraulic pulsator’s controller. For further research, it is necessary to redesign the test rig for carrying such measurements in a reliable and repetitive manner.

6. Conclusions

In general, the purpose of the research was to provide a detailed performance comparison between the single-stage pinch mode valve and the multi-stage pinch mode valve which incorporated three pinch gaps in series in the flow channel. To accomplish this, the authors designed and manufactured the prototypes, and then examined their performance across a prescribed range of excitation inputs.
To summarize, the three-stage prototype reveals a superior performance when compared to its single-stage counterpart. The increase in the performance of the three-stage prototype is 55%. Note that the three-stage valve features a sequence of several air gaps in the solenoid for the magnetic flux to pass through. The air gaps are the elements of the largest reluctance, therefore, the amount of current to generate equivalent flux density in the flow channel is increased. At the same time the three-stage valve is superior in terms of the slope factor variation. At low flow rates the largest slope factor of the three-stage valve is 4.5 times higher than the single-stage valve and augmented by 1.5 times at higher flow rates. Moreover, the three-stage valve exhibits the bilinear behaviour at the highest current level which was not observed in the single-stage prototype.
On a general note, the multi-stage pinch mode valve concept further development may be hampered by its magnetic circuit performance. Although the fluid in the channel is activated in several locations, its performance does not increase proportionally with the number of stages in the flow channel for the same magnetic flux induced in the structure. The authors plan to modify the multi-stage prototype of the valve to improve the dynamic range of the magnetic circuit by proposing a different topology.

Author Contributions

Conceptualization, M.K. and J.Ž.; methodology, M.K.; software, Z.S.; validation, J.Ž., J.G. and B.S.; resources, B.S.; writing—original draft preparation, J.G., J.Ž. and M.S.; writing—review and editing, M.K. and B.S.; supervision, M.K. and B.S.; project administration, B.S. All authors have read and agreed to the published version of the manuscript.

Funding

The authors wish to acknowledge the kind support of the Czech Science Foundation (Grantová agentura České republiky—GACR) and the National Science Centre (Narodowe Centrum Nauki—NCN, Poland)—grant IDs: GACR 21-45236L (CZ) and 2020/39/I/ST8/02916 (PL).

Data Availability Statement

The data generated throughout the described research can be made available upon a reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Goldasz, J.; Sapinski, B. Verification of magnetorheological shock absorber models with various piston configurations. J. Intell. Mater. Syst. Struct. 2013, 24, 1846–1864. [CrossRef]
  2. Žáček, J.; Šebesta, K.; Mohammad, H.; Jeniš, F.; Strecker, Z.; Kubík, M. Experimental Evaluation of Modified Groundhook Car Suspension with Fast Magnetorheological Damper. Actuators 2022, 11, 354. [CrossRef]
  3. Li, G.; Huang, Q.; Hu, G.; Ding, R.; Zhu, W.; Zeng, L. Semi-active fuzzy cooperative control of vehicle suspension with a magnetorheological damper. J. Intell. Mater. Syst. Struct. 2023, 1045389X2311573. [CrossRef]
  4. Xia, D.; Fu, J.; Li, W.; Han, G.; Du, X.; Luo, L.; Yu, M. Incremental proportion integration differentiation control of all-terrain vehicle magnetorheological suspension system under low-frequency disturbances. Smart Mater. Struct. 2023, 32, 075019. [CrossRef]
  5. Yang, J.; Sun, S.; Ezani, S.; Gong, N.; Deng, L.; Zhang, S.; Li, W. New magnetorheological engine mount with controllable stiffness characteristics towards improved driving stability and ride comfort. Smart Mater. Struct. 2022, 31, 125009. [CrossRef]
  6. Chen, S.; Li, R.; Du, P.; Zheng, H.; Li, D. Parametric Modeling of a Magnetorheological Engine Mount Based on a Modified Polynomial Bingham Model. Front. Mater. 2019, 6. [CrossRef]
  7. Strecker, Z.; Jeniš, F.; Kubík, M.; Macháček, O.; Choi, S.B. Novel approaches to the design of an ultra-fast magnetorheological valve for semi-active control. Materials (Basel). 2021, 14. [CrossRef]
  8. Kubík, M.; Šebesta, K.; Strecker, Z.; Jeniš, F.; Goldasz, J.; Mazůrek, I. Hydrodynamic response time of magnetorheological fluid in valve mode: model and experimental verification. Smart Mater. Struct. 2021, 30, 125020. [CrossRef]
  9. Wereley, N.M.; Cho, J.U.; Choi, Y.T.; Choi, S.B. Magnetorheological dampers in shear mode. Smart Mater. Struct. 2008, 17, 015022. [CrossRef]
  10. Gołdasz, J.; Sapiński, B. Application Of CFD To Modeling Of Squeeze Mode Magnetorheological Dampers. Acta Mech. Autom. 2015, 9, 129–134. [CrossRef]
  11. Carlson, J.D.; Goncalves;, F.D.; Catanzarite, M.D.; Dobbs, R.D. Controllable magnetorheological fluid valve, devices, and methods 2008.
  12. Lee, T.-H.; Kang, B.-H.; Choi, S.-B. A quasi-static model for the pinch mode analysis of a magnetorheological fluid flow with an experimental validation. Mech. Syst. Signal Process. 2019, 134, 106308. [CrossRef]
  13. Gołdasz, J.; Sapiński, B. Magnetostatic Analysis of a Pinch Mode Magnetorheological Valve. Acta Mech. Autom. 2017, 11, 229–232. [CrossRef]
  14. Kubík, M.; Gołdasz, J.; Macháček, O.; Strecker, Z.; Sapiński, B. Magnetorheological fluids subjected to non-uniform magnetic fields: experimental characterization. Smart Mater. Struct. 2023, 32, 035007. [CrossRef]
  15. Kubik, M.; Goldasz, J.; Machacek, O.; Sapinski, B. Design of a Pinch Mode Magnetorheological Flow Bench: Magnetic Field Analysis. In Proceedings of the ACTUATOR 2022; International Conference and Exhibition on New Actuator Systems and Applications; 2022; pp. 1–3.
  16. Goldasz, J.; Kluszczynski, K.; Sapinski, B. Fluid Flow Pinched by Near-Wall Bingham Plastic Zones: Simulation Study. In Proceedings of the 2018 19th International Conference on Research and Education in Mechatronics (REM); IEEE, 2018; pp. 48–51.
  17. Gong, X.; Ruan, X.; Xuan, S.; Yan, Q.; Deng, H. Magnetorheological Damper Working in Squeeze Mode. Adv. Mech. Eng. 2014, 6, 410158. [CrossRef]
  18. Kim, B.-G.; Yoon, D.-S.; Kim, G.-W.; Choi, S.-B.; Tan, A.S.; Sattel, T. Design of a Novel Magnetorheological Damper Adaptable to Low and High Stroke Velocity of Vehicle Suspension System. Appl. Sci. 2020, 10, 5586. [CrossRef]
  19. Gołdasz, J.; Sapiński, B. Magnetostatic Analysis of a Pinch Mode Magnetorheological Valve. Acta Mech. Autom. 2017, 11, 229–232. [CrossRef]
  20. Ocalan, M.; McKinley, G.H. Rheology and microstructural evolution in pressure-driven flow of a magnetorheological fluid with strong particle–wall interactions. J. Intell. Mater. Syst. Struct. 2012, 23, 969–978. [CrossRef]
  21. Schümann, M.; Odenbach, S. The microstructure of magnetorheological materials characterized by means of computed X-ray microtomography. Phys. Sci. Rev. 2023, 8, 1487–1511. [CrossRef]
  22. Wang, N.; Liu, X.; Sun, S.; Królczyk, G.; Li, Z.; Li, W. Microscopic characteristics of magnetorheological fluids subjected to magnetic fields. J. Magn. Magn. Mater. 2020, 501, 166443.
  23. Shen, Y.; Hua, D.; Liu, X.; Li, W.; Krolczyk, G.; Li, Z. Visualizing rheological mechanism of magnetorheological fluids. Smart Mater. Struct. 2022, 31, 025027. [CrossRef]
  24. Zhang, L.; Gu, S.; Guo, S.; Tamiya, T. A Magnetorheological Fluids-Based Robot-Assisted Catheter/Guidewire Surgery System for Endovascular Catheterization. Micromachines 2021, 12, 640. [CrossRef]
Preprints 87434 g001
Figure 1. Mechanisms of MR fluid operating modes: flow, pinch ; Δp – pressure drop, Q – flow rate, deff – effective diameter, D – diameter.
Figure 1. Mechanisms of MR fluid operating modes: flow, pinch ; Δp – pressure drop, Q – flow rate, deff – effective diameter, D – diameter.
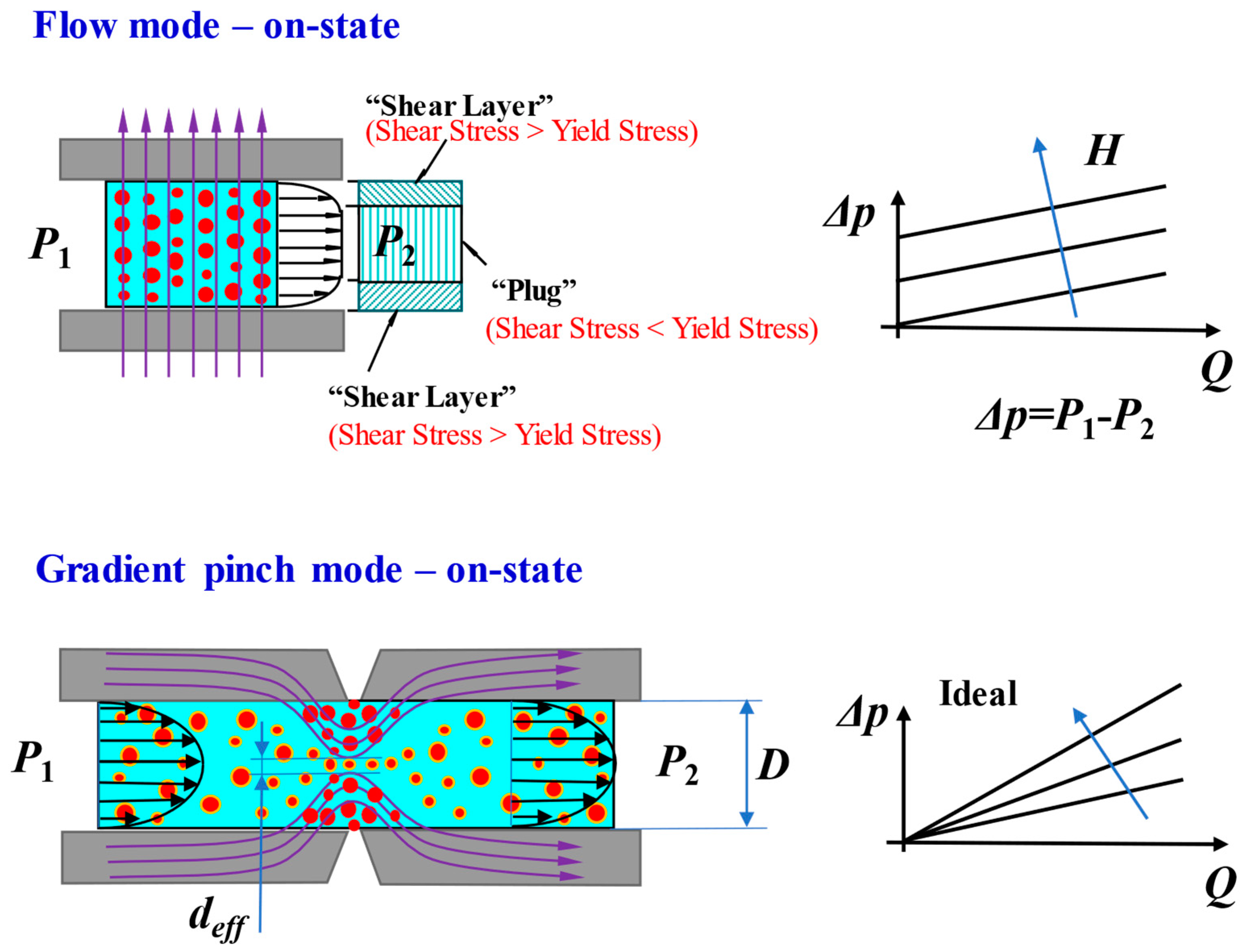
Preprints 87434 g001
Preprints 87434 g002
Figure 2. Rig layout (left); actual setup (right); (1) floating piston, (2) frame, (3) hydraulic pulsator, (4) electromagnetic coil, (5) pinch gap, (6) magnetic flux lines, (7) position sensor, (8) pressure and (9) temperature sensor, (10) MR fluid and (11) Hall probe.
Figure 2. Rig layout (left); actual setup (right); (1) floating piston, (2) frame, (3) hydraulic pulsator, (4) electromagnetic coil, (5) pinch gap, (6) magnetic flux lines, (7) position sensor, (8) pressure and (9) temperature sensor, (10) MR fluid and (11) Hall probe.
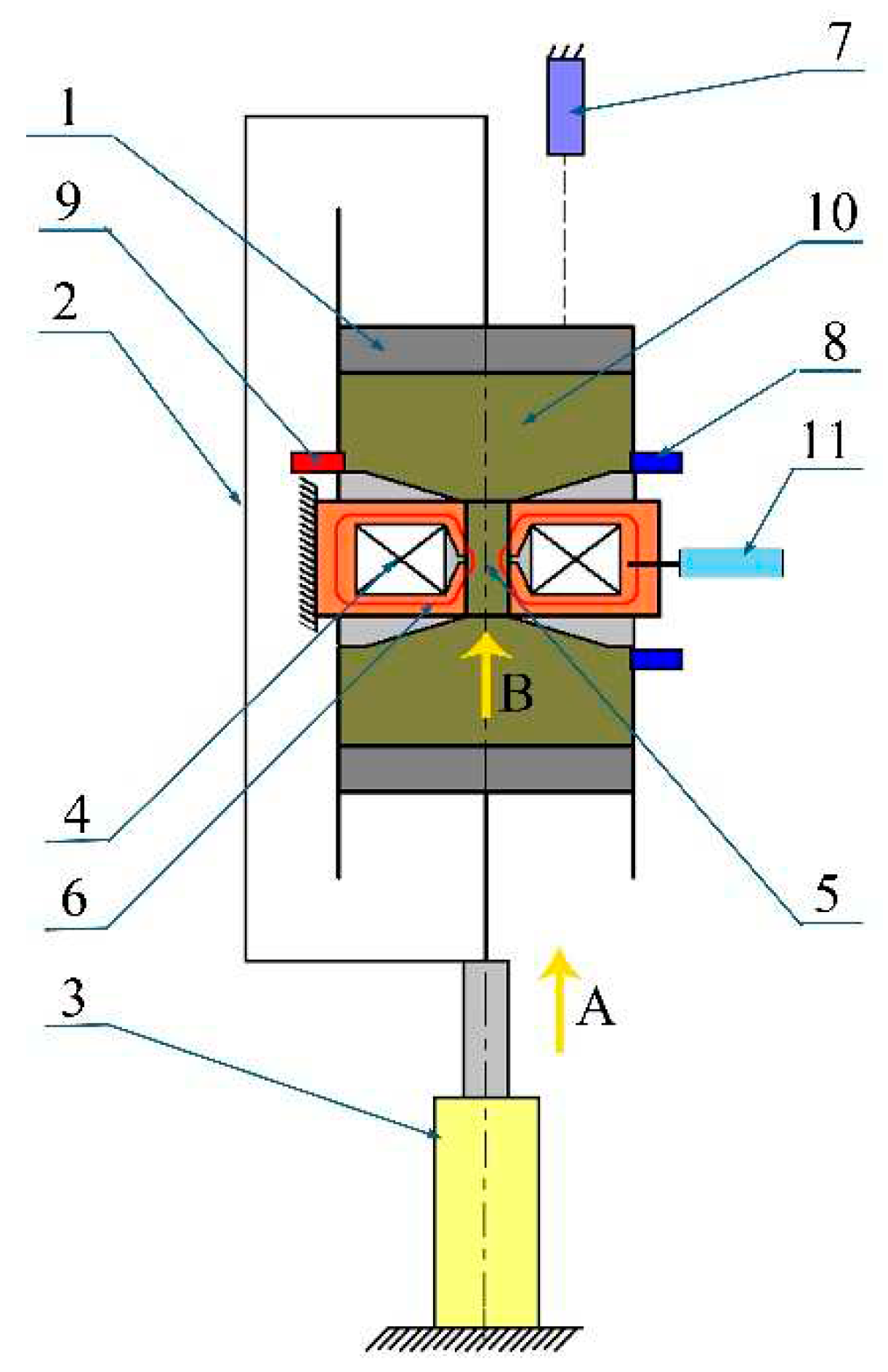
Preprints 87434 g002
Preprints 87434 g003
Figure 3. Input excitation wave form (blue) position x; (orange) velocity v.
Figure 3. Input excitation wave form (blue) position x; (orange) velocity v.
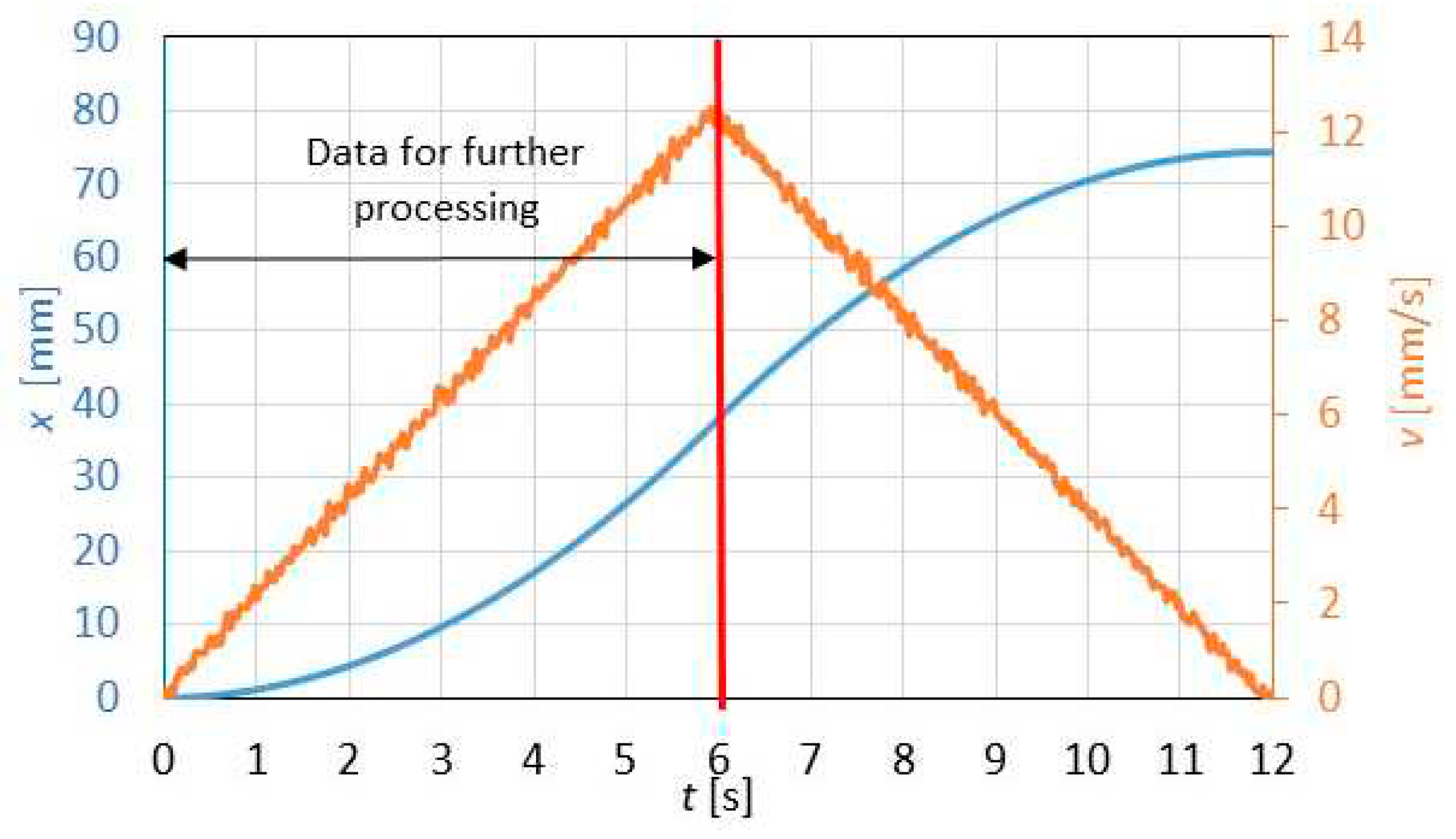
Preprints 87434 g003
Preprints 87434 g004
Figure 4. Layout of the single-stage MR valve (left), prototype cross-section (middle), fabricated parts (right); (1) magnetic circuit, (2) non-magnetic spacer, (3) coil, (4) thru-hole channel, (5) air gap, (6) magnetic flux lines.
Figure 4. Layout of the single-stage MR valve (left), prototype cross-section (middle), fabricated parts (right); (1) magnetic circuit, (2) non-magnetic spacer, (3) coil, (4) thru-hole channel, (5) air gap, (6) magnetic flux lines.
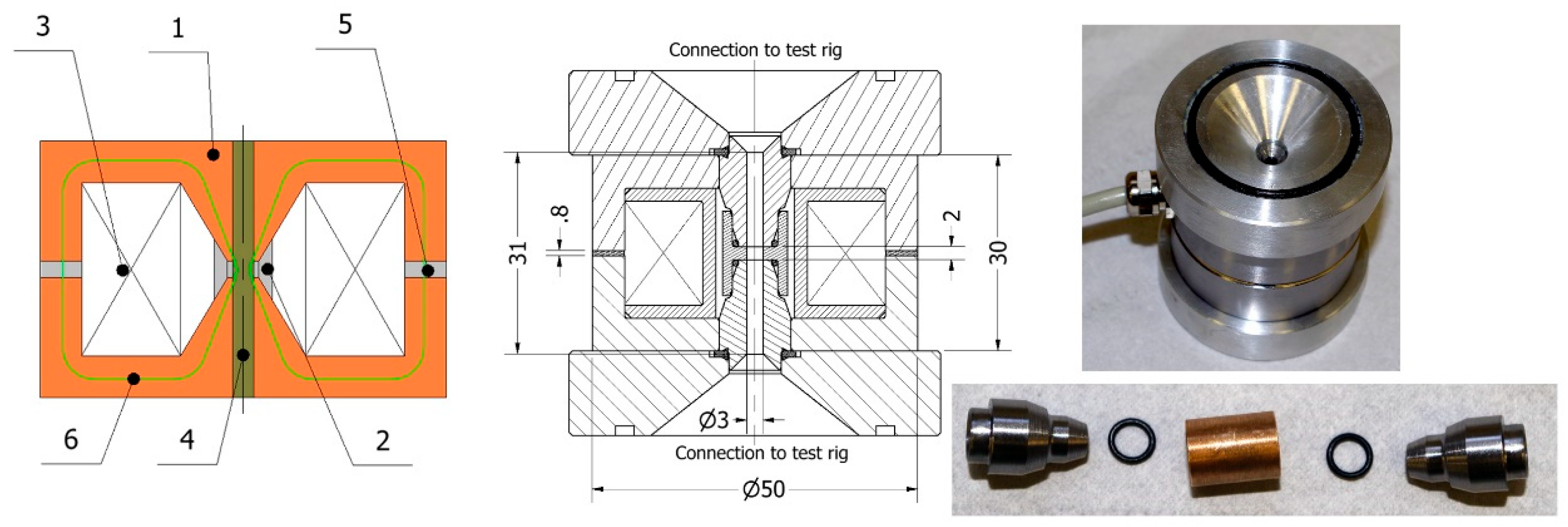
Preprints 87434 g004
Preprints 87434 g005
Figure 5. Layout of the three-stage MR valve incl. fabricated parts (left), prototype cross-section (middle), three-stage assembly (right); (1) magnetic circuit, (2) non-magnetic spacers, (3) magnetic poles, (4) coil, (5) thru-hole channel, (6) air gap, (7) magnetic flux lines.
Figure 5. Layout of the three-stage MR valve incl. fabricated parts (left), prototype cross-section (middle), three-stage assembly (right); (1) magnetic circuit, (2) non-magnetic spacers, (3) magnetic poles, (4) coil, (5) thru-hole channel, (6) air gap, (7) magnetic flux lines.
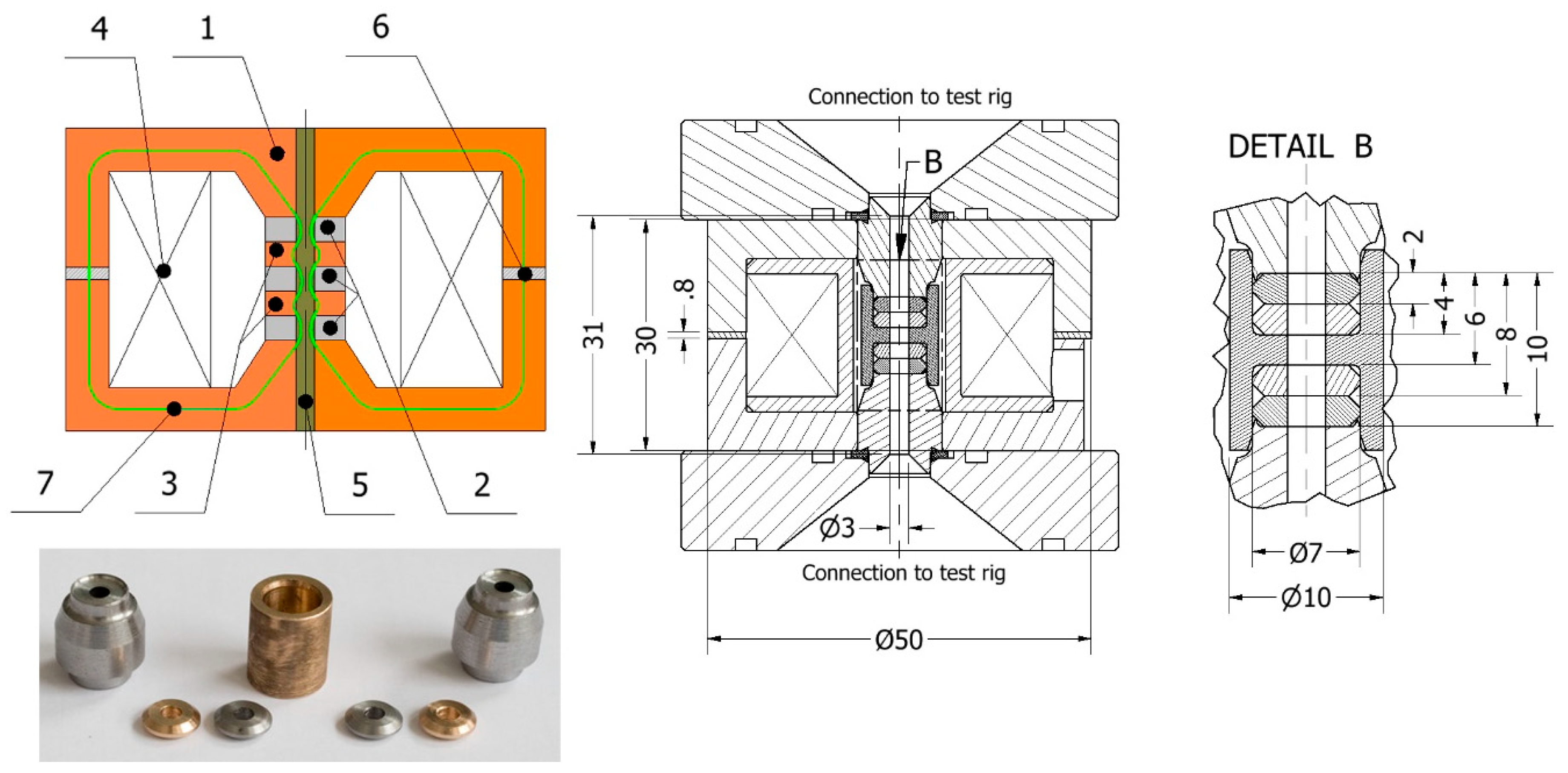
Preprints 87434 g005
Preprints 87434 g006
Figure 6. Simplified geometry of single-stage assembly (left) and the three-stage valve (right) for FE analyses; (orange) low carbon steel, (gray) bronze or aluminum, (green) MR fluid and (white) copper.
Figure 6. Simplified geometry of single-stage assembly (left) and the three-stage valve (right) for FE analyses; (orange) low carbon steel, (gray) bronze or aluminum, (green) MR fluid and (white) copper.
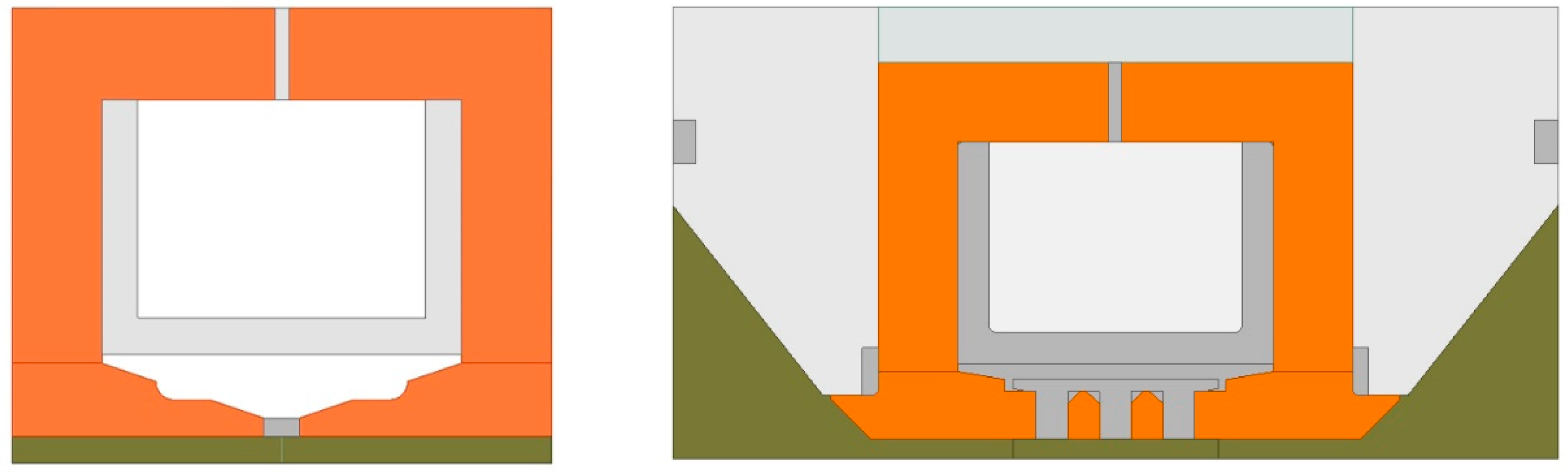
Preprints 87434 g006
Preprints 87434 g007
Figure 7. Experimental verification of the FE models.
Figure 7. Experimental verification of the FE models.
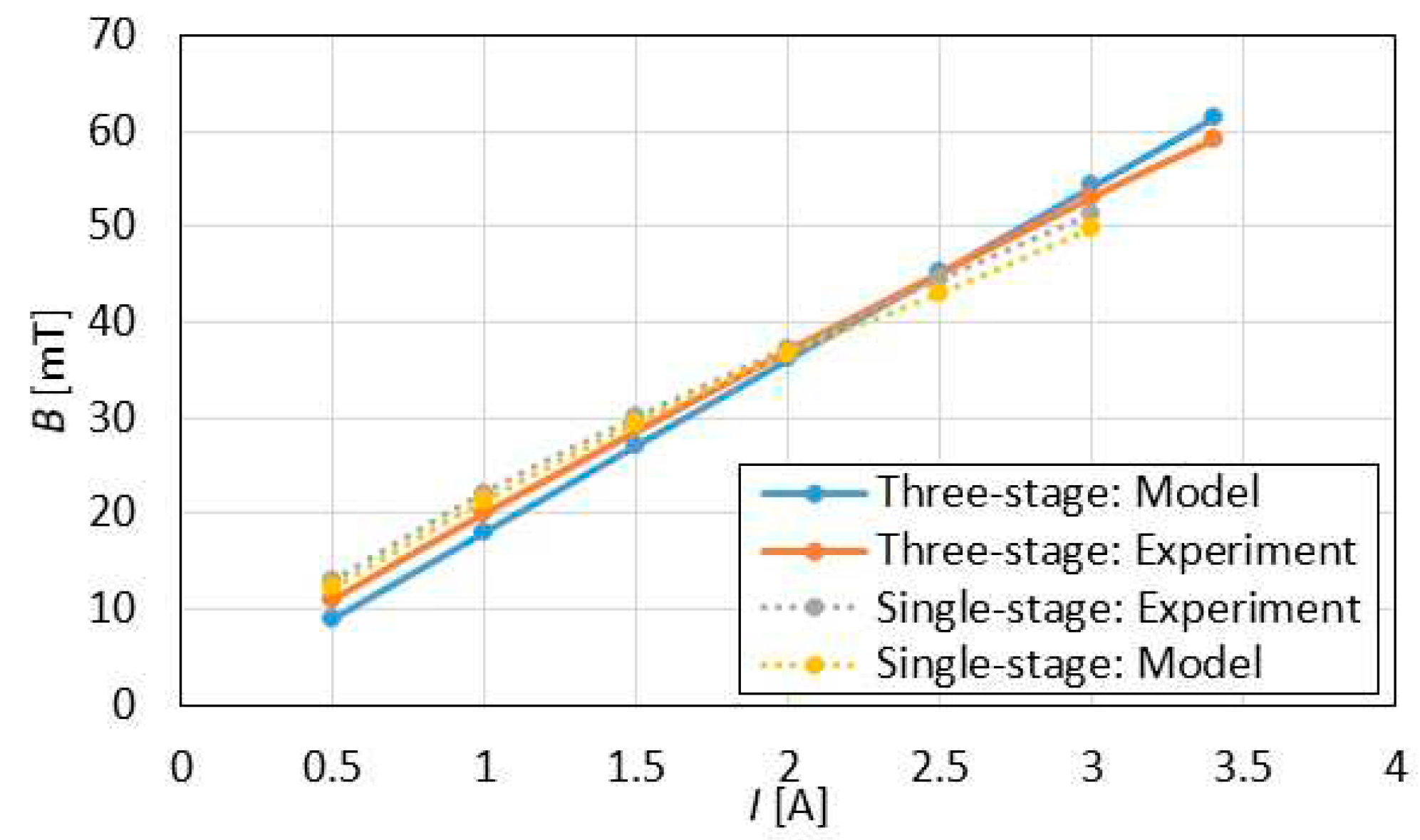
Preprints 87434 g007
Preprints 87434 g008
Figure 8. Single-stage valve model (left) & zoomed-in magnetic flux density maps (right) at (a) I=3 A, (b) I=2 A and (c) I=1 A.
Figure 8. Single-stage valve model (left) & zoomed-in magnetic flux density maps (right) at (a) I=3 A, (b) I=2 A and (c) I=1 A.
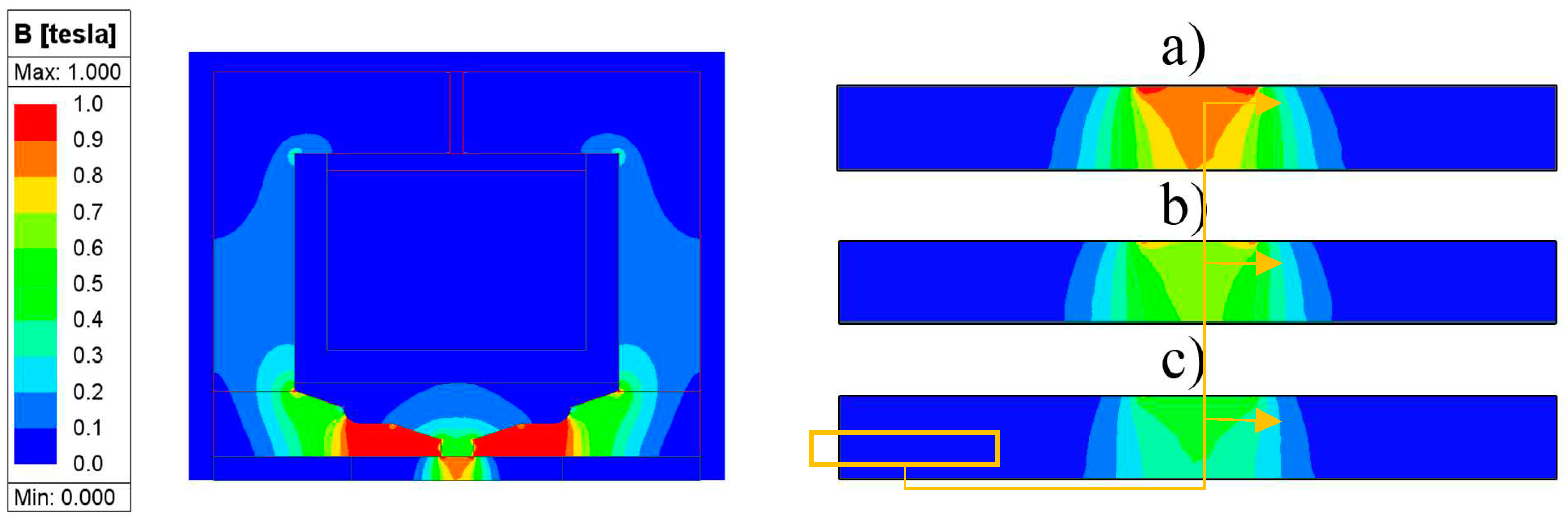
Preprints 87434 g008
Preprints 87434 g009
Figure 9. Three-stage valve (left) & zoomed-in magnetic flux density maps (right) at (a) I=3.4 A, (b) I=3 A, (c) I=2 A and (d) I=1 A.
Figure 9. Three-stage valve (left) & zoomed-in magnetic flux density maps (right) at (a) I=3.4 A, (b) I=3 A, (c) I=2 A and (d) I=1 A.
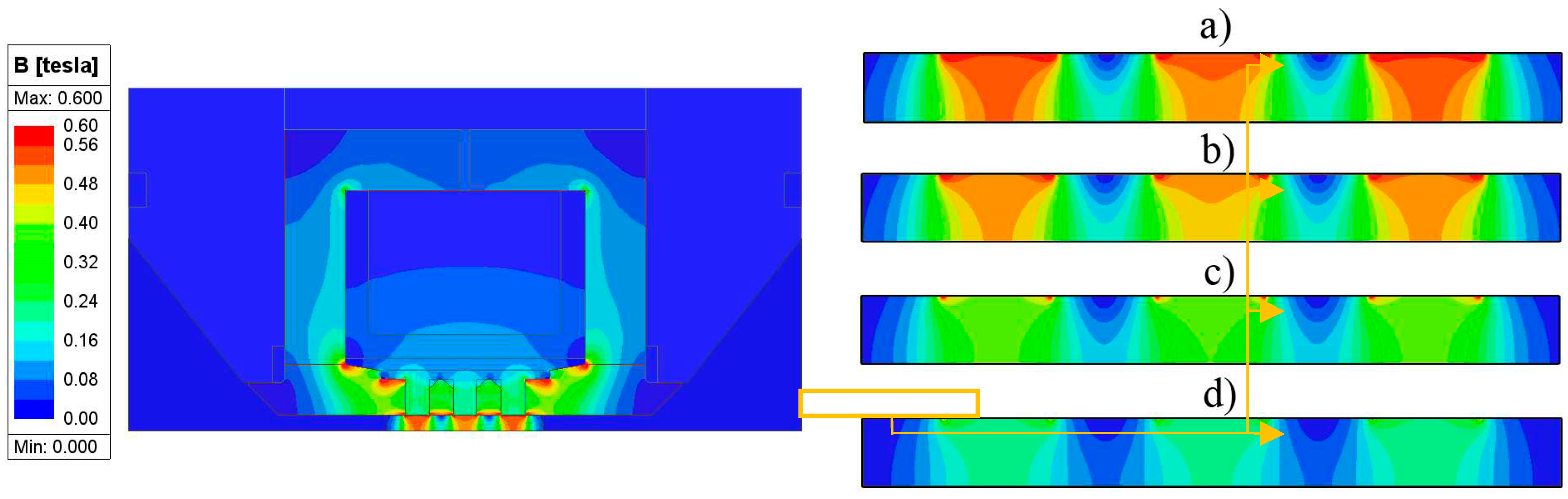
Preprints 87434 g009
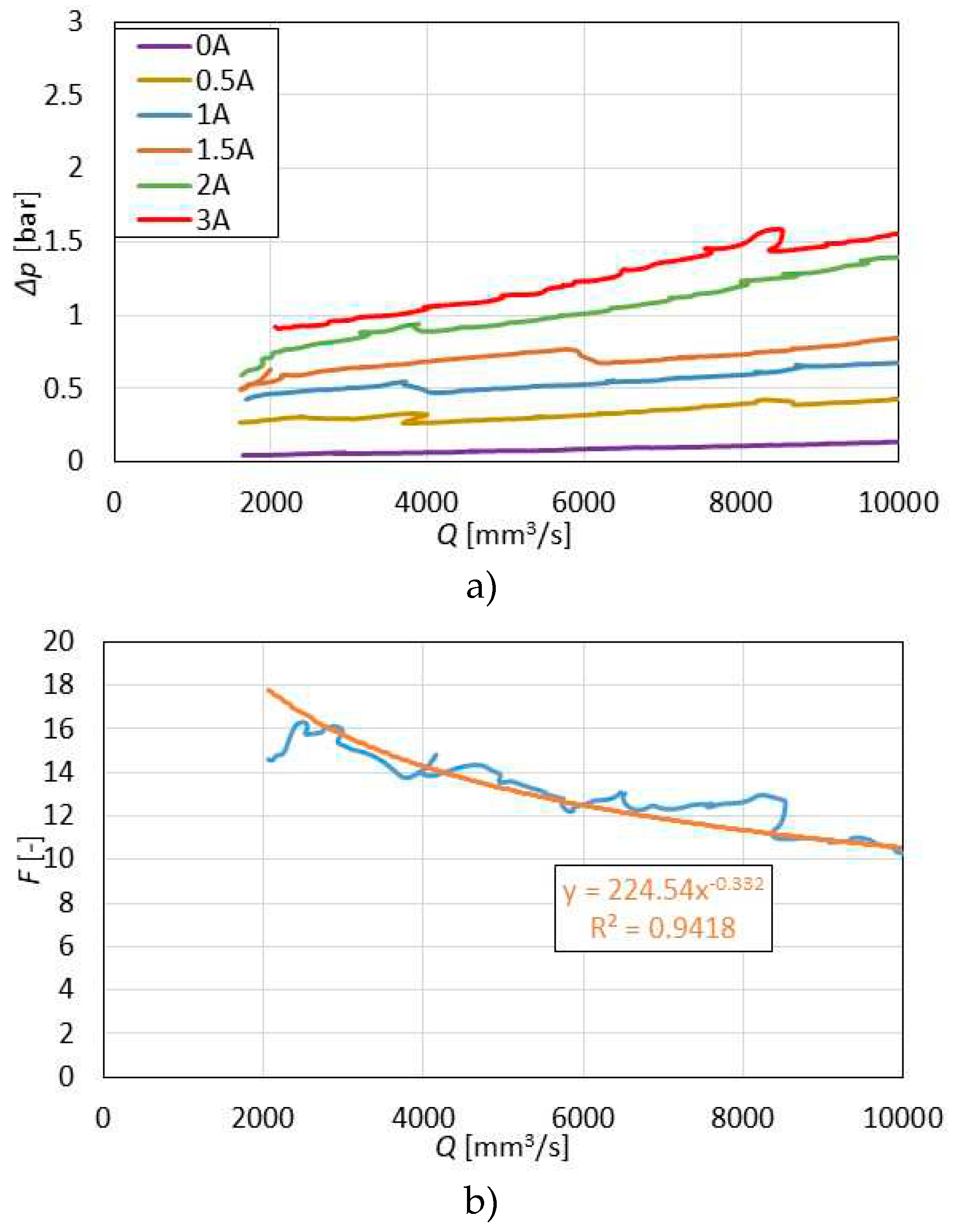
Preprints 87434 g010
Figure 10. Single-stage pinch mode valve: a) pressure drop vs flow rate, b) dynamic range (0-3A).
Figure 10. Single-stage pinch mode valve: a) pressure drop vs flow rate, b) dynamic range (0-3A).
Preprints 87434 g010
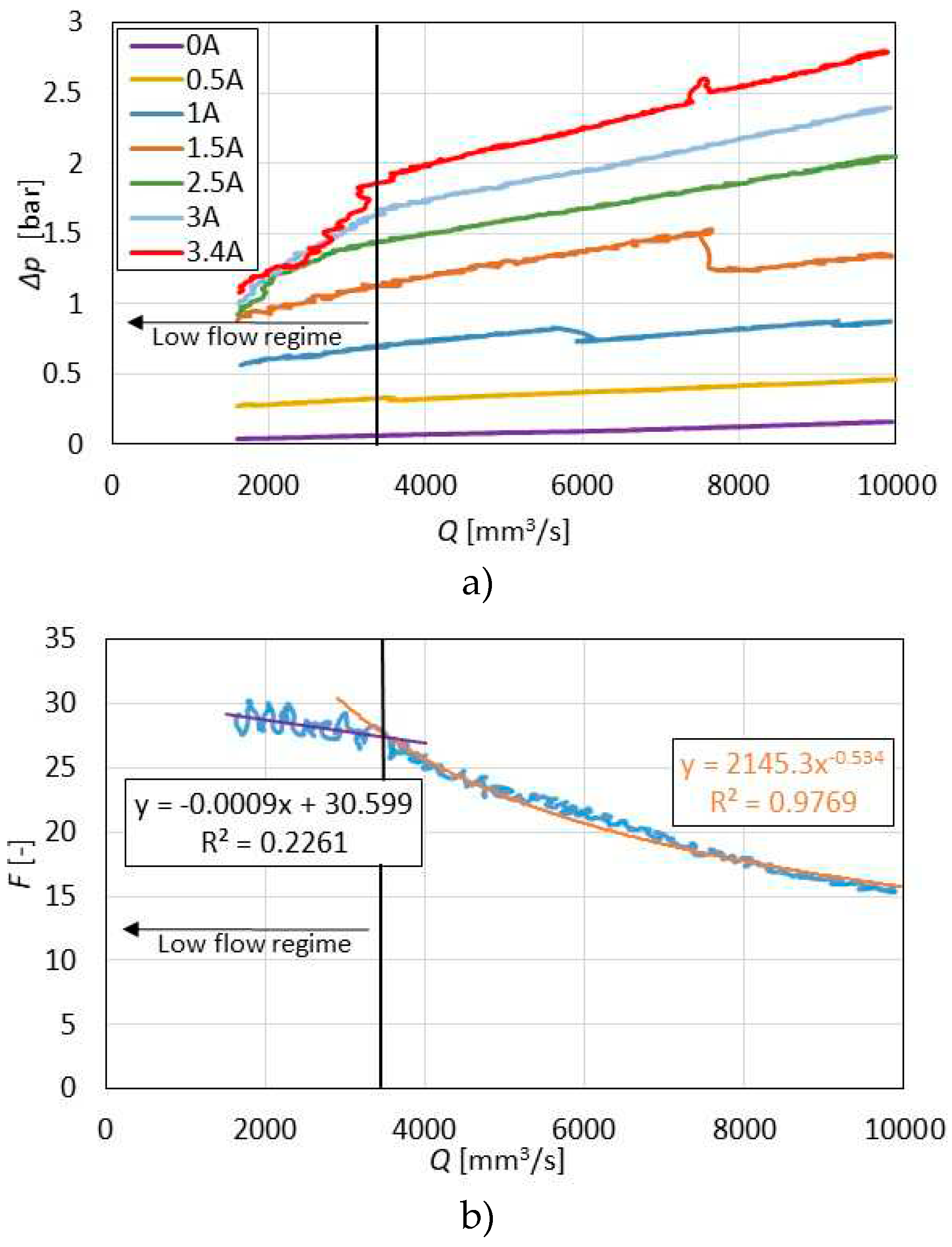
Preprints 87434 g011
Figure 11. Three-stage pinch mode valve: a) pressure drop vs flow rate, b) dynamic range (0-3A).
Figure 11. Three-stage pinch mode valve: a) pressure drop vs flow rate, b) dynamic range (0-3A).
Preprints 87434 g011
Preprints 87434 g012
Figure 12. Three-stage pinch valve: repeatability of the experiment, I=3.4 A.
Figure 12. Three-stage pinch valve: repeatability of the experiment, I=3.4 A.
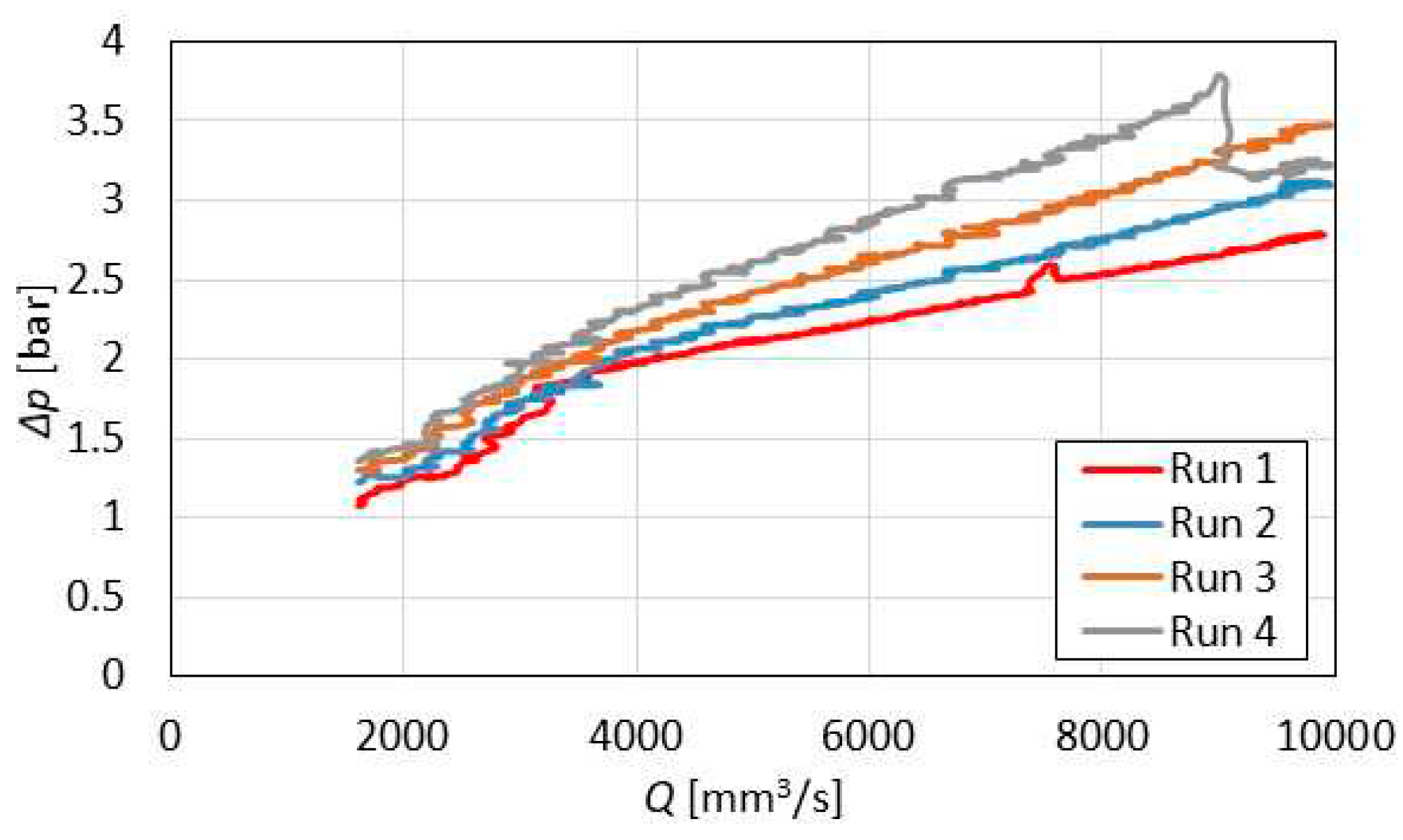
Preprints 87434 g012
Preprints 87434 g013
Figure 13. Valves’ performance comparison.
Figure 13. Valves’ performance comparison.
Preprints 87434 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated