Prerpints.org logo
Preprint
Article

Multiple Sclerosis Recognition via Wavelet Entropy and PSO-Based Neural Network

Altmetrics

Downloads

188

Views

94

Comments

0

This version is not peer-reviewed

Submitted:

09 October 2023

Posted:

10 October 2023

You are already at the latest version

Alerts
Abstract
This paper presents a novel approach for the recognition of multiple sclerosis (MS) using wavelet entropy and a Particle Swarm Optimization (PSO)-based neural network. MS is a complex neurological disorder with diverse clinical manifestations, often challenging to diagnose accurately. In this study, we leverage wavelet entropy (WE) as a feature extraction method to capture intricate patterns within brain imaging data. These extracted features are then employed to train a neural network model optimized through PSO to enhance classification accuracy. Experimental results on a dataset comprising MS and healthy control subjects demonstrate the effectiveness of our proposed approach, viz., WE-PSONN, which achieves a sensitivity of 91.95±1.15, a specificity of 92.36±0.88, a precision of 92.28±0.88, an accuracy of 92.16±0.90. The combination of advanced signal processing techniques and machine learning optimization holds promise for improving the early diagnosis and management of MS, offering potential benefits to both patients and healthcare providers.
Keywords: 
Subject: Computer Science and Mathematics  -   Computational Mathematics

1. Introduction

Multiple sclerosis (MS) is a chronic and often disabling neurological condition that primarily affects the central nervous system [1], comprising the brain and spinal cord. It is considered an autoimmune disease, which means that the immune system mistakenly targets and damages the protective covering of nerve fibers called myelin [2]. This damage disrupts the normal flow of electrical impulses along the nerves, leading to a wide range of neurological symptoms [3].
The symptoms of MS can vary significantly from person to person, making it a highly unpredictable condition. Common symptoms include fatigue, muscle weakness, difficulty walking, numbness or tingling sensations, problems with coordination and balance, and visual disturbances [4]. These symptoms can come and go, or they may persist and worsen over time. In some cases, individuals with MS may experience more severe symptoms, such as difficulty with speech, cognitive impairments [5], and issues with bladder and bowel control [6].
While the exact cause of MS remains unknown, it is believed to involve a complex interplay of genetic and environmental factors. There is currently no cure for multiple sclerosis [7], but various treatments are available to manage symptoms, reduce the frequency of relapses, and slow the progression of the disease. These treatments often include medications, physical therapy, and lifestyle modifications to improve overall well-being and quality of life for individuals living with MS [8].
Traditional MS recognition methods have several shortcomings, which have led to the development and adoption of more advanced diagnostic techniques. Some of the main shortcomings [9] of traditional MS recognition methods include (i) Reliance on Clinical Symptoms: Traditional MS diagnosis often relies on clinical symptoms alone. Since MS symptoms can be nonspecific and mimic other conditions [10], this approach may lead to delayed or misdiagnosis, as many other diseases can produce similar symptoms [11]. This delay can hinder early intervention and treatment, potentially allowing the disease to progress. (ii) Lack of Objectivity: Clinical assessment of MS is subjective and can vary from one healthcare provider to another. The lack of objective, quantifiable measures [12] make it challenging to establish a definitive diagnosis and monitor disease progression accurately. (iii) Invasive Procedures: Historically, diagnosing MS required invasive procedures such as a lumbar puncture (spinal tap) [13] to analyze cerebrospinal fluid for abnormalities. These procedures can be uncomfortable and carry some risks.
Recently, scholars have tended to use machine learning methods to recognize MS. Machine learning methods [14] are a subset of artificial intelligence techniques that enable computers to learn from data and make predictions or decisions without being explicitly programmed [15]. These methods involve the development of algorithms that can analyze and interpret patterns in large datasets, automatically adjusting their parameters to improve performance over time. Machine learning encompasses various approaches, including supervised learning [16] (where models are trained on labeled data to make predictions), unsupervised learning [17] (for discovering patterns and structures in data), and reinforcement learning [18] (for decision-making in dynamic environments). These methods have wide-ranging applications, from natural language processing and image recognition to autonomous robotics and recommendation systems, and are fundamental in enabling computers to perform tasks that require learning from experience. Lopez [19] employed the Haar wavelet transform and logistic regression (LR) method. Han, et al. [20] used an adaptive genetic algorithm (AGA) to detect MS. Zhao, et al. [21] proposed the Dirichlet mixture of Gaussian processes with split-kernel (DMGPS) to identify MS. Han, et al. [22] proposed using Hu moment invariant (HMI) to classify MS.
This paper proposes a novel method that combines wavelet entropy (WE) and a particle swarm optimization-based neural network (PSONN). The contributions of our study are below:
  • We are the first to propose the WE-PSONN method to recognize MS.
  • Our WE-PSONN gets better results than four state-of-the-art approaches.

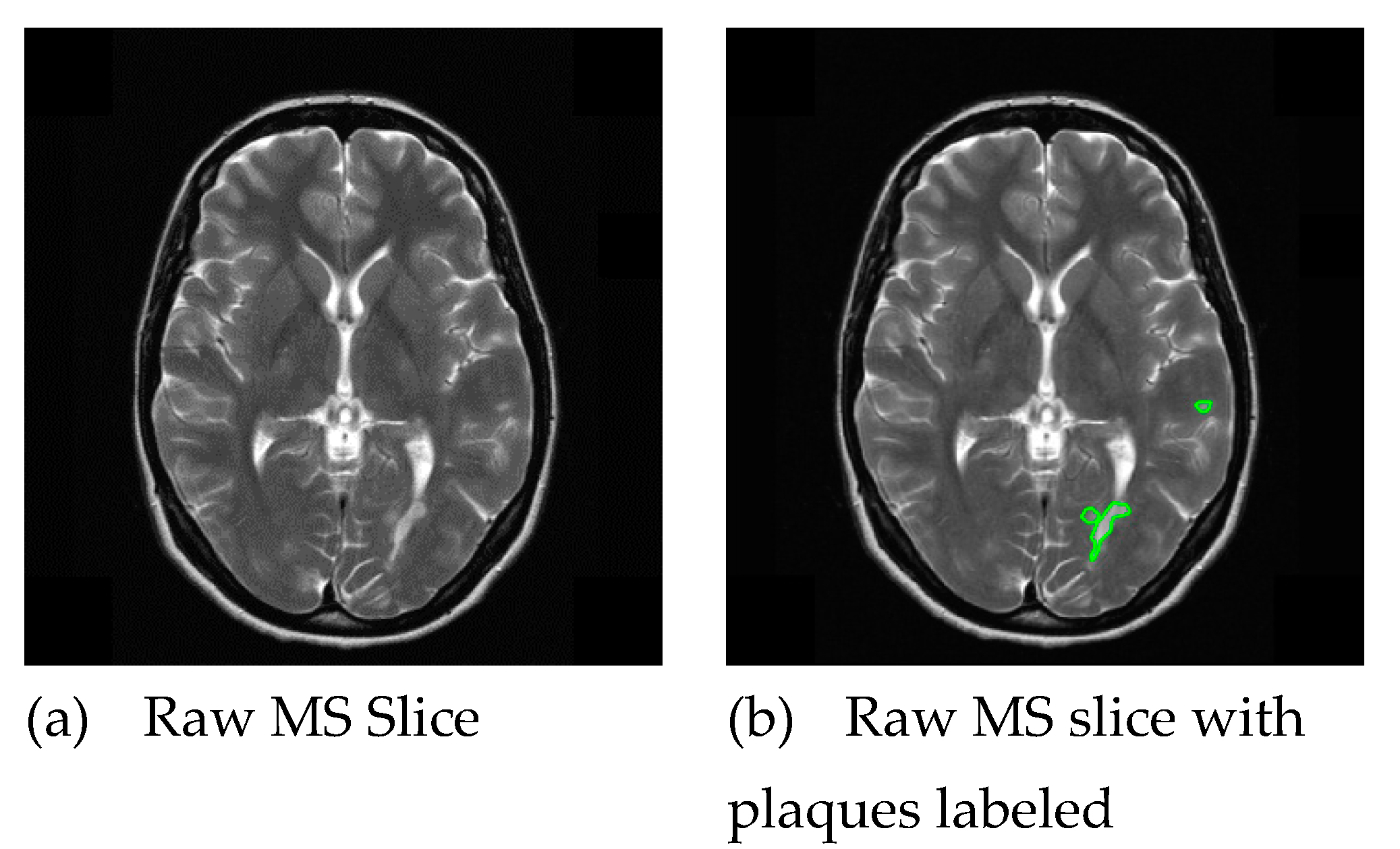
2. Dataset

The dataset is from Ref [20]. Its demographic description is listed in Table 1, where two categories exist: (i) MS; and (ii) healthy control (HC). Figure 1 shows one sample of MS.
Data harmonization [25] is the process of bringing together and standardizing data from different sources or formats to make it consistent and compatible for analysis, integration, or other purposes. The goal of data harmonization is to create a unified and cohesive dataset that can be used for various analytical, reporting, or decision-making tasks. Histogram stretching (HS) [26], also known as contrast stretching or intensity stretching, is a technique in image processing that aims to improve the contrast and visibility of an image by expanding the range of pixel intensities. It involves linearly scaling the intensity values of an image so that the minimum and maximum values span the entire available range, typically from 0 to 255 in an 8-bit image [27]. HS can enhance the visual appearance of an image, making details more distinguishable and improving its overall quality. HS is often used in image enhancement and preprocessing to make images more suitable for subsequent analysis or visualization. HS is used in our method due to its ease of implementation. Suppose α denotes the original brain slice, and β stands for the processed brain slice. Let w , v denote the coordinates, HS operation HS : α ↦ β is defined via:
β w , v = α w , v − α l α h − α l ,
where α l , α h stand for the lowest and highest grayscale intensity values of α , respectively.
α l = min w ⁡ min v ⁡ α ( w , v ) α h = max w ⁡ max v ⁡ α ( w , v ) .

3. Methodology

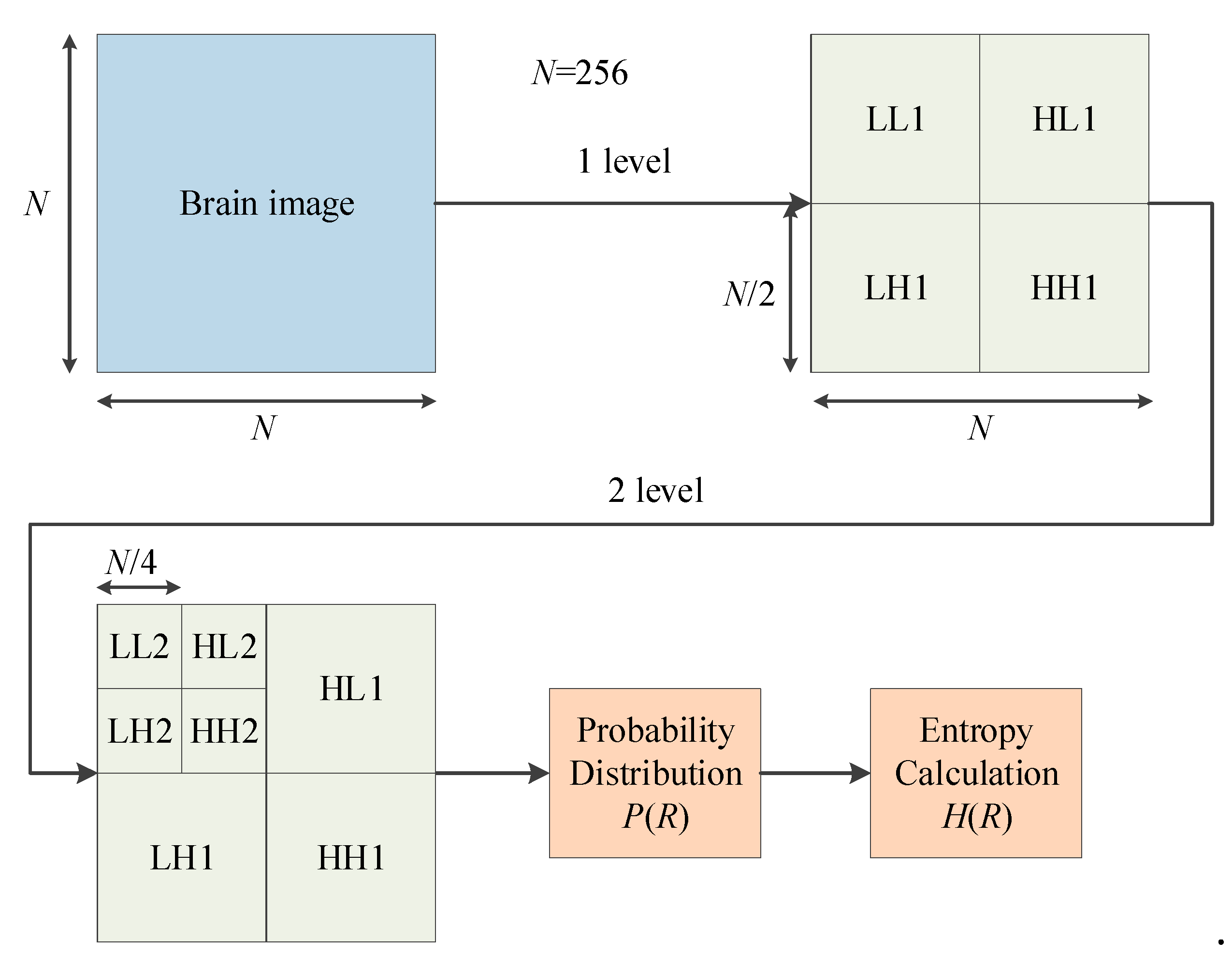
3.1. Wavelet Entropy

Wavelet entropy [28] is a mathematical and statistical measure used in signal processing and data analysis to characterize the complexity or irregularity of a signal or time series data. It is derived from the concept of wavelet transform, which is a mathematical technique for decomposing a signal into different frequency components and analyzing their variations over time [29]. Wavelet entropy quantifies the amount of information or disorder within these frequency components and is particularly useful in fields like neuroscience [30], finance, and environmental science for analyzing complex and non-stationary signals. To compute wavelet entropy, one typically follows these steps:
  • Step 1: Wavelet Transform
The first step involves applying the wavelet transform to the time series data [31]. This transform breaks down the signal into different scales, allowing for the analysis of both low and high-frequency components.
  • Step 2: Probability Distribution
After obtaining the wavelet coefficients, a probability distribution P R is created to represent the magnitude of each scale. This distribution characterizes how the signal's energy is distributed across different scales or frequencies.
  • Step 3: Entropy Calculation
Wavelet entropy [32] is then calculated based on the probability distribution. It measures the unpredictability or randomness within the signal. Higher wavelet entropy values indicate greater complexity, while lower values suggest more regular or predictable patterns.
Shannon entropy is used since it is the originator of modern information theory. Suppose a variable R is discrete and random, and it falls within the value set r 1 , r 2 , … , r n with probability mass function of P R , the Shannon entropy is defined as:
H R = E − ln ⁡ P R ,
where H is the entropy, and E represents the expected value operation. If the set of possible values of R is finite, the formula above is transformed as:
H R = − ∑ i = 1 n P r i log b ⁡ P r i ,
where b is the base of the log function, determining the unit of Shannon entropy.
There are seven coefficient matrices (Figure 2) after a 2-level 2D-DWT [33], with four in size of 64×64 and three 128-by-128. By using this method, the dimension of the feature vector is reduced from the origin 256×256=65,536 to only seven effectively.
In all, wavelet entropy offers advantages over traditional entropy measures, especially for analyzing signals with varying frequency content and non-stationary behavior. It can capture intricate patterns and fluctuations in time series data, making it a valuable tool for understanding complex systems and processes in various scientific and engineering disciplines.

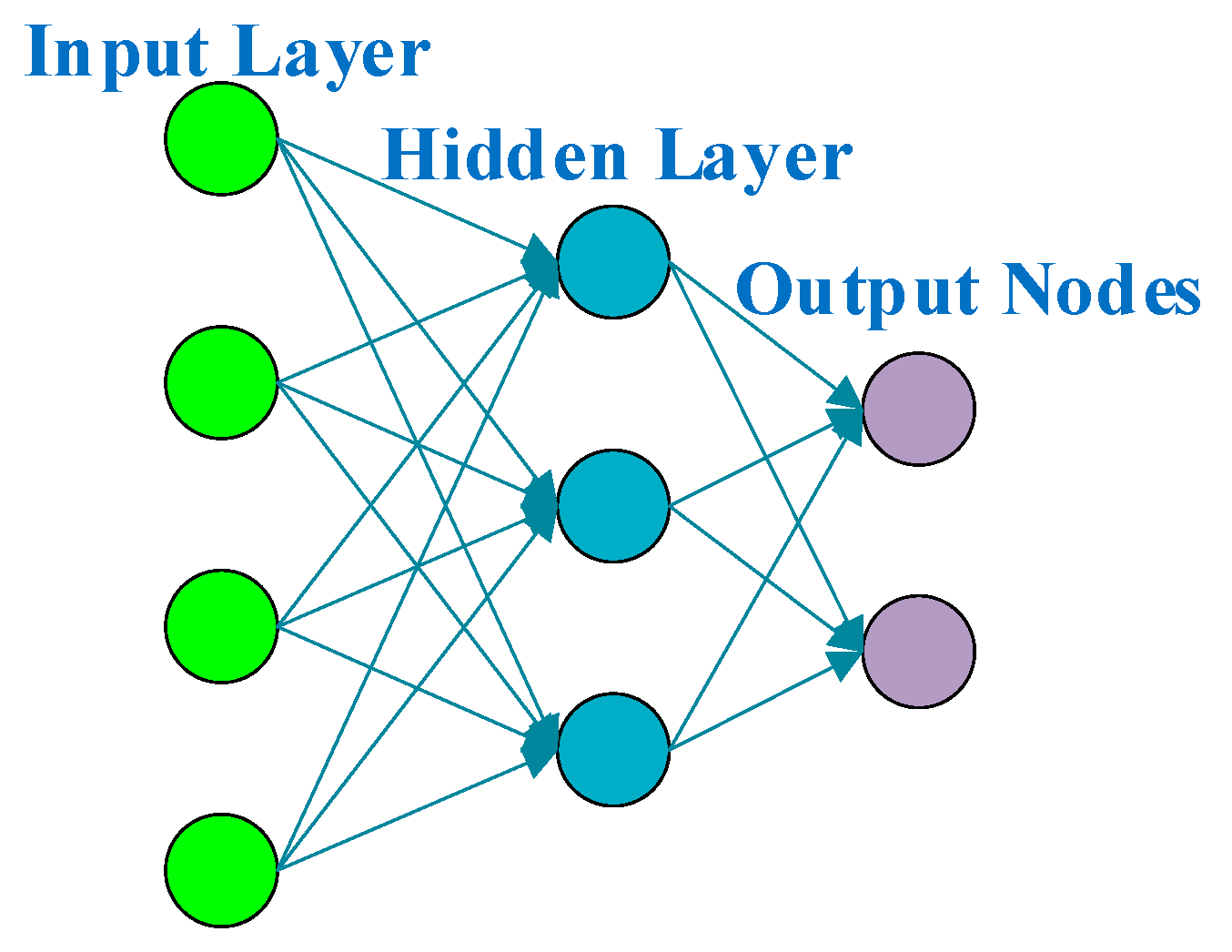
3.2. Feedforward Neural Network

A feedforward neural network (FNN) [34], often simply called a feedforward network, is a fundamental type of neural network architecture used in machine learning and deep learning. It represents the simplest form of neural network, where information flows in one direction [35], from input to output, without any feedback loops or recurrent connections [36]. Here's a more detailed explanation in four paragraphs:
A FNN consists of multiple layers of interconnected nodes or neurons (Figure 3). These layers typically include an input layer, one or more hidden layers, and an output layer [37]. Each neuron in a layer is connected to every neuron in the subsequent layer, but there are no connections that loop back within the same layer or to previous layers. Each connection between neurons has an associated weight, which is adjusted during training to enable the network to learn and make predictions [38].
The operation of a FNN involves a simple forward propagation of information. Input data is fed into the input layer, and it propagates through the network layer by layer [39]. Neurons in each layer perform a weighted sum of their inputs and pass the result through an activation function. This output then becomes the input for the next layer. The final output is obtained at the output layer [40]. This process is deterministic and does not involve any recurrent or feedback connections.
Activation functions play a crucial role in feedforward networks. They introduce nonlinearity into the model, allowing the network to learn complex relationships in data [41]. Common activation functions include the sigmoid, hyperbolic tangent (tanh), and rectified linear unit (ReLU) functions [42]. These functions determine the output of a neuron based on its weighted input sum and introduce the concept of thresholds and saturation points [43].
FNNs are trained using various supervised learning algorithms, with the most popular being backpropagation. During training, the network learns to adjust its weights to minimize the difference between its predictions (output) and the target values in the training data. This is typically done by computing gradients of an error or loss function with respect to the network's weights and then adjusting the weights [44] in the direction that reduces the error. This process is repeated iteratively until the network's performance on the training data reaches a satisfactory level [45].

3.3. PSO-Based Neural Network

A particle swarm optimization-based neural network (PSONN) is a combination of two distinct computational techniques: particle swarm optimization (PSO) [46] and feedforward neural networks (FNNs).
PSO [47] is a heuristic optimization algorithm inspired by the social behavior of birds or fish swarming, where individual particles adjust their positions in search of an optimal solution. FNNs, on the other hand, are a class of machine learning models inspired by the human brain that can learn and make predictions from data. Combining PSO with FNNs aims to improve the training and optimization process of neural networks [48].
PSO is an optimization algorithm that simulates the behavior of a swarm of particles in a multidimensional search space. Each particle represents a potential solution to the optimization problem. These particles iteratively update their positions and velocities based on their own experiences and the experiences of their peers in the swarm. PSO is particularly useful for finding global optima in complex, high-dimensional search spaces. In the context of neural networks, PSO can be applied to optimize the weights and biases of the network to minimize a specific cost or error function [49].
In a PSONN, the PSO algorithm [50] is used to optimize the weights and biases of the neural network. Each particle in the PSO swarm corresponds to a set of neural network weights and biases. The objective is to find the combination of weights and biases that minimizes the error or cost function associated with the neural network's performance on a specific task. PSO guides the search in weight space [51], helping the neural network converge to a more optimal solution. The fitness function used in PSO is often related to the neural network's error on a training dataset.
PSONNs offer advantages in optimizing neural network architectures, making them more efficient and capable of solving complex problems. They are used in various applications, including pattern recognition, time series prediction, feature selection, and optimization of deep neural networks. By combining the strengths of PSO's global search capabilities with the learning and generalization abilities of FNNs, this approach can enhance the performance and efficiency of neural network models, making them more suitable for real-world applications. In the future, we shall try more advanced and recent optimization methods [52].

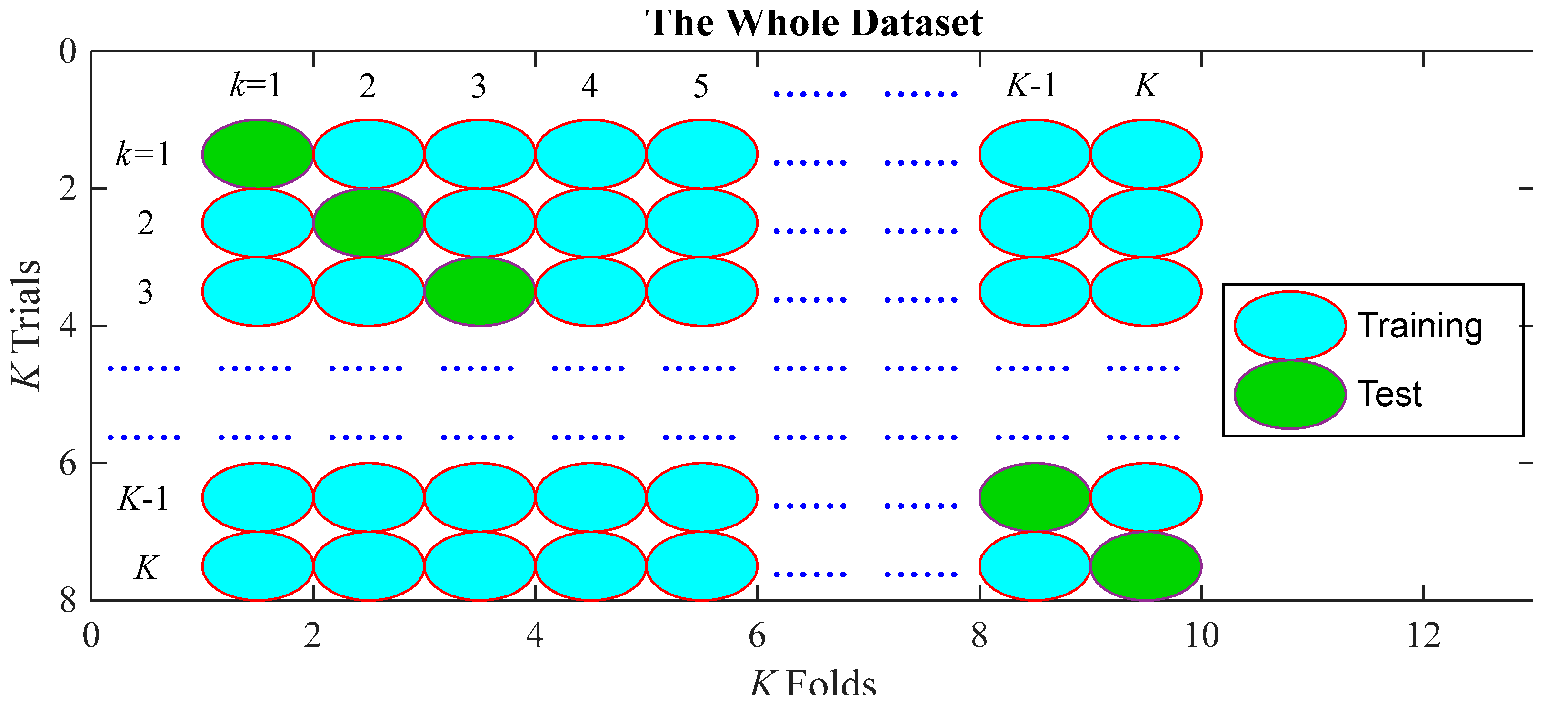
3.4. 10-Fold Cross Validation

K -fold cross-validation is a widely used technique in machine learning and model evaluation that helps assess the performance of a predictive model while maximizing the use of available data [53]. It involves splitting the dataset into K subsets, or "folds," where K is typically a positive integer like 10. The process can be summarized in four key aspects:
Step 1: Dataset Splitting. The first step in K -fold cross-validation is to divide the dataset into K roughly equal-sized parts or folds. Each fold represents a subset of the data, and these subsets are often randomly selected to ensure that the cross-validation process is not biased by the order of the data.
Step 2: Training and Testing. K -fold cross-validation then proceeds through K iterations. During each iteration, one of the K folds is held out as the test set, while the remaining K -1 folds are used as the training set. This means that every data point in the dataset is used for testing exactly once.
Step 3: Model Training and Evaluation. In each iteration, a predictive model (e.g., a machine learning algorithm) is trained on the training set, and its performance is evaluated on the corresponding test set. Common performance metrics, such as accuracy, precision, recall, or mean squared error, are computed to assess how well the model generalizes to unseen data [54].
Step 4: Cross-Validation Results. After completing all K iterations, K separate performance metrics are obtained, one for each fold. These metrics are typically averaged to produce a single, overall performance measure that provides a more robust estimate of how well the model is likely to perform on new, unseen data. This average performance metric is often used to compare different models or tuning parameters [55]. Figure 4 shows the diagram of K -fold cross validation.
K -fold cross-validation is a valuable technique for several reasons. It helps in assessing a model's performance more reliably than a single train-test split because it uses all available data for both training and testing [56]. It also provides insights into the model's stability and generalization performance by examining its performance on different subsets of the data. Additionally, K -fold cross-validation is particularly useful when the dataset is limited in size, as it allows for more efficient and effective use of the available data for model evaluation. Overall, it is a key tool for model selection, hyperparameter tuning, and assessing a model's expected performance in real-world applications.

3.5. Measure on Z runs

Suppose we carry out K -fold cross-validation Z runs. Suppose the confusion matrix M ( z ) over z -th run ( z = 1,2 , … , Z ) is
M z = m 11 ( z ) m 12 ( z ) m 21 ( z ) m 22 ( z )
where the four elements m 11 , m 12 , m 21 , m 22 represent TP, FN, FP, and TN, respectively. Here P means the positive category, MS, and N is the negative category, HC.
The sensitivity [57] (symbolized as f 1 ), specificity [58] (symbolized as f 2 ), precision (symbolized as f 3 ), and accuracy (symbolized as f 4 ) of z -th run are defined as:
f 1 ( z ) = m 11 ( z ) m 11 z + m 12 ( z ) f 2 ( z ) = m 22 ( z ) m 21 z + m 22 ( z ) f 3 ( z ) = m 11 ( z ) m 11 z + m 21 ( z ) f 4 ( z ) = m 11 z + m 22 ( z ) m 11 z + m 12 z + m 21 z + m 22 ( z ) , z = 1,2 … , Z .
The F1 score [59] of z -th run f 5 z is defined as
f 5 z = 2 × f 3 ( z ) × f 1 ( z ) f 3 ( z ) + f 1 ( z ) = 2 × m 11 ( z ) 2 × m 11 z + m 12 z + m 21 z .
Matthews correlation coefficient (MCC) [60] of z -th run ι 6 ( z ) is:
f 6 ( z ) = m 22 ( z ) × m 11 ( z ) − m 21 ( z ) × m 12 ( z ) m 21 ( z ) + m 11 ( z ) × m 11 ( z ) + m 12 ( z ) × m 22 ( z ) + m 21 ( z ) × m 22 ( z ) + m 12 ( z )
Fowlkes–Mallows index (FMI) [61] of z -th run f 7 ( z ) is defined as:
f 7 ( z ) = m 11 ( z ) m 11 ( z ) + m 21 ( z ) × m 11 ( z ) m 11 ( z ) + m 12 ( z )
After running up all the Z runs, we deduce the mean and standard deviation (MSD, symbolized as a k ± b k , k = 1 , … , 7 ) are defined below:
a k = 1 Z × ∑ z = 1 Z f k ( z ) b k = 1 Z − 1 × ∑ z = 1 Z f k z − a k 2 , k = 1,2 , … , 7
The receiver operating characteristic (ROC) curve and the area under the curve (AUC) are reported based on Z runs.

4. Results and Discussions

4.1. Statistical Analysis

Table 2 shows the statistical analysis of our WE-PSONN method, which achieves a sensitivity of 91.95±1.15, a specificity of 92.36±0.88, a precision of 92.28±0.88, an accuracy of 92.16±0.90, an F1 score of 92.11±0.92, an MCC value of 84.32±1.79, and an FMI of 92.12±0.91.

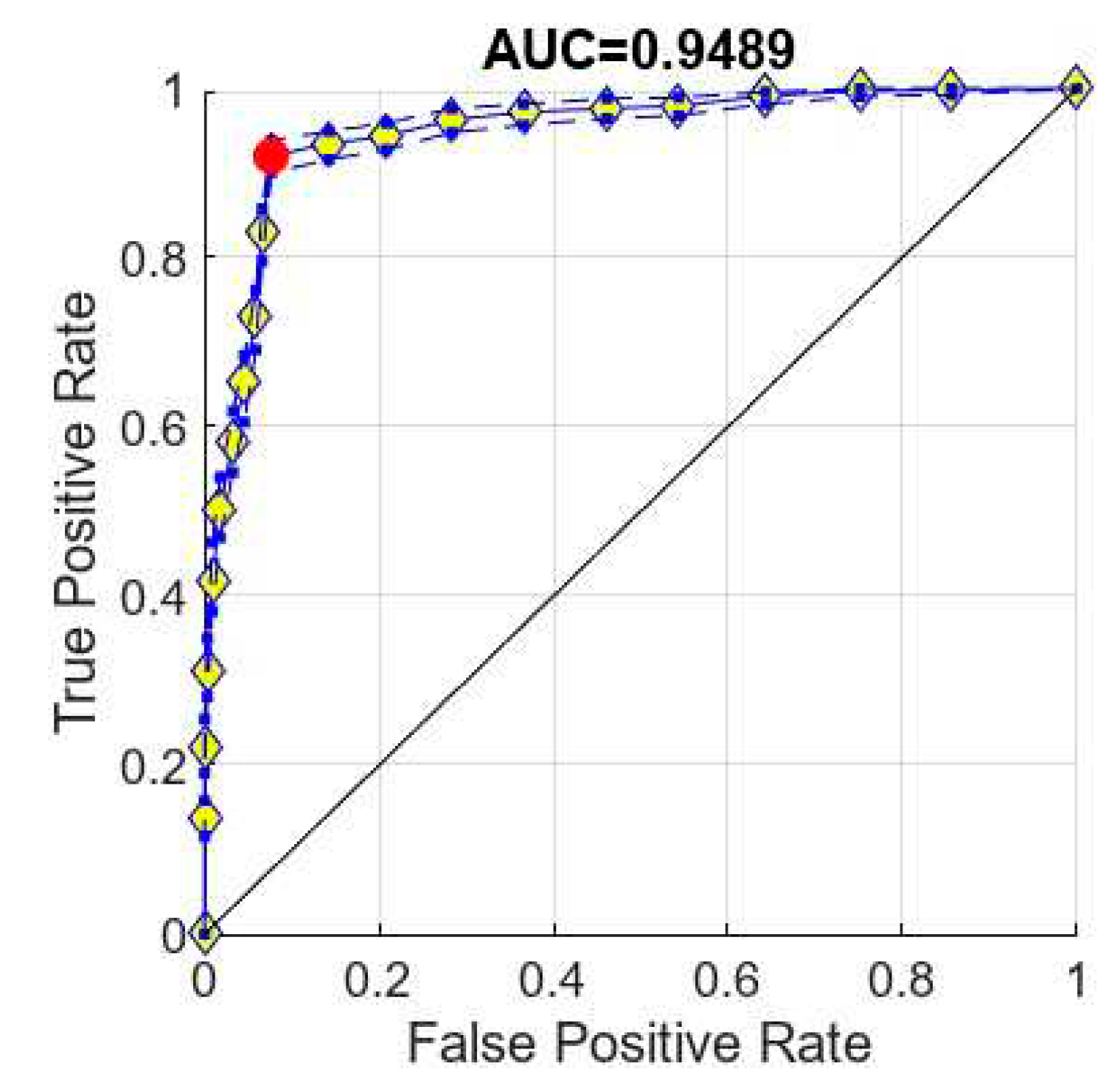
4.2. ROC Curve

The ROC curve is a graphical representation used in machine learning and statistics to evaluate the performance of binary classification models. It is a plot that illustrates the trade-off between a model's true positive rate (TPR, sensitivity) and its false positive rate (FPR, i.e., 1 - specificity) across different threshold values. The ROC curve is created by plotting TPR (sensitivity) on the y-axis against FPR (1 - specificity) on the x-axis at various threshold values. Each point on the curve corresponds to a different threshold setting for the classification model. A diagonal line in the ROC space (from [0,0] to [1,1]) represents random guessing, where the model's performance is no better than chance.
A perfect classifier would have a ROC curve that hugs the upper-left corner of the plot, with TPR equal to 1 and FPR equal to 0. The closer the ROC curve is to the upper-left corner, the better the model's performance in distinguishing between the two classes. The area under the ROC curve (AUC) is also a commonly used metric to quantify the overall performance of a classification model. AUC ranges from 0 to 1, with higher values indicating better model performance. Figure 5 shows the AUC of our WE-PSONN method is 0.9489.

4.3. PSO versus AGA

Han, et al. [20] use WE as a feature and AGA as the optimization algorithm. The AGA is a variant of the traditional Genetic Algorithm (GA) that incorporates adaptive mechanisms to improve the algorithm's performance during the optimization process [62]. Genetic Algorithms are a type of evolutionary algorithm inspired by the process of natural selection and genetics. They are used for solving optimization and search problems by iteratively evolving a population of candidate solutions to find the best solution or approximate the optimal solution [63].
We compare our method with AGA [20], and the comparison results are displayed in Table 3. It shows the PSO is better than AGA in all seven measures. The reason may be the parameter sensitivity. PSO typically has fewer algorithm parameters to tune compared to AGAs, making it easier to set up and less sensitive to parameter choices. AGAs often require careful tuning of parameters such as mutation rates, crossover rates, and selection mechanisms, which can be challenging but also provide more flexibility for customization.

4.4. Comparison with State-of-the-Art Algorithms

We compare our method with three state-of-the-art approaches: LR [19], DMGPS [21], and HMI [22]. Table 4 shows the proposed WE-PSONN gives better results than other state-of-the-art approaches. The reason is twofold, shown below.
First, WE is a good feature extractor [64] because it quantifies the complexity or irregularity of signals in a multi-scale fashion, allowing it to capture important information at various levels of detail. By decomposing a signal into different frequency components using wavelet transform and then measuring the entropy of these components, it provides a robust and informative representation of the signal's characteristics. High wavelet entropy values indicate increased complexity and fine-grained details in the signal, while low values suggest more regular and predictable patterns. This adaptability to different signal complexities makes wavelet entropy a valuable feature for a wide range of applications, including signal processing, image analysis, and biomedical signal classification, as it can effectively discriminate between various signal types and highlight relevant features.
Second, PSO can optimize the hyperparameters of the neural network, such as the learning rate, the number of hidden layers, and the number of neurons in each layer. This automatic tuning process can lead to better convergence and faster training. PSO is a global optimization technique, which means it explores a wide range of parameter settings for the neural network. This can help ensure that the model does not get stuck in local optima and finds a better overall solution.

5. Conclusions

In conclusion, this study demonstrates a promising approach to improving the accuracy of multiple sclerosis diagnosis. By leveraging wavelet entropy for feature extraction and optimizing neural network parameters with a Particle Swarm Optimization (PSO) algorithm, the research shows the potential for more precise and reliable identification of this complex neurological condition. The combination of advanced signal processing [65,66] techniques and machine learning methods offers a valuable contribution to the field of medical image analysis [67,68], paving the way for enhanced early detection and management of multiple sclerosis, ultimately benefiting patients and healthcare providers alike.
Further research and validation of this approach hold the potential to advance our understanding and treatment of multiple sclerosis. We shall explore advanced feature selection techniques [69] to identify the most relevant wavelet entropy features for multiple sclerosis recognition. This could involve employing machine learning algorithms or domain-specific knowledge to optimize feature extraction [70]. Also, conducting larger-scale clinical studies to validate the WE-PSONN model's performance on diverse patient populations. Gathering data from multiple healthcare institutions can help assess the model's generalizability and robustness.

Funding

This research did not receive any grants.

Acknowledgment

We thank all the anonymous reviewers for their hard reviewing work.

Conflict of Interest

The author declares there is no conflict of interest regarding the publication of this paper.

References

  1. Kornbluh, A.B.; Kahn, I. Pediatric Multiple Sclerosis. Semin. Pediatr. Neurol. 2023, 46, 101054. [Google Scholar] [CrossRef] [PubMed]
  2. Quigley, S.; Asad, M.; Doherty, C.; Byrne, D.; Cronin, S.; Kearney, H. Concurrent diagnoses of Tuberous sclerosis and multiple sclerosis. Mult. Scler. Relat. Disord. 2023, 71, 104586. [Google Scholar] [CrossRef] [PubMed]
  3. Maroto-García, J.; Martínez-Escribano, A.; Delgado-Gil, V.; Mañez, M.; Mugueta, C.; Varo, N.; de la Torre. G.; Ruiz-Galdón, M. Biochemical biomarkers for multiple sclerosis. Clin. Chim. Acta 2023, 548, 117471. [Google Scholar] [CrossRef] [PubMed]
  4. Chagot, C.; Vlaicu, M.B.; Frismand, S.; Colnat-Coulbois, S.; Nguyen, J.P.; Palfi, S. Deep brain stimulation in multiple sclerosis-associated tremor. A large, retrospective, longitudinal open label study, with long-term follow-up. Mult. Scler. Relat. Disord. 2023, 79, 104928. [Google Scholar] [CrossRef] [PubMed]
  5. Lunin, S.; Novoselova, E.; Glushkova, O.; Parfenyuk, S.; Kuzekova, A.; Novoselova, T.; Sharapov, M.; Mubarakshina, E.; Goncharov, R.; Khrenov, M. Protective effect of exogenous peroxiredoxin 6 and thymic peptide thymulin on BBB conditions in an experimental model of multiple sclerosis. Arch. Biochem. Biophys. 2023, 746, 109729. [Google Scholar] [CrossRef]
  6. E Freedman, D.; Krysko, K.M.; Feinstein, A. Intimate partner violence and multiple sclerosis. Mult. Scler. J. 2023. [Google Scholar] [CrossRef] [PubMed]
  7. Cerri, S.; Hoopes, A.; N. Greve, D.; Muhlau, M.; Van Leemput, K. A Longitudinal Method for Simultaneous Whole-Brain and Lesion Segmentation in Multiple Sclerosis. Arxiv 2020, arXiv:2008.05117, doi:arXiv:2008.05117.
  8. Atapour, M.; Maghaminejad, F.; Ghiyasvandian, S.; Rahimzadeh, M.; Hosseini, S. The psychometric properties of the Persian version of the Multiple Sclerosis Self-Management Scale-Revised: A cross-sectional methodological study. Heal. Sci. Rep. 2023, 6, e1515. [Google Scholar] [CrossRef]
  9. Shafiee, A.; Soltani, H.; Athar, M.M.T.; Jafarabady, K.; Mardi, P. The prevalence of depression and anxiety among Iranian people with multiple sclerosis: A systematic review and meta-analysis. Mult. Scler. Relat. Disord. 2023, 78, 104922. [Google Scholar] [CrossRef]
  10. Eisler, J.J.; Disanto, G.; Sacco, R.; Zecca, C.; Gobbi, C. Influence of Disease Modifying Treatment, Severe Acute Respiratory Syndrome Coronavirus 2 Variants and Vaccination on Coronavirus Disease 2019 Risk and Outcome in Multiple Sclerosis and Neuromyelitis Optica. J. Clin. Med. 2023, 12, 5551. [Google Scholar] [CrossRef]
  11. Turčić, A.; Radovani, B.; Vogrinc. ; Habek, M.; Rogić, D.; Gabelić, T.; Zaninović, L.; Lauc, G.; Gudelj, I. Higher MRI lesion load in multiple sclerosis is related to the N-glycosylation changes of cerebrospinal fluid immunoglobulin G. Mult. Scler. Relat. Disord. 2023, 79, 104921. [Google Scholar] [CrossRef] [PubMed]
  12. Karaaslan, Z.; Şengül-Yediel, B.; Yüceer-Korkmaz, H.; Şanlı, E.; Gezen-Ak, D.; Dursun, E.; Timirci-Kahraman. ; Baykal, A.T.; Yılmaz, V.; Türkoğlu, R.; et al. Chloride intracellular channel protein-1 (CLIC1) antibody in multiple sclerosis patients with predominant optic nerve and spinal cord involvement. Mult. Scler. Relat. Disord. 2023, 78, 104940. [Google Scholar] [CrossRef]
  13. Chisari, C.G.; Guadagno, J.; Adjamian, P.; Silvan, C.V.; Greco, T.; Bagul, M.; Patti, F. A post hoc evaluation of the shift in spasticity category in individuals with multiple sclerosis-related spasticity treated with nabiximols. Ther. Adv. Neurol. Disord. 2023, 16. [Google Scholar] [CrossRef] [PubMed]
  14. Zhang, Y.; Yang, J.; Wang, S.; Dong, Z.; Phillips, P. Pathological brain detection in MRI scanning via Hu moment invariants and machine learning. J. Exp. Theor. Artif. Intell. 2016, 29, 299–312. [Google Scholar] [CrossRef]
  15. Lasalvia, M.; Gallo, C.; Capozzi, V.; Perna, G. Discrimination of Healthy and Cancerous Colon Cells Based on FTIR Spectroscopy and Machine Learning Algorithms. Appl. Sci. 2023, 13, 10325. [Google Scholar] [CrossRef]
  16. Kiyak, E.O.; Ghasemkhani, B.; Birant, D. High-Level K-Nearest Neighbors (HLKNN): A Supervised Machine Learning Model for Classification Analysis. Electronics 2023, 12, 3828. [Google Scholar] [CrossRef]
  17. Han, G.; Wang, Y.; Liu, J.; Zeng, F. Low-light images enhancement and denoising network based on unsupervised learning multi-stream feature modeling. J. Vis. Commun. Image Represent. 2023, 96. [Google Scholar] [CrossRef]
  18. Liu, X.; Li, Z. Dynamic multiple access based on deep reinforcement learning for Internet of Things. Comput. Commun. 2023, 210, 331–341. [Google Scholar] [CrossRef]
  19. Wu, X.; Lopez, M. Multiple Sclerosis Slice Identification by Haar Wavelet Transform and Logistic Regression. Advances in Materials, Machinery, Electrical Engineering (AMMEE 2017). LOCATION OF CONFERENCE, ChinaDATE OF CONFERENCE.
  20. Han, J.; Hou, S.-M. Multiple Sclerosis Detection via Wavelet Entropy and Feedforward Neural Network Trained by Adaptive Genetic Algorithm. International Work-Conference on Artificial Neural Networks. LOCATION OF CONFERENCE, SpainDATE OF CONFERENCE; pp. 87–97.
  21. Zhao, Y.; Chitnis, T. Dirichlet Mixture of Gaussian Processes with Split-kernel: An Application to Predicting Disease Course in Multiple Sclerosis Patients. 2022 International Joint Conference on Neural Networks (IJCNN). LOCATION OF CONFERENCE, ItalyDATE OF CONFERENCE; pp. 1–8.
  22. Han, J.; Hou, S.-M. A Multiple Sclerosis Recognition via Hu Moment Invariant and Artificial Neural Network Trained by Particle Swarm Optimization. International Conference on Multimedia Technology and Enhanced Learning. LOCATION OF CONFERENCE, United KingdomDATE OF CONFERENCE; pp. 254–264.
  23. MRI Lesion Segmentation in Multiple Sclerosis Database. eHealth laboratory, University of Cyprus, 2021.
  24. Zhang, Y.-D.; Pan, C.; Sun, J.; Tang, C. Multiple sclerosis identification by convolutional neural network with dropout and parametric ReLU. J. Comput. Sci. 2018, 28, 1–10. [Google Scholar] [CrossRef]
  25. Gleason, J.L.; Tamburro, R.; Signore, C. Promoting Data Harmonization of COVID-19 Research in Pregnant and Pediatric Populations. JAMA 2023, 330, 497–498. [Google Scholar] [CrossRef] [PubMed]
  26. Norris, C.J.; Kim, S. A Use Case of Iterative Logarithmic Floating-Point Multipliers: Accelerating Histogram Stretching on Programmable SoC. 2023 IEEE International Symposium on Circuits and Systems (ISCAS). LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE; pp. 1–5.
  27. Wang, S.-H.; Sun, J.; Phillips, P.; Zhao, G.; Zhang, Y.-D. Polarimetric synthetic aperture radar image segmentation by convolutional neural network using graphical processing units. J. Real-Time Image Process. 2017, 15, 631–642. [Google Scholar] [CrossRef]
  28. Dwivedi, D.; Chamoli, A.; Rana, S.K. Wavelet Entropy: A New Tool for Edge Detection of Potential Field Data. Entropy 2023, 25, 240. [Google Scholar] [CrossRef]
  29. Hua, F.; Ling, T.; He, W.; Liu, X. Wavelet Entropy-Based Method for Migration Imaging of Hidden Microcracks by Using the Optimal Wave Velocity. Int. J. Pattern Recognit. Artif. Intell. 2022, 36. [Google Scholar] [CrossRef]
  30. Wang, S.; Li, Y.; Shao, Y.; Cattani, C.; Zhang, Y.; Du, S. Detection of Dendritic Spines Using Wavelet Packet Entropy and Fuzzy Support Vector Machine. CNS Neurol. Disord. - Drug Targets 2017, 16, 116–121. [Google Scholar] [CrossRef]
  31. Wang, J.J. COVID-19 Diagnosis by Wavelet Entropy and Particle Swarm Optimization. Proceedings of 18th International Conference on Intelligent Computing (ICIC), Xian, PEOPLES R CHINA, Aug 07-11; pp. 600–611.
  32. Janani, A.S.; Rezaeieh, S.A.; Darvazehban, A.; Keating, S.E.; Abbosh, A.M. Portable Electromagnetic Device for Steatotic Liver Detection Using Blind Source Separation and Shannon Wavelet Entropy. IEEE J. Electromagn. Rf Microwaves Med. Biol. 2022, 6, 546–554. [Google Scholar] [CrossRef]
  33. Tao, Y.; Scully, T.; Perera, A.G.; Lambert, A.; Chahl, J. A Low Redundancy Wavelet Entropy Edge Detection Algorithm. J. Imaging 2021, 7, 188. [Google Scholar] [CrossRef] [PubMed]
  34. Valluri, D.; Campbell, R. ; Ieee. On the Space of Coefficients of a Feedforward Neural Network. In Proceedings of International Joint Conference on Neural Networks (IJCNN), Broadbeach, AUSTRALIA, Jun 18-23.
  35. Yotov, K.; Hadzhikolev, E.; Hadzhikoleva, S.; Cheresharov, S. A Method for Extrapolating Continuous Functions by Generating New Training Samples for Feedforward Artificial Neural Networks. Axioms 2023, 12, 759. [Google Scholar] [CrossRef]
  36. Zhang, Y.; Wu, L. Improved image filter based on SPCNN. Sci. China Inf. Sci. 2008, 51, 2115–2125. [Google Scholar] [CrossRef]
  37. Admon, M.R.; Senu, N.; Ahmadian, A.; Majid, Z.A.; Salahshour, S. A new efficient algorithm based on feedforward neural network for solving differential equations of fractional order. Commun. Nonlinear Sci. Numer. Simul. 2023, 117. [Google Scholar] [CrossRef]
  38. Abernot, M.; Delacour, C.; Suna, A.; Gregg, J.M.; Karg, S.; Todri-Sanial, A. Two-Layered Oscillatory Neural Networks with Analog Feedforward Majority Gate for Image Edge Detection Application. 2023 IEEE International Symposium on Circuits and Systems (ISCAS). LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE; pp. 1–5.
  39. Sharma, S.; Achlerkar, P.D.; Shrivastava, P.; Garg, A.; Panigrahi, B.K. Combined SoC and SoE Estimation of Lithium-ion Battery using Multi-layer Feedforward Neural Network. 2022 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES). LOCATION OF CONFERENCE, IndiaDATE OF CONFERENCE; pp. 1–6.
  40. Le, X.-K.; Wang, N.; Jiang, X. Nuclear mass predictions with multi-hidden-layer feedforward neural network. Nucl. Phys. A 2023, 1038. [Google Scholar] [CrossRef]
  41. Yurtkan, K.; Adalier, A.; Tekgüç, U. Student Success Prediction Using Feedforward Neural Networks. Romanian J. Inf. Sci. Technol. 2023, 2023, 121–136. [Google Scholar] [CrossRef]
  42. Wang, S.-H.; Zhang, Y.-D. Advances and Challenges of Deep Learning. Recent Patents Eng. 2022. [Google Scholar] [CrossRef]
  43. Zhou, J. Logistics inventory optimization method for agricultural e-commerce platforms based on a multilayer feedforward neural network. Pakistan Journal of Agricultural Sciences 2023, 60, 487–496. [Google Scholar] [CrossRef]
  44. Ben Braiek, H.; Khomh, F. Testing Feedforward Neural Networks Training Programs. ACM Trans. Softw. Eng. Methodol. 2023, 32, 1–61. [Google Scholar] [CrossRef]
  45. R, S.; Sheshappa, S.N.; Vijayakarthik, P.; Raja, S.P. Global Pattern Feedforward Neural Network Structure with Bacterial Foraging Optimization towards Medicinal Plant Leaf Identification and Classification. Int. J. Adv. Comput. Sci. Appl. 2022, 13. [Google Scholar] [CrossRef]
  46. Bidyanath, K.; Singh, S.D.; Adhikari, S. Implementation of genetic and particle swarm optimization algorithm for voltage profile improvement and loss reduction using capacitors in 132 kV Manipur transmission system. Energy Rep. 2023, 9, 738–746. [Google Scholar] [CrossRef]
  47. Karami, M.R.; Jaleh, B.; Eslamipanah, M.; Nasri, A.; Rhee, K.Y. Design and optimization of a TiO2/RGO-supported epoxy multilayer microwave absorber by the modified local best particle swarm optimization algorithm. Nanotechnol. Rev. 2023, 12. [Google Scholar] [CrossRef]
  48. S. Wang, "Magnetic resonance brain classification by a novel binary particle swarm optimization with mutation and time-varying acceleration coefficients," Biomedical Engineering-Biomedizinische Technik, vol. 61, pp. 431-441, 2016.
  49. Ghaeb, J.; Al-Naimi, I.; Alkayyali, M. Intelligent Integrated Approach for Voltage Balancing Using Particle Swarm Optimization and Predictive Models. J. Electr. Comput. Eng. 2023, 2023, 1–14. [Google Scholar] [CrossRef]
  50. Karpat, E.; Imamoglu, F. Optimization and Comparative Analysis of Quarter-Circular Slotted Microstrip Patch Antenna Using Particle Swarm and Fruit Fly Algorithms. Int. Arab. J. Inf. Technol. 2023, 20, 624–631. [Google Scholar] [CrossRef]
  51. Katipoğlu, O.M.; Yeşilyurt, S.N.; Dalkılıç, H.Y.; Akar, F. Application of empirical mode decomposition, particle swarm optimization, and support vector machine methods to predict stream flows. Environ. Monit. Assess. 2023, 195, 1–21. [Google Scholar] [CrossRef]
  52. Wang, S.-H.; Wu, X.; Zhang, Y.-D.; Tang, C.; Zhang, X. Diagnosis of COVID-19 by Wavelet Renyi Entropy and Three-Segment Biogeography-Based Optimization. Int. J. Comput. Intell. Syst. 2020, 13, 1332–1344. [Google Scholar] [CrossRef]
  53. de Sousa, I.A.; Reis, I.A.; Pagano, A.S.; Telfair, J.; Torres, H.d.C. Translation, cross-cultural adaptation and validation of the sickle cell self-efficacy scale (SCSES). Hematol. Transfus. Cell Ther. 2023, 45, 290–296. [Google Scholar] [CrossRef] [PubMed]
  54. Yu, Q.; Guo, J.; Gong, F. Construction and Validation of a Diagnostic Scoring System for Predicting Active Pulmonary Tuberculosis in Patients with Positive T-SPOT Based on Indicators Associated with Coagulation and Inflammation: A Retrospective Cross-Sectional Study. Infect. Drug Resist. 2023, ume 16, 5755–5764. [Google Scholar] [CrossRef]
  55. Ton, V. Validation of a mathematical model of ultrasonic cross-correlation flow meters based on industrial experience. Flow Meas. Instrum. 2023, 93. [Google Scholar] [CrossRef]
  56. Mahmood, Q.K.; Jalil, A.; Farooq, M.; Akbar, M.S.; Fischer, F. Development and validation of the Post-Pandemic Fear of Viral Disease scale and its relationship with general anxiety disorder: a cross-sectional survey from Pakistan. BMC Public Heal. 2023, 23, 1739. [Google Scholar] [CrossRef] [PubMed]
  57. Liyanage, V.; Tao, M.; Park, J.S.; Wang, K.N.; Azimi, S. Malignant and non-malignant oral lesions classification and diagnosis with deep neural networks. J. Dent. 2023, 137, 104657. [Google Scholar] [CrossRef] [PubMed]
  58. Ivanov, I.G.; Kumchev, Y.; Hooper, V.J. An Optimization Precise Model of Stroke Data to Improve Stroke Prediction. Algorithms 2023, 16, 417. [Google Scholar] [CrossRef]
  59. Bansal, S.; Gowda, K.; Kumar, N. Multilingual personalized hashtag recommendation for low resource Indic languages using graph-based deep neural network. Expert Syst. Appl. 2024, 236. [Google Scholar] [CrossRef]
  60. Abirami, L.; Karthikeyan, J. Digital Twin-Based Healthcare System (DTHS) for Earlier Parkinson Disease Identification and Diagnosis Using Optimized Fuzzy Based k-Nearest Neighbor Classifier Model. IEEE Access 2023, 11, 96661–96672. [Google Scholar] [CrossRef]
  61. Alkawsi, G.; Al-Amri, R.; Baashar, Y.; Ghorashi, S.; Alabdulkreem, E.; Tiong, S.K. Towards lowering computational power in IoT systems: Clustering algorithm for high-dimensional data stream using entropy window reduction. Alex. Eng. J. 2023, 70, 503–513. [Google Scholar] [CrossRef]
  62. Dejene, M.; Palanivel, H.; Senthamarai, H.; Varadharajan, V.; Prabhu, S.V.; Yeshitila, A.; Benor, S.; Shah, S. Optimisation of culture conditions for gesho (Rhamnus prinoides.L) callus differentiation using Artificial Neural Network-Genetic Algorithm (ANN-GA) Techniques. Appl. Biol. Chem. 2023, 66, 1–14. [Google Scholar] [CrossRef]
  63. Nakamura, H.; Zhang, J.; Hirose, K.; Shimoyama, K.; Ito, T.; Kanaumi, T. Generating simplified ammonia reaction model using genetic algorithm and its integration into numerical combustion simulation of 1 MW test facility. Appl. Energy Combust. Sci. 2023, 15. [Google Scholar] [CrossRef]
  64. Zhang, Y.; Wang, S.; Huo, Y.; Wu, L.; Liu, A. FEATURE EXTRACTION OF BRAIN MRI BY STATIONARY WAVELET TRANSFORM AND ITS APPLICATIONS. J. Biol. Syst. 2010, 18, 115–132. [Google Scholar] [CrossRef]
  65. Chen, Y.; Yu, Q.; Lu, Y. Pulsar Timing Array Detections of Supermassive Binary Black Holes: Implications from the Detected Common Process Signal and Beyond. Astrophys. J. 2023, 955, 132. [Google Scholar] [CrossRef]
  66. Zhou, C.R.; Wang, Z.T.; Yang, S.W.; Xie, Y.H.; Liang, P.; Cao, D.; Chen, Q. Application Progress of Chemometrics and Deep Learning Methods in Raman Spectroscopy Signal Processing. Chinese Journal of Analytical Chemistry 2023, 51, 1232–1242. [Google Scholar] [CrossRef]
  67. Kolhar, M.; Aldossary, S.M. Privacy-Preserving Convolutional Bi-LSTM Network for Robust Analysis of Encrypted Time-Series Medical Images. AI 2023, 4, 706–720. [Google Scholar] [CrossRef]
  68. Wu, D.; Li, L.; Wang, J.; Ma, P.; Wang, Z.; Wu, H. Robust zero-watermarking scheme using DT CWT and improved differential entropy for color medical images. J. King Saud Univ. - Comput. Inf. Sci. 2023, 35. [Google Scholar] [CrossRef]
  69. Zhang, Y.-D.; Wang, S.-H.; Yang, X.-J.; Dong, Z.-C.; Liu, G.; Phillips, P.; Yuan, T.-F. Pathological brain detection in MRI scanning by wavelet packet Tsallis entropy and fuzzy support vector machine. SpringerPlus 2015, 4, 1–16. [Google Scholar] [CrossRef]
  70. Shandilya, S.K.; Srivastav, A.; Yemets, K.; Datta, A.; Nagar, A.K. YOLO-based segmented dataset for drone vs. bird detection for deep and machine learning algorithms. Data Brief 2023, 50, 109355. [Google Scholar] [CrossRef]
Preprints 87304 g001
Figure 1. Sample of MS.
Figure 1. Sample of MS.
Preprints 87304 g001
Preprints 87304 g002
Figure 2. Diagram of 2-level 2D-DWT.
Figure 2. Diagram of 2-level 2D-DWT.
Preprints 87304 g002
Preprints 87304 g003
Figure 3. Diagram of an FNN.
Figure 3. Diagram of an FNN.
Preprints 87304 g003
Preprints 87304 g004
Figure 4. Diagram of K -fold cross validation.
Figure 4. Diagram of K -fold cross validation.
Preprints 87304 g004
Preprints 87304 g005
Figure 5. RoC curve of our WE-PSONN.
Figure 5. RoC curve of our WE-PSONN.
Preprints 87304 g005
Table 1. Demographic characteristics.
Table 1. Demographic characteristics.
Category NS NS Gender (m/f) Age
MS [23] 38 676 17/21 34.1 ± 10.5
HC [24] 26 681 12/14 33.5 ± 8.3
(NS: Number of Subjects, NS: Number of slices).
Table 2. Statistical Analysis (Unit: %).
Table 2. Statistical Analysis (Unit: %).
Run f 1 f 2 f 3 f 4 f 5 f 6 f 7
1 92.60 91.63 91.65 92.11 92.13 84.23 92.13
2 90.38 90.90 90.79 90.64 90.59 81.28 90.59
3 93.05 93.83 93.74 93.44 93.39 86.88 93.39
4 90.68 93.10 92.88 91.89 91.77 83.81 91.77
5 90.09 91.34 91.17 90.71 90.62 81.43 90.63
6 92.46 92.66 92.59 92.56 92.52 85.11 92.52
7 92.75 92.51 92.48 92.63 92.61 85.26 92.61
8 93.20 92.80 92.78 93.00 92.99 86.00 92.99
9 91.86 92.80 92.69 92.34 92.27 84.67 92.27
10 92.46 92.07 92.05 92.26 92.25 84.53 92.25
MSD 91.95±1.15 92.36±0.88 92.28±0.88 92.16±0.90 92.11±0.92 84.32±1.79 92.12±0.91
Table 3. PSO versus AGA.
Table 3. PSO versus AGA.
Method f 1 f 2 f 3 f 4 f 5 f 6 f 7
AGA [20] 91.91±1.24 91.98±1.36 91.97±1.32 91.95±1.19 91.92±1.20 83.89±2.41 91.92±1.19
PSO (Ours) 91.95±1.15 92.36±0.88 92.28±0.88 92.16±0.90 92.11±0.92 84.32±1.79 92.12±0.91
Table 4. Method Comparison.
Table 4. Method Comparison.
Method f 1 f 2 f 3 f 4 f 5 f 6 f 7
LR [19] 89.63±1.75 90.48±1.45 90.34±1.43 90.06±1.44 89.98±1.47 80.13±2.87 89.98±1.47
DMGPS [21] 88.99±1.20 88.56±1.13 88.54±1.05 88.78±0.95 88.76±0.96 77.56±1.91 88.77±0.96
HMI [22] 91.67±1.41 91.73±0.77 91.70±0.78 91.70±0.97 91.67±1.00 83.40±1.98 91.67±0.99
WE-PSONN (Ours) 91.95±1.15 92.36±0.88 92.28±0.88 92.16±0.90 92.11±0.92 84.32±1.79 92.12±0.91
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated