Preprint

Article

Practical and Rapid Motor Sizing Technigue using Existing Electrical Motor

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Ju Lee^*

Ju Lee^*

This version is not peer-reviewed

Submitted:

10 October 2023

Posted:

11 October 2023

You are already at the latest version

Alerts

Abstract

The electrical motor design requires a lot of work and resources. In the field, motor designers need to decide on competitive motor sizing quickly to compete with other motor suppliers. Generally, it requires expensive FEM S/W to get accurate motor sizing results, but buying and maintaining many licenses is costly. Moreover, it needs some patience to get the result from FEM analysis. In this paper, the motor sizing technique using an existing production motor is presented to respond to urgent requests from customers without using FEM analysis. In order to enhance the fidelity of the result, magnetic flux loss by magnet coating and non-linear characteristics are considered during the motor sizing process. The proposed sizing method was verified by comparison to the FEM analysis and test result and showed reasonable confidence in them. Also, this method has the substantial advantage of outputting accurate results instantly without taking any time. It helps with the modification design of electrical motors without using expensive FEM S/W and a certain level of skill or experience.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Permanent magnet synchronous motors have been used in various applications for centuries for their many advantages, such as high efficiency, high torque-to-current, torque-to-volume ratios, compact structure, and fast dynamic response. [1,2,3,4,5,6,7,8,9,10,11]

In particular, due to the global movement to reduce greenhouse gases, electrification is rapidly occurring in the automotive area. As a result, the adoption of electric motors to replace internal combustion engines and hydraulics, which are existing power sources, is increasing. Additionally, high-output and compact-size electric motors are required to improve vehicle efficiency. [2,7,10,12]

Moreover, like Moore’s Law, computer performance has improved dramatically, and as a result, the calculation speed of FEM S/W required for electric motor design and analysis has also improved dramatically. Therefore, multiple design models can be calculated more quickly, and various system phenomena can be solved using software such as finite element analysis tools.[13] However, many commercial tools are expensive to purchase and maintain, making owning and maintaining many licenses burdensome unless the company or research institute is well-funded. Therefore, in most cases, it is difficult for many motor design engineers to use commercial software simultaneously with limited licenses, so a way to operate it efficiently is needed.

In the field, motor design engineers are frequently asked by their customers to design and quote electric motors that meet desired performance within a short period of time. In the case of the expert with enough experience or lots of evaluated data and design references, there may be no risk in responding to this. However, it would be such challenging work under time constraints in most cases. In addition, price competition among motor manufacturers is intensifying due to an extension of electric motor adoption to many applications. Furthermore, the market price needs to lower gradually, making it more difficult to profit. In this case, most motor manufacturers can convert existing electric motors into a platform to increase production and lower manufacturing costs. This method can significantly reduce new investments by manufacturing key components, such as the rotor and stator core, using the same tooling used to produce conventional products, changing the stack lengths and windings differently to meet the required performance. Additionally, the development period can be shortened, minimizing the resources required for development.

Nevertheless, as mentioned earlier, it is often impossible to use expensive motor design analysis S/W promptly to respond to the tight time given by customers for electric motor design.

Therefore, an effective motor sizing method that can be used in the field is proposed to solve this problem in this paper. To this end, a standard model to be used as a platform design was selected first, and evaluation and analysis data by FEM for this motor were collected as the reference data.

Then, the relationship between coil diameter, number of turns, and lamination length, which are design variables used when determining motor size, was derived for the fundamental parameters of the motor, such as resistance, inductance, and Ke.

In order to increase the accuracy of calculations, torque under load, torque ripple, and demagnetization characteristics of permanent magnets, which are nonlinear characteristics that change with the increase in Ampere-Turn condition, were databased within the sizing process template by performing FEM analysis on the standard model. This process only needs to be performed once for the standard model, and there is no need to analyze it using expensive FEM S/W every time motor sizing is needed in the future. In this way, using the results in the database of the preformed template and the relationship between the three design variables (coil diameter, number of turns, and stacking length) and the motor performance, the characteristics of the motor can be quickly calculated, and specifications that meet the requirements can be found in seconds effectively.

In summary, the sizing method proposed in this paper has the substantial advantage of designing an electric motor that meets the requirements quickly, regardless of the designer’s experience and skill level, without using expensive S/W.

The motor sizing technique presented in this paper was verified by comparing it with the FEM calculation results first. Then, prototype samples were built and tested to verify the method’s effectiveness.

2. Detail of Analysis Model

The basic model to be used in this paper is a permanent magnet synchronous motor (PMSM) designed for automotive electric power steering systems and its configuration is shown in Figure 1. Since the steering system requires an electric motor with low cogging and ripple torque[2,6,7,8,9,14], the surface permanent magnet synchronous motor(SPMSM) with a skew in the stator or rotor is mainly used, and this model has a 3-step skewed rotor. The main parameters for the basic model used in the sizing calculation in this paper are shown in Table 1, and these are the results of verifying consistency through comparison of test and analysis values.

3. Sizing Theories and Procedure

3.1. Magnet Flux Loss

There are several magnet materials to be used in the electrical motor. Among them, the NdFeB sintered magnet is suitable for design for high power density and compact size motors due to their excellent magnetic characteristics and is used in various applications. In addition, this magnet requires a coating treatment on the surface to prevent magnetic performance degradation due to damage such as cracks and corrosion, and there are coating options of various materials and thicknesses, as shown in Table 2

According to the research in [15], there is a difference in the magnetic performance of permanent magnets depending on the presence or absence of coating, as shown in Figure 2. Because the proportion of the raw materials of the magnet itself decreases depending on the coating thickness in the overall size of the magnet as described in Figure 3. And it would be expected that the thicker the coating, the greater the magnetic loss of the magnet. Additionally, it can be expected that the smaller the size of the magnet and the shorter the axial length, the greater the effect of magnetic flux loss. In the case of motors with high output power, such as vehicle traction motors, the coating thickness ratio to the magnet’s size is tiny, so that this effect can be ignored. However, in the case of an electric power steering (EPS) motor in vehicles that requires an output of around or less than 1kw, the magnetic flux loss component due to the thickness of the magnet coating can act as the root cause of errors between the design value and the actual measurement.

Therefore, it needs to consider the loss component of magnetic flux by the coating thickness of the magnet at motor design, especially small power electrical motor. In this paper, a method of considering the magnetic flux loss was applied by comparing the volume of the magnet raw material to the total volume of the selected magnet as shown in Equation (1) in order to reduce the error between the motor sizing results and the actual test value.

L_{p} = 1 - \frac{V_{r}}{V_{o}}

(1)

In the equation, Lp is the magnet flux loss, Vr is the raw material volume of the magnet, and Vo is the overall magnet volume, including coating.

Since the two-dimensional shape and dimensions of the standard model have already been designed, the two-dimensional area of the magnet is determined. When calculating the motor sizing, once the coating material and thickness are determined, the area of the magnet raw material is calculated. And assuming the axial length, the magnetic flux loss for the magnet of the desired length can be calculated using Equation (1)

Figure 4 is the result of calculating the magnetic loss of the magnet for each coating according to the stack length using the standard model using Equation (1).

According to these results, it can be seen that the magnetic loss tends to increase as the lamination length becomes short and the coating thickness becomes thick, and this was reflected in this sizing process to reduce errors with test results.

3.2. Back-EMF Constant(Ke)

The Back electromotive force(Bak-EMF) is an essential indicator in understanding an electric motor’s performance. It is calculated as the induced voltage generated per unit speed as shown in Equation (2) and is determined by many design parameters as shown in Equation (3).

E = K_{e} ω

(2)

In the equation, E is the back-EMF voltage, Ke is the back-emf constant, and

ω

is the angular velocity.

K_{e} = \frac{P Z Φ}{2 π a} = \frac{P Z B L_{s t k}}{2 π a}

(3)

In the Equation, P is pole number, Z is total series turns,

Φ

is total magnetic flux per pole, B is magnetic flux density, Lstk is active stack length, a is parallel number of conductors.

According to the above Equation (3), the back electromotive force is proportional to the number of turns and stack length, which are variables to be used when motor sizing. Therefore, it can be calculated easily using Equation (4) from the design variables an

K_{e 2} = K_{e 1} \frac{Z_{2}}{Z_{1}} \frac{L_{s t k 2}}{L_{s t k 1}} \frac{L_{p 1}}{L_{p 2}}

(4)

where

K_{e 1}

K_{e}

of base model with

Z_{1}

turns and

L_{s t k 1}

stack length,

L_{p 1}

is the magnetic flux loss of base model,

K_{e 2}

K_{e}

of modification model to be design with

Z_{2}

turns and

L_{s t k 2}

stack length at

L_{p 2}

of magnetic flux loss.

The calculation result for the

K_{e}

by combining the stack length and the number of turns using Equation (4) is shown in Figure 5. This sizing study considered the stack from 10mm to 90mm and winding from 10 to 40 turn cases.

3.3. Motor Inductance

The motor inductance is a parameter affected by many design variables, such as the intensity of magnetic flux, number of turns, and length of stacking, as shown in Equation (5).

L = \frac{λ}{i} = \frac{N^{2}}{R} = \frac{N Φ}{i} = \frac{N B l_{s t k}}{i}

(5)

where L is motor inductance,

λ

is total magnetic flux linkage, i is current, N is total series turns,

Φ

is magnetic flux in coil, R is magnetic reluctance, B is magnetic flux density, and lstk is stack length.

As the ampere turn condition increases, the inductance may differ from the result obtained by the above Equation (5) due to magnetic saturation in the magnetic circuit, and as magnetic saturation becomes more severe, the the difference becomes large. However, for an efficient and rapid calculation method in this paper, the design was assumed under ampere-turn conditions where magnetic saturation does not occur, and the inductance was calculated using the Equation of the linear relationship. In this way, the inductance for all combinations of turns and stacked length can be calculated as shown in Figure 6, the same as Ke calculated previously.

3.4. Current Density

The current density of a motor is related to the coil’s durability and the motor’s temperature characteristics. The lower the current density, the better the motor characteristics, but the size increases, so selecting an appropriate current density level is necessary.

Most electric power steering motors have a completely sealed structure, and due to the behavior of instantaneous operation, they use a cooling method by natural convection without an additional cooling device. Therefore, selecting a current density level in the range of 15 to 25 Arms/mm2 at the maximum current condition is generally appropriate.

The coil diameter of the motor to be designed can be determined using the input current and number of parallel circuits as shown in Equation (6) and Equation (7) below.

J_{c} = \frac{\frac{I_{a}}{a}}{\frac{π {D_{c}}^{2}}{4}} = \frac{4 I_{a}}{π a {D_{c}}^{2}}

(6)

D_{c} = \sqrt{\frac{4 I_{a}}{J_{c} π a}}

(7)

Figure 7 below shows the current density calculation result according to the coil diameter with two parallel circuits at 100A input current condition.

3.5. Winding Capability Study

Since the 2-D shape of the basic model has already been defined, it is possible to predict the maximum number of turns that can be wound using the actual drawing, as shown in Figure 8. It is advisable to consider the outer coil diameter, including the insulation coating layers and slot insulator component in slots, to minimize differences from the actual product, as shown in the Figure.

In this way, it is possible to create a winding capability database of the base model for a wide range of coil diameters, as shown in Figure 9.

3.6. Resistance

The general formula for electrical resistance is as follows.

R = ρ_{c} \frac{l_{c}}{A_{c}}

(8)

where R is motor resistance,

ρ_{c}

is the resistivity of the coil,

l_{c}

is the total length of the coil and

A_{c}

is the cross-section area of the coil.

The length of the conductor can be calculated by Equation (9) to Equation (15) using the parameters defined in Figure 10.

R_{c} = \frac{D_{c}}{2} = \frac{D_{s o} - D_{s i}}{2} + D_{s i}

(9)

In the equation,

R_{c}

and

D_{c}

are the radius and diameter center dimension of the coil wound on the stator,

D_{s o}

and

D_{s i}

are the outer and inner diameter of the stator core as defined in Figure 10.

All the parameters defined in the figure can be calculated as follows.

θ_{1} = \frac{360}{Q}

(10)

where, Q is the number of stator slot and

θ_{1}

is the one slot angle.

θ_{2} = arcsin (\frac{W_{s t}}{2 R_{c}})

(11)

where,

W_{s t}

is the teeth widht of stator core and

θ_{2}

is half slot coil pitch angle.

θ_{3} = \frac{θ_{1}}{2} - θ_{2}

(12)

θ_{4} = θ_{2} + \frac{θ_{3}}{2}

(13)

τ_{s} = 2 R_{c} sin θ_{4}

(14)

where,

τ_{s}

is one coil pitch.

In addition,

L_{e x t}

defined in Figure 10 is a length depending on the thickness of the slot insulator used for slot insulation. Assuming that the coil at the end turn area is formed in a semicircle as large as the coil pitch dimension, the coil length per turn

l_{c 1}

and resistance per turn

R_{c 1}

are as follows.

l_{c 1} = 2 (L_{s t} + \frac{π τ_{s}}{2} + L_{e x t})

(15)

R_{c 1} = ρ_{c} \frac{l_{c 1}}{A_{c}}

(16)

And using the given number of turns

N_{p h}

and parallel circuits a, the phase resistance can be calculated as shown in Equation (17). Also, using copper’s resistance temperature coefficient

α_{c}

, the resistance value at a specific temperature condition(t degrees) changes can be calculated using Equation (18).

R_{p h} = R_{c 1} \frac{N_{p h}}{a}

(17)

R_{p h} (t) = R_{p h} (1 + α_{c} (t - R T))

(18)

In the equation,

α_{c}

is the temperature coefficient of copper as 3.93 x 10

^{- 8}

Ω

In this sizing technique, only the coil diameter, number of turns, and lamination length are design variables, and by using Equation (15) to Equation (18), resistance values for all cases by different condition can be calculated.

3.7. Torque Constant Saturation, Torque Ripple and Demagnetization

The torque constant Kt is the torque per unit current and, like the back electromotive force constant

K_{e}

, is a parameter that represents the unique characteristics of the electric motor. This Kt decreases due to the magnetic saturation effect of the magnetic circuit in the motor as the current increases. Because of this magnetic saturation phenomenon, the term Kt saturation is used to refer to the change in

K_{T}

In a sinusoidal drive three-phase motor, the back-EMF constant(

K_{E}

) and torque constant(

K_{T}

) has the following specific relationship.

K_{T} = \frac{\sqrt{3}}{2} K_{E}

(19)

The relationship in Equation (19) shows the ideal condition established with no effect from magnetic saturation or temperature. From this relationship, the ratio of the Kt value between at no load and at a specific load current condition can be defined as in Equation (20) below.

K_{s} = 1 - \frac{K_{T 1}}{K_{T 0}}

(20)

Where

K_{s}

is the saturation ratio of torque constant comparing between a torque constant

K_{T 1}

at a specific current condition and the torque constant

K_{T 0}

without current condition defined from Equation (19).

When the saturation of the torque constant increases, the torque value generated from the motor decreases compared to the basic model, and torque ripple tends to increase.

These non-linear characteristics must be calculated in advance for each ampere turn condition using the basic model through FEM analysis S/W that allows precise calculation. In this way, when an urgent sizing request is made by a customer at any time, the results of non-linear characteristics for all ampere-turn that has been reviewed in advance can be used as a lookup table to increase prediction precision and enable rapid response without performing FEM S/W analysis.

Also, the demagnetization of PMSM is another characteristic showing a nonlinear trend due to the demagnetization curve having a knee point at a particular coercivity condition.

In this paper, the nonlinear analysis was performed from 50 to 5000 ampere-turn, and non-linearity data on Kt, torque ripple, and demagnetization were secured in advance to build a database as shown in Figure 11 and Figure 12.

3.8. Torque-Speed Performance

The design of an electric motor is to find parameters such as magnetic flux, inductance, and resistance that satisfy the voltage equation and torque equation expressed in Equation (21) and Equation (22)[3,17].

T = P_{n} \{Φ_{a} i_{a} + (L_{d} - L_{q}) i_{d} i_{q}\}

(21)

{(L_{d} i_{d} + Φ_{a})}^{2} + {(L_{q} i_{q})}^{2} = {(\frac{V_{o m}}{ω})}^{2}

(22)

In the equation, T is torque,

P_{n}

is the pole pair number of the magnet,

Φ_{a}

is magnetic flux linkage,

L_{d}

and

L_{q}

are the d- and q-axis inductance,

i_{d}

and

i_{q}

are d- and q-axis current,

V_{o m}

is voltage and

ω

is angular velocity.

The torque-speed characteristic is one of the final performances determined by the fundamental parameters such as resistance, inductance and magnetic flux linkage of an electric motor, and there can be countless combinations of these parameters to satisfy the performance. Among these results, the optimal decision as an electric motor designer is to select the smallest size electric motor in consideration of price.

Using the three parameters of back-EMF constant(Ke), resistance and inductance, which are the fundamental parameters of the motor described previously, the required torque and speed characteristics can be calculated within the given constraints such as input voltage and current limits.

The magnetic flux linkage

Φ_{a}

cab be obtained using Equation (23) and Equation (24).

E_{0} = \frac{K_{e 2}}{ω}

(23)

Φ_{a} = \frac{E_{0}}{ω_{e m}}

(24)

Where

E_{0}

is the back-EMF without load current,

K_{e 2}

is the calculated value from Equation (4),

ω

is mechanical rotation velocity. It has a relationship as 1/pole pair with electrical rotation velocity

ω_{e m}

3.9. Sizing Procedure

The procedure for the sizing technique proposed in this paper is shown in Figure 13. First, it is necessary to define the target values for the performance parameters such as

K_{e}

, resistance, inductance, etc, of the electric motor to be designed. Then, determine the magnet coating specifications to be applied to the motor, calculate the magnetic flux loss components of the magnets as described in section 3.1, and calculate the Ke matrix and inductance matrix for stack length and series turns based on the reference model as explained in section 3.2 to section 3.3. Afterwards, the stack length for each turn that satisfies the requirements is selected from the calculated

K_{e}

and inductance results.

The current density of the coil is calculated using the given current value, and a coil diameter with a current density that meets the requirements is selected as described in section 3.4. And the maximum number of turns is determined by the winding capability database of the base model, as explained in section 3.5.

The next step is to calculate resistance values based on section 3.6 for combinations of coil diameter, number of turns, and stack length that satisfy Ke, inductance, and current density. These combinations are checked using the database to see if nonlinear characteristics such as torque ripple and demagnetization are satisfied, as explained in section 3.7. The Torque-Speed(T-N) characteristic calculation is performed using the determined parameters if all conditions are satisfied. Otherwise, it needs to adjust the requirements as described in section 3.8.

The results can be checked at a glance as soon as the requirements are input because all of these processes do not require a separate nonlinear calculation process using FEM S/W or any additional calculation.

4. Verification

The proposed sizing method in this paper was verified by comparing with FEM analysis and test results using actual samples in this section.

4.1. Study Case1

The requirements for the first study case are summarized in Table 3 and Figure 14. The given condition for the sizing performance is at 6.6VrmsLL, 109Arms, and 23DegC.

The sizing result by the suggested motor sizing technique according to the sizing process described in Figure 13 is summarized in Table 4 and Figure 16. This result was compared to the FEM analysis shown in Figure 15 and the sample test. As a comparison, the proposed sizing method shows a reasonable deviation from the FEM analysis and actual test result, as marked with parentheses in the Table instantly. The values in the parentheses mean the differences compared to the value by sizing result.

4.2. Study Case2

Table 5 and Figure 17 summarize the requirements for the second study case. The given condition for the sizing performance is at 6.0VrmsLL, 113Arms, and 23DegC.

The sizing result for the second study case has similar to the FEM analysis and actual test result except for torque ripple and demagnetization ratio as shown in Table 6 and Figure 18. It looks like considerable deviations compared with the percentage unit for the demag. ratio and torque ripple comparison, but it is not a big difference compared with the absolute values.

As the verification result by two kinds of motor specification, the proposed sizing technique shows good fidelity to the FEM analysis and test result even though it does not need long calculation time, unlike expensive FEM S/W.

5. Conclusion

This paper proposes a practical and rapid sizing method for existing platform motors that could reduce production costs using key components such as rotor core, stator core, Etc. The motor parameters to be designed are calculated using the equations and based on the parameters of the base model. The magnetic flux loss by magnet coating is considered to increase the result’s accuracy. And the nonlinear characteristics, such as torque ripple and demagnetization, were reflected by setting up the database through accurate FEM results in advance to enhance the fidelity of the result. This nonlinear calculation by FEM requires only once when setting up the database for the base model. As the verification for this method using 2 study cases specification, the proposed sizing results show good confidence comparison to FEM and test result.

This method will be helpful to modify the design based on the production design within a short time, regardless of the skill level and experiences of the motor designer, without using the expensive FEM S/W.

For future works, it needs to be studied further to improve the calculation accuracy for the non-linear parameters such as torque ripple, demagnetization, and inductance, which could be affected easily by magnetic saturation.

Author Contributions

Conceptualization, Y.K. and J.H.; methodology, Y.K. and J.H..; software, Y.K.; validation, Y.K.; formal analysis, Y.K. and J.H.; investigation, Y.K. and J.H.; resources, X.X.; data curation, Y.K.; writing—original draft preparation, Y.K.; writing—review and editing, Y.K.; visualization, Y.K.; supervision, J.L.; project administration, J.L., All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

Hendershot, J.R.; Miller, T.J.E. Design of Permanent Magnet Brushless Machines, 2nd ed.; Motor Design Books LLC, 2010. [Google Scholar]
Islam, R.; Husain, I.; Fardoun, A.; McLaughlin, K. Permanent Magnet Synchronous Motor Magnet Designs with Skewing for Torque Ripple and Cogging Torque Reduction. IEEE Transaction 2007, 7, 1552–1559. [Google Scholar] [CrossRef]
Lipo, T.A. Introduction to AC Machine Design; IEEE Press Wiley, 2017. [Google Scholar]
Gieras, J.F. Permanent Magnet Motor Technology, 3rd ed.; CRC Press, 2010. [Google Scholar]
Hamdi, E.S. Design of Small Electrial Machines; Wiley, 1994. [Google Scholar]
Fei, W.; Zhu, Z.Q. Comparison of Cogging Torque Reduction in Permanent Magnet Brushless Machines by Conventional and Herringbone Skewing Techniques. IEEE Transaction on Energy Conversion 2013, 28, 664–674. [Google Scholar] [CrossRef]
Islam, M.S.; Mir, S.; Sebastian, T. Issues in Reduction the Cogging Torque of Mass-Produced Permanent-Magnet Brushless DC Motor. IEEE Transaction on Industry Application 2004, 40, 813–820. [Google Scholar] [CrossRef]
Hanselman, D.C. Effect pf skew, pole count and slot count on brushless motor radial force, cogging torque and back emf. IEE Proc.-Electr. Power Appl. 1997, 144, 325–330. [Google Scholar] [CrossRef]
Wang, X.; Yang, Y.; Fu, D. Study of cogging torque in surface-mounted permanent magnet motors with energy method. Journal of Magnetism and Magnetic Materials 2003, 267, 80–85. [Google Scholar] [CrossRef]
Bianchi, N.; Blolgnani, S. Design techniques for reducing cogging torque in surface-mounted PM motors. IEEE Trans. Ind. Appl. 2002, 38, 1259–1265. [Google Scholar] [CrossRef]
Hwang, S.M.; Eom, J.B.; et al. Various design techniques to reduce cogging torque by controlling energy variation in permanent magnet motors. IEEE Trans. on Magn. 2001, 37, 2806–2809. [Google Scholar] [CrossRef]
Colin McKerracher, Electric Vehicle Outlook 2023, September 2017, BloombergNEF. 20 September 2023; 17.
Jung, T.C. A study on IPMSM basic design using per-unit design methods and construction of non-linear data set. Ph.D, Hanyang University, Korea, 2016. [Google Scholar]
Harrer, M.; Pfeffer, P. Steering Handbook; Springer, 2016. [Google Scholar] [CrossRef]
Liu, Y. Discussion on several principal problems aroused from measuring high performance permanent magnetic materials. International Journal of Applied Electromagnetics and Mechanics 2017, 55, 1–27. [Google Scholar] [CrossRef]
Ju.Lee, K.C. Kim, J.S.Ahn, S.H.Won, Design and Control of IPMSM, Intervision, Korea, 2007, pp.10-35.
Shigeo Morimoto, Design, Analysis, and Control of Interior PM Synchronous Machines, October 3rd, 2004. IEEE Industry Applications Society Annual Meeting Seattle. Chapter8. p.8.1-p.8.8. 3 October.

Figure 1. Design Base Model

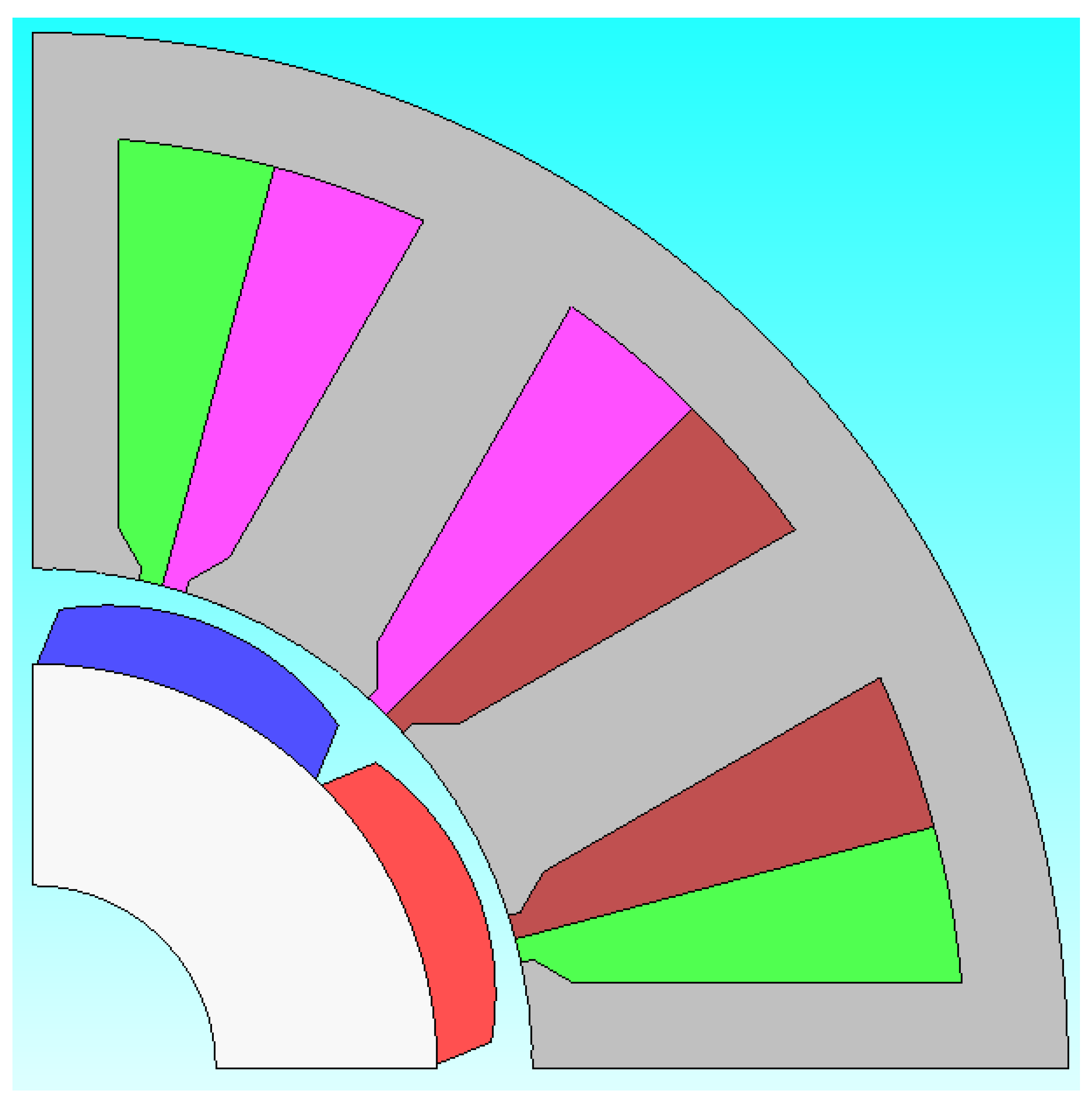
Figure 2. Magnet B-H Curve Comparison between with and without Coating on Surface

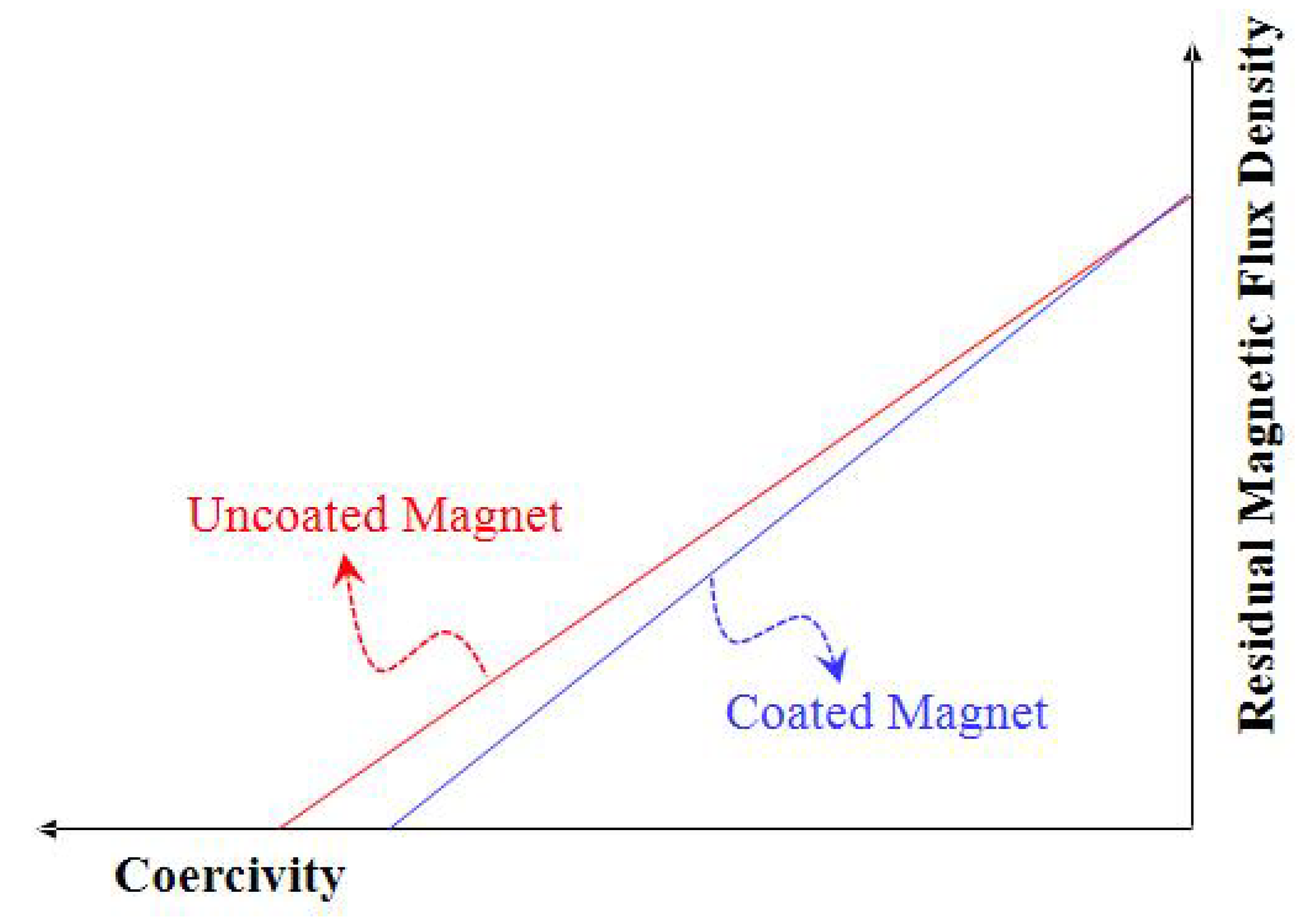
Figure 3. Cross-Section of Magnet including Coating

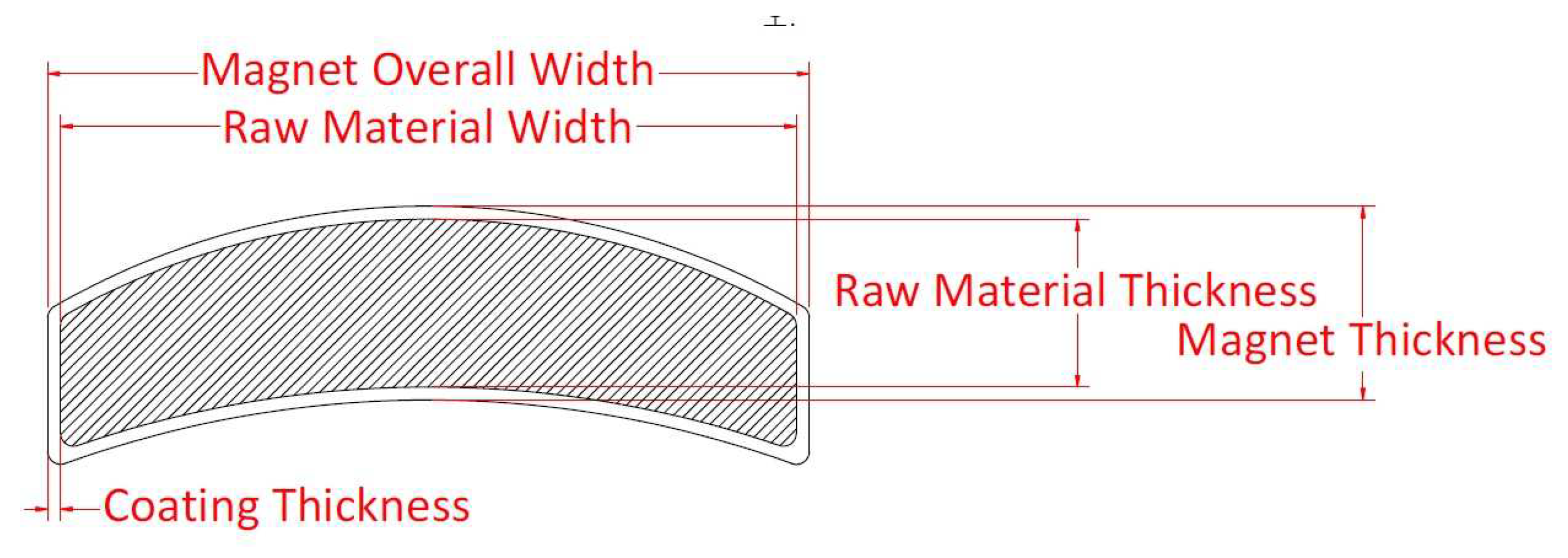
Figure 4. Magnet Flux Loss Calculation Result by Coating and Stack Length

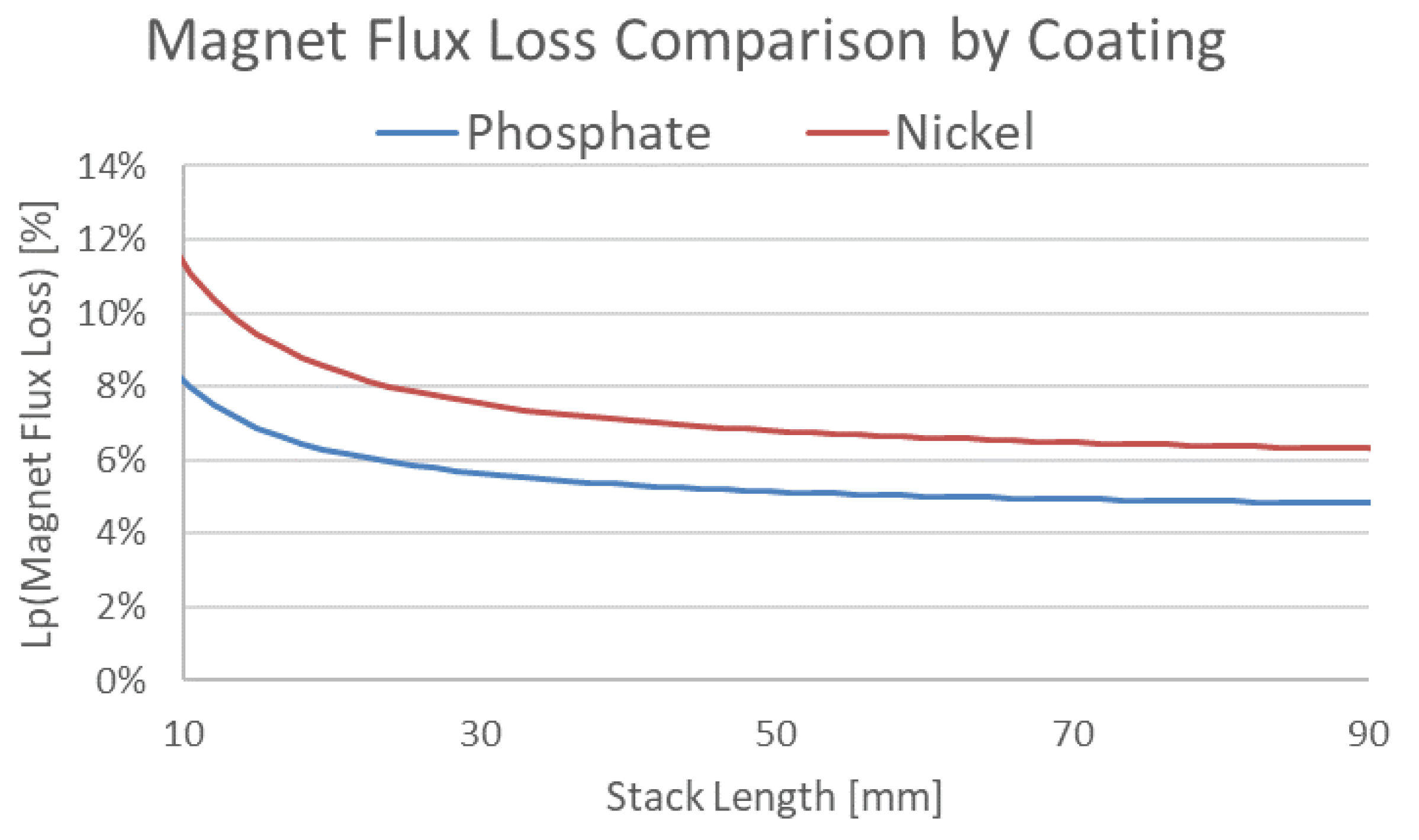
Figure 5. Back-EMF Constant(Ke) Matrix Calculated by Turns and Stack Length Combination

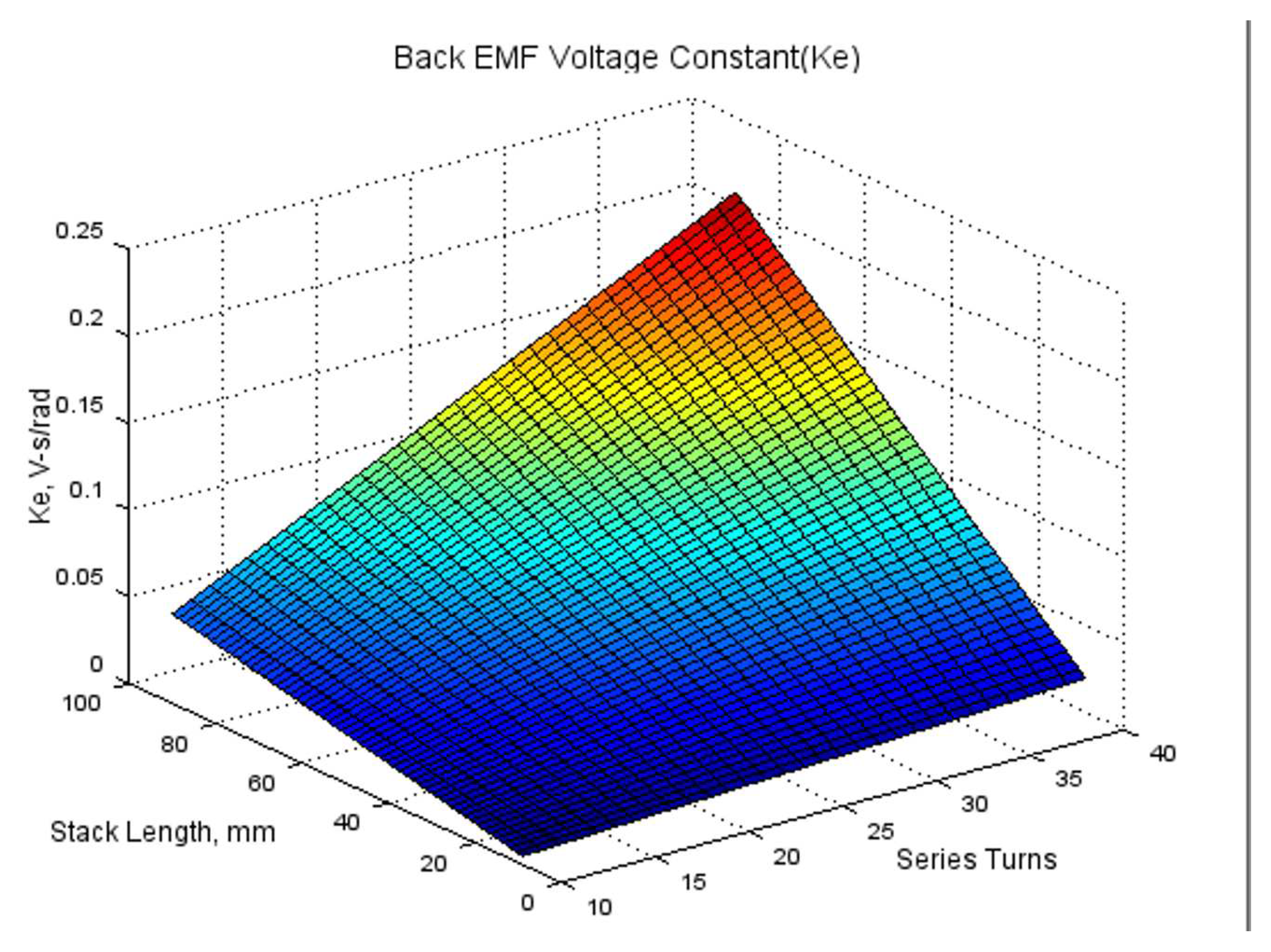
Figure 6. Inductance Matrix Calculated by Turns and Stack Length Combination

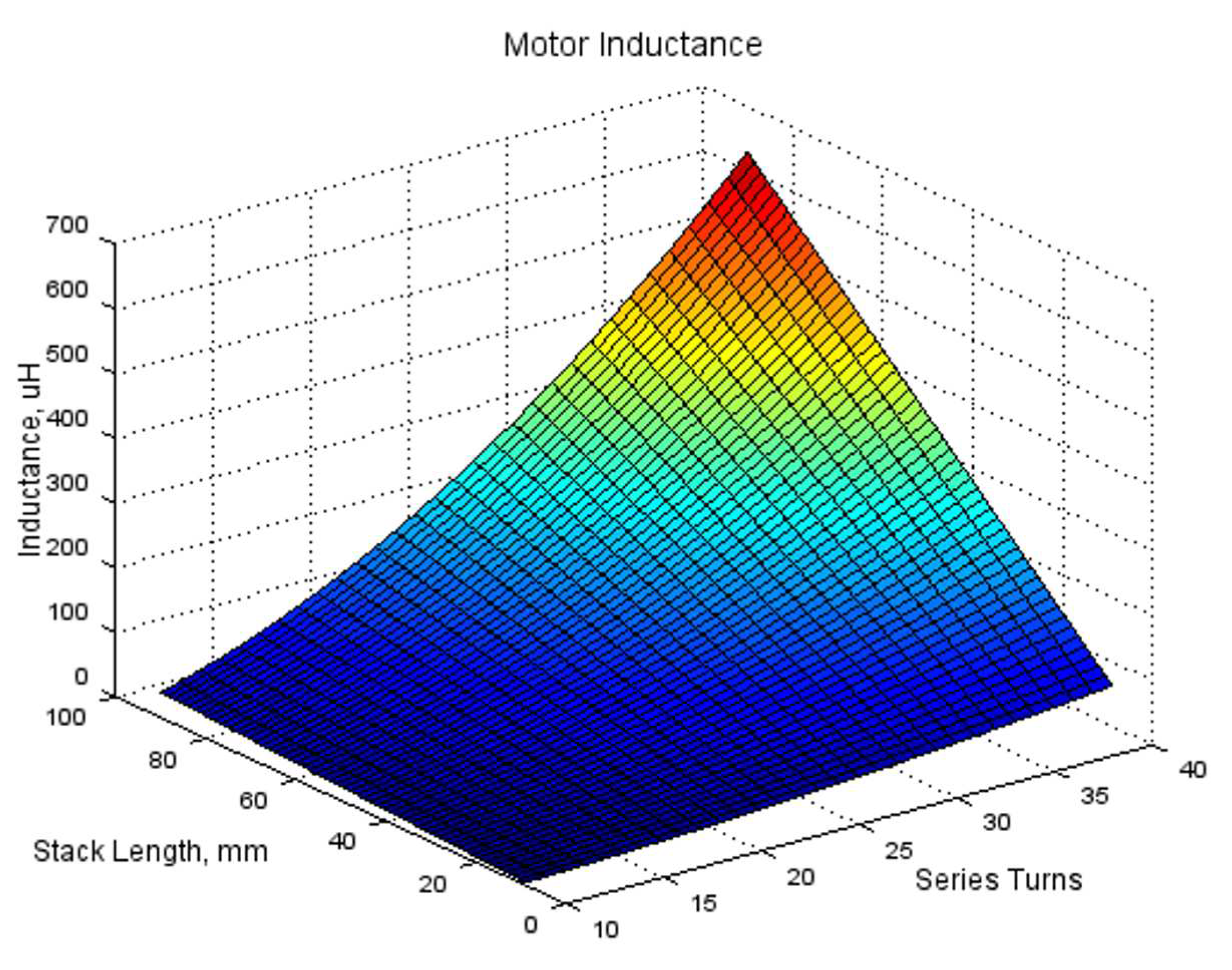
Figure 7. Example of the Current Density Calculation by Coil Diameter

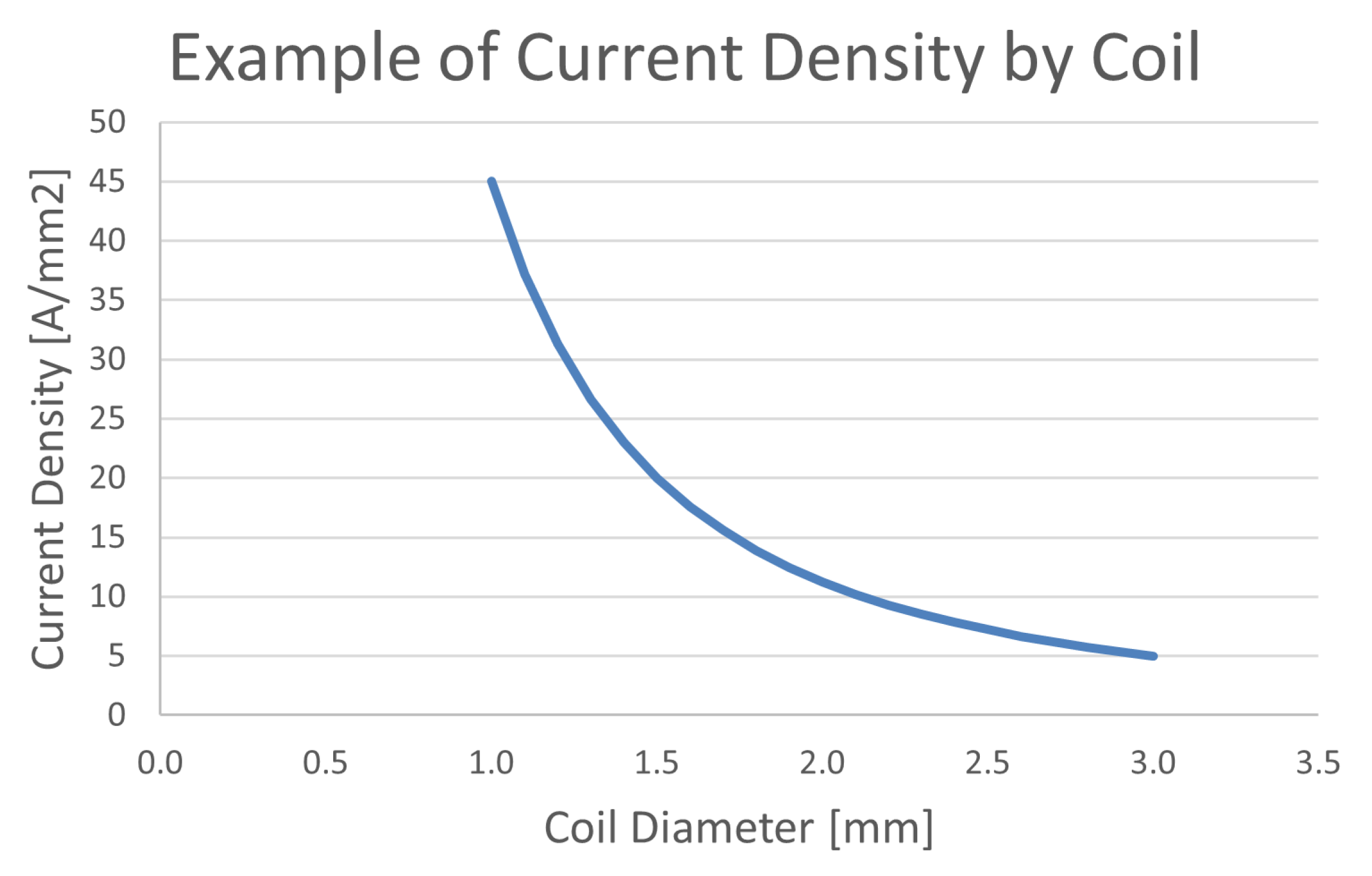
Figure 8. Example of the Winding Capability Study using Drawing

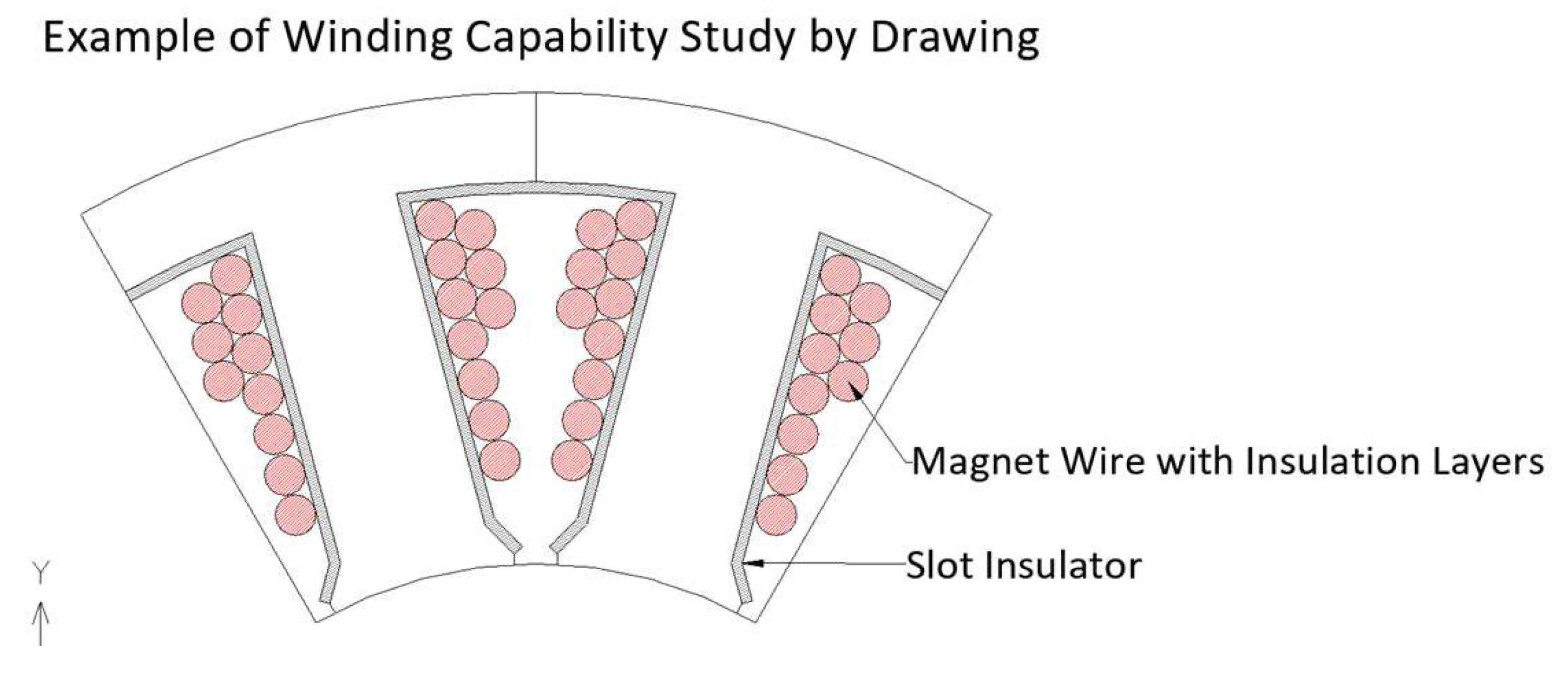
Figure 9. Winding Capability Result : Max Winding Turn by Coil Diameter

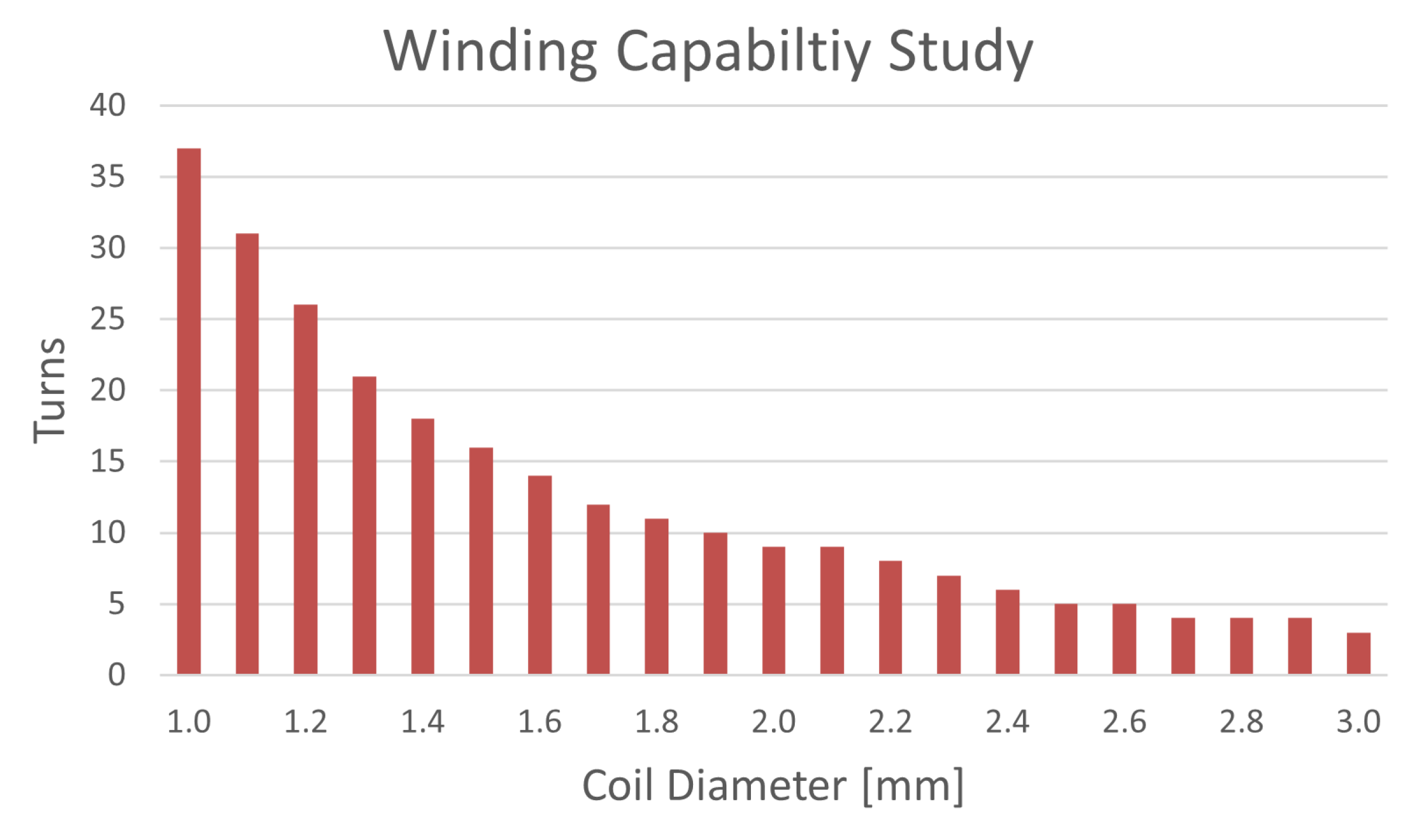
Figure 10. Parameters for calculating winding resistance

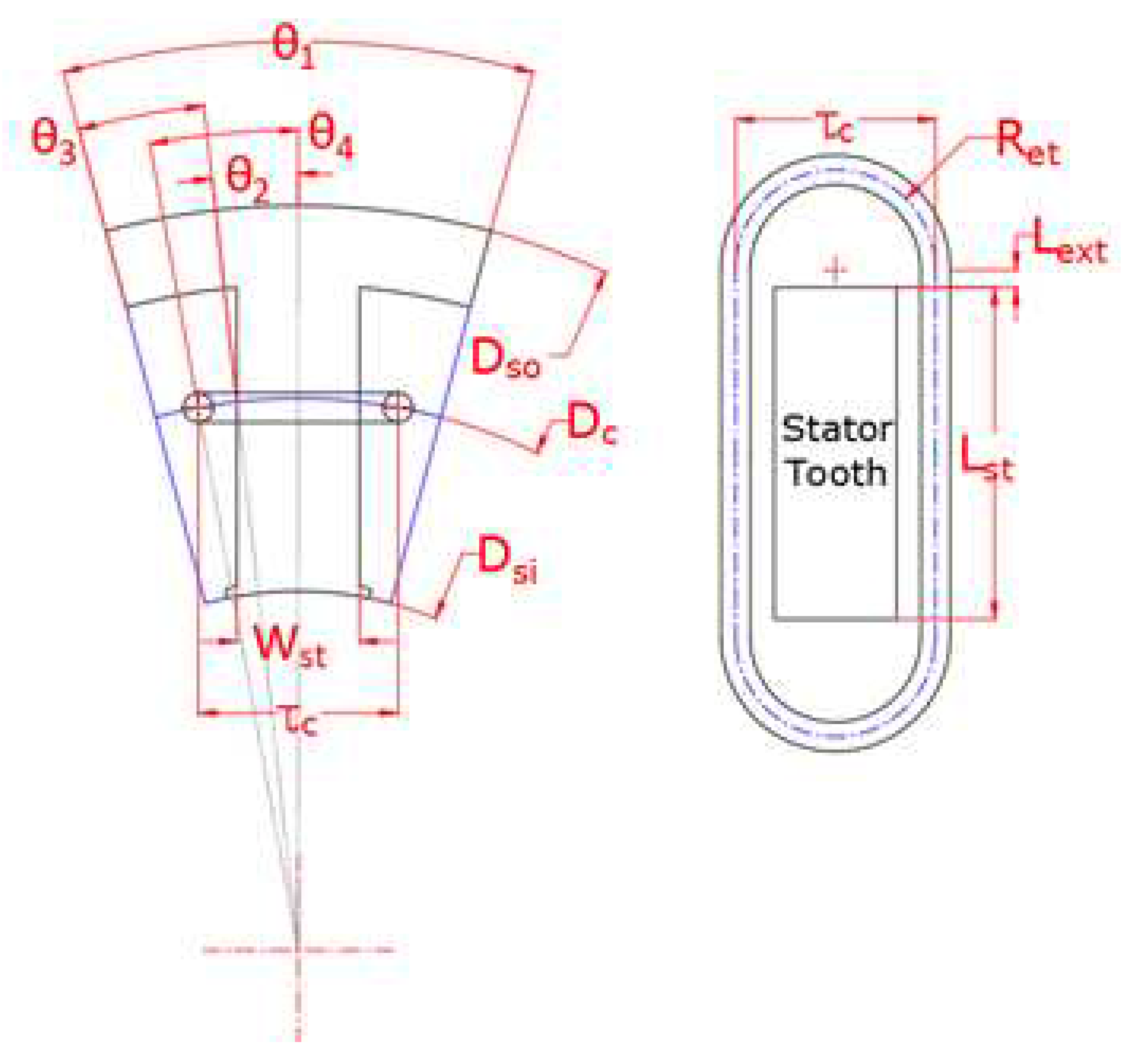
Figure 11. Kt and Torque Ripple by Ampere-Turns

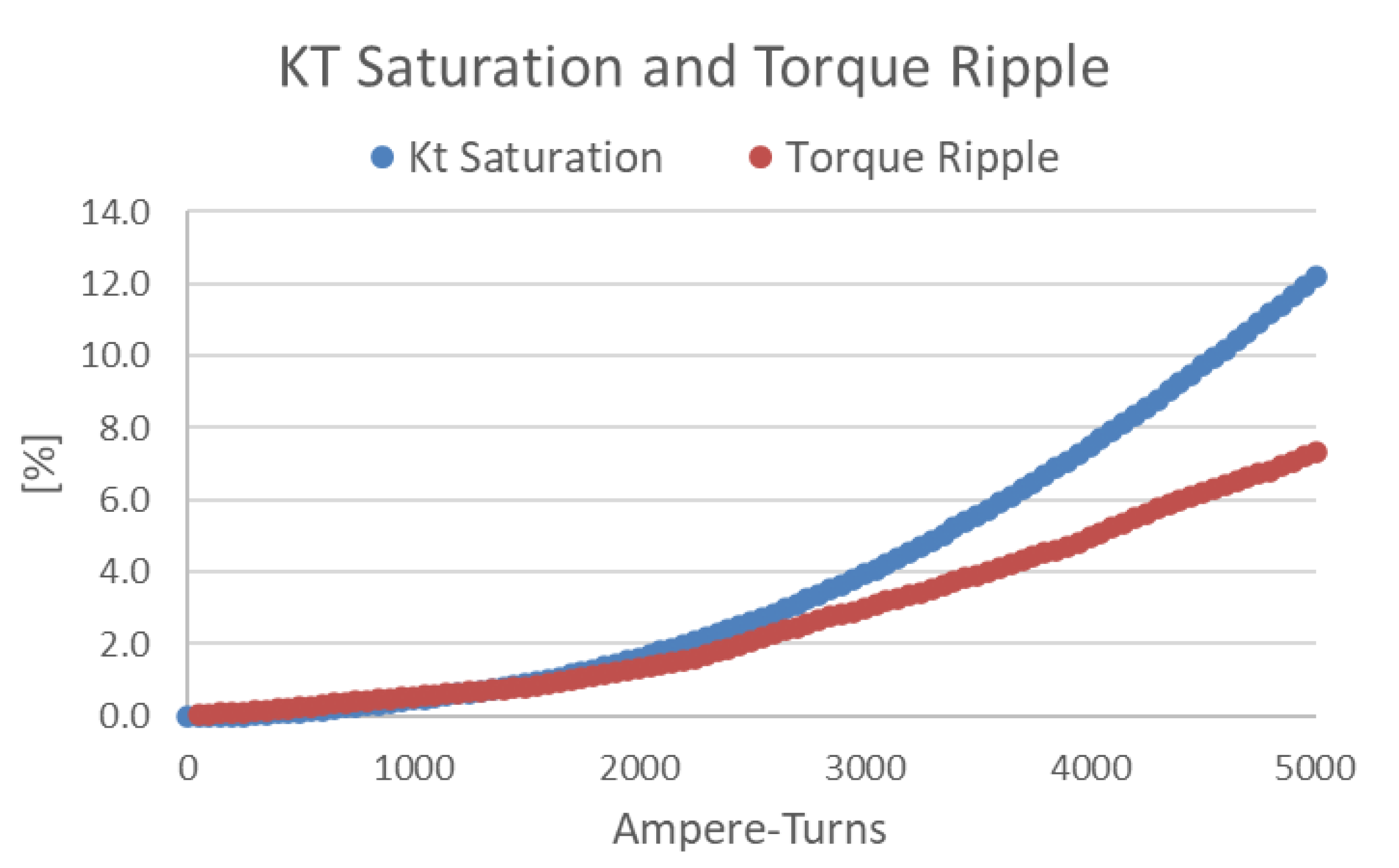
Figure 12. Demagnetization by Ampere-Turns and Temperature

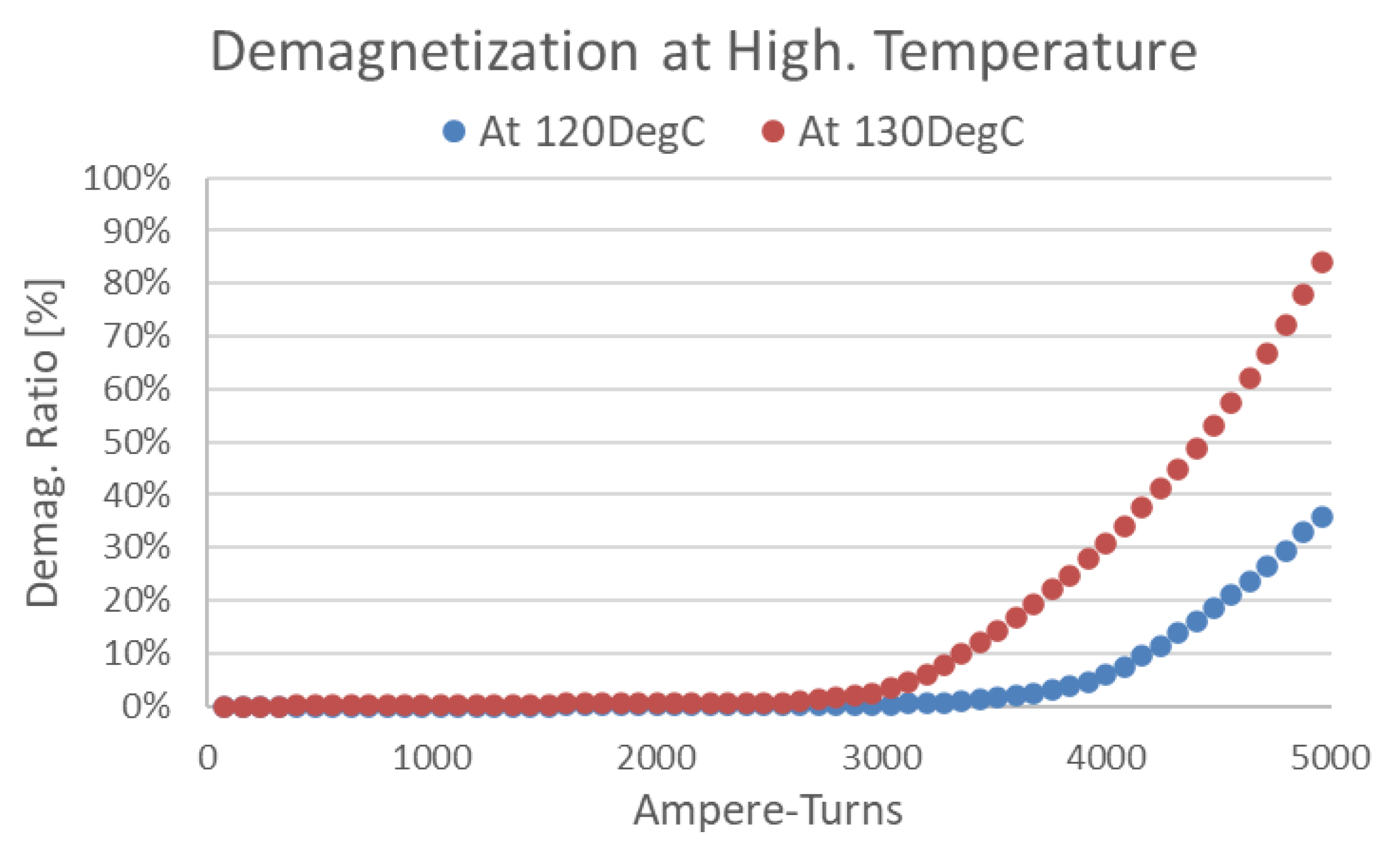
Figure 13. Process Flow of Motor Sizing

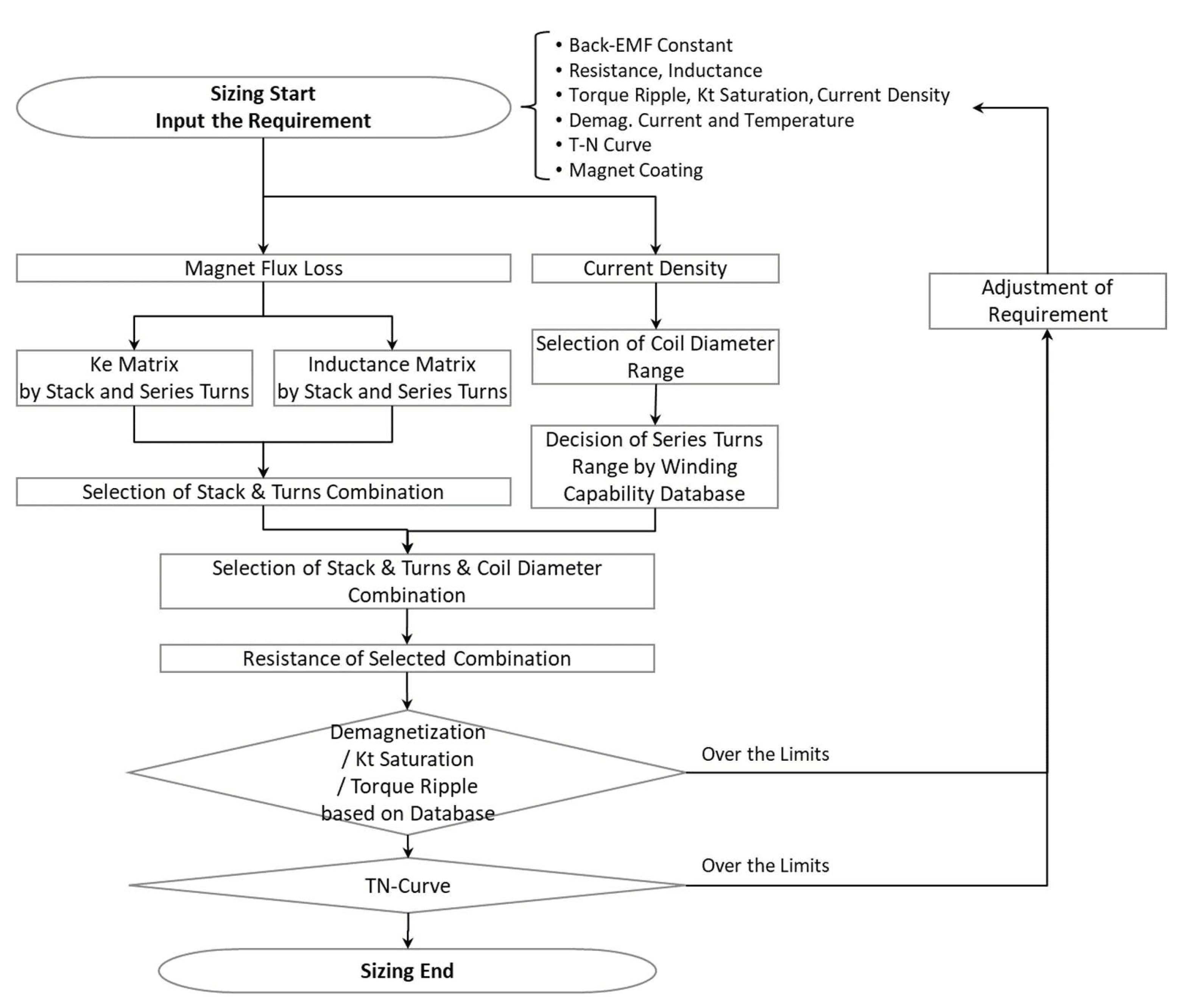
Figure 14. Performance Requirement for the Study Case1

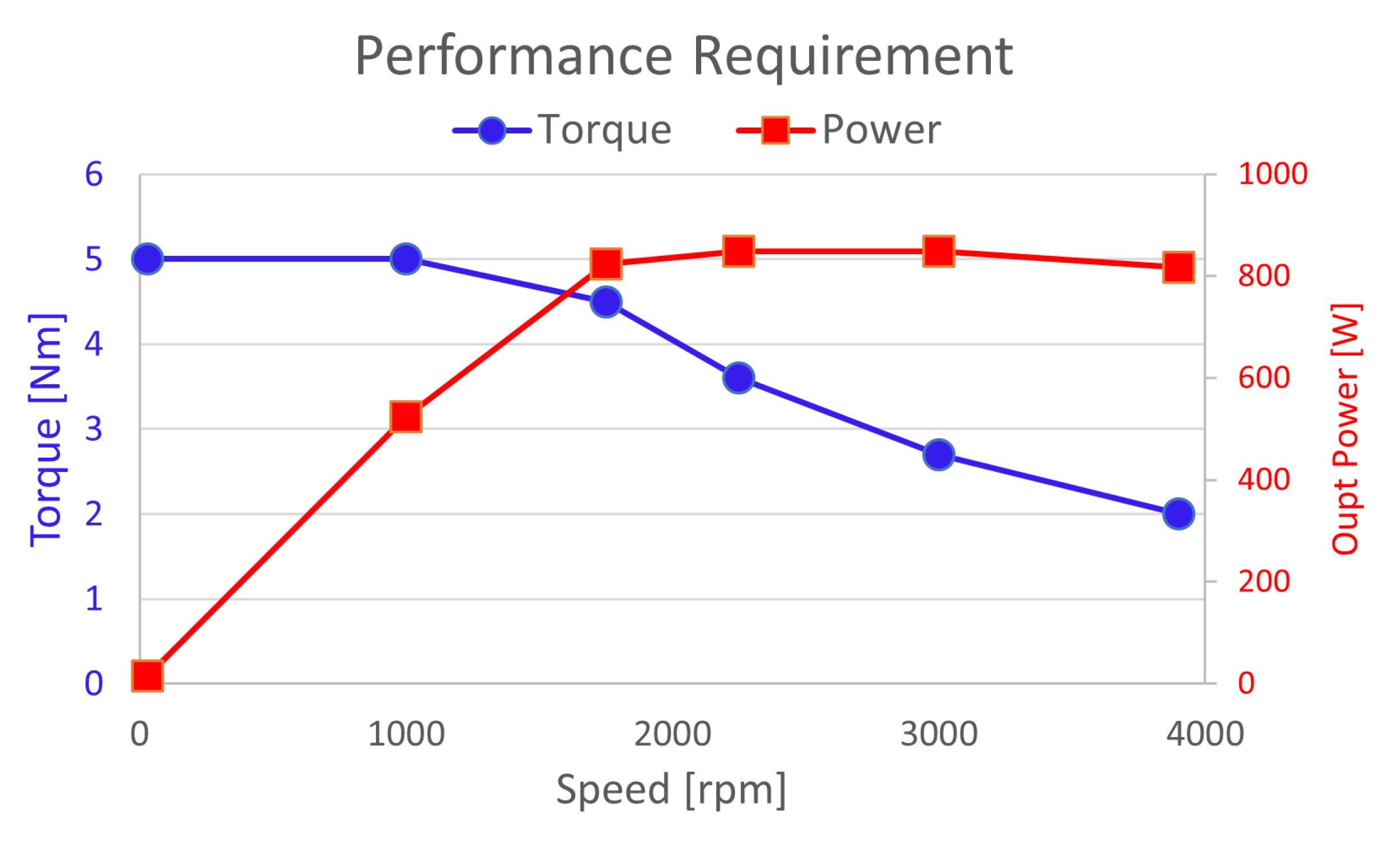
Figure 15. Magnetic Flux Line and Density Distribution for FEM Analysis Model at 154Apk, Current Angle 0Elec.Deg.

Figure 16. Torque-Speed Performance Comparison for the Study Case1

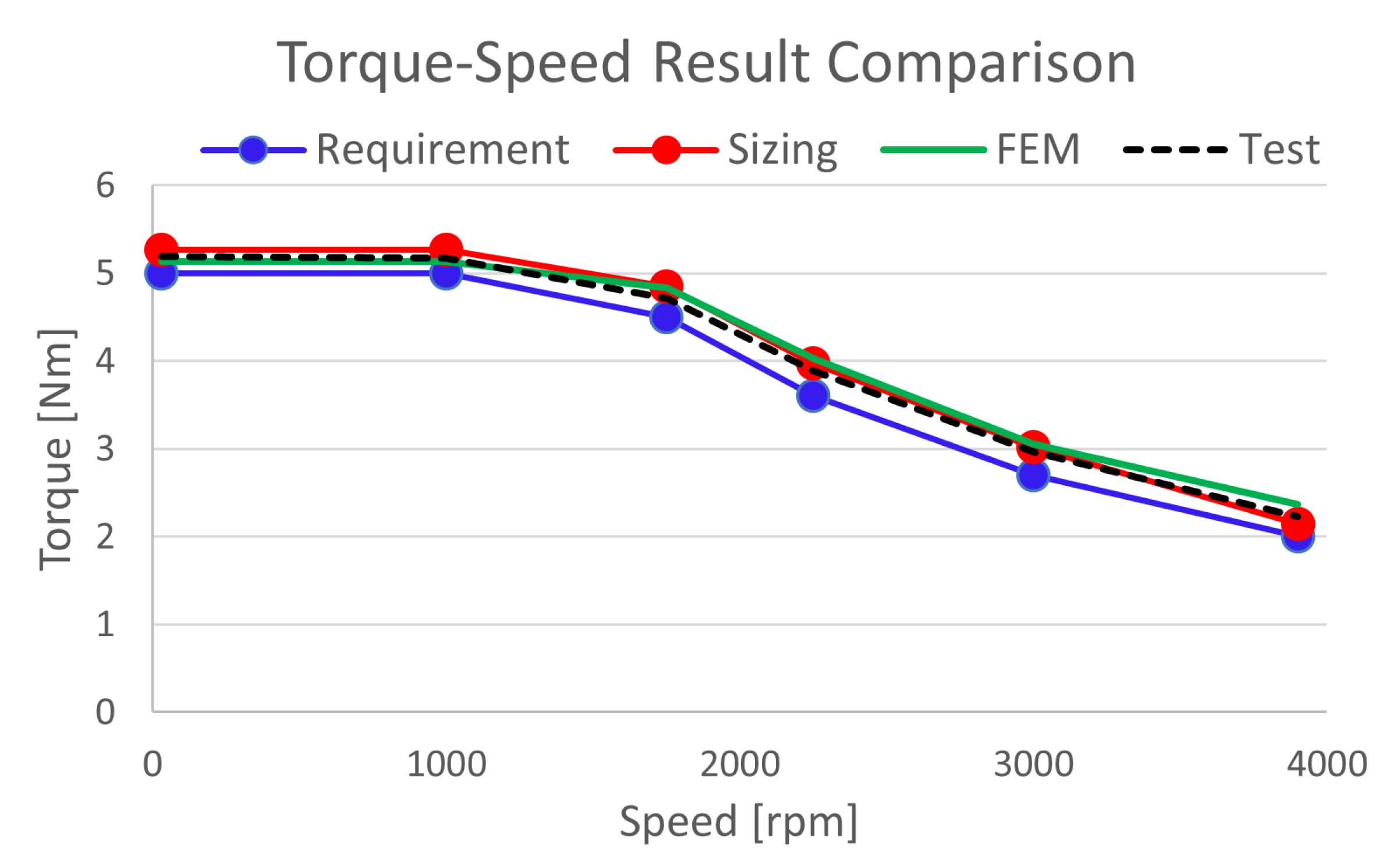
Figure 17. Performance Requirement for the Study Case2

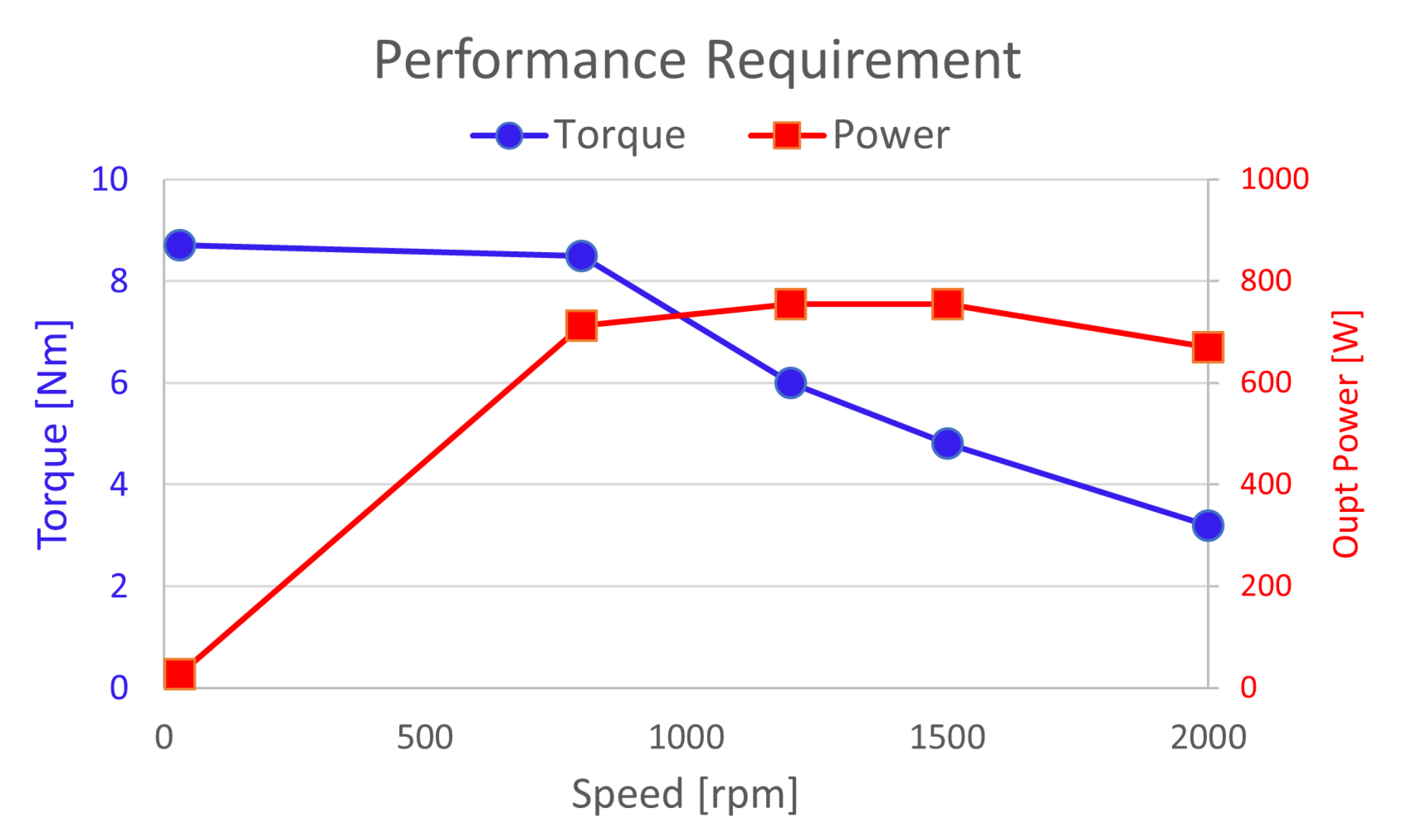
Figure 18. Torque-Speed Performance Comparison for the Study Case2

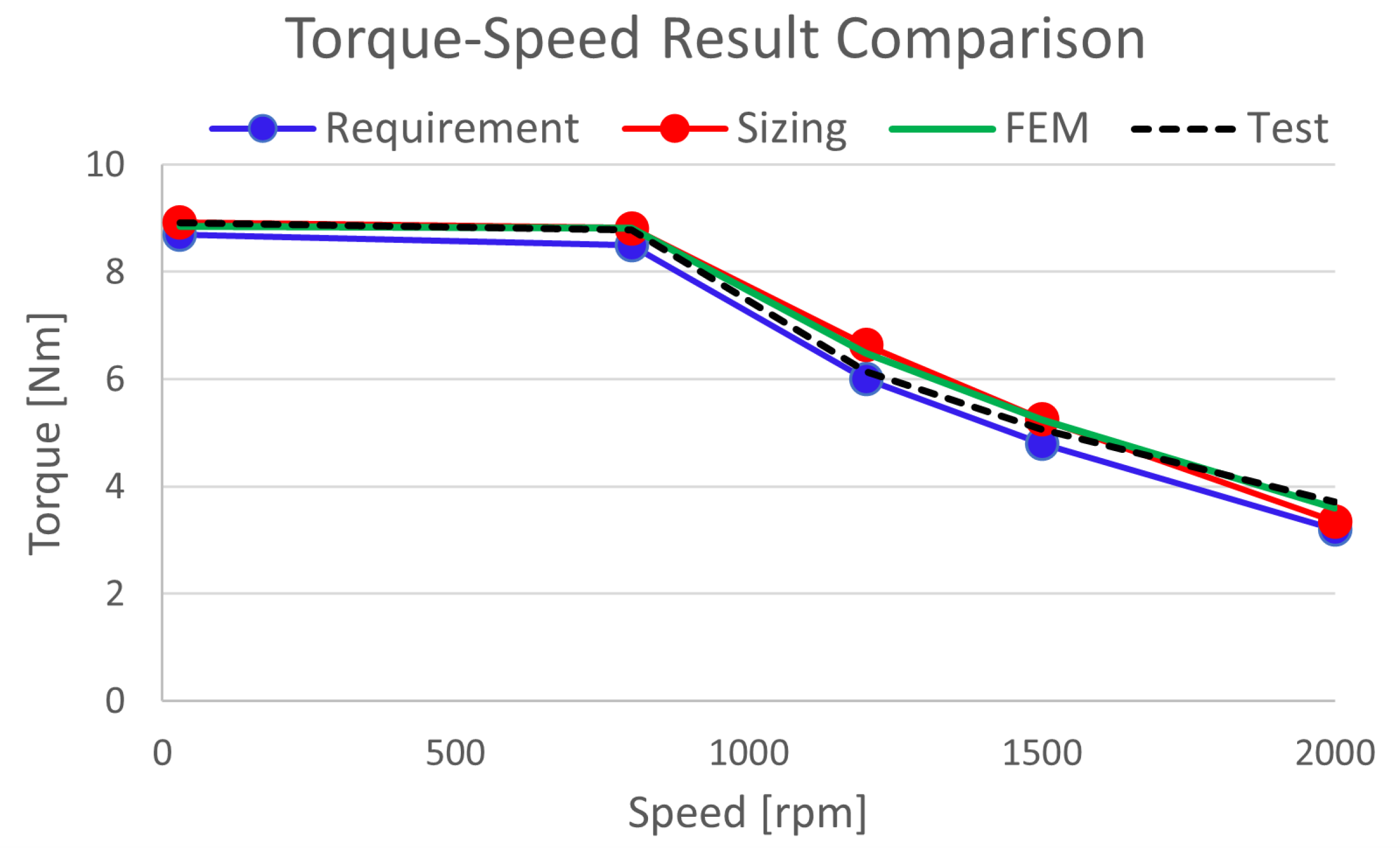
Table 1. Motor Parameters for Design Base Model

Parameters	Values	Unit
Resistance	11.8	mOhm
Synchronous Inductance	53.1	uH
Back-EMF Constant	0.0384	V-s/rad
Stack Length	37.5	mm
Coil Dia-Meter	2	mm
Series Turns	18	Turns
Residual Flux Density of PM	1.37	Tesla
Coercivity of PM	1030	kA/m

Table 2. Magnet Coating Comparison

Surface Treatment	Thickness[um]
Phosphate	0.1- 0.5
Nickel	10-20
Zinc	8-20
Cupper	10-20
Epoxy	15-20

Table 3. Requirement for the Study Case1 Motor

Parameters	Values	Unit
Resistance	Max 14	mOhm
Synchronous Inductance	57 - 63	uH
Back-EMF Constant(Ke)	0.04 - 0.044	V-s/rad
Max Phase Current	109	Arms
Current Density	10-25	A/mm
Demag. Currnet	167.4	A
Demag. Tempeature	130	Deg.C
Demag. Ratio	Max 5	%
Kt Saturation	Max 5	%
Torque Ripple	Max 4	%
Rated Torque @30rpm	Min 5	Nm

Table 4. Sizing Result and Comparison for the Study Case1 Motor

Parameters	Unit	Sizing Result	FEM Analysis	Test Result
Coil Diameter	mm	2.0	2.0	2.0
Series Turns	Turns	18	18	18
Stack Length	mm	40.5	40.5	40.5
Resistance	mOhm	11.32	11.32	11.9(5%)
Inductance	uH	57.4	58.5(2%)	59(3%)
Ke	V-s/rad	0.0416	0.0415(0%)	0.0415(0%)
Demag. Ratio	%	3.37	3.5(4%)	3.21(5%)
Torque Ripple	%	2.57	2.31(10%)	2.91(13%)
Torque@30rpm	Nm	5.26	5.13(2%)	5.18(2%)
Torque@3900rpm	Nm	2.05	2.29(12%)	2.23(9%)
Total Calculation Time	-	<1sec.	around 1.5Hr	-

Table 5. Requirement for the Study Case2 Motor

Parameters	Values	Unit
Resistance	Max 18	mOhm
Synchronous Inductance	80 - 90	uH
Back-EMF Constant(Ke)	0.067 - 0.074	V-s/rad
Max Phase Current	103	Arms
Current Density	10-25	A/mm
Demag. Currnet	176	A
Demag. Tempeature	130	Deg.C
Demag. Ratio	Max 5	%
Kt Saturation	Max 5	%
Torque Ripple	Max 4	%
Rated Torque @30rpm	Min 8.7	Nm

Table 6. Sizing Result and Comparison for the Study Case2 Motor

Parameters	Unit	Sizing Result	FEM Analysis	Test Result
Coil Diameter	mm	2.2	2.2	2.2
Series Turns	Turns	16	16	16
Stack Length	mm	73.5	73.5	73.5
Resistance	mOhm	15.1	15.1(0%)	15.5(5%)
Inductance	uH	83.8	82.6(1%)	81(3%)
Ke	V-s/rad	0.0675	0.0675(0%)	0.0675(0%)
Demag. Ratio	%	1.58	1.4(11%)	1.2(23%)
Torque Ripple	%	2.2	2.4(9%)	2.7(23%)
Torque@30rpm	Nm	8.93	8.85(1%)	8.91(0%)
Torque@2000rpm	Nm	3.34	3.6(8%)	3.71(11%)
Total Calculation Time	-	<1sec.	around 1.5Hr	-

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer