Prerpints.org logo
Preprint
Article

Acceleration of Neutral Atoms by Strong Short-wavelength Short-range Electromagnetic Pulses

Altmetrics

Downloads

73

Views

22

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

10 October 2023

Posted:

11 October 2023

You are already at the latest version

Alerts
Abstract
Nondipole terms in the atom-laser interaction arising due to the presence of a magnetic component in an electromagnetic wave and its inhomogeneity lead to nonseparability of the center-of-mass (CM) and electron variables in the neutral atom and, as a consequence, to its acceleration. We investigate this effect as well as the accompanying excitation and ionization processes for the hydrogen atom in strong (1012 - 2×1014 W/cm2) linearly polarized short-wavelength (5eV ≲ℏω≲ 27 eV) electromagnetic pulses of about 8 fs duration. The study has been carried out within the framework of a hybrid quantum-quasiclassical approach in which the coupled time-dependent Schrödinger equation for an electron and the classical Hamilton equations for the CM of an atom are simultaneously integrated. Optimal conditions with respect to the frequency and intensity of the electromagnetic wave for the acceleration of atoms without their noticeable ionization are found in the analyzed region.
Keywords: 
Subject: Physical Sciences  -   Atomic and Molecular Physics

1. Introduction

The influence of nondipole effects ∼ 1 / c on various atomic processes in strong laser fields arising due to the presence of a magnetic component in the laser field and its inhomogeneity is currently being intensively and widely investigated (see, for example [1,2,3,4,5,6,7,8,9,10,11,12,13,14], and references therein) 1. In particular, their influence on the “stabilization” of atoms at high laser intensities (the probability of ionization reaches a plateau significantly below unity) [9] and the generation of high harmonics (even harmonics appear in the atomic emission spectrum, which are forbidden in the dipole approximation) [14] is predicted. However, nondipole effects, leading to nonseparability of the center of mass (CM) and electron variables in an atom interacting with a laser pulse have practically not been explored [15], as we believe, due to the computational complexity of the problem at hand. Even in the simplest case, in the problem of a hydrogen atom interacting with laser radiation, taking into account these terms, which “entangle” the electron and proton variables in the Hamiltonian of the problem, leads to the need to solve the six-dimensional time-dependent Schrödinger equation.
Nevertheless, the problem of the hydrogen atom in a strong laser field ( 10 14 W / c m 2 ) taking into account the motion of the proton (due to the nondipole effect of nonseparability of the CM in this case), was investigated within the framework of the quantum-quasiclassical method in Melezhik’s recent work [16]. In this approach, the electron is treated quantum mechanically and the CM motion classically. Thus, the Schrödinger equation for the electron and the classical Hamilton equations for the CM variables that are nonseparable due to nondipole effects stimulated by strong laser fields, are integrated simultaneously. In particular, it was shown that with an increase in photon energy from 1.5 eV to 13.6 eV, the hydrogen atom can be accelerated to a velocity of ∼ 2 m / s at an intensity of 10 14 W / c m 2 and pulse duration ∼ 2 fs, which does not contradict the available experimental result [1], where it was possible to accelerate helium and neon atoms to a velocity of ∼ 50 m / s in femtosecond laser pulses of intensity 8 × 10 15 W / c m 2 with photon energy 1.0-1.5 eV. The problem is attractable due to new possible applications in both fundamental and applied physics. Therefore, some evaluation of atom acceleration by strong laser fields have already been made (see, for example [15,17,18,19]).
In this work, we explore the possibility of accelerating the hydrogen atom, as well as its excitation and ionization by strong ( 10 12 - 2 × 10 14 W/cm 2 ) linearly polarized short-wavelength (5eV ≲ ℏ ω ≲ 27 eV) electromagnetic pulses of about 8 fs duration. The investigation is performed in the framework of the quantum-quasiclassical approach [16], the main elements of which in relation to the problem under consideration are described in Section 2. In Section 3, we present the results of nondipole calculations of acceleration, excitation and ionization of the hydrogen atom by high-intensity laser fields. In the considered range of laser field parameters (intensity and frequency), optimal conditions for atomic acceleration were found. It is also shown that the influence of nondipole effects in the considered range of laser intensities and frequencies on the values of ionization and excitation of the atom is insignificant. The last section is devoted to a short conclusion.

2. Theoretical Method

We study the dynamics of a hydrogen atom in a strong laser field linearly polarized along the z-axis and propagating along the y-axis. Assuming a sine-squared carrier envelope for the laser pulse, the vector potential of the laser field is given by
A ( r , t ) = z ^ E 0 ω sin 2 ( π t N T ) sin ( ω t − k · r ) ,
where E 0 the strength of the field defined by the field intensity I = ϵ 0 c E 0 2 / 2 ( ϵ 0 is the vacuum permittivity), ω is the frequency of the laser field, and k = k y ^ = ω / c y ^ and c are the wave-vector and the speed of light, respectively. Here, N shows the number of optical cycles of the period T = 2 π / ω which are included in the laser pulse.
By going beyond the dipole approximation and expanding the space dependent A to the first order of ω y / c , the vector potential A , and the electric E = − d A d t and magnetic B = ∇ × A fields of the laser pulse take the forms
A ( r , t ) = z ^ E 0 ω sin 2 ( π t N T ) sin ( ω t ) − ω c y cos ( ω t ) ,
E ( r , t ) = − z ^ E 0 sin 2 ( π t N T ) cos ( ω t ) + ω c y sin ( ω t ) − z ^ E 0 1 2 N sin ( 2 π t N T ) sin ( ω t ) − ω c y cos ( ω t ) ,
B ( r , t ) = − x ^ E 0 c sin 2 ( π t N T ) cos ( ω t ) .
The Lorentz force acting on each constituent particle of the hydrogen atom (with charge q i = ± e , mass m i and momentum p i ) is of the form F i = q i E + q i m i p i × B where i = 1 , 2 denotes the electron and proton, respectively. Passing to the coordinates of CM ( R = ( m 1 r 1 + m 2 r 2 ) / M , P = p 1 + p 2 ) and relative motion ( r = r 1 − r 2 , p = m 2 M p 1 − m 1 M p 2 ), the interaction potential U between the atom and the electromagnetic field follows (hereafter except where otherwise noted we use atomic units e 2 = ℏ = m 1 = 1 )
U = − E 0 sin 2 ( π t N T ) cos ( ω t ) + 1 2 N sin ( 2 π t N T ) sin ( ω t ) z − E 0 ω c sin 2 ( π t N T ) sin ( ω t ) − 1 2 N sin ( 2 π t N T ) cos ( ω t ) y z + y Z + Y z − E 0 c sin 2 ( π t N T ) cos ( ω t ) y p z − z p y μ ˜ + Y p z − Z p y μ + y P z − z P y M ,
where M = m 1 + m 2 , μ = m 1 m 2 M and μ ˜ = m 1 m 2 m 2 − m 1 . After neglecting the term proportional to 1 / M and using μ ≈ μ ˜ ≈ m 1 = 1 , the interaction potential can be divided into a term dependent only on relative coordinates
U 1 ( r , t ) = − E 0 sin 2 ( π t N T ) cos ( ω t ) + 1 2 N sin ( 2 π t N T ) sin ( ω t ) z − E 0 ω c sin 2 ( π t N T ) sin ( ω t ) − 1 2 N sin ( 2 π t N T ) cos ( ω t ) y z − E 0 c sin 2 ( π t N T ) cos ( ω t ) L ^ x ,
where L ^ x = y p z − z p y is the x-component of the angular momentum operator of electron relative to proton, and a coupling term
U 2 ( r , R , t ) = − E 0 ω c sin 2 ( π t N T ) sin ( ω t ) − 1 2 N sin ( 2 π t N T ) cos ( ω t ) × y Z + z Y − E 0 c sin 2 ( π t N T ) cos ( ω t ) Y p z − Z p y .
Thus, the total Hamiltonian of the system turns into
H ( r , R , t ) = P 2 2 M + h 0 ( r ) + U 1 ( r , t ) + U 2 ( r , R , t ) ,
where h 0 ( r ) = p 2 2 μ − 1 r shows the Hamiltonian of a unit-charged particle with the reduced mass μ in attractive Coulomb field. It is worth reminding that in the dipole approximation, the spatial dependence of the vector field A is neglected, thus the magnetic field effect is excluded and the separation of the CM becomes possible which eventually results in the Hamiltonian of the form H ( r , t ) = h 0 ( r ) + r · E ( t ) , where E ( t ) = E ( r = 0 , t ) (see (3)).
Since for the hydrogen atom P = M V ≫ μ v , we can apply the quantum-quasiclassical approach [20,21,22,23] where the heavy CM is considered to be a classical object and the light electron relative to the proton is treated quantum mechanically. Hence, our problem is reduced to the simultaneous integration of the following system of coupled equations
i ∂ ∂ t ψ ( r , t ) = h 0 ( r ) + U 1 ( r , t ) + U 2 ( r , R , t ) ψ ( r , t ) ,
d d t P = − ∂ ∂ R H e f f R ( t ) , P ( t ) ,
d d t R = + ∂ ∂ P H e f f R ( t ) , P ( t ) ,
with the effective Hamiltonian
H e f f R , P = P 2 2 M + 〈 ψ ( r , t ) | U 2 ( r , R , t ) | ψ ( r , t ) 〉 ,
while the initial wave function is supposed to be the hydrogen atom wave function of the ground state ψ ( r , t = 0 ) = ϕ 100 ( r ) and the initial conditions for the CM position and momentum are
R ( t = 0 ) = 0 , P ( t = 0 ) = 0 .
We integrate the time-dependent three dimensional Schrödinger equation (9) by applying a 2D discrete-variable representation method (DVR) [24] and simultaneously integrate the Hamilton equations of motion (10,11) with the Störmer-Verlet method [25] adapted in [16,22,23] for the quantum-quasiclassical case:
P ( t n + Δ t 2 ) = P ( t n ) − Δ t 2 ∂ ∂ R H e f f R ( t n ) , P ( t n + Δ t 2 ) , R ( t n + Δ t ) = R ( t n ) + Δ t 2 { ∂ ∂ P H e f f R ( t n ) , P ( t n + Δ t 2 ) + ∂ ∂ P H e f f R ( t n + Δ t ) , P ( t n + Δ t 2 ) } , P ( t n + Δ t ) = P ( t n + Δ t 2 ) − Δ t 2 ∂ ∂ R H e f f R ( t n + Δ t ) , P ( t n + Δ t 2 ) .
Once the wave-packet ψ ( r , t ) and R ( t ) and P ( t ) of the CM are found during the time interval 0 ≤ t ≤ T o u t of the laser pulse action, we can calculate the ionization and excitation probabilities [26], and analyse the acceleration of the atom.

3. Results and Discussion

3.1. Excitation and Ionization

In Figure 1 we demonstrate the calculated dependence on the laser frequency ω of the population P g ( ω ) of the ground state of the hydrogen atom after its interaction with a linearly polarized laser pulse of intensity I = 10 14 W / c m 2 . The results of calculations of the probabilities of excitation P e x ( ω ) and ionization P i o n ( ω ) of the atom for the same laser frequencies, intensity and pulse duration are also presented in the same figure. Here, the total pulse duration is fixed at T o u t = N T = 100 π a.u. ≈ 7.6 fs which requires increased number of included optical cycles N by increasing frequency ω . The populations of the ground state of the atom P g ( ω ) were obtained with the standard procedure of projection at the end of the pulse ( t = T o u t ) of the calculated electron wave-packet ψ ( r , ω , t = T o u t ) onto the ground state ϕ 100 ( r ) of the unperturbed atom
P g ( ω ) = ∣ 〈 ψ | ϕ 100 〉 ∣ 2 = ∣ ∫ ψ ( r , ω , T o u t ) ϕ 100 ( r ) d r ∣ 2 .
To evaluate the probability of excitation of an atom by a laser pulse P e x ( ω ) = ∑ n > 1 ∞ P n ( ω ) we applied the following procedure. The calculation of the populations P n ( ω ) of 2 ≤ n ≤ 8 states was carried out in exactly the same way as the population of the ground state (15). To take into account the populations P n ( ω ) of states from n = 9 and above, we used the “interpolation” procedure proposed in our previous work [26]. The probability of ionization of the atom P i o n ( ω ) is calculated using the formula P i o n ( ω ) = 1 − P g ( ω ) − P e x ( ω ) [26].
The first thing that catches our eye in Figure 1 is the resonant peaks in the probabilities P e x ( ω ) near the frequencies ω = 0.37 , 0.44 , 0.47 a.u., defined by the resonant conditions
ℏ ω = 1 2 n 2 − 1 2 n ′ 2
corresponding to the transitions
H n = 1 + ℏ ω → H n ′ , n ′ = 2 , 3 , 4 .
It should be noted that in the resonance condition (16) we do not take into account the perturbation of the excited state n ′ due to the dynamic Stark effect, which can give significant corrections with increasing field intensity, especially for highly excited states. The origin of the resonant peaks at P e x ( ω ) due to one-photon transitions (17) is clearly confirmed by the calculated time-dynamics of the populations P n ( ω , t ) → t → T o u t P n ( ω ) of low-lying states (up to n = 5 ) of the hydrogen atom for some frequencies, including near resonant ones at ω = 0.36a.u., 0.44a.u. and 0.48a.u. (see Figure 2(c-e)). However, the position of the peak ω = 0.24a.u. is not described by the resonance condition (16). Nevertheless, the calculated time-dynamics of populations P n ( t ) shown in Figure 2(b) clearly demonstrates the dominance of transition n = 1 → n ′ = 4 (17) in the population P e x ( ω ) at ω = 0.24a.u.. It is clear that the resonant condition for this transition can be described by the formula
2 ℏ ω = 1 2 n 2 − 1 2 n ′ 2 ,
with 2 ℏ ω ≈ 0.47 a.u. for n = 1 and n ′ = 4 . That is, the peak in P e x ( ω ) at ω = 0.24 a.u. is formed due to a two-photon transition n = 1 → n ′ = 4 . Some contribution of the state n = 3 in P e x ( ω ) at this frequency is also considerable because 2 ℏ ω = 0.48 a.u. is also close to the resonant frequency of 0.44 a.u. for the transition to the state n ′ = 3 . As one can see in the Figure 2(a), the excitation at the frequency ω = 0.22 a.u. has also a two-photon character due to the resonant transition to n ′ = 3 .
Note also that the positions of peaks in P e x ( ω ) exactly coincide with the positions of the minima in the population of the ground state P g ( ω ) in frequency regions, especially in the regions near ω ∼ (0.22-0.24)a.u. and ω ∼ (0.4-0.48)a.u. where ionization is suppressed. The marked areas of ionization suppression are near two-photon resonant excitation to the states n = 3 , 4 and one-photon excitations to the states n = 3 , 4 and 5. The suppression of ionization near the one-photon excitation to the state n = 2 at ω = 0.37 a.u. is only slightly noticeable. As the frequency increases and approaches the ionization threshold ω t = 0.5a.u., ionization begins to increase sharply, up to a point ω i = 0.52a.u. above the threshold, where P i o n ( ω i ) = P g ( ω i ) . Beyond this point, the probability of ionization decreases monotonically with increasing frequency. Note also that at the threshold point ω t = 0.5a.u the probability of excitation is equal to the probability of ionization P e x ( ω t ) = P i o n ( ω t ) .
In Figure 2 we present the calculated time dynamics of the population probabilities of low-lying states for various laser pulse frequencies. Frequencies ω = 0.36a.u., ω = 0.44a.u. and ω = 0.48a.u. in Figure 2(c,d,e) correspond to one-photon excitation into atomic levels n = 2 , 3 , 4 and 5 (see also Figure 1) while Figure 2(a,b) related to ω = 0.22a.u. and ω = 0.24a.u. illustrate the time dynamics of population through a two-photon transition. Moreover, in the cases ω = 0.22a.u., 0.24a.u., 0.44a.u. and 0.48a.u., the processes of excitation of an atom has the two-step character through an intermediate metastable state: the process begins with a transition to the first excited state of the atom n = 2 , which begins to depopulate rapidly by transition to higher states due to the resonant interaction of the atom with the laser pulse. This two-step mechanism is most clearly visible in the cases ω = 0.22a.u. and 0.24a.u.. The resonant population of the lowest excited state n = 2 which is observed at the frequency ω = 0.36a.u. (Figure 2(c)) is a one-step process and occurs directly without any transitions to an intermediate state. Figure 2(f), ω = 0.8a.u., illustrates a non-resonant case of atomic excitation and relates to the case of above ionization threshold excitation of the atom. It can be seen that in the latter case, all populated low-lying levels of the atom, with the exception of n = 2 , are metastable. They are depopulated at the end of the laser pulse, after which only a small part of atoms remains in the excited n = 2 state.

3.2. Acceleration of Neutral Atoms

Figure 2 also shows the results of calculating the time-dynamics of the acceleration of a neutral hydrogen atom by a laser pulse of various frequencies. Here are the CM velocities of an atom in the direction of propagation of the laser pulse V y ( ω , t ) calculated as a function of time. It should be noted that in all cases considered, with the exception of ω = 0.8a.u., the acceleration of the atom CM repeats the time dynamics of the population of the most populated level. In the case of the above threshold ionization with ω = 0.8a.u., the velocity of the CM monotonically increases with time, reaching a maximum at the end of the pulse ( t = T o u t = 314a.u.), while the populations of all low-lying atomic levels grow to the point of maximum intensity of the laser pulse (at the point t = T o u t / 2 ) and begin to depopulate after its passage. At the end of the laser pulse, only a small part of the atoms in the n = 2 state remains in the excited state.
The correlation between the time dynamics of the CM velocity of the atom V y ( ω , t ) and the population probability P n ( t ) of the most populated level demonstrated in Figure 2 confirms the mechanism of acceleration of an atom by a laser pulse due to the acceleration of a spatially inhomogeneous electron cloud in excited states by ponderomotive forces for a frequency below the ionization threshold. In the region of laser frequencies exceeding the ionization threshold (see case ω = 0.8a.u.), we observe acceleration of the atom CM even after passing the critical point t > T o u t / 2 , when the atom is depopulated. The growth in this region V y ( ω = 0.8 , t ) occurs due to ionized electrons, the value of which is significant here (see Figure 1).
Actually, presented in Figure 3, the calculated dependencies on the laser frequency of the total probability of excitation and ionization of atom P e x ( ω ) + P i o n ( ω ) and the momentum P y ( ω ) = M V y ( ω ) of its accelerated CM demonstrate their strong correlation with each other. This is a clear demonstration of what is the root cause of the acceleration of the CM of an atom by a laser field. This is the generation of a non-zero dipole moment between proton and electron cloud that, under the action of electromagnetic pulse, has transferred either to the excited state of the atom or to its continuum. Thus, we see that in the case of noticeable ionization of an atom, in addition to the acceleration of the neutral atom itself as a whole, the acceleration of the electron falling into the continuous spectrum also contributes to the acceleration of the atom CM. Naturally, for practical purposes of accelerating neutral atoms, one should use frequency regions of laser radiation in which ionization is suppressed compared to the excitation of the atom. In this regard, the frequencies near the two-photon resonances ( n = 3 , 4 ) ω ∼ (0.22-0.24)a.u and one-photon resonances ( n = 3-5) ω ∼ (0.42-0.48)a.u. (see Figure 1) are promising.
In Figure 4 we present the results of calculations for resonant frequencies ω = 0.24a.u., 0.48a.u. and ω = 0.8a.u. of the dependence of the velocity V y ( ω , I ) of the atom CM on the radiation intensity I. Noteworthy is the linear dependence of the calculated curves for all given frequencies on this double-logarithmic scale. Moreover, the slopes of the presented curves, with the exception of the frequency ω = 0.24a.u., are the same on a double logarithmic scale, which corresponds to the linear dependence of the the CM velocity on the intensity: V y ( ω , I ) ∝ I . However, the angle of inclination of the curve ω = 0.24a.u. increases, which gives in this case exactly the quadratic dependence of the velocity of the atomic CM in the considered range of intensities: V y ( ω = 0.24 , I ) ∝ I 2 . The physical interpretation of the discovered effect is the following. All cases of acceleration of the CM of the atom considered here, except for ω = 0.24a.u., correspond to the single-photon mechanism discussed above. In this case, the effect of accelerating the CM to velocity V y ( ω , I ) is proportional to the photon number density in the laser pulse (i.e. intensity I), which is clearly demonstrated in Figure 4. In the case of ω = 0.24a.u., the process has two-photon origin, in which the acceleration of the CM to a velocity V y ( ω = 0.24 , I ) is proportional to the square of the photon number density in the laser pulse, which leads to a quadratic dependence V y ( ω = 0.24 , I ) ∝ I 2 which we observe in Figure 4. It should be noted that the proportionality coefficients of V y ( ω = 0.48 , I ) and V y ( ω = 0.80 , I ) to the intensity I are slightly decreasing by increasing intensity to I > 10 14 W / c m 2 . This feature can be interpreted as a complete depopulation of the ground state into excited states and a continuous spectrum of the atom at this region of intensities.

3.3. Influence of Nondipole Effects on Excitation and Ionization Processes

We have also analyzed the influence on the excitation and ionization processes of the nondipole effects. Table 1 illustrates the deviation of P g ( ω ) and P e x ( ω ) calculated in dipole and nondipole approaches. We see that the influence of nondipole effects in the considered range of frequencies on the excitation and ionization of the atom is insignificant. The relative deviation does not exceed the value 0.5 × 10 − 3 .

4. Conclusions

We have investigated the acceleration of a hydrogen atom in strong ( 10 12 - 2 × 10 14 W/cm 2 ) linearly polarized short-wavelength (5eV ≲ ℏ ω ≲ 27 eV) electromagnetic pulses of about 8 fs duration. The study was carried out within the framework of the hybrid quantum-quasiclassical approach, in which the coupled time-dependent Schrödinger equation for an electron and the classical Hamilton equations for the atom CM were simultaneously integrated. It was found that the origin of atomic acceleration is the transition of a part of the electron cloud, under the action of electromagnetic wave, from the ground to excited states and, as a consequence, acceleration of the atom.
The optimal conditions with respect to the frequency and intensity of the electromagnetic pulse for the acceleration of atoms without their noticeable ionization are found in the analyzed region. We have shown that most prospective in this regard are the regions of one-photon resonances n = 3-5 ( ω = ( 0.4 − 0.48 ) a.u.) and two-photon resonances n = 3,4 ( ω = ( 0.22 − 0.24 ) a.u.). We have shown that for intensity I = 2 × 10 14 W / c m 2 the hydrogen atom is maximally accelerated at ω = 0.48a.u. to velocity V y ≃ 700 c m / s . At frequency ω = 0.24a.u., the acceleration is noticeably less than this value and reaches 500 c m / s ; however, due to the two-photon mechanism of excitation of the atom at this frequency, a further increase in intensity should lead to a more significant acceleration than at ω = 0.48a.u. due to the established dependence for the two-photon resonance V y ∝ I 2 . In this regard, it seems also interesting to consider for acceleration of atoms the three-photon excitation mechanism due to the supposed dependence V ∝ I 3 in this case. However, it is clear that this effect can start to be considerable at rather high laser intensities. Nevertheless, it looks promising to investigate the region of three-photon resonances for rather high intensities due to the cubic dependence on the intensity of the CM velocity here; however this demands special consideration.
It seems to us that among the current tasks of further research into the possibility of accelerating atoms by electromagnetic radiation is the inclusion of spatial inhomogeneity of a laser beam in the computational scheme and its generalization to helium and neon atoms, where experimental data are more reachable [1,15,17]. It is also worth considering in our approach the influence of laser radiation polarization on the acceleration of an atom and the possibility of obtaining twisted atoms in this case.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

This work was supported by the Russian Science Foundation under Grant No. 20-11-20257.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
CM center-of-mass
DVR discrete-variable representation

Note

1
Here, c = 1 / α = 137 is the speed of light in the atomic system of units (a.u.).

References

  1. Eichmann, U.; Nubbemeyer, T.; Rottke, H.; Sandner, W. Acceleration of neutral atoms in strong short-pulse laser fields. Nature 2009, 461, 1261–1264. [Google Scholar] [CrossRef] [PubMed]
  2. Kylstra, N.J.; Worthington, R.A.; Patel, A.; Knight, P.L.; De Aldana, J.R.V.; Roso, L. Breakdown of stabilization of atoms interacting with intense, high-frequency laser pulses. Phys. Rev. Lett. 2000, 85, 1835–1838. [Google Scholar] [CrossRef] [PubMed]
  3. Hemmers, O.; et. al. Dramatic Nondipole Effects in Low-Energy Photoionization: Experimental and Theoretical Study of Xe 5s. Phys. Rev. Lett. 2003, 91, 053002–053005. [Google Scholar] [CrossRef] [PubMed]
  4. Førre, M.; Hansen, J.P.; Kocbach, L.; Selstø, S.; Madsen, L.B. Nondipole ionization dynamics of atoms in superintense high-frequency attosecond pulses. Phys. Rev. Lett. 2006, 97, 043601–043604. [Google Scholar] [CrossRef] [PubMed]
  5. Reiss, H.R. Limits on tunneling theories of strong-field ionization. Phys. Rev. Lett. 2008, 101, 043002–043005. [Google Scholar] [CrossRef] [PubMed]
  6. Smeenk, C.T.L.; Arissian, L.; Zhou, B.; Mysyrowicz, A.; Villeneuve, D.M.; Staudte, A.; Corkum, P.B. Partitioning of the linear photon momentum in multiphoton ionization. Phys. Rev. Lett. 2011, 106, 193002–193005. [Google Scholar] [CrossRef]
  7. Ludwig, A.; Maurer, J.; Mayer, B. W.; Phillips, C. R.; Gallmann, L.; Keller, U. Breakdown of the dipole approximation in strong-field ionization. Phys. Rev. Lett. 2014, 113, 243001–243005. [Google Scholar] [CrossRef]
  8. Chelkowski, S.; Bandrauk, A. D.; Corkum, P. B. Photon momentum sharing between an electron and an ion in photoionization: From one-photon (photoelectric effect) to multiphoton absorption. Phys. Rev. Lett. 2014, 2014 113, 263005–263009. [Google Scholar] [CrossRef]
  9. Førre, M.; Simmonsen, A. S. Nondipole ionization dynamics in atoms induced by intence xuv laser fields. Phys. Rev. A 2014, 90, 053411–053420. [Google Scholar] [CrossRef]
  10. Klaiber, M.; Hatsagortsyan, K. Z.; Wu, J.; Luo, S. S.; Grugan, P.; Walker, B. C. Limits of strong field rescattering in the relativistic regime. Phys. Rev. Lett. 2017, 118, 093001–093006. [Google Scholar] [CrossRef]
  11. Ilchen, M.; et. al. Symmetry breakdown of electron emission in extreme ultraviolet photoionization of argon. Nat. Commun. 2018, 9, 4659–4666. [Google Scholar] [CrossRef] [PubMed]
  12. Maurer, J.; Keller, U. Ionization in intense laser fields beyond the electric dipole approximation: concepts, methods, achievements and future directions. J. Phys. B 2021, 54, 094001–094018. [Google Scholar] [CrossRef]
  13. Førre, M. Nondipole effects and photoelectron momentum shifts in strong-field ionization by infrared light. Phys. Rev. A 2022, 106, 013104–013110. [Google Scholar] [CrossRef]
  14. Mishra, M.; Kalita, D. J.; Gupta, A. K. Breakdown of dipole approximation and its effect on high harmonic generation. Eur. Phys. J. D 2012, 66, 169–173. [Google Scholar] [CrossRef]
  15. Bray, A. W.; Eichmann, U.; Patchkovskii, S. Dissecting strong-field excitation dynamics with atomic-momentum spectroscopy. Phys. Rev. Lett. 2020, 124, 233202–233207. [Google Scholar] [CrossRef]
  16. Melezhik, V.S. Quantum-quasiclassical analysis of center-of-mass nonseparability in hydrogen atom stimulated by strong laser fields. J. Phys. A: Math. Theor. 2023, 56, 154003–154017. [Google Scholar] [CrossRef]
  17. Maher-McWilliams, C.; Douglas, P.; Barker, P. F. Laser-driven acceleration of neutral particles. Nat. Photonics 2012, 6, 386–390. [Google Scholar] [CrossRef]
  18. Wang, P. X.; Wei, Q.; Cai, P.; Wang, J. X.; Ho, Y. K. Neutral particles pushed or pulled by laser pulses. Opt. Lett. 2016, 2016 41, 230–233. [Google Scholar] [CrossRef]
  19. Cai,P. ; Zha, J. J.; Xie, Y. J.; Wei, Q.; Wang, P. X. Rydberg-atom acceleration by tightly focused intence laser pulses. Phys. Rev. A 2019, 99, 053401–053406. [Google Scholar] [CrossRef]
  20. Melezhik, V.S.; Schmelcher, P. Quantum energy flow in atomic ions moving in magnetic fields. Phys. Rev. Lett 2000, 84, 1870–1873. [Google Scholar] [CrossRef]
  21. Melezhik, V.S.; Cohen, J.S.; Hu, C.Y. ; Stripping and excitation in collisions between p and He+(n≤3) calculated by a quantum time-dependent approach with semiclassical trajectories Phys. Rev. A 2004, 69, 032709–032721. [Google Scholar] [CrossRef]
  22. Melezhik, V.S.; Idziaszek, Z.; Negretti, A. Impact of ion motion on atom-ion confinement-induced resonances in hybrid traps. Phys. Rev. A 2019, 100, 063406–063417. [Google Scholar] [CrossRef]
  23. Melezhik, V.S. Improving efficiency of sympathetic cooling in atom-ion and atom-atom confined collisions. Phys. Rev. A 2021, 103, 053109–053121. [Google Scholar] [CrossRef]
  24. Melezhik, V.S.; Baye, D. Nonperturbative time-dependent approach to breakup of halo nuclei. Phys. Rev. C 1999, 59, 3232–3239. [Google Scholar] [CrossRef]
  25. Hairer, E.; Lubich, C.; Wanner, G. Geometric numerical integration illustrated by the Störmer–Verlet method. Acta numerica 2003, 12, 399–450. [Google Scholar] [CrossRef]
  26. Shadmehri, S.; Melezhik, V.S. A hydrogen atom in strong elliptically polarized laser fields within discrete variable representation. Laser Phys. 2023, 33, 026001–026014. [Google Scholar] [CrossRef]
Preprints 87459 g001
Figure 1. The calculated dependences on ω of the ground state probability P g ( ω ) , probabilities of atomic excitation P e x ( ω ) and ionization P i o n ( ω ) for the laser intensity 10 14 W / c m 2 and 7.6fs pulse duration.
Figure 1. The calculated dependences on ω of the ground state probability P g ( ω ) , probabilities of atomic excitation P e x ( ω ) and ionization P i o n ( ω ) for the laser intensity 10 14 W / c m 2 and 7.6fs pulse duration.
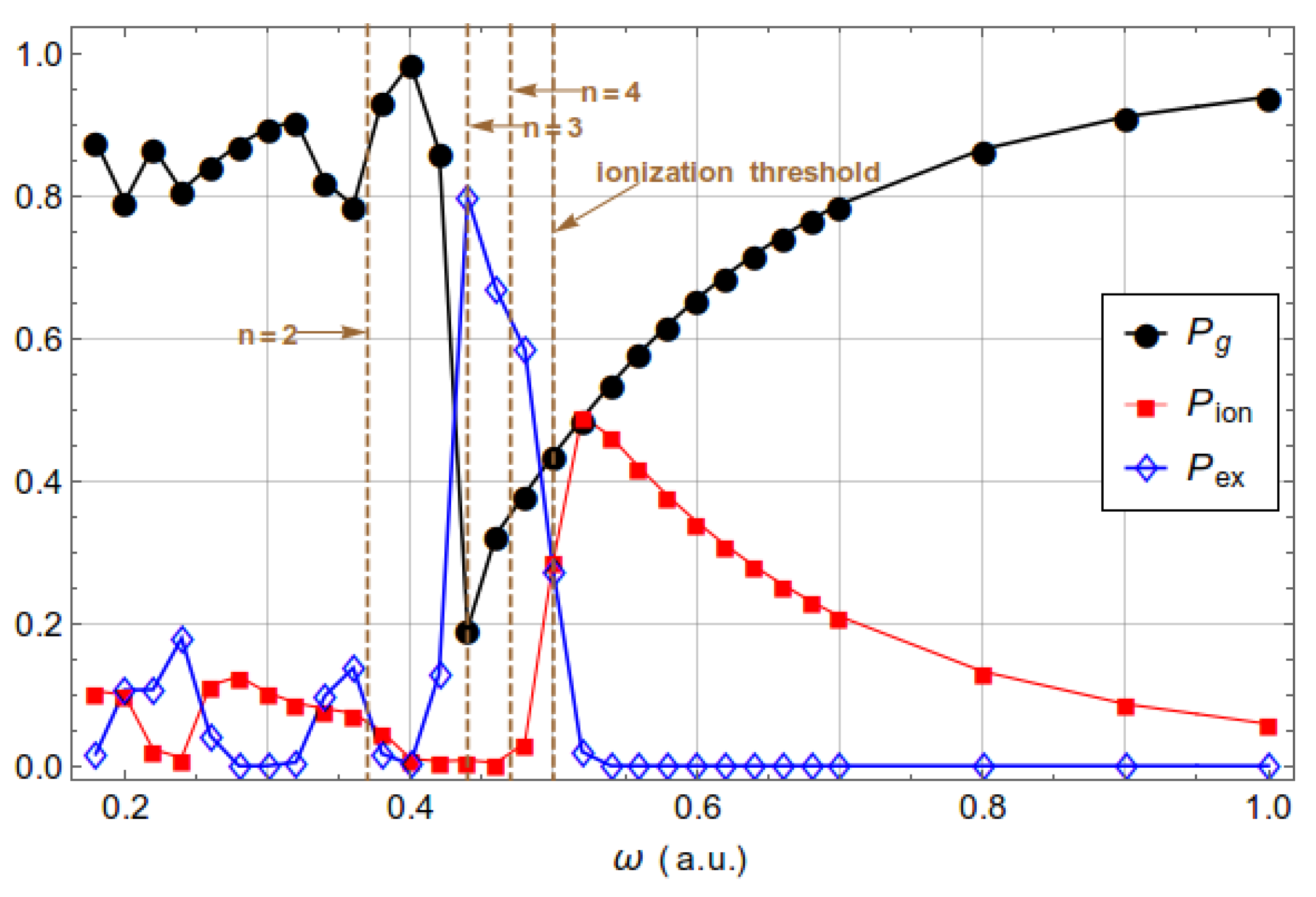
Preprints 87459 g001
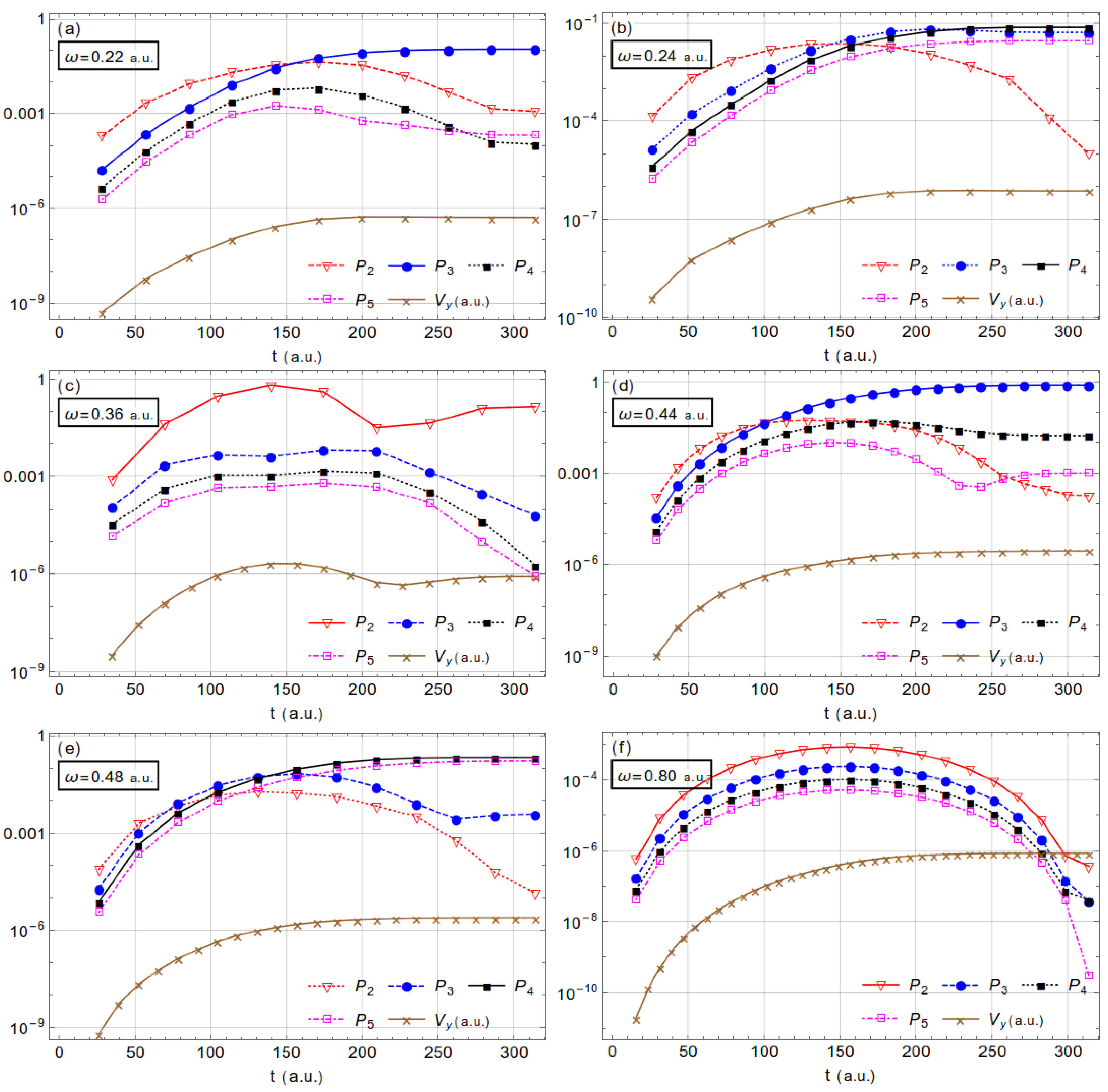
Preprints 87459 g002
Figure 2. The calculated time-dynamics of population probabilities P n ( ω , t ) for low-lying states n = 2-5 and the atomic CM velocity V y ( ω , t ) in the direction of the pulse spreading. The calculations are performed for frequencies (a) ω = 0.22 a.u., (b) ω = 0.24 a.u., (c) ω = 0.36 a.u., (d) ω = 0.44 a.u., (e) ω = 0.48 a.u., and (f) ω = 0.80 a.u. of a laser field with 10 14 W / c m 2 intensity and 7.6fs pulse duration.
Figure 2. The calculated time-dynamics of population probabilities P n ( ω , t ) for low-lying states n = 2-5 and the atomic CM velocity V y ( ω , t ) in the direction of the pulse spreading. The calculations are performed for frequencies (a) ω = 0.22 a.u., (b) ω = 0.24 a.u., (c) ω = 0.36 a.u., (d) ω = 0.44 a.u., (e) ω = 0.48 a.u., and (f) ω = 0.80 a.u. of a laser field with 10 14 W / c m 2 intensity and 7.6fs pulse duration.
Preprints 87459 g002
Preprints 87459 g003
Figure 3. The calculated dependence on the laser frequency of the total probability for atomic excitation and ionization P e x ( ω ) + P i o n ( ω ) together with the momentum P y ( ω ) = M V y ( ω ) of the atomic CM at the end of the pulse duration t = T o u t = 7.6 fs. The calculations are performed for a laser intensity of 10 14 W / c m 2 . The vertical black dashed line indicates the ionization threshold of the atom at ω t = 0.5a.u..
Figure 3. The calculated dependence on the laser frequency of the total probability for atomic excitation and ionization P e x ( ω ) + P i o n ( ω ) together with the momentum P y ( ω ) = M V y ( ω ) of the atomic CM at the end of the pulse duration t = T o u t = 7.6 fs. The calculations are performed for a laser intensity of 10 14 W / c m 2 . The vertical black dashed line indicates the ionization threshold of the atom at ω t = 0.5a.u..
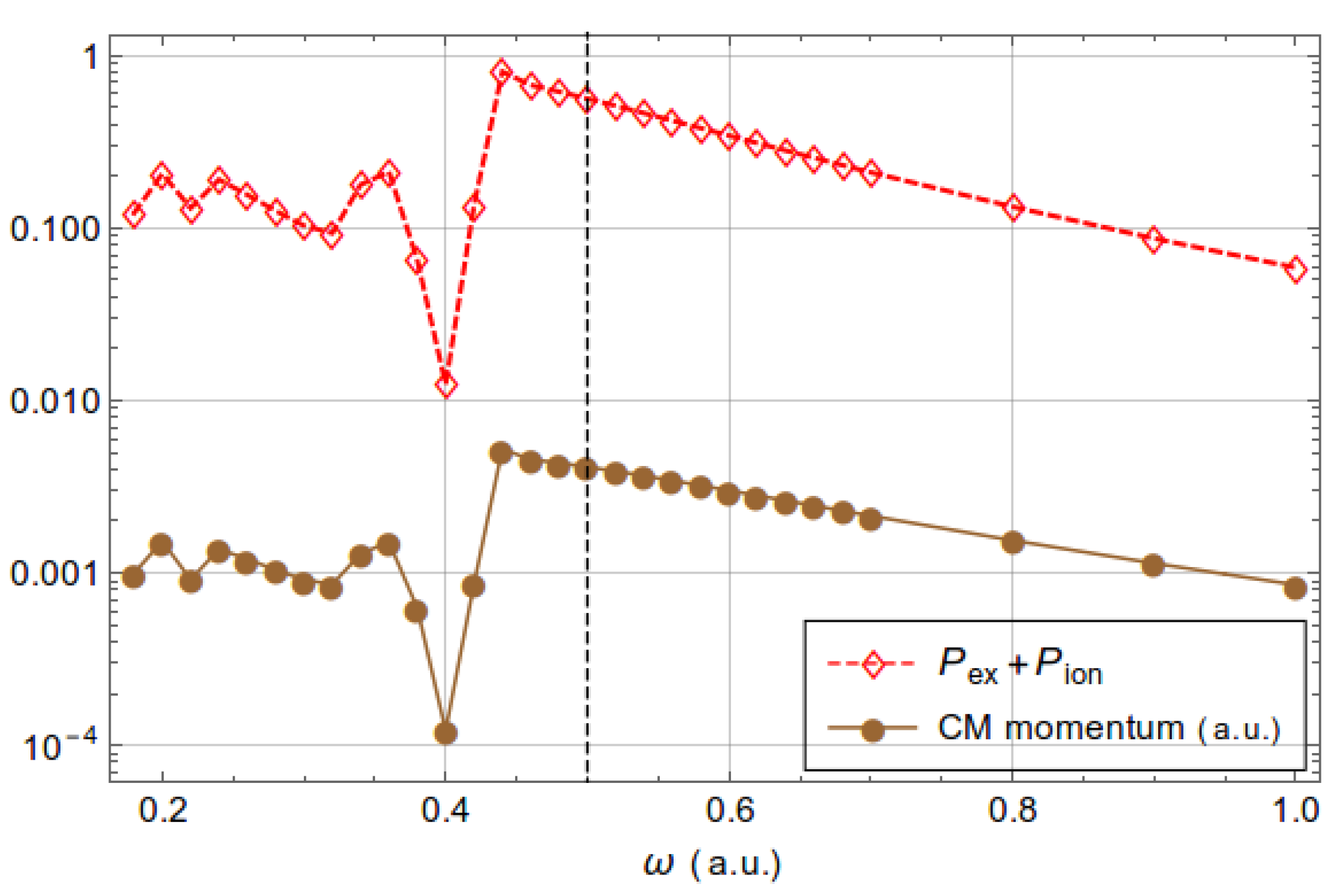
Preprints 87459 g003
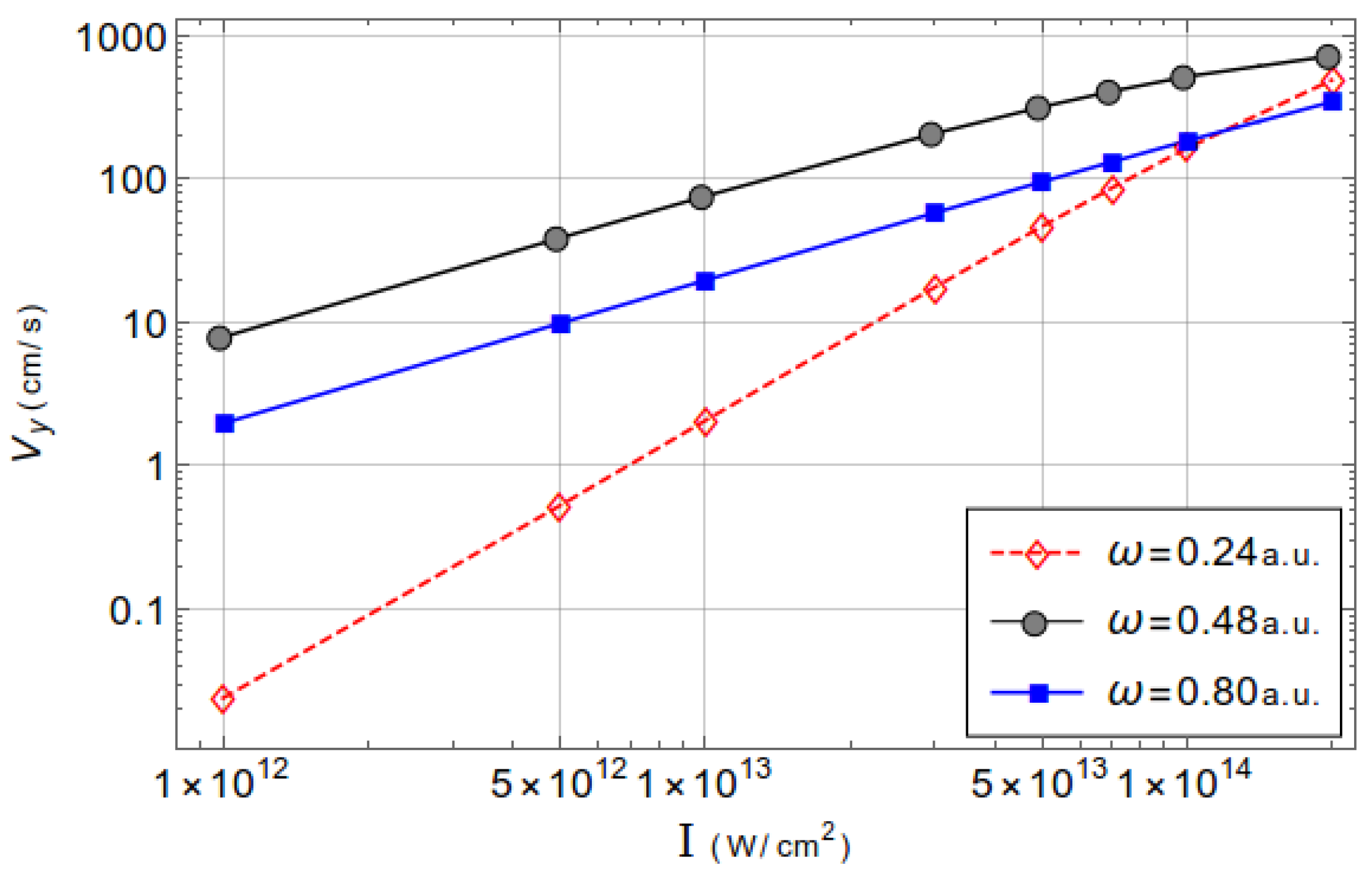
Preprints 87459 g004
Figure 4. The calculated dependence on laser intensity of the CM velocity in the y-direction.
Figure 4. The calculated dependence on laser intensity of the CM velocity in the y-direction.
Preprints 87459 g004
Table 1. The probabilities of the population of the ground state P g and total excitation P e x calculated in the dipole and nondipole approaches for a few laser frequencies with intensity 10 14 W / c m 2 and duration 7.6 fs.
Table 1. The probabilities of the population of the ground state P g and total excitation P e x calculated in the dipole and nondipole approaches for a few laser frequencies with intensity 10 14 W / c m 2 and duration 7.6 fs.
P g P e x
ω Dipole Nondipole Δ P 1 Dipole Nondipole Δ P 1
0.30 0.896815 0.896805 1.05E-05 6.3410E-05 6.3414E-05 6.59E-05
0.40 0.987600 0.987599 1.34E-06 2.3058E-03 2.3052E-03 2.51E-04
0.48 0.382308 0.382294 3.54E-05 5.8582E-01 5.8568E-01 2.37E-04
0.52 0.488483 0.488465 3.74E-05 1.9974E-02 1.9984E-02 4.84E-04
0.80 0.867150 0.867131 2.20E-05 4.6748E-07 4.6756E-07 1.64E-04
1.00 0.941058 0.941045 1.39E-05 4.8210E-07 4.8218E-07 1.68E-04
1 Δ P = P D i p o l e − P N o n d i p o l e P D i p o l e
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated