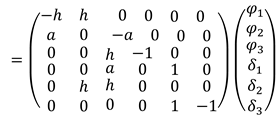A Novel Method of Jacobian Contours to Evaluate the Influence Line in Statically Determinate Structure

Preprint

Article

A Novel Method of Jacobian Contours to Evaluate the Influence Line in Statically Determinate Structure

Altmetrics

Downloads

103

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

09 October 2023

Posted:

12 October 2023

You are already at the latest version

Alerts

Abstract

Influence lines are indispensable tools for visualizing and analyzing the dynamic variations in force factors induced by external loads within structural systems. Among these methods, the energetic approach stands as a widely employed technique, rooted in the fundamental principle of work done by changing forces. It enables engineers to transform intricate structural analysis problems into manageable ones by exploring the first derivatives of the radius vector, which represent infinitesimal velocity or displacement. This methodology seamlessly interweaves concepts such as carrier motion, relative motion, and the construction of mechanisms, bringing fresh perspectives to the analysis of influence lines. In this article, we explore the nuances of these novel methods within the domain of mechanism theory. Through comprehensive elaboration and analysis, we elucidate the underlying principles and practical applications of Jacobian contours. Crucially, we introduce a straightforward, rapid, and programmable approach, promising to revolutionize influence line determination in structural engineering. This method bridges the gap between theory and practice, offering the potential to elevate the accuracy, efficiency, and adaptability of influence line analysis. As such, it represents a significant advancement in the field of structural and applied mechanics, with broad-reaching implications for engineering practice.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Structural engineering, as a field dedicated to ensuring the stability and safety of various architectural marvels, relies heavily on the ability to understand and predict the behavior of structures under the influence of external forces [1]. At the heart of this endeavor lies the construction of influence lines—graphical representations that provide invaluable insights into how internal forces within a structure respond to applied loads. These influence lines are fundamental tools in the arsenal of structural engineers, guiding critical decisions in design, maintenance, and safety assessment [2].

Among the multitude of methods employed to craft these influential diagrams, the energetic method has long stood as a stalwart choice. Rooted in the principle of the work of changing forces, the energetic method is a powerful approach for evaluating the distribution of internal forces under varying load conditions. However, the journey from real-world forces to the abstract realm of influence lines is far from straightforward. It involves a transformation of the problem, turning it into a challenge of first derivatives of the radius vector—essentially, an exploration of infinitesimal velocities and displacements within the structural system [3].

In recent years, the field of structural engineering has seen a paradigm shift, driven by advances in computational tools and mathematical techniques. One of the most promising and modern approaches that have emerged to tackle the intricate problem of influence line analysis is the method of Jacobian contours [4]. This method, which get hitched concepts from carrier and relative motion, mechanism theory, Assur groups with zero degrees of freedom, and other related fields, offers a fresh perspective on how we can harness the power of computation to analyze structures.

In this article, we establish a framework through these innovative methods, exposing a new and highly efficient approach to constructing influence lines for statically determined structures. Our aim is to bridge the gap between theory and practice, shedding light on the theoretical foundations, computational techniques, and practical applications of the Jacobian contours’ method.

As we navigate this exploration, we will witness how the Jacobian contours method brings together intricate forces and geometry. It is a versatile and powerful tool, offering the promise of more accurate, efficient, and insightful structural analyses. The knowledge gleaned from this method has the potential to revolutionize how we approach structural engineering challenges and contribute to the development of safer, more resilient, and more innovative structures in the future. In recent years, advancements in computational tools and mathematical techniques have ushered in new approaches to influence line analysis. One such innovative method is the use of Jacobian matrices or related mathematical concepts. This method has found relevance in diverse engineering domains and has been implemented. Zhu et al. [5] presented an improved model-free adaptive control (iMFAC) method that utilizes event-triggered transmission and quantization, employing Jacobian matrices for control and system analysis. In [6], Huang et al. focused on geometric error compensation in 5-axis machine tools using kinematic transformation models and Jacobi matrices. Qin et al. [7] discussed contour deviation estimation and compensation, relying on Jacobi matrices in the context of precision turning for compensation and estimation of contour in slow tool servo precision turning for complicated curved surfaces. On the other hand, in the electrical field. Song et et al. [8] introduced an optimization algorithm for electrical impedance tomography, employing Jacobian-related techniques to improve image quality. In robotics, Wu et al. [9] presented a hand-eye coordination control system for an acupuncture robot, emphasizing control strategies and precision, which aligns with the broader theme of employing mathematical methods, including the Jacobian method. In this paper, we explore the utilization of Jacobian contours as a novel method to evaluate influence lines in statically determined structures. Building on the concepts and techniques from the literature review and the broader field of engineering, we enquire into the theoretical foundations, and computational approaches, of this innovative method. Through these explorations, we aim to showcase the versatility and interdisciplinary relevance of Jacobian-related methods in enhancing accuracy and efficiency in structural engineering analyses.

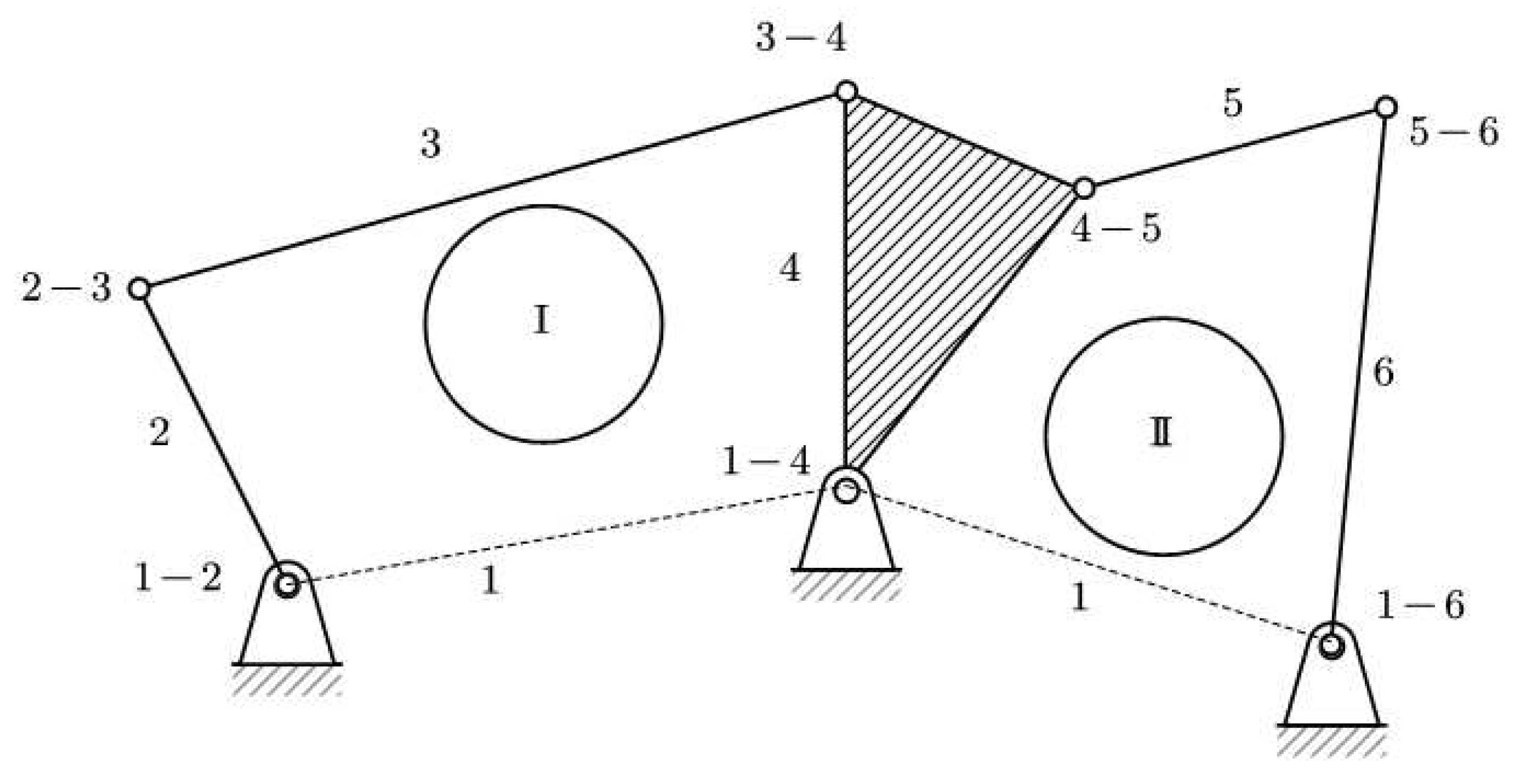
For this purpose, first we will briefly explain the Jacobians method in mechanism. In a mechanism [10,11,12,13,14], the geometric dimensions as well as the kinematic dimensions of the leading link or links, i.e., positions, velocities, and accelerations, are known. All the kinematic magnitudes of the other links forming the Assur groups are required. Let's analyze a 4-bar mechanism with four nodes (Figure 1). The simplest low-pair joint mechanism consists of 4 links and 4 joints and forms a closed contour [13].

For the closed contour, the vector equation (equation 1) is always true, consisting of vectors located in the links of the mechanism, which form the contour [12].

\vec{A B} + \vec{B C} + \vec{C D} + \vec{D A} = \vec{0}

(1)

This equation can be expressed as equation 2:

A B \cdot \vec{e_{2}} + B C \cdot \vec{e_{3}} - C D \cdot \vec{e_{4}} - D A \cdot \vec{e_{1}} = \vec{0}

(2)

For each unit vector

\vec{e}

, we rotate it to form a narrow angle and make its projections on the

x

and

y

axes. The projection in

x

and

y

of the vector equation 2 are respectively equation 3 and 4.

Φ_{1} = A B \cdot \cos φ_{2} + B C \cdot \cos φ_{3} - C D \cdot \cos φ_{4} - D A \cdot \cos φ_{1} = 0

(3)

Φ_{2} = A B \cdot \sin φ_{2} + B C \cdot \sin φ_{3} - C D \cdot \sin φ_{4} - D A \cdot \sin φ_{1} = 0

(4)

So, for planar mechanisms with nodes of the fifth class, the number of contours from which vector polygons are formed will be equal to (equation 5)

K = \frac{n - 2}{2} = g - n + 1 = 4 - 4 + 1 = \frac{4 - 2}{2} = 1

(5)

Where

g

are nodes,

n

are links of mechanism.

A six-link mechanism has two contours and from them result four equations for analysis. Which means that, as many links of Assur groups we have, we will have as many unknown ones as possible. So, we have

2 K

nonlinear equations with

2 K

unknowns. These nonlinear equations are almost always solved cyclically [15].

In the Assur groups, two links are missing, the leader and the base, if the mechanism has a degree of freedom.

Figure 2. 6-bar mechanism with rotation simple joint.

So, we can calculate the number of contours as shown in equation 6.

K = (g = 7) - (n = 6) + 1 = \frac{(n = 6) - 2}{2} = 2

(6)

2. Iterative Solution

The function

= {(Φ_{1}, Φ_{2}, \dots, Φ_{n})}^{T}

depending on several parameters, will be decomposed in the Taylor series [16] up to the first term for all variables, therefore it is presented with the vector sign (equation 7 and 8)

\vec{Φ} ({\vec{q}}_{i} + ∆ \vec{q}) = \vec{Φ} ({\vec{q}}_{i}) + \frac{\partial \vec{Φ} (\vec{q_{i}})}{\partial {\vec{q}}_{i}} \cdot ∆ \vec{q} + \dots = \vec{Φ} ({\vec{q}}_{i}) + J (\vec{q_{i}}) \cdot ∆ \vec{q} + \dots = \vec{0}

(7)

\vec{q} = \{\begin{matrix} q_{1} \\ \dots \\ q_{n} \end{matrix}\}; ∆ \vec{q} = \{\begin{matrix} ∆ q_{1} \\ \dots \\ ∆ q_{n} \end{matrix}\}

(8)

The term

\frac{\partial \vec{Φ} (\vec{q_{i}})}{\partial {\vec{q}}_{i}}

is called Jacobian matrix and it is shown on equation 9.

J = \frac{\partial \vec{Φ} (\vec{q_{i}})}{\partial {\vec{q}}_{i}} = (\begin{matrix} \frac{\partial Φ_{1}}{\partial q_{1}} \dots & \frac{\partial Φ_{1}}{\partial q_{n}} \\ \frac{\partial Φ_{2}}{\partial q_{1}} \dots & \frac{\partial Φ_{2}}{\partial q_{n}} \end{matrix})

(9)

And the difference [8] can be expressed as (equation 10)

∆ q = - J^{- 1} (q_{i}) \cdot Φ (q_{i})

(10)

Also, the new vector can be expressed in equation 11

{\vec{q}}_{i + 1} = {\vec{q}}_{i} + ∆ \vec{q} = \{\begin{matrix} q_{1, i + 1} \\ \dots \\ q_{n, i + 1} \end{matrix}\} + \{\begin{matrix} ∆ q_{1, i} \\ \dots \\ ∆ q_{n, i} \end{matrix}\}

(11)

The loop is terminated when the conditions

|∆ q| < ε

ose

|Φ (q_{i + 1})| < ε

are met. This Newton-Raphson method [12] converges quickly, but it also depends on the starting value, that it may not converge if the starting value is taken too far from the correct solution.

3. Calculation of real displacements and velocities by the method of contours

Derivate with time the contour functions

Φ = {(Φ_{1}, Φ_{2}, \dots, Φ_{n})}^{T}

and determine the virtual displacement or velocity.

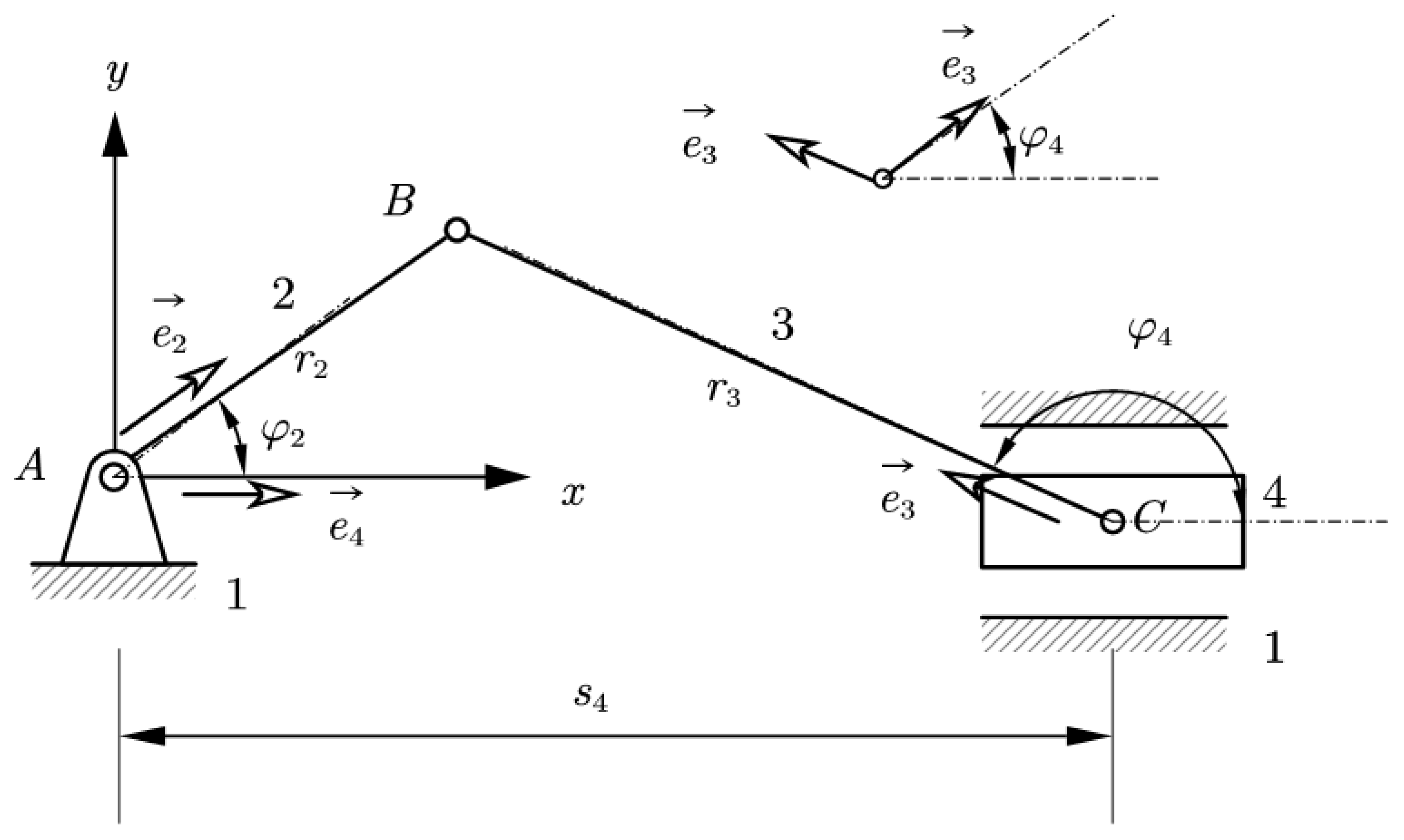
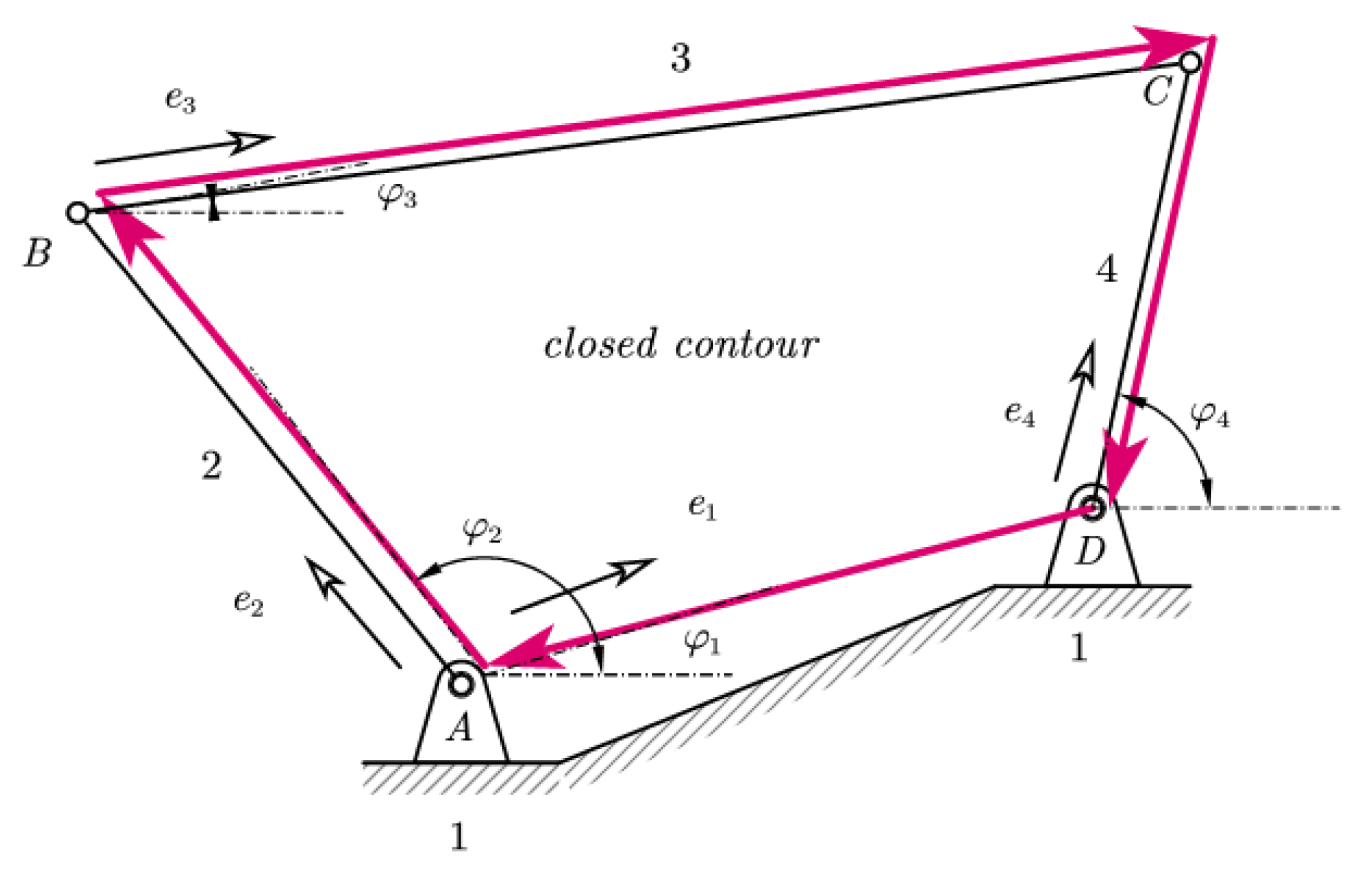
Figure 3. 4-bar mechanism with a slide link.

For the example 4-bar mechanism we can write:

\vec{A B} + \vec{B C} + \vec{C A} = \vec{0}

A B \cdot \vec{e_{2}} - B C \cdot \vec{e_{3}} - C A \cdot \vec{e_{4}} = \vec{0}

. Then we have

Φ_{1} = r_{2} \cdot \cos φ_{2} - r_{3} \cdot \cos φ_{3} - s_{4} = 0,

and

Φ_{2} = r_{2} \cdot \sin φ_{2} - r_{3} \cdot \sin φ_{3} = 0

. Therefore, the velocities and displacements are as shown on equations 12 and 13:

\frac{d Φ_{1}}{d t} = - r_{2} \cdot \sin φ_{2} \frac{d φ_{2}}{d t} + r_{3} \cdot \sin φ_{3} \frac{d φ_{3}}{d t} - \frac{d s_{4}}{d t} = 0 \to d Φ_{1} = - r_{2} \cdot \sin φ_{2} d φ_{2} + r_{3} \cdot \sin φ_{3} d φ_{3} - d s_{4} = 0

(12)

\frac{d Φ_{2}}{d t} = r_{2} \cdot \cos φ_{2} \frac{d φ_{2}}{d t} - r_{3} \cdot \cos φ_{3} \frac{d φ_{3}}{d t} = 0 \to d Φ_{2} = r_{2} \cdot \cos φ_{2} d φ_{2} - r_{3} \cdot \cos φ_{3} d φ_{3} = 0

(13)

By separating the known

d φ_{2}

from the unknown

d φ_{3}, d s_{4}

, the above equation can be written in matrix form as shown in equation 14, 15 and 16.

(\begin{matrix} r_{3} \cdot \sin φ_{3} & - 1 \\ - r_{3} \cdot \cos φ_{3} & 0 \end{matrix}) \cdot (\begin{matrix} d φ_{3} \\ d s_{4} \end{matrix}) = (\begin{matrix} r_{2} \cdot \sin φ_{2} \\ - r_{2} \cdot \cos φ_{2} \end{matrix}) d φ_{2}

(14)

J = \frac{\partial \vec{Φ} (\vec{q_{i}})}{\partial {\vec{q}}_{i}} = (\begin{matrix} \frac{\partial Φ_{1}}{\partial φ_{3}} & \frac{\partial Φ_{1}}{\partial s_{4}} \\ \frac{\partial Φ_{2}}{\partial φ_{3}} & \frac{\partial Φ_{2}}{\partial s_{4}} \end{matrix}) = (\begin{matrix} r_{3} \cdot \sin φ_{3} & - 1 \\ - r_{3} \cdot \cos φ_{3} & 0 \end{matrix})

(15)

(\begin{matrix} d φ_{3} \\ d s_{1} \end{matrix}) = J^{- 1} \cdot [(\begin{matrix} r_{2} \cdot \sin φ_{2} \\ - r_{2} \cdot \cos φ_{2} \end{matrix}) d φ_{2}]

(16)

From the kinematics of planar motion [17,18], we draw the conclusion that the velocity vector is normal to the solid radius and is related to the relation (equation 17)

\vec{v_{B}} = \vec{v_{O p}} + \vec{ω} \times \vec{O_{p} B} = \vec{x} + \vec{y}

(17)

Figure 4. Virtual displacement or velocity for a simple bar.

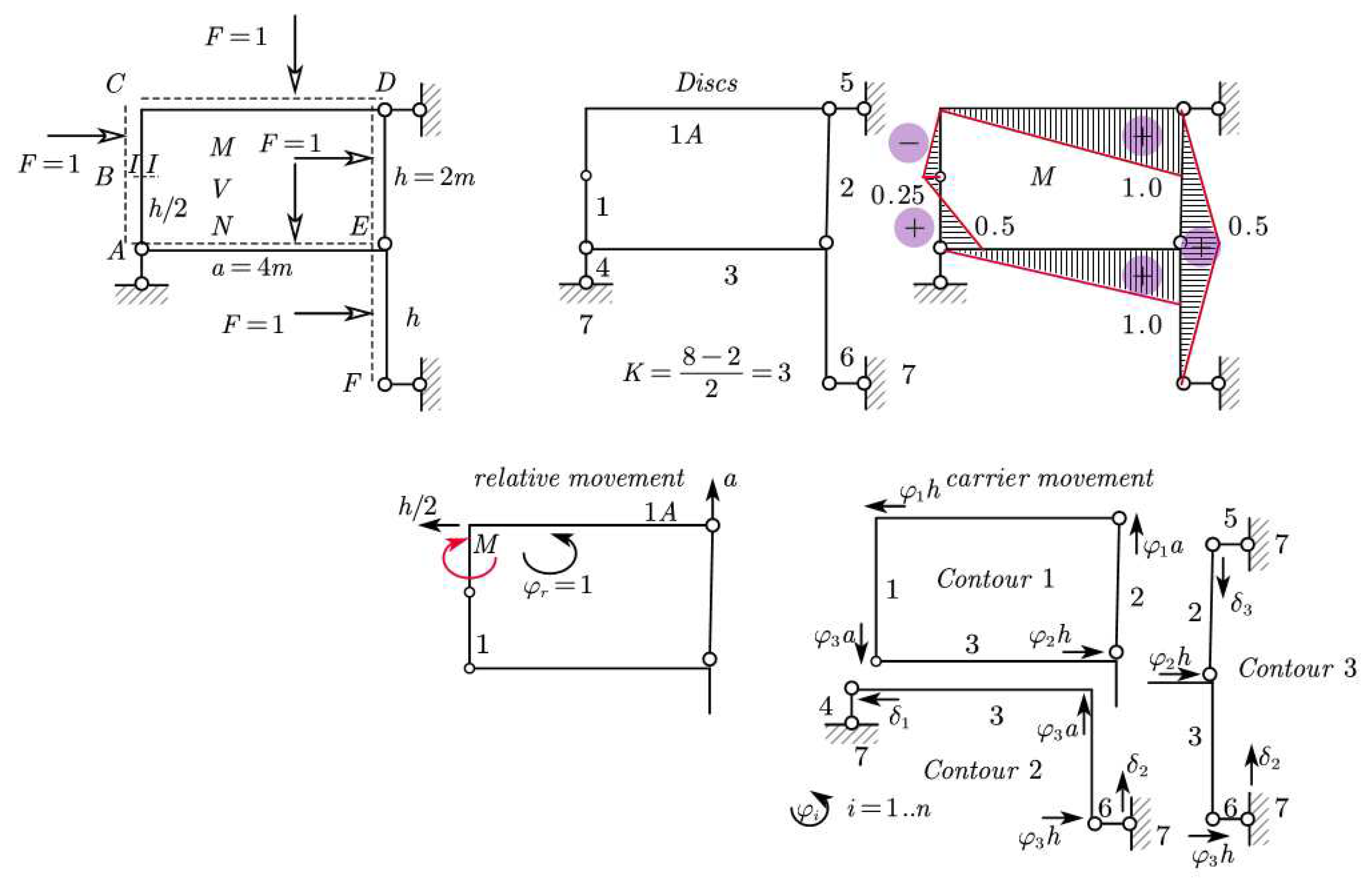
4. Influence line on statically determined structures

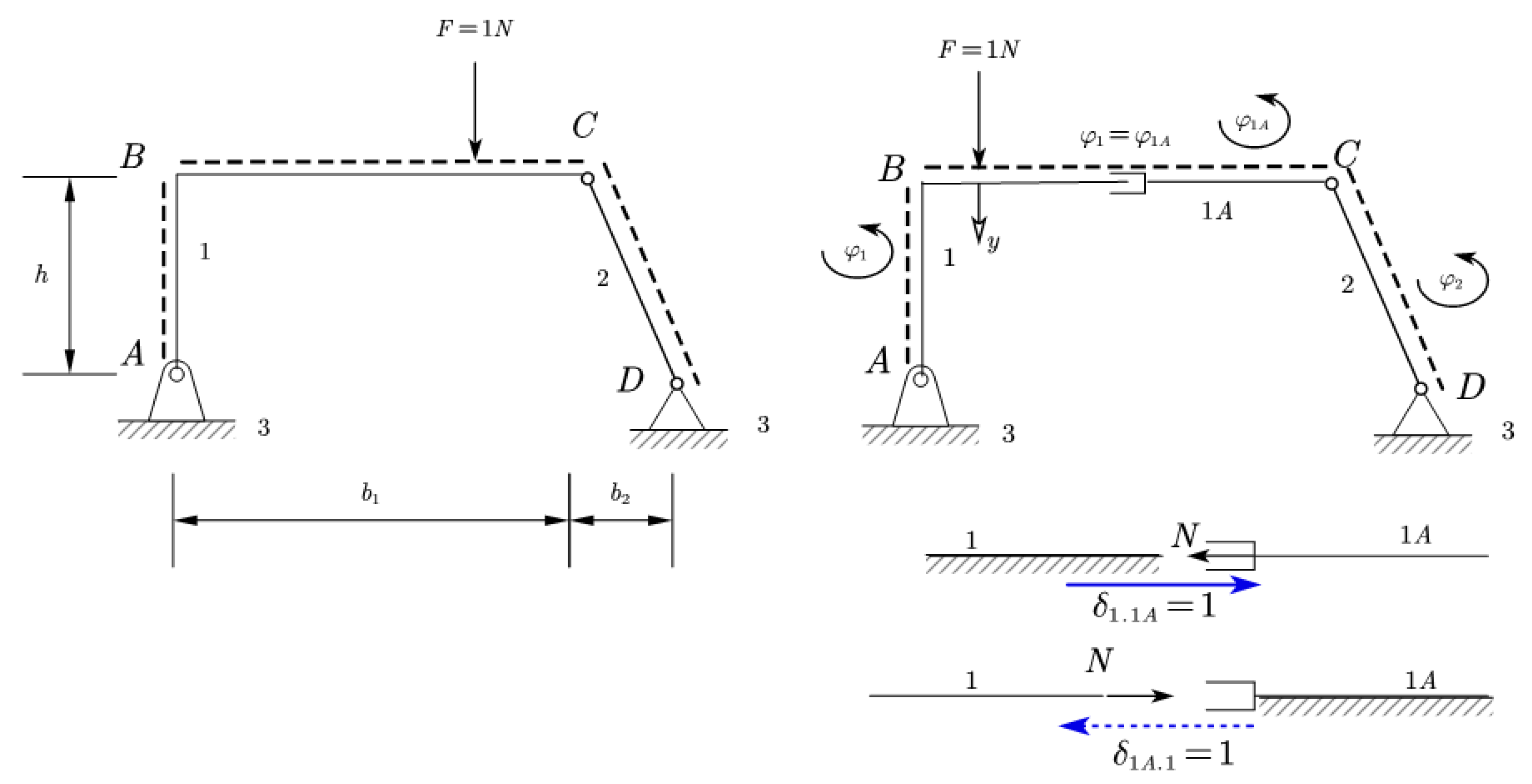
Moving loads in a structure cause changes in reactions, internal forces, and displacements of its points, as shown in Figure 5. Since the number 1 has the property that if it is multiplied by any number, it does not change the latter, as well as the fact that the material is linearly elastic, the driving force is accepted as 1 unit, and graphs of the changes of these factors are constructed and placed on the path of movement of the force. The force is assumed to move with almost zero velocity, to eliminate inertial forces, and to use static equations. These graphs are called the influence line of the respective factor [20]. Applying the principle of virtual displacements [21], since we have only two factors in the structure, we write equation 18.

F \cdot y + M \cdot φ_{1} - M \cdot φ_{1 A} = 0 \to 1 \cdot y - M \cdot (φ_{1 A} - φ_{1}) = 0

(18)

where:

φ_{1 A} - φ_{1} = φ_{1.1 A} = 1

and

M = y

represents the relative motion of disc

1 A

with respect to

1

, which is rotational around section

B

, since the disc was split into two parts

1

and

1 A

Consequently, the line of influence of the factor, i.e.,

M

represents the departure from the path

y

of the points of the path during the movement of the force.

The influence line of a certain factor is the same as the departure or “derailment” from the Path in the mechanism obtained by the removal of a certain obstacle, caused by a relative movement of "1" unit. A relative displacement of 1 unit is called a discontinuity or assembly error. Let's review the force factors, nodes, and discontinuity 1 unit in turn.

4.1. Influence line of normal force.

Figure 6. Influence line of normal force.

So, the solution will be as shown in equation 19.

\sum δ A = - N \cdot δ_{1.1 A} + F \cdot y = 0

(19)

4.2. Influence line of shear force

The influence line for the shear force will be as shown in Figure 7, and the solution will be as shown in equation 20.

\sum δ A = - N \cdot δ_{1.1 A} + F \cdot y = 0

(20)

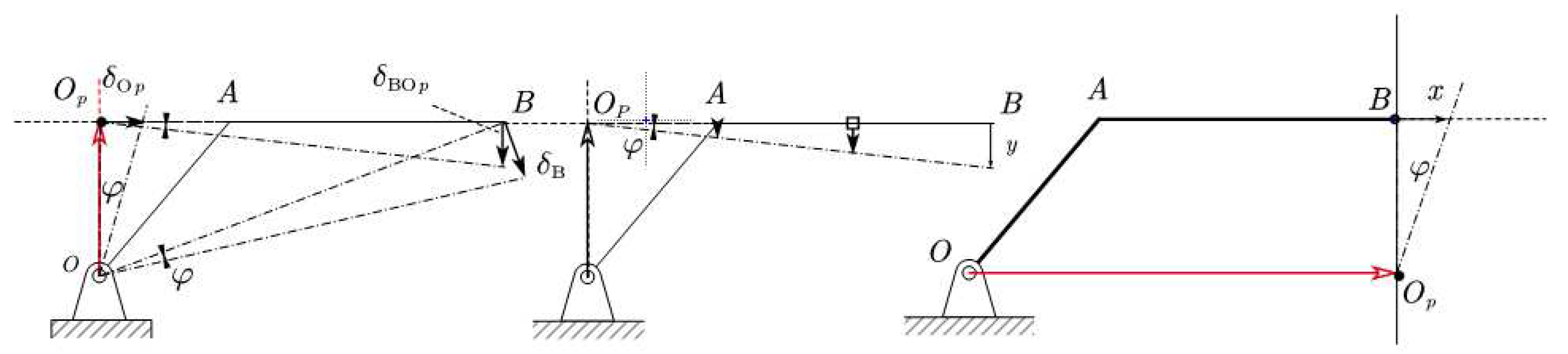
5. The geometric meaning of Jacobians

For the closed contour, figure 5, we can write the corresponding vector equation.

\vec{A B} + \vec{B E} + \vec{E C} + \vec{C D} + \vec{D A} = \vec{0}

(21)

Let us take the variation of the above closed contour vector equation (equation 22).

\vec{δ_{A B}} + \vec{δ_{B E}} + \vec{δ_{E C}} + \vec{δ_{C D}} + \vec{δ_{D A}} = \vec{0}

(22)

More specifically, knowing the virtual rotation angles of the discs we have (equation 23), as shown below:

\vec{φ_{1}} \times \vec{A B} + \vec{φ_{1}} \times \vec{B E} + \vec{φ_{1 A}} \times \vec{E C} + \vec{φ_{2}} \times \vec{C D} + \vec{0} \times \vec{D A} = \vec{0}

(23)

Projecting it along both the horizontal and vertical axes, we derive two equations to find the angles. In the general case, we default to the virtual angles to the counter-clockwise sense that also shows with the positive sign [22].

Figure 8. The geometric meaning of Jacobians method in a 4-bar mechanism.

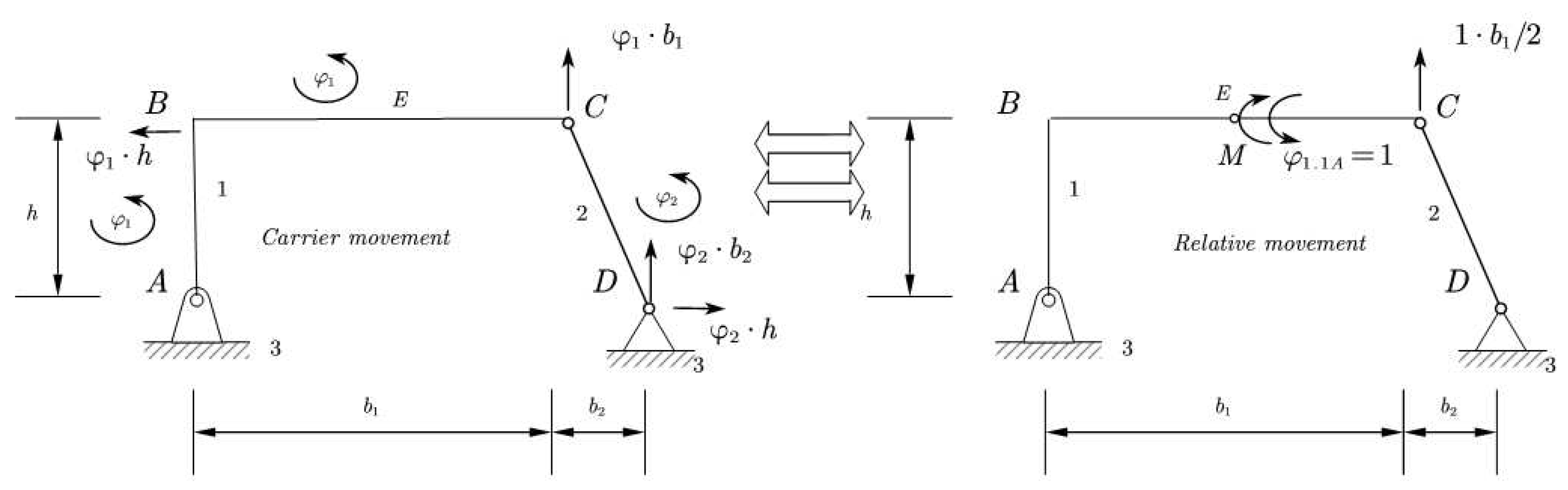
In horizontal direction we have

- φ_{1} \cdot h + φ_{2} \cdot h = 0

. In vertical direction we have

φ_{1} \cdot \frac{b_{1}}{2} + φ_{1 A} \cdot \frac{b_{1}}{2} + φ_{2} \cdot b_{2} = 0

When the points are located on ground link (not movable), they are stationary and therefore have zero displacements. By introducing the concept of relative motion, we naturally also have carrier motion and can write that

φ_{1.1 A} = φ_{1 A} - φ_{1} = \pm 1 \to φ_{1 A} = \pm 1 + φ_{1}

In this case, we have the carrier movement with the links of the statically undetermined structure and the mechanism only with the relative movement

φ_{1.1 A} = \pm 1

, the sign depends on the force factor. Internal factors [23,24], from the principle of action and counteraction, do not perform work during the carrier movement. These factors do work only during relative motion, equal to one unit by the factor and in the opposite direction to the factor (equation 24).

φ_{1} \cdot \frac{b_{1}}{2} \pm 1 \cdot \frac{b_{1}}{2} + φ_{1} \cdot \frac{b_{1}}{2} + φ_{2} \cdot b_{2} = φ_{1} \cdot b_{1} \pm 1 \cdot \frac{b_{1}}{2} + φ_{2} \cdot b_{2} = \vec{0}

(24)

Written in the form of a matrix equation, where one side represents the work in the carrier motion and the other side the work in the relative motion, is given as follows (equation 25)

(\begin{matrix} - h & h \\ b_{1} & b_{2} \end{matrix}) (\begin{matrix} φ_{1} \\ φ_{2} \end{matrix}) = (\begin{matrix} 0 \\ \mp 1 \cdot b_{1} / 2 \end{matrix})

(25)

The carrier work matrix also represents the Jacobian, since the first derivatives represent the velocity vector, which is proportional to the displacement [19]. This is also the geometric meaning of the Jacobian, which represents the matrix of infinitesimal displacements in the carrying motion of the contours, which, for a given structure, is invariant and applies to all internal factors wherever they are located on the contour.

Figure 9. Carrying and relative motion of the contours.

6. Application of Jacobian Method

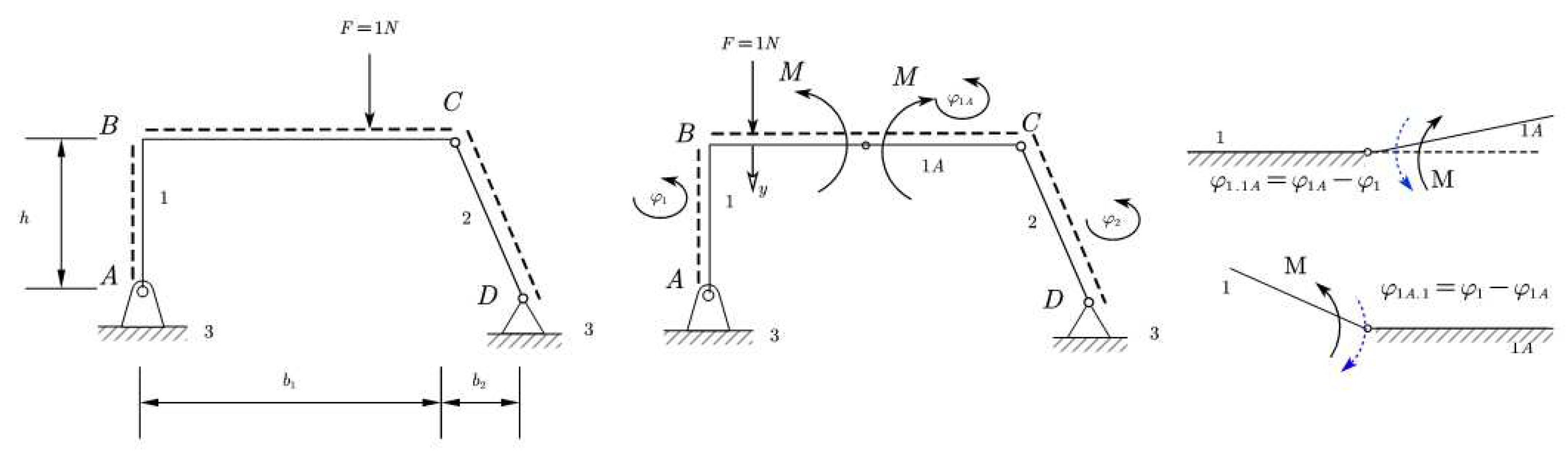
The following Figure 10 represent, step by step, an application of the Jacobian method to a statically determined structure. The first case is for internal moment, the second case is for shear force, and the last is for normal force [25,26].

6.1. Application for internal moment

Let’s see the application of this method for the internal moment. The steps are shown in Figure 10.

The Jacobian matrix can be written as shown in equations 26 and 27.

(26)

(27)

Relative motion and solution of the system will be:

R = (\begin{matrix} - h / 2 \\ a \\ \begin{matrix} 0 \\ 0 \\ \begin{matrix} 0 \\ 0 \end{matrix} \end{matrix} \end{matrix})

and

(\begin{matrix} φ_{1} \\ φ_{2} \\ \begin{matrix} φ_{3} \\ δ_{1} \\ \begin{matrix} δ_{2} \\ δ_{3} \end{matrix} \end{matrix} \end{matrix}) = J^{- 1} R = (\begin{matrix} 0.75 \\ 0.25 \\ \begin{matrix} - 0.25 \\ - 0.5 \\ \begin{matrix} 1 \\ 1 \end{matrix} \end{matrix} \end{matrix})

whereas

φ_{1 A} = 1 - φ_{1} = - 0.25

“Derailment” from the paths in this case will be as Table 1.

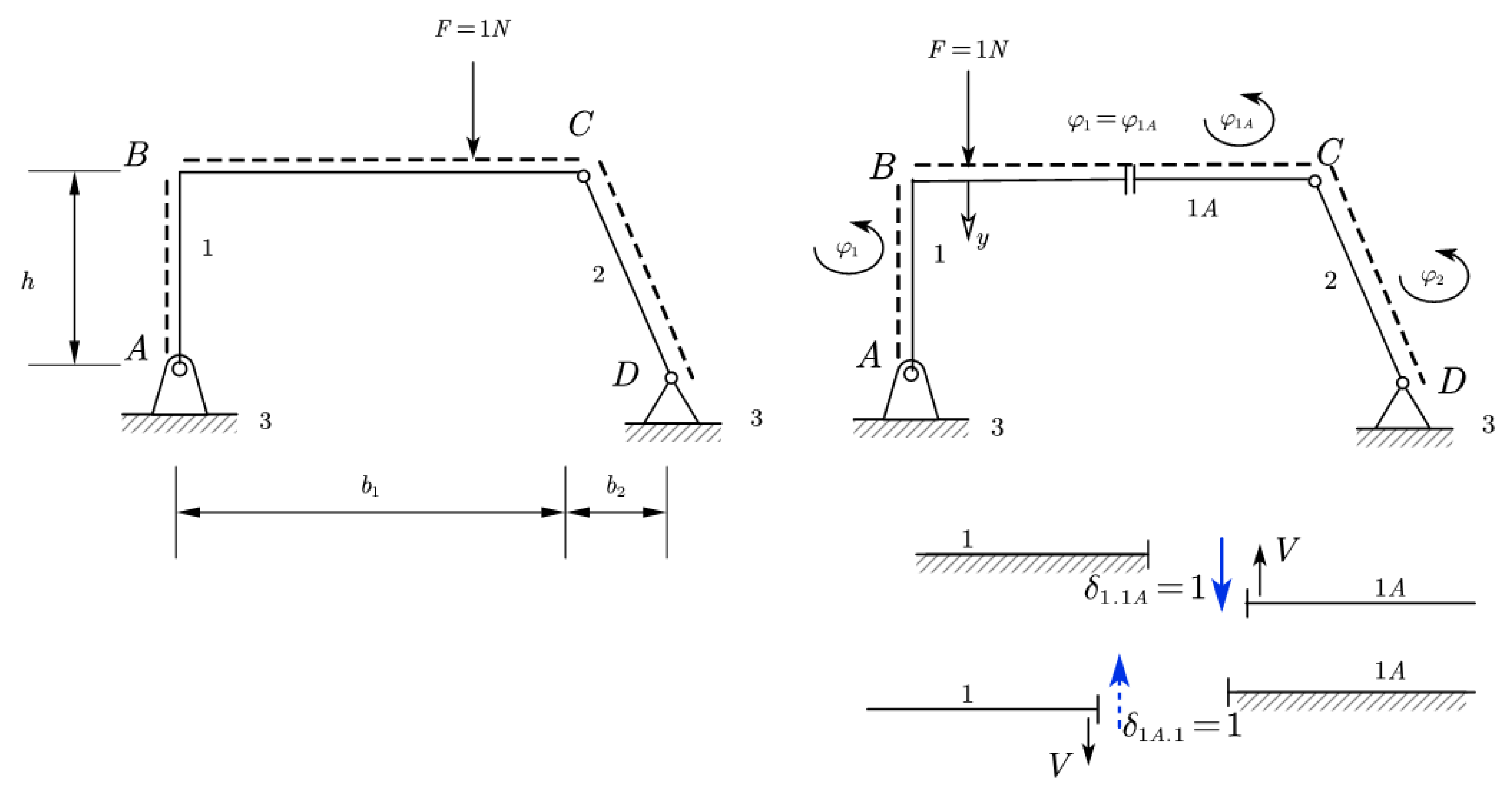
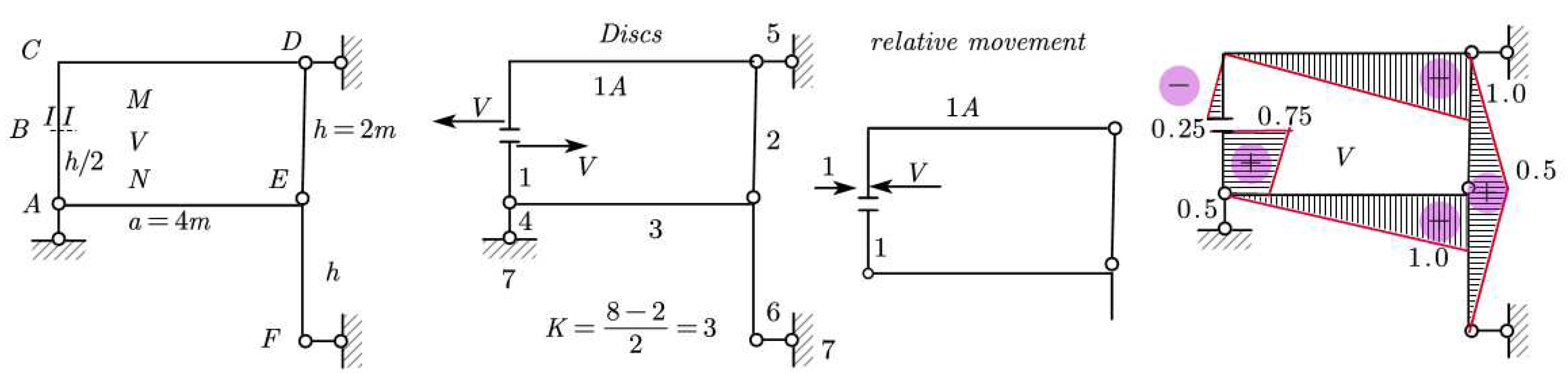
6.2. Application for shear force

For the shear force we will have Figure 11:

Relative motion and solution of the system will be:

R = (\begin{matrix} 1 \\ 0 \\ \begin{matrix} 0 \\ 0 \\ \begin{matrix} 0 \\ 0 \end{matrix} \end{matrix} \end{matrix})

and

(\begin{matrix} φ_{1} \\ φ_{2} \\ \begin{matrix} φ_{3} \\ δ_{1} \\ \begin{matrix} δ_{2} \\ δ_{3} \end{matrix} \end{matrix} \end{matrix}) = J^{- 1} R = (\begin{matrix} - 0.25 \\ 0.25 \\ \begin{matrix} - 0.25 \\ - 0.5 \\ \begin{matrix} 1 \\ 1 \end{matrix} \end{matrix} \end{matrix})

whereas

φ_{1 A} = φ_{1} = - 0.25

“Derailment” from the paths in this mentioned case will be as Table 2.

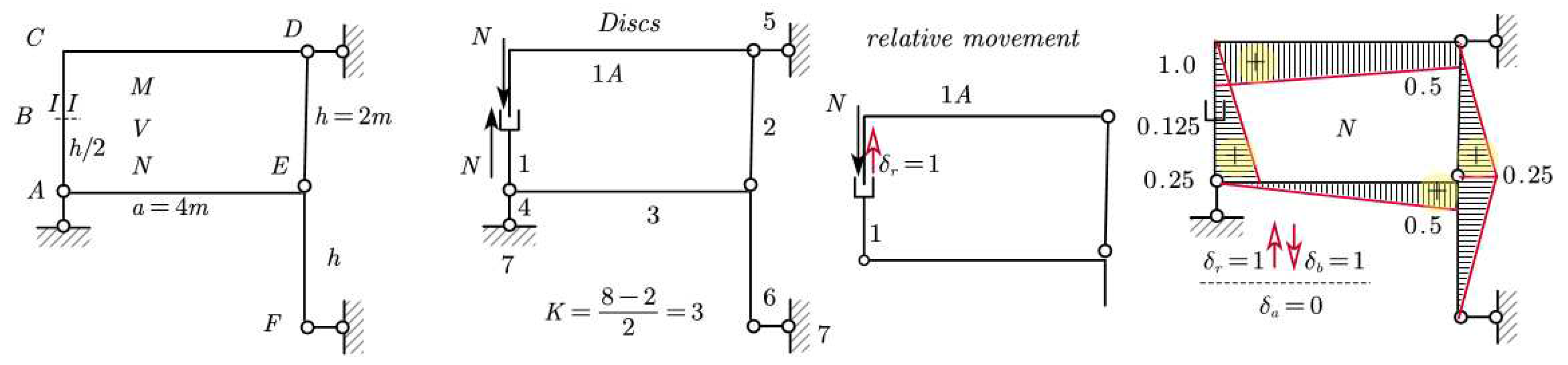
6.2. Application for the normal force

For the normal force applications, the case can be shown as Figure 12:

Relative motion and solution of the system will be:

R = (\begin{matrix} 0 \\ 1 \\ \begin{matrix} 0 \\ 0 \\ \begin{matrix} 0 \\ 0 \end{matrix} \end{matrix} \end{matrix})

and

(\begin{matrix} φ_{1} \\ φ_{2} \\ \begin{matrix} φ_{3} \\ δ_{1} \\ \begin{matrix} δ_{2} \\ δ_{3} \end{matrix} \end{matrix} \end{matrix}) = J^{- 1} R = (\begin{matrix} 0.125 \\ 0.125 \\ \begin{matrix} - 0.125 \\ - 0.25 \\ \begin{matrix} 0.5 \\ 0.5 \end{matrix} \end{matrix} \end{matrix})

whereas

φ_{1 A} = φ_{1} = 0.125

“Derailment” from the paths in this case will be as Table 3.

To examine deeper into the significance of our findings and their broader implications within the fields of structural engineering and applied mechanics there are some aspects to discuss as following.

Invariance of the Jacobian Matrix: One of the key findings of our study is the invariance of the Jacobian matrix for statically determined structures. This finding underscores the robustness and reliability of the Jacobian matrix as a tool for analyzing and predicting the behavior of such structures under varying load conditions. This invariance property provides engineers and designers with a powerful and consistent means to assess structural responses.

Geometric Interpretation of the Jacobian: Our work has revealed a geometric interpretation of the Jacobian matrix, shedding light on its tangible significance. It represents a chain of infinitesimal vector displacements forming a closed contour, projected in both the x and y dimensions. This geometric understanding enhances our grasp of the intricate interplay between forces and geometry within statically determined systems. This insight into the geometric nature of the Jacobian matrix has implications far beyond our study, as it enriches the toolbox of structural engineers by offering a more intuitive perspective on structural behavior.

Pre-Construction of the Jacobian Matrix: Our approach introduces the concept of pre-constructing the Jacobian matrix before the actual mechanism is built. This proactive strategy streamlines the analysis process by eliminating constraints considered in the study, paving the way for a systematic and efficient evaluation of influence lines. The pre-construction methodology introduced here holds great potential for accelerating the analysis of statically determined structures, potentially reducing both time and computational resources required for such evaluations.

Loading Characteristics of Mechanisms: Our study has illuminated an intriguing aspect of the mechanisms derived from statically determined structures. These mechanisms experience loading primarily through the relative movement of one unit, typically in the opposite direction or sense from the previously established internal factor. Understanding these loading characteristics is invaluable for engineers and designers, as it provides insights into how forces are distributed and how mechanisms respond to changes in load conditions. This insight could prove pivotal in optimizing the design and performance of various mechanical systems.

Behavior of Discs and Derailments: Our findings have also offered insights into the behavior of discs within the context of statically determined structures. Notably, discs do not extend, and derailment is represented as the rotation of the Path around the point of zero derailment. These observations deepen our understanding of the intricate mechanics governing these structures and contribute to a more comprehensive knowledge base in the field of structural engineering.

The invariance and geometric significance of the Jacobian matrix, along with the concept of pre-construction, loading characteristics, and behavior of elements like discs, collectively advance our understanding of structural behavior.

7. Conclusions

In conclusion, our study has introduced a novel method utilizing Jacobian contours to evaluate influence lines in statically determined structures. Through our exploration of this innovative approach, several key insights and findings have emerged. Firstly, we have established that the Jacobian matrix remains invariant for statically determined structures. This invariance underscores the fundamental nature of the Jacobian as a robust tool for analyzing the behavior of such structures under varying loads and conditions. Furthermore, we have unveiled the geometric significance inherent in the Jacobian matrix. It serves as a representation of the chain of infinitesimal vector displacements forming a closed contour, projected in both the x and y dimensions. This geometric interpretation enhances our understanding of the Jacobian's role in elucidating the intricate relationships between forces and geometry within statically determined systems. One notable aspect of our method is the pre-construction of the Jacobian matrix before the actual mechanism is built. By removing the constraints we consider, we lay the foundation for a systematic and efficient analysis of influence lines. This proactive approach streamlines the process of understanding and predicting structural responses. Intriguingly, our study has revealed that the mechanism derived from a statically determined structure experiences loading solely through the relative movement of one unit, which occurs in the opposite direction or sense to the previously established internal factor. This insight sheds light on the nuanced interplay between forces and movements within these structures, offering valuable information for engineers and designers.

Finally, our findings indicate that discs within this framework do not extend, and derailment signifies the rotation of the path around the point of zero derailment. This observation provides a deeper understanding of how elements within statically determined structures behave under various conditions, adding to the body of knowledge in structural engineering. In summary, our novel method of employing Jacobian contours has illuminated various facets of influence line analysis in statically determined structures. It has enriched our comprehension of the Jacobian's invariance, geometric significance, and pre-construction role. Moreover, it has unveiled the unique loading characteristics of mechanisms derived from such structures and clarified the behavior of discs and derailments. These findings collectively contribute to advancing the field of structural engineering, providing engineers with powerful tools to enhance the safety and efficiency of load-bearing structures.

Author Contributions

Conceptualization, O.K. and A.S.; methodology, O.K.; software, A.S.; validation, A.S., O.K. and K.D.; formal analysis, R.M.; investigation, K.D.; resources, A.S.; data curation, M.G.; writing—original draft preparation, O.K.; writing—review and editing, K.D and M.G.; visualization, K.D.; supervision, O.K.; project administration, O.K and R.M. All authors have read and agreed to this version of the manuscript.

Funding

The authors would like to thank Technical University of Liberec on Student Grant Competition SGS-2023–3401.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Park, H. Structural Design and Numerical Analysis of Hoisting Device of Test Bed for Aircraft Engine. Appl. Mech. 2023, 4, 407-420. [CrossRef]
Fiorillo, G., & Ghosn, M. (2015). Application of influence lines for the ultimate capacity of beams under moving loads. Engineering Structures, 103, 125–133. [CrossRef]
Young, B. W. (1981). Energy methods of structural analysis. Macmillan Education UK. [CrossRef]
Wang, K., Dong, H., Spyrakos-Papastavridis, E., Qiu, C., & Dai, J. S. (2022). A repelling-screw-based approach for the construction of generalized Jacobian matrices for nonredundant parallel manipulators. Mechanism and Machine Theory, 176, 105009. [CrossRef]
Zhu, P., Jin, S., Bu, X., & Hou, Z. (2023). Improved model-free adaptive control for mimo nonlinear systems with event-triggered transmission scheme and quantization. IEEE Transactions on Cybernetics, 53(9), 5867–5880. [CrossRef]
Huang, N., Jin, Y., Bi, Q., & Wang, Y. (2015). Integrated post-processor for 5-axis machine tools with geometric errors compensation. International Journal of Machine Tools and Manufacture, 94, 65–73. [CrossRef]
Qin, F.-Z., Ma, J.-W., Jia, Z.-Y., Li, G.-L., & Zhang, J.-Z. (2022). Estimation and compensation for deviation of contour in slow tool servo precision turning for complicated curved surface. Journal of Mechanical Science and Technology, 36(8), 4185–4196. [CrossRef]
Song, Z., Wen, J., Wan, N., Ma, J., Hu, Y., Zhang, Y., Gao, Z., Zheng, M., & Li, J. (2023). An optimization algorithm h-gvspm for electrical impedance tomography. IEEE Sensors Journal, 23(5), 4518–4526. [CrossRef]
Wu, K., Li, B., & Zhang, Y. (2022). Design and experimental research of hand–eye coordination control system for acupuncture robot. Journal of Mechanics in Medicine and Biology, 22(07), 2250058. [CrossRef]
Koça, O., Sulejmani, A., & Alimhilli, P. (2021). Direct method of rigidity using Mathcad Software. In IOP Conference Series: Materials Science and Engineering (Vol. 1024, No. 1, p. 012093). IOP Publishing. [CrossRef]
Dedieu, JP. (2015). Newton-Raphson Method. In: Engquist, B. (eds) Encyclopedia of Applied and Computational Mathematics. Springer, Berlin, Heidelberg. [CrossRef]
Sulejmani, Anis, Odhise Koça, and Klodian Dhoska. "METHOD OF PRINCIPAL ORIENTATION IN MOHR’S SPACE." Journal of Southwest Jiaotong University 58.2 (2023). [CrossRef]
Lumi, D., Sulejmani, A., Dhoska, K., & Koça, O. (2022). Study of the strengthened state near the forces for the semi-plan. Pollack Periodica, 17(2), 98-103. [CrossRef]
Sulejmani, Anis, and Odhise Koça. "Development of Optimal Transmission Rate of the Kinematic Chain by using Genetic Algorithms Coded in Mathcad." International Journal of Innovative Technology and Interdisciplinary Sciences 4.4 (2021): 792-803.
G.M. PHILLIPS, P.J. TAYLOR, Theory and Applications of Numerical Analysis (Second Edition), Academic Press, 1996, Pages 440-441, ISBN 9780125535601, (https://www.sciencedirect.com/science/article/pii/B9780125535601500185). [CrossRef]
Zhang, L. Y., Li, Y., Cao, Y. P., & Feng, X. Q. (2014). Stiffness matrix-based form-finding method of tensegrity structures. Engineering structures, 58, 36-48.
Dhoska, K., Lumi, D., Sulejmani, A., & Koça, O. (2022). Measurement uncertainty for mechanical resistance of manufactured steel bar. Pollack Periodica, 17(2), 104-108. [CrossRef]
Sulejmani, A.; Koça, O. Fatigue of Mechanical Structures from Cyclic Wind Actions. Environ. Sci. Proc. 2023, 26, 78. [CrossRef]
Koça, O., Sulejmani, A., & Dhoska, K. (2021). Pressure distribution on rolling-slide contact problem. Pollack Periodica, 16(1), 71-76. [CrossRef]
J. Phys. Chem. 1952, 56, 6, 799–800 Publication Date:June 1, 1952 . [CrossRef]
Helmke, U., Hüper, K. (1997). The Jacobi Method: A Tool for Computation and Control. In: Byrnes, C.I., Datta, B.N., Martin, C.F., Gilliam, D.S. (eds) Systems and Control in the Twenty-First Century. Systems & Control: Foundations & Applications, vol 22. Birkhäuser, Boston, MA. [CrossRef]
Drmač, Z., Hari, V., Slapničar, I. (2002). Advances in Jacobi Methods. In: Drmač, Z., Hari, V., Sopta, L., Tutek, Z., Veselić, K. (eds) Applied Mathematics and Scientific Computing. Springer, Boston, MA. [CrossRef]
O.Koça, Analyse des Spannungszustandes fur Kontaktprobleme bei Abwalzung mit Gleiten. Anwendung dieser Theori auf Zahnráder” Referim. Laboratorium fur Techniche Mechanik. Universitat Paderborn (GH), Germany 1992.
Karnovsky, I.A., Lebed, O. (2010). Influence Lines Method. In: Advanced Methods of Structural Analysis. Springer, Boston, MA. [CrossRef]
Çelik, M.; Noble, T.; Jorge, F.; Jian, R.; Ó Brádaigh, C.M.; Robert, C. Influence of Line Processing Parameters on Properties of Carbon Fibre Epoxy Towpreg. J. Compos. Sci. 2022, 6, 75. [CrossRef]
Mittelstedt, C. (2021). Principle of Virtual Displacements. In: Structural Mechanics in Lightweight Engineering. Springer, Cham. [CrossRef]

Figure 1. 4-bar mechanism with rotation simple joint.

Figure 5. Method to evaluate influence line of a unit force.

Figure 7. Influence line of shear force.

Figure 10. Application of Jacobian Method in a statically determined structure for internal moment.

Figure 11. Application of Jacobian Method in a statically determined structure for shear force.

Figure 12. Application of Jacobian Method in a statically determined structure normal force.

Table 1. Derailment for different paths in internal momentum applications.

Path AB	Path BC	Path CD	Path DE	Path AE
$- δ_{1}$	$- δ_{1} - φ_{1} h / 2$	$0$	$0$	$0$
$- δ_{1} - φ_{1} h / 2$	$δ_{B h} - φ_{1 A} h / 2$	$δ_{3}$	$φ_{2} h$	$- φ_{3} a$
0.5	-0.25	0	0	0
-0.25		1	0.5	1

Table 2. Derailment for different paths in shear force applications.

Path AB	Path BC	Path CD	Path DE	Path AE
$- δ_{1}$	$- δ_{1} - φ_{1} h / 2 - 1$	$0$	$0$	$0$
$- δ_{1} - φ_{1} h / 2$	$- δ_{1} - φ_{1} h - 1$	$δ_{3}$	$φ_{2} h$	$- φ_{3} a$
0.5	-0.25	0	0	0
0.75	0	1	0.5	1

Table 3. Derailment for different paths in normal force applications.

Path AB	Path BC	Path CD	Path DE	Path AE
$- δ_{1}$	$- δ_{1} - φ_{1} h / 2$	$1$	$0$	$0$
$- δ_{1} - φ_{1} h / 2$	$- δ_{1} - φ_{1} h$	$δ_{3}$	$φ_{2} h$	$- φ_{3} a$
0.25	0.125	1	0	0
0.125	0	0.5	0.25	0.5

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Novel Method of Jacobian Contours to Evaluate the Influence Line in Statically Determinate Structure

Abstract

1. Introduction

2. Iterative Solution

3. Calculation of real displacements and velocities by the method of contours

4. Influence line on statically determined structures

4.1. Influence line of normal force.

4.2. Influence line of shear force

5. The geometric meaning of Jacobians

6. Application of Jacobian Method

6.1. Application for internal moment

6.2. Application for shear force

6.2. Application for the normal force

7. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe