Preprint
Article
Mathematical Modeling of Non-small Cell Lung Cancer Biology Through the Experimental Data on Cell Composition and Growth of Patient-Derived Organoids
Altmetrics
Downloads
136
Views
118
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
10 October 2023
Posted:
12 October 2023
You are already at the latest version
Alerts
Abstract
Mathematical models of non-small cell lung cancer are powerful tools that use clinical and experimental data to describe various aspects of tumorigenesis. The developed algorithms capture phenotypic changes in the tumor and predict changes in tumor behavior, drug resistance, and clinical outcomes of anti-cancer therapy. The aim of this study was to propose a mathematical model that predicts the changes in the cellular composition of patient-derived tumor organoids over time with a perspective of translation of these results to the parental tumor, and therefore to possible clinical course and outcomes for the patient. Using the data on specific biomarkers of cancer cells (PD-L1), tumor-associated macrophages (CD206), natural killer cells (CD8), and fibroblasts (αSMA) as input, we proposed a model that accurately predicts the cellular composition of patient-derived tumor organoids at a desired time point. Combining the obtained results with “omics” approaches will improve our understanding of the nature of NSCLC. Moreover, their implementation into clinical practice will facilitate a decision-making process on treatment strategy and develop a new personalized approach in anti-cancer therapy.
Keywords:
Subject: Medicine and Pharmacology - Oncology and Oncogenics
1. Introduction
Non-small cell lung cancer (NSCLC) is one of the deadliest forms of cancer worldwide. Lung cancer organoids are three-dimensional cell aggregates grown from tumor cells in vitro. Unlike traditional monolayered cell cultures, patient-derived tumor organoids (PDTOs) preserve cellular architecture, mutations, and growth of their parental tumor [1,2]. In this respect, exploring the properties of patient-derived organoids represents an attractive option to explore tumor organization, evolution, and complex behavior in controlled conditions.
Mathematical models are often used to evaluate drug responses in infectious and oncologic disorders to predict the outcome of proposed therapy [3,4]. They are also used to assess the efficacy of vaccines. In this regard, nearly any signaling or metabolic pathway is describable as a combination of mathematical equations in the system [5,6,7]. Previously, several authors already proposed mathematical models of tumor growth (rev. in [8]). In such mathematical models, an ordinary differential equation (ODE) is an equation for a function of an independent variable that involves several derivatives characterizing its behavior. The systems of differential equations make it possible to address more complex problems. For instance, it would be possible to assess tumor size using the data on its cellular composition. In perspective, advanced mathematical models will define a time window most suitable for the surgery.
Moreover, several known mathematical models predict the malignancy of lung cancer. Some of these models use imaging data and the results of clinical tests (rev. in [9]), the others – the patients' genetics, such as mutations and specific biomarkers. As believed, efficient mathematical models with good prediction performance will improve the detection of lung cancer at early stages due to the facilitation of its diagnosis.
In the present paper, we apply a computational approach to assess the parameters of a mathematical model simulating the time-dependent counts of cellular subpopulations in patient-derived organoids. The proposed mathematical model originates from the models of lung cancer progression previously developed by Geng et al. [10]. This model accounts for four subpopulations of cancer and tumor-associated cells. Using this approach, we systematically explored changes in the cell composition of PDTOs. Here, our aim was to develop a mathematical model for prediction of changes in the cellular composition of organoids with a perspective of translating these results into the respective parental tumor which potentially can be used as a part of patient condition assessment and NSCLC prognosis.
2. Materials and Methods
2.1. Patients
The material was obtained from 16 patients from the first oncological hospital (Moscow, Russian Federation) and Novgorod Regional hospital (Veliky Novgorod, Russian federation) after surgery. The mean age was 65 years (SD 4.1), 13 of the patients were men (81%) and 3 were women (19%). All the patients have undergone thoracotomic lobectomy due to non-small cell lung cancer (NSCLC). A mathematical model was developed based on data obtained from patient-derived organoid culture of NSCLC.
2.2. Generation of PDTOs
Tumor sample was placed into basal DMEM/F12 (PanEco, Russia) culture medium supplemented with 1x penicillin-streptomycin (PanEco) and delivered to the lab on ice immediately after the surgery. In the lab, the tissue was finely chopped into small pieces using surgical scissors and then immersed in 10 mL of DMEM/F12 growth medium. This medium was supplemented with 1% Penicillin-Streptomycin (PenStrep) and 1 mg mL-1 of collagenase I (Gibco). Afterward, the minced tissue was allowed to incubate at 37°C for 1.5 hours with gentle and slow agitation.
Following the incubation, the digested tissue suspension was filtered through a 70-μm cell strainer (Falcon). The resulting cell suspension was then subjected to centrifugation at 1,500 rpm for 5 minutes at a temperature of 18–20°C. The pellet obtained after centrifugation was washed with HBSS and subsequently resuspended in 6 mL of fresh growth medium suitable for organoid culture. This organoid culture medium consisted of DMEM/F12 supplemented with 20 ng mL-1 of basic fibroblast growth factor (bFGF, 10014-HNAE, SinoBiological, China), 50 ng mL-1 of human epidermal growth factor (EGF, ab55566, Abcam), N2 supplement (PanEco, Moscow, Russia), NeuroMax (PanEco, Moscow, Russia), 10 mM Glutamax (Gibco), 1 mM N-acetyl cysteine (Sigma), 10 mM nicotinamide (Sigma), 10 μM Y27631 (ab120129, Abcam), 15 μM HEPES (Sigma), and 1% Penicillin-Streptomycin (PenStrep). The total cell count was determined using a hemocytometer, and a portion of the collected cells was preserved by freezing for subsequent flow cytometry analysis.
To generate free-floating NSCLC organoids, 96-well plates were initially coated with a 1% w/v agarose solution in Milli-Q water, applying 50 μL to each well. This agarose coating was allowed to solidify at room temperature for approximately 20–30 minutes. Subsequently, a collagen-based gel solution containing resuspended tumor cells was prepared using the SANATO 3D culture gel kit (#FTBM0051, Phystech Biomed, Russia) and 1% (v/v) SANATO reagent (#FTBM0050, Phystech Biomed, Russia) following the manufacturer's protocol. Next, 25 μL gel domes, each containing 50,000 cells, were dispensed into individual wells, and the gel was allowed to solidify at 37°C for 20 minutes. After the gel had set, 100 μL of organoid growth medium was added to each well, and the plates were placed in an incubator. The incubation was carried out at 37°C in a humidified atmosphere with 5% CO2. The growth medium was replaced every other day throughout the entire experiment. Over a period of 14 days, the organoids were subject to daily examination, during which their size and morphology were observed using bright-field microscopy with an AxioVert.A1 microscope (Zeiss, Oberkochen, Germany).
2.3. Flow cytometry
Harvested organoids were centrifuged (1,500 rpm, 5 min, r.t.). The pellet was resuspended in basal DMEM/F12 cell culture medium (1 mL/plate). Then, equal volume of 0.1% collagenase I was added and the samples were incubated for 90 min at 37°C with shacking. After the incubation, the cells were washed and resuspended in versene (0.48 mM EDTA, pH 7.4). The resuspended cells were fixed in 4% formaldehyde for 15 min at room temperature and washed twice in excess of 1X PBS. After washing the cells were resuspended in 0.1% TRITON X-100 prepared in 1x PBS and incubated for 15 min at room temperature. Then the cells were incubated with primary antibodies for 1h, in dark, and on ice. The following primary antibodies were used in this study: rabbit Alexa Fluor® 647 monoclonal anti-human antibodies directed to mannose receptor/CD206 (ab195192, Abcam), mouse monoclonal anti-human antibodies directed to CD8α (ab33786, Abcam), rabbit recombinant anti-human antibodies directed to PD-L1 (ab205921, Abcam), rabbit recombinant anti-human antibody directed to α-smooth muscle actin/αSMA (ab124964, Abcam). After the incubation, the cells were washed twice in ice-cold Versene and resuspended in 1x PBS, Then, the samples were incubated with secondary antibodies for 30 min, in dark, and on ice. The following secondary antibodies were used: goat anti-rabbit IgG H&L conjugated with Alexa Fluor® 647, preadsorbed (ab150083, USA) and goat anti-mouse IgG H&L conjugated with Alexa Fluor® 647 (ab150115, Abcam). After the incubation, the cells were washed with Versene and subjected to flow cytometry.
2.4. Mathematical approaches used in this study
The obtained results were analyzed on PC using Python 3.7. Libraries numpy 1.24.2, maptplotlib 3.7.1 were used for data processing. The scipy 1.10.1 was used to solve the differential equations system.
3. Results
3.1. General work flow
In this study, we present a diagram to visualize the interactions of cells within NSCLC tumors and generated the tumor-specific microenvironment based on the previously published data on their cell composition [11]. We converted the diagram into a system of differential equations (1) to describe the changes in subpopulations of cells in time. We also performed flow cytometry analysis of PDTOs to identify four main subpopulations of cells expressing the specific biomarkers (Table 1). Then, we solved the system of differential equations using the assessments of several parameters previously reported by others (Table 2).
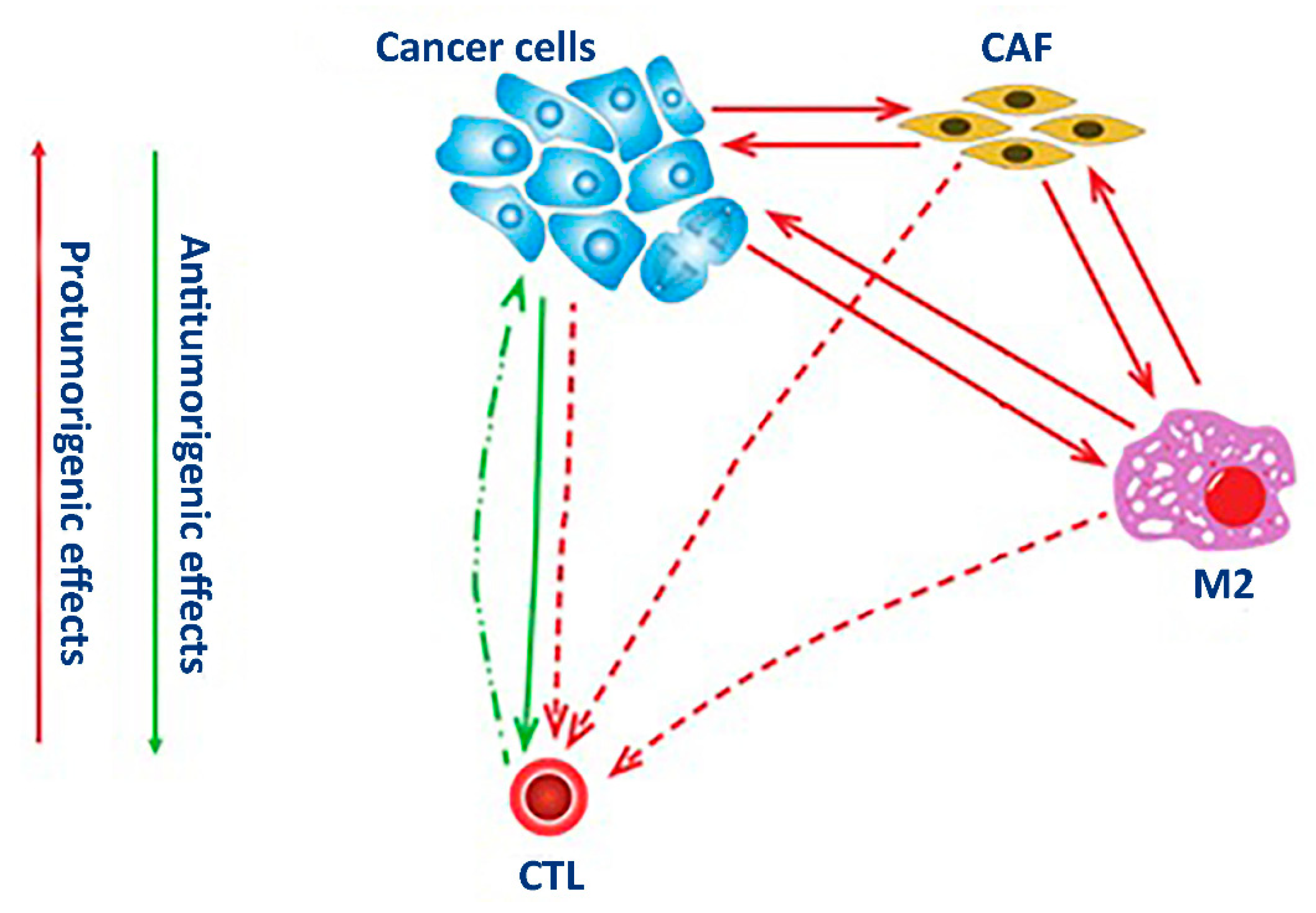
Figure 1.
The logic model of NSCLC organoid tumor microenvironment. Cancer cells (CAN) promote the activation of stromal cells into cancer-associated fibroblasts (CAF) and the polarization of macrophages toward the M2 phenotype (M2). These cells stimulate each other and suppress the anti-tumor activity of cytotoxic lymphocytes - CTL (red arrows). Contrarily, their anti-tumor activity is stimulated by specific antigens on the surface of some tumor cells (green arrows).
Figure 1.
The logic model of NSCLC organoid tumor microenvironment. Cancer cells (CAN) promote the activation of stromal cells into cancer-associated fibroblasts (CAF) and the polarization of macrophages toward the M2 phenotype (M2). These cells stimulate each other and suppress the anti-tumor activity of cytotoxic lymphocytes - CTL (red arrows). Contrarily, their anti-tumor activity is stimulated by specific antigens on the surface of some tumor cells (green arrows).
3.2. Mathematical model
The mechanistic model describing the interaction of cells in NSCLC tumor is defined by the system of differential equations (1):
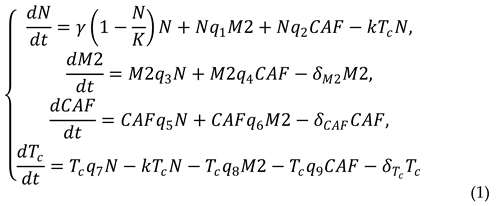
where t – time in days, N – number of cancer cells, M2 – number of M2-polarized (tumor-associated) macrophages, CAF – number of cancer-associated fibroblasts, Tc – number of cytotoxic T-cells. The values of γ, K, q1, k, q3, δM2, δTc were previously assessed by others (see Table 2). The remaining parameters, namely q2, q4, q5, q6, δCAF, q7, q8. q9 (Table 3), were assessed by us using the quantity of cells measured in PDTOs on days 7, 14, and 21 by flow cytometry for PDTOs developed from various tumors. Performing the calculations, we assumed that all assessed parameters had to be above zero. The results of calculations are represented in Table 4.
3.3. Solving the system of differential equations
The system of differential equations (1) can be written in vector form dZ/dt=F(Z) where
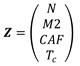
In time interval between i and i + 1, the system of differential equations can be approximated by the system of difference equations in form (2) using the experimental data obtained for individual tumors.
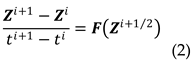
Vector Z i+1⁄2 was calculated using interpolation formulas (3) and (4) for non-negative and strictly positive elements, respectively.
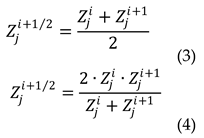
To the reference, j – was number of the element in the vector Z.
Since all parameters that we needed to estimate were introduced in equations (2) linearly, this system was written as a system of linear equations (5)
AQ = B
In this case, A and vector B were calculated from terms of the equations (2). Elements of the vector Q were the parameters that we needed to estimate. The number of columns of the matrix A and dimensions of the vector Q were equal to 8, i.e. the number of parameters that we needed to estimate. The number of rows in the matrix A and dimensions of the vector B depended on how many measurements were made and should not be less than 8. Since the system of equations (5), was overdetermined, it was solved by the method of least squares (6):
Q = (AT x A) −1 x A TB
The results of calculations are presented in Table 4.
To implement the above methodology, we developed a program in Python. The program accepts input data (the results of flow cytometry experiments performed in two time points at least) in Microsoft Excel format and predicts changes in cell composition of PDTOs. To avoid negative values for the parameters listed in Table 3, we adjusted the published values of known parameters as indicated in the last column of Table 2.
Using the proposed mathematical model, describing the interactions in four subpopulations of tumor cells, we explored how the cellular composition of PDTOs could change from day 7 to day 14 of the experiment (Figure 2). The results demonstrated that the predicted changes in subpopulations of cells, except the ratio of PDL1-positive cells in sample donated by patient 8, were describable by functions without local extrema between the desired time points (Figure 2). In the last case (Figure 2a), the ratio of PDL1-positive cells kept increasing from the day 7 and reached the maximum at day 11 of the experiment. In the sample donated by patient 9, the changes in the subpopulation of CD206-positive cells did not exceed 2%, whereas the ratio of αSMA-positive cells changed by a fraction of a percent (Figure 2b). In samples with the prevalence of PDL1- and CD8-positive cells (patients 13 and 14, the predicted changes in subpopulations of other cells (αSMA, CD206, and CD8 – in the former and αSMA, CD206 и PDL1 – in the latter cases, respectively), did not exceed a fraction of a percent (Figure 2c and d). Contrarily, the ratios of PDL1- and CD8-positive cells in samples 13 and 14 samples progressively increased by factors 1.5 and 1.4, respectively.
4. Discussion
In this paper, we analyzed changes in four subpopulations of cells in PDTOs originated from NSCLC tumors. PD-L1-positive cells represented a prominent cancer phenotype capable of suppressing the adaptive arm of immune systems. The cells expressing αSMA were typically of mesenchymal origin. The authors of experimental studies often considered αSMA as a specific biomarker of CAFs. NSCLC tumor cells positive for CD206 and CD8 represented tumor-associated macrophages and cytotoxic T-cells.
Similar to other cell-specific biomarkers, the expression of PD-L1 also occurs in healthy cells, such as immune and epithelial cells, particularly under inflammatory conditions, such as autoimmune responses, chronic infection, and sepsis [15]. The binding of PD-L1 to the inhibitory checkpoint molecule PD-1 located on the surface of activated immune cells activates an inhibitory signal that helps the targeted cells bypass surveillance by immune cells. In this regard, the expression of PD-L1 by cancer cells lets them evade the host immune system. Recruiting stromal and immune cells allows cancer cells to bundle up an immunosuppressive microenvironment. This tumor-specific microenvironment is suitable for the proliferation of cancer cells. It also facilitates the development of drug resistance (Figure 1).
The expression of αSMA mainly occurs in connective tissues in mesenchymal cells, such as vascular endothelial cells and smooth muscle cells. In fibroblasts, αSMA becomes induced upon their activation following an injury. In the lung, the presence of αSMA-positive fibroblasts is evident in fibrotic tissues and tumors [16]. As a part of a tumor, the activated fibroblasts establish direct contact with the cancer cells. Moreover, cancer cells influence their gene expression by soluble factors promoting the acidification of the surrounding milieu and establishing the hypoxic conditions in the core of the tumor. Participating in the secretion and deposition of extracellular matrix [17] by tumors, CAFs provide them with structural support and improve their resistance to anti-cancer drugs (Figure 1).
The mannose receptor CD206 is a surface receptor of M2 macrophages. Unlike CD86-positive (M1) macrophages participating in the development of inflammatory response, M2 macrophages suppress inflammation and contribute to wound healing [18]. The polarization of macrophages to either M1 or M2 phenotype is reversible. For instance, recruiting M1 macrophages by tumor cells induces their repolarization to the M2 phenotype [19]. After repolarization, M2 macrophages become tumor-associated macrophages (TAM). Sustaining in the tumor microenvironment, TAMs promote tumor growth and cancer progression (Figure 1) by producing various growth factors and cytokines, such as IL6, FGF, and VEGFA. These cytokines stimulate angiogenesis, tumor cell proliferation, and invasion. Expressing immunosuppressive cytokines (e.g., IL10 and TGFβ), TAMs suppress the activation of T-cells. TAMs also contribute to the production of extracellular matrix. In turn, covering the tumor with a layer of extracellular protects tumor cells from apoptosis and improves their resistance to anti-cancer therapies.
The CD8 protein is a specific receptor of cytotoxic T lymphocytes. This receptor participates in their interaction with antigen-presenting cells. In the body, cytotoxic CD8-positive T cells kill pathogens and eliminate cancer cells [20]. However, some CD8-positive T-cells acquire unresponsiveness to cancer cells due to prolonged exposure to TCR signaling by cognate antigen. Chronic exposure to the antigen in the tumor microenvironment induces the genes of inhibitory receptors, such as PD-1. Although these cells remain in the tumor microenvironment, they stop expressing the proinflammatory cytokines (IFNγ, TNF, and IL2) and rarely proliferate [21]. The exhausted CD8-positive cells contribute to tumor survival by driving tumor cells to impair the immune attack and recruiting other cells to reprogram the immune milieu. Interaction with CAFs also suppresses T lymphocyte activity [22] by inhibiting the differentiation of CD8-positive T cells and disabling their tumor reactivity to benefit the cancer cells (Figure 1).
Recently, other authors proposed several mathematical models linking the cellular composition of tumors with various aspects of tumorigenesis. Dean E.A. et al. [23] constructed a mathematical model that linked the level of circulating tumor DNA with the metabolic activity of B lymphoma targeted with a T-cell-based therapy against chimeric antigen receptor (CAR). Analyzing the results of PET scans, the authors found a strong correlation between the named parameters (r2 = 0.61, p = 0.0001). However, they did not see an evident correlation after the exclusion of patients in remission because the metabolic activity of the tumor might reach either the maximum or upper detection limit. They also saw an even stronger correlation (r2 = 0.79, p = 0.0007) among the same individuals two months later due to a decline in tumor metabolic activity caused by a therapeutic response. Based on the obtained results, Dean E.A. et al. concluded that their assessments of tumor metabolic rate could be more precise if they considered heterogeneity of patients’ ctDNA.
Pedersen R.K. et al. developed a mathematical model that used measurable changes in subpopulations of tumor cells to describe the establishment of metastatic niches [24]. Analyzing the experimental data obtained by others, the authors explored the clinical value of various processes, such as the proliferation of cancer stem cells, their differentiation, attachment, and detachment from the niche. Combining mathematical analysis and computer simulations, Pedersen R.K. et al. concluded that routine medical tests, such as blood and bulk marrow sampling, provide limited information about cellular interactions in the niche and clonal composition of participating stem cells. The authors also proposed that future studies could improve our understanding of how the metastatic niches niche form and develop and help to optimize the effects of low-dose chemotherapy.
Meade W. et al. reported a mechanistic mathematical model that predicts the effectiveness point of drugs used for prostate cancer [25]. Analyzing the dynamics of patients’ PSA and androgen levels, the authors discovered two indicators of treatment failure. The first is the amount of androgen receptors on the surface of cancer cells, and the second is the ratio of androgen to PSA in patients’ blood. In the first case, the number of androgen receptors had to exceed a threshold value, whereas, in the second case, the ratio of androgen to PSA should fall. Both indicators predicted the loss of the therapeutic effect with high accuracy (87.3 and 88.7%, respectively). The authors concluded that using their model in clinical practice could timely advise physicians on changing the therapy.
Ait Oumghar I. et al. presented a mechanobiological bone remodeling model that couples cellular activities, mechanical stimuli, and the changes in bone mineral density during breast cancer therapy [26]. The authors programmed and implemented the model algorithm on MATLAB software and simulated different scenarios for treatment with tamoxifen and aromatase inhibitors. Ait Oumghar I. et al. assessed their effects on bone remodeling. They also predicted how the bone volume fraction and the associated bone density loss would change over a period of time. The authors also estimated the damaging effect of each treatment regimen. Based on the results of their study, Ait Oumghar I. et al. identified the combination of chemotherapy, tamoxifen, and aromatase inhibitors, followed by the combination of chemotherapy and tamoxifen as the most risky regimen for bone damage. In addition, they confirmed this conclusion by the clinical observations of patients with breast cancer. In this regard, Ait Oumghar’s model is suitable for choosing an appropriate combination of treatments for individual patients and testing new therapeutic agents.
Larsson et al. constructed quantitative models of the time-dependent transcriptional variation of patient-derived glioblastoma cells [27]. To build the models, the authors followed the barcoded glioblastoma cells and their progeny over three weeks. They recorded the changes in morphological characteristics and the growth rate of cancer cells. Using computational simulation, the authors discovered a hierarchical organization of the cell. They also showed that cells experienced significant phenotyping changes during their lifetime, which were somehow patient-specific. In turn, the tested therapeutic agents inhibited the specific states of the cells and altered their differentiation. In this regard, the model proposed by Larssen et al. could predict how a drug therapy affected the cancer cells in a time-dependent manner and serve for evaluation of new experimental drugs.
In turn, the mathematic model reported in this study allowed us to estimate the scale of changes in the four most abundant subpopulations of cells previously discovered in NSCLC tumors (Table 4) and create a computer program to predict changes in cellular composition of PDTOs using the results of flow cytometry experiments performed at two data points (Figure 2). We found that prevalence of some cells in PDTO over the others suppresses their growth (Figure 2c and d). Cytotoxic CD8-positive cells may interfere with PDL1-positive, mostly the cancer cells (Figure 2a and b). In Figure 2a, the ratio of PDL1-positive cells in the sample kept declining starting from day 11 of the experiment. On the other hand, the fraction of CD8-positive cells rapidly increased. The opposite scenario occurred in PDTOs donated by patient 9 (Figure 2b), where cytotoxic CD8-positive cells became nearly undetectable on day 14. Contrarily, the ratio of PDL1-positive cells stabilized at 3% after a steady decline. In turn, the deviations between some predicted values and experimental data indicated that the developed computer program needs improvement.
According to the previously published data, some antigens considered in our study, such as α-SMA and PDL1 (Table 2), are not strictly limited to CAFs and cancer cells, respectively. In this regard, some cancer cells do not express PD-L1. However, expressing PD-L1 helps cancer cells to avoid immune surveillance [28,29]. Moreover, a certain percentage of M2 also expresses PD-L1 [30]. Therefore, the number of PD-L1-expressing macrophages shall be subtracted from the total number of PD-L1-positive cells. In turn, some cancer cells express α-SMA because α-SMA is one of the known biomarkers of epithelial-mesenchymal transition. However, the number of non-fibroblast α-SMA-positive cells in our experimental conditions was negligible by measuring the cellular composition in the experimental block. In addition to the above, a systematic literature review was conducted throughout the model study pathway to more accurately reproduce intercellular interactions. Quantification of double-labeled cells and taking them into account would improve the accuracy of the made predictions.
In turn, the presented mathematic model also has several limitations. First, we performed this study on a limited number of patients. Respectively, a higher sample size would improve the accuracy of our predictions. Second, our prediction power is time-limited since we used the experimental data obtained at three different time points - on days 7, and 14 of the experiment. Respectively, getting out of this time interval will lower the accuracy of our assessments. Third, although organoids are similar to their parental tumors in many aspects [31], their prolonged culturing in vitro would result in different clinical phenotypes due to the isolation of organoids from the host immune and endocrine system. The organoids do not experience pressure from the approaching immune cells. The growth factors that the organoids receive with culture medium are not necessarily the same and in the same concentrations as the ones delivered to the tumor in vivo. [32]. Fourth, the ability of organoids to recruit new cells is limited to the cells already present in the well at plating. Fifth, the model does not consider changes in minor subpopulations of cells.
5. Conclusions
The proposed mathematical model allowed us to range previously unknown parameters characterizing the intercellular interactions in PDTOs obtained from NSCLC tumors. The following implementation of this model into computer application lets us predict the changes in the four most abundant subpopulations of NSCLC tumor cells: PD-L1-positive cancer cells, α-SMA-positive CAFs, CD206-positive TAM, and CD8-positive cytotoxic T-lymphocytes. Although the proposed mathematic model has several limitations and the developed software still needs improvement, in perspective, they would fit into clinical practice to estimate the probability of tumor relapse and survivability of the patients. At the time, we are planning a follow-up study on a new cohort of patients to increase the accuracy of computer applications. We anticipate that the improved version of the computer application would be able to contribute to a solid foundation for developing new NSCLC models, confirm the results of diagnostic tests and make predictions on the cellular composition of tumors using the available clinical data of individual patients, with no need for additional statistical data.
Author Contributions
Conceptualization, V. Makarov, M. Durymanov, and Y. Rumyantsev; methodology, M. Durymanov, A. Mezentsev and Y. Rumyantsev; resources, R. Sulimanov, Komal Zahid and Lilian Ismail; investigation, M. Durymanov and A. Mezentsev; data curation, M. Durymanov and I. Laskov; software, K. Koshelev and I. Laskov; formal analysis, K. Koshelev, A. Mezentsev and I. Laskov; writing — Y. Rumyantsev; writing—review and editing, M. Durymanov and A. Mezentsev.; visualization, A. Mezentsev and I. Laskov; supervision, V. Makarov; project administration, V. Makarov; funding acquisition, V. Makarov. All authors have read and agreed to the published version of the manuscript.
Funding
The work was financed by the Ministry of Science and Higher Education of the Russian Federation within the framework of state support for the creation and development of a World-Class Research Centers “Digital Biodesign and Personalized Healthcare”, project # 075–15-2022–306.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Ethic Committee of Sechenov University (protocol code 12 and January 15, 2023) for studies involving humans.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rossi, R.; De Angelis, M.L.; Xhelili, E.; Sette, G.; Eramo, A.; De Maria, R.; Cesta Incani, U.; Francescangeli, F.; Zeuner, A. Lung Cancer Organoids: The Rough Path to Personalized Medicine. Cancers (Basel) 2022, 14. [Google Scholar] [CrossRef]
- Li, Y.; Gao, X.; Ni, C.; Zhao, B.; Cheng, X. The application of patient-derived organoid in the research of lung cancer. Cell Oncol (Dordr) 2023, 46, 503–519. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Shen, J.; Zou, X. Mathematical modeling and dynamical analysis of anti-tumor drug dose-response. Math Biosci Eng 2022, 19, 4120–4144. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez Messan, M.; Yogurtcu, O.N.; McGill, J.R.; Nukala, U.; Sauna, Z.E.; Yang, H. Mathematical model of a personalized neoantigen cancer vaccine and the human immune system. PLoS Comput Biol 2021, 17, e1009318. [Google Scholar] [CrossRef] [PubMed]
- Voit, E.O. The best models of metabolism. Wiley Interdiscip Rev Syst Biol Med 2017, 9. [Google Scholar] [CrossRef] [PubMed]
- Bag, A.K.; Mandloi, S.; Jarmalavicius, S.; Mondal, S.; Kumar, K.; Mandal, C.; Walden, P.; Chakrabarti, S.; Mandal, C. Connecting signaling and metabolic pathways in EGF receptor-mediated oncogenesis of glioblastoma. PLoS Comput Biol 2019, 15, e1007090. [Google Scholar] [CrossRef] [PubMed]
- Santarpia, M.; Aguilar, A.; Chaib, I.; Cardona, A.F.; Fancelli, S.; Laguia, F.; Bracht, J.W.P.; Cao, P.; Molina-Vila, M.A.; Karachaliou, N.; et al. Non-Small-Cell Lung Cancer Signaling Pathways, Metabolism, and PD-1/PD-L1 Antibodies. Cancers (Basel) 2020, 12. [Google Scholar] [CrossRef] [PubMed]
- Tabassum, S.; Rosli, N.B.; Binti Mazalan, M.S.A. Mathematical Modeling of Cancer Growth Process: A Review. Journal of Physics: Conference Series 2019, 1366, 012018. [Google Scholar] [CrossRef]
- Feng, Y.; Li, X.; Wang, Y. Establishment of a mathematical model for predicting malignancy of lung cancer complicated with Talaromyces Marneffei infection and its chest imaging characteristics. Results in Physics 2021, 25, 104312. [Google Scholar] [CrossRef]
- Geng, C.; Paganetti, H.; Grassberger, C. Prediction of Treatment Response for Combined Chemo- and Radiation Therapy for Non-Small Cell Lung Cancer Patients Using a Bio-Mathematical Model. Sci Rep 2017, 7, 13542. [Google Scholar] [CrossRef]
- Popper, H.H. Manipulation of the immune system by non-small cell lung cancer and possible therapeutic interference. Cancer Drug Resist 2020, 3, 710–725. [Google Scholar] [CrossRef]
- Unni, P.; Seshaiyer, P. Mathematical Modeling, Analysis, and Simulation of Tumor Dynamics with Drug Interventions. Comput Math Methods Med 2019, 2019, 4079298. [Google Scholar] [CrossRef] [PubMed]
- Dritschel, H.; Waters, S.L.; Roller, A.; Byrne, H.M. A mathematical model of cytotoxic and helper T cellinteractions in a tumour microenvironment. Letters in Biomathematics 2018, 5, S36–S68. [Google Scholar] [CrossRef]
- Eftimie, R.; Eftimie, G. Investigating Macrophages Plasticity Following Tumour-Immune Interactions During Oncolytic Therapies. Acta Biotheor 2019, 67, 321–359. [Google Scholar] [CrossRef] [PubMed]
- Qin, W.; Hu, L.; Zhang, X.; Jiang, S.; Li, J.; Zhang, Z.; Wang, X. The Diverse Function of PD-1/PD-L Pathway Beyond Cancer. Front Immunol 2019, 10, 2298. [Google Scholar] [CrossRef] [PubMed]
- Hinz, B.; Celetta, G.; Tomasek, J.J.; Gabbiani, G.; Chaponnier, C. Alpha-smooth muscle actin expression upregulates fibroblast contractile activity. Mol Biol Cell 2001, 12, 2730–2741. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, P. Cancer-stromal interactions: Role in cell survival, metabolism and drug sensitivity. Cancer Biol Ther 2011, 11, 150–156. [Google Scholar] [CrossRef]
- Sobolev, V.V.; Tchepourina, E.; Korsunskaya, I.M.; Geppe, N.A.; Chebysheva, S.N.; Soboleva, A.G.; Mezentsev, A. The Role of Transcription Factor PPAR-γ in the Pathogenesis of Psoriasis, Skin Cells, and Immune Cells. Int J Mol Sci 2022, 23. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, X.; Liu, L.; Wang, J.; Wu, J.; Sun, C. Role of macrophages in tumor progression and therapy (Review). Int J Oncol 2022, 60. [Google Scholar] [CrossRef]
- Raskov, H.; Orhan, A.; Christensen, J.P.; Gögenur, I. Cytotoxic CD8(+) T cells in cancer and cancer immunotherapy. Br J Cancer 2021, 124, 359–367. [Google Scholar] [CrossRef]
- Guan, Y.; Kraus, S.G.; Quaney, M.J.; Daniels, M.A.; Mitchem, J.B.; Teixeiro, E. FOLFOX Chemotherapy Ameliorates CD8 T Lymphocyte Exhaustion and Enhances Checkpoint Blockade Efficacy in Colorectal Cancer. Front Oncol 2020, 10, 586. [Google Scholar] [CrossRef]
- Xie, Q.; Ding, J.; Chen, Y. Role of CD8(+) T lymphocyte cells: Interplay with stromal cells in tumor microenvironment. Acta Pharm Sin B 2021, 11, 1365–1378. [Google Scholar] [CrossRef] [PubMed]
- Dean, E.A.; Kimmel, G.J.; Frank, M.J.; Bukhari, A.; Hossain, N.M.; Jain, M.D.; Dahiya, S.; Miklos, D.B.; Altrock, P.M.; Locke, F.L. Circulating tumor DNA adds specificity to PET after axicabtagene ciloleucel in large B-cell lymphoma. Blood Adv 2023, 7, 4608–4618. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, R.K.; Andersen, M.; Skov, V.; Kjær, L.; Hasselbalch, H.C.; Ottesen, J.T.; Stiehl, T. HSC Niche Dynamics in Regeneration, Pre-malignancy, and Cancer: Insights From Mathematical Modeling. Stem Cells 2023, 41, 260–270. [Google Scholar] [CrossRef] [PubMed]
- Meade, W.; Weber, A.; Phan, T.; Hampston, E.; Resa, L.F.; Nagy, J.; Kuang, Y. High Accuracy Indicators of Androgen Suppression Therapy Failure for Prostate Cancer-A Modeling Study. Cancers (Basel) 2022, 14. [Google Scholar] [CrossRef] [PubMed]
- Ait Oumghar, I.; Barkaoui, A.; Ghazi, A.E.; Chabrand, P. Modeling and simulation of bone cells dynamic behavior under the late effect of breast cancer treatments. Med Eng Phys 2023, 115, 103982. [Google Scholar] [CrossRef] [PubMed]
- Larsson, I.; Dalmo, E.; Elgendy, R.; Niklasson, M.; Doroszko, M.; Segerman, A.; Jörnsten, R.; Westermark, B.; Nelander, S. Modeling glioblastoma heterogeneity as a dynamic network of cell states. Mol Syst Biol 2021, 17, e10105. [Google Scholar] [CrossRef]
- Schildhaus, H.U. [Predictive value of PD-L1 diagnostics]. Pathologe 2018, 39, 498–519. [Google Scholar] [CrossRef]
- Liu, J.; Li, C.; Seery, S.; Yu, J.; Meng, X. Identifying optimal first-line interventions for advanced non-small cell lung carcinoma according to PD-L1 expression: A systematic review and network meta-analysis. Oncoimmunology 2020, 9, 1746112. [Google Scholar] [CrossRef]
- Gordon, S.R.; Maute, R.L.; Dulken, B.W.; Hutter, G.; George, B.M.; McCracken, M.N.; Gupta, R.; Tsai, J.M.; Sinha, R.; Corey, D.; et al. PD-1 expression by tumour-associated macrophages inhibits phagocytosis and tumour immunity. Nature 2017, 545, 495–499. [Google Scholar] [CrossRef]
- Li, Y.; Chan, J.W.Y.; Lau, R.W.H.; Cheung, W.W.Y.; Wong, A.M.; Wong, A.M.; Wong, N.; Ng, C.S.H. Organoids in Lung Cancer Management. Front Surg 2021, 8, 753801. [Google Scholar] [CrossRef] [PubMed]
- Qi, X.; Prokhorova, A.V.; Mezentsev, A.V.; Shen, N.; Trofimenko, A.V.; Filkov, G.I.; Sulimanov, R.A.; Makarov, V.A.; Durymanov, M.O. Comparison of EMT-Related and Multi-Drug Resistant Gene Expression, Extracellular Matrix Production, and Drug Sensitivity in NSCLC Spheroids Generated by Scaffold-Free and Scaffold-Based Methods. Int J Mol Sci 2022, 23. [Google Scholar] [CrossRef] [PubMed]
Figure 2.
Model-predicted dynamics of cell quantity in organoid from 7-th to 14-th day of incubation. a) Patient 8; b) Patient 9; c) Patient 13; d) Patient 14. PD-L1 – cancer cells, CAF – cancer-associated fibroblasts, M2 – M2 polarized macrophages, CD8 – cytotoxic T-cells.
Figure 2.
Model-predicted dynamics of cell quantity in organoid from 7-th to 14-th day of incubation. a) Patient 8; b) Patient 9; c) Patient 13; d) Patient 14. PD-L1 – cancer cells, CAF – cancer-associated fibroblasts, M2 – M2 polarized macrophages, CD8 – cytotoxic T-cells.
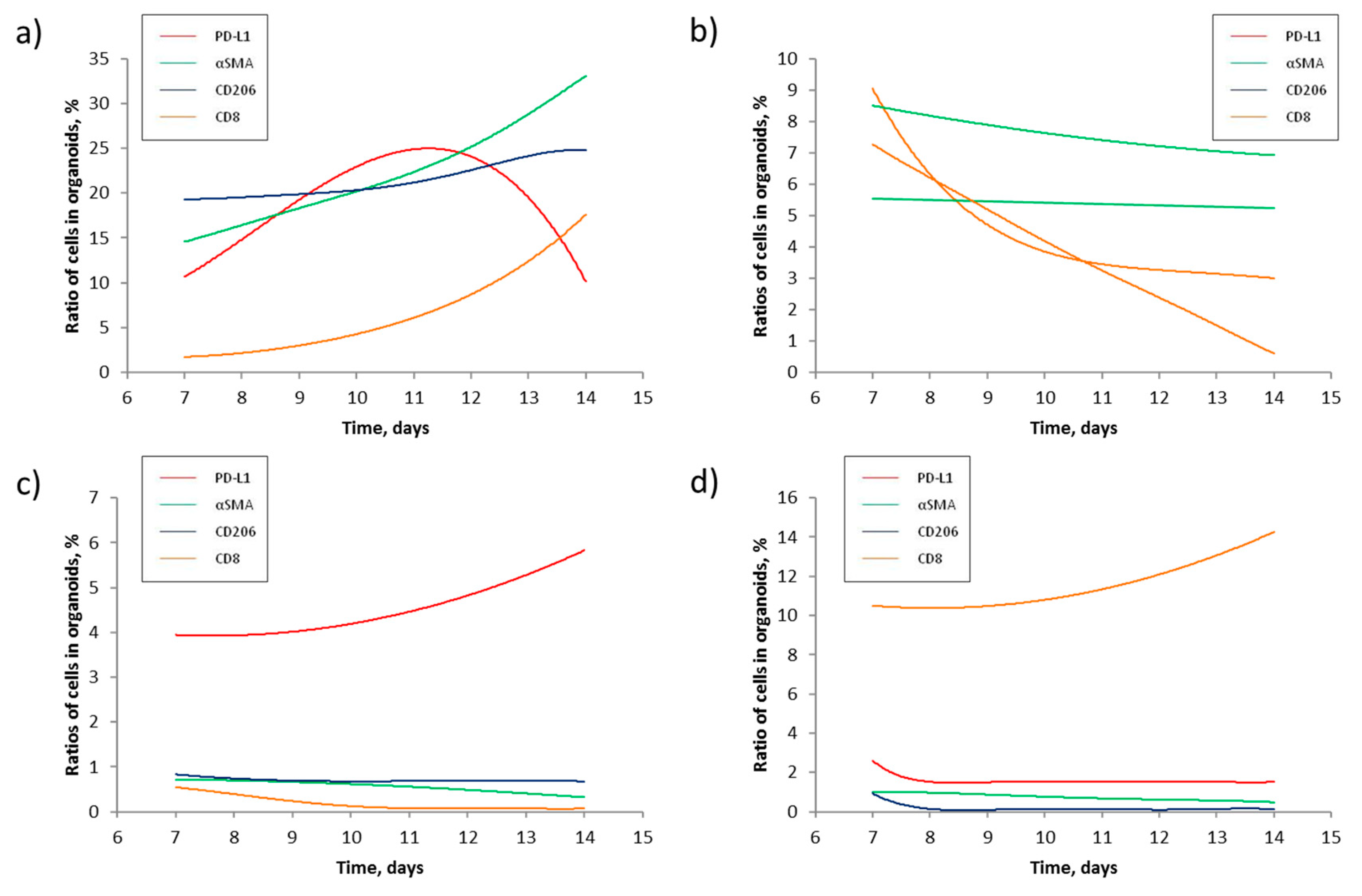
Table 1.
Cell-specific biomarkers used in flow cytometry experiments.
| Type of cells | Cell-specific biomarker |
|---|---|
| Cancer cells | PD-L1 |
| Cancer-associated fibroblasts | αSMA |
| M2-polarized macrophages | CD206 |
| Cytotoxic lymphocytes | CD8 |
Table 2.
Previously assessed parameters of mathematical model.
| Parameter | Definition | Published value | References | Adjusted value |
|---|---|---|---|---|
| γ | Growth rate of cancer cells | 0.05 – 0.44 day−1 | [12,13] | 0.05 day−1 |
| K | Final number of cancer cells | 109 – 3.3 × 109 day | [14] | 106 day−1 |
| q1 | Stimulation of cancer cells by M2-polarized macrophages | 0.4 day−1 | [14] | 4 x 10−5 day−1 |
| q3 | Stimulation of M2 macrophages by cancer cells | 4 x 10−8 day−1 | [14] | 4×10−8 day−1 |
| δM2 | Death rate of M2-polarized macrophages from natural causes | 0.2 day−1 | [13] | 0.2 day−1 |
| k | Number of cancer cells eliminated by cytotoxic cells | 3.4 x 10−10 - 1 x 10−3 cell −1 day −1 | [13] | 0.001 cell−1 day−1 |
| δTc | Death rate of cytotoxic cells | 2 x 10−3 – 1 day −1 | [13] | 0.1 day−1 |
Table 3.
Previously assessed parameters of mathematical model.
| Parameter | Definition | Dimension |
|---|---|---|
| q2 | Stimulation of cancer cells by cancer-associated fibroblasts | day−1 |
| q4 | Stimulation of M2-polarized macrophages by cancer-associated fibroblasts | day−1 |
| q5 | Stimulation of cancer-associated fibroblasts by cancer cells | day−1 |
| q6 | Stimulation of cancer-associated fibroblasts by M2-polarized macrophages | day−1 |
| q7 | Stimulation of cytotoxic T cells by cancer cells | day−1 |
| q8 | Suppression of cytotoxic T cells by M2-polarized macrophages | day−1 |
| q9 | Suppression of cytotoxic T cells by tumor-associated macrophages | day−1 |
| δCAF | Death rate of cancer-associated fibroblasts | day−1 |
Table 4.
Previously assessed parameters of mathematical model.
| Parameter | Calculated values, day−1 |
|---|---|
| q2 | 0.0001–0.005 |
| q4 | 0.0001–0.001 |
| q5 | 0–0.00001 |
| q6 | 0.00001–0.001 |
| q7 | 0.0009–0.0015 |
| q8 | 0–0.00001 |
| q9 | 0–0.00001 |
| δCAF | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







