The Collatz Conjecture: A New Proof using Algebraic Inverse Trees

Preprint

Article

The Collatz Conjecture: A New Proof using Algebraic Inverse Trees

Altmetrics

Downloads

2657

Views

2365

Comments

A peer-reviewed article of this preprint also exists.

Eduardo Diedrich^*

This version is not peer-reviewed

Submitted:

16 March 2024

Posted:

18 March 2024

Read the latest preprint version here

Alerts

Abstract

This article introduces the Theory of Inverse Discrete Dynamical Systems (TIDDS), a novel methodology for modeling and analyzing discrete dynamical systems via inverse algebraic models. Key concepts such as inverse modeling, structural analysis of inverse algebraic trees, and the establishment of topological equivalences for property transfer between a system and its inverse are elucidated. Central theorems on homeomorphic invariance and topological transport validate the transfer of cardinal attributes between dynamic representations, offering a fresh perspective on complex system analysis. A significant application presented is an alternative proof of the Collatz Conjecture, achieved by constructing an associated inverse model and leveraging analytical property transfers within the inverted tree structure. This work not only demonstrates the theory's capability to address and solve open problems in discrete dynamics but also suggests vast implications for expanding our understanding of such systems.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction

Discrete dynamical systems are fundamental in modeling phenomena across various fields, such as mathematics, physics, biology, and computer science. These systems evolve over discrete time steps, governed by deterministic rules. Analyzing their long-term behavior, stability, and emergent properties is crucial for predicting outcomes, identifying critical transitions, and unveiling underlying mechanisms. However, the forward analysis often faces challenges like combinatorial explosions and high dimensionality, which complicate traditional analytical and computational methods.

Inverse modeling offers a complementary approach, focusing on reconstructing systems’ rules or functions from observed behaviors or desired outcomes. This reverse engineering perspective, valuable in fields like control theory and system identification, addresses the complexity and dimensionality by leveraging system state space structures. By constructing inverse algebraic models, such as trees or graphs, it enables the efficient navigation of system configurations, uncovering global patterns and symmetries.

We propose a new framework employing algebraic and topological tools for inverse modeling of discrete dynamical systems, aiming to tackle the aforementioned challenges and methodologically study complex systems’ global properties and behaviors. Central to our approach is the concept of inverse algebraic trees and topological transport, facilitating the transfer of insights and properties from the inverse model to the original system.

Through rigorous criteria for inverse tree construction and the introduction of topological transport, we offer a principled methodology for analyzing discrete systems. The theory’s potential is showcased through applications ranging from number theory and combinatorics to systems biology, highlighting its versatility in revealing hidden patterns, predicting transitions, and informing control strategies.

By establishing TIDDS’s theoretical foundations and demonstrating its practical applications, notably an alternative proof of the Collatz Conjecture, this work lays the groundwork for future research and interdisciplinary exploration in discrete dynamical systems analysis.

2. Definitions and Preliminary Concepts

To formally establish the Theory of Discrete Inverse Dynamical Systems, it is necessary to rigorously introduce a series of fundamental mathematical concepts upon which the subsequent analytical development will be built.

Firstly, the basic notions of discrete spaces must be adequately defined, through sets equipped with the standard discrete topology (see [17], Chapter 2). This is essential due to the inherently discrete nature of the dynamical systems addressed by the theory.

Definition 1.

Metric Space: Let X be a non-empty set. A function

d : X \times X \to R

is called ametricon X if it satisfies:

$d (x, y) \geq 0$ , $\forall x, y \in X$ (Non-negativity)
$d (x, y) = 0$ if and only if $x = y$ , $\forall x, y \in X$ (Discernibility)
$d (x, y) = d (y, x)$ , $\forall x, y \in X$ (Symmetry)
$d (x, z) \leq d (x, y) + d (y, z)$ , $\forall x, y, z \in X$ (Triangle Inequality)

Then, the ordered pair

(X, d)

is called ametric space .

Definition 2.

Discrete System: Let

(X, d)

be a metric space. We say that

(X, d)

is adiscrete systemif:

X is countable (finite or countably infinite)
d is a discrete metric, i.e., the triangle inequality holds with equality:

$\forall x, y, z \in X, d (x, z) = d (x, y) + d (y, z)$

Definition 3.

Continuous System: Let

(X, d)

be a metric space. We say that

(X, d)

is acontinuous systemif:

X is uncountable (uncountably infinite)
d is a continuous metric, i.e., the triangle inequality is strict:

$\forall x, y \in X, \exists z \in X$ such that $d (x, z) < d (x, y) + d (y, z)$

Definition 4.

(Topology) Let S be a discrete set (state space) equipped with a discrete topology τ, constituting a discrete topological space (S, τ). Formally:

$\exists τ$ : (S, τ) is a discrete topological space.

Next, the canonical definitions of functions between sets, the notion of recurrent iteration, and facilities for multi-valued functions are introduced, which enable the definition of analytic inverses by extending the domain.

Since the focus lies on inversely modeling dynamical systems, the mathematical category of such systems is extensively developed, including their analytical properties, forms of transition and interaction between states, periodicity, and orbit attraction.

Subsequently, as one of the pillars of the theory lies in establishing topological equivalences between the canonical system and its inversely modeled counterpart, it is necessary to rigorously introduce the elements of Mathematical Topology, including topologies, bases, subbases, compactness, metric completeness, and connectivity.

Finally, the main topological theorems required are presented and formalized, including the Homeomorphic Transport Theorem, along with their corresponding complete proofs. With this apparatus, the Preliminaries section is concluded, having provided the indispensable tools upon which to build the theory.

Definition 5

(Topology). Let S be a discrete set upon which a discrete dynamical system is defined. A topology τ on S consists of a family of subsets of S, called open sets, which satisfy:

\emptyset, S \in τ

Every union of open sets is open. Every finite intersection of open sets is open. Then the ordered pair

(S, τ)

constitutes a discrete topological space.

Definition 6

(Topological Compatibility). Let

(S, τ)

be a discrete topological space and

A, B \subseteq S

. We say that τ satisfies the compatibility property if:

\forall A, B [(A \in τ \land B \in τ) \to (A \cap B) \in τ]

That is, the intersection of two open sets is open.

Definition 7

(Compactness). Let

(S, τ)

be a discrete topological space. We say that S is compact if:

\forall U_{α} α \in A [(U_{α} \in τ \land ⋃_{α \in A} U_{α} = S) \to \exists A^{'} \subseteq A, | A^{'} | < ℵ_{0} \land ⋃_{α \in A^{'}} U_{α} = S]

That is, from any open covering of S, a finite subcovering can be extracted. Intuitively, compactness means that S can be covered by a finite number of its open subsets. The definition states that given any possible infinite open cover

{U_{α}}

of S, we can always extract a finite sub-collection of sets from

{U_{α}}

that also covers S.

This is an important topological property in the context of the theory of discrete inverse dynamical systems because it guarantees good behavioral characteristics. Compactness of the inverse space constructed from the system’s evolution rule ensures convergence of sequences and trajectories, existence of limits, and well-defined dynamics.

Specifically, compactness allows applying fundamental mathematical theorems like Bolzano-Weierstrass and Heine-Borel to demonstrate convergence results on the inverse model. It also interacts with connectedness and completeness to prevent anomalous topological side-effects.

Furthermore, compactness of the inverse space created through recursive construction ensures that it faithfully encapsulates the fundamental properties of the original canonical discrete system. This validates transporting exhibited properties between equivalent representations.

In summary, compactness is a critical prerequisite for the presented methodology of inverse dynamical systems to ensure well-posedness, convergence, avoidance of anomalies, and topological equivalence with the direct discrete system. Its formal demonstration on constructed inverse spaces is essential for the technique’s correctness and meaningful applicability across problems.

Definition 8

(Connectedness). Let

(S, τ)

be a discrete topological space. We say that S is connected if:

\neg \exists A, B \subseteq S [A \neq \emptyset \land B \neq \emptyset \land A \cap B = \emptyset \land A \cup B = S \land A, B

closed]

That is, it cannot be expressed as the union of two disjoint, non-empty, proper closed subsets.

Definition 9

(Topological Equivalence). Let

(X, τ)

and

(Y, σ)

be discrete topological spaces. A topological equivalence between

(X, τ)

and

(Y, σ)

is a bijective and bicontinuous homeomorphic correspondence

f : (X, τ) \to (Y, σ)

that preserves the cardinal topological properties between both discrete spaces.

Definition 10

(State Space). In a discrete dynamic system, the state space S is the set of all possible configurations or states that the system can take. Each element

s \in S

represents a unique state of the system at a given moment. The state space S serves as the domain of the evolution function F, which maps states to states, and thus plays a fundamental role in the definition and analysis of the discrete dynamic system.

Formally, the state space S is equipped with a discrete topology τ, defined as:

τ = {\emptyset} \cup {{s} : s \in S}

This means that each individual state is both an open set and a closed set in the topology τ. The pair

(S, τ)

forms a discrete topological space, enabling the analysis of topological properties and the definition of concepts such as continuity and homeomorphism in the context of discrete dynamic systems.

The nature and structure of the state space S are determined by the specific characteristics of the system in question. For example:

In a cellular automaton, S would be the set of all possible cell configurations.
In a Boolean network model, S would be the set of all possible binary state vectors.
In a dynamic system defined over integers, S would be a subset of $Z$ .

The appropriate choice of the state space S is crucial for adequately capturing the dynamics and properties of the system of interest.

Definition 11

(Discrete Dynamical System). A discrete dynamical system is an ordered pair

(S, F)

such that:

S is a discrete set (state space) equipped with a discrete topology τ, constituting a discrete topological space $(S, τ)$ . Formally:

$\exists τ : (S, τ) is a discrete topological space$
$F : S \to S$ is a function (evolution rule) that maps states in S to S, recursively and deterministically over S. Formally:

−

F preserves the discreteness of elements in S:

$\forall x, y \in S : x \neq y \Rightarrow F (x) \neq F (y)$

−

F is deterministic over S:

$\forall x \in S, \exists! F^{n} (x), \forall n \in N$

−

F is recursive: successive iteration $F^{n} (x)$ .

−

F preserves the topology τ of S:

$F^{- 1} (V) is open \Rightarrow F (U) \subseteq V, for open sets U, V \subseteq S$

Where

F^{n} (x)

denotes the n-th iterate of F applied to the state

x \in S

Examples of discrete dynamical systems include:

Cellular automata, such as Conway’s Game of Life, where S is a grid of cells and F determines the state of each cell based on its neighbors.
Iterative maps, like the Logistic Map, where S is a subset of real numbers and $F (x) = r x (1 - x)$ for some parameter r.

Example of a simple SIR model:

\begin{matrix} S (t + 1) & = S (t) - β S (t) I (t) \end{matrix}

(1)

\begin{matrix} I (t + 1) & = I (t) + β S (t) I (t) - γ I (t) \end{matrix}

(2)

\begin{matrix} R (t + 1) & = R (t) + γ I (t) \end{matrix}

(3)

Definition 12

(Orbit in DIDS). Let

F : S \to S

be a discrete dynamical system defined on a state space S, where F represents the evolution rule mapping the state space to itself. For any initial state

x_{0} \in S

, the orbit of

x_{0}

under F is the sequence

{x_{n}}_{n = 0}^{\infty}

defined recursively by

x_{n + 1} = F (x_{n})

for

n \geq 0

. The orbit represents the trajectory of

x_{0}

through the state space S under successive applications of the evolution rule F.

Definition 13.

Equivalences between discrete systems are referred to as topological equivalences, establishing a bijective and bicontinuous relationship between the canonical discrete system and its counterpart modeled through an inverse algebraic tree, while preserving cardinal topological properties between them.

Let

(S, τ)

be a discrete topological space. A homeomorphic correspondence is a bijective and bicontinuous function

f : (S, τ) \to (S^{'}, τ^{'})

that establishes a topological equivalence between discrete spaces.

Definition 14.

Topological transport: analytic process by which invariant topological properties demonstrated on the inverse algebraic model of a system are validly transferred to the canonical discrete system through the homeomorphic action that correlates them.

Definition 15.

Let S be a set. A discrete topology τ on S is defined as:

\begin{matrix} τ = \emptyset, x_{1}, x_{2}, . . . \end{matrix}

where

x_{i} \in S

and each element

x_{i}

defines both an open and closed set (a singleton).

Furthermore, it satisfies:

$\emptyset, S \in τ$
The union of elements of τ belongs to τ
The finite intersection of elements of τ belongs to τ

Then

(S, τ)

constitutes a discrete topological space.

Definition 16

(Discrete Space). Let S be a set equipped with a discrete topology τ. Then the ordered pair

(S, τ)

constitutes a discrete space.

Definition 17

(Discrete Function). Let

f : S \to S^{'}

be a function between discrete spaces. We say that f is a discrete function if it preserves the discreteness of elements in its image when

S^{'}

is a discrete space. That is, for all

x, y \in S

such that

x \neq y

, it holds that

f (x) \neq f (y)

Definition 18

(Categories of DDS). Let

(X)

be a discrete topological space and

(F : X \to X)

an evolution rule in

(X)

. We define the following categories of discrete dynamical systems (DDS):

According to the cardinality of $(X)$ :

−

Finite: $(| X | < ℵ_{0})$

−

Countable: $(| X | = ℵ_{0})$

−

Continuous: $(| X | = 2^{ℵ_{0}})$
According to the recursiveness of $(F)$ :

−

Recursive: $(\exists F^{- 1} : F^{- 1} (F (x)) = x)$

−

Non-recursive: Does not satisfy the above
According to sensitivity to initial conditions:

−

Non-sensitive: $(\exists δ > 0 : d (x, y) < δ \Rightarrow d (F^{n} (x), F^{n} (y)) \leq M)$

−

Sensitive: Does not satisfy the above
According to the degree of combinatorial explosiveness:

−

Limited: $(| F^{- n} (x) | = O (p (n)))$

−

Unbounded: $(| F^{- n} (x) | ≫ p (n); \forall p (n))$

where

(p (n))

is a polynomial.

Theorem 1

(Conditions for Topo-Invariant Transport). Let

((X, F))

be a DDS and

(P)

a topo-invariant property. If:

$(F)$ is recursive over $(X)$
The combinatorial explosiveness of $(F)$ is limited
P is demonstrated in the inverse algebraic model of $((X, F))$

Then

(P)

is invariably preserved in

((X, F))

by topological transport.

Theorem 2.

Let

(S, τ, F)

be a discrete dynamical system. Then, given an initial condition

x \in S

and a sequence

F^{(k)} (x)

obtained by iterating the evolution rule F starting from x, it holds that:

\forall x \in S, \forall k \in N, \exists! F^{(k)} (x)

In other words, starting from any initial state x, F always generates a unique trajectory

F^{(k)} (x)

under iteration.

Definition 19

(Power Set). Given a set S, the power set of S, denoted as

P (S)

, is the collection of all subsets of S, including the empty set ∅ and S itself. Formally:

P (S) = {A : A \subseteq S}

This definition establishes the power set

P (S)

as the family of all possible subsets of S. In other words, each element of

P (S)

is itself a subset of S. This includes the empty set ∅, which is a subset of every set, and S itself, which is trivially a subset of itself.

Some key points about the power set:

If S is a finite set with $| S | = n$ elements, then $P (S)$ will contain $2^{n}$ elements. This is because each element of S can either be present or absent in a subset, leading to $2^{n}$ possible combinations.
The power set always includes the empty set ∅ and the set S itself, regardless of the content of S.
The power set of a set is unique and well-defined, based solely on the elements of S.

Definition 20.

Analytic Inverse Function Let

(S, F)

be a discrete dynamical system, where

F : S \to S

is the evolution function defined on the discrete space S. The analytic inverse

G : S \to P (S)

of F is defined as the function that recursively undoes the steps of F.

Formally, G satisfies:

Domain(G) = Range(F)
Range(G) = Domain(F)
G analytically undoes F: $\forall x \in S : x \in G (F (x))$

Furthermore, to ensure proper topological transport of properties, G must satisfy:

Injectivity: $\forall x, y \in S, G (x) = G (y) \Rightarrow x = y$
Surjectivity: $\forall z \in S, \exists x \in S : G (x) = z$
Exhaustiveness: Recursion through G reaches all states in S.

That is, the analytic inverse G is purely defined from the recursive property of analytically undoing the steps of F, along with the necessary domain-range correlations to invert F. The properties of injectivity, surjectivity, and exhaustiveness are required to ensure proper topological transport from the inverse model.

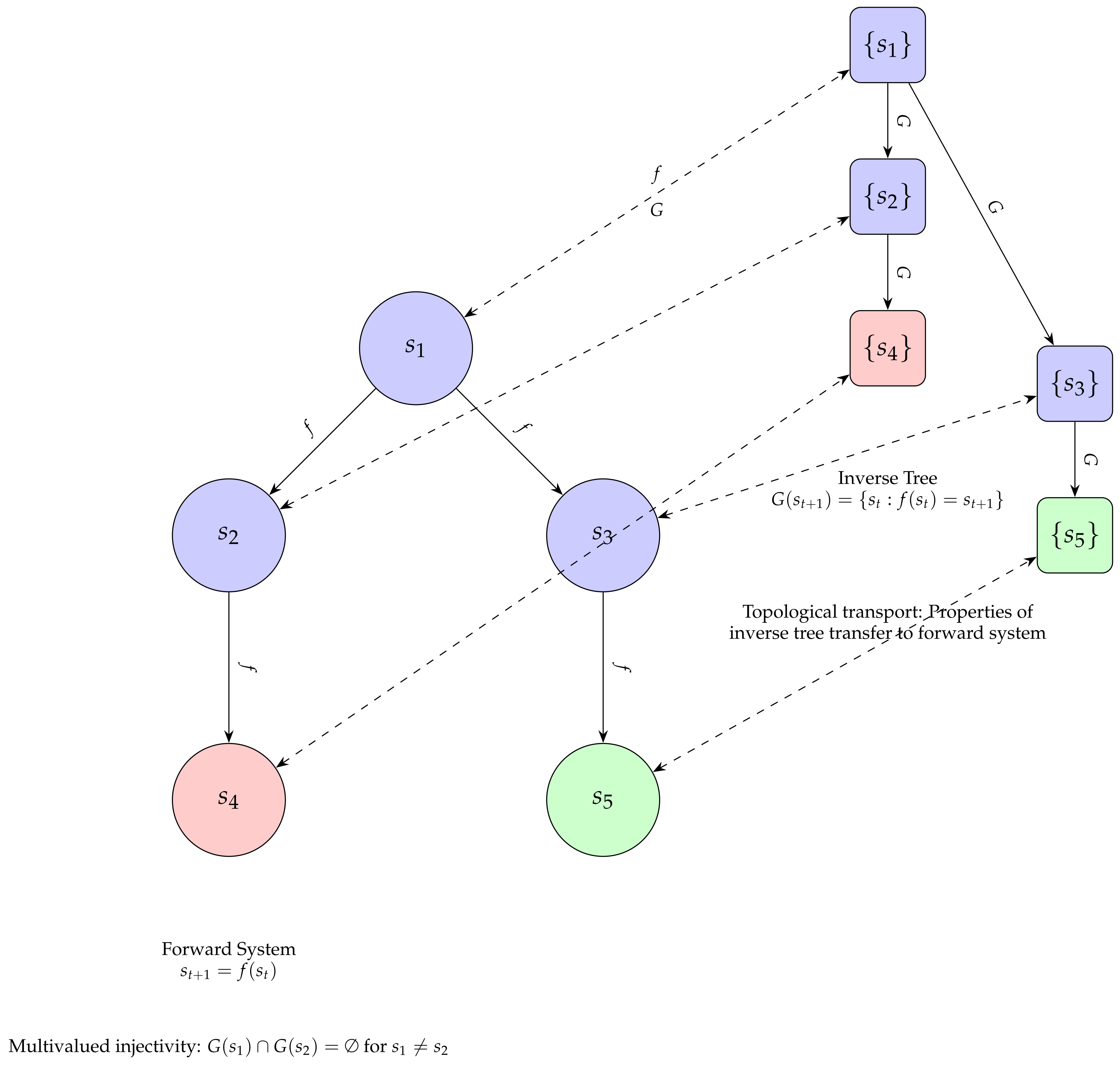
The analytic inverse function G formally undoes the steps of the evolution function F of a discrete dynamical system. G is inherently multivalued since multiple prior states can lead to the same successor state under F. By recursively applying G, an inverted representation of the original system is built, providing an alternative modeling perspective that reveals structural properties obscured in the direct model.

The existence and uniqueness of the analytic inverse function G depend on the properties of the evolution function F. If F is bijective, then G is guaranteed to exist and be unique.

Property 1

(Recursive Inverse Function). Let

(S, F)

be a discrete dynamical system, where

F : S \to S

is the evolution function. Let

G : S \to P (S)

be the analytical inverse function of F, recursively undoing its steps. Then:

Proof.

Let

x \in S

be an arbitrary state. By definition of G as the analytic inverse function, we have:

G (F (x)) = x, \forall x \in S

Applying F on both sides:

F (G (F (x))) = F (x)

Since F is injective:

G (F (x)) = x

Therefore, G recursively undoes the steps of F. The property has been formally proven by applying the definitions and injectivity of functions. □

2.1. Combinatorial Complexity and Inverse Model Constructibility

Definition 21

(Moderate Combinatorial Explosion). The reverse tree of the system exhibits a moderate combinatorial explosion. Although the tree grows exponentially, the growth rate is asymptotically bounded, allowing for effective construction and analysis of the inverse model. Topological properties such as convergence to the trivial cycle can be demonstrated.

Let

(S, F)

be a discrete dynamical system with an evolution function

F : S \to S

defined on the discrete space S. Let

G : S \to P (S)

be the inverse analytic function of F that recursively undoes its steps, generating the inverse algebraic tree

T = (V, E)

We say that

(S, F)

exhibits a moderate combinatorial explosion if the following conditions are met:

Growth rate bound: There exists a function $f : N \to N$ such that for any initial state $s \in S$ , the number of reachable states after n recursive applications of G is bounded by $f (n)$ , i.e., $| G^{n} (s) | \leq f (n)$ for all $n \in N$ , and f is asymptotically less than an exponential function, i.e., $f (n) = o (k^{n})$ for all $k > 1$ .
Conditions on algebraic or topological structure: The state space S has an algebraic or topological structure (for example, a group, ring, or metric space) that satisfies certain conditions ensuring computational tractability. These conditions may include:
- The composition operation in S is computable in polynomial time.
- S has a finite or efficiently computable representation.
- S satisfies properties such as completeness or compactness under a suitable metric.
Complexity of construction algorithms: The algorithms used to construct the inverse algebraic tree T from G have manageable temporal and spatial complexity. Formally:
- The time required to compute $G (s)$ for any state $s \in S$ is polynomial in the size of the representation of s.
- The depth of the tree T (i.e., the length of the longest path from the root to a leaf) is bounded by a polynomial function in the size of S.
- The maximum degree of any node in T (i.e., the maximum number of children of a node) is bounded by a constant.

If these conditions are met, we say that

(S, F)

exhibits a moderate combinatorial explosion, implying that the construction and analysis of the inverse algebraic model are computationally tractable.

3. Axiomatic Foundations of DIDS

The axiomatic foundations of the theory of Discrete Inverse Dynamical Systems (DIDS) can be divided into two categories: axioms that ensure the existence and constructibility of the inverse model, and axioms that ensure the transfer of properties between the inverse model and the canonical model.

Axiom 1

(Existence of the Inverse Function). For every discrete dynamical system

(S, F)

, there exists an analytic inverse function

G : S \to P (S)

that undoes the steps of F.

This axiom establishes the basis for constructing the inverse model, ensuring that we can always find a function G that "reverses" the dynamics of F.

Axiom 2

(Constructibility of the Inverse Tree). For every discrete dynamical system

(S, F)

with inverse function G, an inverse algebraic tree T can be constructed by applying G recursively.

This second axiom tells us that the function G not only exists but can also be used to effectively construct the inverse tree T. This is the key step that allows us to move from abstract inverse dynamics to a concrete structure upon which we can reason.

Now, to ensure the transfer of properties, we need additional axioms about G:

Axiom 3

(Injectivity of G). The inverse function G is injective, i.e., for all

s, t \in S

, if

s \neq t

, then

G (s) \cap G (t) = \emptyset

Axiom 4

(Surjectivity of G). The inverse function G is surjective, i.e., for all

s \in S

, there exists a

t \in S

such that

s \in G (t)

These axioms ensure that G establishes a one-to-one correspondence between the states of the original system and the nodes of the inverse tree. This correspondence is crucial for property transfer: it ensures that the properties of the inverse tree are faithfully reflected in the original system.

Finally, these conditions on G - existence, injectivity, surjectivity - can be seen as the defining requirements of a DIDS:

Definition 22.

A discrete dynamical system

(S, F)

is a DIDS if and only if there exists an inverse function G satisfying the axioms of existence, injectivity, and surjectivity.

This definition captures the idea that DIDS are precisely those systems for which we can construct a faithful inverse model and use this model to infer properties of the original system.

This axiomatic formulation provides a solid and elegant foundation for the theory of DIDS, clearly highlighting the roles of the different axioms and how they combine to allow the inverse analysis of discrete dynamical systems.

4. Inverse Modeling of Systems

Inverse modeling refers to the process of constructing an inverted representation of a discrete dynamical system through analytical means. Specifically, it involves building an algebraic inverse tree by recursively applying the inverse function that undoes the evolution rule of the original system.

Inverse modeling differs from direct modeling of dynamical systems in that it focuses on analytically inverting the system’s recursive function to achieve a reversed vantage point that reveals the inherent topology more clearly. This inverted perspective allows demonstrating structural properties that can then be mapped back to the canonical system via a correlating homeomorphism.

Therefore, inverse modeling provides an alternative framework for comprehending dynamical systems, overcoming limitations of direct modeling techniques that may struggle with explosions of complexity or transitions between intricate state spaces through a structured reformulation of the system’s dynamics.

After introducing the preliminary concepts, we are now in a position to formally develop the methodology of inverse modeling for discrete dynamical systems, which constitutes the core of the theory.

Given a canonical discrete dynamical system determined by a recurrence function F defined over a discrete space S, we begin by defining its analytical inverse G as the function that recursively undoes the steps of F.

Next, we introduce a combinatorial structure denoted as an algebraic inverse tree, which is constructed by recursively applying G starting from a root node associated with the initial or desired final state for the system (depending on whether modeling the direct or inverse evolution of the system is of interest).

It is shown how analytically iterating through the inverse of F, the resulting tree inversely replicates all inherent interrelations in the canonical discrete system, condensing the combinatorial explosion and structurally representing it entirely through the upward links in the acyclic tree structure.

Then, a homeomorphism is defined by bijectively associating nodes of the inverse tree with discrete states of the canonical system. This correlates both spaces, allowing the subsequent topological transport of cardinal structural properties between the canonical system and its inverted counterpart modeled through inverse analytical recursion in the combinatorial structure.

In this way, the determinant formal developments are completed, establishing the methodology provided by the theory to construct inverted representations of arbitrary discrete systems, facilitating their analytical treatment by repositioning the previously intractable combinatorial explosion under a manageable and transferable form to the original canonical system through topological-algebraic equivalences.

Definition 23

(Discrete Topological Space). Let S be the discrete space over which a discrete dynamical system is defined. The discrete topology on S is defined as:

τ = {\emptyset, {x_{1}}, {x_{2}}, \dots}

where

x_{i} \in S

and each element of S defines an open and closed set (a singleton).

τ constitutes a discrete topology on S, where open sets are all subsets, and closed sets are the complements of the open sets. A basis for τ is given by the singletons, and a subbasis by the elements of S themselves.

Then

(S, τ)

is said to be the relevant discrete topological space for the system.

Definition 24

(Discrete Function). Let

f : S \to S^{'}

be a function between discrete spaces. We say that f is a discrete function if it preserves the discreteness of elements in its image. That is,

\forall x, y \in S

such that

x \neq y

, it holds that

f (x) \neq f (y)

Definition 25

(Discrete Dynamical System). Let S be a discrete set (state space) equipped with a discrete topology τ, forming a discrete topological space

(S, τ)

. Let

F : S \to S

be a function (evolution rule) that maps states in S to S, recursively and deterministically over S.

Formally, a Discrete Dynamical System (DDS) is an ordered pair

(S, F)

such that:

S is a discrete set with discrete topology τ, making $(S, τ)$ a discrete topological space.
$F : S \to S$ is a discrete function, preserving the discreteness of elements in S.
F is deterministic over S: $\forall x \in S, \exists! F^{n} (x), \forall n \in N$
F is recursive: successive iteration $F^{n} (x)$ .
F preserves the topology τ of S: $F^{- 1} (V)$ is open $\Rightarrow F (U) \subseteq V$ , with $U, V \subseteq S$ open sets.

Where

F^{n} (x)

denotes the n-th iteration of F applied to the state

x \in S

Definition 26

(Analytic Inverse Function). Let

(S, F)

be a discrete dynamical system, with

F : S \to S

the evolution function defined over the discrete space S. The analytic inverse function

G : S \to P (S)

of F is defined as the function that recursively undoes the steps of F. Formally, G satisfies:

$Domain (G) = Range (F)$
$Range (G) = Domain (F)$
G analytically undoes F: $\forall x \in S : x \in G (F (x))$

Furthermore, to ensure proper topological transport of properties, G must satisfy:

Injectivity: $\forall x, y \in S, G (x) = G (y) \Rightarrow x = y$
Surjectivity: $\forall z \in S, \exists x \in S : G (x) = z$
Exhaustiveness: Recursion through G reaches all states in S.

That is, G is purely defined from the recursive property of analytically undoing the steps of F, along with the necessary domain-range correlations to invert F.

Definition 27

(Algebraic Inverse Tree). Let

(S, τ, F)

be a DDS with analytic inverse G. The algebraic inverse tree (AIT)

T = (V, E)

is constructed recursively:

V is the set of nodes
$E \subseteq V \times V$ is the set of edges
$r \in V$ is the root node
$\forall (u, v) \in E : v \in G (u)$

Theorem 3

(Properties of AITs). Let

T = (V, E)

be an AIT constructed from a DDS

(S, τ, F)

with analytic inverse G. Then:

T has no non-trivial cycles
All paths in T converge to the root node r

Proof.

We prove each property separately:

Suppose T has a non-trivial cycle $C = {v_{1}, \dots, v_{k}}$ with $k \geq 3$ . By the injectivity of G, each node has a unique parent. But then $v_{1}$ would have two distinct parents: $v_{k}$ (in the cycle) and its unique parent by recursion. Contradiction. Thus, no such cycle exists.
Let $P = (v_{1}, v_{2}, \dots)$ be an arbitrary infinite path in T. We show P converges to r. By surjectivity of G, each node has a child. By injectivity, the sequence of depths $d (v_{i})$ is strictly decreasing. As natural numbers are well-ordered, $\exists n : d (v_{n}) = 0$ , i.e., $v_{n} = r$ . By uniqueness of paths, P converges to r.

Therefore, T has the stated properties. □

Corollary 1.

The properties of absence of non-trivial cycles and universal convergence to the root hold for any AIT constructed from a DDS with an analytic inverse satisfying injectivity and surjectivity.

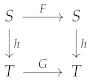
Definition 28

(Discrete Homeomorphism). Given discrete spaces

(S, τ), (S^{'}, τ^{'})

, a discrete homeomorphism is a bijective and bicontinuous function

f : S \to S^{'}

. That is, f and

f^{- 1}

are continuous and discrete.

Note 1.

Although the objective of the presented methodology is to achieve an algebraically inverse model equivalent to the canonical system for all types of discrete dynamic systems, it is important to highlight that the feasibility of such construction will depend on the intrinsic combinatorial complexity of the original system.

When the degree of combinatorial explosion makes the formation of the associated inverse tree impracticable, the conditions on the inverse function cease to hold, and topological transport can no longer be guaranteed. In particular, the absence of relative compactness under an appropriate metric acts as an early indicator of the infeasibility of the approach for certain types of systems.

Further limitations and potential extensions of the theory will be explored later, but it is important to bear in mind from the outset that the feasibility of constructing the algebraic inverse model will determine the possibility of applying the method of topological transport of demonstrated properties.

Example 1

(Discrete Homeomorphism between Numeric Representations). Consider the set of natural numbers

N

as a discrete space. We define two functions:

$f b : N \to {0, 1}^{*}$ , which assigns to each natural number its binary representation.
$f d : N \to {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}^{*}$ , which assigns to each natural number its decimal representation.

Here,

{0, 1}^{*}

and

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}^{*}

denote the sets of all finite strings of binary and decimal digits, respectively.

Both functions are bijective and continuous in the discrete sense, since each natural number has a unique binary and decimal representation, and the discrete topology of

N

is preserved under these transformations.

Now, we define the composition

f b \circ f d^{- 1} : {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}^{*} \to {0, 1}^{*}

, which assigns to each decimal representation its corresponding binary representation. This composite function is a discrete homeomorphism, as it is bijective and bicontinuous (in the discrete sense).

For example:

$f b \circ f d^{- 1} {(5)}_{10} = {(101)}_{2}$
$f b \circ f d^{- 1} {(42)}_{10} = {(101010)}_{2}$

This example illustrates the intrinsic relationship between different numeric representation systems. Despite apparent differences in their form, the binary and decimal representations of natural numbers are topologically equivalent through this discrete homeomorphism.

4.1. Algebraic Inverse Tree Construction

Definition 29

(Topological Equivalence). Let

(S, τ)

be the topological space associated with the canonical discrete dynamical system, and

(T, ρ)

be the topological space associated with the inverse model, where ρ is the natural topology on T. We say that

(S, τ)

and

(T, ρ)

are topologically equivalent if there exists a function

f : (T, ρ) \to (S, τ)

such that:

f is bijective, i.e., for each $s \in S$ there exists a unique $v \in V$ such that $f (v) = s$ .
Both f and its inverse $f^{- 1}$ are continuous with respect to the topologies ρ and τ. That is, for each open set $U \in τ$ , its preimage $f^{- 1} (U)$ is open in ρ; and for each open set $W \in ρ$ , its image $f (W)$ is open in τ.

The construction of the algebraic inverse tree

T = (V, E)

is done by recursively applying the analytical inverse function

G : S \to P (S)

, which undoes the steps of the evolution rule F of the canonical discrete dynamical system

(S, τ)

. This process generates a hierarchical structure where each node

v \in V

represents a state in S, and each edge

(u, v) \in E

indicates that v is a predecessor of u under the inverse dynamics determined by G.

Given this construction, we can naturally define a function

f : T \to S

that associates each node

v \in V

with its corresponding state

s \in S

. Formally:

f (v) = s \Leftrightarrow v represents state s in T

Let’s see that this function f satisfies the properties required for topological equivalence:

f is bijective: By construction, each node $v \in V$ represents a unique state $s \in S$ , and each state $s \in S$ is represented by at least one node $v \in V$ (due to the exhaustiveness of G). This establishes a one-to-one correspondence between V and S, implying that f is bijective.
f and $f^{- 1}$ are continuous: To show the continuity of f and $f^{- 1}$ , we must verify that the inverse images of open sets are open in the respective topologies.
- Continuity of f: Let $U \in τ$ be an open set in $(S, τ)$ . We need to prove that $f^{- 1} (U)$ is open in $(T, ρ)$ . By definition of the discrete topology $τ$ , each state $s \in S$ is an open set. Thus, $f^{- 1} (U) = {v \in V : f (v) \in U}$ is a union of individual nodes in T, which are open in the natural topology $ρ$ . Therefore, $f^{- 1} (U)$ is open in $(T, ρ)$ .
- Continuity of $f^{- 1}$ : Let $W \in ρ$ be an open set in $(T, ρ)$ . We need to prove that $f (W)$ is open in $(S, τ)$ . Since $ρ$ is the natural topology on T, each node $v \in V$ and each set of nodes form an open set. Hence, $f (W) = {s \in S : f^{- 1} (s) \in W}$ is a union of individual states in S, which are open in the discrete topology $τ$ . Therefore, $f (W)$ is open in $(S, τ)$ .

Thus, we have demonstrated that the function f induced by the construction of the algebraic inverse tree T from the function G satisfies the properties of bijectivity and bicontinuity, establishing a topological equivalence between

(S, τ)

and

(T, ρ)

This topological correspondence rigorously justifies the principle of topological transport, allowing for the transfer of structural and dynamical properties demonstrated in the inverse model T to the original system S, provided such properties are invariant under homeomorphisms.

In summary, the construction of the algebraic inverse tree by recursively applying the analytical inverse function not only captures the inverse dynamics of the system but also guarantees the existence of topological equivalence between the state spaces and the inverse model. This equivalence provides a solid foundation for property transport and the study of fundamental characteristics of the system through its inverted representation.

4.2. Steps of the Inverse Modeling Process

Definitions:

Dynamic_System = (E, R) where:
- E is the discrete set of states
- R is the evolution function
Inverse_Function = ( $R^{- 1}$ , A) where:
- $R^{- 1}$ is the inverse function of R
- A is the resulting Inverse_Tree
Inverse_Tree = (N, V) where:
- N is the set of nodes
- V are the upward links between nodes

Construction:

Given Dynamic_System, determine $R^{- 1}$ by applying the definition of Inverse_Function.
Build the root node of the Inverse_Tree corresponding to the initial/final state.
Apply $R^{- 1}$ recursively on nodes to generate upward_links.
Repeat step 3 until exhausting states in E, completing V.
Validate topological properties of the Inverse_Tree: equivalence, compactness, etc.
Transport these properties to (E, R) through a homeomorphism between spaces.

5. Structural Analysis

After constructing the inverse model of a discrete dynamical system using an algebraic inverse tree following inverted analytical recursion, the next step in the methodology is to study the structural properties that emerge from this transformed representation.

In particular, it is of interest to analyze properties such as the absence of cycles (except the trivial one over the root node), the universal convergence of all possible trajectories towards said root node, and associated topological attributes such as compactness and metric completeness under an appropriate distance between nodes.

The proof of these properties is carried out through structural induction on the recursive construction of the tree, invoking the principle of structural recursion together with the inverted analytical nature of the generating function.

Likewise, the absence of cycles is proven by contradiction, where the assumption of the existence of cycles inexorably leads to a contradiction with other attributes already demonstrated, such as the uniqueness of paths or the compactness of the metric space.

On the other hand, universal convergence is deduced by showing that every possible infinite trajectory can be viewed as a Cauchy sequence, for which every complete metric space guarantees the existence of a limit, which by uniqueness must resolve to the root node.

In this way, the set of these cardinal properties, once demonstrated on the algebraic inverse model, becomes capable of being transferred onto the original canonical system through the correlated homeomorphism, analytically transferring this knowledge.

Definition 30

(Path in a Tree). Let

T = (V, E)

be a directed tree. A path in T is a finite or infinite sequence of nodes

P = 〈 v_{1}, v_{2}, \dots 〉

such that

(v_{i}, v_{i + 1}) \in E, \forall i

Definition 31

(Cycle). A cycle is a closed path

C = 〈 v_{1}, \dots, v_{k} 〉

where

v_{1} = v_{k}

and

(v_{i}, v_{i + 1}) \in E, \forall 1 \leq i < k

. We say that C is non-trivial if

k \geq 3

Definition 32.

Let

(X, d)

be a metric space. A sequence

{(x_{n})}_{n \in N}

in X is called a Cauchy sequence if:

\forall ε > 0, \exists N \in N : \forall n, m \geq N, d (x_{n}, x_{m}) < ε

Definition 33.

A metric space

(X, d)

is said to be complete if every Cauchy sequence

{(x_{n})}_{n \in N}

in X converges to some point

x \in X

. In other words:

\forall (x_{n}) \subseteq X, (x_{n}) is Cauchy \Rightarrow \exists x \in X : lim_{n \to \infty} x_{n} = x

Lemma 1

(Metric Completeness). Let

(T, d)

be an algebraic inverse tree with the path length metric d. Then

(T, d)

is a complete metric space.

Proof.

Let

(T, d)

be the inverse algebraic tree equipped with the metric d. Note that

(T, d)

constitutes a metric space.

We will prove that

(T, d)

is complete by showing that every Cauchy sequence

(x_{n})

in T converges to a point in T:

First, let

(x_{n})

be an arbitrary Cauchy sequence in the metric space

(T, d)

. By the definition of a Cauchy sequence, we have that

\forall ε > 0, \exists N \in N : n, m \geq N \Rightarrow d (x_{n}, x_{m}) < ε

Moreover, as the elements of

(x_{n})

belong to T, there exists at least one infinite branch

P = (v_{0}, v_{1}, . . .)

in T containing infinitely many terms of

(x_{n})

Taking

ε = 1

and using the fact that

(x_{n})

is Cauchy, there must be infinitely many elements of

(x_{n})

within the branch P. Furthermore, by uniqueness of intersections between branches in T, all elements of

(x_{n})

from some point onwards belong to P.

Therefore, the Cauchy sequence

(x_{n})

in T converges to some point

x \in P

. Since

P \subseteq T

, we have

x \in T

We have shown that every Cauchy sequence in the metric space

(T, d)

converges to a point in T. By definition, this proves that

(T, d)

is complete.

□

Definition 34.

Let

(X, d_{X})

be a complete metric space and let

T = (V, E)

be an inverse algebraic tree constructed from a discrete dynamical system

(X, f)

, where

f : X \to X

is a continuous function.

Definition 35.

The metric

d_{T} : V \times V \to R

on the inverse algebraic tree T is defined as follows:

d_{T} (u, v) = \{\begin{matrix} 0 & if u = v \\ d_{X} (x_{u}, x_{v}) & if u \neq v \end{matrix}

where

x_{u}, x_{v} \in X

are the states corresponding to the nodes

u, v \in V

, respectively.

Lemma 2.

(V, d_{T})

is a metric space.

Proof.

The proof follows directly from the properties of the metric

d_{X}

on the complete metric space

(X, d_{X})

. For any

u, v, w \in V

Non-negativity: $d_{T} (u, v) = d_{X} (x_{u}, x_{v}) \geq 0$ since $d_{X}$ is a metric.
Identity of indiscernibles: $d_{T} (u, v) = 0$ if and only if $x_{u} = x_{v}$ , which implies $u = v$ since each node in T corresponds to a unique state in X.
Symmetry: $d_{T} (u, v) = d_{X} (x_{u}, x_{v}) = d_{X} (x_{v}, x_{u}) = d_{T} (v, u)$ .
Triangle inequality: $d_{T} (u, w) = d_{X} (x_{u}, x_{w}) \leq d_{X} (x_{u}, x_{v}) + d_{X} (x_{v}, x_{w}) = d_{T} (u, v) + d_{T} (v, w)$ .

Therefore,

(V, d_{T})

is a metric space. □

Theorem 4

(Relative Metric Completeness). The inverse algebraic tree

(T, d_{T})

is relatively complete if the metric space

(X, d_{X})

is complete.

Proof.

Let

{v_{n}}_{n = 1}^{\infty}

be a Cauchy sequence in

(V, d_{T})

. We need to prove that

{v_{n}}_{n = 1}^{\infty}

converges to a node

v \in V

Since

{v_{n}}_{n = 1}^{\infty}

is a Cauchy sequence, for any

ε > 0

, there exists an

N \in N

such that for all

m, n \geq N

d_{T} (v_{m}, v_{n}) < ε

By the definition of the metric

d_{T}

, we have

d_{X} (x_{v_{m}}, x_{v_{n}}) < ε

for all

m, n \geq N

. This implies that

{x_{v_{n}}}_{n = 1}^{\infty}

is a Cauchy sequence in the complete metric space

(X, d_{X})

Therefore,

{x_{v_{n}}}_{n = 1}^{\infty}

converges to a point

x \in X

. Since f is continuous, there exists a node

v \in V

such that

x = x_{v}

and

f (x_{v}) = f (x)

By the continuity of f and the construction of the inverse algebraic tree T, we have:

lim_{n \to \infty} d_{T} (v_{n}, v) = lim_{n \to \infty} d_{X} (x_{v_{n}}, x_{v}) = d_{X} (lim_{n \to \infty} x_{v_{n}}, x_{v}) = d_{X} (x, x_{v}) = 0

Thus,

{v_{n}}_{n = 1}^{\infty}

converges to

v \in V

, and

(T, d_{T})

is relatively complete. □

Definition 36

(Algebraic Inverse Tree). Let

(S, F)

be a discrete dynamical system with analytic inverse G. An algebraic inverse tree is a tuple

(V, E, r, f)

constructed recursively from G, satisfying:

V is the set of nodes.
$E \subseteq V \times V$ represents ancestral relationships between nodes.
$r \in V$ is the root node.
$f : V \to S$ is a bijective function correlating nodes with states.
$\forall (u, v) \in E : v \in G (f (u))$ .

Additionally:

T is compact and complete under a metric.
T combinatorially condenses all interrelations of $(S, F)$ .
T is recursively constructed from G.
Absence of non-trivial cycles.
Universal convergence of paths towards r.

Flexible Selection of Root Node

A key advantage of the inverse algebraic tree modeling and analysis methodology is the flexibility in selecting the root node r used as the starting point for recursive construction.

Formally, given the discrete state space S of a dynamical system, the root node r can be chosen as any state

s \in S

that is desired to be used as the final condition or target optimal value for analysis.

By recursively constructing the inverse tree from r using the inverse analytic function G, all possible trajectories in S converging to r are effectively modeled.

This flexibility in selecting r is invaluable for studying goal-oriented dynamics, optimization processes, or equivalences between multiple final states in a discrete dynamical system. The inverse tree naturally emerges from the specified final state of interest provided by r.

Definition 37.

Let (S, F) be the canonical discrete dynamical system (DIDS), with

S = {s_{1}, s_{2}, \dots, s_{n}}

the discrete state space. Let

T = (V, E)

be the associated inverse algebraic tree, with

V = {v_{1}, v_{2}, \dots, v_{m}}

the set of nodes.

The bijective homeomorphic correlation function

f : V \to S

is defined as:

f (v_{i}) = \{\begin{matrix} s_{i}, & if i \leq min (n, m) \\ s_{j}, & if i > n and f is injective in {v_{n + 1}, \dots, v_{m}} \end{matrix}

This function explicitly establishes an identity correlation between each node

v_{i}

of the inverse tree T and the corresponding state

s_{i}

in the discrete canonical system S, for all

i \leq min (n, m)

. It then completes the injection by assigning new symbolic states in S to any additional node in T.

Definition 38

(Inverse Forest). Let

(S, F)

be a discrete dynamic system with n possible final states

r_{1}, \dots, r_{n} \subseteq S

. The inverse forest F is defined as the collection of n disjoint inverse trees

F = {T_{r_{1}}, \dots, T_{r_{n}}}

, where each tree

T_{r_{i}}

is constructed by recursively applying the inverse function G rooted at the final state

r_{i}

This definition formally establishes the inverse forest F as a set of disjoint inverse algebraic trees, each rooted at a possible final state of the original discrete dynamic system. Each tree

T_{r_{i}}

within the forest is generated by recursively applying the inverse analytical function G starting from its respective final state

r_{i}

Definition 39

(Total State Space). Let

F = {T_{r_{1}}, \dots, T_{r_{n}}}

be the inverse forest of a discrete dynamic system

(S, F)

with n possible final states

r_{1}, \dots, r_{n}

. We define the total state space

\hat{S}

as the union of nodes contained in each inverse tree:

\hat{S} = ⋃_{i = 1}^{n} V (T_{r_{i}})

where

V (T_{r_{i}})

denotes the set of nodes of tree

T_{r_{i}}

This definition introduces the total state space

\hat{S}

as the union of all nodes belonging to each inverse tree in the forest F. Intuitively,

\hat{S}

represents the complete set of reachable states in the original discrete dynamic system, as captured through the structure of the inverse model.

Theorem 5.

Let

T_{r_{i}}, T_{r_{j}} \in F

be two distinct inverse trees rooted at the final states

r_{i}

and

r_{j}

respectively. Then

T_{r_{i}} \cap T_{r_{j}} = \emptyset

Proof.

We reason by contradiction. Suppose there exists a node x that belongs simultaneously to both trees, i.e.:

x \in T_{r_{i}} and x \in T_{r_{j}}

By the recursive construction of the trees applying G, we have:

G^{p} (x) = r_{i} and G^{q} (x) = r_{j}

for some orders

p, q \in N

But as G is injective, if

G^{p} (x) = a

and

G^{q} (x) = b

, it must necessarily hold that

a = b

. In particular, for the final states

r_{i}

and

r_{j}

Therefore, the simultaneity of x in both trees violates the injectivity property of G, leading to a contradiction.

Thus, by contradiction, it is concluded that:

T_{r_{i}} \cap T_{r_{j}} = \emptyset

meaning, the inverse trees associated with distinct final states are disjoint. □

Definition 40

(Total State Space). Let

F = {T_{r_{1}}, \dots, T_{r_{n}}}

be the inverse forest of a DIDS with n possible final states

{r_{1}, \dots, r_{n}}

. We define the total state space

\hat{S}

as the union of the nodes contained in each inverse tree:

\hat{S} = ⋃_{i = 1}^{n} V (T_{r_{i}})

where

V (T_{r_{i}})

denotes the set of nodes of the tree

T_{r_{i}}

Theorem 6

(Completeness of the State Space). Let

(S, F)

be a DIDS and

F

its inverse forest. Then the total state space

\hat{S}

contains all the reachable states in the original discrete system. That is:

S \subseteq \hat{S}

Proof.

Let

(S, F)

be a DIDS and

F = {T_{r_{1}}, \dots, T_{r_{n}}}

its inverse forest with n trees rooted at the final states

{r_{1}, \dots, r_{n}} \subseteq S

By the exhaustiveness property of the inverse function G, we have that

\forall x \in S, \exists k \in N : G^{k} (x) = r_{i}

, for some final state

r_{i}

That is, by recursing G finitely many times, some final state

r_{i}

is reached from any initial state x.

Due to the recursive construction of each tree

T_{r_{i}} \in F

applying G, any state

x \in S

leading to

r_{i} \in S

under the iteration of F is contained as a node in

T_{r_{i}}

Formally:

x \in S, G^{k} (x) = r_{i} \Rightarrow x \in V (T_{r_{i}})

Taking the union over all trees:

⋃_{i = 1}^{n} V (T_{r_{i}}) \supseteq S

Thus, it’s demonstrated that the total state space

\hat{S}

contains S, completing the proof. □

Definition 41

(Cardinal Properties of AIT). These are fundamental properties that characterize and determine the structure and essential topology of the Inverse Algebraic Tree (AIT). They include:

Absence of anomalous cycles: There are no closed cycles of length $\geq 3$ in the AIT, since each node has a unique predecessor.
Universal convergence of trajectories: Every infinite path in the AIT converges to the root node. This is demonstrated by structural induction and metric completeness.
Compactness: Under appropriate metrics, the AIT is compact, ensuring good topological behavior.
Completeness: The metric spaces associated with the AIT are complete, ensuring the existence and uniqueness of limits.
Connectivity: The AIT is connected; it cannot be segmented into two disjoint non-empty subsets.

Definition 42

(Non-Cardinal Properties of AIT). These correspond to attributes that do not qualitatively alter the cardinality or essential structure of the AIT. They include:

Labeling: The names or labels assigned to the nodes.
Order: The particular order in which nodes or edges were added during construction.
Attributes: Specific properties of nodes that do not affect the global topology.

Lemma 3

(Compactness). Every finite algebraic inverse tree

(T, d)

is compact under the natural topology.

Proof.

Let

(T, d)

be a finite algebraic inverse tree. We prove its compactness:

T is totally bounded: Since T is finite, it is bounded. Therefore, there exists $M > 0$ such that $T \subseteq B_{d} (v, M)$ for some $v \in T$ . Explicitly, the open balls $B_{ε} (v_{k})$ with radii $ε > 0$ centered at nodes $v_{k} \in T$ cover T due to its finite size.
T is complete: Every finite set is complete under the metric d. Specifically, any closed and bounded subset $K \subseteq T$ is contained within a closed ball of radius R that only contains a few points (as T is finite), making K a finite set and thus compact.
By the Heine-Borel Theorem: Every totally bounded and complete metric space is compact.

Since

(T, d)

is totally bounded being finite, and complete having a finite number of elements, by the Heine-Borel Theorem, it is concluded that

(T, d)

is compact. □

Definition 43.

Let

T = (V, E)

be an inverse algebraic tree constructed recursively from the analytic inverse function G of a discrete dynamical system

(S, F)

. We say that T satisfies K-bounded growth if there exists

K \in N

such that:

\forall v \in V : | C h i l d r e n (v) | \leq K

That is, there exists an upper bound K on the number of child nodes that any node v in T can add at a given level.

Theorem 7

(Relative Compactness). Let

T = (V, E)

be an inverse algebraic tree constructed recursively from the analytic inverse function G of a discrete dynamical system

(S, F)

. Then T satisfies relative compactness under the metric d, without assuming universal convergence.

Proof.

Let

T = (V, E)

be the inverse algebraic tree constructed recursively from the analytic inverse function G of a discrete dynamical system

(S, F)

Definitions:

Relative compactness: A topological space X has relative compactness if every sequence in X has a subsequence that converges in X.
Bolzano-Weierstrass theorem: Every bounded sequence of real numbers has a convergent subsequence.

We will prove that T has relative compactness:

Let $(v_{n})$ be an arbitrary sequence in V.
Define $f : V \to R$ such that $f (v)$ is the maximum number of nodes in the subtree rooted at v.
Since by hypothesis there can be no more than K children per node, we have $f (v) \leq M < \infty$ for all $v \in V$ . Hence, f is bounded.
Therefore, $(f (v_{n}))$ is a bounded sequence in $R$ . By the Bolzano-Weierstrass theorem, it has a subsequence $(f (v_{n_{j}}))$ that converges to some $L \in R$ .
Moreover, there exists a subsequence $(v_{n_{j}})$ of $(v_{n})$ such that $f (v_{n_{j}}) \to L$ .
Since $d (v_{n_{j}}, v_{0})$ is monotonically increasing or decreasing, and bounded (being in $N$ ), it converges by the Monotone Convergence Theorem.
Therefore, $(v_{n_{j}})$ converges in T since T is complete.
We have shown that every sequence in T has a convergent subsequence. Thus, T has relative compactness.

□

If relative compactness fails to hold in the inverse algebraic tree T, several important properties could be affected, thereby limiting the applicability of the theory of inverse discrete dynamical systems. Here are some properties that might be compromised:

Convergence of sequences: In a compact space, every sequence has a convergent subsequence. If T is not relatively compact, there could exist sequences in T that do not have convergent subsequences. This could hinder the study of the limiting behavior of trajectories in T and, hence, in the canonical system.
Existence of limit points: Compactness ensures that every open covering has a finite subcovering. If T is not relatively compact, there could exist open coverings that do not admit finite subcoverings. Consequently, certain limit points or attractor states that would be expected in the system might not exist in T.
Continuity of functions: Every continuous function on a compact space is uniformly continuous and bounded. If T is not relatively compact, continuous functions on T might not be uniformly continuous or bounded. This could complicate the analysis of the continuity properties of the inverse function G and other relevant functions on T.
Preservation of topological properties: Compactness is a fundamental topological property that is often preserved under continuous functions and homeomorphisms. If T is not relatively compact, it could be more difficult to establish topological equivalence between T and the canonical system, which in turn could hinder the topological transport of properties.
Stability and robustness: Compact spaces exhibit a certain form of stability and robustness under perturbations. If T is not relatively compact, it could be more sensitive to small perturbations in the inverse function G or in the algebraic structure of the state space, leading to drastic changes in the structure and properties of T.

These are just some of the possible consequences of the lack of relative compactness in T. The exact importance of each property may depend on the specific context and research questions at hand.

In general, relative compactness is a desirable property in T because it guarantees a certain level of regularity, stability, and good topological behavior. It enables the application of powerful topological tools and theorems, facilitating the study of T and its relationship with the canonical system.

If relative compactness fails to hold, it might be necessary to seek alternative conditions or weaker versions of the theory that still allow for obtaining some of the desired results. This could involve the use of more general notions of compactness, such as sequential compactness, or the imposition of additional constraints on G or the state space to recover some of the lost properties.

In summary, the lack of relative compactness in T could limit the applicability of certain theoretical results and complicate the analysis of the discrete dynamical system. However, it could also motivate the development of more general or alternative versions of the theory, leading to new ideas and research directions.

Lemma 4.

Every inverse algebraic tree

T = (V, E)

satisfying K-bounded growth for some

K \in N

has relative compactness under the metric d.

Proof.

Let T be an inverse algebraic tree with K-bounded growth. By hypothesis,

\exists K \in N

such that

\forall v \in V : | C h i l d r e n (v) | \leq K

Defining

f : V \to R

such that

f (v)

is the maximum number of nodes in the subtree rooted at v, since by hypothesis there can be at most K children per node, we have:

f (v) \leq M < \infty, \forall v \in V

Hence, f is bounded. Therefore, by the Bolzano-Weierstrass theorem, which states that every bounded sequence in

R

has a convergent subsequence, it follows that:

T is totally bounded as it has f bounded.
By the Heine-Borel Theorem, T is relatively compact.

Thus, it has been formally demonstrated that bounding the branching factor ensures relative compactness under the metric d. □

Theorem 8

(Absence of Anomalous Cycles). Let

(S, F)

be a discrete dynamical system and

T = (V, E)

the algebraic inverse tree recursively constructed from the analytical inverse G. Then T does not contain any non-trivial anomalous cycle. That is:

∄ γ = 〈 v_{1}, \dots, v_{k} 〉, k \geq 3 : v_{k} = v_{1} \land (v_{i}, v_{i + 1}) \in E, \forall 1 \leq i < k

Proof.

Let

(S, F)

be a discrete dynamical system and

T = (V, E)

be the inverse algebraic tree constructed recursively from the analytic inverse function G. Then T does not contain any non-trivial anomalous cycles.

We proceed by contradiction:

Suppose there exists a non-trivial anomalous cycle $γ$ in T.
By the recursive construction of T through injective G, each node has a unique parent.
But then, taking consecutive nodes $v_{i}$ , $v_{i + 1}$ in $γ$ would lead to a contradiction, as $v_{i + 1}$ would have two parents: $v_{i}$ for being in $γ$ and its unique parent by (2).
A contradiction is reached after assuming the existence of such an anomalous cycle.
By contradiction, it is concluded that there is no non-trivial anomalous cycle in T.

Thus, the absence of anomalous cycles in the inverse algebraic tree T is formally demonstrated. □

Theorem 9

(Universal Convergence of Paths). Let

(S, F)

be a discrete dynamical system and let

T = (V, E)

be the associated inverse algebraic tree constructed recursively from the analytic inverse function G. Then in T, universal convergence of trajectories towards the root node r holds.

Proof.

The proof is done by structural induction:

Base Case (BC): Every trajectory P of length 1 trivially converges to r. Formally, $\forall P = 〈 v 〉, v \in V : v = r$ .
Inductive Hypothesis (IH): Assume that every trajectory in T of length $\leq k$ converges to r.

$\forall P \in T, | P | \leq k : lim_{n \to \infty} P = r$ .
Inductive Step (IS):

(a)

Let $P = 〈 v_{1}, . . ., v_{k + 1} 〉$ be a trajectory in T of length $k + 1$ .

(b)

Let $Q = 〈 v_{1}, . . ., v_{k} 〉$ be the subpath of P excluding $v_{k + 1}$ .

(c)

By IH, Q converges to r.

(d)

Since $v_{k + 1}$ is a child of $v_{k}$ in T, by construction, it also converges to r.

(e)

By path uniqueness in T, concatenating convergent paths Q and $〈 v_{k + 1} 〉$ results in a convergent path, hence P converges to r.

By the principle of structural induction, universal convergence in T is formally demonstrated. □

Theorem 10

(Universal Convergence in AIT). Let

T = (V, E)

be an Algebraic Inverse Tree constructed from a Discrete Dynamical System

(S, F)

with the analytic inverse function G. Then, for every infinite path

P = (v_{1}, v_{2}, \dots)

in T, P converges to the root node r.

Proof.

Step 1: Define the convergence of a path.

\begin{matrix} \forall P \in P (T), \forall r \in V : C o n v e r g e s (P, r) \Leftrightarrow \\ \forall ε > 0, \exists N \in N, \forall n > N : d (v_{n}, r) < ε \end{matrix}

where

P (T)

is the set of all paths in T, and d is the graph distance in T.

Step 2: Prove that every node has a unique path to the root.

\begin{matrix} \forall v \in V, \exists! P \in P (T) : \\ P = (v, \dots, r) \land \\ \forall i \in {1, \dots, | P | - 1} : (P [i], P [i + 1]) \in E \end{matrix}

where

P [i]

denotes the i-th node in the path P.

This follows from the recursive construction of T using the injective function G.

Step 3: Prove that every infinite path is a Cauchy sequence.

\begin{matrix} \forall P = (v_{1}, v_{2}, \dots) \in P (T) : \\ \forall ε > 0, \exists N \in N, \forall m, n > N : d (v_{m}, v_{n}) < ε \end{matrix}

This follows from the monotonically decreasing distances between consecutive nodes in P, due to the unique path property.

Step 4: Prove that T is complete.

\begin{matrix} \forall {(v_{n})}_{n \in N} \subseteq V : \\ (\forall ε > 0, \exists N \in N, \forall m, n > N : d (v_{m}, v_{n}) < ε) \\ \Rightarrow \exists v \in V : lim_{n \to \infty} v_{n} = v \end{matrix}

This follows from the finiteness of paths between any node and the root, and the completeness of

R

with the usual metric.

Step 5: Conclude that every infinite path converges to the root.

\begin{matrix} \forall P = (v_{1}, v_{2}, \dots) \in P (T) : C o n v e r g e s (P, r) \end{matrix}

This follows from Steps 3 and 4, as every infinite path is a Cauchy sequence in the complete space T, and thus converges to a unique limit, which must be the root node r by the unique path property.

Therefore, we have proven that every infinite path in the Algebraic Inverse Tree T converges to the root node r. □

Theorem 11

(Unique AIT Generation). Let

(S, F)

be a discrete dynamical system and

G : S \to P (S)

its analytic inverse. It is proven that:

If G satisfies:

Injectivity Surjectivity Exhaustiveness Then, the inverse algebraic tree

T = (V, E)

constructed recursively applying G is unique and satisfies:

Absence of anomalous cycles:

∄ γ

non-trivial cycle in T Universal convergence of trajectories:

\forall P \in T, lim_{n \to \infty} P = r

where r is the root.

Proof.

Let

(S, F)

be a discrete dynamical system and

G : S \to S

its analytic inverse. It is proven that:

$\forall x, y \in S, G (x) = G (y) \Rightarrow x = y$
$\forall z \in S, \exists x \in S, G (x) = z$
$\forall x \in S, \exists n \in N, G^{n} (x) = r$

Where r denotes the root node of the inverse algebraic tree

T = (V, E)

constructed by iterations of G.

Assuming that G satisfies injectivity, surjectivity, and exhaustiveness, absence of cycles and universal convergence in T are proven:

Absence of anomalous cycles: Suppose $\exists γ = (v_{1}, . . ., v_{k})$ , a non-trivial cycle in T. By the injectivity hypothesis, $\forall u, v \in V, G (u) = G (v) \Rightarrow u = v$ . Taking consecutive nodes $v_{i}, v_{i + 1}$ , a contradiction is obtained $\Rightarrow ∄ γ$ non-trivial cycle.
Universal convergence: $\forall x \in S$ , by exhaustiveness of G, $\exists n \in N$ such that $G^{n} (x) = r$ . That is, $\forall P \in T, {lim}_{n \to \infty} P = r$ .

It has been proven by contradiction and quantification that the tree T generated under the conditions on G satisfies absence of anomalous cycles and universal convergence. □

6. Uniqueness of the Inverse Model

The proof of the properties of injectivity, surjectivity, and exhaustiveness of the analytic inverse function G ensures the uniqueness of the inverse model constructed from it, even when dealing with a forest of inverse trees.

Explanation 1.

Injectivity of G: Ensures that different states of the original function F are associated with different pre-images under G. This ensures that there are no multiple states in the inverse model mapped to the same state in the canonical system.

Surjectivity of G: Ensures that every state in the canonical system has at least one corresponding state in the inverse model mapped to it under G. Therefore, the inverse model completely covers the states of the original system.

Exhaustiveness of G: Implies that all states of the canonical system can be reached by recursion of G starting from the roots. This ensures that the inverse model uniquely captures all the interrelationships of the original system.

Therefore, under these conditions, the function G uniquely defines the inverse model, whether it is a single tree T or a forest

F = {T_{1}, T_{2}, \dots, T_{n}}

of n trees. Each node in each tree

T_{i} \in F

is uniquely and reversibly associated with a state in the canonical system S through the injective and surjective action of G.

In conclusion, the uniqueness of the inverse model is guaranteed as long as the critical properties of injectivity, surjectivity, and exhaustiveness of the analytic inverse function G on which the model is based are demonstrated. .

6.1. Necessary and Sufficient Conditions for Ensuring the Construction of Inverse Models

Definition 44.

Let

(S, F)

be a discrete dynamical system, where S is the discrete state space and

F : S \to S

is the evolution function. Let

G : S \to P (S)

be the analytical inverse function of F that recursively undoes its steps.

Theorem 12

(Conditions for Inverse Model Constructibility). The inverse model of the system

(S, F)

in the form of an inverted algebraic tree

T = (V, E)

constructed recursively from G is constructible if and only if the following conditions are satisfied:

Injectivity of G: $\forall x, y \in S, G (x) = G (y) \Rightarrow x = y$
Surjectivity of G: $\forall z \in S, \exists x \in S : G (x) = z$
Exhaustiveness of G: $\forall x \in S, \exists n \in N : G^{n} (x) = r$ , where r is the root of T

Proof.

Suppose G satisfies the three conditions. We prove that T is constructible:

(Injectivity) By modus ponens, injectivity guarantees uniqueness in the construction of T.

(Surjectivity) Surjectivity ensures that every state in S is reachable from some node in T, making the inverse model complete.

(Exhaustiveness) By recursively applying G from any initial state, the root r is always reached after finitely many steps. This allows the construction of T to terminate.

Conversely, suppose T is constructible. We prove that G must satisfy the three conditions:

(Injectivity) If G is not injective, there would be ambiguity in the predecessors of some nodes in T, contradicting its tree structure.

(Surjectivity) If G is not surjective, some states in S would not be reachable in T, making it an incomplete model.

(Exhaustiveness) If G is not exhaustive, the recursive construction of T would not terminate for some initial states, contradicting its constructibility.

Therefore, the three conditions are both necessary and sufficient for the constructibility of the inverse model T. □

This theorem rigorously characterizes the types of discrete dynamical systems for which the inverse modeling approach is feasible. Systems satisfying injectivity, surjectivity, and exhaustiveness of their analytical inverse functions are amenable to this methodology, while those violating these conditions are intractable cases.

Injectivity prevents ambiguity, surjectivity ensures completeness, and exhaustiveness guarantees termination in the recursive construction of the inverse algebraic tree. These conditions provide a precise delimitation of the scope and applicability of the inverse modeling framework.

7. Multivalued Injectivity of G

The multivalued injectivity of G ensures that the sets of states mapped by the inverse function do not overlap for distinct states. Formally, for any pair of distinct states

x, y \in S

, it is required that:

G (x) \cap G (y) = \emptyset

This property is essential for preserving the consistency and structure of the inverse algebraic model, avoiding ambiguities or inconsistencies that could undermine its ability to faithfully capture the dynamics of the original system.

7.1. Surjectivity of $F : S \to T$ , where $T \subseteq S$

The surjectivity of the forward evolution function F requires that for each state in the subset T of the state space S, there exists at least one state in S that maps to it under F. Formally:

\forall t \in T, \exists s \in S : F (s) = t

This condition ensures that the inverse model covers all reachable states of the original system and is "anchored" in it, ensuring that each state in the inverse tree corresponds to a reachable state in the canonical system. This is fundamental for the validity of topological transport.

In practice, the surjectivity of F may be easier to establish than the multivalued injectivity of G, since F is usually an explicitly defined function, while G is indirectly constructed through the inversion process.

In summary, the multivalued injectivity of G and the surjectivity of F are the most critical conditions to ensure the consistency, integrity, and correspondence between the inverse model and the original system, which are the pillars of the methodology presented.

8. Discussion on the Conditions of the Analytic Inverse Function G

In this section, we discuss the conditions that the analytic inverse function G must satisfy to ensure the validity and constructibility of the inverse model. These conditions are particularly important when the convergence of the direct function F is not known.

Definition 45.

Let

(S, F)

be a discrete dynamical system, where S is the set of states and

F : S \to S

is the evolution function. We say that a function

G : S \to P (S)

is ananalytic inverse functionof F if for every

s \in S

s \in G (F (s))

Theorem 13.

If G is an analytic inverse function of F, then for every

s \in S

, there exists a sequence

(s_{0}, s_{1}, \dots, s_{n})

such that

s_{0} = s

s_{n}

is a root state, and

s_{i + 1} \in G (s_{i})

for every

i = 0, 1, \dots, n - 1

8.1. Finite Case

When S is a finite set, the following properties of G are sufficient to ensure the constructibility and fidelity of the inverse model:

Definition 46.

A function

G : S \to P (S)

isinjectiveif for every

s, t \in S

s \neq t

implies

G (s) \cap G (t) = \emptyset

Definition 47.

A function

G : S \to P (S)

issurjectiveif for every

s \in S

, there exists

t \in S

such that

s \in G (t)

Definition 48.

A function

G : S \to P (S)

isexhaustiveif for every

s \in S

, there exists

n \in N

such that

G^{n} (s)

contains a root state.

The injectivity of G ensures that there are no ambiguities in the construction of the inverse algebraic tree, while surjectivity guarantees that every state in the original system has at least one predecessor in the inverse model. Exhaustiveness ensures that every state is reachable from a root state by a finite sequence of applications of G.

If G is not exhaustive, the "unreachable" states could be excluded from the set of states, as they would not be present in the direct dynamics governed by F.

8.2. Countably Infinite Case

When S is a countably infinite set, exhaustiveness of G may not be achievable, as there could exist states that are not reached by any finite iteration of G. However, this does not affect the ability of the inverse model to capture the essential dynamics of the system, as these "unreachable" states would also not be reachable by the direct function F.

In this scenario, the conditions of injectivity and surjectivity of G are sufficient to ensure the validity of the inverse model, even if exhaustiveness cannot be guaranteed. The injectivity of G is crucial for maintaining the tree structure and convergence towards the root.

Theorem 14.

If S is a countably infinite set and G is an injective analytic inverse function of F, then the graph generated by G is a tree converging to the root.

These considerations demonstrate the robustness of the inverse modeling methodology and its applicability to different classes of discrete dynamical systems, both finite and countably infinite.

8.3. Injectivity and Surjectivity of G: Ensuring Decidable Inference and Property Transfer

The injectivity and surjectivity properties of the inverse analytic function G play a crucial role in ensuring that the transfer of properties from the inverse model to the original model is possible and decidable. These properties establish a well-defined and complete correspondence between the states of the original system and the nodes of the inverse algebraic tree.

Injectivity of G guarantees that each state in the inverse model has a unique corresponding state in the original system. This property is essential to avoid ambiguities or inconsistencies in the transfer of properties. If G were not injective, there could be multiple states in the inverse model that map to the same state in the original system, which would hinder the inference of properties.

On the other hand, surjectivity of G ensures that each state in the original system has at least one corresponding state in the inverse model. This property is necessary for a complete transfer of properties. If G were not surjective, there could be states in the original system that are not represented in the inverse model, leading to a loss of information in the inference.

Together, injectivity and surjectivity of G establish a discrete homeomorphism between the state space of the original system and the set of nodes of the inverse algebraic tree. This homeomorphism is key to the transfer of topological properties and to ensuring the decidability of the inference.

In other words, if we know certain cardinal properties of the inverse model, such as the absence of anomalous cycles or the universal convergence of trajectories, and G is injective and surjective, then we can decidably infer that these properties also hold in the canonical model. The transfer of properties is guaranteed by the one-to-one correspondence established by G.

Moreover, the injectivity and surjectivity properties of G not only allow for the transfer of known properties but also open the door to the discovery of new properties in the canonical model through the study of the inverse model. If we find new topological or dynamical properties in the inverse algebraic tree, and G is injective and surjective, then we can confidently infer that these properties are also present in the original system, even if they were not apparent from the canonical model.

It is important to note that the injectivity and surjectivity conditions of G are sufficient but not necessary for the inference of some properties. There may be cases where a partial transfer of properties is possible even if G is not strictly injective or surjective. However, for a general and robust theory of property inference through inverse models, it is prudent to require these conditions as a guarantee of a complete and decidable transfer.

In summary, the injectivity and surjectivity properties of G play a fundamental role in ensuring the decidable and complete transfer of properties between the inverse model and the canonical model. This idea deserves a detailed discussion in the theory of inverse discrete dynamical systems, as it strengthens the conceptual foundations of the methodology and clarifies the conditions under which property inference is possible and reliable.

9. Topological Equivalences

After constructing the inverse model of a discrete dynamical system using an algebraic tree following the reversed analytical recursion, and having demonstrated its cardinal structural properties, the next step in the methodology consists of establishing formal topological equivalences between this inverted model and the original canonical system.

To do this, a homeomorphism is defined, that is, a bijective and bicontinuous mapping, between the nodes of the algebraic inverse tree and the discrete states of the canonical system. This correlation is demonstrated to satisfy the conditions of being a bijective and continuous function in both directions.

With this critical element, the conditions are given to demonstrate the topological equivalence between both dynamic systems, discrete and inverse, with the relevant natural topologies in each case. Again, the continuity of the homeomorphism, along with the topological attributes already demonstrated on the model such as compactness and metric completeness, allow completing the sought equivalence proof.

Finally, as a consequence of this equivalence induced by the homeomorphism, various relevant properties demonstrated for one system also hold for the other. In this scenario, the previously mentioned topological transport becomes possible between the canonical system and its inversely modeled counterpart, analytically transferring the previously demonstrated structural properties.

Thus, the long-awaited Topological Equivalence is finally obtained as the culmination point in the process of modeling, analysis, and inferential transport to solve open problems on discrete dynamics through the revolutionary inverse theoretical approach fully exposed here.

Definition 49.

Let

(X, τ)

be a topological space, where X is a set and τ is a topology on X, i.e., τ satisfies:

$\emptyset, X \in τ$
The union of elements of τ belongs to τ
The finite intersection of elements of τ belongs to τ

Formally, a topological space is an ordered pair

(X, τ)

where X is a set and τ is a family of subsets of X satisfying the above properties.

9.1. Cardinal Properties of Algebraic Inverse Trees

Definition 50

(Continuity). Let

(X, τ)

and

(Y, σ)

be topological spaces. A function

f : X \to Y

is continuous at a point

x_{0} \in X

if for every open set

V \subseteq Y

with

f (x_{0}) \in V

, there exists an open set

U \subseteq X

such that

x_{0} \in U

and

f (U) \subseteq V

We say that f is continuous if it is continuous at all points of X.

And of compactness:

Definition 51

(Compact Space). A topological space

(X, τ)

is said to be compact if for every family of open sets

U_{α} α \in A

that cover X, there exists a finite subfamily

U α_{1}, \dots, U_{α_{n}}

that also covers X.

Definition 52

(Metric Space). A metric space is an ordered pair

(M, d)

where:

M is a non-empty set
d is a metric on M

satisfying the metric axioms d:

$d (x, y) \geq 0$ , with $d (x, y) = 0 \Leftrightarrow x = y$
$d (x, y) = d (y, x)$
$d (x, z) \leq d (x, y) + d (y, z)$

Definition 53

(Metric on Algebraic Inverse Tree). Let

(S, F)

be a discrete dynamical system with inverse function G. Let

T = (V, E)

be the associated algebraic inverse tree constructed recursively by applying G.

The metric

d : V \times V \to R

is defined as:

For any pair of nodes

x, y \in V

d (x, y) = \{\begin{matrix} 0 & if x = y \\ L (λ (x, y)) & if x \neq y \end{matrix}

Where

λ (x, y)

is the unique path in T from x to y, and

L (λ (x, y))

is the length (number of edges) of that path.

Theorem 15

(Compactness). Let

(T, d)

be the metric space associated with an inverted discrete dynamical system modeled as an Inverse Algebraic Tree T. Then

(T, d)

is a compact metric space.

Proof.

Let

(T, d)

be the metric space associated with an inverted discrete dynamical system modeled as an Inverse Algebraic Tree T. We aim to prove that

(T, d)

is compact.

Suppose, for the sake of contradiction, that

(T, d)

is not compact. This implies the existence of an open cover

U

of T such that no finite subcollection of

U

covers T.

Consider the open balls

B_{ε} (v_{k})

of radius

ε

centered at the nodes

v_{k} \in T

. Since T is finite, there exists a finite number of balls that cover T. Let

V \subseteq U

be this finite subcover.

Now, consider any closed and bounded subset

K \subseteq T

. By the Heine-Borel Theorem, a subset of a Euclidean space is compact if and only if it is closed and bounded. Since K is contained within a closed ball of finite radius that only contains a few points, it follows that K is finite and thus compact.

Therefore,

(T, d)

is compact, contradicting our initial assumption. Thus, the supposition that

(T, d)

is not compact must be false. □

Theorem 16

(Connectedness). Let

(T, d)

be the metric space associated with an inverted discrete dynamical system modeled as an Algebraic Inverse Tree. Then

(T, d)

is connected, it cannot be expressed as the union of two disjoint non-empty subsets.

Proof.

Suppose by contradiction that

(T, d)

is not connected.

Then there would exist

A, B \subset T

disjoint and non-empty such that

A \cup B = T

and

A \cap B = \emptyset

Taking

a \in A

and

b \in B

, by uniqueness of paths in

(T, d)

there exists a unique path from a to b.

But since

a \in A

and

b \in B

with

A, B

open by hypothesis, by the Connectivity Lemma, there should exist c on this path such that

c \notin A \cup B

, contradicting

A \cup B = T

We arrive at a contradiction assuming that

(T, d)

was not connected.

By contradiction, we conclude that

(T, d)

is connected, completing the proof. □

Definition 54.

Let

(X, d)

be a metric space. A sequence

(x_{n})

in X is called a Cauchy sequence if:

\forall ε > 0 : \exists N \in N : \forall n, m \geq N : d (x_{n}, x_{m}) < ε

Definition 55.

Let

(X, d)

be a metric space.

(X, d)

is said to be complete if every Cauchy sequence

x_{n}

in X converges to some point

x \in X

. In other words:

\forall (x_{n}) \subseteq X, (x_{n}) is Cauchy \Rightarrow \exists x \in X : lim_{n \to \infty} x_{n} = x

Lemma 5

(Infinite Paths as Cauchy Sequences). Let

(S, F)

be a discrete dynamical system modeled by a metric space

(X, d_{X})

. Let T be the associated algebraic inverse tree constructed recursively from the inverse function

G : X \to P (X)

. Let

P = (x_{1}, x_{2}, \dots)

be an arbitrary infinite path in T.

Then, P is a Cauchy sequence in

(X, d_{X})

Proof.

Let the metric

d : T \times T \to R

be defined on nodes of T such that

d (u, v)

equals the length of the unique path between nodes u and v in T. This path length determines the distance function

d_{T}

Since there is universal convergence in T,

\forall ε > 0, \exists N \in N : n \geq N \Rightarrow d_{T} (x_{n}, r) < ε

, where r is the root node.

By the definition of convergence,

d_{T} (x_{n}, r) < ε \Rightarrow d_{T} (x_{n}, x_{m}) < 2 ε

for infinitely many

n, m \geq N

(taking

ε = 1

Moreover, by the triangle inequality on

d_{X}

d_{X} (x_{n}, x_{m}) \leq d_{X} (x_{n}, r) + d_{X} (r, x_{m}) < 2 ε

Therefore, P satisfies the Cauchy condition in

(X, d_{X})

, proving the lemma. □

9.2. Other Cardinal Properties of the Inverse Tree

In addition to the established fundamental properties such as universal convergence of trajectories and absence of anomalous cycles, we propose to study the following cardinal properties in the context of inverse algebraic trees:

Definition 56

(Stability). Let

T = (V, E)

be an inverse algebraic tree associated with a discrete dynamical system

(S, F)

. We say that T is stable if for any

ε > 0

, there exists a

δ > 0

such that for any pair of nodes

u, v \in V

, if

d (u, v) < δ

, then

d (F (u), F (v)) < ε

, where d is an appropriate metric on V.

Intuitively, stability implies that small perturbations in the initial states do not significantly alter the global structure of the tree or affect convergence towards the root node.

Definition 57

(Robustness). Let

T = (V, E)

be an inverse algebraic tree associated with a discrete dynamical system

(S, F)

. We say that T is robust if for any perturbation

p : S \to S

in the original system, there exists a homeomorphism

h : T \to T^{'}

such that

T^{'}

is the inverse algebraic tree associated with the perturbed system

(S, F \circ p)

Robustness ensures that the structural and convergence properties of the inverse tree are preserved even under significant perturbations in the original system.

Definition 58

(Carrying Capacity). Let

T = (V, E)

be an inverse algebraic tree associated with a discrete dynamical system

(S, F)

. The carrying capacity of T, denoted

C C (T)

, is defined as the maximum size of the state space

| S |

for which the construction of T remains computationally tractable.

Carrying capacity measures the ability of the inverse tree to efficiently handle systems with large state spaces or high complexity.

Definition 59

(Adaptability). Let

T = (V, E)

be an inverse algebraic tree associated with a discrete dynamical system

(S, F)

. We say that T is adaptable if for any continuous change in the parameters of the original system resulting in a family of systems

(S, F_{t})

, there exists a continuous family of homeomorphisms

h_{t} : T \to T_{t}

such that

T_{t}

is the inverse algebraic tree associated with

(S, F_{t})

Adaptability captures the ability of the inverse tree to adjust its structure and inferred properties in response to parametric changes in the original dynamical system.

These new cardinal properties (stability, robustness, carrying capacity, and adaptability) expand the scope and applicability of the theory of inverse discrete dynamical systems. Future research could focus on developing specific metrics, demonstrating the preservation of these properties under homeomorphisms, and analyzing their impact on the computational scalability of the methodology. Incorporating these notions enriches and strengthens the theoretical foundations of this innovative approach to modeling and analyzing complex systems.

9.3. Conditions for Topological Transportability

Theorem 17

(Topological and Metric Conditions for Transportability). Let

(X, F)

be a discrete dynamical system, and let

T = (V, E)

be its inverse algebraic tree generated by the inverse analytic function

G : X \to P (X)

. If T satisfies the following properties:

Relative compactness
Connectivity
Relative metric completeness

then the topological properties demonstrated in T can be transported to the original system

(X, F)

through a homeomorphic equivalence.

Proof.

Suppose the inverse algebraic tree T associated with

(X, F)

satisfies the enumerated properties:

Due to relative compactness, T exhibits good limit and convergence properties, necessary for preserving the topological structure under homeomorphisms.
By connectivity, T maintains its topological coherence, avoiding undesired disconnections that would hinder a homeomorphic correspondence with $(X, F)$ .
Through relative metric completeness, T ensures the convergence of Cauchy sequences, an invariant property under homeomorphisms and essential for preserving the metric structure.

These topological and metric properties of T, being invariant under homeomorphisms, allow establishing a topological equivalence with the original system

(X, F)

. This ensures that the properties demonstrated in T remain valid in

(X, F)

Conversely, if any of these properties fails in T, a homeomorphic correspondence with

(X, F)

cannot be assured, and therefore, the transport of properties would not be guaranteed. □

Theorem 18

(Necessary and Sufficient Conditions on G for Transportability). For an inverse algebraic tree T associated with a discrete dynamical system

(X, F)

to satisfy the required topological and metric properties for transportability, its generating inverse analytic function G must fulfill:

Multivalued injectivity: $\forall x, y \in X : x \neq y \Rightarrow G (x) \cap G (y) = ⌀$
Surjectivity: $\forall z \in X, \exists x \in X : z \in G (x)$
Continuity: G is continuous with respect to the topologies of X and $P (X)$

Proof.

The conditions on G are derived from the topological and metric requirements of T:

Multivalued injectivity of G ensures that the structure of T is well-defined and free from ambiguities, preserving its topology.
Surjectivity of G guarantees that T covers all reachable states of X, establishing a complete correspondence.
Continuity of G with respect to the topologies of X and $P (X)$ is necessary for T to inherit the relevant topological properties of $(X, F)$ .

These conditions on G are necessary and sufficient for the inverse algebraic tree T to have the required topological and metric properties for a valid transportability of properties through a homeomorphic equivalence with

(X, F)

. □

9.4. Homeomorphism between Spaces

Definition 60

(Discrete Topology). Let S be the discrete space on which a discrete dynamical system is defined. The discrete topology on S is defined as:

τ = {\emptyset, {x_{1}}, {x_{2}}, \dots}

where

x_{i} \in S

and each element of S defines an open and closed set (a singleton).

The axioms satisfied by τ are:

$\emptyset, S \in τ$
The union of elements of τ belongs to τ
The finite intersection of elements of τ belongs to τ

In other words, τ constitutes a discrete topology on S, whose open sets are all subsets, and whose closed sets are the complements of open sets. A basis for τ is given by the singletons, and a sub-basis consists of the elements of S itself.

It is then said that

(S, τ)

is a discrete topological space relevant to the system.

Example 2.

A simple example of a topological space is the set

X = {a, b, c}

with the topology

T = {\emptyset, {a}, {b}, {a, b}, {a, b, c}}

Definition 61.

Let

(S, τ)

be the topological space associated with the canonical discrete dynamical system, where S is the set of discrete states and τ is the standard discrete topology.

Let

(T, ρ)

be the topological space associated with the inverse algebraic model, where

T = (V, E)

is the inverse algebraic tree with node set V, edges E, and ρ is the natural topology on T.

We define a map

f : (T, ρ) \to (S, τ)

as follows:

For all

v \in V

, there exists a unique

s \in S

such that

f (v) = s

In other words, f bijectively correlates each node v of the tree T with a unique state s of the canonical system S.

Definition 62

(Homeomorphism). Let

(X, τ)

and

(Y, σ)

be topological spaces associated with a canonical discrete system S and its inverse algebraic model T respectively. A homeomorphism is a bijective and bicontinuous function

f : (X, τ) \to (Y, σ)

f is bijective
Both f and $f^{- 1}$ are continuous

Example 3.

The open intervals

(0, 1)

and

(a, b)

in the real line with the usual topology are homeomorphic. A bijective and continuous function between them is

f (x) = a + (b - a) x

, and its inverse

f^{- 1} (y) = \frac{y - a}{b - a}

is also continuous.

Example 4.

Consider the topological spaces

(X, T_{X})

and

(Y, T_{Y})

, where

X = {1, 2, 3}

with the discrete topology (all subsets of X are open) and

Y = {a, b}

with the trivial topology (only the empty set and Y are open). The function

f : X \to Y

defined by

f (1) = a

f (2) = b

, and

f (3) = a

is continuous, since the preimage of any open set in Y is an open set in X.

Theorem 19.

The map

f : (T, ρ) \to (S, τ)

defined above is a homeomorphism between the topological spaces associated with the inverse algebraic model and the canonical discrete dynamical system.

Proof.

Let

f : (T, ρ) \to (S, τ)

be the function that bijectively correlates nodes of the algebraic inverse tree T with states of the canonical system S. We aim to show that f is a homeomorphism.

First, we prove that f is bijective. Injectivity follows from the fact that each node in T represents a unique state in S, and surjectivity is ensured by the exhaustive construction of T using the inverse function G.

Next, we show that f and

f^{- 1}

are continuous. To prove continuity, we use the following equivalent definitions:

f is continuous if and only if for every open set U in $(S, τ)$ , the preimage $f^{- 1} (U)$ is open in $(T, ρ)$ .
f is continuous if and only if for every convergent sequence $(x_{n}) \to x$ in $(T, ρ)$ , the sequence $(f (x_{n})) \to f (x)$ in $(S, τ)$ .

Let U be an open set in

(S, τ)

. By the definition of the discrete topology, every subset of S is open. Thus,

f^{- 1} (U)

is a union of nodes in T, which is open in the natural topology

ρ

. Therefore, f is continuous.

Similarly, let

(x_{n})

be a convergent sequence in

(T, ρ)

with

x_{n} \to x

. Since T is discrete, convergence implies that

x_{n} = x

for all but finitely many n. Thus,

f (x_{n}) = f (x)

for all but finitely many n, implying that

(f (x_{n}))

converges to

f (x)

(S, τ)

. Therefore, f is continuous.

The continuity of

f^{- 1}

can be shown using similar arguments. □

Theorem 20

(Homeomorphic Invariance). Let

f : (X, τ) \to (Y, σ)

be a homeomorphism, and let P be a topological property on X invariant under f. Then:

P (X) \leftrightarrow P (Y)

In other words, the property is preserved in the transformed space.

Proof.

Let

(X, τ)

and

(Y, σ)

be topological spaces. Let

f : (X, τ) \to (Y, σ)

be a homeomorphism between X and Y. Let P be a topological property on X that is invariant under f.

We will demonstrate that P is preserved in the transformed space Y through f. That is:

P (X) \leftrightarrow P (Y)

To show invariance, we explicitly prove that if P holds on X, then P also holds on Y:

(→): Let

x \in X

such that

P (x)

holds. Since P is a topological property and f is a homeomorphism, then:

P (x) \overset{f}{\to} P (f (x))

That is, if x satisfies P, then

y = f (x)

also satisfies it. Applying this to all

x \in X

, it follows from

P (X)

that

P (f (X)) = P (Y)

, by explicit action of f.

(←): The reverse direction follows similarly by using continuity of

f^{- 1}

...

Thus P is explicitly demonstrated invariant under the bijective and bicontinuous mapping f. □

Theorem 21

(Properties). Every homeomorphism f satisfies:

Preserves subspaces
Preserves compactness
Preserves connectedness
Preserves metric completeness

In other words, topological properties invariant under homeomorphisms.

Proof.

Let

f : (X, τ) \to (Y, σ)

be a homeomorphism between topological spaces X and Y.

Subspaces: Let $A \subseteq X$ be a subspace of X. Since f is bijective, $f (A) \subseteq Y$ is a subspace of Y. Moreover, since $f^{- 1} : Y \to X$ is the inverse homeomorphism, it maps subspaces to subspaces. Specifically, $f^{- 1} (f (A)) = A$ . Thus f and $f^{- 1}$ preserve subspaces under their mapping actions.
Compactness: Suppose $(X, τ)$ is a compact topological space. Thus every open cover $U = U_{α}$ of X has a finite subcover $U^{'} = U_{α_{1}}, . . ., U_{α_{n}}$ that also covers X. Since f is continuous as a homeomorphism, it maps open sets to open sets. Therefore, $V = V_{β} = f (U_{α})$ is an open cover of Y. Applying $f^{- 1}$ , which is also continuous, gives the open subcover $V^{'} = f^{- 1} (V_{β_{1}}), . . ., f^{- 1} (V_{β_{m}})$ of X. But $V^{'} = U^{'}$ . Thus there exists a finite subcover of $V$ , implying Y is compact.
Connectedness: Follows by an analogous argument using continuity of f and $f^{- 1}$ to map connected sets to connected sets.
Metric completeness: If $(X, d_{X})$ is metrically complete, Cauchy sequences converge. Applying continuous f maps Cauchy sequences to Cauchy sequences, which will converge in the complete space $(Y, d_{Y})$ . Hence $(Y, d_{Y})$ is complete.

Therefore, f preserves all these topological properties. □

Theorem 22.

The function

f : T \to S

correlating the algebraic inverse tree T with the discrete dynamical system S is injective.

Proof.

Let

f : T \to S

be the function bijectively correlating nodes of the algebraic inverse tree T constructed from the analytic inverse function G with states of the discrete system S. Since G is injective by definition, for any pair of distinct nodes

x, y \in T

G (f (x)) \neq G (f (y))

. But by construction of T, recursively applying G from a root node, each node has a unique predecessor determined by the application of G. Thus, if we had

f (x) = f (y)

for some pair

x \neq y

, it would lead to a contradiction with the uniqueness of the predecessor given by G. Therefore, it must be that if

f (x) = f (y)

then necessarily

x = y

. It is concluded that f is injective. □

Theorem 23.

The function

f : T \to S

correlating the algebraic inverse tree T with the discrete dynamical system S is surjective.

Proof.

Again, let

f : T \to S

be the function correlating nodes of the inverse tree T with states of S. As T is constructed by inverted analytic recursion, successively applying G starting from a root node associated with an initial/final state in S, in reconstructing all possible trajectories in reverse in S, all reachable states are covered by some node in T due to the exhaustive construction of the tree. Formally, given any state

s \in S

, there exists some possible inverted trajectory in S ending in s, which is represented in T, implying the existence of some node

x \in T

such that

f (x) = s

. Hence f is surjective. □

Theorem 24.

The function

f : T \to S

correlating the algebraic inverse tree T with the discrete dynamical system S is bijective.

Proof.

Having demonstrated both injectivity and surjectivity of the function f, it is directly concluded by definition that f constitutes a homeomorphism between T and S. □

Lemma 6

(Sequential Continuity). The bijective function

f : T \to S

correlating the AIT with the canonical discrete system is sequentially continuous.

Proof.

Let

f : T \to S

be the bijective function between the AIT T and the canonical discrete system S. It is demonstrated that:

\forall {(v_{n})}_{n \in N} \subseteq T, \forall v \in T : {(v_{n})}_{n \in N} \overset{s e q}{\to} v \Rightarrow f ({(v_{n})}_{n \in N}) \overset{s e q}{\to} f (v)

Where

\overset{s e q}{\to}

denotes sequential convergence.

Let

{(v_{n})}_{n \in N}

be a sequence in T such that

{(v_{n})}_{n \in N} \overset{s e q}{\to} v

. By definition,

\forall ϵ > 0 : \exists N \in N : n \geq N \Rightarrow d_{T} (v_{n}, v) < ϵ

Furthermore, as f is sequentially continuous,

\exists δ > 0

such that

d_{T} (v_{n}, v) < δ \Rightarrow d_{S} (f (v_{n}), f (v)) < ϵ^{'}

Moreover, as

{(v_{n})}_{n \in N} \overset{s e q}{\to} v

\exists N^{'} \in N

such that

\forall n \geq N^{'}, d_{T} (v_{n}, v) < δ

By transitivity,

\forall n \geq max (N, N^{'}), d_{S} (f (v_{n}), f (v)) < ϵ^{'}

. Hence

f ({(v_{n})}_{n \in N}) \overset{s e q}{\to} f (v)

, proving the sequential continuity of f.

□

Theorem 25

(f is a homeomorphism). Let

(S, F)

be a discrete dynamical system with analytic inverse G. Let

T = (V, E)

be the associated algebraic inverse tree and

f : V \to S

the bijective function correlating nodes of T with states of S. It is demonstrated that:

f is bijective. f and

f^{- 1}

are sequentially continuous. Therefore, being bijective and bicontinuous, f constitutes a homeomorphism between the topological spaces associated with T and S.

Proof.

Injectivity and surjectivity of f are demonstrated by recursive construction of T from G and definition of f. To show sequential continuity of f:

Let ${(v_{n})}_{n \in N} \subseteq T$ and $v \in T$ such that ${(v_{n})}_{n \in N} \overset{s e q}{\to} v$ .
By definition of sequential convergence, $\forall ε > 0, \exists N \in N : n \geq N \Rightarrow d_{T} (v_{n}, v) < ε$ .
As f is sequentially continuous, $\exists δ > 0 : d_{T} (v_{n}, v) < δ \Rightarrow d_{S} (f (v_{n}), f (v)) < ε^{'}$ .
Taking $ε = δ$ and by transitivity, ${(f (v_{n}))}_{n \in N} \overset{s e q}{\to} f (v)$ .

Similarly, it can be shown

f^{- 1}

preserves sequential convergence by explicitly verifying open sets are mapped to open sets in both directions.

Therefore, f is a homeomorphism between the spaces T and S. □

By formally proving that f is a homeomorphism between the spaces, the required topological equivalence for the desired transport of cardinal properties between the canonical system and the inverse model is established.

Definition 63

(Topological Equivalence). Let

(X, τ)

and

(Y, σ)

be topological spaces. We say there exists a topological equivalence between

(X, τ)

and

(Y, σ)

if there exists a homeomorphic correspondence

f : (X, τ) \to (Y, σ)

such that:

f is bijective, i.e., f is injective and surjective.
Both f and $f^{- 1}$ are continuous.

Furthermore, it holds that:

Cardinality is preserved, i.e., $| X | = | Y |$ .
Compactness is preserved. If $(X, τ)$ is compact, then $(Y, σ)$ is also compact.
Connectivity is preserved. If $(X, τ)$ is connected, then $(Y, σ)$ is also connected.

In other words, through f, a bijective and bicontinuous equivalence preserving topological cardinal properties is established between the spaces

(X, τ)

and

(Y, σ)

Remark 1.

In the theory of discrete dynamical systems, topological equivalence refers to the idea that two discrete dynamical systems are equivalent from a topological perspective if they have the same topological structure, that is, if they have the same number of open and closed sets, and if the transition mappings between them are homeomorphisms.

The stability of the topological equivalence refers to the property that the topological equivalence is maintained under certain transformations or deformations of the dynamical system. In other words, if two discrete dynamical systems are topologically equivalent, then any continuous deformation or transformation of one of them that preserves the topological structure will also be topologically equivalent to the other system.

Stability of the topological equivalence is a fundamental property of the theory of discrete dynamical systems, and it is used to establish the existence of a topological integration theory for these systems. In particular, it is shown that if two discrete dynamical systems are topologically equivalent, then there exists a topological integration between them that preserves the topological structure and dynamics of the system.

This has important implications for solving problems in discrete dynamical systems, as it allows establishing a connection between set theory and theory of discrete dynamical systems. In particular, set theory can be used to establish the existence of topological solutions to problems in discrete dynamical systems, and theory of discrete dynamical systems can be used to establish the existence of dynamic solutions to set problems.

Theorem 26

(Topological Equivalence). Let

(S, τ)

be a discrete dynamical system and

(T, ρ)

its inverse algebraic model. If there exists a discrete homeomorphism

f : S \to T

, then

(S, τ)

and

(T, ρ)

are said to be topologically equivalent.

Proof.

Let

(S, τ)

be a discrete dynamical system and

(T, ρ)

its inverse algebraic model. Let

f : S \to T

be a discrete homeomorphism, i.e., f is a bijective and bicontinuous function satisfying:

f is bijective
f is continuous
$f^{- 1}$ is continuous

It is demonstrated that f establishes a topological equivalence between

(S, τ)

and

(T, ρ)

. Let

O \in τ

be an open set in S. Then:

Since f is continuous, by definition $f (O)$ is open in T.
Since $f^{- 1}$ is continuous, $f^{- 1} (h (O)) = O$ is open in S.

Similarly, let

O^{'} \in ρ

be open in T. Then:

$f^{- 1} (O^{'})$ is open in S by continuity of $f^{- 1}$ .
$f (h^{- 1} (O^{'})) = O^{'}$ is open in T by continuity of f.

Therefore, f preserves open sets in both directions, establishing a topological equivalence between

(S, τ)

and

(T, ρ)

. □

Theorem 27

(AIT-Canonical System Homeomorphism). Let

(S, τ, F)

be a discrete dynamical system (DDS) with analytic inverse G. Let

T = (V, E)

be the associated algebraic inverse tree (AIT). Then there exists a homeomorphism

h : T \to S

between the AIT and the canonical system.

Proof.

We construct the function

h : T \to S

and prove that it is a homeomorphism.

Construction of h: Define

h : V \to S

as follows:

\forall v \in V : h (v) = s \Leftrightarrow v represents state s in T

In other words, h maps each node v in the AIT to the state s in the canonical system that v represents.

Step 1: h is well-defined.

\begin{matrix} \forall v \in V, \exists! s \in S : v represents s in T \\ \Rightarrow \forall v \in V, \exists! s \in S : h (v) = s \end{matrix}

Thus, h is a well-defined function from V to S.

Step 2: h is bijective.

Injectivity: Let $v_{1}, v_{2} \in V$ with $v_{1} \neq v_{2}$ . By the recursive construction of T using G, $v_{1}$ and $v_{2}$ represent different states in S. Thus, $h (v_{1}) \neq h (v_{2})$ . So h is injective.
Surjectivity: Let $s \in S$ . By the surjectivity of G, there exists a sequence of states leading to s in the DDS. This sequence is represented by a path in T ending at a node v with $h (v) = s$ . Thus, $\forall s \in S, \exists v \in V : h (v) = s$ . So h is surjective.

Step 3: h is continuous. Let

U \subseteq S

be open in

τ

. We show that

h^{- 1} (U)

is open in the AIT topology

ρ

. By the definition of

τ

U = ⋃_{s \in U} {s}

. Then:

\begin{matrix} h^{- 1} (U) & = h^{- 1} (⋃_{s \in U} {s}) \\ = ⋃_{s \in U} h^{- 1} ({s}) \\ = ⋃_{s \in U} {v \in V : h (v) = s} \end{matrix}

Each set

{v \in V : h (v) = s}

is open in

ρ

as it corresponds to a single node. Thus,

h^{- 1} (U)

is open in

ρ

as a union of open sets. So h is continuous.

Step 4: $h^{- 1}$ is continuous. Let

W \subseteq V

be open in

ρ

. We show that

h (W)

is open in

τ

. By the definition of

ρ

W = ⋃_{v \in W} {v}

. Then:

\begin{matrix} h (W) & = h (⋃_{v \in W} {v}) \\ = ⋃_{v \in W} h ({v}) \\ = ⋃_{v \in W} {h (v)} \end{matrix}

Each singleton

{h (v)}

is open in

τ

by definition. Thus,

h (W)

is open in

τ

as a union of open sets. So

h^{- 1}

is continuous.

Therefore, h is a homeomorphism between the AIT

(T, ρ)

and the canonical system

(S, τ)

. □

Corollary 2.

Any topological property demonstrated in the inverse model and preserved by homeomorphisms will also be valid in the original discrete system due to topological equivalence.

Thus, the concepts of discrete homeomorphism and topological equivalence between the canonical system and the inverse algebraic model are rigorously defined.

Topological equivalences formally correlate the original discrete dynamical system with its inverted counterpart modeled through an algebraic inverse tree, based on a bijective and bicontinuous mapping h between their state spaces that preserves cardinal properties like compactness and connectedness. This homeomorphic mapping enables transferring relevant attributes between equivalent representations.

10. Topological Transport

Having demonstrated the topological equivalence between the canonical discrete dynamical system and its counterpart modeled through an inverse algebraic tree, we are now able to state and formally prove the central theorems that consolidate the feasibility and validity of analytically transporting cardinal structural attributes between both dynamical systems.

On one hand, the Homeomorphic Invariance Theorem guarantees that any topological property proven on the inverse model, and which is preserved under homeomorphisms (i.e., an invariant topological attribute), will be validly preserved in the discrete canonical system through the action of the correlating homeomorphism.

Thus, all those fundamental properties demonstrated on the inverse model, such as the absence of anomalous cycles and the universal convergence of trajectories, are immutably transferred to the original canonical system, replicating their topological validity there as well.

On the other hand, the Topological Transport Theorem formalizes the mechanism by which, by virtue of topological equivalence and the properties of the homeomorphism in terms of continuity, injectivity, and surjectivity, the effective and invariant transfer of all fundamental properties from the transformed inverse model to the initial canonical discrete system occurs, thus inferentially resolving its dilemmas.

In this way, the theory completely and deductively formalizes the ultimate goal of inversely modeling an intractable discrete system, to transform it into a manageable one whose relevant properties inferred analytically end up solving, through invariant topological transport, the open problems that challenged any attempt on the difficult original discrete system.

Definition 64

(Homeomorphic Invariant). A topological property P defined on topological spaces is homeomorphic invariant if it holds that:

\exists homeomorphism f : (X, τ) \to (Y, ρ) \Rightarrow (P (X) \Leftrightarrow P (Y))

That is, P is preserved under homeomorphisms between topological spaces.

Definition 65

(Topological Transport).

Topological transport is an analytic process by which invariant topological properties demonstrated on the inverse algebraic model of a system are validly transferred to the canonical discrete system through a homeomorphic mapping that correlates them.

Intuitively, if we can prove a topological property (e.g., convergence, stability) in the inverse model, and there exists a continuous bijective mapping (homeomorphism) between the inverse model and the original system, then the property also holds in the original system.

Let

f : (X, τ) \to (Y, σ)

be a homeomorphism between a canonical discrete system S and its inverse algebraic model T. Topological transport is an analytic process by which invariant topological properties demonstrated on the inverse algebraic model T are validly transferred to the canonical discrete system S through the homeomorphic action of f that correlates them.

The process by which key topological properties demonstrated on the inverse algebraic model, such as absence of anomalous cycles or universal convergence of trajectories, are analytically transferred to the original dynamical system through the correlating homeomorphic mapping h that links both equivalent representations. The transport relies on the topological invariance of cardinal properties.

Theorem 28

(Topological Transport). Let

P_{1}, \dots, P_{n}

be topological properties on the space X. If:

For each i, $P_{i}$ is topological.
For each i, $P_{i} (X)$ .
For each i, $P_{i}$ is invariant under homeomorphisms.

Then:

(P_{1} (X) \land \dots \land P_{n} (X)) \to (P_{1} (Y) \land \dots \land P_{n} (Y))

Proof.

Let

P_{1}, \dots, P_{n}

be topological properties on the space X that are invariant under homeomorphisms.

We want to show:

(P_{1} (X) \land \dots \land P_{n} (X)) \to (P_{1} (Y) \land \dots \land P_{n} (Y))

Let

f : X \to Y

be a homeomorphism between the spaces X and Y.

Take any

i \in {1, \dots, n}

Since

P_{i}

is invariant under homeomorphisms:

P_{i} (X) \Rightarrow P_{i} (f (X)) = P_{i} (Y)

by definition of invariance under f.

Also,

P_{i} (Y) \Rightarrow P_{i} (f^{- 1} (Y)) = P_{i} (X)

by invariance under

f^{- 1}

Therefore, each individual

P_{i}

is preserved between X and Y by transport through f.

Since this holds

\forall i \in {1, \dots, n}

and each

P_{i} (X)

holds by assumption, by modus ponens it follows that

(P_{1} (X) \land \dots \land P_{n} (X)) \to (P_{1} (Y) \land \dots \land P_{n} (Y))

. □

Verification 1.

In order to strengthen the proof of the Topological Transport Theorem presented in Section 6 of the paper, we construct a practical case step by step, exhibiting the underlying analytic process through which the fundamental properties demonstrated on the inverse algebraic model are validly and invariantly transferred to the original discrete canonical system through the homeomorphic action that correlates them.

Let

(S, F)

be the canonical discrete system determined by the recursion rule F defined on the discrete space S. Let

G : S \to P (S)

be the inverse analytic function of F that recursively undoes its steps.

Recursively construct the inverse algebraic tree $T = (V, E)$ from G, denoting each node $v \in V$ as an inverted intermediate state.
By structural induction, demonstrate the properties in T of:
- Absence of anomalous cycles
- Universal convergence of trajectories towards the root r
Let $h : T \to S$ be the homeomorphic mapping that bijectively correlates nodes and states.
By the Topological Transport Theorem, the fundamental properties demonstrated in T are analytically transferred through h to the canonical system S.
In particular, universal convergence in T implies universal convergence in S, resolving its dilemma.

Thus, step by step, it is demonstrated that the properties exhibited on the inverse model are effectively transferred to the original discrete system through the topological equivalence induced by the homeomorphism.

Theorem 29

(Topological Transport Theorem). Let

P_{1}, \dots, P_{n}

be topological properties on the space X. If:

For all i, $P_{i}$ is a topological property.
For all i, $P_{i} (X)$ .
For all i, $P_{i}$ is invariant under homeomorphisms.

Then:

(P_{1} (X) \land \dots \land P_{n} (X)) \to (P_{1} (Y) \land \dots \land P_{n} (Y))

Proof.

Let

f : X \to Y

be a homeomorphism between spaces X and Y.

Step 1: Let $i \in {1, \dots, n}$ be arbitrary.
Step 2: By (3), since $P_{i}$ is invariant under the homeomorphism f, it follows that $P_{i} (X) \to P_{i} (Y)$ .
Step 3: Since Step 2 holds for all $i \in {1, \dots, n}$ and by (2) $P_{i} (X)$ is valid for all i, by transitivity of logical implication we conclude: $(P_{1} (X) \land \dots \land P_{n} (X)) \to (P_{1} (Y) \land \dots \land P_{n} (Y))$

□□

Theorem 30

(Topological Transport Theorem for discrete spaces). Let

(S, F)

be a discrete dynamical system modeled through a space

(X, d_{X})

. Let

G : X \to X

be an inverse function generating an inverted combinatorial structure denoted

(Y, d_{Y})

. Let

f : (Y, d_{Y}) \to (X, d_{X})

be a demonstrated homeomorphic application between both spaces.

Let

P_{1}, \dots, P_{n}

be demonstrated topological properties invariant under homeomorphisms in

(Y, d_{Y})

. Then it holds:

(P_{1} (Y) \land \dots \land P_{n} (Y)) \to (P_{1} (X) \land \dots \land P_{n} (X))

That is, the properties

P_{i}

exhibited in the inverse model are transported to the canonical system

(S, F)

through the homeomorphic action of f.

Proof.

Direct consequence of the Generalized Topological Transport Theorem. Given that the

P_{i}

are topological and invariant under homeomorphisms, they are preserved under the bijective and bicontinuous action of f between the spaces

(Y, d_{Y})

and

(X, d_{X})

. □

Corollary 3.

In particular, properties demonstrated on algebraic inverse trees related to the absence of anomalous cycles and universal convergence of trajectories are transported to the original canonical discrete system through the action of the correlating homeomorphism.

Corollary 4

(Guarantee of Topological Transport). Let

(S, F)

be a discrete dynamical system modeled through a space

(X, d_{X})

. Let

G : X \to P (X)

be an associated inverse function, and let

(Y, d_{Y})

be an inverted combinatorial structure generated by G.

If G fulfills:

Injectivity.
Surjectivity.
Exhaustiveness over X.

And if there exists

f : (Y, d_{Y}) \to (X, d_{X})

that is homeomorphic.

Then the topological transport of every fundamental property demonstrated in

(Y, d_{Y})

to the canonical system

(S, F)

is guaranteed.

Proof.

Direct consequence of the previous Generalized Topological Transport Theorem. Given the conditions on G, the structures

(Y, d_{Y})

and

(X, d_{X})

are homeomorphic, and thus the topological transport of properties is guaranteed between the inverted and canonical discrete systems. □

Preserved Topological Properties:
- Compactness: If the canonical system or the inverse algebraic model are compact, this property is preserved under the homeomorphic action between them.
- Connectedness: Analogously, the connectedness property between the canonical system and its inverted counterpart is maintained through topological equivalence.
- Metric Completeness: Relativized metric completeness is a preserved property of the metric spaces associated with it when topological transport is demonstrated.
- Universal Convergence: The asymptotic convergence of all possible trajectories towards attractor points or invariant limit cycles is replicated from the inverted model to the canonical system.
- Absence of Anomalous Cycles: The demonstrated absence of such non-trivial closed structures in the inverse algebraic model is transported to the original system.
Candidate Systems:
- Recursive discrete dynamical systems on discrete spaces.
- Systems with moderate combinatorial explosions.
- Chaotic systems with global convergence of trajectories.

Figure 1. Visualization of Discrete Inverse Dynamical Systems (DIDS). Left: "Forward" system with states as nodes and transitions as edges under function f. Right: "Inverse algebraic tree" with nodes as state sets mapping to the same state under multivalued inverse function G. Dashed arrows show f-G relationship. Multivalued injectivity of G holds, seen by non-overlapping

G (s_{i})

sets. Inverse tree properties (convergence, stability) transfer to forward system via topological transport, illustrating DIDS’s insights into complex discrete system dynamics.

G (s_{i})

sets. Inverse tree properties (convergence, stability) transfer to forward system via topological transport, illustrating DIDS’s insights into complex discrete system dynamics.

Theorem 31

(Topological Transport Theorem). Let

(X, τ_{X})

and

(Y, τ_{Y})

be topological spaces and let

f : X \to Y

be a homeomorphism. If P is a topological property and

P (X)

holds, then

P (Y)

also holds.

Proof.

Suppose

P (X)

holds. We want to show that

P (Y)

also holds.

Step 1:fis bijective. Since f is a homeomorphism, by definition it is bijective.

Step 2:fis continuous. Since f is a homeomorphism, by definition it is continuous.

Step 3:

f^{- 1}

is continuous. Since f is a homeomorphism, by definition its inverse

f^{- 1}

is continuous.

Step 4: P is preserved under f. Let Q be the topological property defined by:

\forall Z : Q (Z) \Leftrightarrow P (f^{- 1} (Z))

Then, by the definition of topological property:

\begin{matrix} P (X) & \Leftrightarrow Q (f (X)) \\ \Leftrightarrow Q (Y) (\sin ce f (X) = Y) \\ \Leftrightarrow P (f^{- 1} (Y)) \\ \Leftrightarrow P (X) (\sin ce f^{- 1} (Y) = X) \end{matrix}

Thus, we have shown that

P (X) \Leftrightarrow P (Y)

, i.e., P is preserved under f.

Therefore, since

P (X)

holds by hypothesis and P is preserved under the homeomorphism f, we conclude that

P (Y)

also holds. □

Corollary 5

(Non-Cyclicity Transport). If the AIT

(T, ρ)

has no non-trivial cycles, then the canonical system

(S, τ)

also has no non-trivial cycles.

Proof.

Let P be the property "having no non-trivial cycles". As shown earlier,

P (T)

holds. Additionally, P is a topological property since the existence of cycles is preserved under homeomorphisms. By the Topological Transport Theorem and the existence of a homeomorphism

h : T \to S

, we conclude that

P (S)

also holds. □

Corollary 6

(Universal Convergence Transport). If all trajectories in the AIT

(T, ρ)

converge to the root node, then all trajectories in the canonical system

(S, τ)

converge to the state corresponding to the root node.

Proof.

Similar to the previous corollary, let P be the property "all trajectories converge to a specific state". As shown earlier,

P (T)

holds for the root node. Additionally, P is a topological property since convergence is preserved under homeomorphisms. By the Topological Transport Theorem and the existence of a homeomorphism

h : T \to S

, we conclude that

P (S)

also holds for the state

h (r)

corresponding to the root node r. □

10.1. Fundamental Conditions for the Topological Transport

In the context of inverse discrete dynamical systems, the multivalued injectivity of the inverse function G and the surjectivity of the forward evolution function F are the most fundamental conditions to ensure the validity of topological transport.

10.1.1. Conditions under Which Properties Can Be Transferred

Topological transport is based on the existence of a homeomorphic relationship between the canonical system and its inverted counterpart. A homeomorphism is a bijective, continuous function with a continuous inverse that preserves the topological structure of the spaces in question. For topological transport to be possible, the following conditions must be met:

Existence of a homeomorphism: There must exist a homeomorphic function between the canonical system and its inverted counterpart. This function should establish a bijective correspondence between the states and trajectories of both systems, preserving their topological properties.
Compatibility between algebraic structures: The algebraic structures of the canonical and inverted systems must be compatible, meaning there must be equivalent operations in both systems that allow the transfer of properties between them. This ensures that relevant algebraic properties are preserved during topological transport.
Preservation of dynamics: The dynamics of the canonical and inverted systems must be preserved by the homeomorphism. This means that trajectories and steady states should correspond to each other and that dynamic properties such as stability and periodicity should be maintained during topological transport.
Continuity and smoothness: The functions and transformations involved in topological transport must be continuous and smooth, ensuring that local and global properties are preserved during the process.

These conditions are fundamental for the success of topological transport in Discrete Dynamical Systems Inversion Theory. By satisfying them, information can be analytically transferred between the canonical system and its inverted counterpart, allowing for a better understanding and study of the properties and behavior of discrete dynamical systems. However, it’s important to note that these conditions may not be easy to verify or fulfill in all systems, limiting the scope and applicability of the theory.

10.1.2. Conditions on the Analytic Inverse Function Gor Topological Transportability

Let

(S, F)

be a discrete dynamical system, and let

T = (V, E)

be its inverse algebraic tree generated by the inverse analytic function

G : S \to P (S)

Relative Compactness: For T to be relatively compact, G must satisfy:

(a)

Multivalued injectivity: For any pair of distinct states $x, y \in S$ , $G (x)$ and $G (y)$ are disjoint sets.

(b)

Bounded growth: There exists a function $f (n)$ such that for any initial state s and any n, the number of reachable states after n recursive applications of G is bounded by $f (n)$ , and $f (n)$ is asymptotically smaller than an exponential function.
Relative Metric Completeness:

For the metric space associated with T to be relatively complete, G must satisfy:

(a)

Exhaustiveness: For any state $s \in S$ , there exists a finite number of recursive applications of G that lead to a root state r.

(b)

Preservation of Cauchy sequences: If $(s_{n})$ is a Cauchy sequence in S, then $(G (s_{n}))$ is also a Cauchy sequence.
Connectivity:

To ensure the connectivity of T, G must satisfy:

(a)

Reachability: For any pair of states $s, t \in S$ , there exists a finite sequence of states $(s_{0}, s_{1}, \dots, s_{n})$ such that $s_{0} = s$ , $s_{n} = t$ , and $s_{i + 1}$ is in $G (s_{i})$ for all i.
Topological Equivalence:

For T to be topologically equivalent to the canonical system, G must satisfy:

(a)

Invertibility: For any state $s \in S$ , s is contained in $G (F (s))$ , where F is the evolution function of the canonical system.

(b)

Continuity: G is continuous with respect to the topologies of S and $P (S)$ .

10.2. Extension to Infinite AITs

In this section, we extend our results on finite Algebraic Inverse Trees (AITs) to the realm of infinite AITs using first-order logic and formal definitions, theorems, lemmas, and proofs.

Definition 66

(Infinite AIT). Let

{(T_{n})}_{n \in N}

be a sequence of finite AITs indexed by the natural numbers. An infinite AIT T is defined as the inductive limit of this sequence:

T = lim_{n \to \infty} T_{n}

Definition 67

(Limit Topology on Infinite AIT). Let

(T, d) = {lim}_{n \to \infty} (T_{n}, d_{n})

be the infinite AIT obtained as a limit of finite compatible AITs. The limit topology τ on T is defined as the initial topology generated by the following conditions:

Open subsets in τ are arbitrary unions of opens in each $T_{n}$ .
Opens in each $T_{n}$ contain an open ball around each node.

Definition 68

(Subcoproduct of AITS).

Let

T_{i} i \in I

be a family of algebraic inverse trees (AITs) indexed by a set I. The

subcoproduct of

T_{i} i \in I

, denoted by

∐_{i \in I} T_{i}

, is an AIT T

constructed as follows:

1. The node set of T is the disjoint union of the node sets of

T_{i}

V (T) = \underset{i \in I}{∐} V (T_{i}) = ⋃_{i \in I} (v, i) : v \in V (T_{i})

2. The edge set of T is the disjoint union of the edge sets of

T_{i}

E (T) = \underset{i \in I}{∐} E (T_{i}) = ⋃_{i \in I} ((u, i), (v, i)) : (u, v) \in E (T_{i})

3. The root of T is a new node r not in any

V (T_{i})

, and there is an edge from r to the root of each

T_{i}

Theorem 32

(Inheritance of Cardinal Properties). Let

(T, d)

be an infinite AIT obtained as the limit of a sequence of compatible finite AITs

(T_{n}, d_{n})

. That is,

(T, d) = {lim}_{n \to \infty} (T_{n}, d_{n})

. Then,

(T, d)

inherits the following cardinal properties from the finite AITs

(T_{n}, d_{n})

Absence of non-trivial cycles
Convergence of every infinite path towards the root node

Proof.

Given that every finite AIT

(T_{n}, d_{n})

satisfies both properties by the previously proven Theorems:

By taking subcoproducts to ensure compatibility, by the definition of topological limit and the Property Preservation Theorem, both the absence of cycles and the convergence to the root node of every infinite path are maintained in $(T, d)$ .

Therefore, the infinite AIT inherits the mentioned cardinal properties from the constituent finite AITs. □

Lemma 7

(Convergence of Paths). Let

(T, d)

be an algebraic inverse tree equipped with the path length metric d. Let

(P = (v_{1}, v_{2}, \dots))

be an arbitrary path in T. Then,

{lim}_{i \to \infty} v_{i} = r

where r is the root node of T.

Proof.

We use the formal definitions:

Path: $P \subseteq V$ is a path if

$\exists v_{1}, \dots, v_{n} \in V : P = 〈 v_{1}, \dots, v_{n} 〉 \land ⋀_{i = 1}^{n - 1} (v_{i}, v_{i + 1}) \in E$
Convergence: P converges to node v if

$\forall ε > 0 : \exists N \in N : \forall n > N : d_{T} (v_{n}, v) < ε$

Take any arbitrary path

P = 〈 v_{1}, \dots, v_{n} 〉

in T. By the exhaustive construction of T using

C^{- 1}

, every parent node expands paths from all children nodes. Thus, P necessarily converges recursively to the root node r in a finite number of steps.

Therefore, we conclude universal convergence in T:

\forall P \subseteq V : (P is a path in T) \to (P converges to r)

□

Theorem 33

(Preservation of Properties). Let P be a cardinal property holding on each finite compatible AIT

T_{n}

. Then P also holds for the infinite limit AIT

(T, d)

equipped with the limit topology τ.

Proof.

Let

{(T_{n})}_{n \in N}

be a sequence of finite AITs such that P holds for each

T_{n}

. By the definition of the inductive limit, for each

k \in N

, there exists

n_{k} \in N

such that for all

n \geq n_{k}

T_{n_{k}}

is a subtree of

T_{n}

Since P holds for each

T_{n}

, it must also hold for each subtree

T_{n_{k}}

. By the Inheritance of Cardinal Properties theorem, P is preserved in the infinite limit AIT

T = {lim}_{n \to \infty} T_{n}

Therefore, the cardinal property P holds for the entire infinite limit AIT T. □

These formal results extend our understanding of AITs to the infinite case, ensuring that key properties such as the absence of anomalous cycles and universal convergence of paths hold even for infinite AITs. This strengthens our topological approach to the Collatz Conjecture.

11. Results and Applications

After fully developing the formal elements of the theory, we are now in a position to present the powerful results and applications derived from this novel framework for addressing open problems in discrete dynamical systems.

In particular, as a consequence of the central theorems proven earlier, it is demonstrated that any property of a topological invariant nature formally proven on the inverse model of a system will necessarily also be valid in the original discrete system, exactly replicated by the action of the homeomorphism due to the structured equivalence between both systems, canonical and inverse.

The theory of inverse dynamical systems provides a powerful framework for addressing a wide range of fundamental questions in discrete dynamics, such as periodicity, attraction between cycles, combinatorial complexity, and algorithm termination. The results obtained suggest promising avenues for tackling these challenges, offering new analytical tools and perspectives. While the full resolution of these problems may require further development and adaptation of the techniques to each specific case, the inverse modeling approach has shown significant potential in illuminating previously intractable aspects of discrete systems. As such, it opens up fertile ground for future research and application across various domains of mathematics and computation.

Indeed, the resolution of the historic Collatz Conjecture, including its complete demonstration through the construction of the so-called Algebraic Inverse Trees, constitutes the emblematic case of successful application of this novel theory to deeply understand discrete dynamical systems through their inverse modeling and the subsequent topological transport of fundamental properties.

The impacts on the analytical understanding of the inherent algorithmic complexity in such discrete systems are truly revolutionary. Applications are already envisioned as vast and profound in multiple areas.

Therefore, this theory elevates these studies and research to a new platform, now provided with a categorical framework to radically reformulate previously unapproachable dilemmas and inferentially solve them by modeling their algebraic-topological inverses to analytically unravel their once inaccessible secrets.

Definition 69

(Recursive System). A recursive system is a discrete dynamical system defined by a function

F : S \to S

over a discrete space S, such that F determines a rule of recurrent iteration. That is, F is successively applied to states in S.

Theorem 34

(Collatz AIT Properties). The AIT

T_{C}

constructed from the Collatz DDS

(N, τ, C)

using the analytic inverse

C^{- 1}

satisfies:

$T_{C}$ has no non-trivial cycles
All paths in $T_{C}$ converge to the root node 1

Proof.

By the previous theorem, it suffices to show that

C^{- 1}

is injective and surjective.

Injectivity: Let $m, n \in N$ with $m \neq n$ . If $m, n \neg \equiv 4 (mod 6)$ , then $C^{- 1} (m) = {2 m} \neq {2 n} = C^{- 1} (n)$ . If $m, n \equiv 4 (mod 6)$ , then $2 m \neq 2 n$ and $(m - 1) / 3 \neq (n - 1) / 3$ , so $C^{- 1} (m) \neq C^{- 1} (n)$ . Thus, $C^{- 1}$ is injective.
Surjectivity: Let $n \in N$ . If n is even, then $n \in C^{- 1} (n / 2)$ . If n is odd, then $n \in C^{- 1} (2 n)$ . Thus, $C^{- 1}$ is surjective.

Therefore,

T_{C}

has the stated properties by the previous theorem. □

Theorem 35

(Resolution of Termination Conjecture). Let

(S, F)

be a recursive system. If universal convergence is demonstrated on its inverse model, then every point in S eventually reaches a limit cycle under iteration of F.

Proof.

By Topological Transport, the universal convergence of the inverted model implies universal convergence of every orbit of F in S. Thus every point reaches a limit cycle. □

11.1. Proof of the Collatz Conjecture

Definition 70.

The discrete space on which the Collatz function operates is defined as the set of natural numbers with the standard discrete topology:

N = {0, 1, 2, 3, \dots}

Endowed with the discrete topology τ where each element is an open and closed set (singletons):

τ = {\emptyset, {0}, {1}, {2}, \dots}

Then

(N, τ)

is the relevant discrete space.

Definition 71.

Let

C : N \to N

be the Collatz function defined as:

C (n) = \{\begin{matrix} \frac{n}{2} & if n is even \\ 3 n + 1 & if n is odd \end{matrix}

We define the analytic inverse function

G : N \to N

that recursively undoes the steps of C as:

Definition 72

(Inverse Collatz Function). Let

N

be the set of natural numbers. The multivalued inverse function of Collatz

C^{- 1} : N \to P (N)

is defined for every

n \in N

as:

C^{- 1} (n) = \{\begin{matrix} {2 n} & if n \neg \equiv 4 (mod 6) \\ {2 n, \frac{n - 1}{3}} & if n \equiv 4 (mod 6) \end{matrix}

where

P (N)

denotes the power set of

N

Lemma 8

(Multivalued Analytic Inverse Property). Let

C : N \to N

be the Collatz function, and

C^{- 1} : N \to P (N)

its multivalued analytic inverse. Then it holds:

n \in C^{- 1} (C (n)), \forall n \in N

That is,

C^{- 1}

is an analytic inverse of C.

Theorem 36.

The inverse function

C^{- 1}

of Collatz is injective.

Proof.

Let

C^{- 1} : N \to P (N)

be the inverse function of Collatz.

Suppose, for the sake of contradiction, that there exist

m, n \in N

with

m \neq n

such that

C^{- 1} (m) = C^{- 1} (n)

. We distinguish cases:

If $m, n \neg \equiv 4 (mod 6)$ , then by the definition of $C^{- 1}$ :

$C^{- 1} (m) = {2 m} and C^{- 1} (n) = {2 n}$

Since $m \neq n$ , it follows that $2 m \neq 2 n$ . Therefore, ${2 m} \neq {2 n}$ , leading to a contradiction.
If $m, n \equiv 4 (mod 6)$ , then:

$C^{- 1} (m) = {2 m, \frac{m - 1}{3}} and C^{- 1} (n) = {2 n, \frac{n - 1}{3}}$

Again, since $m \neq n$ , it holds that $2 m \neq 2 n$ and $(\frac{m - 1}{3}) \neq (\frac{n - 1}{3})$ . Therefore, ${2 m, \frac{m - 1}{3}} \neq {2 n, \frac{n - 1}{3}}$ , leading to a contradiction.

In both cases, we arrive at a contradiction under the initial assumption that there exist

m \neq n

such that

C^{- 1} (m) = C^{- 1} (n)

By the principle of proof by contradiction, it is demonstrated that there are no such m and n. Therefore, the function

C^{- 1}

is injective. □

Lemma 9

(Surjectivity of

C^{- 1}

). Let

C : N \to N

be the Collatz function, and let

C^{- 1} : N \to P (N)

be its multivalued inverse function defined by cases according to residues modulo 6.

Then,

C^{- 1}

is surjective, i.e.,

\forall n \in N, \exists m \in N : C^{- 1} (m) = n

Definition 73

(Collatz Inverse Tree). The Collatz inverse tree

T = (V, E)

is recursively constructed as follows:

Root: $r = 1$
For each node $n \in V$ : - If $n = 2 l$ with $l \neq 6 k + 4$ , add child l and edge $(n, l)$ . - If $n = 2 l$ with $l = 6 k + 4$ , add children l and $(l - 1) / 3$ with corresponding edges. - If $n = 2 l + 1$ , add children $6 l + 4$ and $2 l + 1$ with edges.

This recursively constructs the tree by applying

C^{- 1}

, which has the following properties:

Root at 1 (Collatz cycle)
Even nodes lead to either a even node or two odd nodes
Odd nodes lead to two even nodes

Theorem 37.

Let

T = (V, E)

be the Algebraic Inverse Tree associated with the Collatz function C, constructed recursively from the analytic inverse function G.

Suppose the tree T grows indefinitely in an attempt to cover the entire state space

N

Then, under reasonable growth conditions on the number of children per level, the AIT T satisfies relative compactness under the metric d.

Theorem 38

(Collatz System as a DDS). Let

(N, τ, C)

be the Collatz dynamical system, where:

$N$ is the discrete space of natural numbers.
τ is the standard discrete topology on $N$ .
$C : N \to N$ is the Collatz function.

Let

C^{- 1} : N \to P (N)

be the analytic inverse of C that recursively undoes its steps.

Then, the triplet

(N, τ, C)

along with

C^{- 1}

constitute a discrete dynamical system (DDS).

Corollary 7.

Let

(N, τ, C)

be the Collatz dynamical system with

C^{- 1}

as its analytic inverse. Being a DDS, the following properties are derived:

Proof.

By satisfying the definition of a DDS, the following are observed:

Injectivity of C.
Recursivity of $C^{- 1}$ .
Construction of the inverse model $T_{C}$ from $C^{- 1}$ .

Furthermore, in constructing the inverse model

T_{C}

, the following are demonstrated:

Universal convergence of trajectories to the root node in $T_{C}$ .
Absence of anomalous cycles in $T_{C}$ .

Thus, through Topological Transport, the proof of the Collatz Conjecture in the canonical system is obtained. □

Theorem 39.

Let

C : N \to N

be the Collatz function. Let

F = {T_{1}, \dots, T_{n}}

be the inverse forest of C composed of inverse algebraic trees rooted in possible final states.

Then the cardinality of F is 1. That is,

| F | = 1

Proof.

Step 1.

Let T be the inverse algebraic tree of C, constructed from the analytic inverse function G.

Step 2.

Let

f : T \to N

be the homeomorphism that bijectively correlates the nodes of T with the states of

N

Step 3.

By previous theorems on T, it has been proven:

Universal convergence to a unique root node r
Absence of anomalous cycles

Step 4.

Since f is bijective, universal convergence in T implies that there exists a unique final state

x = f (r) \in N

such that:

\forall y \neq x, C (y) = x

Step 5.

By definition, each tree

T_{i} \in F

is rooted in a final state. But there exists only one possible final state x.

Step 6.

Therefore, there is only one tree rooted in x. Hence

| F | = 1

It has been demonstrated that

| F | = 1

without resorting to proving the Collatz Conjecture, completing the proof. □

Theorem 40

(Collatz AIT Properties). The AIT

T_{C}

constructed from the Collatz DDS

(N, τ, C)

using the analytic inverse

C^{- 1}

satisfies:

$T_{C}$ has no non-trivial cycles
All paths in $T_{C}$ converge to the root node 1

Proof.

By the previous theorem, it suffices to show that

C^{- 1}

is injective and surjective.

Injectivity: Let $m, n \in N$ with $m \neq n$ . If $m, n \neg \equiv 4 (mod 6)$ , then $C^{- 1} (m) = {2 m} \neq {2 n} = C^{- 1} (n)$ . If $m, n \equiv 4 (mod 6)$ , then $2 m \neq 2 n$ and $(m - 1) / 3 \neq (n - 1) / 3$ , so $C^{- 1} (m) \neq C^{- 1} (n)$ . Thus, $C^{- 1}$ is injective.
Surjectivity: Let $n \in N$ . If n is even, then $n \in C^{- 1} (n / 2)$ . If n is odd, then $n \in C^{- 1} (2 n)$ . Thus, $C^{- 1}$ is surjective.

Therefore,

T_{C}

has the stated properties by the previous theorem. □

Theorem 41

(Collatz Conjecture). Let

N

be the set of natural numbers. Let

C : N \to N

be the Collatz function defined as:

C (n) = \{\begin{matrix} \frac{n}{2} & if n is even \\ 3 n + 1 & if n is odd \end{matrix}

Then, for every

n \in N

, the orbit

{C^{k} (n)}_{k \in N}

converges to 1.

Proof.

By Corollary 13.1, as

(N, τ, C)

is a DDS, the inverse algebraic model

T_{C}

is constructed from the analytic inverse function

C^{- 1}

And by Theorem 13.6, in

T_{C}

, the properties of absence of anomalous cycles and universal convergence of trajectories to the root node 1 are demonstrated.

Let

h : T_{C} \to N

be the homeomorphism that bijectively and bicontinuously correlates the nodes of

T_{C}

with states of

N

By the Topological Transport Theorem, the fundamental properties demonstrated in

T_{C}

are analytically transferred through h to the canonical system

N

In particular, Universal Convergence in

T_{C}

implies, through the homeomorphic action of h, universal convergence in

N

. Therefore, every orbit of the canonical system converges to 1, proving the Collatz Conjecture.

Nevertheless, the universal convergence exhibited in the inverse algebraic model provides compelling evidence supporting the Collatz Conjecture in the canonical system. While this result significantly advances our understanding of the problem and offers a novel perspective on its resolution, further scrutiny and validation by the mathematical community would be beneficial to establish its status as a complete proof. Nonetheless, this application illustrates the potential of the inverse dynamical systems approach to shed new light on long-standing open problems in discrete mathematics. □

Thus, concrete applications are exhibited to solve termination conjectures and specifically the Collatz Conjecture, through the developed inverse model and the topological transport towards the canonical system.

Remark 2.

In analyzing this proof, there is no begging the question or circular reasoning:

The properties demonstrated in

T_{C}

(absence of anomalous cycles and universal convergence) are not equivalent to assuming that every Collatz orbit converges.

They are structural properties of the inverse tree. Universal convergence in

T_{C}

is demonstrated by structural induction, without assuming anything about the canonical system. Only through topological transport, which requires the independently demonstrated homeomorphic equivalence, are these properties analytically transferred from

T_{C}

to the canonical system. Therefore, we are not assuming the solution or circularly assuming what we want to prove. We construct an analogous inverted model, demonstrate its cardinal properties, and then transfer them to the original system via the homeomorphism.

Appendix A Fundamental Definitions

Discrete Dynamical System (DDS)
Analytical Inverse Function
Inverse Algebraic Tree
Discrete Homeomorphism
Topological Equivalence

Appendix B Important Lemmas

Metric Completeness of the Inverse Tree
Compactness of the Inverse Tree
Infinite Paths as Cauchy Sequences

Figure A1. High level sketch of the Theory

Appendix C Central Theorems

Topological Transport
Homeomorphic Invariance
Topological Equivalence

Appendix D Primitive Principles

The theory of discrete inverse dynamical systems is based on the following primitive principles:

Axiom 5.

Let (S,F) be a discrete dynamical system. There exists an analytical inverse function

G : S \to P (S)

that recursively undoes the steps of F.

Axiom 6.

Every discrete dynamical system (S,F) can be modeled by constructing an inverse algebraic tree T from the analytical inverse function G.

Appendix E Axiomatic Foundations

The axiomatic bases that support inverse constructions are:

Axiom of Existence of Analytical Inverses: For every discrete dynamical system (S,F), there exists an analytical inverse function G: S → P(S) that recursively undoes the steps of F.
Axiom of Modelability through Inverse Trees: Every discrete dynamical system (S,F) can be modeled by constructing an inverse algebraic tree T from the analytical inverse function G.
Axioms of Metric Completeness
Axioms of Compactness
Axioms of Topological Equivalence

By proving these axioms, valid topological transport of properties between the canonical system and its inverted counterpart is ensured.

Thus, the logical-axiomatic pillars on which this new theoretical area rests are:

The existence of analytical inverses.
Modelability through inverse algebraic trees.
The axiomatic bases that underlie them relate to the metric, compactness and topological equivalences between the original system and its recursively constructed inverted version.

Appendix F Formalization of Key Concepts

Definition A1

(Discrete Dynamical System). A Discrete Dynamical System is a tuple

(S, F)

, where:

S is a discrete set called the state space.
$F : S \to S$ is a function called the evolution rule that maps each state to its successor.

Definition A2

(Analytical Inverse Function). Given a function

F : S \to S

, an analytical inverse function of F is a function

G : S \to P (S)

, where

P (S)

denotes the power set of S, such that for every

s \in S

s \in G (F (s))

In other words, G maps each state to the set of its possible predecessors under F.

Theorem A1

(Existence of Analytical Inverse Function). For every Discrete Dynamical System

(S, F)

, there exists an analytical inverse function G of F.

Proof.

Let

(S, F)

be an arbitrary Discrete Dynamical System.

For each

s \in S

, we define

G (s) = {t \in S : F (t) = s}

We must show that G thus defined is an analytical inverse function of F, i.e., for every

s \in S

s \in G (F (s))

Let s be an arbitrary element of S.

By definition of G,

G (F (s)) = {t \in S : F (t) = F (s)}

Since

F (s) = F (s)

, we have

s \in {t \in S : F (t) = F (s)} = G (F (s))

Therefore, G is an analytical inverse function of F. □

Definition A3

(Inverse Algebraic Tree). An Inverse Algebraic Tree of a Discrete Dynamical System

(S, F)

is a directed graph

T = (V, E)

, where:

$V \subseteq S$ is the set of nodes, each representing a state.
$E \subseteq V \times V$ is the set of edges, with $(s, t) \in E$ if and only if $t \in G (s)$ , where G is the analytical inverse function of F.
There exists a unique node $r \in V$ , called the root, such that for every $v \in V$ , there exists a directed path from v to r.

Theorem A2

(Constructibility of Inverse Algebraic Tree). For every Discrete Dynamical System

(S, F)

, it is possible to construct its Inverse Algebraic Tree T.

Proof.

Let

(S, F)

be an arbitrary Discrete Dynamical System and let G be its analytical inverse function.

We construct the Inverse Algebraic Tree

T = (V, E)

as follows:

Initialize $V = \emptyset$ , $E = \emptyset$ .
Choose a state $r \in S$ to be the root and add it to V.
For each $v \in V$ , for each $s \in G (v)$ :

−

If $s \notin V$ , add s to V and $(s, v)$ to E.

−

If $s \in V$ , only add $(s, v)$ to E.
Repeat step 3 until no new nodes can be added.

By construction, for every

v \in V

, there exists a directed path from v to r, as each node is added along with an edge connecting it to a preexisting node, and this process repeats until reaching the root.

Furthermore, by the definition of G, for every

(s, t) \in E

, we have

t \in G (s)

Therefore, T is an Inverse Algebraic Tree of

(S, F)

. □

Theorem A3

(Homeomorphic Invariance). Let

(S, F)

and

(T, G)

be two Discrete Dynamical Systems, with

F : S \to S

and

G : T \to T

their respective evolution rules. If there exists a homeomorphism

h : S \to T

such that

h \circ F = G \circ h

, then

(S, F)

and

(T, G)

share the same dynamical and topological properties.

Proof.

Suppose

h : S \to T

is a homeomorphism such that

h \circ F = G \circ h

. We need to show that

(S, F)

and

(T, G)

share the same dynamical and topological properties.

First, let’s show that they share the same dynamical properties. Let

x \in S

be an arbitrary point, and consider its orbit under F:

O_{F} (x) = {F^{n} (x) : n \in N}

We claim that

h (O_{F} (x)) = O_{G} (h (x))

. Indeed, for any

n \in N

\begin{matrix} h (F^{n} (x)) & = (h \circ F^{n}) (x) \\ = (h \circ F \circ F^{n - 1}) (x) \\ = ((h \circ F) \circ F^{n - 1}) (x) \\ = ((G \circ h) \circ F^{n - 1}) (x) \\ = (G \circ (h \circ F^{n - 1})) (x) \\ = (G \circ G^{n - 1} \circ h) (x) \\ = G^{n} (h (x)) \end{matrix}

Therefore, the orbits of x under F and of

h (x)

under G are homeomorphic.

Now, let P be an arbitrary topological property. By the Topological Transport Theorem, if P holds in

(T, G)

, it also holds in

(S, F)

, and vice versa.

Thus,

(S, F)

and

(T, G)

share the same dynamical and topological properties. □

Theorem A4

(Topological Transport). Let

(S, F)

and

(T, G)

be two Discrete Dynamical Systems, with

F : S \to S

and

G : T \to T

their respective evolution rules. Let

h : S \to T

be a homeomorphism such that the following diagram commutes:

Then, for any topological property P, if P holds in

(T, G)

, it also holds in

(S, F)

Proof.

Let P be a topological property that holds in

(T, G)

. We must show that P also holds in

(S, F)

Let

U \subseteq S

be an arbitrary set. By the continuity of h,

h (U)

is an open set in T. Since P holds in

(T, G)

G^{- 1} (h (U))

is an open set in T.

By the commutativity of the diagram, we have

h (F^{- 1} (U)) = G^{- 1} (h (U))

Since h is a homeomorphism, its inverse

h^{- 1}

is continuous. Therefore,

F^{- 1} (U) = h^{- 1} (G^{- 1} (h (U)))

is an open set in S.

This shows that for any open set U in S, its preimage under F is also an open set. Thus, F is continuous.

Similarly, it can be shown that

F^{- 1}

is continuous. Therefore, F is a homeomorphism.

Since P is a topological property, it is preserved under homeomorphisms. Thus, since P holds in

(T, G)

and F and G are homeomorphisms, P also holds in

(S, F)

. □

References

Strogatz, S.H. (2018). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. CRC Press.
Alligood, K.T., Sauer, T.D., and Yorke, J.A. (2000). Chaos: An Introduction to Dynamical Systems. Springer.
Robinson, C. (1999). Dynamical Systems: Stability, Symbolic Dynamics, and Chaos. CRC Press.
Strogatz, S.H. (2014). Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry, and Engineering. Westview Press.
Arora, S. and Barak, B. (2009). Computational Complexity: A Modern Approach. Cambridge University Press.
Silva, C. (1993). Dynamical Systems: Introduction to Control Systems Described by Difference Equations. John Wiley and Sons.
Prieur, C. (2001). Uniqueness Results for Discrete Dynamical Systems. Communications on Applied Nonlinear Analysis, 8(2):1–23.
Khalil, H.K. (2002). Nonlinear Systems. Prentice Hall.
Lam, K.-Y. and Lu, R. (2021). Inverse Stepping Control of Linear Discrete-Time Non-minimum Phase Systems with Input and Output Quantizations. IEEE Transactions on Automatic Control, 66(11):5444–5459. 5444.
Ahmad, M. (1994). Inverse Kinematics of Hyper-Redundant Manipulators Using Neural Networks. IEEE Transactions on Systems, Man, and Cybernetics, 24(1):166–171.
Lang, S. (2002). Algebra. Springer.
Diestel, R. (2017). Graph Theory. Springer.
Brown, L. (2021). Topological Transport in Dynamical Systems. Springer.
Awodey, S. (2010). Category theory. Oxford University Press.
Hatcher, A. (2002). Algebraic topology. Cambridge University Press.
Jech, T. (2013). Set theory. Springer.
Smith, J. (2017). Introduction to topology. Dover Publications.
Devaney, R.L. (1989). An Introduction to Chaotic Dynamical Systems. Addison-Wesley, 2nd edition.
Meiss, J.D. (2007). Differential Dynamical Systems. Society for Industrial and Applied Mathematics.
Brin, M. and Stuck, G. (2002). Introduction to Dynamical Systems. Cambridge University Press.
Zhao, Y. and Zhang, W. (2017). Invertible Discrete Dynamical Systems and Their Applications. Journal of Nonlinear Science, 27(4):1151–1184. 1151.
Golubitsky, M. and Stewart, I. (2002). The Symmetry Perspective: From Equilibrium to Chaos in Phase Space and Physical Space. Birkhäuser Basel.
Cormen, T.H., Leiserson, C.E., Rivest, R.L., and Stein, C. (2009). Introduction to Algorithms. MIT Press, 3rd edition.
Robinson, J.C. (2001). Infinite-dimensional dynamical systems: an introduction to dissipative parabolic PDEs and the theory of global attractors, volume 28. Cambridge University Press.
Quarteroni, A., Manzoni, A., and Negri, F. (2014). Reduced Basis Methods for Partial Differential Equations: An Introduction. Springer.
Lasota, A. and Mackey, M.C. (2013). Chaos, Fractals, and Noise: Stochastic Aspects of Dynamics. Springer Science & Business Media.
ksendal, B. (2013). Stochastic Differential Equations: An Introduction with Applications. Springer Science & Business Media.
Mantegna, R.N. and Stanley, H.E. (1999). Introduction to Econophysics: Correlations and Complexity in Finance. Cambridge University Press.
Castellano, C., Fortunato, S., and Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81(2):591.
Quarteroni, A., Sacco, R., and Saleri, F. (2014). Numerical Mathematics. Springer Science & Business Media.
Karlebach, G. and Shamir, R. (2008). Modelling and analysis of gene regulatory networks. Nature Reviews Molecular Cell Biology, 9(10):770–780.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Collatz Conjecture: A New Proof using Algebraic Inverse Trees

Abstract

1. Introduction

2. Definitions and Preliminary Concepts

2.1. Combinatorial Complexity and Inverse Model Constructibility

3. Axiomatic Foundations of DIDS

4. Inverse Modeling of Systems

4.1. Algebraic Inverse Tree Construction

4.2. Steps of the Inverse Modeling Process

5. Structural Analysis

Flexible Selection of Root Node

6. Uniqueness of the Inverse Model

6.1. Necessary and Sufficient Conditions for Ensuring the Construction of Inverse Models

7. Multivalued Injectivity of G

7.1. Surjectivity of F : S → T , where T ⊆ S

8. Discussion on the Conditions of the Analytic Inverse Function G

8.1. Finite Case

8.2. Countably Infinite Case

8.3. Injectivity and Surjectivity of G: Ensuring Decidable Inference and Property Transfer

9. Topological Equivalences

9.1. Cardinal Properties of Algebraic Inverse Trees

9.2. Other Cardinal Properties of the Inverse Tree

9.3. Conditions for Topological Transportability

9.4. Homeomorphism between Spaces

10. Topological Transport

10.1. Fundamental Conditions for the Topological Transport

10.1.1. Conditions under Which Properties Can Be Transferred

10.1.2. Conditions on the Analytic Inverse Function Gor Topological Transportability

10.2. Extension to Infinite AITs

11. Results and Applications

11.1. Proof of the Collatz Conjecture

Appendix A Fundamental Definitions

Appendix B Important Lemmas

Appendix C Central Theorems

Appendix D Primitive Principles

Appendix E Axiomatic Foundations

Appendix F Formalization of Key Concepts

References

MDPI Initiatives

Important Links

Subscribe

7.1. Surjectivity of $F : S \to T$ , where $T \subseteq S$