Prerpints.org logo
Preprint
Article

The Electron-Phonon Interaction at Vicinal Metal Surfaces Measured with Helium-Atom Scattering

This is a preprint, it has not been peer-reviewed.

Submitted:

12 October 2023

Posted:

13 October 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
It has been recently demonstrated that inelastic helium-atom scattering from conducting surfaces can provide a direct measurement of the surface electron-phonon coupling constant (mass-enhancement factor ) via the temperature- or the incident-energy-dependence of the Debye-Waller exponent. The analysis of previous published as well as unpublished helium atom scattering diffraction data from the vicinal surfaces of copper (Cu(11),  = 3,5,7) and aluminium (Al(221) and Al(332)) permits to extract  for this class of surfaces, suggesting an enhancement with respect to the corresponding data for the low-index surfaces (111) and (001) above a possible roughening transition temperature. The specific role of steps as compared to that of terraces is briefly discussed.
Keywords: 
  -  

1. Introduction

The interest in vicinal crystal surfaces, whose planes form a small angle with a low-index plane (e.g., (001), (111) or (110) in cubic crystals), goes much beyond pure crystallography. Ideal vicinal surfaces are characterized by sets of equally-spaced steps separated by low-index terraces. Their structure and stability with respect to faceting, reconstruction and roughening transitions have been the subject of several experimental studies with He atom scattering (HAS) and related theoretical works [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. The early interest in vicinal surfaces was motivated by their expected role as natural templates for the epitaxial growth of functional nanostructures [21,22,23,24], and in heterogeneous catalysis [25]. The topological and the quasi-one-dimensionality (quasi-1D) features of steps are argued to be reflected in their electronic and vibrational properties, hence in the local electron-phonon (el-ph) interaction, thus opening new horizons for quasi-1D superconductivity in topological materials [26,27,28,29].
In a previous work [30], it has been shown that helium-atom scattering (HAS) can provide a direct information on the surface el-ph interaction at a conducting surface, as expressed by the total mass-enhancement factor λ, via the temperature- or incident-momentum-dependence of the HAS Debye-Waller (DW) exponent. The value of λ derived in this way (hereafter denoted λHAS) has been reported for several metal surfaces [31] and overlayers [32], graphene [33], topological semimetals [34,35,36,37], layered dichalcogenides [38,39], 2D superconductors [40], and low- and multi-dimensional surfaces [41]. In this paper we extend this study to high-index metal surfaces, by re-analysing previous HAS diffraction measurements on the vicinal surfaces of copper Cu(11α) (α = 3,5,7 [42,43], α = 2,5 [44,45,46] (Figure 1, left)) and aluminium Al(221) and Al(332) [46,47] (Figure 1, right). It is shown that the DW exponent -2W(T,ki), whether as a function of the surface temperature T or of the incident He beam wavevector ki, carries distinct information about the el-ph interaction associated with either steps or terraces. Lapujoulade et al. [42,43] observed that the typical linear slope of -2W(T,ki) for increasing temperature Cu(11α),, becomes suddenly steeper above a certain temperature TR, of the order or above room temperature, indicative of a surface roughening transition. In the light of the el-ph theory of the DW exponent, it is shown in Section 3 that this kind of roughening transition actually yields an increase of the local el-ph interaction, similarly to what recently reported for a semiconductor surface [48].

2. Theory

The specular HAS intensity is written as a function of the incident wavevector ki and surface temperature T in the form
I ( k i , T ) = I 0 ( k i )   e − 2 W ( k i , T ) = I ( k i , 0 )   e 2 W ( k i , 0 ) e − 2 W ( k i , T )
The wavevector dependence of the prefactor I 0 ( k i ) is conveniently described at small ki by a power law, I 0 ( k i ) ∝ k i η , where η ( > 1 ) depends on the atom-surface interaction as well as on the supersonic beam source design and operating conditions [30,50].
The present el-ph theory of HAS from conducting surfaces [30,31] links the surface el-ph mass-enhancement factor λHAS to the dependence of the DW exponent on temperature or incident momentum through the two equations
λ H A S = − π ϕ 2 n s a c ∂ ln I ( k i , T ) k i z 2 ∂ ( k B T ) ,
λ H A S = − π ϕ 2 n s a c ∂ ln [ k i − η I ( k i , T ) ] ( k B T ) ∂ k i z 2 ,
respectively. Here φ is the surface work function, ns the effective number of surface atomic layers involved in the surface el-ph interaction, and ac the surface unit cell area. For vicinal surfaces, ac is here approximated by that of the terraces between two neighbour parallel steps. The power law for I 0 ( k i ) ensures that the measured I ( k i , T ) at a given surface temperature T vanishes for both ki → 0 and ki → ∞. It will therefore have a maximum at ki = ki, max, where ∂ I ( k i , max , T ) / ∂ k i = 0. By combining this condition with Equations (1) and (3), the latter can be expressed as:
λ H A S = π ϕ 4 n s a c η k B T   k i z , max 2 .
Note that, by inserting Equation (4) into (3), k i z , max 2 can be obtained from:
1 k i z , max 2 = − 2 ∂ ln [ k i − η I ( k i , T ) ] η   ∂ k i z 2 ,
and is therefore dependent on the surface temperature.
As discussed in Ref. [30], when the effects of the attractive surface potential depth D are not completely negligible in specular HAS, they can be approximately accounted for by replacing k i z 2 in Equation (2) with k ¯ i z 2 = k i z 2 + 2 m D / ℏ 2 (Beeby correction [51]), where m is the He atom mass and the potential depth D can directly be obtained from the analysis of HAS bound-state resonances [52]. Classically, the Beeby correction is equivalent to assuming that the He-surface interaction occurs at the maximum speed acquired by the He atom under the effect of the attractive potential. When the ki—dependence of the HAS intensity is used instead of its temperature dependence to derive λHAS, Equation (4) has the advantage that the information on the electron-phonon interaction is all within the factor k i z , max 2 , to which the Beeby correction can be directly added.

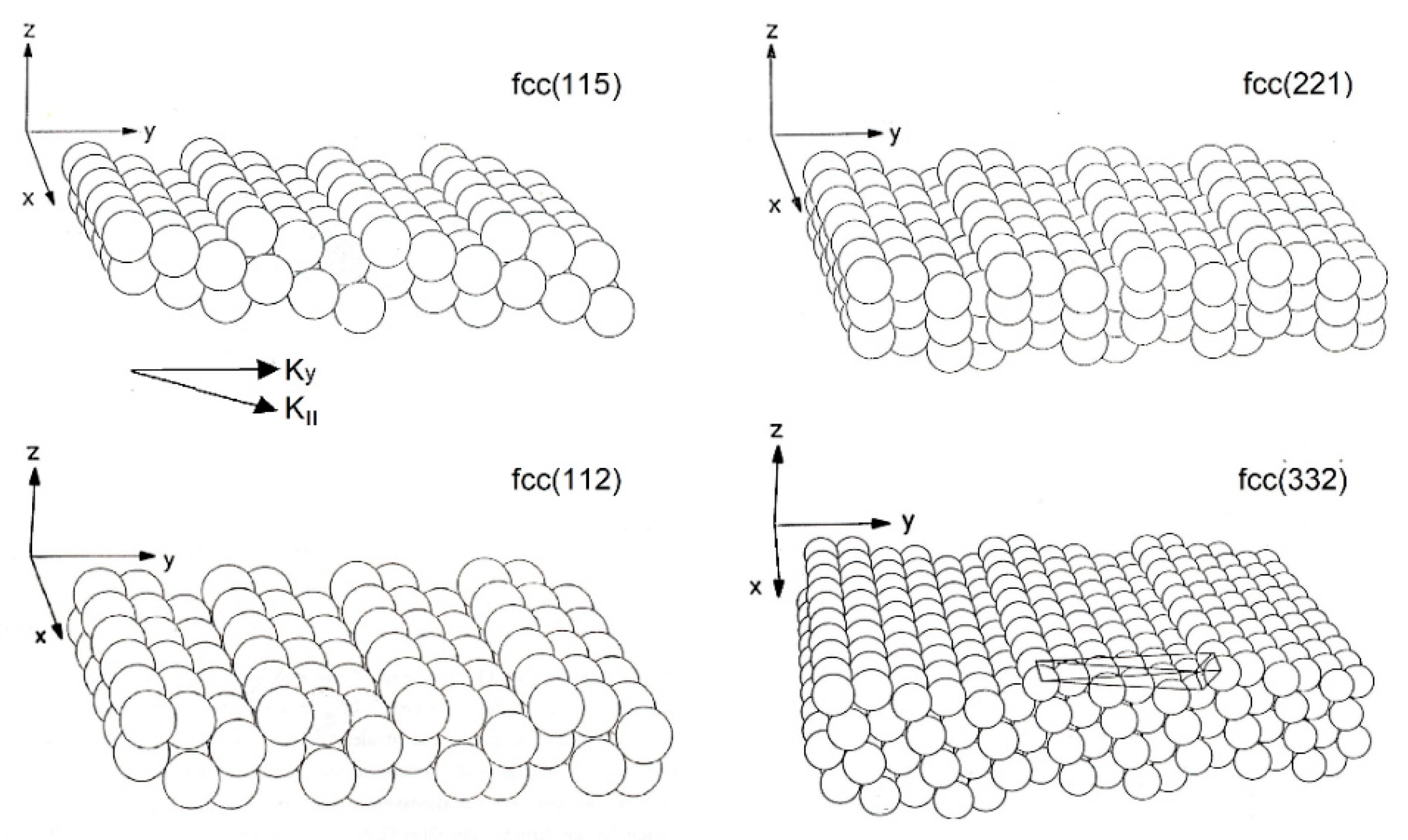
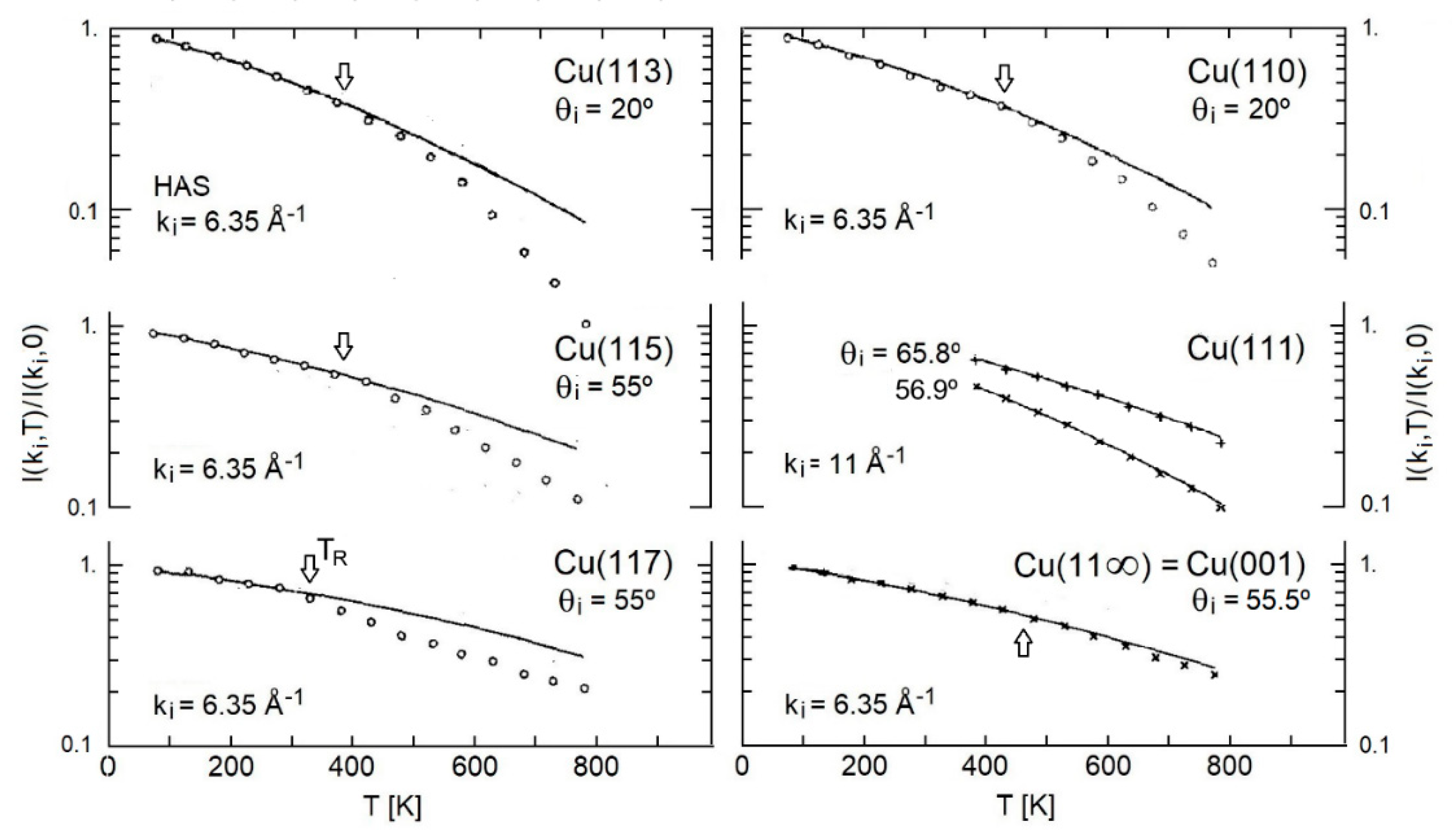
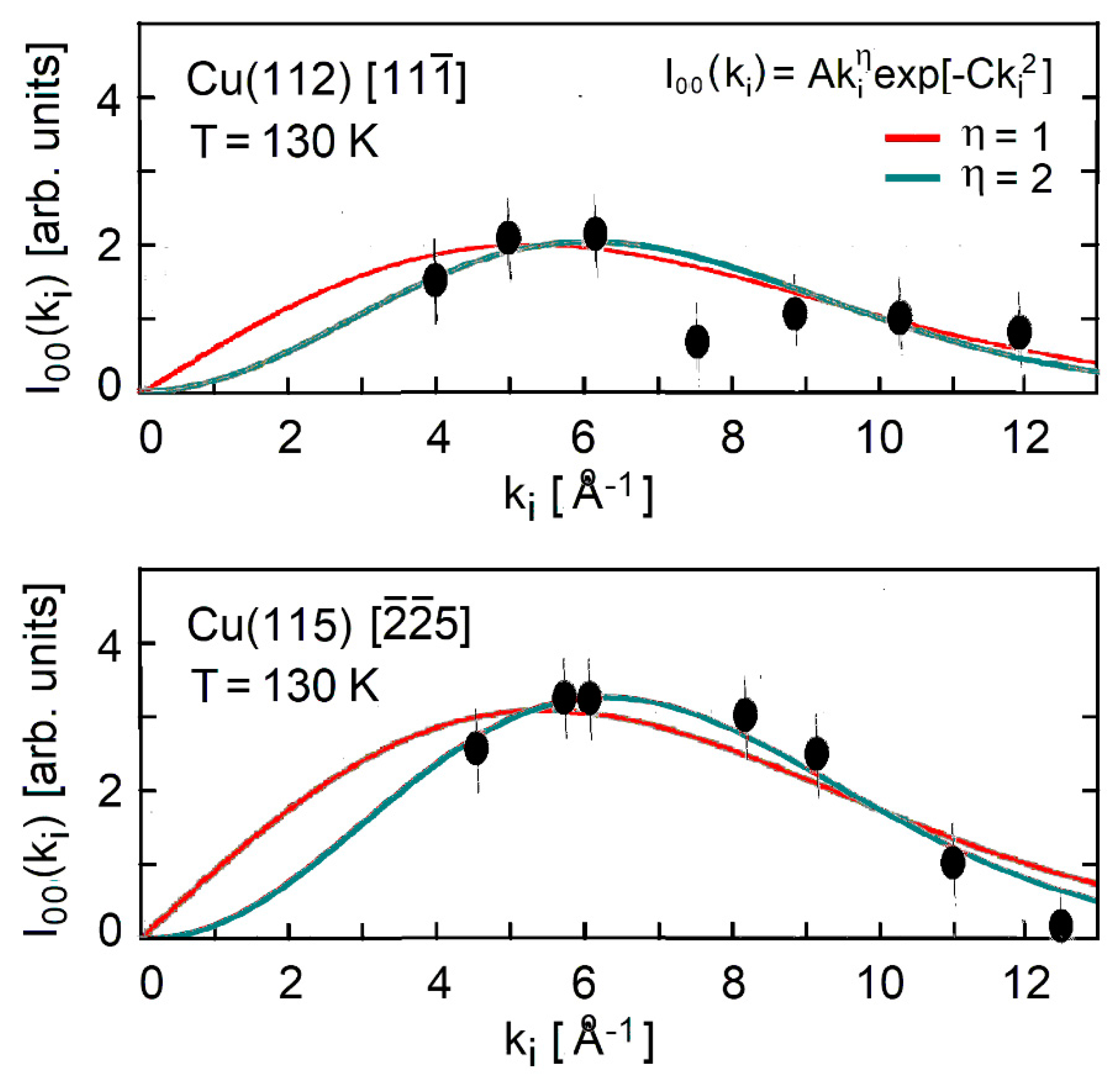
3. The Copper Vicinal Surfaces Cu(11α)

A selection of HAS specular reflectivity data measured by Lapujoulade et al. [42,43] as a function of the surface temperature for the vicinal surfaces of copper (11α), with α = 3,5,7, is reproduced in Figure 2 (left) and compared with the data for the low-index surfaces (110), (111) and (001) (α = 0,1,∞) (right). The reflectivity data, normalized to the extrapolated zero-temperature value I(ki,0), are plotted on a logarithmic scale so as to give the profile of the DW exponent, with the corresponding He beam incident wavevectors ki and angles θi indicated in the panels. The HAS experimental points have been fitted by Lapujoulade et al. (full lines) [42,43] with a theory for the DW temperature dependence based on a He-surface atom phenomenological potential, the surface dynamics represented by a surface Debye temperature of the order of 230 K, and adjustable parameters for the Beeby correction, for the so-called Armand effect, and for anharmonic corrections, the latter in order to account for the high-temperature deviations from the expected linearity.
All this appears to be largely insufficient to explain the sudden increase of slope observed above some temperature TR of the order of room temperature for Cu(117), or larger for Cu(115), Cu(113) and even Cu(110), while the fit is excellent for the densely-packed surfaces (111) and (001), which show a regular behaviour up the highest measured temperature of 800 K. This has led Lapujoulade et al. [8,9] to consider these data as a clear evidence for a roughening transition, promoted by, and affecting first, the step rows, with TR its critical temperature.
The values of λHAS derived by means of Equation (2) from the data of Figure 2 below (light face) and above (bold face) the roughening transition are given in Table 1, with the input data taken from the indicated references. The work function φ = 4.53 eV measured by Gartland et al. [49] for the Cu(112) has been adopted for the other vicinal surfaces. This is however very close to that of Cu(001), which actually is the terrace plane for α = 3,5,7. The Cu(001) terrace values are then used also for ns, and ac.
Below the roughening transition the intensity slope used in the calculation is that of the interpolating line calculated by Lapujoulade et al. shown in Figure 2 [30] and including anharmonic corrections, while above the transition the experimental intensity ratio at the two temperatures T1 and T2 given in Table 1 has been used. No evidence of any roughening was found for the closed-packed surface Cu(111). For this surface two different sets of data from Ref. [30] are reproduced in Figure 2, corresponding to the different incident angles. Although the slopes are rather different, the corresponding values of λHAS given in Table 1 are about the same, as expected. For the Cu(001) surface, two different values of λHAS are associated with the slight increase of the intensity slope observed with respect to the fitting curve, although this small effect can be hardly associated to a real transition rather than to a gradual increase of surface disorder.
An interesting result from this analysis is the appreciable increase of the electron-phonon interaction above the roughening transition. As anticipated above, this appears to be consistent with what was recently reported for a CdTe surface [48], although the mechanism for the electron-phonon interaction at a roughened metal surface may be rather different from that for an intrinsic semiconductor surface. It should be noticed that disorder activates additional scattering channels at the expense of ordinary specular and diffraction channels. Thus, a steeper decay of the DW exponent observed at increasing temperature above the disorder threshold may be in part an effect of opening new competitive scattering channels, rather than an indication of larger electron-phonon interaction. On the other hand, below that threshold the observed increase of λHAS has a solid basis, relying on the localization of both electronic and phonon excitations, conferring a quasi-one-dimensional character to step dynamics. Phonon softening at steps [59] may be viewed as a manifestation of a larger local electron-phonon interaction.
The HAS angular distributions reported by Miret-Artés et al. [45] for the Cu(112) and the Cu(115) vicinal surfaces, respectively measured along the [ 11 1 ¯ ] and [ 5 ¯ 5 ¯ 2 ] directions, give the specular intensity from the vicinal plane (θi = 45°) for seven different values of the incident ki at the same temperature of about 130 K. The measured specular intensities, plotted in Figure 3, give indication of a maximum value k i z , max 2 around 15 Å-2 for both surfaces [45]. For the (115) surface the fit of the specular intensity with the function
I 00 ( k i ) = A k i η exp [ − C k i 2 ] ,
where the exponential represents the DW factor and A and C are two fitting constants, suggests η = 2 with k i , max ≅     7.0 Å-1 rather than η = 1 with k i , max ≅     5.5 Å-1. For the (112) surface the dip in the intensity at ki = 7.5 Å-1 is presumably due to a bound-state resonance, and does not allow to clearly distinguish between the fits with the two values of η and the respective values of ki,max given in Table 2. The corresponding values of λHAS for the two surfaces Cu(112) and Cu(115) at T = 130 K, obtained from Equation (4) for both η = 1 and 2, are given in Table 2. Clearly the values of λHAS increase with η . The quality of the fits in Figure 3 for Cu(115) would suggest η = 2, but the resulting values of λHAS , even with η = 1, turn out to be systematically larger than those obtained from the temperature dependence of the DW exponent, and more consistent with the values found above the roughening transition temperature.
It should be noted that the terraces of the Cu(112) surfaces are (111) surfaces, while the terraces of the other Cu(11α) surfaces (α=3,5,7) are (001) planes. For vicinal surfaces with a short inter-step period and a densely packed terraces like Cu(112) the actual crystallographic unit cell area (ac = 15.9 Å2) should be a better choice. In this case λHAS drops to 0.10 for η = 1 (close to that of Cu(001) and Cu(111)) and 0.16 for η = 2 (Table 2).
It appears, however, as a general fact that λHAS increases in moving from high-index to intermediate vicinal surfaces. The largest λHAS of the Cu(11α) series derived from the DW temperature-dependence is found for α = 5. Such an increase of the surface el-ph interaction can be associated to the presence of steps, as long as they are sufficiently localized but not too far apart. Localization of the surface electronic states at the Fermi level can also stay behind the increase of λHAS above the roughening transition.
Table 1. shown in Figure 2 (from ref. [42]) for ordered (low-temperature interval) and roughened (high-temperature interval, bold face figures) Cu(11α), Al(221) and Al(332) vicinal surfaces. No roughening transition has been observed for Cu(111). For comparison, the mass-enhancement factor reported for Al(111) is λHAS = 0.30 [30].
Table 1. shown in Figure 2 (from ref. [42]) for ordered (low-temperature interval) and roughened (high-temperature interval, bold face figures) Cu(11α), Al(221) and Al(332) vicinal surfaces. No roughening transition has been observed for Cu(111). For comparison, the mass-enhancement factor reported for Al(111) is λHAS = 0.30 [30].
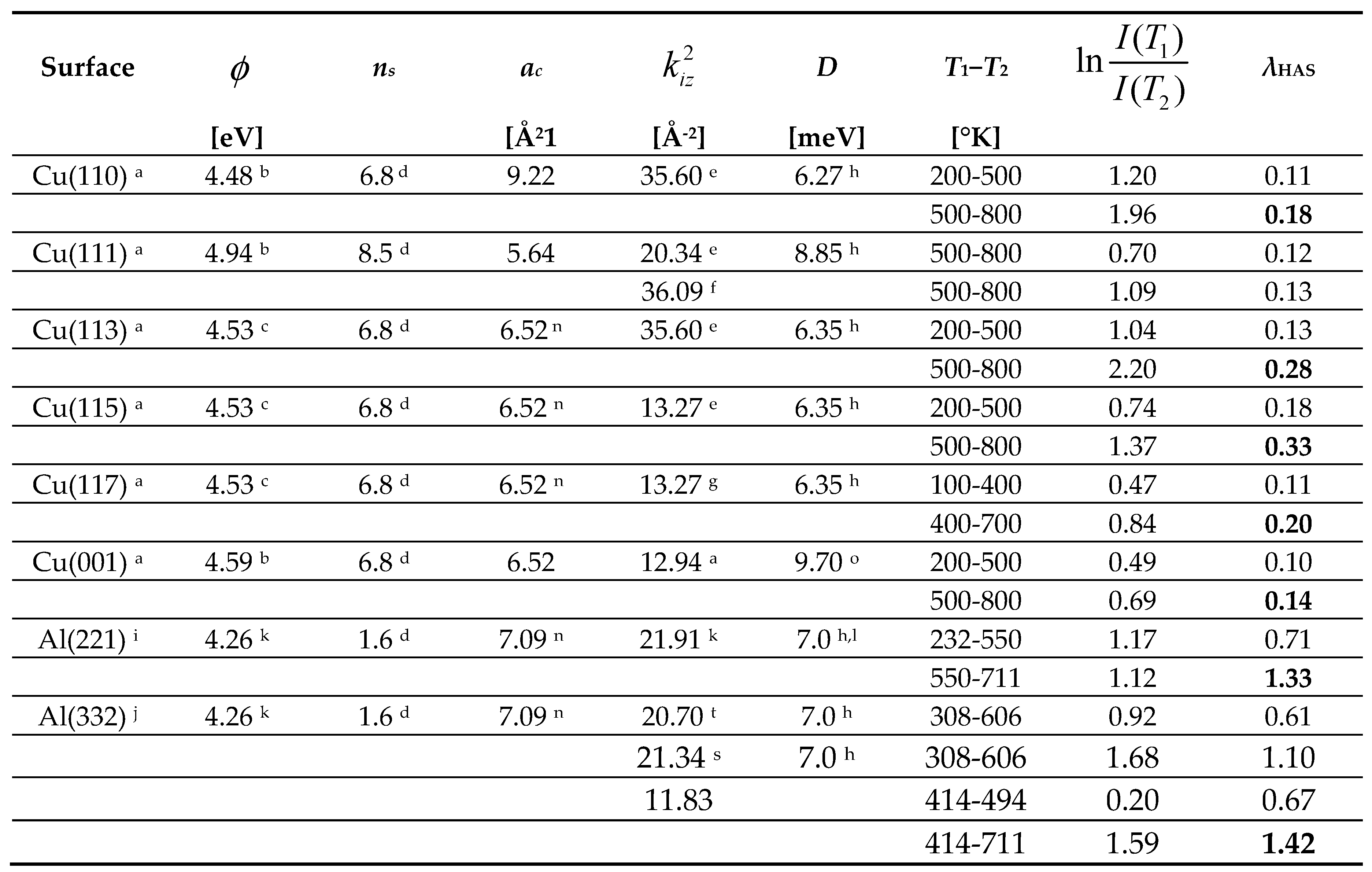
Preprints 87641 i001
a) Refs. [42,43]. b) Ref. [49]. c) The value measured for Cu(112) [49] is adopted for all present vicinal surfaces. d) Value for the corresponding terrace surface from Ref. [30]. e) Ref. [42]; for Cu(111) from data in Figue 2 with θI = 65.8º. f) For Cu(111) from data in Figure 2 with θI =56.9º. g) Ref. [43]. h) Ref. [52].i) Refs. [46,54,55]. j) Refs. [46,47,55]. k) Ref. [53] .l) Potential depth for the (001) surface; the one for the terrace (111) surface not available. m) Diffuse elastic intensity (Figure 13 of Ref. [47]). n) Unit cell area of the corresponding terrace surface. o) Ref. [56]. t) Specular scattering from terrace surface (Figure 6a [46,47]). s) Specular scattering from the (332) surface (Figure 6a [46,47]).
Table 2. Electron-phonon mass-enhancement factor λHAS derived from the dependence of the specular HAS intensity on the incident wavevector (Eqs. (3,4)). Values equal to those of the line above are omitted.
Table 2. Electron-phonon mass-enhancement factor λHAS derived from the dependence of the specular HAS intensity on the incident wavevector (Eqs. (3,4)). Values equal to those of the line above are omitted.
Surface φ ns ac ki,max D T η λHAS
[eV] [Å21 [Å-1] [meV] [K]
Cu(112) a 4.53 b 6.8 c 5.64 d ~5.0 8.25 e 130 1 0.29
~6.5 2 0.45
15.9 i ~5.0 8.25 e 130 1 0.10
~6.5 2 0.16
Cu(115) a 4.53 b 6.8 c 6.52 d ~5.5 6.35 e 130 1 0.26
~7.0 2 0.38
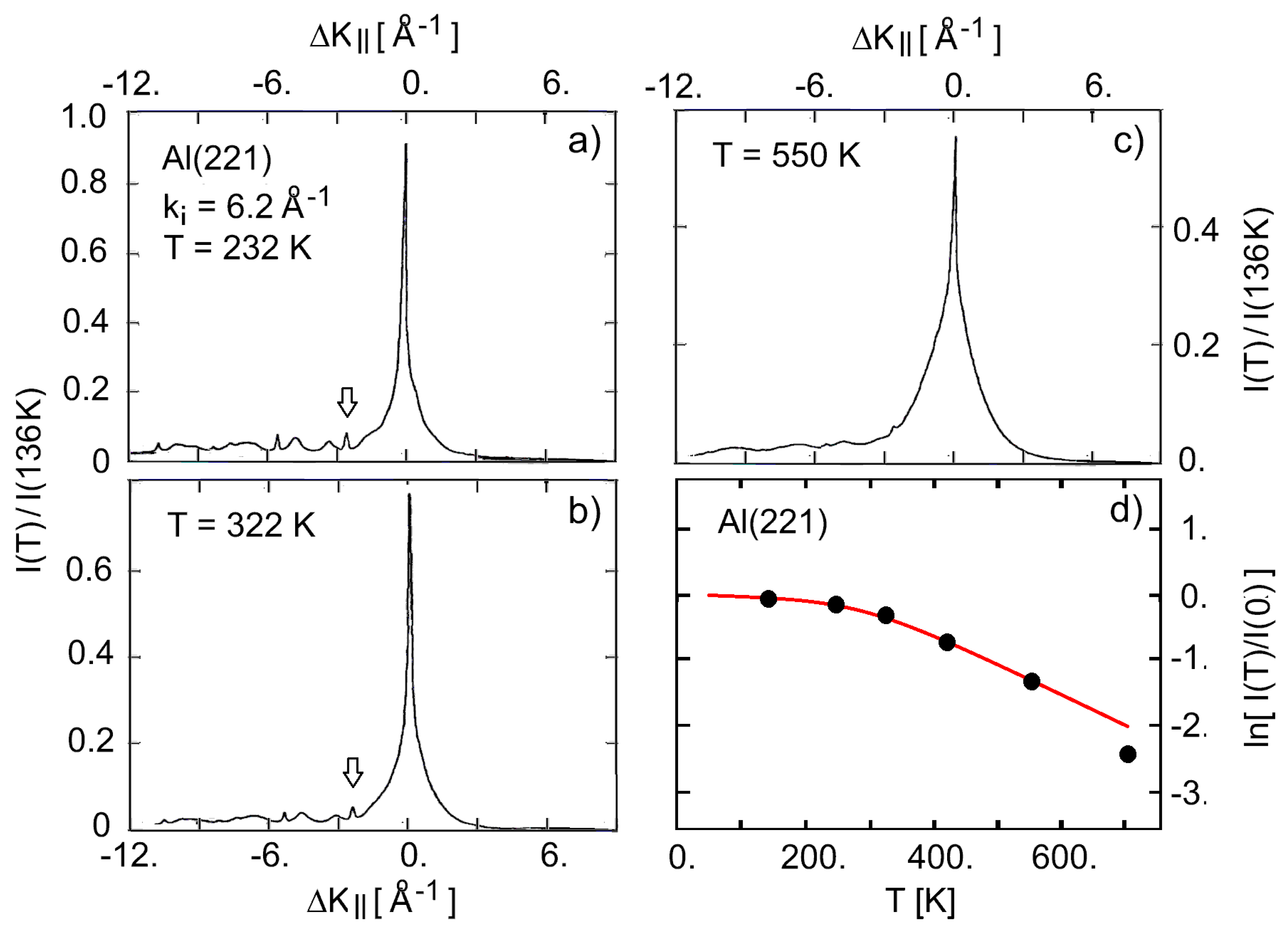
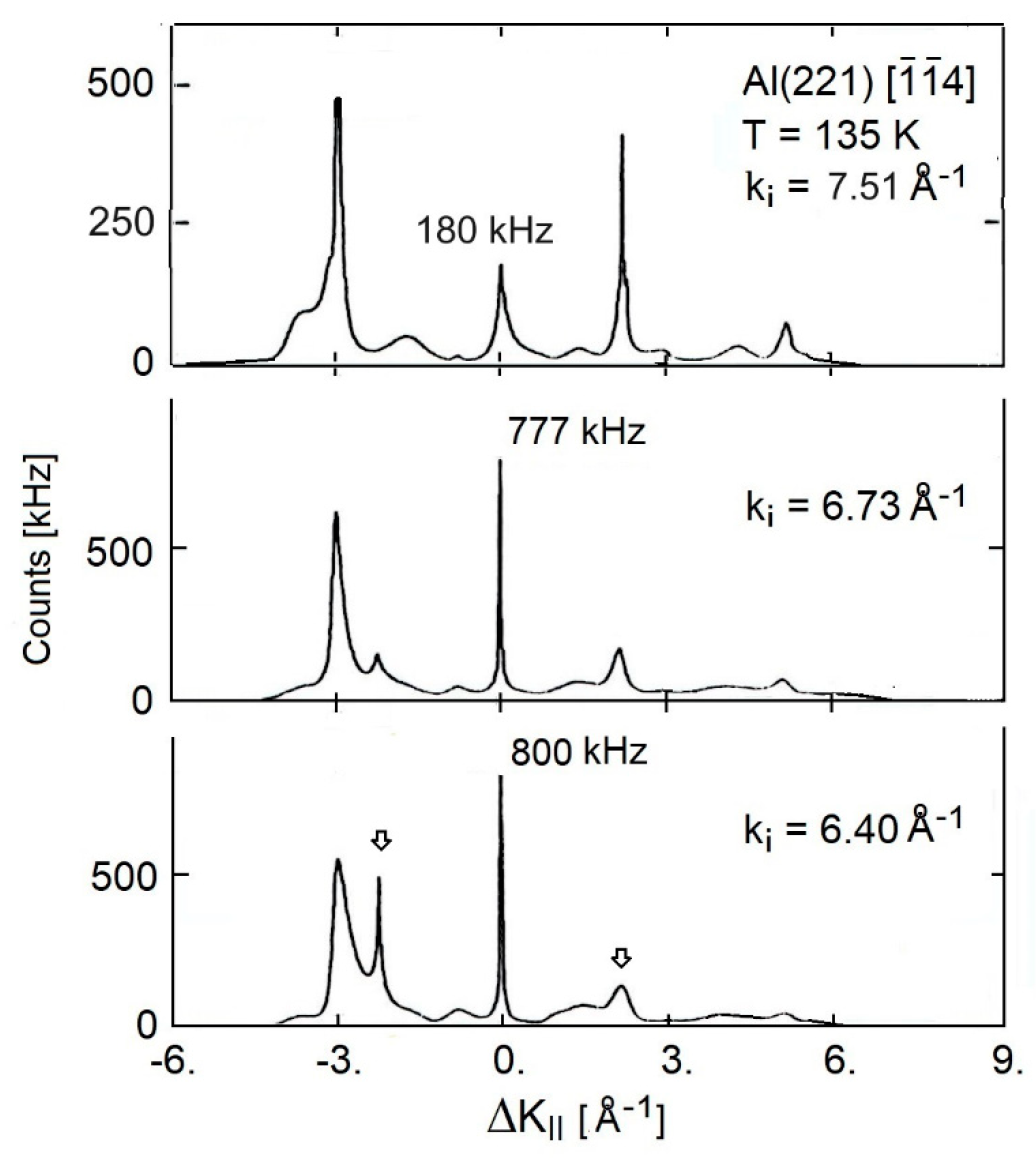
Al(221) f 4.26 h 1.6 c 7.09 d ~6.5 7.0 e 135 1 0.72
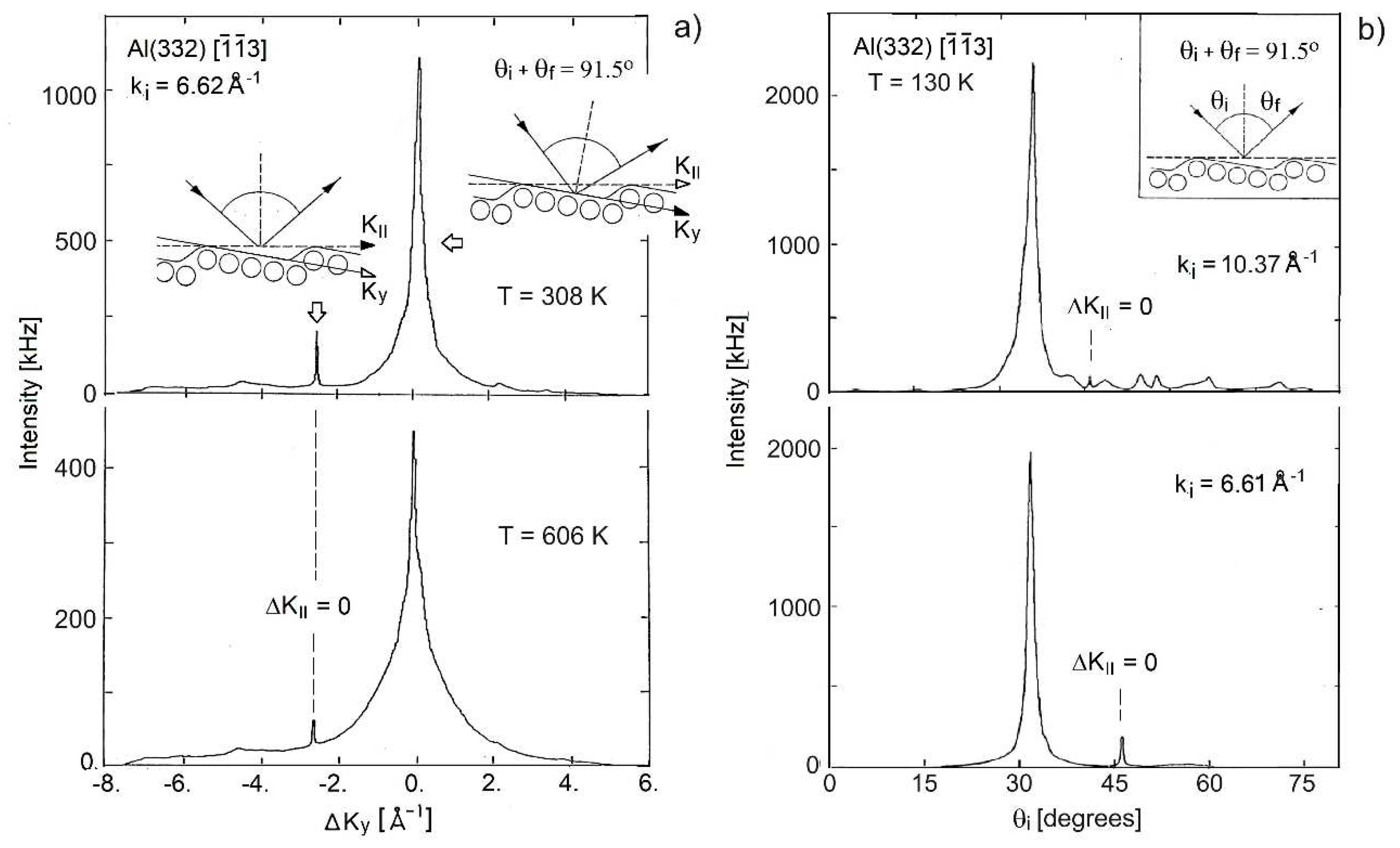
Al(332) g 4.26 h 1.6 c 7.09 d ~7.2 7.0 e 130 1 0.61
a) Ref. [45]; b) Ref. [49]; the value measured for Cu(112) is also used for Cu(115). c) Value for the corresponding terrace surface from Ref. [30]. d) Unit cell area of the corresponding terrace surface. i) Cu(112) unit cell area. e) Ref. [52]. The (111) terrace value is used for Cu(112). f) Refs. [46,54,55]. g) Refs. [46,47,55]. h) Ref. [53].

4. The Aluminium Vicinal Surfaces Al(221) and Al(332)

The HAS intensity at a scattering angle θ i + θ f = 91.5º has been measured for the vicinal surfaces Al(221) [46,54,55] and Al(332) [46,47,55], both as a function of the surface temperature and incident wavevector. Figure 4a–c reproduces some of the HAS spectra from the Al(221) surface measured by Witte et al. [54,55] at three different surface temperatures and given incident wavevector ki = 6.2 Å-1. They are plotted as functions of the parallel wavevector change Δ K ∥ in the direction [ 1 ¯ 1 ¯ 4 ] normal to the steps. The specular scattering from the crystallographic surface occurs at Δ K ∥ = 0, while the specular scattering from terraces occurs at about ±2.4 Å-1, the sign corresponding to either the up-hill or down-hill scattering configuration. Panel (d) shows the DW exponent derived from the full set of data points reported by Witte et al. and a coth ( θ D / 2 T ) fit (red full line), where θD = 790 K is the aluminium Debye temperature [58]. The corresponding λHAS from Equation (2) and the parameters listed in Table 1, when referred to the approximate linear behaviour in the temperature interval 232-550 K, is 0.71. The experimental point at 712 K clearly deviates from the fitting curve, with the larger DW slope in the high-T range giving λHAS = 1.33. Such a large increase above 550 K could be interpreted as an effect of surface roughening, similar to what is observed in Cu(11α). Clearly, more measurements in this range should be made available in order to confirm this interpretation.
The value of λHAS found for Al(221) below 550 K is, however, much larger than the one found for the Al(111) surface (λHAS = 0.30, see Table 2 of Ref. [30]), as well as the bulk value λ = 0.43 ± 0.05 [57], but it almost coincides with the value of λHAS = 0.72 derived via Equations (3,4) from the wavevector dependence of the specular HAS intensity at T = 135 K and for η = 1 (Figure 5). It may be argued that also for the vicinal surface Al(221) a robust increase of the el-ph interaction occurs with respect to that of the low-index surfaces, with a further increase above 550 K as a possible effect of roughening. Note that in Al(221) the specular scattering from the crystallographic (221) surface is still larger than (or comparable to) that from the (111) terraces (small arrows in Figure 4 and Figure 5), despite the fairly large inter-step distance of 8.74 Å.
The vicinal surface Al(332) (Figure 6), with its 14.30 Å inter-step distance, exhibits instead a dominant HAS specular scattering from (111) terraces ( Δ K y = 0 , see Figure 1), and only small sharp peaks from the periodic array of steps of the (332) surface ( Δ K ∥ = 0). Figure 6, adapted from Lock et al. [46,47], shows the changes of the HAS specular intensities from both terraces and step arrays observed by changing either temperature at a given ki (Figure 6(a)), or ki at a given temperature (Figure 6(b)). In the first case, Equation (2), applied to scattering from terraces with the parameters listed in Table 1 and the temperature interval 308–606 K, λHAS = 0.61. The same value is obtained in the second case from Eqs. (3-5), with η = 1 and the ki interval 6.61-10.37 Å-1. The same consistency was found for Al(221), which strongly supports the choice η = 1.
It is noted that λHAS for Al(332), although still larger than that of Al(111), turns out to be smaller than that found for Al(221). An interesting question is whether this is due to the different sources of data used for Al(332) (specular HAS from (111) terraces) and Al(221) (specular HAS from the (221) surface, actually from the periodic array of steps). The temperature- and incident wavevector-dependence of the small peaks at Δ K ∥ = 0 in Figure 6 permits to compare what amounts to terraces and those of steps and to assess the respective contributions to the surface electron-phonon coupling. The second row of Al(332) data in Table 1 shows indeed that λHAS derived from the temperature dependence of the small Δ K ∥ = 0 peak is increased to 1.10, which brings the surface electron-phonon coupling of Al(223) above that of Al(221) and much above that of the Al(111) low-index surface. A similar increase can probably be extracted from the ki—dependence of Δ K ∥ = 0 peak, although the very small peak at the higher wavevector is hidden in the background.
The temperature dependence of the elastic scattering spectra from Al(223) terraces measured by Lock et al. [46,47] around Δ K y = 0 for a fixed incident wavevector ki = 4.93 Å-1, reproduced in Figure 7, can hardly be used to extract λHAS due to the partial superposition to an additional peak growing with increasing temperature at positive values of Δ K y . This has been attributed to a temperature-driven instability towards faceting at steps. Nevertheless, the value of λHAS = 0.66 obtained from Equation 2 in the lowest temperature interval (414-494 K) (see Table 1, 3rd row for Al(332)), where the specular scattering intensity from (111) terraces is still dominant, is consistent with the terrace values derived from Figure 6. At larger temperatures, where faceting instability occurs, it can make sense to consider the areas of the double peak features and to take the logarithm of the ratio of two areas measured at two different temperatures, in order to have an overall qualitative information on the electron-phonon interaction. The 4th row for Al(332) in Table 1 gives λHAS as obtained in this way over the entire 414-711 K temperature range. The comparatively large value of λHAS = 1.42 is consistent with what found at the higher temperature for Al(221) (1.33) and attributed to a roughening transition, in analogy to what was reported for copper vicinal surfaces.

5. Conclusions

The method of extracting the electron-phonon interaction (mass enhancement factor λHAS) at conducting surfaces from the Debye-Waller exponent of helium-atom scattering [30], has been applied to the analysis of existing HAS data on Cu and Al vicinal surfaces. It is found that the electron-phonon interaction of the vicinal surfaces analysed in the present work is generally larger than that of the corresponding low-index surface of the terraces between two neighbouring steps. Such increase of λHAS is attributed to the specific contribution of steps. The case of Al(332) is illuminating in this respect, because it permits to compare λHAS obtained from the HAS reflectivity of (111) terraces to that obtained from the HAS reflectivity of the crystallographic surface (332).
More intriguing is the pronounced increase of λHAS at higher temperature where some form of disorder appears such as roughening or terrace faceting. It has been noticed above that disorder activates additional scattering channels, which subtract intensity to specular and diffraction scattering, producing a steeper decay with temperature of the DW exponent. It is expected that disorder induced by increasing temperature starts from steps were atoms are more loosely bound at their lattice positions. On the other hand, the larger contributions of step atoms to λHAS than that of terrace atoms, as found in the present analysis, is likely to be due to the step localization of both electronic and phonon excitations, which acquire a quasi-one-dimensional character, so that the phonon softening at steps [59] may be linked to the larger local electron-phonon interaction.
The present work has been stimulated by existing HAS measurements which were not intended for the derivation of λHAS, the method being unknown at those times. There have been very interesting HAS investigations also on the clean and Fe-covered Pt(997)
surfaces [60] where the normalization of HAS diffraction spectra measured at several different temperatures does not permit the evaluation of λHAS. We hope that this study will stimulate new HAS studies explicitly designed for the derivation of both λHAS and the mode-selected λQν. The recent studies on the possible superconductivity enhancement as an effect of surface disorder [61] offer further good reasons for new HAS studies specifically aiming at the derivation of the electron-phonon interaction at stepped surfaces and conducting surfaces with various types of disorder.

Acknowledgements

SMA would like to thank the support of Fundación Humanismo y Ciencia.

References

  1. C. Comsa, G. Mechtersheimer, B. Poelsema, S. Tomoda Direct Evidence for Terrace Bending from He Beam Scattering on Pt(997), Surf. Sci. 89, 123 (1979).
  2. J. Harris, A. Liebsch, G. Comsa, G. Mechtersheimer, B. Poelsema, S. Tomoda, Refraction effects in atom scattering from stepped surfaces, Surf. Sci. 118, 279 (1982).
  3. J. Villain, D.R. Grempel, J. Lapujoulade, Roughening transition of high-index crystal faces: the case of copper, J. Phys. F 15, 809 (1985).
  4. M. den Nijs, E. K. Riedel, E. H. Conrad, and T. Engel, Roughening of Stepped Metal Surfaces, Phys. Rev. Lett. 55, 1689 (1985) Erratum: Phys. Rev. Lett. 57, 1279 (1986).
  5. E. H. Conrad, L. R. Allen, D. L. Blanchard, T. Engel, Kosterlitz-Thouless roughening at the Ni(113) surface, Surf. Sci. 187, 265 (1987).
  6. E. H. Conrad, R. M. Aten, D. S. Kaufman, L. R. Allen, T. Engel, M. den Nijs, E. K. Riedel, Observation of surface roughening on Ni(115), J. Chem. Phys. 84, 1015 (1986); E: J. Chem. Phys. 85, 4756 (1986).
  7. A. Bartolini, F. Ercolessi, and E. Tosatti, “Magic” Vicinal Surfaces Stabilized by Reconstruction, Phys. Rev. Lett. 63, 872 (1989).
  8. J. Lapujoulade, B. Salanon, F. Fabre, and B. Loisel, The Roughening Transition of Vicinal Surfaces, in Kinetics of Ordering and Growth at Surfaces, ed. by M. G. Lagally (Plenum Press, New York, 1990) p. 355, and references therein.
  9. J. Lapujoulade, The roughening transition at metal surfaces, Surf. Sci. Rep. 20, 191 (1994).
  10. E. Hahn, H. Schief, V. Marsico, A. Fricke, and K. Kern, Orientational Instability of Vicinal Pt Surfaces Close to (111), Phys. Rev. Lett. 72, 3378 (1994).
  11. J. W. M. Frenken and P. Stoltze, Are Vicinal Metal Surfaces Stable?, Phys. Rev. Lett. 82, 3500 (1999).
  12. E. Le Goff, L. Barbier, L. Masson, and B. Salanon, Vicinal surfaces: free energy, terrace width distribution and step correlation functions, Surf. Sci. 432, 139(1999).
  13. P. Nozières, The roughening transition of vicinal surfaces, Eur. Phys. J. B 24, 383–386 (2001).
  14. E. G. Michel (ed.), Vicinal surfaces, J. Phys.: Condens. Matter, 15, E01 (2003); a special section collecting ten contributions on the expected relevant role of vicinal surfaces in different areas of surface science.
  15. C. Barreteau, F. Raouafi, M.-C. Desjonquères, D. Spanjaard, Modelisation of transition and noble metal vicinal surfaces: energetics, vibrations and stability, J. Phys.: Cond. Matter 15, S3171 (2003).
  16. J. L. F. Da Silva, C. Barreteau, K. Schroeder, and S. Blügel, All-electron first-principles investigations of the energetics of vicinal Cu surfaces, Phys. Rev. B 73, 125402 (2006).
  17. D. K. Yu, H. P. Bonzel, and M. Scheffler, The stability of vicinal surfaces and the equilibrium crystal shape of Pb by first principles theory, New Journal of Physics 8, 65 (2006).
  18. P. Hecquet, Stability of vicinal surfaces and role of the surface stress, Surf. Sci. 604, 834 (2010).
  19. L. Guin, M. E. Jabbour, L. Shaabani-Ardali, L. Benoit-Maréchal, and N. Triantafyllidis, Stability of Vicinal Surfaces: Beyond the Quasistatic Approximation, Phys. Rev. Lett. 124, 036101 (2020).
  20. L. Guin, M.E. Jabbour, L. Shaabani-Ardali, and N. Triantafyllidis, Revisiting step instabilities on crystal surfaces. Part I: The quasistatic approximation, J. Mech. Phys. Solids, 156, 104574 (2021); Part II: General theory, J. Mech. Phys. Solids, 156, 104582 (2021).
  21. V. Marsico, M. Blanc, K. Kuhnke, and K. Kern, Discrete Row Growth at Vicinal Surfaces ,Phys. Rev. Lett. 78, 94 (1997).
  22. K. Kuhnke and K. Kern, Vicinal metal surfaces as nanotemplates for the growth of low-dimensional structures, J. Phys.: Condens. Matter 15, S3311, (2003).
  23. T.-Y. Lee, S. Sarbach, K. Kuhnke , K. Kern, Growth and surface alloying of Fe on Pt(997), Surf. Sci. 600, 3266 (2006).
  24. Ch. Tegenkamp, Vicinal surfaces for functional nanostructures, J. Phys.: Condens. Matter 21, 013002 (2009).
  25. B. L. M. Hendriksen, M. D. Ackermann, R. van Rijn, D. Stoltz, I. Popa, O. Balmes, A. Resta, D. Wermeille, R. Felici, S. Ferrer, and J. W. M. Frenken, The role of steps in surface catalysis and reaction oscillations, Nature Chem. 2, 730 (2010).
  26. L.-F. Zhang, L. Flammia, L. Covaci, A. Perali and M. V. Miloševic, Multifaceted impact of a surface step on superconductivity in atomically thin films, Phys. Rev. B 96, 104509 (2017).
  27. Y. Xu, G. Jiang, J. Chiu, L. Miao, E. Kotta, Y. Zhang, R. R. Biswas, and L.A. Wray, Connection topology of step edge state bands at the surface of a three-dimensional topological insulator, New J. Phys. 20, 073014 (2018).
  28. Z.-H. Wang, F. Xu, L. Li, R. Lü, B. Wang, and W.-Q. Chen, One-dimensional topological superconductivity at the edges of twisted bilayer graphene nanoribbons, Phys. Rev. B 100, 094531 (2019).
  29. L. X. Xu, Y.Y Y. Xia, S. Liu, Y. W. Li, L.Y. Wei, H. Y. Wang, C. W. Wang, H. F. Yang, A. J. Liang, K. Huang , T. Deng, W. Xia, X. Zhang, H. J. Zheng, Y. J. Chen, L. X. Yang, M. X. Wang, Y. F. Guo , G. Li, Z. K. Liu, and Y. L. Chen, Evidence of a topological edge state in a superconducting non-symmorphic nodal-line semimetal, Phys. Rev. B 103, L201109 (2021).
  30. J. R. Manson, G. Benedek, S. Miret-Artés, Atom scattering as a probe of the surface electron-phonon interaction at conducting surfaces, Surf. Sci. Rep. 77,100552 (2022).
  31. J. R. Manson, G. Benedek, and Salvador Miret-Artès, Electron–Phonon Coupling Strength at Metal Surfaces Directly Determined from the Helium Atom Scattering Debye–Waller Factor, J. Phys. Chem. Lett. 7, 1016 (2016); 7, 1691 (2016).
  32. G. Benedek, Salvador Miret-Artès, J. P. Toennies, and J. R. Manson, Electron-Phonon Coupling Constant of Metallic Overlayers from Specular He-Atom Scattering, J. Phys. Chem. Lett. 9, 76−83 (2018).
  33. G. Benedek, J. R. Manson, and S. Miret-Artés, The Electron-Phonon Coupling Constant for Single-Layer Graphene on Metal Substrates Determined from He Atom Scattering, PCCP 23, 7553 (2021).
  34. G. Benedek, S. Miret-Artès, J. R. Manson, A. Ruckhofer, W. E. Ernst, and A. Tamtögl, Origin of the Electron-Phonon Interaction of Topological Semimetal Surfaces Measured with Helium Atom Scattering, J. Phys. Chem. Letters 11, 1927-1933 (2020).
  35. A. Tamtögl, P. Kraus, N. Avidor, M. Bremholm, E. M. J. Hedegaard, Bo B. Iversen, M. Bianchi, Ph. Hofmann, J. Ellis, W. Allison, G. Benedek, and W. Ernst, Electron-Phonon Coupling and Surface Debye Temperature of Bi2Te3(111) from Helium Atom Scattering, Phys. Rev. B 95, 195401 (2017).
  36. A. Ruckhofer, D. Campi, M. Bremholm, Ph. Hofmann, G. Benedek, M. Bernasconi, W. E. Ernst, and A. Tamtögl, THz Surface Excitations and Electron-Phonon Coupling in Bi2Se3(111) from Helium Atom Scattering, Phys. Rev. Res. 2, 023186 (2020).
  37. A. Ruckhofer, G. Benedek, M. Bremholm, W. E. Ernst, and A. Tamtögl, “Observation of Dirac Charge-Density Waves in Bi2Te2Se”, Nanomaterials 13, 476 (2023).
  38. G. Anemone, M. Garnica, M. Zappia, P. Casado Aguilar, A. Al Taleb, C.-N. Kuo, C. S. Lue, A. Politano, G. Benedek, A. L. Vázquez de Parga, R. Miranda, and D. Farías, Experimental determination of surface thermal expansion and electron-phonon coupling constant of 1T-PtTe2, 2D Materials 7, 025007 (2020).
  39. G. Anemone, P. Casado Aguilar, M. Garnica, F. Calleja, A. Al Taleb, C.-N. Kuo, C. S. Lue, A. Politano, A. L. Vàzquez de Parga, G. Benedek, D. Farìas, and R. Miranda, Electron-phonon coupling in superconducting 1T-PdTe2, npj 2D Materials and Applications 5, 25 (2021).
  40. G. Benedek, J. R. Manson, S. Miret-Artés, A. Ruckhofer, W. E. Ernst, A. Tamtögl, and J. P. Toennies, Measuring the Electron-Phonon Interaction in Two-Dimensional Superconductors with He Atom Scattering, Condens. Matter 5, 79 (2020); E: Condens. Matter 6, 54 (2021).
  41. G. Benedek, J. R. Manson, and S. Miret-Artés, The Electron–Phonon Interaction of Low-Dimensional and Multi-Dimensional Materials from He Atom Scattering, Advanced Materials 32, 2002072 (2020).
  42. J. Lapujoulade, J. Perreau and A. Kara, The Thermal Attenuation of Elastic Scattering of Helium from Copper Single Crystal Surfaces, Surf. Sci. 129, 59 (1983).
  43. J. Lapujoulade, Y. Lejay and N. Papanicolaou, Diffraction of Helium from a Stepped Surface: Cu(117)—An Experimental Study, Surf. Sci. 90 (1979) 133.
  44. G. Witte, J. Braun, A. Lock, and J.P. Toennies, Helium-atom-scattering study of the dispersion curves of step-localized phonons on Cu(211) and Cu(511), Phys. Rev. B 52, 2165 (1995).
  45. S. Miret-Artés, J. P. Toennies, and G. Witte, Surface-scattering study of the interaction potential of He atoms with the step edges of the Cu(211) and Cu(511) vicinal surfaces, Phys. Rev. B 54, 5881 (1996).
  46. A. Lock, Untersuchung der Struktur und Dynamik von gestuften Metall-Einkrill-oberflächen mittels Helium-Atomstreuung (Max-Planck-Institut für Strömungsforschung, Göttingen, Bericht 2/1991) ISSN 0436-1199.
  47. B.J. Hinch, A. Lock, H. H. Madden, J. P. Toennies, and G. Witte, Helium-atom scattering investigation of facetting of the Al stepped (332) surface, Phys. Rev. B 42, 1547 (1990).
  48. C.I. Medel-Ruiz, J.R. Molina-Contreras, C. Frausto-Reyes, J.R. Sevilla-Escoboza, H. Pérez Ladron de Guevara, Influence of the surface roughness on electron-phonon interaction in an intrinsic CdTe single crystal, Physica B 603 (2021) 412785.
  49. P.O. Gartland, S. Berge, B.J. Slagsvold, Photoelectric work function of a copper single-crystal for (100), (110), (111) and (112) faces, Phys. Rev. Lett. 28 (1972) s738.
  50. In Ref. [30], Eq. (151), the exponent γ ≡ -η is used, with the value γ = -1.
  51. J.L. Beeby, Scattering of helium atoms from surfaces, J. Phys. Chem. 4, L359 (1971).
  52. G. Vidali, G. Ihm, H.-Y. Kim, and M. W. Cole, Surf. Sci. Rep. 12, 133-181 (1991).
  53. J. Grepstad, P. Gartland, B. Slagsvold, Anisotropic workfunction of of clean and smooth low-index faces of aluminium, Surf. Sci. 57, 348 (1976). The (111) terrace workfunction is used for the two vicinal surfaces.
  54. G. Witte, Characterization of structure and dynamics of clean and adsorbate covered oxide and metal surfaces, Thesis (Georg-August Universität Göttingen, 1995).
  55. A. Lock, J. P. Toennies, G. Witte, Surface Phonons at Stepped Metal Surfaces, J. El. Spect. Rel. Phen., 54-55, 309 (1999).
  56. J. Lapujoulade, Y. Lejay and G. Armand, The Thermal Attenuation of Coherent Elastic Scattering of Noble Gas From Metal Surfaces ,Surface Sci. 95, 107 (1980).
  57. G. Grimvall, The Electron-Phonon Interaction in Metals, North-Holland, New York, 1981.
  58. J.R. Noonan, H.L. Davis, J. Vac. Sci. Technol. A8, 2671 (1990).
  59. Y. Zhang and D.J. Flannigan, Imaging Nanometer Phonon Softening at Crystal surface Steps with 4D Ultrafast Electron Microscopy, Nano Lett. 21, 7332 (2021).
  60. T.-Y. Lee, S. Sarbach, K. Kuhnke, K. Kern, Growth and surface alloying of Fe on Pt(997), Surf. Sci. 600, 3266 (2006).
  61. Quanxin Hu, Fazhi Yang, Xingyu Wang, Jiajun Li, Wenyao Liu, Lingyuan Kong , Shiliang Li, Lei Yan, Jinpeng Xu , and Hong Ding, Surface superconductivity emerged from disordered surface in undoped BaFe2As2, Phys. Rev. Materials 7, 034801 (2023).
Preprints 87641 g001
Figure 1. The structure of the (115) and (112) (left) and of the (221) and (332) (right) vicinal surfaces of a monoatomic face-centered cubic (fcc) crystal (adapted from [46]). The orthogonal coordinates used in the paper are those of the vicinal surface; the wavevector component normal to steps lying in the terrace plane is here denoted K||.
Figure 1. The structure of the (115) and (112) (left) and of the (221) and (332) (right) vicinal surfaces of a monoatomic face-centered cubic (fcc) crystal (adapted from [46]). The orthogonal coordinates used in the paper are those of the vicinal surface; the wavevector component normal to steps lying in the terrace plane is here denoted K||.
Preprints 87641 g001
Preprints 87641 g002
Figure 2. The specular HAS intensity as a function of temperature, normalized to its T = 0 value, for the copper vicinal surfaces (11α) with α = 3,5,7 (left) and low-index surfaces (right), as measured by Lapujoulade et al. [42,43] with a He-beam incident momentum ki = 6.35 Å-1 (ki = 11 Å-1 for Cu(111)) and the incident angles θi given in the panels. The arrows indicate the roughening transition temperature TR [42]; the slight slope increase for Cu(001) above 460 K can hardly be distinguished from an effect of anharmonicity [42].
Figure 2. The specular HAS intensity as a function of temperature, normalized to its T = 0 value, for the copper vicinal surfaces (11α) with α = 3,5,7 (left) and low-index surfaces (right), as measured by Lapujoulade et al. [42,43] with a He-beam incident momentum ki = 6.35 Å-1 (ki = 11 Å-1 for Cu(111)) and the incident angles θi given in the panels. The arrows indicate the roughening transition temperature TR [42]; the slight slope increase for Cu(001) above 460 K can hardly be distinguished from an effect of anharmonicity [42].
Preprints 87641 g002
Preprints 87641 g003
Figure 3. Specular HAS intensity as a function of the incident wavevector for the copper vicinal surfaces Cu(112) and Cu(115), measured at a surface temperature of 130 K along the directions normal to the steps [ 11 1 ¯ ] and [ 22 5 ¯ ] , respectively, (●, from Miret-Artés et al. [45]). Solid lines show the fits of the HAS data with Equation (6) (reproduced in the upper panel) with two different values of the exponent η.
Figure 3. Specular HAS intensity as a function of the incident wavevector for the copper vicinal surfaces Cu(112) and Cu(115), measured at a surface temperature of 130 K along the directions normal to the steps [ 11 1 ¯ ] and [ 22 5 ¯ ] , respectively, (●, from Miret-Artés et al. [45]). Solid lines show the fits of the HAS data with Equation (6) (reproduced in the upper panel) with two different values of the exponent η.
Preprints 87641 g003
Preprints 87641 g004
Figure 4. (a–c) HAS spectra from the Al(221) surface around the specular peak at three different surface temperatures and the same incident wavevector ki = 6.2 Å-1 as functions of the parallel wavevector change in the direction [ 1 ¯ 1 ¯ 4 ] normal to the steps [54]. Intensities are given in units of the specular intensity at T = 136 K. The arrows in panels (a,b) indicate the positions of possible features from down-hill terrace specular scattering. (d) Temperature dependence of the DW exponent. The linear part of the fit (red full line) gives λHAS = 0.71, whereas the experimental slope in the 550-712 K range gives λHAS = 1.33.
Figure 4. (a–c) HAS spectra from the Al(221) surface around the specular peak at three different surface temperatures and the same incident wavevector ki = 6.2 Å-1 as functions of the parallel wavevector change in the direction [ 1 ¯ 1 ¯ 4 ] normal to the steps [54]. Intensities are given in units of the specular intensity at T = 136 K. The arrows in panels (a,b) indicate the positions of possible features from down-hill terrace specular scattering. (d) Temperature dependence of the DW exponent. The linear part of the fit (red full line) gives λHAS = 0.71, whereas the experimental slope in the 550-712 K range gives λHAS = 1.33.
Preprints 87641 g004
Preprints 87641 g005
Figure 5. HAS spectra from the Al(221) surface at the surface temperature of 135 K for three different incident wavevectors ki as functions of the parallel wavevector change Δ K ∥ in the direction [ 1 ¯ 1 ¯ 4 ] normal to the steps (adapted from [46]). The exponential drop of the specular intensity ( Δ K ∥ = 0) at larger ki (see Equation (6)) is evident at ki = 7.51 Å-1 (top panel). The maximum specular intensity is located at ki,max ≅ 6.5 Å-1. The arrows in the lowest panel indicate the positions of possible features from either up-hill (positive Δ K ∥ ) or down-hill (negative Δ K ∥ ) terrace specular scattering.
Figure 5. HAS spectra from the Al(221) surface at the surface temperature of 135 K for three different incident wavevectors ki as functions of the parallel wavevector change Δ K ∥ in the direction [ 1 ¯ 1 ¯ 4 ] normal to the steps (adapted from [46]). The exponential drop of the specular intensity ( Δ K ∥ = 0) at larger ki (see Equation (6)) is evident at ki = 7.51 Å-1 (top panel). The maximum specular intensity is located at ki,max ≅ 6.5 Å-1. The arrows in the lowest panel indicate the positions of possible features from either up-hill (positive Δ K ∥ ) or down-hill (negative Δ K ∥ ) terrace specular scattering.
Preprints 87641 g005
Preprints 87641 g006
Figure 6. (a) Elastic HAS spectra from Al(332) along the direction [ 1 ¯ 1 ¯ 3 ] normal to the steps in the up-hill orientation, at two different surface temperatures (302 K and 605 K) and a given incident wavevector ki = 6.62 Å-1 as functions of the wavevector change parallel to the terrace (adapted from Lock et al. [46,47]). The insets show the up-hill scattering configuration, either specular with respect to the (332) surface (left) and yielding a small elastic peak, or specular with respect to the (111) terraces (right), and yielding a strong peak. (b) Same as panel (a), but for different incident wavevectors (ki = 10.37 and 6.61 Å-1) at a given surface temperature of 130 K, and as functions of the incident angle. The inset illustrates the up-hill scattering configuration from the vicinal surface (113) with a scattering angle of 91.5º. As in panel (a), the large peaks come from terrace scattering, while the scattering from the (332) surface ( Δ K ∥ = 0) yields very small peaks.
Figure 6. (a) Elastic HAS spectra from Al(332) along the direction [ 1 ¯ 1 ¯ 3 ] normal to the steps in the up-hill orientation, at two different surface temperatures (302 K and 605 K) and a given incident wavevector ki = 6.62 Å-1 as functions of the wavevector change parallel to the terrace (adapted from Lock et al. [46,47]). The insets show the up-hill scattering configuration, either specular with respect to the (332) surface (left) and yielding a small elastic peak, or specular with respect to the (111) terraces (right), and yielding a strong peak. (b) Same as panel (a), but for different incident wavevectors (ki = 10.37 and 6.61 Å-1) at a given surface temperature of 130 K, and as functions of the incident angle. The inset illustrates the up-hill scattering configuration from the vicinal surface (113) with a scattering angle of 91.5º. As in panel (a), the large peaks come from terrace scattering, while the scattering from the (332) surface ( Δ K ∥ = 0) yields very small peaks.
Preprints 87641 g006
Preprints 87641 g007
Figure 7. Elastic specular HAS spectra from the (111) terraces of Al(332) at different temperatures and fixed incident wavevector, showing for increasing temperature the rise of an additional peak attributed to faceting or increasing disorder (adapted from Lock et al. [46,47]).
Figure 7. Elastic specular HAS spectra from the (111) terraces of Al(332) at different temperatures and fixed incident wavevector, showing for increasing temperature the rise of an additional peak attributed to faceting or increasing disorder (adapted from Lock et al. [46,47]).
Preprints 87641 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated