Prerpints.org logo
Preprint
Article

Neural Networks-based Image Denoising Methods

Altmetrics

Downloads

131

Views

53

Comments

0

This version is not peer-reviewed

3D Computer Vision and Smart Building and City, 2nd Volume

Submitted:

12 October 2023

Posted:

13 October 2023

You are already at the latest version

Alerts
Abstract
Image denoising has been one of the important problems in the field of computer vision, and it has a wide range of practical value in many applications, such as medical image processing, image enhancement, and computational photography. Traditional image denoising methods are usually based on hand-designed features and filters, but these methods perform poorly under complex noise and image structures. In recent years, the rapid development of neural network technology has revolutionized the image-denoising task. This paper introduces the knowledge about neural networks and image denoising, explores the impact of neural networks on image denoising, and how is it possible to denoise images by neural networks. It also summarises other image-denoising methods and finally points out the challenges and problems faced by image-denoising at present. Some possible new development directions are proposed to provide new solutions for image-denoising researchers and to promote the development of the field.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction of Image Denoising

Image denoising is a crucial image processing technique that aims to remove or reduce unwanted noise from digital images [1]. Noise in images typically appears as random variations in brightness or color caused by various factors such as electronic interference, sensor limitations, low-light conditions, or compression artifacts [2]. As shown in Figure 1, with a clear image on the left and a noise-contaminated image on the right, the image with noise very much affects the visual perception, so, the image denoising process is needed [3,4]. The goal of image denoising is to enhance the visual quality of an image by preserving important image details while suppressing or eliminating noise.
One common approach to image denoising is the use of mathematical algorithms and filters. These algorithms analyze the pixel values in the image and apply various mathematical operations to estimate and separate the noise from the actual image content. Popular techniques include mean filters [5], median filters [6], and Gaussian filters [7], each with its advantages and trade-offs in terms of noise reduction and preservation of image details.
Another powerful method for image denoising is using machine learning, particularly deep learning models like convolutional neural networks (CNNs) [8,9,10]. These models are trained on large datasets of noisy and clean images to learn complex patterns and relationships between noisy and noise-free images. Once trained, they can effectively remove noise from new, unseen images. This approach often outperforms traditional filtering methods, especially when dealing with complex and non-uniform noise patterns.
Image denoising plays a critical role in various applications, including medical imaging, surveillance, photography, and computer vision. In medical imaging, for example, denoising helps improve the accuracy of diagnoses by providing clearer and more accurate images for analysis [11,12]. In photography, it enhances the quality of images captured in low-light conditions or with less advanced camera equipment. In computer vision, denoising contributes to more reliable object detection, recognition, and tracking by reducing the impact of noise on image-based algorithms.
In summary, image denoising is the process of removing or reducing unwanted noise from digital images to enhance their visual quality and make them more suitable for analysis, interpretation, or presentation. This can be achieved through various mathematical filters and algorithms or by leveraging machine learning techniques like deep neural networks. Image denoising is a fundamental step in many applications where image quality is critical, ranging from medical imaging to photography and computer vision [13].
The article structure of this review is distributed as follows: Section 2 focuses on what a neural network is and the range of applications of neural networks. the structure of each layer of an NN, and also examines the training of NNs as well as the learning methods of NNs, and the role of normalized networks. Section 3 deals with the role of neural networks in image denoising. Section 4 describes other methodological techniques for image denoising. Section 5 examines the application of GAN in image denoising. Section 6 summarises the difficulties of current challenges in image denoising.

2. Neural Networks

2.1. Introduction of Neural Networks

A neural network, often referred to as an artificial neural network (ANN) or simply a neural net, is a computational model inspired by the structure and functioning of the human brain [14]. It is a fundamental component of machine learning and deep learning, used for a wide range of tasks, including pattern recognition, classification, regression, and more [15].
A neural network is composed of interconnected processing units called neurons or artificial neurons [16]. These neurons are organized into layers, typically consisting of an input layer, one or more hidden layers, and an output layer. Each neuron receives input from neurons in the previous layer, processes that input, and produces an output that may be used as input for neurons in the subsequent layer.
Neurons in a neural network apply an activation function to the weighted sum of their inputs. This introduces non-linearity into the model [17], enabling it to learn complex relationships in data. Common activation functions include the sigmoid, ReLU (Rectified Linear Unit), and tanh (hyperbolic tangent) [18].
Neural networks learn from data through a process called training. During training, the network adjusts its internal parameters (weights and biases) to minimize the difference between its predictions and the actual target values in the training dataset. This optimization is typically achieved using gradient-based techniques like backpropagation, which compute the gradient of the error [19] concerning the network's parameters and update them accordingly.
Neural networks with multiple hidden layers are referred to as deep neural networks or deep learning models [20]. These networks have gained significant popularity in recent years due to their ability to automatically learn hierarchical features from data, making them well-suited for tasks like image recognition, natural language processing, and speech recognition.
Neural networks have a wide range of applications across various domains. They are used in image classification (e.g., CNNs for image recognition), natural language processing (e.g., RNNs for text generation), recommendation systems (e.g., collaborative filtering with neural networks), and more. They have also achieved remarkable results in fields like computer vision, speech recognition, and autonomous driving.

2.2. Structure of NNs

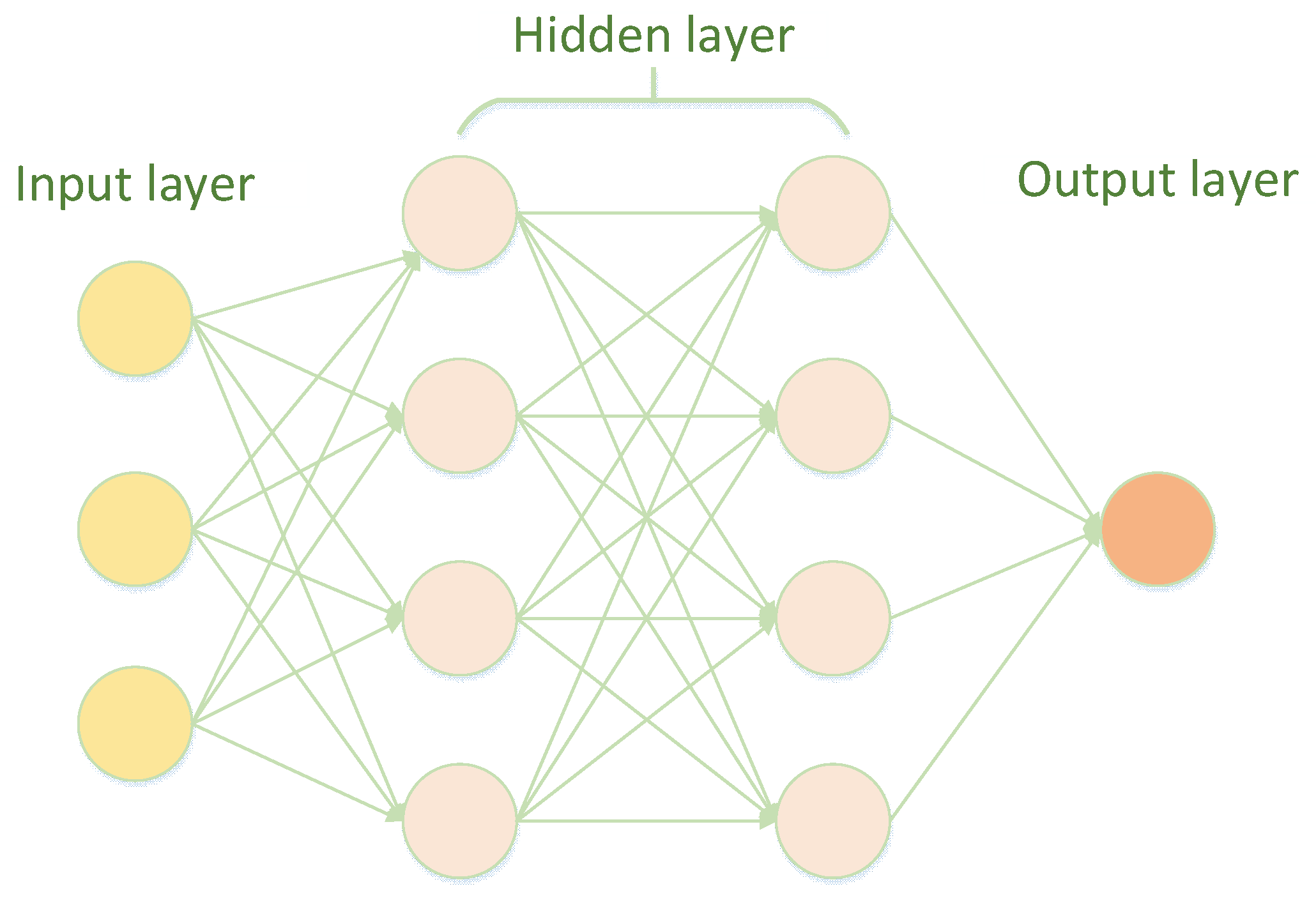
The basic structure of a neural network consists of interconnected processing units called neurons or nodes. These neurons are organized into layers [21], typically divided into three main types: the input layer, hidden layers, and the output layer. The structure of a neural network is shown in Figure 2 below.
The input layer is the first layer of a neural network. Its purpose is to receive raw input data and pass it to the next layer. Each neuron in the input layer represents a feature or dimension of the input data [22]. For example, in an image classification task, each neuron in the input layer may correspond to a pixel's intensity value.
Between the input and output layers, there can be one or more hidden layers. These layers are where the neural network performs its computations and learns complex patterns from the input data [23]. Neurons in the hidden layers take the weighted sum of their inputs, apply an activation function (e.g., ReLU, sigmoid, or tanh), and pass the result as output to the next layer [24]. The depth and size (number of neurons) of the hidden layers are crucial factors in determining the network's capacity to model complex relationships in data.
The output layer is the final layer of the neural network, and it produces the network's predictions or outputs. The number of neurons in the output layer depends on the specific task [25]. For instance, in a binary classification task, there might be one neuron in the output layer representing the probability of belonging to one class and another neuron representing the probability of belonging to the other class. In a multi-class classification task, the number of output neurons matches the number of classes [26].
Neurons in adjacent layers are connected by weighted connections, and each connection has an associated weight. These weights are crucial parameters that the network learns during training. They determine the strength of the influence one neuron has on another [27]. Learning involves adjusting these weights to minimize the difference between the network's predictions and the actual target values in the training data [28].

2.3. Training and Learning Methods of NN

Training neural networks involves optimizing the network's parameters (weights and biases) to make accurate predictions or perform a specific task [29]. Two key components of training neural networks are the loss function and the optimization algorithm [30].
Loss Function: The loss function, also known as the cost function or objective function, is a crucial part of training a neural network. It quantifies the difference between the network's predictions and the actual target values in the training dataset. The goal during training is to minimize this loss function. Common loss functions include mean squared error (MSE) for regression tasks and categorical cross-entropy for classification tasks [31]. Choosing an appropriate loss function depends on the nature of the problem being solved [32].
Backpropagation: Backpropagation is the primary algorithm used to train neural networks. It's a gradient-based optimization technique that calculates the gradients of the loss function concerning the network's parameters. These gradients indicate how the loss would change if the parameters were adjusted slightly. The chain rule of calculus is employed to efficiently compute these gradients layer by layer, starting from the output layer and working backward through the network [33]. Once the gradients are known, an optimization algorithm adjusts the parameters in a way that reduces the loss. The most commonly used optimization algorithms include stochastic gradient descent (SGD), Adam, and RMSprop.
Epochs and Batches: Training a neural network is an iterative process that typically involves processing the entire training dataset multiple times, where each complete pass through the dataset is called an epoch. Training can be further divided into mini-batches, where a subset of the data is used for each weight update iteration. The batch size is a hyperparameter that influences training efficiency and the quality of the learned model. Larger batch sizes can lead to faster convergence but require more memory, while smaller batch sizes may offer better generalization at the cost of slower training.

2.4. Regularization of NNs

Regularization methods in neural networks are techniques used to prevent overfitting, which occurs when a model fits the training data too closely and fails to generalize well to unseen data [34]. Overfitting can result in poor model performance and reduced ability to make accurate predictions on new data [35]. Here are some common regularization methods used in neural networks:
L1 and L2 Regularization (Weight Decay): L1 and L2 regularization, also known as weight decay, are popular techniques to prevent overfitting by adding a penalty term to the loss function [36]. In L1 regularization, the penalty is proportional to the absolute values of the weights, encouraging sparsity in the model [37]. In L2 regularization, the penalty is proportional to the squared values of the weights, which discourages large weight values. These regularization terms help to keep the model's weights smaller, reducing the risk of overfitting [38].
Dropout: Dropout is a regularization technique where a random fraction of neurons in the network is deactivated (set to zero) during each training iteration [39]. This prevents any specific neuron from becoming overly reliant on certain features in the input data, forcing the network to learn more robust representations. Dropout has been particularly effective in deep neural networks and is a widely used regularization method.
Early Stopping: Early stopping is a simple but effective regularization technique. It involves monitoring the model's performance on a validation dataset during training. Training is halted when the validation performance starts deteriorating, indicating that the model is overfitting. Early stopping helps find the point at which the model generalizes well without memorizing the training data [40].
Data Augmentation: Data augmentation is a regularization technique primarily used in computer vision tasks. It involves applying random transformations to the training data, such as cropping, rotation, or flipping, to artificially increase the size of the training dataset. This makes the model more robust to variations in the input data and can help prevent overfitting [41].
Batch Normalization: Batch normalization is a regularization technique that normalizes the inputs of each layer in a neural network by adjusting the mean and variance of the activations within mini-batches of data [42]. This helps stabilize training and can act as a form of regularization by reducing internal covariate shifts. It has been shown to improve the training and generalization of deep neural networks.

3. Neural Networks for Image Denoising

Neural networks have proven to be highly effective for image denoising, a critical task in image processing. Traditional image-denoising methods often rely on handcrafted filters and heuristics, but neural networks offer a data-driven approach that can learn intricate noise patterns and remove noise from images in a more sophisticated manner [43]. Here's how neural networks are used for image denoising:
CNNs are commonly used for image denoising due to their ability to capture local spatial dependencies in images. These networks consist of multiple convolutional layers, which are particularly adept at learning features and patterns in image data. The network architecture can be designed with an encoder-decoder structure, where the encoder extracts relevant features from the noisy image, and the decoder generates a denoised version by upscaling the features [44].
The training process requires a dataset of noisy-clean image pairs. The noisy images serve as input, while the corresponding clean versions are the target outputs. During training, the neural network learns to map noisy images to their corresponding clean counterparts. This process involves minimizing a loss function that measures the difference between the network's predictions and the ground truth clean images. Common loss functions include MSE or perceptual loss, which leverages pre-trained models like VGG to capture perceptual quality.
Regularization methods, such as dropout and L1/L2 regularization, can be applied to prevent overfitting during training [38]. These techniques help ensure that the network generalizes well to new, unseen noisy images. Additionally, data augmentation can be used to increase the diversity of training examples by introducing variations in the noisy data.
Once trained, the neural network can be applied to denoise new or unseen images. The noisy image is passed through the trained model, and the network's predictions provide the denoised image. The neural network's ability to remove noise from images is particularly valuable in applications such as medical imaging, surveillance, and photography, where image quality is critical for analysis and interpretation [45].

4. Other Methods for Image Denoising

Median filtering is a non-linear filtering technique that replaces each pixel's value with the median value of the neighboring pixels [6]. It is effective at removing impulse noise (salt-and-pepper noise) while preserving edges and fine details in the image. Median filtering is simple and computationally efficient but may not be as effective for other types of noise. Median filtering is a process where the pixel values within a certain window are selected and arranged in ascending order, and the median of these values is selected as the new central pixel value. The whole process can be represented in Figure 3, using a window size of 3 × 3 and a median of 4 instead of the original central pixel value of 6 . Median filtering is particularly effective for pretzel noise, as the pixel values of pretzel noise are usually located at the ends of the aligned pixel values [46]. It is therefore easier to remove.
Gaussian filtering is a linear filtering technique that convolves the image with a Gaussian kernel. It is effective at reducing Gaussian noise, which is a type of noise characterized by its statistical properties [47]. Gaussian filtering is widely used for smoothing and denoising, but it may blur fine details in the image. If x is used as the centre in the window, then the weight of a particular point y can be found by equation.
G y = 1 2 π σ 2 e − x − y 2 2 σ 2 ,
where σ is the standard deviation of the pixel values in the window. As the value of σ increases, the filtering effect becomes better. But the less clear the image is.
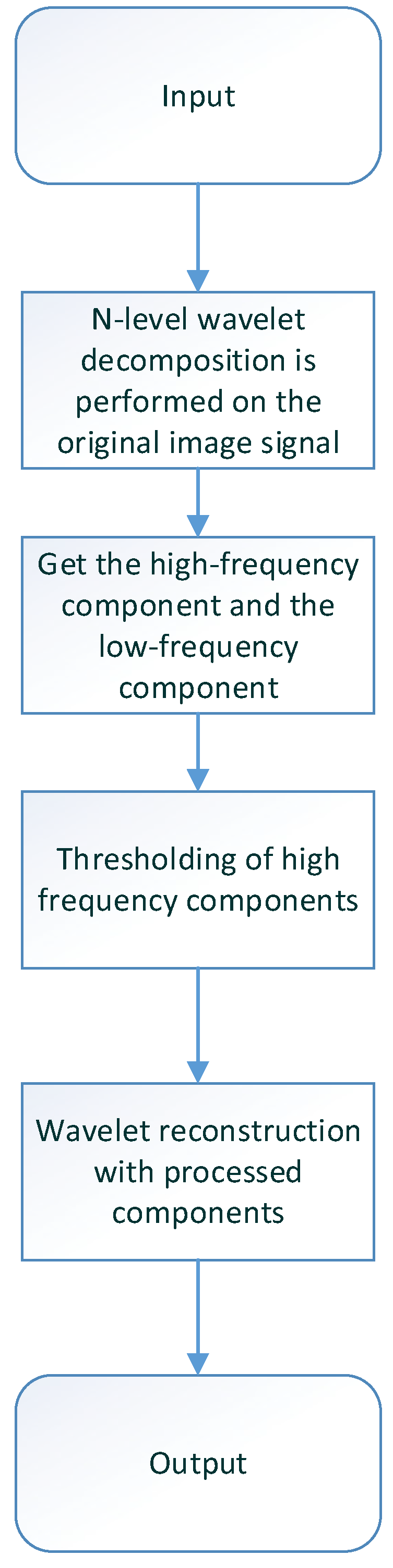
Wavelet denoising is based on wavelet transforms, which decompose the image into different frequency components. By thresholding or shrinking the wavelet coefficients in the high-frequency bands, wavelet denoising can remove noise while preserving image features and edges [48,49]. Wavelet-based methods are suitable for a wide range of noise types. The flowchart of denoising an image using wavelets is shown in Figure 4.
Non-Local Means (NLM): NLM is a powerful denoising technique that exploits the redundancy in natural images. It estimates the noise-free pixel value of each pixel by averaging similar patches from the image, giving more weight to patches that are closer in content to the target patch [50]. NLM is effective at removing various types of noise, including Gaussian and salt-and-pepper noise [51].
Total variation denoising is a regularization-based method that aims to preserve edges while removing noise. It minimizes the total variation (the sum of the absolute differences between neighboring pixel values) of the denoised image [52,53,54]. This method is suitable for images with piecewise smooth structures.
BM3D (Block-Matching and 3D Filtering): BM3D is a state-of-the-art denoising method that operates in two stages [55]. First, it groups similar blocks of pixels in the image and estimates a 3D representation of the image patches. Then, it applies collaborative filtering to remove noise. BM3D is highly effective for denoising natural images and has achieved excellent results in various applications [56].

5. GAN for Image Denoising

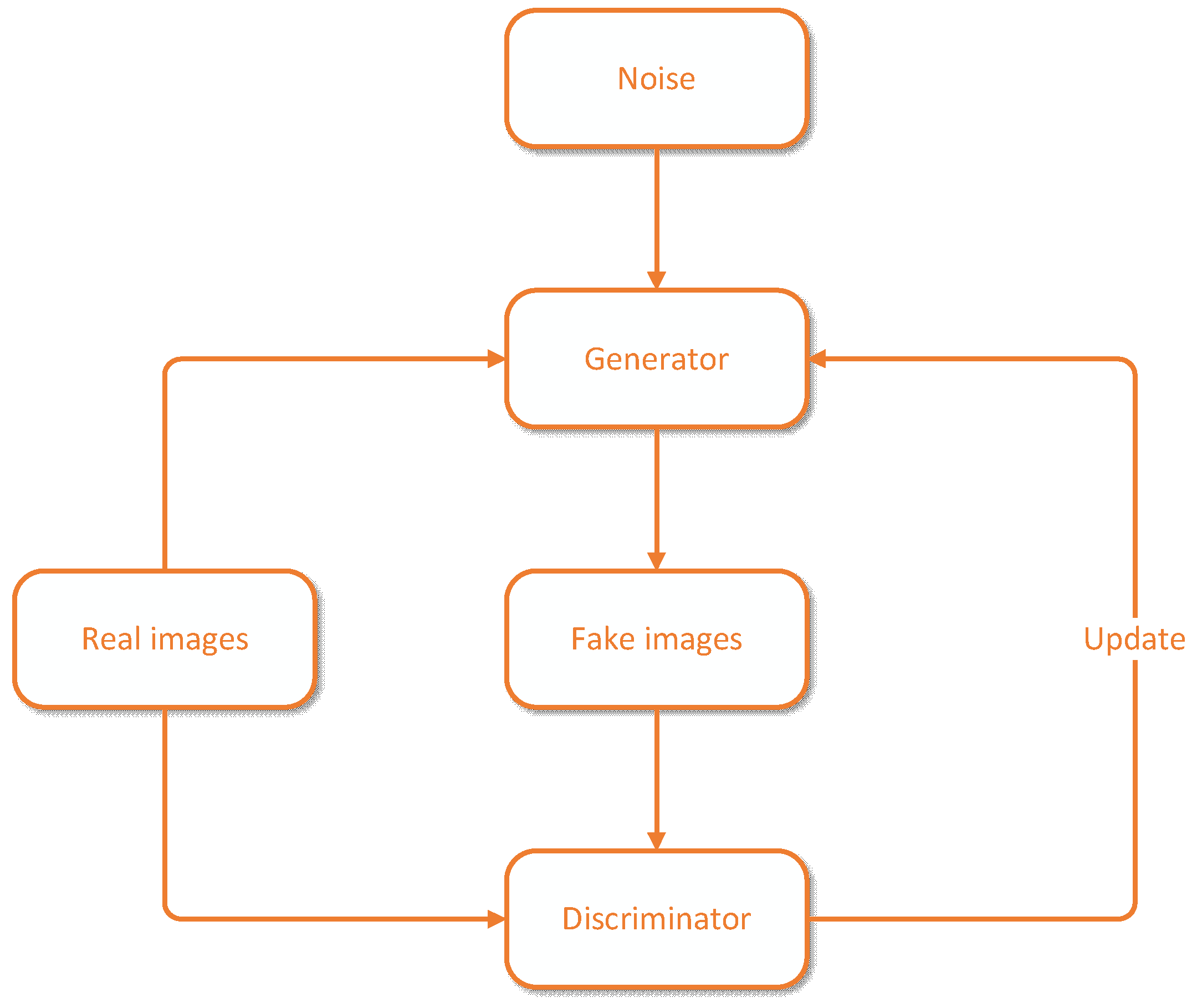
In the context of image denoising, a GAN typically consists of two neural networks: a generator and a discriminator. The generator network takes a noisy image as input and attempts to produce a clean, denoised version of the image as its output [57]. The discriminator network tries to distinguish between real (clean) images and the generated (denoised) images. The GAN network structure is shown in Figure 5.
The training of a denoising GAN involves a competitive process between the generator and discriminator. The generator aims to produce denoised images that are indistinguishable from real clean images, while the discriminator tries to differentiate between real and generated images. The training process seeks to find a balance where the generator produces high-quality denoised images, and the discriminator becomes less effective at telling them apart from clean images [58]. GANs use two distinct loss functions during training:
(i)
Generator Loss: This loss encourages the generator to produce denoised images that are realistic and similar to clean images. It is typically based on a measure of dissimilarity between the generated and clean images.
(ii)
Discriminator Loss: The discriminator loss encourages the discriminator to correctly classify real and generated images. It is often based on binary cross-entropy, aiming to minimize the difference between the discriminator's predictions for real and generated images.
As the GAN training progresses, the generator becomes increasingly proficient at denoising images, while the discriminator becomes less capable of distinguishing between real and generated images [44]. The output of the generator at the end of training is a denoised version of the noisy input image [59].
GAN-based denoising methods can be computationally intensive and require careful tuning of hyperparameters. Furthermore, they may generate denoised images that preserve some degree of noise as they aim to maintain realism [60]. Therefore, the choice of denoising method, whether GAN-based or traditional, should depend on the specific requirements and constraints of the task at hand.

6. Challenges of Image Denoising

Image denoising is a crucial preprocessing step in various applications, but it comes with several challenges: (i) Different types of noise, such as Gaussian noise, salt-and-pepper noise, or speckle noise, can affect images. These noise types have distinct statistical properties and require different denoising approaches. Handling multiple types of noise within a single image or adapting to variable noise levels can be challenging. (ii) Image-denoising algorithms must strike a balance between reducing noise and preserving important image details. Aggressive noise reduction can lead to the loss of fine textures and edges, while overly conservative denoising may not effectively remove noise.
Some advanced denoising techniques, especially those based on deep learning or complex mathematical models, can be computationally intensive. Real-time or resource-constrained applications may struggle with the computational demands of these methods.

Funding

This research did not receive any grants.

Acknowledgment

We thank all the anonymous reviewers for their hard reviewing work.

References

  1. T. A. Soomro, L. Zheng, A. J. Afifi, A. Ali, S. Soomro, M. Yin, et al., "Image Segmentation for MR Brain Tumor Detection Using Machine Learning: A Review," IEEE Reviews in Biomedical Engineering, vol. 16, pp. 70-90, 2023. [CrossRef]
  2. P.-H. Dinh, "Medical image fusion based on enhanced three-layer image decomposition and Chameleon swarm algorithm," Biomedical Signal Processing and Control, vol. 84, p. 104740, 2023. [CrossRef]
  3. M. Genzel, J. Macdonald, and M. März, "Solving Inverse Problems With Deep Neural Networks – Robustness Included?," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 45, pp. 1119-1134, 2023. [CrossRef]
  4. P. Ma, J. Ren, G. Sun, H. Zhao, X. Jia, Y. Yan, et al., "Multiscale Superpixelwise Prophet Model for Noise-Robust Feature Extraction in Hyperspectral Images," IEEE Transactions on Geoscience and Remote Sensing, vol. 61, pp. 1-12, 2023. [CrossRef]
  5. P. Nair and K. N. Chaudhury, "Fast High-Dimensional Bilateral and Nonlocal Means Filtering," IEEE Transactions on Image Processing, vol. 28, pp. 1470-1481, 2019. [CrossRef]
  6. S. A. Villar, S. Torcida, and G. G. Acosta, "Median Filtering: A New Insight," Journal of Mathematical Imaging and Vision, vol. 58, pp. 130-146, 2017.
  7. M. L. Psiaki, "The blind tricyclist problem and a comparative study of nonlinear filters: A challenging benchmark for evaluating nonlinear estimation methods," IEEE Control Systems Magazine, vol. 33, pp. 40-54, 2013. [CrossRef]
  8. K. Zhang, Y. Li, W. Zuo, L. Zhang, L. V. Gool, and R. Timofte, "Plug-and-Play Image Restoration With Deep Denoiser Prior," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 44, pp. 6360-6376, 2022.
  9. F. Olayah, E. M. Senan, I. A. Ahmed, and B. Awaji. (2023). AI Techniques of Dermoscopy Image Analysis for the Early Detection of Skin Lesions Based on Combined CNN Features. Diagnostics 13(7). [CrossRef]
  10. S. R. Nayak, D. R. Nayak, U. Sinha, V. Arora, and R. B. Pachori. (2023). An Efficient Deep Learning Method for Detection of COVID-19 Infection Using Chest X-ray Images. Diagnostics 13(1). [CrossRef]
  11. D. J. Lin, S. S. Walter, and J. Fritz, "Artificial Intelligence–Driven Ultra-Fast Superresolution MRI: 10-Fold Accelerated Musculoskeletal Turbo Spin Echo MRI Within Reach," Investigative Radiology, vol. 58, 2023.
  12. U. S. Kamilov, C. A. Bouman, G. T. Buzzard, and B. Wohlberg, "Plug-and-Play Methods for Integrating Physical and Learned Models in Computational Imaging: Theory, algorithms, and applications," IEEE Signal Processing Magazine, vol. 40, pp. 85-97, 2023.
  13. L. Zhuang, L. Gao, B. Zhang, X. Fu, and J. M. Bioucas-Dias, "Hyperspectral Image Denoising and Anomaly Detection Based on Low-Rank and Sparse Representations," IEEE Transactions on Geoscience and Remote Sensing, vol. 60, pp. 1-17, 2022.
  14. L. V. Jospin, H. Laga, F. Boussaid, W. Buntine, and M. Bennamoun, "Hands-On Bayesian Neural Networks—A Tutorial for Deep Learning Users," IEEE Computational Intelligence Magazine, vol. 17, pp. 29-48, 2022. [CrossRef]
  15. K. Yamazaki, V.-K. Vo-Ho, D. Bulsara, and N. Le. (2022). Spiking Neural Networks and Their Applications: A Review. Brain Sciences 12(7). [CrossRef]
  16. C. Xu, W. Zhang, Z. Liu, and L. Yao, "Delay-induced periodic oscillation for fractional-order neural networks with mixed delays," Neurocomputing, vol. 488, pp. 681-693, 2022. [CrossRef]
  17. Y. Zhang, "Smart detection on abnormal breasts in digital mammography based on contrast-limited adaptive histogram equalization and chaotic adaptive real-coded biogeography-based optimization," Simulation, vol. 92, pp. 873-885, 2016. [CrossRef]
  18. A. Onan, "Bidirectional convolutional recurrent neural network architecture with group-wise enhancement mechanism for text sentiment classification," Journal of King Saud University - Computer and Information Sciences, vol. 34, pp. 2098-2117, 2022. [CrossRef]
  19. Y. Zhang, "Remote-Sensing Image Classification Based on an Improved Probabilistic Neural Network," Sensors, vol. 9, pp. 7516-7539, 2009. [CrossRef]
  20. S. Cuomo, V. S. Di Cola, F. Giampaolo, G. Rozza, M. Raissi, and F. Piccialli, "Scientific Machine Learning Through Physics–Informed Neural Networks: Where we are and What’s Next," Journal of Scientific Computing, vol. 92, p. 88, 2022. [CrossRef]
  21. N. M. U. Din, A. Assad, R. A. Dar, M. Rasool, S. Ul Sabha, T. Majeed, et al., "RiceNet: A deep convolutional neural network approach for classification of rice varieties," Expert Systems with Applications, vol. 235, Article ID: 121214, 2024. [CrossRef]
  22. Q. Shi, X. Tang, T. Yang, R. Liu, and L. Zhang, "Hyperspectral Image Denoising Using a 3-D Attention Denoising Network," IEEE Transactions on Geoscience and Remote Sensing, vol. 59, pp. 10348-10363, 2021. [CrossRef]
  23. Y. D. Zhang, "A novel algorithm for all pairs shortest path problem based on matrix multiplication and pulse coupled neural network," Digital Signal Processing, vol. 21, pp. 517-521, 2011. [CrossRef]
  24. C. Tian, Y. Xu, and W. Zuo, "Image denoising using deep CNN with batch renormalization," Neural Networks, vol. 121, pp. 461-473, 2020. [CrossRef]
  25. S.-H. Wang and M. A. Khan, "WACPN: A Neural Network for Pneumonia Diagnosis," Computer Systems Science and Engineering, vol. 45, pp. 21-34, 2023. [CrossRef]
  26. C. Tian, L. Fei, W. Zheng, Y. Xu, W. Zuo, and C.-W. Lin, "Deep learning on image denoising: An overview," Neural Networks, vol. 131, pp. 251-275, 2020. [CrossRef]
  27. T. Zhong, W. Wang, S. Lu, X. Dong, and B. Yang, "RMCHN: A Residual Modular Cascaded Heterogeneous Network for Noise Suppression in DAS-VSP Records," IEEE Geoscience and Remote Sensing Letters, vol. 20, pp. 1-5, 2023. [CrossRef]
  28. Y. Zhang and J. M. Gorriz, "Modern Forms and New Challenges in Medical Sensors and Body Area Networks," Journal of Sensor and Actuator Networks, vol. 11, p. 79, 2022. [CrossRef]
  29. A.F. Mirza, M. Mansoor, M. Usman, and Q. Ling, "Hybrid Inception-embedded deep neural network ResNet for short and medium-term PV-Wind forecasting," Energy Conversion and Management, vol. 294, Article ID: 117574, 2023. [CrossRef]
  30. M. J. Colbrook, V. Antun, and A. C. Hansen, "The difficulty of computing stable and accurate neural networks: On the barriers of deep learning and Smale’s 18th problem," Proceedings of the National Academy of Sciences, vol. 119, p. e2107151119, 2022. [CrossRef]
  31. A. Saleh Ahmed, W. H. El-Behaidy, and A. A. A. Youssif, "Medical image denoising system based on stacked convolutional autoencoder for enhancing 2-dimensional gel electrophoresis noise reduction," Biomedical Signal Processing and Control, vol. 69, p. 102842, 2021. [CrossRef]
  32. J. Ma, J. Chen, M. Ng, R. Huang, Y. Li, C. Li, et al., "Loss odyssey in medical image segmentation," Medical Image Analysis, vol. 71, p. 102035, 2021. [CrossRef]
  33. C. Wang, M. Li, R. Wang, H. Yu, and S. Wang, "An image denoising method based on BP neural network optimized by improved whale optimization algorithm," EURASIP Journal on Wireless Communications and Networking, vol. 2021, p. 141, 2021. [CrossRef]
  34. S. Wang, "Bionic Artificial Neural Networks in Medical Image Analysis," Biomimetics, vol. 8, p. 211, 2023. [CrossRef]
  35. J. Ojih, A. Rodriguez, J. J. Hu, and M. Hu, "Screening outstanding mechanical properties and low lattice thermal conductivity using global attention graph neural network," Energy and Ai, vol. 14, Article ID: 100286, 2023. [CrossRef]
  36. S. Shin, M. Kwon, S. Kim, and H. So, "Prediction of Equivalence Ratio in Combustion Flame Using Chemiluminescence Emission and Deep Neural Network," International Journal of Energy Research, vol. 2023, Article ID: 3889951, 2023. [CrossRef]
  37. S.-H. Wang and M. A. Khan, "VISPNN: VGG-inspired stochastic pooling neural network," Computers, Materials & Continua, vol. 70, pp. 3081-3097, 2022. [CrossRef]
  38. Y. Ma, B. Wei, P. Feng, P. He, X. Guo, and G. Wang, "Low-Dose CT Image Denoising Using a Generative Adversarial Network With a Hybrid Loss Function for Noise Learning," IEEE Access, vol. 8, pp. 67519-67529, 2020. [CrossRef]
  39. Z. Zhu, "A Survey of Convolutional Neural Network in Breast Cancer," Comput Model Eng Sci, vol. 136, pp. 2127-2172, 2023. [CrossRef]
  40. J. Wang, "Artificial intelligence for visually impaired," Displays, vol. 77, p. 102391, 2023. [CrossRef]
  41. Z. Wang, G. Feng, H. Wu, and X. Zhang, "Data hiding during image processing using capsule networks," Neurocomputing, vol. 537, pp. 49-60, 2023. [CrossRef]
  42. F. Kong, F. Liu, K. Xu, and X. Shi, "Why does batch normalization induce the model vulnerability on adversarial images?," World Wide Web, vol. 26, pp. 1073-1091, 2023. [CrossRef]
  43. K. Wei, Y. Fu, and H. Huang, "3-D Quasi-Recurrent Neural Network for Hyperspectral Image Denoising," IEEE Transactions on Neural Networks and Learning Systems, vol. 32, pp. 363-375, 2021. [CrossRef]
  44. Z. Huang, J. Zhang, Y. Zhang, and H. Shan, "DU-GAN: Generative Adversarial Networks With Dual-Domain U-Net-Based Discriminators for Low-Dose CT Denoising," IEEE Transactions on Instrumentation and Measurement, vol. 71, pp. 1-12, 2022. [CrossRef]
  45. Y. Zhang, Y. Tian, Y. Kong, B. Zhong, and Y. Fu, "Residual Dense Network for Image Restoration," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 43, pp. 2480-2495, 2021.
  46. G. Perrot, S. Domas, and R. Couturier, "How separable median filters can get better results than full 2D versions," The Journal of Supercomputing, vol. 78, pp. 10118-10148, 2022. [CrossRef]
  47. K. Ito and K. Xiong, "Gaussian filters for nonlinear filtering problems," IEEE Transactions on Automatic Control, vol. 45, pp. 910-927, 2000.
  48. S.-F. Wang, W.-K. Yu, and Y.-X. Li, "Multi-Wavelet Residual Dense Convolutional Neural Network for Image Denoising," IEEE Access, vol. 8, pp. 214413-214424, 2020. [CrossRef]
  49. C. Tian, M. Zheng, W. Zuo, B. Zhang, Y. Zhang, and D. Zhang, "Multi-stage image denoising with the wavelet transform," Pattern Recognition, vol. 134, 2023. [CrossRef]
  50. H. Li and C. Y. Suen, "A novel Non-local means image denoising method based on grey theory," Pattern Recognition, vol. 49, pp. 237-248, 2016. [CrossRef]
  51. T. Tasdizen, "Principal components for non-local means image denoising," in 2008 15th IEEE International Conference on Image Processing, 2008, pp. 1728-1731.
  52. C. Yi, Y. Lv, Z. Dang, and H. Xiao. (2016). A Novel Mechanical Fault Diagnosis Scheme Based on the Convex 1-D Second-Order Total Variation Denoising Algorithm. Applied Sciences 6(12). [CrossRef]
  53. L. Condat, "A Direct Algorithm for 1-D Total Variation Denoising," IEEE Signal Processing Letters, vol. 20, pp. 1054-1057, 2013. [CrossRef]
  54. K. Liu, W. Xu, H. Wu, and A. A. Yahya, "Weighted hybrid order total variation model using structure tensor for image denoising," Multimedia Tools and Applications, vol. 82, pp. 927-943, 2023. [CrossRef]
  55. D. Yang and J. Sun, "BM3D-Net: A Convolutional Neural Network for Transform-Domain Collaborative Filtering," IEEE Signal Processing Letters, vol. 25, pp. 55-59, 2018. [CrossRef]
  56. Y. Wen, Z. Guo, W. Yao, D. Yan, and J. Sun, "Hybrid BM3D and PDE filtering for non-parametric single image denoising," Signal Processing, vol. 184, p. 108049, 2021. [CrossRef]
  57. Q. Lyu, D. Xia, Y. Liu, X. Yang, and R. Li, "Pyramidal convolution attention generative adversarial network with data augmentation for image denoising," Soft Computing, vol. 25, pp. 9273-9284, 2021. [CrossRef]
  58. D. M. Vo, D. M. Nguyen, T. P. Le, and S.-W. Lee, "HI-GAN: A hierarchical generative adversarial network for blind denoising of real photographs," Information Sciences, vol. 570, pp. 225-240, 2021. [CrossRef]
  59. C. Saharia, J. Ho, W. Chan, T. Salimans, D. J. Fleet, and M. Norouzi, "Image Super-Resolution via Iterative Refinement," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 45, pp. 4713-4726, 2023.
  60. A. You, J. K. Kim, I. H. Ryu, and T. K. Yoo, "Application of generative adversarial networks (GAN) for ophthalmology image domains: a survey," Eye and Vision, vol. 9, p. 6, 2022. [CrossRef]
Preprints 87612 g001
Figure 1. Comparison of noisy image and original image.
Figure 1. Comparison of noisy image and original image.
Preprints 87612 g001
Preprints 87612 g002
Figure 2. Neural network structure.
Figure 2. Neural network structure.
Preprints 87612 g002
Preprints 87612 g003
Figure 3. Median filter calculation method.
Figure 3. Median filter calculation method.
Preprints 87612 g003
Preprints 87612 g004
Figure 4. Wavelet denoising flowchart.
Figure 4. Wavelet denoising flowchart.
Preprints 87612 g004
Preprints 87612 g005
Figure 5. GAN network structure diagram.
Figure 5. GAN network structure diagram.
Preprints 87612 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated