Membrane Potential: The Mathematical Problem

Preprint

Article

Membrane Potential: The Mathematical Problem

Altmetrics

Downloads

133

Views

Comments

This version is not peer-reviewed

Submitted:

12 October 2023

Posted:

13 October 2023

You are already at the latest version

Alerts

Abstract

The generation and maintenance of membrane potential is considered a fundamental element of the cellular machinery. They are based on elements of physics and chemistry. Mathematics is used to validate the equations and evaluate the results. However, this computation process can lead to a misunderstanding of the phenomena involved or to the masking of crucial events. It is even possible that the calculation no longer corresponds to the hypothesis considered. Membrane theory is no exception to these trivial considerations, which are essential for normal theory validation.

Keywords:

Subject: Biology and Life Sciences - Biophysics

1. Introduction

This is the latest in a series of articles on membrane theory and the problems it raises.

Any diffusion? [1]
The enigma of ion pumps [2]
The Tamagawa experiment [3]
The ignored shape [4]
The mathematical problem

In the first article we demonstrated that simple diffusion or facilitated diffusion cannot be at the origin of membrane potential (MP). In biology and biophysics, the principles used daily in industry and recognized as valid in chemistry and physics are often distorted or incorrectly applied. However, it is a fundamental theory and a basic assumption from which many cellular processes derive. If a basic assumption is wrong, then many of our conclusions may need to be revised.

The second pointed out that diffusion at the microscopic level is also questionable. If theory dictates the presence of ion channels in the membrane, then we must accept that the operating conditions are in line with the underlying theoretical conditions. The electrostatic interactions involved do not allow ion channels to function as hypothesized.

The third article showed that there can be a potential difference in an electrolyte solution even in the absence of diffusion. The adsorption principle is widely accepted in chemistry and helps to overcome certain contradictions in membrane theory.

The fourth paper looks at the intermediate level, the cell, and also at the level directly above it, the tissue. The shape of the cell offers properties that can modify the behavior of our hypotheses and lead us to results that are totally at odds with our theories.

This fifth and final chapter deals with the mathematical problems associated with the use of physical-chemical theories in membrane theory. We will see that some of the equations used do not describe the observed phenomena, in contradiction with all established scientific principles.

2. Material and Discussion

2.1. Bad domain

We’re used to saying that the quantity of ions needed to generate the membrane potential is so small that ion concentrations on either side of the membrane are barely altered. At the same time, the theory of action potential propagation involves tenuous sequential phenomena at the level of small patches of membrane.

Taking into account our initial hypotheses, we can therefore state that the ionic quantities involved in both the membrane potential and the action potential are very small and indirectly measurable. Indeed, the quantity of ions involved is merely the result of a computation based on an electrical equation. This is the well-known equation where the capacitance

C_{m}

is equal to the electrical charge

q_{K}

divided by the voltage difference

E_{m}

across the capacitor. It is then easy to deduce the number

m_{i}

of ions needed to obtain this charge by dividing the total charge by the value of the elementary charge e.

\begin{matrix} C_{m} = \frac{q_{K}}{E_{m}} \end{matrix}

(1)

\begin{matrix} m_{i} = \frac{E_{m} C_{m}}{e} \end{matrix}

(2)

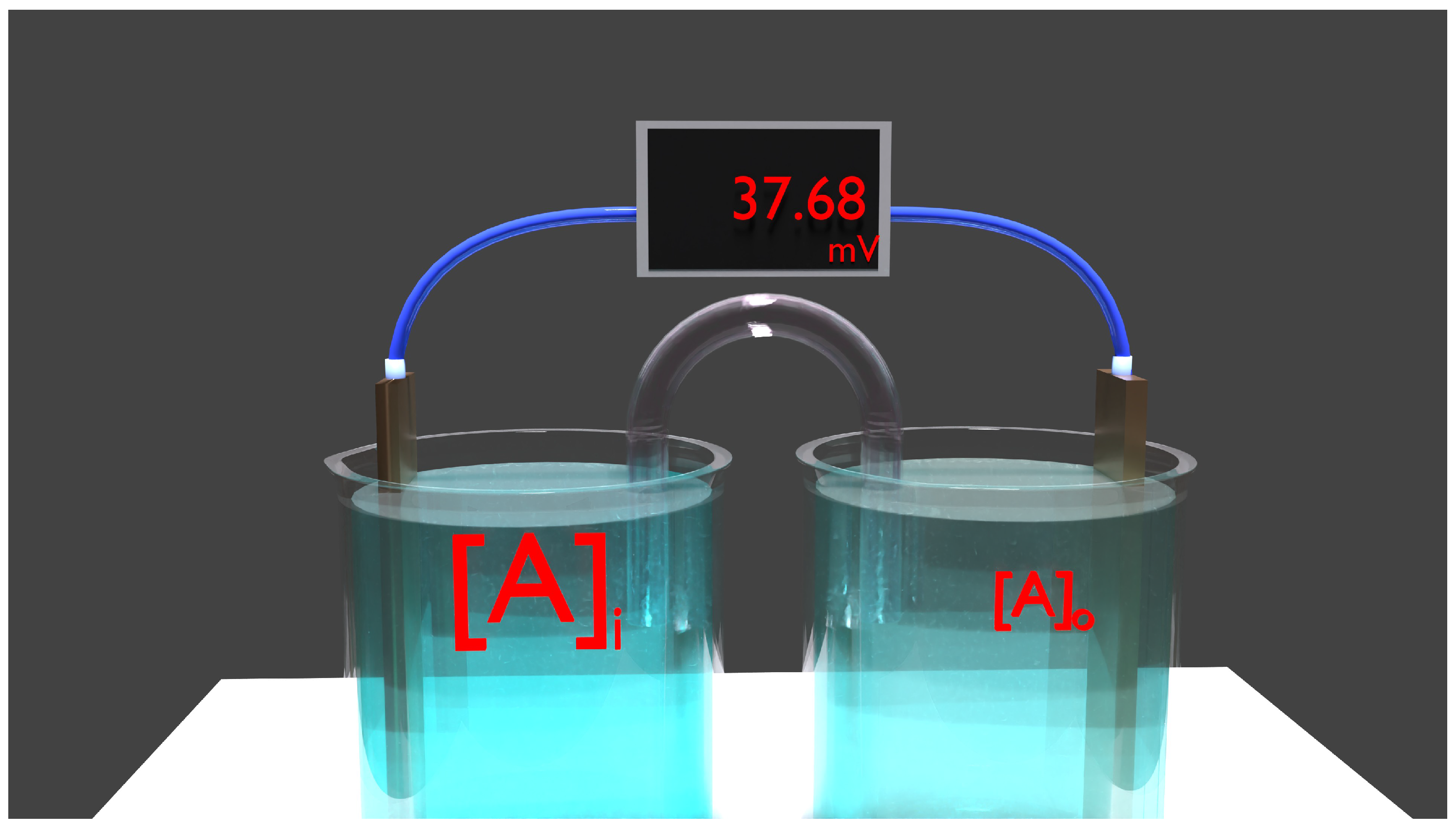
Moreover, most likely, theories insist that only a thin layer close to the membrane is affected by ionic changes. Figure 1 shows how this asymmetrical situation looks, where the ions are not evenly distributed. It is not possible to predict the external concentration of potassium because in one case, for sodium, we are using a volume that is far greater than that in which the potassium ions are concentrated. We obtain a much lower concentration because we measure the concentrations of the various ions via the same volume. This thin layer acts as a virtual electrode for the electrical capacity of the membrane.

It would be wiser to consider the subdomain, or rather the microdomain [5], in which the phenomenon occurs. Of course, in doing so, the variations in concentrations would certainly be greater, but would be much more appropriate to the variations we want to measure. In any case, the calculations we make are absolutely incorrect since they are based on supposedly homogeneous concentrations and cell volumes that are also supposed to be ideal, since they are limited to a sphere or cylinder. These conditions are far removed from the cell shapes we observe and, in our thinking, we are imposing that the surface of the outer membrane be populated by ions, which can only distort our calculations and predictions.

2.2. Inhomogeneity

The Goldman-Hodgkin-Katz equation (GHK eq.) hypothetically gives the value of the membrane potential, and it is clearly specified that this is a value valid only for steady state.

\begin{matrix} E_{m} = \frac{R T}{n F} ln (\frac{P_{K} {[K^{+}]}_{o u t} + P_{N a} {[N a^{+}]}_{o u t} + P_{C l} {[C l^{-}]}_{i n}}{P_{K} {[K^{+}]}_{i n} + P_{N a} {[N a^{+}]}_{i n} + P_{C l} {[C l^{-}]}_{o u t}}) \end{matrix}

(3)

\begin{matrix} E_{m} = \frac{R T}{n F} ln (\frac{{[K^{+}]}_{o u t}}{{[K^{+}]}_{i n}}) \end{matrix}

(4)

It is interesting to note that in the GHK complete equation 3, the permeability coefficient of an ion can be particularly preponderant when its value is large relative to other permeabilities. If we consider that potassium, due to its concentration and ability to act in the reaction, is of great importance, then the equation can be reduced to the second simplified form of the equation 4.

It is all the more important to note that the simplified form completely eliminates the notion of permeability, which we felt was absolutely essential in the original reasoning.

The major criticism that remains, and which has already been mentioned in the previous section, is the inhomogeneity of the ionic distribution as we conceive it in theory. What about the membrane, which is considered ideal, whereas current theory [6] is far from it? If we accept the current scientific position, then we have to admit that there is more than just a discrepancy between hypothesis and reality and that the membrane potential hypothesis needs to be revised.

The GHK equation cannot relate the facts we describe or hypothesize. Any scientific theory and any equation that supports that theory must show or be able to reproduce the observed facts. This is not the case, either in form or in substance.

To arrive at a hypothesis closer to reality, we would certainly have to take into account the volumes where these ions are located, but this would certainly complicate our task, as these volumes are not as ideal as we assume.

2.3. Electronic or non-electronic

The equation 4 is a trivial form of the Nernst equation. It is hard to say what its field of application is and chemists are unequivocal: electrochemistry. It is clear from this that we are talking about electron exchange, chemical reactions, and, in particular, redox. Moreover, these chemical redox reactions can and must be put into equations.

Figure 2. Nernst

The equation 5 shows a device called concentration cells. This, for example, works with copper electrodes and two separate compartments containing a dissolved copper salt (

C u C l^{2}

) but at different concentrations. Our equation obviously applies to this situation and is, fortunately, reminiscent of the situation we encounter in the living cell.

\begin{matrix} E = \frac{R T}{2 F} ln (\frac{{[C u^{2 +}]}_{l e f t}}{{[C u^{2 +}]}_{r i g h t}}) \end{matrix}

(5)

We need a chemical equation for the most concentrated compartment at left:

\begin{matrix} C u_{(l i q)}^{2 +} + 2 e^{-} ⇌ C u_{(s o l)} \end{matrix}

(6)

Very simply, a

C u^{2 +}

ion (which is in liquid form) forms a neutral copper atom in solid metallic form, with the addition of 2 electrons. This formula is reversible. In the other compartment, of course, we have exactly the opposite.

\begin{matrix} C u_{(s o l)} ⇌ C u_{(l i q)}^{2 +} + 2 e^{-} \end{matrix}

(7)

A neutral copper atom in solid metallic form forms a

C u^{2 +}

ion (which is in liquid form) and donates 2 electrons. This formula is reversible. Therefore, there is a transfer of ions from one compartment to another, from the more concentrated to the less concentrated. But this transfer does not take place by diffusion!

The current produced is located in an external electrical circuit where the electrons circulate. This current depends on the volumes involved, the concentrations, and the surface and shape of the electrodes. The reactions we have just described are not balanced, and suggest a negentropic phenomenon. Of course, this is not the case. The reactions continue until the concentrations are equal and the voltage difference is zero. There is irreversibility.

There is a change of state in each compartment: an ion becomes a metal on the left and takes 2 electrons, which are given by the reaction on the right where a metal loses 2 electrons to form an ion, but the left compartment becomes more negative with each reaction and the right compartment more positive, whereas we know that, on the contrary, voltage decreases. Equilibrium is ensured by the saline bridge between the two compartments, which contains a hypertonic saline solution that is supposed to play no part in the redox equations. By migration, i.e. under the influence of the electric field generated by the difference in charges between the compartments, 2 negative charges go to the right, while 2 positive ones go to the left.

If this were not the case, the voltage would rise to extremely dangerous levels as long as the circuit is closed. This never happens. Even when the circuit is open, the voltage does not exceed a few tens of volts: this is the open-circuit voltage. This limitation is due to the progressive increase in the electric field, which prevents any ionic migration and blocks the phenomenon.

The biological version is quite different, proposing a negentropic hypothesis in which diffusion is able to overcome the barrier of the electric field and the same weak force is able to separate matter in the absence of electrodes or electrical circuits. It seems that extraordinary stories are always more pleasing to our eyes and ears, but that does not mean that they can be verified scientific hypotheses. We have a positive multiionic system (sodium-potassium) that works bidirectionally with a constant electric field: this is nonsense. The polyionic hypothesis has never been reproduced in a laboratory, which is also extraordinary. Even Nernst, when he discovered a diffusion potential, was with ions of extreme mobility (

H^{+}

) compared to others [7]. He never demonstrated or hypothesized polyionic diffusion of the same sign but in the opposite direction. Not a single video is capable of showing us a single electric migration of ions of the same charge moving in opposite directions: none and for good reason.

2.4. Lack of dimension

Whereas chemistry is capable of predicting the quantities of products resulting from chemical reactions by establishing balanced equations, biology has taken the habit and ease of ignoring quantities, often limiting itself to concentration values alone.

It is true that chemistry sometimes does the same, but this is because it specifies the values to be taken into account in the initial conditions. A chemical reaction is a matter of numbers, most of which are expressed in volumes we know. Concentrations and volumes are related values. If the volumes are identical, it is often possible to omit them from the equation. Chemistry must be precise in terms of quantities, or we will end up with incomplete reactions that do not meet the expected quality criteria.

In biology, for example, in Figure 3, the Gibbs-Donnan equilibrium is often used to demonstrate that a potential difference can be generated by simple diffusion, and the demonstration is based on very simple equations [8].

At the start, we have the concentrations, on the left:

\begin{matrix} [P r^{-}] = [K^{+}] = x, [C l^{-}] = 0 \end{matrix}

(8)

At the start, we have the concentrations, on the right:

\begin{matrix} [C l^{-}] = [K^{+}] = x, [P r^{-}] = 0 \end{matrix}

(9)

And when equilibrium is reached, on the left we have:

\begin{matrix} [P r^{-}] = x, [K^{+}] = x + y, [C l^{-}] = y \end{matrix}

(10)

And when equilibrium is reached, on the right we get:

\begin{matrix} [P r^{-}] = 0, [K^{+}] = x - y, [C l^{-}] = x - y \end{matrix}

(11)

We have always subtracted or added concentrations to other concentrations, and we’ve never been shocked or questioned. This is what is taught, what must be learned and held to be right. However, we know that concentration is the quantity of a product (

K C l

, for example) per unit liter, not the quantity actually contained in the experiment. It is possible to say that the transfer is equivalent to adding or removing a certain amount of ions from one compartment or the other. This quantity is proportional to the concentration AND to the volume in which this concentration is expressed. This calculation is only valid if the two volumes considered are equal. In biology, this is never the case.

The results are always wrong.

The search for a solution for a Gibbs-Donnan equilibrium is therefore ill-founded, as it is inapplicable. Biology does not respect one of the most important principles of chemistry: rigor. Working with concentrations rather than quantities is a good way of forgetting reality and constructing false hypotheses from false results.

2.5. Inequalities

Chemistry, on the other hand, always seeks to balance reactions. Even in electrochemistry, this same principle is respected, and it is because the speed of reactions can be different between half-cells that there will be a current. This current only flows because an electrical circuit exists and is connected AND closed. If there are inequalities in reactions, they are known, and chemistry always takes them into account.

Biology has no such concerns. The membrane potential is negentropic and unbalanced. It presents a theory that is certainly marvelous, but far removed from current knowledge. The theory is idealized to the point of reductionism, masking the importance of molecular relationships, both chemical and electrostatic.

With the advent of information technology, we are relying more and more on simulation, with software that respects OUR initial conditions but is not always accurate or scientifically sound. Simulation must represent and reproduce observed facts. Today, we imagine facts and try to make them true through simulation. This is not science. We have reached the age where we are able to fabricate facts to make theory follow our inventions.

2.6. Out of range

If we refer to scientific principles, it seems normal and logical to study variations in the membrane potential to find its origins and understand its variations within physiological limits. The principles of homeostasis should lead us to use values within living limits. However, validation of the GHK equation eludes this essential obligation. Although the external concentration of potassium is most often around

5 m M

[9], we use values several dozen times higher to support our hypotheses.

We seem incapable of limiting ourselves to the limits of the living world, even though we know very well that any living being would be totally incapable of withstanding such potassium concentrations. So what is the value of equations that are validated with numbers outside acceptable limits?

Wouldn’t it be desirable and logical to limit ourselves, as we do in most scientific fields, to measured areas, and to understand that outside such a framework we risk losing the substance of the phenomenon and its explanation?

Is it normal that mathematical simulation is limited to copying or reproducing curves obtained experimentally [10]? Does this validate the model? Not really.

It is entirely possible to create mathematical equations that reproduce the curves observed in nature. This graphic expression is not a validation of the theory. If we look at the HH model, the parameters of the curves have simply been computed from two points: the value of the resting potential and the maximum value of the spike. Everything else was found by adjusting the parameters to fit the curve, but without experimental validation. We have never experimentally recorded the values of the sodium or potassium permeability curves. However, their authors had formally warned us: The explanation given is only partial and seeks to explain only part of the phenomenon. The reality is more complex, but it escapes us for the moment.

3. Conclusions

This final article in the series showed that, beyond scientific, morphological, and functional considerations, the theory supporting the generation of membrane potential is also mathematically flawed. The hypotheses proposed do not stand up to simple anatomical examination and are largely incompatible with current theories and observed facts. They cannot simply be computed or simulated, but must be based on observations, as is the rule. Theory must keep pace with the current state of knowledge, rather than remain an unchanging, uncriticizable perpetual dogma [11].

Science can only move forward if its members keep an open mind and accept criticism, which must, of course, be well-argued. Let us hope that such a day will come one day soon.

Author Contributions

Conceptualization, B.D. and H.T. and V.M.; investigation, B.D.; writing—original draft preparation, B.D. and H.T. and V.M; writing—review and editing, B.D. and H.T. and V.M; visualization, B.D.; All authors have read and agreed to the published version of the manuscript.

Funding

This work was not subsidized.

Conflicts of Interest

The authors declare no conflict of interest.

References

Delalande, B.; Tamagawa, H.; Matveev, V. Membrane Potential: Any Diffusion? [CrossRef]
Delalande, B.; Tamagawa, H.; Matveev, V. Membrane Potential: The Enigma of Ion Pumps. [CrossRef]
Delalande, B.; Tamagawa, H.; Matveev, V. Membrane Potential: The Tamagawa Experiment. [CrossRef]
Delalande, B.; Tamagawa, H.; Matveev, V. Membrane Potential: The Ignored Shape 2023. [CrossRef]
Álvarez, R.; Escribá, P.V. Structural Basis of the Interaction of the G Proteins, Gαi1, Gβ1γ2 and Gαi1β1γ2, with Membrane Microdomains and Their Relationship to Cell Localization and Activity. Biomedicines 2023, 11, 557. [Google Scholar] [CrossRef] [PubMed]
Mayor, S.; Bhat, A.; Kusumi, A. A Survey of Models of Cell Membranes: Toward a New Understanding of Membrane Organization. Cold Spring Harbor Perspectives in Biology 2023, 15, a041394. [Google Scholar] [CrossRef] [PubMed]
Maex, R. On the Nernst–Planck equation. Journal of Integrative Neuroscience 2017, 16, 73–91. [Google Scholar] [CrossRef] [PubMed]
Donnan, F.G. Theory of membrane equilibria and membrane potentials in the presence of non-dialysing electrolytes. A contribution to physical-chemical physiology. Journal of Membrane Science 1995, 100, 45–55. [Google Scholar] [CrossRef]
Wallin, B.G. The Relation between External Potassium Concentration, Membrane Potential and Internal Ion Concentrations in Crayfish Axons. Acta Physiologica Scandinavica 1967, 70, 431–448. [Google Scholar] [CrossRef] [PubMed]
Clay. Determining K+ channel activation curves from K+ channel currents often requires the Goldman–Hodgkin–Katz equation. Frontiers in Cellular Neuroscience 2009. [CrossRef]
Drukarch, B.; Wilhelmus, M.M.M. Thinking about the action potential: the nerve signal as a window to the physical principles guiding neuronal excitability. Frontiers in Cellular Neuroscience 2023, 17. [Google Scholar] [CrossRef] [PubMed]

Figure 1. Artistic view of a patch of membrane with a scaled distribution of the ions present inside and outside the cell. The outside is at the top. Sodium = yellow, potassium = purple, and chlorine is green. The quantity of ions represented is proportional to the concentrations usually measured. Potassium is clearly visible on the outer surface of the cell membrane, as described in the steady-state theory of the GHK equation. It is not possible to compute a conduction for external potassium since the volumes are not equal.

Figure 3. Illustration of the Gibbs-Donnan problem and the search for equilibrium. We show a simple, ideal situation and, to simplify our thinking, we visually show equal compartments, which imposes on us a visual solution that would be fair. Unfortunately, in biology, such conditions are difficult, if not impossible, to achieve. It’s difficult to know the volumes involved. Proteins are represented as ribbons. Potassium is shown in violet and chlorine in green.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Membrane Potential: The Mathematical Problem

Abstract

1. Introduction

2. Material and Discussion

2.1. Bad domain

2.2. Inhomogeneity

2.3. Electronic or non-electronic

2.4. Lack of dimension

2.5. Inequalities

2.6. Out of range

3. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe