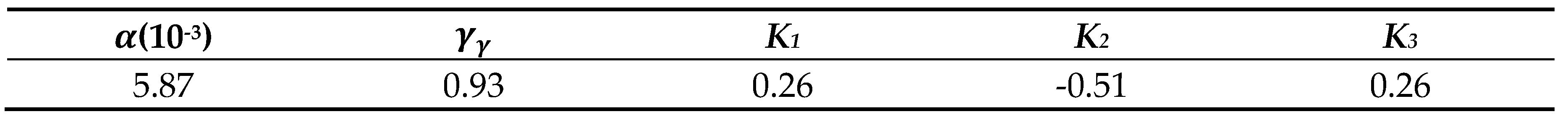Prerpints.org logo
Preprint
Article

Effect of Soil Anisotropy on Ground Motion Characteristics

Altmetrics

Downloads

75

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 October 2023

Posted:

13 October 2023

You are already at the latest version

Alerts
Abstract
Soil transverse isotropy results in different stiffness characteristics in the horizontal and vertical directions. However, the effect is usually neglected in the seismic motion analysis. In this study, an equivalent linear anisotropic soil model was established based on the finite element method and investigated the impact of anisotropic parameters on ground motion at the site under various seismic wave inputs. It is found that the anisotropic parameters have a more significant effect for the seismic waves with the dominant frequency closer to the fundamental frequency of the site. As an example, the soil dynamic parameters in Shanghai Yangshan Port were calibrated by a series of bending elements, resonance columns, and cyclic triaxial tests. The influences of anisotropy on the peak ground acceleration (PGA) and response spectrum are studied for Yangshan Port. Addi-tionally, the standard design response spectra considering the soil anisotropy were provided. A comparison reveals that the existing isotropic design response spectrum may lead to dangerous seismic design for the structures at Yangshan port.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

To improve the seismic design of structures, it is necessary to conduct site-specific seismic motion analysis to understand the characteristics of ground motion at the site. Earthquakes have resulted in significant economic losses and casualties. Earthquakes have the potential to inflict significant destruction upon various types of structures, encompassing inland buildings [1], hydraulic structures [2], and subterranean constructions [3]. Numerous scholars have extensively researched the seismic resilience of architectural structures [4,5,6,7]. The analysis of structures for seismic resistance utilizes a range of methodologies, encompassing response spectrum analysis, the base shear method, and time history analysis. The response spectrum method is extensively utilized as the predominant seismic analysis approach in engineering practice. The response spectrum is obtained by calibrating the ground motion characteristics at the specific site. Consequently, numerous scholars have researched the seismic design of structures based on the seismic motion characteristics at the site [7,8,9].
Soil dynamic constitutive models can be categorized into total stress models and effective stress models, considering the aspects of stress transmission and inter-particle contact. The effective stress model offers superior capability in addressing the issue of seismic liquefaction [10,11,12]. Regarding the issue of seismic ground motion response, researchers commonly employ the total stress model for analysis. The total stress models include elastic-plastic model [13,14,15,16,17,18,19], nonlinear model [20,21,22] and equivalent linear model [23]. Traditional elastoplastic models such as the Mohr-Coulomb model [24] and the Drucker-Prager model [25], can be integrated with boundary interface theory [15,16,17], kinematic hardening theory[13,14], and nested yield surface theory [18,19] to account for the effects of cyclic loading. Although elastoplastic model theory effectively describes the hysteresis characteristics and nonlinearity of soils, its computational complexity and significant workload make it inconvenient for engineering applications. Researchers employ nonlinear models [21,22] based on the Masing criteria to depict the nonlinearity and hysteresis characteristics of soils. While these nonlinear models simplify the workload associated with elastoplastic models, they still entail a certain level of complexity. The linear model offers the advantages of low workload and low complexity, allowing for the consideration of soil nonlinearity and hysteresis characteristics through the application of an equivalent concept. Hence, the most widely utilized approach at present is the equivalent linear model, which has evolved from linear models. Schnabel [18] initially pioneered the development of the frequency-domain equivalent linear model within the SHAKE program. Idriss et al. [26] modified the expression of damping in the SHAKE program and developed the SHAKE91 program. With the development of commercial software, the SHAKE and SHAKE91 programs have been integrated into software such as EERA and DEEPSOIL. The SAHKE program demonstrates limited proficiency in effectively addressing anisotropic challenges.
Soil anisotropy has aroused great interest in recent years. Zhang et al. [27,28] and Teng [29] investigated the impact of soil anisotropy on excavation-induced effects in excavations. Wei et al. [30], Soe et al. [31], and Zhang et al. [32] investigated the impact of soil anisotropy on tunnel design and construction. Peric et al. [33], and Ai et al. [34,35] investigated the impact of anisotropy on the design of pile foundations. It has been found that there is anisotropy in the soil under small strain conditions. Bentil [36] has delved into the anisotropy of the small-strain shear modulus by conducting bending element experiments. The consideration of soil anisotropy in seismic response analysis of soil layers has been scarce among scholars, primarily due to the complexities involved in studying anisotropy, seismic loads, and their associated intricacies. Considering the lack of relevant researches, and to maintain the coherence and rigor of scientific inquiry, this study investigates the impact of anisotropy on the seismic response of the site using a finite element method with an anisotropic time-domain equivalent linear model.

2. Soil dynamic characteristics

2.1. Linear viscoelastic model

The viscoelastic Kelvin model (a spring connected in parallel with a sticky pot) is used to reflect the hysteresis of the soil under cyclic loading. The stress-strain relationship is described by Equation (1):
τ = G γ + η G γ ˙
where G is the shear modulus; τ is the shear stress; γ is the shear strain; η G is the shear viscosity coefficient, as given in Equation (2):
η G = 2 G D ω
where D is the damping ratio; ω is the circular frequency.

2.2. Modulus and damping models

The key to the effective linearization method is to determine the relationship between the shear modulus ratio and the damping ratio with the shear strain. Hyperbolic models are widely used to describe nonlinear soil behavior under cyclic loading, such as the Pyke model and the Stokoe model [37]. In this study, the improved Stokoe mode is selected to fit the relationship between the shear modulus ratio and shear strain, as given in Equation (3):
G n o r m = G G max = 1 1 + r / r r α
where G n o r m is the normalized shear modulus, r r is the reference strain; α is the fitting parameter; the definition of r r is different from the Harden-Drnevich model ( r r = τ m a x / G m a x ).
Zhang et al’s. [38] formula is adopted to describe the relationship between D and G n o r m as follow:
D = K 1 G n o r m 2 + K 2 G n o r m + K 3
where K 1 、 K 2 、 K 3 are the model fitting parameters.

2.3. Effects of anisotropy

The notation for an anisotropic material used herein is: the y -axis (the vertical direction) represents the direction of the anisotropy, and the x , z -plane is the plane of isotropy. The stress-strain increment equation for an anisotropic material can be written as follows (5) [39].
δ ε x δ ε y δ ε z δ γ x y δ γ y z δ γ z x = 1 E h - v v h E v - v h h E h 0 0 0 - v h v E h 1 E v - v h v E h 0 0 0 - v h h E h - v v h E v 1 E h 0 0 0 0 0 0 1 G h v 0 0 0 0 0 0 1 G v h 0 0 0 0 0 0 1 G h h δ σ x δ σ y δ σ z δ σ x y δ σ y z δ σ z x
where E v and E h Young's moduli in the vertical and horizontal directions, respectively; V h h and V v h Poisson's ratios for horizontal strains from a horizontal and vertical strain, respectively; V h v Poisson's ratio for vertical strains from a horizontal strain; G v h and G h v shear moduli in the vertical plane; and G h h shear modulus in the horizontal plane.
The anisotropy ratios A R G and A R E for the shear modulus and Young's modulus are respectively defined as:
A R G = G h h G v h
A R E = E h E v
Under the undrained condition, these Poisson's ratios [40] needs to satisfy the additional relationships ( v v h = 0.5 , v h h + v h v = 1 ). Therefore, one can further get the following equations [40]:
v h h = 1 − v h v = 1 − A R E ⋅ v v h
v h v = E h E v ⋅ v v h = A R E ⋅ v v h
G h h = A R E ⋅ E v 2 ( 2 − A R E ⋅ v v h )
G v h = G h v = 1 A R G A R E ⋅ E v 2 ( 2 − A R E ⋅ v v h )

3. Simulation of time-domain equivalent linear model for anisotropic soil layers

3.1. Input Ground Motion

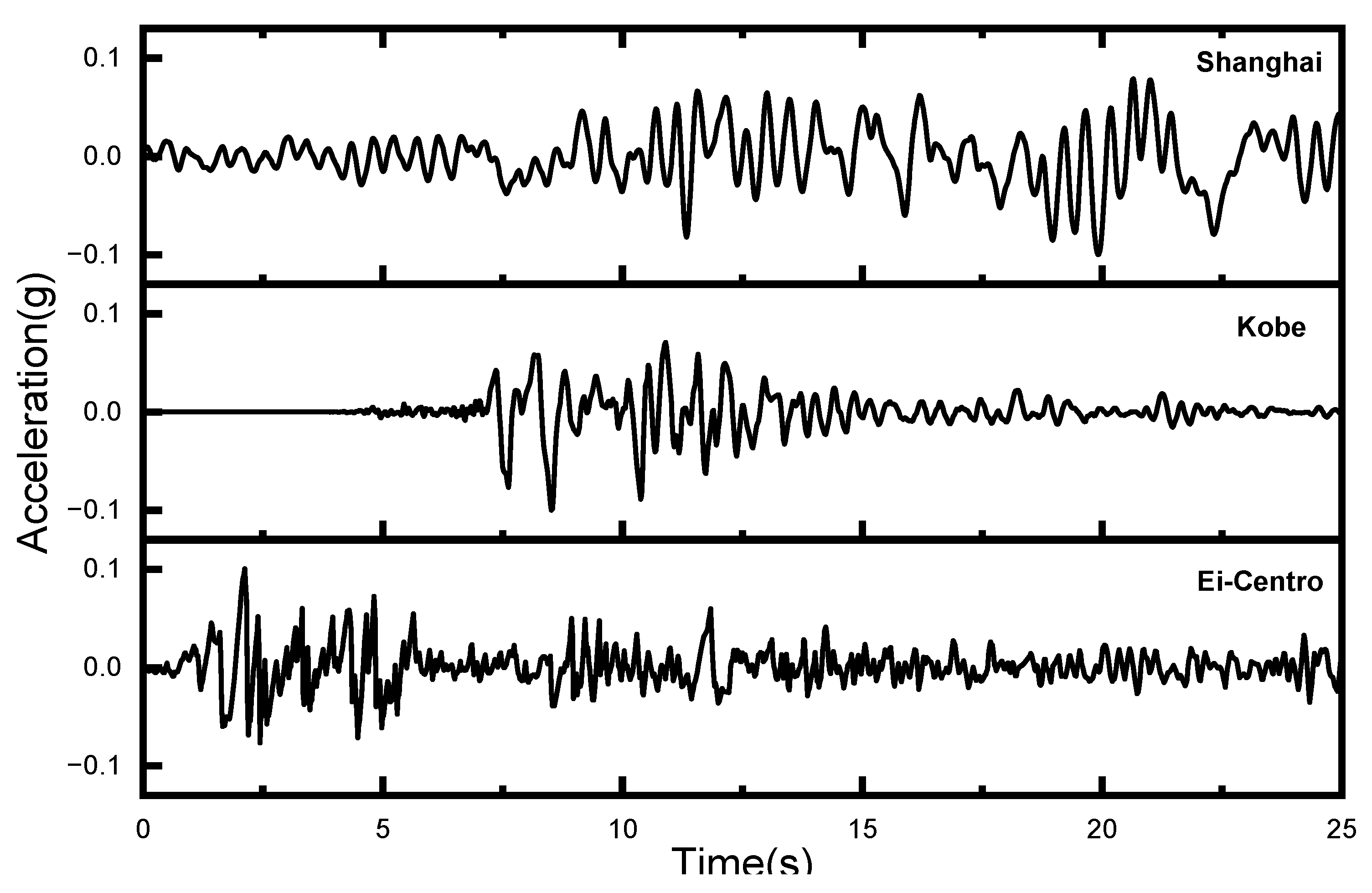
In the Eurocode 8 [41], sites are classified according to the average shear wave velocity in upper 30m thick soil profile. Therefore, the soil layer thickness is selected as 30m. Also, three seismic waves are chosen: Ei-Centro Wave, Shanghai Wave, and Kobe Wave. The amplitudes of these seismic waves were adjusted to have a peak acceleration of 0.1g. Figure 1 illustrates the three seismic waves.

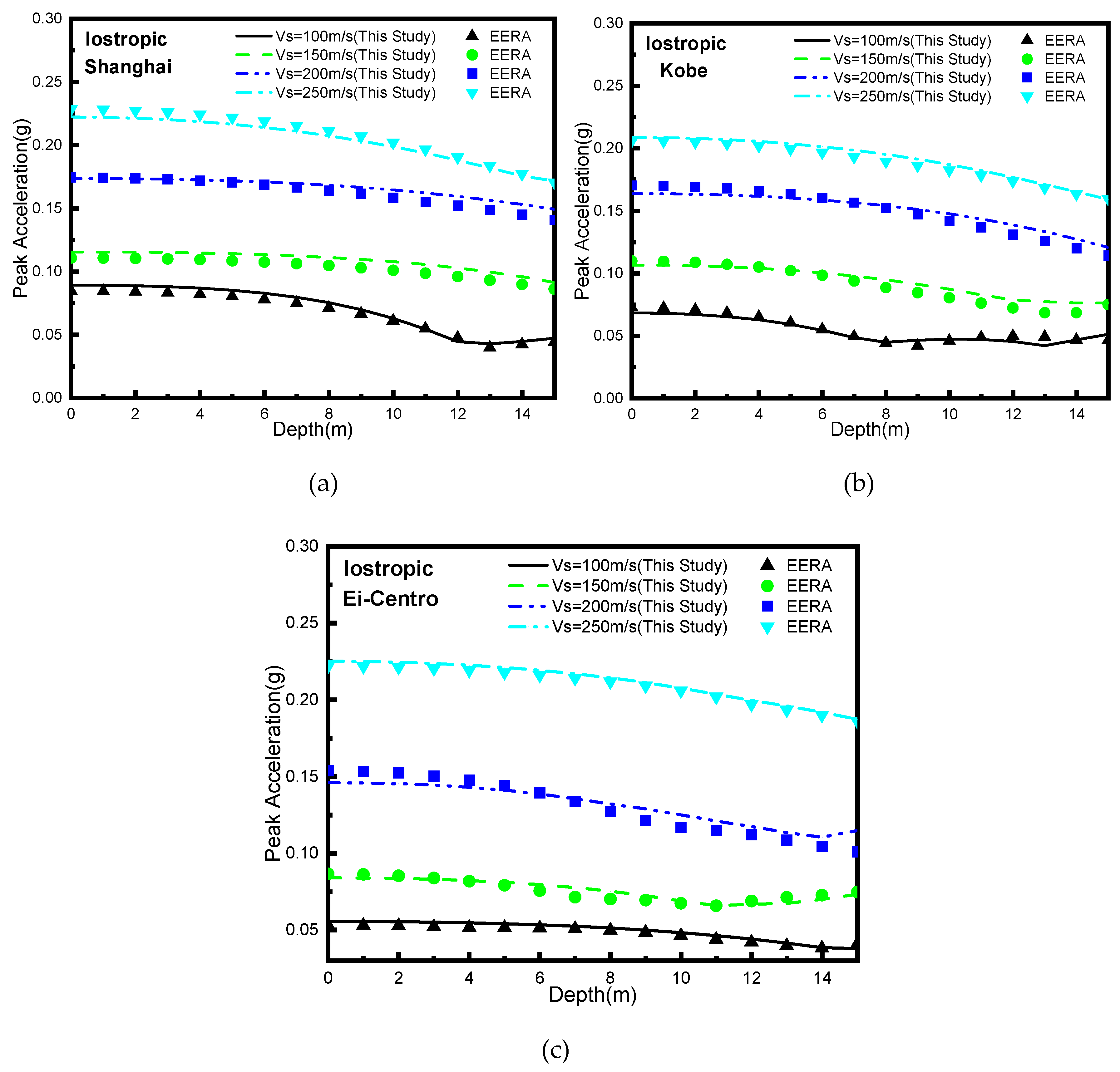
3.2. Isotropic soil layer

This subsection is used to verify the validity of the established finite element method with an anisotropic time-domain equivalent linear model in the isotropic case studies. The shear modulus model chosen here is the Seed-Idriss mode [42], and the damping curve model used is the Idriss mode [26]. Table 1 presents the model parameters. The properties of the soil layers are shown in Table 2.
Figure 2 illustrates the comparison of the peak ground acceleration (PGA) with depth, considering three seismic records, namely Ei-Centro Wave, Shanghai Wave, and Kobe Wave, along with four soil conditions. They exhibit good agreements with the results obtained from the classical seismic analysis code EERA.

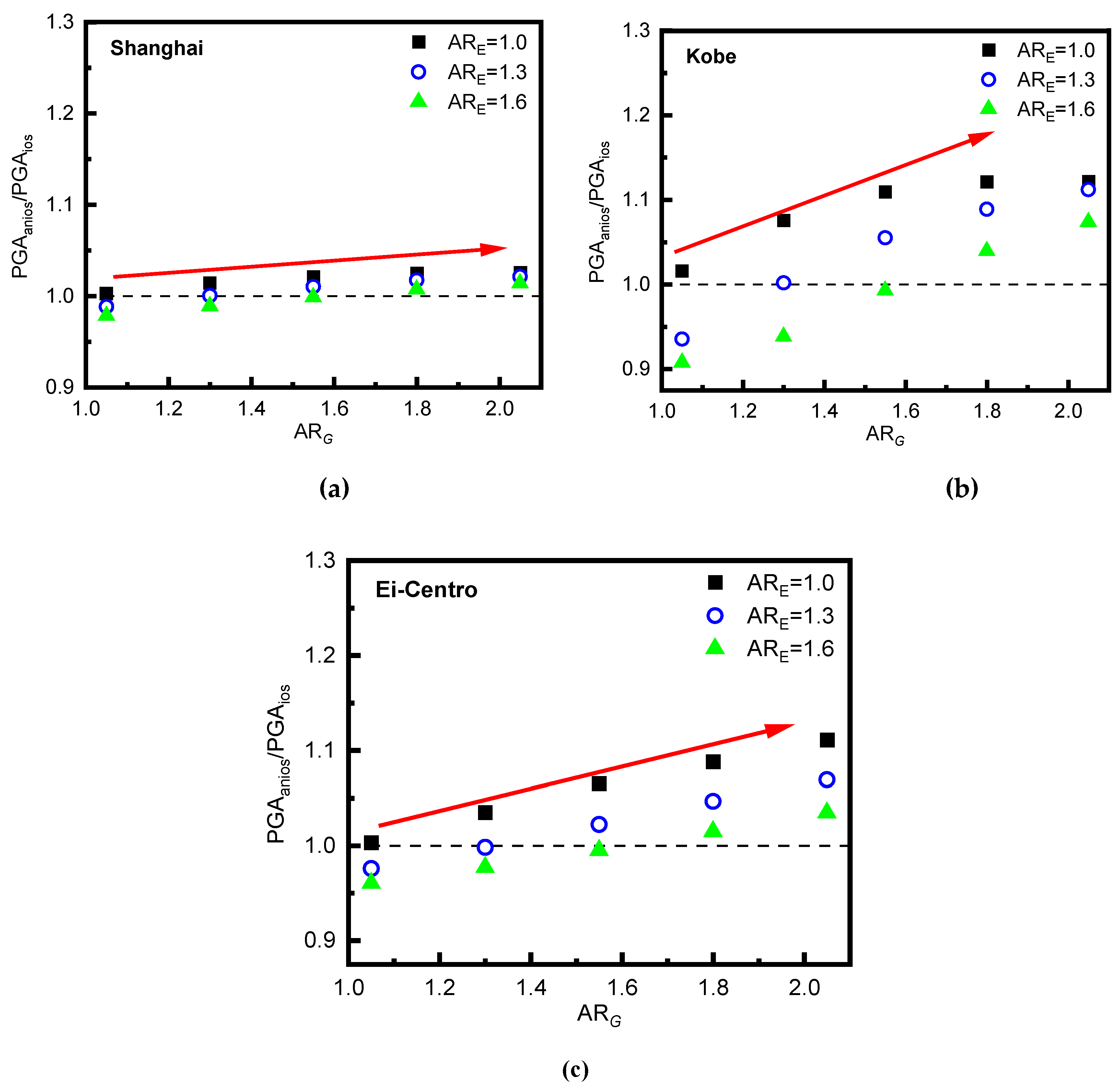
3.3. The Influence of Anisotropic Parameters

It should be noted that this study assumes a consistent relationship between G v h − γ and G h h − γ . Different anisotropic parameter ( A R E =1.00, 1.30, 1.60; A R G =1.05, 1.30, 1.55, 1.80, 2.05) were selected for a 30-meter-thick layer of soft soil with a shear wave velocity of 150m/s. Detailed parameters are listed in Table 3.
P G A a n i o s / P G A i o s is the ratio between the peak ground acceleration obtained at an anisotropic site and that obtained at an isotropic site. Figure 3 shows that, with A R E increasing, P G A a n i o s / P G A i o s gradually decreases. Conversely, as A R G increases, PGA has an obvious increase. Especially when inputting Kobe wave, the PGA of anisotropic conditions exceeds that of isotropic conditions up to 14% with A R G increasing. Consequently, considering soil anisotropy is essential in analyzing site conditions for seismic response.
To assess the impact of anisotropy on the seismic response, the dominant frequency of the seismic waves and the fundamental frequency of the site are further discussed as listed in Table 4, where the fundamental frequency of the site is calculated using Equation (12) [43]:
f g = 1 T g = V S i / 4 ∑ i = 1 n H i
where the symbol " f g " represents the fundamental frequency of the site; " T g " refers to the site's characteristic period; the variable " H i " denotes the thickness of individual soil layers; whereas " V S i " represents the wave velocity specific to each respective soil layer.
As shown in Figure 3, the Ei-Centro and Kobe waves have significant influences on the P G A a n i o s / P G A i o s , while Shanghai wave has a relatively slight effect. From Table 4, compared with the dominant frequency of the Shanghai wave, those of the Kobe wave and Ei-Centro waves are closer to the fundamental frequency of the site. The waves with the dominant frequencies closer to the fundamental frequencies of sites may result in more significant effect of anisotropy. Therefore, detailed investigations on the effects of the soil anisotropy on the seismic response of Shanghai Yangshan Port site are conducted as an example.

4. Seismic response of Shanghai Yangshan Port

4.1. Input seismic wave

The seismic characteristics of Yangshan Port are examined in this study through the analysis of artificial seismic wave data from Shanghai. According to the site classification method specified in the "Code for Seismic Design of Buildings" (GB 50011-2010) [44], the Yangshan Port area belongs to the fourth category of site. Based on the linear elastic soil layer, the ground acceleration time history is inverted to bedrock to obtain the bedrock acceleration time history [45].

4.2. Calculation model and parameters of soil layer

Most of the topsoil in Yangshan port is soft clay, and there is sand soil in the lower layer. Through the geological investigation, the site of Yangshan Port consists of four typical soil layers: clay layer, silty clay layer, muddy silty clay, and sand soil layer. According to Hou [46], the A R E values for this area range from 1.6 to 2.40. Li [47] reported A R G values ranging from 1.08 to 1.39 for Shanghai soil, while Ng [48] stated the values were between 1.07 and 1.38. Considering the earlier discussion on the suppression effect of A R E and the promotion effect of A R G on PGA, an A R E value of 1.6 and an A R G value of 1.4 were chosen to model the unfavorable conditions. Detailed borehole data for the soil layers are provided in Table 5.
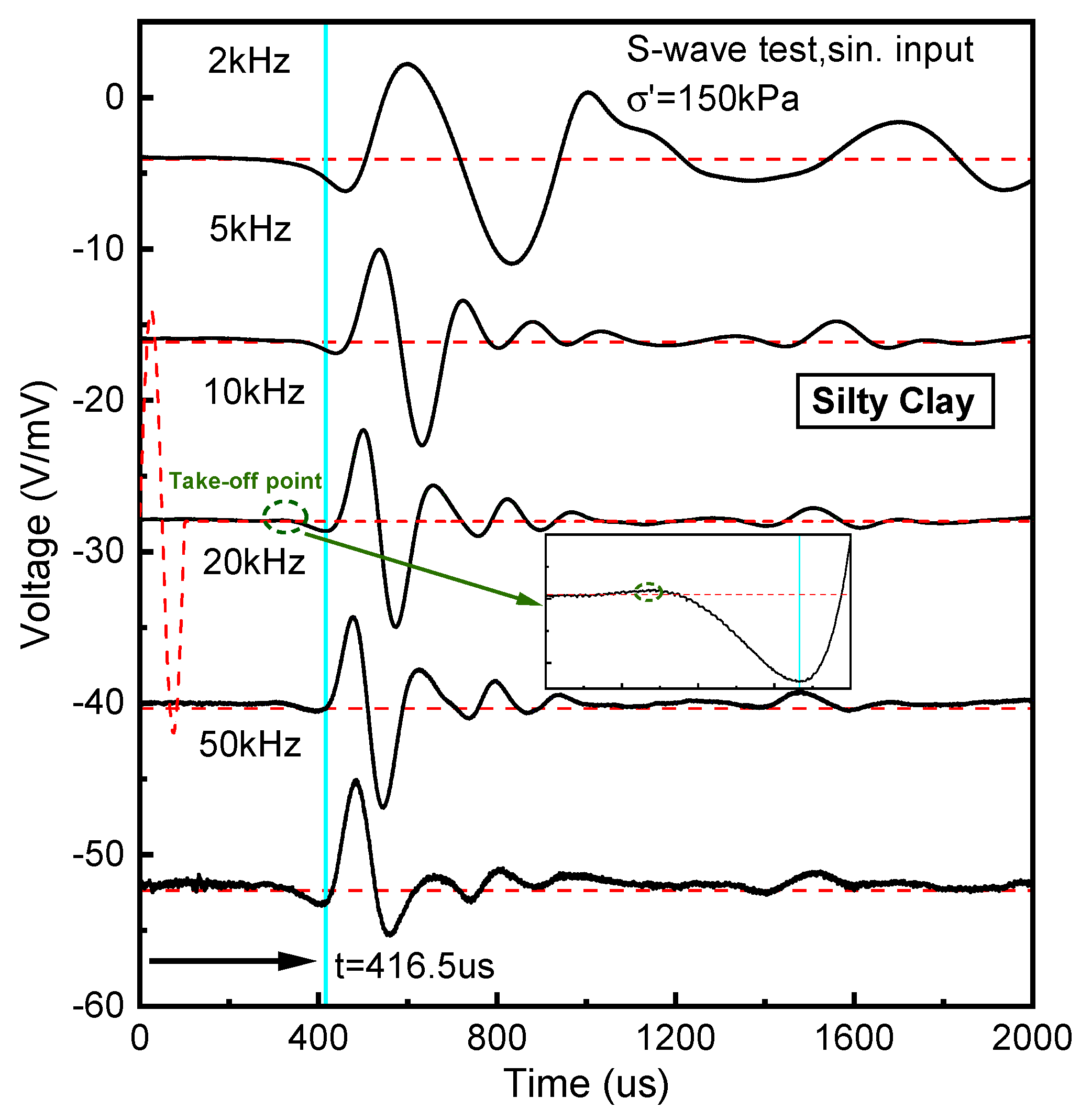
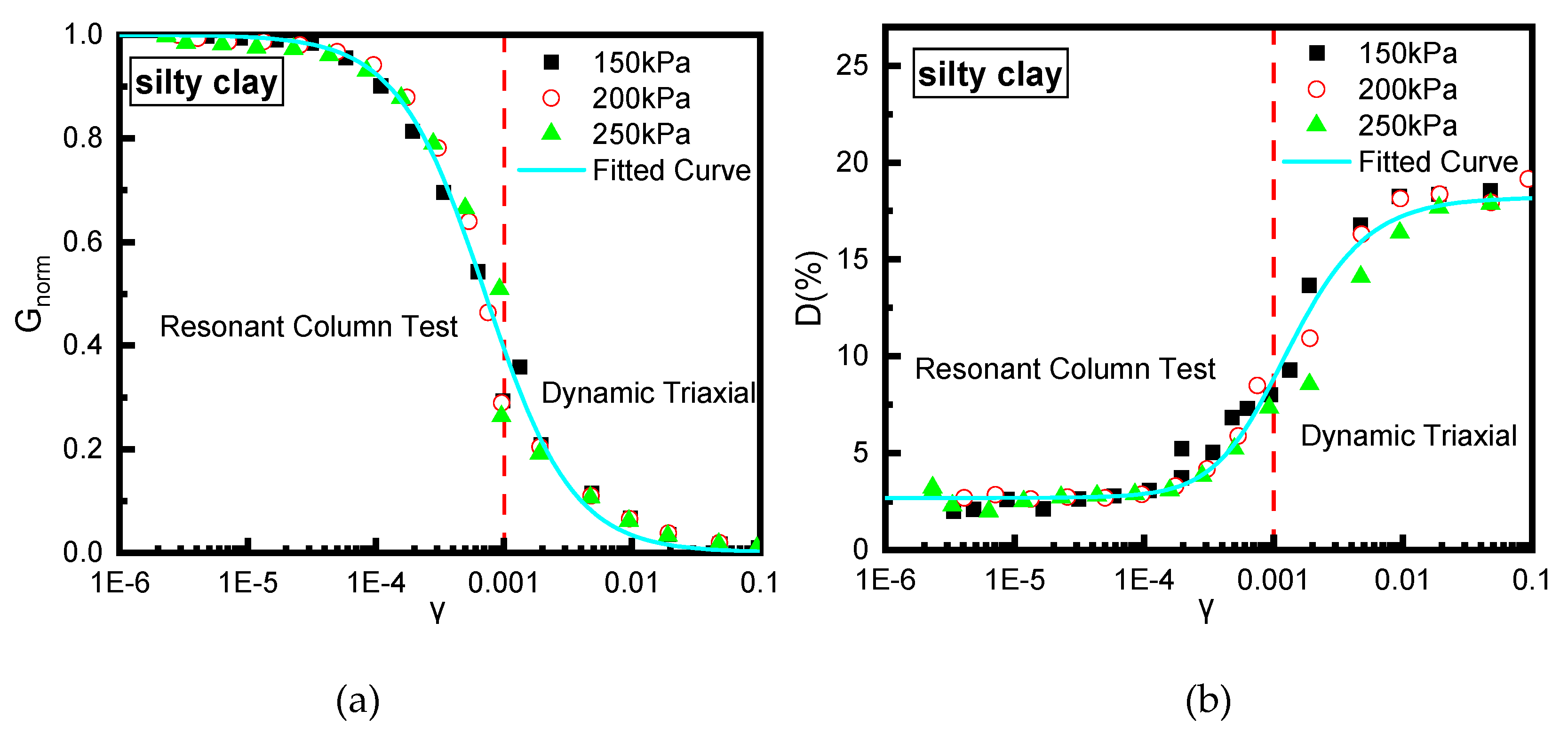
Resonance column and cyclic triaxial tests were conducted to obtain G n o r m − γ and D − γ curves for clay, silty clay layer and muddy silty clay. The design confining pressures are 150 kPa, 200 kPa, and 250 kPa. The experimental results pertaining to silty clay are specifically analyzed in this study. Figure 4 illustrates the S-wave output signals of the bending element in the silty clay specimen subjected to a confining pressure of 150 kPa across different input frequencies. Furthermore, the G 0 value derived from the bending element tests is approximately 1.1 to 1.2 times greater than the results obtained from the resonant column tests, which aligns with the outcomes reported by Yang et al. [49] and Gu et al. [50,51]. The reason behind this is that the results of the bending element tests specifically relate to the localized stiffness of the shear wave propagation path, while the resonant column offer insights into the overall stiffness characteristics of the specimens [49,50,51]. This confirms the accuracy of the resonant column test. Simultaneously, Yang et al. [49], Gu et al. [50,51], and Youn et al. [52] propose to determine G 0 based on the resonant column test.
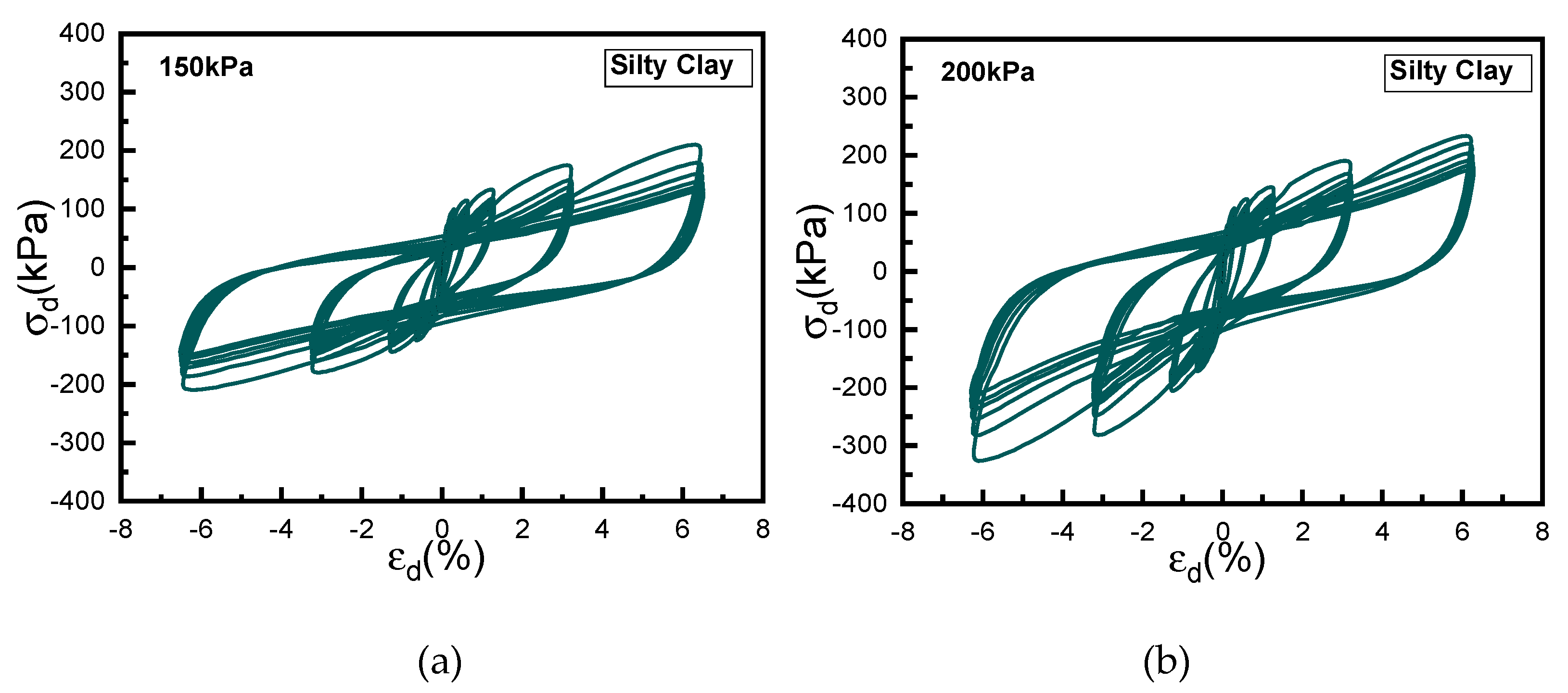
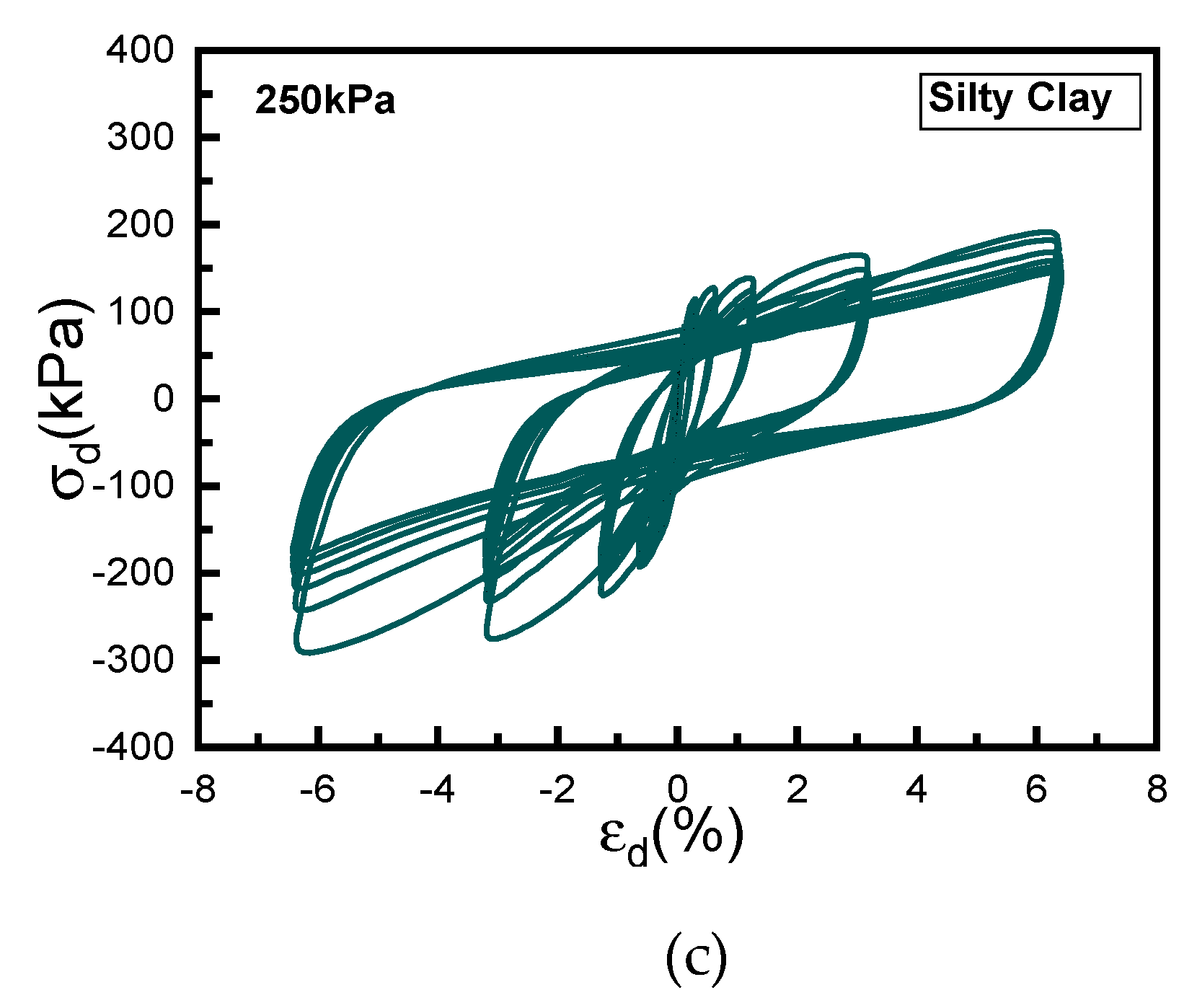
The cyclic triaxial experiments were performed employing strain control. To mitigate the influence of cyclic loading on subsequent tests, the number of cycles for each loading stage was limited to six. Figure 5 depicts the outcomes of the cyclic triaxial tests conducted on the silty clay. The modulus degrades as the strain increases, while it amplifies with the elevated confining pressure. Through fitting analysis, we obtained the G n o r m − γ and D − γ curves for clay in the Yangshan Port site. Figure 6 depicts the curve of best fit for the silty clay specimen. For the other soil layers, the model parameters calibrated from the resonance column and the cyclic triaxial tests are also provided in Table 6.

4.3. Results

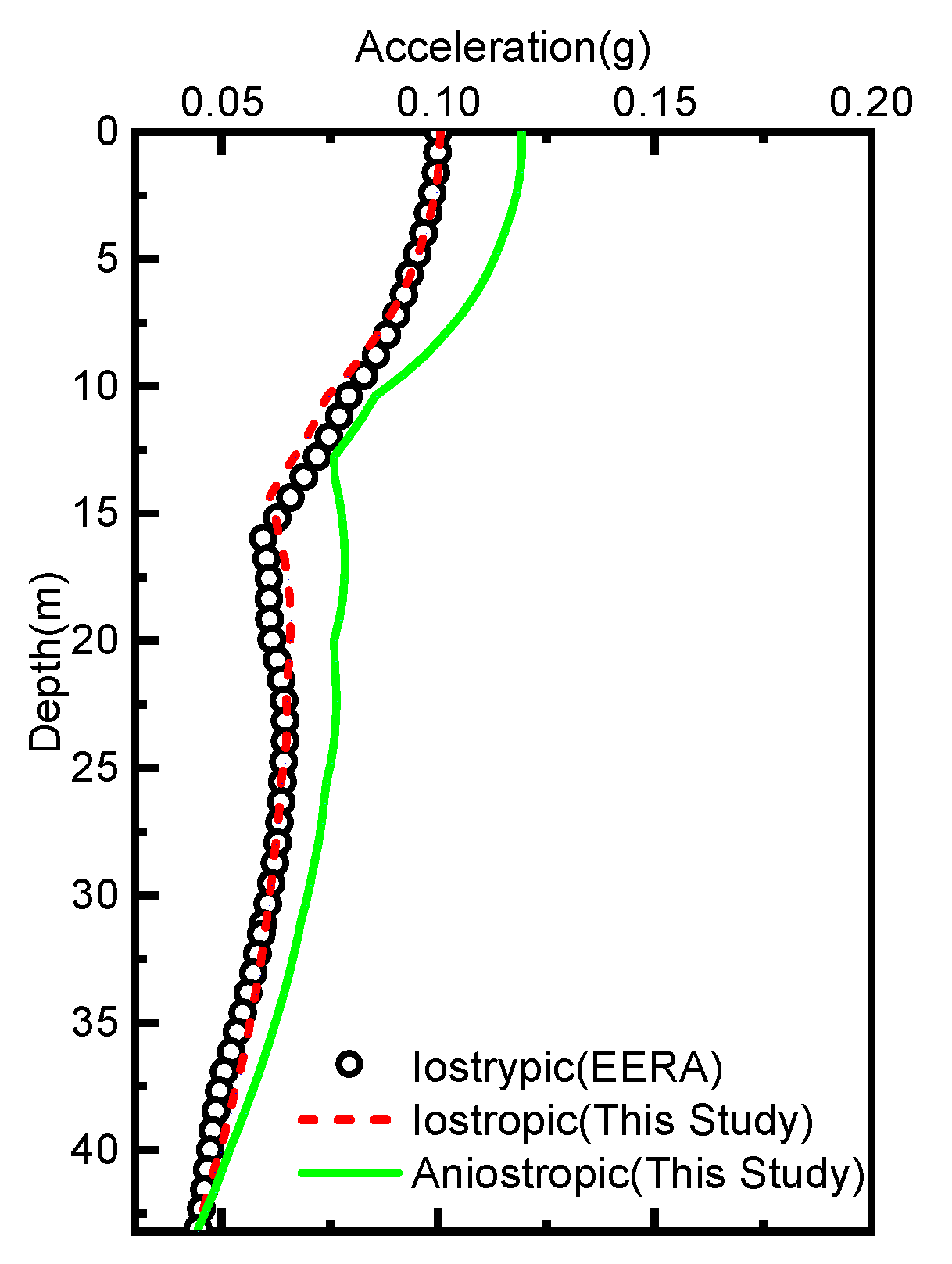
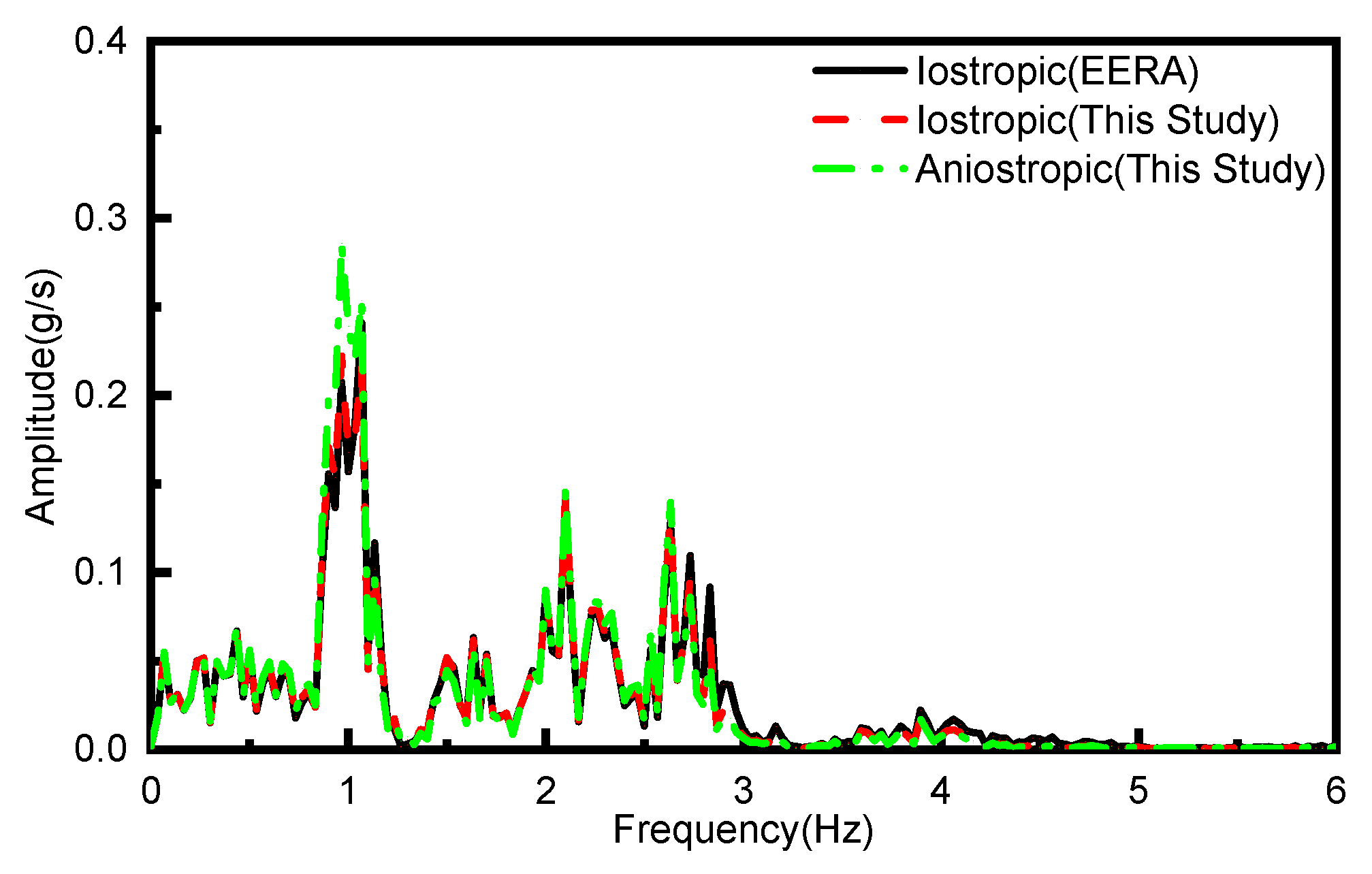
In this case study, the Shanghai wave is adjusted to have the peak ground acceleration of to 0.1g. Figure 7 and Figure 8 show the changes in peak acceleration along the depth and the ground peak acceleration spectrum, respectively. It is evident that, when the proposed calculation model reduces to the isotropic scenario, it aligns well with the results obtained from EERA. However, when considering the soil anisotropy, the PGA increases by 19.70%; the peak value of the ground response spectrum undergoes a significant increase of 28.82% at 1 Hz.
To further explore the design response spectrum of Yangshan Port, the ground motion responses of the site under different seismic intensities (0.1g, 0.15g, 0.2g, 0.25g, 0.3g) are studied. Based on the 5% damped ground acceleration response spectrum of different intensities, the least squares method by Andreotti [53] et al. was used to calibrate the design response spectrum. The shape function of the design response spectrum is as follows [54]:
β ( T ) = 1 + ( β max − 1 ) T T 0   0 ≤ T ≤ T 0 β max T 0   ≤ T ≤ T g β max ( T g T ) χ T g   ≤ T ≤ T m
where T 0 is the period associated with the initial inflection point, established at 0.1s. T g signifies the characteristic period. Since this study focuses on a certain soil layer in Yangshan Port, the characteristic period ( T g ) can be calculated according to Equation (12), which is 0.92s. T m is the cutoff period, χ represents the attenuation index, and β m a x denotes the plateau value.
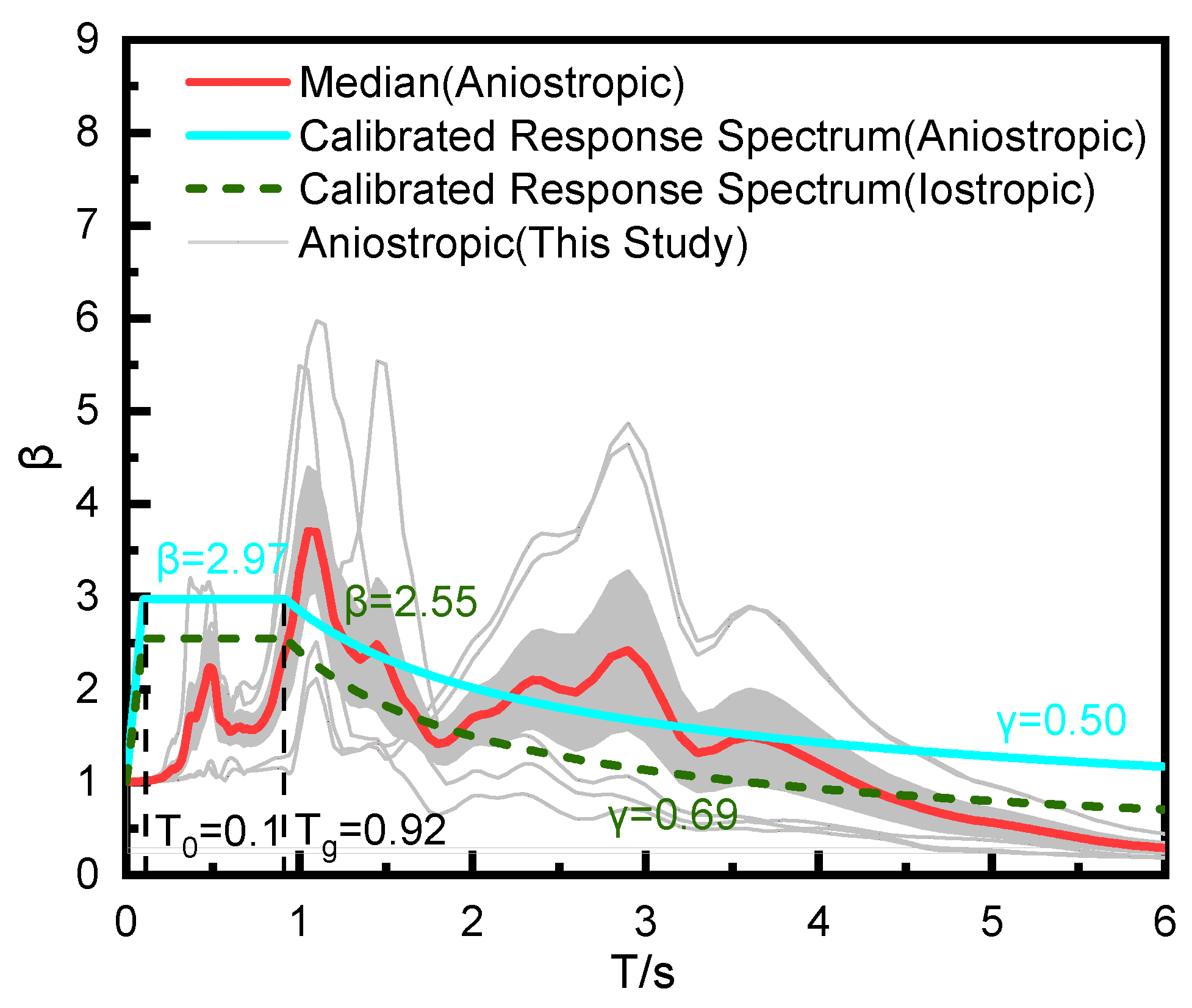
The gray lines in Figure 9 are the ground response spectrums at different intensities with a consideration of soil anisotropy. The upper and lower bounds of the gray area are the 16th to 84th percentil, respectively, showing the region with a probability range of 16% to 84% for the occurrence of seismic events. Red line represents the average of the response spectrum curve. Using the shape function given in Equation (13), the 5% damped design response spectrum for the Yangshan Port is calibrated as the blue line.
In addition, based on the same process, the design response spectrum for the isotropic site is calibrated as the green line, of which plateau value ( β ) is 2.55, the characteristic period ( T g ) is 0.92s, and the attenuation index ( χ ) is 0.69.
Compared with the isotropic one, the anisotropic one has a higher design response spectrum, with a plateau value ( β ) of 2.97, a characteristic period ( T g ) of 0.92s, and an attenuation index ( χ ) of 0.50. After accounting for anisotropy, the plateau value ( β ) of the standard design response spectrum increased by 16.47%. Therefore, when using the isotropic design response spectrum for the seismic design of structures at Shanghai Yangshan port, it may lead to dangerous results.

5. Conclusions

This study establishes a model for analyzing the dynamic behavior of anisotropic soil layers with equivalent linear viscoelasticity. The effects of different anisotropy values of three typical seismic waves on site ground motions are investigated. It is found that the anisotropy ratios for the shear modulus ( A R G ) has a promoting effect on the peak ground acceleration (PGA), while the anisotropic ratio of undrained Young's modulus( A R E ) has an inhibitory effect on peak ground acceleration (PGA) in the site earthquake response problem. The impact of anisotropy on the ground motion of the site becomes more significant when seismic waves have the dominant frequencies closer to the fundamental frequencies of sites.
The study futher takes the Yangshan Port site as an example to calibrated the seismic motion parameters of the Yangshan Port soil layer based on cyclic triaxial tests and resonant column tests, and studied the seismic motion characteristics of the anisotropic site of Yangshan Port.
It is found that the consideration of site anisotropy leads to significant increases in both the peak ground acceleration (PGA) and the peak of ground acceleration spectrum for the Yangshan Port site. The design response spectrum calibrated for an anisotropic site is higher than the design response spectrum calibrated for an isotropic site. When conducting seismic design of buildings, the design response spectrum obtained by using isotropic site ground motion response calibration may be more dangerous.

Acknowledgments

This work was supported by the National Key Research and Development Program of China (No. 2021YFB2600700) and the Natural Science Foundation of Shanghai (No. 23ZR1468500).

References

  1. Tong, X.; Hong, Z.; Liu, S.; Zhang, X.; Xie, H.; Li, Z.; Bao, F. Building-damage detection using pre-and post-seismic high-resolution satellite stereo imagery: A case study of the May 2008 Wenchuan earthquake. ISPRS Journal of Photogrammetry and Remote Sensing. 2012, 68, 13–27. [Google Scholar] [CrossRef]
  2. Zhang, M.; Jin, Y. Building damage in Dujiangyan during Wenchuan earthquake. Earthquake Engineering and Engineering Vibration. 2008, 7, 263–269. [Google Scholar] [CrossRef]
  3. An, X.; Shawky, A.A.; Maekawa, K. The collapse mechanism of a subway station during the Great Hanshin earthquake. Cement and concrete composites. 1997, 19, 241–257. [Google Scholar] [CrossRef]
  4. Joyner, M.D.; Gardner, C.; Puentes, B.; Sasani, M. Resilience-Based seismic design of buildings through multiobjective optimization. Engineering Structures. 2021, 246, 113024. [Google Scholar] [CrossRef]
  5. Morandi, P.; Butenweg, C.; Breis, K.; Beyer, K.; Magenes, G. Latest findings on the behaviour factor q for the seismic design of URM buildings. Bulletin of Earthquake Engineering. 2022, 20, 5797–5848. [Google Scholar] [CrossRef]
  6. Leyva, H.; Bojórquez, J.; Bojórquez, E.; Reyes-Salazar, A.; Carrillo, J.; López-Almansa, F. Multi-objective seismic design of BRBs-reinforced concrete buildings using genetic algorithms. Structural and Multidisciplinary Optimization. 2021, 64, 2097–2112. [Google Scholar] [CrossRef]
  7. Jiang, J.; El Nggar, H.M.; Xu, C.; Zhong, Z.; Du, X. Effect of ground motion characteristics on seismic fragility of subway station. Soil Dynamics and Earthquake Engineering. 2021, 143, 106618. [Google Scholar] [CrossRef]
  8. Mo, T.; Wu, Q.; Li, D.Q.; Du, W. Influence of ground motion characteristics (velocity pulse and duration) on the pile responses in liquefiable soil deposits. Soil Dynamics and Earthquake Engineering. 2022, 159, 107330. [Google Scholar] [CrossRef]
  9. Zhang, X.; Tang, L.; Ling, X.; Chan, A.H.C.; Lu, J. Using peak ground velocity to characterize the response of soil-pile system in liquefying ground. Engineering geology. 2018, 240, 62–73. [Google Scholar] [CrossRef]
  10. Dammala, P.K.; Kumar, S.S.; Krishna, A.M.; Bhattacharya, S. Dynamic soil properties and liquefaction potential of northeast Indian soil for non-linear effective stress analysis. Bulletin of Earthquake Engineering. 2019, 17, 2899–2933. [Google Scholar] [CrossRef]
  11. Markham, C.S.; Bray, J.D.; Macedo, J.; Luque, R. Evaluating nonlinear effective stress site response analyses using records from the Canterbury earthquake sequence. Soil Dynamics and Earthquake Engineering. 2016, 82, 84–98. [Google Scholar] [CrossRef]
  12. Chen, G.; Wang, Y.; Zhao, D.; Zhao, K.; Yang, J. A new effective stress method for nonlinear site response analyses. Earthquake Engineering & Structural Dynamics. 2021, 50, 1595–1611. [Google Scholar]
  13. Li, Z.; Liu, H. An isotropic-kinematic hardening model for cyclic shakedown and ratcheting of sand. Soil Dynamics and Earthquake Engineering. 2020, 138, 106329. [Google Scholar] [CrossRef]
  14. Elia, G.; Rouainia, M. Investigating the cyclic behaviour of clays using a kinematic hardening soil model. Soil Dynamics and Earthquake Engineering. 2016, 88, 399–411. [Google Scholar] [CrossRef]
  15. Moghadam, S.I.; Taheri, E.; Ahmadi, M.; Ghoreishian Amiri, S.A. Unified bounding surface model for monotonic and cyclic behaviour of clay and sand. Acta Geotechnica. 2022, 17, 4359–4375. [Google Scholar] [CrossRef]
  16. Cheng, X.; Du, X.; Lu, D.; Ma, C.; Wang, P. A simple single bounding surface model for undrained cyclic behaviours of saturated clays and its numerical implementation. Soil Dynamics and Earthquake Engineering. 2020, 139, 106389. [Google Scholar] [CrossRef]
  17. Shi, Z.; Huang, M. Intergranular-strain elastic model for recent stress history effects on clay. Computers and Geotechnics. 2020, 118, 103316. [Google Scholar] [CrossRef]
  18. Elbadawy, M.A.; Zhou, Y.G.; Liu, K. A modified pressure dependent multi-yield surface model for simulation of LEAP-Asia-2019 centrifuge experiments. Soil Dynamics and Earthquake Engineering. 2022, 154, 107135. [Google Scholar] [CrossRef]
  19. Mroz, Z. On the description of anisotropic workhardening. Journal of the Mechanics and Physics of Solids. 1967, 15, 163–175. [Google Scholar] [CrossRef]
  20. Chen, G.; Wang, Y.; Zhao, D.; Zhao, K.; Yang, J. A new effective stress method for nonlinear site response analyses. Earthquake Engineering Structural Dynamics. 2021, 50, 1595–1611. [Google Scholar] [CrossRef]
  21. Hardin, B.O.; Drnevich, V.P. Shear modulus and damping in soils: measurement and parameter effects (terzaghi leture). Journal of the soil mechanics and foundations division. 1972, 98, 603–624. [Google Scholar] [CrossRef]
  22. Hardin, B.O.; Drnevich, V.P. Shear modulus and damping in soils: design equations and curves. Journal of the Soil mechanics and Foundations Division. 1972, 98, 667–692. [Google Scholar] [CrossRef]
  23. Schnabel, P.B. SHAKE, a computer program for earthquake response analysis of horizontally layered sites. Report No. EERC 72-12, University of California, Berkeley, 1972.
  24. Wang, J.P.; Xu, Y. A non-stationary earthquake probability assessment with the Mohr–Coulomb failure criterion. Natural Hazards and Earth System Sciences. 2015, 15, 2401–2412. [Google Scholar] [CrossRef]
  25. Luo, C.; Yang, X.; Zhan, C.; Jin, X.; Ding, Z. Nonlinear 3D finite element analysis of soil–pile–structure interaction system subjected to horizontal earthquake excitation. Soil Dynamics and Earthquake Engineering. 2016, 84, 145–156. [Google Scholar] [CrossRef]
  26. Idriss, I.M.; Sun, J.I. A Computer program for conducting equivalent linear seismic response analysis of horizontally layered soil deposits. Users manual for SHAKE91, 1992.
  27. Zhang, R.; Wu, C.; Goh, A.T.; Böhlke, T.; Zhang, W. Estimation of diaphragm wall deflections for deep braced excavation in anisotropic clays using ensemble learning. Geoscience Frontiers. 2021, 12, 365–373. [Google Scholar] [CrossRef]
  28. Zhang, R.; Li, Y.; Goh, A.T.; Zhang, W.; Chen, Z. Analysis of ground surface settlement in anisotropic clays using extreme gradient boosting and random forest regression models. Journal of Rock Mechanics and Geotechnical Engineering. 2021, 13, 1478–1484. [Google Scholar] [CrossRef]
  29. Teng, F. A Simplified Expression for Ground Movements Induced by Excavations in Soft Clay. In Proceedings of the 2nd International Symposium on Asia Urban GeoEngineering; Springer: Singapore, 2018; pp. 93–115. [Google Scholar]
  30. Wei, F.; Wang, H.; Zeng, G.; Jiang, M. Seepage flow around twin circular tunnels in anisotropic ground revealed by an analytical solution. Underground Space. 2023, 10, 1–14. [Google Scholar] [CrossRef]
  31. Soe, T.E.E.; Ukritchon, B. Three-dimensional undrained face stability of circular tunnels in non-homogeneous and anisotropic clays. Computers and Geotechnics. 2023, 159, 105422. [Google Scholar] [CrossRef]
  32. Zhang, W.; Li, Y.; Wu, C.; Li, H.; Goh, A.T.C.; Liu, H. Prediction of lining response for twin tunnels constructed in anisotropic clay using machine learning techniques. Underground space. 2022, 7, 122–133. [Google Scholar] [CrossRef]
  33. Perić, D.; Tran, T.V.; Miletić, M. Effects of soil anisotropy on a soil structure interaction in a heat exchanger pile. Computers and Geotechnics. 2017, 86, 193–202. [Google Scholar] [CrossRef]
  34. Ai, Z.Y.; Ye, J.M.; Zhao, Y.Z. The performance analysis of energy piles in cross-anisotropic soils. Energy. 2022, 255, 124549. [Google Scholar] [CrossRef]
  35. Ai, Z.Y.; Ye, J.M. Thermo-mechanical analysis of pipe energy piles in layered cross-isotropic soils. Energy. 2023, 277, 127757. [Google Scholar] [CrossRef]
  36. Bentil, O.T.; Zhou, C.; Zhang, J.; Liu, K.K. Cross-anisotropic stiffness characteristics of a compacted lateritic clay from very small to large strains. Canadian Geotechnical Journal. 2023 (ja).
  37. Stokoe, K.H.; Darendeli, M.B.; Andrus, R.D.; Brown, L.T. Dynamic soil properties: laboratory, field and correlation studies. In Earthquake geotechnical engineering; 1999. pp. 811–845.
  38. Zhang, M.; Liao, W.M.; Wang, Z.J. Statistical analysis of the relationship between dynamic shear modulus ratio and damping ratio and shear strain of cohesive soil. Earthquake Engineering and Engineering Vibration. 2013, 33, 256–262. [Google Scholar]
  39. Nishimura, S. Cross-anisotropic deformation characteristics of natural sedimentary clays. Géotechnique. 2014, 64, 981–996. [Google Scholar] [CrossRef]
  40. Teng, F.C.; Ou, C.Y.; Hsieh, P.G. Measurements and numerical simulations of inherent stiffness anisotropy in soft Taipei clay. Journal of Geotechnical and Geoenvironmental Engineering. 2014, 140, 237–250. [Google Scholar] [CrossRef]
  41. CEN (European Committee for Standardization) Eurocode 8: Design of structures for earthquake, 2004.
  42. Seed, H.B. Soil moduli and damping factors for dynamic response analyses. Reoprt, 1970: EERC 70-10.
  43. Forte, G.; Chioccarelli, E.; De Falco, M.; Cito, P.; Santo, A.; Iervolino, I. Seismic soil classification of Italy based on surface geology and shear-wave velocity measurements. Soil Dynamics and Earthquake Engineering. 2019, 122, 79–93. [Google Scholar] [CrossRef]
  44. Ministry of Housing and Urban-Rural Development of the People's Republic of China (Code for seismic design of buildings) GB 50011-2010. Beijing: China Architecture Building Press. In Chinese, 2010.
  45. Dong, F.F.; Chen, G.X.; Jin, D.D. Comparison of one-dimensional equivalent linear and two-dimensional nonlinear analysis of seismic effect characteristics in Quanzhou Basin. Journal of Disaster Prevention and Mitigation Engineering. 2014, 34, 154–160. [Google Scholar]
  46. Hou, Y.M.; Wang, J.H.; Zhang, L.L. Finite-element modeling of a complex deep excavation in Shanghai. Acta Geotechnica. 2009, 4, 7–16. [Google Scholar] [CrossRef]
  47. Li, Q.; Ng, C.W.W.; Liu, G.B. Determination of small-strain stiffness of Shanghai clay on prismatic soil specimen. Canadian geotechnical journal. 2012, 49, 986–993. [Google Scholar] [CrossRef]
  48. Ng, C.W.W.; Li, Q.; Liu, G.B. Experimental study on the measurement of anisotropic shear modulus of undisturbed Shanghai soft clay using bending elements. Chinese Journal of Geotechnical Engineering. 2013, 35, 150–156. [Google Scholar]
  49. Yang, J.; Liu, X. Shear wave velocity and stiffness of sand: the role of non-plastic fines. Géotechnique. 2016, 66, 500–514. [Google Scholar] [CrossRef]
  50. Gu, X.; Yang, J.; Huang, M. Laboratory measurements of small strain properties of dry sands by bender element. Soils and Foundations. 2013, 53, 735–745. [Google Scholar] [CrossRef]
  51. Gu, X.Q.; Yang, J.; Huang, M.S.; Gao, G.Y. Bending element, resonant column and cyclic torsional shear tests for the determination of shear modulus of sand. Chinese Journal of Geotechnical Engineering. 2016, 38, 740–746. [Google Scholar]
  52. Youn, J.U.; Choo, Y.W.; Kim, D.S. Measurement of small-strain shear modulus G max of dry and saturated sands by bender element, resonant column, and torsional shear tests. Canadian Geotechnical Journal. 2008, 45, 1426–1438. [Google Scholar] [CrossRef]
  53. Andreotti, G.; Famà, A.; Lai, C.G. Hazard-dependent soil factors for site-specific elastic acceleration response spectra of Italian and European seismic building codes. Bulletin of Earthquake Engineering 2018, 16, 5769–5800. [Google Scholar] [CrossRef]
  54. Ministry of Housing and Urban-Rural Development of the People's Republic of China (Standard for seismic design of hydraulic structures) GB 51247-2018. Beijing: China Architecture Building Press. In Chinese, 2018.
Preprints 87647 g001
Figure 1. Seismic wave time history curve.
Figure 1. Seismic wave time history curve.
Preprints 87647 g001
Preprints 87647 g002
Figure 2. Comparison of results for homogeneous soil layer with iostropic: (a) Shanghai; (b) Kobe; (c) Ei-Centro.
Figure 2. Comparison of results for homogeneous soil layer with iostropic: (a) Shanghai; (b) Kobe; (c) Ei-Centro.
Preprints 87647 g002
Preprints 87647 g003
Figure 3. Normalized peak ground acceleration scatter plot: (a) Shanghai;(b) Kobe; (c) Ei-Centro.
Figure 3. Normalized peak ground acceleration scatter plot: (a) Shanghai;(b) Kobe; (c) Ei-Centro.
Preprints 87647 g003
Preprints 87647 g004
Figure 4. BE S-wave signals in silty clay specimen.
Figure 4. BE S-wave signals in silty clay specimen.
Preprints 87647 g004
Preprints 87647 g005aPreprints 87647 g005b
Figure 5. Partial results of cyclic triaxial testing (silty clay): (a) 150kpa; (b) 200kpa; (c) 250kpa.
Figure 5. Partial results of cyclic triaxial testing (silty clay): (a) 150kpa; (b) 200kpa; (c) 250kpa.
Preprints 87647 g005aPreprints 87647 g005b
Preprints 87647 g006
Figure 6. (a) G n o r m − γ ;(b) D − γ .
Figure 6. (a) G n o r m − γ ;(b) D − γ .
Preprints 87647 g006
Preprints 87647 g007
Figure 7. Peak acceleration along depth.
Figure 7. Peak acceleration along depth.
Preprints 87647 g007
Preprints 87647 g008
Figure 8. Ground acceleration spectrum.
Figure 8. Ground acceleration spectrum.
Preprints 87647 g008
Preprints 87647 g009
Figure 9. 5% damped design response spectrum for Yangshan Port.
Figure 9. 5% damped design response spectrum for Yangshan Port.
Preprints 87647 g009
Table 1. Model parameters.
Table 1. Model parameters.
Preprints 87647 i001
Table 2. Isotropic soil example.
Table 2. Isotropic soil example.
Preprints 87647 i002
Table 3. Example parameters.
Table 3. Example parameters.
Preprints 87647 i003
Table 4. Site fundamental frequency and seismic wave dominant frequency.
Table 4. Site fundamental frequency and seismic wave dominant frequency.
Preprints 87647 i004
Table 5. Soil layer information of Yangshan port.
Table 5. Soil layer information of Yangshan port.
Preprints 87647 i005
Table 6. The soil parameters of the Yangshan Port site.
Table 6. The soil parameters of the Yangshan Port site.
Preprints 87647 i006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated