Prerpints.org logo
Preprint
Article

Evolutionary Reinforcement Learning of Neural Network Controller for Acrobot Task — Part2: Genetic Algorithm

Altmetrics

Downloads

77

Views

31

Comments

0

This version is not peer-reviewed

Submitted:

13 October 2023

Posted:

13 October 2023

You are already at the latest version

Alerts
Abstract
Evolutionary algorithms find applicability in reinforcement learning of neural networks due to their independence from gradient-based methods. To achieve successful training of neural networks using evolutionary algorithms, careful considerations must be made to select appropriate algorithms due to the availability of various algorithmic variations. The author previously reported experimental evaluations on Evolution Strategy for reinforcement learning of neural networks, utilizing the Acrobot control task. In this study, Genetic Algorithm is adopted as another instance of major evolutionary algorithms. Experimental results demonstrate that there was no statistically significant difference between the experimental performances of GA and ES, but the priority of generations and offsprings was different; GA performed better with a greater number of generations while ES performed better with a greater number of offsprings. Eight hidden units were the best among four variations (4, 8, 16 or 32 units), which aligns with previous study using ES.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Neural networks can be effectively trained using gradient-based methods for supervised learning tasks, where labeled training data are available. However, when it comes to reinforcement learning tasks where labeled training data are not provided, neural networks demand the utilization of gradient-free training algorithms. Evolutionary algorithms [1,2,3,4,5] find applicability in the reinforcement learning of neural networks due to their independence from gradient-based methods.
Evolution Strategy [6,7], Genetic Algorithm [8,9,10,11], and Differential Evolution [12,13,14] stand as representative evolutionary algorithms. To achieve successful training of neural networks using evolutionary algorithms, careful considerations must be made regarding: i) selecting appropriate algorithms due to the availability of various algorithmic variations, and ii) designing hyperparameters as they significantly impact performance. The author previously reported experimental evaluations on Evolution Strategy for reinforcement learning of neural networks, utilizing the Acrobot task [15]. In this study, Genetic Algorithm is adopted as another instance of major evolutionary algorithms.

2. Acrobot control task

As a task that requires reinforcement learning to solve, this study employs Acrobot control task provided at OpenAI Gym. Figure 1 shows a screenshot of the system. This task is the same as that in the previous study; details on this task were described in Part1 [15]. The same method for scoring fitness of a neural network controller (eq.(1) in Part1) was employed again in this study.

3. Neural networks

In the previous study using ES [15], the author employed a three-layered feedforward neural network known as a multilayer perceptron (MLP [16,17]) as the controller. The same MLP is utilized again in this study.
Figure 2 illustrates the topology of the MLP. The feedforward calculations were described in Part1 [15]. In both of this study and the previous one, the MLP serves as the policy function: action(t) = F(observation(t)). The input layer consists of six units, each corresponding to the values obtained by an observation. To ensure the input value falls within the range [-1.0, 1.0], the angular velocity of θ1 (θ2) is divided by 4 π ( 9 π ). The output layer comprises one unit, and its output value is directly applied as the torque to the joint.

4. Training of neural networks by genetic algorithm

A three-layered perceptron, as depicted in Figure 2, includes M+L unit biases and NM+ML connection weights, resulting in a total of M+L+NM+ML parameters. Let D represent the quantity M+L+NM+ML. For this study, the author sets N=6 and L=1, leading to D=8M+1. The training of this perceptron is essentially an optimization of the D-dimensional real vector. Let x = ( x 1 , x 2 , . . . , x D ) denote the D-dimensional vector, where each x i corresponds to one of the D parameters in the perceptron. By applying the value of each element in x to its corresponding connection weight or unit bias, the feedforward calculation in eqs. (2)-(6) can be processed.
In this study, the D-dimensional vector x is optimized using Genetic Algorithm [8,9,10,11]. GA treats x as a chromosome (a genotype vector) and applies evolutionary operators to manipulate it. The fitness of x is evaluated based on eq. (1) described in Part1 [15]. Figure 3 illustrates the GA process. Steps 1-3 are the same as those in Evolution Strategy, which are described in Part1 [15]. Step 1 initializes vectors y 1 , y 2 , …, y λ randomly within a predefined range, denoted as m i n , m a x D , where λ represents the number of offsprings. In Step 2, the values in each vector y c (c=1, 2, ..., λ ) are fed into the MLP, which subsequently controls the Acrobot system for a single episode consisting of 200 time steps. The fitness of y c is evaluated based on the outcome of the episode. In Step 3, the evolutionary training loop concludes upon meeting a preset condition. A straightforward example of such a condition is reaching the limit number of fitness evaluations.
The term “elites” refers to the highest performing offspring vectors. To leverage the optimal solutions found thus far, elite vectors are maintained as potential parents for genetic crossover. Initially, the elite population is empty. Let E denote the number of elite vectors. From the union of the E elites and the λ offsprings, the best E vectors (i.e., vectors with the top E fitness scores) are saved as new Elites. Step 5 consists of crossover and mutation operations. During Step 5.1, new λ offspring vectors are generated by applying the crossover operator to the union of the elite vectors z 1 , z 2 , . . . , z E and the vectors y 1 , y 2 , . . . , y λ . A single offspring is produced through a single crossover, which involves randomly selecting two parents from the union set. This process is repeated λ times to generate new λ offspring vectors. In this study, the blend crossover method (BLX-α) [18] is utilized. The new offspring vectors replace the current population y 1 , y 2 , . . . , y λ . Any element of the new offspring vectors is truncated to the domain [ m i n , m a x ] if the element exceeds the domain. In Step 5.2, the mutation probability is applied to each element in the new offspring vectors, resulting in their reinitialization to a uniformly randomly generated number within the domain.

5. Experiment

In the previous study using ES, the number of fitness evaluations included in one experiment trial was set to 5,000 [15]. The number of new offsprings generated per generation ( λ ) was either of (a) 10 and (b) 50. The number of generations for each case of (a) or (b) was 500 and 100 respectively. The total number of fitness evaluations were 10 × 500 = 5,000 for (a) and 50 × 100 = 5,000 for (b). The experiments using GA in this article employed the same settings. The hyperparameter settings for GA are shown in Table 1. The number of elite individuals to be preserved, denoted as E, was set to 20% of the λ offsprings for both (a) and (b). The parameter α for the blend crossover was set to the conventional value of 0.5. The mutation probability was set as 1/D, where D is the genotype length. The value of D varied according to the number of hidden units M in the MLP. For instance, if M = 4 then D = 8M + 1 = 33, resulting in a mutation probability of 1/33.
The domain of genotype vectors, m i n , m a x D , was kept consistent with the previous experiment [15], i.e., [-10.0, 10.0]D. The number of hidden units M was also consistently set to the four variations: 4, 8, 16, and 32. An MLP with either of 4, 8, 16, or 32 hidden units underwent independent training 11 times. Table 2 presents the best, worst, average, and median fitness scores of the trained MLPs across the 11 trials. Each of the two hyperparameter configurations (a) and (b) in Table 1 was applied.
Upon comparing the scores in Table 2 between configurations (a) and (b), it is evident that the values obtained using configuration (a) are higher than those obtained using configuration (b). This result indicates that configuration (a) outperforms configuration (b). The Wilcoxon signed rank test confirmed that this difference is statistically significant (p<.01). Hence, in this study, increasing the number of generations rather than the number of offspring allowed GA to discover superior solutions. Note that the reverse was true for ES [15], i.e., configuration (b) was significantly better than configuration (a) (p<.01).
This difference arises from the distinction in reproduction methods between GA and ES. The reproduction method of GA can generate offsprings that are distant from the parents, especially in the early stages of exploration. As a result, GA excels in broad exploration. On the other hand, the reproduction method of ES, when set with a small step size, produces offsprings that are close to the parents even in the early stages of exploration, making ES adept at local exploration. Comparing configurations (a) and (b), (a) can enhance local exploration more than (b), while conversely, (b) can promote broad exploration more than (a). Generally, achieving a proper balance between exploration and exploitation is crucial for successfully optimizing solutions using stochastic multi-point search methods. Therefore, configuration (a) is considered more desirable in GA as it complements exploitation, and configuration (b) is deemed preferable in ES as it complements exploration. This conclusion aligns with the findings of the author’s previous study using the pendulum task [19].
Next, upon comparing the fitness scores obtained using configuration (a) among the four variations of M (the number of hidden units), it is observed that the scores with M=4 are worse than those of M=8, 16 and M=32. The Wilcoxon rank sum test confirmed that (1) the difference between M=4 and either of M=8 or 16 is statistically significant (p<.05), and (2) the difference between M=4 and M=32 is also statistically significant (p<.1). No other difference was found to be statistically significant. This result indicates that 4 hidden units are not sufficient for this task, which is consistent with the previous study [15]. Since M=8 was not significantly inferior to M=16 or M=32, it can be concluded that, in this task, M=8 was the best choice in terms of performance and model size.
Figure 4 presents learning curves of the best, median, and worst runs among the 11 trials where the configuration is (a). Note that the horizontal axis of these graphs is in a logarithmic scale. The shapes of these graphs are similar to the results of the previous experiment using ES [15], and the manner in which the best fitness score became larger along with the progression of evaluation counts showed a common pattern between ES and GA. The random solutions for the first evaluation have fitness values almost exclusively at 0.0. The graphs in Figure 4 show increases in fitness from 0.1 to 0.2 by approximately the first 100 evaluations, which corresponds to 2% of the total 5,000 evaluations. Afterward, over the remaining 4,900 evaluations, the fitness gradually rises to around 0.4 to 0.45. For all the four M variations, even in the worst trials the final fitness scores are not significantly worse than the corresponding best trials. This indicates that GA could robustly optimize the MLP so that the variance was small within the 11 trials. In the case of M=16 (Figure 7(iii)), the fact that the fitness evaluation value of the worst trial is not near 0.0 from the beginning, but rather exceeds 0.2, is likely due to the random initialization of a solution that happened to be a good one. Despite starting the optimization with the better initial solution than those in the other 10 trials, this particular trial eventually became the worst among the 11 trials. This suggests that commencing optimization from better initial solutions is not necessarily desirable, as premature convergence can hinder the subsequent evolution of solutions.
Figure 5a illustrates the actions by the MLP and the heights py(t) (see eq. (1) in Part1 [15]) in the 200 steps prior to training, while Figure 5b displays the corresponding actions and heights after training. In this scenario, the MLP employed 8 hidden units, and the configuration (a) in Table 1 was utilized. These graphs also bear a resemblance to the graphs in the previous study with ES [15]. As a distinguishing feature, when comparing Figure 5a after the training by GA with Figure 8b in the previous article using ES [15], it can be observed that, for the case of GA, during the latter 100 steps in the episode, there is an oscillation in the range of heights greater than 0.4. In the previous case of ES, such oscillations were not present; instead, a larger oscillation in height was observed, spanning from a value close to the minimum of 0.0 to a value close to the maximum of 1.0. Supplementary videos are provided which demonstrate the motions of the chain23. By examining the chain motion achieved by the GA-trained MLP in the video, it becomes evident that during the latter 100 steps, only the second chain beyond the joint portion was rotated while keeping the first chain up to the joint portion in an inverted state. As a result, the free end of the second chain was maintained at a height greater than 0.4, allowing for a higher fitness evaluation value. The best MLP trained by ES was not capable of achieving this kind of control [15]. This difference is likely to stem from the fact that GA explores solutions more broadly and searches for a greater diversity of solutions compared with ES. However, even in the case of GA, it was not possible to maintain the entire chain in an inverted state and bring the free end of the chain to the highest position at 1.0, which was the same as the result with ES.

6. Statistical test to compare GA with ES

The author conducted a Wilcoxon signed rank test to investigate whether there was a statistically significant difference between the fitness scores obtained from the previous experiment using ES [15] and those from the experiment using GA. The data used for this test included the 32 values reported in Table 2 of Part1 [15] (the data obtained using ES) and the corresponding 32 values shown in Table 2 of this article (the data obtained using GA). The test result indicated that there was no statistically significant difference between these sets of data (p > .1). However, when conducting separate tests for configurations (a) and (b), it was found that with configuration (a), GA was significantly superior to ES (p < .01), while with configuration (b), ES was significantly superior to GA (p < .01). As mentioned earlier, it is desirable to increase the number of offsprings for ES to complement exploration, and to increase the number of generations for GA to complement exploitations. This observation was confirmed by the test result.

7. Conclusion

In this study, Genetic Algorithm was applied to the reinforcement learning of a neural network controller for the Acrobot task, and the result was compared with that previously reported in Part1 [15] where ES was applied to the same task. The findings from this study are summarized as follows:
(1)
In terms of the parameter settings for Genetic Algorithm, two approaches were employed: one with more generations and less offsprings (Table 2(a)), and the other with less generations and more offsprings (Table 2(b)). Based on the experimental results, it was observed that increasing generations significantly led to better solutions (p < .01). Interestingly, this result was opposite to that observed in the case of Evolution Strategy [15]. This indicates that the priority of generations and offsprings varies depending on the algorithm.
(2)
Four different numbers of units in the hidden layer of the multilayer perceptron were compared: 4, 8, 16, and 32. The experimental results revealed that, in the case of 4 units, significantly inferior performance was obtained compared to the other three configurations. For 8 units, there was no statistically significant difference compared to 16 and 32 units. Therefore, from the perspective of the trade-off between performance and model size, 8 units in the hidden layer were found to be the optimal choice. This finding aligns with previous study using Evolution Strategy [15].
The author plans to further apply and evaluate another evolutionary algorithms to the same task and compare the performance with those by GA and ES.

Acknowledgments

The author conducted this study under the Official Researcher Program of Kyoto Sangyo University.
1
https://www.gymlibrary.dev/environments/classic_control/acrobot/.
2
http://youtu.be/JoQXURiP8RY.
3
http://youtu.be/kP9nSD3zQMU.

References

  1. Bäck, T., & Schwefel, H. P. (1993). An overview of evolutionary algorithms for parameter optimization. Evolutionary computation, 1(1), 1-23. [CrossRef]
  2. Fogel, D. B. (1994). An introduction to simulated evolutionary optimization. IEEE transactions on neural networks, 5(1), 3-14. [CrossRef]
  3. Bäck, T. (1996). Evolutionary algorithms in theory and practice: evolution strategies, evolutionary programming, genetic algorithms. Oxford university press.
  4. Eiben, Á. E., Hinterding, R., & Michalewicz, Z. (1999). Parameter control in evolutionary algorithms. IEEE Transactions on evolutionary computation, 3(2), 124-141.
  5. Eiben, A. E., & Smith, J. E. (2015). Introduction to evolutionary computing. Springer-Verlag Berlin Heidelberg.
  6. Schwefel, H. P. (1984). Evolution strategies: A family of non-linear optimization techniques based on imitating some principles of organic evolution. Annals of Operations Research, 1(2), 165-167. [CrossRef]
  7. Beyer, H. G., & Schwefel, H. P. (2002). Evolution strategies–a comprehensive introduction. Natural computing, 1, 3-52.
  8. Goldberg, D.E., Holland, J.H. (1988). Genetic Algorithms and Machine Learning. Machine Learning 3, 95-99. [CrossRef]
  9. Holland, J. H. (1992). Genetic algorithms. Scientific american, 267(1), 66-73.
  10. Mitchell, M. (1998). An introduction to genetic algorithms. MIT press.
  11. Sastry, K., Goldberg, D., & Kendall, G. (2005). Genetic algorithms. Search methodologies: Introductory tutorials in optimization and decision support techniques, 97-125.
  12. Storn, R., & Price, K. (1997). Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. Journal of global optimization, 11, 341-359. [CrossRef]
  13. Price, K., Storn, R. M., & Lampinen, J. A. (2006). Differential evolution: a practical approach to global optimization. Springer Science & Business Media.
  14. Das, S., & Suganthan, P. N. (2010). Differential evolution: A survey of the state-of-the-art. IEEE transactions on evolutionary computation, 15(1), 4-31. [CrossRef]
  15. Okada, H. (2023). Evolutionary reinforcement learning of neural network controller for Acrobot task – Part1: evolution strategy. Preprints.org, doi: 10.20944/preprints202308.0081.v1.
  16. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning internal representations by error propagation. Parallel distributed processing: explorations in the microstructure of cognition, vol. 1: foundations. MIT Press, Cambridge, MA, USA, 318-362.
  17. Collobert, R., & Bengio, S. (2004). Links between perceptrons, MLPs and SVMs. In Proceedings of the twenty-first international conference on Machine learning (ICML 04). Association for Computing Machinery, New York, NY, USA, 23. [CrossRef]
  18. Eshelman, L.J. & Schaffer, J.D. (1993). Real-coded genetic algorithms and interval-schemata, Foundations of Genetic Algorithms, 2, 187-202. [CrossRef]
  19. Okada, H. (2023). An evolutionary approach to reinforcement learning of neural network controllers for pendulum tasks using genetic algorithms, International Journal of Scientific Research in Computer Science and Engineering, 11(1), 40-46.
Preprints 87719 g001
Figure 1. Acrobot system1.
Figure 1. Acrobot system1.
Preprints 87719 g001
Preprints 87719 g002
Figure 2. Topology of the MLP.
Figure 2. Topology of the MLP.
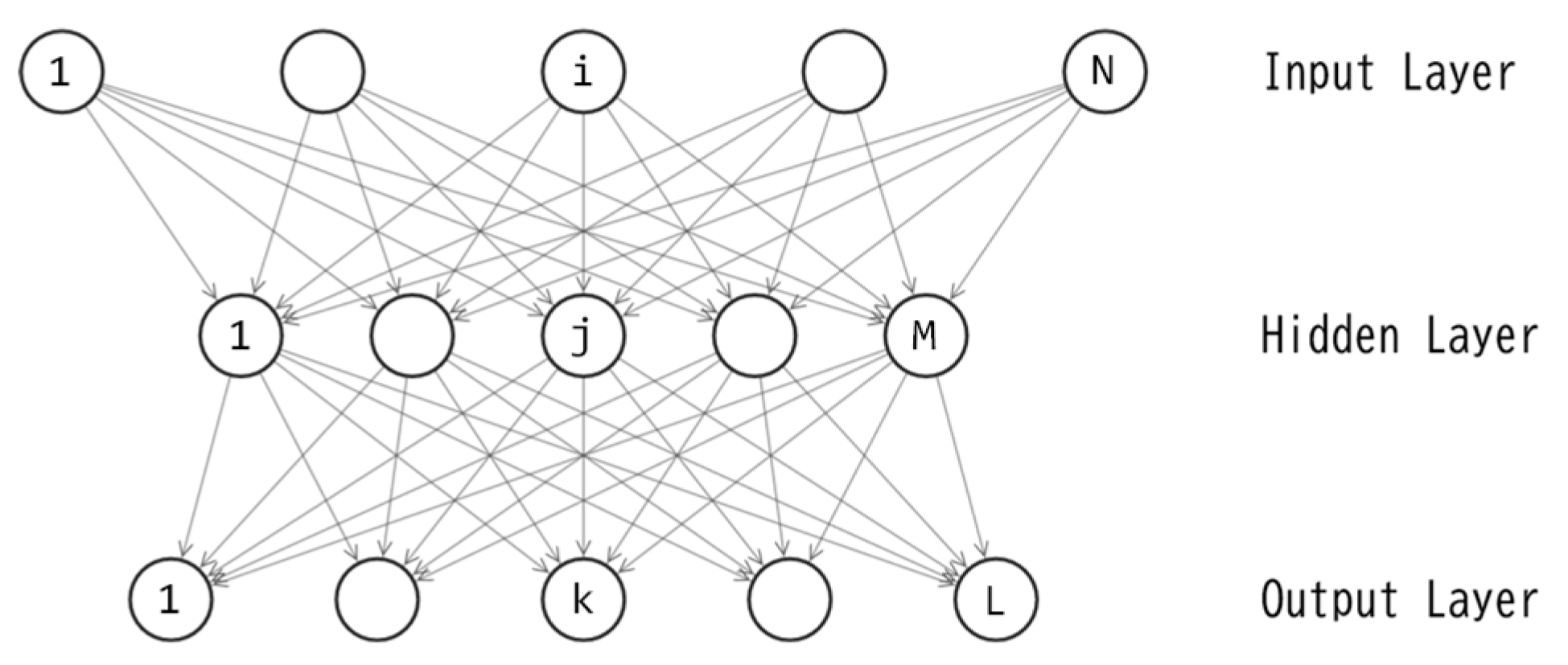
Preprints 87719 g002
Preprints 87719 g003
Figure 3. Process of Genetic Algorithm.
Figure 3. Process of Genetic Algorithm.
Preprints 87719 g003
Preprints 87719 g004
Figure 4. Learning curves of MLP with M hidden units.
Figure 4. Learning curves of MLP with M hidden units.
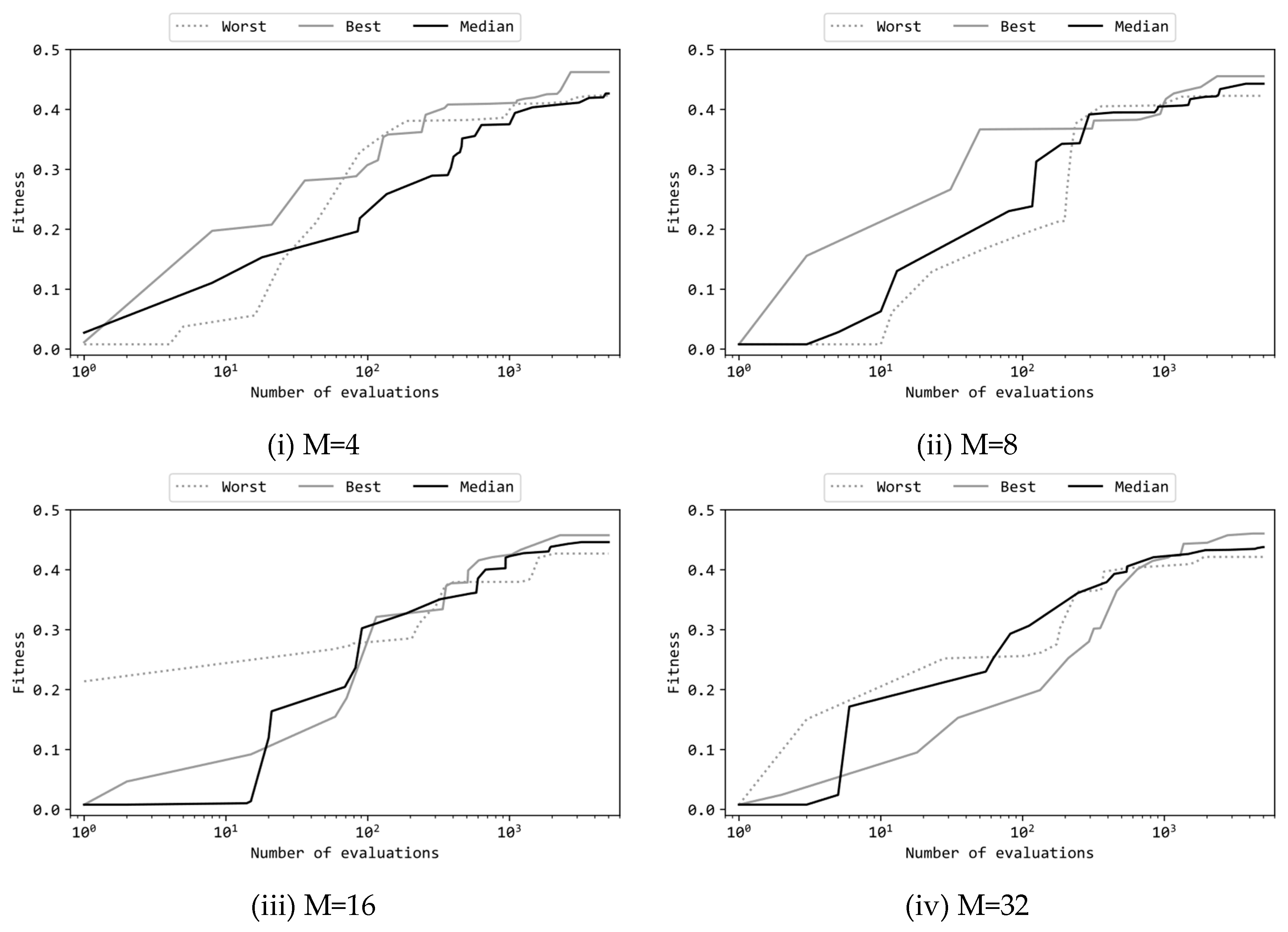
Preprints 87719 g004
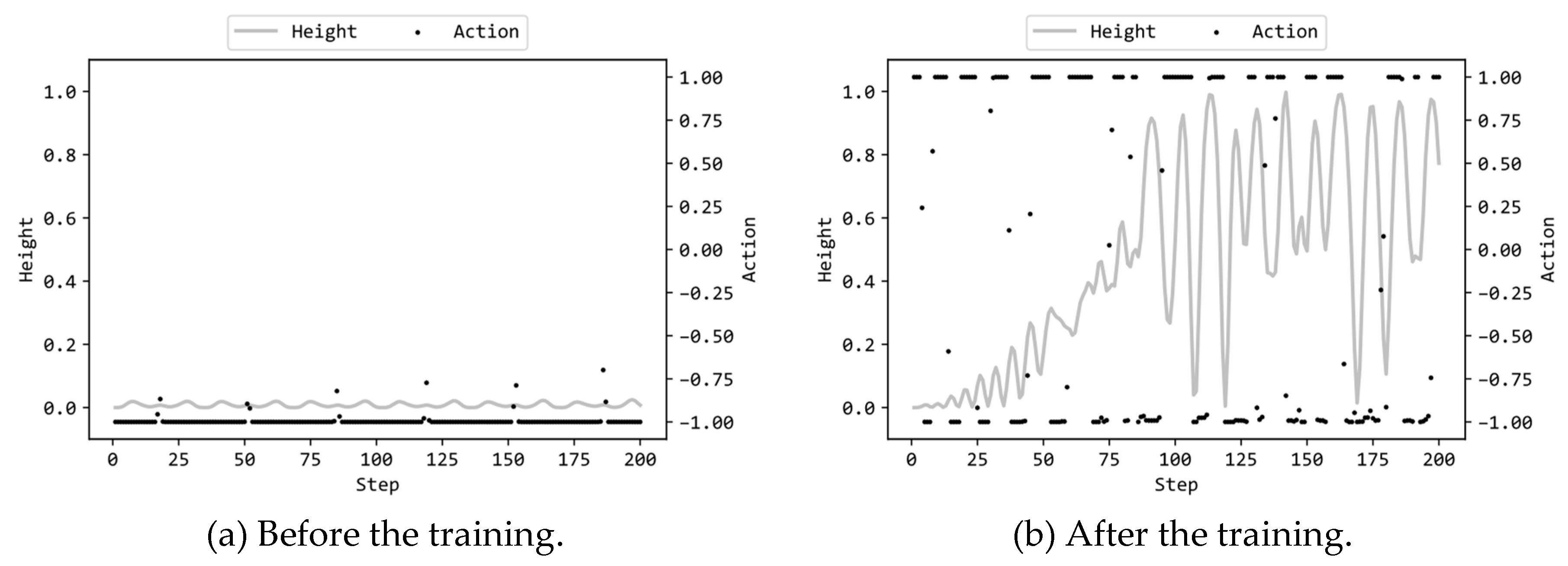
Preprints 87719 g005
Figure 5. MLP actions and the height py(t) in an episode.
Figure 5. MLP actions and the height py(t) in an episode.
Preprints 87719 g005
Table 1. GA Hyperparameters.
Table 1. GA Hyperparameters.
Hyperparameters (a) (b)
Number of offsprings ( λ ) 10 50
Generations 500 100
Fitness evaluations 10 × 500=5,000 50 × 100=5,000
Number of elites (E) 10 × 0.2=2 50 × 0.2=10
α for blend crossover 0.5 0.5
Mutation probability 1/D 1/D
Table 2. Fitness Scores among 11 Runs.
Table 2. Fitness Scores among 11 Runs.
M Best Worst Average Median
(a) 4 0.462 0.423 0.433 0.427
8 0.455 0.423 0.442 0.443
16 0.458 0.427 0.443 0.446
32 0.460 0.421 0.441 0.438
(b) 4 0.452 0.398 0.428 0.432
8 0.434 0.407 0.421 0.426
16 0.435 0.382 0.416 0.422
32 0.418 0.396 0.408 0.410
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated