Prerpints.org logo
Preprint
Article

A Comparative Analysis of Machine Learning Techniques for National Glacier Mapping: Evaluating Performance Through Spatial Cross-Validation in Perú.

Altmetrics

Downloads

175

Views

77

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 October 2023

Posted:

13 October 2023

You are already at the latest version

Alerts
Abstract
Accurately glacier mapping is crucial for understanding climate change impacts, but existing efforts may be biased due to overlooking spatial autocorrelation during map validation. To address this, we compared several widely used machine learning algorithms as gradient boosting machines (GBM), k-nearest neighbor (KNN) and random forest (RF) with parametric logistic regression (GLM) and an unsupervised remote sensing-based method (NDSI) for mapping Peru's glacier regions in a thoughtful experimental setup. Spatial and non-spatial cross-validation methods were used to evaluate model’s performance and compared with a fully independent test set. Performance differences of up to 18% were found between bias-reduced (spatial) and overoptimistic (non-spatial) cross-validation results when compared to independent test set, emphasizing the need to consider spatial autocorrelation when using machine learning for glacier mapping. K-nearest neighbors (KNN) was the overall best model across regions consistently demonstrating the highest performance followed by logistic regression (LR) and gradient boosting machines (GBM). Our novel validation approach, accounting for spatial characteristics, provides valuable insights for glacier mapping studies and future efforts on glacier retreat monitoring. Incorporating this approach improves the reliability of glacier mapping, guiding future national-level initiatives.
Keywords: 
Subject: Environmental and Earth Sciences  -   Water Science and Technology

1. Introduction

Tropical glaciers are sensitive indicators of climate change [1] and vital dry season sources for drinking water, agriculture, and livelihood of many people that depends upon them [2].
Tropical Andean glaciers are among the fastest shrinking and largest contributors to sea level rise on Earth. Over the period from 1975 to 2020 Southern Peruvian Andes have receded by ∼32 % and are now at less than half their original size [3,4]. Most recent studies reported a glacier recession in the Cordillera Blanca of −46 % between 1930 and 2016 [5]. This has bought effects in spatiotemporal alterations in both quantity and quality of mountain water resources [2,6,7] specially this reliance increases sharply during drought conditions [8].
Accurate extraction of glacier areas and continuous monitoring of glacier morphology are fundamental prerequisites for glacier research, as they provide crucial information for assessing hydrologic risks and facilitating climate change mitigation efforts [9].
For example, recent studies focusing on hydrologic modeling of glacier contribution to watersheds in the tropical Andes have utilized multi-temporal estimates of glacier area derived from remotely sensed data to describe the effect that glacier change has had and will have on water resources for this region [10,11].
Due to the arduous, time-consuming, and subjective nature of manually delineating glacier boundaries, numerous techniques have been devised to automatically delineate glacier outlines using primarily multispectral imagery [1], this technique has been proven to generate equivalent accuracy compared to manual digitization techniques when a large sample of glaciers is analyzed [12]. Several studies have been carried out to map glaciated areas on a local and regional scale in Peru using remote sensing techniques [1,6,11,13] as well as in continental scale [9].
The prevailing and currently operational technique employed for delineating debris-free glaciers in the Peruvian Andes relies on the utilization of a Normalized Difference Snow Index (NDSI) threshold [12,14]. However, it is important to note that different threshold values can yield varying results [15]. Although the threshold limit may need to be adjusted for specific regions [10,13], it is commonly kept constant at approximately 0.35 to 0.55 in the literature [1].
Machine learning (ML) is commonly used to build geospatial prediction models [16,17,18,19,20] and has been universally employed in geoscientific research such as global soil properties mapping [21,22,23], landslide susceptibility [24], climate change studies [25], and wildfire risk mapping. Specially several machine learning approaches have been suggested for glacier mapping studies [26,27,28,29]. To be sure that observed glacier changes are related to real changes rather than caused by imprecise determination of the outline, the accuracy of the outlines must be known [30]. This measure is also appropriate to assess the significance of any derived relative changes in glacier size.
Geospatial prediction of environmental variables often relies on map accuracy assessment [31,32], classical map accuracy assessment is rooted in sampling theory [33,34] in which an unbiased estimate of map accuracy is obtained.
Several approaches can be chosen in order to accomplish accuracy assessment [35]. A classical procedure is to evaluate model performance and associated errors by randomly selecting a number of test observations that are set aside at the model calibration stage and only used to quantify model prediction error [36]. While the best method is simply using a completely independent test sample, this is not always feasible [33,34].
A possible solution is K-fold cross validation (K-CV)[37,38,39]. K-CV is a resampling-based technique for the estimation of a model's predictive performance [38]. The basic idea behind K-CV is to split an existing dataset into training and test sets using a user-defined number of partitions. First, the dataset is divided into k partitions or folds. The training set consists of k − 1 partitions and the test set of the remaining partition. The model is trained on the training set and evaluated on the test partition. A repetition consists of k iterations for which every time a model is trained on the training set and evaluated on the test set.
Each partition serves as a test set once. The procedure is repeated k-times and finishes when each unique subset has been used for testing once. A further improvement of this approach is the repetition of the K-CV: the whole procedure is repeated, producing a set of random samples each time. This approach is called the repeated k-fold CV method (RK-CV).
In environmental sciences, observations are often spatially dependent [24,40]. Subsequently, they are affected by underlying spatial autocorrelation by a varying magnitude. Although cross-validation is a particularly well-established approach for model assessment of supervised machine-learning models [39,41,42,43] it is generally agreed that most ML methods in spatial applications do not consider relative location and neighborhood features and that they analyze pixels regardless of their surroundings [44], and hence completely ignoring the spatial dependent and heterogeneity of spatial processes [16]. Therefore, the direct application of ML to geospatial data without accounting for the potential spatial autocorrelation could lead to biased outcomes. It is clear from many studies [40,44,45] that unaddressed spatial autocorrelation generates problems, such as overoptimistic fit of models, omitted information and/or biased (suboptimal) and therefore model performance estimates from conventional cross-validation leads to optimistically biased estimates of map accuracy [20,36,43] due to the similarity of training and test data in a non-spatial partitioning setup when using any kind of cross-validation for tuning or validation [36,43,46].
Several papers including [36,47] have investigated the over-optimistic accuracy estimates by promoting SP-CV methods. These methods start from the premise that spatial proximity of data points in the calibration and test data folds is to be avoided. This is commonly achieved by spatial blocking in K-CV [39,47]. The general overview from the literature [44] is that visible progress has been made recently in the development of spatial machine learning modelling. The current standard for modeling is to use a classic ML algorithm, and some sort of spatial cross-validation method (SP-CV). Therefore, cross-validation approaches that adapt to this problem should be used in any kind of performance evaluation when spatial data is involved [48,49].
A common approach is block-CV (BLK-CV) which divides all samples into contiguous blocks, and then avoids the selection of samples within the same block as both training and validation samples [47]. As an example [36,43] used K-Means clustering to split samples into five folds based on sample data’s locations. The validity of these procedure was empirically tested by [36,40,43]. They found that BLK-CV better approximate the error obtained when predicting species distribution and above ground forest biomass (AGB).
Overall, the intention of this work is to demonstrate the need for spatial cross validation when using machine learning in geospatial classification of glacier land cover when the aim is to estimate a biased-reduced predictive performance. The following objectives (and hypotheses) are addressed:
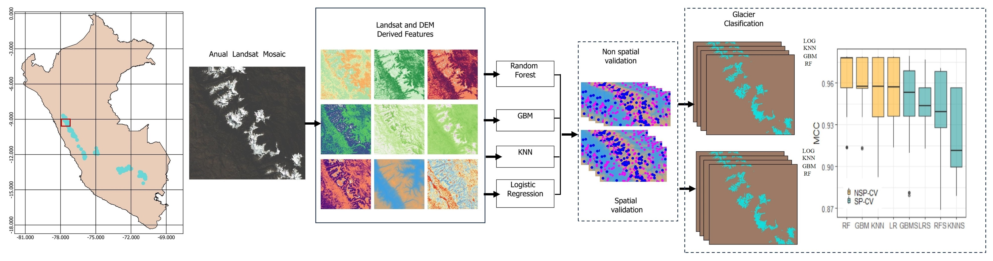
  • The study compares the predictive performance of machine learning algorithms: k-nearest neighbors, Random Forest, Gradient Boosting Machines, and classical statistic models: logistic regression in glacier mapping. It is expected that the machine learning algorithms will demonstrate significantly higher predictive performance.
  • The study also examines the predictive performance of classification algorithms when spatial and non-spatial cross-validation methods are used. It is hypothesized that non-spatial partitioning methods will yield over-optimistic results due to the presence of spatial autocorrelation.
  • Additionally, the study investigates the effects of spatial clustering on the distribution of errors in the analyzed algorithms for glacier mapping. It is anticipated that non-spatial models will exhibit spatial autocorrelation in their errors.

2. Materials and Methods

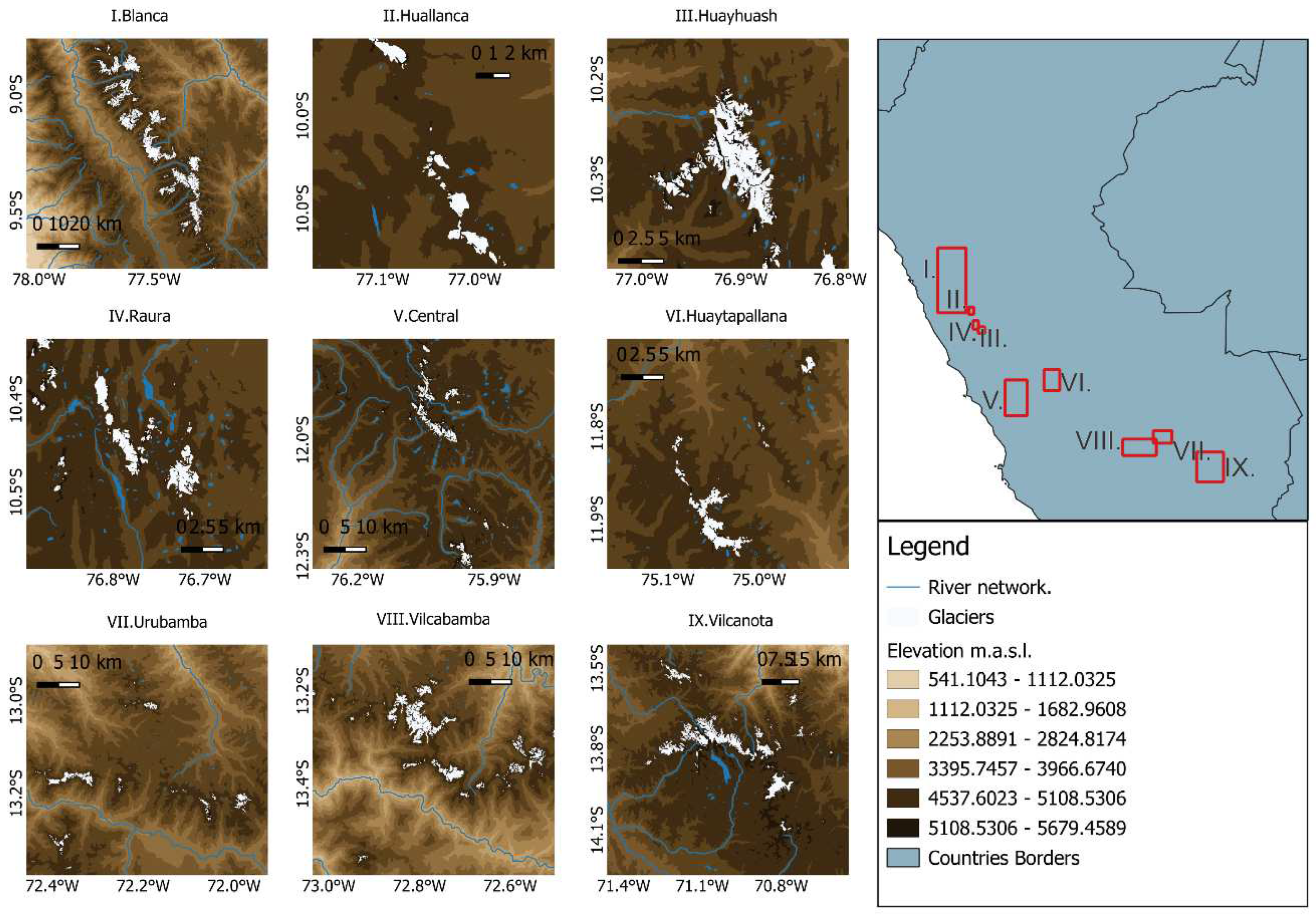
2.1. Study Area

Peru encompasses the largest concentration of tropical glaciers worldwide. About 70 % of all tropical glaciers, covering an area of 1602.96 km2 are located there [50]. According to [51] the glacierized areas of the Peruvian Andes can be divided into three subregions based on their temperature, precipitation, and humidity characteristics:
  • R1 is the northern wet outer tropics, with a high mean annual humidity of 71 %, nearly no seasonality of the temperature and a total annual precipitation of 815 mm. R1 includes the Cordillera Blanca, Central, Chonta, Huagoruncho, Huallanca, Huayhuash, Huaytapallana, La viuda and Raura.
  • R2 is the southern wet outer tropics, with moderate mean annual humidity of 59 %, an annual variability of the mean monthly temperature of about 4 ◦C and a total annual precipitation of 723 mm. R2 includes the Cordillera Vilcabamba, Urubamba, Vilcanota, Carabaya and Apolobamba.
  • R3 is the dry outer tropics, with low mean annual humidity of 50 %, a mean annual temperature of −4.0 ◦C and low total annual precipitation of 287 mm. R3 includes the Cordillera Ampato and Coropuna.
The three subregions experience a dry season from May to September, coinciding with the austral winter, and a wet season from October to April, corresponding to the austral summer [51]. During the wet season, the glaciers predominantly accumulate mass, while the lower portions of the glaciers experience ablation consistently throughout the year.
This study focusses in R1 and R2 glacier subregions (Figure 1), excluding glaciers form R3 subregion, hence reducing the number of Cordilleras analyzed. From the entire National Glacier Inventory (hereafter NGI) [52], we identified 9 glacier Cordilleras as show in Table 1. Nevertheless, in order to ensure the broad applicability of our findings, we carefully select Cordilleras that provide a comprehensive representation of the glacier distribution in Peru, particularly all selected study areas span proximally 90% of the glaciated surface of Cordilleras of Perú [52]. Blanca (40.20%), Central (3.80%), Huallanca (0.47%), Huayhuash (4.75%), Huaytapallana (1.92%), Raura (2.29%), Urubamba (2.11%), Vilcabamba (9.05%) and Vilcanota (22.96%).
Additionally, the majority of selected glaciers have been studied in term of hydrology, ablation and dynamics, especially the Cordillera Blanca and Cordillera Vilcanota have been intensely studied the in recent years [3,11,50,53,54].

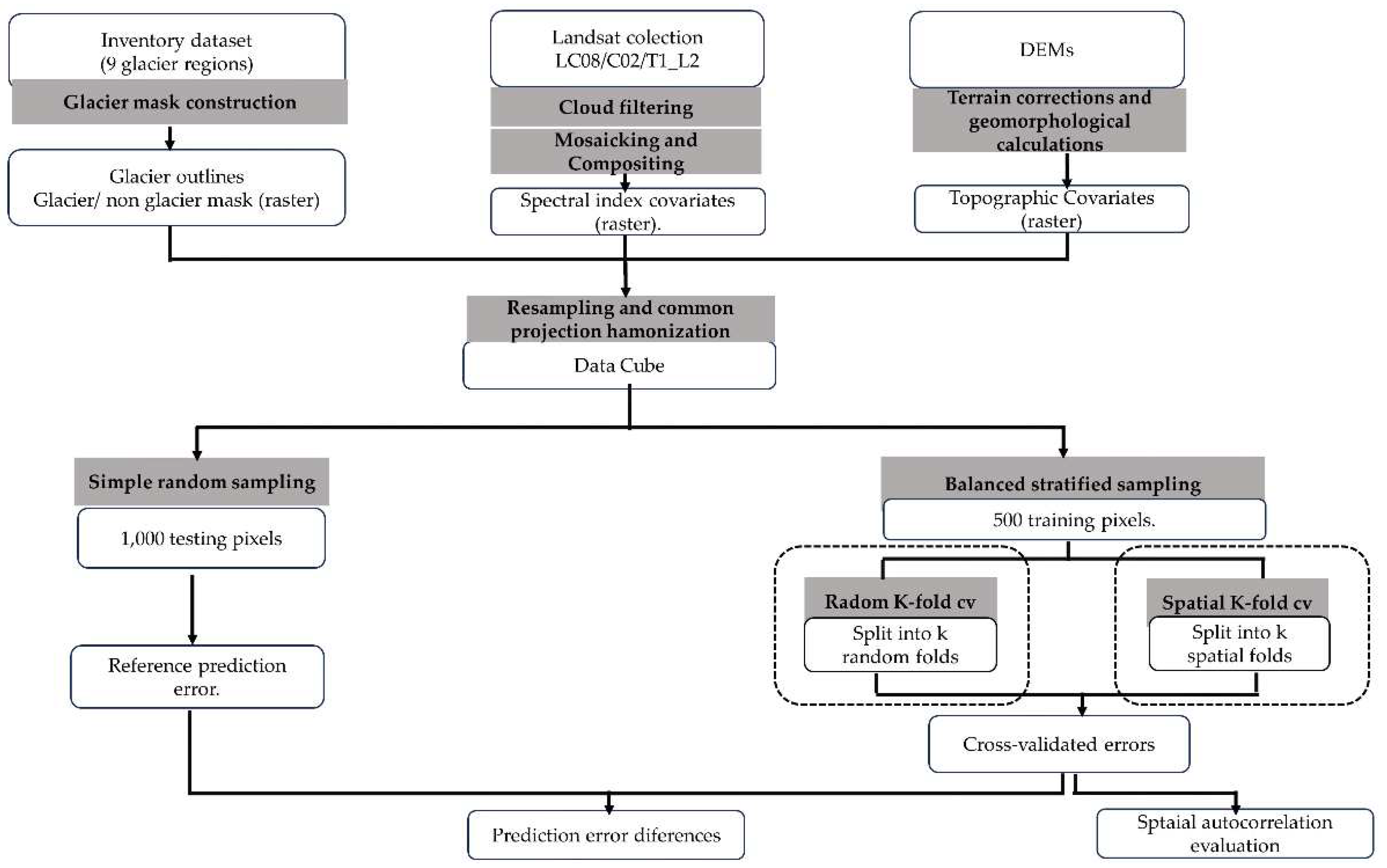
2.2. Data Acquisition

2.2.1. Glacier Inventory

The analysis was conducted using the National Glacier Inventory (NGI) dataset provided by [52] as the reference data. This dataset consisted of polygonal vector data representing glacier areas delineated using mostly Sentinel 2 and Landsat data and high-resolution Google Earth images with field survey studies.
NGI is a shape file of the 2017-2018 glacier outlines for the main glaciated mountain regions in the Peruvian Andes, covering the entirety of Peru with information concerning their code name, date of acquisition and remote sensing sensor used for delineation. To prepare the data for classification, the glacier outlines from the NGI were used to generate a binary raster mask I(x) of 30 m grid size with values 0/1 corresponding to non-glacier/glacier pixels which is achieved after Equation (1):
I x = 1 ,   i f   p i x e l   b e l o n g s   t o   g l a c i e r   c l a s s     0 ,     o t h e r w i s e .
Finally, the labels were projected to Universal Transverse Mercator (UTM) projection (UTM Zone 18S for subregion R1 and UTM Zone 19S for subregion R2). This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

2.2.2. Landsat Data and Processing

Landsat data corresponding to the period 2017–2018 were obtained from Landsat Collection 2 Level 2 and Tier 1 surface reflectance (SR) products [55] available online: https://www.usgs.gov/landsat-missions/landsat-collection-2-surface-reflectance (accessed on 1 July 2023). The Landsat image collections used were accessed and processed in the Google Earth Engine (GEE) platform [56]. For each selected glacier sub-region, a monthly composite was created using atmospherically corrected and topographic calibrated Landsat 8 OLI reflectance data imagery from the Tier 1 LANDSAT/LC08/C02/T1_L2 collection. The Landsat image collections used were accessed and processed in the Google Earth Engine (GEE) platform [56].
Table 1 provides an overview of the spectral characteristics of the OLI bands of Landsat-8. A more in-depth explanation of the Landsat Data processing steps is given below.
All available images from 2017 with a cloud cover less than 80% during the dry season (June and July) were filtered and selected. This period corresponds to the end of the ablation period, minimizing the potential confusion caused by transient snow cover, which could degrade the quality of the data and hinder accurate glacier discrimination [11,57]. In our study case, the implementation gets least cloudy scenes during the desired month in the dry season and nearby dates.
For the cloud masking we used the Band Quality Assessment (QA_PIXEL) information available in the Landsat Collection 2 Level 2 and Tier 1 surface reflectance (SR) images. Then we applied a spectral transformation by scale and offset parameters based on [58]. We created annual image composites for 2017 year using GEE’s image-reducing methods, having as an input all the cloud-masked Landsat scenes available in GEE’s Landsat collection that met our filter criteria. Finally, we got an annual Landsat mosaic composite conformed of Blue, Green, Red, NIR, SWIR1, SWIR2 reflectance bands for each AOI.

2.2.3. Normalized Difference Snow Index (NDSI)

The Normalized Difference Snow Index (NDSI) is a widely used index to separate snow from other land coverages, and therefore it is also useful to identify glacier coverage. Subsequently, NDSI has been extensively used for glacier mapping [6,9,10,11,59]. We computed NDSI values from each reflectance composite using Equation (2):
N D S I = ( ρ G r e e n − ρ S W I R ) /   ( ρ G r e e n + ρ S W I R ) ,
wheree ρ G r e e n   is the surface reflectance in the green band and ρ S W I R is the surface reflectance in the SWIR band. The use of NDSI as only mean of glacier detection is a common approach in glacier mapping generally with acceptable results [57,60,61]. In this work, we utilized the Normalized Difference Snow Index (NDSI) both as a covariate and as an independent method for delineating glacier outlines.

2.2.4. Digital Elevation Model (DEM)

The significance of topographic characteristics in glacier classification has been demonstrated, as the distinction between debris-covered and non-covered glaciers based solely on reflectance properties is practically impossible [12,30,59]. Accordingly, 10 topographic parameters including elevation, slope, aspect, profile curvature, plan curvature, longitudinal curvature, cross-sectional curvature, maximum curvature and minimum curvature were generated using SAGA GIS [62] using the 30-meter resolution JAXA’S ALOS WORLD 3D DEM downloaded from https://opentopography.org/ through the R package elevatr (https://github.com/jhollist/elevatr) for each glacier region under study.

2.2.5. Pixel Sampling and Classification Matrix Assembly

We build a label-predictors classification matrix by combining the NGI raster mask, Landsat surface reflectance derived products and topographic parameters as is explained in the following section.
Although it is common approach in glacier mapping to use all available pixel in a given reflectance scene [9,57], processing each pixel might be redundant for regional or national scale mapping specially with high spatial resolution (i.e.,30 meters) images and specially in an experiment-benchmark based studies. As such, computing resources were prioritized to process only a sample of pixels in each Cordillera.
Therefore, a stratified random sampling approach (SRS) [40,63] was employed to select a balanced sampling of pixels for each glacier region under study, hence the training samples were a subset of the available pixels within each scene, this approach is common in glacier mapping via machine learning [29,64]. Finally, all covariates and label rasters were harmonized to UTM Zone 18S and UTM Zone 19S glacier Cordilleras within subregion R1 an R2 respectively. This was done before cropping, resampling to 30 meters of spatial resolution and stacking. After preparing the data-cubes, the complete stacks of label-covariate rasters were discretized to 5,000 training pixels over all studied glacier Cordilleras (Table 2). With this harmonized dataset, each glacier area was processed one by one in the main workflow, allowing the implementation of modeling methods for individual study areas. Overall, all Landsat mosaic composite images cover a total area of 42 135 km2.

2.3. Machine Learning Classifiers

A large variety of machine learning (ML) methods have been used for spatial prediction and more specially in glacier mapping [28,42,64,65]. However, the focus of this paper is on the evaluation of CV methods. Thus, similar to previous cross validation comparison studies [36,43,45], we selected just a small amount of ML methods for our experiments: Random Forest (RF), Gradient Boosted Machines (GMB) and Weighted k-Nearest Neighbors (KKN), additionally a statistical model, Logistic Regression (LG). A detailed explanation of each model is outside of the scope of this study, but a brief summary is given for each model with relevant references for each.

2.3.1. Logistic Regression

The binary logistic regression takes the dependent variable in the form of binary data as presence (1) and absence (0) and linearly relates to the independent variable(s) [66]. Using an exponential function (sigmoid function), it calculates the probability of each input sample for classification. The multinomial binary logistic regression can be written as follows:
Z = a + ∑ i = 1 n b i x i
P ( Z ) = 1 1 + e − Z ,
where P(Z) is the probability; Z is a parameter; a is the intercept and b i ’s are the coefficients for independent variables x i ’s; the i index is for each covariate. Usually, the probability value of 0.5 is used to categorize data of either presence or absence class, and thereby compute the classification metrics (i.e., accuracy).

2.3.2. k-Nearest Neighbors

The Weighted k-Nearest Neighbors (KNN) algorithm is a supervised learning method which uses kernel functions to weight the neighbors according to their distances [67]. KNN classifies data points based on the closest k training samples in the feature space. It considered as non -parametric because KNN makes no statistical assumption about the data. KNN is a common classification algorithm used in remote sensing data mining applications and it has been widely used for mapping glacier surfaces [64,68].
Clustering with the k-means algorithm has the significant advantages of ease of interpretation, a high degree of flexibility and computational efficiency; however, its main disadvantage lies in the need to specify a priori the number of k clusters (Kopczewska, 2022). Moreover, three hyper-parameters have to be set: the number of nearest neighbors (k), the distance and the kernel are needed to set before training a KNN. In this research we implemented KNN using the knnn package for R (https://github.com/KlausVigo/kknn)

2.3.3. Random Forest

Random forest (RF) belongs to the group of ensemble learners, which builds upon a large number of basic model structures called Decision Trees (DT) that are trained in parallel. RF and merges the results of these DT together to get a more accurate and stable prediction compared to a single DT [69]. For each DT, a random subset of the training sample and a random subset of the classification features are used [69], hence each DT is trained independently.
Currently RF is the most common machine learning method used for geospatial predictions and is widely acknowledge for its general accuracy and successful applications in diverse geoscientific problems [17,19,22,49,70,71,72,73,74].
To train an RF model, some hyper-parameters should be selected, among others, the number of individual decision trees (ntree) and the number of features selected at each split of the trees (mtry). In this study the number of trees is kept at a moderate size of 100 to 500 trees for a balance between computational efficiency and predictive stability [75].

2.3.4. Gradient Boosting Machines

Gradient Boosting Machines (GBM) were first presented in [76], is another type of model based of ensemble learners. To generate the final prediction results, GBM could use weak learners in a sequential learning process, in the form of an ensemble of weak predictions such as DT. Unlike RF, in GBM Decision Tree learners (DT) are trained sequentially. GBM is a useful practical tool for different predictive tasks, and it can consistently provide more accurate results than the conventional single machine learning models [77,78,79]. A downside of GBM compared to RF, is that GBM has more hyperparameters that need to be calibrated.

2.4. Implementation

All modeling analyses were conducted using the R programming language, an open-source statistical software [80]. The algorithm implementations from several packages were employed, including gbm (https://github.com/harrysouthworth/gbm) for boosted regression trees [76], kknn [81] for weighted k-nearest neighbor classification (KNN), ranger [82] for random forest (RF) modeling based on [69].

2.5. Model Evaluation Metrics

2.5.1. Matthews Correlation Coefficient (MCC)

Evaluating binary classifications is a pivotal task in statistics and machine learning, because it can influence decisions in multiple areas.
To evaluate the accuracy of the models in binary classification problems, we employ the Matthews correlation coefficient (MCC), Equation 3, as an established and robust error measurement metric [83]. The MCC is derived from Cramér's V and is applied to a 2 × 2 traditional confusion matrix, consisting of true positives (TP), true negatives (TN), false negatives (FN), and false positives (FP):
M C C = T P × T N − F P × F N T P + F N × T P + F N × T N + F P × T N + F N
Given the number of experiments we ran in each glacier region, we focused solely on MCC for sequent comparative analysis because this was proved to be a balanced, more reliable summary of binary classification error than accuracy, F1 score and Kappa[83,84]. We choose not to use Kappa coefficient as is has proven to not to be a reliable measure of accurate classification and is difficult to interpret [85].
The Matthews correlation coefficient instead, generates a high score only if the classifier correctly predicted most of the positive data instances and most of the negative data instances, and if most of its positive predictions and most of its negative predictions are correct. A high Matthews correlation coefficient (close to +1) means always high values for all the four basic rates of the confusion matrix: true positive rate (TPR), true negative rate (TNR), positive predictive value (PPV), and negative predictive value (NPV).
It should be emphasized that in the classification results presented in this study, no manual modification of glacier outlines/areas was conducted, contrary to common practice. Although such modifications are typically carried out to improve classification accuracy, evaluating the effectiveness of these procedures is challenging due to their irreproducibility [12]. Moreover, attributing the accuracy results solely to manual corrections would undermine the primary objective of this study, which is to assess the accuracy of the algorithm and cross-validation method itself. This was important in our work as we needed to automatically analyze and compare different algorithm-dataset combinations.

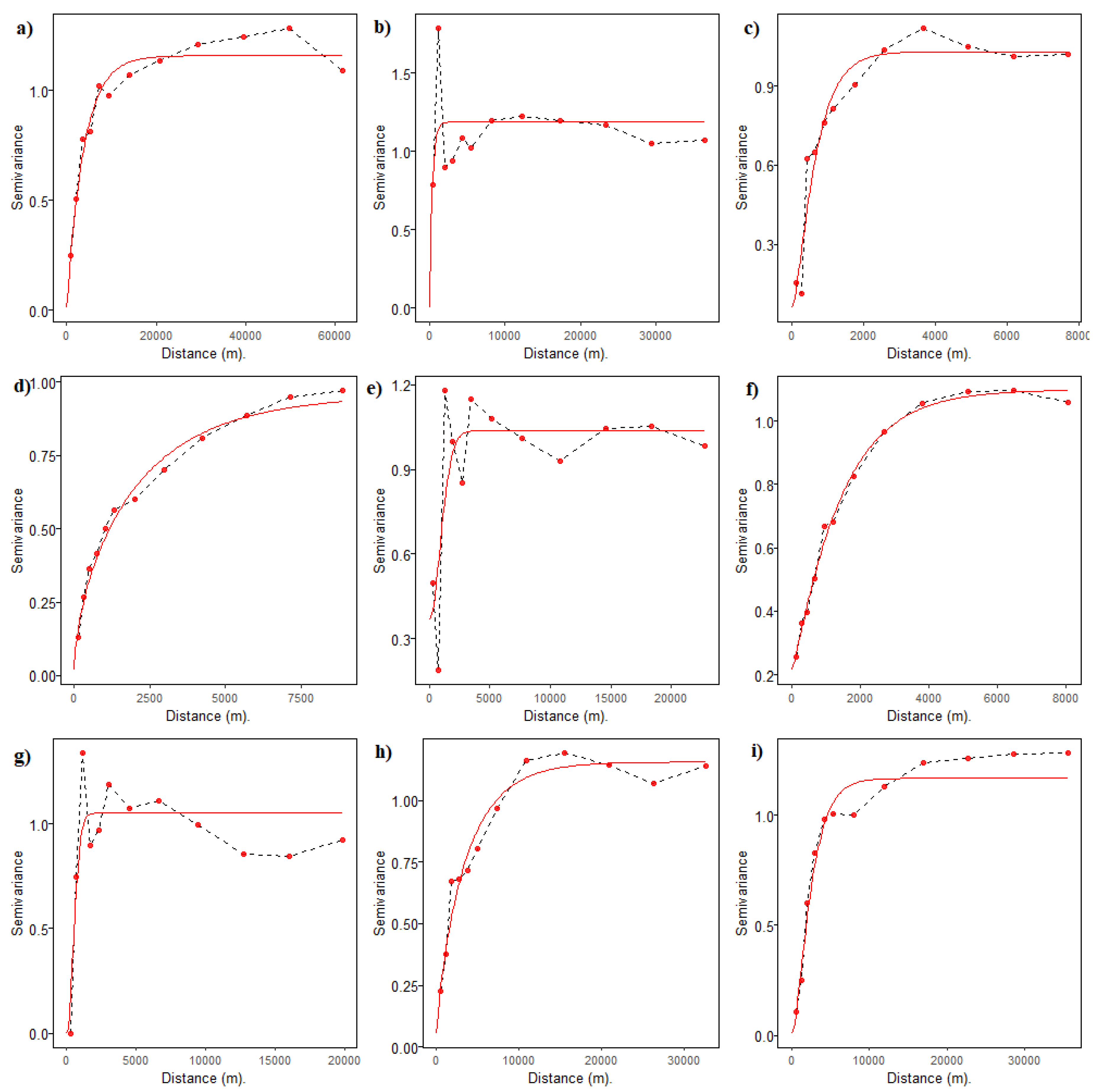
2.5.2. Moran’s I

Another way to assess the quality of a model applied on geographical data is that degree of spatial autocorrelation of errors [20]. Preferably the spatial autocorrelation of errors should be minimized or even eliminated, which would imply that the model performs similarly in space and that there are minimal (or no) subregions with strong patterns of over- or underestimated values [45,49]. The Moran’s I metric (MI) can be used for detect and quantify global spatial autocorrelation [86]. Therefore, Moran’s I were estimate from the absolute error of each model averaged for all repetitions for each glacier area.
MI varies from −1 to +1. A positive value means similar values happen in close proximity, while a negative value shows that dissimilar values are spatially grouped close to each other. A value close to zero shows no spatial autocorrelation for the variable, indicative of a spatially random process; in the latter case, the assumption of independence, essential for many statistical methods, is met [73].
In all cases Moran’s I was tested under Monte Carlo simulation and were derived from nearest neighbor spatial weights matrices based on k = 5 nearest neighbors using the R library spdep [87].

2.5.3. Spatial Autocorrelation of Glacier Class

Although cross-validation is a particularly well-established approach for model assessment of supervised machine-learning models [39,41,42,43] a particular issue is that spatial autocorrelation in the data can invalidate model validation approaches because an observation point cannot serve as spatially independent validation of nearby training data points [45]. Even so when the data points are spatially clustered, conventional cross-validation leads to optimistically biased estimates of map accuracy [45,49]. Therefore, when machine learning models are directly applied to spatial data we need to considering if spatial autocorrelation is present and to what extent [36].
To better understand the effect of spatial autocorrelation in our validation approaches, we test for spatial autocorrelation on class labels using indicator variogram analysis (Equation 6). The indicator semivariogram γ I can be inferred from the indicator class data using the estimator [32,88,89,90,91]:
γ I U k ; h = 1 2 n h ∑ i = i n ( h ) i U k ; x − i U k ; x + h ± ∆ h 2 ; k = 1 , … , m − 1
where U 1 , … , U m possible clases exist (in our case two classes for glacier and non- glacier surface, i.e., m = 2), n ( h ) is the number of pairs of indicator data that are a distance h ± ∆ h apart, finally the indicator random function or indicator transform i U k ; x of N ( x ) is defined using Equation 7:
I U k ; h = 1   i f   N x ∈   U 1 , … , U k             0   i f   N x ∈   U k + 1 , … , U m ; k = 1 , … , m − 1 .
where N x denotes the value of the random variable at pixel x . Since we already have binary class labels, we can readily apply equation 3 without apply the indicator transform in equation 2.
In order to model the indicator semivariograms for each glacier dataset, we employed various model specifications including the exponential, spherical, Gaussian, and Matern functions. Variograms were fitted by weighted least squares using N j / h j 2 as weights, where N j denotes number of points pairs in the j-th lag and h j 2 is the corresponding lag distance. The model that yielded the smallest residual sum of squares when compared to the sample variogram was selected as the final model. The variogram models were implemented using the gstat package for R [92,93].

2.6. Spatial Vs. Non-Spatial CV Comparison Experiment

Our experimental benchmark (illustrated in Figure 2) is mainly composed of 4 steps. Step 1 deals with the construction of training data and prediction locations from the entire dataset. In step 2 the prediction locations are applied to calculate the reference prediction error M C C r e f . This reference error is used to check which CV method can provide more accurate and unbiased predictions. In step 3 we implement both NSP-SP and SP-CV methods on the training dataset. This implementation provides estimated prediction errors M C C C V of each CV method. In step 4 we calculate the absolute difference ( d C V ) of the two error values, M C C r e f and M C C C V .

2.6.1. Step 1: Construction of Sample Data and Prediction Locations

In order to assess the accuracy of different CV methods, it is crucial to incorporate an unbiased reference prediction error is an indispensable element to include in the benchmarks. Therefore, CV methods cannot be implemented directly in the entire dataset, the dataset should be divided into two parts, one containing training data to implement CV methods, and the other containing prediction locations (test data) to provide a standard quasi real prediction error i.e., ( M C C r e f ). Therefore, the initial stage of the experiments involves the creation of sample datasets and prediction datasets for each Cordillera [46].
For the test data, we employed simple random sampling to generate 1000 independent sampled pixels for each glacier region being investigated, which served as the prediction locations. In contrast, the training samples were selected using a designed stratified sampling approach to ensure a balanced representation of the two classes [33,94]. This was done because it has been proven that class imbalanced in machine learning model can produce highly overoptimistic biased result [95].

2.6.2. Step 2: Calculate Reference Prediction Error

Since randomly independent prediction locations are directly used as the test set, the calculated value of reference prediction error M C C r e f can completely depict all model’s unbiased performances [34,40]. First, all the available training samples are used to build the benchmark models. Then, these models are used to predict in the independent test locations to obtain the reference error M C C r e f based on the prediction of the machine learning models at the prediction locations and the true class values. As mentioned earlier, the incorporation of the reference prediction error enables us to assess and compare the potential biases of machine learning models in the context of glacier classification.

2.6.3. Step 3: Calculate the Prediction Error of Each CV Method

In this stage we employed two cross-validation strategies to assess the predictive power of our models and generate the prediction error ( M C C C V ). The first strategy involved a standard K-fold cross-validation approach (NSP-CV), where observations were randomly divided into V subsets, ignoring any structure of spatial dependence in the data. The models were then trained iteratively on V-1 sets, with each subset V serving as a test set in a different iteration. The predicted vector of glacier and non-glacier land cover classes was used to calculate cross-validation error statistics, we focused on Matthew correlation coefficient (MCC). In our study, we used K = 5, representing five-fold cross-validation.
The second strategy, known as spatial K-fold CV (SP-CV), differs from random K-fold CV (NSP-CV) by considering the spatial structure of the data when partitioning observations into subsets. The objective is to group observations into spatially homogeneous clusters that are larger in size than the range of spatial autocorrelation, thereby achieving independence between cross-validation folds. In this work, we adopted the spatial cross-validation approach proposed by [47], and utilized by [43] which utilizes k-means clustering to mitigate the influence of spatial autocorrelation. In contrast to non-spatial cross-validation, spatial cross-validation partitions the data into spatially disjoint subsets, reducing the impact of spatial autocorrelation.
For the second CV scenario (i.e., SP-CV) we developed novel code to accommodate the specific characteristics of our dataset and research objectives. Since k-fold cross-validation is commonly used and well-known among machine learning practitioners [41,96], we provided a detailed explanation of the spatial cluster-based implementation instead in Figure 3:
In all experiments, k was set to 5. Both 10 and 5 are the most commonly used values in CV [36]. Then, each CV method was implemented 50 times (i.e., 50 repeated five-fold partitioning setting was chosen for performance estimation of M C C C V for each model). Thus, 250 models were fitted and tested at each glacier region and the average M C C C V was derived to account for random errors [36].

2.6.4. Step 4: Calculate CV Method’s Prediction Error Difference

After step 2 and step 3, we obtain the reference prediction error M C C r e f and the evaluation result of every CV method ( M C C C V ). By comparing them, we can find out which CV method produces more realistic results. For this purpose, we use the CV method’s prediction error difference ( d C V ) as a quantitative metric. We calculate by subtracting from and getting the absolute value ( d C V = M C C C V − M C C r e f ). When is closer to zero, the corresponding CV method’s performance is considered better.

2.7. Satistical Comparison of Model Results

In order to determine the influence of the two different validation scenarios on model performance, a paired t-test was carried out to see if there were significant differences in the results between models. The analysis was based on modified paired t-test [97] considering as factor the model and validation strategy used and as dependent variable the classification performance measure (i.e., MCC). The null hypothesis establishes that average differences between models’ results (i.e., MCC) are negligible, then both cross-validation approaches behave equally. For analyzing the results, we examined the p-values. Prior to applying the t-test, a Shapiro-Wilk test was conducted to confirm the normal distribution of the experimental results, as required by the test as in [98].

3. Results and Discussion

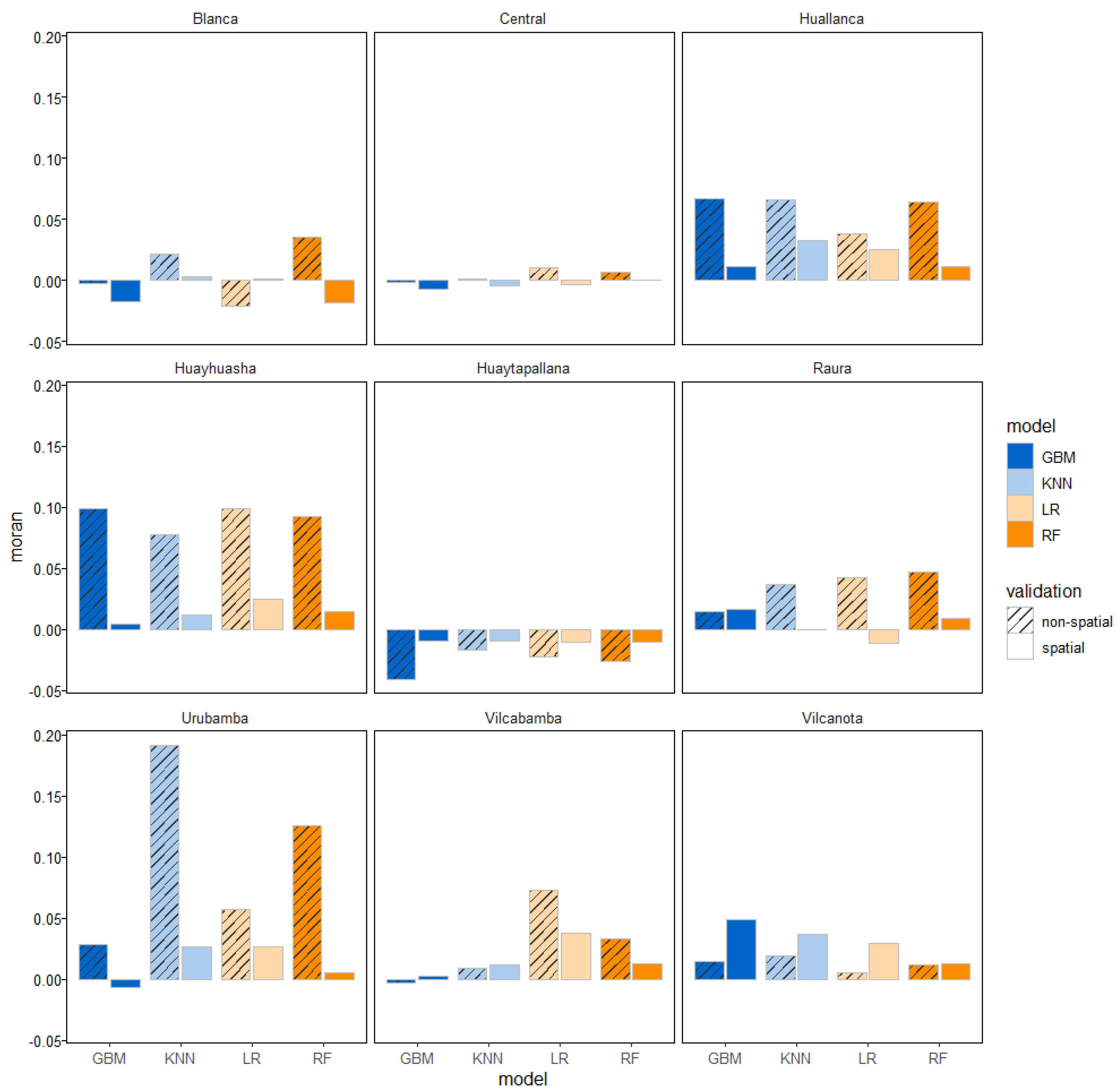
3.1. Spatial Autocorrelation

Semivariograms were calculated for the glacier class indicator variable for each glacier area under study to confirm the presence of spatial autocorrelation in the datasets.
Figure 4 shows the experimental and fitted indicator variograms for each glacier data set for 1000 test pixels, the semivariograms were rescaled by variance of each indicator variable to facilitate comparison across datasets. The parameters of the indicator variogram models of the 9 data sets are given in Table 3.
In general, it is clear that the glacier class sampled at 30 m resolution presents a significant spatial correlation, the smallest range of spatial dependence was found for cordilleras Central, Urubamba and Huallanca with ranges from 0.37, 0.68 and 0.87 Km respectively, and the largest range was found for cordillera Blanca (5.42 Km).
For some glacier regions the indicator semivariograms display a very large nugget effect and a short-range structure (i.e., Central, Huaytapallana and Urubamba), as well as bigger kappa parameters, indicating a fairly constant spatial process in those cases. But in general, relative larger ranges and smaller nugget effects occur for the majority of other regions. For instance, in the cordillera Blanca case, the indicator variogram shows that at a 30 m resolution km spatial resolution, glacier class presents a significant spatial correlation up to 5.42 km (Figure 4). This spatial autocorrelation can notably be observed in almost all cases, where clusters of homogeneous glacier class values are present. The cordillera Blanca region exhibited a larger range due to its considerably larger area (13,963 Km2). The absence of similar range behavior in other areas can be attributed to the substantial differences in the overall size and extent of each individual region because glaciers assume a size and flow rate that are in balance with local climate [15].
Given the relatively high sampling intensity (and resulting proximity) of glacier class pixels selected for this work, and the long range of spatial autocorrelation in the data (i.e., 5 km), it is obvious that any given randomly selected test pixel will not be independent from a large number of neighboring pixels, thereby violating the core hypothesis of model validation (i.e., the independence between training and test sets). This result probably doesn’t hold for the regions for which variograms revealed poor spatial structure like Central, Huaytapallana and Urubamba Cordilleras. This suggest that a spatial cross validation method could possibly be useful in this context [36].
It is worth to note that no stationarity assumptions are needed since the indicator variograms are simply used as a means to describe the spatial structure of the data, rather than to perform a model based inferential spatial prediction of a spatial process.

3.2. Model Specification

For the benchmark, all models were trained using either default hyperparameter values and/or recommendations from the literature that were specifically tailored to our case data. A detailed summary of the models and hyperparameters is shown in the Table 4.

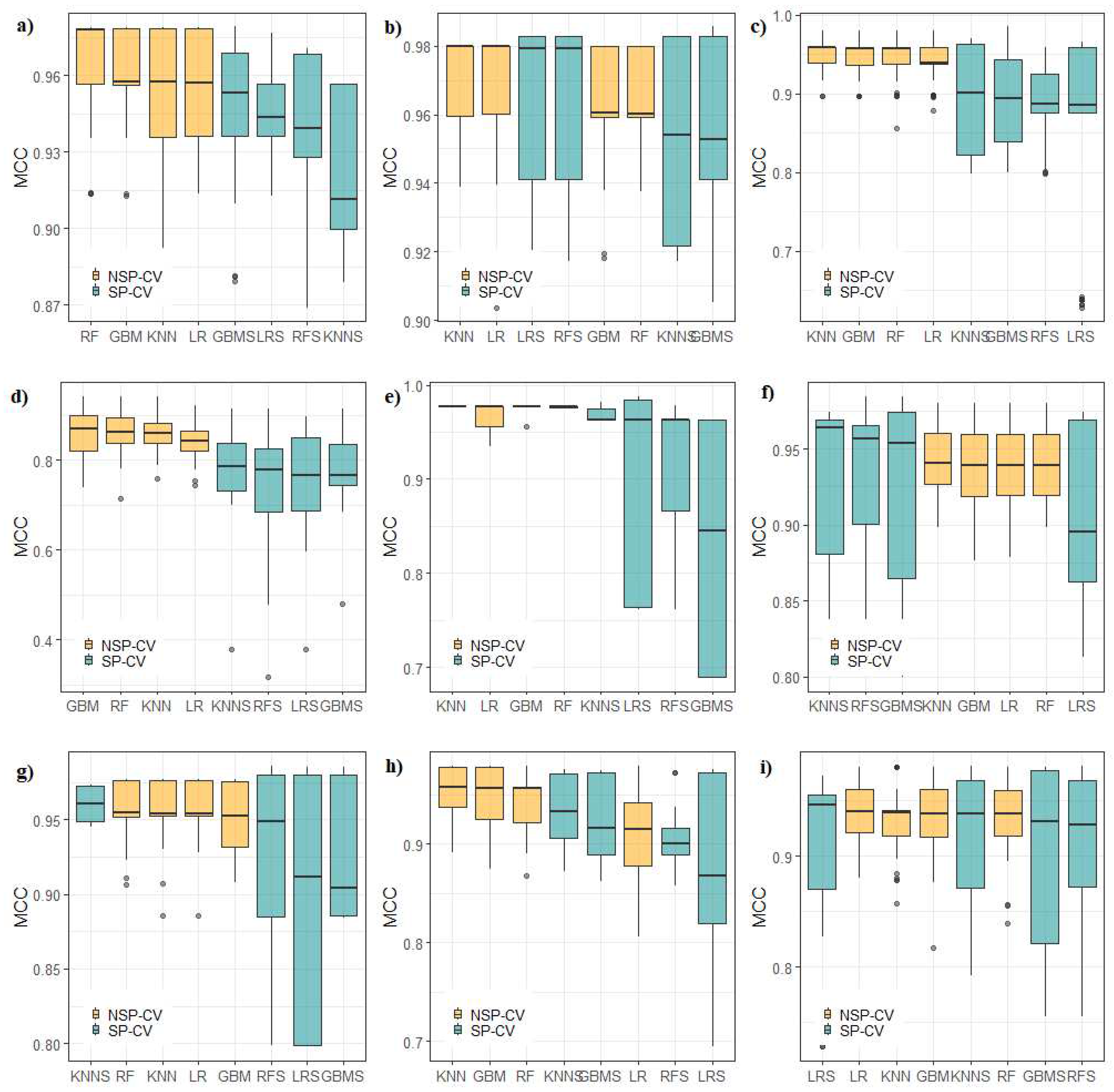
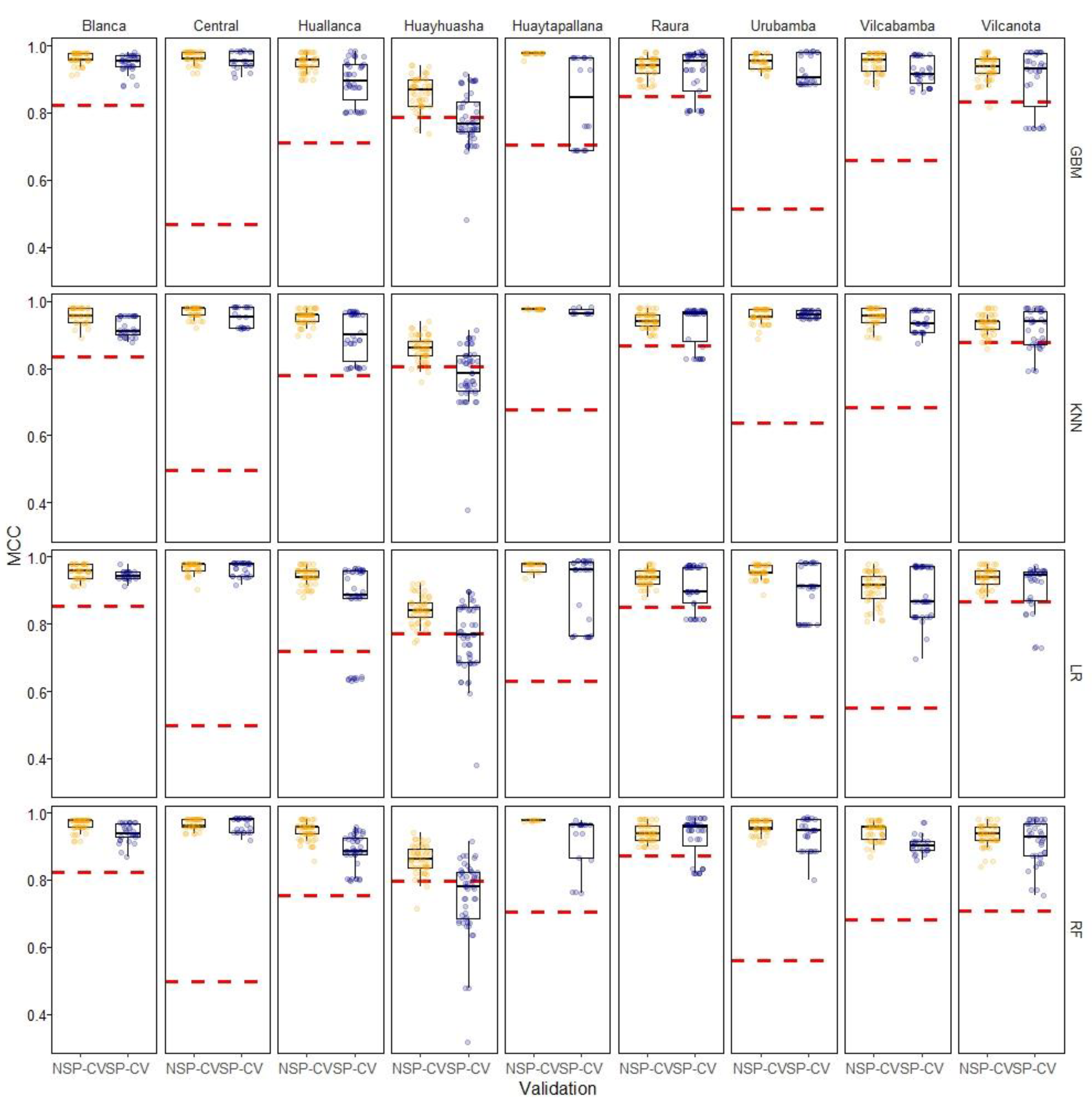
3.3. Spatial Vs. Non-Spatial CV Comparison Experiment

Figure 5 shows the results of our experimental benchmark. It is possible to identify the models that exhibit superior and inferior performance in both scenarios. In NSP-CV settings, K-nearest neighbors (KNN) was the overall best model across regions consistently demonstrating the highest performance followed by logistic regression (LR) and random forest (RF). The SP-CV settings, generally shown lower MCC values, K-nearest neighbors (KNN) remained as the overall best model in almost all regions, followed by gradient boosting machines (GBM) and logistic regression (LR), in Cordillera Blanca and Central respectively. Some studies have found that KNN shows the best predictive performance in spatial settings [81,99] although this is generally not the case [43,100,101,102].
Although SP-CV generally shows lower MCC results than NSP-CV, this is not always the case, especially in Cordillera Central, Raura, Urubamba, and Vilcanota. We hypothesize that these results are connected with the degree of spatial autocorrelation/clustering of the glacier class in these specific Cordilleras. For example, Cordilleras Central and Urubamba present almost a pure nugget effect, which could have generated the mixed response of MCC to both validation approaches. Hence, it is impossible to distinguish the effect of SP-CV from NSP-CV in the presence of weak spatial autocorrelation.
Surprisingly logistic regression (LR) demonstrates good performance in some cases in this quasi-linear problem, without clear evidence of being surpassed by models such as random forest (RF) and boosted trees (GBM) in some cases, as commonly acknowledged in other geospatial contexts [17,43,74]. This result shows the importance of traditional parametric approaches in spatial modeling which make this algorithm a valid choice, especially if the differences in predictive accuracy compared to black-box models are small
Concerning the poor performance of random forest (RF), the literature generally agrees upon its general applicability in geospatial contexts as a "go-to" model [17,43,60,74,103]. RF uses "bagging" (bootstrap aggregation). As spatial data is correlated, this resampling violates the assumption of independent and identically distributed (i.i.d.) data units, which is fundamental to bootstrapping. [104] provided evidence that these limitations could lead to inferior prediction performance of RF under spatial dependence, and this could be the reason for the observed performance of RF.
There were notable differences in the distribution of the estimated MCC between the spatial and nonspatial settings (i.e., M C C S P − C V and M C C N S P − C V ). Figure 6 shows the results for both CV methods for each glacier region under study along the reference error M C C r e f in red doted horizontal lines.
First and foremost, it can be seen than almost in all cases the SP-CV and NSP-CV methods produced quite different results in terms of MCC, it is also remarkable that the proposed SP-CV, which consider the clustered nature of the data, produce closer evaluation results to the reference prediction MCC than NPS-CV in almost all cases. This suggests that SP-CV may produce bias reduced spatial predictions when using ML models for glacier mapping, especially when training locations area scare and highly clustered as is usual in glacier monitoring and mapping. As expected, the SP-CV results shown high variance for all models.
Upon careful examination of Figure 6, Cordillera Central, Urubamba, and Vilcabamba, it can be found quite high differences between CV-MCCs and the test MCC (dotted red lines in Figure 6), regardless of the validation approach. It seems that, in those particular cases, both CV methods are incapable of estimating the true error of the models. This indicates the presence of biased results, even when employing the spatial cross-validation approach suggested in this study. Although there could be multiple reasons to explain these results, we hypothesize that they are due to possible overfitting of the models in those specific areas.
A more detailed analysis can be found in Table 5 that shows the mean MCC grouped by Cordillera and CV method as well the difference regard to the test reference MCC (in parenthesis). For example, Cordillera Blanca mean MCC for NSP-CV models is 0.949, while mean MCC for SP-CV models is 0.928, and their difference with respect to the reference independent test (i.e., M C C r e f 0.844) are 0.1054 and 0.0845 respectively.
Overall, the spatial 5- fold CV led to a slightly decline in model’s MCC (i.e., about - 4%) respect to the non-spatial k fold method. Likewise, the SP-CV yields a sharp decline in biases ( d C V ). compared to the reference MCC evaluated at the test-sets (i.e., about - 18%).
Furthermore, SP-CV’s evaluation results were much closer to the reference prediction error than the results of NSP-CV for all glacier regions under study. This shows that the proposed method, which considers the spatial structure of the data in the evaluation of the model could indeed provide a reasonable unbiased result. To further strengthen this observation, it is important to analyze the individual model’s discrepancy between the SP-CV and NSP-CV MCC estimates obtained in the benchmark’s settings, which will be explored in the subsequent section.

3.4. Satistical Comparison of Model Results

We carried out a comparative statistical analysis of the results using non-parametric statistical tests to compare the performances of all the considered models. Table 6 shows the t-statistics and the p-values (in parenthesis) of paired t-test comparison for the MCC results obtained after the 50-repeteated 5-fold CV using the two types of cross-validation for each glacier region (p-values < 0.05 means that there is a significance statistical difference between cross-validated MCC results and p-value > 0.05 means that both cross-validation approaches yield equal results).
Based on the statistical analysis, considering the results of the paired t-test, it is not definitively conclusive to assert that spatial cross-validation (SP-CV) yields significantly different Matthew’s correlation coefficient (MCC) estimates compared to non-spatial cross-validation (NPS-CV) in the majority of cases with exception of remarkable cases that need further clarification:
For Cordillera Blanca only GBM and KNN models showed significant differences (p-value < 0.05). For Cordillera Huallanca, Huayhuash and Vilcabamba RF was the only model that showed significant differences. For Cordillera Huaytapallana only GBM showed significant differences. For Cordillera Urubamba only LR showed significant differences.
Some algorithms showed no sensitivity to the cross-validation method (i.e., KNN and LR). Since KNN is the best model overall in all cases regardless the CV method, this suggests that KNN can produce more reliably estimates of error, and at the same time the best performing predictions. On the other hand, some algorithms were quite sensible to the cross-validation method. RF showed, especially RF showed significant differences between SP-CV MCC’s and NP-CV MCC’s. In all those cases, the null hypothesis establishes that average differences between error’s models (i.e., MCC) are non-negligible. Therefore, this difference can be attributed to an overoptimistic bias in nonspatial performance estimates in the presence of spatial autocorrelation [36,43,46,72,74].
However, it should be noted that these results may slightly vary depending on the data distribution within each fold and the randomization in each repetition, which can impact the comparison tests [43]. Nonetheless, given the considerable number of repetitions in the experiments, these results are generally robust.
While our results align with previous studies, such as those by [43,105] and [45] suggesting that non-spatial performance estimates tend to be significantly “superior´’ to spatial performance estimates, it is important to note that our experiments do not allow for such a definitive statement in all cases. The observed differences in performance between spatial and non-spatial estimates in our study may not be as pronounced or statistically significant regardless of the classification algorithm.

3.5. Spatial Autocorrelation of Errors

Is traditionally acknowledge that when applying standard ML models in a spatial prediction setting, errors could remain depended in space due to failing to account for spatial dependency or heterogeneity in important explanatory variables or in model architecture [72,106,107]
Correspondences between predicted and label class data were indicator coded. If the class of the test sampled pixel matched with that of the prediction class, an indicator code 1 was assigned to that sample pixel. Conversely, an indicator code 0 was given to sites where the predicted class differed from the test class. These values were identified as classification errors and obtained through the 50 repeated spatial 5-fold either spatial and non-spatial cross-validation (i.e., SP-CV and NSP-CV) and then aggregated through a simple majority vote approach for all repetitions. Next, we analyzed spatial autocorrelation of the indicator-coded data using Moran's I.
Figure 7 shows that regardless of the type of modeling algorithm, there were low MI values with statistically non-significant p-values, (i.e., p values greater to 0.05). At first it seems that SP-CV could possibly reduce the spatial dependence of errors compared to NSP-CV which shows generally higher MI values (i.e., spatial correlated errors). Thus, suggesting that in our SP-CV validation method, spatial structure of errors is completely eliminated in all glacier regions but not in NSP-CV. But a closer inspection of p-values (not shown in figure) suggest that the Null hypothesis should not be rejected and the spatial error patterns are almost random in both cross-validation scenarios.
Urubamba was the only exception in terms of significant MI p-values, especially when KNN model was applied, indicating the occurrence of spatial correlated errors. Overall, after either SP-CV and NSP-CV methods, the errors’ spatial structure was completely absorbed by almost all the models in all the glacier regions (statistically non-significant p-values) regardless the CV approach.
These results suggest that our expectation that the inclusion of spatial information in SP-CV method is supposed to capture the spatial autocorrelation of errors better than the NSP-CV doesn’t hold for glacier classification errors in the Tropical Andes using machine learning algorithms.

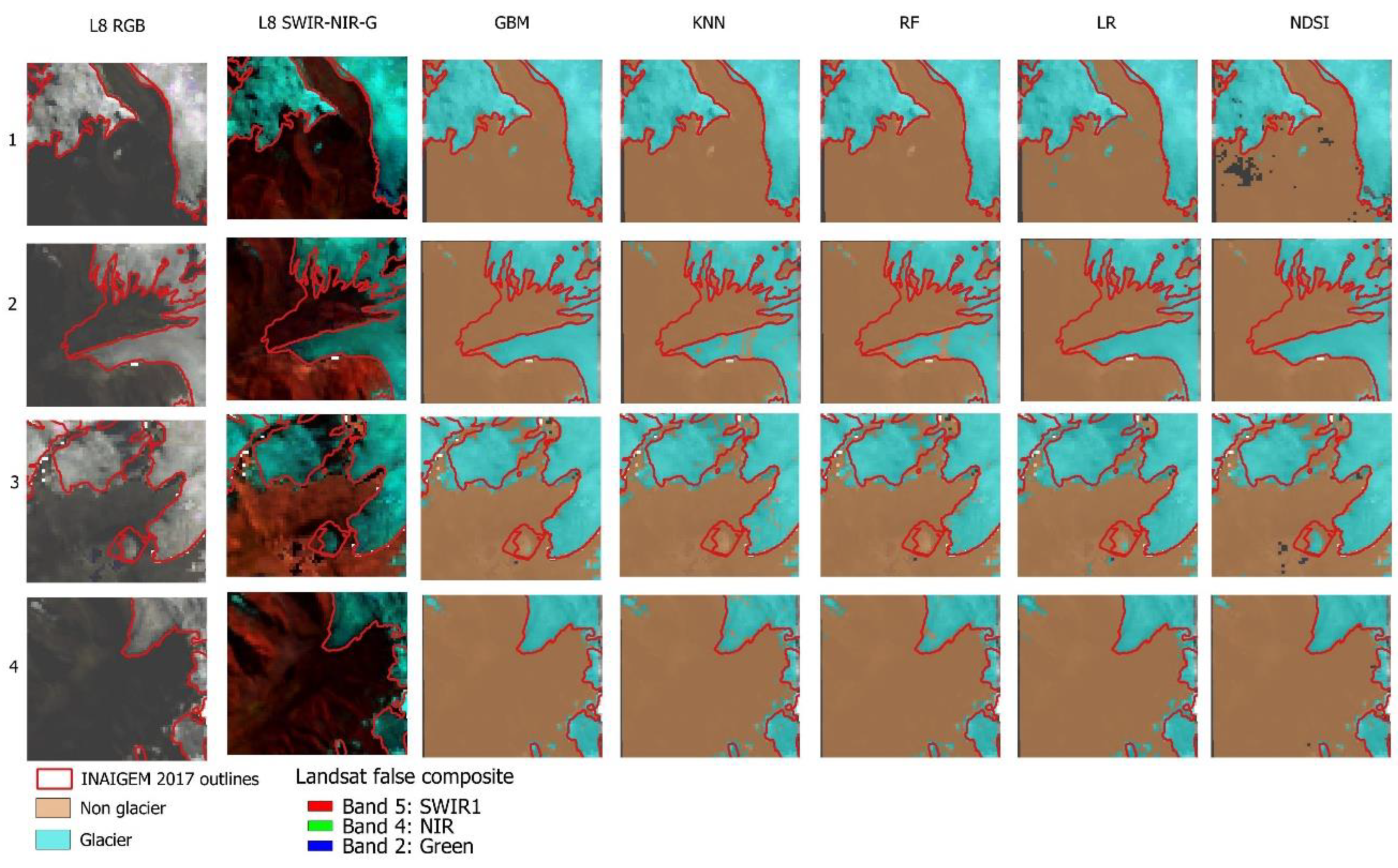
3.6. Spatial Predictions

Finally, we generated glacier outline maps over all studied regions using trained models to visually inspect and compare the predictions. For predict glacier class we took the approach of [108] described in [45]. We used all available pixels of each area to fit the final prediction models. As the error estimates from such a model are invalid, error estimates derived from the blocked cross-validation methods should still be used. This approach favors final prediction quality over perfect accuracy of error estimates. It has the advantage of using all the data and thus likely being the best predictor, particularly for smaller datasets. It has the disadvantage that the error estimates from the cross-validation no longer apply perfectly to the predictions, as they were made with slightly different models.
To analyze the predictions in greater detail we show a set of predictions on four small areas within Cordillera Blanca (Figure 8). Overall, the spatial distribution of the model predictions is quite similar. Here, KNN is not clearly the best predictor all around, as all the outlined maps exhibit a strong agreement with the NGI outline. There are, however, certain areas showing overestimation and underestimation of glacier surfaces. Notably, overestimation is noticeable, particularly near the glacier periphery of NGI in inset 3. In inept 2 we observe some areas of underestimation, where glaciers areas were misclassified as non-glacier, especially in the case of KNN and RF algorithms.
These classification errors could be attributed, to some extent, to the compositing and cloud filtering of Landsat 8 images in GEE. This filtering process might lead to the improper detection of transient snow areas, which are then mistaken for glaciers. Importantly, this phenomenon is not observed in other prediction areas. This highlights the significance of the cloud filtering algorithm, as snow pixels can seriously undermine the performance of machine learning models of glacier classification. Additionally, the spatial resolution of Landsat imagery used in this study can introduce a substantial number of mixed pixels—pixels that encompass both the glacier and the surrounding terrain. To address the former issue, a series of recommended algorithms has been previously suggested [57].
The debris-free outline map generated using the NDSI approach exhibits a high degree of similarity with the NGI outlines, although not perfect, probably due to NDSI being the current operational method for glacier mapping in Perú [11,52]. Although high similar, differences exist because our approach uses Landsat 8 imagery, whereas the NGI uses Sentinel 2 and Landsat 8 as well.
Prior studies have already concluded that debris-free ice can be accurately mapped using simple methods, such as the band ratio of the Red/NIR bands of Landsat or S2 data [26,42,53,64,109]. While our primary objective was to compare the predictive classification errors of machine learning algorithms using spatially distributed glacier class data, it's important to note that NDSI and band ratio approaches remain robust and widely used methods in remote sensing-based glacier monitoring. As this research demonstrates, these methods should not be dismissed. Nevertheless, evaluating the classification errors of glacier mapping using these approaches requires a proper assessment, typically involving a comparison with high-resolution satellite images [30,109], a procedure which is highly manual and inefficient. Therefore, we hope that a statistically sound approach could enhance current national glacier mapping efforts.

3.7. Methodological Limitations of the Study

Although machine learning (ML) has been effectively used to map glaciers in recent years [110], for example, [64] used approaches such as K-nearest neighbors (KNN), while [111,112] employed Random Forest (RF). The use of deep learning segmentation algorithms has been recently suggested for glacier mapping [42,110]. However, the computational cost can be high, limiting nationwide mapping efforts at the moment. Additionally, deep learning approaches have disadvantages compared to conventional machine learning algorithms, as spatial validation methods cannot be readily applied to them.
Some limitations detected in this work concern primarily the training/testing pixel sampling schema. When using multi-spectral optical satellite data for glacier mapping, an independent validation sample is usually not used, and maps are validated either manually [5,53,57] or through a comparison with high-resolution satellite images [30,109]. On the other hand, some studies used an independent sample [9] as a means of validation. We would argue that the size of the training and validation samples would inevitably affect the classification and validation results.
We acknowledge that hyperparameter tuning would likely yield better results or slightly alter the best model's outcomes [107]. A few previous studies have tested the effects of hyperparameter tuning and spatial cross-validation. For example, [43] implemented hyperparameter tuning in both spatial and non-spatial settings with mixed results. Therefore, here we fixed the hyperparameters for ease of comparison between the proposed validation methods, a similar approach that has been used by [36].
We also hypothesize that the size of the validation blocks needs calibration, as previous results suggested [36]. The size of the blocks should be substantially larger than the range of spatial autocorrelation in the model residuals to provide a reliable error estimate.
In general, we suggest that more work needs to be done to (1) incorporate different pixel sampling schemes and sample sizes into consideration, (2) develop experimental benchmarks that incorporate hyperparameter tuning, and (3) understand the effect of the spatial dimensions of validation blocks on the possible reduction of error estimates.

4. Conclusions

Here we have experimentally explored the effects of machine learning algorithm and cross validation in terms of glacier classification performance. If spatial dependence in the validation approach is not taking into account, our study provides that with the exception of Cordillera Blanca, Huayhuash and Vilcanota where Random Forest, GBM and logistic regression respectively outperforms in terms of Matthew correlation coefficient, KNN outperformed other models. In the SP-CV settings, the results change sightly, K-nearest neighbors (KNN) remained as the overall best model in almost all regions, followed by gradient boosting machines (GBM) and logistic regression (LR) in Cordillera Blanca and Central respectively. More importantly, we found that non-spatial cross validation leads to overoptimistic performance results (up to 18%), especially in the presence of spatial autocorrelation. Although these differences are not always statistically significant, we would recommend to use spatial CV instead of non-spatial CV for estimating the prediction performance of machine models when using spatial data, as only this ensures the assessment of bias-reduced predictive performance results, and as the error estimates are always conservative, this is especially important when the corresponding results form the basis of conservation and policy making.

Author Contributions

Conceptualization, Marcelo Bueno; Data curation, Marcelo Bueno and Brigitte Macera ; Formal analysis, Marcelo Bueno; Investigation, Marcelo Bueno; Methodology, Brigitte Macera ; Software, Marcelo Bueno; Supervision, Nilton Montoya; Validation, Marcelo Bueno and Nilton Montoya; Writing – original draft, Marcelo Bueno; Writing – review & editing, Marcelo Bueno and Nilton Montoya.

Funding

This study was funded by the National Council for Science, Technology, and Technological Innovation (CONCYTEC) of Peru and the Newton Fund of England. N_ 005-2019-PROCIENCIA. Peru

Data Availability Statement

The data presented in this study is available in Zenodo repository at: https://doi.org/10.5281/zenodo.8220980. Additionally, the code to replicate our process can be found in the following GitHub repository: https://github.com/kundun14/glacier_mapping_peru.

Acknowledgments

This study was developed within the framework of the NewtonPaulet Fund based RAHU project which is implemented by CONCYTEC Peru and UKRI (NERC grant no. NE/S013210/1).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Veettil, B.K.; Kamp, U. Remote Sensing of Glaciers in the Tropical Andes: A Review. International Journal of Remote Sensing 2017, 38, 7101–7137. [Google Scholar] [CrossRef]
  2. Drenkhan, F.; Carey, M.; Huggel, C.; Seidel, J.; Oré, M.T. The Changing Water Cycle: Climatic and Socioeconomic Drivers of Water-related Changes in the Andes of Peru. WIREs Water - Wiley Online.
  3. Salzmann, N.; Huggel, C.; Rohrer, M.; Silverio, W.; Mark, B.G.; Burns, P.; Portocarrero, C. Glacier Changes and Climate Trends Derived from Multiple Sources in the Data Scarce Cordillera Vilcanota Region, Southern Peruvian Andes. The Cryosphere 2013, 7, 103–118. [Google Scholar] [CrossRef]
  4. Taylor, L.S.; Quincey, D.J.; Smith, M.W.; Potter, E.R.; Castro, J.; Fyffe, C.L. Multi-Decadal Glacier Area and Mass Balance Change in the Southern Peruvian Andes. Frontiers in Earth Science 2022, 10. [Google Scholar] [CrossRef]
  5. Silverio, W.; Jaquet, J.-M. Glacial Cover Mapping (1987–1996) of the Cordillera Blanca (Peru) Using Satellite Imagery. Remote Sensing of Environment 2005, 95, 342–350. [Google Scholar] [CrossRef]
  6. Durán-Alarcón, C.; Gevaert, C.M.; Mattar, C.; Jiménez-Muñoz, J.C.; Pasapera-Gonzales, J.J.; Sobrino, J.A.; Silvia-Vidal, Y.; Fashé-Raymundo, O.; Chavez-Espiritu, T.W.; Santillan-Portilla, N. Recent Trends on Glacier Area Retreat over the Group of Nevados Caullaraju-Pastoruri (Cordillera Blanca, Peru) Using Landsat Imagery. Journal of South American Earth Sciences 2015, 59, 19–26. [Google Scholar] [CrossRef]
  7. Juen, I.; Kaser, G.; Georges, C. Modelling Observed and Future Runoff from a Glacierized Tropical Catchment (Cordillera Blanca, Perú). Global and Planetary Change 2007, 59, 37–48. [Google Scholar] [CrossRef]
  8. Buytaert, W.; Moulds, S.; Acosta, L.; De Bièvre, B.; Olmos, C.; Villacis, M.; Tovar, C.; Verbist, K.M.J. Glacial Melt Content of Water Use in the Tropical Andes. Environ. Res. Lett. 12 114014 2017. [Google Scholar] [CrossRef]
  9. Turpo Cayo, E.Y.; Borja, M.O.; Espinoza-Villar, R.; Moreno, N.; Camargo, R.; Almeida, C.; Hopfgartner, K.; Yarleque, C.; Souza, C.M. Mapping Three Decades of Changes in the Tropical Andean Glaciers Using Landsat Data Processed in the Earth Engine. Remote Sensing 2022, 14, 1974. [Google Scholar] [CrossRef]
  10. Muñoz, R.; Huggel, C.; Drenkhan, F.; Vis, M.; Viviroli, D. Comparing Model Complexity for Glacio-Hydrological Simulation in the Data-Scarce Peruvian Andes. Journal of Hydrology: Regional Studies 2021, 37, 100932. [Google Scholar] [CrossRef]
  11. Veettil, B.K. Glacier Mapping in the Cordillera Blanca, Peru, Tropical Andes, Using Sentinel-2 and Landsat Data. Singapore Journal of Tropical Geography 2018, 39, 351–363. [Google Scholar] [CrossRef]
  12. Paul, F.; Barrand, N.E.; Baumann, S.; Berthier, E.; Bolch, T.; Casey, K.; Frey, H.; Joshi, S.P.; Konovalov, V.; Bris, R.L.; et al. On the Accuracy of Glacier Outlines Derived from Remote-Sensing Data. Annals of Glaciology 2013, 54, 171–182. [Google Scholar] [CrossRef]
  13. López-Moreno, J.I.; Fontaneda, S.; Bazo, J.; Revuelto, J.; Azorin-Molina, C.; Valero-Garcés, B.; Morán-Tejeda, E.; Vicente-Serrano, S.M.; Zubieta, R.; Alejo-Cochachín, J. Recent Glacier Retreat and Climate Trends in Cordillera Huaytapallana, Peru. Global and Planetary Change 2014, 112, 1–11. [Google Scholar] [CrossRef]
  14. INAIGEM Manual Metodológico de Inventario Nacional de Glaciares; Instituto Nacional de Investigación en Glaciaresy Ecosistemas de Montaña: Huaraz, 2017.
  15. Raup, B.; Racoviteanu, A.; Khalsa, S.J.S.; Helm, C.; Armstrong, R.; Arnaud, Y. The GLIMS Geospatial Glacier Database: A New Tool for Studying Glacier Change. Global and Planetary Change 2007, 56, 101–110. [Google Scholar] [CrossRef]
  16. Gao, B.; Stein, A.; Wang, J. A Two-Point Machine Learning Method for the Spatial Prediction of Soil Pollution. International Journal of Applied Earth Observation and Geoinformation 2022, 108, 102742. [Google Scholar] [CrossRef]
  17. Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.M.; Gräler, B. Random Forest as a Generic Framework for Predictive Modeling of Spatial and Spatio-Temporal Variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef] [PubMed]
  18. Janowicz, K.; Gao, S.; McKenzie, G.; Hu, Y.; Bhaduri, B. GeoAI: Spatially Explicit Artificial Intelligence Techniques for Geographic Knowledge Discovery and Beyond. International Journal of Geographical Information Science 2020, 34, 625–636. [Google Scholar] [CrossRef]
  19. Meyer, H.; Reudenbach, C.; Wöllauer, S.; Nauss, T. Importance of Spatial Predictor Variable Selection in Machine Learning Applications – Moving from Data Reproduction to Spatial Prediction. Ecological Modelling 2019, 411, 108815. [Google Scholar] [CrossRef]
  20. Nikparvar, B.; Thill, J.-C. Machine Learning of Spatial Data. ISPRS International Journal of Geo-Information 2021, 10, 600. [Google Scholar] [CrossRef]
  21. Bonfatti, B.R.; Demattê, J.A.M.; Marques, K.P.P.; Poppiel, R.R.; Rizzo, R.; Mendes, W. de S.; Silvero, N.E.Q.; Safanelli, J.L. Digital Mapping of Soil Parent Material in a Heterogeneous Tropical Area. Geomorphology 2020, 367, 107305. [Google Scholar] [CrossRef]
  22. Gupta, S.; Papritz, A.; Lehmann, P.; Hengl, T.; Bonetti, S.; Or, D. Global Mapping of Soil Water Characteristics Parameters— Fusing Curated Data with Machine Learning and Environmental Covariates. Remote Sensing 2022, 14, 1947. [Google Scholar] [CrossRef]
  23. Hengl, T.; Mendes de Jesus, J.; Heuvelink, G.B.M.; Ruiperez Gonzalez, M.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global Gridded Soil Information Based on Machine Learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [PubMed]
  24. Brenning, A. Spatial Prediction Models for Landslide Hazards: Review, Comparison and Evaluation. Natural Hazards and Earth System Sciences 2005, 5, 853–862. [Google Scholar] [CrossRef]
  25. Rolnick, D.; Donti, P.L.; Kaack, L.H.; Kochanski, K.; Lacoste, A.; Sankaran, K.; Ross, A.S.; Milojevic-Dupont, N.; Jaques, N.; Waldman-Brown, A.; et al. Tackling Climate Change with Machine Learning 2019.
  26. Baraka, S.; Akera, B.; Aryal, B.; Sherpa, T.; Shresta, F.; Ortiz, A.; Sankaran, K.; Ferres, J.L.; Matin, M.; Bengio, Y. Machine Learning for Glacier Monitoring in the Hindu Kush Himalaya 2020.
  27. Caro, A.; Condom, T.; Rabatel, A. Climatic and Morphometric Explanatory Variables of Glacier Changes in the Andes (8–55°S): New Insights From Machine Learning Approaches. Frontiers in Earth Science 2021, 9. [Google Scholar] [CrossRef]
  28. Li, X.; Wang, N.; Wu, Y. Automated Glacier Snow Line Altitude Calculation Method Using Landsat Series Images in the Google Earth Engine Platform. Remote Sensing 2022, 14, 2377. [Google Scholar] [CrossRef]
  29. Lu, Y.; Zhang, Z.; Huang, D. Glacier Mapping Based on Random Forest Algorithm: A Case Study over the Eastern Pamir. Water 2020, 12, 3231. [Google Scholar] [CrossRef]
  30. Paul, F.; Huggel, C.; Kääb, A. Combining Satellite Multispectral Image Data and a Digital Elevation Model for Mapping Debris-Covered Glaciers. Remote Sensing of Environment 2004, 89, 510–518. [Google Scholar] [CrossRef]
  31. Abriha, D.; Srivastava, P.K.; Szabó, S. Smaller Is Better? Unduly Nice Accuracy Assessments in Roof Detection Using Remote Sensing Data with Machine Learning and k-Fold Cross-Validation. Heliyon 2023, 9, e14045. [Google Scholar] [CrossRef]
  32. Tsendbazar, N.-E.; De Bruin, S.; Fritz, S.; Herold, M. Spatial Accuracy Assessment and Integration of Global Land Cover Datasets. Remote Sensing 2015, 7, 15804–15821. [Google Scholar] [CrossRef]
  33. Brus, D.J.; Kempen, B.; Heuvelink, G.B.M. Sampling for Validation of Digital Soil Maps. European Journal of Soil Science 2011, 62, 394–407. [Google Scholar] [CrossRef]
  34. Wadoux, A.M.J.-C.; Heuvelink, G.B.M.; de Bruin, S.; Brus, D.J. Spatial Cross-Validation Is Not the Right Way to Evaluate Map Accuracy. Ecological Modelling 2021, 457, 109692. [Google Scholar] [CrossRef]
  35. Brus, D.J. Sampling for Digital Soil Mapping: A Tutorial Supported by R Scripts. Geoderma 2019, 338, 464–480. [Google Scholar] [CrossRef]
  36. Ploton, P.; Mortier, F.; Réjou-Méchain, M.; Barbier, N.; Picard, N.; Rossi, V.; Dormann, C.; Cornu, G.; Viennois, G.; Bayol, N.; et al. Spatial Validation Reveals Poor Predictive Performance of Large-Scale Ecological Mapping Models. Nat Commun 2020, 11, 4540. [Google Scholar] [CrossRef] [PubMed]
  37. Bengio, Y.; Grandvalet, Y. No Unbiased Estimator of the Variance of K-Fold Cross-Validation. J. Mach. Learn. Res. 5, 1089–1105.
  38. An Introduction to Statistical Learning: With Applications in R; James, G. , Witten, D., Hastie, T., Tibshirani, R., Eds.; Springer texts in statistics; Springer: New York, 2013; ISBN 978-1-4614-7137-0. [Google Scholar]
  39. Schratz, P.; Becker, M.; Lang, M.; Brenning, A. Mlr3spatiotempcv: Spatiotemporal Resampling Methods for Machine Learning in R. arXiv:2110.12674 [cs, stat], arXiv:2110.12674 [cs, stat] 2021.
  40. De Bruin, S.; Brus, D.J.; Heuvelink, G.B.M.; Van Ebbenhorst Tengbergen, T.; Wadoux, A.M.J.-C. Dealing with Clustered Samples for Assessing Map Accuracy by Cross-Validation. Ecological Informatics 2022, 69, 101665. [Google Scholar] [CrossRef]
  41. Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics; Springer New York: New York, NY, 2009; ISBN 978-0-387-84857-0. [Google Scholar]
  42. Lu, Y.; Zhang, Z.; Shangguan, D.; Yang, J. Novel Machine Learning Method Integrating Ensemble Learning and Deep Learning for Mapping Debris-Covered Glaciers. Remote Sensing 2021, 13, 2595. [Google Scholar] [CrossRef]
  43. Schratz, P.; Muenchow, J.; Iturritxa, E.; Richter, J.; Brenning, A. Hyperparameter Tuning and Performance Assessment of Statistical and Machine-Learning Algorithms Using Spatial Data - ScienceDirect. 2019.
  44. Kopczewska, K. Spatial Machine Learning: New Opportunities for Regional Science. Ann Reg Sci 2022, 68, 713–755. [Google Scholar] [CrossRef]
  45. Roberts, D.R.; Bahn, V.; Ciuti, S.; Boyce, M.S.; Elith, J.; Guillera-Arroita, G.; Hauenstein, S.; Lahoz-Monfort, J.J.; Schröder, B.; Thuiller, W.; et al. Cross-Validation Strategies for Data with Temporal, Spatial, Hierarchical, or Phylogenetic Structure. Ecography 2017, 40, 913–929. [Google Scholar] [CrossRef]
  46. Wang, Y.; Khodadadzadeh, M.; Zurita-Milla, R. Spatial+: A New Cross-Validation Method to Evaluate Geospatial Machine Learning Models. International Journal of Applied Earth Observation and Geoinformation 2023, 121, 103364. [Google Scholar] [CrossRef]
  47. Brenning, A. Spatial Cross-Validation and Bootstrap for the Assessment of Prediction Rules in Remote Sensing: The R Package Sperrorest. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium; IEEE: Munich, Germany, July, 2012; pp. 5372–5375. [Google Scholar]
  48. Meyer, H.; Pebesma, E. Machine Learning-Based Global Maps of Ecological Variables and the Challenge of Assessing Them. Nat Commun 2022, 13, 2208. [Google Scholar] [CrossRef]
  49. Milà, C.; Mateu, J.; Pebesma, E.; Meyer, H. Nearest Neighbour Distance Matching Leave-One-Out Cross-Validation for Map Validation. Methods Ecol Evol 2022, 13, 1304–1316. [Google Scholar] [CrossRef]
  50. Seehaus, T.; Malz, P.; Sommer, C.; Lippl, S.; Cochachin, A.; Braun, M. Changes of the Tropical Glaciers throughout Peru between 2000 and 2016 – Mass Balance and Area Fluctuations; Glaciers/Remote Sensing, 2019.
  51. Sagredo, E.A.; Lowell, T.V. Climatology of Andean Glaciers: A Framework to Understand Glacier Response to Climate Change. Global and Planetary Change 2012, 86–87, 101–109. [Google Scholar] [CrossRef]
  52. INAIGEM Inventario Nacional de Glaciares; Instituto Nacional de Investigación en Glaciaresy Ecosistemas de Montaña. 2018.
  53. Drenkhan, F.; Guardamino, L.; Huggel, C.; Frey, H. Current and Future Glacier and Lake Assessment in the Deglaciating Vilcanota-Urubamba Basin, Peruvian Andes. Global and Planetary Change 2018, 169, 105–118. [Google Scholar] [CrossRef]
  54. Kozhikkodan Veettil, B.; de Souza, S.F. Study of 40-Year Glacier Retreat in the Northern Region of the Cordillera Vilcanota, Peru, Using Satellite Images: Preliminary Results. Remote Sensing Letters 2017, 8, 78–85. [Google Scholar] [CrossRef]
  55. Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary Analysis of the Performance of the Landsat 8/OLI Land Surface Reflectance Product. Remote Sensing of Environment 2016, 185, 46–56. [Google Scholar] [CrossRef]
  56. Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sensing of Environment 2017, 202, 18–27. [Google Scholar] [CrossRef]
  57. Paul, F.; Bolch, T.; Kääb, A.; Nagler, T.; Nuth, C.; Scharrer, K.; Shepherd, A.; Strozzi, T.; Ticconi, F.; Bhambri, R.; et al. The Glaciers Climate Change Initiative: Methods for Creating Glacier Area, Elevation Change and Velocity Products. Remote Sensing of Environment 2015, 162, 408–426. [Google Scholar] [CrossRef]
  58. Roy, D.P.; Kovalskyy, V.; Zhang, H.K.; Vermote, E.F.; Yan, L.; Kumar, S.S.; Egorov, A. Characterization of Landsat-7 to Landsat-8 Reflective Wavelength and Normalized Difference Vegetation Index Continuity. Remote Sensing of Environment 2016, 185, 57–70. [Google Scholar] [CrossRef]
  59. Burns, P.; Nolin, A. Using Atmospherically-Corrected Landsat Imagery to Measure Glacier Area Change in the Cordillera Blanca, Peru from 1987 to 2010 - ScienceDirect. Remote Sensing of Environment 2014. [Google Scholar] [CrossRef]
  60. Wang, J.; Tang, Z.; Deng, G.; Hu, G.; You, Y.; Zhao, Y. Landsat Satellites Observed Dynamics of Snowline Altitude at the End of the Melting Season, Himalayas, 1991–2022. Remote Sensing 2023, 15, 2534. [Google Scholar] [CrossRef]
  61. Wang, X.; Wang, J.; Che, T.; Huang, X.; Hao, X.; Li, H. Snow Cover Mapping for Complex Mountainous Forested Environments Based on a Multi-Index Technique. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2018, 11, 1433–1441. [Google Scholar] [CrossRef]
  62. Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1; Climate and Earth System Modeling. 2015. [Google Scholar]
  63. de Gruijter, J.; Brus, D.; Bierkens, M.; Knotters, M. (Eds.) Sampling for Natural Resource Monitoring; 1st ed.; Springer: Wageningen University Wageningen University and Research Centre and Research Centre Alterra, 2006. 2006. [Google Scholar]
  64. Alifu, H.; Vuillaume, J.-F.; Johnson, B.A.; Hirabayashi, Y. Machine-Learning Classification of Debris-Covered Glaciers Using a Combination of Sentinel-1/-2 (SAR/Optical), Landsat 8 (Thermal) and Digital Elevation Data. Geomorphology 2020, 369, 107365. [Google Scholar] [CrossRef]
  65. Prieur, C.; Rabatel, A.; Thomas, J.-B.; Farup, I.; Chanussot, J. Machine Learning Approaches to Automatically Detect Glacier Snow Lines on Multi-Spectral Satellite Images. Remote Sensing 2022, 14, 3868. [Google Scholar] [CrossRef]
  66. Das, P.; Pandey, V. Use of Logistic Regression in Land-Cover Classification with Moderate-Resolution Multispectral Data. J Indian Soc Remote Sens 2019, 47, 1443–1454. [Google Scholar] [CrossRef]
  67. Taunk, K.; De, S.; Verma, S.; Swetapadma, A. A Brief Review of Nearest Neighbor Algorithm for Learning and Classification. In Proceedings of the 2019 International Conference on Intelligent Computing and Control Systems (ICCS); May 2019; pp. 1255–1260. [Google Scholar]
  68. Huang, Z. Extensions to the K-Means Algorithm for Clustering Large Data Sets with Categorical Values. Data Mining and Knowledge Discovery 1998, 2, 283–304. [Google Scholar] [CrossRef]
  69. Breiman, L. Random Forests. Machine Learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
  70. Chen, Q.; Miao, F.; Wang, H.; Xu, Z.; Tang, Z.; Yang, L.; Qi, S. Downscaling of Satellite Remote Sensing Soil Moisture Products Over the Tibetan Plateau Based on the Random Forest Algorithm: Preliminary Results. Earth and Space Science 2020, 7. [Google Scholar] [CrossRef]
  71. de Graaf, I.E.M.; Sutanudjaja, E.H.; van Beek, L.P.H.; Bierkens, M.F.P. A High-Resolution Global-Scale Groundwater Model. Hydrol. Earth Syst. Sci. 2015, 19, 823–837. [Google Scholar] [CrossRef]
  72. Georganos, S.; Grippa, T.; Niang Gadiaga, A.; Linard, C.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E.; Kalogirou, S. Geographical Random Forests: A Spatial Extension of the Random Forest Algorithm to Address Spatial Heterogeneity in Remote Sensing and Population Modelling. Geocarto International 2021, 36, 121–136. [Google Scholar] [CrossRef]
  73. Hu, L.; Chun, Y.; Griffith, D.A. Incorporating Spatial Autocorrelation into House Sale Price Prediction Using Random Forest Model. Transactions in GIS - Wiley Online Library.
  74. Sekulić, A.; Kilibarda, M.; Heuvelink, G.B.M.; Nikolić, M.; Bajat, B. Random Forest Spatial Interpolation. Remote Sensing 2020, 12, 1687. [Google Scholar] [CrossRef]
  75. Probst, P.; Wright, M.N.; Boulesteix, A. Hyperparameters and Tuning Strategies for Random Forest. WIREs Data Mining Knowl Discov 2019, 9. [Google Scholar] [CrossRef]
  76. Friedman, J.H. Stochastic Gradient Boosting. Computational Statistics & Data Analysis 2002, 38, 367–378. [Google Scholar] [CrossRef]
  77. Zhang, J.; Li, X.; Liu, Q.; Zhao, L.; Dou, B. An Extended Kriging Method to Interpolate Soil Moisture Data Measured by Wireless Sensor Network; Water Resources Management/Remote Sensing and GIS. 2016. [Google Scholar]
  78. Xing, C.; Chen, N.; Zhang, X.; Gong, J. A Machine Learning Based Reconstruction Method for Satellite Remote Sensing of Soil Moisture Images with In Situ Observations. Remote Sensing 2017, 9, 484. [Google Scholar] [CrossRef]
  79. Yoshida, T.; Murakami, D.; Seya, H. Spatial Prediction of Apartment Rent Using Regression-Based and Machine Learning-Based Approaches with a Large Dataset. J Real Estate Finan Econ 2022. [Google Scholar] [CrossRef]
  80. R Core Team R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing 2013.
  81. Uddin, S.; Haque, I.; Lu, H.; Moni, M.A.; Gide, E. Comparative Performance Analysis of K-Nearest Neighbour (KNN) Algorithm and Its Different Variants for Disease Prediction. Sci Rep 2022, 12, 6256. [Google Scholar] [CrossRef]
  82. Wright, M.N.; Ziegler, A. Ranger : A Fast Implementation of Random Forests for High Dimensional Data. J. Stat. Soft. 2017, 77. [Google Scholar] [CrossRef]
  83. Chicco, D.; Warrens, M.J.; Jurman, G. The Matthews Correlation Coefficient (MCC) Is More Informative Than Cohen’s Kappa and Brier Score in Binary Classification Assessment. IEEE Access 2021, 9, 78368–78381. [Google Scholar] [CrossRef]
  84. Chicco, D.; Jurman, G. The Advantages of the Matthews Correlation Coefficient (MCC) over F1 Score and Accuracy in Binary Classification Evaluation. BMC Genomics 2020, 21, 6. [Google Scholar] [CrossRef] [PubMed]
  85. Foody, G.M. Explaining the Unsuitability of the Kappa Coefficient in the Assessment and Comparison of the Accuracy of Thematic Maps Obtained by Image Classification. Remote Sensing of Environment 2020, 239, 111630. [Google Scholar] [CrossRef]
  86. Anselin, L. Lagrange Multiplier Test Diagnostics for Spatial Dependence and Spatial Heterogeneity. Geographical Analysis 1988, 20, 1–17. [Google Scholar] [CrossRef]
  87. Bivand, R.S.; Pebesma, E.; Gómez-Rubio, V. Applied Spatial Data Analysis with R; Springer New York: New York, NY, 2013; ISBN 978-1-4614-7617-7. [Google Scholar]
  88. Bierkens, M.F.P.; Burrough, P.A. The Indicator Approach to Categorical Soil Data. Journal of Soil Science - Wiley Online Library.
  89. Cressie, N.A.C. Statistics for Spatial Data; Revised edition.; John Wiley & Sons, Inc: Hoboken, NJ, 2015; ISBN 978-1-119-11517-5. [Google Scholar]
  90. Easterling, W.; Apps, M. Assessing the Consequences of Climate Change for Food and Forest Resources: A View from the IPCC. In Increasing Climate Variability and Change; Salinger, J., Sivakumar, M.V.K., Motha, R.P., Eds.; Springer-Verlag: Berlin/Heidelberg, 2005; ISBN 978-1-4020-3354-4. [Google Scholar]
  91. Goovaerts, P. AUTO-IK: A 2D Indicator Kriging Program for the Automated Non-Parametric Modeling of Local Uncertainty in Earth Sciences. Computers & Geosciences 2009, 35, 1255–1270. [Google Scholar] [CrossRef]
  92. Pebesma, E.; Bivand, R.S. Classes and Methods for Spatial Data: The Sp Package. 2005, 21.
  93. Gräler, B.; Pebesma, E.; Heuvelink, G. Spatio-Temporal Interpolation Using Gstat. The R Journal 2016, 8, 204. [Google Scholar] [CrossRef]
  94. Walvoort, D.J.J.; Brus, D.J.; de Gruijter, J.J. An R Package for Spatial Coverage Sampling and Random Sampling from Compact Geographical Strata by K-Means. Computers & Geosciences 2010, 36, 1261–1267. [Google Scholar] [CrossRef]
  95. Chabalala, Y.; Adam, E.; Ali, K.A. Exploring the Effect of Balanced and Imbalanced Multi-Class Distribution Data and Sampling Techniques on Fruit-Tree Crop Classification Using Different Machine Learning Classifiers. Geomatics 2023, 3, 70–92. [Google Scholar] [CrossRef]
  96. Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press. 2016. [Google Scholar]
  97. Nadeau, C.; Bengio, Y. Inference for the Generalization Error. Machine Learning 2003, 52, 239–281. [Google Scholar] [CrossRef]
  98. Guillén, A.; Martínez, J.; Carceller, J.M.; Herrera, L.J. A Comparative Analysis of Machine Learning Techniques for Muon Count in UHECR Extensive Air-Showers. Entropy 2020. [Google Scholar] [CrossRef]
  99. Pacheco, A. da P.; Junior, J.A. da S.; Ruiz-Armenteros, A.M.; Henriques, R.F.F. Assessment of K-Nearest Neighbor and Random Forest Classifiers for Mapping Forest Fire Areas in Central Portugal Using Landsat-8, Sentinel-2, and Terra Imagery. Remote Sensing 2021, 13, 1345. [Google Scholar] [CrossRef]
  100. Bansal, M.; Goyal, A.; Choudhary, A. A Comparative Analysis of K-Nearest Neighbor, Genetic, Support Vector Machine, Decision Tree, and Long Short Term Memory Algorithms in Machine Learning. Decision Analytics Journal 2022, 3, 100071. [Google Scholar] [CrossRef]
  101. Hoef, J.M.V.; Temesgen, H. A Comparison of the Spatial Linear Model to Nearest Neighbor (k-NN) Methods for Forestry Applications. PLOS ONE 2013, 8, e59129. [Google Scholar] [CrossRef]
  102. Vega Isuhuaylas, L.A.; Hirata, Y.; Ventura Santos, L.C.; Serrudo Torobeo, N. Natural Forest Mapping in the Andes (Peru): A Comparison of the Performance of Machine-Learning Algorithms. Remote Sensing 2018, 10, 782. [Google Scholar] [CrossRef]
  103. Behrens, T.; Viscarra Rossel, R.A. On the Interpretability of Predictors in Spatial Data Science: The Information Horizon. Sci Rep 2020, 10, 16737. [Google Scholar] [CrossRef]
  104. Saha, A.; Basu, S.; Datta, A. Random Forests for Spatially Dependent Data. Journal of the American Statistical Association 2023, 118, 665–683. [Google Scholar] [CrossRef]
  105. Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving Performance of Spatio-Temporal Machine Learning Models Using Forward Feature Selection and Target-Oriented Validation. Environmental Modelling & Software 2018, 101, 1–9. [Google Scholar] [CrossRef]
  106. Jiang, Z. A Survey on Spatial Prediction Methods. IEEE Trans. Knowl. Data Eng. 2019, 31, 1645–1664. [Google Scholar] [CrossRef]
  107. Liu, X.; Kounadi, O.; Zurita-Milla, R. Free Full-Text | Incorporating Spatial Autocorrelation in Machine Learning Models Using Spatial Lag and Eigenvector Spatial Filtering Features. 2022.
  108. Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Soft. 2008, 28. [Google Scholar] [CrossRef]
  109. Kochtitzky, W.H.; Edwards, B.R.; Enderlin, E.M.; Marino, J.; Marinque, N. Improved Estimates of Glacier Change Rates at Nevado Coropuna Ice Cap, Peru. J. Glaciol. 2018, 64, 175–184. [Google Scholar] [CrossRef]
  110. Mohajerani, Y.; Jeong, S.; Scheuchl, B.; Velicogna, I.; Rignot, E.; Milillo, P. Automatic Delineation of Glacier Grounding Lines in Differential Interferometric Synthetic-Aperture Radar Data Using Deep Learning. Sci Rep 2021, 11, 4992. [Google Scholar] [CrossRef]
  111. Khan, A.A.; Jamil, A.; Hussain, D.; Taj, M.; Jabeen, G.; Malik, M.K. Machine-Learning Algorithms for Mapping Debris-Covered Glaciers: The Hunza Basin Case Study. IEEE Access 2020, 8, 12725–12734. [Google Scholar] [CrossRef]
  112. Zhang, J.; Jia, L.; Menenti, M.; Hu, G. Glacier Facies Mapping Using a Machine-Learning Algorithm: The Parlung Zangbo Basin Case Study. Remote Sensing 2019, 11, 452. [Google Scholar] [CrossRef]
Preprints 87668 g001
Figure 1. The geographical location of selected study areas inthis work, Perú. Background is a JAXA’S ALOS WORLD 3D DEM and reference glacier surfces from the National Inventory of Glaciers produced on 2017. All plotting was done in QGIS 3.30.1-'s-Hertogenbosch.
Figure 1. The geographical location of selected study areas inthis work, Perú. Background is a JAXA’S ALOS WORLD 3D DEM and reference glacier surfces from the National Inventory of Glaciers produced on 2017. All plotting was done in QGIS 3.30.1-'s-Hertogenbosch.
Preprints 87668 g001
Preprints 87668 g002
Figure 2. Flowchart of the processing steps presented in this study.
Figure 2. Flowchart of the processing steps presented in this study.
Preprints 87668 g002
Preprints 87668 g003
Figure 3. The spatial CV process used in this study.
Figure 3. The spatial CV process used in this study.
Preprints 87668 g003
Preprints 87668 g004
Figure 4. Experimental (points) and fitted rescaled indicator variograms (curves) for the data set with 1000 pixels. a)Blanca, b)Central, c) Huallanca, d) Huayhuasha, e) Huaytapallana, f) Raura, g) Urubamba, h) Vilcabamba and i) Vilcanota.
Figure 4. Experimental (points) and fitted rescaled indicator variograms (curves) for the data set with 1000 pixels. a)Blanca, b)Central, c) Huallanca, d) Huayhuasha, e) Huaytapallana, f) Raura, g) Urubamba, h) Vilcabamba and i) Vilcanota.
Preprints 87668 g004
Preprints 87668 g005
Figure 5. The final results (Matthew Correlation Coefficient M C C C V ) of experimental benchmarks after applying algorithm 1 on the 9 studied areas. a)Blanca, b)Central, c) Huallanca, d) Huayhuasha, e) Huaytapallana, f) Raura, g) Urubamba, h) Vilcabamba and i) Vilcanota.
Figure 5. The final results (Matthew Correlation Coefficient M C C C V ) of experimental benchmarks after applying algorithm 1 on the 9 studied areas. a)Blanca, b)Central, c) Huallanca, d) Huayhuasha, e) Huaytapallana, f) Raura, g) Urubamba, h) Vilcabamba and i) Vilcanota.
Preprints 87668 g005
Preprints 87668 g006
Figure 6. The final results (Matthew Correlation Coefficient M C C C V ) of experimental benchmarks desegregated by model type and study area. Reference error of each model M C C r e f in red doted horizontal lines are used for calculated d C V = M C C C V − M C C r e f .
Figure 6. The final results (Matthew Correlation Coefficient M C C C V ) of experimental benchmarks desegregated by model type and study area. Reference error of each model M C C r e f in red doted horizontal lines are used for calculated d C V = M C C C V − M C C r e f .
Preprints 87668 g006
Preprints 87668 g007
Figure 7. Moran's I results of cross-validation error.
Figure 7. Moran's I results of cross-validation error.
Preprints 87668 g007
Preprints 87668 g008
Figure 8. Maps of the spatial predictions of compared models. NDSI is added as a comparison. Reference National Glacier Inventory in red contour is overlay as a reference.
Figure 8. Maps of the spatial predictions of compared models. NDSI is added as a comparison. Reference National Glacier Inventory in red contour is overlay as a reference.
Preprints 87668 g008
Table 1. OLI and TIRS bands description, information. The visible part of the electromagnetic spectrum is covered by bands 1–4 and 8 with resolution of 30 m, except for bands 8 that has a resolution of 15 m. The NIR is covered by band 5 with a resolution of 30 m. The SWIR is covered by bands 6 and 7 with a resolution of 30 m.
Table 1. OLI and TIRS bands description, information. The visible part of the electromagnetic spectrum is covered by bands 1–4 and 8 with resolution of 30 m, except for bands 8 that has a resolution of 15 m. The NIR is covered by band 5 with a resolution of 30 m. The SWIR is covered by bands 6 and 7 with a resolution of 30 m.
Name and Resolution (m) Spectral Range um Band Number
Coastal/ Aerosol (30 m) 0.435–0.451 Band 1
Blue (30 m) 0.452–0.512 Band 2
Green (30 m) 0.533–0.590 Band 3
Red (30 m) 0.636–0.673 Band 4
Near InfraRed (NIR) (30 m) 0.851–0.879 Band 5
Short Wave InfraRed 1 (SWIR 1) (30 m) 1.566–1.651 Band 6
SWIR 2 (30 m) 2.107–2.294 Band 7
Table 2. Allocation of Training and Test Samples within Respective Cordillera Regions.
Table 2. Allocation of Training and Test Samples within Respective Cordillera Regions.
Cordillera LS81 Composite
Total area (Km2)		 Non glacier
samples		 Glacier
samples		 Test
samples
Cordillera Blanca 13 963.1 248 217 1000
Cordillera Central 5957.4 248 245 1000
Cordillera Huallanca 271.9 247 238 1000
Cordillera Huayhuash 344.5 246 250 1000
Cordillera Huaytapallana 2 489.8 246 200 1000
Cordillera Raura 322.3 247 245 1000
Cordillera Urubamba 1818 248 184 1000
Cordillera Vilcabamba 4 221.3 247 218 1000
Cordillera Vilcanota 6 179.7 246 242 1000
Total 42 135 2719 2511 9000
1 Landsat 8.
Table 3. Rescaled Indicator Variogram Parameters for 1000 Pixels Across Cordillera Regions.
Table 3. Rescaled Indicator Variogram Parameters for 1000 Pixels Across Cordillera Regions.
Cordillera Model1 Range (m) C02 C3 kappa
Cordillera Blanca Mat 5428.204 3.57E-04 0.0355 0.5
Cordillera Central Exp 371.4613 0 0.00475 -
Cordillera Huallanca Mat 874.5616 1.14E-03 0.0184 1
Cordillera Huayhuash Mat 3160.411 2.54E-03 0.1477 0.3
Cordillera Huaytapallana Mat 1320.108 2.21E-03 0.004013 10
Cordillera Raura Mat 1999.836 1.68E-02 0.07002 0.6
Cordillera Urubamba Mat 684.1284 0 0.00736 10
Cordillera Vilcabamba Mat 5326.374 1.30E-03 0.0264 0.4
Cordillera Vilcanota Mat 3288.231 3.19E-04 0.03816 1.2
1 Mat: Matern, M. Stein's parameterization.; Exp: exponential model. 2 C0: Nugget effect, and 3: Sill.
Table 4. Selected hyperparameter data types and chosen values for each algorithm. Notations of hyperparameters from the respective R packages were used. p is the number of features.
Table 4. Selected hyperparameter data types and chosen values for each algorithm. Notations of hyperparameters from the respective R packages were used. p is the number of features.
Algorithm Reference Hyperparameter Type Default
Gradient Boosting Machines (GBM)1 [76] n.trees Integer 100
n.minobsinnode Integer 10
shrinkage Numeric 0.1
distribution Nominal bernoulli
Random Forest (RF) [69] num.trees Integer 500
mtry Integer Sqrt(p)
min.node.size Integer 1
max.depth Integer 0
Weighted k-Nearest Neighbors (KKN) https://github.com/KlausVigo/kknn k Integer 10
distance Integer 2
kernel Nominal gaussian
Logistic Regression (LR) family Nominal binomial
1 Algorithm symbols used on result´s analysis.
Table 5. Mean Matthew Correlation Coefficients grouped by Cordillera and CV method.
Table 5. Mean Matthew Correlation Coefficients grouped by Cordillera and CV method.
Glacier region SP-CV1 MCC NSP-CV2 MCC
Cordillera Blanca 0.928(0.0845)3 0.949(0.1054)
Cordillera Central 0.937(0.446) 0.954(0.4624)
Cordillera Huallanca 0.877(0.1201) 0.937 (0.1800)
Cordillera Huayhuash 0.753(0.0196) 0.830(0.0576)
Cordillera Huaytapallana 0.904(0.1979) 0.968(0.2617)
Cordillera Raura 0.915(0.0532) 0.931(0.0699)
Cordillera Urubamba 0.906(0.3082) 0.930(0.3317)
Cordillera Vilcabamba 0.891(0.2067) 0.917(0.2326)
Cordillera Vilcanota 0.906(0.0618) 0.929(0.0847)
1 SP-CV: spatial cross validation, 2: NSP-CV: non spatial cross validation, 3: difference regard to the test reference MCC ( M C C C V − M C C r e f ) in parenthesis.
Table 6. Modified paired t-test, t-statistics and the p-values (in parenthesis) of paired t-test comparison for the MCC obtained after the 50-repeteated 5-fold CV using the two types of cross-validation for each glacier region.
Table 6. Modified paired t-test, t-statistics and the p-values (in parenthesis) of paired t-test comparison for the MCC obtained after the 50-repeteated 5-fold CV using the two types of cross-validation for each glacier region.
Glacier region LR RF GBM KNN
Cordillera Blanca 0.05971(0.4763) 1.155 (0.1267) 1.678 (0.04711) 1 2.061
(0.02229) 1
Cordillera Central 0.2374(0.4066) 0.8284 (0.2057) 0.6774 (0.2506) 1.391
(0.08516)
Cordillera Huallanca 1.202 (0.1174) 1.9135 (0.03076) 1 1.4590 (0.07545) 1.366
(0.08895)
Cordillera Huayhuash 1.44537 (0.07735) 1.6833 (0.04933) 1 1.64397 (0.05329) 1.64590 (0.0530)
Cordillera Huaytapallana 1.3271 (0.09530) 1.5579 (0.06284) 1.910303 (0.03092) 1 253.484
-
Cordillera Raura 0.76974 (0.2225) 0.34939 (0.3641) 0.4885 (0.3136) 0.3651
(0.3582)
Cordillera Urubamba 1.59805 (0.04823) 1 0.93018 (0.1784) 1.2942 (0.1008) 0.0655
(0.4739)
Cordillera Vilcabamba 0.20655 (0.4186) 1.61089 (0.04681) 1 0.9120 (0.1831) 1.3423 (0.09283)
Cordillera Vilcanota 0.84632 (0.2007) 0.62994 (0.2658) 0.7284 (0.2348) 0.48702 (0.3142)
1 Modified paired t-test significance statistical difference between cross-validated MCC results (p-value < 0.05).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated