Preprint
Article
Work Fluctuations in Ergotropic Heat Engines
This version is not peer-reviewed.
Submitted:
11 October 2023
Posted:
13 October 2023
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
We study the work fluctuations in ergotropic heat engines, namely two-strokes quantum Otto engines where the work stroke is designed to extract the ergotropy (the maximum amount of work by a cyclic unitary evolution) from a couple of quantum systems at canonical equilibrium at two different temperatures, whereas the heat stroke thermalizes back the systems to their respective reservoirs. We provide an exaustive study for the case of two qutrits whose energy levels are equally spaced at two different frequencies by deriving the complete work statistics. By varying the values of temperatures and frequencies, only three kinds of optimal unitary strokes are found: the swap operator U1, an idle swap U2 (where one of the qutrits is regarded as an effective qubit), and a non trivial permutation of energy eigenstates U3, which indeed corresponds to the composition of the two previous unitaries, namely U3 = U2U1. While U1 and U2 are Hermitian (and hence involutions), U3 is not. This point has an impact on the thermodynamic uncertainty relations (TURs) which bound the signal-to-noise ratio of the extracted work in terms of the entropy production. In fact, we show that all TURs derived from a strong detailed fluctuation theorem are violated by the transformation U3.
Keywords:
quantum thermodynamics
; quantum heat engines
; thermodynamic uncertainty relations
; two-stroke Otto cycles
; ergotropy
supplementary.zip (991.23KB )
Introduction
A quantum description of thermodynamic heat engines has lately become necessary to consider physical systems at the mesoscale and nanoscale [1,2,3], such as nanojunctions thermoelectrics [4], quantum dots [5], and biological [6,7] or chemical [8] systems. The optimal transport theory also has recently been embedded in a thermodynamic quantum framework [9]. At the quantum level, the fluctuations of the thermodynamic variables play a fundamental role, due to the discrete spectral structure of quantum systems.
The probability distributions of a set of thermodynamic variables are related to the entropy production through the so-called fluctuation theorems, which in general can be expressed as [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]
where refers to the backward process, i.e. to the time-reversed process identified by p [for a self-contained derivation of Eq. (1) see Appendix A and Eq. (A22)]. Through this relation, the symmetries of the processes set relevant constraints on the statistics of the variables . Another class of relations that connects the statistical properties of mesoscopic and nanoscopic systems to the entropy production is given by the so-called thermodynamic uncertainty relations (TURs) [9,26,29,30,31,32,33,34,35,36,37,38,39]. It has been shown that there is a strong connection between fluctuation theorems and TURs, i.e. every fluctuation theorem implies a specific TUR [32]. Note that the converse does not hold: it was recently found in Ref. [38] a TUR which does not stem from any fluctuation theorem.
Thermodynamic engines which admit a straightforward quantum description are the ones based on the Otto cycle [28,35,36,40,41,42,43,44,45,46,47,48] since the work and heat exchanged are unambiguously identified by their respective distinct strokes. The case considered in this paper, namely a two-stroke Otto cycle, is outlined in Figure 1, where the working fluid is represented by two qutrits.
In the case of an engine based on a two-stroke Otto cycle the full probability distribution of work and heat has been retrieved for two qudits [35] and for two bosonic modes [36] as working fluids, where the transformation for the work extraction is the unitary partial-swap interaction. The two-stroke Otto engine is particularly interesting with respect to its well-known four-stroke version because it allows to extract the maximum amount of work in the adiabatic step of the cycle by a single unitary operation, the so-called ergotropy [49,50,51,52,53]. Note that the extraction of the ergotropy necessarily depends also on the transformation that couples the systems. We will show here that, if the systems are qudits with dimension larger than two, unitary evolutions different from the swap interaction can increase the extracted work.
We will define a procedure for determining the unitary interaction that provides the maximum work from two multilevel systems A and B for a given choice of the relevant parameters, i.e. the frequency gaps and of the qudits and the temperatures and of the reservoirs. Then we take the specific case of a working fluid described by two qutrits and classify all the transformations that extract the ergotropy. Specifically, we find three different kinds of optimal unitary strokes: the swap operator , an idle swap (where one of the qutrits is regarded as an effective qubit), and a non trivial permutation given by a composition of the two previous unitaries, namely . Each transformation extracts the ergotropy from a different regime defined by the frequency gaps and of the two qutrits and by the temperatures and of the baths. By deriving the characteristic function of work and heat, we evaluate the work statistics and the entropy production for every case. Note that a complete description of a quantum ergotropic heat engine and of the procedure for determining the work statistics is detailed in Appendix A. Then, we focus on the trade-off between ergotropy extraction and relative fluctuations , i.e. the inverse of the signal-to-noise ratio (SNR). The evaluation of the fluctuations allows us to establish the relation between the variance of the work and the mean entropy production in terms of the TURs. A standard reference TUR bounds the fluctuations with the inverse of the entropy production as follows [29]
We show that all the three ergotropic transformations violate this TUR. Moreover, is proved to beat all the TURs derived by the strong fluctuation theorem where the forward and backward processes in Eq. (1) are related by the same condition .
The paper is structured as follows. In Section 1 we define the procedure for determining the transformations extracting the ergotropy in the case where the working fluid is described by two qudits with generic dimensions and . Then, in Section 2 we apply our procedure to the case of two qutrits. In particular, in Section 2.1 we classify all the transformations extracting the ergotropy and their properties. In Section 2.2 we evaluate the maximum work extracted by each transformation in terms of the frequency gaps and the temperatures. In Section 2.3 we study the mean entropy production related to each interaction. In Section 2.4 we derive the work distributions. Finally, in Section 2.5 we find the relative fluctuations of work, compare the corresponding SNR to the bounds provided by the most relevant TURs and discuss the assumptions required for these TURs to hold. In Section 3 we draw our conclusions.
1. Materials and Methods
In this work we fix the Planck and Boltzmann constants to natural units, i.e. . We consider two qudits A and B in a product of Gibbs states, i.e.
where is the Hamiltonian of the system , each one with equally-spaced energy levels, and denotes the corresponding partition function, and the inverse temperature. The number states in the expansion of the Hamiltonians are eigenstates of the occupation number . Without loss of generality, we fix .
We use the state in Eq. (3) as input to a two-stroke Otto engine. As depicted in Figure 1, the process starts with the two qudits in thermal equilibrium with their baths, at temperature and . Afterwards, the two qudits are isolated from their baths and we make them interact through a unitary evolution in order to extract the ergotropy. The procedure for the ergotropy extraction will be detailed in the following. Once the work has been extracted through the interaction, we reset the two qudits to their equilibrium state by re-connecting them via weak coupling to their thermal baths. The sequential repetition of this process leads to our two-stroke cyclic engine.
We fix the convention of positive work for the extraction from the system and positive heat for the absorption from the reservoirs. Then, in each cycle the average energy change in system A due to the unitary stroke corresponds to the average heat released by the hot reservoir A, namely . Similarly, for the cold reservoir, , and, for the first law of thermodynamics, the average work is given by . Correspondingly, the average entropy production reads . Our goal is the investigation of an ergotropic heat engine based on the two-qudit system described above, i.e. an engine extracting the maximum work by exploiting the difference of frequency and temperature between the systems A and B. In other words, we are looking for the unitary transformations U mapping the input into a state such that the average extracted work is maximized, i.e.
where here is the Hamiltonian of the system. The evolution that extracts the ergotropy was identified in Ref. [49] as the one minimizing the final energy . In the present case, where the initial state has no coherence, namely it is diagonal in the energy basis, the ergotropic evolution is the transformation that permutes the eigenstates of the input state so that the magnitude order of the energy levels is reversed with respect to the corresponding occupation fractions. More explicitly, if we take the occupation fractions of the system in descending order, the transformation permutes the related eigenstates to set the corresponding energy levels in ascending order. If the input state already displays this configuration, then the state is called passive and no transformation can extract work. In summary, since unitary transformations preserve the spectrum, the ergotropy is extracted by reversing all possible population inversion with respect to the energy levels. In the following, we provide a re-visited analysis of the first level maximization strategy developed in Ref. [50].
The procedure of ergotropy extraction can be formalized in a compact way for two subsystems A and B of dimension and as follows. We consider two different permutations and of the energy eigenstates with respect to their lexicographic order. The permutation sorts them so that the corresponding eigenvalues are set in ascending order, i.e.
where the vector of eigenvalues satisfies . Similarly, the permutation rearranges the occupation numbers of the initial state in descending order, namely,
and is such that . Then we can straightforwardly find the transformation which minimizes the final energy from
implying that the ergotropic transformation can be expressed as
For instance, take two qubits in a Gibbs state
Then the energies pertaining to the levels and are and , respectively, while the related occupation fractions are and . If we have and or the symmetric case where both the order relations are reversed, the transformation that swaps with , namely , extracts the ergotropy. This result appears immediately if we consider the permutation matrices and , which in this case read
where is the Heaviside function. The operator promptly identifies the ergotropic transformations and the corresponding ergotropic regimes, since
This simple example shows how the extraction of the ergotropy is entirely determined by the order relations between the parameters. In particular, the initial state of an equally-spaced two-qudit engine is described for any dimension of the qudits by a first partial order over the frequencies and a second one over the products . These order relations identify four basic partially-ordered sets (posets). In the two-qubit example, the ergotropy can only be extracted if the initial state belongs to or , where the bar denotes the same poset with A and B switched. The states belonging to the remaining two sets are passive.
The description in terms of posets becomes more complex in higher dimension. For a state as in Eq. (3), the ordering procedure for the ergotropy extraction needs to establish if and if for every pair of natural numbers and .
Even if the simplest non-trivial case would be a system made of a qubit and a qutrit, here, as mentioned above, we consider a two-qutrit system, so that we can use the results for the two-stroke swap Otto engine with two qudits with equal dimension studied in Ref. [35] as a benchmark. In this scenario, each of the four basic posets mentioned above is further partitioned in four subsets, defined by the order relations and , with or and may be A or B. The total number of posets determining the regimes for the ergotropy extraction is then sixteen. We expect some of them to be passive regimes, i.e. the input state defined by those parameters is passive. As for the others, we will show that a specific transformation can extract the ergotropy from different regimes, as we noted for the two-qubit case with the swap in the regimes and .
2. Results
2.1. Ergotropic transformations
As mentioned above, we can jointly classify all the ergotropic transformations U and the corresponding ergotropic regimes by inspecting the permutations and .
In the two-qutrit case we have four posets identified by and for , and four identified by and for . We find different permutations and for each of the corresponding four posets, i.e. four distinct transformations. We show them associated to the corresponding poset in Figure 2. Note that, for what concerns , we have to distinguish three inequivalent cases identified by the relative position of points on the axis according to the value of the ratio .
In summary, and are simply the identity I (i.e. no reordering is needed) for and , respectively. For and , both and are given by the swap , namely
or, equivalently, , using the cycle notation and the lexicographic ordering where the elements of the cycles are related to the kets as .
For and , both and are given by
Finally, for and , both and are given by
We notice that and are not invariant under swap symmetry. In particular, reads
while
The unitary operators , and are also Hermitian and hence self-inverse. Notice also that
and, similarly, .
The product together with the composition rules for , and explored above allows to find the ergotropic transformations for each ergotropic regime identified by combining an poset with a poset. In particular, we remark that the ergotropic transformations resulting from the product must be again , , and . They are five overall, considering the identity too, which pertains to initial passive states. We provide a direct visualization of the landscape of ergotropic transformations in Figure 3, Figure 4 and Figure 5. Having set , each figure is linked to a different regime for the ratio . As outlined in Figure 2, we can identify three distinct ranges of with two critical values, namely and . For each case, we show the ergotropic transformation related to each poset. In particular, we set in Figure 3, in Figure 4 and in Figure 5. Firstly, we observe that in the first two cases all the transformations found above appear (except , which pertains to the regime ). In the case of Figure 5, is never present and the number of passive regimes becomes four. Notice that in the region , it is possible to take the limits and . In this case, one of the passive regimes disappears and most of the parameter region is dominated by the swap. On the contrary, approaching the critical point we see that the region where the swap extracts the ergotropy shrinks until it vanishes at the critical point. In the second case, in Figure 4, the swap plays again a role, but the passive regimes grow as well until, at the critical point , the ergotropic region of vanishes and is replaced for by passive regimes. Of course, at , the whole frequency subset is passive.
Let us inspect more in detail the non-trivial ergotropic transformations , , and . The swap clearly commutes with the total number operator, namely
On the other hand, the evolutions and act asymmetrically on the two systems, since they perform a permutation of the frequency levels of as if the system identified by the smallest frequency gap (B when the ergotropy is extracted by and A when it is extracted by ) were a two-level system, being its intermediate level left unaffected. Thus, we name as idle swap. In fact, for this asymmetry we have .
Differently from , the idle swaps and enjoy the conservation laws
As for , being the composition of the standard and the idle swap, we name it double swap. We noticed above that is not Hermitian. Indeed, one finds out that the double swap has multiplicative order six, namely , as it can be inferred from the cycle notation in Eq. (14). Furthermore, the double swap does not commute with any linear combination of and . In Appendix A, we prove that, if the transformation commutes with a linear combination of and , then all work and heat moments are proportional each another and hence the mean entropy production is proportional to the mean extracted work, as we will explicitly show for , and in the next Sections.
2.2. Ergotropy
Now we are ready to provide the mean work of Eq. (4) extracted by each ergotropic transformation. In the case of the swap , the ergotropy can be expressed in terms of units and reads
In the case of the idle swaps and we obtain
and
Here we recognize the action described above: the lower frequency qutrit is taken as a qubit whose gap is for and for , so that the extracted work is proportional to and , respectively. As expected, the work extracted from is obtained from the one extracted by just by swapping A with B. From Eqs. (20-22) one also verifies that
where the ratio is a relevant parameter, as we will find in the following.
In the case of the double swap, we have
Here we see the effects of the atypical behavior of : the extracted work is not proportional to any frequency gap. On the contrary the frequencies and appear multiplied with different weights. Notice that for one has and from the second line of Eq. (24) the double swap extracts the same work as , i.e. . Instead, for , namely , one has and . Finally, for we have and again . In Figure 6 we represent the ergotropy extraction in the case . In particular, we set the ratio , as in Figure 3, with . Note that the pretended discontinuities in the transitions between different ergotropic regions are just cusps, as it can be recognized in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11.
In these figures, we show specific examples of ergotropy extraction as a function of , by fixing all the other parameters. Figure 7 displays the case , with . Therefore, this is not a critical point and for varying we span all the non-equivalent ergotropic transformations. The black dot line displays the work extracted from the standard swap , so that we can see how it is outperformed by the other unitaries outside its own ergotropic regime. Moreover, the solid lines, corresponding to and , show that the regime of operation of an ergotropic heat engine is enlarged with respect to the swap Otto engine. In Figure 8 we consider the critical point , which represents the transition between the cases in Figure 3 and Figure 4, where the ergotropic regime of the standard swap vanishes. Indeed, here we do not have any ergotropic contribution from , except for the limiting case , where the work extracted coincides with the one provided by , identified by the red point. In Figure 9 we show the ergotropy as a function of for the critical point , which is the transition point between the cases of Figure 4 and Figure 5. As expected, the double swap is never required to extract the ergotropy. The maximum work is extracted by the idle swap for , by the standard swap for and by for . For the case of Figure 5, we fix in Figure 10. As in the previous case, is not needed and, furthermore, there are two more passive regions. Finally, in the last example in Figure 11, we plot the ergotropy for the ideal case , by setting to 0 and finite large values for and . In particular, the high value of allows to see that the extracted work is large when is large, except for the limiting case (in such case indeed we would have , implying ).
In summary, in the regime of operation of the standard swap Otto engine, i.e. , the work extraction may be improved by replacing the swap with the permutation . Moreover, the idle swaps and even allow to enlarge the range of operation of the heat engine.
2.3. Entropy production
Let us now evaluate the mean entropy production of the quantum heat engine in order to study its relation with the work fluctuations and to explore the validity or violation of TURs. As mentioned in Section 1, the mean entropy production is given by
We can evaluate the moments of W and through the derivatives of the characteristic function, according to Eqs. (A27) and (A28) of Appendix A. Due to the conservation laws for , and as in Eqs. (18) and (19), according to Eq. (A34), we have
where for , for , and for . Hence, the entropy production of , and is proportional to their pertaining work, and one has
where , and are given in Eqs. (20), (21) and (22), respectively.
Eq. (26) does not hold for , and the entropy production explicitly is given by
Note that in all cases the mean entropy production is positive and depends only on the ratios between frequency and temperature and not on the bare frequencies.
2.4. Work distribution
We can now provide the explicit expression for the distribution of work pertaining to each ergotropic transformation. As shown in Appendix A [see Eq. (A15)], we have
where is the energy distribution of the input state, namely
while is the energy conditional distribution after the evolution U, given the input energy levels n and m, i.e.
In the case of the standard swap , the conditional distribution reads , and hence
which is a 5-point distribution. Explicitly, upon naming , one has
A specific example is plotted in Figure 12. Eq. (33) is consistent with the general result given in Ref. [35] for the work distribution in swap engines based on two qudits.
Now we focus on the idle swap . Due to its asymmetric action on systems A and B, the conditional distribution is slightly more complicated and reads
where ⨁ denotes the sum . Hence, one retrieves the following 3-point distribution
An example is depicted in Figure 13.
Similarly, in the case of one has
Finally, since , for the double swap we readily find
and then one obtains the following 7-point distribution
A specific example is provided in Figure 14.
2.5. Work fluctuations and TURs
Here we evaluate the relative fluctuations of the work extracted by the ergotropic transformations and compare them to the lower bounds identified by different thermodynamic uncertainty relations (TURs).
We can find the relative fluctuations as the ratio between the variance of the extracted work and the square of its mean value, namely , with . The second moment of the extracted work can be obtained from the characteristic function as in Eqs. (A28) and (A29), and one has
For the standard swap one obtains
which is in agreement with the general result of the swap engine with two qudits of Ref. [35]. As expected, the fluctuations of the standard swap are invariant under swapping A and B.
For the idle swap , we have
As for the ergotropy in Eqs. (21) and (22), the expression for is simply obtained by exchanging A with B in Eq. (41). Note that the fluctuations of both the standard and the idle swap depend only on the products .
This is not the case for the double swap , which depends also on the frequency ratio as follows
For all the ergotropic transformations the fluctuations are minimized in the limiting case where for one qutrit and for the other one. In the case of the swap, being naturally invariant under swap symmetry, we can either set to zero and to infinity or the other way around. On the contrary, the case of the idle and the double swap is asymmetric and we achieve the minimum of the fluctuations for in the case of and for in the case of and . Here we mainly focus on the transformations that extract the ergotropy in the same poset identified by the products . In particular, we choose the poset defined by , where the optimal evolutions are , and . In the case of the double swap , the minimization has to be performed also on the frequency ratio and the infimum is obtained for . The optimization of the fluctuations over the whole span of the parameters readily provides
Therefore, it turns out that and achieve smaller fluctuations than .
We will now investigate if damping the noise comes together with the extraction of the ergotropy. While for this is always the case, the same is not true for and . The idle swap extracts the ergotropy for , where the condition for the minimization of fluctuations corresponding to does not hold. Interestingly, in that region it is the ergotropy extractor. Within the ergotropic region of , we need to take , which provides . For , on the contrary, the condition on the ratios for optimal fluctuations is compatible with the extraction of ergotropy, but with the additional constraint . The minimization over x then sets it to , and, as discussed after Eq. (24), for that frequency ratio . To sum up, if we aim to optimize the noise inside the ergotropic regimes of each ergotropic transformation, we find that the best performance is achieved by the standard swap, since
In this last regime where ergotropy extraction and minimal noise coexist, we finally note that the standard swap extracts more work than the idle and double swap. In fact, one has
We remark that the results found so far do imply that the standard swap is the best operation in terms of fluctuations and extracted work in the optimal limiting case , but the same does not hold for intermediate values of , as we shall see in the following.
Now we compare the relative fluctuations of the ergotropic engine in asymptotic and non-asymptotic cases with the bounds derived from the most significant TURs. We recall that the double swap is not Hermitian. Therefore, as remarked in the Appendix after Eq. (A26), could violate all the TURs based on the equivalence between forward and backward processes. On the other hand, we already know from previous works [35] that the swap itself breaks the standard TUR in Eq. (2). We study in Figure 15 the violation of the standard TUR as a function of in conditions of minimal fluctuations, independently from the ergotropic regime. Namely, in the case of (red dashed line), (purple solid line) and (blue dot-dashed line) the free variable is with . Just for , we also need . We remark that here we are not focusing on the ergotropy extraction, but only on the properties of the evolutions , and in terms of work fluctuations. We find that all the three ergotropic transformations break the standard thermodynamic uncertainty relation. In particular, the violation due to is impressive. As found in [35], when the evolution is the standard swap the relative fluctuations for the extracted work satisfies
The variation of Eq. (46) from the standard TUR explains the slight violation found in Figure 15, where the lower bound from the standard TUR is displayed as a black dotted line. Similarly to , also and satisfy Eq. (46). In fact,
where
which satisfies
The fluctuations originated from , instead, can break the TUR in Eq. (46). Such violation stems from the asymmetry of the process described by , which is not Hermitian. Indeed, we note that a necessary condition for the TURs in Eqs. (2) and (46) to hold is the equivalence between forward and backward process, i.e. . Moreover, note that the double swap is the only transformation whose fluctuations depend also on the frequency ratio, while leaving the mean entropy as a function of just and . Therefore, in this case we can optimize over a third parameter without changing the lower bound of the TUR.
The violation of the TUR in Eq. (46) by can be found also in realistic cases, i.e. even if we do not set the parameters to the values minimizing the fluctuations. Actually, these cases are the most relevant to be considered, not only because closer to experimental applications but especially because they keep into account the ergotropy extraction provided by the different evolutions. For instance, consider the case of Figure 7, where , , and is left free. Correspondingly, in Figure 16 we plot the signal-to-noise ratio (SNR) of the extracted work for each transformation in its ergotropic regime, together with the lower bound of Eq. (2) (dotted lines). Firstly, note that the double swap violates the TUR even if we are far from the optimal conditions on the parameters maximizing the SNR. Second, the TUR is violated in both regimes where extracts the ergotropy (). Third, differently from what we found in the case of optimal conditions, and can achieve better SNRs than the standard swap where the ergotropy is extracted.
The standard TUR is not the only relevant lower bound which we show in Figure 16. The tightest TUR that cannot be violated by any time-symmetric process was found in Ref. [33] and, applied to the extracted work, reads
where is the inverse of the function . Therefore, we expect that nor neither can violate this TUR, while in principle can. This is what we see in Figure 16, where the dot-dashed lines corresponds to the lower bound determined by Eq. (50): the SNR identified by the double swap is the only one that can violate the tight TUR, also within its ergotropic regime.
We focus more in detail on the violation of the TURs above in Figure 17, Figure 18 and Figure 19, where we plot the SNRs for the three evolutions both for optimal values of the parameters independently from the ergotropy extraction and within the corresponding ergotropic regime. In particular, Figure 17 displays the performance of the standard swap . Here we set , which implies that the fluctuations are minimized for large . As increases, the signal-to-noise ratio approaches the inverse of the minimal fluctuations, namely , in agreement with Eq. (43). Again, we find a slight violation of the standard TUR (dotted line).
In Figure 18 we show the performance of the idle swap where it maximizes the SNR (first panel) and where it extracts the ergotropy (second panel). Therefore, in the former case we set and retrieve the optimization of the SNR for large values of , as in Eq. (43). In the regime where extracts the ergotropy, as in Eq. (44), we find an optimal SNR approaching for and an almost negligible violation of the standard TUR. Neither the standard nor the idle swap violate the tight TUR in Eq. (50), displayed as a dashed-dotted line.
The case of the double swap, displayed in Figure 19, is radically different. If we neglect the conditions for the ergotropy extraction, here we can optimize also over the frequency ratio and we can set it to zero, while , implying that we expect to find the optimal SNR for large , as in Eq. (43). Again, the standard TUR is violated, but, compared with the previous cases, the corresponding bound is saturated for larger values of , where the SNR approaches its maximum. Most importantly, the tight TUR of Eq. (50) is also violated, both when the SNR is optimized (first panel) and when the ergotropy is extracted (second panel).
We also compare the SNR of with the loosest bound that always holds for time-symmetric processes [21,31,34] given by
The bound from Eq. (51) is displayed as a brown line in Figure 19. The violation that we find is a consequence of the fact that is not Hermitian.
In the second panel of Figure 19, as mentioned above, we explore the performance of the double swap in its ergotropic regime, where . The best performance is obtained for , where the amount of work extracted by is the same as the one extracted by (red line in Figure 19). We also plot the case , in blue. We get a worse SNR, but still can observe a violation of all the TURs derived for time-symmetric processes.
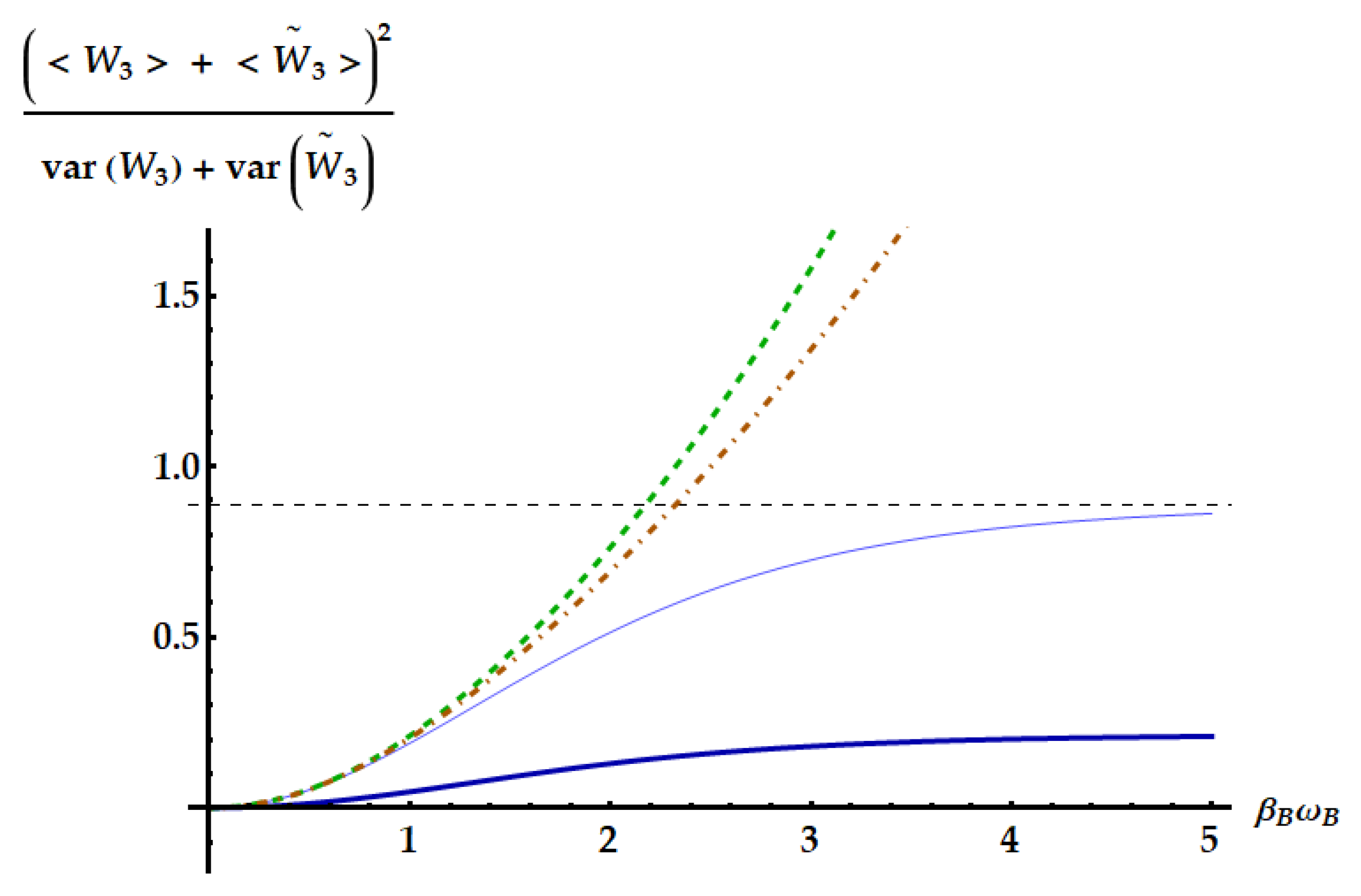
The only TURs that can set a bound which cannot be violated by are those obtained without posing the symmetry between forward and backward process. In fact, the TURs in Eqs. (50) and (51) have been generalized respectively in Refs. [39] and [32] by releasing the assumption that forward and backward processes share the same distribution of the stochastic variables. These new bounds are given by
and
where the quantities with subscript B are referred to the backward process and . In the case of , the statistics of W for the backward process is easily found since . Hence, outputs the same work statistics as provided that systems A and B are swapped. Then, , and can be obtained from Eqs. (24), (28) and (42) simply swapping labels A and B. Note also that the bounds (right-hand sides) given by the TURs in Eqs. (52) and (53) depend only on the products , while the corresponding bounded quantities depend also on the frequency ratio .
In Figure 20, we compare the reciprocal of the left-hand sides of Eqs. (52) and (53) for with the corresponding bounds as a function of with fixed . In this regime maximizes the SNR. We show the two limiting cases (thick dark-blue curve) and (thin light-blue curve) together with the bounds obtained from the TURs in Eqs. (52) and (53), identified by the dot-dashed brown curve and the dashed green curve, respectively. Note that these TURs are never violated and, as expected, the first is tighter than the second. Having set , the maximum is asymptotically reached for and , and amounts to (dashed horizontal line in Figure 20).
3. Conclusions
We devised a consistent description of ergotropic heat engines for the optimal work extraction from a couple of quantum systems which are cyclically restored to the canonical equilibrium at two different temperatures. We provided an exhaustive study for the case of two qutrits with equally-spaced energy levels by deriving the optimal ergotropic transformations, the statistics of the extracted work and the mean entropy production. We focused on the relative fluctuations of the work extracted by each ergotropic transformation and showed that one of them, the double swap , violates many common TURs, specifically the ones based on the assumption that the distributions of the extracted work for the forward and backward process are the same.
The application of our procedure to systems with higher dimension is promising because it will lead to the generalization of the ergotropic transformations found for the qutrit case and will allow to find new transformations which, as shown in this work, may possibly extract more work on average with lower fluctuations with respect to the two-stroke Otto engines based on qudits.
4. Conclusions
This section is not mandatory, but can be added to the manuscript if the discussion is unusually long or complex.
5. Patents
This section is not mandatory, but may be added if there are patents resulting from the work reported in this manuscript.
Acknowledgments
This material is based upon work supported by the EU H2020 QuantERA ERA-NET Cofund in Quantum Technologies project QuICHE, and by the Italian MUR through PRIN 2022. C.M. acknowledges support from the PNRR MUR Project PE0000023-NQSTI.
Appendix A
Let us describe the two-stroke Otto engines. We consider two quantum systems A and B (with Hamiltonians and ) initially at thermal equilibrium with their own reservoirs and (with Hamiltonians and ) at inverse temperatures and . Without loss of generality we take . We assume weak coupling between systems and reservoirs, so that we can represent the initial state as the tensor product of canonical density matrices, namely
where . We perform a two-strokes cyclic heat engine by isolating the two quantum systems from the reservoir at ; extracting work by a unitary transformation U acting on the two systems up to time ; reconnecting the two quantum systems to their respective reservoirs by weak coupling to achieve complete thermalization at . We remark that the unitary U incorporates the free evolution of the two systems and their interaction obtained by external (possibly time-dependent) driving protocols, with the condition of being cyclic, namely such that initial and final Hamiltonian coincide, i.e. for both A and B.
The average value of the work extracted on a cycle corresponds to the opposite of the variation of the internal energy of A and B during the unitary stroke U, i.e.
During the thermalization stroke each system comes back to equilibrium, namely system A absorbs the average heat from the hot reservoir, and system B dumps on the cold one. In our convention the cycle operates as a heat engine when , , and . Clearly, the first law is obtained as . At each cycle the two quantum systems come back to their respective equilibrium states, and hence the average entropy production per cycle simply corresponds to .
Let us now describe the above thermodynamical cycle by a set of stochastic trajectories which correctly reproduce the mean values of all thermodynamic variables by an average of stochastic variables over all possible trajectories. We adopt an operational approach based on complete energy measurements at different times [2,16,23] as in the typical derivation of Jarzynski equality [12]. This approach will allow us to study the complete statistics of work extraction and heat exchanges, and in particular to evaluate the fluctuations of work and their relation with the entropy production.
Figure A1.
Scheme for the stochastic description of a cycle of the Otto two-stroke engine. Labels A and B identify the two systems operated by the engine as a working fluid, and are the corresponding reservoirs. The unitary U is the transformation extracting work, while and are the energy-preserving unitaries for the thermal relaxation of each system with its pertaining reservoir.
Figure A1.
Scheme for the stochastic description of a cycle of the Otto two-stroke engine. Labels A and B identify the two systems operated by the engine as a working fluid, and are the corresponding reservoirs. The unitary U is the transformation extracting work, while and are the energy-preserving unitaries for the thermal relaxation of each system with its pertaining reservoir.
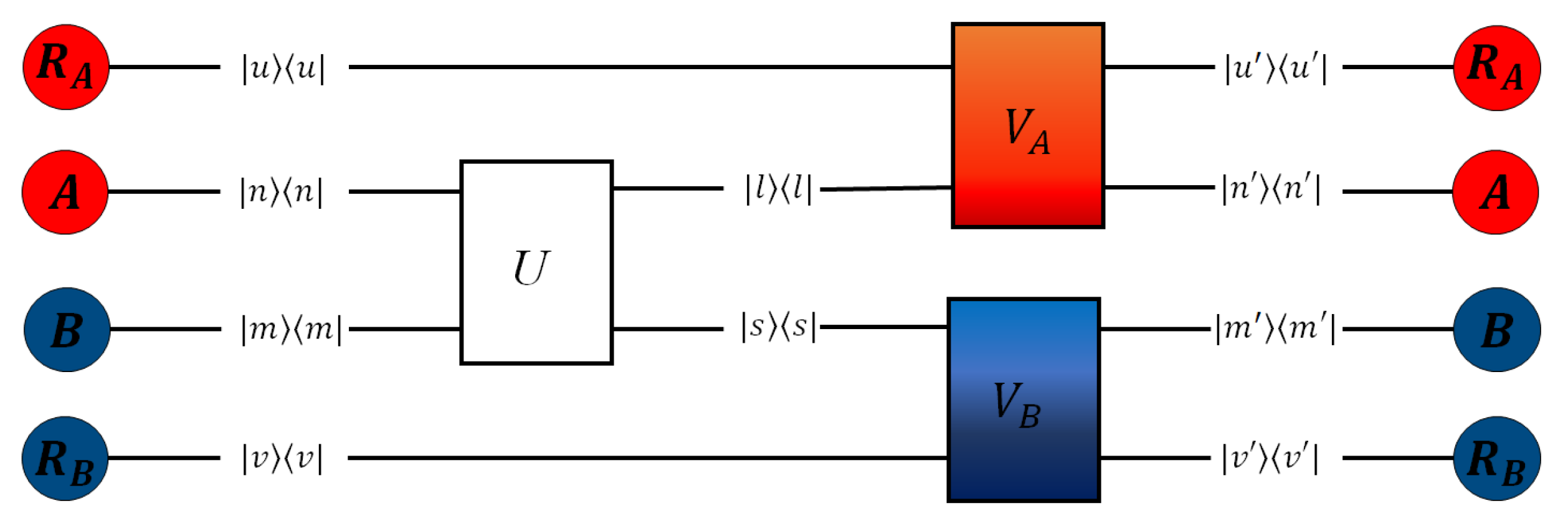
As depicted in Figure A1, we identify a single stochastic trajectory by the outcomes of the sequential fine-grained energy measurements of at the beginning of the cycle ; of at the end of the work stroke operated by U; and finally of at the end of the thermalization stroke . We denote by , with , the unitary operator representing the joint evolution of system X and reservoir by weak coupling and energy-preserving interaction up to complete thermal equilibrium at . By respecting the order of the above measurements, we denote by the stochastic trajectory corresponding to the sequence of outcomes, namely
with corresponding energy eigenvalues
We could denote by the eigenvector pertaining to the eigenvalue of Hamiltonian , with , but we will generally write instead of since in the following it will be clear from the context (and with the help of Figure A1) the respective Hilbert space of all eigenvectors.
Let us now evaluate the probability of occurence of a specific trajectory . Since the initial state is given by Eq. (A1), the probability for the initial outcomes is given by the product of Gibbs weights, namely
The conditional probability pertaining to the energy measurements of A and B with outcomes l and s after the unitary stroke U, given initial outcomes n and m, writes
Finally, the conditional probability for the thermalization stage is given by
It follows that the probability of the trajectory is given by
One easily identifies the functions of stochastic variables in correspondence to the thermodynamical variables of interest for each trajectory. Clearly, the work contribution corresponds to
On the other hand, the heat released by reservoirs A and B corresponds to
since we describe the thermalization with each reservoir by weak coupling and energy-preserving interactions [15].
By weighting each possible trajectory with its probability of occurrence we obtain the joint probability for extracting work W along with heat exchanges and as follows
Since models the complete thermalization by the reservoir , one has
for arbitrary density matrix of system X. This fact can be used to simplify Eq. (A11) by summing on all reservoir indexes . Hence, can be rewritten in terms of measurements outcomes only on systems A and B, namely
Eq. (A13) allows one to study the complete statistics of an ergotropic heat engine. The first principle of thermodynamics for the cycle is recovered since the average variation of the internal energy correctly gives zero, as shown as follows
One also has , where is the average variation of the internal energy of A during the unitary stroke, whose expectation can be obtained by averaging over all trajectories. Similarly, , where has corresponding stochastic values given by .
By introducing the trajectories for the thermalization stroke, we remark that the present result allows us to refine the approach of Refs. [33,35,36], where the stochastic values of were identified with (and analogously for with ). In fact, notice that the relation does not generally hold at the trajectory level. Anyway, since corresponds to the average of over the trajectories, for increasing number of cycles the discrepancy between the stochastic variables and remains bounded by the finite energy of system A, whereas both and increase linearly with the number of cycles, thus providing . Analogous point applies for the variables and .
All results about the stochastic efficiency of the heat engines given in Refs. [35,36] rigorously hold for defined in terms of , namely . One could refine and compare the results for defined as by means of the probability distribution presented here in Eq. (A13). The subtle difference between these two definitions of stochastic efficiency was already discussed in Ref. [45], where the thermalization in a two-stroke Otto engine was modeled by the quantum jump method.
The probability of work extraction is the marginal of in Eq. (A13) with respect to the heat exchanges, and one has
Let us now consider a backward protocol where the measurements on the quantum systems and the reservoirs are performed in the reverse ordering, along with the time-reversal evolution of all interactions. The initial state for the backward protocol is again taken as the product of canonical density matrices, namely as in Eq. (A1). By assuming that all Hamiltonians are invariant under time-reversal at all times [17,18,23], the backward protocol is then equivalent to follow Figure A1 from the right to the left, along with the replacement of , and U with , and , respectively.
We can compare the forward and the backward protocols by the probability of a trajectory and the probability for the occurrence of the specular reverse trajectory with the same measurement outcomes, namely . The comparison between the forward and the backward protocol is made by the logarithm of the probabilities, which defines the stochastic entropy generated along a trajectory as [18]
Since each identifies a corresponding backward trajectory , the fluctuation theorem simply follows as
In the present case, using Eq. (A8) and the cancellation between forward and backward conditional probabilities for both and , one obtains
and hence
where we used Eqs. (A10). As for the case of the stochastic work , notice that also depends only on the reduced set of indexes pertaining to the unitary stroke operated by U. The probability of the stochastic entropy is then given by
From Eq. (A20) one correctly recovers the equivalent identities .
Since from definition (A16) one has we easily derive the detailed fluctuation theorem as follows
Indeed, by analogous derivation, for any set of odd stochastic variables such that , one has
In particular, since , we can also write [17,20,22,24]
where
and identifies the distribution of the backward process, described by the transformation instead of U. We recall here that the relation holds for the stochastic variables, namely at the trajectory level.
When the unitary operator U is of the form
with unitary Hermitian and arbitrary phases , notice that one has the symmetry
Typically, this happens when the time-dependent protocol that actualizes the unitary evolution U is a time-symmetric driving [2,17,20]. We remark that the TUR in Eq. (50) derived from the fluctuation theorem of Eq. (A22) implicitly assumed the condition .
Let us now consider in more detail the joint probability . The full statistics of W and is equivalently contained in the characteristic function given by the Fourier transform
Here, and denote the counting parameters for W and , so that all moments and correlations can be recovered as
Using Eq. (A24) and applying the delta functions in the integrals of Eq. (A27) one obtains
Recalling Eq. (A1), one easily verifies the identity , which corresponds to the fluctuation theorem of Eq. (A17). In fact, one has
In terms of the characteristic function, we notice that the detailed fluctuation theorem of Eq. (A23) is translated into the symmetry
In the presence of a symmetry in the unitary stroke achieved by U such that for a real one has
from Eq. (A29) one obtains the corresponding property
i.e. the characteristic function becomes a function of a single variable. It follows that , and from Eq. (A28) one obtains the symmetry relations
namely the stochastic variables W and are perfectly correlated. Moreover, since , one has . It also follows that the average entropy is simply proportional to the average work, namely
The effect of a strong symmetry as Eq. (A32) can be seen directly on the joint probability . In fact, by using the last expression in Eq. (A33) for in the inverse Fourier transform of Eq. (A27), one easily obtains
namely one has the perfect correlation . In this case, one also recognizes that the stochastic -efficiency defined as the ratio , is a self-averaging quantity and has no fluctuations, since .
References
- Li, N.; Ren, J.; Wang, L.; Zhang, G.; Hänggi, P.; Li, B. Colloquium: Phononics: Manipulating heat flow with electronic analogs and beyond. Rev. Mod. Phys. 2012, 84, 1045–1066. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 1–58. [Google Scholar] [CrossRef] [PubMed]
- Benenti, G.; Casati, G.; Saito, K.; Whitney, R. S. Fundamental aspects of steady-state conversion of heat to work at the nanoscale. Physics Reports 2017, 694, 1–124. [Google Scholar] [CrossRef]
- Dubi, Y.; Di Ventra, M. Colloquium: Heat flow and thermoelectricity in atomic and molecular junctions. Rev. Mod. Phys. 2011, 83, 131–155. [Google Scholar] [CrossRef]
- Josefsson, M.; Svilans, A.; Burke, A. M.; Hoffmann, E. A.; Fahlvik, S.; Thelander, C.; Leijnse, M.; Linke, H. A quantum-dot heat engine operating close to the thermodynamic efficiency limits. Nat. Nanotech. 2018, 13, 920–924. [Google Scholar] [CrossRef] [PubMed]
- Ritort, F. Nonequilibrium Fluctuations in Small Systems: From Physics to Biology. Adv. Chem. Phys. 2008, 137, 31–123. [Google Scholar]
- Gnesotto, F. S.; Mura, F.; Gladrow, J.; Broedersz, C. P. Broken detailed balance and non-equilibrium dynamics in living systems: a review. Rep. Prog. Phys. 2018, 81. [Google Scholar] [CrossRef]
- Rao, R.; Esposito, M. Nonequilibrium Thermodynamics of Chemical Reaction Networks: Wisdom from Stochastic Thermodynamics. Phys. Rev. X 2016, 6, 041064. [Google Scholar] [CrossRef]
- Van Vu, T.; Saito, K. Thermodynamic Unification of Optimal Transport: Thermodynamic Uncertainty Relation, Minimum Dissipation, and Thermodynamic Speed Limits. Phys. Rev. X 2023, 13, 011013. [Google Scholar] [CrossRef]
- Gallavotti, G.; Cohen, E. G. D. Dynamical Ensembles in Nonequilibrium Statistical Mechanics. Phys. Rev. Lett. 1995, 74, 2694–2697. [Google Scholar] [CrossRef]
- Jarzynski, C. Equilibrium free-energy differences from nonequilibrium measurements: A master-equation approach. Phys. Rev. E 1997, 56, 5018–5035. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Crooks, G. E. Nonequilibrium Measurements of Free Energy Differences for Microscopically Reversible Markovian Systems. J. Stat. Phys. 1998, 90, 1481–1487. [Google Scholar] [CrossRef]
- Piechocinska, B. Information erasure. Phys. Rev. A 2000, 61, 062314. [Google Scholar] [CrossRef]
- Jarzynski, C.; Wójcik, D. K. Classical and Quantum Fluctuation Theorems for Heat Exchange. Phys. Rev. Lett. 2004, 92, 230602. [Google Scholar] [CrossRef] [PubMed]
- Talkner, P.; Hänggi, P. The Tasaki–Crooks quantum fluctuation theorem. J. Phys. A 2007, 40, F569–F571. [Google Scholar] [CrossRef]
- Andrieux, D.; Gaspard, P.; Monnai, T.; Tasaki, S. The fluctuation theorem for currents in open quantum systems. New J. Phys. 2009, 11, 043014. [Google Scholar] [CrossRef]
- Esposito, M.; Harbola, U.; Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 2009, 81, 1665–1702. [Google Scholar] [CrossRef]
- Esposito, M.; Van der Broeck, C. Three Detailed Fluctuation Theorems. Phys. Rev. Lett. 2010, 104, 090601. [Google Scholar] [CrossRef] [PubMed]
- Campisi, M.; Talkner, P.; Hänggi, P. Fluctuation Theorems for Continuously Monitored Quantum Fluxes. Phys. Rev. Lett. 2010, 105, 140601. [Google Scholar] [CrossRef] [PubMed]
- Merhav, N.; Kafri, Y. Statistical properties of entropy production derived from fluctuation theorems. J. Stat. Mech. 2010, 12, P12022. [Google Scholar] [CrossRef]
- Sinitsyn, N. A. Fluctuation relation for heat engines. J. Phys. A 2011, 44, 405001. [Google Scholar] [CrossRef]
- Campisi, M.; Hänggi, P.; Talkner, P. Quantum fluctuation relations: Foundations and applications. Rev. Mod. Phys. 2011, 83, 771–791. [Google Scholar] [CrossRef]
- Campisi, M. Fluctuation relation for quantum heat engines and refrigerators. J. Phys. A 2014, 47. [Google Scholar] [CrossRef]
- Hänggi, P.; Talkner, P. The other QFT. Nat. Phys. 2015, 11, 108–110. [Google Scholar] [CrossRef]
- Vo, V. T.; Van Vu, T.; Hasegawa, Y. Unified approach to classical speed limit and thermodynamic uncertainty relation. Phys. Rev. E 2020, 102, 062132. [Google Scholar] [CrossRef] [PubMed]
- Salazar, D. S. P. Bound for the moment generating function from the detailed fluctuation theorem. Phys. Rev. E 2023, 107, L062103. [Google Scholar] [CrossRef] [PubMed]
- Mohanta, S.; Saha, M.; Venkatesh, B. P.; Agarwalla, B. K. Bounds on nonequilibrium fluctuations for asymmetrically driven quantum Otto engines. Phys. Rev. E 2023, 108, 014118. [Google Scholar] [CrossRef]
- Barato, A. C.; Seifert, U. Thermodynamic Uncertainty Relation for Biomolecular Processes. Phys. Rev. Lett. 2015, 15, 158101. [Google Scholar] [CrossRef] [PubMed]
- Gingrich, T. R.; Horowitz, J. M.; Perunov, N.; England, J. L. Dissipation Bounds All Steady-State Current Fluctuations. Phys. Rev. Lett. 2016, 116, 120601. [Google Scholar] [CrossRef]
- Proesmans, K.; Van den Broeck, C. Discrete-time thermodynamic uncertainty relation. Europhys. Lett. 2017, 119, 20001. [Google Scholar] [CrossRef]
- Potts, P. P.; Samuelsson, P. Thermodynamic uncertainty relations including measurement and feedback. Phys. Rev. E 2019, 100, 052137. [Google Scholar] [CrossRef]
- Timpanaro, A. M.; Guarnieri, G.; Goold, J.; Landi, G. T. Thermodynamic uncertainty relations from exchange fluctuation theorems. Phys. Rev. Lett. 2019, 123, 090604. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, Y.; Van Vu, T. Fluctuation Theorem Uncertainty Relation. Phys. Rev. Lett. 2019, 123, 110602. [Google Scholar] [CrossRef] [PubMed]
- Sacchi, M. F. Multilevel quantum thermodynamic swap engines. Phys. Rev. A 2021, 104, 012217. [Google Scholar] [CrossRef]
- Sacchi, M. F. Thermodynamic uncertainty relations for bosonic Otto engines. Phys. Rev. E 2021, 103, 012111. [Google Scholar] [CrossRef] [PubMed]
- Van Vu, T.; Saito, K. Thermodynamics of Precision in Markovian Open Quantum Dynamics. Phys. Rev. Lett. 2022, 128, 140602. [Google Scholar] [CrossRef] [PubMed]
- Salazar, D. S. P. Thermodynamic uncertainty relations from involutions. Phys. Rev. E 2022, 106, L062104. [Google Scholar] [CrossRef] [PubMed]
- Francica, G. Fluctuation theorems and thermodynamic uncertainty relations. Phys. Rev. E 2022, 105, 014129. [Google Scholar] [CrossRef] [PubMed]
- Feldmann, T.; Geva, E.; Kosloff, R.; Salamon, P. Heat engines in finite time governed by master equations. Am. J. Phys. 1996, 64, 485–492. [Google Scholar] [CrossRef]
- Rezek, Y.; Kosloff, R. Irreversible performance of a quantum harmonic heat engine. New J. Phys. 2006, 8, 83. [Google Scholar] [CrossRef]
- Quan, H. T.; Liu, Y.; Sun, C. P.; Nori, F. Quantum thermodynamic cycles and quantum heat engines. Phys. Rev. E 2007, 76, 031105. [Google Scholar] [CrossRef] [PubMed]
- Thomas, G.; Johal, R. S. Coupled quantum Otto cycle. Phys. Rev. E 2011, 83, 031135. [Google Scholar] [CrossRef]
- Abah, O.; Roßnagel, J.; Jacob, G.; Deffner, S.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Single-Ion Heat Engine at Maximum Power. Phys. Rev. Lett. 2012, 109, 203006. [Google Scholar] [CrossRef] [PubMed]
- Campisi, M.; Pekola, J.; Fazio, R. Nonequilibrium fluctuations in quantum heat engines: theory, example, and possible solid state experiments. New J. Phys. 2015, 17, 035012. [Google Scholar] [CrossRef]
- Peterson, J. P. S.; Batalhão, T. B.; Herrera, M.; Souza, A. M.; Sarthour, R. S.; Oliveira, I. S.; Serra, R. M. Experimental Characterization of a Spin Quantum Heat Engine. Phys. Rev. Lett. 2019, 123, 240601. [Google Scholar] [CrossRef]
- Piccione, N.; De Chiara, G.; Bellomo, B. Power maximization of two-stroke quantum thermal machines. Phys. Rev. A 2021, 103, 032211. [Google Scholar] [CrossRef]
- Gramajo, A. L.; Paladino, E.; Pekola, J.; Fazio, R. Fluctuations and stability of a fast-driven Otto cycle. Phys. Rev. B 2023, 107, 195437. [Google Scholar] [CrossRef]
- Allahverdyan, A. E. Maximal work extraction from finite quantum systems. EPL 2004, 67, 565–571. [Google Scholar] [CrossRef]
- Allahverdyan, A. E.; Johal, R. S.; Mahler, G. Work extremum principle: Structure and function of quantum heat engines. Phys. Rev. E 2008, 77, 041118. [Google Scholar] [CrossRef] [PubMed]
- Francica, G.; Binder, F. C.; Guarnieri, G.; Mitchison, M. T.; Goold, J.; Plastina, F. Quantum Coherence and Ergotropy. Phys. Rev. Lett. 2020, 125, 180603. [Google Scholar] [CrossRef] [PubMed]
- Biswas, T.; obejko, M.; Mazurek, P.; Jałowiecki, K.; Horodecki, M. Extraction of ergotropy: free energy bound and application to open cycle engines. Quantum 2022, 6, 841. [Google Scholar] [CrossRef]
- Salvia, R.; De Palma, G.; Giovannetti, V. Optimal local work extraction from bipartite quantum systems in the presence of Hamiltonian couplings. Phys. Rev. A 2023, 107, 012405. [Google Scholar] [CrossRef]
Figure 1.
Scheme of a quantum thermodynamic engine based on the two-stroke Otto cycle with two qutrits as working fluid. In the first stage, the qutrits A and B with frequency and are at thermal equilibrium with the corresponding baths at temperature and , respectively, with . In the second stage, the two systems are isolated and allowed to interact through a unitary evolution extracting work W. Finally, in the last stage, the systems A and B are allowed to relax to the corresponding thermal baths, implying that A absorbs the heat and B releases the heat , thus restoring the initial condition.
Figure 1.
Scheme of a quantum thermodynamic engine based on the two-stroke Otto cycle with two qutrits as working fluid. In the first stage, the qutrits A and B with frequency and are at thermal equilibrium with the corresponding baths at temperature and , respectively, with . In the second stage, the two systems are isolated and allowed to interact through a unitary evolution extracting work W. Finally, in the last stage, the systems A and B are allowed to relax to the corresponding thermal baths, implying that A absorbs the heat and B releases the heat , thus restoring the initial condition.
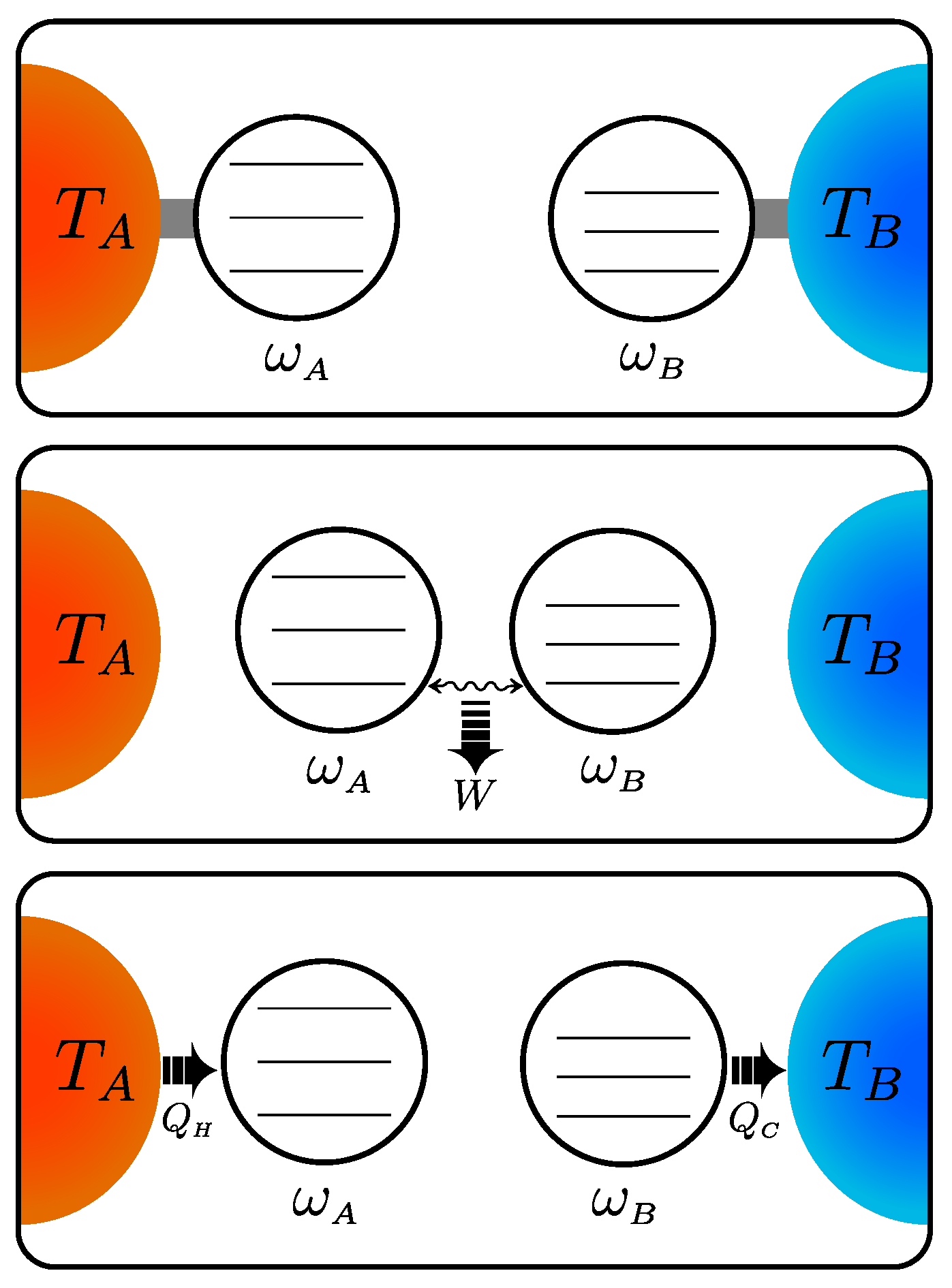
Figure 2.
Scheme of the transformations realizing the permutations and in the different regimes identified by in the former case and by in the latter. We show these regimes by fixing and the three inequivalent cases for the temperature ratio and studying and for increasing . As increases, we find that both the permutations are given by the identity (black thin line), (purple thick line), (blue dotdashed line), and the swap (red dashed line).
Figure 2.
Scheme of the transformations realizing the permutations and in the different regimes identified by in the former case and by in the latter. We show these regimes by fixing and the three inequivalent cases for the temperature ratio and studying and for increasing . As increases, we find that both the permutations are given by the identity (black thin line), (purple thick line), (blue dotdashed line), and the swap (red dashed line).
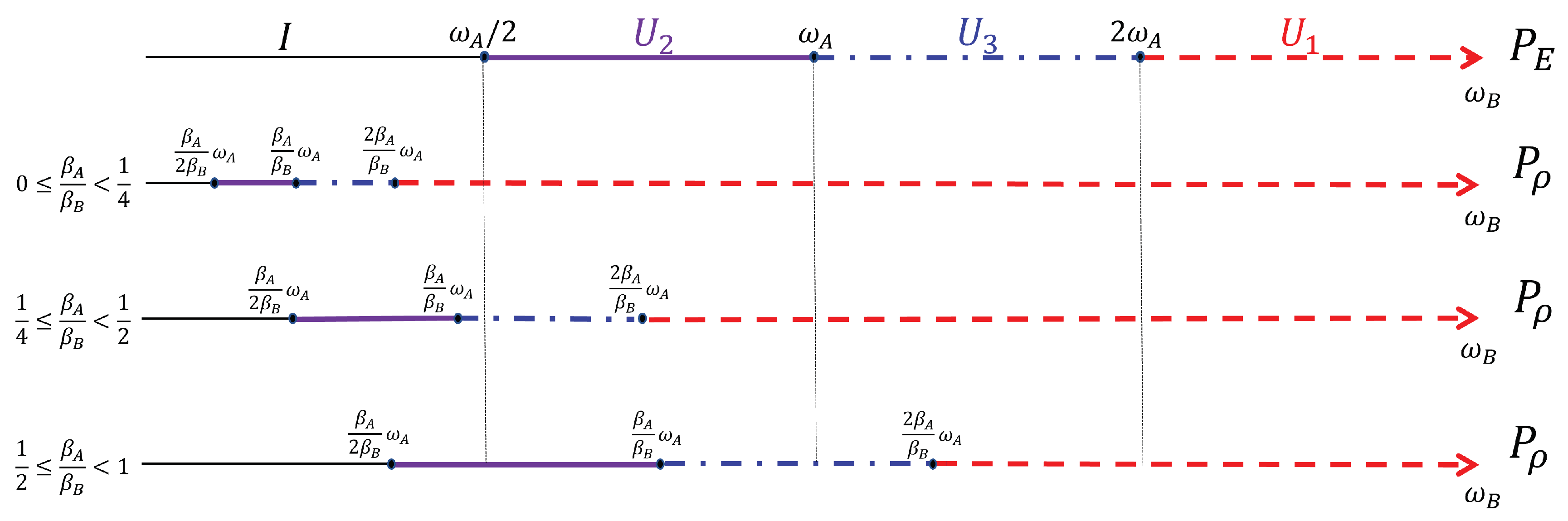
Figure 3.
First case: . Here, specifically, .
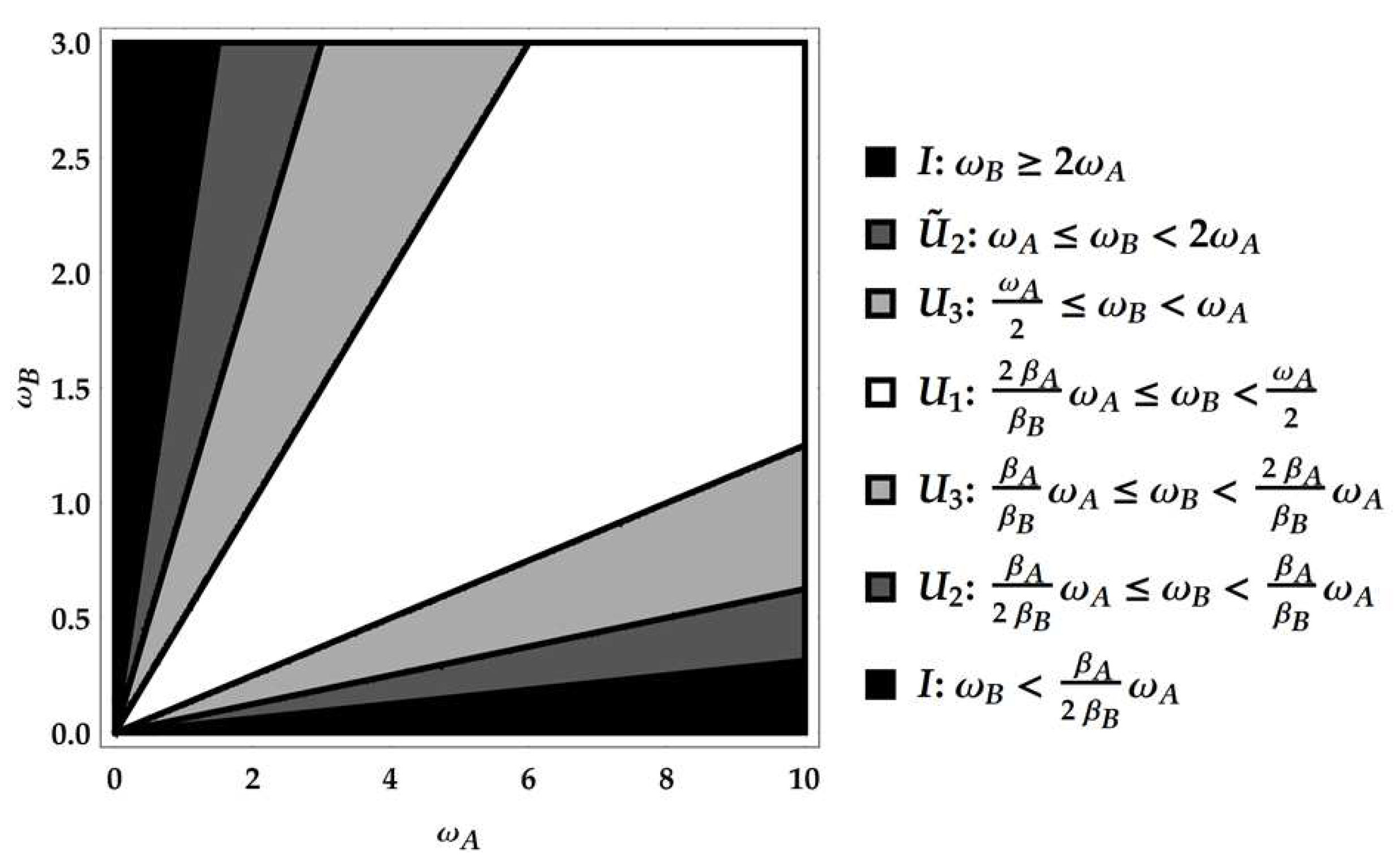
Figure 4.
Second case: . Here, specifically, .
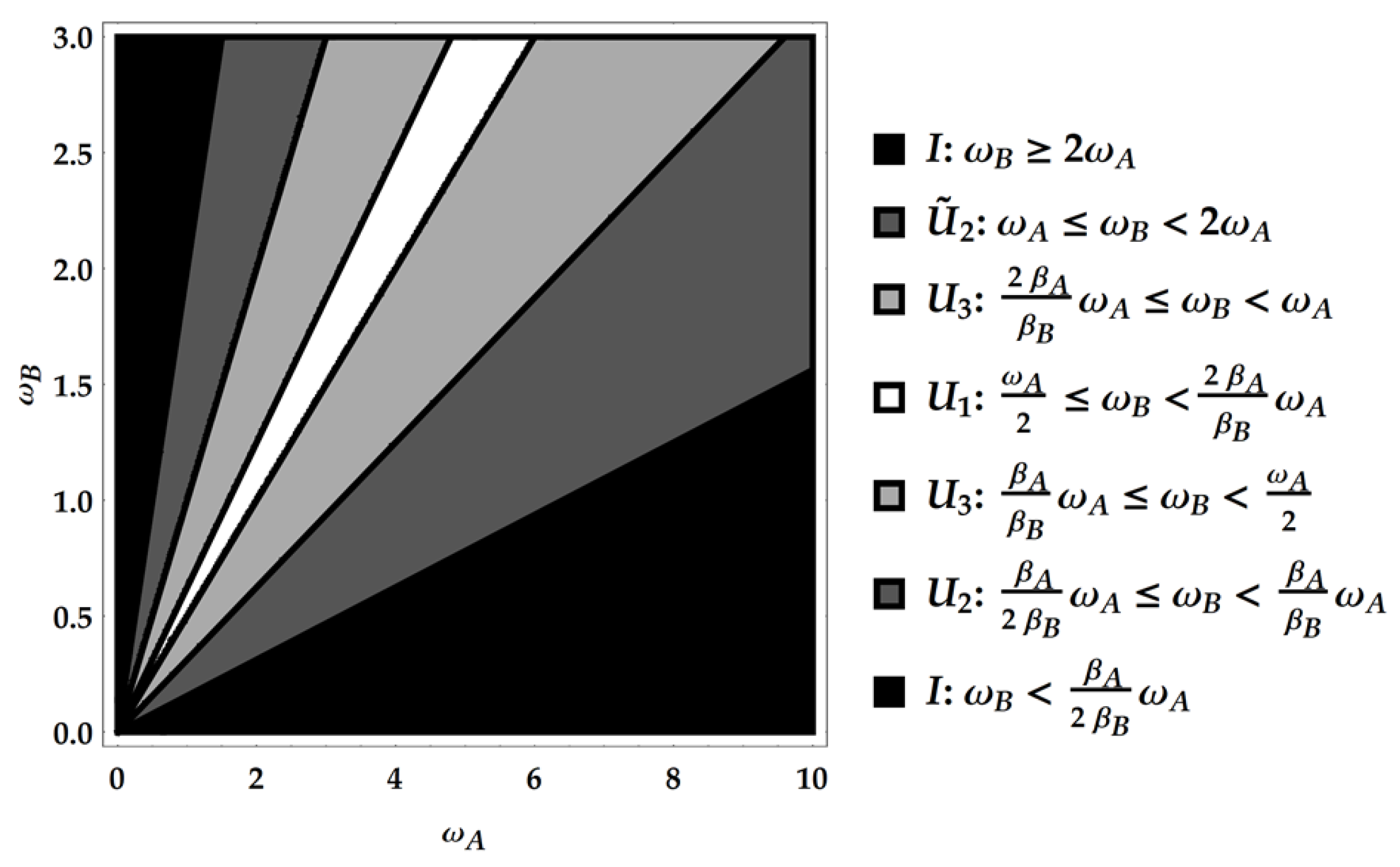
Figure 5.
Third case: . Here, specifically, .
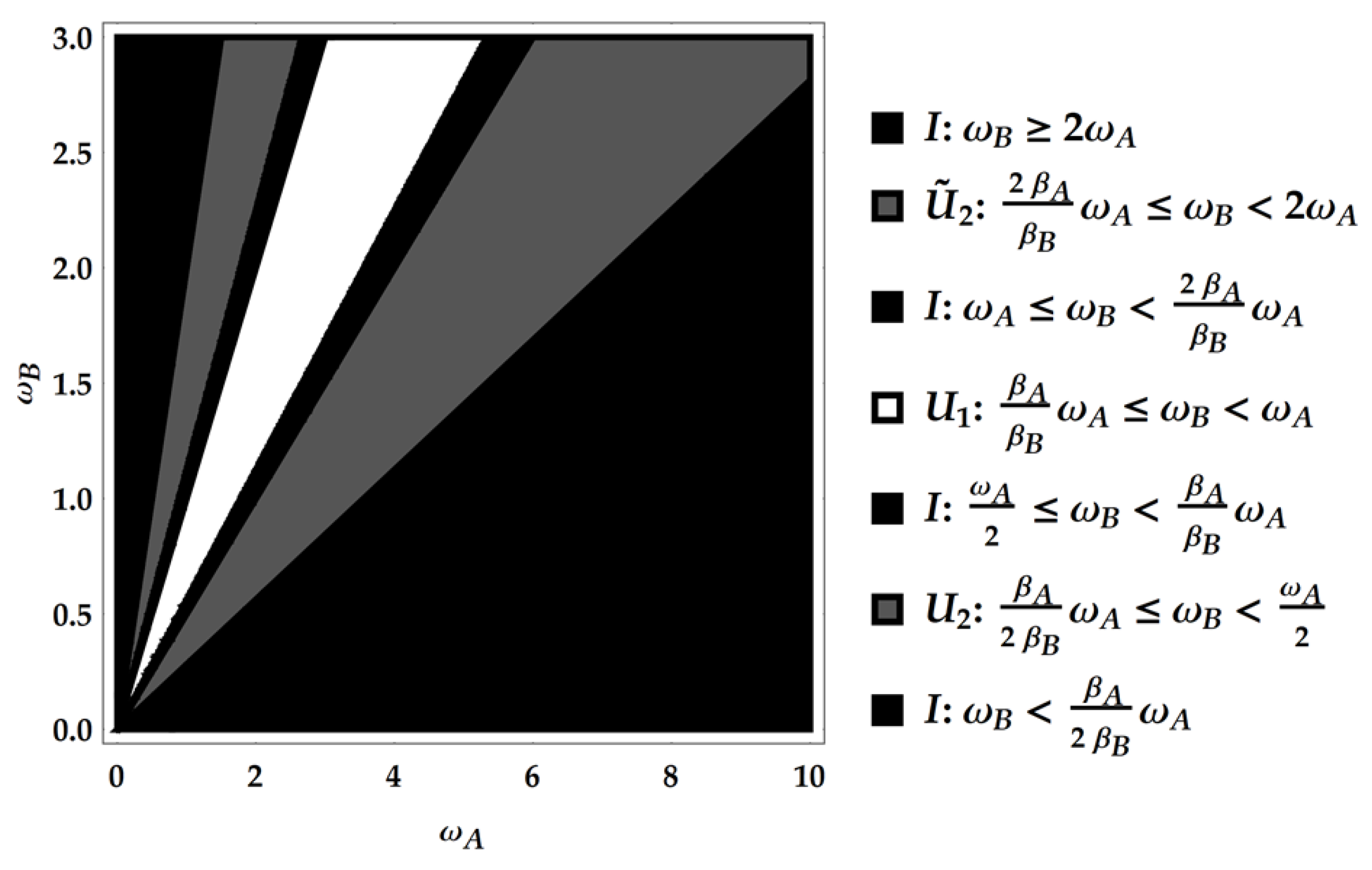
Figure 6.
Ergotropy extraction in the case . Here and .

Figure 7.
Ergotropy as a function of in the case , with , , . Purple solid lines: idle swaps () and (). Blue dot-dashed line: double swap . Red dashed line: standard swap inside the corresponding ergotropic regime. Black dotted line: standard swap for any such that the extracted work is positive.
Figure 7.
Ergotropy as a function of in the case , with , , . Purple solid lines: idle swaps () and (). Blue dot-dashed line: double swap . Red dashed line: standard swap inside the corresponding ergotropic regime. Black dotted line: standard swap for any such that the extracted work is positive.

Figure 8.
Ergotropy as a function of at the critical point , with , , . The red mark identifies the tangent point where the standard swap (dotted black line) and the double swap (blue dashed-dotted line) extracts the same amount of work at . The purple solid curves identify the ergotropy extracted by () and ().
Figure 8.
Ergotropy as a function of at the critical point , with , , . The red mark identifies the tangent point where the standard swap (dotted black line) and the double swap (blue dashed-dotted line) extracts the same amount of work at . The purple solid curves identify the ergotropy extracted by () and ().
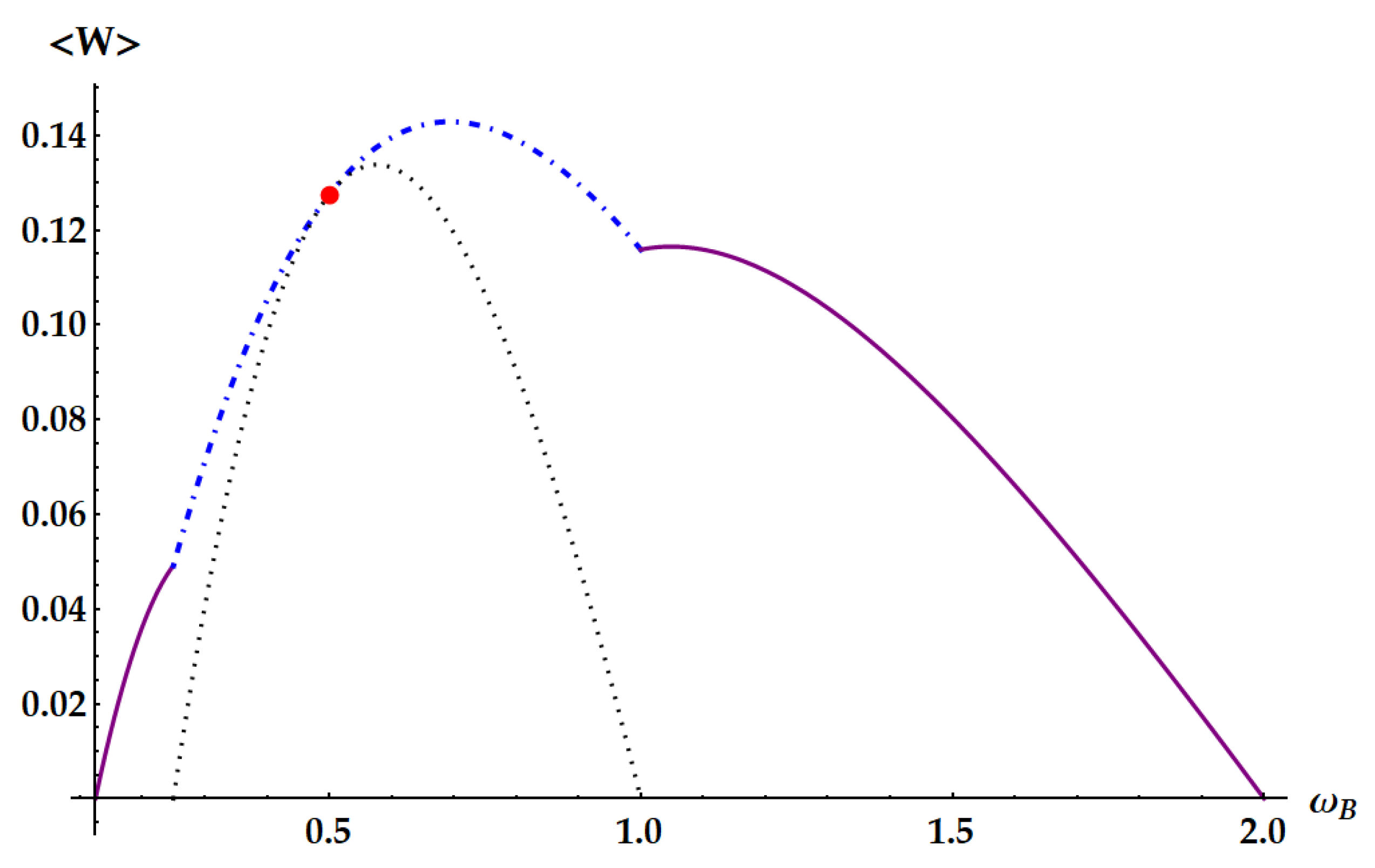
Figure 9.
Ergotropy as a function of in the critical case , with , , . Dashed red line: standard swap for . Purple solid lines: idle swaps for and for .
Figure 9.
Ergotropy as a function of in the critical case , with , , . Dashed red line: standard swap for . Purple solid lines: idle swaps for and for .
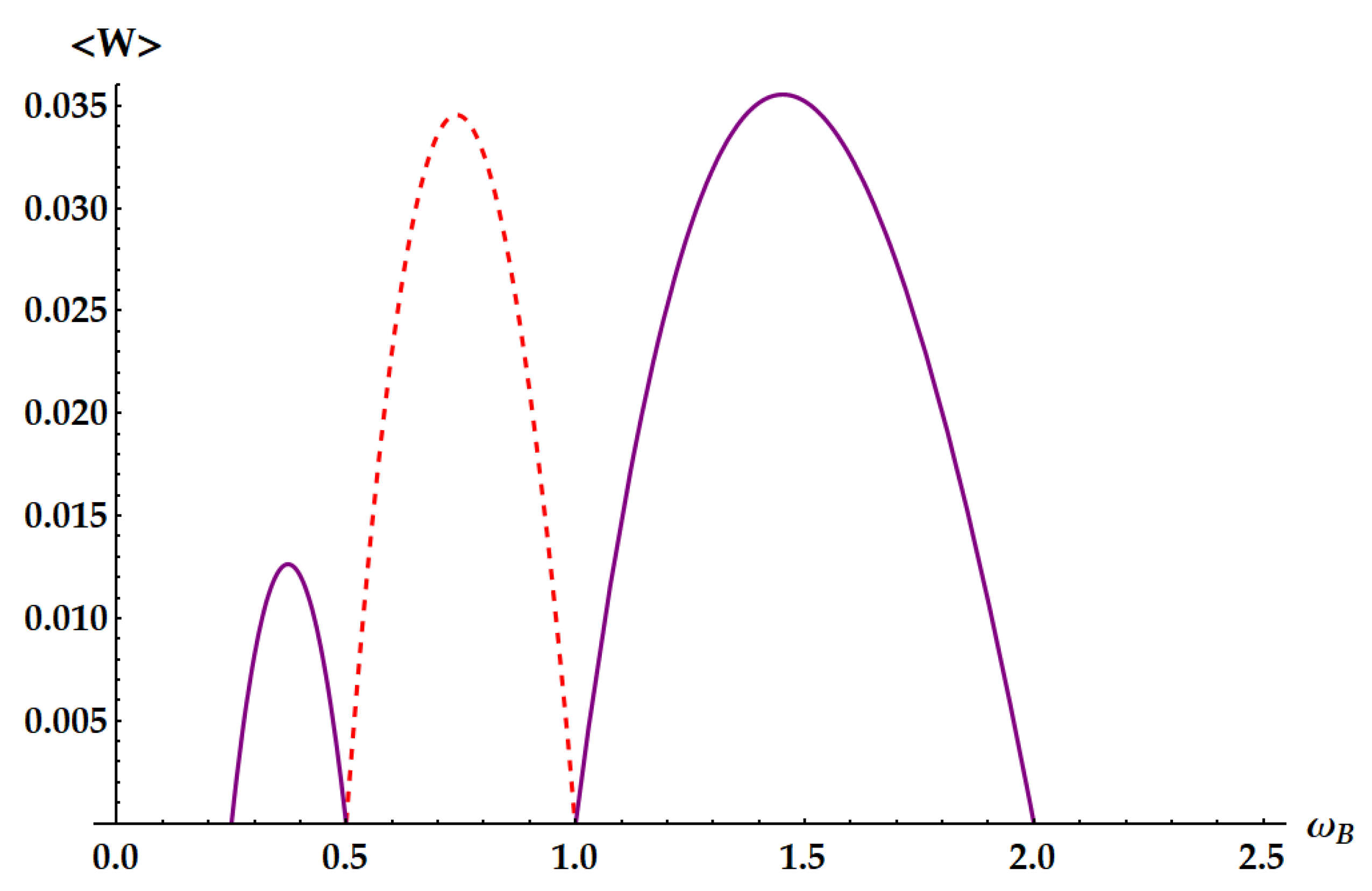
Figure 10.
Ergotropy as a function of in the case , with , , . Dashed red line: standard swap for . Purple solid lines: idle swaps for and for .
Figure 10.
Ergotropy as a function of in the case , with , , . Dashed red line: standard swap for . Purple solid lines: idle swaps for and for .
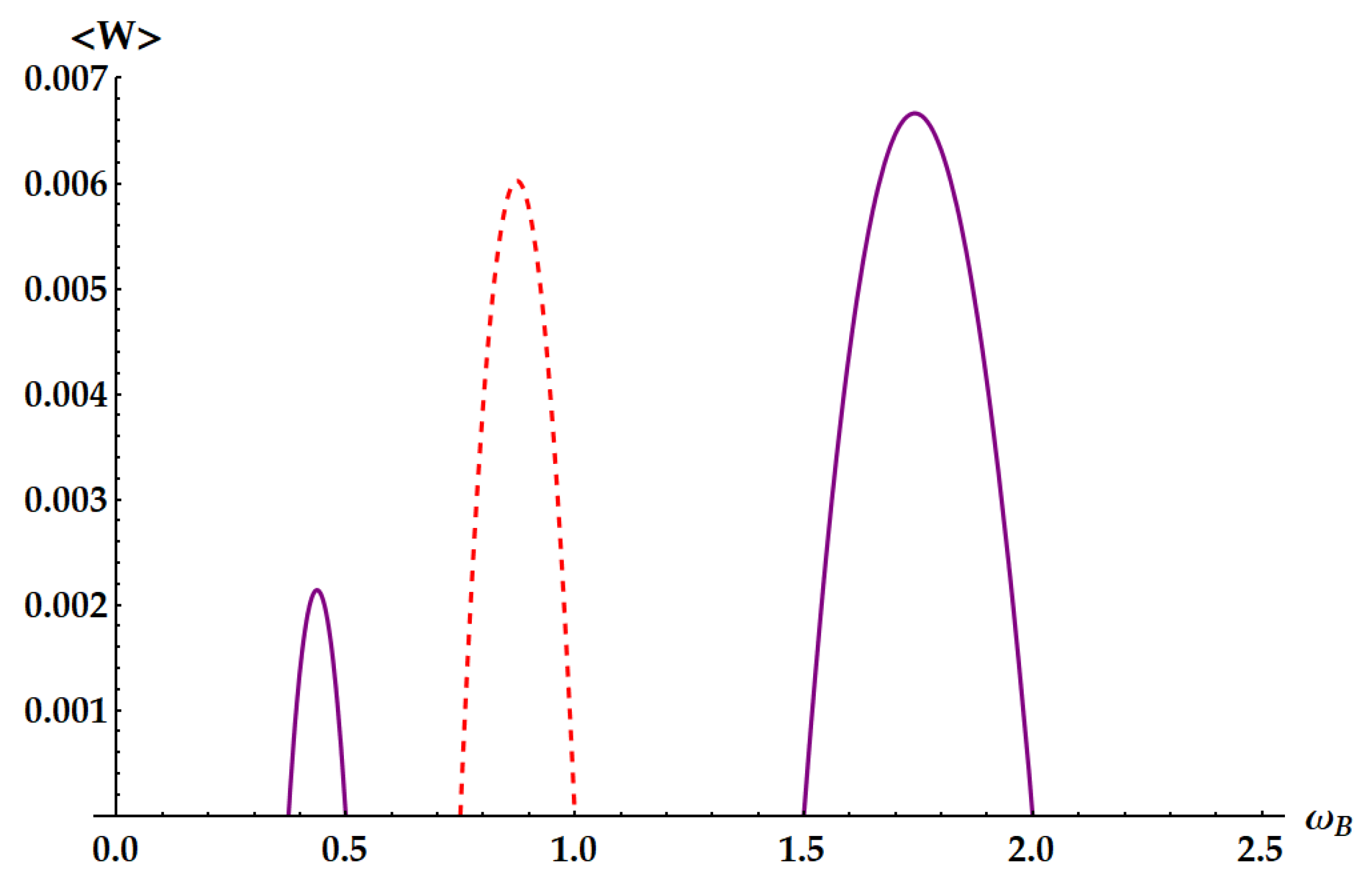
Figure 11.
Ergotropy as a function of in the limiting case , with , , . Blue dot-dashed line: double swap . Red dashed line: standard swap inside the corresponding ergotropic regime. Purple solid line: idle swap . Black dotted line: standard swap for any such that the extracted work is positive.
Figure 11.
Ergotropy as a function of in the limiting case , with , , . Blue dot-dashed line: double swap . Red dashed line: standard swap inside the corresponding ergotropic regime. Purple solid line: idle swap . Black dotted line: standard swap for any such that the extracted work is positive.
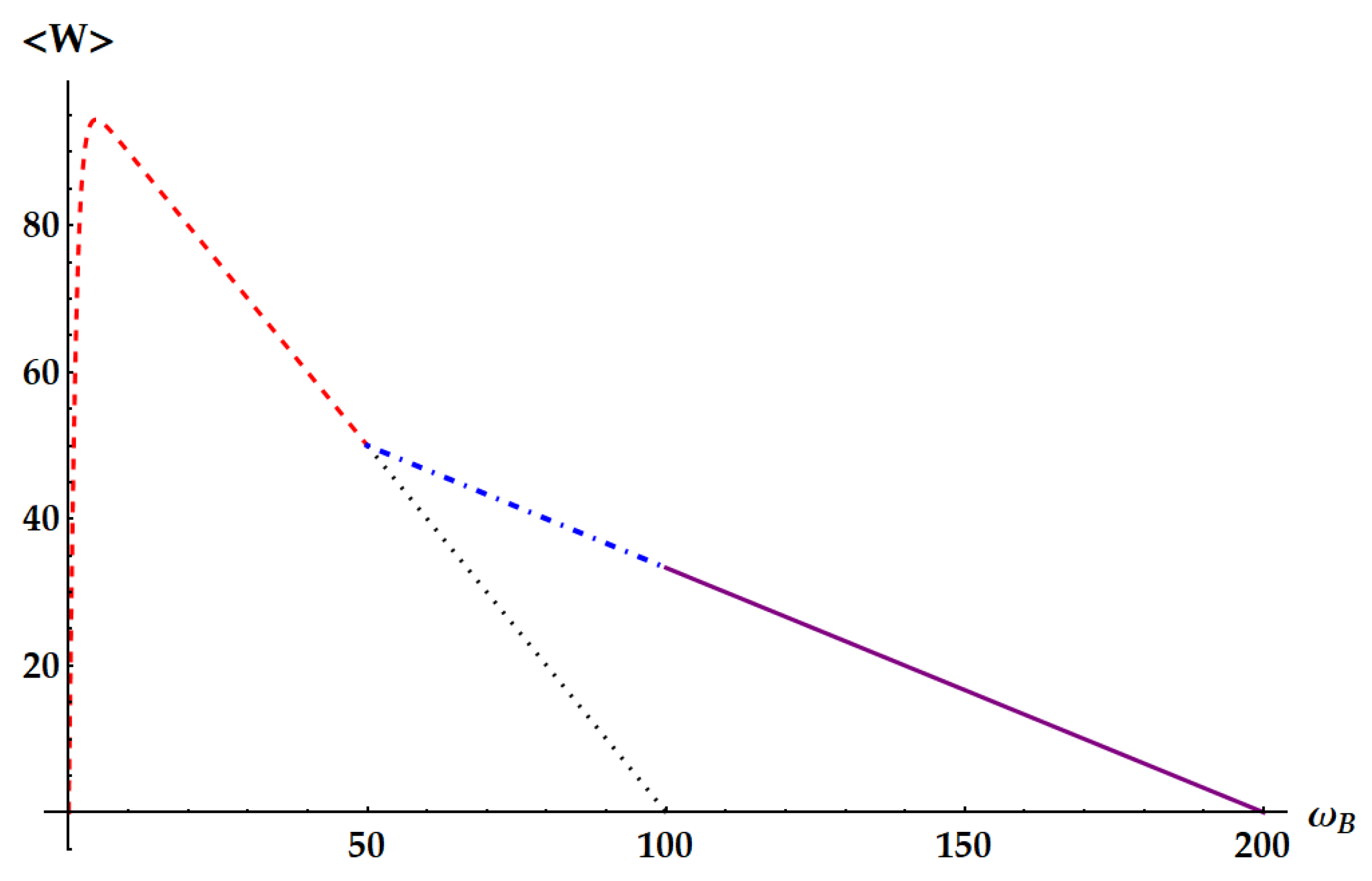
Figure 12.
Distribution of the work extracted by the standard swap in units. We set and .
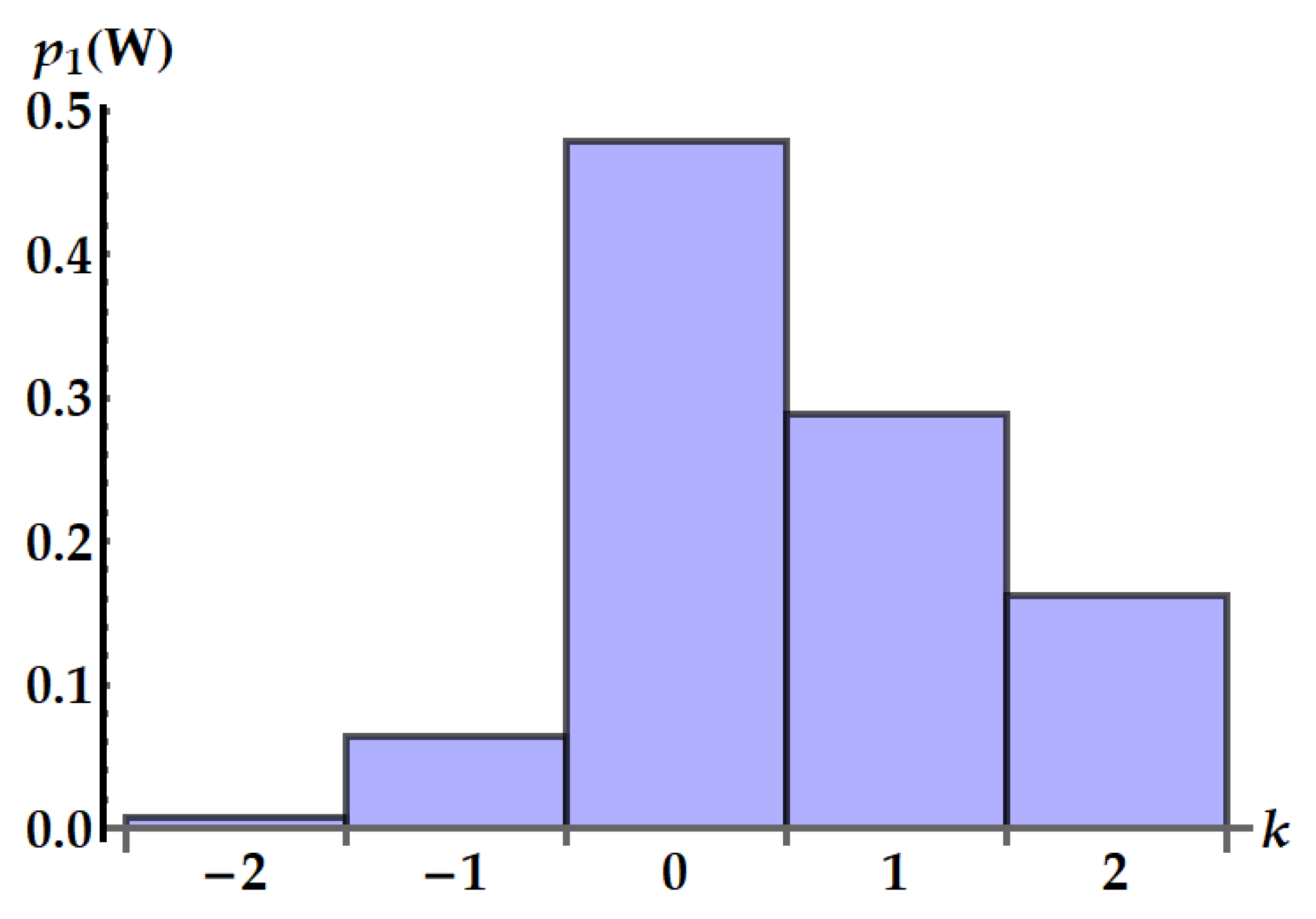
Figure 13.
Distribution of the work extracted by the idle swap in units. We set and .
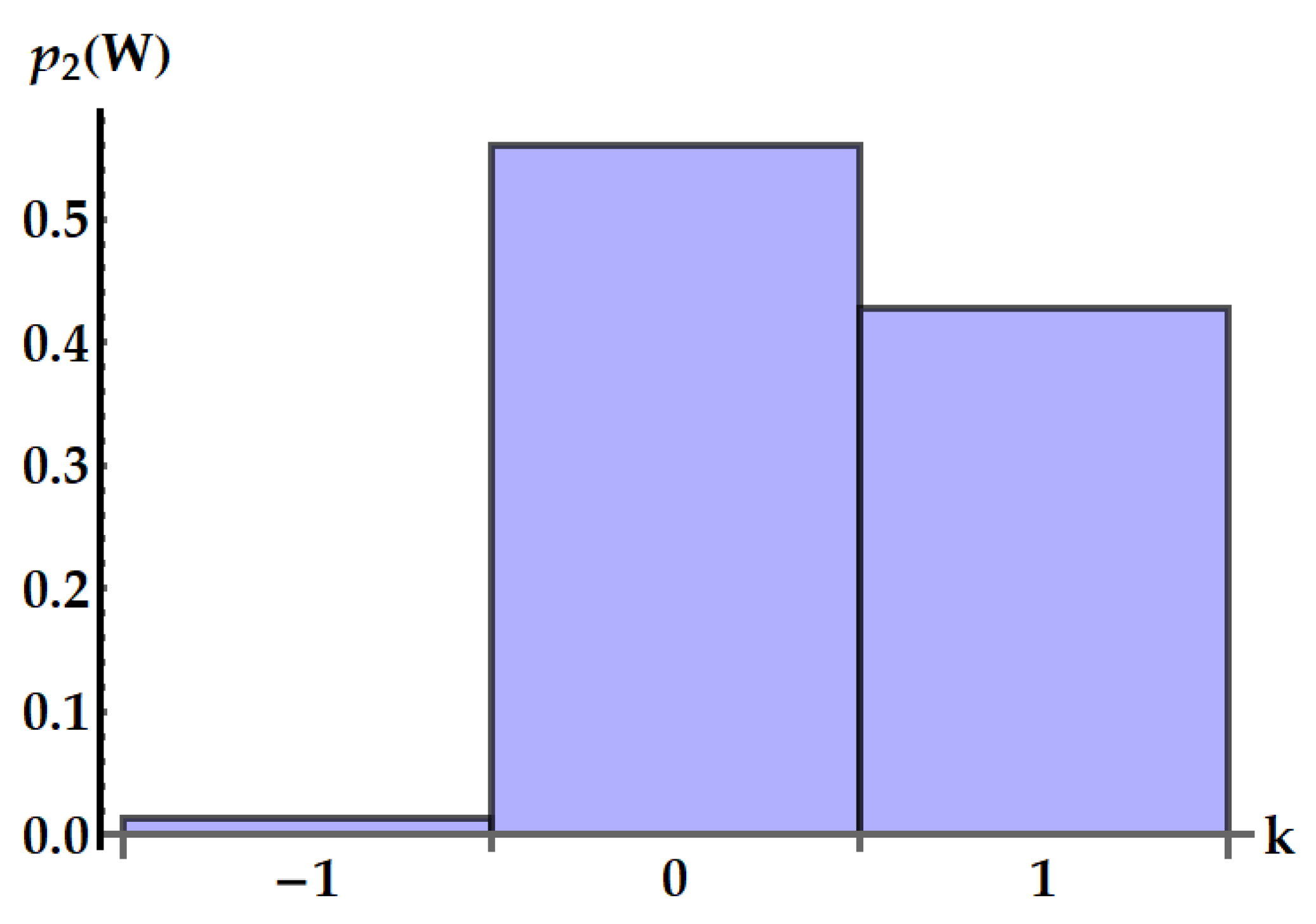
Figure 14.
Distribution of the work extracted by the double swap in units in the case . We set and .
Figure 14.
Distribution of the work extracted by the double swap in units in the case . We set and .
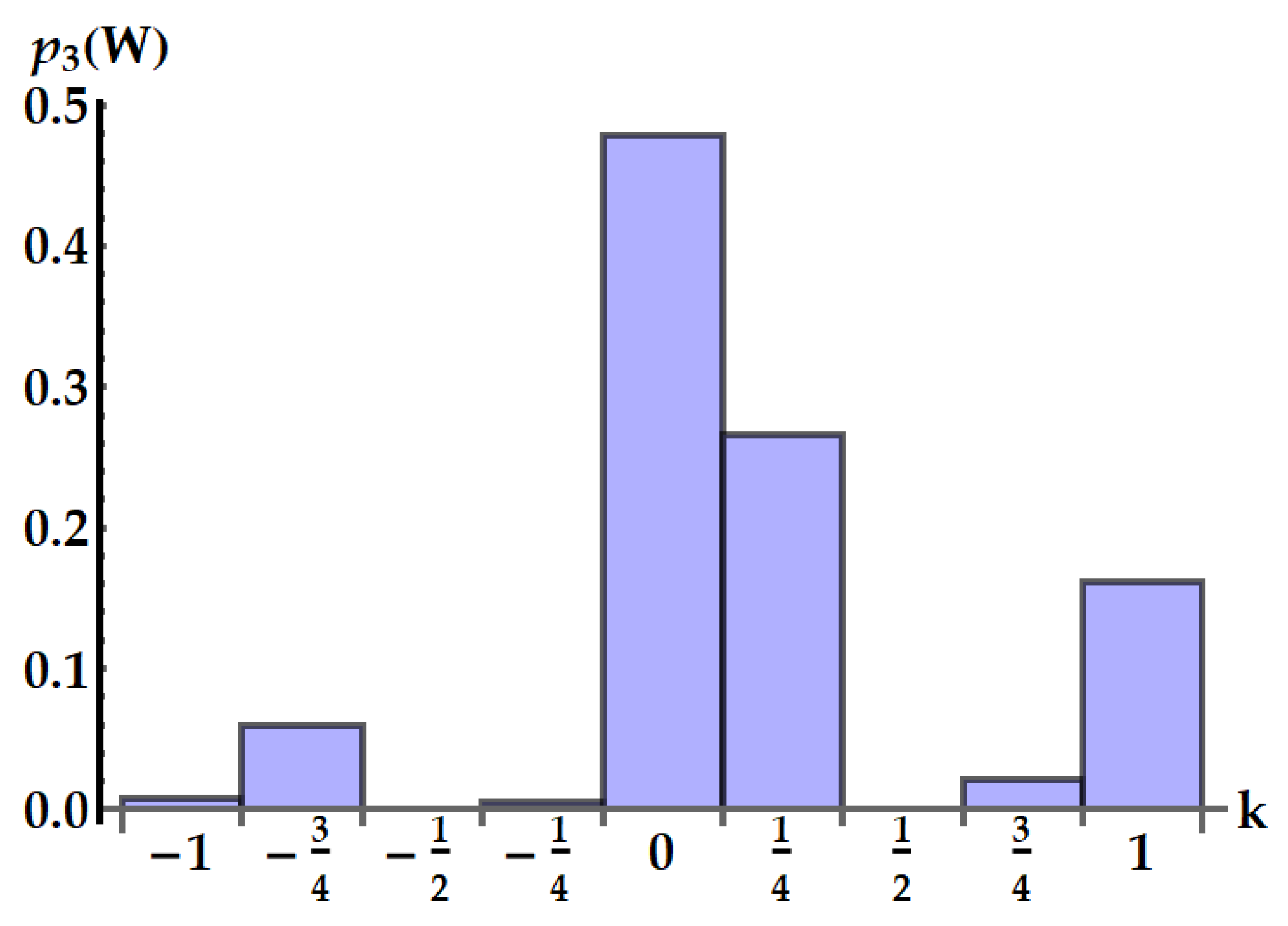
Figure 15.
Product of the relative fluctuations with the mean entropy production, which is lower bounded by 2 in the standard TUR of Eq. (2) and by a function of the mean entropy in Eq. (50). We set . The plot shows the violations due to the standard swap (red dashed line), the idle swap (solid purple line) and the double swap (blue dot-dashed line) as a function of .
Figure 15.
Product of the relative fluctuations with the mean entropy production, which is lower bounded by 2 in the standard TUR of Eq. (2) and by a function of the mean entropy in Eq. (50). We set . The plot shows the violations due to the standard swap (red dashed line), the idle swap (solid purple line) and the double swap (blue dot-dashed line) as a function of .
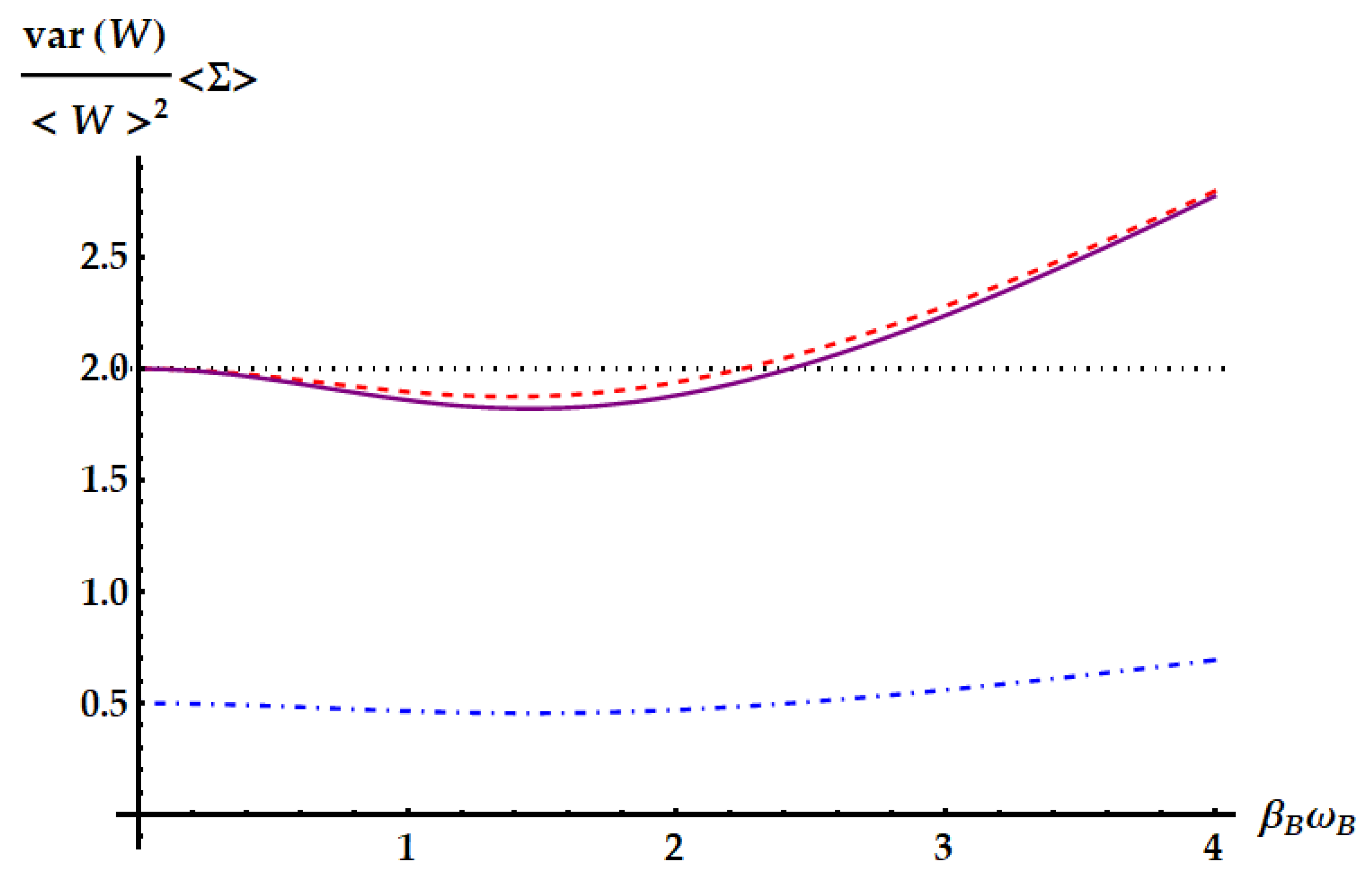
Figure 16.
SNRs obtained from the ergotropy extraction of the example and parameters as in Figure 7. The vertical dashed lines separate different the ergotropic regimes. We have the idle swaps for and for (purple lines), the double swap for and for (blue lines) and for (red line). The solid curves display the SNR. The dotted and dot-dashed lines show the upper bounds provided by the standard TUR in Eq. (2) and the tight TUR in Eq. (50). In the region , corresponding to the non-Hermitian unitary , strong violations of both TURs are apparent.
Figure 16.
SNRs obtained from the ergotropy extraction of the example and parameters as in Figure 7. The vertical dashed lines separate different the ergotropic regimes. We have the idle swaps for and for (purple lines), the double swap for and for (blue lines) and for (red line). The solid curves display the SNR. The dotted and dot-dashed lines show the upper bounds provided by the standard TUR in Eq. (2) and the tight TUR in Eq. (50). In the region , corresponding to the non-Hermitian unitary , strong violations of both TURs are apparent.

Figure 17.
SNR of the work extracted by the standard swap (solid line) in ideal optimal conditions, with . The dotted and dot-dashed lines display the upper bound from the standard TUR in Eq. (2) and the tight TUR in Eq. (50), respectively. The dashed horizontal line highlights the asymptotic limit of the SNR.
Figure 17.
SNR of the work extracted by the standard swap (solid line) in ideal optimal conditions, with . The dotted and dot-dashed lines display the upper bound from the standard TUR in Eq. (2) and the tight TUR in Eq. (50), respectively. The dashed horizontal line highlights the asymptotic limit of the SNR.
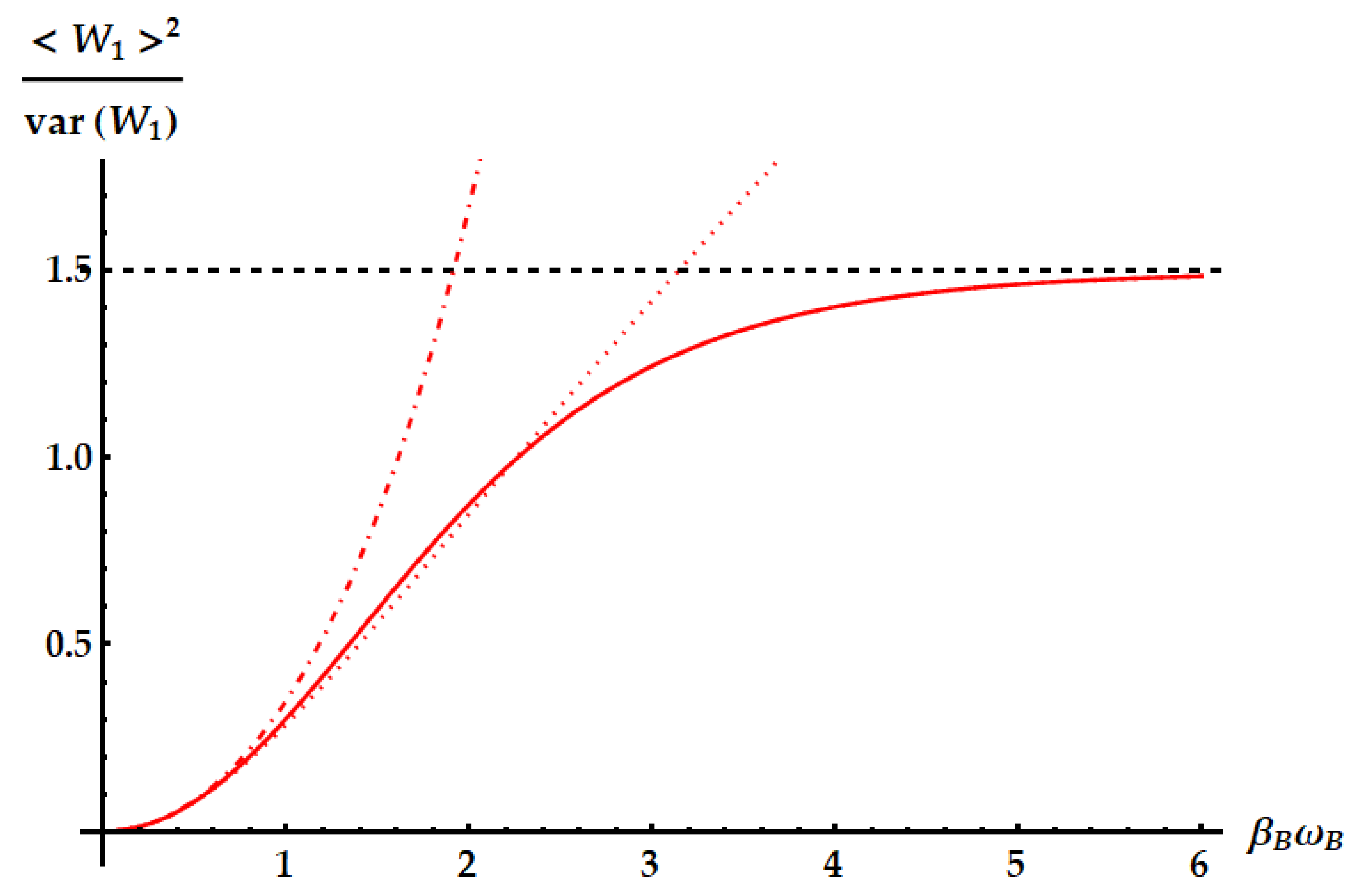
Figure 18.
SNR of the work extracted by the idle swap (solid lines). The dotted lines display the upper bound from the standard TUR in Eq. (2), while the dot-dashed lines display the upper bound from the tight TUR in Eq. (50). The dashed horizontal lines highlight the limit of the SNR. Up panel: conditions for the maximum SNR independently from the ergotropy extraction, namely . Here we set . Bottom panel: conditions for the maximum SNR within the ergotropic regime of , namely . Here we set .
Figure 18.
SNR of the work extracted by the idle swap (solid lines). The dotted lines display the upper bound from the standard TUR in Eq. (2), while the dot-dashed lines display the upper bound from the tight TUR in Eq. (50). The dashed horizontal lines highlight the limit of the SNR. Up panel: conditions for the maximum SNR independently from the ergotropy extraction, namely . Here we set . Bottom panel: conditions for the maximum SNR within the ergotropic regime of , namely . Here we set .
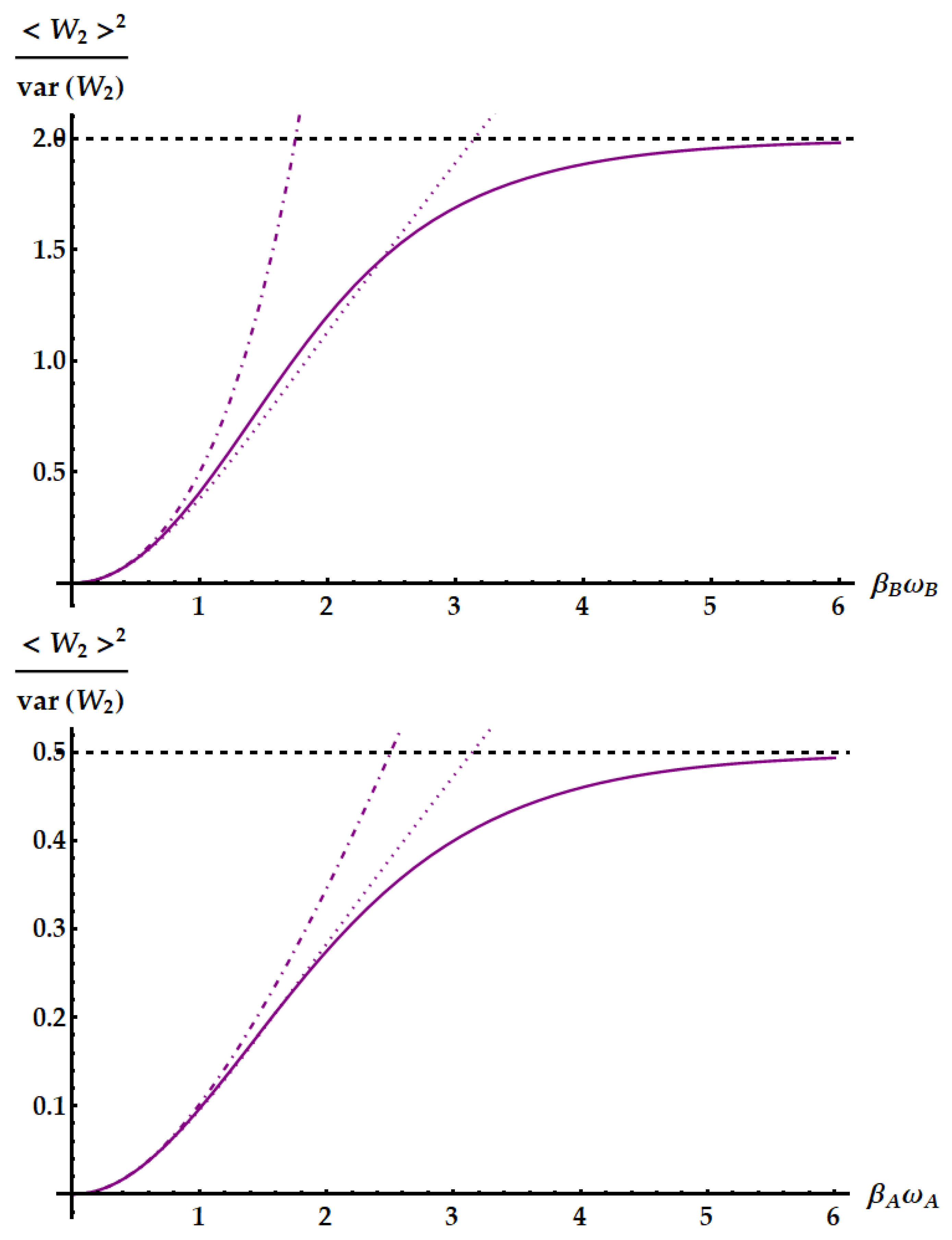
Figure 19.
SNR of the work extracted by the double swap . The dotted and dot-dashed lines display the upper bound from the standard TUR in Eq. (2) and the tight TUR in Eq. (50). The dashed brown lines display the bound from the loosest TUR for time-symmetric processes in Eq. (51). The dashed horizontal lines highlight the limit of the SNR. Up panel: conditions for the maximum SNR independently from the ergotropy extraction, namely and . Here we set . The solid blue line displays the SNR. Bottom panel: conditions for the maximum SNR within the ergotropic regime of , namely and . Here we set and show the cases obtained from two different choices of the frequency ratio. The red line displays the choice optimizing the SNR, i.e. , which reduces the statistics of the work extracted by the double swap to the one extracted by the standard swap. The blue solid line displays the case .
Figure 19.
SNR of the work extracted by the double swap . The dotted and dot-dashed lines display the upper bound from the standard TUR in Eq. (2) and the tight TUR in Eq. (50). The dashed brown lines display the bound from the loosest TUR for time-symmetric processes in Eq. (51). The dashed horizontal lines highlight the limit of the SNR. Up panel: conditions for the maximum SNR independently from the ergotropy extraction, namely and . Here we set . The solid blue line displays the SNR. Bottom panel: conditions for the maximum SNR within the ergotropic regime of , namely and . Here we set and show the cases obtained from two different choices of the frequency ratio. The red line displays the choice optimizing the SNR, i.e. , which reduces the statistics of the work extracted by the double swap to the one extracted by the standard swap. The blue solid line displays the case .
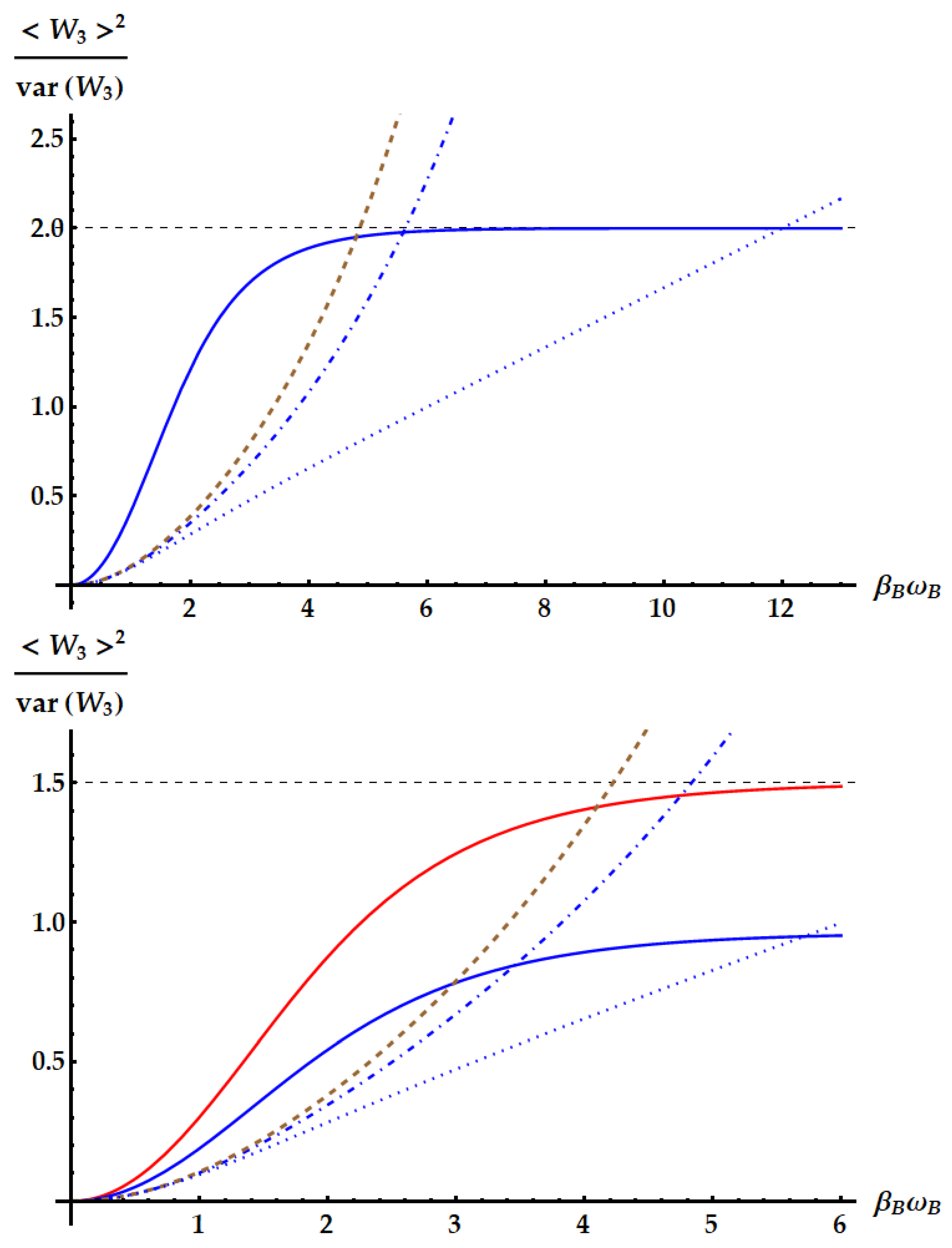
Figure 20.
Ratio between the squared sum of the mean works extracted in the forward () and backward () processes and the sum of the corresponding variances as a function of (solid lines). We set . We display the cases (dark-blue thick line) and (light-blue thin line). The dot-dashed brown and the dashed green curve represent the upper bounds given by Eqs. (52) and Eq. (53), respectively. The dashed black horizontal line identifies the asymptotic value, which amounts to and is achieved for both and .
Figure 20.
Ratio between the squared sum of the mean works extracted in the forward () and backward () processes and the sum of the corresponding variances as a function of (solid lines). We set . We display the cases (dark-blue thick line) and (light-blue thin line). The dot-dashed brown and the dashed green curve represent the upper bounds given by Eqs. (52) and Eq. (53), respectively. The dashed black horizontal line identifies the asymptotic value, which amounts to and is achieved for both and .
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Downloads
103
Views
50
Comments
0
Subscription
Notify me about updates to this article or when a peer-reviewed version is published.
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated






