Preprint
Article
Fast Converging Gauss-Seidel Iterative Algorithm for Massive MIMO Systems
Altmetrics
Downloads
83
Views
13
Comments
0
A peer-reviewed article of this preprint also exists.
Submitted:
13 October 2023
Posted:
16 October 2023
You are already at the latest version
Alerts
Abstract
For massive multiple-input multiple-output (MIMO) communications, the minimum mean square error (MMSE) scheme provides close to optimal recognition but involves inverting the high-dimensional matrix. A Gauss-Seidel (GS) detector based on conjugate gradient and Jacobi iteration (CJ) joint processing is introduced to address this problem. Firstly, the signal is initialized with the best of the three initialization regimes for faster algorithm convergence. Secondly, the signal is processed together with CJ. Finally, the pre-processed result is transferred to the GS detector. The simulation results indicate that the proposed iterative algorithm has a lower BER performance than the GS and improved iterative scheme based on GS in channels with different correlation levels.
Keywords:
Subject: Computer Science and Mathematics - Signal Processing
1. Introduction
Massive multiple-input multiple-output (MIMO) is a pioneering technology for expanding channel capacity without increasing spectrum width [1]. Compared to traditional MIMO art, more users can be served at the same time on the same frequency with massive MIMO that can increase network capacity [2] and data transmission rates [3]. However, the signals are subject to interference from other antennas during transmission, which create an order of magnitude higher complexity to detect the required signal. Therefore, a detector for massive MIMO needs to be designed at the receiver side that can achieve low complexity and high performance.
Maximum likelihood [4] detection algorithm finds the signal closest to the transmitted signal by rounding through all the received signals, but the high complexity of traversal makes them difficult to apply in practice. In order to mitigate the cost of computing, linear detection schemes are recommended to obtain near-optimal detection performance, commonly known as zero-forced [5] algorithm and minimum mean squared error (MMSE) [6] detection algorithm. A highly complex matrix inversion is used in the MMSE method, which is unfriendly in practice.
Avoidance of inverse operations on high-dimensional matrices, a few iterative algorithms have emerged based on MMSE detection algorithm. Depending on the iterative approach, they can be classified into the following three categories. The first category is the iterative algorithm based on gradient search. The convergence speed of the steepest descent [7] iterative algorithm, influenced by the initial point, becomes slower when approaching the final estimated signal. The conjugate gradient (CG) [8] detection algorithm is offered to increase the speed of convergence, but a complex pre-processing process is required. The second category is repetitive methods that rely on series expansion, like the Neumann series expansion algorithm [9], where the complexity is acceptable if the quantity of series expansion terms is less than 3, but high complexity arises if the quantity of level expansion levels is larger than or equal to 3. The third group is that rely on iterative schemes for solving linear equations. The common ones are Jacobi iterative method [10], successive over relaxation (SOR) iterative algorithm [11], Richardson iterative algorithm [12], Gauss-Seidel (GS) [13] iterative algorithm, etc. Such detection algorithms reverse the matrices into solving a system of linear equations, which has a strong stepwise nature and high requirements for the filter matrix.
There is a limit to what can be achieved using a single algorithm to detect [14]. Therefore, the combination of different detection algorithms in a complementary manner can further improve the detection capability. A hybrid iterative algorithm combining adaptive damped Jacobi and conjugate gradient was proposed in the literature [15], which requires several iterations to achieve near-optimal performance. The literature [16] indicates that combining QR with traditional techniques to detect provides excellent manifestations and effectively improves the plant throughput. In the literature [17], a hybrid iterative algorithm has been suggested that further reduces the complexity of the ML detection algorithm by using a sphere decoding algorithm suitable for high signal-to-noise ratio and an easy-to-use DM algorithm. The literature [18] proposes the JAGS detection such as QR-MLD, on algorithm, which is initialized by the Jacobi method and then estimated by GS, but the convergence speed is slow. The preprocessing Gauss-Seidel iterative algorithms [19,20] use the preprocessing matrix to transform the original linear equation into a completely new linear equation, which results in a faster convergence rate in the new framework. However, complex preprocessing processes create additional computational difficulties.
1.1. Contributions
This study utilizes a low-complexity iterative algorithm for signal detection based on solving linear equations to address the high cost associated with the inverse operation of MMSE detection. By analyzing the nature of massive MIMO system, a new initialization method is used, which can obtain an initial solution closer to the final solution than other initialization methods. An improved Gauss-Seidel iterative algorithm based on conjugate gradient and Jacobi (CJ) joint preprocessing is proposed, which can be described as CJGS iterative method. The proposed algorithm attempts to combine CG and Jacobi iteration to accelerate the convergence of GS. Then the GS detector is employed to converge faster and iterate less.
Simulation manifestations show that the BER ability of the CJGS iterative scheme outperforms the traditional Gauss-Seidel repetitive method and improved iterative program based on GS, regardless of the channel correlation. It is less complex, requiring fewer iterations to achieve MMSE detection ability. Therefore, the suggested scheme is superior in the balance of complexity and detection efficiency.
1.2. Paper Outline
The remainder of the article is structured as follows: Section 2 describes the system model for large-scale MIMO, the channel model, and the principles of the MMSE detection algorithm. The third part discusses the proposed detection algorithm. In the fourth part, the BER performance of the proposed algorithm is analyzed in comparison with existing results. Then calculate the complexity of the proposed algorithm. Conclusions are obtained in the fifth part.
1.3. Notation
Vectors and matrices are displayed in bold lowercase and bold uppercase letters respectively. Scalars are represented in lowercase letters. The operators and indicate matrix inverse and Hermitian transpose. The identity matrix is represented by . denotes the element in row i, column j of the matrix . The result after the i-th iteration is the vector .
2. Massive MIMO System Model
The uplink of an uncoded massive MIMO system is studied, which consists of antennas configured at the received side serving single-antenna users within the same time-frequency resource [21]. Figure 1 illustrates schematic diagram. And is much greater than .
The dimensional symbol vector transmitted by total users in the meantime is , where is the symbol vector sent by the th user and is the set of modulated symbols. The channel gain between the antennas at the receiving and transmitting form the channel matrix
Then the reception signal vector has the form
where denotes a dimensional complex Additive White Gaussian Noise(AWGN) vector with zero mean, and covariance matrix is . To simplify the operation, equation (1) is transformed into an analogue real-valued model as
The assumption is that there is perfect channel state information available at the receiving end.
2.1. Channel Model
In practical large-scale MIMO communications, channels are generally correlated. The detection is getting complicated when channels are correlated. Considering the correlation between the transceiver and received antennas in massive MIMO communications, Kronecker’s channel model [22] is described by
where Hi,i,d denotes the independent identically distributed complex channel fading matrix, and denote the degree of channel correlation between the receiving and transmitting antennas, respectively.
where and represent the random phases of the transmit and receive antennas that are uniformly distributed, respectively. Assuming that and are known at the base station side, the channel correlation scenarios are classified into four types according to the different values taken by, which are as follows [23].
(1) and , the channel is independent and identically distributed.
(2) and , the channel is user-side relevant.
(3) and , the channel is base station side related.
(4) and , the channel is fully correlated.
2.2. MMSE Detection
Applied at the recipient side of a massive MIMO communication, the MMSE iterative scheme offers near-optimal detection performance by degrading inaccuracies of the transmitted and received signals [24]. Estimation of the transmitted signal using MMSE detection method is expressed in terms of [25]
where denotes the Gram matrix, represents the matched filter. The MMSE detection method has computational complexity, so it is difficult to apply in practice.
3. Proposed Algorithm
The MMSE detection algorithm has near sub-optimal detection performance when applied to large-scale MIMO systems, which generates a high exponential level of complexity. The algorithm is difficult to re-engineer in hardware devices. This paper applies the CJGS iterative algorithm to signal detection in massive MIMO communication. The scheme can be broken down three parts: initialization, CJ joint processing and GS iterative estimation, and the block method of the CJGS detection is shown in Figure 2. During the initial stage, the optimal initial value is selected to speed up convergence. In the CJ joint processing phase, the CG iteration is used to select the optimal search direction and combined with Jacobi iteration to reduce the number of subsequent iteration cycles. In the GS iteration estimation phase, Gauss-Seidel iteration is used to converge quickly, thus improving the overall detection performance of the massive MIMO system.
3.1. GS Iterative Estimation
When GS is used for signal detection at the receiving end of a massive MIMO communication, the GS scheme can be executed according to the following steps.
1. matrix decomposition. If there are fewer antennas at the user site than at the base station site for massive MIMO communication, the channels tend to be orthogonal to each other. The MMSE filter matrix is a positive definite matrix with diagonal dominance [26]. Matrix A can be divided into
where , and denote the diagonal matrix, the strict upper triangular matrix and the strict lower triangular matrix of matrix A respectively.
2. Calculate the initial value .
3. GS iterative estimation. The signal estimation formula of GS iterative algorithm is
3.2. Initialization
The initial estimate has an impact on the computational complexity, the convergence speed and the number of subsequent iterations required in massive MIMO signal detection. Traditional detection algorithms generally have zero vectors as initial values, which are far away from the final estimate, so convergence is slower. When the matrix is a Hermitian positive definite matrix, the GS repetitive scheme converges for any initial solution [27]. For this reason, two initialization schemes are proposed below. We perform performance simulations of the two initialization schemes in Chapter 4, with the initial estimated value of the zero vector as the reference object.
1. In a given massive MIMO, the quantity of transmitting and receiving antennas is set. Thus, estimation of the initial solution by means of a linear transformation of the number estimating the initial solution, which can avoid matrix inversion operations and further limit computing power.
2. The diagonal elements of the matrix is dominant in massive MIMO communication. Therefore, the elements of matrix A can be grouped into diagonal elements that are not negligible and non-diagonal elements that are negligible, i.e. . The computational complexity of inverting the matrix could decreased by replacing with
3.3. CJ Joint Processing
CJ joint processing combines CG and Jacobi to pre-iterate the initialized signal, taking advantage of the good convergence of the CG initial iteration. It is CJ joint processing that reduces the number of cycles required for subsequent iterative estimation.
The CG [8] detection algorithm searches in the direction conjugate to the gradient until the search converges the residuals to zero. The CG iteration algorithm gives a good initial detection direction, but the pre-processing step generates high complexity over many iterations of the loop. Therefore, we choose one conjugate gradient iteration to avoid the increase in complexity.
In the CG iterative algorithm, it is known that the initial residuals and the starting conjugate search direction are assumed to be and , respectively. Then the result for the CG iterative algorithm after one iteration is
where is the search step.
The expression for the signal estimate of the Jacobi iterative algorithm [10] applied to massive MIMO communication is
Using the CG iterative algorithm as the starting value of Jacobi iterative scheme, the result after one repetition of Jacobi can be given,
Combined with the description of the above, the CJGS iterative algorithm is shown in Algorithm 1.
| Algorithm 1. CJGS iterative algorithm |
| Input: y H B U |
| Initialization: |
| 1. |
| 2. |
| 3. |
| 4. |
| 5. |
| CJ joint processing: |
| 6. |
| 7. |
| 8. |
| 9. |
| GS iterative estimation: |
| For i=2 do |
| 10. |
| End |
| Output: |
4. Simulation Results and Analysis
MMSE detection algorithms are employed as a benchmark, approximating optimal detection. Firstly, the bit error ratio (BER) of five algorithms, including GS, CPGS, PGS and JAGS iterative algorithms, is compared in uncorrelated and correlated channels, respectively. The MMSE scheme is utilized as a reference object. Its performance is not very different from that of the best detection system. Then, the initial values of the CJGS iterative algorithm are simulated and examined. Finally, a comparison of the computational difficulty for the above-mentioned methods has been made. Where i is the scheme’s number of iterations.
4.1. BER Performance
A comparison and analysis of the BER performance of different iterative algorithms with different antenna configurations is shown in Figure 3. The channel matrix is independent and identically distributed, that is , . Signal modulation is 16-QAM.
In Figure 3a, it is clear that all schemes have excellent BER performance after a modest quantity of rounds, and that the CJGS scheme has improved BER performance over the other repetition methods for the identical number of rounds. The BER of the CJGS and JAGS iterative algorithms is after two iterations, but the gap between them is 8 dB. Therefore, the CJGS iterative method is better. From Figure 3b, it can be noticed that the CJGS iterative scheme requires three iterations, while the other four iterative schemes require more than seven iteration cycles to achieve the ability of MMSE scheme when the MIMO antenna configuration is . If the signal-to-noise ratio (S/N) is 20 dB, BER achievable by the CJGS iterative method is after 3 iterations, and the BER achievable by GS, CPGS, JAGS and PGS after 7 iterations are , , and ,respectively. From Figure 3c, it can be shown that with the MIMO antenna configuration of , CJGS, GS and JAGS can achieve better BER performance after 2 iterations, but the BER performance of CPGS and PGS is not very good.
Furthermore, by keeping at a fixed value and increasing , all algorithms can gain the identical BER in a fraction of the repetitions from Figure 3a,b. Conversely, if remains fixed and increases, all algorithms need a higher signal-to-noise ratio to get the identical results, and the quantity of receptions required increases from Figure 3b,c.
Figure 4 is a comparison and analysis of the BER behavior of different iterative algorithms. The antenna configurations are different. The channel matrix satisfies as , . Signal modulation is 16-QAM.
In Figure 4a, with the MIMO antenna configuration of , the performance of the other four iterative algorithms after running five iterations is still worse than that of the CJGS iterative algorithm in one iteration. The minimum BER achieved by MMSE detection is , while the BER of the CJGS iteration is after one iteration. From Figure 4b, the CJGS iterative scheme provides much more superior performance when the MIMO antenna configuration is , which converges faster than the remaining iterative methods From Figure 4c, it can be found that the CJGS iterative algorithm after three iterations can achieve the identical effects as the MMSE detection scheme if the S/N is 16 dB.
A comparison and analysis of BER performance for different algorithms with different antenna configurations is shown in Figure 5. The channel matrix satisfies as , . Signal modulation is 16-QAM.
The detection performance of the GS, CPGS, JAGS and PGS iterative algorithms is less satisfactory for an iteration number of one in Figure 5, while the CJGS iterative algorithm achieves a desirable performance close to MMSE detection. All iterative algorithms become better in detection performance as the number of iterations increases. As shown in Figure 5 and Figure 3, all algorithms require more iterations to achieve optimal performance when the transmit-side antenna is correlated. If the MIMO antenna configured is set to and the BER reaches , the required S/N ratio for CJGS is 20 dB, while the S/N ratio requirement for PGS and JAGS iterations is 24 dB. Therefore, the proposed algorithms are more suitable for channel scenarios where correlation exists on the transmit side of large-scale MIMO systems.
In Figure 6, the fully correlated channel was concerned, i.e., , . The BER performance of the GS iterative algorithm, CPGS iterative method, JA-GS detection algorithm, PGS detection method and CJGS iterative algorithm are compared and analyzed for different antenna configurations with 16-QAM modulation.
As shown in Figure 6, the detection capability of all the algorithms becomes better with more repetitions. From Figure 6a, the designed algorithm is shown to perform as well as the performance of MMSE detection at one iteration when the MIMO antenna configuration is , while all other iterations require more than five iterations to achieve the same results. If the S/N ratio is 16 dB, the BER achievable by the MMSE detection algorithm is , while the BER of the CJGS iterative algorithm is after five iterations. Thus, the CJGS iterative method can achieve a lower BER. From Figure 6b, it can be observed that to achieve the performance of MMSE detection when the MIMO antenna configuration is , the CJGS iterative algorithm needs to perform 3 iterations, while the other four iterative algorithms need more than 7 iteration cycles. From Figure 6c, there has been evidence that all algorithms achieve lower BER after five iterations when the MIMO antenna configuration is , but the suggested method has superior performance for equal iterations.
According to the previous description, near MMSE detection performance is achieved with proposed method with only a few iterations. The novel scheme outperforms the other four iterative algorithms. A reduction in the quantity of received side and increase in the sending side, then the ratio between them decreases. The proposed algorithm still shows a reliable performance, which can be well adapted to both channel-uncorrelated and channel-correlated scenarios.
As shown in Figure 7, baseline1, baseline2 and baseline3 are the initial values of schemes 1, 2 and zero vector mentioned in Chapter 3, part B, respectively. When the Massive MIMO antenna configuration is , the number of iterations is two and the baseband modulation method is 16-QAM, the CJGS iterative method has superior BER performance and faster convergence when initial values proposed in scheme 1 are used.
4.2. Complexity Analysis
In massive MIMO communications, computational cost is a critical metric for signal detection algorithms [28]. The sophistication of the CJGS iterative scheme consists of three parts: initialization, Conjugate Gradient and Jacobi co-processing and GS iteration estimation, and only the number of true multiplicative operations of the method is considered in the analysis. The computation of and is only once required, which is the same as the MMSE detection algorithm. Therefore, this part of the calculation is ignored and only the complexity of the subsequent steps is analyzed. One real multiplication is noted as one real multiplication times, the multiplication of a complex number with a constant is noted as two real multiplication times, and the multiplication of two complex numbers is noted as four real multiplication times.
The complexity of : it involves multiplying a constant and a vector of with a complexity of .
The complexity of Conjugate Gradient and Jacobi co-processing:
The complexity of : it involves multiplying a matrix of and a vector of , with a complexity of .
The complexity of : it concerns multiplying a vector of and a vector of , with a complexity of . And it involves multiplying a matrix of and a vector of , with a complexity of . It concerns multiplying a vector of and a vector of , with a complexity of .
The complexity of : it involves multiplying a constant and a vector of , with a complexity of 2U. The complexity of is .
The complexity of the GS iteration: the calculation of involves multiplying twice a matrix of and a vector of with a complexity of .
Hence, total complexity of CJGS algorithm is .Taken together, the computational complexity of the various algorithms is shown in Table 1.
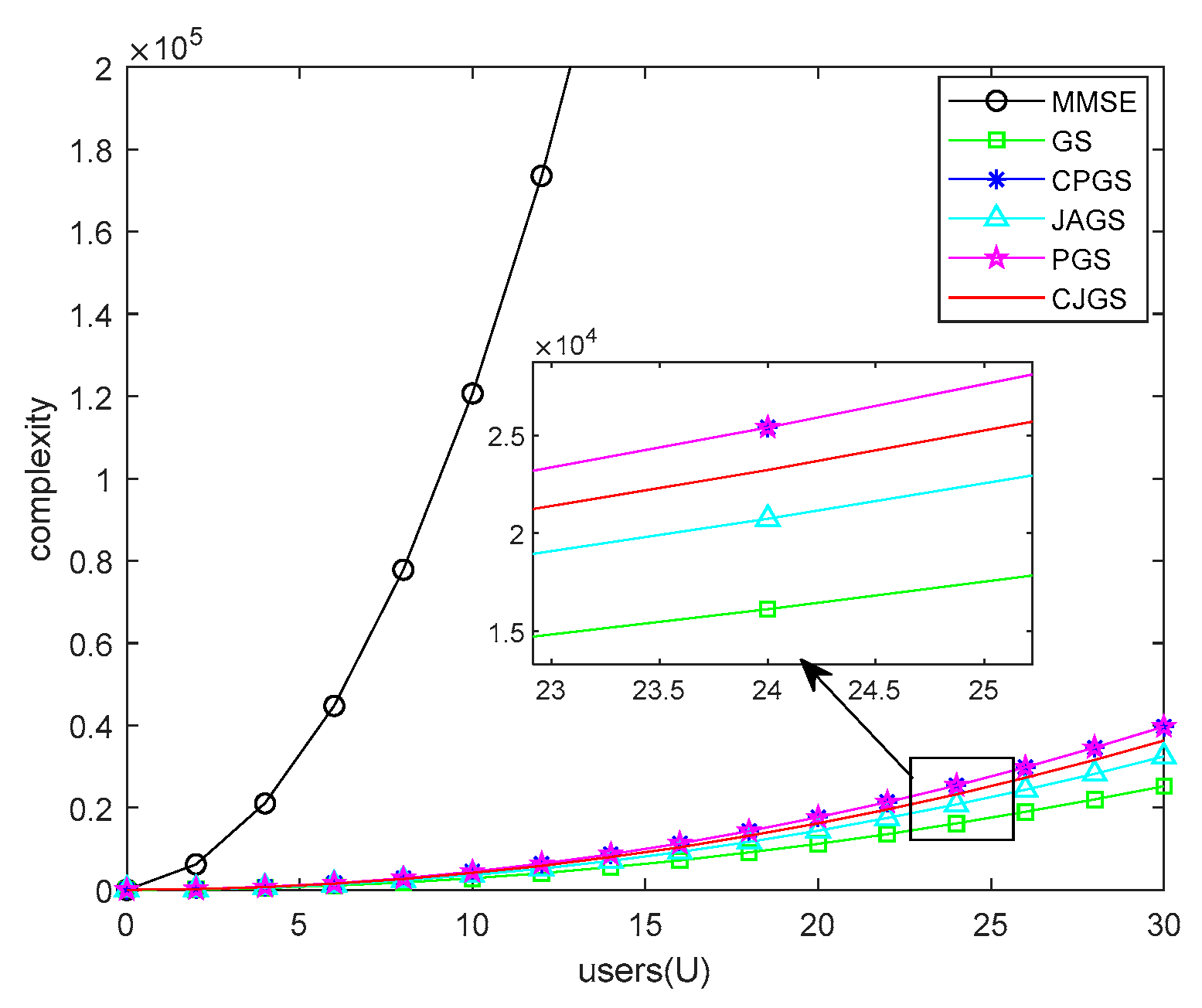
In Figure 8, the complexity of the different algorithms for MIMO systems are compared. Base station antenna count is 128 and user-side antenna count ranges from 0 to 30 with three iterations. The suggested algorithm is much less complex than MMSE scheme whose complexity is .
5. Conclusion
In this work, the Gauss-Seidel iterative algorithm based on joint processing conjugate gradient and Jacobi iteration for massive MIMO communication was introduced. CG and Jacobi iterations are used in combination with GS iterations to enhance convergence and improve BER performance. Through theoretical and simulation analysis, the suggested method in this work is not easily affected by the degree of channel correlation. Only a small number of rounds are required to achieve the result of the MMSE detection scheme. For various antenna configurations, the CJGS algorithm performs markedly superior to other detection schemes. Unfortunately, precoding and soft decision techniques can be added in subsequent studies to further improve the reliability of detection, although the analysis in this study only considers the influence of channel correlation and antenna configuration.
Funding
This research was funded by Natural Science Foundation of Ningxia, grant number 2023AAC03741. This research was funded by Science and Technology Plan of Gansu Province, grant number 23YFGA0047.
References
- Kumar, A., Gupta, M. A review on activities of fifth generation mobile communication system. AEJ-Alexandria Engineering Journal, 2017, vol.57, no.2, p.1125-1135. [CrossRef]
- S. P, R.S. Miriyala, N. Matsa, et al. Capacity Evaluation of MIMO System: with and without Successive Interference Cancellation, In Proceedings of the 7th International Conference on Computing Methodologies and Communication (ICCMC). The Erode (India), 2023, p. 27-31. [CrossRef]
- Albreem, M.A., Salah, W., Kumar, A., et al. Low Complexity Linear Detectors for Massive MIMO: A Comparative Study. IEEE Access, 2021, vol. 9, p. 45740-45753. [CrossRef]
- Wang, Y.N., Xiao, Y., Dan, L.L, et al. On the BER Performance of Constant Envelope OFDM in Frequency Selective MIMO Channels with ML Detection. IEEE Wireless Communications Letters, 2023, p. 1. [CrossRef]
- Zhou, M., Li, J.M., Wan, A., et al. Rate analysis of ZF receiver for uplink cell-free massive MIMO systems with D2D communications. Physical Communication, 2023, vol.58, p. 102024. [CrossRef]
- Kalachikov, A.A., Shelkunov, N.S. Performance Evaluation of the Detection Algorithms for MIMO Spatial Multiplexing Based on Analytical Wireless MIMO Channel Models. In Proceedings of 2018 XIV International Scientific-Technical Conference on Actual Problems of Electronics Instrument Engineering (APEIE). The Novosibirsk (Russia), 2018, p. 180-183. [CrossRef]
- Deng, Q., Liang, X., Wang, X., et al. Fast Converging Iterative Precoding for Massive MIMO Systems: An Accelerated Weighted Neumann Series-Steepest Descent Approach. IEEE Access, 2020, vol. 8, p. 50244-50255. [CrossRef]
- Wei, Y., Zhao, M.M., Hong, M., et al. Learned Conjugate Gradient Descent Network for Massive MIMO Detection. IEEE Transactions on Signal Processing,2020, vol. 68, p. 6336-6349. [CrossRef]
- Liu, X., Zhang, Z., Wang, X., et al. A Low Complexity High Performance Weighted Neumann Series-based Massive MIMO Detection. In Proceedings of 28th Wireless and Optical Communications Conference (WOCC), The Beijing (China), 2019, p. 1-5. [CrossRef]
- Lee, Y. Decision-aided Jacobi iteration for signal detection in massive MIMO systems. Electronic Letter, 2017, vol 53, no. 23, p. 1552-1554. [CrossRef]
- Xu, Y.H., Wang, J. Signal Detection Algorithm Based on SOR Algorithm in Massive MIMO System. In Proceedings of 14th IEEE International Conference on Signal Processing (ICSP), The Beijing (China), 2018, p. 662-667. [CrossRef]
- Gao, X., Dai, L., Yuen, C., et al. Low-Complexity MMSE Signal Detection Based on Richardson Method for Large-Scale MIMO Systems. In Proceedings of 2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall), The Vancouver (Canada), 2014, p. 1-5. [CrossRef]
- Shahabuddin, S., Hautala, I., Juntti, M., et al. ADMM-Based Infinity-Norm Detection for Massive MIMO: Algorithm and VLSI Architecture. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2021, vol. 29, no. 4, p. 747-759. [CrossRef]
- Park, S. Kalman Combining Based Iterative Detection and Decoding for MIMO Systems with Hybrid ARQ. IEEE Transactions on Vehicular Technology, 2023, vol.72, no.2, p. 2040-2050. [CrossRef]
- Dong, Y.Y., Zhang Z.Y., Chen, L., et al. A low-complexity precoding method based on the steepest descent algorithm for downlink massive MIMO systems. In Proceedings of IEEE/CIC International Conference on Communications in China (ICCC), The Beijing (China), 2018, p. 17-21. [CrossRef]
- Kumar, A., Gour, N., Sharma, H., et al. Hybrid detection techniques for 5G and B5G M-MIMO system. Alexandria Engineering Journal, 2023, vol.75, p. 429-437. [CrossRef]
- Chang, M.X., Su, S.L. Complexity-reduced maximum-likelihood hybrid detection for MIMO systems. IET Communications, 2023, vol. 17, no.7, p. 829-841. [CrossRef]
- Albreem, M.A.M., El-Saleh, A.A., Juntti, M. Linear Massive MIMO Uplink Detector Based on Joint Jacobi and Gauss-Seidel Methods. In Proceedings of 2020 16th International Conference on the Design of Reliable Communication Networks DRCN. The Milan (Italy), 2020, p. 1-4. [CrossRef]
- Wu, Z., Ge, L., You, X., et al. Efficient near-MMSE detector for large-scale MIMO systems. In Proceedings of 2017 IEEE International Workshop on Signal Processing Systems (SiPS), The Lorient (France), 2017, p. 1-6. [CrossRef]
- Ahmad, M., Zhang, X., Khoso, I.A., et al. High-Precision Iterative Preconditioned Gauss–Seidel Detection Algorithm for Massive MIMO Systems. Electronics, 2022, vol.11, no.22, p.3806. [CrossRef]
- Shahabuddin, S., Juntti, M., Studer, C. ADMM-based infinity norm detection for large MU-MIMO: Algorithm and VLSI architecture. In Proceedings of 2017 IEEE International Symposium on Circuits and Systems (ISCAS), 2017, p. 1-4. [CrossRef]
- KHOSO, A.I., ZHANG, X.F., SHAIKH, H. A., et al. Improved Gauss–Seidel detector for large-scale MIMO systems. IET Commun,2022, vol. 16, no.4, p. 291–302. [CrossRef]
- Zhou, J., Hu, J., Chen, J., et al. Biased MMSE soft-output detection based on conjugate gradient in massive MIMO. In Proceedings of IEEE 11th International Conference on ASIC (ASICON), The Chengdu (China), 2015, p. 1-4. [CrossRef]
- Chataut, R., Akl, R., Dey, U.K. Massive MIMO Uplink Signal Detector for 5G and Beyond Networks. In Proceedings of the IEEE Texas Symposium on Wireless and Microwave Circuits and Systems (WMCS), The Waco (USA), 2022, p. 1-7. [CrossRef]
- Mi, S.C., Zhang, J.Y., Fan, F.j., et al. Low complexity detection algorithms based on ADMIN for massive MIMO. China Communications. [CrossRef]
- Chinnusami, M., Ravikumar, C., Priya, S., et al. Low Complexity Signal Detection for Massive MIMO in B5G Uplink System. IEEE Access, 2023, p.1-11. [CrossRef]
- Chataut, R., Akl R., Dey, U. K., et al. SSOR Preconditioned Gauss-Seidel Detection and Its Hardware Architecture for 5G and Beyond Massive MIMO Networks. Electronics, 2021, vol.10. no. 5. p.578. [CrossRef]
- Wang, Z., Xu, W., Xia, Y., et al. A New Randomized Iterative Detection Algorithm for Uplink Large-scale MIMO Systems. IEEE Transactions on Communications, 2023, p.1. [CrossRef]
- G. Blanchard and R. Loubere, High-order conservative remapping with a posteriori MOOD stabilization on polygonal meshes, 2015, Available from: http://www.emn.fr/z-info/choco-solver/ [last accessed May 2011].
- R. Boggs, J. Bozman, and R. Perry, Reducing downtime and business loss: adressing business risk with effective technology, Tech. Report Technical report 91-18, InternationalData Corporation (IDC), Sernageomin, 2002.
- S. Elbaum, A. G. Malishevsky, and G. Rothermel, Test case prioritization: A family of empirical studies, IEEE Trans. Softw. Eng. 28 (Feb. 2002), no. 2, 159–182.
- G. Rothermel, A safe efficient regression test selection technique, ACM Trans. Soft. Eng. Methodology 6 (1997), no. 2, 173–210. MR 2000f:91046.
- G. Rothermel, M. J. Harrold, C. W. Hirt, A. A. Amsden, and J. L. Cook, A safe efficient regression test selection technique, ACM Trans. Soft. Eng. Methodology 6 (1998), no. 2, 173–210.
- A. Schulz and G. Doblhammer, Aktueller und Zukünftiger Krankenbestand von Demenz in Deutschland auf Basis der Outinedaten der AOK. (Current and future number of people suffering from dementia in Germany based on routine data from the AOK.), Versorgungs-Report (Piscataway, NJ, USA) (C. Gnster, J. Klose, and N. Schmacke, eds.), IEEE Press, 2012, pp. 161–175.
- S. Yoo and M. Harman, Pareto efficient multi-objective test case selection, (Proceedings Of The 2007 International Symposium On Software Testing And Analysis, London, UK), 2007, pp. 140–150.
Figure 1.
Signal detection framework for massive MIMO communications.
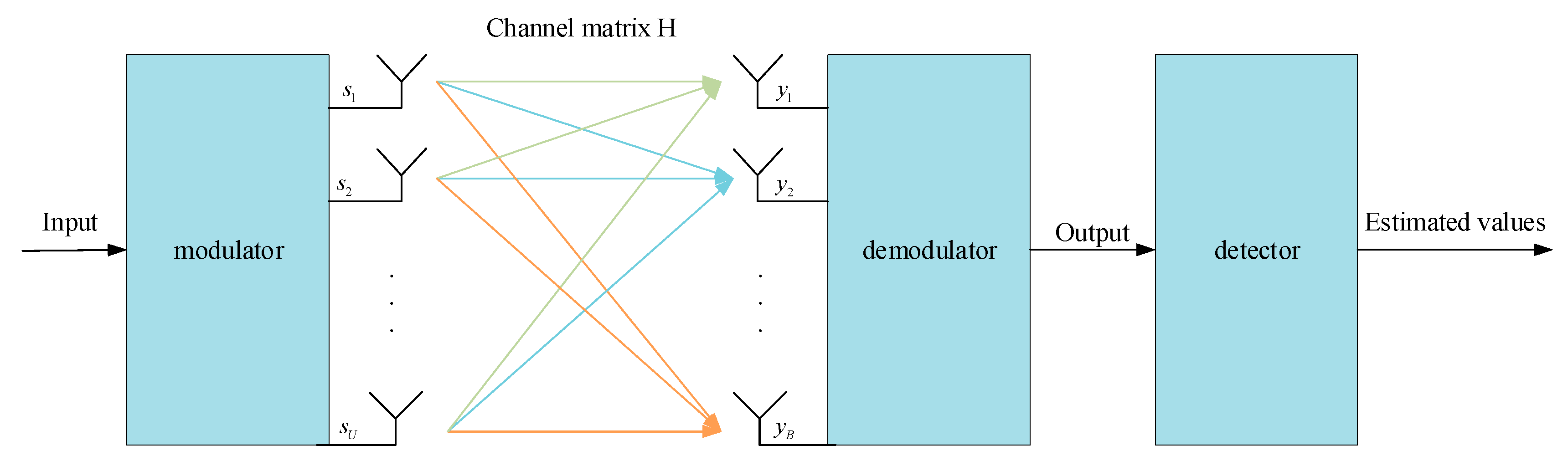
Figure 2.
Block diagram of the CJGS detector.
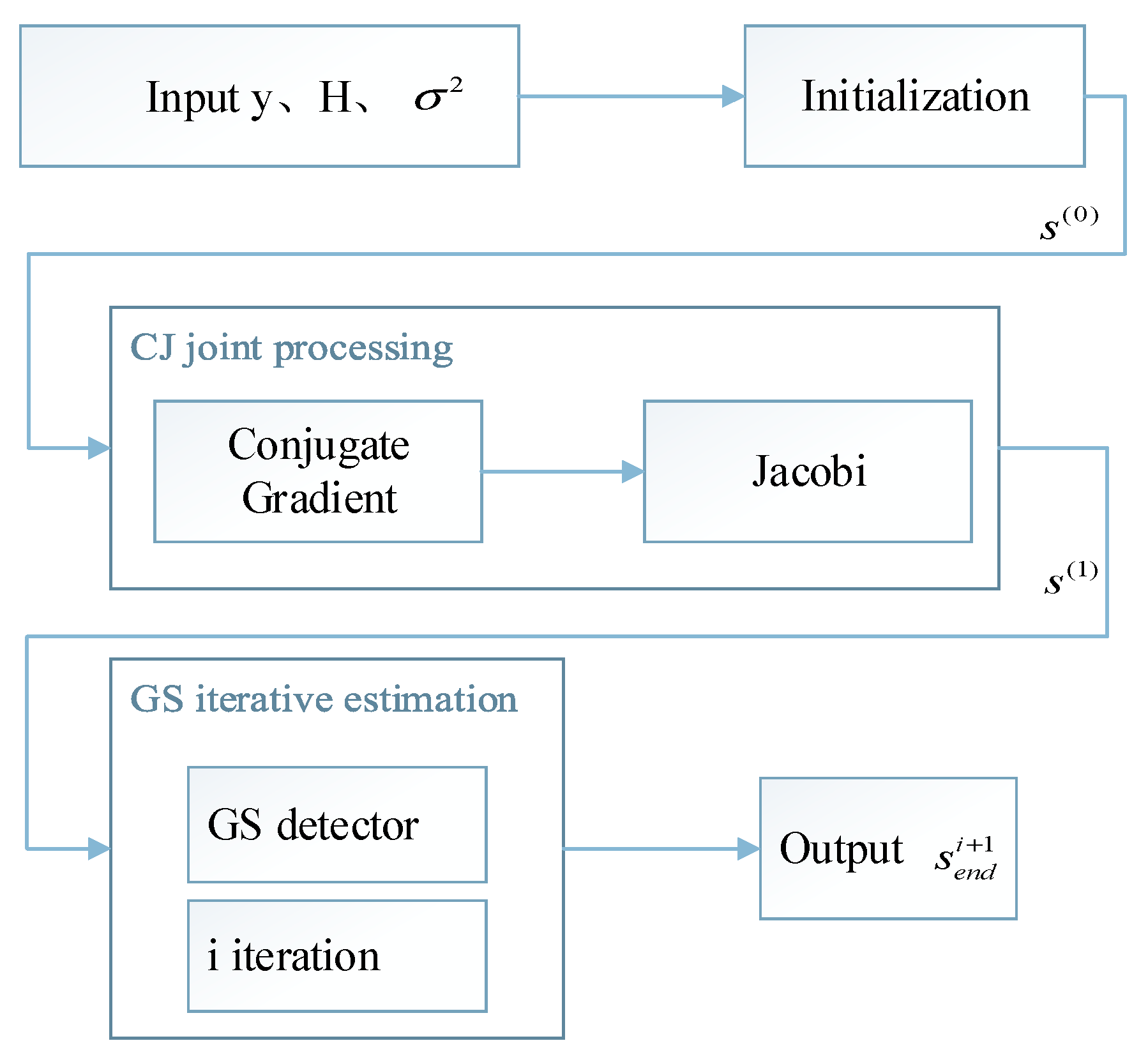
Figure 3.
BER performance for independent and identically distributed channels.
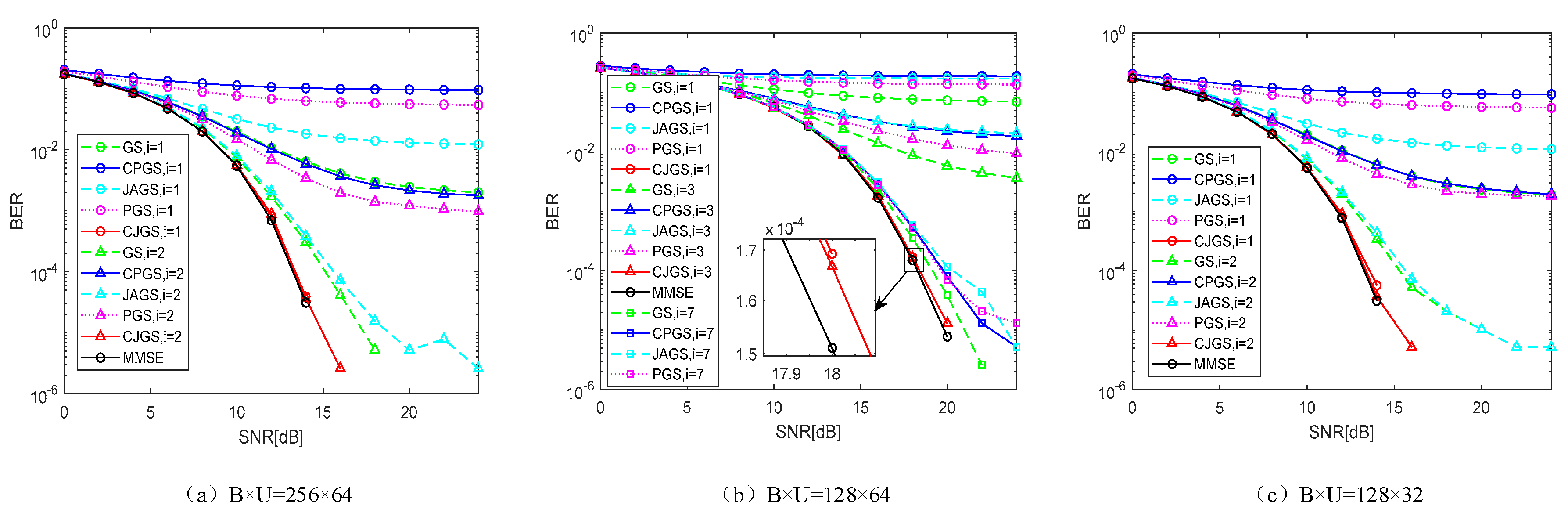
Figure 4.
BER performance for related channel in base station side.
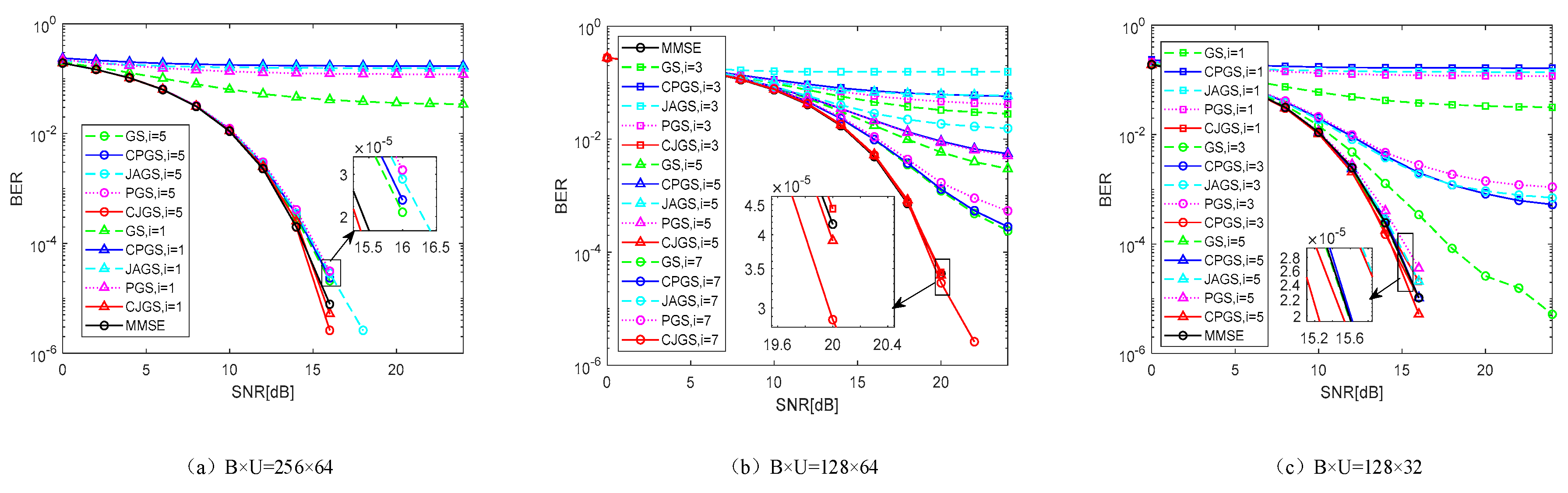
Figure 5.
BER performance for related channels on the user side.
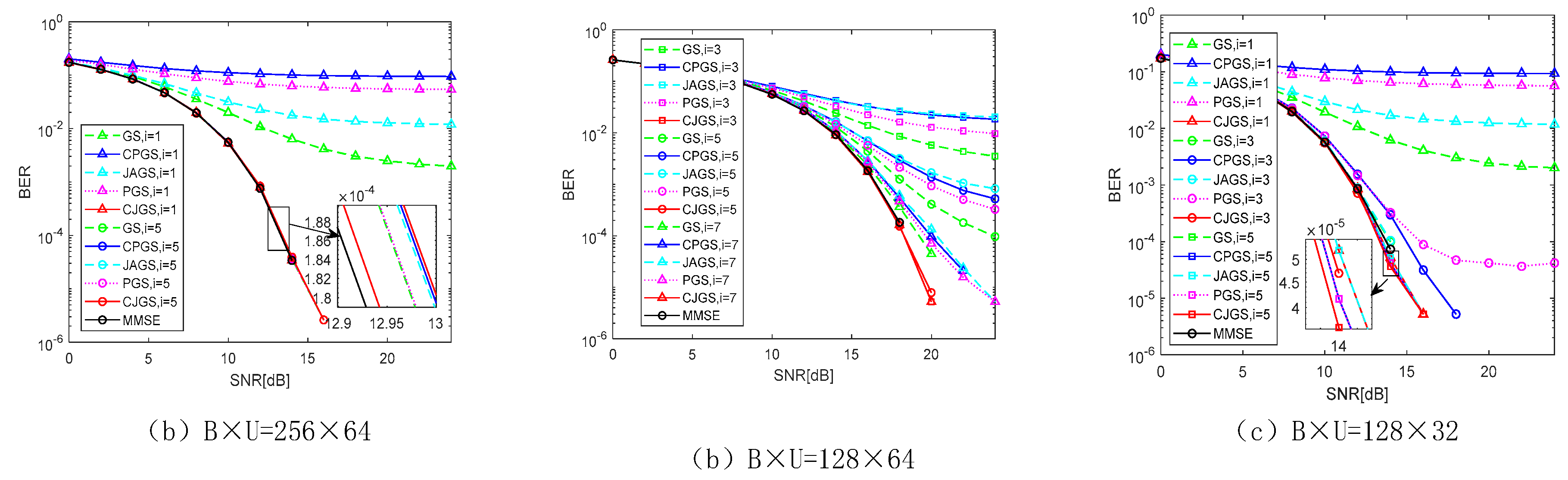
Figure 6.
BER performance for fully correlated channel.
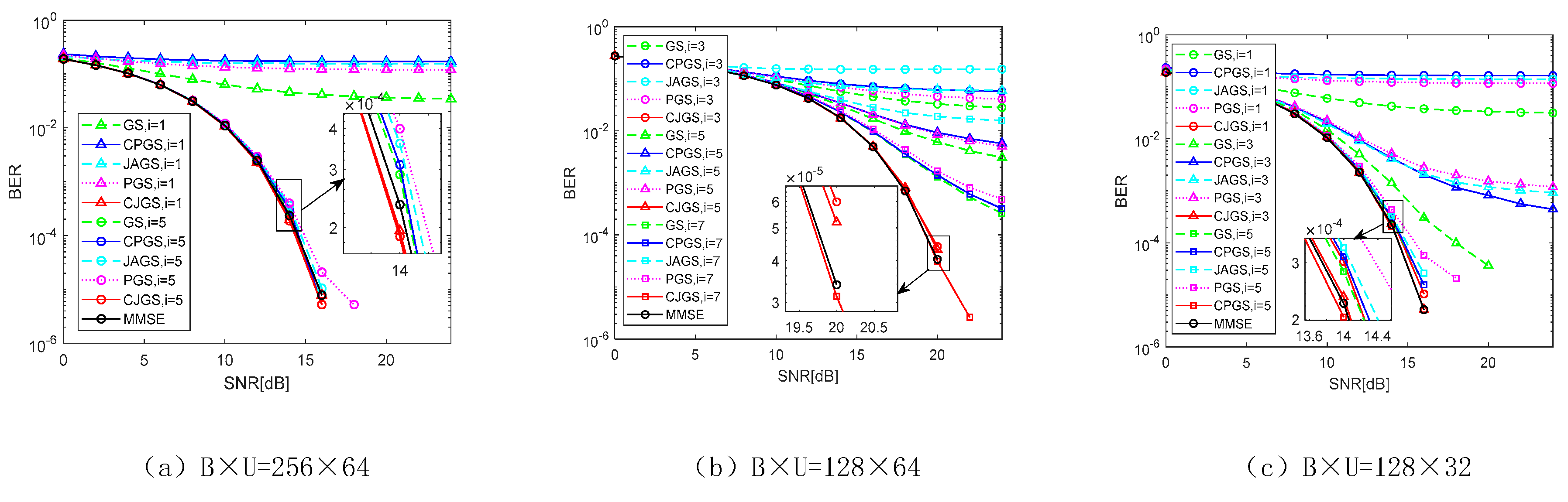
Figure 7.
BER performance comparison of the CJGS iterative algorithm with different initial values.
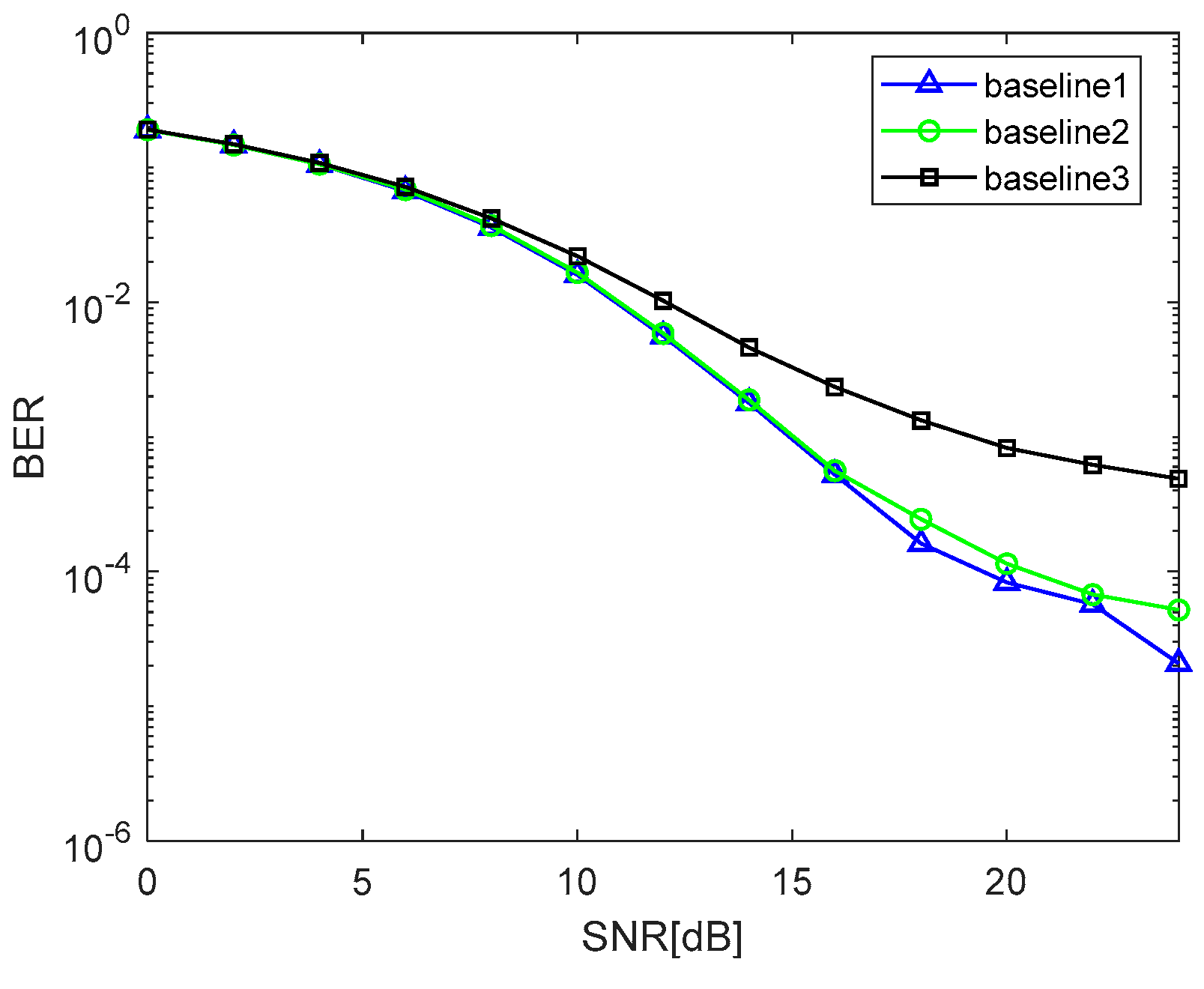
Figure 8.
Comparison of algorithmic complexity.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





