Preprint
Review
A Review of Pool Boiling Processes Based on Bubble Dynamics Parameters
This version is not peer-reviewed.
Submitted:
13 October 2023
Posted:
16 October 2023
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
Pool boiling is extensively utilized in various fields, such as electronics cooling, battery cooling, nuclear power plants, and chemical processing. In the process of temperature control through boiling, the generation and transportation of bubbles play a crucial role in calculating the heat transfer capacity of the system. Therefore, it holds immense significance to gain a profound understanding of the mechanisms underlying bubble formation, growth, and detachment. Currently, numerous mechanistic explanations and empirical correlations have been proposed to elucidate various parameters of bubbles during the boiling process. These findings were considered valuable references in selecting appropriate boiling media and designing efficient heating surfaces. To comprehensively present the progress of bubble formation and heat transfer during the boiling process, the forces exerted on the bubbles was highlighted in this article. And a meticulous review on bubble force analysis and correlation formulas pertaining to various relevant parameters (e.g. nucleation sites density, bubble growth rate, detachment diameter, detachment frequency) were conducted. This review article also were expected to provide a novel foundation for further exploration of enhanced boiling heat transfer.
Keywords:
Subject:
Engineering - Energy and Fuel Technology1. Introduction
In the context of ongoing industrialization and informatization, electronic devices have become increasingly miniaturized and highly integrated, especially in sectors such as automotive, artificial intelligence, and data centers [1,2]. As a consequence, the heat dissipation challenges from these advancements have become severe. The heat flux of individual chips can reach as high as 100-1000 W/cm2, which exceeds the cooling capacity of traditional air cooling techniques [3,4,5]. Therefore, the immersion boiling cooling method, which provides excellent heat transfer efficiency and uniform temperature distribution, has attracted considerable attention. Boiling can transfer a large amount of heat and control the wall temperature effectively. For instance, the latent heat released by a unit mass of water during boiling can raise the temperature of about five times its own mass from 0 °C to 100 °C. Currently, the heat dissipation capacity of boiling cooling can achieve as high as 202 W/cm2, which is about six times higher than that of traditional air cooling methods[6]. Therefore, the boiling cooling technology is widely used in various fields, such as nuclear power plants [7], air-conditioning units [8], heat pipes [9], rocket engines [10], battery cooling [11], electronics cooling [12,13] to meet the needs of various industries. Boiling can be broadly categorized into two types: pool boiling and flow boiling. Pool boiling, in particular, has significant advantages in terms of passive cooling without the need for pump work. This feature allows for a remarkable reduction in energy consumption, making it widely adopted in various industries [14].
In pool boiling, heat is applied to a solid surface immersed in a liquid contained in a vessel or pool. As the surface temperature increases, a thin layer of liquid in direct contact with the surface reaches its boiling point and undergoes phase change, forming small vapor bubbles. These bubbles detach from the surface and rise through the liquid due to buoyancy. Pool boiling, as a passive method of heat transfer through phase change, relies solely on the buoyancy effect to facilitate the cooling process. This characteristic not only gives pool boiling a high heat transfer efficiency but also provides it with several advantageous features. First, it requires minimal maintenance due to its self-sustaining nature. Second, pool boiling eliminates the need for pump induction, resulting in simplified system design and lower energy consumption. Third, the packaging and implementation of pool boiling systems are relatively easy, making the deployment suitable for various applications. In the process of realizing temperature control with pool boiling, the rate of heat transfer during boiling is largely determined by the amount of bubbles generated and transferred. Thus, understanding the mechanism of bubbles formation, growth and detachment is crucial for enhancing heat transfer.
In the process of pool boiling, the bubbles will cycle nucleation, growth, detachment, and nucleation again, as shown in Figure 1, after the bubble detaches from the heated surface during pool boiling, the region will be temporarily devoid of bubbles for new bubbles. During the early stage of boiling, when the heated wall surface meets the superheating criteria, nucleation sites are formed at the concave pits and cracks on the wall, inducing bubble nucleation. Then bubbles growth through the combined effects of the thermal boundary layer, micro-convection, and micro-liquid layer. In this process, the bubbles are mainly subject to the surface tension Fs , the liquid static pressure Fp and the excess vapor pressure Fm, the role of the gravitational force is usually negligible. When the bubble detachment force exceeds the force dragging the bubble, the bubble detaches from heated surfaces. The superheated wall continues to undergo convective heat transfer with the liquid until the nucleation conditions are met again and the bubble cycle is repeated.
Evaluation of the correlations of the boiling heat transfer coefficient and the heat flux showed that the key parameters affecting the boiling heat transfer process include the active nucleation site density Ns , bubble growth rate, bubble detachment diameter Dd and bubble detachment frequency f. Among them, the nucleation site density Ns is related to the surface conditions and temperature field, the bubble growth rate and the detachment diameter Dd are closely related to the force balance model, and the bubble detachment frequency f is determined by the bubble growth period tg and the bubble waiting period tw. The complex relationship of the above parameters can be represented by the relationship diagram shown in Figure 2.
Many researchers have proposed empirical correlations for various bubble-related parameters, force balance models, heat flux and heat transfer coefficients in the boiling process. However, there are strict constraints on the use of these empirical correlations, and it is often difficult to obtain ideal results outside of their own experimental conditions[15]. The prediction of various parameters of bubble dynamics always relies on accurate boiling heat transfer mechanisms, and these theoretically derived parameters of bubble dynamics will, in turn, affect subsequent heat transfer calculations, making accurate prediction of the boiling process significantly more difficult [16]. Therefore, the goal of this paper is that mathematical descriptions of the various stages of bubble behavior and force analysis are reviewed and summarized, and the accuracy and applicability of these models are further analyzed to provide valuable references for subsequent boiling heat transfer calculations and heat transfer enhancement.
2. Bubble nucleation
The formation of bubbles in boiling is now generally categorized into two types: homogeneous nucleation and heterogeneous nucleation. And the conditions for homogeneous nucleation are more demanding and require the liquid to be superheated to a sub-stable state [17], such as heating water in a smooth cup through a microwave. It needs to be noted that the superheated liquid is very unstable and may induce violent boiling by slight perturbation, causing liquid splashed out of the container, which is also known as the burst boiling phenomenon. Heterogeneous nucleation is the formation of bubbles on heated surfaces with the help of nucleation sites and is the main form of boiling [18] . Compared with the heterogeneous nucleation, homogeneous nucleation symmetric uniform model is easier to be described by mathematics, thus many researchers took advantage of the relative simplicity of modeling conditions for homogeneous nucleation to assist the calculation of heterogeneous nucleation mechanism.
2.1. Homogeneous nucleation
Homogeneous nucleation tends to form in superheated water when liquids are heated uniformly on smooth surfaces [17], such as heating smooth test tubes, microwaving water in a clean cup and releasing the pressure rapidly at high temperature. Superheated water is very unstable, the slightest disturbance may induce the liquid to boil violently and splash out of the container, so it is necessary to pay attention to precautions in life, for example, adding zeolite in the test tube, putting chopsticks in the cup, and so on.
In the case of low boiling point liquids stored under high pressure, if the integrity of the container is compromised, the pressure will rapidly drops below the saturation vapor pressure, which could lead to the rapid expansion of liquid or even cause explosions, resulting in safety hazards. This phenomenon is also known as boiling liquid expanding vapor explosion (BLEVE) [19]. BLEVE is also found in thermal micro-electric mechanical systems [20], laser-assisted phase change systems[21] and transient cooling of hot surfaces in the metal processing industry [22].
2.2. Heterogeneous nucleation
Rough surfaces with pits, crevices, and cracks are more likely to retain gas and induce bubble nucleation, the heating effect is also stronger than flat region, as shown in Figure 3 [23]. The superheating around the bubbles is not uniform due to the presence of the thermal boundary layer and micro-liquid layer, making the growth of bubbles in non-homogeneous boiling more complex than in homogeneous boiling.
It is widely recognized that bubbles form from pre-existing gas nuclei within the surface cavities, and cavities that cannot trap gas are hardly active nucleation sites. S.G. Bankoff [24] simplified the cavity to a conical cavity, where the condition for trapping the gas is that the contact angle needs to be greater than the cone angle of the cavity,i.e., θ > π - 2α, as shown in Figure 4. Cornwell [25] synthesized the effect of microscopic roughness in the cavity and extended the bubble trapping criterion to various shapes, proposing that the gas trapping surface should satisfy: θ > π - α - cos−1(1/S), where S is the dimensionless surface parameter, which is the wetted area of the rough surface divided by the projected area of the surface i.e., S = Sactual / Sprojected . The Cornwell criterion is in agreement with the Bankoff criterion when the cavity is a tapered cavity. Both equations indicate that hydrophobic surfaces(large contact angles) are more likely to trap gas and form nucleation sites than hydrophilic surfaces(small contact angles).
The formation of nucleation sites requires not only pre-existing gas, but also a certain degree of superheat to induce nucleation growth of the bubbles. A combination of force equilibrium and thermodynamic equilibrium is currently commonly used to calculate the required superheat of the bubble embryo, i.e., it is predicted by Equation (3) obtained by combining the Young-Laplace equation and the Clausius-Clapeyron equation, as shown in Equations (1) and (2),
where
Hsu [26] argued that a range of cavity sizes can be activated in heated surfaces, rather than the specific size predicted by Equation (1). Therefore, he proposed a nucleation criterion that depends on the properties of the thermal boundary layer at the heated wall, as shown in Figure 5. The bubble embryo will nucleate successfully when the liquid temperature in the thermal boundary layer reaches the vapor bubble temperature i.e., when the relative height to the wall surface h = hb. The liquid temperature Equation (4) is obtained by solving the transient one-dimensional heat transfer equation, and the bubble temperature is obtained from Equation (3). Thus Hsu obtained a quadratic equation whose solution bounds the range of the nucleation cavity size as shown in Equation (5).
In Equation (5), the angle is the shape angle formed by the embryonic bubble and the surface measured from the liquid side when the bubble temperature is equal to the liquid temperature, as shown in Figure 5. The shape angle is related to surface tension and hydrophilicity and the more hydrophilic, the smaller the angle . It is important to note that during boiling, cavities may still settle after activation to produce bubbles, resulting in a rapid rise in local surface temperature. Qi and Klausner [27] studied the heterogeneous nucleation of artificial cylindrical cavities fabricated on silicon substrates with diameters ranging from 8 to 60 µm and depths of 45 µm, and observed that bubble nucleation during the boiling process shows an intermittent pattern, with the cavities experiencing a few minutes of silence before nucleating again. They attributed this phenomenon to the enhanced convection induced by bubble boiling, which led to the thinning of the boundary layer and thus inhibited nucleation at certain locations. Therefore, the stability of nucleation sites during boiling is also an important factor that should be considered in surface design.
Based on the nucleation radius model proposed by Hsu [26] , water with high surface tension and high latent heat and Novec-649 fluoride liquid with low surface tension and low latent heat are selected as the research objects in this paper to investigate the effect of different shape angles on their nucleation radius. The thickness of the thermal boundary layer recommended by Liu et al. [28] is taken to calculate, and the boiling is assumed to be saturated boiling i.e., . The physical properties of water and Novec-649 fluoride (p0 =1 bar) are shown in Table 1. Based on the data in the table and Equation (5), the relationship between the range of nucleation radius and wall superheat for water and Novec-649 at different shape angles is obtained in Figure 6, where the middle part of the curves indicates the range of nucleation radius. It can be seen from the figure that, according to the nucleation radius model proposed by Hsu [26], the nucleation radius range of boiling increases with increasing shape angle, which also verifies that the stronger the hydrophobicity is, the easier the nucleation is, and the superheat degree does not have much effect on the nucleation radius after reaching a certain standard.
For heterogeneous nucleation, the nucleation sites density Ns is defined as the number of cavities present on the heated surface where bubbles grow per unit of heated surface area [31]. The active nucleation sites density is essential for the determination of boiling heat flux and heat transfer coefficient.
Sakashita and Kumada [32] calculate the density of active nucleation sites by Equation (7), which is the function of cavity radius Rc and Jakob number Ja, and Ja is a dimensionless measure of wall superheat shown in Equation (6). In the following relation, the constant C2 was determined from experimental data, and the cavity size Rc was calculated using the Hsu and Graham model [33].
Xiao et al.[34] proposed a theoretical model of nucleation site density based on the statistical properties of the boiling process. They obtained the cumulative size distribution of the active nucleation sites density based on the correlation of Wang and Dhir [35]. The value of nucleation sites density was expressed by calculating the minimum nucleation cavity density and the maximum nucleation cavity size:
Suszko and El-Genk [36] synthesized the conservation of energy and expressed the nucleation site density calculation equation in terms of bubble detachment diameter, bubble departure frequency, and Jacob number as follows, where Archimedean number .
From the perspective of enhanced boiling, boiling surfaces are often expected to have lower nucleation onset (ONB) and denser nucleation sites, thus generating more phase transitions and transferring more heat at low superheat. Cornwell [25] criterion can be applied to a wide range of irregular surfaces and provide a valuable reference for surface cavity design. According to this criterion, the wall contact angle of the liquid should be as large as possible, i.e., more hydrophobic. Bourdon et al.[37] also noted that hydrophobic surfaces have lower boiling onset temperatures and higher heat transfer coefficients than hydrophilic surfaces under low superheat conditions. It should be noted, however, that while hydrophobic surfaces are more likely to nucleate, bubbles on hydrophilic surfaces are more likely to detach. Jo et al.[38] found that hydrophobic surfaces have lower boiling onset superheat and higher boiling heat transfer coefficients than hydrophilic surfaces, but their critical heat flux (CHF) is lower, which may be caused by the excessive bubble size on hydrophobic surfaces results in no liquid wetting underneath the bubbles [39]. Therefore, some researchers [40,41] have also tried to achieve better heat transfer by combining hydrophobic and hydrophilic surfaces on the same surface.
It needs to be explained that the above criteria(Figure 4, Figure 5 and Figure 6), can only be applied to ordinary rough surfaces. However, as shown in Figure 7, more and more complex surface structures are being used to enhance boiling heat transfer, such as metal foams [42], nanostructures [43], porous media [44], and so on. How to describe the disordered microstructure of these complex surfaces by mathematical logic is the urgent problem that still needs to be solved. Moreover, the force analysis of bubbles has an important effect on the disordered microstructure, so the research on force analysis of bubbles is reviewed in order to investigate the mechanism of growth and detachment of bubbles after nucleation.
3. Mechanical analysis of the bubble
The forces on the bubbles have a great influence on the state of motion and shape of the bubbles in the process of growth and separation of bubbles after nucleation, and it is very important to analyze and model the forces acting on the bubbles. The growth and separation of bubbles on solid surfaces are affected by various forces such as surface tension, buoyancy, drag force, etc. Among these forces, they can be divided into the lifting force that separates the bubbles, such as buoyancy, internal pressure of the gas, etc., as well as the resistance force that makes the bubbles attach to the heated surfaces, such as surface tension, drag force, etc. In the early boiling stage, the impact of lift is less than the resistance, the bubble to stay attached to the solid wall. When the bubble growth to a certain size, the influence of lift began to exceed the resistance, the bubble from the heated surface detachment, quickly rise to the liquid surface and broken.
In order to research the growth and detachment of bubbles during boiling, many researchers have mathematically modeled the forces on bubbles. Klausner et al.[46] theoretically analyzed the forces on bubbles in flow boiling and provided expressions for various forces. Their theory suggests that the growth and detachment of bubbles on heated surface perpendicular to the direction of gravity are subjected to a combination of surface tension Fs , unsteady drag force Fdu , shear lift Fsl , buoyancy Fb , hydrodynamic pressure force Fh and contact pressure force Fcp . Among these forces, the surface tension Fs originates from the area between the bubble and the wall and acts along the bubble interface, which tries to prevent the bubble from detaching; the unsteady drag force Fdu originates from the bubble growth process, also known as the bubble growth force Fg , which includes the resistance caused by the asymmetric bubble growth Fd and the dynamic effects induced by the unsteady fluids, such as the additional mass force Fi ; the contact pressure Fcp is induced by the difference in pressure between the inside and outside of the bubble, which acts in the direction perpendicular to the heated surface.
For flow boiling, there will also be a shear lift force Fsl due to the flow of the liquid as well as a liquid flow force Fh , where the shear lift force Fsl acts perpendicular to the direction of the flow and tries to lift the bubbles off the walls.Van Helden et al.[47] believe that this force is influenced by Bernoulli suction and vortex volume. To calculate it, Mei and Klausner [48] proposed a relation based on the assumption of spherical bubbles in an infinite flow field at low Reynolds number and related it to the Auton’s relation [49] for the shear lift of bubbles in viscous flow at low tension rates, giving a relation for the shear lift in a wide range of Reynolds numbers:
where is the dimensionless flow shear rate and CL is the lift-off coefficient, expressed as:
The liquid flow force Fh is derived from the differential pressure generated by the liquid flow, which is given by:
Thus, its mechanics are described as:
In pool boiling, the flow velocity u of the liquid can be approximated as 0, so for pool boiling, Fh and Fsl can be neglected, i.e.,
Klausner’s mechanical model [46] has been applied and improved by many researchers, Thorncroft et al.[50] proposed the static force wall contact pressure Fcp as well as the first term of the unsteady resistance Fdu should be neglected and the second coefficient of Fdu was changed from 1.5 to 2, and the wall contact pressure Fcp was modified to obtain the mechanical equilibrium of the bubble detachment in the pool boiling as:
Jiang et al.[51] modified Klausner and Thorncroft’s model by proposing a different growth force equation and considering the drag force caused by the wake of the bubble after it leaves in the force model. They proposed that as the bubble grows, the vapor in the bubble and the liquid expelled around the bubble will exert a growth or inertial force on the bubble. They modelled this inertial force on the basis of the growth rate of the bubbles and developed a dynamic boiling model that takes into account the effects of evaporation action at the contact line and heat transfer from the thermal boundary layer, and which also takes into account the change in the contact angle during the growth of the bubbles. Wang et al.[52] made some modifications in the coefficients and considered the Marangoni stress acting on the bubbles, which is a stress gradient caused by the temperature difference, and the greater the liquid subcooling, the greater the effect of Marangoni force. Bhati et al.[53] and Paruya et al.[54] on the other hand, proposed that for bubbles in boiling, the effect of contact pressure can be neglected.
Siddharth [55] performed further calculations on the volume of the truncated sphere and modified the drag coefficient. Among these models, Klausner, Wang and Siddharth’s model is more widely used for reference, the specific relational equations they propose are listed in the Table 2, where Rcur =5Rb , is the radius of curvature at the bottom of the bubble and Cd is the drag coefficient, which is obtained by the rate of growth of the radius of the bubble [56] , whose expression is .
Bucci et al.[57] took high-speed video and infrared thermometry to modify these formulas by quantifying these forces. They conducted a series of experimental studies on the growth and departure of single isolated bubbles under boiling conditions in a horizontal pool. By contouring the liquid-gas interface, they calculated these external forces acting on the bubbles. These forces versus time during bubble growth and detachment are shown in Figure 8. Bucci et al. argue that the force balance approach relies on predicting, for example, the rate of change of bubble momentum, which is very small, to give a basis for the viscous drag Fd and inertial force Fi of the bubble, leading to experiments with very high demands on the precision of the measurements. This relationship makes it difficult to obtain the desired results for bubble detachment radius prediction by force balance methods.
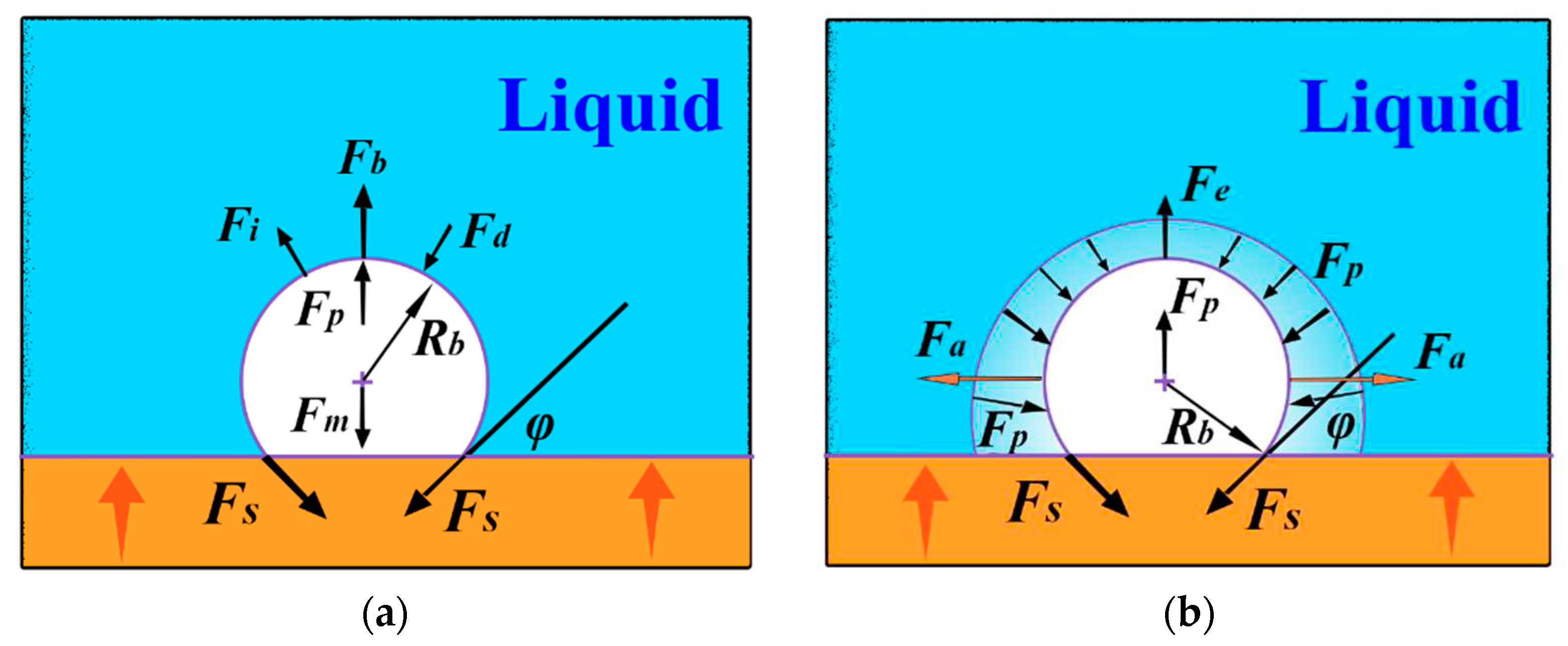
In all of the above models, the researchers used Archimedes’ principle for the calculation of buoyancy, i.e.,
Fb=ρlgV. It should be noted that Archimedes’ law can only be applied to the bubbles after they detached from the wall, and for the bubbles that have not yet been detached, Archimedes’ law does not apply because the part of the bubble that is in contact with the wall is not subjected to the pressure of the fluid [58].
Liu et al.[59] calculated the pressure on the bubble surface by spherical coordinate integration and considered the effect of the micro-liquid layer at the bottom of the bubble on the overall pressure. The receding contact angle was taken in their calculations , which was obtained by photographing the state of the bubble before it detached. The forces on the bubble in their mechanical model include the surface tension FS , the liquid pressure FP , the gravity FG , the momentum change force Fe , and the internal pressure of the bubble Fm , the instantaneous expansion force acting on the boundary of the bubble Fa , which is oriented perpendicular to the boundary of the bubble, and the combined force acting on the bubble was denoted as FZ . The comparison between Wang et al.[52] proposed force model and Liu et al.[59] is shown in Figure 9, and the computational equations of various forces are shown in Table 3, where H denotes the height from the wall to the liquid surface, is the ratio of the area of the micro-fluid layer to the area of the bottom of the bubble, denotes the heat flux at the gas-liquid interface around the bubble, and Ss denotes the area of the gas-liquid interface, with the negative sign indicating that the direction is along the direction of gravity. In its assumptions, the radius of the micro-fluid layer is approximately twice the radius of the dry portion.
It can be seen from the equation that the bubble force is also affected by the liquid level height H in Liu et al. model, which provides a new insight for the design of the boiling system, and Kopchikov et al.[60] also pointed out that the boiling heat transfer coefficient increases significantly with the reduction of liquid height when the liquid height is reduced to a certain value.
Liu et al.[59] proposed the formula p=ρlgh for liquid pressure, however, the effect of external air pressure should also be taken into account due to the adhesion of the bubbles to the wall, i.e., p= ρlgh + p0 . The integration of the actual liquid pressure on the bubble in combination with the external pressure results in:
The relationship between bubble growth and systemic pressure has also been confirmed by many researchers. Labuntsov et al.[61] and Akiyama et al.[62] pointed out that the bubble growth rate decreases with increasing pressure, Miglani et al.[63] and Gao et al.[64] observe that the higher the pressure, the smaller the diameter of the bubble detachment.
A review of these forces shows that the bubble forces are related to the density of the liquid, the surface tension, wall wettability, and the growth rate of the bubbles, so all these physical properties of the liquid should be taken into account when selecting a boiling medium. The equilibrium of forces on the bubbles is critical for the prediction of the bubble detachment diameter, which is discussed in Section 4.3. The analytical difficulties among these forces are that the first-order and second-order derivatives of bubble size with respect to time contained in unsteady resistance Fdu are difficult to predict accurately, and the ever-changing mass transfer process also keeps the center of mass of the bubbles in an unsteady state, and an accurate bubble growth and detachment model will help in the calculation of these variable quantities.
4. Bubble growth and detachment model
Mahmoud et al.[65] conducted an experimental study on the growth of bubbles in saturated pool boiling of deionized water on the surface of pure copper under atmospheric and sub-ambient pressures. The measurements were conducted using a high speed, high resolution camera, and the complete cycle of bubbles from nucleation, growth, detachment to nucleation again is shown in the Figure 10. They also evaluated existing uniform and non-uniform bubble growth models based on experimental data [66]. They found that the existing models are difficult to unify after summarizing these studies, most of which are only applicable under the experimental conditions of the proposers themselves, and suggested that the phenomenon may be caused by the excessive differences in the mechanisms affecting bubble kinetics (growth rate, departure diameter, frequency), fluid properties and surface microstructure. They also point out the difficulty of modelling uniform boiling for the prediction of bubble growth rates in nuclear boiling under many operating conditions, but it can provide a reference for calculations of non-uniform boiling. Modelling of bubble growth during uniform and non-uniform boiling is presented in detail next.
4.1. Bubble growth in uniform boiling
The second-order non-linear type ordinary differential equation as shown in Equation (17) for the bubble when uniformly heated can be obtained from the mass conservation equation and momentum conservation equation of the bubble, which is obtained based on the following simplifying assumptions.
(i) Bubbles grow in an infinite medium and that their growth has spherical symmetry;
(ii) The surrounding fluid is a Newtonian fluid with constant properties;
(iii) The bubbles are assumed to be unaffected by external forces;
(iv) The pressure and temperature inside the bubble are uniform;
(v) Due to mass transfer at the interface, the liquid around the bubble is assumed to flow at a velocity of ;
(vi) There is no translational or rotational motion in bubble growth.
The homogeneous nucleation of bubbles was categorized into three distinct phases by Mahmoud [66]: surface tension growth, inertial growth, and thermal diffusion growth, as shown in Figure 11.
In the surface tension growth phase, the initial equilibrium radius of the bubble is R0 , which is obtained from the pressure difference between inside and outside the bubble and the surface tension equilibrium as pv - pl∞ = 2σ/R, i.e., the Young-Laplace equation. And the temperature of the bubble is equal to the temperature of the surrounding liquid, i.e., Tv = TL∞ . In this case, the velocity and acceleration are so small that the liquid inertia terms (the first and second terms in Equation (17) are negligible and the dynamic growth of the bubble is driven by the pressure difference.
In the inertial growth phase of the bubbles (R10R0 ), the radius of the bubble is significantly larger than the initial radius R0 . Therefore, the third term on the right hand side of surface tension Equation (17) becomes negligible and bubble growth will be dominated by liquid inertia. It is worth mentioning that the time scales of the first and second phases are very small, in the order of microseconds. For example, Sernas et al.[67] and Forster et al.[68] reported a weakening of the dynamic effect after 50μs (based on experimental measurements) and 100μs (based on numerical analysis), respectively.
During the thermal diffusion growth phase, evaporation occurs at the bubble surface and a thin thermal boundary layer forms around the bubble, called the “cooling effect [69] “. As a result, the vapor temperature drops from the initial superheat to the saturation temperature, so that the vapor pressure pv equals the liquid pressure pl∞ (system pressure). This makes the left term of Equation (17) zero and the dynamic effect no longer drives bubble growth, and it is the temperature difference that drives bubble growth.
Although the above differential equation does not have an analytic solution, each of the individual growth stages in it has an approximate solution or a complete numerical solution. For example, Rayleigh [66] simplified the bubble growth problem by neglecting the surface tension phase, ignoring the vapor-liquid density ratio (ρv /ρl ), and assuming that the bubble grows isothermally (no heat transfer), i.e., (pv -pl∞) remains constant, to obtain a Rayleigh solution Equation (18) to inertia-controlled growth, which shows that the radius increases linearly with time, i.e., the bubble grows at a constant rate.
The energy equation need be coupled with the kinetic Equation (17) in order to combine the heat transfer with the bubble growth problem. The coupling between the two equations is usually realized through the pressure difference term (pv -pl∞) in Equation (17), e.g., the well-known Clausius-Clapeyron equation (Equation (19)), which allows to relate the pressure difference term to the liquid superheat term (Tl∞ -Tv ). The liquid temperature at the bubble interface is equal to the vapor temperature in thermodynamic equilibrium, which can be obtained from the solution of the transient energy equation without an internal heat source Equation (20), and the boundary conditions at the bubble interface take the second type of boundary conditions (heat flux is known). Thus, the solutions of Equations (17) and (19) with appropriate initial and boundary conditions are able to describe the complete bubble growth problem, and these equations can be solved by numerical calculations
Since the numerical solution does not provide an explicit expression for the bubble radius and the kinetic effect of the bubble is only important for a short time interval at the beginning, many researchers have ignored the complex initial growth phases (surface tension growth and inertial growth) and given an approximate analytical solution for the asymptotic phase in which the radius of the bubble is proportional to the square root of time (i.e., R ∝ t0.5 ).And the asymptotic solution can be obtained simply from equations such as the energy balance Equation (21) if the temperature gradient (∂T/∂r)r=R is known.
A comparison of correlations for uniform boiling [70,71,72,73,74,75] was conducted and shown in Table 4. In the following correlations, Ja is the Jacob number and the expression is , is the thermal diffusivity and the expression is . These correlations were compared with pool boiling experiments by Mahmoud et al.[65] It was found that for bubble growth at atmospheric pressure, the prediction curve of the formula proposed by Fritzd et al.[70] is most consistent with the experimental curves, with relative errors between 18.5% and 31.6%; for the conditions at 0.5 bar and 0.15 bar, these homogeneous models are difficult to coincide with the experimental curves.
The growth rate of bubbles is mainly related to the Ja number and the thermal diffusivity of the liquid in uniform growth models from Table 4. Early studies considered the rate to be proportional to the square root of time, while later studies mostly took the form of dimensionless numbers to describe the bubble growth rate in uniform growth models.
4.2. Bubble growth in non-uniform boiling
The growth of bubbles in non-uniform boiling is more complex and unpredictable compared to the situation in uniform boiling. The radius R is mostly proportional to t0.5 in the most of the above discussed correlations, while the time exponent can be less than 0.5 in the non-uniform boiling, e.g., Strenge et al.[76] measured the growth of bubbles during saturated boiling of n-pentane and ether at atmospheric pressure and found that the radius of the bubbles conforms to the relation R∝tn , where n takes values in the range of 0.19 ~ 0.475. The main difference in the modeling of bubble growth during the asymptotic stage of non-uniform boiling lies in the assumptions made on the heat transfer mechanism of the bubbles. The researchers assumed two main mechanisms, one in which the increase in bubble mass originates mainly from the evaporation of liquid in the micro-fluid layer below the bubble; and the other is attributed to the evaporation of the thermal boundary layer around the bubble surface.
It is now generally accepted that bubble growth is attributed to the action of the micro-fluid or thermal boundary layer, as shown in schematic Figure 12. In Figure 12a, bubble growth driven from evaporation of the boundary layer carried by the bubbles from the boiling surface. In Figure 12b, the bubbles protrude outside the wall thermal boundary layer (WTBL) and grow from microlayer evaporation. The mechanism in Figure 12c is similar to that in Figure 12a, except that the thermal boundary covers only a part of the bubble. In Figure 12d, the growth of the bubble come from the combined effect of the micro-fluid layer and the thermal boundary layer around the bubble.
Mahmoud et al.[66] concluded that models based only on micro-fluid layer evaporation are difficult to explain bubble growth and can only reach good agreement with the results under certain specific experimental conditions after a detailed evaluation of several mathematical models of the micro-fluid layer. Bubble growth is mainly promoted by evaporation from the thermal boundary layer around the bubble, and the effect of the micro-liquid layer is relatively small for some fluids such as water, for example.
4.2.1. Thermal boundary layer bubble growth modeling
Bubbles in non-uniform boiling are not homogeneous spheres, which are usually calculated as truncated spheres, and the heat in a thermal system usually comes from the superheated wall at the bottom of the bubble. In this regard, Zuber [77] modified the uniform growth model proposed by Fritz and Ende [70] to capture the superheat in non-uniform boiling processes. The model takes a uniform thickness based on a “thin boundary layer” approximation of the interfacial heat balance. There is only one heat flux vector pointing towards the inner bubble interface in uniform boiling. On the contrary, in non-uniform boiling, a part of the heat can be transferred towards the bubble surface as a temperature potential (Tmax -Tsat ) and another part of the heat can be transferred towards the liquid as a temperature potential (Tmax -TLb ). In other words, the temperature of the liquid within the boundary layer around the bubble has a peak Tmax , and decays toward the bubble interface and the liquid body. This peak temperature is assumed to be equal to the boiling surface temperature Tw and the heat flux qLb to the liquid body is assumed to be equal to the wall heat flux. And a factor b is used to correct for the effect of bubble curvature on the temperature gradient under the assumption of a flat interface, , and the recommended value is obtained by comparing with the experimental data. The energy balance at the bubble interface in non-uniform boiling was corrected to Equation (22) to obtain the bubble radius in Equation (23).
A relaxation phenomenon exists in all fields of physics, whereby when a system in equilibrium is perturbed, it requires a delay time to return to its initial equilibrium state, and this process shows exponential regression. Van Stralen [78] launched a study on the growth model of bubbles with the help of this concept. As the bubble expands radially, these superheated fluids accumulate around the bubble up to a certain height y, which measured from the boiling surface, and it may be less than or equal to the bubble height. He assumed that the boundary layer around the bubble up to this height has a uniform thickness and referred to it as the “relaxation layer”. Thus, the bubble was assumed to increase in size due to evaporation at spherical segments whose height was less than the bubble height, as if the bubble were partially heated. Van Stralen also assumed that the liquid superheat in the “relaxation layer” decreases exponentially with time from its initial maximum (Tw ), as in Equation (24). Van Stralen used the bubble detachment time td as the characteristic time in Equation (24) based on the assumption that bubble growth followed the relaxation law. This correlation performed an energy balance for partially heated bubbles, and incorporated the time-dependent superheating term into the relationship. Its calculation result (Equation (25)) is similarly to that of the Plesset and Zwick [71] model for uniform boiling, but his model was also multiplied by the factor b∗ defined by Equation (26), which represents the proportion of the bubble surface area covered by the superheated liquid layer.
The “relaxed boundary layer” model proposed in Equation (25) predicted all the data well in terms of trend and numerical value, with deviation errors within 15% for a wide range of superheat and low and medium pressure conditions [66]. The limitation of this model is that the bubble detachment period td and the radius of detachment Rd must be known in advance. The departure time and radius were taken directly from the experimental data in the above calculation. Therefore, accurate bubble detachment diameter and bubble detachment period need to be calculated first for exact calculation.
4.2.2. Empirical modeling of bubble growth
Many models for bubble growth in non-uniform boiling have been proposed based on experimental data. Cole and Shulman [79] measured bubble growth in saturated boiling of toluene, acetone, pentane, carbon tetrachloride, methanol, and water on a smooth metallic zirconium belt at different wall superheat levels. They evaluated a number of homogeneous growth models based on their data and concluded that the experimental growth factor β = f(Ja) would be smaller than the homogeneous model due to nonuniform superheating in nonuniform boiling. They relate their data in the form given by Equation (27), and the empirical constant 2.5 and the exponent 0.75 to the Jacob number were taken(mostly 1 in uniform boiling).
Du et al.[80] synthesized experimental data from various researches on saturation boiling of water on copper, stainless steel, nickel and silver surfaces at different pressures and wall superheat, and proposed fitting these data with the formula by Equation (28), where the growth factor β depends on Ja and the exponent of time, n, depends on the system pressure in Mpa. The exponent n varies equally as the main factor controlling the growth rate varies,. This is because growth is much more influenced by the inertial growth stage at low pressures; whereas growth is mainly controlled by heat transfer under high pressure ambient conditions.
Benjamin and Balakrishnan [81] collected saturated pool boiling data for a variety of liquids (including water, CCl4 , et al.) on metal surfaces in the horizontal direction from the literature, and they proposed Equation (30) to fit these data based on their collection, in which the correction factor B = 1.55 for water, CCl4 , and n-hexane; and B = 0.645 for n-pentane and acetone.
The accuracy of the above relation was evaluated by Mahmoud et al.[66] based on experimental data from non-uniform boiling and it was found that the Du et al.[80] model has better performance at atmospheric pressure, while Benjamin et al.[81] model showed better accuracy at low and medium pressures. The better performance of the model at sub-atmospheric pressure may be due to the incorporation of the Archimedes number that takes into account the effect of gravity, which is neglected in all other empirical models.
4.3. Bubble detachment diameter
The bubble detachment diameter is the equivalent diameter of the bubble after it leaves the heated surface during boiling, which is an important parameter in determining the boiling heat transfer coefficient. Bubble detachment diameter is usually determined by mathematical calculations with the aid of force balances or experimental measurements using a high-speed camera to capture the boiling process of a single bubble image at present. Such measurements are limited to low heat flux, i.e., the early stage of boiling, and neighboring bubbles collide with each other and form larger bubble sizes with high heat flux, which is difficult to obtain through theoretical analysis.
It is generally accepted that the prediction of bubble departure diameter requires information about the surface tension, wall wettability, contact angle, heat flux, wall superheat and thermal diffusivity. Many correlations equation for bubble departure diameter have been established by considering factors such as pressure, surface roughness, interfacial properties, and cavity radius in conjunction with the thermophysical properties of the fluid. Fazel et al.[82] conducted nucleation pool boiling experiments on a horizontal bar heater with aqueous solutions of electrolytes such as NaCl, KNO3 and Na2SO4 as working fluids and measured the bubble kinetic parameters. They found that the bubble detachment diameter increased with increasing boiling heat flux and electrolyte concentration based on the experimental results. Thus they obtained a bubble detachment diameter prediction model for a wide range of heat fluxes and concentrations by combining the boiling heat flux and the dynamic viscosity as shown in Equation (31). The model predicts the bubble detachment diameters from experimental data with errors of 2%, 10% and 5% for NaCl solution, KNO3 solution and Na2SO4 solution, respectively.
Phan et al.[83] modified Fritz’s relational equation to propose a new correlation to predict bubble detachment diameter for organic fluids based on the concepts of macroscopic and microscopic contact angles with the following assumptions: (i) Maximum bubble volume is determined by force balance based on the concept of macroscopic and microscopic contact angles. (ii) Bubbles growth comes from evaporation of the liquid microlayer and the maximum bubble volume is related to the conservation of mass. (iii) Mass transfer during the rewetting stage of the liquid is assumed to be negligible. They related the bubble departure diameter to the contact angle and thermophysical properties of the fluid to obtain Equation (32). The model predicted the experimental data for bubble departure diameters at low superheat and low subcooling within ±30% and was valid for contact angle values from 0° to 90°. However, the proposed correlations show large deviations in comparison to the experimental results at high concentrations.
Nam et al.[84] conducted experiments by fabricating separated microcavities by forming CuO nanostructures on silicon substrates with superhydrophobic surfaces. Their results showed that the bubble departure diameter of water became 2.5 times smaller and the growth period 4 times shorter compared to that on the silicon substrate. They proposed a model for bubble detachment diameter by balancing the buoyancy and surface tension force acting on the bubble based on Fritz [85] model, ignoring other forces such as viscous drag and liquid inertial force. They found that the effect of wettability on bubble dynamics has been demonstrated experimentally on superhydrophilic surfaces and used the root term to express the effect of contact angle.
Suszko and El Genk [36] carried out experiments on smooth and rough copper surfaces under saturated boiling conditions with PF-5060 liquid and a heat flux of 0.5 W/cm2 . The surface roughness of the rough surfaces varied about 0.21-1.79 μm, and the roughness of the these surfaces varied isometrically at intervals of 0.039 μm. They derived correlations between bubble detachment diameter and bubble growth period for two surfaces. For the smooth surface Equation (34) and the rough surface Equation (35), the correlations predicted experimental data with errors of ±15% and ±8%, respectively.
Bovard et al.[86] conducted an experimental study of horizontal cylindrical heaters during pool boiling of pure liquids (e.g., water, ethanol, and acetone) with heat fluxes ranging from 10-100 kW/m2. They also considered heating rod materials such as aluminum, stainless steel 316A, copper and brass with different surface roughness from copper and aluminum (0.03-0.43μm). They used Buckingham’s π-theorem to derive the dimensionless correlation Equation (36) for the bubble departure diameter, taking into account the different forces acting on the growing bubbles according to the dimensionless parameters (e.g., Bond number, Capillary number, Jacob number, and heat diffusion coefficient), and the experimental data predicted error bands were less than ±15%. In the relation, the Capillary number , where denotes the kinetic viscosity, denotes the velocity of bubble motion, , , , , .
Kumar et al.[87] considered the effect of wall superheat and liquid properties through the Jacob, proposing that the gas density and latent heat in the Jacob partially incorporate the effect of system pressure, and expressing the effect of solid-liquid-gas interfacial interaction on bubble detachment through the term. Therefore, Kumar et al.[87] synthesized the role of the Jacob number index in the Cole [88] model and Du et al.[80] model, and the effect of contact angle in the Fritz [85] model and Phan et al.[83] model. A prediction equation applicable to nucleate boiling individual bubbles was proposed with the following constant , which ignored the effects of neighboring bubble interactions and lateral motion of the liquid. The model was able to obtain errors within 25% for 90% of the data in comparison with other experimental data.
Most of the above correlation equations consider the bubble force equilibrium, and the refinement of the force analysis will help more accurate detachment size prediction. Researchers usually enhance heat transfer by reducing the detachment radius in practice. Dong et al.[89] conducted experiments on microstructured and nanostructured surfaces and found that reducing the bubble departure diameter and increasing the departure frequency can accelerate the bubble departure since the nanostructures essentially retard bubble merging and prevent the formation of a vapor film on the surface. Wang et al.[90] fabricated a kind of thin liquid film with the help of nanoporous membranes, utilized the capillary force under the pore size to maintain the liquid film height, and controlled the bubble detachment size below the millimeter level by the very low liquid film height, and obtained an ultra-high critical heat flux of 1.85 kW/cm2. Lim et al.[91] on the other hand, obtain better heat transfer with the help of a matrix arrangement of hydrophobic patterns and hydrophilic surfaces, the bubble departure diameter and bubble location are controlled by the size and spacing of the patterns.
5. Bubble departure frequency
The bubble cycle period and bubble departure frequency are inverses of each other, and both of them are important bubble dynamics parameters affecting the boiling heat transfer coefficient. The bubble period is the time interval between the first nucleation and the second nucleation in the boiling process, which is usually divided into two parts: the bubble waiting period and the bubble growth period [92]. The bubble cycle is usually divided into two parts: the bubble waiting cycle and the bubble growth cycle. The frequency is usually measured by recording the total number of bubbles emerging from the cavity per unit time, the single-cavity bubble frequency during boiling can be expressed as:
5.1. Bubble growth period tg
The bubble growth period has a direct effect on the detachment frequency of bubbles and therefore has a significant impact on the boiling heat transfer. It is defined as the time interval between the start of bubble growth and the departure of the bubble from the same cavity on the heating surface, i.e., the time it takes for a bubble to grow from its initial size to its detachment size.
Zuber [77] presented a correlation for the bubble growth period by considering the bubble departure diameter, the liquid thermal diffusion coefficient and the dimensionless Jacob number. It is considered that the bubble growth period is proportional to the square of the bubble departure diameter with Equation (39), where b is an empirical constant whose size varies from 1 to .
Hatton and Hall[93] analyzed the Plesset and Zwick[71] ‘s expression for the bubble growth rate and considered Zuber [77] ‘s parameters. A new bubble growth period relation Equation (40) is proposed by eliminating the Jacob number and considering the cavity radius, which suggests that the bubble growth period is positively proportional to the square of the bubble departure diameter and the nucleation cavity radius:
Lee et al.[94] considered the growth period of bubbles is to be proportional to the Jacob, departure diameter and liquid density based on different boundary conditions and working fluids, and the bubble growth period is proposed to be:
5.2. Bubble waiting period tw
Another important parameter of bubble dynamics affecting the surface heat flux during nucleation boiling is the bubble waiting time. It is defined as the time interval between the detachment of the bubble and the start of next nucleation from the same cavity, representing the process by which the superheated wall activate nucleation site by natural convection. Han et al.[95] proposed an expression for the waiting period based on the guidelines of bubble nucleation and potential flow theory, and they obtained an explicit form Equation (42) for the waiting period by simplifying the temperature distribution equation. This relationship shows that the bubble waiting period decreases with increasing wall superheat for a certain cavity radius.
Hsu et al.[96] developed a detailed analysis of the relationship between cavity size and bubble waiting time for a given wall temperature. The exact radius value of the nucleation cavity in the experiment is difficult to be calculated. Thus they analyzed the fluid temperature line and bubble equilibrium temperature profile to obtain the minimum bubble waiting time, their model is shown in Equation (43).
Van Stralen et al.[97] established a relationship between the bubble waiting period and the bubble growth period for monolithic liquids, and they found that the bubble waiting period is about three times the bubble growth period in the same nucleation cavity, i.e.,:
5.3. Bubble departure frequency
The equations mentioned above for bubble growth period and waiting period show that the bubble departure frequency largely depends on the wall superheat, the fluid thermophysical properties, the angle of contact, the size of the cavity, and the interaction between neighboring bubbles. Jakob and Fritz [98] found an inverse relationship between bubble departure frequency and departure diameter in pool boiling experiments with water and liquid nitrogen. Jakob [99] assumed that the bubble growth period and the bubble waiting period satisfy a certain relationship and corrected it by adding factors such as the thermophysical properties and surface tension, thus the correlation Equation (45) was obtained.
Sakashita et al.[100] proposed a correlation of bubble departure frequency of high-pressure water on a rectangular plate at high heat flux, and their experiments observed that heat flux and pressure no longer have a significant effect on the detachment frequency at high heat flux, and gave a relation Equation (46) for the detachment frequency at this time. This expression includes the density property, kinematic viscosity property and surface tension, and the effect of the detachment radius on it was ignored.
Miglani et al.[63] conducted experiments on the surface of an inconel alloy during high-pressure pool boiling of the refrigerant R-134a, with heat fluxes ranging from 2.5 kW/m2 to 12 kW/m2. And a dimensionless correlation between the bubble generation frequency and the modified boiling point was proposed based on their experimental results and using a regression relation, as shown in Equation (47), where .
Hamzekhani et al.[101] established a correlation of bubble departure frequency from experimental data of pool boiling of water and NaCl solutions at low and medium heat fluxes at standard atmospheric pressure. The Buckingham’s π-theory were used to performed a dimensionless analysis for the influential parameters such as departure diameter, departure frequency, surface tension, gravitational acceleration, gas-liquid density difference, heat flux, etc. And three π-terms were obtained as shown in Equation (48).
Several researchers [102,103,104] proposed to use the form of to describe the relationship between the detachment frequency and the detachment radius of bubbles. Cole [102] analyzed the force balance between the buoyancy force and the drag force on the bubbles and derived the correlation equation of based on the experimental data. McFadden and Grassmann [103] supplemented the magnitude analysis for all dynamic variables, adopting 0.56 as an empirical constant in their experiments. Ivey [104] analyzed experimental observations on bubbles with different bubble detachment sizes and concluded that the value of the constant C should be taken as 0.90 when Dd < 3mm. Zhang et al.[105] compared three mentioned above correlations with boiling bubble data for different liquids and surface materials, which included R-113 on a glass surface [106] and water on the surface of 316SS stainless steel [107] , indium tin oxide (ITO) surfaces [108], copper metal surfaces [109,110] and metallic zirconium (Zr) surfaces [102]. The comparison results are shown in Figure 13a.
Zhang et al.[105] analyzed the heat transfer process in the bottom region of the boiling cycle, and proposed that the heat transfer leading to bubble re-growth consists of two parts, i.e., rewetting of the surrounding superheated liquid and heat conduction between the solid and the gas, which they model as transient heat conduction at a semi-infinite wall with convective boundary conditions and they got the correlation Equation (49), where , . Figure 13b shows the comparison between the predicted straight line of Equation (49) and the experimental value, the straight line is obtained by different physical properties of the wall and the liquid, and the experimental and predicted straight lines for the same conditions have the same color.
The above relational equations show that the bubble departure frequency is correlated with the bubble departure diameter in different forms, and the accurate prediction of the departure radius makes the prediction of the bubble departure frequency more difficult. In addition to the bubble detachment diameter, the bubble departure frequency is also affected by various surface properties and liquid properties. A better correlation formula may be obtained by a dimensionless analysis of parameters such as surface roughness, cavity dimensions, system pressure, and wall superheating conditions.
6. Boiling heat transfer coefficient h and heat flux q
Boiling heat transfer coefficient and boiling heat flux are the most important two parameters to measure heat transfer effect of the boiling process, the former determines the wall superheat at equilibrium, the latter determines the heat taken away per unit time. The traditional methods of measuring the heat flux of pool boiling mainly include the Joule effect method, and temperature gradient method and thermoelectric effect method, etc. [111] The Joule effect method utilizes the voltage and current applied to the heating element to directly calculate the heat flux, and is suitable for systems where the boiling surface area is larger [112]. The gradient method determines the boiling surface temperature gradient by measuring the temperature difference between solid layers and obtains a linear temperature distribution under steady state conditions, and the heat flux is calculated by Fourier’s law [113,114,115].The principle of the thermoelectric effect method, on the other hand, is that materials with anisotropic thermal conductivity generate an electric field with a transverse component in the main axis of the material when heat passes through it due to the Seebeck effect, thus enabling the heat flux to be obtained by detecting the electrical signal, which allows for the ultra-fast response and is suitable for transient heat flux measurements [116] . With the continuous development of Machine Learning, the image [117,118] and acoustic signals [119] of boiling are detected in order to develop a boiling heat flux measurement system with the aid of the Convolutional Neural Networks (CNNs)[120] and Multilayer Perceptron Neural Networks (MLPNNs) [121].
Accurate prediction equations for boiling heat transfer coefficient and heat flux can help us to predict the experimental heat transfer intensity in advance, as well as to verify the experimental results. Kim [122] reviewed bubble heat transfer models of pool boiling based on enhanced convection, transient conduction, microlayer evaporation, and three-phase line mechanisms, a large number of correlation formulas for determining boiling heat transfer coefficients based on experimental results and theoretical analyses were compiled. And Kim found that most of the heat transfer models were developed based on a combination of factors such as heat flux, pressure, geometrical dimensions, thermo-physical properties, and surface liquids. Mohanty et al.[123] also suggested that the accuracy of the equations was highly dependent on a proper and accurate mathematical description of the bubble behavior in reviewing the prediction equations for boiling heat transfer coefficients and heat flux.
6.1. Boiling heat transfer coefficient h
It is been widely recognized that predicting the boiling heat transfer coefficient through modelling theoretically or empirical relational equations from experimental data. And these correlations also reduce time and economic cost compared to measuring experimentally. Therefore, it is necessary to explore the boiling heat transfer coefficients(HTC) for various combinations of surfaces and liquids.
Jung et al.[124] conducted a pool boiling experiment on a horizontal smooth tube with an outer diameter of 19 mm with various refrigerants, such as CFC-123, CFC-11, HCFC-142b, HFC-134a, CFC-12, HCFC-22, HFC-125 and HFC-32. They reduced the heat flux from 80 kW/m2 to 10 kW/m2 isotropically decreasingly. The Equation (50) was proposed in based on their experimental data, which described the relationship between the boiling heat transfer coefficient and the bubble detachment diameter, the heat flux, the thermal diffusivity, the liquid saturation temperature and the thermophysical properties, where , pr and Tr respectively are the reduced pressure and the reduced temperature i.e., the ratios of the measured values to the critical values.
Jung et al.[125] investigated the experimental data of nucleate boiling pool with several flammable refrigerants such as propylene (R-1270), propane (R-290), isobutane (R-600a), butane (R-600), and dimethyl ether (RE-170), refined the Equation (50) and obtain Equation (51), which was found to agree with the experimental results within an error of ±5.3%.
Rao and Balakrishnan [126] carried out a pool boiling experiments on a 28.9 mm diameter aluminum block for acetone–isopropanol–water and ace-tone–MEK (Methyl Ethyl Ketone)–water ternary systems at atmospheric pressure and standard gravity conditions and proposed a new correlation i.e., Equation (52) to estimate mixture heat transfer coefficients in terms of an ideal heat transfer coefficient and a correction term, which is within 16% error compared to the experimental results. The equation includes the bubble detachment diameter, heat flux, thermal diffusivity, surface tension, pressure, surface roughness, and thermophysical properties of the fluid:
where , indicates the effect of wall physical properties and liquid physical properties on boiling.
Judd and Hwang [127] et al. proposed to divide the heated surface into bubble zones and natural convection zones and performed the calculation of convective heat transfer coefficient. Fazel and Mahboobbour [128] carried out further calculations on this theory and experimentally verified the saturated pool boiling of aqueous ethylene glycol solutions with different concentrations at atmospheric pressure. They assumed that the boiling surface maintains a uniform temperature and used Newton’s law of cooling to measure the boiling heat transfer to obtain Equation (53), where hnc is natural convective heat transfer coefficient affected by bubbles given by Mikic and Rohsenow [129]. This predicted equation is within 12% relative error compared to the experimental results.
6.2. Heat flux q
Models for the calculation of heat flux have also been developed by many researchers. Due to the perturbations caused by bubble generation and detachment, the boiling system usually be divided into different zones for the calculation of heat transfer, which can be mainly divided into the natural convection zone without bubble generation, the bubble zone, and the peripheral zone affected by the bubbles. Based on above assumption, Han and Griffth [130] expressed the total heat flux in terms of natural convective and transient heat transfer due to thermal boundary reconstruction. Mikic and Rohsenow [129] modified the Han and Griffth [130] model and the effect of heating characteristics was given extra thought. They developed a total heat flux that includes the heat flux of transient conduction and the heat flux of natural convection, where transient conduction is expressed in terms of bubble detachment diameter, nucleation site density, detachment frequency, wall superheat, and thermophysical properties of the fluid. Then Judd and Hwang [127] modified the Mikic and Rohsenow [129] thermal model by including the heat flux of evaporation from the micro-fluid layer at the bottom of the bubble and expressing it in terms of vapor volume, active nucleation site density, liquid density, latent heat of vaporization, and bubble detachment frequency. Paul and Abdel-Khalik [131], on the other hand, expressed the boiling heat flux by considering heat flux of phase change, natural convection and forced convection.
Yu and Cheng [132] modeled heat transfer in pool boiling based on the fractal distribution of nucleation locations on the boiling surface. On the computational model proposed by Mikic and Rohsenow [129], they divided the boiling heat flux density qtotal into phase change heat flux qb , micro-fluid layer evaporation heat flux qme and heat flux density qnc , and validated the model with the help of experimental data from Wang and Dhir at different contact angles [133]. The experimental data at different contact angles were verified and good agreement was obtained, and the expression of the total nucleation boiling heat flux is expressed in Equation (54).
Chu et al.[134] further analyzed the theoretical research proposed by Han and Griffith[130]. Then the heat transfer was further described combining the transient conduction heat flow qtc due to bubble thermal boundary reconstruction and the evaporation heat flux qme of the liquid micro-fluid layer. The weighted average distribution of bubble growth time and bubble waiting time was adopted for the two kinds of heat flux, and their new descriptive model is shown in Equation (55).
Sateesh et al.[135] proposed a modified model for pool boiling heat transfer considering the effect of sliding bubbles on the vertical heated surface. They used four different heat transfer mechanisms, i.e., latent heat of microlayer evaporation, transient conduction of thermal boundary reconstruction, natural convection, and vertical heated surface sliding bubble heat transfer, and the total heat flux was calculated as Equation (56), where the suffix of subscript s denotes the sliding bubbles and the superscript m denotes the modified model.
Kaniowski et al.[30] performed pool boiling experiments on microchannels of different heights and arrangements with Novec-649 at atmospheric pressure, visualization images of vapor bubbles were made, the diameters of bubble departure and the frequency of departure from the surface were measured. Based on the model of transient conduction proposed by Mikic and Rohsenow [129] and the model of natural convection proposed by Han and Griffth [130], the total heat flux can be determined ultimately from the relationship from Equation (57) to Equation (60), where β is the thermal expansion coefficient.
The proposed prediction models of Yu et al.[132] , Sateesh et al.[135] and Chu et al.[134] was compared with experimental data measured by Wang et al.[133], and the result is shown in Figure 14a by Mohanty et al.[123] The comparison shows that about 80% of the experimental data obtain within 25% of the error with the predictive models proposed by Yu et al.[132] and Sateesh et al.[135] while the Chu and Yu [134] exhibit a low degree of agreement with experimental data. Sateesh et al.[135] model is the best fit for the working conditions at high heat flux, and further validation was carried out by Mohanty et al.[123] The Figure 15b shows the results of the heat flux model given by Sateesh et al. in comparison with three different pool boiling heat flux experiments i.e., the pool boiling of water on the vertical surface which was conducted by Wang and Dhir [133], the pool boiling of R134a on the horizontal tube which was conducted by Barthu and Hahne [136], the pool boiling of propane on the horizontal tube surface which was conducted by Luke and Gorenflo [137]. As can be seen from the Figure 14b, Sateesh et al.[135] model has a prediction error within ±25% from the results of the three sets of experimental data.
It is well known that the relationship between the heat flux q and the heat transfer coefficient h is from Newton’s law of cooling. In the prediction of the heat transfer coefficient h and the heat flux q, if the wall superheat is known, it can be quickly through one quantity to get the value of the other, and the appropriate choice should be made according to the demand in relevant experiments.
In order to solve the heat transfer problem during boiling, many researchers [138,139,140] have attempted to solve the complex flow and heat transfer problems during boiling by means of Computational Fluid Dynamics (CFD). For the simulation of boiling processes by CFD, various bubble correlations can be used to check the accuracy of the simulation. Although CFD simulations have been very successful and widely used in predicting single-phase flows, their effectiveness for two-phase flows has not been fully realized [141], and CFD also has difficulty in accurately describing a variety of complex structural surfaces. For unstudied boiling cases, the difficulty of CFD modeling and the degree of similarity to other conditions should be weighed to decide whether to adopt mathematical formulation models or CFD models.
By reviewing various behaviors of bubbles in the boiling process, it can be found that the complexity and unpredictability of boiling mainly come from the complex coupling relationship between the mass transfer brought by bubble nucleation as well as growth, and the energy transfer brought by thermal convection as well as phase change. Besides, the parameters in the boiling process are changing from moment to moment, which affects and is affected by other bubble characteristic quantities.
7. Conclusions
In this work, the mechanism and mathematical correlations of each period of bubbles were reviewed and analyzed, the conclusions were made as follows:
(1) Whether bubbles can nucleate or not depends on the shape as well as size of the cavities on the surface, the wall wettability, and the wall superheat. And stronger heat transfer will activate more nucleation sites when the wall superheat rises. The detailed requirement for heat transfer coefficient or critical heat flux should be considered for the selection of wettability, e.g., hydrophilic walls lead to higher critical heat flux while hydrophobic walls require lower initial nucleation criteria. The density of active nucleation sites is affected by a variety of factors (e.g., cavity shape and size, wall wettability, heat flux, wall superheat, and system pressure), and the proposal of various complex reinforced surfaces requires improvement in the nucleation theory and the prediction of nucleation sites density.
(2) Bubbles in growth period and detachment period mainly are affected by the surface tension and the differential pressure between bubble inside and outside, and the former prevents the bubble detachment while the latter induces the bubble rise. The buoyancy force is also included in the internal and external differential pressure force as the effectiveness of pressure difference due to heights different. The force analysis of bubbles helps researchers determine the bubble detachment size better. This paper proposes that the influence of ambient pressure should also be considered for the force analysis, and the relevant calculation results can further explain the role of ambient pressure on the influence of boiling.
(3) The growth rate of bubbles is mainly determined by the liquid density , the latent heat hlv , the isobaric specific heat cpl , the surface tension , and the wall superheat . And the growth of bubbles mainly comes from the evaporation of heat transfer in the thermal boundary layer. Van Stralen’s [78] relaxation model can predict the bubble radius more accurately, but the bubble detachment diameter Dd is needed in advance. The bubble detachment radius ranges from micrometers to centimeters under different working conditions [105]. Currently, the common methods for predicting the radius of bubble detachment include the force analysis method [59] and dimensionless analysis [86].
(4) Most of the studies on the relational equations for the bubble detachment frequency f need to be calculated by the boiling heat transfer coefficient h or the heat flux q, which is contrary to the commonly expected need to calculate the heat transfer coefficient or the heat flux with the help of the bubble detachment frequency, so it is worthwhile to further study how to exclude these two parameters from the correlation equations, and replace them with other factors such as the wall superheat for calculation instead.
In the current study, the bubble dynamics correlations provided in the literature are always highly specific to the experimental data observed by themselves, and the agreement always reduce when these correlations are used to predict experimental data from other researchers. This is attributed to the fact that these correlations depend on a variety of influential parameters, which include the thermal physical properties of the fluid, contact angle, gravitational acceleration, bubble growth rate, bubble growth period, bubble waiting period, cavity dimensions, surface roughness, heat flux or wall superheat, system pressure, and so on. But usually, only some of the highly correlated factors were selected to make the correlation guess based on their own experimental data, and some other factors were ignored. Therefore, in order to obtain a universal correlation formula, it is necessary to conduct a full range of experiments and inferences, taking all factors into account, which requires a very sophisticated experimental design and a complex integration process. In actual engineering situations, the number of factors to be considered can be narrowed down to meet the actual needs as well as to reduce the cost, and the boiling enhancement study can be carried out in specific directions, for example, the heat transfer study on different wettability surfaces, liquid level heights, and other conditions.
Acknowledgments
This work has been supported by the National Natural Science Foundation of China (No. 52076185), the Natural Science Foundation of Zhejiang Province (No. LZ19E060001).
Abbreviations
| \Nomenclature | |||
| Abbreviations | Greek symbols | ||
| Ar | Archimedes number | thermal diffusivity(m2 s-1) | |
| Ca | Capillary number() | density(kg m-3) | |
| CL | lift-off coefficient | difference | |
| Cp | specific heat at constant pressure(J kg-1K-1) | dynamic viscosity (kg m-1s-1) | |
| Dd | bubble departure diameter (m) | kinematic viscosity (m2s-1) | |
| f | bubble departure frequency (s-1) | thermal boundary layer thickness (μm) | |
| Fb | buoyancy force(N) | surface tension (N m-1) | |
| Fdu | unsteady drag force(N) | contact angle (°) | |
| Fm | excess vapor pressure (N) | shape angle (°) | |
| Fp | liquid static pressure(N) | ||
| Fs | surface tension(N) | Superscripts | |
| g | gravitational acceleration(m s-2) | + | non-dimensional |
| h | heat transfer coefficient(W m-2 K-1) | ||
| H | height of liquid(m) | Subscripts | |
| hlv | latent heat of vaporization (J kg-1) | c | cavity |
| Ja | Jakob number() | d | bubble departure |
| k | thermal conductivity (W m-1 K-1) | l | liquid phase |
| Nu | Nusselt number | max | maximum |
| Ns | active nucleation site density (m-2) | me | microlayer evaporation |
| p | pressure (bar) | min | minimum |
| Pr | Prandtl number | nc | natural convection |
| q | heat flux (W m-2) | r | reduced property |
| Ra | surface roughness (μm) | sat | saturation condition |
| Rb | bubble radius (m) | tc | transient conduction |
| Rc | cavity radius (m) | s | heating surface |
| S | dimensionless surface parameter | v | vapor phase |
| T | temperature (K) | w | wall |
| t | time (s) | bulk | |
| tw | bubble waiting period (s) | ||
| tg | bubble growth period (s) | ||
| v | specific volume(m3 kg-1) | ||
References
- Wu, X.; Huang, J.; Zhuang, Y.; Liu, Y.; Yang, J.; Ouyang, H.; Han, X. Prediction Models of Saturated Vapor Pressure, Saturated Density, Surface Tension, Viscosity and Thermal Conductivity of Electronic Fluoride Liquids in Two-Phase Liquid Immersion Cooling Systems: A Comprehensive Review. Appl. Sci. 2023, 13, 4200. [Google Scholar] [CrossRef]
- Wu, X.; Li, C.; Yang, J.; Liu, Y.; Han, X. Theoretical and experimental research on flow boiling heat transfer in microchannels for IGBT modules. Int. J. Heat Mass Transf. 2023, 205. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, M.; Jiang, Y.; Liu, J. Two-stage multichannel liquid–metal cooling system for thermal management of high-heat-flux-density chip array. Energy Convers. Manag. 2022, 259, 115591. [Google Scholar] [CrossRef]
- Sun, Y.; Tang, Y.; Zhang, S.; Yuan, W.; Tang, H. A review on fabrication and pool boiling enhancement of three-dimensional complex structures. Renew. Sustain. Energy Rev. 2022, 162. [Google Scholar] [CrossRef]
- Chu, H.; Yu, X.; Jiang, H.; Wang, D.; Xu, N. Progress in enhanced pool boiling heat transfer on macro- and micro-structured surfaces. Int. J. Heat Mass Transf. 2023, 200. [Google Scholar] [CrossRef]
- Kang, D.; Lee, J.; Chakraborty, A.; Lee, S.-E.; Kim, G.; Yu, C. Recent Advances in Two-Phase Immersion Cooling with Surface Modifications for Thermal Management. Energies 2022, 15, 1214. [Google Scholar] [CrossRef]
- Pham, M.; Bois, G.; Francois, F.; Baglietto, E. Assessment of State-of-the-art multiphase CFD modeling for subcooled flow boiling in reactor applications. Nucl. Eng. Des. 2023, 411. [Google Scholar] [CrossRef]
- Kuczyński, W.; Charun, H.; Piątkowski, P.; Bałasz, B.; Chliszcz, K. A regressive model for dynamic impulsive instabilities during the condensation of R134a, R1234ze(E) and R1234yf refrigerants. Int. J. Heat Mass Transf. 2021, 169, 120963. [Google Scholar] [CrossRef]
- Liu, Y.; Bao, K.; Yan, Y.; Ouyang, H.; Han, X. Investigation on the influence of different heat transmission distances on thermo-hydrodynamic characteristics of pulsating heat pipes. Appl. Therm. Eng. 2023, 234. [Google Scholar] [CrossRef]
- Wei, R.; Hu, C.; Yang, J.; Wu, F.; Hu, J.; Li, F.; Li, C. Pressure-drop characteristics of CO2 boiling flow in the regenerative-cooling channel of an Mg/CO2 powder rocket engine for Mars missions. Acta Astronaut. 2022, 199, 153–160. [Google Scholar] [CrossRef]
- Wang, Y.; Li, C.; Wen, X.; Cai, W.; Jiang, Y.; Wen, C.; Wang, Y.; Hu, L.; Yu, H.; Zhu, H.; et al. Experimental studies on two-phase immersion liquid cooling for Li-ion battery thermal management. J. Energy Storage 2023, 72. [Google Scholar] [CrossRef]
- Narumanchi, S.; Troshko, A.; Bharathan, D.; Hassani, V. Numerical simulations of nucleate boiling in impinging jets: Applications in power electronics cooling. Int. J. Heat Mass Transf. 2008, 51, 1–12. [Google Scholar] [CrossRef]
- Birbarah, P.; Gebrael, T.; Foulkes, T.; Stillwell, A.; Moore, A.; Pilawa-Podgurski, R.; Miljkovic, N. Water immersion cooling of high power density electronics. Int. J. Heat Mass Transf. 2019, 147, 118918. [Google Scholar] [CrossRef]
- Fan, S.; Duan, F. A review of two-phase submerged boiling in thermal management of electronic cooling. Int. J. Heat Mass Transf. 2020, 150, 119324. [Google Scholar] [CrossRef]
- Mahmoud, M.; Karayiannis, T. Pool boiling review: Part I – Fundamentals of boiling and relation to surface design. Therm. Sci. Eng. Prog. 2021, 25, 101024. [Google Scholar] [CrossRef]
- Ghazivini, M.; Hafez, M.; Ratanpara, A.; Kim, M. A review on correlations of bubble growth mechanisms and bubble dynamics parameters in nucleate boiling. J. Therm. Anal. Calorim. 2021, 147, 6035–6071. [Google Scholar] [CrossRef]
- Hasan, M.N.; Monde, M.; Mitsutake, Y. Lower limit of homogeneous nucleation boiling explosion for water. Int. J. Heat Mass Transf. 2011, 54, 3226–3233. [Google Scholar] [CrossRef]
- Nimkar, N.D.; Bhavnani, S.H.; Jaeger, R.C. Effect of nucleation site spacing on the pool boiling characteristics of a structured surface. Int. J. Heat Mass Transf. 2006, 49, 2829–2839. [Google Scholar] [CrossRef]
- Salla, J.; Demichela, M.; Casal, J. BLEVE: A new approach to the superheat limit temperature. J. Loss Prev. Process. Ind. 2006, 19, 690–700. [Google Scholar] [CrossRef]
- Zhao, Z.; Glod, S.; Poulikakos, D. Pressure and power generation during explosive vaporization on a thin-film microheater. Int. J. Heat Mass Transf. 2000, 43, 281–296. [Google Scholar] [CrossRef]
- Li, J.; Peterson, G.; Cheng, P. Mechanical nonequilibrium considerations in homogeneous bubble nucleation for unsteady-state boiling. Int. J. Heat Mass Transf. 2005, 48, 3081–3096. [Google Scholar] [CrossRef]
- Islam, A.; Monde, M.; Woodfield, P.L.; Mitsutake, Y. Jet impingement quenching phenomena for hot surfaces well above the limiting temperature for solid–liquid contact. Int. J. Heat Mass Transf. 2008, 51, 1226–1237. [Google Scholar] [CrossRef]
- Petersen, K.; Rahbarimanesh, S.; Brinkerhoff, J. Progress in physical modelling and numerical simulation of phase transitions in cryogenic pool boiling and cavitation. Appl. Math. Model. 2023, 116, 327–349. [Google Scholar] [CrossRef]
- Bankoff, S.G. Entrapment of gas in the spreading of a liquid over a rough surface. AIChE J. 1958, 4, 24–26. [Google Scholar] [CrossRef]
- Cornwell, K. On boiling incipience due to contact angle hysteresis. Int. J. Heat Mass Transf. 1982, 25, 205–211. [Google Scholar] [CrossRef]
- Hsu, Y. On the Size Range of Active Nucleation Sites on a Heating Surface. Journal of Heat Transfer 1962, 207–213. [Google Scholar] [CrossRef]
- Qi, Y.; Klausner, J.F. Heterogeneous nucleation with artificial cavities. Journal of Heat Transfer 2005, 127, 1189–1196. [Google Scholar] [CrossRef]
- Liu, X.; Zou, Q.; Yang, R. Theoretical analysis of bubble nucleation in liquid film boiling. Int. J. Heat Mass Transf. 2022, 192. [Google Scholar] [CrossRef]
- Iyer, S.; Kumar, A.; Coventry, J.; Lipiński, W. Modelling of bubble growth and detachment in nucleate pool boiling. Int. J. Therm. Sci. 2023, 185. [Google Scholar] [CrossRef]
- Kaniowski, R.; Pastuszko, R. Pool boiling experiment with Novec-649 in microchannels for heat flux prediction. Exp. Therm. Fluid Sci. 2023, 141. [Google Scholar] [CrossRef]
- Nam, Y.; Aktinol, E.; Dhir, V.K.; Ju, Y.S. Single bubble dynamics on a superhydrophilic surface with artificial nucleation sites. Int. J. Heat Mass Transf. 2011, 54, 1572–1577. [Google Scholar] [CrossRef]
- Hiroto Sakashita, T.K. Method for predicting boiling curves of saturated nucleate boiling. International Journal of Heat and Mass Transfer 2001, 44, 673–682. [Google Scholar] [CrossRef]
- Hsu, Y.Y.; Graham, R.W. .An analytical and experimental study of the thermal boundary layer & ebullition cycle in nucleate boiling[J], 1961.
- Xiao, B.; Jiang, G.; Zheng, D.; Chen, L.; Liu, B. Calculation of Active Nucleation Site Density in Boiling Systems. Res. J. Appl. Sci. Eng. Technol. ` 2013, 6, 587–592. [Google Scholar] [CrossRef]
- Wang, C.H.; Dhir, V.K. Effect of Surface Wettability on Active Nucleation Site Density During Pool Boiling of Water on a Vertical Surface. ASME Journal of Heat and Mass Transfer 1993, 115, 659–669. [Google Scholar] [CrossRef]
- Suszko, A.; El-Genk, M.S. Saturation boiling of PF-5060 on rough Cu surfaces: Bubbles transient growth, departure diameter and detachment frequency. Int. J. Heat Mass Transf. 2015, 91, 363–373. [Google Scholar] [CrossRef]
- Bourdon, B.; Di Marco, P.; Rioboo, R.; Marengo, M.; De Coninck, J. Enhancing the onset of pool boiling by wettability modification on nanometrically smooth surfaces. Int. Commun. Heat Mass Transf. 2013, 45, 11–15. [Google Scholar] [CrossRef]
- Jo, H.; Ahn, H.S.; Kang, S.; Kim, M.H. A study of nucleate boiling heat transfer on hydrophilic, hydrophobic and heterogeneous wetting surfaces. Int. J. Heat Mass Transf. 2011, 54, 5643–5652. [Google Scholar] [CrossRef]
- Mahmoud, M.; Karayiannis, T. Pool boiling review: Part II – Heat transfer enhancement. Therm. Sci. Eng. Prog. 2021, 25, 101023. [Google Scholar] [CrossRef]
- Hsu, C.-C.; Lee, M.-R.; Wu, C.-H.; Chen, P.-H. Effect of interlaced wettability on horizontal copper cylinders in nucleate pool boiling. Appl. Therm. Eng. 2017, 112, 1187–1194. [Google Scholar] [CrossRef]
- Jo, H.; Kaviany, M.; Kim, S.H.; Kim, M.H. Heterogeneous bubble nucleation on ideally-smooth horizontal heated surface. Int. J. Heat Mass Transf. 2014, 71, 149–157. [Google Scholar] [CrossRef]
- Shi, J.; Feng, D.; Chen, Z.; Ma, Q. Numerical study of a hybrid thermal lattice Boltzmann method for pool boiling heat transfer on a modeled hydrophilic metal foam surface. Appl. Therm. Eng. 2023, 229. [Google Scholar] [CrossRef]
- Wang, X.; Xu, J.; Jiang, H.; Liu, Y.; Li, X.; Shan, D.; Guo, B. Achieving robust and enhanced pool boiling heat transfer using micro–nano multiscale structures. Appl. Therm. Eng. 2023, 227. [Google Scholar] [CrossRef]
- Lv, Z.; An, Y.; Huang, C. Enhanced pool boiling heat transfer by adding metalized diamond in copper porous materials. Appl. Therm. Eng. 2023, 226. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, Y.; Ni, L.; Jiang, J.; Yu, Y.; Pan, Y.; Zhu, Z. Fabrication of tungstate metal foams as efficient catalysts for dimethyl sulfoxide oxidation in a microreactor. J. Ind. Eng. Chem. 2024, 129, 445–455. [Google Scholar] [CrossRef]
- Klausner, J.; Mei, R.; Bernhard, D.; Zeng, L. Vapor bubble departure in forced convection boiling. Int. J. Heat Mass Transf. 1993, 36, 651–662. [Google Scholar] [CrossRef]
- Van Helden WG, J.; Van Der Geld CW, M.; Boot PG, M. Forces on bubbles growing and detaching in flow along a vertical wall. International Journal of Heat and Mass Transfer 1995, 38, 2075–2088. [Google Scholar] [CrossRef]
- Mei, R.; Klausner, J.F. Unsteady force on a spherical bubble at finite Reynolds number with small fluctuations in the free-stream velocity. Phys. Fluids A: Fluid Dyn. 1992, 4, 63–70. [Google Scholar] [CrossRef]
- Auton, T.R. The lift force on a spherical body in a rotational flow. J. Fluid Mech. 1987, 183, 199–218. [Google Scholar] [CrossRef]
- Thorncroft, G.E.; Klausner, J.F. BUBBLE FORCES AND DETACHMENT MODELS. Multiph. Sci. Technol. 2001, 13, 42. [Google Scholar] [CrossRef]
- Jiang, Y.Y.; Osada, H.; Inagaki, M.; Horinouchi, N. Dynamic modeling on bubble growth, detachment and heat transfer for hybrid-scheme computations of nucleate boiling. Int. J. Heat Mass Transf. 2013, 56, 640–652. [Google Scholar] [CrossRef]
- Xueli Wang a B Z W B, Jinjia Wei C a, Bengt Sundén. Correlations for prediction of the bubble departure radius on smooth flat surface during nucleate pool boiling. International Journal of Heat and Mass Transfer 2019, 132, 699–714. [Google Scholar] [CrossRef]
- Bhati, J.; Paruya, S. Numerical simulation of bubble dynamics in pool boiling at heated surface. Int. J. Heat Mass Transf. 2020, 152. [Google Scholar] [CrossRef]
- Paruya, S.; Bhati, J.; Akhtar, F. Numerical model of bubble shape and departure in nucleate pool boiling. Int. J. Heat Mass Transf. 2021, 180, 121756. [Google Scholar] [CrossRef]
- Iyer, S.; Kumar, A.; Coventry, J.; Lipiński, W. Mechanistic modelling of bubble growth in sodium pool boiling. Appl. Math. Model. 2023, 117, 336–358. [Google Scholar] [CrossRef]
- Beer, H.; Best, R.; Hahne, H.; et al. Nucleate Boiling: Bubble Growth and Dynamics. Heat Transfer in Boiling 1977, 21–52. [Google Scholar]
- Bucci, M.; Buongiorno, J.; Bucci, M. The not-so-subtle flaws of the force balance approach to predict the departure of bubbles in boiling heat transfer. Physics of Fluids 2021, 33. [Google Scholar] [CrossRef]
- Lima, S.F. Using surface integrals for checking Archimedes’ law of buoyancy. European Journal of Physics 2012, 33, 101–113. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Y.; Fei, G.; Zhou, T.; Zhao, C. Effects of surface wettability on bubble departure and critical heat flux: A parametric study based on 3-D dynamic force analysis model. Int. J. Therm. Sci. 2023, 186. [Google Scholar] [CrossRef]
- Kopchikov, I.A.; Voronin, G.I.; Kolach, T.A.; et al. Liquid boiling in a thin film. International Journal of Heat and Mass Transfer 1969, 12, 791–796. [Google Scholar] [CrossRef]
- Labuntsov, D. Study of the growth of bubbles during boiling of saturated water within a wide range of pressures by means of high-speed moving pictures. Teplofizika Vysokikh Temperatur 1964, 2, 446–453. [Google Scholar]
- Akiyama, M.; Tachibana, H.; Ogawa, N. Effects of system pressure on bubble growth rate. Trans, JSME 1969, 35, e126. [Google Scholar]
- Miglani, A.; Joo, D.; Basu, S.; Kumar, R. Nucleation dynamics and pool boiling characteristics of high pressure refrigerant using thermochromic liquid crystals. Int. J. Heat Mass Transf. 2013, 60, 188–200. [Google Scholar] [CrossRef]
- Gao, W.; Qi, J.; Yang, X.; Zhang, J.; Wu, D. Experimental investigation on bubble departure diameter in pool boiling under sub-atmospheric pressure. Int. J. Heat Mass Transf. 2019, 134, 933–947. [Google Scholar] [CrossRef]
- Mahmoud, M.; Karayiannis, T. Bubble growth on a smooth metallic surface at atmospheric and sub-atmospheric pressure. Int. J. Heat Mass Transf. 2023, 209. [Google Scholar] [CrossRef]
- Mahmoud, M.; Karayiannis, T. Bubble growth models in saturated pool boiling of water on a smooth metallic surface: Assessment and a new recommendation. Int. J. Heat Mass Transf. 2023, 208. [Google Scholar] [CrossRef]
- Sernas, V.; Hooper, F.C. The initial vapor bubble growth on a heated wall during nucleate boiling. International Journal of Heat and Mass Transfer 1969, 12, 1627–1630. [Google Scholar] [CrossRef]
- Forster, H.K.; Zuber, N. Growth of a Vapor Bubble in a Superheated Liquid. J. Appl. Phys. 1954, 25, 474–478. [Google Scholar] [CrossRef]
- Plesset, M.S.; Zwick, S.A. The Growth of Vapor Bubbles in Superheated Liquids. J. Appl. Phys. 1954, 25, 493–500. [Google Scholar] [CrossRef]
- Fritz, W.; Ende, W. Über den verdampfungsvorgang nach kinematographischen aufnahmen an dampfblasen. Physikalische Zeitschrift Der Sowjetunion 1936, 37, 391–401. [Google Scholar]
- Plesset, M.S.; Zwick, S.A. The Growth of Vapor Bubbles in Superheated Liquids. J. Appl. Phys. 1954, 25, 493–500. [Google Scholar] [CrossRef]
- Forster, H.K.; Zuber, N. Growth of a Vapor Bubble in a Superheated Liquid. J. Appl. Phys. 1954, 25, 474–478. [Google Scholar] [CrossRef]
- Scriven, L. On the dynamics of phase growth. Chem. Eng. Sci. 1959, 10, 1–13. [Google Scholar] [CrossRef]
- Avdeev, A.A.; Zudin, Y.B. Inertial-thermal governed vapor bubble growth in highly superheated liquid. Heat Mass Transf. 2005, 41, 855–863. [Google Scholar] [CrossRef]
- Mikic, B.B.; Rohsenow, W.M.; Griffith, P. On bubble growth rates. International Journal of Heat and Mass Transfer 1970, 13, 657–666. [Google Scholar] [CrossRef]
- Strenge, P.H.; Orell, A.; Westwater, J.W. Microscopic study of bubble growth during nucleate boiling. AIChE Journal 1961, 7, 578–583. [Google Scholar] [CrossRef]
- Zuber, N. The dynamics of vapor bubbles in nonuniform temperature fields. Int. J. Heat Mass Transf. 1961, 2, 83–98. [Google Scholar] [CrossRef]
- Van Stralen, S. The mechanism of nucleate boiling in pure liquids and in binary mixtures—part I. Int. J. Heat Mass Transf. 1966, 9, 995–1020. [Google Scholar] [CrossRef]
- Cole, R.; Shulman, H.L. Bubble growth rates at high Jakob numbers. International Journal of Heat and Mass Transfer 1966, 9, 1377–1390. [Google Scholar] [CrossRef]
- Du, J.; Zhao, C.; Bo, H. A modified model for bubble growth rate and bubble departure diameter in nucleate pool boiling covering a wide range of pressures. Appl. Therm. Eng. 2018, 145, 407–415. [Google Scholar] [CrossRef]
- Benjamin, R.; Balakrishnan, A. Nucleate pool boiling heat transfer of pure liquids at low to moderate heat fluxes. Int. J. Heat Mass Transf. 1996, 39, 2495–2504. [Google Scholar] [CrossRef]
- Alavi Fazel, S.A.; Shafaee, S.B. Bubble dynamics for nucleate pool boiling of electrolyte solutions[J], 2010.
- Phan, H.T.; Caney, N.; Marty, P.; Colasson, S.; Gavillet, J. A model to predict the effect of contact angle on the bubble departure diameter during heterogeneous boiling. Int. Commun. Heat Mass Transf. 2010, 37, 964–969. [Google Scholar] [CrossRef]
- Nam, Y.; Aktinol, E.; Dhir, V.K.; Ju, Y.S. Single bubble dynamics on a superhydrophilic surface with artificial nucleation sites. Int. J. Heat Mass Transf. 2011, 54, 1572–1577. [Google Scholar] [CrossRef]
- Friz, W. Maximum volume of vapor bubbles. Phys. Z. 1935, 36, 379–354. [Google Scholar]
- Bovard, S.; Asadinia, H.; Hosseini, G.; Fazel, S.A.A. Investigation and experimental analysis of the bubble departure diameter in pure liquids on horizontal cylindrical heater. Heat Mass Transf. 2016, 53, 1199–1210. [Google Scholar] [CrossRef]
- Kumar, N.; Ghosh, P.; Shukla, P. Development of an approximate model for the prediction of bubble departure diameter in pool boiling of water. Int. Commun. Heat Mass Transf. 2021, 127, 105531. [Google Scholar] [CrossRef]
- Cole, R. Bubble frequencies and departure volumes at subatmospheric pressures. AIChE J. 1967, 13, 779–783. [Google Scholar] [CrossRef]
- Dong, L.; Quan, X.; Cheng, P. An experimental investigation of enhanced pool boiling heat transfer from surfaces with micro/nano-structures. Int. J. Heat Mass Transf. 2014, 71, 189–196. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, R. Ultrahigh Flux Thin Film Boiling Heat Transfer Through Nanoporous Membranes. Nano Lett. 2018, 18, 3096–3103. [Google Scholar] [CrossRef]
- Lim, D.Y.; Bang, I.C. Controlled bubble departure diameter on biphilic surfaces for enhanced pool boiling heat transfer performance. International Journal of Heat and Mass Transfer 2020, 150, 119360. [Google Scholar] [CrossRef]
- Marie, A.; Cioulachtjian, S.; Lips, S.; Sartre, V. Thermal interactions between nucleation sites and the solid wall during pool boiling of a pure fluid: A review. Int. J. Therm. Sci. 2022, 174, 107388. [Google Scholar] [CrossRef]
- Hatton, A.P.; Hall, I.S. Photographic study of boiling on prepared surfaces. Proc. 3rd int. heat transfer conf. Aiche Journal 1966, 4, 24–37. [Google Scholar]
- Lee, H.C.; Oh, B.D.; Bae, S.W.; et al. Single bubble growth in saturated pool boiling on a constant wall temperature surface. International Journal of Multiphase Flow 2003, 29, 1857–1874. [Google Scholar] [CrossRef]
- Chi-Yeh H, Griffith, Peter The mechanism of heat transfer in nucleate pool boiling. International Journal of Heat and Mass Transfer 1965, 8, 887–904. [CrossRef]
- Hsu, Y.Y.; Graham, R.W. Transport Processes in Boiling and Two-Phase Systems[J], 1986.
- Van Stralen S J D, Sohal M S, Cole R; et al. Bubble growth rates in pure and binary systems: Combined effect of relaxation and evaporation microlayers. International Journal of Heat and Mass Transfer 1975, 18, 453–467.
- Jakob, M.; Fritz, W. Versuche über den Verdampfungsvorgang. Forschung auf dem Gebiet des Ingenieurwesens A 1931, 2, 435–447. [Google Scholar] [CrossRef]
- Jakob, M. Heat Transfer, Chapter 29, 1: New York: Wiley and Sons, 1949.
- Sakashita, H.; Ono, A. Boiling behaviors and critical heat flux on a horizontal plate in saturated pool boiling of water at high pressures. Int. J. Heat Mass Transf. 2009, 52, 744–750. [Google Scholar] [CrossRef]
- Hamzekhani, S.; Falahieh, M.M.; Kamalizadeh, M.R.; Nazari, Z. Experimental study on bubble departure frequency for pool boiling of water/NaCl solutions. Heat Mass Transf. 2015, 51, 1313–1320. [Google Scholar] [CrossRef]
- Cole, R. A photographic study of pool boiling in the region of the critical heat flux. AIChE J. 1960, 6, 533–538. [Google Scholar] [CrossRef]
- McFadden, P.; Grassmann, P. The relation between bubble frequency and diameter during nucleate pool boiling. Int. J. Heat Mass Transf. 1962, 5, 169–173. [Google Scholar] [CrossRef]
- Ivey, H.J. Relationships between bubble frequency, departure diameter and rise velocity in nucleate boiling. International Journal of Heat and Mass Transfer 1967, 10, 1023–1040. [Google Scholar] [CrossRef]
- Zhang, L.; Gong, S.; Lu, Z.; Cheng, P.; Wang, E.N. A unified relationship between bubble departure frequency and diameter during saturated nucleate pool boiling. Int. J. Heat Mass Transf. 2020, 165, 120640. [Google Scholar] [CrossRef]
- Kim, J.; Kim, M.H. On the departure behaviors of bubble at nucleate pool boiling. International Journal of Multiphase Flow 2006, 32, 1269–1286. [Google Scholar] [CrossRef]
- Goel, P.; Nayak, A.K.; Kulkarni, P.P.; Joshi, J.B. Experimental study on bubble departure characteristics in subcooled nucleate pool boiling. Int. J. Multiph. Flow 2017, 89, 163–176. [Google Scholar] [CrossRef]
- Gerardi C, Buongiorno J, Hu L-W; et al. Measurement of nucleation site density, bubble departure diameter and frequency in pool boiling of water using high-speed infrared and optical cameras[J], 2009.
- Han, C.-Y. The mechanism of heat transfer in nucleate pool boiling[D]. Massachusetts Institute of Technology, 1962.
- Chang, Y.; Ferng, Y. Experimental investigation on bubble dynamics and boiling heat transfer for saturated pool boiling and comparison data with previous works. Appl. Therm. Eng. 2019, 154, 284–293. [Google Scholar] [CrossRef]
- Sapozhnikov, S.Z.; Mityakov, V.Y.; Mityakov, A.V. Heatmetry: The science and practice of heat flux measurement[M]. Springer Nature, 2020.
- McHale, J.P.; Garimella, S.V. Nucleate boiling from smooth and rough surfaces – Part 1: Fabrication and characterization of an optically transparent heater–sensor substrate with controlled surface roughness. Exp. Therm. Fluid Sci. 2012, 44, 456–467. [Google Scholar] [CrossRef]
- Cao, Z.; Wu, Z.; Sundén, B. Heat transfer prediction and critical heat flux mechanism for pool boiling of NOVEC-649 on microporous copper surfaces. Int. J. Heat Mass Transf. 2019, 141, 818–834. [Google Scholar] [CrossRef]
- Upadhyay, A.; Kumar, B.; Kumar, N.; Raj, R. Simultaneous enhancement of critical heat flux and heat transfer coefficient via in-situ deposition of ionic liquids during pool boiling. Int. J. Heat Mass Transf. 2023, 208. [Google Scholar] [CrossRef]
- Yu, X.; Xu, N.; Yu, S.; Han, Y.; Chu, H. Effect of orthogonal channel structure on the heat transfer in pool boiling and its heat flux prediction model. Int. J. Therm. Sci. 2023, 187. [Google Scholar] [CrossRef]
- Konopko, L.A.; Nikolaeva, A.A.; Huber, T.E.; Kobylianskaya, A.K. Miniaturized Heat-Flux Sensor Based on a Glass-Insulated Bi–Sn Microwire. Semiconductors 2019, 53, 662–666. [Google Scholar] [CrossRef]
- Rassoulinejad-Mousavi, S.M.; Al-Hindawi, F.; Soori, T.; Rokoni, A.; Yoon, H.; Hu, H.; Wu, T.; Sun, Y. Deep learning strategies for critical heat flux detection in pool boiling. Appl. Therm. Eng. 2021, 190, 116849. [Google Scholar] [CrossRef]
- Suh, Y.; Bostanabad, R.; Won, Y. Deep learning predicts boiling heat transfer. Sci. Rep. 2021, 11, 1–10. [Google Scholar] [CrossRef]
- Barathula, S.; Chaitanya, S.; Srinivasan, K. Evaluation of machine learning models in the classification of pool boiling regimes up to critical heat flux based on boiling acoustics. Int. J. Heat Mass Transf. 2023, 201. [Google Scholar] [CrossRef]
- Dunlap, C.; Pandey, H.; Weems, E.; Hu, H. Nonintrusive heat flux quantification using acoustic emissions during pool boiling. Appl. Therm. Eng. 2023, 228. [Google Scholar] [CrossRef]
- Hobold, G.M.; da Silva, A.K. Visualization-based nucleate boiling heat flux quantification using machine learning. Int. J. Heat Mass Transf. 2019, 134, 511–520. [Google Scholar] [CrossRef]
- Kim, J. Review of nucleate pool boiling bubble heat transfer mechanisms. Int. J. Multiph. Flow 2009, 35, 1067–1076. [Google Scholar] [CrossRef]
- Mohanty, R.L.; Das, M.K. A critical review on bubble dynamics parameters influencing boiling heat transfer. Renewable and Sustainable Energy Reviews 2017, 78, 466–494. [Google Scholar] [CrossRef]
- Jung, D.; Kim, Y.; Ko, Y.; Song, K. Nucleate boiling heat transfer coefficients of pure halogenated refrigerants. Int. J. Refrig. 2003, 26, 240–248. [Google Scholar] [CrossRef]
- Jung, D.; Lee, H.; Bae, D.; Oho, S. Nucleate boiling heat transfer coefficients of flammable refrigerants. Int. J. Refrig. 2004, 27, 409–414. [Google Scholar] [CrossRef]
- Rao, G.V.; Balakrishnan, A. Heat transfer in nucleate pool boiling of multicomponent mixtures. Experimental Thermal and Fluid Science 2004, 29, 87–103. [Google Scholar]
- Judd, R.L.; Hwang, K.S. A Comprehensive Model for Nucleate Pool Boiling Heat Transfer Including Microlayer Evaporation. Journal of Heat Transfer 1976, 98, 623–629. [Google Scholar] [CrossRef]
- Fazel, S.A.; Mahboobpour, M. Pool boiling heat transfer in monoethyleneglycol aqueous solutions. Exp. Therm. Fluid Sci. 2013, 48, 177–183. [Google Scholar] [CrossRef]
- Mikic, B.B.; Rohsenow, W.M. A New Correlation of Pool-Boiling Data Including the Effect of Heating Surface Characteristics. J. Heat Transf. 1969, 91, 245–250. [Google Scholar] [CrossRef]
- Han, C.; Griffith, P. The Mechanism of Heat Transfer in Nucleate Pool Boiling Part L. International Journal of Heat and Mass Transfer 1965, 8, 887–903. [Google Scholar]
- Paul, D.D.; Abdel-Khalik, S.I. A statistical analysis of saturated nucleate boiling along a heated wire. International Journal of Heat and Mass Transfer 1983, 26, 509–519. [Google Scholar] [CrossRef]
- Yu, B.; Cheng, P. A Fractal Model for Nucleate Pool Boiling Heat Transfer. J. Heat Transf. 2002, 124, 1117–1124. [Google Scholar] [CrossRef]
- Wang, C.H.; Dhir, V.K. Effect of Surface Wettability on Active Nucleation Site Density During Pool Boiling of Water on a Vertical Surface. Journal of Heat Transfer 1993, 115, 659–669. [Google Scholar] [CrossRef]
- Chu, H.; Yu, B. A new comprehensive model for nucleate pool boiling heat transfer of pure liquid at low to high heat fluxes including CHF. Int. J. Heat Mass Transf. 2009, 52, 4203–4210. [Google Scholar] [CrossRef]
- Sateesh, G.; Das, S.K.; Balakrishnan, A. Analysis of pool boiling heat transfer: effect of bubbles sliding on the heating surface. Int. J. Heat Mass Transf. 2005, 48, 1543–1553. [Google Scholar] [CrossRef]
- Barthau, G.; Hahne, E. Nucleation site density and heat transfer in nucleate pool boiling of refrigerant R 134a in a wide pressure range[C]. 3rd European thermal sciences conference (Heidelberg, 10-13 September 2000), 2000: 731-736.
- Luke, A.; Gorenflo, D. Heat transfer and size distribution of active nucleation sites in boiling propane outside a tube. Int. J. Therm. Sci. 2000, 39, 919–930. [Google Scholar] [CrossRef]
- Zueter, A.F.; Tareen, M.S.; Newman, G.; Sasmito, A.P. Dynamic CFD modeling coupled with heterogeneous boiling for deep two phase closed thermosyphons in artificial ground freezing. Int. J. Heat Mass Transf. 2023, 203. [Google Scholar] [CrossRef]
- Yan, P.; Jin, H.; He, G.; Guo, X.; Ma, L.; Yang, S.; Zhang, R. CFD simulation of hydrodynamics in a high-pressure bubble column using three optimized drag models of bubble swarm. Chem. Eng. Sci. 2019, 199, 137–155. [Google Scholar] [CrossRef]
- Mohammed, H.I.; Giddings, D.; Walker, G.S. CFD simulation of a concentrated salt nanofluid flow boiling in a rectangular tube. Int. J. Heat Mass Transf. 2018, 125, 218–228. [Google Scholar] [CrossRef]
- Kharangate, C.R.; Mudawar, I. Review of computational studies on boiling and condensation. Int. J. Heat Mass Transf. 2017, 108, 1164–1196. [Google Scholar] [CrossRef]
Figure 1.
Various stages of bubbles in pool boiling process.
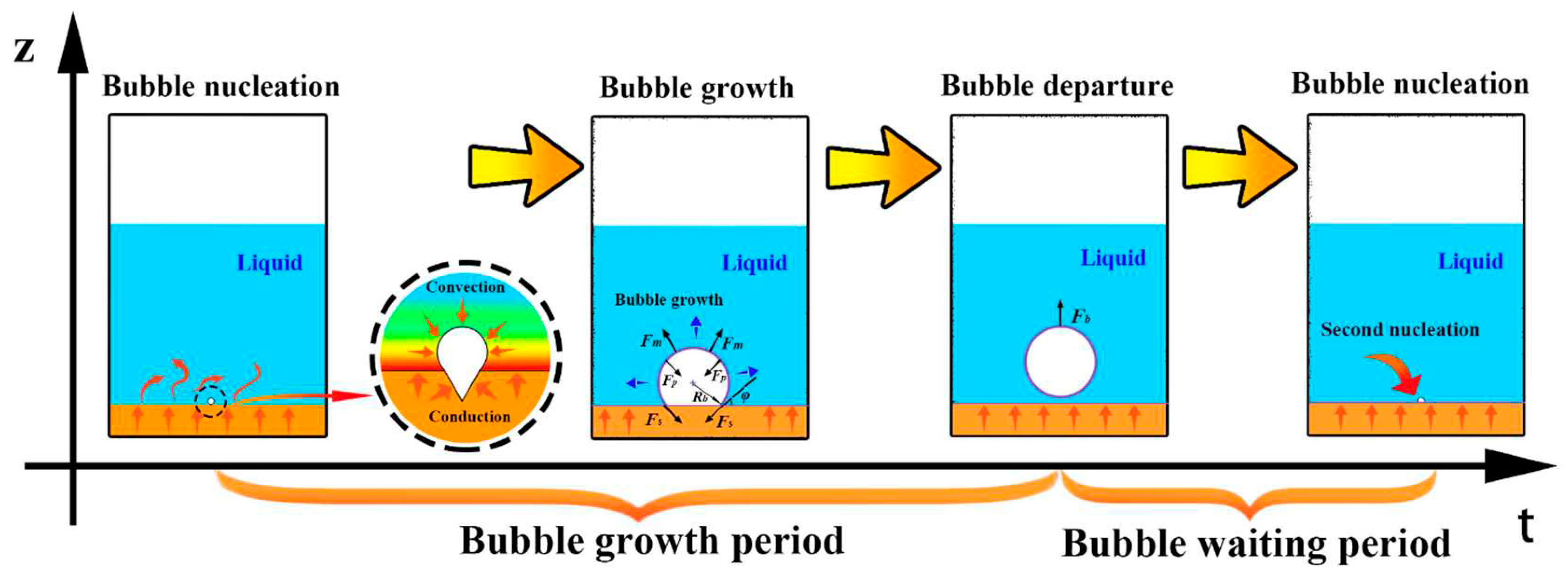
Figure 2.
Complex relationship of various bubble parameters.
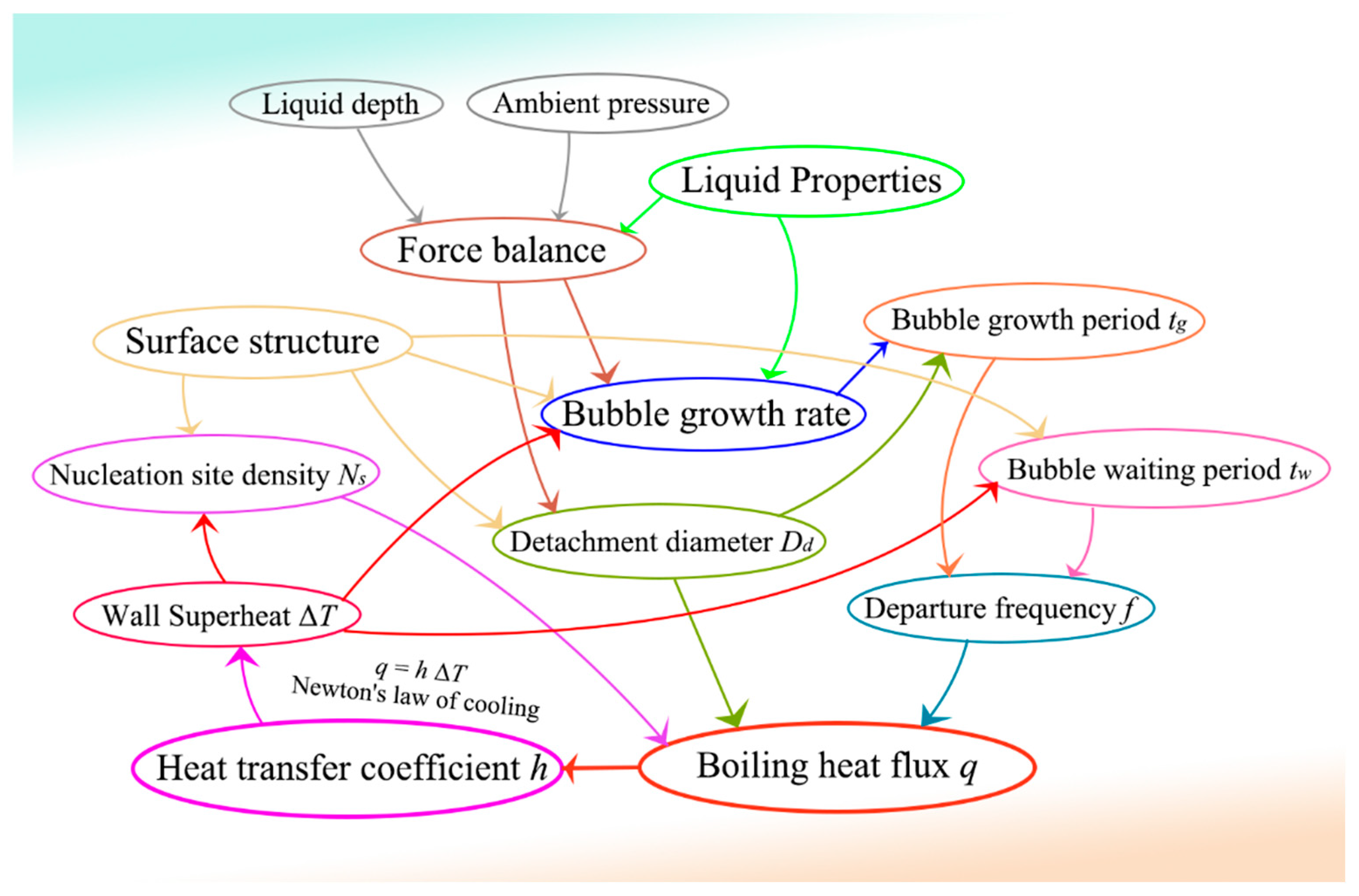
Figure 3.
Pits and crevices are more likely to entrap gas [23].
Figure 3.
Pits and crevices are more likely to entrap gas [23].
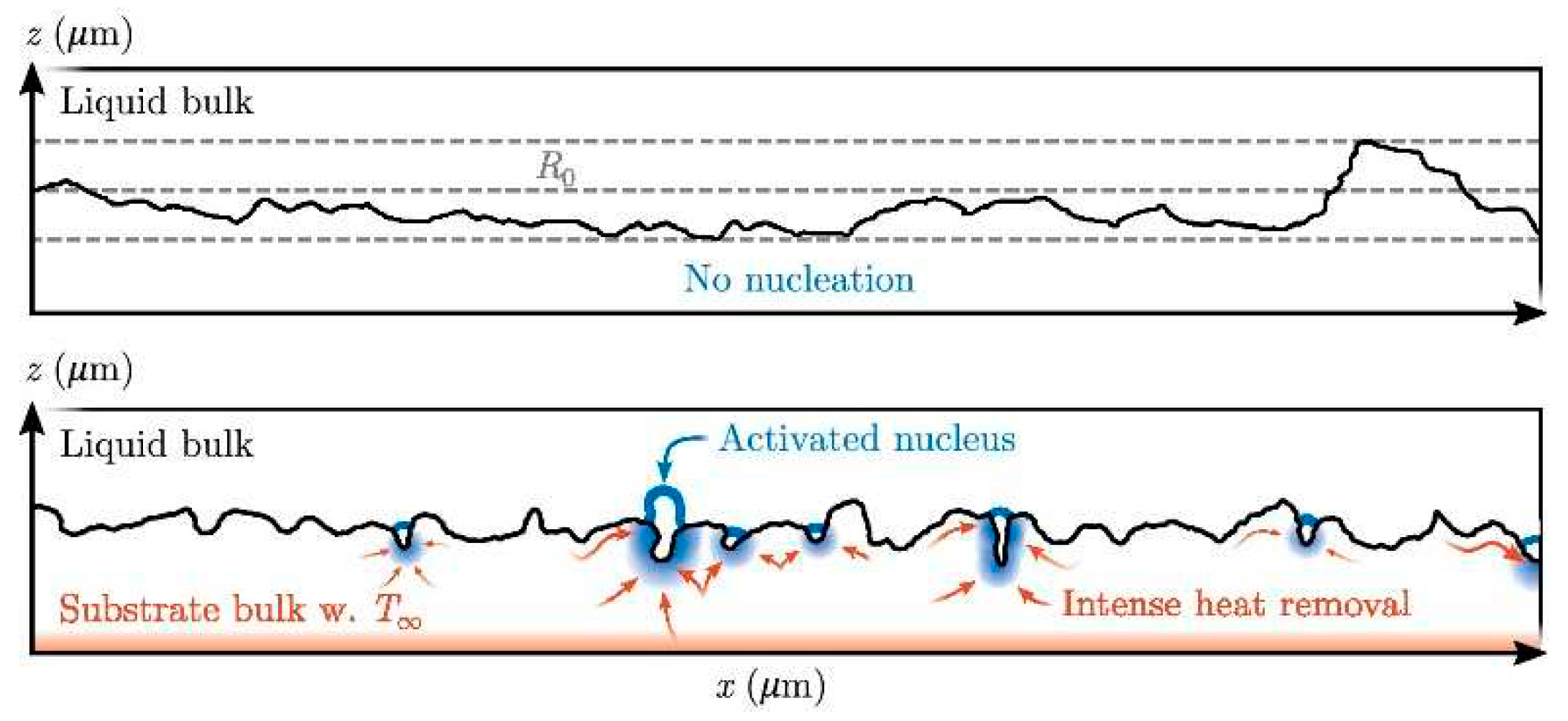
Figure 4.
Schematic of the gas entrapment proposed by Bankoff [24].
Figure 4.
Schematic of the gas entrapment proposed by Bankoff [24].
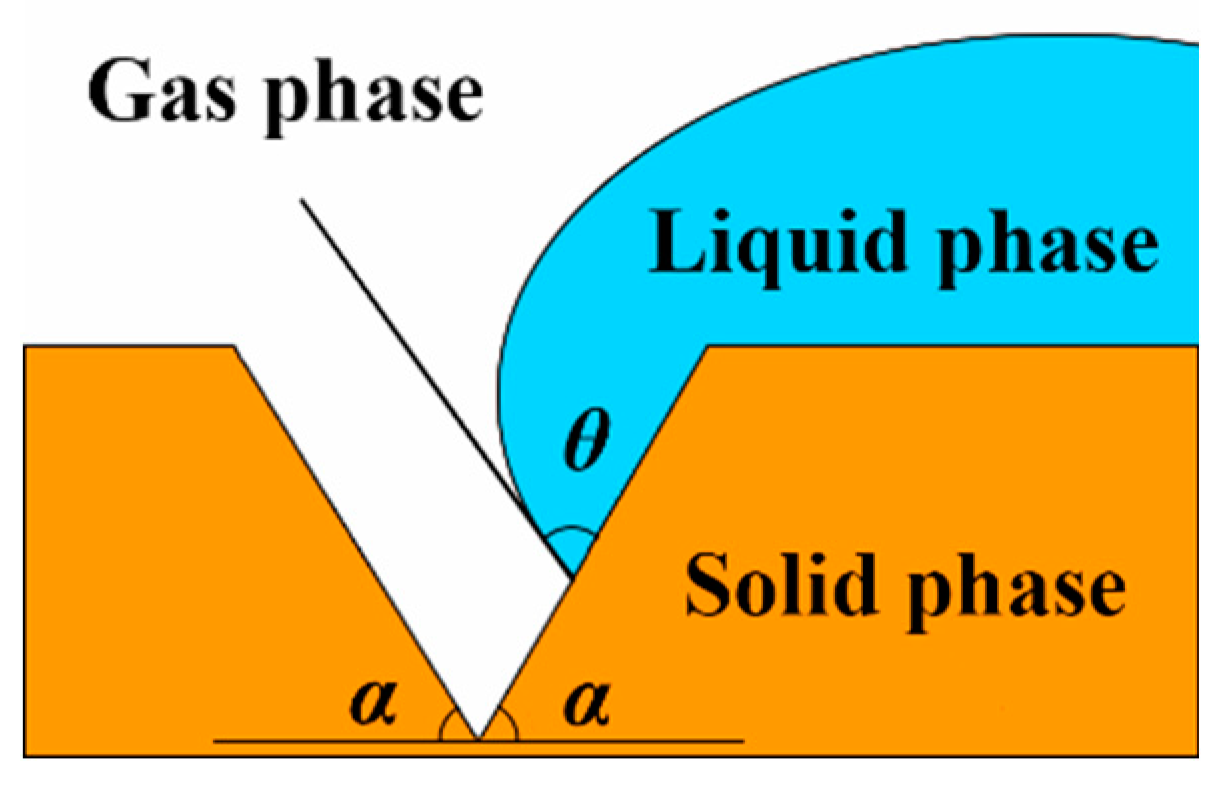
Figure 5.
Schematic diagram of the thermal boundary layer nucleation model proposed by Hsu [26].
Figure 5.
Schematic diagram of the thermal boundary layer nucleation model proposed by Hsu [26].
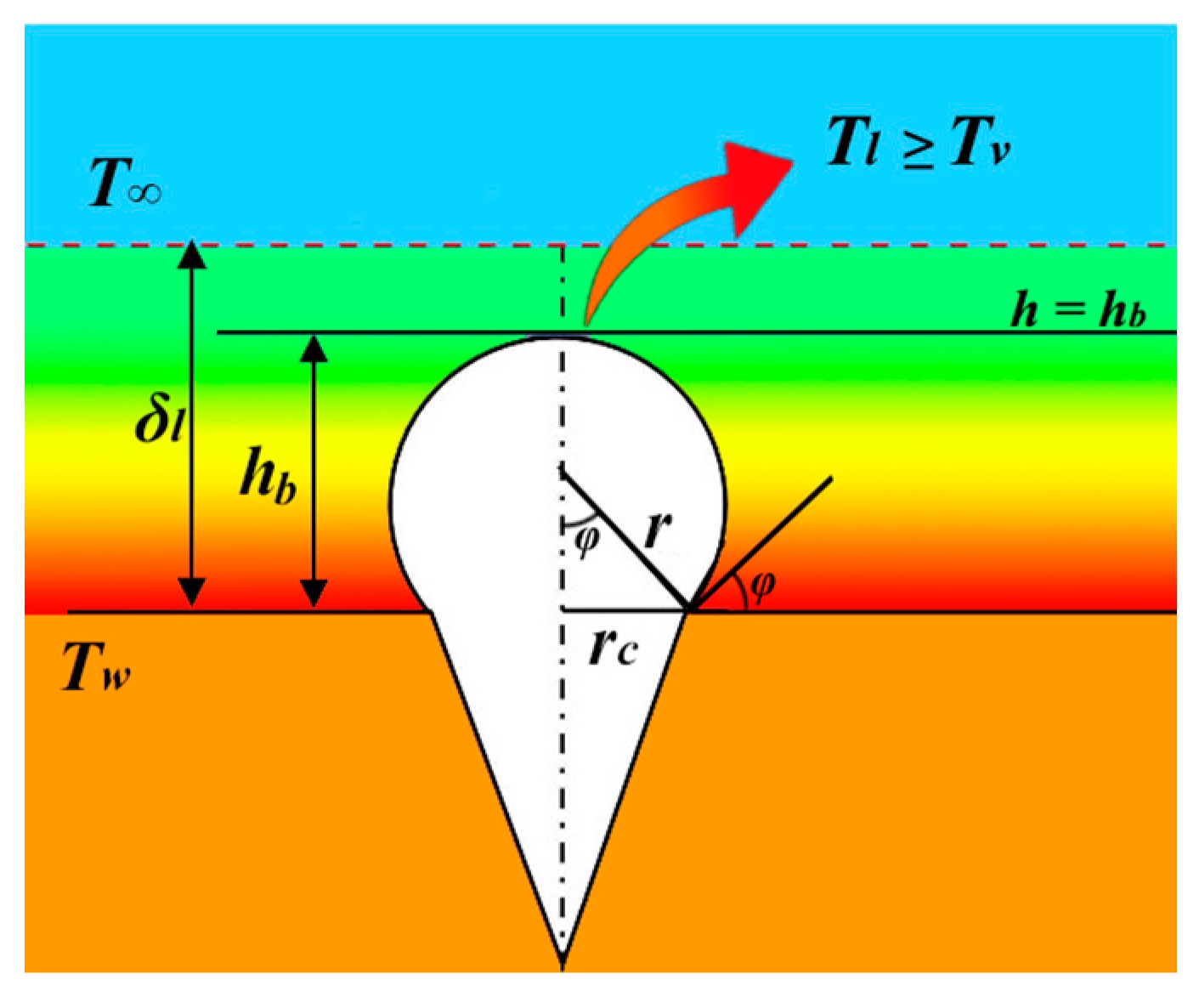
Figure 6.
Radius range of nucleation radius at different shape angles (a) Water (b) Novec-649.
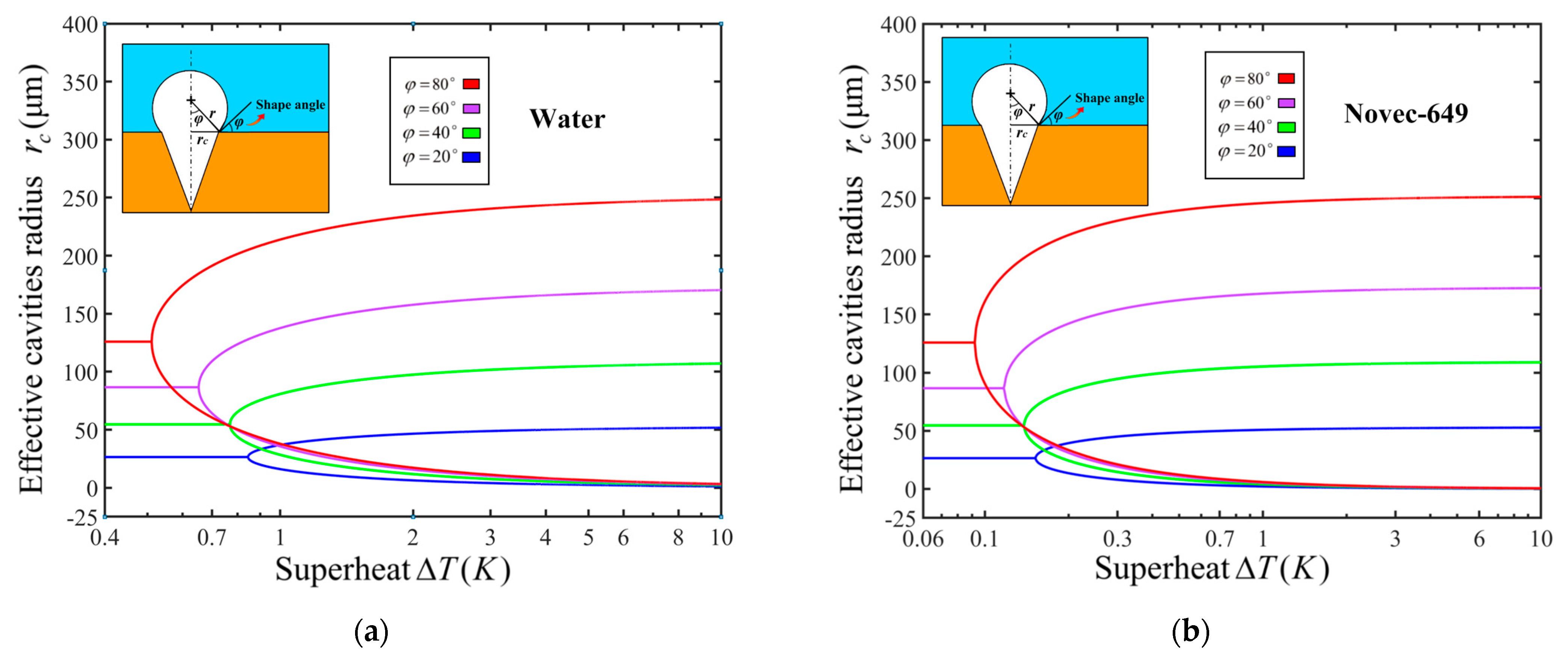
Figure 7.
Surfaces of three complex structures (a) Nanostructures [43] (b)Porous media structure [44](c)Copper metal foam structure [45].

Figure 8.
Bubble growth images and mechanical calculations at wall temperature 113 °C, p=1 bar [57].
Figure 8.
Bubble growth images and mechanical calculations at wall temperature 113 °C, p=1 bar [57].
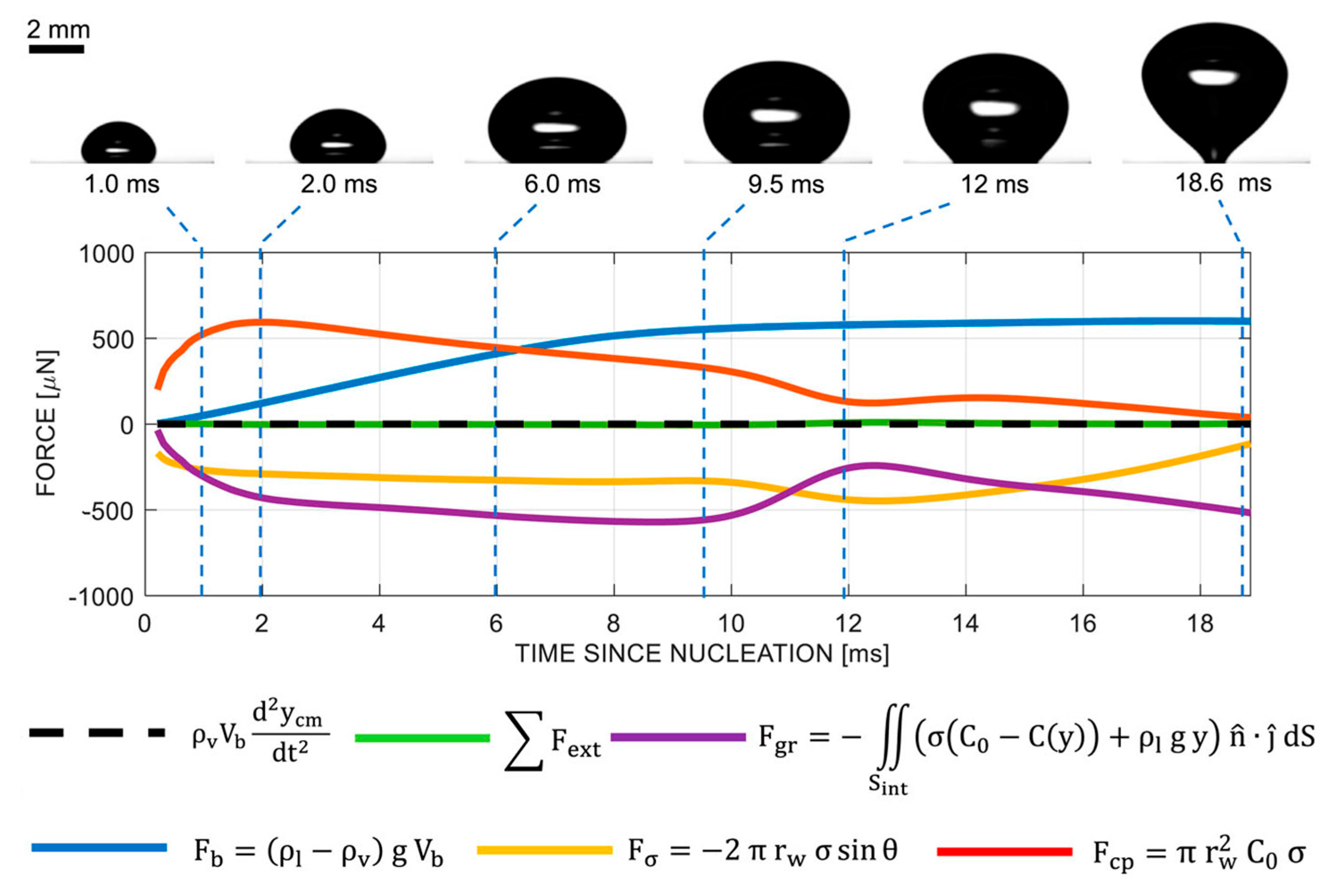

Figure 11.
Different growth stages of homogeneous nucleation [66].
Figure 11.
Different growth stages of homogeneous nucleation [66].
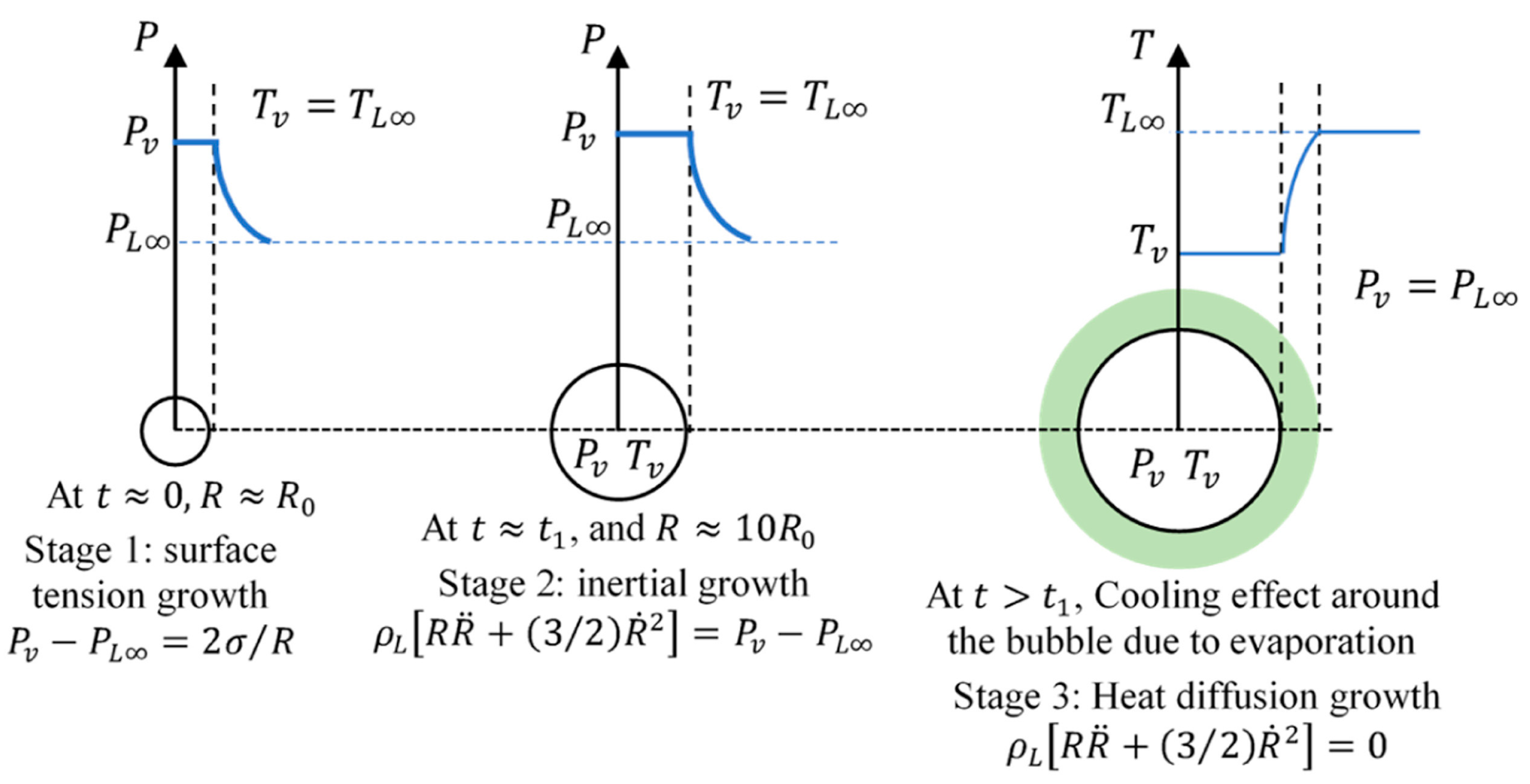
Figure 12.
Different growth modes of heterogeneous nucleating bubbles [66].
Figure 12.
Different growth modes of heterogeneous nucleating bubbles [66].
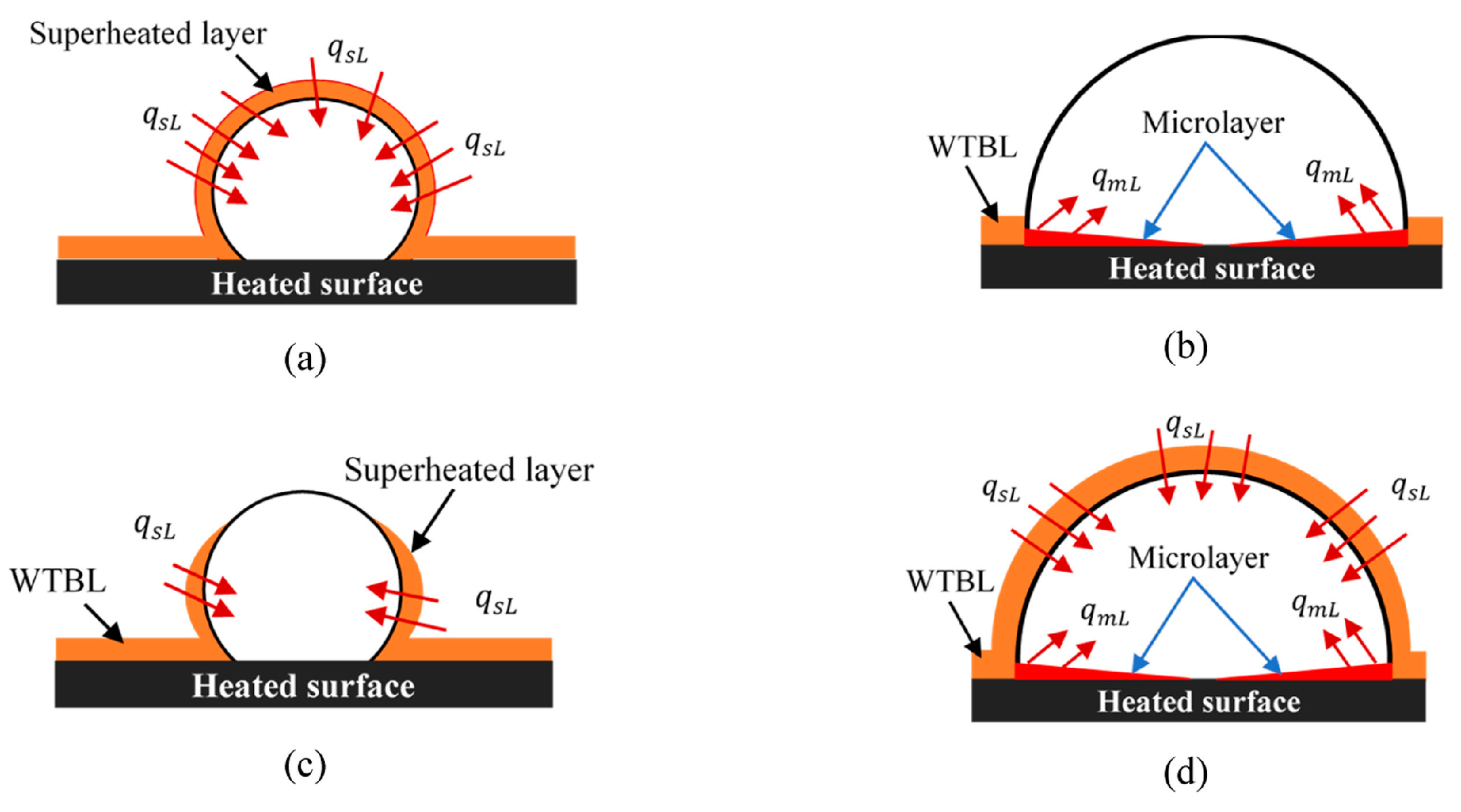
Figure 13.
Comparison between different theories and experimental results [105] (a) Comparison of the three models of Cole et al. with experimental results (b) Comparison of Zhang’s model with experimental results.
Figure 13.
Comparison between different theories and experimental results [105] (a) Comparison of the three models of Cole et al. with experimental results (b) Comparison of Zhang’s model with experimental results.
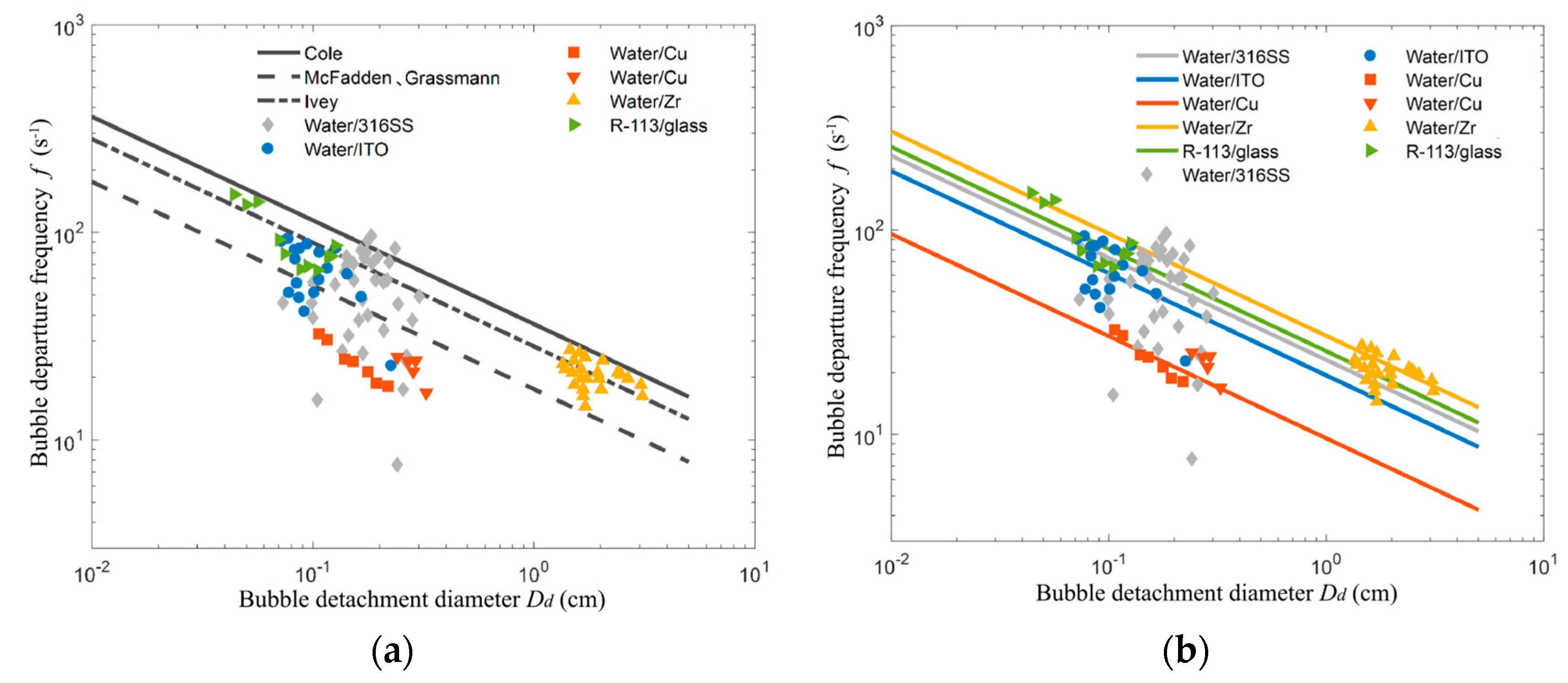
Figure 14.
Comparison of multiple heat flux prediction models with experimental results [123] (a) Comparison of three heat flux prediction models with Wang and Dhir’s experimental boiling heat flux (b) Comparison of the Sateesh boiling heat flux density prediction model with three experimental boiling heat flux density results.
Figure 14.
Comparison of multiple heat flux prediction models with experimental results [123] (a) Comparison of three heat flux prediction models with Wang and Dhir’s experimental boiling heat flux (b) Comparison of the Sateesh boiling heat flux density prediction model with three experimental boiling heat flux density results.
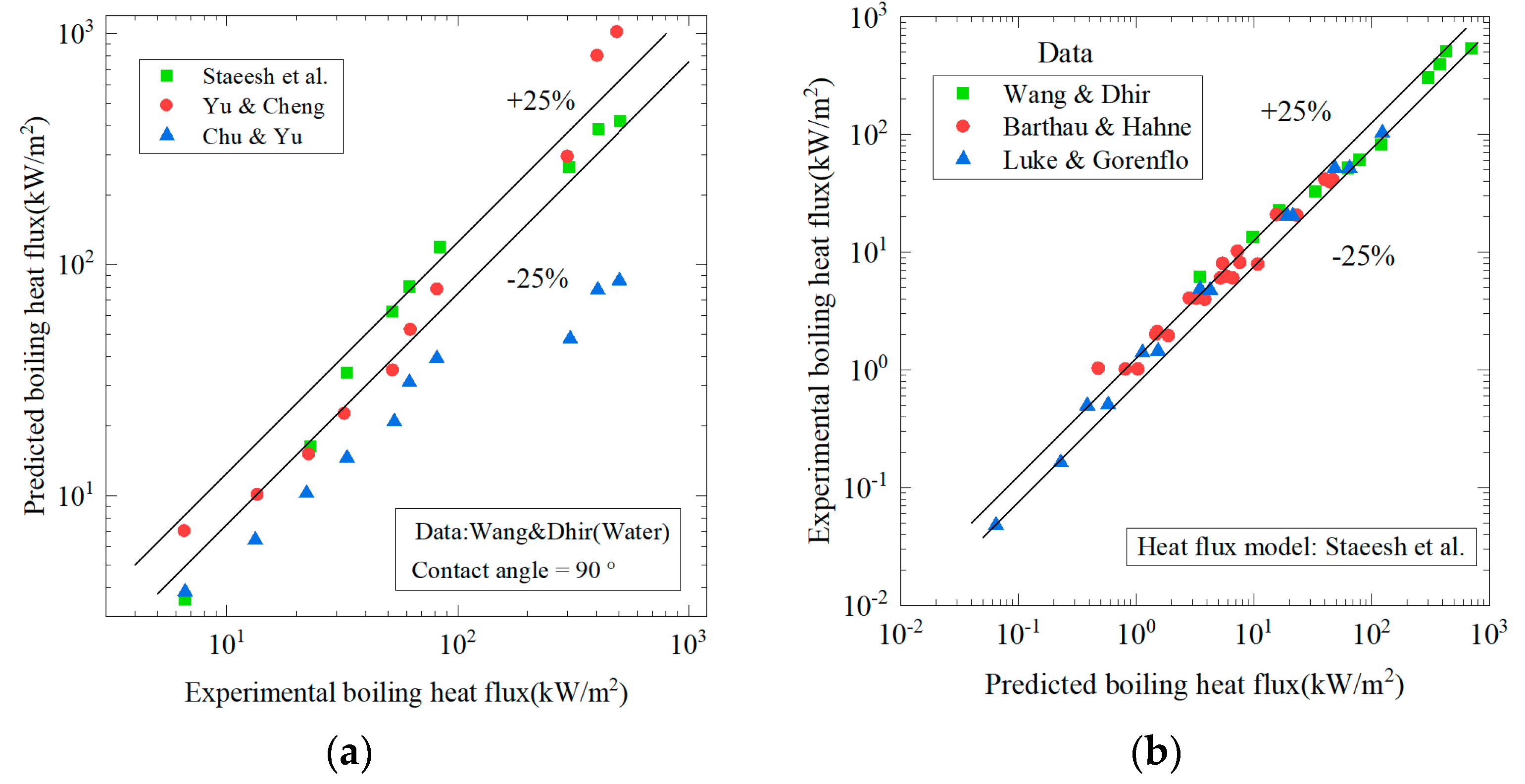
Table 1.
Physical properties of water and Novec-649 fluoride liquid.
| Ref. | Liquid density (kg/m3 ) |
Vapor density (kg/m3 ) |
Surface tension (mN/m) |
Latent heat (kj/kg) |
Saturation temperature(°C) |
|---|---|---|---|---|---|
| Water [29] | 958.35 | 0.597 | 59 | 2256.5 | 100 |
| Novec-649 [30] | 1513 | 13.42 | 10.8 | 88 | 49 |
Table 2.
Bubble force equations for three types of detachment.
| Klausner[46] model | Wang[52] model | Siddharth[55] model | |
|---|---|---|---|
| Fs | |||
| Fb | |||
| Fcp | |||
| Fd | |||
| Fi |
Table 3.
Liu et al. [59] Proposed bubble force equations.
Table 3.
Liu et al. [59] Proposed bubble force equations.
| Types of forces | Equation expressing a relation |
|---|---|
| Fs | |
| FP |
|
| FG | |
| Fe | |
| Fm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated