Algorithm on Transform Fractal Domain AA-F

Preprint

Article

Algorithm on Transform Fractal Domain AA-F

Altmetrics

Downloads

Views

Comments

Alen Pérez Labardi^*

This version is not peer-reviewed

Submitted:

11 October 2023

Posted:

16 October 2023

You are already at the latest version

Alerts

Abstract

In this work we present a novel steganography algorithm, based on Fractal Transform domain, combined with the principles of Cryptography. The proposed method uses a private key, which will indicate which segment of the image will be taken and encoded with the Fractal Transform, to then insert the secret bits in the transformed coefficients, thus generating the stego image.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

Introduction

At the moment, it exists the danger that our information, confidential many times, it can be, for not wanted people: consulted, modified, destroyed; we can also be harmed so that it is harmed, for an external agent, the protocols of authorizations, being impeded to consent to our own data. The information in I traffic it can be easily intercepted. In front of the desire of confidentiality you can suffer an interception attack; in front of the authentication desire we can be supplanted; in front of the desire of integrity of our information we can suffer modifications and even destruction of our own information; in front of the desire of authenticity we can suffer falsification attacks. It is for it that different forms have been adopted for the protection of the information, since the risks of being intercepted are very high. For such a reason, the use of the Cryptography and the modern Steganography plays a significant paper in the society for the security and protection of the information.

1. Steganography

The Modern Steganography is a group of technical and methods that allow to hide information inside such digital files as: audio, video and images. This investigation area this divided in two branches:

Steganography in the Domain of the Frequencies (DF).
Steganography in the Space Domain (DE).

The first one consists on taking advantage of the noises in the frequency to insert the information. The second group acts for example about the redundancy that possess the digital files, when considering the less significant bits of the images to insert the information or in parts of the same one that I lower some established approach they are defined as less important or redundant. In general the idea that the Steganography continues is to send the hidden message (E) hidden in a message of innocuous appearance (C) that will serve of camouflage. This is, an steganographyc function is applied

f (E, C) = O

, it is sent by an insecure channel the result that it can be seen without problems by third. Finally, the sender receives the object O and applying the inverse function

f^{- 1} (O) = E

it can recover the hidden message.

Then, an stego - algorithm is the algorithm steganographyc that indicates as carrying out the procedure of incorporation of the message

{(\nabla}_{O})

that we want to maintain secretly in the payee and the extraction

{(\nabla}_{E});

in the previous example:

{f : = \nabla}_{O},

{f^{- 1} : = \nabla}_{E} .

On the other hand, because the Steganographyc is invasive, that is to say, leaves prints in the means of used transport, they exist technical that try to detect these changes, even using complex statistical mechanisms, those which, until the moment, alone they end up offering level of probability of existence of a message hidden in a payee. These techniques implemented in software can make the detection work, for diverse analytic roads; to the study and application of them is what is denominated Steganalysis [3,17].

2. The Fractal

The fractals is mathematical sets with a high grade of complexity that can model many natural phenomena. The work with the fractals and their associate concepts have become important tools in diverse areas of the natural sciences, mainly because the modeling of fractals doesn't suppose that the studied objects have good properties of continuity and softness. One of their characteristics but important it is that it allows the characterization of irregularities that cannot be by means of the Euclidean Geometry, what allows the study of broken into fragments objects that they present regarding invariance the scale change and to describe objects that are considered mathematically too complex. In the fractals one can observe the self- similarity property. In principle this self - similarity is infinite, but alone in the case of the mathematical fractals, the alone natural fractals presents an I number finite of levels self - similar; also, although resemblances, don't possess a completely exact likeness. To this property of statistical invariance of the one climbed is denominated statistical self-similarity [8,10,11]. In general, the fractals is irregular, rough, porous or broken into fragments objects and that, also, they present these properties to the same grade in all the scales, that is to say that these objects present the same form if they are seen from a distance or closely. Inside the variety of applications of the fractals they are included: the study of the landscape and of the complexity of the costs, music's generation and in diverse art ways, seismology, mechanics of floors, creation of video games (in particular graphics of biological environments), technical of analysis of series of prices, the creation of amplifications of digital pictures [10,14] and the Compression of Images [10,18].

2.1. Compression of Images

The compression of images plays an important paper in the storage of images with a smaller cost, as well as in the quick transmission of data. Undoubtedly when compressing and then to decompress these data can get lost information, the one which, many times it is not perceived by the human eye or it is redundant, and the efficient compression methods are those that are able to extract the essence of the image, it stops later, when decompressing, to reproduce a very near image to the original one. In the nature many objects maintain a self - likeness that you can represent as the atractor of a Iterated System Functions (IFS) [10,11], such it is the case of the clouds, ferns, plants, hoist, bushes, among others.

In the year of 1987 two mathematicians of the Technological Institute of Georgia, Michael Barnsley and Alan Sloan, formed Iterated Systems Inc., a company with base in Atlanta where the development of the fractal theory is used applied to the compression [12,13]. One of the products but acquaintances are the Encyclopedia it Registers, published by Microsoft Corp. that includes in a CD - Rom 700 pictures to color, in their it finishes version of 1997 they incorporate but of 30000 articles, pictures and maps. Another product is the Fractal Imager, a program that receives an image file, preferably in format. JPG, and it compresses it in another fractal image format (. FIF) that you can decompress and to do with the Fractal Viewer, increasing sections from her to any level.

The first outline of compression of this published type, was Arnauds Jacquin doctoral thesis, student of Barnsley, in 1989 [2]. Other important contributions gave them Y. Fisher [18], R. D. Boss and E. W. Jacobs [7] among other [14].

2.2 Iterated System Functions

To compress images with IFS leaves of the application of the following theorem (Collage):

Supposes that one has

S_{i} : R^{n} \to R^{n}

function with

i = 1, \dots, m

and suppose that for all i one has

|S_{i} (x) - S_{i} (y)| \leq c |x - y|

, for all

x, y \in R^{n},

con

0 < c < 1 .

E \subset R^{n}

compact and not empty, then:

D (E, F) \leq D (E, \cup_{i = 1}^{m} S_{i} (E)) \frac{1}{1 - c},

Where F is the invariant set of those

S_{i}

and

D

the metric of Hausdorff [10].

The previous theorem guarantees that the invariant set can be a good approach of the initial group if the union of small copies this near this, because in this case one

D (E, F)

he would come closer to zero. In this sense and I eat consequence of this theorem, the following result tells us that a compact group can approach as much as it is wanted, under the metric Hausdorff, for a combined self - similar and invariance of an IFS. If the group is but complicated, this one can see as the overlapping of several combined invariant of several IFS.

Corollary:

E \subset R^{n}

compact and not emmpty. For all

0 < δ < 1

exists a Iterated System Function (IFS)

S_{1}, . ., S_{n}

with invariant set

F

such that

D (E, F) < δ

. [10].

Then one works an image in scale of gray with all the tones of gray between white and black and to see them as

z = f (x, y)

, where the smallest value of

f

it is white and high the black. It will be assumed that

f : I \times I \to I

, where

I = [0, 1]

. The methods of compression of images can be evaluated using the compression reason that is the reason of the memory required to keep the image like collection of pixels and the memory required to keep the representation of the image in compressed form. A file of around 720KB you can compress in FIF in 12KB, for a compression reason of 720:12, that is to say, 60:1.

The applications tune they are in general rotations, reflections, adjournments, contractions or changes in the coordinated axes that can be represented for:

v_{i} (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} a_{i} & b_{i} \\ c_{i} & d_{i} \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) + (\begin{matrix} e_{i} \\ f_{i} \end{matrix})

(1)

On the other hand, they can be used different metric to measure the distance between two images, two of them are the metric rms and the metric sup that it is but simple:

d_{r m s} (f, g) = \sqrt{\sum_{i = 1}^{n} \sum_{j = 1}^{m} {(f (x_{i}, y_{j}) - g (x_{i}, y_{j}))}^{2}}

(2)

d_{r m s} (f, g) = {s u p}_{(x, y) \in I^{2}} | f (x, y) - g (x, y) |

(3)

To compress images in scale of gray they are considered the following functions [10]:

w_{i} (\begin{matrix} x \\ y \\ z \end{matrix}) = (\begin{matrix} a_{i} & b_{i} & 0 \\ c_{i} & d_{i} & 0 \\ 0 & 0 & s_{i} \end{matrix}) (\begin{matrix} x \\ y \\ z \end{matrix}) + (\begin{matrix} e_{i} \\ f_{i} \\ o_{i} \end{matrix}),

(4)

where

s_{i}

it controls the contrast and

o_{i}

the shine of

w_{i}

D_{i}

R_{i}

the domain and the range respectively of

v_{i}

, o sea

v_{i} (D_{i}) = R_{i}

;

\cup R_{i} = I^{2}

R_{i} \cap R_{j} = \emptyset

, for

i \neq j

. To compress an image

f_{0}

coarse with finding the atractor

f = x_{W}

del IFS, this is

W (f) = w_{1} (f) \cup w_{2} (f) \cup \dots \cup w_{N} (f) = f .

Then to code the image needs to be

D_{i}, R_{i}, w_{i}

and to decode it, it would be applied

W

repeatedly to any initial image until the distance to

x_{W}

be "acceptable". The good thing serious to find the atractor of the IFS, but it is enough to find an image

f^{'}

, that in some step of the iteration this near

f

, that is to say

d_{r m s} (f, f^{'})

be small.

Finally, to code an image using some outline that uses the elements of the Fractal Theory, partition the image it is needed by some collection of ranges

R_{i}

; for each

R_{i}

he notices of some collection of images a

D_{i}

that he has an rms error small when it is applied in

R_{i}

and for I finish of the equation (4) they are determined

a_{i}, b_{i}, c_{i}, d_{i}, e_{i}, f_{i}, e_{i}, f_{i}, s_{i}

o_{i}

. With this it is obtained

W = \cup w_{i},

that it codes the original image, to this process is denominated Fractal Transformed. Storing these coefficients is but efficient that to keep the map of pixels of an image, it is for it that one says that when transforming in fractal way an image it is in a compression process.

3. Steganography Algorithm AA-Fractal

In this section our proposal of steganographyc algorithm is described. This designed to solve fundamental questions, say you robustness and security. The first one means that the information that hides in the image is resistant to diverse manipulations for third, such as: format change and treatment of the image with software specialized to improve their quality. On the other hand the security resides in the use of a key or key that alone it is of the knowledge of the originator and the receiver of the message. Both questions and other similar ones were approached in section 3.1 in detail.

An Steganographyc Algorithm this compound for an Algorithm of Concealment (∆) and an Algorithm of Recovery (Λ) [3]. It counts, also, basically, with the following conditions initials for their operation:

Digital information that wants to transmit in a hidden way (S).
Cover: I file digital where the digital information will be introduced S.

In this work it was used as cover an image I, for what we will hide certain quantity of information E in I. Be ∆ the concealment algorithm, this will have as entrance the information E and the cover I, this is: ∆(E,I). The algorithm returned the covered with the hidden information I*, therefore:

∆ (E, I) → I*.

He took to

l

as base for the longitude of the binary sequence of the secret message

S = {s_{i} : 0 \leq i \leq 2 l - 1)}

, where

s_{i}

they are the secret bits whose value is 0 or 1, the image is a bits map of size

n

m

and

l : = m i n {n, m}

. The places where the secret message will be hidden they are determined by a pseudo- random binary sequence defined by means of

K = {k_{0}, \dots, k_{l - 1}}

, which worked as symmetrical key [1,16].

I.: Insert Process.

Partition of the image.

The partition process is carried out in two stages:

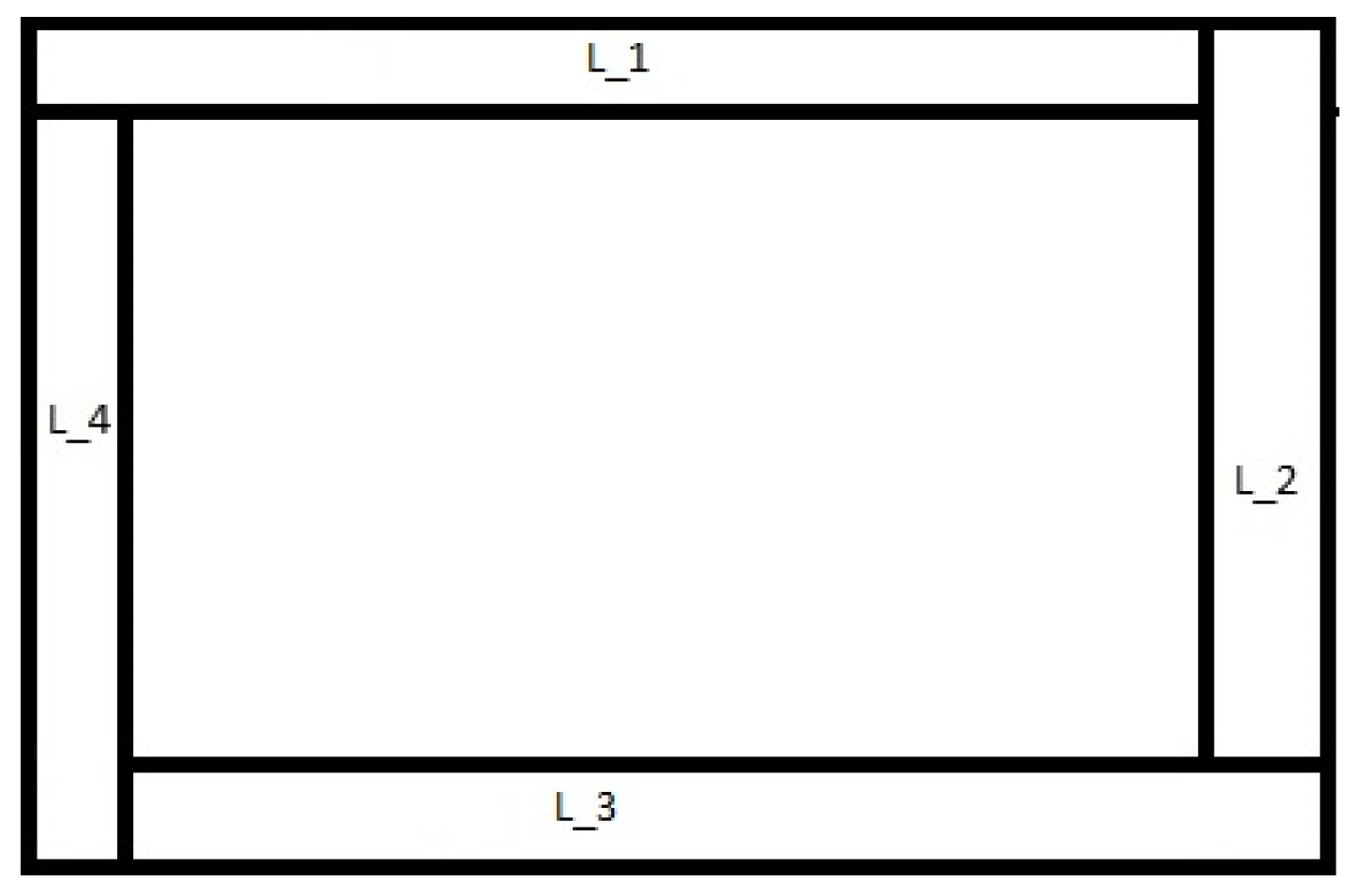
In the first place partition all the borders of the image with a wide of 2 pixels like sample the Figure 1.

In second place each border

L_i

partition in size blocks 2x2 pixels, what would be in the sets

L_{i j} = \{m_{j} : m a t r i x o f 2 x 2, m_{j} \in L_{i}\}; i = 1, 3; j = 0 . . (\frac{m}{2} - 1)

L_{i j}^{*} = \{m_{j} : m a t r i x o f 2 x 2, m_{j} \in L_{i}\}; i = 2, 4; j = 0 . . (\frac{n}{2} - 1)

The insert process is dependent of a secret key

K = {k_{0}, \dots, k_{l - 1}}

and the information that is wanted to hide

S = {s_{i} : 0 \leq i \leq 2 l - 1)}

, then you comes in the following way:

1: Beginning
2: Input: S, K, L_ij /*

L_{i j} : = L_{i j} \cup L_{i j}^{*}

*/
3: For i = 1 to 4 do
4: For j = 0 to

l - 1

do
5: If

K_{i} = 1

then
6: C := Compression _ Fractal _ Image (

L_{i j}

); /* C = [s, o, a, b, c, d, e, f]: See (4) */
7: C[2] := C[2] + K_i +s_i; /* Here the information is inserted, C = [s, o*, a, b, c, d, e, f]. */
8:

l

:= Decompression _ Fractal _ Image ( C ); /* matrix generated from the new fractal code C */
9:

L_{i j} ≔ l

; /* the generated matrix substitutes to the original one. */
10: End_If
11: End_for j
12: End_for i
13: Return

{(L}_{i j}

);
16: END.
Finally is carried out the inverse process of partition with the borders

L_{i j}

modified and you returns the resulting image.

II.: Recovery process.

The extraction of the information is carried out from a similar way to the previous process, what they extract the bits identified by the sequence instead of being inserted (key)

K = \{k_{1}, \dots, k_{l - 1}\}

binary pseudo - random, this is:

1: Beginning
2: Input: K, L_ij /*

L_{i j} : = L_{i j} \cup L_{i j}^{*}

*/
3: For i = 1 to 4 do
4: For j = 0 to

l - 1

do
5: If

K_{i} = 1

then
6: C := Compression _ Fractal _ Image (

L_{i j}

);
7: r :=

(C [2] {+ K}_{i}) m o d 2

; /* Here recovers the information. */
8:                                 S := Add _ to _ the_List( r );
9:             End_If
10:     End_for j
11: End_for i
12: Return S:
13: END

3.1 About AA-Fractal

In principle the Compression Fractal of an image consists on partition this in n parts (submatrix) and to apply him the Fractal Transformed (FT) to each one of them, I process theoretically simple but not at computer level, that is to say, the time of execution of the particionamiento and compression of an image is computational expensive [10]. It is for it that in the algorithm AA-Fractal alone you partition parts of the image: the borders, action that is carried out to obtain a group of matrix of 2x2, that they are the case but simple to calculate the FT. On the other hand they are the images .BMP to be these a virgin format in the sense that they are not compressed, what is ideal to experience when introducing him information and to apply him the different types of compression of images and to check the steganographyc characteristic of robustness, this is that quantity of inserted information can recover when changing among formats.

One of the fundamental aspects of the proposed algorithm resides where the information is inserted after having carried out the particionamiento process, that is to say, when taking a matrix of 2x2 like the pixels are worked to be able to apply the FT. In a process of compression fractal the usual thing serious to apply the FT to the group formed by the four pixels of the sub-image:

{p_{00}, p_{01}, p_{10}, p_{11}}

, but this would weaken the robustness of the algorithm for what takes the group formed by the bits but significant of each pixel, this is:

p_{i j} = {[b_{0}, \dots, b_{3}, b_{4}, \dots, b_{7}]}_{2};

p_{i j}^{*} = {[b_{4}, \dots, b_{7}]}_{2};

\{p_{00}^{*}, p_{01}^{*}, p_{10}^{*}, p_{11}^{*}\} .

It is important to point out that the prosecution of images, say you: softened, filtrate, mask, detection of borders, they are carried out on the less significant bits, what consolidates the robustness of the algorithm and their strength regarding the format change.

The capacity of the proposed algorithm this certain one for the size of the key that is used a bit of secret information since is inserted by each bit different from 0 of the key, and keeping in mind that the key is of longitude 128 bits generated pseudo-aleatorily (it possesses the same quantity of zeros and some) it would be in

4 * \frac{128}{2} = 256

bits of information that allows to insert in the cover.

Finally the theoretical security of AA - Fractal rests about the ignorance of the key, or what is the same thing that you leave of the image was coded in way fractal. As the key it is of 128 bits, the quantity in ways that they could have been chosen to insert the information in the first sub-border is

2^{128}

; supposing that an attacker chooses a key aleatorily and that when recovering the information of the first sub-border she had "sense", she would have to be proven that the extracted information of the other 3 sub-borders also has "sense" and that the concatenation of them produces a chain of coherent bits finally. Here one of the principles of the Cryptography has been used [10] : "the strength of a cryptographic algorithm should reside alone in the ignorance of the key, not in the ignorance of the algorithm in question", what reinforces its security.

4. Steganography Algorithms with Fractal Technique

Inside the consulted bibliography they were of great interest for their similar outline to the proposed algorithm the following works:

Kamal Gulati: ¨Information Hiding Using Fractal Encoding¨, 2003 [9]: This work uses technical of code fractal to identify in that leave of the image the secret information it will be introduced. The image is partition in regions domain D (blocks domain) and regions ranges R (blocks range). a bookstore of domains is built separated in two groups: $D_{0}$ and $D_{1}$ . The outline insert of the information is basically the following one: for each $R_{i}$ the best block is looked for $D_{i^{*}}$ such that $d (D_{i^{*}}, R_{i}) \leq m i n {e : d (D_{i^{* *}}, R_{i}) = e, D_{i^{* *}} \in G$ , where d it is a metric and ${G = D}_{0}$ if the i - th secret bit that leaves to it inserts it is 0 ó ${G = D}_{1}$ in another way.
Dilip Vishwakarma: “ Efficient Information Hiding Technique Using Steganography”, 2012 [6]: This work uses technical of fractal code to identify in that leave of the image the secret information it will be introduced. They intend 3 algorithms:

i.

The image is partitioned regions domain according to the quadrants of the image and to take alone $D_{I}, D_{I I I}$ (blocks domain) and regions ranges R (blocks range). When inserting the information: for each $R_{i}$ the best block is looked for $D_{i^{*}}$ such that $d (D_{i^{*}}, R_{i}) \leq m i n {e : d (D_{i^{* *}}, R_{i}) = e, D_{i^{* *}} \in G}$ , where d it is a metric and ${G = D}_{I}$ if the i th secret bit that will insert is 0 or ${G = D}_{I I I}$ in another way.

ii.

Similar to the Algorithm 1, but one works alone with integer numbers.

iii.

The image is partitioned in regions domain according to the quadrants of the image and to take alone $D_{I}, D_{I I I}$ (blocks domain) and regions ranges R (blocks range). When inserting the information: for each $R_{i}$ the best block is looked for $D_{i^{*}}$ such that the less significant bits of both sub-images coincides and also $d (D_{i^{*}}, R_{i}) \leq m i n {e : d (D_{i^{* *}}, R_{i}) = e, D_{i^{* *}} \in G}$ , where d it is a metric and ${G = D}_{I}$ if the i-th secret bit that leaves to it inserts it is 0 o ${G = D}_{I I I}$ in another way.
Fadhil Salman Abed: “A Proposed Encoding and Hiding Text in an Image by using Fractal Image Compression”, 2012 [4]: The image is partitioned in regions domain D (blocks domain) and regions ranges R (blocks range). The FT is calculated for each $R_{i}$ , being a list of coefficients of lineal functions ( $s_{i} * x + o_{i}$ ) stored in the way [ ${[s}_{1}, o_{1}]$ ₁, …, [ $s_{n}, o_{n}$ ]_n ], where n it is the quantity of elements that R possesses. As $0 < s_{i} < 1$ , what is equivalent to that $s_{i} = 0 . n_{1} n_{2} n_{3} n_{4} n_{5}$ , taking the first 5 figures after the 0, the information that is wanted to hide is transformed to its decimal value into code ASCII after being calculated with RSA and inserted in you finish them three positions.
Dr. Tawfiq Abdulkhaleq Abbas: “Steganography Using Fractal Images Technique”, 2014 [5]: He takes a map of pixels RGB (. BMP), it locates which they are the regions fractals in the image and it introduces the information in this lease in the following way: 1 bit in the Red one, 1 bit in the Green and 3 bits in the Blue. The longitude of the block range can vary its size between 2x2 and 32x32.
Richa Gupta: “Digital Image Encoding Scheme using Fractal Approach”, 2018 [15]: He takes a map of pixels RGB (. BMP) and it converts it to scale of gray, it locates which they are the regions fractals in the image and it introduces the information in this lease but in the original image. BMP in the following way: 1 bit in the Red one, 1 bit in the Green and 3 bits in the Blue.

The previous algorithms present some difficulties which were paid by the algorithm AA-Fractal:

Time of execution (for an image of fixed square size): Partitioned an image in pxp blocks (p is multiple of 2) it requires $t_{p}$ seconds. Then in $t_{p}$ seconds they are calculated $\frac{n^{2}}{p^{2}}$ sub-images. Find for each region $R_{i}$ their corresponding one $D_{i}$ it requires $t_{R P}$ seconds. To introduce the information requires $t_{I}$ seconds. Then, basically, for each algorithm, the time of execution is:

$T = t_{p} + t_{R P} + t_{I} .$

On the other hand an deterministic algorithm P( ) with capacity by heart limitless that partitioned images in pxp blocks, would calculate

\frac{n^{2}}{p^{2}}

sub-images in

t_{p}

seconds. As their time of execution it is dependent alone of the quantity of sub-images that should calculate, this is, to smaller size of p bigger time of execution, its relationship with the entrance will be lineal. Then find the lineal dependence of

t_{2}

regarding

t_{p}

in the following way:

\frac{(\frac{n^{2}}{p^{2}})}{t_{p}} = \frac{(\frac{n^{2}}{2^{2}})}{t_{2}},

t_{p} = \frac{(\frac{n^{2}}{p^{2}})}{(\frac{n^{2}}{2^{2}})} * t_{2},

t_{p} = \frac{2^{2}}{p^{2}} * t_{2} .

In the Table 1 a comparative of the mentioned algorithms is shown and the one proposed in this work. Here they are considered same in each algorithm the time of partitionedof the ranges and the domains, also the time of search of the domains for each range. The first column corresponds to the name of the algorithms, the second its time of execution in function of

t_{p}, t_{R P}

t_{I}

; and the third in function of

t_{2}, t_{R P}

t_{I}

. Notice you that AA-Fractal (AA-F) it possesses a more small because alone time of execution you partitioned leaves of the image and to that domains are not calculated, this is, he decreases the time of

2 * t_{2} {+ t}_{R P} + t_{I}

t_{2} {+ t}_{R P} + t_{I}

, but I neither eat domains they are compared for each range we obtain

t_{2} + t_{I}

. Finally the time for partitioned an image square nxn in sub-images of 2x2 according to the algorithm P () they are needed

t_{2}

seconds, what would be in a total of

\frac{n}{2} * \frac{n}{2} = \frac{n^{2}}{4}

calculated sub-images. To the partitioned in AA-Fractal they are obtained

4 * \frac{n}{2} = 2 n

sub-images in x seconds, then:

\frac{(\frac{n^{2}}{2^{2}})}{t_{2}} = \frac{2 n}{x},

x = \frac{2 n * t_{2}}{\frac{n^{2}}{2^{2}}} = \frac{2^{2} * 2 n * t_{2}}{n^{2}},

x = \frac{2^{3}}{n} * t_{2} .

As the images that one works in all the mentioned algorithms and in the one proposed they have a minimum of 256x256 resolution it formulates it previous it would be finally in:

x = \frac{2^{3}}{2^{8}} * t_{2},

x = \frac{1}{2^{5}} * t_{2}

2.: Robustness: The previously mentioned algorithms lack characteristic one of the main ones that an Stego-system should possess: the robustness. This algorithms insert the information in the less significant bits of the image through fractals technical without considering that when varying some few bits of the stego image the result from the FT when trying to recover the information it can be gravely altered, this is, a simple change among image format, say you of. BMP to. JPG and then to. BMP, a prosecution of the image for to increase him / to diminish him the shine and/or contrast or to enhance the borders it would commit the extraction of the secret information totally.

Conclusions

In this investigation you presents a novel Steganographyc algorithm based on the Domain of the Fractal Transform. The same one makes use principles of the Cryptography, by means of which a high grade of security of the Steganographyc system is reached, guaranteeing this way the level of confidentiality and privacy that it demands today in the world of the security information.

References

A. Menezes, P. van Oorschot, S. Vanstone. Handbook of Applied Cryptography. CRC Prees. 1996.
A.E, Jacquin. A Fractal Theory of Iterated Markov Operators whit Applications to Digital Imagen Coding. PhD Thesis. Georgia Institute of Technology. August 1989.
A.Soria-Lorente, R. Manuel Sánchez, A. M. Ramírez Aberasturis. Steganographicalgorithm of privatekey. Revista de investigación. G.I.E Pensamiento Matemático, Vol. III, No 2, pp. 059–072, ISSN 2174-0410. 2013.
A. Fadhil. A Proposed Encoding and Hiding Text in an Image by using Fractal Image Compression. International Journal on Computer Science and Engineering (IJCSE).Vol. 4 No. 01. ISSN : 0975-3397. January 2012.
A. Tawfiq A., K. Hassanein H. Steganography Using Fractal Images Technique. IOSR Journal of Engineering (IOSRJEN). Vol. 04, Issue 02. ISSN (e): 2250-3021, ISSN (p): 2278-8719. February 2014.
D. Vishwakarma, S. Maheshwari, S Joshi. Efficient Information Hiding Technique Using Steganography. International Journal of Emerging Technology and Advanced Engineering. Volume 2, Issue 1. ISSN 2250-2459. January 2012.
E.W. Jacobs, R.D.Boss. Fractal Image Compression Using Iterated Transforms: Applications to DTED. IEEE Military Communcations Conference. October 11-14, 1992. [CrossRef]
J.E. Hutchinson. Fractals and Self-Similarity. Indiana University Journal of Mathematics 30, 713–747. 1981.
K. Gulati. Information Hiding Using Fractal Encoding. Master of Technology. School of Information Technology Indian Institute of Technology, Bombay, Mumbai. January 2003.
M. Alfaro A., M. Murillo T., A. Soto A. Fractales. Revista digital: Matemática, Educación e Internet (www.cidse.itcr.ac.cr/revistamate/). ISBN 978-9968-641-03-6. 2010.
M. Bansal, S. K. Ranade. A review on fractal image compression. International Journal of Advances in Computing and Information Technology. ISSN 2277–9140. July 2012.
M. Barnsley, A. Sloan. Methods and apparatus for image compression by iterated function system. United States Patent #4.941.193.
M. Barnsley, A. Sloan. Methods and apparatus for processing digital data. United States Patent #5.065.447.
M. Barnsley. Fractal modelling of real world images. The Science of Fractal Images, H.O. Peitgen an D. Saupe (eds.). Springer Verlag, New York. 1988. [CrossRef]
R. Gupta, D. Mehrotra, R. K. Tyagi, R. Kumar: Digital Image Encoding Scheme using Fractal Approach. IEEE 978-1-5386-2615-3. 2018. [CrossRef]
S. Rani, H. Kaur. Technical Review on Symmetric and Asymmetric Cryptography Algorithms. International Journal of Advanced Research in Computer Science. Volume 8, No. 4, Special Issue. ISSN09765697. May 2017. [CrossRef]
V. Yadav, P. Sharma. A review paper on Steganography. International Journal of Advance Engineering and Research Development. Volume 2, Issue 5, e-ISSN(O): 2348-4470. May 2015.
Y. Fisher. Fractal Image Compression. SIGGRAPH ’ 92. Course Notes. 1992.

Figure 1.

Table 1. Comparison of the times of execution of the mentioned algorithms and the one proposed.

ALGORITHM	$TIME OF EXECUTION (t_{p}$ )	$TIME OF EXECUTION (t_{2}$ )
A-I	${2 * t}_{4} + t_{R P} + t_{I}$	$t_{2} + t_{R P} + t_{I}$
A-II	${2 * t}_{4} + t_{R P} + t_{I}$	$t_{2} + t_{R P} + t_{I}$
A-III	${2 * t}_{8} + t_{R P} + t_{I}$	$\frac{1}{2} {* t}_{2} + t_{R P} + t_{I}$
A-IV	${2 * t}_{32} + t_{R P} + t_{I}$	${\frac{1}{2^{3}} * t}_{2} + t_{R P} + t_{I}$
A-V	${2 * t}_{32} + t_{R P} + t_{I}$	${\frac{1}{2^{3}} * t}_{2} + t_{R P} + t_{I}$
AA-F	${\frac{1}{2^{5}} * t}_{2} + t_{I}$	${\frac{1}{2^{5}} * t}_{2} + t_{I}$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Algorithm on Transform Fractal Domain AA-F

Abstract

Introduction

1. Steganography

2. The Fractal

2.1. Compression of Images

2.2 Iterated System Functions

3. Steganography Algorithm AA-Fractal

3.1 About AA-Fractal

4. Steganography Algorithms with Fractal Technique

Conclusions

References

MDPI Initiatives

Important Links

Subscribe