Conjugate Gradient Least Squares Algorithm for OFDM Nonlinear Equalization in Intelligent Future IoT Transportation Systems

Preprint

Article

Conjugate Gradient Least Squares Algorithm for OFDM Nonlinear Equalization in Intelligent Future IoT Transportation Systems

Altmetrics

Downloads

134

Views

Comments

Hani Attar

Mohammad Aljaidi^*

Ayat Alrosan,

Ilhami COLAK,Ahmed Solyman,Ramy Said Agieb

Hani Attar

Mohammad Aljaidi^*

Ayat Alrosan,

Ilhami COLAK,Ahmed Solyman,Ramy Said Agieb

This version is not peer-reviewed

Submitted:

12 October 2023

Posted:

17 October 2023

You are already at the latest version

Alerts

Abstract

Intelligent transportation systems (ITS) have recently evolved rapidly, which requires development of highly trustworthy and effective communication technologies for uses, including vehicle-to-vehicle (V2V) and vehicle-to-everything (V2X) communication; where Orthogonal Frequency Division Multiplexing (OFDM) is regarded as a strong candidate and highly popular option technique among these methods. However, the movement of vehicles introduces Doppler frequencies which produce inter-carrier interference (ICI), that is frequently occurs in V2X channels. This interference has the potential to compromise the integrity of subcarrier orthogonality within OFDM, leading to lower-quality communication and an increased likelihood of data transmission errors. When employing channels with doubly dispersive fading, OFDM necessitates the usage of a complex equalization based on the minimum mean-square error (MMSE) equalizer, which requires channel matrix inversion. Several low-complexity equalizers for OFDM have been developed and are based on band factorization, time domain LSQR (Least-Square QR) iterative computing, and banded minimum mean squared error (BMMSE). This paper proposes Conjugate Gradient Least Squares (CGLS), which is a novel iterative computation algorithm integrated with nonlinear equalizers. The suggested nonlinear equalization technique determines the trade-off between computations and performance. According to simulation data, the suggested nonlinear equalizer performs better than the current BMMSE and linear CGLS algorithms across doubly dispersive fading channels.

Keywords:

Subject: Computer Science and Mathematics - Computer Networks and Communications

1. Introduction

The advent of the Internet of Things (IoT) has brought about a profound transformation in the way modern cities function and engage with technology [1]. The IoT is a network of physical items or "things" equipped with sensors, software, and other technologies to gather and exchange data with connected things and systems over the internet[2]. The following elements of modern cities have been greatly impacted by this integrated ecosystem: Smart Infrastructure, Smart Transportation, Environmental Monitoring, Healthcare, Retail and Commerce, and Energy Management [3]. It is worth noting that the rise of IoT serves as a pivotal catalyst for the advancement of 6G technology[4].

Smart transportation has been profoundly impacted by IoT, which has improved the efficiency, security, and sustainability of numerous modes of transportation [5]. Traffic management, Vehicle-to-vehicle (V2V) and vehicle-to-everything (V2X) communication, predictive maintenance, parking management, autonomous vehicles, ride-sharing and mobility services, eco-friendly transportation, fleet management, traffic data for urban planning, and emergency response are all areas where IoT technologies are being implemented [6]. The traffic management applies IoT sensors and cameras to monitor traffic flow and congestion in real-time, optimize signal timings, and reroute vehicles, where V2V and V2X communication enable real-time transmission of information regarding traffic conditions, accidents, and dangers. The IoT sensors in cars can track different parts' efficiency to tell when the repair is required, minimize downtime, and avoid breakdowns. The IoT technology also enhances the effectiveness and dependability of public transport networks, enabling users to plan their journeys and optimize routes following demand. Moreover, the developed IoT ride-sharing system can connect drivers and passengers in real-time mode, resulting in optimizing the routes and reducing idle trips.

Transportation and energy systems can become more resilient, sustainable, and efficient through the integration of smart grid and IoT-enabled V2X technologies. Through the use of these technologies, Vehicles and the smart grid may communicate more easily, allowing for the storage of excess energy for system stability and charging during periods of low demand[7]. By giving real-time data on energy generation and demand, V2X can also maximize the integration of renewable energy sources into the grid. EVs with V2X capability can act as mobile power sources during emergencies, improving the resilience and dependability of the grid. Charge schedules can be optimized using smart grid technologies, guaranteeing economical and effective charging. Greenhouse gas emissions can be decreased through more environmentally friendly patterns of energy and transportation that result from the cooperation of V2X and smart grids. IoT sensors may track energy usage trends, traffic congestion, and air quality, allowing for data-driven decision-making to reduce negative environmental effects. Policy and regulatory frameworks can be informed by cooperative efforts between the energy and transportation sectors, resulting in a more sustainable and integrated future. Within this context, further investigation into the security of IoT is warranted and may potentially elevate the demand for Blockchain technology[8].

Smart transportation encompasses areas like route optimization, parking, street lighting, accident prevention/detection, road anomalies, and infrastructure. Intelligent Transportation Systems (ITS) have revolutionized modern transportation by leveraging advanced communication technologies. One critical aspect of ITS is the seamless communication between vehicles and infrastructure, known as V2V and V2X communication; where the efficient and reliable exchange of information in these scenarios demands robust communication methods [9].

Due to its capacity to effectively control data transmission through wireless communication channels, Orthogonal frequency division multiplexing (OFDM) has found widespread application in numerous technological fields, such as:

Wireless Communication Standards: OFDM is a key component of wireless communication standards like IEEE 802.11 (Wi-Fi), IEEE 802.16 (WiMAX), and IEEE 802.22 (Wireless Regional Area Network), where it provides high data rates, robustness against multipath fading, and effective spectrum utilization.
Mobile Cellular Networks: 4G (LTE) and 5G cellular networks rely heavily on OFDM. Reducing the effects of signal interference and multipath propagation promotes high data throughput, enhanced spectral efficiency, and higher coverage [10].
Digital Television & Broadcasting: The efficient transmission of multimedia content over the airwaves is made possible by using OFDM in digital television broadcasting standards like Digital Video Broadcasting-Terrestrial (DVB-T) and Digital Audio Broadcasting (DAB) [11].
Wireless Local Area Networks (WLANs): Modern WLAN technologies, including Wi-Fi, use OFDM to speed up data transmission rates, expand indoor coverage, and support multiple concurrent users.
Broadband Internet Access: Fixed broadband wireless systems that use OFDM can deliver high-speed internet access to homes and businesses in locations where installing wired infrastructure is difficult.
Satellite Communications: OFDM is employed in satellite communication systems to efficiently utilize satellite transponders and robust data transmission in challenging atmospheric conditions [12].

Indeed, OFDM is a successful technique for mitigating inter-symbol interference (ISI) in frequency-selective channels, which is achieved by using a cyclic prefix (CP) and dividing the channel into several frequency non-selective sub-channels [13]. Additionally, OFDM employs single-tap equalizers to enhance its performance further in combating ISI. Conversely, the usage of terahertz (THz) frequency bands and the existence of high mobility can result in substantial Doppler shifts, hence causing interference with the orthogonality of OFDM subcarriers. As a result, implementing V2V and V2X wireless communication systems would lead to the emergence of time-varying channels and inter-carrier interference (ICI) [14]. The motivation behind this research stems from the critical importance of reliable and efficient V2X communication in modern transportation systems. Ensuring high-quality communication while managing the challenges posed by Doppler-induced ICI is vital for the safety and effectiveness of V2X applications. By providing a low-complexity yet high-performance solution, this research seeks to enhance the reliability and real-time capabilities of V2X communication systems. To tackle the issue of ICI, several equalization methods have been implemented such as in [15,16]. The work conducted by Jeon et al. [17] introduced a simplistic zero-forcing (ZF) equalization method that was based on a linear representation of channel variations. Unfortunately, the ZF approach demonstrates a limitation in noise amplification, which may result in limitless noise power spectrum densities after the equalization procedure. The sequential detection strategy utilizing the minimum mean square error (MMSE) was developed by Choi et al. [18]. The computational complexity of the MMSE technique may be expressed as O(N ³), where N is the total number of subcarriers. Therefore, the MMSE method may be seen as a sophisticated equalization tool as it needs the inversion of the communication channel matrix. The study of Cai et al. [19] introduced a solution for mitigating ICI with an O(N²) computational complexity, where the approach assumes that the power of ICI is mostly focused on a restricted set of neighboring subcarriers. In the study of Rugini et al. [20], LDL^H factorization in combination with a block decision feedback equalizer (BDFE) methodology was employed to achieve a computational complexity of O(N). Instead of employing the previously described solutions, which function in the frequency domain, Hrycak et al. [21] introduced an alternative linear equalization technique that integrates a time-domain ICI mitigation mechanism.

Research is underway to integrate artificial intelligence into the realm of equalization and channel estimation within Orthogonal Frequency-Division Multiplexing (OFDM) systems. In their work [insert reference], the authors emphasize the critical significance of channel estimation and signal detection within OFDM-based systems. Their study leverages deep neural network (DNN) layers, incorporating long-short-term memory (LSTM) units, to discern signals by acquiring knowledge from both the received signal and channel information. The outcomes of their simulations indicate that the system attains a signal bit error rate that is on par with, and in some cases surpasses, that achieved by conventional techniques[22].

The LSQR (Least-Squares QR) [23] iterative approach is utilized to tackle the difficulties associated with solving systems of least-squares equations, particularly when these equations are of significant size and have a sparse distribution [24]. The LSQR algorithm improves upon the conventional conjugate gradient approach by efficiently solving systems of equations through QR decomposition. This method is particularly beneficial when the required solution emphasizes a minimal L2 norm and the coefficient matrix displays a significant and sparse structure. This technique finds common use in various fields, including machine learning, control systems, image processing, and signal processing [25]. The LSQR method starts with an initial solution approximation and refines it iteratively, progressively improving the result. After each iteration, it calculates the QR decomposition of the coefficient matrix and uses it to update the solution. This approach effectively tackles least-squares problems by ensuring that the solution remains orthogonal to the null space of the coefficient matrix. LSQR is well-suited for handling sparse matrices, especially those with numerous zero components. It also allows for the selection of reliable stopping criteria, ensuring that the solution reaches the desired level of accuracy and ceases to change. To expedite convergence and enhance the algorithm's performance, preconditioning techniques are often integrated with the LSQR algorithm. The LSQR algorithm is well recognized as a reliable and effective approach for solving linear systems and least-squares problems using extensive datasets characterized by sparsity. The algorithm demonstrates a high degree of appropriateness for many applications due to its proficiency in managing sparse matrices and its ability to establish dependable termination criteria. The tasks mentioned above are relevant to the fields of signal and image processing, as well as the discipline of machine learning.

The Conjugate Gradient Least Squares (CGLS) algorithm [26] is an iterative method for solving linear least squares problems of Ax ≈ b, where A is a matrix, x is the solution vector, and b is the observed data vector. The CGLS algorithm aims to find the vector x that minimizes the residual error between the approximated Ax and b. CGLS is a low-complexity iterative method to solve the matrix inversion needed by the MMSE equalizer. This research proposes CGLS as a low-complexity solution for MMSE nonlinear equalizers.

Several research challenges need to be addressed in this study. These include:

(1): Developing an efficient algorithm, such as CGLS, for nonlinear equalization to combat ICI.
(2): Achieving a trade-off between computational complexity and communication performance.
(3): Conducting extensive simulations and experiments to validate the proposed approach across different channel conditions.
(4): Comparing the performance of the proposed CGLS algorithm with existing equalization techniques, such as MMSE and BMMSE.
(5): Investigating the hardware implications and feasibility of implementing the CGLS algorithm in IoT transportation systems.

This study presents the Conjugate Gradient Least Squares (CGLS) algorithm as a viable and computationally efficient method for addressing the issue of inter-carrier interference caused by Doppler effects in V2X communication systems based on OFDM. This study investigates the trade-off between computational complexity and communication quality, showcasing the improved performance of the proposed method in comparison to existing approaches such as MMSE and BMMSE. The research paper also examines the hardware considerations associated with implementing CGLS in Internet of Things (IoT) transportation systems.

2. Orthogonal Frequency Division Multiplexing

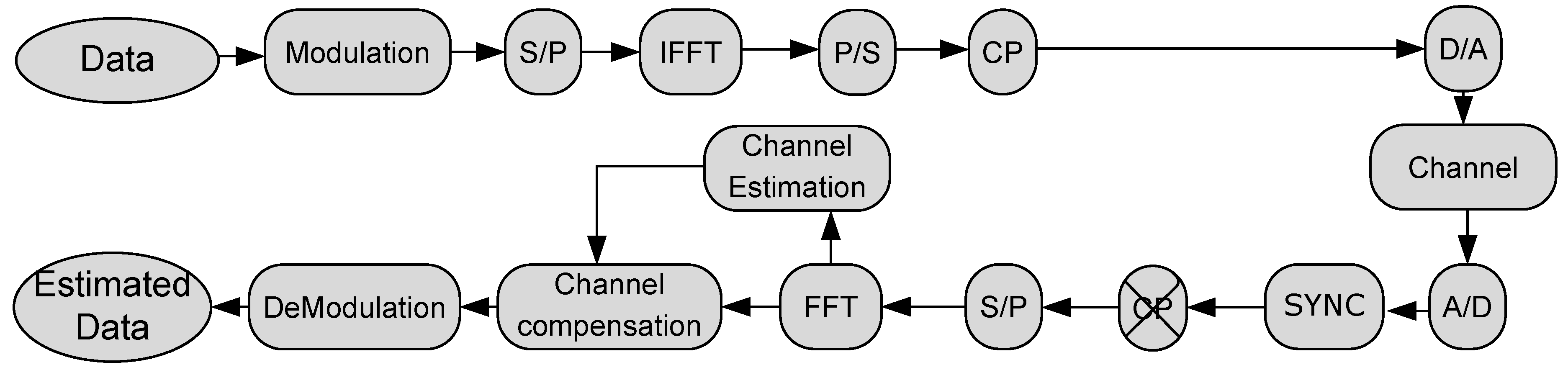
The block diagram of the OFDM system is illustrated in Figure 1, where the modulator functional block modulates the binary stream to symbols. The amount of subcarrier channels is used to divide the data into streams, the serial-to-parallel function is presented here, and some data is assigned to each sub-carrier for transmission. The modulation or mapping method (usually Binary Phase Shift Keying (BPSK), Quadrature Phase Shift Keying (QPSK), or Quadrature Amplitude Modulation (QAM)) is then used to determine the requisite amplitude and phase of the carrier. The Inverse Fast Fourier Transform (IFFT) block is then used to convert this spectral representation of the data into the time domain. A serial data stream is created by combining the many parallel data streams. In contrast, a copy of several subcarriers is added as a cyclic extension by the cyclic extension function block at the end of the OFDM symbol, minding that the copy is put at the very beginning of the symbol. Finally, the signal is upconverted to the desired transmission frequency and converted to an analog signal using a digital to analog (D/A) block.

The receiver's job is to recover useful information from the damaged signal after the channel by analyzing the received signal and restoring it to its original form on the other side of the radio channel, taking into consideration that before performing the signal demodulation, the receiver must correct the flaws using the synchronization function block. The CP is eliminated together with the synchronized signal and the timing signals, and after the CP removal function block, the serial data stream is divided into parallel data streams, where the quantity is the same as the transmitter's number of subcarrier channels. The data streams are demodulated from the OFDM symbols using the Fast Fourier Transform (FFT) function block, and the final symbols are then transformed into a serial signal stream, to start the channel estimation, where the equalization process begins using the estimated channel. Finally, the demodulation function block converts the signal to a binary stream and returns the approximated data to its original form.

3. OFDM Equalization

Time-invariant frequency selective multipath channels affect single-carrier communication systems, necessitating a complex equalizer to maintain quality of service (QoS) with a predetermined likelihood of error. However, employing a single tap equalizer, OFDM can correct the time-invariant multipath channel impact.

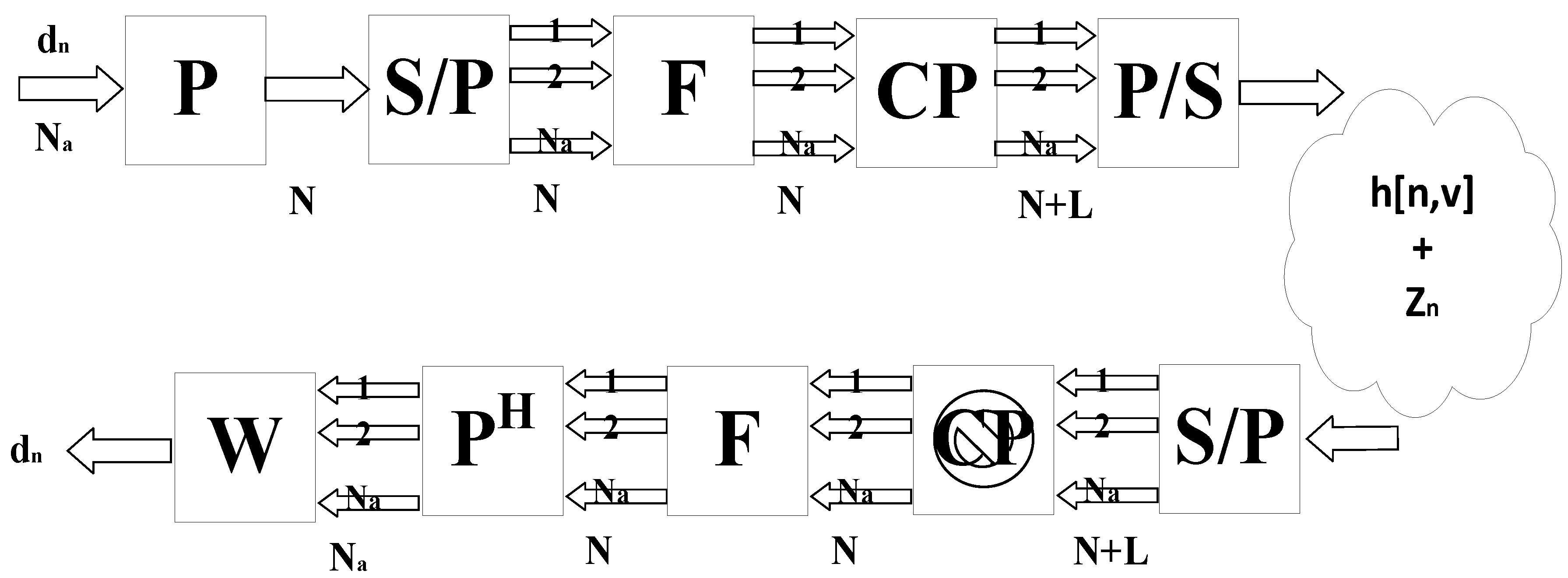
By looking at the block-by-block processing communication system in Figure 2 for a linear time-invariant frequency selective noisy channel [27]; the symbols received are provided by

r_{n} = H F^{*} d_{n} + z_{n}

(1)

where

r_{n}

is the received sequence, H is the

N \times N

channel matrix,

N

is the number of subcarriers,

F

is the discrete Fourier transform (DFT) matrix,

F^{*}

is the IDFT matrix,

d_{n}

is the transmitted data vector in the

n^{t h}

OFDM symbol, and

z_{n}

is a white Gaussian noise in the time domain.

After demodulation and using DFT, the received vector is given by:

{\tilde{r}}_{n} = F H F^{*} d_{n} + {F z}_{n}

(2)

As H is a circulant matrix (because of the cyclic prefix(CP)),

F H F^{*}

becomes a diagonal matrix [28] and the received signal can be equalized by adjusting the phase and amplitude for the received sequence [29], which is the characteristic that is regarded as a key benefit of OFDM, indeed; it simplifies the equalization operation process in multipath fading channels and transfer it to a single tap equalizer problem.

However, this characteristic only applies to frequency-selective multipath channels that are classified as time-invariant [28]. Conversely, this traditional method becomes ineffective in the presence of doubly dispersive fading channels or time-variant fading channels. The Discrete Fourier Transform (DFT) can no longer fully diagonalize the channel matrix, leading to the emergence of Inter-Carrier Interference (ICI) when a frequency offset occurs at the receiver [24]. Additionally, in cases of doubly selective channels, which are characterized by being both time and frequency-selective, OFDM necessitates the use of complex equalizers [29,30].

4. Equalization Strategies for OFDM in Doubly Dispersive Channels:

A multicarrier modulation (MCM) system with a block time that incorporates both the Doppler effect caused by receiver mobility and temporal variability, is prone to sub-carrier orthogonal losses due to the occurrence of ICI [31], resulting in reducing the system’s effectiveness and efficiency. The impact of the ICI becomes significantly more pronounced as increasing the size of the MCM blocks, carrier frequency, and velocity.

A.: Challenges associated with Doppler-induced ICI

The presence of Doppler-induced Inter-Carrier Interference (ICI) in Orthogonal Frequency Division Multiplexing (OFDM) communication systems poses many substantial obstacles that have implications for the dependability and effectiveness of wireless communication. The following is a comprehensive elucidation of the aforementioned challenges:

(1): The frequency shift resulting from the relative motion between the transmitter and receiver is a significant obstacle that must be addressed. When a mobile device, such as a vehicle equipped with vehicle-to-everything (V2X) communication capabilities, is in motion, the Doppler effect induces a modification in the frequency of the received signal. This transition has the potential to result in a lack of synchronization between the nominal frequencies of the OFDM subcarriers.
(2): The phenomenon of loss of orthogonality occurs when subcarriers in an ideal Orthogonal Frequency Division Multiplexing (OFDM) system no longer maintain their orthogonal relationship, resulting in interference between them. Nevertheless, the orthogonality can be disrupted by frequency changes generated by the Doppler effect. When the orthogonality of subcarriers is compromised, inter-carrier interference (ICI) arises due to the leakage of energy from one subcarrier to neighboring subcarriers. The presence of interference has the potential to diminish the quality of the signal that is received.
(3): Symbol interference occurs when there is interference between symbols due to Doppler-induced inter-carrier interference (ICI). Orthogonal Frequency Division Multiplexing (OFDM) is a modulation technique in which each symbol is associated with a group of subcarriers. In the context of inter-symbol interference (ICI), the presence of overlapping or interfering symbols might pose difficulties for the recipient in accurately demodulating and decoding the transmitted data.
(4): The inclusion of Interference-Causing Interactions (ICI) has a detrimental impact on the Signal-to-Noise Ratio (SNR), hence influencing the overall quality of the communication link. Consequently, this results in an increased occurrence of bit errors and a subsequent reduction in data throughput.
(5): The process of channel estimation plays a crucial role in the functioning of OFDM systems as it effectively mitigates the adverse effects of multipath fading and facilitates the implementation of channel equalization techniques. Nevertheless, the presence of Doppler-induced inter-carrier interference (ICI) can give rise to inaccuracies in the estimation of the channel, hence presenting difficulties in effectively tracking and compensating for the time-varying nature of the channel conditions.
(6): The demodulation process might be compromised by ICI, resulting in challenges for the receiver in precisely recovering the sent data. In instances of significant severity, the recipient may have a failure to accurately demodulate symbols, hence leading to the occurrence of communication failures.
(7): Advanced Equalization Techniques: To mitigate the effects of Doppler-induced ICI, sophisticated equalization methods are commonly employed. These approaches include MMSE equalization and iterative techniques such as CGLS. These methods enhance the computational intricacy and may pose difficulties when implementing them in real-time communication systems.
(8): Examples of Doppler-induced ICI affecting the communication quality
(9): Doppler-induced ICI in OFDM-based V2X communication systems can pose significant challenges.
(10): In a high-speed vehicle scenario:

Vehicles A and B are exchanging vital safety information while travelling at a high rate of speed. When both vehicles are stationary, Vehicle A's OFDM signal reaches Vehicle B without interference. However, when both vehicles are moving, the Doppler effect takes place. When the signal reaches Vehicle B, its frequency changes, causing ICI in the OFDM subcarriers at the receiver of Vehicle B. This can cause Vehicle B to misinterpret Vehicle A's vital safety information, which could be dangerous.
(11): In an urban intersection scenario, multiple vehicles communicate traffic information to optimize flow and avoid collisions. As vehicles approach the intersection, Doppler-induced frequency shifts introduce ICI in the received signals, leading to misinterpretations of other vehicles' intentions, potentially causing traffic congestion and increasing accident risks. Additionally, misalignment of signals due to Doppler effects can disrupt traffic signal coordination and cause inefficiencies in traffic management.

These examples demonstrate the importance of addressing ICI in OFDM-based V2X communication systems to ensure smooth operation and safety.

Extensive scholarly investigation has examined the effects of time-selective multipath fading on OFDM systems specifically developed for broadband mobile applications, where numerous endeavours have resulted in establishing limits for errors associated with ICI. Lately, researchers have been investigating numerous strategies aimed at alleviating the effects of ICI within OFDM systems, where the revealed results have been well-documented in multiple academic publications, encompassing references such as [32,33,34].

Despite the superior performance of nonlinear equation approaches, linear methods continue to maintain their significance due to the following reasons:

The linear objects or concepts are characterized by their simplicity.
The nonlinear techniques continue to employ a linear equalizer to mitigate ICI.

Figure 2 illustrates the block diagram of an OFDM system, wherein the transmitted data vector is denoted as

d_{n} = [d_{0}, d_{1} . . . {d_{N_{a} - 1}]}^{T}

, the binary matrix P, which belongs to the set of integers

Z^{N_{a} \times N_{a}}

, the number of subcarriers, denoted as N, can be considered as:

P = [0_{N_{a} \times (N - N_{a}) / 2} I_{N_{a}} 0_{N_{a} \times (N - N_{a}) / 2}]

(3)

The symbol

0_{X \times Y}

represents an X×Y matrix consisting entirely of zero entries while

I_{X}

denotes an X×X matrix. The vector

s_{n}

, denoted as

{[s_{0} s_{1} \dots . . s_{N}]}^{T}

, can be computed using the following equation:

s_{n} = F^{*} P d_{n}

(4)

The symbol F* stated previously denotes the IDFT matrix.

Within the field of communications engineering, the impulse response h(n, v) is a valuable tool for modelling the doubly dispersive channel due to its ability to exhibit time-variance. The variables n and v in this context are representative of the time instant and time delay, respectively. The following matrix representation can express the articulation of this model:

{[H]}_{n, v} : = h (n, {〈n - v〉}_{N})

(5)

In cases where the greatest delay spread is smaller than the cyclic prefix

L

(

N_{h} \leq L

) after the CP is removed, the received samples for the n^th OFDM symbol can be expressed as:

r_{n} = H_{n} d_{n} + z_{n}

(6)

The variable z_n represents Gaussian noise, while H_n, under stationary conditions, is a circulant matrix. The DFT matrix, denoted as F, is employed to demodulate the subcarriers that have been received. The received signal, y, can be obtained using the following formula:

y = F r_{n}

(7)

The equalizer matrix

W_{n} \in C^{N_{a} \times N_{a}}

Operates on the input:

{\tilde{r}}_{n} = P^{H} F H_{n} F^{*} P d_{n} + P^{H} F z = U_{n} d_{n} + {\tilde{z}}_{n}

(8)

Where

U_{n} \in C^{N_{a} \times N_{a}}

is a system matrix (

U_{n} = P^{H} F_{} H_{n} F^{*} P)

The matrix P functions as a protective frequency guard band, effectively mitigating out-of-band emission and eliminating the components in the upper left and right corners. The following notation indicates the representation of the data vector approximation:

{\hat{d}}_{n} = W {\tilde{r}}_{n}

(9)

Where it is known that the channel matrix is given by

{[\tilde{H}]}_{m, k}

equals to

\tilde{h} (m - k, k)

, which is:

\tilde{h} (m, k) = \frac{1}{N} \sum_{n = 0}^{N - 1} \sum_{v = 0}^{N - 1} h (n, v) e^{- j 2 π (v k + m n) / N}

(10)

B.: Zero Forcing and MMSE Block Equalizers

by minimizing

E \{‖d_{n} - W {\tilde{r}}_{n}‖\},

the estimated data of

{\hat{d}}_{Z F}

and

{\hat{d}}_{M M S E}

will be:

{\hat{d}}_{Z F} = {\tilde{H}}^{+} {\tilde{r}}_{n} = {{\tilde{H}}^{H} (\tilde{H} {\tilde{H}}^{H})}^{- 1} {\tilde{r}}_{n}

(11)

{\hat{d}}_{M M S E} = {{\tilde{H}}^{H} (\tilde{H} {\tilde{H}}^{H} + γ^{- 1} I_{N_{a}})}^{- 1} {\tilde{r}}_{n}

(12)

The variables

{\tilde{H}}^{H}, {\tilde{H}}^{+}, I_{N_{A}},

and

γ

represent the conjugate transpose of the channel matrix, the Moore-Penrose pseudo-inverse matrix, the identity matrix of dimensions N_a×N_a, and the SNR [37], respectively. It is postulated that the expected value of the random variable d_n is equal to the expected value of the random variable

{\tilde{z}}_{n}

, both of which are considered to be zero. Additionally, the expected value of the product of d_n and its conjugate transpose is equal to the identity matrix, while the expected value of the product of d_n and the conjugate transpose of

{\tilde{z}}_{n}

is supposed to be zero. Lastly, the expected value of the product of

{\tilde{z}}_{n}

and its conjugate transpose is equal to σ² times the identity matrix.

The ZF equalizer exhibits suboptimal performance due to noise optimization, while the MMSE equalizer demonstrates superior performance for all linear equations. However, the MMSE equalizer is characterized by its high complexity, requiring

O ({N_{a}}^{3})

complex operations. This complexity becomes problematic for larger values of N_a.

The real-time implementation of IoT transportation systems can be greatly impacted by the computing complexity of algorithms such as the MMSE equalizer. IoT devices, which frequently have limited processing power and memory, may be strained by this complexity. For activities like autonomous vehicle control, traffic management, and vehicle-to-vehicle communication, real-time processing is crucial, and the time needed for MMSE equalization could cause unacceptably long delays.

Battery-powered Internet of Things devices may have a shorter operating life because of higher energy consumption brought on by the computational complexity of MMSE equalization. An additional constraint on scalability is the increase in linked devices and data streams. Complex equalization techniques might cause delays that compromise the stability of the signal, resulting in communication failures or erratic data delivery.

To overcome computational difficulties, certain IoT transportation systems can use specialized hardware accelerators or coprocessors; nevertheless, these can raise the complexity and cost of the system. For IoT transportation system designers, choosing the right algorithm is essential. For real-time operation, lower-complexity algorithms might be chosen.

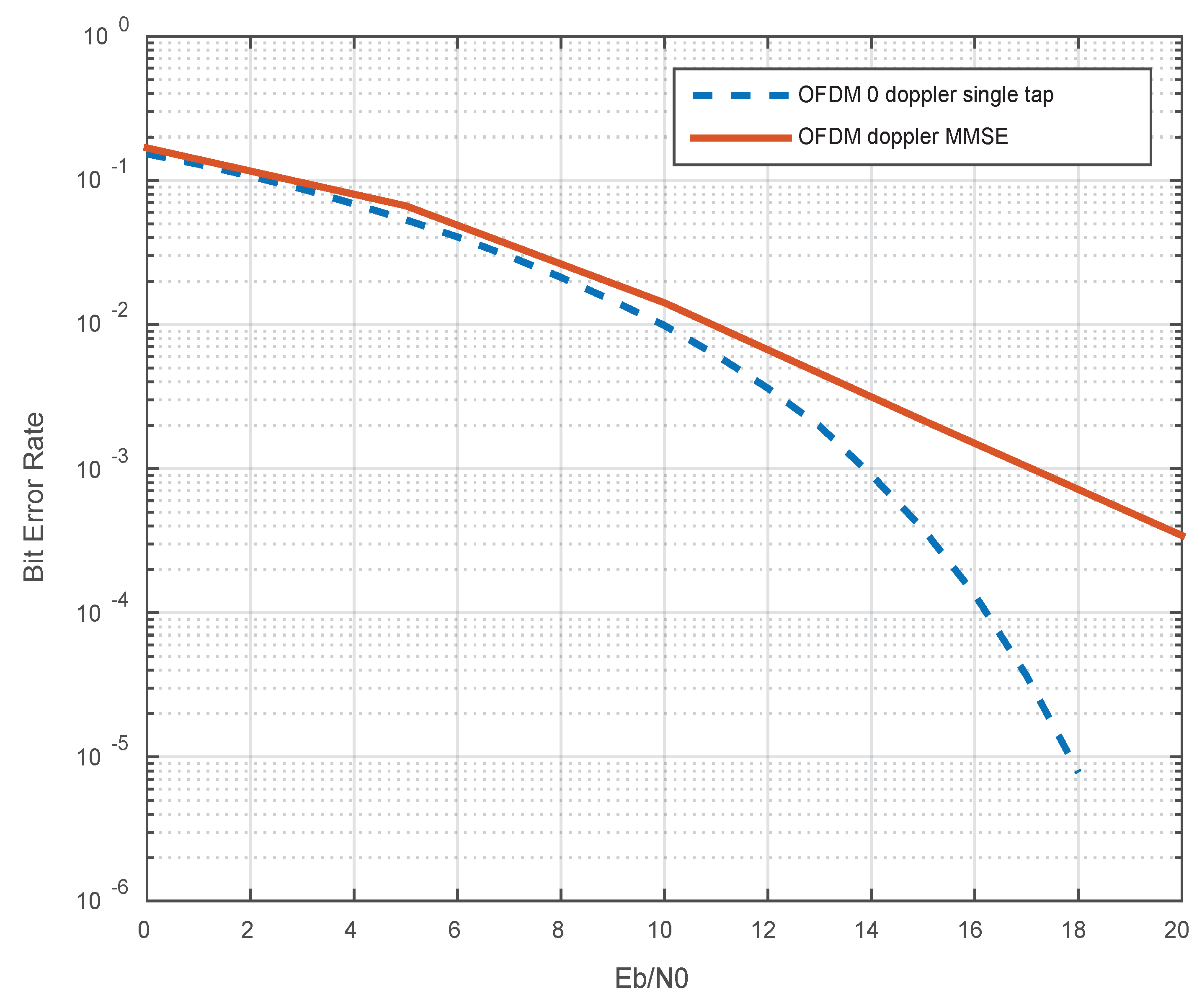
In a channel environment that remains constant over time, OFDM utilizes a single-tap equalizer. Conversely, when dealing with a channel that varies with time, the OFDM system employs the MMSE equalizer. The comparison of the bit error rate (BER) performance for these two scenarios is illustrated in Figure 3.

Figure 3 demonstrates that employing single-tap equalizers within the OFDM system leads to exceptional performance, characterized by significantly reduced complexity. However, when single-tap equalization is applied to a channel with doubly dispersive characteristics, it results in subpar performance that cannot be effectively harnessed. As depicted in Figure 3, the use of MMSE equalization proves to be advantageous when dealing with a doubly dispersive channel.

5. Proposed Conjugate Gradient Least Squares Algorithm:

Although the MMSE equalizers perform superior to other linear equalization techniques, their complexity makes them impractical for scenarios involving long symbols, such as broadcasting applications. This is primarily due to the computationally intensive matrix inversion process, as indicated by equation (12). Many alternative equalizers have been devised to tackle the intricacies connected with MMSE equalization. According to the references [35,36], it has been found that doubly dispersive channels tend to produce a channel matrix in the frequency domain that is virtually banded. A low-complexity solution in the form of a serial MMSE equalizer was offered in [38] as a reaction. As described in reference [32], an alternative approach proposes a low-complexity equalizer implemented in a banded structure. These low-complexity equalizers demonstrate performance outcomes that are substantially the same or comparable to the block MMSE method while effectively decreasing the computational cost.

The MMSE equations pose a challenge due to the computational complexity associated with matrix inversion, as demonstrated in equation (12). One innovative way to simplify the MMSE equations is to execute the matrix inversion iteratively.

The block iterative methods effectively solve the linear system of equations AX = B, where A is a sparse, rectangular, or square matrix of dimensions m × n (where m is greater than or equal to n). These methods are particularly suitable for solving least squares problems using block approaches, offering three primary advantages. Initially, it is probable to compute solutions for many right-hand sides, which proves advantageous in various practical scenarios, such as pursuing solutions over numerous right-hand vectors in multi-objective optimization. In the context of the second feature, it has been observed that the utilization of block approaches can enhance the rate of convergence in comparison to right-sided one-sided solutions. This improvement can be attributed to the iterative examination of several pathways within a Krylov subspace. The third characteristic pertains to the computational efficiency achieved by linear systems with significantly large matrix coefficients, which can permit efficient calculation.

In the cited references [24,25,37], the authors employed the iterative LSQR approach to solve the challenge of channel matrix inversion, particularly for unconditional matrices. This method demonstrates exceptional performance by efficiently ending iterations at an early stage, hence reducing computational complexity. This method is typically advisable when the maximum channel delay is limited. Recently, a novel iterative technique called CGLS has been introduced[26].

The CGLS algorithm is a highly effective iterative approach for addressing large and sparse linear least-squares problems. The hybrid process, which combines elements of the Conjugate Gradient (CG) and Least Squares (LS) methods, is particularly advantageous when dealing with a large and sparse coefficient matrix and seeking a solution with a small 2-norm. This technology's application spans multiple disciplines, encompassing machine learning, control systems, signal processing, and image processing.

The CGLS algorithm is a dependable and effective method for addressing linear least-squares problems that are both big in size and sparse in nature. The 2-norm of the residual vectors is decreased through the utilization of the conjugate gradient approach and the least squares method, ultimately leading to the identification of a solution that minimizes the 2-norm of the residual vectors. The suitability of this method for a wide range of applications, such as machine learning and image processing, is attributed to its ability to handle sparse matrices efficiently, ensure global convergence, and accommodate preconditioning techniques. Preconditioning methods can enhance the durability and convergence rate of the algorithm.

A.: Comparison between CGLS and LSQR

The techniques LSQR and CGLS are useful in communications engineering for tackling difficult and poorly populated linear least squares issues. These techniques work especially well for matrices with sparse elements and dense right-hand sides. While LSQR employs an iterative strategy and has remarkable performance in solving linear least squares problems, independent of their sparseness or density, CGLS is a trustworthy method for addressing sparse linear least squares issues on a large scale. Both approaches have effective, adaptable regularization algorithms that can handle ill-posed scenarios.

CGLS uses the conjugate gradient approach when tackling least squares issues, while LSQR employs the QR decomposition approach. Both techniques work well when used on sizable matrices with sparse populations. CGLS may show rapid convergence when conditions are favourable, whereas LSQR may offer greater resilience. The LSQR and CGLS algorithms have a computational complexity of O(k*(n+m)*m) and O(k*n*m), respectively. Depending on the situation's specifics, various algorithms' computational complexity can change.

B.: Conjugate Gradient Basics

The CG approach has proven to be an effective iterative technique for solving systems of linear equations. Specifically, computational geometry addresses problems of the following nature.

\hat{g} = \arg \min {‖b - A \tilde{g}‖}^{2}

(13)

In the field of communications engineering, when working with a positive definite matrix A, the CG method provides an iterative approach for efficiently computing the solution vector g, effectively reducing computational complexity. This approach differs from direct techniques, which require the calculation of

\hat{g} = A^{- 1} b

. Another noteworthy computational geometry technique in this context is the CGLS method.

In contrast to the traditional CG method, the CGLS algorithm can accommodate non-square matrices, hence eliminating the need for computing the regularised Gramme matrix. As a result, the CGLS method emerges as a feasible choice for solving systems of linear equations (Ax = b) and least squares (LS) problems (

m i n {‖A x - b‖}_{2}

), in which matrix A can be regarded as an efficient linear operator. The CGLS algorithm utilizes the Golub-Kahan bidiagonalization method, which is specifically designed for solving the equation

A^{T} A x = A^{T} b

The CGLS algorithm is based on the Golub-Kahan bidiagonalization process applied to matrix A, much to the LSQR approach. The LSQR method has been mathematically compared with the CGLS algorithm in addressing least squares issues. The LSQR algorithm differs from the CGLS algorithm by the Golub-Kahan bi-diagonalization technique and the Lanczos process. As a more modern approach to approximating least squares solutions, the LSMR method, a variation of LSQR, is introduced [38]. Similar to the MINRES approach, the LSMR method is particularly effective at resolving equations of the form

A^{T} A x = A^{T} b

. The following normal equation has been discovered to work exceptionally well with the LSQR methodology:

(A^{T} A + λ^{2} I) x = A^{T} b

(14)

The LSQR and CGLS algorithms show convergence but ultimately reach the same solutions. It is important to note that the CGLS algorithm converges faster and needs fewer iterations to get the required result. The CGLS approach, which offers enhanced computing efficiency and decreased costs due to its rapid solution convergence, can address the problem with the inversion matrix in the MMSE equalizer more successfully.

C.: CGLS Algorithm

The objective of the CGLS method is to estimate the solution of the linear problem given as:

A^{T} A x = A^{T} b

(15)

m i n {‖A x - b‖}_{2}

(16)

Hestenes and Stiefel initially proposed the resolution of the least squares problem [39] in the context of the CGLS method. The construction of a sequence of estimated solutions will be facilitated by the utilization of an initial solution approximation.

The CGLS algorithm is a frequently used iterative method employed to solve linear least squares problems. It is particularly well-suited for situations where the coefficient matrix is both large and sparse, leading to efficient computational performance and memory utilization. The CGLS technique finds application in various domains, including signal processing, image reconstruction, and solving linear systems. Here, we provide an in-depth overview of the CGLS algorithm.

The objective of this task is to find a solution for the linear least squares problem, denoted as Ax ≈ b. In this problem, A represents a matrix, x represents the solution vector, and b represents the vector of observed data.

Algorithmic Steps:

Initialization:

Start with an initial estimate of the solution vector, x₀ (e.g., all zeros).
Compute the initial residual vector, r₀ = b - Ax₀.

Iteration:

For each iteration, denoted by the variable k, starting from 1 and continuing indefinitely until convergence is achieved:

The computation of the search direction vector, pₖ, can be achieved by taking the transpose of matrix A, denoted as Aᵀ, and multiplying it by the residual vector rₖ.

The step size, denoted as αₖ (also known as the scaling factor), can be computed using

αₖ = (rₖᵀrₖ) / (pₖᵀApₖ).

update the solution vector: The updated solution vector can be expressed as xₖ₊₁ = xₖ + αₖpₖ.

The residual vector can be updated in an iterative process: rₖ₊₁ = rₖ - αₖApₖ

The convergence of the solution can be assessed by monitoring either the norm of the residual vector or the change in the solution.

If the convergence requirements have been satisfied, terminate the iteration process.

Alternatively, proceed to the subsequent iteration.

Termination:

Upon the algorithm's convergence or upon reaching a predetermined number of iterations, the solution vector x shall be returned. The solution vector provided is an approximate solution to the initial least squares problem.

Key Features and Considerations for The Conjugate Gradient Least Squares:

(1): The CGLS method is particularly advantageous in the context of large and sparse matrices due to its ability to circumvent the explicit construction of normal equations (AᵀA).
(2): The methodology utilizes an iterative strategy, consistently enhancing the solution vector x and diminishing the residual error.
(3): The CGLS algorithm is considered to be memory-efficient due to its ability to operate without the need for keeping a huge dense matrix.

The CGLS algorithm is a commonly employed technique for effectively addressing linear least squares problems, encompassing activities such as solving equation systems, reconstructing images, and optimizing objectives. The technique in question exhibits mathematical resemblances to the Conjugate Gradient algorithm and is regarded as being more precise owing to its capability to circumvent explicit computation of the matrix product at each iteration. The computational complexity of the CGLS algorithm is determined by the number of iterations required to achieve a specified degree of accuracy. This complexity is impacted by factors such as the issue size, features of the matrix involved, and the behavior of the convergence process. In contrast to other algorithms, the CGLS algorithm does not possess a predetermined temporal complexity. Instead, its temporal behavior is characterized by the number of iterations required for achieving convergence. The condition number (κ) of the coefficient matrix (A) is the primary factor influencing the number of iterations in CGLS. The CGLS's convergence behavior can be significantly impacted by the condition number, which expresses how sensitive the issue is to variations in the data or input.

The i needed for CGLS to reach a particular level of accuracy is often estimated using the following formula:

i = \sqrt{k} l o g (ε)

(17)

Whereas

Matrix A's condition number is k.

The intended accuracy or tolerance is represented by

ε

Remember that this is only an approximate estimate, and the real number of iterations may differ depending on the specifics of the problem, the selection of the stopping criterion, and the matrix A's attributes.

It is worth saying that the complexity of the MMSE equalizer is The time complexity of matrix inversion is typically cubic in the size of the matrix

O ({N_{a}}^{3})

, making it impractical for large matrices.

D.: Linear CGLS Equalizer

The dispersion doubly channel matrix exhibits both maximum Doppler shift and delay spread. Therefore, the system matrix

\tilde{H}

exhibits a significantly large condition number, making it challenging to employ the CGLS equivalent directly

\tilde{H}

. However, the H-banded form can be utilized to mitigate the complexity involved.

The computation of the equalizer matrix W_n is restricted to the initial sub-Q and super-diameters of H ̃, which represents the fractional domain channel matrix. This computation involves the utilization of a binary masking matrix M, which contains certain elements as follows:

M (m, n) = \{\begin{matrix} 1 0 \leq |m - n| \leq Q \\ 0 Q < |m - n| < N_{a} \end{matrix}

(18)

The dimensions of the matrix are indicated on the masked matrix.

B_{n} = M ⊙ \tilde{H}

(19)

The MMSE equalizer can be defined analogously based on the masked matrix [26], where ⊙ represents element-wise multiplication.

W_{n, M M S E} = {B_{n}^{H} (B_{n} B_{n}^{H} + γ^{- 1} I_{N_{a}})}^{- 1}

(20)

The inclusion of Q off-diagonal components above and below the main diagonal in the band structure of

B_{n}

leads to the formation of a band structure for the matrix

(B_{n} B_{n}^{H})

. This approach simplifies the computation of the MMSE equaliser in equation (12). However, as the value of (19) is time-dependent, the estimation

{\hat{d}}_{n} = W_{n, M M S E} {\tilde{r}}_{n}

can be obtained without explicitly stating the specific value of

W_{n, M M S E}

The equation for the CGLS equalizer is as follows:

B_{n}^{H} B_{n} {\hat{d}}_{Z F} = B_{n}^{H} {\tilde{r}}_{n}

(21)

The normal equation is derived by excluding the noise term

{\tilde{z}}_{n}

from equation (12), and then replacing

\tilde{H}

with

B_{n}

. Finally, the equation is multiplied on the left by

B_{n}^{H}

. The aim is to minimize the norm of the difference between the product of matrix B_n and the vector

{\hat{d}}_{Z F} - {\tilde{r}}_{n}

, denoted as

‖B_{n} {\hat{d}}_{Z F} - {\tilde{r}}_{n}‖

, may be demonstrated to yield an approximation of the linear least squares problem during the i^th iteration of the CGLS algorithm.

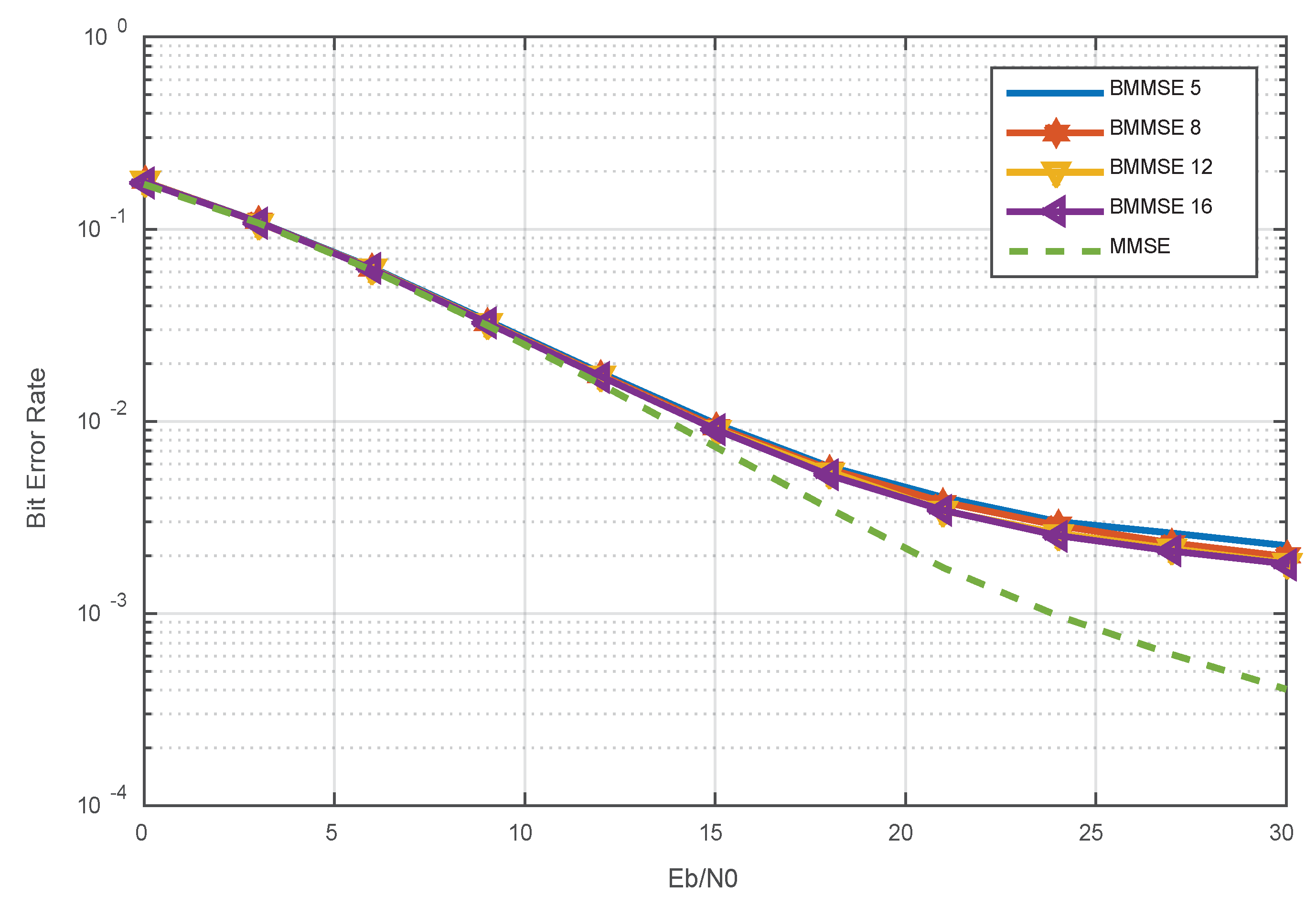
Figure 4 presents a noteworthy trade-off relationship between the number of sub-diagonals

Q

inside the channel matrix and two crucial performance metrics, namely the bit error rate (BER) and computational complexity. As the quantity of sub-diagonals escalates, there is a consistent decline in the BER, which signifies enhanced fidelity of the signal and augmented capabilities for error correction. Nevertheless, the decrease in BER is accompanied by a rise in computational complexity, as the system is required to handle a larger amount of data. The presented figure demonstrates a significant observation: the increase in sub-diagonals from 5 to 16 results in a minimal improvement in BER, indicating that the decrease in errors diminishes beyond a certain threshold. Therefore, it is deemed advantageous to achieve a harmonious equilibrium by opting for the selection of five sub-diagonals. The decision made successfully strikes a balance between intricacy and effectiveness, providing a significant standard for evaluating the system's efficacy in mistake handling and computing requirements management.

The exclusion of noise effects in a zero-forcing equalizer amplifies noise and modeling mistakes, affecting the system's overall performance. Similarly, the CGLS equalizer functions on the same concept, disregarding the influence of noise. The number of iterations is a crucial factor in determining the effectiveness of the CGLS approach. By carefully choosing the number of repetitions, it is possible to decrease system errors to a similar extent as obtained through MMSE equalization. Nevertheless, a high number of iterations can substantially impact the noise levels and mistakes in the modelling process, given the heavy reliance of CGLS inputs on approximations.

E.: Regularized CGLS Equalizer

The estimated data

{\tilde{d}}_{M M S E}

from (12, 19) can be written in one of the following two forms:

{\hat{d}}_{M M S E} = {{\tilde{H}}^{H} (\tilde{H} {\tilde{H}}^{H} + γ^{- 1} I_{N_{a}})}^{- 1} {\tilde{r}}_{n}

(22)

{\hat{d}}_{M M S E} = {(\tilde{H} {\tilde{H}}^{H} + γ^{- 1} I_{N_{a}})}^{- 1} {\tilde{H}}^{H} {\tilde{r}}_{n}

(23)

by left multiplying with

({\tilde{H}}^{H} \tilde{H} + γ^{- 1} I_{N_{a}})

, we can get:

({\tilde{H}}^{H} \tilde{H} + γ^{- 1} I_{N_{a}}) {\hat{d}}_{M M S E} = {\tilde{H}}^{H} {\tilde{r}}_{n}

(24)

which is equivalent to the regularized least squares (RLS) problem

(A^{T} A + λ^{2} I) x = A^{T} b

to minimize

m i n {‖(\begin{matrix} A \\ λ \end{matrix}) x - (\begin{matrix} b \\ 0 \end{matrix})‖}_{2}

, CGLS equalizer.

Working with the complete

\tilde{H}

matrix can pose challenges, resulting in the formation of the B_n matrix. Consequently, the problem of MMSE equalization can be formulated as follows:

(B_{n} B_{n}^{H} + γ^{- 1} I_{N_{a}}) {\hat{d}}_{M M S E} = B_{n}^{H} {\tilde{r}}_{n}

(25)

It can be demonstrated that the CGLS method can be utilized to get an approximate solution to the regularised least squares equation. Within this theoretical framework, the CGLS method incorporates two dual regularisation parameters: the number of iterations and the Signal-to-Noise Ratio (SNR) represented by the symbol γ. As mentioned above, the combination reduces the amplification of noise and improves the system's overall performance.

The attractiveness of CGLS stems from its numerical stability, intrinsic organizational skills, and the low arithmetic complexity of

O (N_{a} (Q + 1) i)

6. Advanced Nonlinear Equalization Techniques for Enhanced OFDM Performance

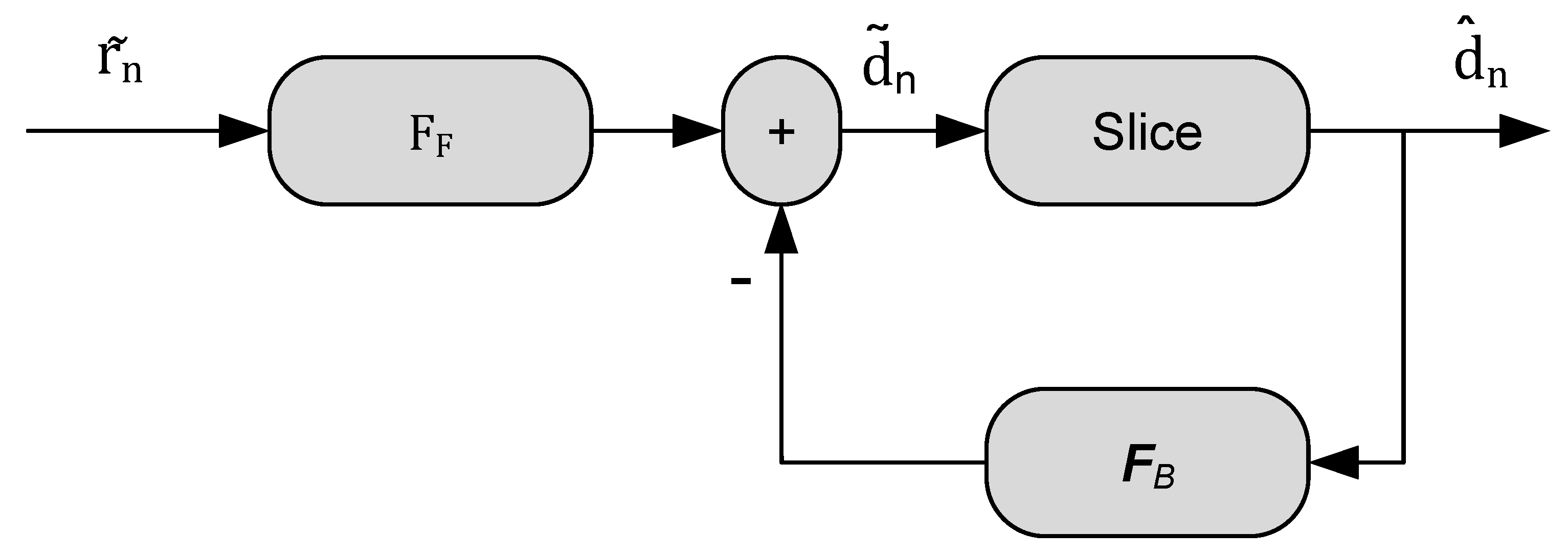
Two cutting-edge methods for equalization techniques are proposed to improve the efficiency of the OFDM systems. The first approach entails creating a low-complexity CGLS based on a banded decision feedback Equalizer (CGLS-BDFE) for OFDM, specially designed to handle the complexity presented by nonlinear equalization. This innovative method prioritizes efficiency and decreased complexity while minimizing the ICI present in OFDM.

The idea of an RLS-CGLS sliding window equalizer is also explored. This method uses the CGLS method and the RLS algorithm. A sliding window equalization system is being developed to address the dynamic changes in the OFDM channel efficiently. This strategy tries to improve performance while enabling adaptation to the shifting channel circumstances frequently seen in real-world situations.

These two solutions demonstrate the dedication to enhancing communication effectiveness and dependability in difficult channel circumstances. They also represent substantial breakthroughs in OFDM equalization strategies.

A.: Low Complexity CGLS-based Block Decision Feedback Equalizer for OFDM (Nonlinear equalizer).

The block decision feedback equaliser (BDFE) was initially proposed in reference [40] as a means to improve the performance of the MMSE equalizer. This enhancement is accomplished by employing a recursive methodology for data detection, which emphasizes the detection of individual data points sequentially, in contrast to the simultaneous detection of all data points as exhibited by previous techniques. The strategy mentioned above follows sequential detection, a widely employed technique in multi-user detection in DS-CDMA systems.

An innovative equalizer was developed by combining the CGLS and MMSE-BDFE methods, aiming to simplify the complexity of the MMSE-BDFE equalizer while improving its performance. The suggested equalizer utilizes the CGLS algorithm to address and reduce band approximation inaccuracies properly. Furthermore, the proposed method integrates a band LDL^H factorization technique with a DFE, enhancing performance while avoiding increased complexity. The methods proposed were utilized to develop the design of both feedforward (F_F) and feedback (F_B) filters, as depicted in Figure 5. This strategy successfully reduces the error, which is represented as

e = {\tilde{d}}_{n} - d_{n}

. It is important to mention that F_B is designed in a manner that adheres to a rigid upper triangular structure, which enables the utilization of a consecutive cancellation mechanism during the feedback process.

Under the standard assumption of correct prior judgments, denoted as

{\hat{d}}_{n} = d_{n}

, the error vector can be mathematically represented as:

e = F_{F} {\tilde{r}}_{n} - (F_{B} + I_{N_{a}}) d_{n}

(26)

The relationship between F_F and F_B is determined using the minimizing of mean square error (MSE) criterion as stated in reference [40].

F_{F} = {(F_{B} + I_{N_{a}}) ({\tilde{H}}_{α}^{H} {\tilde{H}}_{α} + γ^{- 1} I_{N_{a}})}^{- 1} {\tilde{H}}_{α}^{H} = (F_{B} + I_{N_{a}}) W_{M M S E}

(27)

by applying the band approximation

{\tilde{H}}_{α} = B_{n}

F_{F} = (F_{B} + I_{N_{a}}) {(B_{n} B_{n}^{H} + γ^{- 1} I_{N_{a}})}^{- 1} B_{n}^{H}

(28)

The structure of the feedforward filter can be described as a sequential combination of two components: a low-complexity MMSE equalizer and an upper triangular matrix denoted as F_B+I_Na, which has a unit diagonal. The full construction of both the F_F and F_B filters was thoroughly discussed in [40], providing a comprehensive explanation of their design. The task at hand entailed the clarification of the autocorrelation matrix associated with the error vector e.

R_{e e} = σ^{2} (F_{B} + I_{N_{a}}) {(B_{n} B_{n}^{H} + γ^{- 1} I_{N_{a}})}^{- 1} {(F_{B} + I_{N_{a}})}^{H}

(29)

where

σ^{2}

is the noise variance. By using the LDL^H, (29) is obtained:

M = B_{n} B_{n}^{H} + γ^{- 1} I_{N_{a}} = L D L^{H}

(30)

Within this situation, the symbol L indicates the lower triangular matrix with a unit diagonal, while the symbol D denotes the diagonal matrix. Minimizing the expected error E{e²} can be achieved by establishing the following relationship, which simplifies the process.

F_{B} = L^{H} - I_{N_{a}}

(31)

which reduces

R_{e e}

diagonal.

F_{F}

can be expressed by:

F_{F} = L^{H} W_{M M S E} = L^{H} M^{- 1} B_{n}^{H} = D^{- 1} L^{- 1} B_{n}^{H}

(32)

Despite the apparent complexity of equations (30) and (31), the utilization of the CGLS method, considering the diagonal nature of D, the banded structure of B, and the lower triangular and banded properties of L, reveals that the banded CGLS-BDFE exhibits remarkably low computational complexity. In the context of signal processing, the feedforward filter is a type of filter that operates by processing the input signal in a forward direction.

OFDM equalizers

d_{n} = F_{F} {\tilde{r}}_{n}

(33)

{\tilde{r}}_{n} = F_{F}^{- 1} d_{n} = B^{- H} D L d_{n}

(34)

from equation(32 and 33), it can be shown that:

D L = (B_{n} B_{n}^{H} + γ^{- 1} I_{N_{a}}) L^{- H}

(35)

{\tilde{r}}_{n} = B_{n}^{- H} (B_{n} B_{n}^{H} + γ^{- 1} I_{N_{a}}) L^{- H} d_{n} = (B_{n} + B_{n}^{- H} γ^{- 1}) L^{- H} d_{n}

(36)

which can be solved efficiently using the CGLS algorithm.

The computational complexity of the CGLS-BDFE equalizer is highly similar to that of the RLS- CGLS equalizer, resulting in a total of O (N (Q+1) i) complex operations.

The uncoded BER performance analysis for OFDM using the CGLS-BDFE equalizer is conducted via simulations spanning 100,000 multicarrier blocks. This assessment pertains to an OFDM setup characterized by parameters N=128, N_A=96, L=8, and QPSK modulation scheme. The channel is simulated by a set of Rayleigh channels with the spread of RMS delay for three sample cycles. The channel model uses the same statistics as [14], including the maximum Doppler spreading of 15 % carrier spacing.

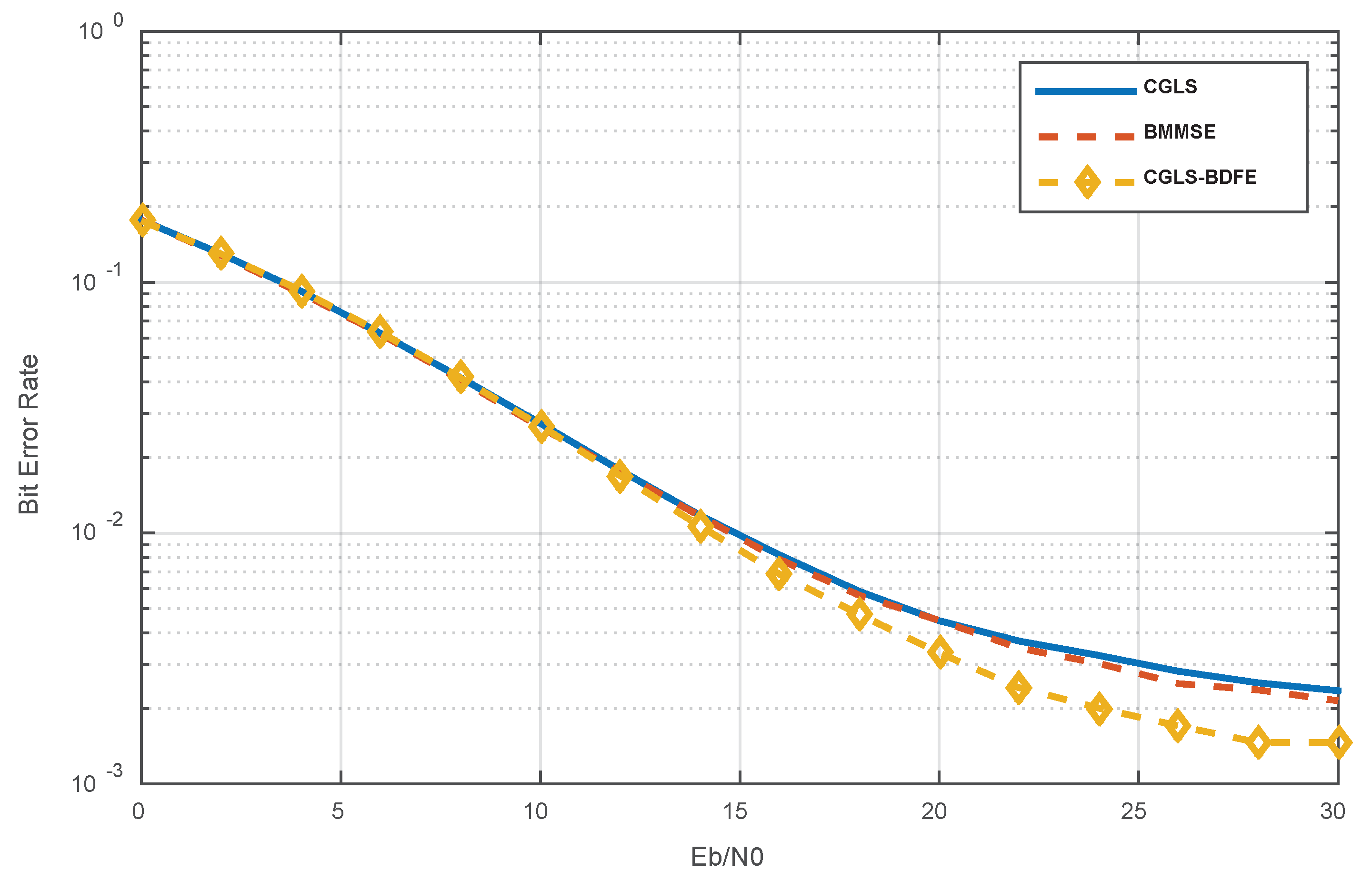
Figure 6 illustrates a comparative analysis of OFDM systems employing Q=5. The comparison includes the utilization of CGLS, BMMSE, and CGLS-BDFE equalizers. The graphical depiction in Figure 6 reveals that the CGLS-BDFE equalizer achieves the highest level of performance, while the BMMSE and CGLS equalizers exhibit nearly comparable performance. Through our simulation results, it is evident that the nonlinear approach significantly enhances performance, achieving an improvement of nearly 5 dB. Notably, the CGLS-BDFE equalizer demonstrates the highest level of performance, while the BMMSE and CGLS equalizers exhibit closely comparable performance. Specifically, it's noteworthy that achieving the same bit error rate requires 20 dB for the CGLS-BDFE nonlinear equalizer, while both the BMMSE and CGLS linear equalizers necessitate 25 dB.

B.: RLS-CGLS Sliding Window Equalizer

The authors of [41] proposed using sliding window equalization to reduce the complexity often associated with the MMSE equalizer. The proposed methodology involves dividing the process of inverting a large matrix into a sequence of smaller matrix inversions. As an illustration, the computational complexity of matrix inversion, specifically for an N×N matrix, is sometimes expressed as O(N³). Let us consider a hypothetical scenario in which the value of N is set to 96. In this case, the processes' complexity would amount to a total of 884,736 complicated operations.

Nevertheless, the total complexity can be reduced by segmenting the inversion process into smaller computations. In this case, the 96 symbols can be computed using a window 9. By doing so, the overall complexity decreases to 69,984, calculated as 9 raised to the power of 3, multiplied by 96.

The central idea is to choose a condensed window from the broader banded system matrix Bn, aiming to estimate symbols for a particular subcarrier. The focal point of energy associated with the symbol of interest is centered within this specific window, while the surrounding components are disregarded. The method mentioned above is executed systematically, wherein the window is shifted across all subcarriers within the received multicarrier signal. By employing this approach, the system's complexity being studied is notably reduced while still upholding its overall performance. Using the CGLS algorithm to handle the resultant system with reduced dimensions can effectively enhance the process of simplifying complexity.

Let us examine a scenario in which the detection of the data symbol

d_{k, n}

is required. It is worth noting that the majority of the symbol energy associated with

d_{k, n}

is concentrated on the subcarrier k and its adjacent subcarriers. The estimation of

d_{k, n}

can be achieved by utilizing the following method:

{\hat{d}}_{k, n} = W_{M M S E, k} {\tilde{r}}_{k}

(37)

The vector

{\tilde{r}}_{k} = {[{\tilde{r}}_{k - D} \dots {\tilde{r}}_{k + D}]}^{T}

is defined as a concatenation of the elements. The received vector

\tilde{r}

consists of the symbol

d_{k, n}

and its neighboring symbols. The number of related symbols, denoted as P, equals 2D+1. The sliding window matrix has a size of

(P \times K)

, where K is equal to

(2 Q + 1)

. Here, Q represents the number of sub- and super-diagonals that define the limits of the banded matrix. The MMSE equalizer for the k symbol window is denoted as

W_{M M S E, k}

W_{M M S E, k} = {(B_{n, k} B_{n, k}^{H} + γ^{- 1} I_{k})}^{- 1} B_{n, k}^{H}

(38)

The

B_{n, k}

matrix is a component of the banded system matrix

B_{n}

, which has dimensions P×K. It can be defined as follows:

B_{n, k} = [\begin{matrix} \begin{matrix} B_{k - D, k - Q} & B_{k - D, k - Q + 1} \\ B_{k - D + 1, k - Q} & B_{k - D + 1, k - Q + 1} \end{matrix} & \begin{matrix} \dots & B_{k - D, k + Q} \\ \dots & B_{k - D + 1, k + Q} \end{matrix} \\ \begin{matrix} ⋮ & ⋮ \\ B_{k + D, k - Q} & B_{k + D, k - Q + 1} \end{matrix} & \begin{matrix} ⋮ & ⋮ \\ \dots & B_{k - D, k + Q} \end{matrix} \end{matrix}]

(39)

By implementing this approach, the intricacy linked to the inversion of a

N_{a} \times N_{a}

matrix is converted into N inversions of P×K matrices. The optimization of this reduction in complexity can be enhanced by incorporating the CGLS algorithm to tackle the issue of regularized least squares.

(B_{n, k} B_{n, k}^{H} + γ^{- 1} I_{k}) {\hat{d}}_{k} = B_{n, k}^{H} {\tilde{r}}_{k}

(40)

The degree to which complexity is reduced within the system is contingent upon the size and dimensions of the sliding window matrix P. Significantly, the utilization of a comparatively low value for the parameter P does not significantly affect the overall performance of the system. Furthermore, a notable benefit of this approach is its ability to reduce the need for accurate channel matrix estimation, as it only requires a limited number of channel components. The computational complexity of the sliding window equalization can be denoted as

O (N_{a} P (Q + 1) i_{P \times K})

. Upon initial examination, this may surpass the complexity of existing low-complexity equalizers based on CGLS. However, a substantial disparity arises in the number of iterations required to solve the smaller P×K matrix, denoted as

i_{P \times K}

, which is considerably less than the iterations needed to solve the bigger

N_{a} \times N_{a}

matrix.

An evaluation is undertaken to analyze the performance of OFDM in terms of the uncoded BER. This assessment involves the use of simulations that comprise 100,000 multicarrier blocks. The primary objective of this study is to assess the utilization of the RLS- CGLS sliding window equalizer in the context of employment. In this research, we analyze an OFDM system with specific parameters. The system has a total number of subcarriers, N, equal to 128. The number of active subcarriers, N_A, is 96. The length of the cyclic prefix, L, is 8. The modulation scheme employed is QPSK. The Rayleigh fading channel model is applied using identical parameters in the preceding section, ensuring a fair comparison of the outcomes.

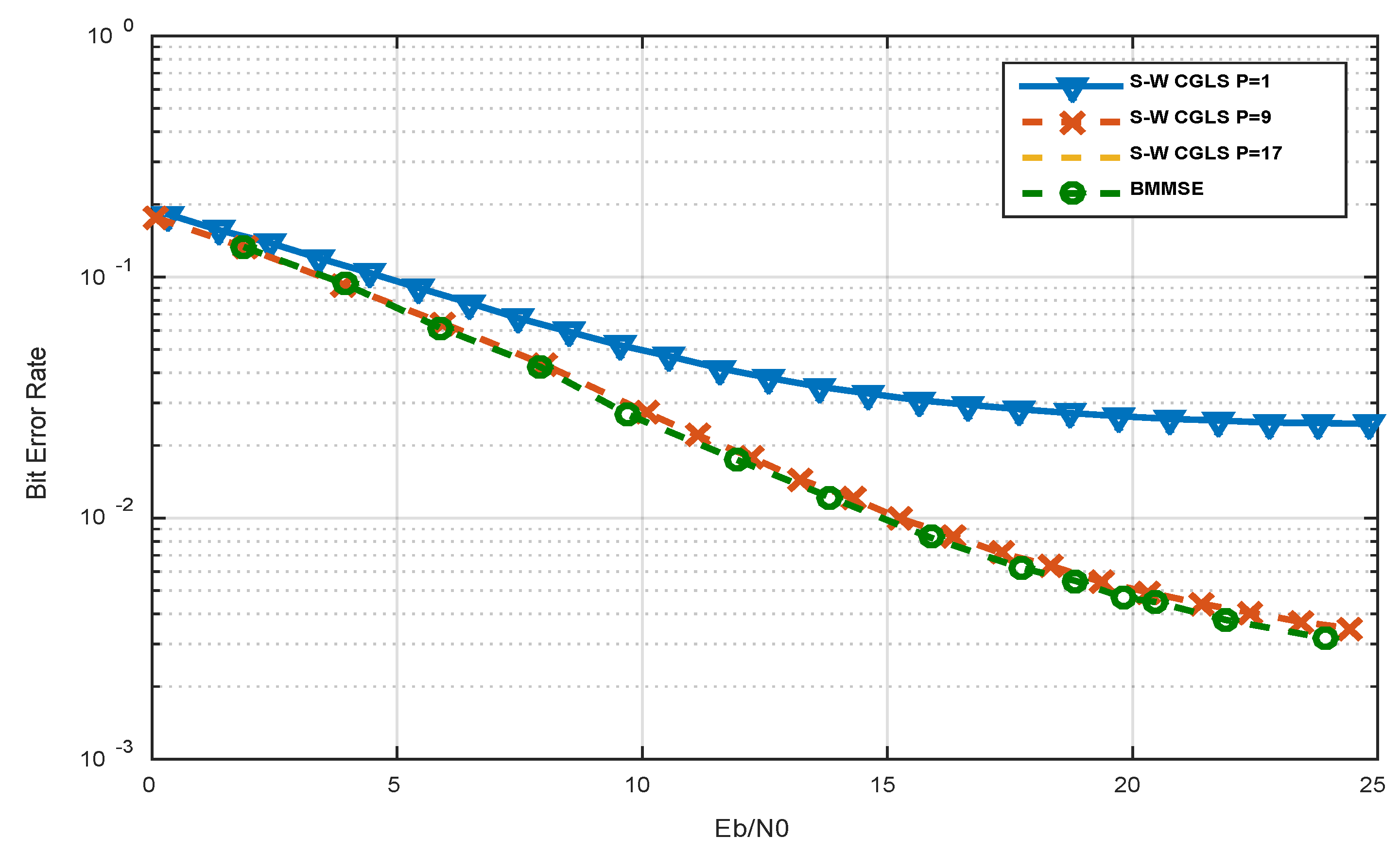
Figure 7 compares the recently introduced RLS- CGLS sliding window equalizer and the banded MMSE equalizer, both operating with a value of Q equal to 5. The findings suggest that the banded MMSE equalizer performs better, while the RLS- CGLS sliding window equalizer shows nearly identical performance in situations with a low SNR. The degree of performance decline depends on the size of the window matrix. The performance of the RLS- CGLS sliding window equalizer is almost identical to BMMSE with much less complexity.

Simulation results conducted in the context of doubly dispersive fading channels reveal the superiority of the proposed CGLS algorithm over the BMMSE method. The nonlinear equalizers introduced in the CGLS algorithm consistently outperform their counterparts regarding bit error rate and overall communication performance. the proposed nonlinear equalization technique determines the trade-off between computations and performance. As nonlinear equalization added some complexity to the overall system it effectively improved performance.

Equalizer selection for OFDM

The selection of an equalizer for an OFDM system is contingent upon various aspects, such as the prevailing channel circumstances, the desired performance specifications, and the computational resources at hand. In scenarios where the channel circumstances exhibit favorable characteristics and there are constraints on computational resources, employing a linear equalizer can be a judicious decision. In scenarios where the channel circumstances exhibit greater severity and computational resources are abundant, alternative equalization techniques such as the zero-forcing equalizer, minimal mean square error equalizer, decision feedback equalizer, BMMSE equalizer, or RLS Sliding Window Equalizer may present more favorable options. Machine learning equalizers are a favorable option for applications that demand optimal performance and have sufficient computational resources at their disposal.

The comparative analysis of several OFDM equalizers, including factors such as computational complexity, performance metrics, as well as their respective strengths and weaknesses, can offer useful insights into the selection process of an appropriate equalizer for a certain application. Table 1 presents a comparative analysis of various OFDM equalizers often employed in wireless communication systems.

Upon comparing various OFDM equalizers, it becomes evident that optimal performance can be achieved by combining the MMSE equalizer with nonlinear equalizers. However, this approach significantly increases computational complexity, rendering it impractical for real-time applications. Hence, a practical strategy involves integrating the BMMSE equalizer with nonlinear equalizers to enhance BMMSE performance while concurrently reducing computational demands. Additional complexity reduction can be attained by utilizing iterative algorithms specifically developed for addressing the computationally intensive task of channel matrix inversion, which constitutes the most resource-intensive aspect of the equalization process. These iterative methods include LDL factorization, LSQR, LSMR, and CGLS.

Table 2 offers a comprehensive comparison of the complexity and performance aspects of these iterative matrix inversion algorithms.

The choice of an iterative matrix inversion algorithm depends on various factors, including the matrix's size, sparsity, desired precision, and available computational resources. LDL factorization is a viable choice when precision is paramount, especially for dense matrices. In scenarios involving sparse matrices where both high accuracy and efficiency are essential, algorithms like LSQR, LSMR, or CGLS may be more appropriate. Among these options, CGLS stands out as the optimal choice for real-time OFDM equalization, offering the lowest computational complexity while maintaining efficiency and accuracy.

The trade-off between computational complexity and performance in the context of IoT transportation systems:

Adaptive approaches are used by the RLS-CGLS Sliding Window Equalizer and the CGLS-BDFE to balance performance and computational complexity. To achieve the ideal balance in IoT transportation systems, they dynamically modify their operations based on observed conditions, predefined thresholds, and real-time requirements. This flexibility is essential to guarantee effective, dependable, and instantaneous communication in settings that are dynamic and resource-constrained.

(1): CGLS-BDFE OFDM equalizer:

Adaptive Iterations: The CGLS-BDFE equalization process is iterative. It adjusts based on the performance that is observed, beginning with fewer iterations. It can balance performance and computational complexity because of its versatility. Fewer iterations are done at first to save computing strain, and if more iterations are needed for better equalization, they are subsequently increased.

Dynamic Complexity Control: While the algorithm is running, it dynamically modifies its complexity. In order to guarantee real-time operation, it starts with modest computational needs, particularly in IoT transportation systems where prompt data processing is essential. To enhance equalization performance, it increases its computational intensity when channel conditions change or data quality deteriorates.

Exchange of value Performance thresholds are established by CGLS-BDFE. It limits the number of repeats if the current performance reaches or surpasses the predetermined threshold, thereby avoiding needless computational overhead. The system automatically increases iterations to improve communication quality when the performance drops below predefined criteria.

Resource-Conscious Design: The algorithm is made to use resources as efficiently as possible. To cut down on energy use, it optimizes data processing and lowers memory use. This resource-aware strategy guarantees that it can function without placing undue computing pressure on IoT devices.

(2): RLS-CGLS OFDM equalizer:

The RLS-CGLS Sliding Window Equalizer is a device that incorporates a sliding window mechanism. By restricting the range of calculations to a smaller sample of data, this method lowers the computational complexity as a whole. It maintains real-time functioning by processing a subset of the data at a time.

Window Size Adjustment: Based on channel conditions and performance needs, the algorithm can modify the sliding window's size. To minimize computational complexity, it might use a smaller window when the circumstances are right. On the other hand, it can widen the window under difficult circumstances in order to collect more information and enhance equalization.

Performance Monitoring: The equalization keeps an eye on the sliding window technique's effectiveness all the time. The status quo is maintained if the present window size and processing complexity satisfy the required performance requirements. On the other hand, it dynamically modifies the window size and processing depth to enhance communication quality if performance deteriorates.

Real-time responsiveness is a top priority for both the CGLS-BDFE and the RLS-CGLS Sliding Window Equalizer. Optimizing computational resources guarantees that IoT transportation systems can manage changing channel conditions and maintain timely data transmission.

The CGLS algorithm can play a vital role in IoT transportation systems, with several hardware implications. It is energy-efficient, making it compatible with low-power processors or specialized hardware accelerators, thus conserving energy. Real-time processing is a critical requirement for IoT applications such as autonomous vehicles and traffic management, and CGLS's iterative and adaptable nature makes it suitable for efficient real-time execution. Parallel computing architectures can enhance CGLS iterations, leading to improved real-time performance. Tailored hardware acceleration units can further boost CGLS performance while keeping energy consumption to a minimum. Scalable hardware designs are adaptable to increasing processing demands as the IoT network grows. Integration with sensors like LiDAR and cameras facilitates seamless data fusion and real-time decision-making. Incorporating redundancy and fault tolerance mechanisms enhances system reliability, even when hardware failures occur. Optimizing memory usage for storing matrices and data reduces the memory footprint of CGLS-based equalization. These hardware considerations are indispensable for achieving efficiency and high performance in IoT transportation solutions.

7. Future Directions

The effectiveness and efficiency of CGLS equalization algorithms could be improved in several ways through future research in the context of IoT transportation systems. These include security considerations, multi-objective optimization, experimental validation, standardization and integration, sparse matrix optimization, machine learning integration, quantum computing applications, robustness to hardware constraints, distributed processing, dynamic resource allocation, hardware acceleration architectures, and cross-layer optimization.

Sparse matrix optimization optimizes CGLS versions for sparse matrices, which can lower computational complexity and improve real-time performance. Using deep learning models or neural networks in machine learning can increase performance and adaptability. Because quantum computing can process data in parallel, it can speed up CGLS-based equalization. Optimizing CGLS for various processor types and memory configurations will result in robustness to hardware limitations. By dividing up equalization responsibilities among network nodes, distributed processing methods can improve scalability and lessen the load on individual devices. Computational complexity and communication quality can be dynamically balanced via dynamic resource allocation.

Architectures for hardware acceleration can further maximize performance and energy efficiency. Security issues include identifying potential weak points in the algorithm and creating defences against attackers. Multi-objective optimization takes into account hardware limits, communication quality, and energy efficiency all at once. To verify the effectiveness of CGLS-based equalization in various IoT transportation scenarios, real-world experiments and comprehensive field trials are conducted as part of the experimental validation process. Cross-layer optimization can be attained by working with researchers in other fields, but standardization and integration efforts can guarantee smooth integration into IoT transportation communication protocols.

8. Conclusions

The Internet of Things (IoT) has ushered in a significant transformation in urban operations, leaving its mark on smart infrastructure, transportation, and energy management. Within the realm of Intelligent Transportation Systems (ITS), IoT's influence has been profound, enhancing efficiency, security, and sustainability across various facets such as traffic management, predictive maintenance, parking solutions, autonomous vehicles, and optimizing emergency response strategies. ITS, driven by advanced communication technologies, represents a paradigm shift in modern transportation, enabling seamless information exchange through vehicle-to-vehicle (V2V) and vehicle-to-everything (V2X) communication.

However, the dynamic nature of V2X communication introduces Doppler frequencies, giving rise to a doubly dispersive channel that degrades the performance of Orthogonal Frequency Division Multiplexing (OFDM) due to inter-carrier interference (ICI).

Addressing the challenge of ICI in OFDM necessitates a critical Minimum Mean Square Error (MMSE) complex equalizer, which, in turn, requires intricate channel matrix inversion, contributing to its overall complexity. Enter the Conjugate Gradient Least Squares (CGLS) algorithm, a novel approach presented in this paper. It integrates an iterative computation method with nonlinear equalization techniques.

The proposed CGLS algorithm demonstrates superior performance compared to existing algorithms, showcasing an improvement of at least 5 dB. This improvement positions it as a promising solution to tackle the challenges posed by Doppler-induced inter-carrier interference in OFDM-based communication systems for ITS. Numerical results reveal that the CGLS-based nonlinear equalizers and precoding methods exhibit rapid convergence and effectively correct equalization parameter estimations.

Despite its lower computational complexity, the proposed CGLS approach can achieve error-rate performance equivalent to that of a precise inversion method. In V2X communication systems with doubly dispersive fading channels, this technique has the potential to enable efficient, high-throughput hardware designs. The algorithm's regularity and simplicity make it well-suited to address the challenges posed by such channels.

In summary, the results of this study underscore how the combination of the CGLS algorithm with nonlinear equalizers can enhance the efficiency and reliability of OFDM systems in challenging communication scenarios. These findings validate the potential of the CGLS-based approach to drive advancements in the realm of ITS and IoT-enabled V2X communication systems.

Author Contributions

Conceptualization, H.A. and M.A.; data curation, H.A.; formal analysis, M.A., A.A. ; funding acquisition, H.A.; investigation, H.A. and M.A. and A.S.; methodology, H.A., M.A. and A.A.; project administration, H.A., M.A. and A.S.; resources, H.A. and A.S.; software, H.A. and M.A. ; supervision, M.A; validation, H.A., M.A., I.C.; writing original draft, H.A.; writing review and editing, M.A., A.A., I.C., A.S. and R.A.; All authors have read and agreed to the published version of the manuscript.

Funding

This research is supported by Zarqa University, Jordan.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to extend their sincere appreciation to Zarqa University for supporting this research.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix 1

Symbol	Notation description
$r_{n}$	The received samples for the n^th OFDM symbol after discarding the CP
H	The $N \times N$ channel matrix
$F$	The DFT matrix
$F^{*}$	The IDFT matrix
$d_{n}$	The transmitted data vector in the $n^{t h}$ OFDM symbol
$z_{n}$	White Gaussian noise in the time domain
${\tilde{r}}_{n}$	Received sequence after demodulation with the DFT
$Z$	The circularly symmetric complex Gaussian random variable
$f_{d}$	The Doppler shift
$h (t)$	The channel impulse response
$z (t)$	Added noise signal
$\hat{d} (t)$	The estimated data vector
$ε$	Mean-square error
$P$	Permutation matrix
$N_{a}$	Active subcarriers
$h (n, v)$	The doubly dispersive channel impulse response
$H$	The doubly dispersive channel (time-variant, circular) convolution matrix
$L$	Cyclic prefix
$y$	The received signal after demodulation by the DFT matrix
$\tilde{H}$	Frequency domain channel matrix
$\tilde{z}$	The noise vector in the frequency domain
$W_{n}$	The equaliser matrix
${\hat{d}}_{Z F}$	Estimated data using ZF equaliser
${\hat{d}}_{M M S E}$	Estimated data using MMSE equaliser
$I_{N_{A}}$	The identity $N_{a} \times N_{a}$ matrix
$γ$	The signal-to-noise ratio (SNR)
$M$	Binary masking matrix
$Q$	The number of the first sub- and super-diagonals
$B_{n}$	The masked equaliser matrix
$W_{n, M M S E}$	The MMSE equaliser
F_F	Decision Feedback Equaliser feed-forward filter
F_B	Decision Feedback Equaliser feedback filter
$L$	The lower triangular matrix with unit diagonal in the $L D L^{H}$ algorithm
$D$	The diagonal matrix in the $L D L^{H}$ algorithm
$B_{n, k}$	The matrix which is part of the equivalent banded system matrix $B_{n}$ with $P \times K$ size
$P$	The width of the sliding window matrix
$\hat{g}$	the symbol representing the variable or parameter that we are trying to determine or estimate.
A	a matrix that acts on g (a vector or another mathematical object).
b	represents the vector of observed data
$A^{T}$	Matrix transpose of matrix A
$I$	Identity matrix
X	represents the solution vector
rₖ	residual vector
αₖ	the scaling factor
xₖ₊₁	The updated solution vector
pₖ	the search direction vector
$ε$	The intended accuracy or tolerance
i	The number of iterations
k	Condition number of the matrix A
${\tilde{H}}^{H}$	The channel matrix conjugate transpose in the frequency domain
$B_{n}^{H}$	The banded channel matrix conjugate transpose in the frequency domain
γ	the Signal-to-Noise Ratio (SNR)
e	the error vector

References

Heidari, N. Navimipour, M. U.-S. C. and Society, and undefined 2022, “Applications of ML/DL in the management of smart cities and societies based on new trends in information technologies: A systematic literature review,” Elsevier, Accessed: Oct. 09, 2022. [Online]. Available: https://www.sciencedirect.com/science/article/pii/S2210670722004061?casa_token=zCUqJfdVMkgAAAAA:yLF30ISenZA3uUXJ2AaPyOU0hkISCpavLxWNPLuz0kiC9bNJ-86d30Zb779lq_NAuQujGkf-SQ3P.
J. Jagannath, N. Polosky, A. Jagannath, F. Restuccia, and T. Melodia, “Machine learning for wireless communications in the Internet of Things: A comprehensive survey,” Ad Hoc Networks, vol. 93, p. 101913, Oct. 2019. [CrossRef]
Z. Lv and W. Shang, “Impacts of intelligent transportation systems on energy conservation and emission reduction of transport systems: A comprehensive review,” Green Technologies and Sustainability, vol. 1, no. 1, p. 100002, Jan. 2023. [CrossRef]
M. Vaezi et al., “Cellular, Wide-Area, and Non-Terrestrial IoT: A Survey on 5G Advances and the Road Toward 6G,” IEEE Communications Surveys and Tutorials, vol. 24, no. 2, pp. 1117–1174, 2022. [CrossRef]
Y. Wu, H. N. Dai, H. Wang, Z. Xiong, and S. Guo, “A Survey of Intelligent Network Slicing Management for Industrial IoT: Integrated Approaches for Smart Transportation, Smart Energy, and Smart Factory,” IEEE Communications Surveys and Tutorials, vol. 24, no. 2, pp. 1175–1211, 2022. [CrossRef]
R. Khan et al., “DSRC Technology in Vehicle-to-Vehicle (V2V) and Vehicle-to-Infrastructure (V2I) IoT System for Intelligent Transportation System (ITS): A Review,” Lecture Notes in Electrical Engineering, vol. 730, pp. 97–106, 2022. [CrossRef]
Goudarzi, F. Ghayoor, M. Waseem, S. Fahad, and I. Traore, “A Survey on IoT-Enabled Smart Grids: Emerging, Applications, Challenges, and Outlook,” Energies 2022, Vol. 15, Page 6984, vol. 15, no. 19, p. 6984, Sep. 2022. [CrossRef]
M. Waseem, M. Adnan Khan, A. Goudarzi, S. Fahad, I. A. Sajjad, and P. Siano, “Incorporation of Blockchain Technology for Different Smart Grid Applications: Architecture, Prospects, and Challenges,” Energies 2023, Vol. 16, Page 820, vol. 16, no. 2, p. 820, Jan. 2023. [CrossRef]
Y. H. Kuo, J. M. Y. Leung, and Y. Yan, “Public transport for smart cities: Recent innovations and future challenges,” Eur J Oper Res, vol. 306, no. 3, pp. 1001–1026, May 2023. [CrossRef]
A. Ahmed Solyman and K. Yahya, “Evolution of wireless communication networks: from 1G to 6G and future perspective,” International Journal of Electrical and Computer Engineering (IJECE), vol. 12, no. 4, pp. 3943–3950, Aug. 2022. [CrossRef]
A. A. Solyman et al., “A low-complexity equalizer for video broadcasting in cyber-physical social systems through handheld mobile devices,” IEEE Access, vol. 8, pp. 67591–67602, 2020. [CrossRef]
Y. Wang, H. Niu, Q. Zhao, L. Wang, Y. Gao, and Z. Lin, “NC-OFDM Satellite Communication Based on Compressed Spectrum Sensing,” Sensors 2022, Vol. 22, Page 3800, vol. 22, no. 10, p. 3800, May 2022. [CrossRef]
Y. Wu and W. Y. Zou, “Orthogonal frequency division multiplexing: A multi-carrier modulation scheme,” IEEE Transactions on Consumer Electronics, vol. 41, no. 3, pp. 392–399, 1995. [CrossRef]
Y. Zhong et al., “Empowering the V2X Network by Integrated Sensing and Communications: Background, Design, Advances, and Opportunities,” IEEE Netw, vol. 36, no. 4, pp. 54–60, Jul. 2022. [CrossRef]
P. Schniter, “Low-Complexity Equalization of OFDM in Doubly Selective Channels,” IEEE Transactions on Signal Processing, vol. 52, no. 4, pp. 1002–1011, Apr. 2004. [CrossRef]
Tauböck, M. Hampejs, P. Švač, G. Matz, F. Hlawatsch, and K. Gröchenig, “Low-complexity ICI/ISI equalization in doubly dispersive multicarrier systems using a decision-feedback LSQR algorithm,” IEEE Transactions on Signal Processing, vol. 59, no. 5, pp. 2432–2436, May 2011. [CrossRef]
Jeon, K. Li, J. R. Cavallaro, and C. Studer, “On the achievable rates of decentralized equalization in massive MU-MIMO systems,” IEEE International Symposium on Information Theory - Proceedings, pp. 1102–1106, Aug. 2017. [CrossRef]
Y. S. Choi, P. J. Voltz, and F. A. Cassara, “On channel estimation and detection for multicarrier signals in fast and selective Rayleigh fading channels,” IEEE Transactions on Communications, vol. 49, no. 8, pp. 1375–1387, Aug. 2001. [CrossRef]
X. Cai and G. B. Giannakis, “Bounding performance and suppressing intercarrier interference in wireless mobile OFDM,” IEEE Transactions on Communications, vol. 51, no. 12, pp. 2047–2056, Dec. 2003. [CrossRef]
L. Rugini and P. Banelli, “Performance analysis of banded equalizers for OFDM systems in time-varying channels,” IEEE Workshop on Signal Processing Advances in Wireless Communications, SPAWC, no. 1, 2007. [CrossRef]
T. Hrycak and G. Matz, “Low-complexity time-domain ICI equalization for OFDM communications over rapidly varying channels,” Conf Rec Asilomar Conf Signals Syst Comput, pp. 1767–1771, 2006. [CrossRef]
K. J. Wong, F. H. Juwono, and R. Reine, “Deep Learning for Channel Estimation and Signal Detection in OFDM-Based Communication Systems,” ELKHA, vol. 14, no. 1, pp. 52–59, Apr. 2022. [CrossRef]
C. Paige and M. A. Saunders, “LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares,” ACM Transactions on Mathematical Software (TOMS), vol. 8, no. 1, pp. 43–71, 1982. [CrossRef]
Tauböck, M. Hampejs, G. Matz, F. Hlawatsch, and K. Gröchenig, “LSQR-Based ICI equalization for multicarrier communications in strongly dispersive and highly mobile environments,” IEEE Workshop on Signal Processing Advances in Wireless Communications, SPAWC, 2007. [CrossRef]
Han and L. N. Wu, “Low complexity LSQR-based block decision feedback equalizer for OFDM systems over rapidly time-varying channels,” 2010 WRI International Conference on Communications and Mobile Computing, CMC 2010, vol. 2, pp. 438–441, 2010. [CrossRef]
M. Hajarian, “Extending the CGLS algorithm for least squares solutions of the generalized Sylvester-transpose matrix equations,” J Franklin Inst, vol. 353, no. 5, pp. 1168–1185, Mar. 2016. [CrossRef]
A. A. Solyman, S. Elgamel, S. Weiss, and J. J. Soraghan, “Hybrid FrFT and FFT based Multimode Transmission OFDM System Based,” The International Conference on Electrical Engineering, vol. 8, no. 8th International Conference on Electrical Engineering ICEENG 2012, pp. 1–12, May 2012. [CrossRef]
H. Attar et al., “Efficient equalisers for OFDM and DFrFT-OCDM multicarrier systems in mobile E-health video broadcasting with machine learning perspectives,” Physical Communication, vol. 42, p. 101173, Oct. 2020. [CrossRef]
Vlachos, A. S. Lalos, and K. Berberidis, “Low-complexity OSIC equalization for OFDM-based vehicular communications,” IEEE Trans Veh Technol, vol. 66, no. 5, pp. 3765–3776, 2017. [CrossRef]
P. Robertson and S. Kaiser, “The effects of doppler spreads in OFDM(A) mobile radio systems,” IEEE Vehicular Technology Conference, vol. 50, no. 1, pp. 329–333, 1999. [CrossRef]
A. A. Solyman, H. Attar, M. R. Khosravi, and B. Koyuncu, “MIMO-OFDM/OCDM low-complexity equalization under a doubly dispersive channel in wireless sensor networks:,” https://doi.org/10.1177/1550147720912950, vol. 16, no. 6, Jun. 2020. [CrossRef]
A. A. Solyman, S. Weiss, and J. J. Soraghan, “Low-complexity LSMR equalisation of FrFT-based multicarrier systems in doubly dispersive channels,” IEEE International Symposium on Signal Processing and Information Technology, ISSPIT 2011, pp. 461–465, 2011. [CrossRef]
P. Schniter, “Low-complexity estimation of doubly-selective channels,” IEEE Workshop on Signal Processing Advances in Wireless Communications, SPAWC, vol. 2004-Janua, no. 4, pp. 200–204, 2004. [CrossRef]
S. Ahmed, M. Sellathurai, S. Lambotharan, and J. A. Chambers, “Low-complexity iterative method of equalization for single carrier with cyclic prefix in doubly selective channels,” IEEE Signal Process Lett, vol. 13, no. 1, pp. 5–8, 2006. [CrossRef]
A. A. Solyman, S. Weiss, and J. J. Soraghan, “Low-complexity LSMR equalisation of FrFT-based multicarrier systems in doubly dispersive channels,” IEEE International Symposium on Signal Processing and Information Technology, ISSPIT 2011, no. 1, pp. 461–465, 2011. [CrossRef]
Fang, L. Rugini, and G. Leus, “Low-complexity block turbo equalization for OFDM systems in time-varying channels,” IEEE Transactions on Signal Processing, vol. 56, no. 11, pp. 5555–5566, 2008. [CrossRef]
C. Paige and M. A. Saunders, “LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares,” ACM Transactions on Mathematical Software (TOMS), vol. 8, no. 1, pp. 43–71, Mar. 1982. [CrossRef]
C. L. Fong and M. Saunders, “LSMR: An iterative algorithm for sparse least-squares problems,” SIAM Journal on Scientific Computing, vol. 33, no. 5, pp. 2950–2971, 2011. [CrossRef]
Hestenes, Magnus R., and Edward Stiefel. "Methods of Conjugate Gradients for Solving Linear Systems." Journal of Research of the National Bureau of Standards 49.6 (1952): 409–436.
Zhang, Z. Wang, C. Pan, S. Chen, and L. Hanzo, “Low-complexity iterative frequency domain decision feedback equalization,” IEEE Trans Veh Technol, vol. 60, no. 3, pp. 1295–1301, Mar. 2011. [CrossRef]
Li, E. Bala, and R. Yang, “Sliding window-frequency domain equalization for multi-mode communication systems,” 9th Annual Conference on Long Island Systems, Applications and Technology, LISAT 2013, 2013, doi: 10.1109/LISAT.2013.6578231. [CrossRef]

Figure 1. OFDM Block diagram.

Figure 2. Block Diagram of an OFDM system [10].

Figure 3. OFDM comparison in time-invariant and time-variant channels environment with a single tap and MMSE equalizers.

Figure 4. Subdiagonal Count vs. BER and Complexity Trade-off Analysis.

Figure 5. BDFE Structure.

Figure 6. Comparison between CGLS, BMMSE, and CGLS-BDFE

(Q = 5)

OFDM equalizers

Figure 6. Comparison between CGLS, BMMSE, and CGLS-BDFE

(Q = 5)

OFDM equalizers

Figure 7. RLS- CGLS sliding window equalizer and the Banded MMSE equalizer BER Comparison

(Q = 5)

Figure 7. RLS- CGLS sliding window equalizer and the Banded MMSE equalizer BER Comparison

(Q = 5)

Table 1. comparison between different OFDM equalization techniques.

Linearity	Equalizer	complexity	Performance	Strengths	Weaknesses
Linear	Zero-forcing equalizer (ZF)	High	Good	Can completely eliminate ISI	May amplify noise, sensitive to channel estimation errors
	Minimum mean square error equalizer (MMSE)	High	Very good	Good performance in noise, robust to channel estimation errors, Offers better BER performance compared to ZF equalizer, especially in noisy channels, Improved noise resilience, and better performance in frequency-selective channels.	May not be able to completely eliminate ISI, has High computational complexity, and not suitable for real-time applications.
	Banded Minimum mean square error equal-izer (BMMSE)	Medium	good to Very good	Can achieve good performance with lower computational complexity than MMSE, can adapt to dynamic channel conditions	may not be able to achieve the best possible performance, less performance compared to MMSE
Non-linear	Decision feedback equalizer (DFE)	Very High	Excellent	Can completely eliminate ISI, has good performance in noise, suitable for severe channel conditions.	Sensitive to channel estimation errors, and high latency.
	RLS Sliding Window Equalizer	High	Very good to excellent	Can adapt to dynamic channel conditions, good performance in noise	Sensitive to channel estimation errors, and high latency, depends on the choice of the window size and the forgetting factor
	Machine learning equalizers (MLEs)	Very High	Very good to excellent	Can achieve the best possible performance, can adapt to dynamic channel conditions	High computational complexity, may require training data

Table 2. Comparison of Iterative Matrix Inversion Algorithms: Complexity and Performance Analysis.

Algorithm	Complexity	Performance	Strengths	Weaknesses
LDL factorization	O(n^3)	Good for dense matrices	Accurate, fast	High memory complexity
LSQR	O(n^2)	Good for sparse matrices	Accurate, fast	May require more iterations than LSMR or CGLS
LSMR	O(n^2)	Good for sparse matrices	Accurate, fast	Fewer iterations are required than LSQR.
CGLS	< O(n^2)	Good for sparse matrices	Accurate, fast	Fewer iterations required than LSQR or LSMR

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Conjugate Gradient Least Squares Algorithm for OFDM Nonlinear Equalization in Intelligent Future IoT Transportation Systems

Abstract

1. Introduction

2. Orthogonal Frequency Division Multiplexing

3. OFDM Equalization

4. Equalization Strategies for OFDM in Doubly Dispersive Channels:

5. Proposed Conjugate Gradient Least Squares Algorithm:

6. Advanced Nonlinear Equalization Techniques for Enhanced OFDM Performance

7. Future Directions

8. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix 1

References

MDPI Initiatives

Important Links

Subscribe