Neutrino Energy Formula Different from the Planck Energy Formula

Preprint

Article

Neutrino Energy Formula Different from the Planck Energy Formula

Altmetrics

Downloads

Views

Comments

Sheng Qin^*

This version is not peer-reviewed

Submitted:

15 October 2023

Posted:

17 October 2023

You are already at the latest version

Alerts

Abstract

This paper is the third application-oriented paper based on the "unified theory of forces" and also addresses the shortcomings of previous research in fully explaining the origin and nature of the weak force. The main conclusions of this paper are as follows: (1) It is argued that neutrinos are generated by the gravitational field, and their generation mechanism is similar to the radiation of photons from electron orbital transitions. Particles undergoing orbital transitions in a gravitational field will emit neutrinos. (2) We rigorously derive the energy formula for neutrinos and demonstrate that the energy formula for neutrinos does not comply with the Planck energy formula. Neutrinos with higher energy have longer wavelengths and are more easily observed in experiments.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

Currently, physicists generally believe that neutrinos belong to the lepton family [1,2] and are considered one of the fundamental particles, similar to electrons. However, the author believes that neutrinos resemble photons from various perspectives, such as their propagation at the speed of light and their nearly zero rest mass. However, we do not differentiate between different types of photons, such as e-photon, μ-photon, and τ-photon. Therefore, the author believes that neutrinos should also not be distinguished as e-neutrino, μ-neutrino, and τ-neutrino.

This study does not involve neutrino oscillation (in fact, we do not yet fully understand the true physical significance of neutrino oscillation) or neutrino spin. Instead, it directly explores the radiation and absorption mechanisms of neutrinos, as well as the properties of neutrinos under these radiation mechanisms, so that experimental physicists can observe the properties of neutrinos from another perspective.

At the same time, this study also complements the shortcomings of our previous research in the "Unified Theory of Forces" [3], which did not discuss the mechanism of the weak force in detail. Modern physics believes that gravitons belong to bosons and should have a spin of 2, which is used to transmit gravity. However, as the author has demonstrated, the origin of all forces in our universe is due to the "energy loss

E_{m i s s i n g}

" [3], and photons are not the main means of force transmission. At the same time, the author believes that our current standard model of physics still cannot explain many phenomena. Therefore, we ignore speculations about gravitons and instead focus on the physical properties of neutrinos based on actual physical mechanisms.

2. Neutrino Radiation Mechanism and Absorption Mechanism

2.1. Discussing Neutrinos as Gravitons

So far, we have not discovered any other fundamental forces besides the electromagnetic force, strong force, and gravitational force, and we have already demonstrated the nature and mechanisms of the electric field, magnetic field, and strong force field [3]. However, at that time, we neglected the explanation of the mechanism of the weak force, specifically the radiation and absorption mechanisms of neutrinos. From past research, we have found that the weak force, or the radiation and absorption of neutrinos, share a common characteristic: a very small interaction radius, much smaller than

10^{- 15} m

[3]. From the probability of detecting neutrinos, we can infer that their interaction radius should be much smaller than the range of the strong force.

The author believes that neutrinos are a material similar to photons, and their radiation mechanism should be the same as that of photons. Among all the fields we currently know: electromagnetic force, strong force, and gravitational force, we first exclude the possibility that neutrinos are generated in the electromagnetic field because neutrinos do not possess the relevant properties of photons. Secondly, we believe that the probability of neutrino generation in the strong force field is not high. Although the range of the strong force is closer to neutrinos, the probability of detecting the strong force is much higher than that of neutrinos. If neutrinos are generated by the orbital transitions of particles in the strong force field, we should be able to detect the interactions between neutrinos and matter with a higher probability.

Therefore, the most reasonable explanation is that neutrinos originate from the gravitational field and are generated by the orbital transitions of particles in the gravitational field, similar to how electrons undergo orbital transitions in the atomic nucleus and emit photons. It is precisely because neutrinos are born in the gravitational field that their interaction radius is so small, as gravity is much weaker compared to electromagnetism.

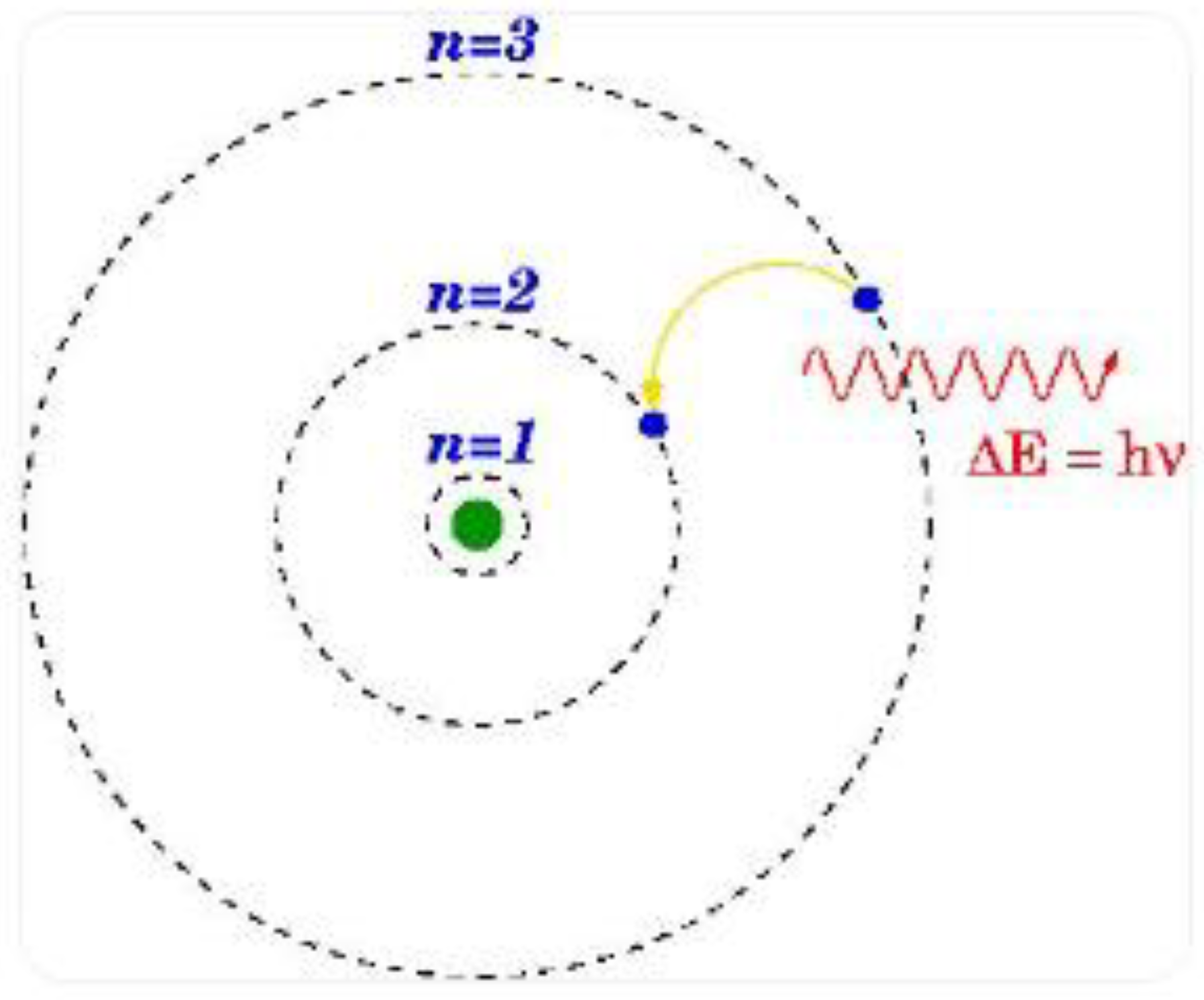
The mechanism of neutrino generation is similar to that of photons, as shown in Figure 1:

Particles can emit neutrinos through orbital transitions in the gravitational field. The author believes that the radiation and absorption mechanisms of neutrinos are generated by the orbital transitions of particles in the gravitational field. We have already demonstrated that all forces originate from the "energy loss

E_{m i s s i n g}

" [3], so both the electric field and the gravitational field ultimately convert the missing energy

E_{m i s s i n g}

into the kinetic energy of particles, such as the motion of electrons outside the atomic nucleus. Therefore, theoretically, electrons outside the atomic nucleus can undergo orbital transitions in both the electric field to emit photons and in the gravitational field to emit neutrinos. This is actually the mechanism by which neutrinos are associated with the electric field in particles, where the kinetic energy of particles can be emitted as both photons and neutrinos.

However, in our current material structure, we hardly see direct neutrino effects produced by gravitational radiation; the neutrinos we currently observe are mostly produced indirectly. The main reason for this is that the primary interaction mode of the matter we currently observe is still electromagnetic force, with a cross section much larger than that of neutrinos. For example, the interaction cross section between gamma rays and matter with the same energy is about

10^{- 23} {c m}^{2}

, while in neutrino reactions, the cross section is approximately

10^{- 40} {c m}^{2}

[4]. Let's compare the electromagnetic force and gravitational force between a proton and an electron. At the same distance, the electromagnetic force is approximately

10^{39}

times larger than the gravitational force. To emit neutrinos with the same transition energy, the transition radius of the neutrino would be much smaller than the orbital radius of the electron in the electromagnetic force.

Of course, for particles with higher energy and closer distance, the probability of particles undergoing gravitational field orbital transitions and emitting neutrinos will be greater.

2.2. Mechanism of Conversion between Electric Field and Gravitational Field

According to the conclusions in the "Unified Theory of Force" [3], the missing energy

E_{m i s s i n g}

that generates electric field and gravitational field will ultimately be converted into the relative motion between matter, which is the kinetic energy

E

of particles.

Taking the example of an electron moving outside the atomic nucleus, its kinetic energy is equivalent for both the electric field and gravitational field. However, we hardly observe direct neutrino radiation from atoms to the outside. This is because, as we have discussed in the "Unified Theory of Force" [3], both photons and neutrinos are inferred to have a minimum static mass

m

. The prerequisite for photon or neutrino radiation is that the transition energy of the particles in the electric field or gravitational field must be greater than or equal to

m C^{2}

Therefore, the prerequisite for gravitational radiation is that the energy generated by the particle's orbital transition in the gravitational field must reach a certain minimum energy. Due to the weakness of gravity, we expect this to be another reason why gravitational radiation is so rare.

Once the particle's orbital transition in the gravitational field meets this condition, gravitational radiation can theoretically occur, resulting in the production of neutrinos. At this point, the energy of the neutrinos does not necessarily come entirely from the energy transition but can also come from the absorption of the particle's kinetic energy. Similar to the radiation of high-energy photons, the energy of photons does not solely come from the particle's orbital transition in the electric field but can also absorb the particle's kinetic energy to increase its own energy. Therefore, in beta decay, the energy of neutrinos is continuous, rather than fixed.

In the particle realm, this equivalence effect of energy allows for the conversion between gravitational field and electric field energy. For example, theoretically, an electron can absorb photons and convert them into electron kinetic energy, and then convert the electron kinetic energy into neutrinos through gravitational radiation. Conversely, particles can absorb neutrinos to gain energy and then emit photons through electromagnetic radiation. However, due to the smallness of gravity and the high frequency and small wavelength of neutrinos (which will be discussed later), this requires particles to be very close to each other and have sufficient energy to form such conversion effects between energies. This is expected to be the essence of the weak interaction we usually observe between particles.

Therefore, the author believes that there is actually no so-called weak force. The essence of the weak force is actually an energy conversion effect of particles under orbital transitions in the gravitational field, similar to stimulated radiation of electrons outside the atomic nucleus.

3. Mechanism of Neutrino Interactions

3.1. Difference between Neutrinos and Photons

In another article, we have discussed the possible structure of photons, which should be formed by particles interacting through the electric field. The internal structure of photons is likely to have a structure similar to positive and negative charges. However, unlike gravity, we have not yet discovered positive gravitons and negative gravitons. Therefore, the microscopic structure of neutrinos may not possess positive or negative properties, but rather be homogeneous. As a result, neutrinos may exhibit many different characteristics in their physical properties:

(1) Currently, we observe in experiments that neutrinos do not participate in electromagnetic interactions, which is consistent with the author's inference that neutrinos serve as the fundamental particles of gravity.

(2) Photons themselves are electrically neutral as a whole; they exhibit phenomena such as polarization changes in a magnetic field. However, in contrast, neutrinos have mass themselves, so they can interact with the gravitational field. We are not clear about the differences this may bring.

(3) If the internal structure of neutrinos is fully identical, that is, if we assume that neutrinos are composed of two (or more) completely identical and symmetrical particles moving in mutual motion, then this will bring about what kind of impact. We are also not clear about this.

3.2. Energy Formula of Neutrinos

The Planck energy formula is not applicable to neutrinos. We have previously discussed the Planck energy formula for photons. The reason why photons adhere to the Planck energy formula is that the particle's charge does not increase with the increase in particle energy [5]. We have derived the Planck energy formula in the previous article and explained its physical significance. However, neutrinos are different.

Below, we will derive the energy formula for neutrinos using the conclusions from the "Unified Theory of Force" [3]. We will adopt the same approach as used in the previous article (for detailed derivation, please refer to the previous article) [5]. Let's assume that two particles, A and B, with equal mass

m_{1}

, have an energy deficit of

{E^{0}}_{m i s s i n g}

between them (ignoring relativistic effects and Lorentz contraction between different reference frames, which we have proven not to exist [6,7], and we have also rigorously demonstrated the true physical reasons for the Lorentz contraction effect of moving objects under electromagnetic forces [5]). It should also be noted that no

E_{f o l l o w}

is generated when accelerating particles A and B because the total energy (kinetic mass) of moving matter is determined by velocity. We have also proven this point:

So, when particles A and B are at rest, under the influence of

{E^{0}}_{m i s s i n g}

, they will attract each other and perform circular motion. The equilibrium radius r is derived from the following formula:

E = G \frac{m_{1} m_{1}}{r}

Therefore, we obtain:

r_{0} = G \frac{m_{1} m_{1}}{{E^{0}}_{m i s s i n g}} = G \frac{{m_{1}}^{2}}{{E^{0}}_{m i s s i n g}}

We assume that particles A and B are simultaneously accelerated to velocity

v

. Initially, particles A and B are far apart (which means that

{E^{0}}_{m i s s i n g}

has not yet been converted into the kinetic energy of particles A and B). After acceleration, particles A and B are attracted to each other by gravitational forces and perform rotational motion around each other. From the perspective of an observer on Earth's coordinate system, the mass of particles A and B after acceleration will become:

m_{B}^{v} = m_{A}^{v} = m_{1}^{v} = m_{1} \sqrt{\frac{1}{1 - \frac{v^{2}}{c^{2}}}}

From the perspective of an observer on Earth's coordinate system, the energy deficit

{E^{v}}_{m i s s i n g}

between particles A and B after acceleration and the equilibrium radius

r_{1}

after the particles merge will become:

{E^{v}}_{m i s s i n g} = {E^{0}}_{m i s s i n g} \sqrt{\frac{1}{1 - \frac{v^{2}}{c^{2}}}}

r_{1} = G \frac{m_{1}^{v} m_{1}^{v}}{{E^{v}}_{m i s s i n g}} = G \frac{{m_{1}}^{2}}{{E^{0}}_{m i s s i n g}} \sqrt{\frac{1}{1 - \frac{v^{2}}{c^{2}}}} = r_{0} \sqrt{\frac{1}{1 - \frac{v^{2}}{c^{2}}}}

This also means that, from the perspective of an observer on Earth, the equilibrium radius

r_{1}

of the mutual motion generated by gravity between particles A and B after acceleration will increase.

We assume that the energy deficit between particles A and B is ultimately converted into the kinetic energy of particles A and B, as shown in the following formula:

{E^{0}}_{m i s s i n g} = {2 \frac{1}{2} m}_{1} {\bar{v}}^{2}

The average velocity

\bar{v}

generated by the mutual attraction between particles A and B when they are at rest is:

\bar{v} = \sqrt{\frac{{E^{0}}_{m i s s i n g}}{m_{1}}}

From the perspective of an observer on Earth's coordinate system, the kinetic energy of particles A and B after acceleration and the average velocity

\overset{̿}{v}

of their mutual rotational motion will be:

{E^{v}}_{m i s s i n g} = 2 \frac{1}{2} m_{1}^{v} {\overset{̿}{v}}^{2}

\overset{̿}{v} = \sqrt{\frac{{E^{v}}_{m i s s i n g}}{m_{1}^{v}}} = \sqrt{\frac{{E^{0}}_{m i s s i n g} \sqrt{\frac{1}{1 - \frac{v^{2}}{c^{2}}}}}{m_{1} \sqrt{\frac{1}{1 - \frac{v^{2}}{c^{2}}}}} = \bar{v}}

Therefore, we obtain that for particles A and B, from the perspective of an observer on Earth, the average velocity at which they mutually rotate around each other remains unchanged before and after acceleration:

\overset{̿}{v} = \bar{v}

Now, if we assume that in the rest state, the motion period of particles A and B in their mutual motion is

T_{0}

, and after being accelerated to velocity

v

, the motion period becomes

T_{1}

. According to the previously derived formulas for the change in velocity and the motion radius of particles A and B during circular motion, we can easily obtain that the circular motion period of particles A and B after acceleration will become:

T_{1} = T_{0} \sqrt{\frac{1}{1 - \frac{v^{2}}{c^{2}}}}

Therefore, the energy formula for particles A and B after acceleration (excluding the energy deficit

{E^{v}}_{m i s s i n g}

between A and B) is:

m_{1}^{v} C^{2} = m_{1} \sqrt{\frac{1}{1 - \frac{v^{2}}{c^{2}}}} ∙ C^{2} = m_{1} C^{2} \frac{T_{1}}{T_{0}}

If we assume that 2

m_{0} \frac{1}{T_{0}} C^{2} + \frac{1}{T_{0}} {E^{0}}_{m i s s i n g} = h_{0}

T_{1} = \frac{1}{ω_{1}}

, then the total energy

{E^{v}}_{A B}

of particles A and B after acceleration and merging is:

{E^{v}}_{A B} = (2 m_{0} C^{2} + {E^{0}}_{m i s s i n g}) \sqrt{\frac{1}{1 - \frac{v^{2}}{c^{2}}}} = h_{0} T_{1} = h_{0} \frac{1}{ω_{1}} = h_{0} \frac{λ}{C}

This is the energy formula for neutrinos, where

ω_{1}

refers to the frequency of neutrinos,

h_{0}

is a constant similar to the Planck constant,

λ

is the wavelength of neutrinos, and

C

is the speed of light.

We find that the energy expression formula

{E^{v}}_{A B}

for neutrinos is different from the Doppler energy formula for photons,

E = h ω

. If we consider particles A and B as the structural components of neutrinos, we will find that the higher the energy of neutrinos, the lower their oscillation frequency, and the longer the wavelength

λ

, which theoretically makes them more likely to interact with matter. The specific formula is as follows:

ω_{1} = \frac{h_{0}}{{E^{v}}_{A B}}

λ = \frac{{C E}^{v}_{A B}}{h_{0}}

The above formulas give completely different conclusions from the commonly seen Planck energy formula.

Perhaps this model may not be applicable to macroscopic objects such as celestial bodies.

4. Conclusion

The author believes that neutrinos are actually a form of matter radiated by microscopic particles undergoing orbital transitions in a gravitational field, similar to photons.

Furthermore, based on the theory of the "Unified Theory of Force" [3] [5], this article rigorously derives the energy formula and other properties of neutrinos, leading to the following important conclusions:

(1) The higher the energy of a neutrino, the lower the observed oscillation frequency

ω

and the larger the wavelength

λ

. This conclusion is contrary to the Planck energy formula.

(2) Due to the larger wavelength

λ

of higher energy neutrinos, theoretically, higher energy neutrinos are more likely to be observed. This can be verified in laboratory experiments.

(3) If neutrinos are particles radiated by orbital transitions in a gravitational field, the best places to observe them would be celestial bodies with higher energy densities, such as neutron stars or the currently recognized black holes. In high-density celestial bodies, neutrino radiation, absorption, and reflection effects may be as common as the absorption and radiation of photons by matter.

References

Remarks on the unified model of elementary particles. Progress of Theoretical Physics. 1962, 28(5), 870–880. [CrossRef]
Gribov, V. N., & Pontecorvo, B. M. (1969). Neutrino astronomy and lepton charge. Physics Letters B. 1969, 28(8), 493–494.
Qin S (2022) Unified Theory of Gravity, Electromagnetic Force, Strong and Weak Forces and their Applications: Theoretical Explanation for Dark Matter. J Phys Chem Biophys. 12:335. [CrossRef]
s: Shao-Min（2017），Post neutrino-oscillation-discovery experiments, 2017. [CrossRef]
ShengQin. 2023. “A Theoretical Explanation and Modification of the Lorentz Contraction Effect, and a Tentative Theoretical Explanation of the Planck Energy Formula E=hω.” OSF Preprints. 4 May. [CrossRef]
Qin S (2022) Derivation of Special Relativity Transformation Formulas without Time Delay Effect and Length Contraction Effect. J Phys Chem Biophys. 12:333.
Qin S (2022) A Possible Explanation for the Twin Paradox and Action at a Distance: The Relative Independence of Space and the Absoluteness of Simultaneity. J Phys Chem Biophys. 12:332. [CrossRef]

Figure 1. Emission mechanism of photons.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Neutrino Energy Formula Different from the Planck Energy Formula

Abstract

1. Introduction

2. Neutrino Radiation Mechanism and Absorption Mechanism

2.1. Discussing Neutrinos as Gravitons

2.2. Mechanism of Conversion between Electric Field and Gravitational Field

3. Mechanism of Neutrino Interactions

3.1. Difference between Neutrinos and Photons

3.2. Energy Formula of Neutrinos

4. Conclusion

References

MDPI Initiatives

Important Links

Subscribe