Prerpints.org logo
Preprint
Article

Teaching Quantum Algorithms Using the Harmonic Oscillator Example

Altmetrics

Downloads

173

Views

54

Comments

0

Submitted:

13 October 2023

Posted:

17 October 2023

You are already at the latest version

Alerts
Abstract
This Article demonstrates how an eigendecomposition problem is inputted into a quantum circuit, how gates are applied in the quantum circuit, and how the output measurements are the correct eigenvalues. This process is known as quantum phase estimation (QPE). A quantum harmonic oscillator example, a foundational quantum physical chemistry problem, is demonstrated within the context of QPE. A particle in a box example, another quantum physical chemistry problem, may be solved by QPE with a caveat. These examples are of the limiting cases of diagonal matrices. Future advances in taking matrix inverses for solving linear sets of equations or finding ground state energies in the Schrödinger equation will use the principles implemented in this Article.
Keywords: 
Subject: Chemistry and Materials Science  -   Theoretical Chemistry

Introduction

The nascent quantum computing field has a number of theoretical algorithms proposed in recent decades, some with a supreme advantage over conventional computers at their specific tasks.[1,2,3,4] The Shor algorithm[3] that can factor large numbers rapidly, breaking current RSA encryption. RSA encryption relies on current computers, even the world’s most powerful, taking far too long, on the timescale of years, to break. However, there exist two extremely powerful applications of quantum computing to physical chemistry, the first of which would entirely transform the field. This application is exactly solving for the ground state energy of the Schrödinger equation for quantum systems.[5,6] The second is solving linear sets of equations which arise in chemical kinetics.[7] Rapid solutions to large linear systems of equations would advance chemical kinetics modeling.[7,8,9,10]
Quantum computers have been shown, in principle, to achieve accurate solutions to the Schrödinger equation for molecules in far less time than needed for equivalent calculations from current and planned exascale computing. In additional to hardware development of quantum computers, programming implementations are necessary to achieve the promise of rapid and nearly perfect quantum mechanical computations with quantum computers. Once achieved, though, such a technology will utterly change the face of the computational chemistry field, because the equilibrium concentrations and rate of any chemical reaction could be reliably known prior to experiment.[1]
The quantum computer solves the Schrödinger eigendecomposition problem.[11,12] If only the ground state energy (eigenvalue of the Schrödinger equation), and not the wavefunctions (eigenvectors) can be precisely obtained at various ionic positions, a variational quantum algorithm could be employed.[13,14] The movement of the ions would be conducted with a classical algorithm, for example conjugate gradient, and the ground state energy would be obtained with a quantum computer.[15,16] This separation is allowed by the Born-Oppenheimer approximation.
An example experimental validation of a quantum computing solution to the Schrödinger equation is the overall reaction energy of the water-gas shift reaction (WGS). The overall reaction energy has been experimentally measured,[17] and a prediction from a quantum computer could be immediately checked. WGS is the leading industrial reaction for producing hydrogen.[18,19] Once validated for accuracy, the goal of solving the Schrödinger equation will be to predict the exact reaction mechanism for any catalyst, at the molecular scale. That way, computational screening of catalysts would be far more tractable and rapid. For example, the exact mechanism of WGS is still not known for certain on the least complex single crystal precious metal catalysts. The molecular catalytic reaction mechanism underpins any improvements in catalyst design. Quantum computing would provide the speedup and accuracy to change this situation in the computational catalysis field.
The current leading computational catalysis method for finding molecular reaction mechanisms is density functional theory (DFT). DFT places all the uncertain part of the Schrödinger equation into a function of the electron density function of space.[20,21] A function of a function is known as a functional. The electron density field is changed over iterations until it is self-consistent, meaning the Schrödinger equation is satisfied, for that particular functional of electron density.[22,23]
The quantum computation of the Schrödinger equation is fundamentally different from its computation with DFT. In a quantum computer, the quantum phase estimation (QPE) circuit[24] extracts the energy levels which are the eigenvalues of the Schrödinger equation for a molecule, solid-state material or any many-body set consisting of nuclei and electrons. The challenge lies in expressing the Hamiltonian operator (left-hand side of Schrödinger equation) containing the kinetic energy and potential energy operators, in the acceptable format of QPE. The acceptable format is an exponential of a Hermitian matrix representing the Hamiltonian operator.[25] Current approaches include split-operator techniques[12] and Taylor series approximations[11,26].

Density functional theory

The time-independent Schrödinger equation which governs elementary particles (electrons and nuclei in the context of physical chemistry) is,
H ^ | Ψ = E | Ψ
H ^ is the Hamiltonian operator. An operator takes one function and returns another function. Unlike matrix algebra, in which a multiplication is taken across a matrix row, down a vector, and summed, an operator, denoted by a hat,   ^ , takes the wave function Ψ , and changes it. Ψ is the wavefunction of all the electrons. Ψ takes in position and returns wave amplitude. E is the energy, and it is a scalar number.
In broad terms, the Hamiltonian operator consists of a kinetic energy operator and a potential energy operator. The kinetic energy operator performs a second-order partial derivative on the wavefunction with respect to space (the ∇ operator). The potential energy operator term of the Hamiltonian operator multiplies the potential energy function dependent upon vector variables for each elementary particle by the wavefunction. The potential energies are the coulombic potential energy of each elementary particle due to each of the other elementary particles. The difficulty in computation is that the positions of the elementary particles are variables and not constants. The result is analytical solutions become too large to solve.
Density functional theory (DFT) gets around analytical solutions with a numerical approach. To begin with, an amplitude is initiated at each point in space. This is a (wave)function because it takes in a location and returns an amplitude.[21] A functional takes the field and changes it.[23] Since it is a function of a function, it is called a functional. DFT derives its name from functionals of the electron density field. (The electron density is the square of the wavefunction amplitude).
Hohenberg,[21] Kohn and Sham[20,23] separate out the Hamiltonian as,
E = ∫ v r n r d r + 1 2 ∫ ∫ n r n r ′ r − r ′ d r d r ′ + G [ n ]
The first term in equation 2 is the static potential energy of each electron in an interacting inhomogeneous electron gas. The potential energy is static because it is due to unmoving nuclei (the Born-Oppenheimer approximation allows this separation). v ( r ) is the potential function of r , the vector indicating position of an electron. n ( r ) is the density of the electron gas at position r . The second term in equation 2 is the potential energy due to one position in the electron density field due to another position in the electron density field.
G [ n ] is functional (function of a function of position) of the electron density. G [ n ] is split into two terms,
G n ≡ T s n + E x c [ n ]
T s [ n ] is the kinetic energy functional. E x c n is the exchange-correlation functional. First, the kinetic energy functional, besides multiplication by constants, takes the second derivative (the momentum operator). There are numerical methods for taking the second derivative at all points in a field. Second, the exchange-correlation functional accounts for two electronic energies that arise. The exchange energy is the stabilization due to electrons being able to exchange among equal energy (also known as degenerate) orbitals. For example, the three p orbitals are at the same energy level, and electrons may exchange between those three. The correlation energy correction is phenomena of how the electrons of a system interact with each other. Further explanation of electron correlation energy is outside of the scope of this article. With all the Hamiltonian operation on the electron density field in place, the field can be changed during numerical iterations to find a self-consistent field. The self-consistent field satisfies the Schrödinger equation for the guessed functional form of electron density for the exchange-correlation energy.
Quantum computing will not work with a guess of the functional form of electron density for the exchange-correlation energy, but rather return to accounting each electron and nucleus with their entangled wavefunctions. Within quantum phase estimation (QPE), the analytical form of the wavefunction will likely remain unknown and unmeasurable. However, the ground state energy, or the phase of the Hamiltonian operator, is the most crucial information.

Quantum phase estimation

QPE is the quantum computing algorithm which solves eigendecomposition problems and underpins many of the prominent quantum algorithms.[27,28,29] QPE extracts the eigenvalues and eigenvectors of a unitary matrix, U . Matrices are in bold font. A unitary matrix times its complex conjugate transpose, by definition, is equal to the identity matrix. For example,
U U * = U * U = I
Here, U * is the complex conjugate transpose of U . I is the identity matrix. By contrast, a Hermitian matrix is equal to its complex conjugate transpose, and the asterisks could be removed from equation 4. A Hermitian matrix is therefore necessarily also unitary. The eigenvalues of a unitary matrix have a norm, or length, of one. The non-complex equivalent of a unitary matrix is an orthonormal matrix. Fortunately, quantum computing gates are square, and the complex conjugate transpose is the inverse, which does not hold true for non-square matrices.
The eigenvectors of a unitary matrix are orthogonal to each other. The significant outcome of this property is that the eigenvalues preserve the overall lengths of the eigenvectors. This property harks back to the probabilities of all the computational bases of qubits, i.e. possible bitstrings measured, summing to one. This property of unitary matrices is known as length preservation. The vector of qubits maintains unit length.
The eigendecomposition equation for U which is executed by QPE is,
U | Ψ = e 2 π i θ | Ψ
In equation 2, the eigenvector is Ψ . The ket notation may be perceived as a vertical vector, the matrix mechanics equivalent. A matrix multiplication is denoted by | in bra-ket notation. The imaginary number is denoted i , where i = − 1 . Equation 5 is set up specifically with the special case of the eigenvalues being of the form e 2 π i θ . For any matrix containing any eigenvalues and eigenvectors, further preparation is necessary to arrive at the form of equation 5. These preparations vary by the type of matrix,[30] are outside the scope of this Article. Nonetheless, θ may be thought of as containing the eigenvalues of a matrix which has been transformed to U . θ may be also be considered converted to radians (unitless) by the multiplicative constant 2 π in equation 5.
The eigenvalues in equation 5 will always lie on the complex unit circle as visualized in Figure 1a. On the complex plane, e i θ is always length 1. The length of a complex number is R e 2 + I m 2 , where R e is the real part and I m is the imaginary part. For example, e 2 π i θ always contains only real parts when θ is a multiple of π 2 (pointing to the left perfectly horizontal). The eigenvalues of equation 5 are unit vectors on the complex plane.
A unitary matrix has advantages in calculation. The dot products of the column vectors of U are zero (inner product) except when dotted with itself, in which case it is 1. This property may be demonstrated with the following unitary matrix and its complex conjugate,
U = 1 2 1 2 − e i θ 1 2 e i θ 1 2
U * = 1 2 − e i θ 1 2 1 2 e i θ 1 2
For demonstration purposes, U may be written as two orthonormal vectors:
U = u 1 u 2
Then, the property of unitary matrices is checked:
U * U = u 1 · u 1 u 1 · u 2 u 2 · u 1 u 2 · u 2
The dot product equaling 1 establishes unit length of the vector. This check is analogous to the norm, in which the algebra is the same. Taking u 1 :
u 1 · u 1 = u 1 = 1 2 2 + − e i θ 1 2 2 = 1 2 + + e i − i θ 1 2 = 1
In equation (6), when the norm (length) of a complex number is taken, the complex conjugate (opposite sign imaginary part) is multiplied with the original complex number.
A unitary matrix with known eigenvalues and eigenvectors may be created. For example, θ = 1 2 , 3 4 . The eigenvalues are placed in the diagonals of the Λ matrix.
D = U Λ U * = 1 2 1 1 − 1 1 e π i 0 0 e 3 π i 2 1 2 1 − 1 1 1 = 1 2 e π i e 3 π i 2 − e π i e 3 π i 2 1 − 1 1 1
D = 1 2 e π i + e 3 π i 2 − e π i + e 3 π i 2 − e π i + e 3 π i 2 e π i + e 3 π i 2
The eigenvalues and eigenvectors of matrix D are then,
λ 1 = e π i   λ 2 = e 3 π i 2
Ψ 1 = 1 2 1 − 1   Ψ 2 = 1 2 1 1
In QPE, the eigenvalues of U are “kicked back” in a Fourier basis, which are extracted by an inverse quantum Fourier transform.[31] The eigenvalues, e 2 π i θ , are kicked back in this way. A quantum Fourier transform (QFT), those eigenvalues are converted back to θ ’s.
A scalar example of e i π 4 is considered (1x1 matrix). This is a rotation of 1 8 around the complex unit circle, as seen in Figure 1b. Therefore, the value of θ is,
θ = 1 8
When applied as a gate in a quantum circuit in QPE, the U matrix is made into a controlled- U matrix. The control is created by adding the identity matrix, I , to the upper left block, and the U matrix to the lower-right block. The upper-right and lower-right blocks of this C U matrix are zeroes. The “controlled” term means that a qubit controls whether or not the gate is applied to another qubit. In QPE, the control qubits are the qubits onto which the phase, or eigenvalue, is kicked back. In the simplifying case of a scalar, the C U matrix is dimension 2x2, with a one in the upper left, and the scalar in the lower-right.
This C U matrix is for the θ in equation 12 is,
C U = 1 0 0 e i π 4
To begin QPE, Hadamard gates, H , are applied to each of the qubits.
H = 1 2 1 1 1 − 1
The Hadamard gate happens the same as the 2-dimensional discrete Fourier transform gate.[32] Each qubit of the compute register will receive the C U matrix 2 q number of times, where q is the qubit number. The zeroeth qubit will receive the C U matrix once, the first qubit will receive the C U matrix twice, and the third qubit will receive the C U matrix four times. These gates and their number of repetitions are shown in Figure 2.
Next, an inverse QFT, Q F T † , block of gates converts the eigenvalue, in the format of e 2 π i θ to the format from which θ may be measured as a computational basis (bitstring). The (forward) QFT block applies the discrete Fourier transform matrix. Here is a 2-dimensional QFT matrix,
W = 1 N 1 1 1 ω   ω = e − 2 π i N   N = 2
W = 1 2 1 1 1 − 1   ω = e − π i = − 1
The result of π radians on the complex unit circle equaling -1 may be observed from Figure 1. Figure 3a displays π rotation with the 1 8 allowed steps due to the maximum precision of 3 qubits. Figure 4 displays the measurement when the precise π rotation is taken. Figure 4 displays how the probability is distributed among possible measurements when a rotation is not on the increments allowed by the precision due to the number of qubits. W is the QFT matrix. ω is the Nth root of unity, and − 1 2 = 1 . N is the dimension.
The Q F T gate for 3 qubits (example here) has dimension 8x8.[32]
Q F T = 1 1 1 1 1 1 1 1 1 ω 1 ω 2 ω 3 ω 4 ω 5 ω 6 ω 7 1 ω 2 ω 4 ω 6 ω 8 ω 10 ω 12 ω 14 1 ω 3 ω 6 ω 9 ω 12 ω 15 ω 18 ω 21 1 ω 4 ω 8 ω 12 ω 16 ω 20 ω 24 ω 28 1 ω 5 ω 10 ω 15 ω 20 ω 25 ω 30 ω 35 1 ω 6 ω 12 ω 18 ω 24 ω 30 ω 36 ω 42 1 ω 7 ω 14 ω 21 ω 28 ω 35 ω 42 ω 49   ω = e − 2 π i N = 8 = 2 2 − 2 i 2
Q F T = 1 1 1 1 1 1 1 1 1 ω − i − i ω − 1 − ω i i ω 1 − i − 1 i 1 − i − 1 i 1 − i ω i ω − 1 i ω − i − ω   1 − 1 1 − 1 1 − 1 1 − 1 1 − ω − i i ω − 1 ω i − i ω 1 i − 1 − i 1 i − 1 − i 1 i ω i − ω − 1 − i ω − i ω
This gate is not directly applied to the three qubits. There are a number of gates applied in sequence.[7]
Finally, the measurements output computational bases or bitstrings. Each qubit, when measured, collapses to a 0 or 1 . Since,
0 ≤ θ < 1
the intervals of θ which result in exact computational bases are,
θ = 1 2 3 = 1 8
The values of θ and their corresponding computational basis are listed in Table 1. A count in binary numbers is spread over the interval of equation 17. When an eigenvalue is not precisely a multiple of the value in equation 18, the probability is spread among computational bases (Figure 5). Statistical sampling of the quantum circuit is accomplished via multiple shots of the circuit. The precision is doubled with each extra qubit, as shown in equation 18, although the gate depth also increases, which is a hardware consideration.
This example has disregarded matrices with eigenvalues not on the complex unit circle, i.e. eigenvalues which are not of the format e 2 π i θ . In fact, the U matrix is constructed from an original matrix which is necessarily Hermitian.[32,33] There is a block matrix form which can make any matrix Hermitian which doubles the matrix dimensions. A ~ is an original Hermitian matrix. U is,
U = e i A ~ 2 π
The eigenvalues are then in the complex unit circle format, e 2 π i θ , where θ was the original eigenvalue before exponentials were taken. There is an expense in taking the matrix exponential. There is a form of the Euler identity which can be applied to exponentials,[34] but there will be computational cost in terms of taking sines and cosines. There is also an infinite series expansion of the matrix exponential, which may be truncated.[30] Obtaining the matrix exponential is left out of the scope of this Article.

Particle in a box

Returning to the Schödinger equation (equation 1), the Hamiltonian operator[35] for a single particle is expanded to yield,[36]
− ℏ 2 2 μ ∇ 2 ψ x − V x ψ x = E ψ x
ℏ is the reduced Planck’s constant. Instead of mass m , a reduced mass is used to combine the mass of the nucleus and electron into one constant. Reduced mass, μ , is defined as μ = m M m + M .   M refers to the mass of the nucleus, and m is the mass of the electron. ψ r is the wavefunction of a single particle. In the particle in a box example, only the Cartesian x dimension is retained.
The problem is visualized as a single subatomic particle sandwiched between two parallel infinite barriers of infinitely high potential, where the subatomic particle cannot be. The constant potential is also set to zero, which causes only the kinetic energy to remain in the Hamiltonian operator.
V r = V 0 r = 0
Equation 20 is then:
− ℏ 2 2 m ∂ 2 ∂ x 2 ψ x = E ψ x
The analytical solution requires conceiving of a function for ψ x such that the left-hand side of equation 22 yields the original ψ x times some constant, which will be the value of E . The solution for ψ x , which is not immediately derived but can be shown to be correct (known as an ansatz), is,
ψ x = A s i n k x + B c o s ( k x )
A , B and k are constants to be obtained shortly. Necessary boundary conditions for solving the particle in a box problem are that the amplitude of the wavefunction must be equal to zero at the walls. Assume the walls to be at 0 and L .
x = 0 ;   ψ x = 0 x = L ;   ψ x = 0
Since the interpretation of the wavefunction is that its square provides the probability of the particle being in the position x . Therefore, according to equation 24, the particle has zero probability of being at the walls.
First, k is solved for. The position of x = 0 is selected to eliminate a term.
ψ 0 = A s i n 0 + B c o s 0 = 0
In equation 25, sin ⁡ 0 = 0 , but cos ⁡ 0 = 1 . Therefore, B = 0 by necessity of satisfying the equation at the boundary condition of x = 0 . The wavefunction is reduced to,
ψ x = A s i n k x
Derivatives of the wavefunction are obtained for further determination of the constants.
d ψ x d x = k A c o s ( k x )
d 2 ψ ( x ) d x 2 = − k 2 A s i n ( k x )
In the right-hand side of equation 27b, the original ψ x = A s i n k x reappeared. Multiple derivatives of the sine and cosine functions repeat in a known cycle. Therefore,
d 2 ψ ( x ) d x 2 = − k 2 ψ ( x )
The second derivative of ψ x with respect to x , d 2 ψ ( x ) d x 2 , is substituted into the Schrödinger equation for the particle in a box problem (equation 22).
− ℏ 2 2 m − k 2 ψ x = E ψ x
ℏ 2 2 m k 2 = E
k = 2 m E ℏ 2
As a side note, ℏ = h 2 π . Plugging k into the wavefunction leaves only A unknown,
ψ x = A s i n 2 m E ℏ 2 x
The other boundary condition provides a route.
ψ L = 0 = A s i n 2 m E ℏ 2 L
Equation 31 is only zero (disregarding the unproductive A = 0 case), when the sine is some integer times π .
2 m E ℏ 2 L = n π ;   n = 1,2 , 3 … , ∞
2 m E ℏ 2 = n π L
In equation 32a, n is not zero, because the equation would not be balanced in that case. The left-hand side of equation 33b fits into equation 30, yielding,
ψ x = A s i n n π L x
The probability of the particle being anywhere along the x dimension must total one. In mathematical terms, the integral of the probability must equal one. This is known as normalizing the wavefunction. Normalization is expressed,
∫ 0 L ψ 2 ( x ) d x = 1
A 2 ∫ 0 L sin 2 ⁡ n π L d x = 1
The solution to the integral is lengthy. However, it has been previously solved[37] and the solution is,
A 2 L 2 = 1 ;   A = 2 L
The wavefunction now has no unknown constants:
ψ x = 2 L sin ⁡ n π L x
Equation 37 may now be substituted in equation 22,
− ℏ 2 2 m ∂ 2 ∂ x 2 2 L sin ⁡ n π L x = E 2 L sin ⁡ n π L x
ℏ 2 2 m 2 L n 2 π 2 L 2 sin ⁡ n π L x = E 2 L sin ⁡ n π L x
ℏ 2 2 m n 2 π 2 L 2 = E
E = ℏ 2 n 2 π 2 2 m L 2
Since the eigenvalue problem is solved, the constant when n = 1 may be placed in the lower right of a 2x2 controlled unitary matrix. The controlled unitary matrix, C U , would then be,
C U = 1 0 0 e 2 π i E
C U = 1 0 0 e 2 π i ℏ 2 π 2 2 m L 2
When n = 2 , the quantity in the lower right-corner is exactly 4 times the current value. Since E increases by integer multipliers, and since there is a 2 π factor before E , representing exactly one revolution around the complex unit circle, the eigenvalue measured by QPE will always be precisely the same for all energy levels. I.e., for any correct energy level, QPE will measure out the correct eigenvalue, or phase. However, there is some information loss, because the allowed energies scale by n 2 . Any integer multiplier will return the correct-appearing result due to the 2 π factor conducting precisely one revolution. Therefore, any n would be indistinguishable from the correct n 2 in this QPE arrangement. The quantum harmonic oscillator, exhibited below

Harmonic oscillator

The harmonic oscillator has a symmetric potential energy which allows for an analytical solution to its energy levels (eigenvalues) and wavefunctions (eigenvectors). The Schrödinger equation with the Hamiltonian operator expanded for the harmonic oscillator example is,
− ℏ 2 2 m d 2 ψ x d x 2 + 1 2 m ω 2 x 2 ψ x = E ψ x
The wavefunction, ψ x , is not derived here, but the correct guess is,
ψ x = C e x p − α x 2 2
C and α are constants. Equation 41 is in the form of a gaussian function, and the tails of a gaussian function diminish to zero. This fact signifies that the wavefunction may be normalized, as essential criteria. Not fully shown here, the constant C cancels in the Schrödinger equation, via an exponent by becoming e 0 . There remain x 2 ψ x polynomial terms and ψ x terms in the analytical solution. The x 2 ψ x coefficients are set equal to obtain α = m ω ℏ . The ψ x coefficients being equal yields,
ℏ ω 2 = E
ℏ ω n + 1 2 = E
Equation 42b also satisfies the Schrödinger equation when multiplied by the integer n = 0,2 , 3 … ∞ , though the proof of this is not included in this Article. (The wavefunction also includes n in these other higher-energy solutions.) ℏ is the reduced Planck’s constant, and ω is the angular velocity, also assumed constant. Both sides of the eigendecomposition equation may be divided by a scalar, ℏ ω . When placed on the complex unit circle, a full revolution occurs after 1, because of the multiplicative 2 π factor. Therefore, only the scalar 1 2 is necessary. When the measured computational basis is 100 , or θ = 1 2 , the solution may be,
E = 1 2 + n ;   n = 0,1 , 2 , … , ∞
n is an integer. For example, 3 2 , π on the complex unit circle, is place exactly at 1 2 , also π on the complex unit circle. The matrix exponential is taken of 1 2 , and the control block is added. The C U matrix is then very similar to the previous C U matrix of equations 13 and 39:
C U = 1 0 0 e i π
The result, after matching with Table 1, will be multiplied by the constant ℏ ω . Figure 4 shows the measurements from the code implementation of QPE. Subsequent to publication, all code will be made publicly available at https://bitbucket.org/ericawalk/ oscillator/src/master/.

Hydrogen atom and larger

The hydrogen atom does include potential energy that is nonzero and dependent upon position, specifically radial distance from the nucleus. I.e., it is more complex than the quantum harmonic oscillator example which experiences symmetric potential energy allowing for an analytical solution. For one electron in a hydrogen atom, the coulombic potential energy function is,[35]
V r = − Z e 2 4 π ϵ 0 r
Z = 1 is the charge of the nucleus. e 2 = 1 is the charge of the electron. ϵ 0 is the permittivity of a vacuum. Permittivity is a measure of how much an electric field can permeate a vacuum. r is the same spatial coordinate, radius.
The energy levels may be analytically solved in a lengthy procedure left out of the scope of this work. The final energy levels of the hydrogen atom are,
E = − μ Z 2 e 4 π 2 2 ϵ 0 2 ℏ 2 n 2
In the case of equation 46, the energy levels scale as 1 n 2 , and therefore do not repeat at constant integer intervals. Therefore, for QPE, the various E ’s for various n ’s would have to be entered into the matrix diagonal. The dimension of the matrix inputted into QPE would increase with every new energy level, and many distinct eigenvalues would be measured. The ground-state energy, when n = 1 , could be placed in a C U matrix and be measured, although the same may be said for nearly any number which follows certain conditions. The advantage of a quantum computer would come in solving multi-electron potential energy rather than the hydrogen atom.
The challenge exists in expressing the coulombic energies among multiple electrons in the potential energy function in a format for QPE. The positions of the electrons are not known and are left as variables in the multi-electron potential energy function. As put forward by Aspuru-Guzik, et al.,[12] every entangled qubit state can represent a point in space. Then, the electronic structure may be tracked over a very short time to obtain the ground state energy. Future work will be writing Hamiltonians as numerical matrices via a finite difference method over the space. With a fine enough mesh due to a large number of entangle qubit states, greater and greater accuracy will be achievable. It is very likely that the matrix exponential via truncated Taylor series approach for quantum computing as demonstrated by Berry, et al.[11,26] will be employed on numerical Hamiltonian matrices. Another related option is to apply full configuration interaction up to a limit of number of electrons (and nuclei).[38,39] A remarkable advantage of quantum computing which has not been available thus far via analytical analysis, is that the wavefunction need not be measured, only the ground state energy.

Conclusions

In order for quantum computers to effect breakthroughs in physical chemistry, the rudiments of algorithms and, equally important, extracting the result, must be rigorously developed and demonstrated. In addition to the quantum harmonic oscillator example, this Article has demonstrated how eigenvalues may be placed in the complex unit circle along with the subsequent steps in measuring out those eigenvalues. While run on a quantum circuit simulator, a quantum computer without noise is predicted to also exactly solve the quantum harmonic oscillator problem in the same way as the simulator employed in this Article. With further programming implementation of many-body quantum systems, the power of quantum computing will be fully harnessed for physical chemistry, and if the hope becomes true, surpass even the most accurate modern computational methods in the field.

Acknowledgements

Coding, simulations and calculations were performed at the Center for Computational Research of the University at Buffalo, the State University of New York. Eugene F. Dumitrescu of the Quantum Information Science group of Oak Ridge National Laboratory is acknowledged for the helpful discussions. Tyler Takeshita, currently a quantum solutions architect at Amazon Web Services, is also acknowledged for the helpful discussions.

References

  1. National Academies of Sciences, Engineering, and Medicine. Quantum Computing: Progress and Prospects; The National Academies Press: Washington, DC, USA, 2019; p. 272. [Google Scholar]
  2. Hidary, J.D. Quantum Computing: An Applied Approach; Springer International Publishing, 2019; p. 379. [Google Scholar]
  3. Shor, P.W. Algorithms for Quantum Computation: Discrete Logarithms and Factoring. Proceedings 35th Annual Symposium on Foundations of Computer Science, 20-22 November 1994; pp. 124–134. [Google Scholar]
  4. Grover, L.K. , From Schrödinger’s Equation to the Quantum Search Algorithm. Pramana 2001, 56, 333–348. [Google Scholar] [CrossRef]
  5. Feynman, R.P. , Simulating Physics with Computers. International Journal of Theoretical Physics 1982, 21, 467–488. [Google Scholar] [CrossRef]
  6. Trabesinger, A. , Quantum Simulation. Nature Physics 2012, 8, 263–263. [Google Scholar] [CrossRef]
  7. Walker, E.A.; Pallathadka, S.A. , How a Quantum Computer Could Solve a Microkinetic Model. J. Phys. Chem. Lett. 2020, 592–597. [Google Scholar] [CrossRef] [PubMed]
  8. Horvatits, C.; Li, D.; Dupuis, M.; Kyriakidou, E.A.; Walker, E.A. , Ethylene and Water Co-Adsorption on Ag/Ssz-13 Zeolites: A Theoretical Study. J. Phys. Chem. C 2020, 124, 7295–7306. [Google Scholar] [CrossRef]
  9. Walker, E.A.; Ravisankar, K.; Savara, A. , Chekipeuq Intro 2: Harnessing Uncertainties from Data Sets, Bayesian Design of Experiments in Chemical Kinetics. ChemCatChem 2020, n/a. [Google Scholar] [CrossRef]
  10. Matera, S.; Schneider, W.F.; Heyden, A.; Savara, A. , Progress in Accurate Chemical Kinetic Modeling, Simulations, and Parameter Estimation for Heterogeneous Catalysis. ACS Catal. 2019, 9, 6624–6647. [Google Scholar] [CrossRef]
  11. Berry, D.W.; Ahokas, G.; Cleve, R.; Sanders, B.C. , Efficient Quantum Algorithms for Simulating Sparse Hamiltonians. Communications in Mathematical Physics 2007, 270, 359–371. [Google Scholar] [CrossRef]
  12. Kassal, I.; Jordan, S.P.; Love, P.J.; Mohseni, M.; Aspuru-Guzik, A. , Polynomial-Time Quantum Algorithm for the Simulation of Chemical Dynamics. PNAS 2008, 105, 18681–18686. [Google Scholar] [CrossRef] [PubMed]
  13. Bravo-Prieto, C.; LaRose, R.; Cerezo, M.; Subasi, Y.; Cincio, L.; Coles, P.J. , Variational Quantum Linear Solver. arXiv 2020. [Google Scholar] [CrossRef]
  14. Cerezo, M.; Arrasmith, A.; Babbush, R.; Benjamin, S.C.; Endo, S.; Fujii, K.; McClean, J.R.; Mitarai, K.; Yuan, X.; Cincio, L. , Variational Quantum Algorithms. arXiv 2020, arXiv:09265. [Google Scholar] [CrossRef]
  15. Kresse, G.; Furthmüller, J. , Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  16. Kresse, G.; Hafner, J. , Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
  17. Nist Chemistry Webbook; National Institute of Standards and Technology. Available online: http://webbook.nist.gov.
  18. Walker, E.; Ammal, S.C.; Terejanu, G.A.; Heyden, A. , Uncertainty Quantification Framework Applied to the Water–Gas Shift Reaction over Pt-Based Catalysts. J. Phys. Chem. C 2016, 120, 10328–10339. [Google Scholar] [CrossRef]
  19. Walker, E.A.; Mitchell, D.; Terejanu, G.A.; Heyden, A. , Identifying Active Sites of the Water–Gas Shift Reaction over Titania Supported Platinum Catalysts under Uncertainty. ACS Catal. 2018, 8, 3990–3998. [Google Scholar] [CrossRef]
  20. Kohn, W.; Sham, L.J. , Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
  21. Hohenberg, P.; Kohn, W. , Inhomogeneous Electron Gas. Physical Review 1964, 136, B864–B871. [Google Scholar] [CrossRef]
  22. Hummer, K.; Harl, J.; Kresse, G. , Heyd-Scuseria-Ernzerhof Hybrid Functional for Calculating the Lattice Dynamics of Semiconductors. Phys. Rev. B 2009, 80, 115205. [Google Scholar] [CrossRef]
  23. Kohn, W.; Sham, L.J. , Quantum Density Oscillations in an Inhomogeneous Electron Gas. Physical Review 1965, 137, A1697–A1705. [Google Scholar] [CrossRef]
  24. Abrams, D.S.; Lloyd, S. , Quantum Algorithm Providing Exponential Speed Increase for Finding Eigenvalues and Eigenvectors. Phys. Rev. Lett. 1999, 83, 5162–5165. [Google Scholar] [CrossRef]
  25. Wang, H.; Kais, S.; Aspuru-Guzik, A.; Hoffmann, M.R. , Quantum Algorithm for Obtaining the Energy Spectrum of Molecular Systems. Phys. Chem. Chem. Phys. 2008, 10, 5388–5393. [Google Scholar] [CrossRef]
  26. Berry, D.W.; Childs, A.M.; Cleve, R.; Kothari, R.; Somma, R.D. , Simulating Hamiltonian Dynamics with a Truncated Taylor Series. Phys. Rev. Lett. 2015, 114, 090502. [Google Scholar] [CrossRef]
  27. Dorner, U.; Demkowicz-Dobrzanski, R.; Smith, B.J.; Lundeen, J.S.; Wasilewski, W.; Banaszek, K.; Walmsley, I.A. , Optimal Quantum Phase Estimation. Phys. Rev. Lett. 2009, 102, 040403. [Google Scholar] [CrossRef] [PubMed]
  28. Paesani, S.; Gentile, A.A.; Santagati, R.; Wang, J.; Wiebe, N.; Tew, D.P.; O’Brien, J.L.; Thompson, M.G. , Experimental Bayesian Quantum Phase Estimation on a Silicon Photonic Chip. Phys. Rev. Lett. 2017, 118, 100503. [Google Scholar] [CrossRef] [PubMed]
  29. D'Ariano, G.M.; Macchiavello, C.; Sacchi, M.F. , On the General Problem of Quantum Phase Estimation. Phys. Lett. A 1998, 248, 103–108. [Google Scholar] [CrossRef]
  30. White, R.E.; Subramanian, V.R. , Computational Methods in Chemical Engineering with Maple; Springer: Verlag Berlin Heidelberg, 2010. [Google Scholar]
  31. Lee, Y.; Joo, J.; Lee, S. , Hybrid Quantum Linear Equation Algorithm and Its Experimental Test on Ibm Quantum Experience. Scientific Reports 2019, 9, 4778. [Google Scholar] [CrossRef] [PubMed]
  32. Coles, P.J.; Eidenbenz, S.; Pakin, S.; Adedoyin, A.; Ambrosiano, J.; Anisimov, P.; Casper, W.; Chennupati, G.; Coffrin, C.; Djidjev, H. , Quantum Algorithm Implementations for Beginners. arXiv 2018, arXiv:1804.03719. [Google Scholar]
  33. Harrow, A.W.; Hassidim, A.; Lloyd, S. , Quantum Algorithm for Linear Systems of Equations. Phys. Rev. Lett. 2009, 103, 150502. [Google Scholar] [CrossRef]
  34. Argentini, G. , A Matrix Generalization of Euler Identity. arXiv 2007. [Google Scholar]
  35. McQuarrie, D.A. , Physical Chemistry: A Molecular Approach; University Science Books: Sausalito, Calif, 1997. [Google Scholar]
  36. Pauling, L.; Wilson, E.B. Introduction to Quantum Mechanics with Applications to Chemistry; Courier Corporation, 2012. [Google Scholar]
  37. Saleem, M. A Particle in a One-Dimensional Box. In Quantum Mechanics; IOP Publishing, 2015; pp. 2-1–2-13. [Google Scholar]
  38. Aspuru-Guzik, A.; Dutoi, A.D.; Love, P.J.; Head-Gordon, M. , Simulated Quantum Computation of Molecular Energies. Science 2005, 309, 1704. [Google Scholar] [CrossRef]
  39. Zimmerman, P.M. , Incremental Full Configuration Interaction. J. Chem. Phys. 2017, 146, 104102. [Google Scholar] [CrossRef] [PubMed]
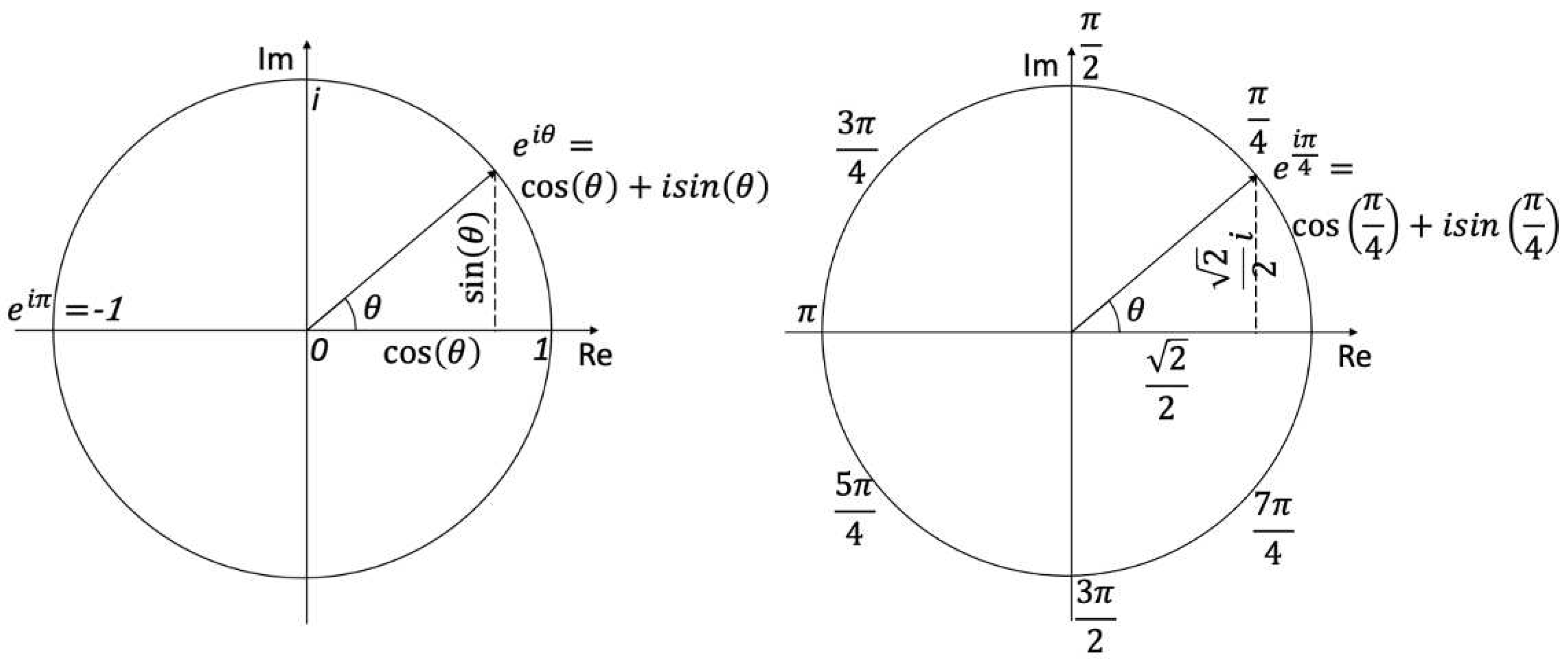
Preprints 87756 g001
Figure 1. (a) Complex number plane and Euler’s identity. (b) One eighth, 1 8 , rotation about the complex unit circle corresponds to e i π 4 .
Figure 1. (a) Complex number plane and Euler’s identity. (b) One eighth, 1 8 , rotation about the complex unit circle corresponds to e i π 4 .
Preprints 87756 g001
Preprints 87756 g002
Figure 2. Reading out the eigenvalues at intervals of θ = 1 8 from the matrix U , the lower right block of the controlled C U . On the zeroeth qubit, q 0 , the C U matrix is applied once ( 2 0 = 1 ). On the first qubit, C U is applied twice, and for the second qubit it is applied four times. Q F T † is the inverse QFT. The measurements corresponding to θ   are listed in Table 1.
Figure 2. Reading out the eigenvalues at intervals of θ = 1 8 from the matrix U , the lower right block of the controlled C U . On the zeroeth qubit, q 0 , the C U matrix is applied once ( 2 0 = 1 ). On the first qubit, C U is applied twice, and for the second qubit it is applied four times. Q F T † is the inverse QFT. The measurements corresponding to θ   are listed in Table 1.
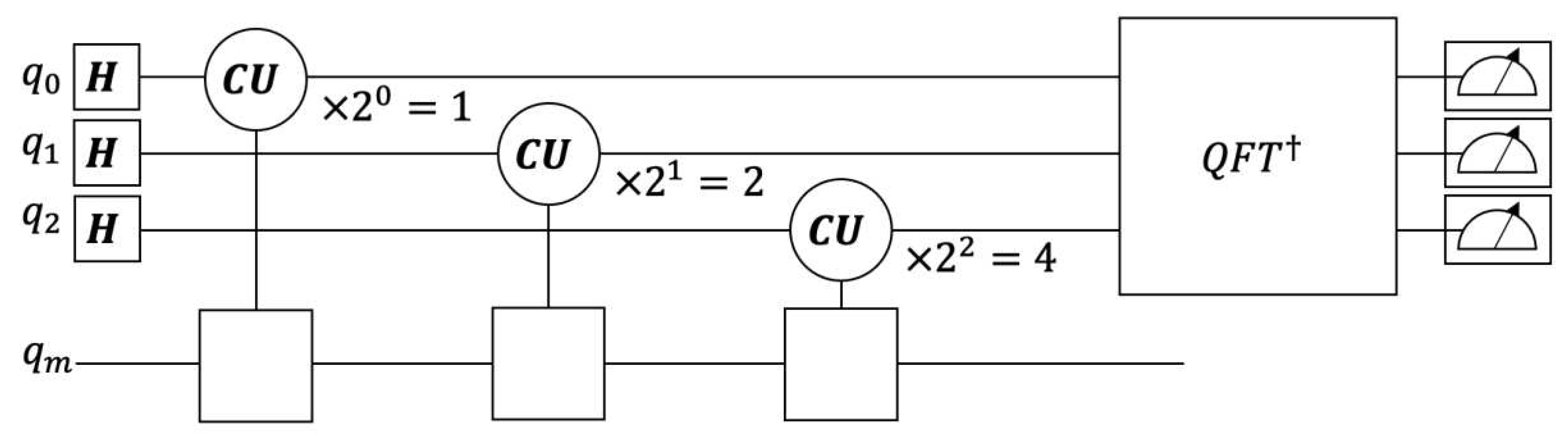
Preprints 87756 g002
Preprints 87756 g003
Figure 3. Precision of rotations around the complex unit circle for 3 qubits. 1 2 3 = 1 8 . (a) π rotation will result in a precise probability during measurement (Figure 4). (b) A rotation not on the allowed increments will distribute probability among possible measurements (Figure 5).
Figure 3. Precision of rotations around the complex unit circle for 3 qubits. 1 2 3 = 1 8 . (a) π rotation will result in a precise probability during measurement (Figure 4). (b) A rotation not on the allowed increments will distribute probability among possible measurements (Figure 5).
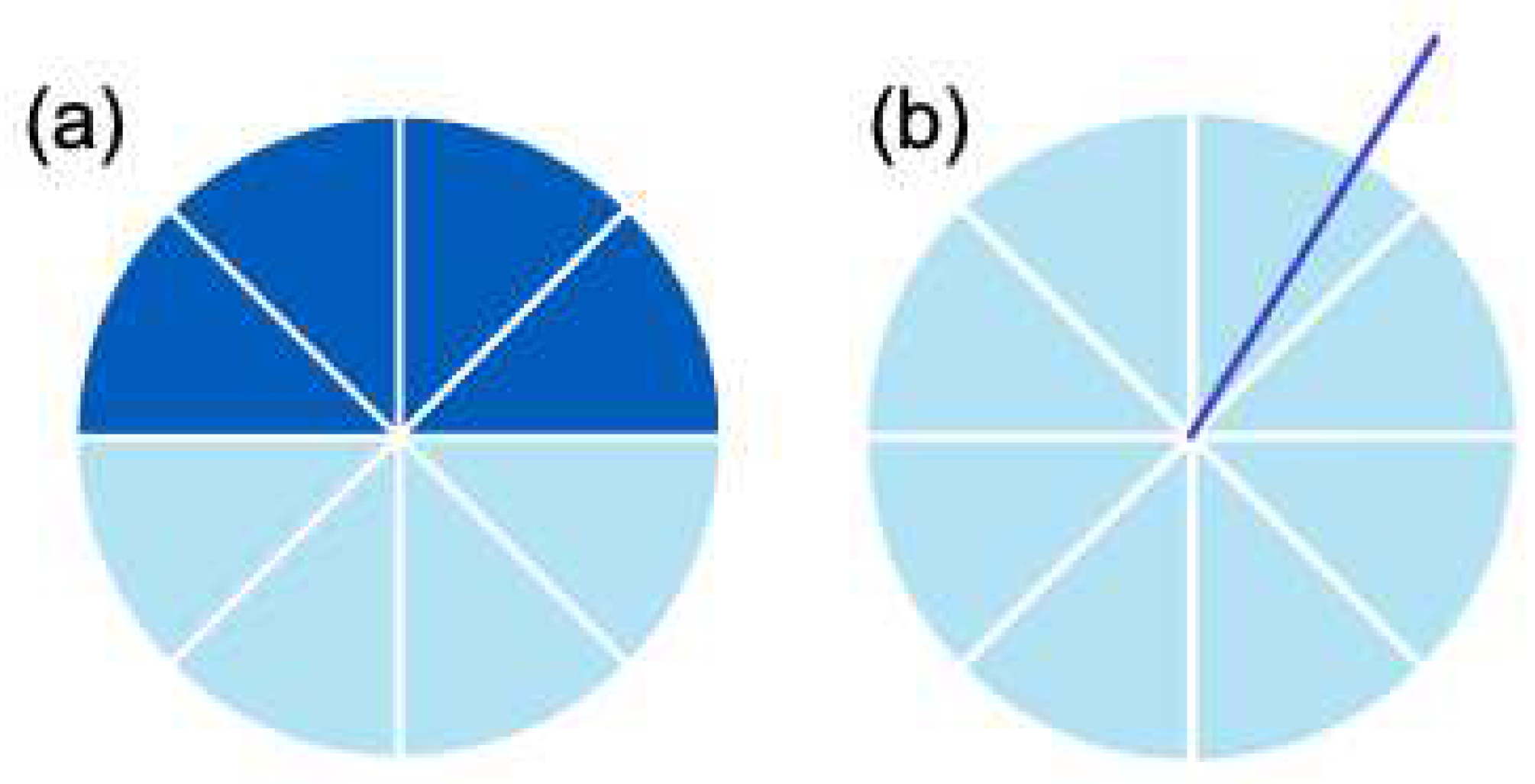
Preprints 87756 g003
Preprints 87756 g004
Figure 4. The harmonic oscillator eigenvalue(s) are measured in the quantum circuit. Due to the precise setup, the probability of reading the eigenvalue(s) correctly are 100%. Checking with Table 1 of the main text, the bitstring 100 , corresponds to 1 2 , the lowest energy harmonic oscillator. The infinitely higher energies of the harmonic oscillator each add 2 π , one full revolution to the complex unit circle. Therefore, the measured bitstring will always be the same for any of those infinite number of energy levels for the harmonic oscillator.
Figure 4. The harmonic oscillator eigenvalue(s) are measured in the quantum circuit. Due to the precise setup, the probability of reading the eigenvalue(s) correctly are 100%. Checking with Table 1 of the main text, the bitstring 100 , corresponds to 1 2 , the lowest energy harmonic oscillator. The infinitely higher energies of the harmonic oscillator each add 2 π , one full revolution to the complex unit circle. Therefore, the measured bitstring will always be the same for any of those infinite number of energy levels for the harmonic oscillator.
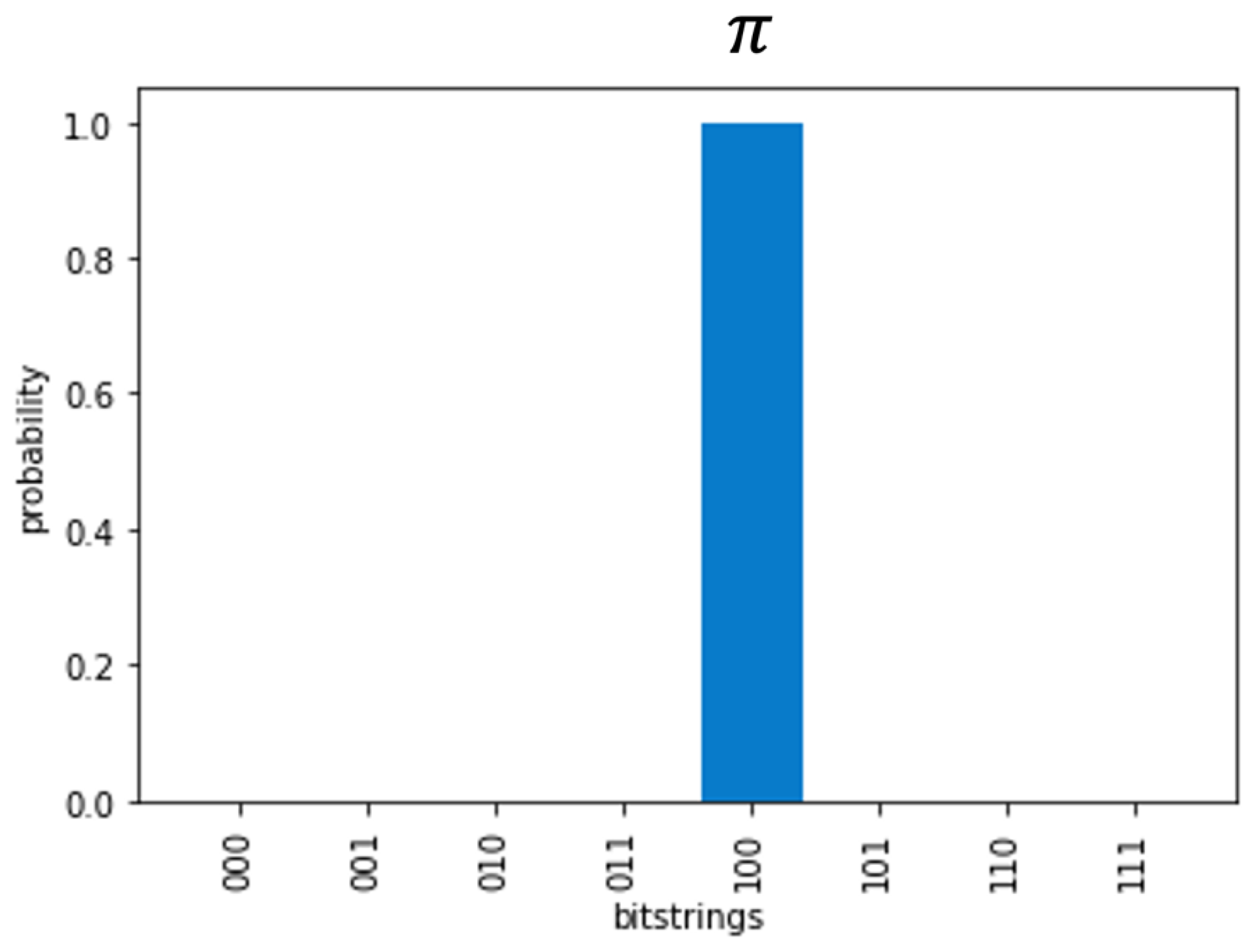
Preprints 87756 g004
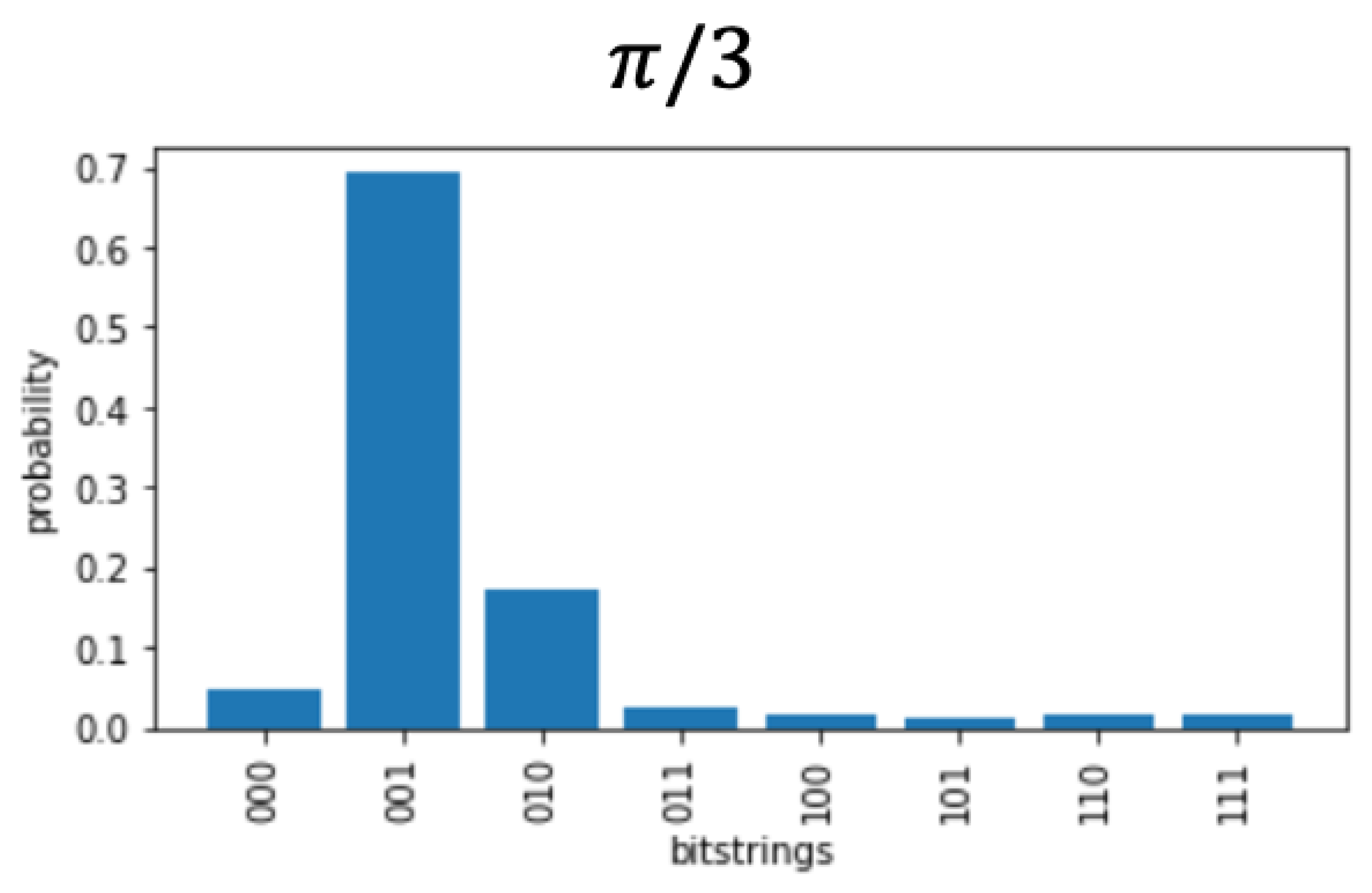
Preprints 87756 g005
Figure 5. A non-precise step in the complex unit circle is π 3 . The exact steps are 1 2 t 2 π , where t is the total number of qubits. Therefore, probability is spread over multiples of 1 8 .
Figure 5. A non-precise step in the complex unit circle is π 3 . The exact steps are 1 2 t 2 π , where t is the total number of qubits. Therefore, probability is spread over multiples of 1 8 .
Preprints 87756 g005
Table 1.
measurement 000 001 010 011 100 101 110 111
θ 0 1 8 1 4 3 8 1 2 5 8 3 4 7 8
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated