Prerpints.org logo
Preprint
Article

Dual-Period Polarization-Dependent Diffraction Gratings Based on a Polymer-Stabilized Liquid Crystal

Altmetrics

Downloads

84

Views

51

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

16 October 2023

Posted:

17 October 2023

You are already at the latest version

Alerts
Abstract
In this paper we demonstrate first ever dual-period diffraction gratings that do not require electrical tuning to obtain the effect of period change. Our method allows for multiplication of the base period by proper modification of the subsequent slits of the grating. The proposed elements are fabricated by selective photopolymerization of a composite based on nematic liquid crystal. The gratings are formed by polymer stabilization of liquid crystal in different orientations of the molecules in selected grating slits to allow for period manipulation. The operating principle is based on changing the phase delay introduced by the slits depending on polarization direction of incident light with respect to the director in each type of slit, which allows to change the grating’s period. The proposed technique was successfully utilized to obtain diffraction gratings with either doubling or tripling of the period.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Composites consisting of liquid crystals (LCs) and polymers have been widely studied over the years. Such materials are usually categorized as polymer-stabilized LCs (PSLCs) or polymer-dispersed LCs (PDLCs) depending on LC to monomer ratio. In case of PSLCs, the polymer network is formed in between LC molecules and stabilizes the molecular arrangement as the concentration of monomer is quite low (<10%) [1]. Such a network allows not only to expand the temperature stability of the LC phase [2,3,4,5] but also to preserve the desired orientation of LC molecules that was initially obtained under the influence of an external factor such as electric field [6,7,8,9,10,11]. When it comes to PDLCs, the polymer concentrations typically range from ~20% to 80% [1]. In such composites the LC and polymer separate during polymerization process and thus LC droplets dispersed in the polymer matrix are formed [12]. In contrast to PSLCs, the molecules within LC droplets are oriented randomly and thus the material is highly scattering when no electric field is applied.
Polymer-doped LCs have been demonstrated to be suitable for applications in optics and photonics, especially when it comes to tunable lenses [13,14,15], diffractive optical elements [2,11,16,17,18,19,20,21], LCDs [4,22,23,24], waveguides [7] and phase shifters [25,26,27]. Stabilization of LC’s molecular arrangement with a polymer network has been used to fabricate various types of lenses including Fresnel zone plates [16] and lenses with electrically tunable focal length [14,15]. However, a huge issue with such lenses is the fact that their performance is strongly dependent on polarization of incident light. When it comes to diffraction gratings, it was demonstrated that such elements can be fabricated based on PDLCs irradiated with a periodic pattern, although external electric field was required for the gratings to operate properly as otherwise the LC within the droplets was oriented randomly [28]. Other groups reported a method of forming PDLC-based [29] and PSLC-based [30] diffraction gratings by introducing the material into LC cells with periodic in-plane switching electrodes. Additionally, LC-based diffraction gratings with no polymer added the material have been demonstrated. In those cases, the gratings were either created by irradiation of photosensitive alignment layers [31,32,33,34,35,36,37] or by introducing the LC into LC cells with periodic electrodes [38]. Moreover, the diffraction efficiencies of the presented LC-based diffraction gratings were dependent on polarization of incident light and the value of applied voltage in case of the ones with periodic electrodes. The concept of dual-period diffraction gratings has also been investigated [39] as such gratings can be highly beneficial for beam steering. Such gratings based on polymer-stabilized blue phase LCs have been demonstrated, however, the polymer was used only to provide stability of the material and the gratings themselves were formed by periodic electrodes [20,21].
The main goal of the presented research was to provide a proof of concept for polymer-stabilized dual-period diffraction gratings operating for linearly polarized light. To achieve this, strong dependence of LC-based diffractive optical elements on polarization direction of incident light was utilized. The fabrication method was relatively simple as it was based on selective polymer-stabilization of electrically controlled orientation of LC molecules in selected slits of each diffraction grating. As a result, stable structures with periodically variable molecular arrangement were formed and, unlike in the case of diffraction gratings based on PDLCs [28] or LC cells with periodic electrodes [20,21]., no external electric field was required for them to operate. Additionally, the polymerization-induced increase in thermal stability of the LC [5] makes the proposed fabrication technique superior to the one based on photoalignment. The fabricated samples were examined in a free space optical setup to prove the possibility of changing the gratings’ period by rotating the polarization direction of incident linearly polarized light. When it comes to application prospects, it is thought that a combination of such gratings, designed to exhibit different period changes, can be used as main discriminator for a polarimeter [40,41,42,43,44]. Moreover, the proposed polarization-dependent dual-period gratings can be utilized as passive elements in spectrometers that allow to change the spectral resolution just by controlling the polarization of incoming light.

2. Materials and methods

2.1. Material preparation

The composite used in the research was based on a nematic LC 5CB (4-Cyano4’-pentylbiphenyl, >99.5%) doped with reactive monomer Bisphenol A dimethacrylate (Sigma Aldrich, >98%, CAS: 3253-39-2) and photoinitiator 4,4’-Bis(diethylamino)benzophenone (Sigma Aldrich, ≥99%, CAS: 90-93-7). The concentration of the dopant was 2.5wt% and the ratio between the monomer and photoinitiator was 9:1. The material was created by mixing the dopant compounds in desired proportions and then adding the LC to ensure a precise measurement of the dopants’ amount. Next, the composite was mixed in ultrasonic bath in temperature above the clearing point of 5CB for 30 minutes to provide uniform distribution of the compounds. The mixed material was introduced into 12µm LC cells with planar alignment layers and ITO coating using capillary forces.

2.2. Design and fabrication

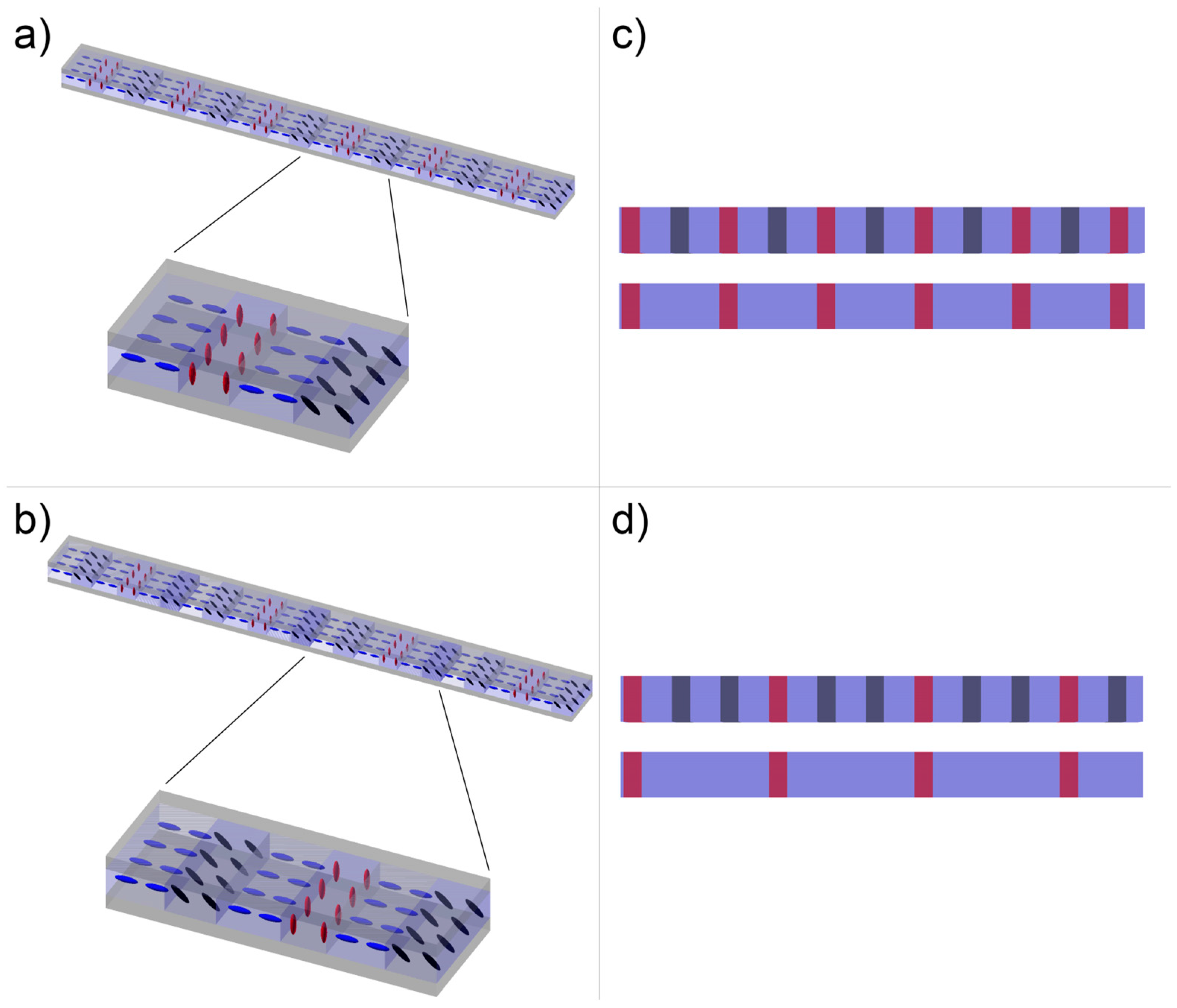
The samples were fabricated by selective irradiation (λ=405nm, I=1mW/cm2, 15 minutes per slit type) with periodic patterns corresponding to the grating’s slits with each designed molecular arrangement of the LC. During polymerization, the LC cell was connected to a function generator to control the orientation of LC molecules. The building block of each diffraction grating consisted of 4 or 6 elements of identical width corresponding to the grating’s slits, which is demonstrated in Figure 1. Regardless of structure design, every other slit was left non-polymerized (planar) and the LC molecules in the other ones were polymerized either under 20V to obtain a homeotropic orientation or under lower voltage to achieve only a tilt of the molecules with respect to the LC cell plane. The LC arrangement in case of a 4-element building block (Figure 1a) was as follows: planar, polymerized with a tilt, planar, polymerized in homeotropic orientation. In case of a 6-element block (Figure 1b), there were two additional slits: planar and polymerized with a tilt. Periodically varying orientations of LC molecules resulted in periodic changes of effective birefringence between the grating’s slits. Consequently, linearly polarized light passing through each type of slits experienced different phase delays. Moreover, the effective birefringence, and thus the introduced phase delay, depends on the relation between the polarization direction and LC director in each slit. The proposed design enabled the creation of gratings with either double (Figure 1c) or triple (Figure 1d) period change with polarization rotation by ensuring that the phase difference between planar slits and the ones with a tilt of LC molecules was equal to integer multiplicity of π for a specific polarization direction.
Preprints 87935 g001
Figure 1. Schematic representation of the designed diffraction gratings. The schemes a) and b) demonstrate the molecular arrangement in each type of diffraction grating as well as zoom on each grating’s building block consisting of: a) 4 elements (double period change), b) 6 elements (triple period change). The schemes c) and d) visualize the polarization-dependent period change of grating a) and b) respectively.
Figure 1. Schematic representation of the designed diffraction gratings. The schemes a) and b) demonstrate the molecular arrangement in each type of diffraction grating as well as zoom on each grating’s building block consisting of: a) 4 elements (double period change), b) 6 elements (triple period change). The schemes c) and d) visualize the polarization-dependent period change of grating a) and b) respectively.
Preprints 87935 g001

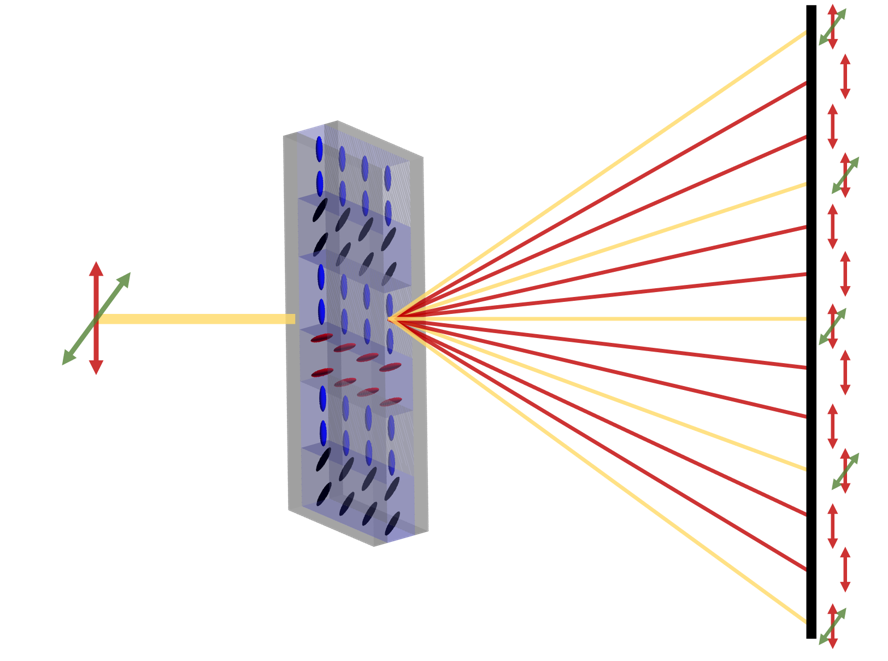
2.3. Analysis of diffraction patterns

The performance of diffraction gratings was analyzed in a free space optical setup consisting of a red laser (λ=660nm) as a light source and a half-wave plate to control the polarization direction of light incident on the sample. The diffraction patterns were observed on a screen set in a distance from the sample that was sufficient to fulfil the small angle approximation ( s i n α ≅ t g α ). The measurements of grating’s period values were conducted under a digital microscope (Keyence VHX 5000) with a sample positioned between crossed polarizers. To ensure that the measured values corresponded to the observed diffraction patterns, the period values were also calculated based on the measured distances between the 0th and 1st diffraction order by approximating the formula:
d s i n α = m λ ,
where d – grating period, α   – diffraction angle, m   – diffraction order and λ – illuminating wavelength. The distance between higher diffraction orders was not considered as for larger diffraction angles the s i n α ≅ t g α approximation would not be valid.

3. Results and discussion

3.1. Diffraction gratings with double period change

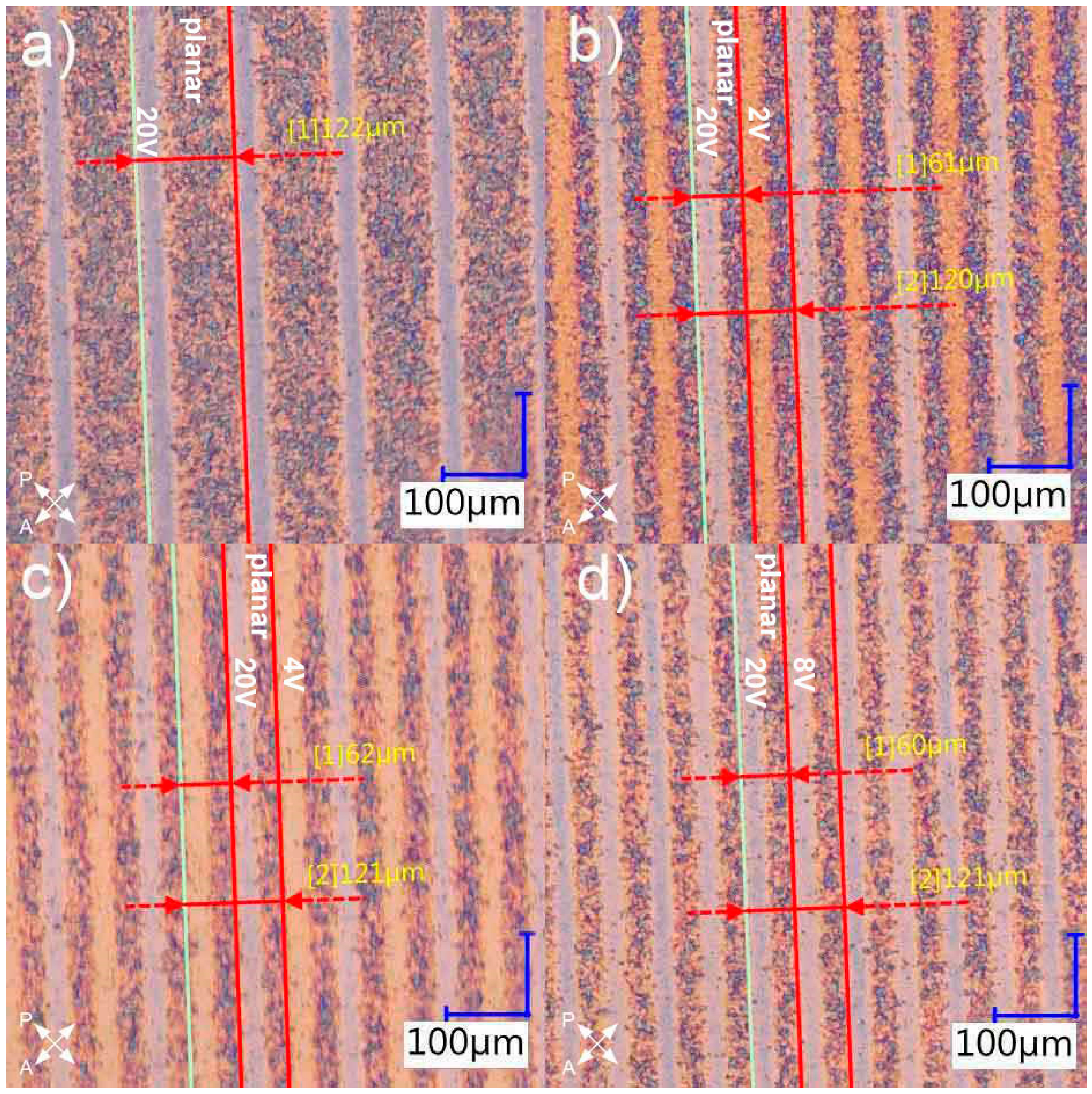
The first samples were designed to exhibit doubling of the grating’s period. The polymerized slits were irradiated interchangeably in two different orientations of LC molecules (homeotropic and tilted), however, the voltage values corresponding to the tilt angle were chosen arbitrarily. This step was aimed at determining the voltage that provided a sufficient tilt of LC molecules to allow for a period change for a specific polarization direction. The fabricated gratings, including the reference one with only larger period, are presented in Figure 2.
Preprints 87935 g002
Figure 2. Comparison of fabricated diffraction gratings observed under a polarizing microscope with crossed polarizers. The reference grating a) has every other slit polymerized under 20V. The gratings b-d have half of the polymerized slits irradiated under 20V and the rest is polymerized under: b) 2V, c) 4V and d) 8V. The remaining slits are not polymerized. Period(s) of each grating are measured with the measurement tools of the microscope.
Figure 2. Comparison of fabricated diffraction gratings observed under a polarizing microscope with crossed polarizers. The reference grating a) has every other slit polymerized under 20V. The gratings b-d have half of the polymerized slits irradiated under 20V and the rest is polymerized under: b) 2V, c) 4V and d) 8V. The remaining slits are not polymerized. Period(s) of each grating are measured with the measurement tools of the microscope.
Preprints 87935 g002
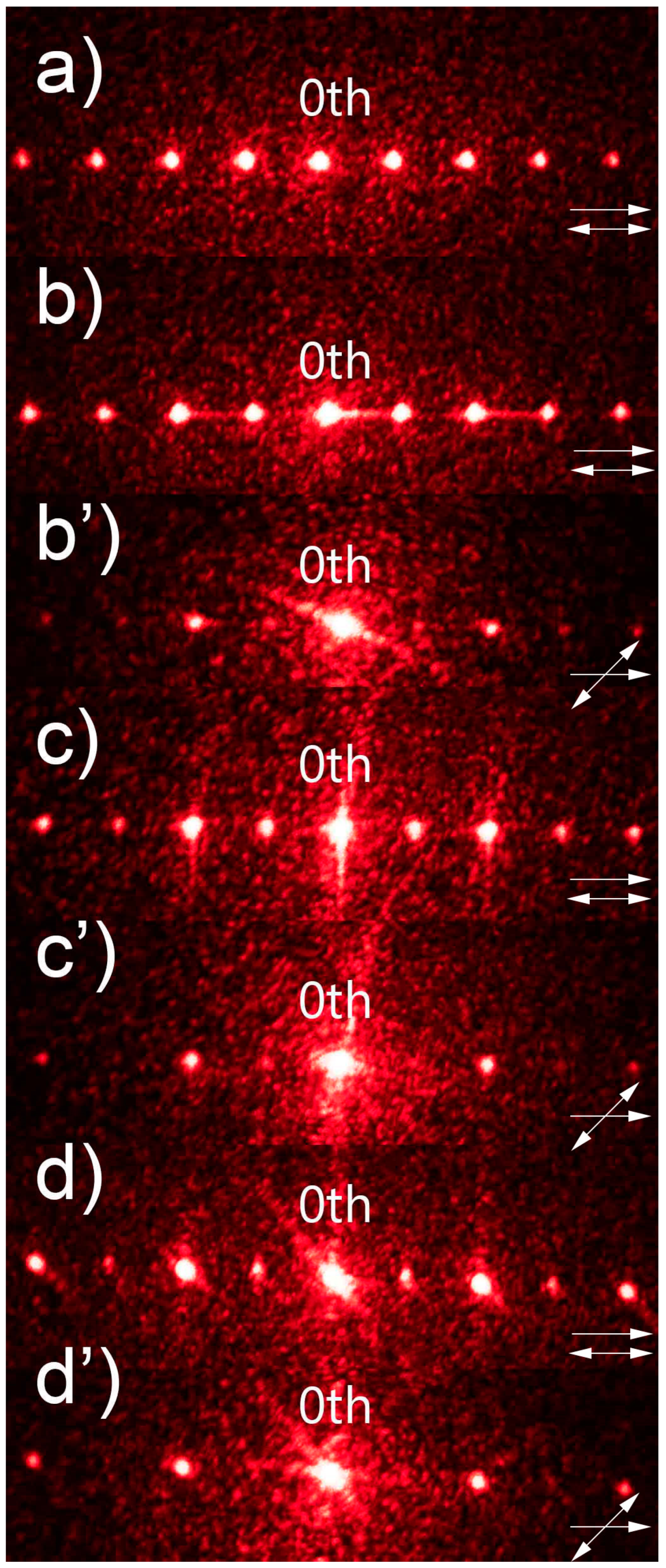
The obtained samples were examined in a free space optical setup and the observed diffraction patterns were compared with the one acquired for the reference sample (Figure 3).
Preprints 87935 g003
Figure 3. Comparison of diffraction patterns observed for the gratings presented in Figure 2. The reference grating (Figure 2a) has only one period so the diffraction pattern is presented for only one polarization direction (picture a)). The other gratings are examined for different polarization directions to observe the period change: (b, b’) Figure 2b, (c, c’) Figure 2c and (d, d’) Figure 2d. The relation between LC director in planar slits and polarization direction is marked in each image. For all the images, 80 pixels correspond to 1cm on the screen.
Figure 3. Comparison of diffraction patterns observed for the gratings presented in Figure 2. The reference grating (Figure 2a) has only one period so the diffraction pattern is presented for only one polarization direction (picture a)). The other gratings are examined for different polarization directions to observe the period change: (b, b’) Figure 2b, (c, c’) Figure 2c and (d, d’) Figure 2d. The relation between LC director in planar slits and polarization direction is marked in each image. For all the images, 80 pixels correspond to 1cm on the screen.
Preprints 87935 g003
The diffraction patterns obtained for the dual-period samples (Figure 3c-d’) clearly demonstrate that it was possible to find a linear polarization direction for which the incident light experienced both a smaller period and the larger one that was identical to the reference sample. In case of the reference diffraction pattern (Figure 3 a), the diffraction efficiency was gradually decreasing for higher diffraction orders. However, for all the other samples (Figure 3b, c, d), the diffraction efficiency for even diffraction orders was higher than for the odd ones. This disproportion in diffraction efficiency was larger for the samples with larger tilt of LC molecules (higher voltage values during polymerization) and such behavior was due to phase mismatch between the non-polymerized slits and half of the polymerized ones. When it comes to the smaller period, it was possible to observe diffraction patterns corresponding to it only for two samples (Figure 3c’, d’). In case of the sample with part of the slits polymerized under 2V (Figure 2b), it was not possible to find a polarization direction for which the change of period could have been observed – the diffraction pattern corresponding to the larger period was visible regardless of polarization direction and the change was observed only in diffraction efficiency (Figure 3b, b’). It was thought that the tilt of LC molecules in the regions polymerized under 2V was too small and thus a necessary phase difference between those slits and the planar ones could not have been obtained. The highest diffraction efficiency in case of the smaller period was obtained for the sample with part of the slits polymerized under 8V (Figure 3d’), which was most likely due to the largest phase difference between those slits and the planar ones. However, improvement in diffraction efficiency for smaller period resulted in worsening of grating’s performance in case of larger period. Moreover, the phase delays between all the slit types could not have been equalized for any polarization direction, whereas in theory it should be possible for polarization direction perpendicular to LC director in the planar slits. This was due to changes of LC’s refractive index resulting from the formation of polymer network [6]. As a result, the diffraction patterns corresponding to smaller grating period were observed for polarization direction at 45 ° + m · 90 ° with respect to LC director. The patterns corresponding to the larger ones were visible for most angles, however, the best results were achieved for m · 90 ° angles between LC director and polarization direction. Overall, the optimal results were obtained for the grating presented in Figure 2d as both a clear period change and high diffraction efficiency for smaller period were achieved (Figure 3d, d’).
To ensure that the observed diffraction patterns corresponded to the measured period values of the fabricated diffraction gratings, the period values calculated based on the measured distance between the 0th and 1st diffraction order were compared with the measured ones for each sample. The measurement results as well as the comparison of period values can be found in Table 1.
Table 1. Comparison of the calculated and measured period(s) of the gratings presented in Figure 2 for two polarization directions corresponding to different period values. The distance between the sample and the screen was 2.7m. The measurement accuracy for the diffraction pattern was 0.025cm (2 pixels), for the grating’s period it was 2µm and 1cm for screen distance.
Table 1. Comparison of the calculated and measured period(s) of the gratings presented in Figure 2 for two polarization directions corresponding to different period values. The distance between the sample and the screen was 2.7m. The measurement accuracy for the diffraction pattern was 0.025cm (2 pixels), for the grating’s period it was 2µm and 1cm for screen distance.
grating measured period [µm] measured distance between 0th and 1st diffraction order [cm] calculated period [µm]
20V 122 1.46 121.9(2.8)
2V/20V 61 2.94 60.7(1.4)
120 1.46 121.8(2.8)
4V/20V 62 2.94 60. 7(1.4)
121 1.46 121.8(2.8)
8V/20V 60 2.95 60.4(1.4)
121 1.46 121.8(2.8)
The results presented in Table 1 prove that the observed diffraction patterns corresponded to the measured period value(s) of each grating within the measurement uncertainty. The differences between the measured and calculated values were within the measurement accuracy. Moreover, small variations (1-2µm) in measured period values between the samples were due to microscope’s measurement accuracy and slight imperfections on the edges of polymerized patterns.

3.2. Diffraction gratings with triple period change

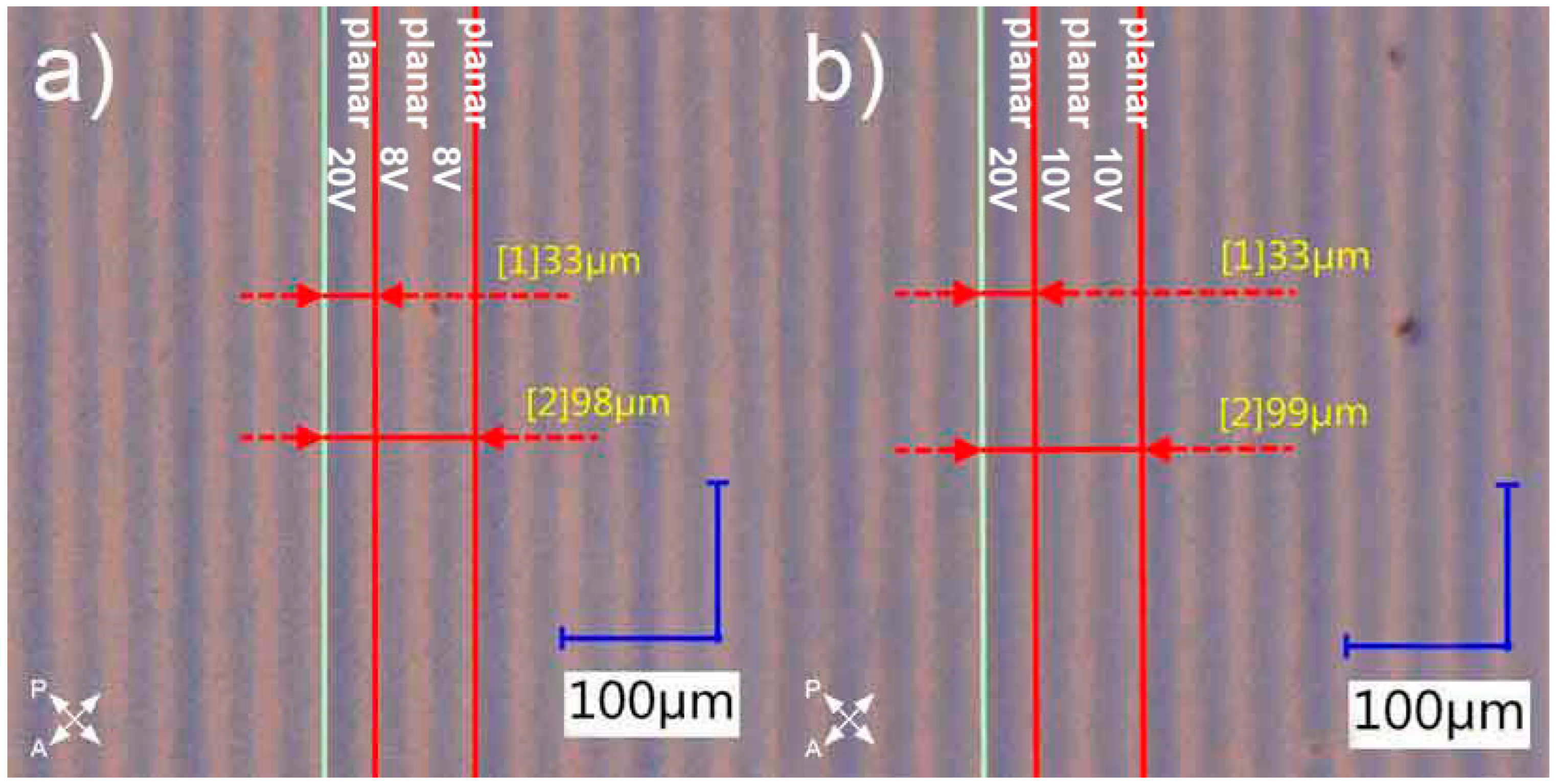
The optimal results obtained previously were the basis for design of the gratings with triple period change. The only difference, compared to the previous design, was that in this case tripling of the period for a specific polarization direction of incident light was desired and thus every third polymerized slit was irradiated under 20V. The voltage values for other slits were chosen based on the previous experiments – for one sample it was 8V as this value gave optimal results and for the other one it was 10V to check how the grating’s performance would change. It was observed that the fabricated samples looked nearly identical under a polarizing microscope as shown in Figure 4.
Preprints 87935 g004
Figure 4. Comparison of fabricated diffraction gratings observed under a polarizing microscope with crossed polarizers. In both cases, every third polymerized slit is polymerized under 20V and the other ones are polymerized under: a) 8V and b) 10V. The remaining slits are not polymerized. Periods of each grating are measured with the measurement tools of the microscope.
Figure 4. Comparison of fabricated diffraction gratings observed under a polarizing microscope with crossed polarizers. In both cases, every third polymerized slit is polymerized under 20V and the other ones are polymerized under: a) 8V and b) 10V. The remaining slits are not polymerized. Periods of each grating are measured with the measurement tools of the microscope.
Preprints 87935 g004
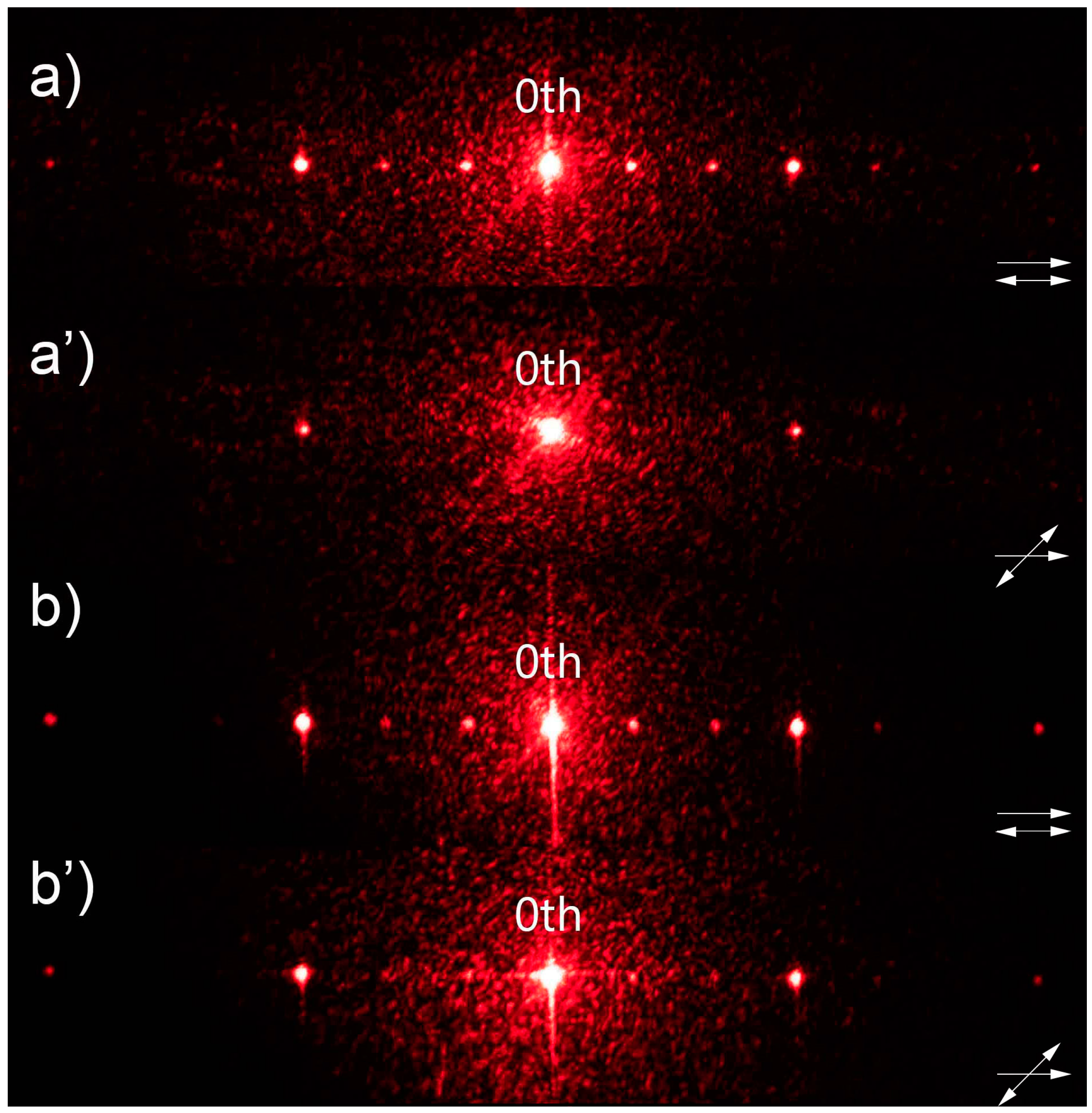
As previously, the gratings were examined in a free space optical setup to investigate their performance and determine if there were any differences between them. The behavior of the sample polymerized under 8V was consistent with previous results. It was possible to find a polarization direction for which the incident light behaved like the slits with a tilt of LC molecules were not present (Figure 5a) and the one for which the diffraction pattern corresponded to the smaller period (Figure 5a’). The performance of the second sample was very similar, however, small differences were observed. The diffraction efficiency for the smaller period was higher compared to Figure 5a’ to the point where it was possible to observe the 2nd diffraction order (Figure 5b’). On the other hand, there were visible traces of the 1st diffraction order corresponding to the larger period in the diffraction pattern observed for the smaller period. This result indicated that voltage values equal to 8V or slightly higher than this would be suitable for obtaining optimal grating’s performance. Moreover, the disproportion in diffraction efficiencies between diffraction orders in the case of larger period was observed for both samples (Figure 5a, b). This type of behavior was consistent with previous results. The only difference was that in this case every third diffraction order had higher efficiency, which was an expected outcome.
Preprints 87935 g005
Figure 5. Comparison of diffraction patterns observed for the gratings presented in Figure 4. The gratings are examined for different polarization directions to observe the period change: (a, a’) Figure 4a and (b, b’) Figure 4b. The relation between LC director in planar slits and polarization direction is marked in each image. For all the images, 80 pixels correspond to 1cm on the screen.
Figure 5. Comparison of diffraction patterns observed for the gratings presented in Figure 4. The gratings are examined for different polarization directions to observe the period change: (a, a’) Figure 4a and (b, b’) Figure 4b. The relation between LC director in planar slits and polarization direction is marked in each image. For all the images, 80 pixels correspond to 1cm on the screen.
Preprints 87935 g005
Additionally, the consistency between the observed diffraction patterns and the measured period values was examined as previously. The results demonstrated in Table 2 prove that the measurements agreed with the calculations within the uncertainty as predicted.
Table 2. Comparison of the calculated and measured periods of the gratings presented in Figure 4 for two polarization directions corresponding to different period values. The distance between the sample and the screen was 2.7m. The measurement accuracy for the diffraction pattern was 0.025cm (2 pixels), for the grating’s period it was 2µm and 1cm for screen distance.
Table 2. Comparison of the calculated and measured periods of the gratings presented in Figure 4 for two polarization directions corresponding to different period values. The distance between the sample and the screen was 2.7m. The measurement accuracy for the diffraction pattern was 0.025cm (2 pixels), for the grating’s period it was 2µm and 1cm for screen distance.
grating measured period [µm] measured distance between 0th and 1st diffraction order [cm] calculated period [µm]
8V/20V 33 5.36 33.23(0.75)
98 1.80 99.0(2.3)
10V/20V 33 5.40 33.00(0.75)
99 1.80 99.0(2.3)

4. Conclusions

The results presented in this paper show that the polarization-dependent properties of LC-based diffractive optical elements can be utilized to create dual-period diffraction gratings operating for linearly polarized light. The gratings were created by selective photopolymerization of the slits with different orientations of LC molecules. This allowed to observe diffraction patterns corresponding either to smaller or larger grating’s period by changing of azimuth of linear polarization of incoming light. It was possible to fabricate diffraction gratings with either double or triple change of the period when voltage values corresponding to the tilt of LC molecules in part of the slits was chosen appropriately. Moreover, it was observed that improvement of diffraction efficiency for smaller period resulted in higher disproportion in diffraction efficiency between diffraction orders in case of larger period. The presented method could be adopted to fabricate dual-period diffraction grating with higher multiplier of the base period (i.e. four, five etc. times larger than base period). Smaller base periods could be obtained by using higher precision of selective photopolymerization i.e. high resolution direct laser writing. One of our long-term goals is to utilize such dual-period gratings for fabrication of a compact spectrometer with switchable resolution and measurement range, where the user can change the range/resolution just by simple mechanical switch connected with properly oriented polarizers.

Author Contributions

Conceptualization, Marta Kajkowska and Miłosz Chychłowski; methodology, Marta Kajkowska, Miłosz Chychłowski and Sławomir Ertman; validation, Marta Kajkowska, Miłosz Chychłowski and Sławomir Ertman; investigation, Marta Kajkowska and Miłosz Chychłowski.; resources Piotr Lesiak; writing—original draft preparation, Marta Kajkowska; writing—review and editing, Miłosz Chychłowski, Sławomir Ertman, Piotr Lesiak.; visualization, Marta Kajkowska, Miłosz Chychłowski and Sławomir Ertman; funding acquisition, Piotr Lesiak.

Funding

The work was supported by the National Science Centre, Poland, under research project no UMO-2020/39/B/ST7/02356

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zhang, H.; Miao, Z.; Shen, W. Development of Polymer-Dispersed Liquid Crystals: From Mode Innovation to Applications. Composites Part A: Applied Science and Manufacturing 2022, 163, 107234. [Google Scholar] [CrossRef]
  2. Yan, J.; Li, Y.; Wu, S.-T. High-Efficiency and Fast-Response Tunable Phase Grating Using a Blue Phase Liquid Crystal. Opt. Lett., OL 2011, 36, 1404–1406. [Google Scholar] [CrossRef]
  3. Chychłowski, M.S.; Kajkowska, M.; Jankiewicz, B.; Bartosewicz, B.; Woliński, T.R.; Lesiak, P. Photopolymerization of 1D Photonic Structures Induced by Nematic–Isotropic Phase Transition in Liquid Crystal. Soft Matter 2023, 19, 3398–3404. [Google Scholar] [CrossRef] [PubMed]
  4. Ge, Z.; Gauza, S.; Jiao, M.; Xianyu, H.; Wu, S.-T. Electro-Optics of Polymer-Stabilized Blue Phase Liquid Crystal Displays. Appl. Phys. Lett. 2009, 94, 101104. [Google Scholar] [CrossRef]
  5. Ono, H.; Emoto, A.; Takahashi, F.; Kawatsuki, N.; Hasegawa, T. Highly Stable Polarization Gratings in Photocrosslinkable Polymer Liquid Crystals. Journal of Applied Physics 2003, 94, 1298–1303. [Google Scholar] [CrossRef]
  6. Kajkowska, M.; Chychłowski, M.; Lesiak, P. Influence of Photopolymerization on Propagation Properties of Photonic Crystal Fiber Infiltrated with Liquid Crystal Mixture. Photonics Letters of Poland 2022, 14, 68–70. [Google Scholar] [CrossRef]
  7. Rutkowska, K.A.; Chychłowski, M. Methods for Polymer-Stabilization of Molecular Orientation in LC-Waveguiding Structures. Photonics Letters of Poland 2018, 10, 11–13. [Google Scholar] [CrossRef]
  8. Chychłowski, M.S.; Ertman, S.; Rutkowska, K.; Strzeżysz, O.; Dąbrowski, R.; Woliński, T.R. Locally-Induced Permanent Birefringence by Polymer-Stabilization of Liquid Crystal in Cells and Photonic Crystal Fibers. Opto-Electronics Review 2018, 26, 242–246. [Google Scholar] [CrossRef]
  9. Rutkowska, K.A.; Chychłowski, M.; Kwaśny, M.; Ostromęcka, I.; Piłka, J.; Laudyn, U.A. Light Propagation in Periodic Photonic Structures Formed by Photo-Orientation and Photo-Polymerization of Nematic Liquid Crystals. Opto-Electronics Review 2017, 25, 118–126. [Google Scholar] [CrossRef]
  10. Wang, J.; McGinty, C.; Reich, R.; Finnemeyer, V.; Clark, H.; Berry, S.; Bos, P. Process for a Reactive Monomer Alignment Layer for Liquid Crystals Formed on an Azodye Sublayer. Materials 2018, 11, 1195. [Google Scholar] [CrossRef]
  11. Lee, S.N.; Chien, L.-C.; Sprunt, S. Polymer-Stabilized Diffraction Gratings from Cholesteric Liquid Crystals. SID Symposium Digest of Technical Papers 1998, 29, 834–837. [Google Scholar] [CrossRef]
  12. Bronnikov, S.; Kostromin, S.; Zuev, V. Polymer-Dispersed Liquid Crystals: Progress in Preparation, Investigation, and Application. Journal of Macromolecular Science, Part B 2013, 52, 1718–1735. [Google Scholar] [CrossRef]
  13. Ren, H.; Fan, Y.-H.; Lin, Y.-H.; Wu, S.-T. Tunable-Focus Microlens Arrays Using Nanosized Polymer-Dispersed Liquid Crystal Droplets. Optics Communications 2005, 247, 101–106. [Google Scholar] [CrossRef]
  14. Presnyakov, V.V.; Galstian, T.V. Electrically Tunable Polymer Stabilized Liquid-Crystal Lens. Journal of Applied Physics 2005, 97, 103101. [Google Scholar] [CrossRef]
  15. Hsu, C.J.; Sheu, C.R. Using Photopolymerization to Achieve Tunable Liquid Crystal Lenses with Coaxial Bifocals. Opt. Express, OE 2012, 20, 4738–4746. [Google Scholar] [CrossRef]
  16. Fan, Y.-H.; Ren, H.; Wu, S.-T. Switchable Fresnel Lens Using Polymer-Stabilized Liquid Crystals. Opt. Express, OE 2003, 11, 3080–3086. [Google Scholar] [CrossRef]
  17. Luo, W.; Ni, M.; Zhou, X.; Peng, H.; Xie, X. Holographic Polymer Nanocomposites with Both High Diffraction Efficiency and Bright Upconversion Emission by Incorporating Liquid Crystals and Core-Shell Structured Upconversion Nanoparticles. Composites Part B: Engineering 2020, 199, 108290. [Google Scholar] [CrossRef]
  18. Wang, K.; Zheng, J.; Gui, K.; Li, D.; Zhuang, S. Improvement on the Performance of Holographic Polymer-Dispersed Liquid Crystal Gratings with Surface Plasmon Resonance of Ag and Au Nanoparticles. Plasmonics 2015, 10, 383–389. [Google Scholar] [CrossRef]
  19. Wang, K.; Zheng, J.; Liu, Y.; Gao, H.; Zhuang, S. Electrically Tunable Two-Dimensional Holographic Polymer-Dispersed Liquid Crystal Grating with Variable Period. Optics Communications 2017, 392, 128–134. [Google Scholar] [CrossRef]
  20. Gao, L.; Zheng, Z.-Z.; Zhu, J.-L.; Han, W.-M.; Sun, Y.-B. Dual-Period Tunable Phase Grating Based on a Single in-Plane Switching. Opt. Lett., OL 2016, 41, 3775–3778. [Google Scholar] [CrossRef]
  21. Yan, J.; Xing, Y.; Li, Q. Dual-Period Tunable Phase Grating Using Polymer Stabilized Blue Phase Liquid Crystal. Opt. Lett., OL 2015, 40, 4520–4523. [Google Scholar] [CrossRef] [PubMed]
  22. He, Z.; Shen, W.; Yu, P.; Zhao, Y.; Zeng, Z.; Liang, Z.; Chen, Z.; Zhang, H.; Zhang, H.; Miao, Z.; et al. Viewing-Angle-Switching Film Based on Polymer Dispersed Liquid Crystals for Smart Anti-Peeping Liquid Crystal Display. Liquid Crystals 2022, 49, 59–65. [Google Scholar] [CrossRef]
  23. Lu, S.-Y.; Chien, L.-C. A Polymer-Stabilized Single-Layer Color Cholesteric Liquid Crystal Display with Anisotropic Reflection. Applied Physics Letters 2007, 91, 131119. [Google Scholar] [CrossRef]
  24. Mucha, M. Polymer as an Important Component of Blends and Composites with Liquid Crystals. Progress in Polymer Science 2003, 28, 837–873. [Google Scholar] [CrossRef]
  25. Zhang, X.; Fan, F.; Zhang, C.-Y.; Ji, Y.-Y.; Wang, X.-H.; Chang, S.-J. Tunable Terahertz Phase Shifter Based on Dielectric Artificial Birefringence Grating Filled with Polymer Dispersed Liquid Crystal. Opt. Mater. Express, OME 2020, 10, 282–292. [Google Scholar] [CrossRef]
  26. Altmann, K.; Reuter, M.; Garbat, K.; Koch, M.; Dabrowski, R.; Dierking, I. Polymer Stabilized Liquid Crystal Phase Shifter for Terahertz Waves. Opt. Express, OE 2013, 21, 12395–12400. [Google Scholar] [CrossRef]
  27. Utsumi, Y.; Kamei, T.; Saito, K.; Moritake, H. Increasing the Speed of Microstrip-Line-Type Polymer-Dispersed Liquid-Crystal Loaded Variable Phase Shifter. IEEE Transactions on Microwave Theory and Techniques 2005, 53, 3345–3353. [Google Scholar] [CrossRef]
  28. Liu, Y.; Shen, J.; Shen, T.; Zheng, J.; Zhuang, S. Electro-Optical Properties and Frequency Response of Polymer-Dispersed Liquid Crystal Gratings Doped with Multi-Walled Carbon Nanotubes. J Mater Sci 2021, 56, 12660–12670. [Google Scholar] [CrossRef]
  29. Huang, C.-Y.; Lin, S.-H. Polarization-Dependent Gratings Based on Polymer-Dispersed Liquid Crystal Cells with In-Plane Switching Electrodes. Polymers 2022, 14, 297. [Google Scholar] [CrossRef] [PubMed]
  30. Habibpourmoghadam, A.; Wolfram, L.; Jahanbakhsh, F.; Mohr, B.; Reshetnyak, V.Y.; Lorenz, A. Tunable Diffraction Gratings in Copolymer Network Liquid Crystals Driven with Interdigitated Electrodes. ACS Appl. Electron. Mater. 2019, 1, 2574–2584. [Google Scholar] [CrossRef]
  31. Crawford, G.P.; Eakin, J.N.; Radcliffe, M.D.; Callan-Jones, A.; Pelcovits, R.A. Liquid-Crystal Diffraction Gratings Using Polarization Holography Alignment Techniques. Journal of Applied Physics 2005, 98, 123102. [Google Scholar] [CrossRef]
  32. Lin, T.; Xie, J.; Zhou, Y.; Zhou, Y.; Yuan, Y.; Fan, F.; Wen, S. Recent Advances in Photoalignment Liquid Crystal Polarization Gratings and Their Applications. Crystals 2021, 11, 900. [Google Scholar] [CrossRef]
  33. Nieborek, M.; Rutkowska, K.; Woliński, T.R.; Bartosewicz, B.; Jankiewicz, B.; Szmigiel, D.; Kozanecka-Szmigiel, A. Tunable Polarization Gratings Based on Nematic Liquid Crystal Mixtures Photoaligned with Azo Polymer-Coated Substrates. Crystals 2020, 10, 768. [Google Scholar] [CrossRef]
  34. Węgłowski, R.; Kozanecka-Szmigiel, A.; Piecek, W.; Konieczkowska, J.; Schab-Balcerzak, E. Electro-Optically Tunable Diffraction Grating with Photoaligned Liquid Crystals. Optics Communications 2017, 400, 144–149. [Google Scholar] [CrossRef]
  35. Kazak, A.A.; Melnikova, E.A.; Tolstik, A.L.; Mahilny, U.V.; Stankevich, A.I. Controlled Diffraction Liquid-Crystal Structures with a Photoalignment Polymer. Tech. Phys. Lett. 2008, 34, 861–863. [Google Scholar] [CrossRef]
  36. Komanduri, R.K.; Oh, C.; Escuti, M.J. 34.4L: Late-News Paper: Polarization Independent Projection Systems Using Thin Film Polymer Polarization Gratings and Standard Liquid Crystal Microdisplays. SID Symposium Digest of Technical Papers 2009, 40, 487–490. [Google Scholar] [CrossRef]
  37. Blinov, L.M.; Cipparrone, G.; Mazzulla, A.; Provenzano, C.; Palto, S.P.; Barnik, M.I.; Arbuzov, A.V.; Umanskii, B.A. Electric Field Controlled Polarization Grating Based on a Hybrid Structure “Photosensitive Polymer-Liquid Crystal. ” Applied Physics Letters 2005, 87, 061105. [Google Scholar] [CrossRef]
  38. Huang, S.-Y.; Huang, B.-Y.; Kang, C.-C.; Kuo, C.-T. Diffraction and Polarization Properties of Electrically–Tunable Nematic Liquid Crystal Grating. Polymers 2020, 12, 1929. [Google Scholar] [CrossRef]
  39. Skigin, D.C.; Depine, R.A. Diffraction by Dual-Period Gratings. Appl. Opt., AO 2007, 46, 1385–1391. [Google Scholar] [CrossRef]
  40. Myhre, G.; Hsu, W.-L.; Peinado, A.; LaCasse, C.; Brock, N.; Chipman, R.A.; Pau, S. Liquid Crystal Polymer Full-Stokes Division of Focal Plane Polarimeter. Opt. Express, OE 2012, 20, 27393–27409. [Google Scholar] [CrossRef] [PubMed]
  41. Cofré, A.; Vargas, A.; Torres-Ruiz, F.A.; Campos, J.; Lizana, A.; del Mar Sánchez-López, M.; Moreno, I. Quantitative Performance of a Polarization Diffraction Grating Polarimeter Encoded onto Two Liquid-Crystal-on-Silicon Displays. Optics & Laser Technology 2017, 96, 219–226. [Google Scholar] [CrossRef]
  42. Garcia-Caurel, E.; De Martino, A.; Drévillon, B. Spectroscopic Mueller Polarimeter Based on Liquid Crystal Devices. Thin Solid Films 2004, 455–456, 120–123. [Google Scholar] [CrossRef]
  43. Honma, M.; Takahashi, N.; Nose, T. Simple Stokes Polarimeter Using a Liquid Crystal Grating with Ternary Orientation Domains. Appl. Opt., AO 2018, 57, 10183–10190. [Google Scholar] [CrossRef] [PubMed]
  44. Lepera, E.; Provenzano, C.; Pagliusi, P.; Cipparrone, G. Liquid Crystal Based Polarization Gratings for Spectro-Polarimetric Applications. Molecular Crystals and Liquid Crystals 2012, 558, 109–119. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated