Preprint

Article

An Experimental Study on the Impact of Minimum Quantity Lubrication Surroundings on the Machined Surface Quality during AISI 1050 Steel Circular Pocket Milling

Altmetrics

Downloads

Views

Comments

Ly Chanh Trung^*,Tran Thien Phuc

This version is not peer-reviewed

Submitted:

16 October 2023

Posted:

17 October 2023

You are already at the latest version

Alerts

Abstract

AISI 1050 steel circular pocket milling under minimum quantity lubrication (MQL) surroundings including nozzle elevation angle, lubricant flow rate, air pressure and cutting speed was studied. The machined surface quality (Ra) was evaluated for Up-milling side and Down-milling side. In this study, to obtain an manifest explanation on the pivotal effective parameters of MQL surroundings and cutting speed on the machined surface quality (Ra) through analyzing Taguchi L9 (34-2) approach and ANOVA calculation to identify those parameters, by utilizing the experimental outcomes to interpret three-dimensional (3D) surface plots and the diagrams of Signal-to-Noise ratios and major impact plots of Mean. The obtained outcomes of optimal operating parameters indicated that the pivotal effective parameters of MQL surroundings are nozzle elevation angle and lubricant flow rate on the machined surface quality. Simultaneously, a quadratic mathematical paradigm generated by using response surface design (RSD) and desirableness function evaluation were utilized to forecast the optimal values of the machined surface quality compared to Taguchi method. The results unveiled that the optimal values of the machined surface quality are adjacent to experimental attained values. The machined surface quality has been significantly improved using MQL surroundings.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

A product in which is fabricated specific shapes or surface characteristics is the salient objective of machining operations. Because high quality products are often manufactured using more extravagant, advanced machines and cutting tools. Therefore, Conditions for machining operation are not only chosen based on geometry and the machined surface quality requirements but also based on optimizing machining parameters to find out the greatest effective factors on machining operations [1]. The elimination of chip inside an encircled region from a flat face of work-part is a feature of pocket milling. The objective of optimizing machining may be different, so pocket milling plays a significant role of numerous subjects of research, because more than 80 percentage of all mechanical parts in which are fabricated by computer numerical controlled (CNC) milling machines in manufacturing industry. The pockets can have even or uneven shape, can be straight or curved edges, and can have islands or holes. Pocket machining optimization is a consistently practical problem and goals of optimization can be the highest possible surface quality, minimum tool wear, shortest time machining, lowest cost of production and minimal energy consumption [2,3]. Because pocket milling is a significant operation on milling machine. Nisar et al. [4] interpreted the significance of machining parameters on dimensional preciseness and the machined surface quality in pocket milling operation through analyzing Taguchi method, grey relational analysis (GRA) and ANOVA calculation to identify an amalgamation of the optimal parameters in machining process. Besides, Sayuti et al. [5] employed the Taguchi optimization method, fuzzy logic and response surface methodology to define the salient machining factors during hard turning of AISI 4140 steel utilizing MQL surroundings and SiO₂ nano-particle to attain the minimal tool wear and the best machined surface quality. Sharma et al. [6] envisaged a systemization that multi-response optimization of process parameters using desirability function analysis during face milling machining of EN31 steel under different machining environments. The results revealed that MQL environment is the most salient factor followed by cutting speed. Sharma et al. [7] also unveiled that the most pivotal effective factors on tool wear and the machined surface quality are determined as cutting speed, lubricant flow rate, distance from spraying nozzle to surface and nozzle elevation angle during EN 31 steel face milling under MQL surroundings utilizing the optimization of manifold output parameters by Taguchi method. The effectiveness of MQL can be further enhanced by optimizing the variables associated with the MQL system. Because the friction between tool-chip interface generate high temperature in the cutting zone during difficult-to-cut material is the main puzzle. Therefore, the best machined surface quality attaining in machining process is a big challenge. Rana et al. [8] reported that the optimal machined surface quality and microhardness of AISI 52,100 alloy steel attained in face milling operation by using Taguchi method to identify an optimal parameter set which is composed of cutting velocity, feed rate, lubricant gathering and flow rate.

Analogously, Masooth et al. [9] reported that Taguchi method was analyzed for optimizing the parameters of milling operation to achieve the minimal machined surface quality under MQL environment which consisted of a very small amount of lubricant and compressed air sprayed out droplets at the tool-chip interface. Moreover, the study was fulfilled in CNC milling process utilizing uncoated and TiAlN coated carbide end mill cutter. This indicates that the cost impacts on machining process. Rana et al. [10] revealed that based on Taguchi-based grey relational analysis to determine the most influential factor on the machined surface quality and temperature was nozzle elevation angle. The scrutiny was performed to optimize multiple responses of nozzle parameters under MQL circumstance during AISI 52,100 alloy steel face milling. Singh et al. [11] also conducted the investigation on the optimization of numerous input parameters under MQL environment during EN 31 alloy steel face milling by applying Taguchi method to determine the best possible levels of input parameters. The results verified that lubricant flow rate is the main influential factor on the machined surface quality. Sharma et al. [12] studied EN 31 face milling under machining environment including MQL and nano-particle through analyzing Taguchi method to identify the simultaneous optimization of the machined surface quality and microhardness. The investigating result pointed out that the lubricant flow rate was the most salient factor because of its high contribution in machining process. With above mentioned discussions, pocket milling machining requires with sophisticated geometries and high dimensional accuracy. Thus, MQL technique not only plays the pivotal role as a replacement for dry machining but also reduces friction and lubrication on the machined surface. MQL technique not only plays the significant role to enhance good machinability of material but also help save the total cost of a machining operation. Consequently, the application of MQL technique is considered as an outstanding alternative compared to normal cutting fluid application. The effect of MQL parameters on machining is the most saliency such as nozzle elevation angle, distance from the nozzle tip to the machined surface, lubricant flow rate and air pressure [13,14,15]. Also, MQL parameters also have different technological parameters such as nano-particle, vegetable oil, cryogenic, and so on. Dubey et al. [16] investigated input parameters such as cutting speed, feed rate, depth of cut and nanoparticle concentration. The aim of the study is to analyze the impact of the different particle size in the cutting fluid and estimates its effect on surface roughness under MQL circumstance as hard turning of AISI 304 steel. Tuan et al. [17] used Box-Behnken experimental design and ANOVA technique to probe the influence of MQL technological parameters using nano-particle oils as a novel solution and its effectiveness on surface roughness in hard turning. Singh et al. [18] found the connection between the machined surface quality and the oscillation of cutting tool that the volume of the oscillation was a pivotally effective factor on the machined surface quality. The exploration fulfilled EN 31 face milling by utilizing hybrid optimization approach to create a deeply graspable interpretation between independent variables and dependent variables. Salur [19] and Ross et al. [20] conducted the study on the impact of various MQL circumstances such as nitrogen in liquid form (LN₂), CO₂ and MQL (CMQL) to enhance the productivity of sustainable manufacturing process. According to evidences from the systematical pilots, CMQL and LN₂ were determined as the most influential cooling environment, reducing friction in tool-chip interface and surface roughness has a considerable decrease. Obviously, many researchers interest the impact of MQL parameters and there are many researches on surface roughness with relation to MQL parameters in turning and milling machining processes. Meher et al. [21] envisaged a comprehensive review that the machining technologies were always non-stop discovered with the type of different machining operations to overcome the drawbacks of traditional machining processes. Especially, the investigation also delivered a systematic synthesis of cutting conditions and various MQL environments to help scientists concentrate on more explorations in various machining processes.

Through study of literature review manifestly pointed out that comprehensive investigation must be fulfilled to attain more effective machining conditions. Thus, the pivotal intention of this scrutiny is to discover the influence of MQL parameters and cutting speed on the machined surface quality in AISI 1050 steel circular pocket milling using Taguchi L₉ (3^4-2) approach to perform the experiment of design in circular pocket milling operation. The experimental matrix was set up four factors including cutting speed, air pressure, lubricant flow rate and nozzle elevation angle with three levels for each factor. In order to identify the salient effective factors on the machined surface quality by controlling and analyzing ANOVA technique combined with the analysis of Signal-to-Noise (S/N) ratios diagram and major impact plots of Means from Taguchi method. Moreover, it is necessary to perform a quadratic equation as a forecast paradigm by using response surface design (RSD) from Minitab 19 software, then the analysis of the influential factors on the machined surface quality based on 3D surface plots. Ultimately, the response optimization method is utilized to optimize one or more response surfaces from RSD approach.

2. Materials and Methods

2.1. Work-part material, CNC machine and endmill cutter

To get a deep grip of this study. First, AISI 1050 material was utilized to perform in circular pocket milling operations, its hardness is 197 HB, dimensions of work-part material given as follow: 50 x 50 x 50 mm³. Table 1 illustrated AISI 1050 steel chemical components. Table 2 depicted AISI 1050 steel mechanical properties. Table 3 represented AISI 1050 steel physical properties. Second, CNC machine is an EMCOMAT FB 450 MC (Austria) vertical milling machine with specification parameters as follows: motor capacity of 10 kW, maximum spindle speed of 5000 rev/min, and the table of dimensions 800 x 400 mm² can withstand a work-part material of 150 kg. Moreover, Machine is also furnished a flood cooling system and an external MQL system with milling operations. 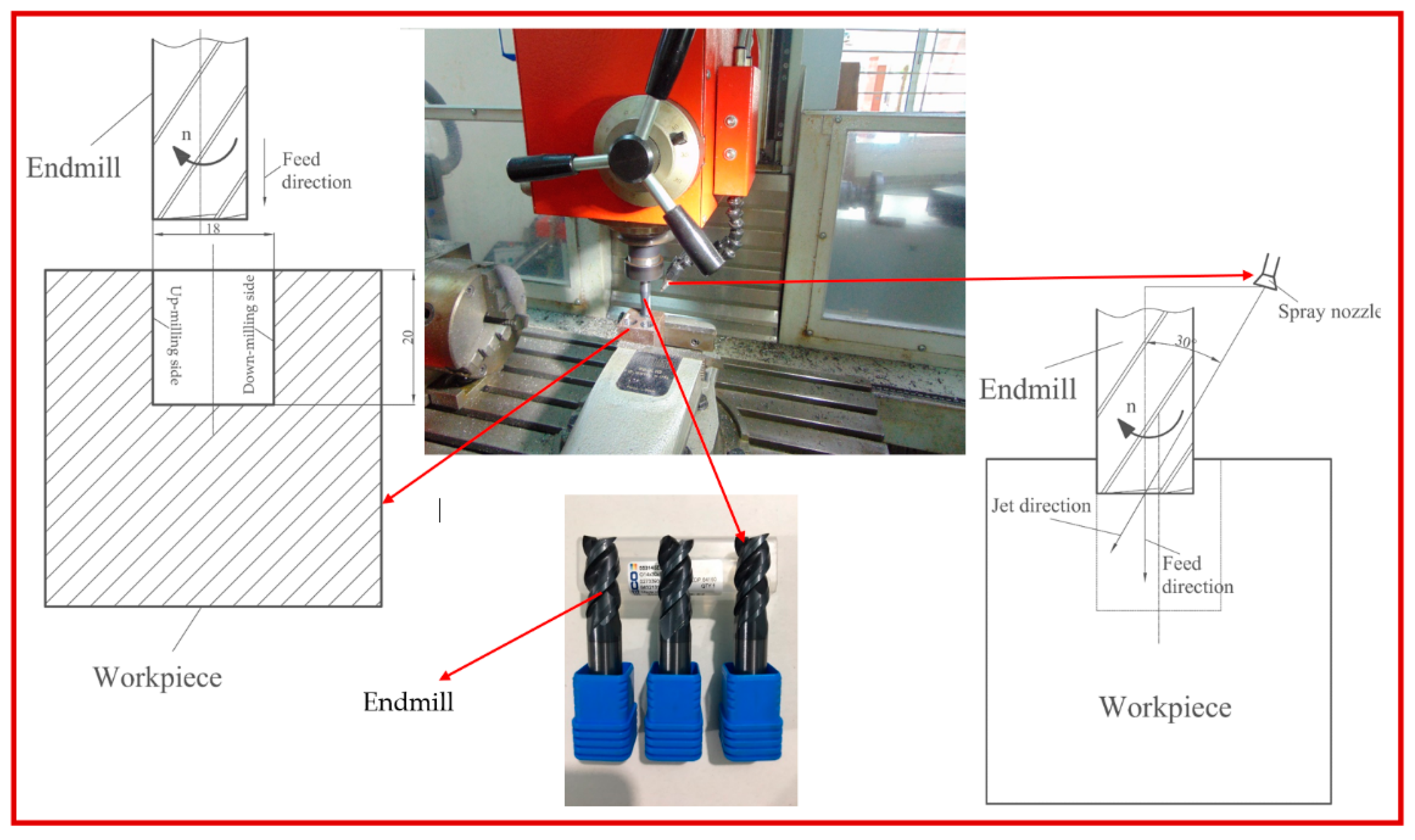Figure 1 described the various parts of the external MQL system in details. Third, the coated solid carbide endmill JS553, type: 553140Z3.0-SIRON-A produced by SECOTOOLS was employed as a key cutter including specification parameters as follows: rake angle: 8^o; helix angle: 48^o; overall length: 85 mm; shank diameter: 14 mm; cutting diameter: 14 mm; corner chamfer width: 0.175 mm; depth of cut maximum in feed direction side: 30 mm; peripheral cutting-edge count: 3.

2.2. Cutting conditions, machining environment and design of experiments

In this study, the cutting speed (V_c) and MQL surroundings were selected as independent variables in circular pocket milling operations. MQL circumstance is composed of input parameters of MQL system. To realize its definition, it can be interpreted that MQL in which is an amalgamation between lubricant and air is sprayed into tool-chip interface through a nozzle with a tiny quantity to lessen the generated temperature in cutting region. In circular pocket milling experiments, three different lubricant flow rate Q (120, 180, 240 ml/h), three different levels of spray nozzle air pressure P (1, 2, 3 bar) and three different levels of spray nozzle angle (30^o, 45^o, 60^o) were utilized as illustrated in Figure 2. Input parameters and their levels were selected based on previous literature review and initial scrutiny [5,6,11]. The various experimental conditions and input parameter’s levels are given in Table 4.

Normally, a full factorial design (FFD) will be chosen for the investigation. However, if the number of factors and levels increase, FFD will have a lot of experiments leading to enhancing cost and spending time to fulfill experiments. Simultaneously, the result of FFD is complicated and has manifold influences and interactions which are unimportant or extraneous. Thus, Taguchi L₉ (3^4-2) [24,25,26] is suggested as a chance to lessen the amount of experiments, cost and time compared to FFD. Table 4 presented the experimental conditions. Table 5 illustrated Taguchi L₉ (3^4-2) with the coded and actual values of experimental design.

2.3. Measurement tool

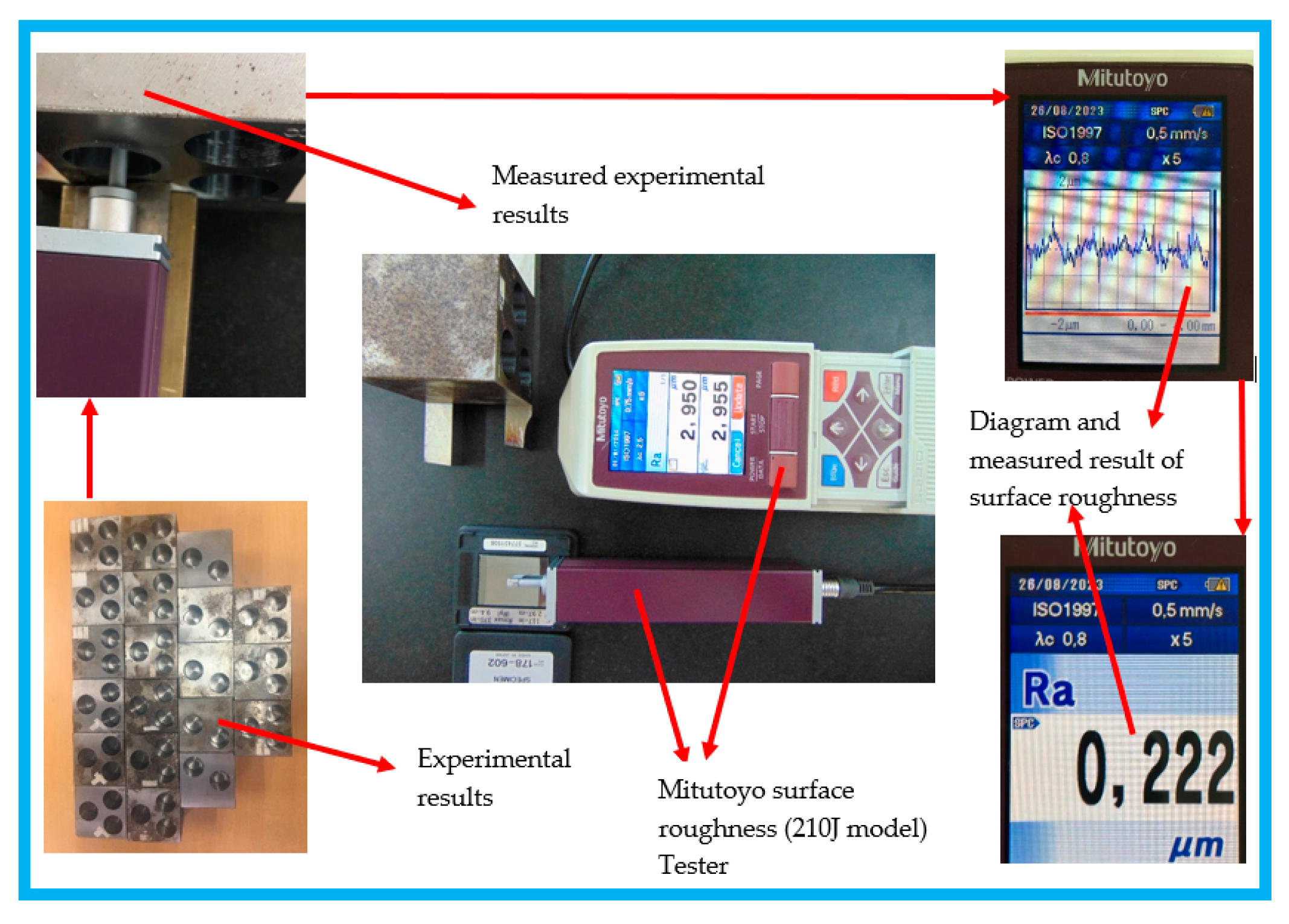
In machining process, the machine surface quality or surface roughness is considered as a pivotal criterion to decide the quality of product. Therefore, with this study, the average values of the machined surface quality (Ra) were measured after each measurement. Mitutoyo surface roughness (model SJ 210) tester was performed for Ra measurements. To measure the machined surface quality. First, the measurement device must be calibrated with a precision preference specimen in advance. Second, the worth of the machined surface quality was measured on the various positions of machined surface to minimize error. Third, the average worth of the machined surface quality was computed.

3. Results and discussion

Circular pocket milling operations are conducted non-stop as per L₉ (3^4-2). Each experiment is carried out with five duplications to lessen the unsteadiness in the output responses. Basically, Taguchi method utilizes a criterion in which is considered as a feature of quality. Especially, the Signal-to-Noise (S/N) ratio diagram is chosen to take the feature of quality into consideration. On the other hand, Taguchi L₉ (3^4-2) also provide an effective analysis to reduce the considerable amount of experiment. There are three significant features given in the Signal-to-Noise ratio diagram to optimize process parameters as follow: the higher-is-better, the lower-is-better and the nominal-is-best. In this paper, arithmetic mean roughness (Ra) for attaining of optimal conditions was scrutinized with both Up-milling side and Down-milling side, and the lower-is-better was chosen to obtain minimum roughness. The experimental results were given in Table 6 and Table 7.

S / N ratio = - 10 {l o g}_{10} (\frac{1}{n} \sum_{i = 1}^{n} y_{i}^{2})

(1)

Where

y_{i}

is the value of achieved response for each experiment duplicated n times and Eq. (1) is utilized to calculate the Signal-to-Noise ratios for 9 experiments. Then, its value is recorded as shown in Table 6 and Table 7.

3.1. Signal-to Noise interpretation

In manufacturing industry, the machined surface quality is evaluated as an index in which is a pivotal criterion for the quality of produce. In the circular pocket milling operation, the machined surface quality of Up-milling side and Down-milling side was controlled by MQL environment and cutting speed. Figure 3 illustrated a circular pocket milling operation and Figure 4 illustrated the experimental results and measured results.

The Signal-to-Noise ratios diagram was utilized to analyzed the impact of each factor level on the machined surface quality. Table 8 and Table 9 presented the average Signal-to-Noise for each response value corresponding to the valuable levels with both Up-milling side and Down-milling side.

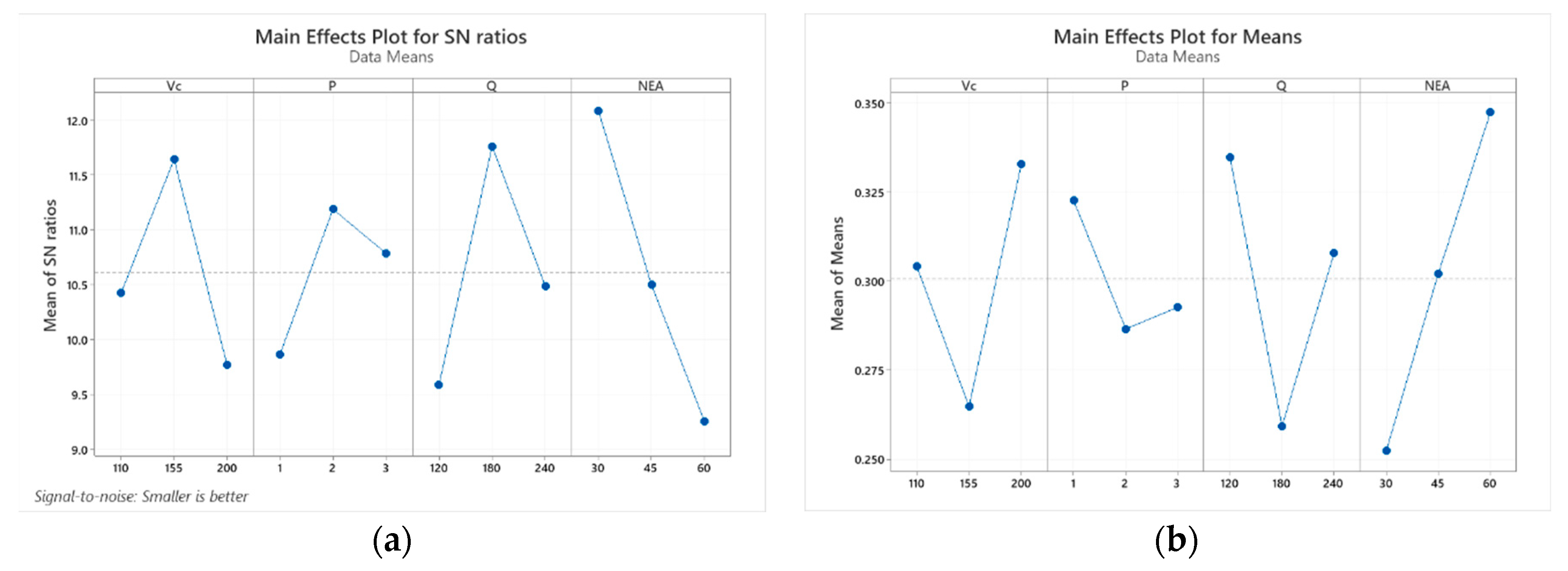
The maximum and minimum values of S/N ratio (main impact) were distinguishable from response table for S/N ratios and response table for Means were given in Table 8 and Table 9. Figure 5 and Figure 6 represent the diagrams of Mean of S/N ratios and Mean of Means which were used for assessment. Figure 5 indicates that the MQL surroundings with input parameters achieved the optimization for the machined surface quality with Up-milling side were determined as V_c2, P₂, Q₂, NEA₁, which were 155 m/min of cutting speed (level 2), 2 bar of air pressure (level 2), 180 ml / hr of lubricant flow rate (level 2), and 30^o of nozzle elevation angle (level 1). From Table 8 depicts the response table for Means, it is concluded that nozzle elevation angle has been regarded as the main effective factor on surface roughness of specimen whereas air pressure has the least impact on the machined surface quality.

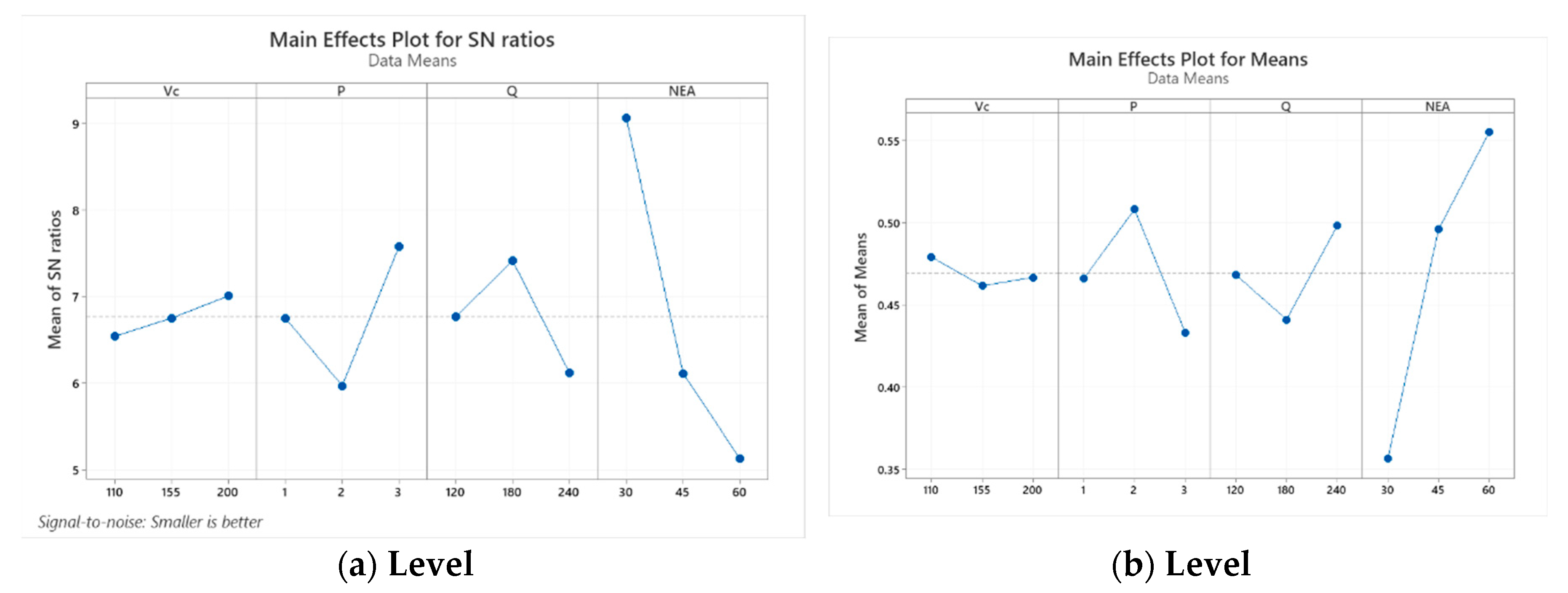
Analogously, Figure 6 indicates that the MQL surroundings with input parameters achieved the optimization for the machined surface quality with Down-milling side were determined as V_c3, P₃, Q₂, NEA₁, which were 200 m/min of cutting speed (level 3), 3 bar of air pressure (level 3), 180 ml / hr of lubricant flow rate (level 2), and 30^o of nozzle elevation angle (level 1). From Table 9 depicts the response table for Means, it is concluded that nozzle elevation angle has been considered as the major effective factor on surface roughness of specimen whereas cutting speed has the least influence on the machined surface quality.

3.2. ANOVA analysis and the impact of the factors

In this study, cutting speed and MQL circumstance with input parameters including lubricant flow rate, nozzle elevation angle, air pressure which are considered as the influential parameters on the machined surface quality. Therefore, ANOVA analysis is crucial to determine the impact of input parameters on output parameters. It is necessary to perform the analysis of mean (ANOM). These results were presented in Table 10 and Table 11 with both Up-milling side and Down-milling side.

η_{mj} = Mean (S / N) = \frac{1}{p} \sum_{i = 1}^{p} {(S / N)}_{i}

(2)

Where η_mj is the average value of S/N ratios in correspondence with each valuable level of each factor. The

p

is the number of mean S/N ratios in correspondence with the valuable levels of each factor. The η_mj was calculated using Eq. (2)

ANOM and ANOVA values of experimental results for the machined surface quality (Ra) were shown in Table 10 and Table 11. Their percentage of contribution of each input variable was taken into consideration to determine the salient level of each input variable. Table 10 for Up-milling side points out that the most significant effective variable on the machined surface quality (Ra) was the nozzle elevation angle with 34.81% percentage of contribution. The other variables impacted on Ra are lubricant flow rate, air pressure and cutting speed with 27.19%, 13.61% and 24.39% respectively. Table 11 for Down-milling side indicates that the percentage contribution of input variables including nozzle elevation angle, lubricant flow rate, air pressure and cutting speed were found out as follow: 57.47%, 16.18%, 20.32% and 6.03% respectively. Therefore, nozzle elevation angle (factor D) is the most key effective factor on Ra with both Up-milling side and Down-milling side.

3.3. Response surface design (RSD) for Ra and the analysis of three-dimensional (3D) surface plots

3.3.1. Response surface design (RSD) for Ra

A mathematical paradigm is generated using Minitab 19 software to stimulate and analyze the relation between input parameters and output parameters. In this study, the experimental outcomes were utilized to generate this paradigm in which is called response surface design (RSD).

Basically, to scrutinize the impact of milling factors inside valuable zone on output parameters and to find out extremum values, a quadratic response surface paradigm is generated into the following Eq. (3):

y = b₀ + b₁.x₁ + b₂.x₂ + b₃.x₃ + b₄.x₄ + b₁₂.x_1.x₂ + b₁₃.x₁.x₃ + b₁₄.x₁.x₄ + b₂₃.x₂.x₃ + b₂₄.x₂.x₄ + b₃₄.x₃.x₄ + b₁₁.x₁² + b₂₂.x₂² + b₃₃.x₃² + b₄₄.x₄²

(3)

Where “y” is the corresponding response, and x₁, x₂, x₃, x₄ are the value of the milling parameters including MQL surroundings and cutting speed. The term “b” is the regression coefficient. Cutting speed and MQL surroundings (lubricant flow rate, air pressure and nozzle elevation angle) impact on the machined surface quality is considered as a quadratic function. Eq. 3 indicates that the relation between the input parameters of MQL environment, cutting speed and the machined surface quality (Ra) as shown below:

Ra = b₀ + b₁. V_c + b₂. P + b₃. Q + b₄.NEA + b₁₂. V_c. P + b₁₃. V_c. Q + b₁₄.V_c.NEA + b₂₃. P. Q + b₂₄. P. NEA + b₃₄. Q. NEA + b₁₁. V_c² + b₂₂. P² + b₃₃. Q² + b₄₄. NEA²

(4)

To be obtained the second order model, it is necessary to conduct two central experiments with the average results as shown in Table 12 and Table 13.

The experimental outcomes were utilized to generate a quadratic mathematical paradigm in which interpreted the relationship between input parameters including cutting speed and MQL surroundings, by filling in input parameters in Eq. (4). The machined surface quality (Ra) paradigm for Up-milling side is generated through response surface design (RSD) as shown below:

Ra = 1.1843 – 0.00642 V_c – 0.1495 P – 0.00698 Q + 0.01079 NEA + 0.000022 V_c. V_c + 0.02103 P. P + 0.000017 Q. Q – 0.000085 NEA. NEA + 0.000280 P. Q
R² = 99.71%

(5)

Analogously, the experimental outcomes were utilized to generate a quadratic mathematical paradigm in which interpreted the relationship between input parameters including cutting speed and MQL surroundings, by filling in input parameters in Eq. (4). The machined surface quality (Ra) paradigm for Down-milling side is generated through response surface design (RSD) as illustrated below:

Ra = 0.061 – 0.00125 V_c + 0.196 P – 0.00420 Q + 0.0255 NEA + 0.000004 V_c V_c – 0.0585 P.P + 0.000012 Q. Q – 0.000210 NEA. NEA + 0.000119 P. Q
R² = 97.84%

(6)

Obviously, from Eq. (5) and Eq. (6) point out that the R² values in the quadratic mathematical paradigms are greater than 80% percentage, in turn, 99.7% and 97.84% for both Up-milling side and Down-milling side. It can be proved that the quadratic mathematical paradigm of response surface for both Up-milling side and Down-milling side is highly suited to the experimental outcomes. Thus, the machined surface quality (Ra) entirely satisfies with the forecast by using the quadratic mathematical paradigm of response surface.

3.3.2. Analysis of three-dimensional (3D) surface plots

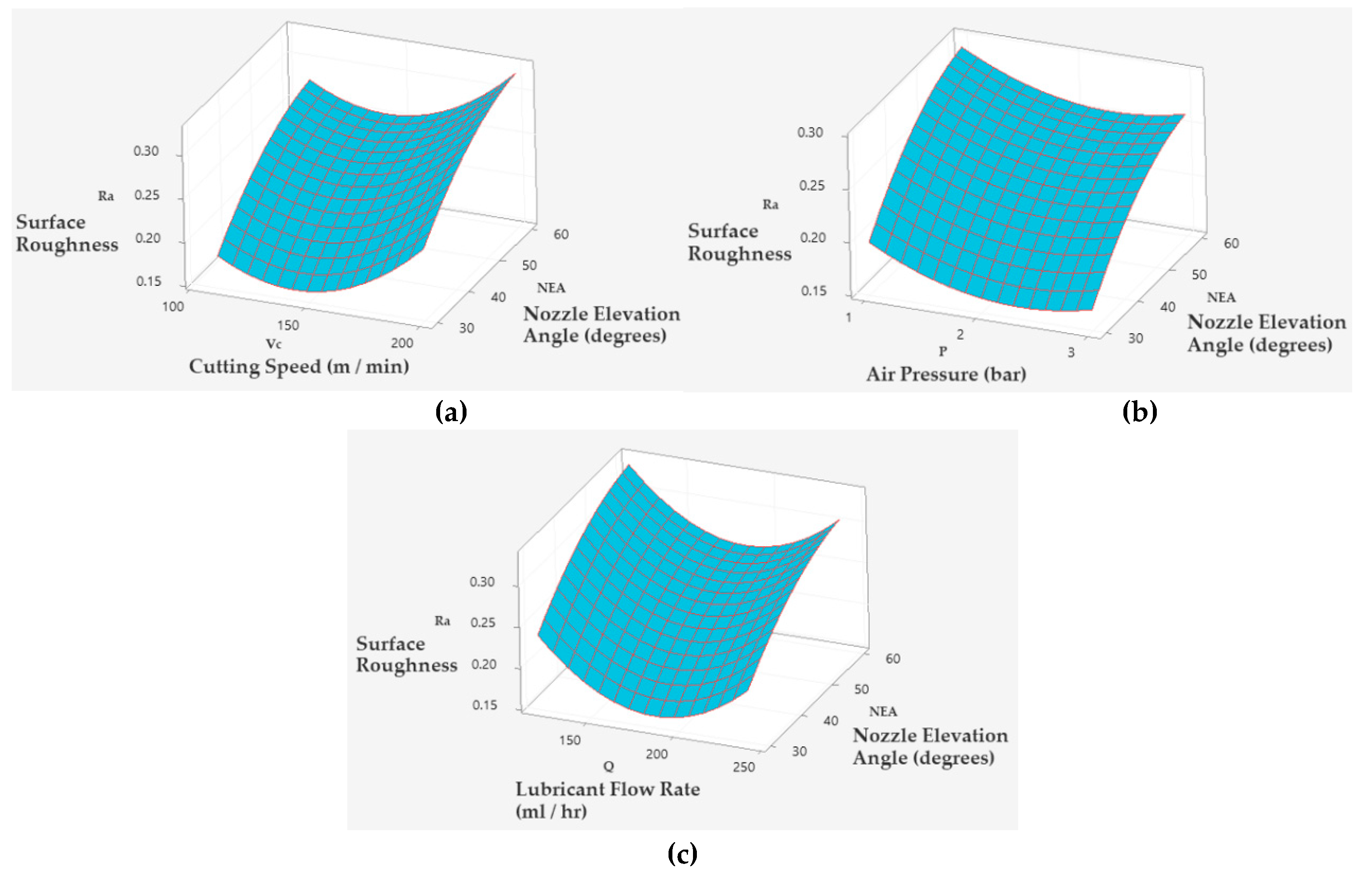
According to the interpretation of Signal-to-Noise and response surface design (RSD) by employing Minitab 19 software, 3D surface plots for Up and Down milling were used for the evaluation on the impact of independent variables on the machined surface quality (Figure 7 and Figure 8).

The impact of the independent variables on the machined surface quality is represented in Figure 7. Figure 7 (a) interprets the machined surface quality increases or decrease depending on the relation between the influence of nozzle elevation angle (NEA) corresponding to various cutting speed. It can be concluded that in the lowest level of nozzle elevation angle, as cutting speed increases, the surface roughness enhances slightly. The optimal machined surface quality is determined corresponding to the lowest level of NEA and the average cutting speed. Figure 7 (b) presents the optimal machined surface quality is determined corresponding to the lowest level of NEA and the average level of air pressure. Figure 7 (c) illustrates that the influence of nozzle elevation angle corresponding to different lubricant flow rate on the machined surface quality. It can be realized that the machined surface quality strongly increases, as lubricant flow rate decreases quickly. The machined surface quality is determined in accordance with the average level of lubricant flow rate and the lowest level of nozzle elevation angle.

The impact of the independent variables on the machined surface quality is represented in Figure 8. Figure 8 (a) interprets that the relation between independent variables including nozzle elevation, cutting speed and dependent variable (Ra). It can be actual expressed when cutting speed slightly increases in accordance with the lowest level of nozzle elevation angle, the machined surface quality (Ra) slightly enhances. It can be concluded that the optimal machined surface quality is determined corresponding to an average cutting speed. Figure 8 (b) presents the optimum achieved machined surface quality depends on the alteration of nozzle elevation angle corresponding to various air pressure levels. Moreover, it can be easily realized when air pressure at the highest surging level in correspondence with the lowest level of nozzle elevation angle, the machined surface quality decreases. The outcome reveals that the optimum machined surface quality is identified corresponding to the highest level of air pressure. Figure 8 (c) illustrates that the influence of nozzle elevation angle at different lubricant flow rate on the machined surface quality. It can be apparent realized that the surface roughness increases slightly, as lubricant flow rate increases quickly. The optimal machined surface quality is determined nearly the average level of lubricant flow rate in correspondence with the lowest level of nozzle elevation angle.

Consequently, from the analysis of response surface graphs with both Up-milling side and Down milling side. It can be pointed out that as nozzle elevation angle increases, surface roughness or the machined surface quality enhances as well.

3.4. Response optimization using desirableness function evaluation

A good way to approach and solve one or more optimal parameters of MQL environment and cutting speed together by utilizing desirableness function evaluation technique. Derringer and Suich suggested this technique in 1980 [27], in which the largest achieved value of desirableness is to identify the optimal answer by using the reduced gradient algorithm. The measured properties of each forecasted response are transformed into a dimensionless desirableness value d [28]. The desirableness function of “Smaller is better” can be written as given in Eq. (7):

d_{i} = 1 i f y_{i} \leq y_{m i n} d_{i} = {(\frac{y_{i} - y_{m a x}}{y_{m i n} - y_{m a x}})}^{r}, y_{m i n} \leq y_{i} \leq y_{m a x}, r \geq 0 d_{i} = 0 i f y_{i} \geq y_{m i n}

(7)

Eq. (7) is interpreted as follow:

y_{i}

is the optimal achieved value of

i

th output parameter.

y_{m i n}

y_{m a x}

: the lower deviation limit and upper deviation limit of

i

th output parameter respectively. The r is the weight in which depends on user’s demand.

Each response has a discrete desirableness index. It can be amalgamated all of discrete desirableness index to generate a singular value written by Eq. (8) below [28]:

d_{G} = \sqrt[w]{d_{1}^{w 1} . d_{2}^{w 2} \dots d_{i}^{w i}}

(8)

Where

d_{i}

is the discrete desirableness of the response

i

w_{i}

is the weight of the response

i

and

w

is the sum of the discrete weights.

Eq. (7) and Eq. (8) indicate that the better the quality of produce, the higher the value of desirableness. Therefore, the parameter

d_{G}

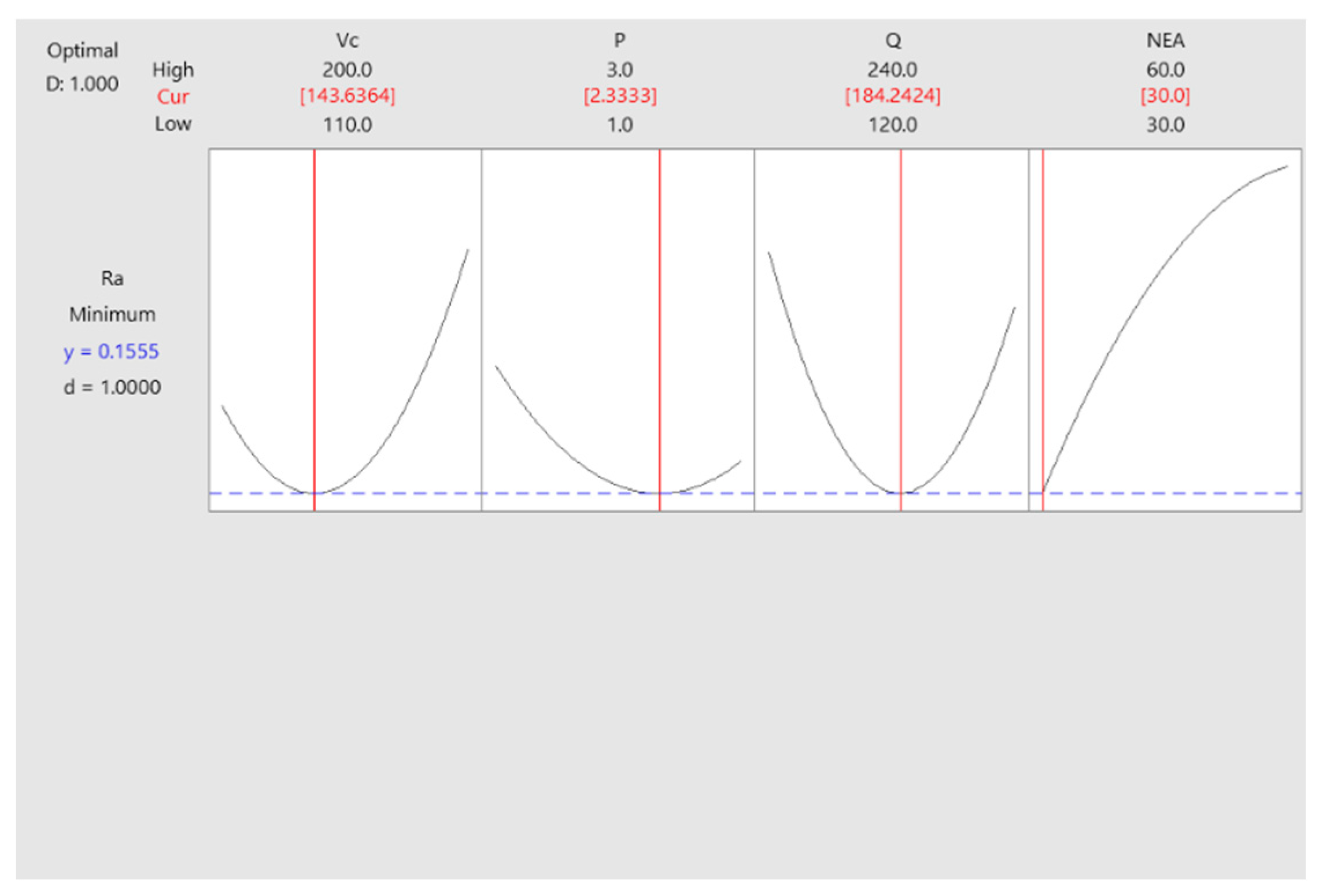
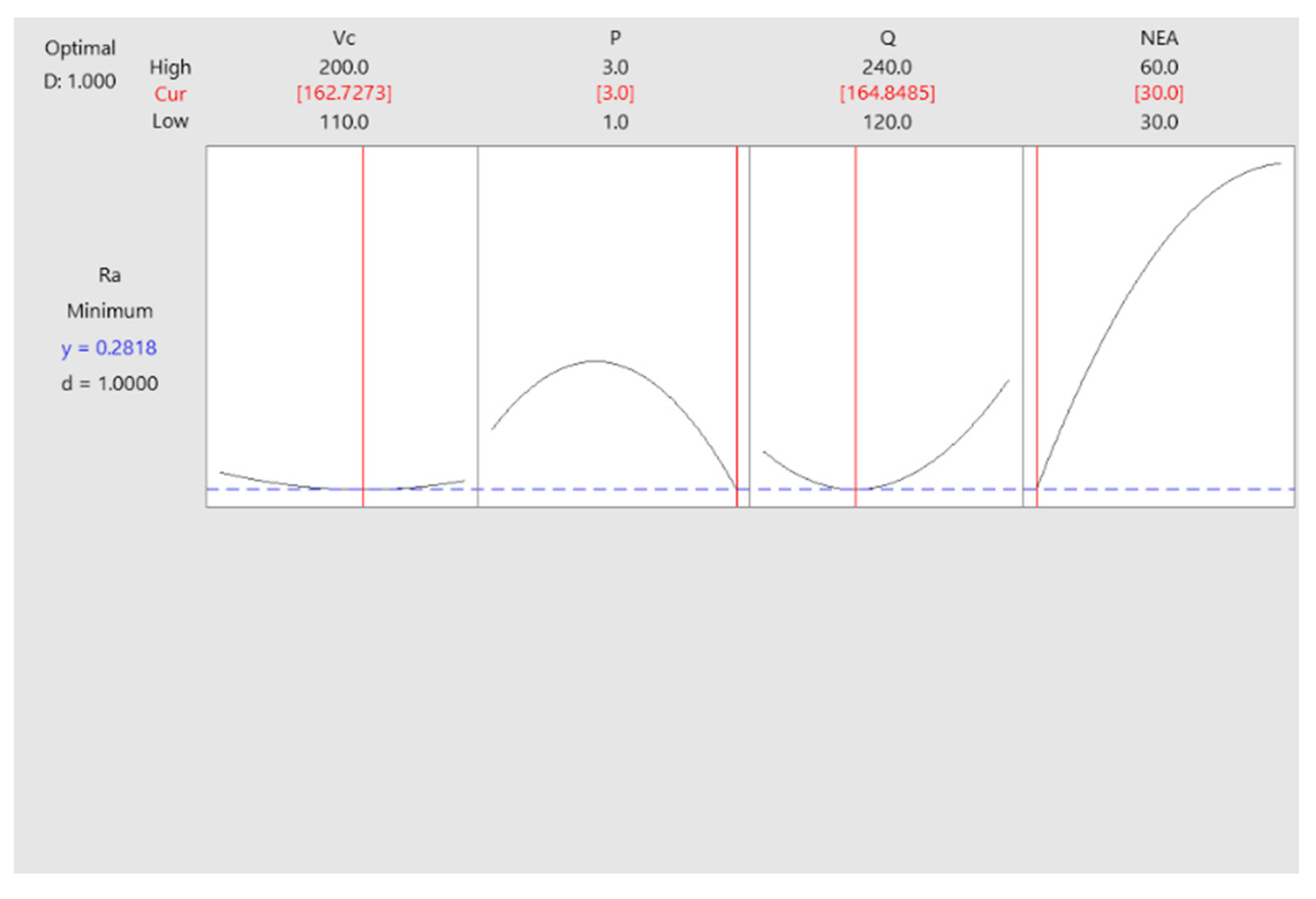
is established through calculating the influential parameter and the optimal value. Table 14 presents that the objective utilized for the machined surface quality is “minimize” and the objective utilized for the input parameters at optimum conditions “in the effective scope”, and then the optimization is fulfilled for an amalgamation of objectives. Based on the optimal values of the anatomized outcomes attained as 0.1555 μm for Ra with Up-milling side and 0.2818 μm for Ra with Down-milling side as shown in Figure 9 and Figure 10. Furthermore, the desirableness values were 1 for Ra with both Up-milling side and Down milling side, as given in Table 14.

3.5. Confirmation experiment

Basically, the optimal experimental outcomes will be considered as the findings after determination of the variable levels through analyzing the optimization by using Taguchi approach verified confirmation experiments. The results of confirmation experiments fulfilled in accordance with the optimal variable levels for the machined surface quality (Ra). Figure 4 and Figure 5 can be easily identified that the optimal variable levels with both Up-milling side (V_c2, P₂, Q₂, NEA₁) and Down-milling side (V_c3, P₃, Q₂, NEA₁) were utilized to calculate the forecasted optimal values of the machine surface quality. Table 15 exhibited the comparison of forecasted optimum values between RSD paradigm and Taguchi approach. The outcomes unveiled that the forecasted and the experimental obtained values are adjacent to together. Obviously, the quadratic mathematical paradigm established from RSD is an efficient instrument to forecast the value of the machined surface quality (Ra) under the impact of MQL surroundings and cutting speed in the scope of conducted trial.

4. Discussion

In MQL system, oil and the compressed air are amalgamated together to be sprayed into tool-chip interface and workpiece into droplets with a very small quantity through a nozzle. Oil plays the role as lubricant, and the compressed air plays the role of the cooling agent. In this study, from the Table 15 mentioned above, it can also be observed that among the four process parameters including cutting speed, air pressure, lubricant flow rate and nozzle elevation angle. Nozzle elevation angle is the pivotal effective parameter, immediately after lubricant flow rate, air pressure and cutting speed which impacts on the machined surface quality. This indicates that MQL parameters play the most significant role during circular pocket milling machining.

On the other hand, from the analysis of 3D surface plots (Figure 7 and Figure 8) indicates that on increasing nozzle elevation angle, the machined surface quality increases. It can be realized that output parameter is sensitive to change in nozzle elevation angle followed by lubricant flow rate. Therefore, it can be concluded that nozzle elevation angle increased with a surge of the machined surface quality, and a decrease of lubricant flow rate for Up-milling side and a slight increase of lubricant flow rate for Down-milling side. This coincides with the previous investigation finished in this studied range [5]. Sayuti et al [5], who reported that the minimum machined surface quality achieved 0,44 μm in accordance with a 30^o nozzle elevation angle in AISI 4140 steel hard turning operation. In this study, the minimum machined surface quality achieved 0.1612 μm and 0.29 μm in accordance with a 30^o nozzle elevation angle in circular pocket milling for both Up-milling side and Down milling side respectively. Obviously, it can be realized that the considerable improvement of the machine surface quality in AISI 1050 circular pocket milling operation compared to AISI 4140 hard turning operation.

Analogously, from Table 15 indicates that the optimal lubricant flow rate achieved 184.2424 ml / hr and 164.8485 ml / hr for Up-milling side and Down-milling side respectively. It is deeply interpreted the current findings have the consensus with the work of Sharma et al [6] and Singh et al [11].

Future scrutiny may be not only opened to analyze the impact of parameters in MQL surroundings on the machined surface quality as rectangle pocket milling, internal cone pocket milling, and so on, but also may be extended the effect of different MQL parameters such as lubrication type (LN₂ + MQL, CO₂ + MQL, vegetable oil) for type of different milling operations.

5. Conclusions

This investigation concentrates on analyzing the impact of MQL surroundings and cutting speed on the machined surface quality (Ra) as AISI 1050 steel circular pocket milling. To get a truly deep realization on the relation between the parameters of MQL environment and cutting speed on Ra through utilizing a quadratic mathematical paradigm of response surface design (RSD) and desirableness function evaluation to forecast the experimental outcomes. Moreover, the parameters of MQL surroundings consist of nozzle elevation angle, lubricant flow rate, air pressure and cutting speed are interpreted through analyzing Taguchi method. Simultaneously, the diagrams of Signal-to-Noise, three-dimensional (3D) surface plots, major impact plots of Means and ANOVA calculation are determined as a strategy for interpreting the optimum effective values of MQL environment and cutting speed on the machine surface quality. The outcomes can be drawn as follows:

*Through the analysis of diagrams such as three-dimensional (3D) surface plots, Signal-to-Noise, major impact plots of Means from Taguchi method. It can be actual realized that the parameters of MQL surroundings including nozzle elevation angle, lubricant flow rate and air pressure is the most significant instrument to estimate the machined surface quality.

*One of the most salient parameters of MQL environment which has the greatest impact on the machined surface quality (Ra) with both Up-milling side and Down milling side is nozzle elevation angle (NEA). Because Analysis of Variance (ANOVA) obviously demonstrated it. Nozzle elevation angle in which impacts on Ra is achieved 34.81% for Up-milling side and 57.47% for Down-milling side.

*Affirmation experiments demonstrate that the quadratic mathematical paradigm establishing by response surface design as AISI 1050 steel circular pocket milling has the value of high square R. It can be genuinely proved the relation between the experimental and forecasted values of response is adjacently identified together. Therefore, the quadratic mathematical paradigm is established utilizing response surface design (RSD) to be formulize the crucial effective parameters of MQL surroundings and cutting speed on the machine surface quality (Ra).

*From analyzing Taguchi technique proves that the various amalgamation between the parameters of MQL environment and cutting speed achieved the optimal outcomes for the machined surface quality (Ra) as 0.2900 μm. It indicates that affirmation experiments give confident outcomes.

Noticeably, the optimal parameters of AISI 1050 steel circular pocket milling operation are composed of cutting speed of 143.6364 m / min, air pressure of 2.3333 bar, lubricant flow rate of 184.2424 ml / hr, and nozzle elevation angle of 30 degrees; cutting speed of 162.7273 m / min, air pressure of 3 bar, lubricant flow rate of 164.8485 ml / hr and nozzle elevation angle of 30 degrees, and are determined through analyzing response surface design (RSD) and desirableness function evaluation corresponding to the optimal machined surface quality of Ra = 0.1555 μm for Up-milling side and Ra = 0.2818 μm for Down-milling side. Thus, RSD paradigm has the highly efficient forecast on the impact of parameters on results and is considered as a useful strategy to optimize output variables.

*Because the value of desirableness function evaluation is 1 for RSD paradigms of Ra with both Up-milling side and Down-milling side. It can be truly realized that desirableness function evaluation in RSD paradigm is an advantageous instrument to forecast the machine surface quality (Ra).

*In this paper, a circular pocket milling operation is anatomized and considered as an experimental and statistical method to find out the optimal parameters of Ra and can be taken the useful solution into consideration when applying safety to manufacturing processes.

Author Contributions

Conceptualization, L. C. T.; methodology, L. C. T.; software, L. C. T.; validation, L. C. T.; formal analysis, L. C. T.; investigation, L. C. T.; resources, L. C. T.; data curation, L. C. T.; writing—original draft preparation, L. C. T.; writing—review and editing, L. C. T. and T. T. P.; visualization, L. C. T.; supervision, T. T. P. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

This study acknowledges the assistance of Mechanical Engineering Laboratory and Mechanical Manufacturing Workshop, Faculty of Mechanical Engineering, Cao Thang Technical College.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

S/N	Signal-to-Noise
ANOM	Analysis of Mean
ANOVA	Analysis of Variance
RSD	Response Surface Design
NEA	Nozzle Elevation Angle
Eq	Equation
Ra	Machined surface quality or surface roughness
FFD	Full factorial design
hr	hour
ml	milli-liter
HB	Brinell Hardness
CNC	Computer Numerical Control
MQL	Minimum Quantity Lubrication

References

Lee, Y.; Resiga, A.; Yi, S.; Wern, C. ; The Optimization of Machining Parameters for Milling Operations by Using the Nelder–Mead Simplex Method. J. Manuf. Mater. Process. 2020, 4, 66. [Google Scholar] [CrossRef]
Mladen., B.; M., Budaka; CNC programming of pocket machining. 16^th International Scientific Conference On Production Engineering - CIM 2017 2017. .
Kariuki, L., W.; E. EIkua, B., W.; G. Nyakoe, N., N.; Generation and optimization of pocket miiling tool paths - A review. Proceedings of 2014 International Conference on Sustainable Research and Innovation 2014. 5.
Nisar, L.; Banday, B.; Amatullah, M.; Farooq, M.; Thoker, A.; Maqbool, A.; Wahid, M. An investigation on effect of process parameters on surface roughness and dimensional inaccuracy using Grey based Taguchi method. Materials Today: Proceedings 2021, 46, 6564–6569. [Google Scholar] [CrossRef]
Sayuti, M., A. Sarhan, A. D.; Salem, F. Novel uses of SiO2 nano-lubrication system in hard turning process of hardened steel AISI4140 for less tool wear, surface roughness and oil consumption. Journal of Cleaner Production 2014, 67, 265–276. [CrossRef]
Sharma, V.; Rana, M.; Singh, T.; Singh, A.; Chattopadhyay, K. Multi-response optimization of process parameters using Desirability Function Analysis during machining of EN31 steel under different machining environments. Materials Today: Proceedings 2021, 44, 3121–3126. [Google Scholar] [CrossRef]
Sharma, V.; Singh, T.; Rana, M.; Singh, K. Multi-output optimization during MQL based face milling of EN-31 steel employing Taguchi coupled grey relational analysis. Materials Today: Proceedings 2022, 65, 3216–3223. [Google Scholar] [CrossRef]
Rana, M.; Singh, T.; Sharma, V.; Saini, A.; Singh, J. Optimization of surface integrity in face milling of AISI 52,100 alloy steel using Taguchi based grey relational analysis. Materials Today: Proceedings 2022, 50, 2105–2110. [Google Scholar] [CrossRef]
Masooth, P.; Jayakumar, V.; Bharathiraja, G. Experimental investigation on surface roughness in CNC end milling process by uncoated and TiAlN coated carbide end mill under dry conditions. Materials Today: Proceedings 2020, 22, 726–736. [Google Scholar]
Rana, M.; Singh, T.; Saini, A.; Singh, J.; Sharma, V.; Singh, M.; Rooprai, R. Multi response optimization of nozzle process parameters in MQL assisted face milling of AISI 52,100 alloy steel using TGRA. Materials Today: Proceedings 2021, 44, 3177–3182. [Google Scholar] [CrossRef]
Singh, T.; Sharma, V.; Rana, M.; Saini, A.; Rooprai, R.; Singh, M. Multi response optimization of process variables in MQL assisted face milling of EN31 alloy steel using grey relational analysis. Materials Today: Proceedings 2021, 47, 4062–4066. [Google Scholar] [CrossRef]
Sharma, V.; Singh, T.; Singh, K.; Rana, M.; Gehlot, A. Optimization of surface qualities in face milling of EN-31 employing hBN nanoparticles-based minimum quantity lubrication. Materials Today: Proceedings, 2022, 69, 303–308. [Google Scholar] [CrossRef]
Masoudi, S.; Vafarda, A.; Hadad, M.; Jafarian, F. Experimental investigation into the effects of nozzle position, workpiece hardness, and tool type in MQL turning of AISI 1045 steel. Materials and Manufacturing Processes 2017. [Google Scholar] [CrossRef]
Yan, L.; Yuan, S.; Liu, Q. Influence of Minimum Quantity Lubrication Parameters on Tool Wear and Surface Roughness in Milling of Forged Steel. CHINESE JOURNAL OF MECHANICAL ENGINEERING, 2012, 25. [Google Scholar] [CrossRef]
Yuan, S.; Liu, Si.; Yan, Lutao.; Xiong, Q.; Experimental evaluation on the effect of the position of the nozzle in end milling under minimum quantity lubrication condition. Applied Mechanics and Materials 2012, 155–156, 42–46.
Dubey, V.; Sharma, K.; Pimenov, D. Prediction of Surface Roughness Using Machine Learning Approach in MQL Turning of AISI 304 Steel by Varying Nanoparticle Size in the Cutting Fluid. lubricants 2022, 10. [Google Scholar] [CrossRef]
Tuan, N.; Long, T.; Ngoc, T. Study of Effects of MoS2 Nanofluid MQL Parameters on Cutting Forces and Surface Roughness in Hard Turning Using CBN Insert. Fluids 2023, 8, 8. [Google Scholar] [CrossRef]
Singh, T.; Sharma, V.; Rana, M.; Singh, K.; Saini, A. GRA based optimization of tool vibration and surface roughness in face milling of hardened steel alloy. Materials Today: Proceedings 2022, 50, 2288–2293. [Google Scholar] [CrossRef]
Salur, E. Understandings the tribological mechanism of Inconel 718 alloy machined under different cooling/lubrication conditions. Tribology International 2022, 174. [Google Scholar] [CrossRef]
Ross, N.; Ganesh, M.; Srinivasan, D.; Gupta, M.; Korkmaz, M.; Krolczyk, J. Role of sustainable cooling/lubrication conditions in improving the tribological and machining characteristics of Monel-400 alloy. Tribology International 2022, 176. [Google Scholar] [CrossRef]
Meher, J.; Nayak, B.; Panda, A.; Kumar, R.; Sahoo, A. Recent research development of CNC based milling machining conditions: A comprehensive review. Materials Today: Proceedings, 2022, 62, 3983–3989. [Google Scholar] [CrossRef]
Meral, G.; Sarikaya, M.; Dilipak, H.; Seker, U. Multi-response Optimization of Cutting Parameters for Hole Quality in Drilling of AISI 1050 Steel. Arab J Sci Eng 2015. [Google Scholar] [CrossRef]
Sari, N.; Yilmaz, M. Investigation of abrasive + erosive wear behaviour of surface hardening methods applied to AISI 1050 steel. Materials and Design 2004, 27, 470–478. [Google Scholar] [CrossRef]
Karna, S.; Sahai, R. An Overview on Taguchi Method. International Journal of Engineering and Mathematical Sciences, 2012, 1, 11–18. [Google Scholar]
Yang, W.; Tarng, Y. Design optimization of cutting parameters for turning operations based on the Taguchi method. Journal of Materials Processing Technology 1998, 84, 122–129. [Google Scholar] [CrossRef]
Karna, S.; Singh, R.; Sahai, R. Application of Taguchi Method in Indian Industry. International Journal of Emerging Technology and Advanced Engineering 2012, 11. [Google Scholar]
Derringer, G.; Suich, R. Simultaneous Optimization of Several Response Variables. Journal of Quality Technology 1980, 12. [Google Scholar] [CrossRef]
Sait, A.; Aravindan, S.; Haq, A. Optimisation of machining parameters of glass-fibre-reinforced plastic (GFRP) pipes by desirability function analysis using Taguchi technique. Int J Adv Manuf Technol 2009, 43, 581–589. [Google Scholar] [CrossRef]

Figure 1. EMCOMAT FB450 machine with MQL setup.

Figure 2. MQL parameters in circular pocket milling operations.

Figure 3. Illustrated a circular pocket milling operation including machine, cutting tool, workpiece and nozzle elevation angle.

Figure 4. illustrated experimental results and recorded surface roughness.

Figure 5. Main effects plot for Up-milling side a) Mean of S/N ratios b) Mean of Means.

Figure 6. Main effects plot for Down-milling side a) Mean of S/N ratios b) Mean of Means.

Figure 7. The response 3D surface plots of Ra with Up-milling side according to change nozzle elevation angle, lubricant flow rate, air pressure and cutting speed.

Figure 8. The response 3D surface plots of Ra with Down-milling side according to change nozzle elevation angle, lubricant flow rate, air pressure and cutting speed.

Figure 9. Response optimization plot for Ra with Up-milling side.

Figure 10. Response optimization plot for Ra with Down-milling side.

Table 1. AISI 1050 steel chemical composition [22,23].

			%Weight
C	Si	Mn	P_max	S_max	Cr	Mo	Ni
0.533	0.293	0.883	0.04	0.012	0.255	0.098	0.183

Table 2. AISI 1050 steel mechanical properties.

Test temperature	Ultimate tensile	0.2% Yield (MPa)	% Elong	Hardness
(^oC)	Strength (MPa)	0.2% Yield (MPa)	% Elong	Hardness
Room	690	365.4	23.7	197

Table 3. AISI 1050 steel physical properties.

Parameters and unit	Value
Density (g / cm³)	7.85
Thermal conductivity (W / mK)	49.8
Elastic Modulus (GPa)	190-210
Special heat capacity (J / g^oC)	0.486
Melting (^oC)	1425 - 1540

Table 4. Experimental Conditions.

Machine Tool	CNC Vertical EMCOMAT FB450 MC
Tool Holder	DIN 69871 / SK40
Endmill Cutter	SECO JS553, type: 553140Z3.0-SIRON-A
Depth of cut, d (mm)	0.5
Cutting Speed, V_c (m / min)	110, 155, 200
MQL surroundings
+Air Pressure P, (bar)	1, 2, 3
+Lubricant flow rate, Q (ml / h)	120, 180, 240
+Lubricant used	Mineral oil
Circular Pocket Depth, CPD (mm)	20
Spraying Distance, SD (mm)	35
Nozzle Elevation Angle, NEA (Degrees)	30^o, 45^o, 60^o

Table 5. Experimental design.

Exp.no	Coded value				Actual value
Exp.no	A	B	C	D	V_c (m/min)	P (bar)	Q (ml/hr)	NEA (degrees)
1	1	1	1	1	110	1	120	30^o
2	1	2	2	2	110	2	180	45^o
3	1	3	3	3	110	3	240	60^o
4	2	1	2	3	155	1	180	60^o
5	2	2	3	1	155	2	240	30^o
6	2	3	1	2	155	3	120	45^o
7	3	1	3	2	200	1	240	45^o
8	3	2	1	3	200	2	120	60^o
9	3	3	2	1	200	3	180	30^o

Table 6. Measured results for Up-milling side, their calculated S/N ratios.

Exp. no	Coded values				Actual values				Measured parameters
	A	B	C	D	V_c	P	Q	NEA	Surface roughness (μm)
									Reading					Average	S/N ratios
									1	2	3	4	5
1	1	1	1	1	110	1	120	30^o	0.273	0.331	0.213	0.351	0.391	0.3118	10.1225
2	1	2	2	2	110	2	180	45^o	0.247	0.226	0.311	0.196	0.271	0.2502	12.0343
3	1	3	3	3	110	3	240	60^o	0.331	0.265	0.219	0.355	0.580	0.3500	9.1186
4	2	1	2	3	155	1	180	60^o	0.228	0.547	0.283	0.190	0.213	0.2922	10.6864
5	2	2	3	1	155	2	240	30^o	0.232	0.197	0.112	0.285	0.223	0.2098	13.5639
6	2	3	1	2	155	3	120	45^o	0.202	0.191	0.234	0.469	0.366	0.2924	10.6805
7	3	1	3	2	200	1	240	45^o	0.346	0.271	0.315	0.483	0.403	0.3636	8.7875
8	3	2	1	3	200	2	120	60^o	0.386	0.485	0.334	0.391	0.402	0.3996	7.9675
9	3	3	2	1	200	3	180	30^o	0.256	0.277	0.219	0.204	0.221	0.2354	12.5639

Table 7. Measured results for Down-milling side, their calculated S/N ratios.

Exp. no	Coded values				Actual values				Measured parameters
	A	B	C	D	V_c	P	Q	NEA	Surface roughness (μm)
									Reading					Average	S/N ratios
									1	2	3	4	5
1	1	1	1	1	110	1	120	30^o	0.284	0.422	0.404	0.326	0.376	0.3624	8.8162
2	1	2	2	2	110	2	180	45^o	0.576	0.525	0.597	0.217	0.668	0.5166	5.7369
3	1	3	3	3	110	3	240	60^o	0.467	0.712	0.338	0.321	0.952	0.5580	5.0673
4	2	1	2	3	155	1	180	60^o	0.387	0.585	0.594	0.535	0.480	0.5162	5.7436
5	2	2	3	1	155	2	240	30^o	0.373	0.397	0.396	0.606	0.312	0.4168	7.6014
6	2	3	1	2	155	3	120	45^o	0.409	0.527	0.367	0.341	0.613	0.4514	6.9088
7	3	1	3	2	200	1	240	45^o	0.270	0.737	0.512	0.784	0.293	0.5192	5.6933
8	3	2	1	3	200	2	120	60^o	0.367	0.471	0.510	0.847	0.758	0.5906	4.5741
9	3	3	2	1	200	3	180	30^o	0.279	0.221	0.558	0.175	0.217	0.2900	10.7520

Table 8. Up-milling side, Response table for S/N ratios and Means.

Level	Factors				Level	Factors
Level	V_c	P	Q	NEA	Level	V_c	P	Q	NEA
1	10.425	9.865	9.590	12.083	1	0.3040	0.3225	0.3346	0.2523
2	11.644	11.189	11.762	10.501	2	0.2648	0.2865	0.2593	0.3021
3	9.773	10.788	10.490	9.258	3	0.3329	0.2926	0.3078	0.3473
Delta	1.871	1.323	2.171	2.826	Delta	0.0681	0.0360	0.0753	0.0949
Rank	3	4	2	1	Rank	3	4	2	1

Table 9. Down-milling side, Response table for S/N ratios and Means.

Level	Factors				Level	Factors
Level	V_c	P	Q	NEA	Level	V_c	P	Q	NEA
1	6.540	6.751	6.766	9.057	1	0.4790	0.4659	0.4681	0.3564
2	6.751	5.971	7.411	6.113	2	0.4615	0.5080	0.4409	0.4957
3	7.006	7.576	6.121	5.128	3	0.4666	0.4331	0.4980	0.5549
Delta	0.466	1.605	1.290	3.928	Delta	0.0175	0.0749	0.0571	0.1985
Rank	4	2	3	1	Rank	4	2	3	1

Table 10. Up-milling side, The impact of the factors on output parameter.

No.	Factors	Mean of S/N ratio in correspondence with response value at the valuable levels			Mean	Max (1,2,3)	Max - Mean	Contribution %	Delta	Rank
No.	Factors	1	2	3	Mean	Max (1,2,3)	Max - Mean	Contribution %	Delta	Rank
1	V_c (m/min)	10.4251	11.6435	9.7729	10.6138	11.6435	1.0296	24.39	1.8706	3
2	P (bar)	9.8654	11.1885	10.7876	10.6138	11.1885	0.5746	13.61	1.3231	4
3	Q (ml / hr)	9.5901	11.7614	10.4899	10.6138	11.7614	1.1476	27.19	2.1713	2
4	NEA (degrees)	12.0833	10.5007	9.2574	10.6138	12.0833	1.4695	34.81	2.8259	1

Table 11. Down-milling side, The impact of the factors on output parameter.

No.	Factors	Mean of S/N ratio in correspondence with response value at the valuable levels			Mean	Max (1,2,3)	Max - Mean	Contribution %	Delta	Rank
No.	Factors	1	2	3	Mean	Max (1,2,3)	Max - Mean	Contribution %	Delta	Rank
1	V_c (m/min)	6.5401	6.7512	7.0064	6.7659	7.0064	0.2405	6.03	0.4663	4
2	P (bar)	6.7510	5.9708	7.5760	6.7659	7.5760	0.8101	20.32	1.6052	2
3	Q (ml / hr)	6.7663	7.4108	6.1206	6.7659	7.4108	0.6449	16.18	1.2902	3
4	NEA (degrees)	9.0565	6.1129	5.1283	6.7659	9.0565	2.2906	57.47	3.9282	1

Table 12. Up-milling side.

No.	MQL and cutting speed factors				Coded factors				The recorded and measured surface roughness results (μm)					Average Ra (μm)
No.	V_c (m/min)	P (bar)	Q (ml / hr)	NEA (degrees)	x₁	x₂	x₃	x₄	Ra1	Ra2	Ra3	Ra4	Ra5	Average Ra (μm)
1	110	1	120	30^o	-1	-1	-1	-1	0.273	0.331	0.213	0.351	0.391	0.3118
2	110	2	180	45^o	-1	0	0	0	0.247	0.226	0.311	0.196	0.271	0.2502
3	110	3	240	60^o	-1	1	1	1	0.331	0.265	0.219	0.355	0.580	0.3500
4	155	1	180	60^o	0	-1	0	1	0.228	0.547	0.283	0.190	0.213	0.2922
5	155	2	240	30^o	0	0	1	-1	0.232	0.197	0.112	0.285	0.223	0.2098
6	155	3	120	45^o	0	1	-1	0	0.202	0.191	0.234	0.469	0.366	0.2924
7	200	1	240	45^o	1	-1	1	0	0.346	0.271	0.315	0.483	0.403	0.3636
8	200	2	120	60^o	1	0	-1	1	0.386	0.485	0.334	0.391	0.402	0.3996
9	200	3	180	30^o	1	1	0	-1	0.256	0.277	0.219	0.204	0.221	0.2354
10	155	2	180	45^o	0	0	0	0	0.292	0.205	0.190	0.198	0.216	0.2202
11	155	2	180	45^o	0	0	0	0	0.360	0.202	0.192	0.221	0.202	0.2354

Table 13. Down-milling side.

No.	MQL and cutting speed factors				Coded factors				The recorded and measured surface roughness results (μm)					Average Ra (μm)
No.	V_c (m/min)	P (bar)	Q (ml / hr)	NEA (degrees)	x₁	x₂	x₃	x₄	Ra1	Ra2	Ra3	Ra4	Ra5	Average Ra (μm)
1	110	1	120	30^o	-1	-1	-1	-1	0.284	0.422	0.404	0.326	0.376	0.3624
2	110	2	180	45^o	-1	0	0	0	0.576	0.525	0.597	0.217	0.668	0.5166
3	110	3	240	60^o	-1	1	1	1	0.467	0.712	0.338	0.321	0.952	0.5580
4	155	1	180	60^o	0	-1	0	1	0.387	0.585	0.594	0.535	0.480	0.5162
5	155	2	240	30^o	0	0	1	-1	0.373	0.397	0.396	0.606	0.312	0.4168
6	155	3	120	45^o	0	1	-1	0	0.409	0.527	0.367	0.341	0.613	0.4514
7	200	1	240	45^o	1	-1	1	0	0.270	0.737	0.512	0.784	0.293	0.5192
8	200	2	120	60^o	1	0	-1	1	0.367	0.471	0.510	0.847	0.758	0.5906
9	200	3	180	30^o	1	1	0	-1	0.279	0.221	0.558	0.175	0.217	0.2900
10	155	2	180	45^o	0	0	0	0	0.869	0.441	0.302	0.517	0.255	0.4768
11	155	2	180	45^o	0	0	0	0	1.116	0.359	0.246	0.522	0.435	0.5356

Table 14. RSD optimization results for responses.

Response	Object.	Optimum Conditions				Lower	Target	Upper	Weights	Import.	Predicted	Desirability
Response	Object.	V_c (m/min)	P (bar)	Q (ml/hr)	NEA (degrees)	Lower	Target	Upper	Weights	Import.	Predicted	Desirability
Ra (Up-milling)	Min.	143.636	2.3333	184.242	30	0.2098	0.2098	1.5	1	1	0.1555	1
Ra (Down-milling)	Min.	162.727	3	164.848	30	0.29	0.29	1.5	1	1	0.2818	1

Table 15. Outcomes of affirmation experiments and forecasted values by RSD paradigm.

No.		V_c (m/min)	P (bar)	Q (ml/hr)	NEA (degrees)	Experimental Result	RSD predicted
Surface Roughness for Up-milling side
1	V_c2, P₂, Q₂, NEA₁ (Taguchi)	155	2	180	30		0.1612
2	V_c, P, Q, NEA (Predicted optimum values from RSD)	143.6364	2.3333	184.2424	30		0.1555
Surface Roughness for Down-milling side
1	V_c3, P₃, Q₂, NEA₁ (Taguchi)	200	3	180	30	0.2900
2	V_c, P, Q, NEA (Predicted optimum values from RSD)	162.7273	3	164.8485	30		0.2818

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer