Aero-Structural Design Optimization of Wind Turbine Blades

Wind energy is becoming increasingly important as a renewable energy source due to its environmental and economic benefits. Wind turbines are key components in wind energy systems, and their performance is critical for efficient power generation. Wind turbine blades are the most critical components as they interact with the wind, and their design has a significant impact on the overall system performance. Therefore, it is essential to optimize the design of wind turbine blades to enhance their efficiency and reduce their costs. This paper presents an aero-structural optimization approach for wind turbine blade design. The optimization aims to maximize the torque generated by the blade while minimizing its mass. The optimization is implemented using DAFoam software for CFD simulation, TACS for FEM simulation, and Mphys under the OpenMDAO framework for fluid-structure interaction between the CFD and FEM. The optimization results show a 6.78% increase in torque and a 4.22% decrease in mass, which demonstrates the effectiveness of the proposed approach. Aerodynamic optimization focuses on maximizing the blade's torque by modifying the blade's shape. The optimization results show that the optimized blade generates more torque than the original blade design. Additionally, structural optimization aims to minimize the blade's mass while maintaining its structural integrity. This is achieved by adjusting the thickness of the blade's cross-section. The proposed aero-structural optimization approach presents an effective solution for the design optimization of wind turbine blades. The approach considers the interaction between the aerodynamic and structural aspects of the blade and optimizes them simultaneously. This leads to an optimized design that is efficient and cost-effective, which is crucial for the widespread adoption of wind energy systems. The results of this study highlight the importance of considering the interaction between the aerodynamic and structural aspects of wind turbine blades and the effectiveness of the proposed optimization approach in enhancing their performance.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

The development of renewable energy sources has become a priority for emerging nations because of the volatile energy market, the depletion of fossil fuels, and the deteriorating environmental conditions. The fundamental idea behind using renewable energy is that it comes from ongoing natural processes. As a result, emerging nations reject the use of fossil fuels and migrate to other sources of energy like wind and solar. The majority of these renewable energy sources significantly reduce CO2 emissions, as suggested by the Intergovernmental Panel on Climate Change (IPCC) [1].

Renewable energy is produced from natural resources that replenish themselves naturally and without human intervention. Wind energy is one of the renewable energy sources that is growing the quickest. As a result, harnessing wind energy to generate electricity is more economical than using coal or gas-fired power plants. Wind energy is one of the renewable energy sources that is growing the quickest. As a result, harnessing wind energy to generate electricity is more economical than using coal or gas-fired power plants. Despite all of its advantages, wind energy's main disadvantage is that power is intermittent. Consequently, another energy source that can be produced on demand must be combined with wind energy. Wind power should be considered an additional energy source rather than the main one.

Only land-based wind power can economically meet humanity's energy demands, claim Zhou et al. [2]. However, only a tiny fraction of this enormous potential for wind energy is now being used [3]. Three thousand years of human history have seen the utilization of wind energy [4]. The use of wind energy peaked during both World Wars, then decreased afterward and again rose as a result of the demise of the petroleum sector in the 1970s [5]. Therefore, modern wind turbines had been built in Denmark by the end of the seventeenth century [6]. The technological complexity of wind turbines makes them difficult to run with a variety of workloads [7].

Expanding the usage of carbon-free technologies that rely on high-potential, renewable energy sources like wind power would require lowering the levelized cost of energy. Modern, highly flexible wind turbine rotors are defined by strongly coupled, multi-physics interactions, which must be captured by advanced computational approaches. As a consequence, computing methods may greatly improve the time-consuming process that occurs in wind turbine blades.

2. Literature Review

Energy is crucial for social and economic progress, and because of rising greenhouse gas emissions and fuel costs, renewable energy sources are gaining popularity. Renewable energy does have certain limitations, too, such intermittent generation and the need for sophisticated design, planning, and control optimization techniques.

Computational optimization techniques for renewable energy design, planning, and control difficulties were demonstrated by Baos et al. in 2011 [8]. The use of heuristic approaches, Pareto-based multi-objective optimization, and parallel processing are intriguing study areas in renewable and sustainable energy, according to one of the review's fascinating results.

A bibliography on wind speed and wind power projections was eventually given by Lei et al. [9]. The incorporation and application of artificial intelligence techniques as well as the blending of diverse statistical models for both long- and short-term forecasts were seen as possible prospects. The papers listed below [10,11,12,13] discuss forecasting techniques for wind energy.

Miller et al. [14] reviewed recent developments in numerical simulation techniques, technology, and applications to wind energy. They also looked at past numerical simulations.

The wind energy business heavily relies on computational fluid dynamics to research innovative turbine designs (CFD).

New tools must be created in order to apply CFD early in the design phase, where lower-fidelity methods like blade element momentum (BEM) are more common. Algorithmic optimization tools are extremely helpful since they reduce the dependency on trial-and-error design.

Rodriguez and Celis proposed that a CFD-based difference model is coupled to a GA-based optimization tool as a thorough method for improving wind turbine blade designs [15]. The findings also show that the ideal airfoil outperforms a NACA 4412 airfoil in terms of lift-to-drag ratios.

Madsen et al. [16] presented the first comprehensive 3-D CFD adjoint-based form optimization of a modern 10 MW offshore wind turbine. In order to compare their findings with the BEM results from their case study and ascertain the value of design optimization based on high-fidelity models, the optimization challenge was matched with a case study from the International Energy Agency (IEA) Wind Task 37.

For high-fidelity aerodynamic shape optimization, the adjoint technique is an effective method for calculating the derivatives of an interest function with respect to a large number of design factors. Open standards were offered by Kenway et al., who also released a thorough analysis of the various adjoint implementation strategies, making recommendations for practical implementation strategies that are accurate, efficient, and affordable [17]. The Jacobian-free method is unquestionably preferable due to its Jacobian-free adjoint methodology.

In addition, Gray et al. proposed the theory and architecture of OpenMDAO in 2019 [18]. This open-source multidisciplinary design optimization (MDO) framework solves coupled systems utilizing Newton-type algorithms and takes use of problem structure via novel hierarchical methodologies. The main goal of MDO is to build interconnected numerical models of challenging engineering systems. There are a number of MDO software frameworks, however none of them completely makes use of cutting-edge methods to solve connected models efficiently.

This study's goal is to present an aero-structural optimization method for wind turbine blade design that aims to maximize torque while lowering mass because none of the earlier literature studies attempted to incorporate the associated performance optimization of wind turbines. While structural optimization aims to minimize bulk while maintaining structural integrity, aerodynamic optimization concentrates on altering the shape of the blade. This approach is crucial for the widespread adoption of wind energy systems since it is both effective and affordable.

3. Materials and Methods

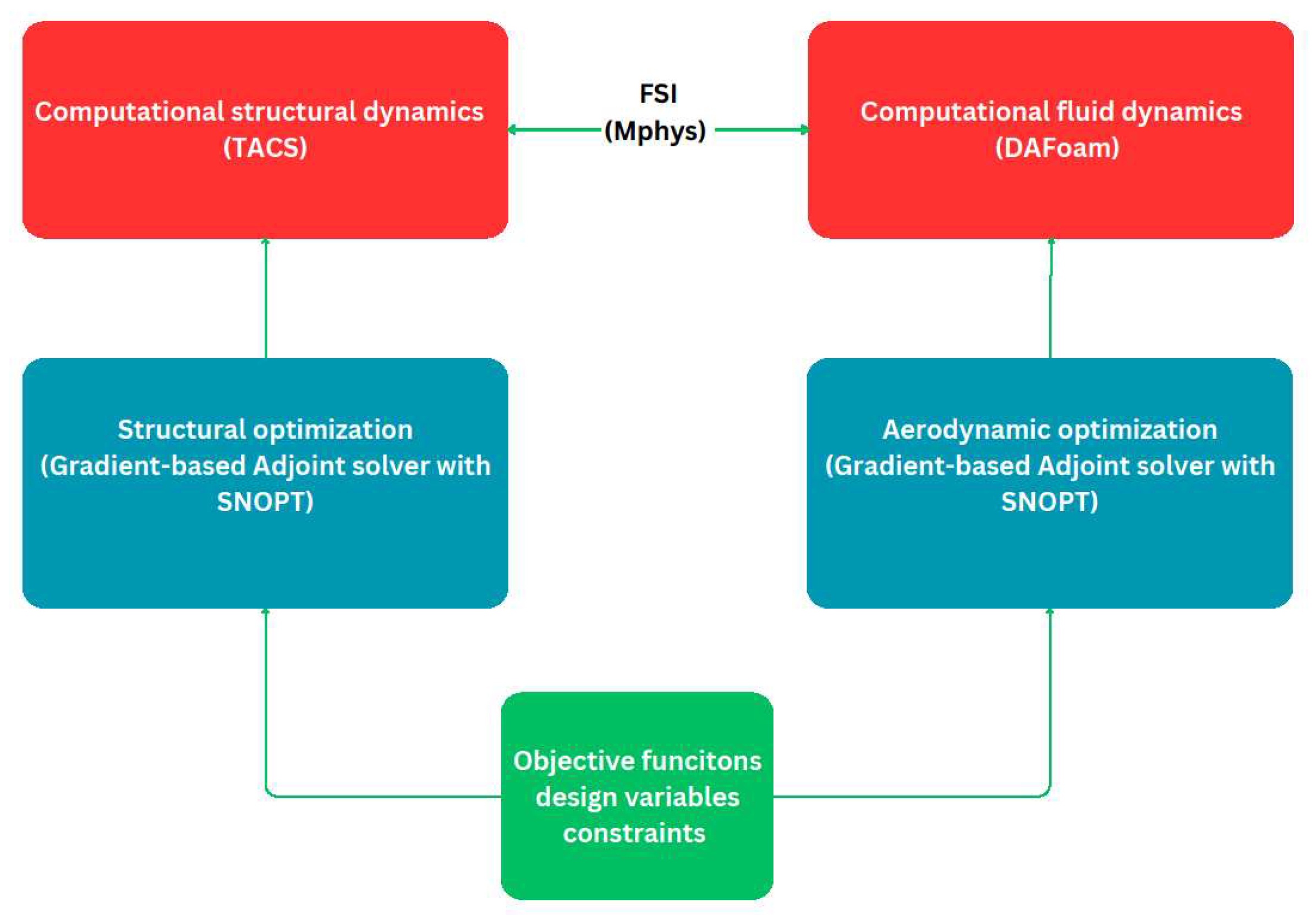
3.1. Aero-structural optimization framework

In spite of having a higher computational cost and implementation effort when compared to low-fidelity solvers, the use of high-fidelity solvers in aero-structural design optimization of wind turbine blades can give improved accuracy and more complete model specification [17]. To manage the high-dimensional and high-fidelity optimization formulations in a tractable numerical problem, gradient-based optimization techniques are required, such as the use of adjoint-based derivative computations. Multiple aero-structural, hydrostructural, aerothermal, aeropropulsive, and aeroelastic MDO issues have been incorporated in the OpenMDAO framework to handle interdisciplinary design optimization challenges in engineering systems [18]. The main functionality of the Python-based, open-source, high-performance computing platform known as OpenMDAO is gradient-based optimization using analytic derivatives. The implementation presented in this paper is based on a two-way fluid-structure interaction (FSI) in the OpenMDAO framework that couples the discrete adjoint with OpenFOAM for High-fidelity Multidisciplinary Design Optimization (DAFoam) [19] and the Toolkit for the Analysis of Composite Structures (TACS) [20] with Mphysics [21]. With competitive speed, scalability, and accuracy, DAFoam employs a discrete adjoint technique without Jacobians. It also offers a Python interface for linking interdisciplinary design optimization.

In this study, we optimize the aero-structural design of wind turbine blades to improve their aerodynamic performance and decrease their mass using the discrete CFD solver DAFoam in combination with the OpenMDO framework. The aerodynamic and structural systems work together; the aerodynamics group gets a mesh as input and creates aerodynamic loads as an output, while the structural group receives these loads as input and generates structural displacements as a result. This method has received a lot of previous research attention, with several studies examining its potential applications in the optimization of aircraft aerodynamics and aero-structural design [22,23,24].

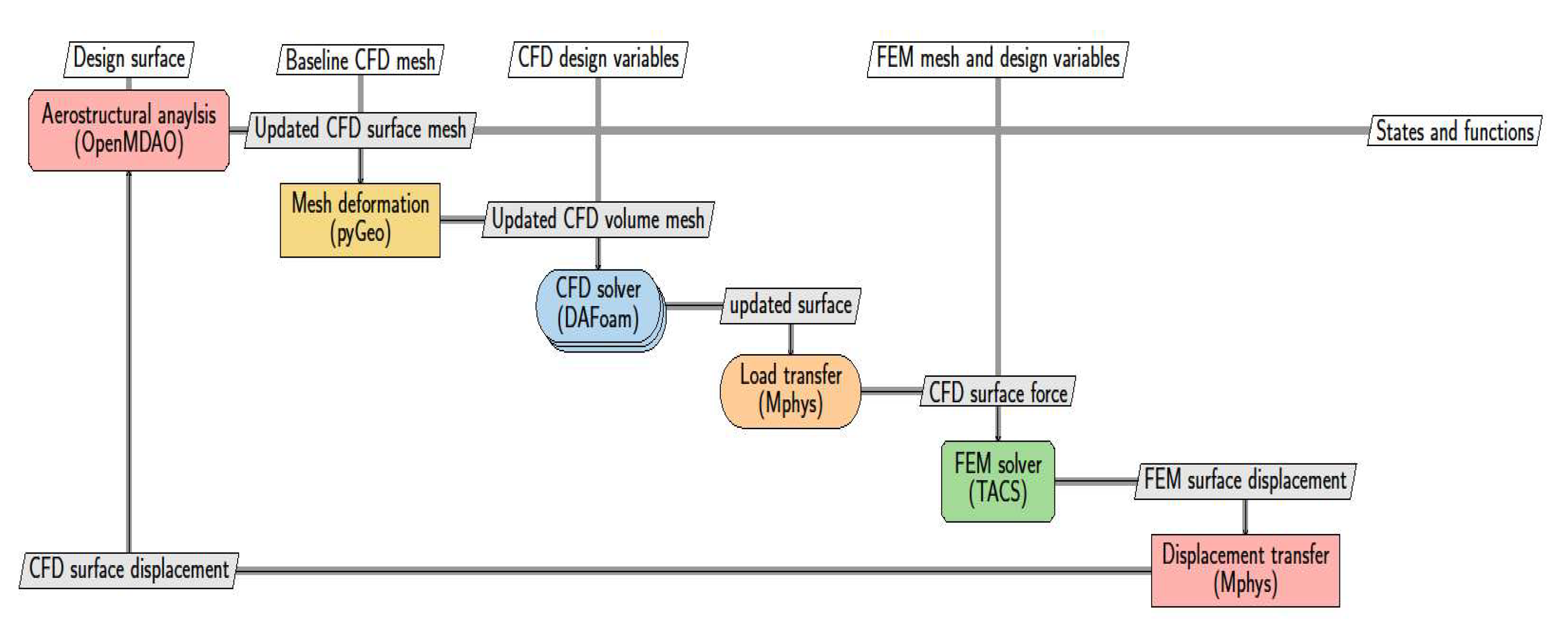
According to the Extended Design Structure Matrix (XDSM) schematic [26] in Figure 1, the MACH [25] is a group of closely connected sub-modules that enable geometry parametrization and deformation, coupled aero-structural analysis, and effective derivatives assessment in an optimization context.

The OpenMDAO framework, which is based on Mach-aero, is used to carry out the optimization procedure [27]. The creation of the structural mesh in MSC Patran and the aerodynamic mesh in pyHyp are both part of the preprocessing stage. The Free-Form Deformation (FFD) method and Non-Uniform Rational B-Splines (NURBS) scheme are used by the geometry parametrization package, pyGeo, to alter the geometry. Surface node displacements are propagated from the revised geometry to the volume mesh through the mesh deformation module IDwarp. For high-fidelity interdisciplinary design optimization, the aerodynamic solver, DAFoam, implements the discrete adjoint using the FD Jacobian technique and Krylov method. While the OpenMDAO/Mphys framework is used to create the aerostructural coupling, FUNtoFEM is used to compute the load and displacement transfer. The Toolkit for the Analysis of Composite Structures (TACS), a structural solution that can deal with both linear and nonlinear geometric structural issues, was employed in this study. PyOptSparse handles the formulation of the optimization problem as well as the data flow between the solvers and the optimizer. The SimpleFoam solver from OpenFOAM is used to simulate steady-state turbulent flow. Figure 2 depicts the entire aero-structural optimization profile.

3.2. RANS-based turbulent simulation

For the conservation of mass and momentum, the Navier-Stokes equations are used to describe a three-dimensional steady incompressible flow.

\nabla . u = 0 .

(1)

\frac{\partial u}{\partial t} + \nabla . (u u) = - \frac{1}{ρ} \nabla \bar{p} + μ \nabla . \nabla u .

(2)

These equations are given as Eqs. 1 and 2, where u denotes the fluid's velocity, p denotes its pressure, d denotes its density, v denotes its dynamic viscosity, and f denotes the absence of an explicit body force. The Spalart-Allmaras model [28] is employed as the turbulence model because it is reliable, effective, converges well, and is simple to use. In Table 1, the boundary conditions are displayed. The initial values for k, ε, νt, ω, ṽ are 0.8375 m²/s², 0.2 m²/s³, 5e-05 m²/s, 12.24 s^-1 and 5e-05 m²/s, respectively. The inlet velocity of the fluid is 7 m/s, and the blade has a rotational velocity of 72 rpm.

3.3. Structural Model

The influence of temperature is not included in the structural simulation employed in this model. As a result, the simulation would be set to isothermal for this chapter. The state equation for the momentum balance has the following structure:

\frac{\partial^{2} (ρ u)}{\partial t^{2}} - \nabla \cdot σ = 0

(3)

where

u

and

σ

are displacement vector and stress tensor, respectively, while

μ_{s}

and

λ

are the material properties. The stress tensor is specified using strain tensor

ε

σ = 2 μ_{s} ε + λ t r (ε) I

(4)

ε = \frac{1}{2} [\nabla u + {(\nabla u)}^{T}]

(5)

Equations (4) and (5) when combined provide the following results:

\nabla \cdot σ = \nabla \cdot (μ_{s} \nabla u) + \nabla \cdot {[μ_{s} (\nabla u)}^{T} + λ I t r (\nabla u)]

(6)

The tweak to the solution technique improves the convergence of a simulation by rearranging terms in Equation (6). The first component of Equation (3) is implicitly solved by OpenFoam, whereas the second term is explicitly solved.

Therefore, by changing the order of phrases, the explicit and implicit components are more evenly distributed. Equation (3) in its modified form has the following form:

\nabla \cdot σ = \nabla \cdot [(2 μ_{s} + λ) \nabla u] + \nabla \cdot {[μ_{s} (\nabla u)}^{T} + λ I t r (\nabla u) - (μ_{s} + λ) \nabla u]

(7)

The traction force boundary condition has the following expression (where

n

is a surface normal to the boundary):

T = σ \cdot n = [(2 μ_{s} + λ) \nabla u] + \nabla \cdot {[μ_{s} (\nabla u)}^{T} + λ I t r (\nabla u) - (μ_{s} + λ) \nabla u] \cdot n

(8)

Only elastic deformation is described by equations (3) to (8). Every substance in nature experiences plastic deformation after it has been subjected to a certain amount of stress. The following is the format of the modified governing equation with plastic term:

\nabla \cdot {μ_{s} \nabla (d u) + {μ_{s} [\nabla (d u)]}^{T} + λ I t r [\nabla (d u)] - [2 μ_{s} (d ε_{p}) + λ I t r (d ε_{p})] = 0

(9)

where

d u

and

d ε_{p}

are incremental displacement vector and incremental plastic strain tensor respectively. Equation (10) undergoes similar modification:

T = σ \cdot n \to d T = d σ \cdot n = (2 μ_{s} + λ) \nabla (d u) + μ_{s} {[\nabla (d u)]}^{T} + λ I t r [\nabla (d u)] - (μ_{s} + λ) \nabla (d u) - [2 μ_{s} (d ε_{p}) + λ I t r (d ε_{p})]

(10)

3.4. Discrete adjoint derivative computation

The torque in our example serves as the objective function

f

, and

x

is the vector of design variables. The adjoint method is utilized to quickly determine the total derivatives

d f / d x

. In the discrete technique, it is expected that the primary solver can provide a discretized form of the governing equations and that the design variable vectors

x R^{n_{x}}

and

ω R^{n_{ω}}

satisfy the discrete residual equations

R (ω, x)

= 0, where R

R R^{n_{ω}}

is the residual vector.

Therefore, the relevant functions are functions of the state variable as well as the design variable:

f = R (ω, x)

. Although there are several functions of relevance,

f

is regarded as a scalar in the following derivations to retain generality. Each new function demands the solution of an additional adjoint system, as will become evident later. The total derivative

d f / d x

is derived using the chain rule:

\underset{1 \times n_{x}}{\underset{⏟}{\frac{d f}{d x}}} = \underset{1 \times n_{x}}{\underset{⏟}{\frac{\partial f}{\partial x}}} + \underset{1 \times n_{ω}}{\underset{⏟}{\frac{\partial f}{\partial ω}}} \underset{n_{ω} \times n_{x}}{\underset{⏟}{\frac{d ω}{d x}}}

(11)

When there are no implicit computations, making the estimation of the partial derivatives

\partial f / \partial x

and

\partial f / \partial ω

very simple. On the other hand, because it is implicitly specified by the residual equations

R (ω, x) = 0

, the total derivative matrix

d ω / d x

is expensive.

We may obtain

d ω / d x

using the chain rule for R. We may then exploit this information to our advantage because the governing equations should always hold. Therefore, the derivatives

d R / d x

must amount to zero:

\frac{d R}{d x} = \frac{\partial R}{\partial x} + \frac{\partial R}{\partial ω} \frac{d ω}{d x} = 0 \Rightarrow \underset{n_{ω} \times n_{x}}{\underset{⏟}{\frac{d ω}{d x}}} = - \underset{n_{ω} \times n_{ω}}{\underset{⏟}{{\frac{\partial R}{\partial ω}}^{- 1}}} \underset{n_{ω} \times n_{x}}{\underset{⏟}{\frac{\partial R}{\partial x}}}

(12)

In Eq. (12), substituting

d ω / d x

from Eq. (11) yields:

\underset{1 \times n_{x}}{\underset{⏟}{\frac{d f}{d x}}} = \underset{1 \times n_{x}}{\underset{⏟}{\frac{\partial f}{\partial x}}} - \overset{ψ^{T}}{\overset{⏞}{\underset{1 \times n_{ω}}{\underset{⏟}{\frac{\partial f}{\partial ω}}} \underset{n_{ω} \times n_{ω}}{\underset{⏟}{{\frac{\partial R}{\partial ω}}^{- 1}}}}} \underset{n_{ω} \times n_{x}}{\underset{⏟}{\frac{\partial R}{\partial x}}}

(13)

We may solve the adjoint equation by transposing the state Jacobian matrix

\partial R / \partial ω

and using,

{[\partial f / \partial ω]}^{T}

as the right-hand side.

\underset{n_{ω} \times n_{ω}}{\underset{⏟}{{\frac{\partial R}{\partial ω}}^{T}}} \underset{n_{ω} \times 1}{\underset{⏟}{ψ}} = \underset{n_{ω} \times 1}{\underset{⏟}{{\frac{\partial f}{\partial ω}}^{T}}}

(14)

The adjoint vector is the

ψ

. When we enter the adjoint vector into Eq. 13 after solving this equation, we obtain the total derivative, which is expressed as:

\frac{d f}{d x} = \frac{\partial f}{\partial x} - ψ^{T} \frac{\partial R}{\partial ω}

(15)

Since the design variable is not explicitly stated in Eq. 14, we only need to solve the adjoint equations once for each function of interest. As a result, its computing cost is related to the number of interesting functions rather than being independent of the number of design variables. This strategy, known as the adjoint technique, provides benefits for many design issues in aeronautical engineering when just a small number of functions are of relevance but where several hundred design variables may be used.

The following four essential steps make up a discrete adjoint implementation, which involves computing the partial derivatives and resolving the adjoint equations:

1) Figuring out the partial derivatives

{[\partial f / \partial ω]}^{T}

and

{[\partial R / \partial ω]}^{T}

2) The adjoint vector

ψ

in the linear Eq. 12 solution.

3) The method of computing the partial derivatives

\partial f / \partial x

and

\partial R / \partial x

4) Calculate the total derivative

d f / d x

using Eq 15.

The four approaches outlined above don't need a specific residual function

R (ω, x)

therefore they may be used with any collection of discrete PDEs.

3.5. Aero-structural coupling

The adjoint formulation indicated above assumes that the state variables of the Finite Element Method (FEM) and Computational Fluid Dynamics (CFD) are combined and solved concurrently, which will result in a bigger Jacobian matrix and increased memory use. To get around this, we solve the aero-structural adjoint in a linked way using a different technique called block Gauss-Seidel, as shown below.

[\begin{matrix} {\frac{\partial R_{C F D}}{\partial w_{C F D}}}^{T} & {\frac{\partial R_{F E M}}{\partial w_{C F D}}}^{T} \\ {\frac{\partial R_{C F D}}{\partial w_{F E M}}}^{T} & {\frac{\partial R_{F E M}}{\partial w_{F E M}}}^{T} \end{matrix}] [\begin{matrix} Ψ_{C F D} \\ Ψ_{F E M} \end{matrix}] = [\begin{matrix} {\frac{\partial f}{\partial w_{C F D}}}^{T} \\ {\frac{\partial f}{\partial w_{F E M}}}^{T} \end{matrix}]

(16)

The abbreviations CFD and FEM, which stand for computational fluid dynamics and finite element method, respectively, refer to the residual and state variables for the solvers. We use DAFoam to solve the CFD adjoint equation:

{\frac{\partial R_{C F D}}{\partial w_{C F D}}}^{T} Ψ_{C F D} = {\frac{\partial f}{\partial w_{C F D}}}^{T}

(17)

According to Kenway et alstudy .'s [29], DAFoam uses a technique known as Jacobian-free adjoint, where automated differentiation is employed to compute partial derivatives and matrix-vector products. DAFoam employs the generalized minimum residual (GMRES) iterative linear equation solver from the PETSc package to solve the adjoint equation [30]. DAFoam employs a layered technique using the additive Schwartz method for global preconditioning, and an incomplete lower and upper (ILU) factorization method with one level of fill-in is utilized for local preconditioning.

The preconditioner matrix

{[\partial R / \partial w]}_{R C}^{T}

is produced to improve convergence by estimating the residuals and linearizing them [31]. Since constructing

{[\partial R / \partial w]}_{R C}^{T}

takes up around 30% of the adjoint runtime, this matrix is only created once and then utilized for the adjoint equation. This results in a considerable decrease in adjoint runtime. The adjoint equation for the FEM component is solved using TACS:

{\frac{\partial R_{F E M}}{\partial w_{F E M}}}^{T} Ψ_{F E M} = {\frac{\partial f}{\partial w_{F E M}}}^{T}

(18)

Without explicitly creating the matrix, automated differentiation is used to determine the non-diagonal portions of the matrix multiplied by a vector.

Using OpenMDAO and MPhys, the aero-structural system was created in a modular manner for adaptability. The components in Figure 1 needed to multiply the state Jacobian matrix by a particular vector and implement ways to compute output based on input. The adjoint total derivative computation was unified by OpenMADO using the MAUD algorithm [32]. In OpenMDAO, a linear block Gauss-Seidel solver with Aitken relaxation was employed to solve the coupled adjoint of CFD and FEM.

3.6. Baseline geometry configuration

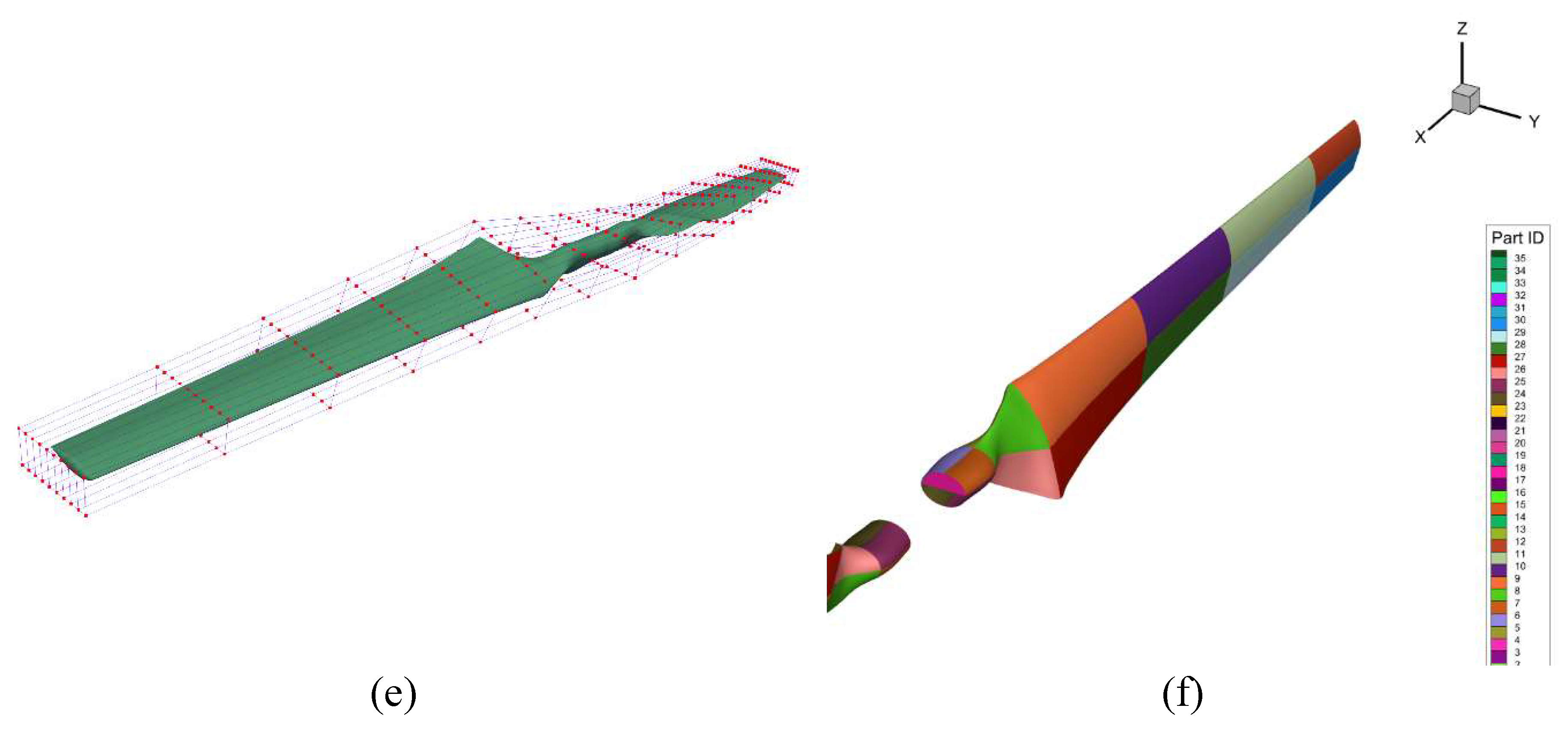
As in our earlier research [33], we used the NREL Phase VI, which has just two blades, as the baseline geometry in this investigation. Regarding the aerodynamic component, the surface mesh as shown in Fig. 3 (c) is constructed in ICEM CFD, and the spherical volume mesh as shown in Fig. 3 (a) is created by extruding the structured surface mesh using the open-source mesh generator pyHyp [34]. Fig. 3 depicts the hyperbolic expansion layer that surrounds the wind turbine blade (b). Additionally, MSC Patran generates a structural finite-element mesh that matches the shape of the outer mold line and incorporates an interior main shear web as seen in Fig. 3 (d). The whole collection of structural elements is made up of thin CQUAD hexahedral shell elements. At the root, which is situated at a distance of about 0.66 from the rotating axis, two identical blades are fastened. In Fig. 3 (e), the FFD points for the aerodynamic optimization are presented, and the aerodynamic form optimization is put into practice. In contrast, Fig. 3 (f) shows the structural design factors as a total of 60 panels with random colors.

3.7. Mesh convergence and validation

Based on the Multi Reference Frame (MRF), a steady-state method used in computational fluid dynamics (CFD) to describe problems with rotating components, a mesh convergence study has been conducted using three levels of mesh: L0, L1, and L2, as shown in Table 2. The wind speed is 7 m/s and the rotor's rotating speed is 72 pm. In order to maintain a value of y+ close to 1, the growth ratio is set to 1.2 and the initial cell height away from the turbine surface is set to 0.00003 m. y+ is the non-dimensional distance from the wall to the first mesh node, and the superscript cross denotes normalization with the axis that used to be the distance.

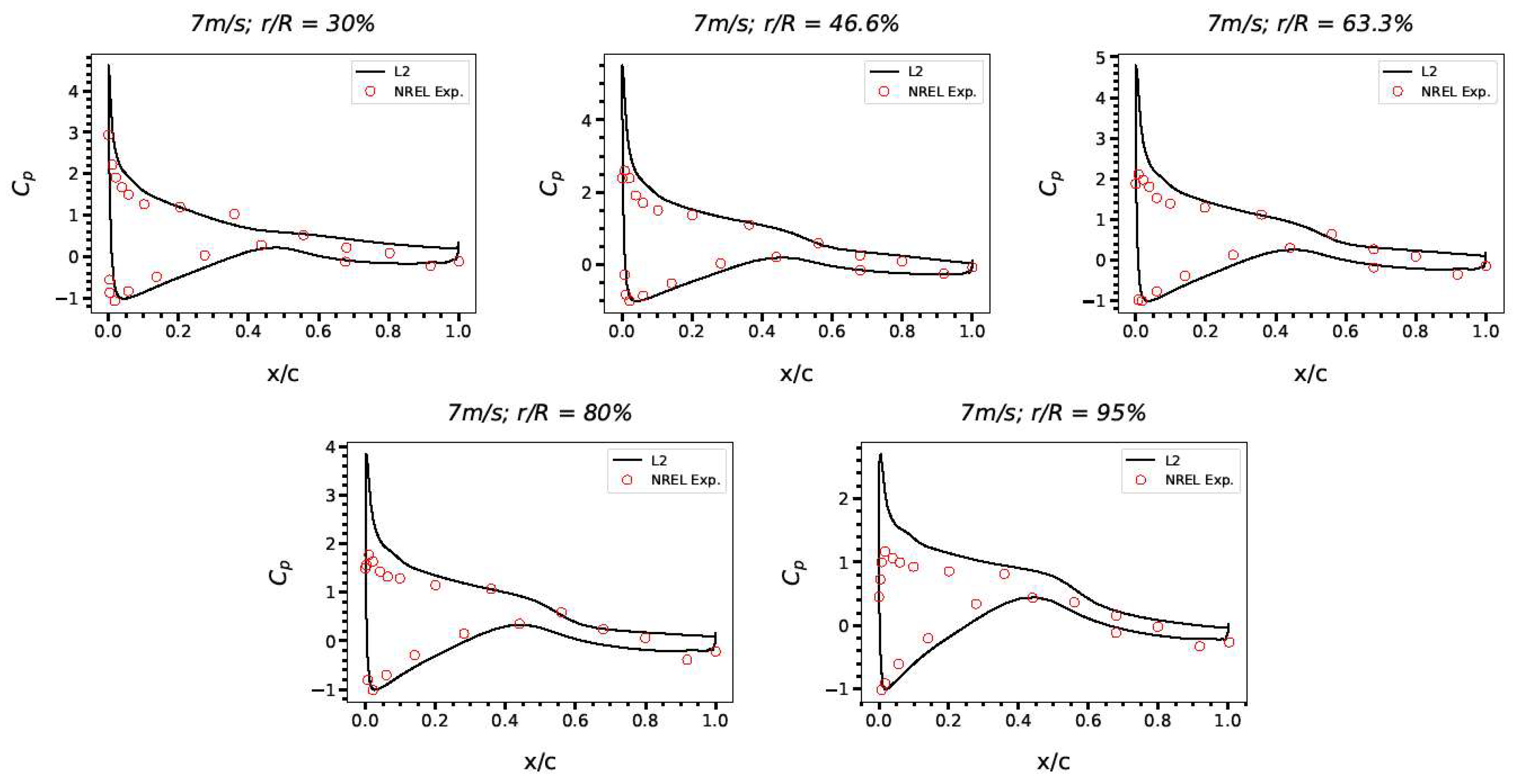
According to Table 2, the torque errors for the three mesh L0, L1, and L2-based CFD simulations are 5.35 percent, 10.19 percent, and 13.63 percent, respectively, when compared to the NREL experimental value. However, owing to the high cost of computing, L2 mesh is utilized in our optimization.

As shown in Fig. 4, the estimated Cp distribution from the CFD simulation using the L2 mesh at the following spans: 30%, 47, 63, 80, and 95% is compared with the experimental data from NREL. The experimental result and the CFD findings agree.

4. Results and Discussion

The configuration for aero-structural optimization is summarized in Table 3. While the structural optimization seeks to minimize mass, the aerodynamic optimization is more concerned with torque. Figure 3 shows a body-fitted FFD box for the blade (e). Only the top 6 layers of FFD points are permitted to shift, creating 240 form variables for the blade as a consequence. This prevents mesh quality issues. Several geometric and physical restrictions, such as a minimal blade volume restriction to prevent the blade volume from falling below three times its baseline volume and thickness restrictions to prevent the blade from becoming too thin, are used to assure practical design.With a maximum non-orthogonality and skewness of 78 degrees and 5.8, respectively, two mesh quality limits are placed on the volume mesh deformation to handle mesh deformation issues. The mesh quality values are calculated using the OpenFOAM checkMesh function, and the constraint derivatives are automatically differentiated using DAFoam. In order to prevent structural failure, an aggregated von-Mises stress limitation is applied together with a panel thickness constraint. The stress constraint value, which is an approximate maximal stress value normalized by the material yield stress, is calculated using the Kreisselmeier-Steinhauser function.

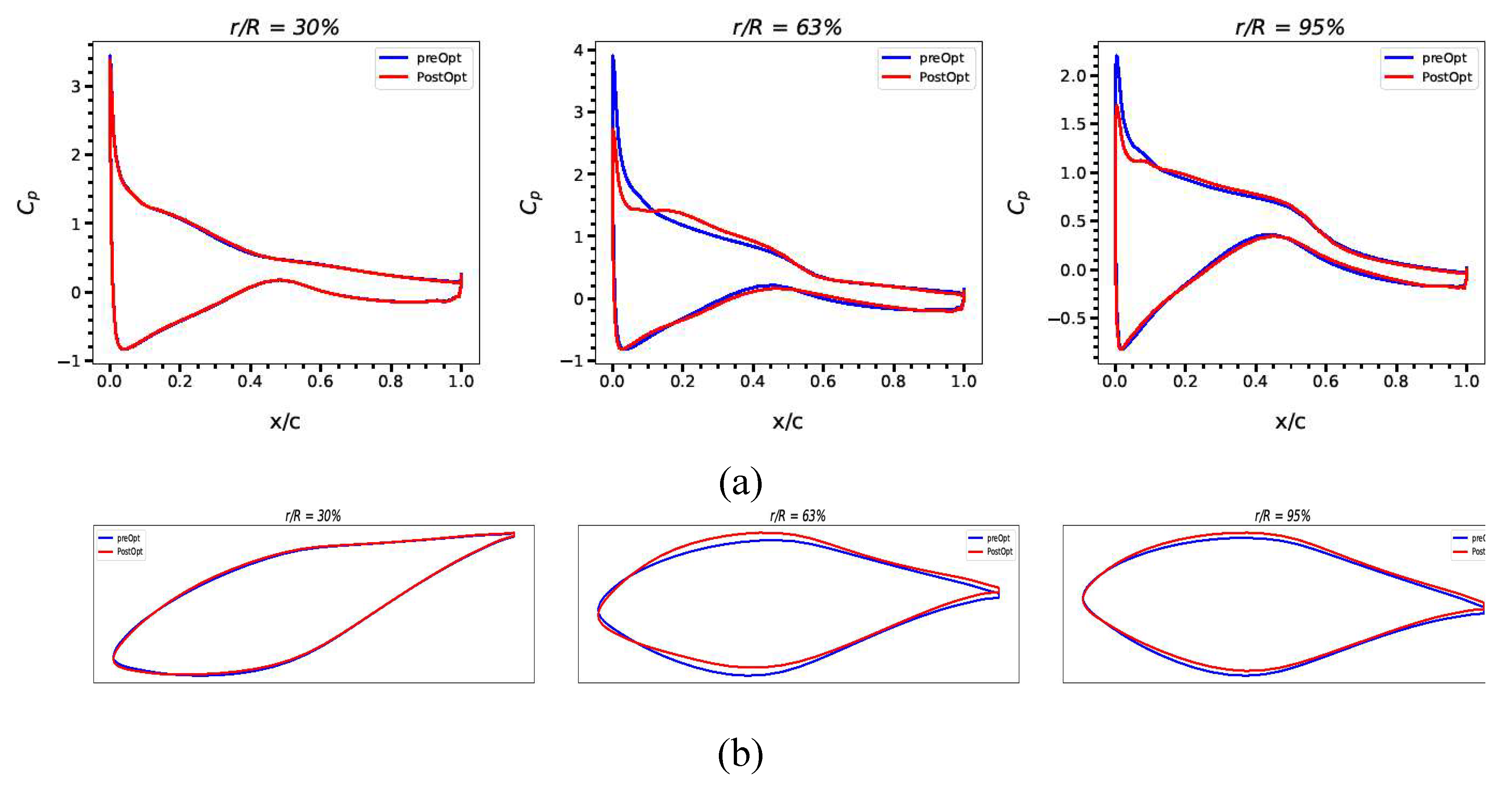
Figure 6 (a) shows that following optimization, the pressure coefficient varies more significantly closer to the tip while being more stable farther away from the root. The cross-section profile of the blade in terms of the three separate sections along the blade is also shown in Figure 6. (b) before and after the optimization. The leading edge and middle portion are improved to provide greater aerodynamic performance.

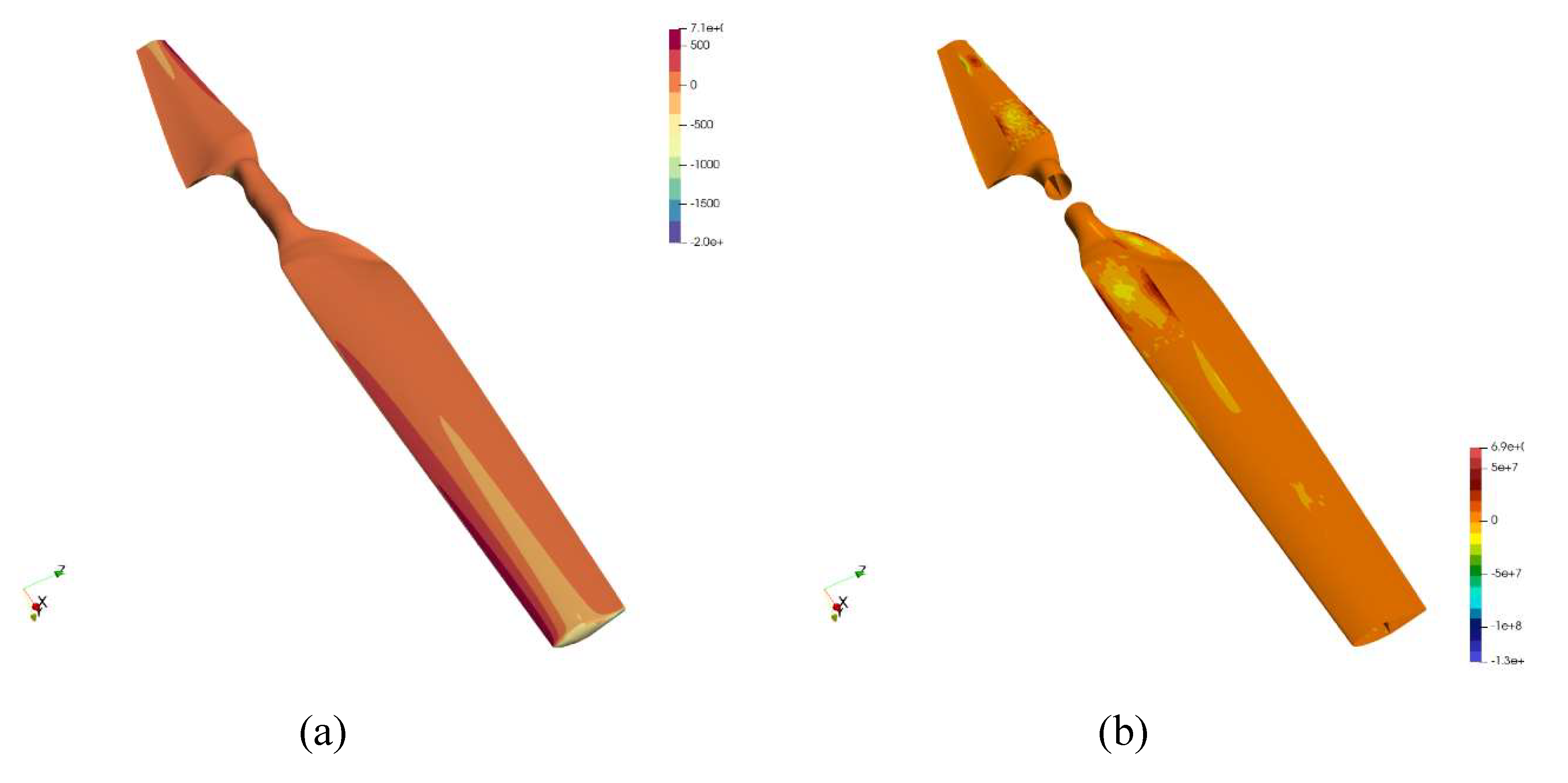
Figure 5. (a) Pressure on the blade on the aerodynamic side; (b) Stress on the structural side.

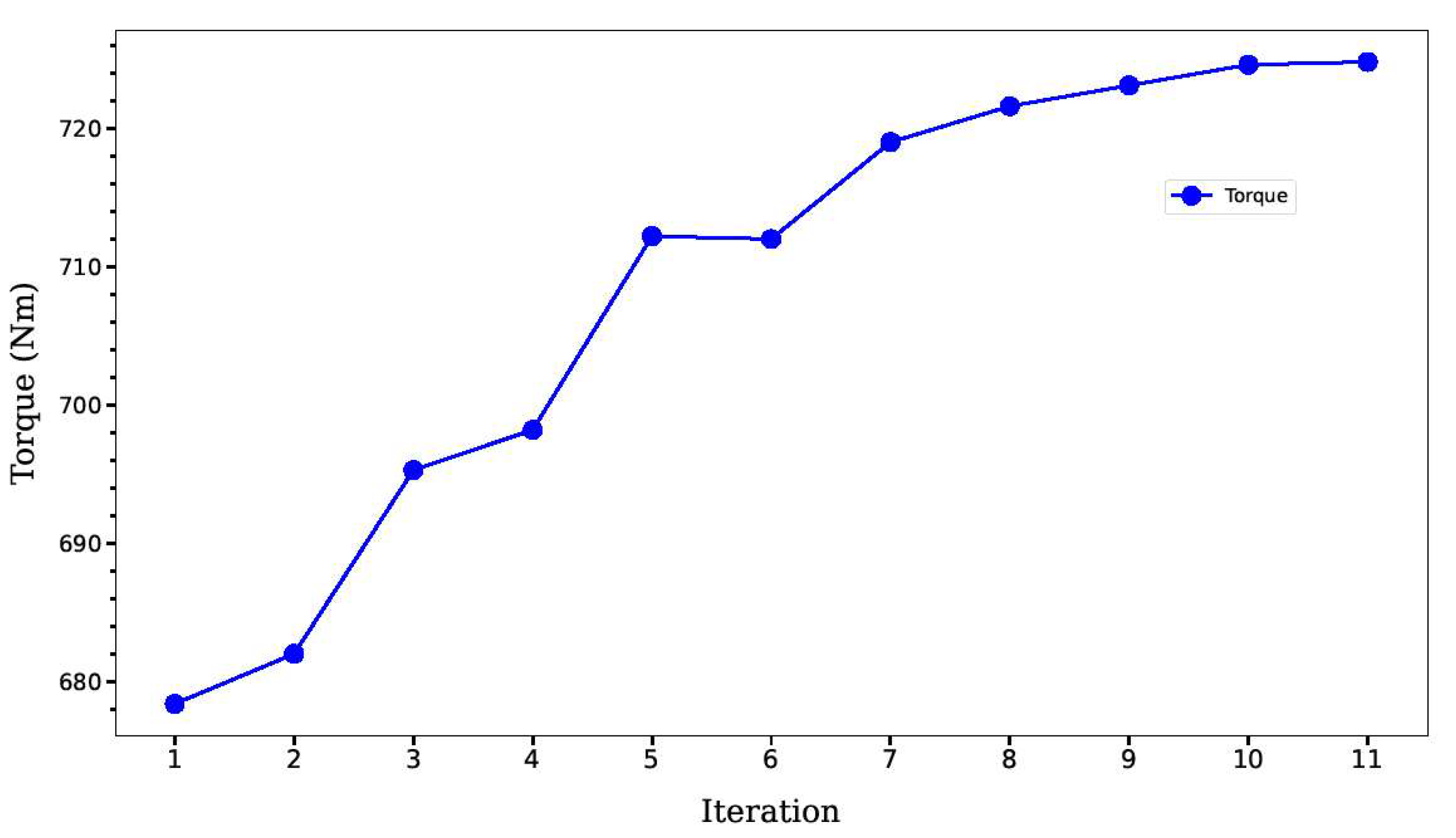
Torque was increased by around 6.78 percent as the main goal of the aerodynamic portion of the aero-structural optimization. The torque production of the wind turbine blade has increased by around 6.78 percent as a result of this optimization procedure. The optimization of the blade's form is responsible for the increase in torque. By improving this aspect, the airflow around the blade may be better managed, which improves the efficiency with which wind energy is transferred to the turbine blades.

The wind turbine's total efficiency and power production have significantly increased thanks to the 6.78 percent rise in torque output. Since the turbine can produce more electricity with the same quantity of wind, this improved efficiency may result in lower energy prices. The optimization procedure may also result in lower maintenance costs due to decreased component wear and tear brought on by better efficiency.

The term "optimization" in the context of blade design refers to the process of changing different blade design parameters in order to accomplish a certain objective. In this instance, the objective is to reduce the blade's bulk while preserving its structural integrity. In order to do this, Mphys is used to shift the aerodynamic load on the blade to its structural component. To distribute the weight properly and lessen stress concentrations, the blade's panels' thickness must be changed.

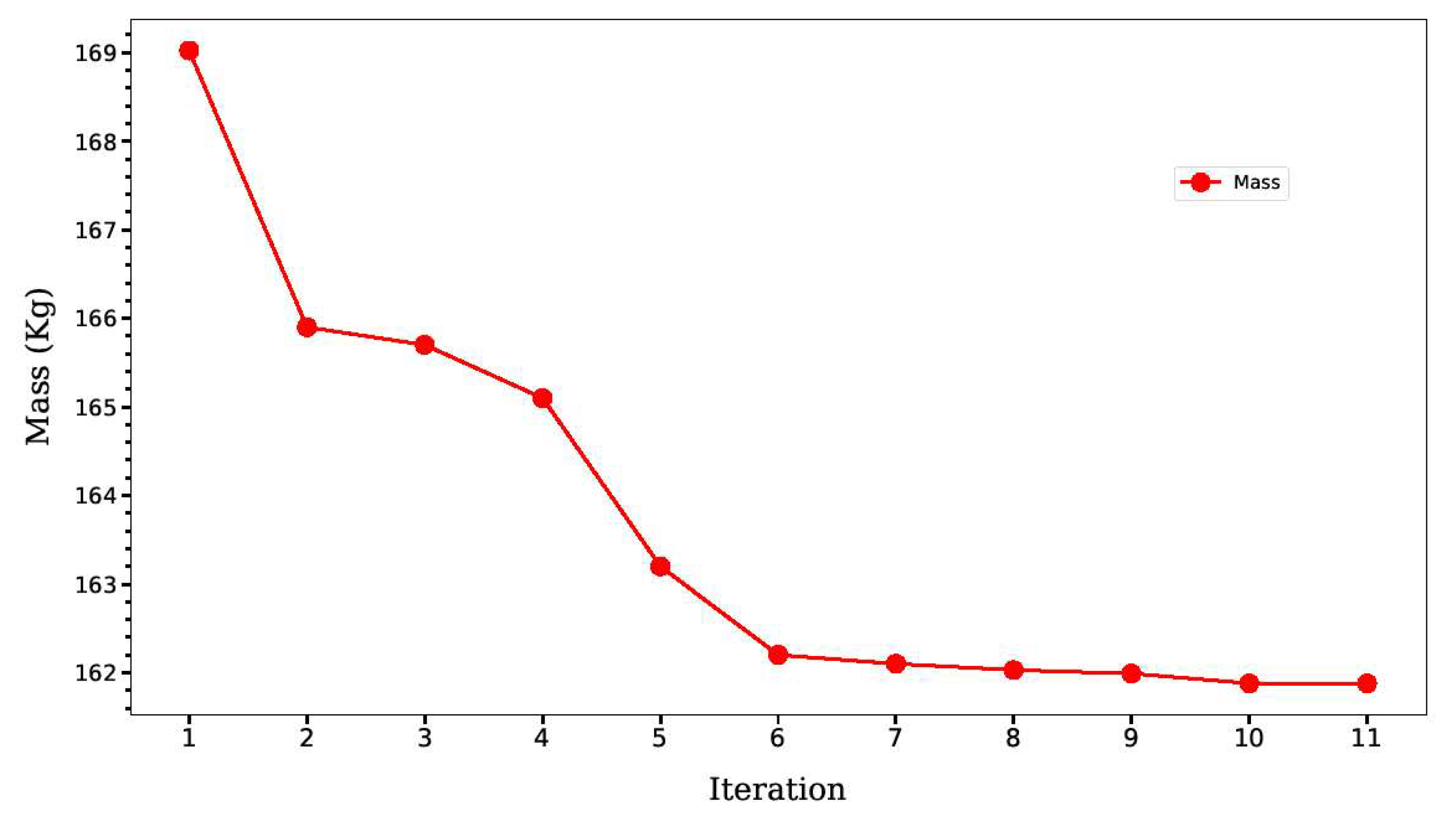
The mass of the blade is continuously measured and recorded throughout the optimization process. The findings are shown in Figure 8, which indicates that with each optimization step, the mass of the blade reduces. After the sixth iteration, the rate of decline slows down, indicating that future tweaks would not result in substantial mass reductions. The mass of the blade has also decreased by 4.22 percent as a consequence of the optimization process, which has the potential to significantly increase the turbine's performance and efficiency.

5. Conclusions

This research has offered an analysis of a wind turbine blade's aero-structural optimization. For the aerodynamic portion of the study, DAFoam software was used, while TACs was used for the structural portion. The OpenMDAO framework was used to implement the fluid-structure interaction between the CFD and FEM. Torque was the goal for the aerodynamic component, while mass reduction was the goal for the structural component.

The findings of the optimization revealed a 6.78 percent increase in torque and a 4.22 percent decrease in mass. These findings show that the aero-structural optimization strategy can significantly boost the efficiency of wind turbine blades. The weight of the turbine may be made lighter overall by lowering the mass of the blade, which lowers the cost of production and shipping. Additionally, a higher torque can boost the turbine's energy production, increasing its effectiveness.

The OpenMDAO framework's integration of DAFoam, TACs, and Mphys made it possible to analyze the wind turbine blade in its whole. The combination of these software tools made it easier to combine the structural and aerodynamic properties of the blade, allowing for design optimization. The outcomes of the optimization show how crucial it is to take into account both the structural and aerodynamic properties of wind turbine blades when designing them.

In conclusion, this work has shown how aero-structural optimization may enhance the performance of wind turbine blades. The optimization's results show that by reducing the bulk of the blade, there is the possibility for considerable increases in energy output and cost savings. Future research might concentrate on improving the optimization method's effectiveness and determining whether it can be used with different kinds of wind turbines.

Author Contributions

Yong Zhao oversees the project and provides the fund as well as the equipments; Sagidolla Batay developed the geometry, CFD analysis and optimization process and wrote the manuscript. Aigerim Baidullayeva assisted with the mesh generation and manuscript. Yong Zhao, Dongming Wei reviewed and edited the manuscript.

Funding

This study is funded by Nazarbayev University through a FDCR grant No. 20122022FD4126.

Data Availability Statement

Data are available upon request to the first author (shaheidula.batai@nu.edu.kz).

Acknowledgments

The authors would like to thank Nazarbayev University for the financial support for this work through a FDCR grant No. 20122022FD4126.

Conflicts of Interest

The authors declare that they have no conflict of interest.

References

Masson-Delmotte, V. , Zhai, P., Pörtner, H.-O., Roberts, D., Skea, J., Shukla, P. R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., “Global warming of 1.5 C. An IPCC Special Report on the impacts of global warming of 1.5°C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty.” Tech. rep., Intergovernmental Panel on Climate Change (IPCC), 2018.
Zhou Y, Luckow P, Smith SJ, Clarke L. Evaluation of Global Onshore Wind Energy Potential 17 and Generation Costs. Environ Sci Technol. 2012, 46, 7857–7864. [Google Scholar] [CrossRef] [PubMed]
Jacobson MZ, Delucchi MA. A Path to Sustainable Energy by 2030. Sci Am. 2009, 301, 58–65. [Google Scholar] [CrossRef] [PubMed]
Şahin, AD. Progress and recent trends in wind energy. Progress in Energy and Combustion Science. 2004, 30, 501–43. [Google Scholar] [CrossRef]
Ackermann T, Söder L. An overview of wind energy-status 2002. Renew Sustainable Energy Rev. 2002, 6, 67–127. [Google Scholar] [CrossRef]
IEA-ETSAP, IRENA. Wind Power: Technology Brief. 2016.
Muskulus, Michael, and Sebastian Schafhirt. Design optimization of wind turbine support structures-a review. Journal of Ocean and Wind Energy 2014, 1, 12–22. [Google Scholar]
Baños R, Manzano-Agugliaro F, Montoya F, Gil C, Alcayde A, Gómez J. Optimization methods applied to renewable and sustainable energy: a review. Renew Sustain Energy Rev 2011, 15, 1753–66. [Google Scholar] [CrossRef]
Lei M, Shiyan L, Chuanwen J, Hongling L, Yan Z. A review on the forecasting of wind speed and generated power. Renew Sustain Energy Rev 2009, 13, 915–20. [Google Scholar] [CrossRef]
Ramirez-Rosado IJ, Fernandez-Jimenez LA, Monteiro C, Sousa J, Bessa R. Comparison of two new short-term wind-power forecasting systems. Renew Energy 2009, 34, 1848–54. [Google Scholar] [CrossRef]
Costa A, Crespo A, Navarro J, Lizcano G, Madsen H, Feitosa E. A review on the young history of the wind power short-term prediction. Renew Sustain Energy Rev 2008, 12, 1725–44. [Google Scholar] [CrossRef]
Sfetsos, A. A comparison of various forecasting techniques applied to mean hourly wind speed time series. Renew Energy 2000, 21, 23–35. [Google Scholar] [CrossRef]
Zhang Y, Wang J, Wang X. Review on probabilistic forecasting of wind power generation. Renew Sustain Energy Rev 2014, 32, 255–70. [Google Scholar] [CrossRef]
Miller A, Chang B, Issa R, Chen G. Review of computer-aided numerical simulation in wind energy. Renew Sustain Energy Rev 2013, 25, 122–34. [Google Scholar] [CrossRef]
Serrano González J, Burgos Payán M, Santos JMR, González-Longatt F. A review and recent developments in the optimal wind-turbine micro-siting problem. Renew Sustain Energy Rev 2014, 30, 133–44. [Google Scholar] [CrossRef]
Chen Z, Blaabjerg F. Wind farm—a power source in future power systems. Renew Sustain Energy Rev 2009, 13, 1288–300. [Google Scholar] [CrossRef]
Yang, X. , Wang, X., Wang, Q., Huang, B., Sørensen, J. N. Aero-structural design optimization of wind turbine blades using high-fidelity CFD and FEA. Renewable Energy 2019, 133, 1012–1026. [Google Scholar] [CrossRef]
Kirschner, M. , Luo, J., & Martins, J. R. R. A. Adjoint-based multidisciplinary design optimization using OpenMDAO. Progress in Aerospace Sciences 2021, 119, 100667. [Google Scholar] [CrossRef]
Ping He, Charles A. Mader, Joaquim R.R.A. Martins, Kevin J. Maki. DAFoam: An open-source adjoint framework for multidisciplinary design optimization with OpenFOAM. AIAA Journal 2020, 58, 2020. [Google Scholar] [CrossRef]
Boopathy, K.; Kennedy, G.J. Parallel Finite Element Framework for Rotorcraft Multibody Dynamics and Discrete Adjoint Sensitivities. 2019. [CrossRef]
Gray, J.S.; Hwang, J.T.; Martins, J.R.R.A.; Moore, K.T.; Naylor, B.A. OpenMDAO: An Open-Source Framework for Multidisciplinary Design, Analysis, and Optimization. Structural and Multidisciplinary Optimization 2019. [CrossRef]
Yan, Z. , Wang, J., Li, Q., Wang, X. Aero-structural design optimization of wind turbine blades using DAFoam and OpenMDO. Journal of Renewable and Sustainable Energy 2022, 14, 023304. [Google Scholar] [CrossRef]
Aerostructural wing optimization of a regional jet considering mission fuel burn N. Bons, J. R. R. A. Aerostructural wing optimization of a regional jet considering mission fuel burn N. Bons, J. R. R. A. Martins, F. Odaguil, and A. P. C. Cuco ASME Open Journal of Engineering, 1011046, 2022. [CrossRef]
Multidisciplinary design optimization framework with coupled derivative computation for hybrid aircraft. A. Sgueglia, ro, P. Schmollgruber, N. Bartoli, E. Benard, J. Morlier, J. Jasa, J. R. R. A. Martins, J. T. Hwang, and J. S. Gray, Journal of Aircraft, 57(4):715–729, 2020. [CrossRef]
Lafage, R. , Defoort, S. In AIAA Aviation 2019 Forum (p. 2990.
Borah, D. , Kenway, G., Martins, J.R.R.A., Alonso, J.J. MACH: An Open-Source, High-Fidelity Framework for Aircraft Multidisciplinary Design Optimization. Aerospace 2018, 5, 121. [Google Scholar] [CrossRef]
Kenway, G. K. , Martins, J. R. R. A., & Alonso, J. J. (2016). MACH-Aero: A tool for multidisciplinary analysis and optimization of aircraft configurations with lifting surfaces. 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, AIAA SciTech Forum, (p. 0568).
Spalart, P. R. , & Allmaras, S. R. (1994). A one-equation turbulence model for aerodynamic flows. La Recherche Aerospatiale, 1-21.
Kenway, G. K. W. , Mader, C. A., He, P., and Martins, J. R. R. A. Effective adjoint approaches for computational fluid dynamics. Progress in Aerospace Sciences 2019, 110, 100542. [Google Scholar] [CrossRef]
Balay, S. , Abhyankar, S., Adams, M. F., Brown, J., Brune, P., Buschelman, K., Dalcin, L., Dener, A., Eĳkhout, V., Gropp, W. D., Kaushik, D., Knepley, M. G., May, D. A., McInnes, L. C., Mills, R. T., Munson, T., Rupp, K., Sanan, P., Smith, B. F., Zampini, S., Zhang, H., and Zhang, H., “PETSc Users Manual,” Tech. Rep. ANL-95/11 - Revision 3.10, Argonne National Laboratory, 2018. [CrossRef]
He, P. , Mader, C. A., Martins, J. R. R. A., and Maki, K. J., “An Aerodynamic Design Optimization Framework Using a Discrete Adjoint Approach with OpenFOAM,” Computers & Fluids, Vol. 168, 2018, pp. 285–303. [CrossRef]
Martins, J. R. , andHwang, J. T. Reviewand unification of methods for computing derivatives of multidisciplinary computational models. AIAA journal 2013, 51, 2582–2599. [Google Scholar] [CrossRef]
Batay S, Kamalov B, Zhangaskanov D, Zhao Y, Wei D, Zhou T, Su X. Adjoint-Based High-Fidelity Concurrent Aerodynamic Design Optimization of Wind Turbine. Fluids 2023, 8, 85. [Google Scholar] [CrossRef]
Secco, N.; Kenway, G.K.W.; He, P.; Mader, C.A.; Martins, J.R.R.A. Efficient Mesh Generation and Deformation for Aerodynamic Shape Optimization. AIAA Journal 2021. [CrossRef]

Figure 1. MACH optimization framework's XDSM diagram.

Figure 2. Profile for multidisciplinary design optimization.

Figure 3. a) Spherical volume mesh; b) Hyperbolic expansion layer; c) Aerodynamic surface mesh; d) Structural mesh; e) FFD points for aerodynamic optimization; f) Structural design variables (in terms of panels with random colors).

Figure 4. Comparison of the pressure coefficients (Cp) from Level 2 mesh and NREL Experimental data.

Figure 6. (a) Cp comparisons before and after the optimization in terms of 30 %, 63% and 95% spanwise section; (b) Shape changes in the cross-section profiles accordingly.

Figure 7. The torque optimization during the aero-structural optimization .

Figure 8. The mass optimization during the aero-structural optimization .

Table 1. Boundary conditions.

Boundary Conditions	blade	inout
Epsilon	epsilonWallFunction	inletOutlet
Nut	nutUSpaldingWallFunction	fixedValue
nuTilda	fixedValue	inletOutlet
K	kqRWallFunction	inletOutlet
Omega	omegaWallFunction	inletOutlet
P	zeroGradient	fixedValue
U	fixedValue	inletOutlet

Table 2. Mesh convergence by comparing the torque result from simulation against experimental value.

Mesh#	L0	L1	L2	NREL Exp.
Mesh type	Fine mesh	Medium mesh	Course mesh	-
Cells (million)	25.3	10.12	2.53	-
Torque (Nm)	743.2	705.1	678.4	785
Error (%)	5.35	10.19	13.63	-

Table 3. Overview of the aero-structural optimization cases.

	Aero-structural optimization
	Aerodynamic optimization	Structural optimization
Objective function	Torque	Mass
Design variables	Blade shape in terms of FFD points	Panel thickness
Constraints	Volume and thickness	Panel thickness and von-mises stress
Quantity of the design variables	240 FFD points	60 panels
Optimization by percentage	↑ 6.78%	↓ 4.22%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer