Prerpints.org logo
Preprint
Article

Microstructures and Deformation Mechanism of Hetero-Structured Pure Titanium under High Strain Rate

Altmetrics

Downloads

104

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

13 October 2023

Posted:

17 October 2023

You are already at the latest version

Alerts
Abstract
This study investigates the microstructures and deformation mechanism of hetero-structured pure titanium under different high strain rates (500 s-1，1000 s-1，2000 s-1). The influence of strain rate on the deformation mechanism is examined. As the strain rate increases, the dominance of dislocation slip decreases while deformation twinning becomes more prominent. Notably, at a strain rate of 2000s-1, nanoscale twin lamellae are activated within grain with a size of 500nm, which is a rarely observed phenomenon in pure Ti. Additionally, martensitic phase transformation is also identified. These findings can greatly enhance our understanding of the mechanical responses of Ti and broaden the potential applications of Ti in dynamic deformation scenarios.
Keywords: 
Subject: Engineering  -   Metallurgy and Metallurgical Engineering

1. Introduction

The usage of pure titanium has been steadily increasing in the fields of chemical, biomedical, and aerospace engineering. This is primarily due to its exceptional corrosion resistance, excellent biological compatibility, and impressive high specific strength[1,2]. As a structural material, pure titanium not only encounters static loads but also confronts challenges from high-speed impact loads. Structural components in industries such as aerospace and defense industries may inevitably be involved in high-speed collision events. Compared to static loading, the mechanical properties and deformation mechanisms of titanium and its alloys undergo significant changes under dynamic loading conditions, especially at high strain rates[3]. Therefore, conducting thorough investigation on the deformation mechanisms of pure titanium at high strain rates is of great significance for promoting the extensive utilization of pure titanium.
Previous studies have indicated that the deformation mechanisms of pure titanium are affected by various factors, including its inherent characteristics (grain size, alloying elements, texture, etc.) and experimental conditions (loading mode, strain rate, temperature, strain level, etc.)[4,5,6,7,8]. In particular, strain rate plays a significant role and significantly influences the deformation behavior of materials. It has been found that higher strain rate facilitates the activation of twinning[9,10]. This is because high strain rate promotes the rapid accumulation of dislocations in localized regions, leading to severe stress concentration. These stress concentration regions provide effective nucleation sites for twinning. [11] t is worth noting that at high strain rates, the heat dissipation process in titanium is relatively slower compared to heat generation. This results in thermal softening during the accumulation of plastic deformation[3]. Consequently, instabilities in plastic flow and the formation of shear bands are observed, exerting a significant impact on the deformation mechanism. In addition, the influence of crystallographic texture on the mechanical behavior and deformation mechanism of pure titanium cannot be underestimated, owing to its low symmetry. Extensive research has revealed that the presence of two distinctly different initial textures results in varying mechanical responses[12].
Besides to strain rate, deformation mechanism of pure titanium also has a strong grain size dependency[13]. Currently, high-speed deformation studies of pure titanium primarily focus on samples with large grain sizes, where deformation are mainly dominated by dislocation slip and various types of twinning[12,14]. However, there has been limited experimental research conducted on the high-speed deformation of pure titanium with hierarchical grain size, thereby impeding an in-depth investigation into grain size effect. In recent years, an innovative approach, microstructural heterogenization, has emerged in the field of materials science. This strategic paradigm has demonstrated a remarkable synergy in enhancing mechanical properties in pure Ti [15]. By incorporating heterogenization in grain size, ranging from coarse to ultra-fine regime, this structure can be served as an ideal model for studying the mechanism change during high-speed deformation processes.
Therefore, this study focuses on hetero-structured pure titanium samples with a hierarchical grain size. A room temperature split Hopkinson pressure bar test was conducted to examine the dynamic mechanical responses of the samples at different strain rates. Microstructural evolution during deformation was characterized using electron backscattering diffraction (EBSD) and transmission electron microscopy (TEM) techniques. Microstructures and deformation mechanism of hetero-structured pure titanium were systematically investigated, with a particular focus on exploring the influence of grain size on twinning under high strain rates.

2. Experimental

In this study, a split Hopkinson pressure bar (ALT1000) compression test was conducted to analyze the mechanical responses of the sample. The compression was performed along the ND (normal direction) axis of Ti samples at room temperature and the compression rate was controlled by adjusting the gas pressure. This allowed for data collection on the sample's dynamic mechanical response at different strain rates (500 s-1, 1000 s-1, 2000 s-1). A schematic diagram of the Hopkinson impact test is illustrated in Figure 1a-1. Figure 1a-2 displays the observation surface of the sample in the transverse direction (TD) plane. Commercially pure titanium was chosen as the material for this investigation. To prepare the initial hetero-structured pure titanium samples with hierarchical grain sizes, a combination of rolling and annealing techniques was employed. The titanium samples underwent cold rolling at 80% reduction, followed by annealing at 480 °C for 5 minutes under vacuum conditions. EBSD observations were carried out using a Zeiss Auriga scanning electron microscope (SEM) with an acceleration voltage of 15 kV and a step size of 50 nm. TEM characterization was performed using FEI TEM at 200 kV. Figure 1b presents the EBSD results of the hetero-structured pure titanium sample. The grain size exhibits a bimodal distribution, with an average grain size of 580 nm for the ultrafine grains and 2.14 μm for the coarse grains (Figure 1b-3). Twinning was not observed in the sample. The grain boundary orientation distribution map (Figure 1b-2) reveals that the proportion of low angle grain boundaries (LAGBs) in the sample is approximately 19.5 %. This indicates that the material has undergone significant recovery of dislocations during the annealing process.

3. Results and Discussion

Figure 2a presents the Hopkinson impact mechanical curves of the hetero-structured pure titanium samples deformed under strain rates of 500 s-1, 1000 s-1, 2000 s-1. It can be observed that the dynamic compressive stress increases continuously with increasing strain, indicating that the sample absorbs impact energy during the impact process. It is important to note that the rapid decrease in flow stress at the end of the curve is due to the termination of the load applied to the Hopkinson bar, rather than material failure. To obtain the true stress-strain curve, it can be calculated based on the compressive engineering stress-strain curve, as depicted in Figure 2b. This relationship can be described as follows:
σ t = σ e ( 1 − ε e )
ε t = − I n ( 1 − ε e )
where σ t and ε t represent the true stress and strain, σ e and ε e represent engineering stress and strain. It can be observed that the increase in true stress is not significant with increasing strain, but there is a noticeable oscillatory pattern. This oscillatory pattern arises stress vibrations which occur when an elastic wave, caused by an impact from a hammer in the test machine, propagates through the test sample and is detected by the load cell[16]. Figure 2c shows the strain hardening capacity of hetero-structured sample under different strain rates, and this is closely related to the deformation mechanism. It can be found that sample subjected to a strain rate 2000 s-1 exhibits a comparatively superior strain hardening capacity. In Figure 2d, the variation trends of different mechanical performance indicators with strain rate are illustrated. It can be seen that the corresponding yield strength (YS), ultimate compressive strength (UCS) and uniform elongation (UE) increase with the increase of strain rate.
During high-speed deformation, a significant portion of the plastic deformation energy is converted into heat energy. Due to insufficient heat dissipation, noticeable local temperature rise occurs, leading to thermal softening of the material. The influence of temperature on the deformation mechanism of the material is crucial, making it necessary to discuss the impact of temperature rise during high-speed deformation. Assuming that all the plastic deformation energy is completely converted into heat energy and not dissipated, the adiabatic temperature rise can be expressed as:
∆ T = β ρ C v ∫ 0 ε f σ T d ε T
where ρ is density, and C v specific heat capacity. σ t and ε t represent the true stress and strain, ε f   is the max strain.   β is a constant known as the Taylor-Quinney factor, which represents the coefficient of plastic deformation work converted into heat. The values of ρ , C v , β are ρ = 4.51 g/cm3, C v = 527 J/(kg·℃), β =0.9[17]. The calculated results base on Equation (3) are shown in Figure 3. At a strain rate of 500 s-1, the theoretical temperature rise is approximately 10 K. As the impact rate increases, the total strain also increases, resulting in an increase in the plastic deformation energy of the corresponding sample and a corresponding increase in adiabatic temperature rise. When the strain rate reaches 2000 s-1, the corresponding theoretical temperature rise is approximately 45 K. Although the temperature rise increases significantly with the strain rate, it is far from reaching the recrystallization temperature. Therefore, we believe that temperature rise of here has little effect on the deformation mechanism, and the emphasis is on the effect of stress.
Figure 4 presents the EBSD results of hetero-structured pure titanium subjected to various strain rates. From the IPF maps depicted in Figure 4a-1, b-1, and c-1, it is evident that the microstructure remains its hetero-structured nature without any signs of recrystallization or significant grain refinement within the samples. After impact tests, a noticeable occurrence of twinning is observed. Through analyzing the orientation differences (Figure 4a-3, b-3, c-3), it can be observed that the predominant twinning type in the three deformed samples is { 11 2 ¯ 2 } compression twins[18]. For pure titanium with HCP structure, { 11 2 ¯ 2 } twinning is activated more readily when the lattice experiences stress along the c-axis[19]. As depicted in the twin boundary map (Figure 4a-2, b-2, c-2), an increase in the percentage of twin boundaries, from 5.4% to 6.2% and 8.6%, is observed when the strain rate increases from 500 s-1 to 1000 s-1 and 2000 s-1. The percentage of twin boundaries is determined by calculating the areal fractions of twin boundaries among all interfaces within the EBSD maps. It is noteworthy that at relatively low strain rates (500 s-1), twinning only occurs in coarse grains due to the notable influence of grain size on twinning behavior in pure titanium[20,21]. However, when the grain size is refined to the ultrafine range, twinning is nearly absent. Only at a strain rate of 2000 s-1 does twinning seem to occur in some smaller grains, as shown in Figure 4c-2. This could be attributed to the unique microstructure of hetero-structured pure titanium and the high stress induced by the ultra-high strain rate, which activates twinning[22]. Additionally, it was found that the proportion of LAGBs does not vary significantly under different strain rates, which suggests a decreased dominance of dislocations in the impact deformation process[23]. Figure 4a-4, b-4 and c-4 illustrate the statistical distribution plots of local misorientation corresponding to impact deformation at different strain rates. By analyzing these plots, the average Local Misorientation difference ( K ¯ ) can be calculated. For strain rates of 500 s-1, 1000 s-1, and 2000 s-1, the K ¯ values are 0.38, 0.54, and 0.59, respectively. The increase in K ¯ indicates a higher level of plastic deformation or a higher density of defects in the sample[24]. Specifically, the sample subjected to a strain rate of 2000 s-1 shows a close K ¯ compared to the sample at 1000 s-1 strain rate, suggesting insignificant dislocation accumulation as the strain rate increases from 1000 s-1 to 2000 s-1. This is consistent with the minimal increase in the proportion of LAGBs shown in Figures 4 b-2 and c-2.
Figure 5a, 5b, and 5c display the pole figures that correspond to the samples deformed under strain rates of 500 s-1, 1000 s-1, and 2000 s-1, respectively. The pole figures reveal a bimodal basal texture, with the highest texture strengths measured at 13.5, 12.8, and 14.6, respectively. There is no significant change in the texture type when compared to the original sample. These results indicate that the strain rate has a minimal effect on the texture. In other words, the influence of texture on the change of deformation mechanism can be ignored.
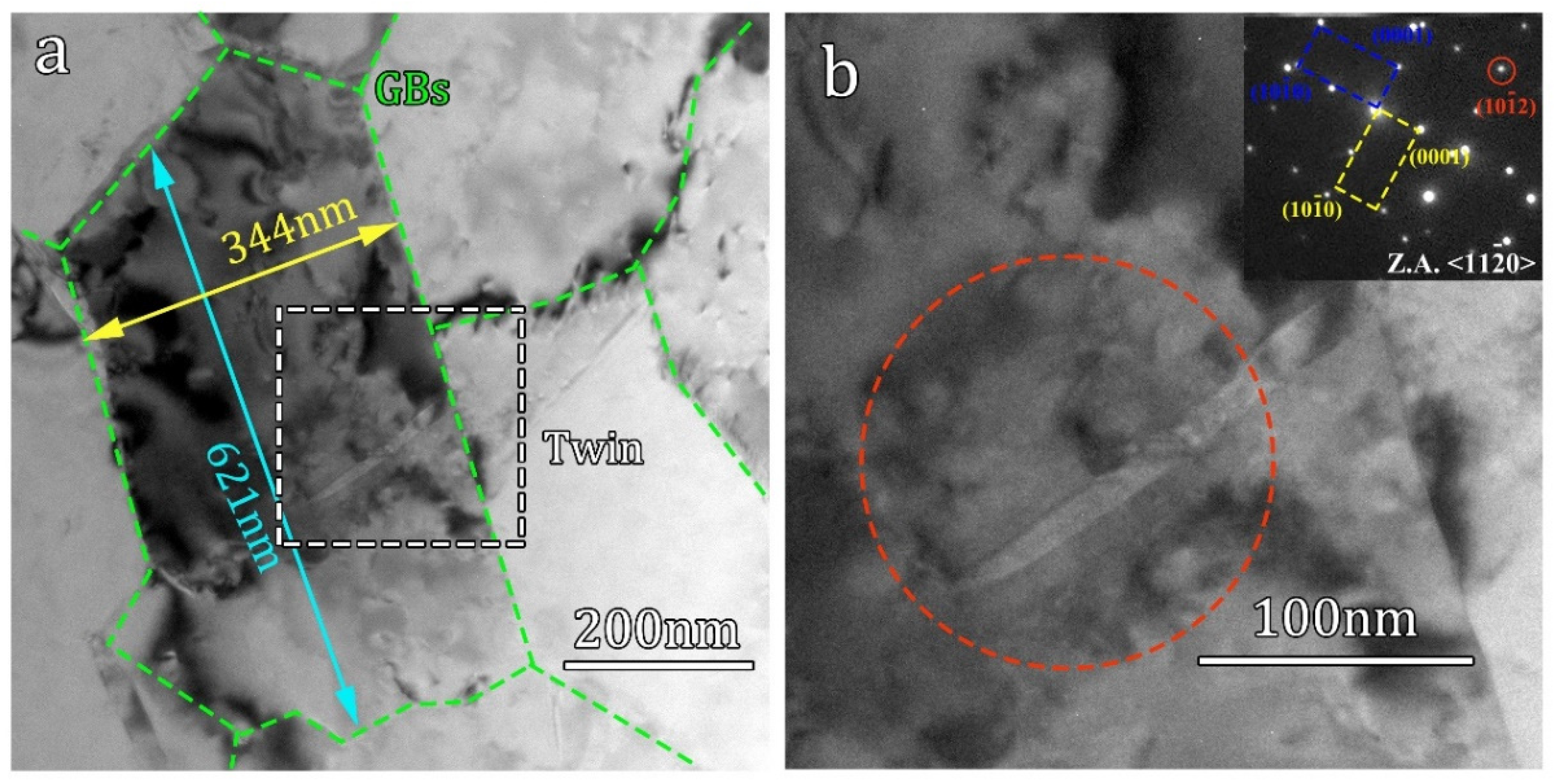
Figure 6a shows a bright-field TEM image of Ti sample deformed at a strain rate of 500 s-1. It can be observed that the deformed sample contains high density of dislocations, which is a typical characteristic of plastic deformation. Twin boundaries are commonly observed within coarse grains, as illustrated by the yellow dotted lines in Figure 6a-1 and 3a-2. For ultrafine grains, no twinning was identified, and dislocation slip is the main deformation mode [25]. When the impact strain rate increases to 1000 s-1, the microstructure of the sample is shown in Figure 6b, revealing a typical deformed structure characterized by a significant presence of defects such as dislocations and twins. Similarly, no twinning is observed in the ultrafine grain region in the sample. Implying that, even at a strain rate of 1000 s-1, twinning is still suppressed in the ultrafine grains. On the other hand, within the coarse grains, a prominent twin boundary is present, accompanied by a significant distribution of dislocations that form a ring-like pattern. In the magnified region (Figure 6b-2), a large number of dislocations can be seen near the twin boundary, indicating that the newly formed twin boundary hinders the slipping of dislocations[26]. Additionally, dislocations are also observed within the twin lamellae.
When the impact strain rate reaches 2000 s-1; due to severer plastic deformation; the microstructure undergoes significant disordering within the grains; as shown in Figure 7. Consequently; the grains exhibit a remarkably high density of defects; making it difficult to distinguish clearly grain boundaries and twin boundaries solely based on morphology (Figure 7a; 4b). Although it has been verified by EBSD observation (Figure 4c-2) that the areal twin percentage is 8.6%. TEM bright-field images at high magnification reveal the formation of dislocation cell structures in certain regions; as depicted by the solid rectangle in Figure 7b. Additionally; Figure 7c-1 and c-2 show the presence of numerous fine needle-like structures; which were not found in the deformed samples at strain rates of 500 s-1 and 1000 s-1. Notably; the characteristics of these structures resemble the needle-like martensitic phases found in titanium alloys. Previous studies have indicated that; under extreme deformation conditions; pure titanium can undergo stress-induced martensitic phase transformation. This transformation refers to a shift from HCP phase to face-centered cubic (FCC) phase; ultimately resulting in the formation of fine needle-like martensitic structures[27,28]
For the hetero-structured pure titanium selected in this study, the grain sizes are generally below 3μm and contain a significant number of ultrafine grains, resulting in a relatively small grain size (Figure 1b-3). Considering the influence of grain size on deformation mechanisms, dislocation slip is the most prevalent deformation mechanism under these grain size[29,30]. On one hand, higher strain rates lead to the activation of more dislocation sources, resulting in the entanglement of dislocations and impeding their motion. This leads to the accumulation and pile-up of a significant number of dislocations, as confirmed by TEM images of the deformed samples. On the other hand, in the hierarchical structure, numerous hetero-structure interfaces exist. These interfaces give rise to hetero-deformation induced (HDI) stress, which in turn leads to a significant accumulation of geometrically necessary dislocations [31,32].
It is generally believed that twinning is unlikely to occur in ultrafine grains[20,29]. However, in the deformed samples under a strain rate of 2000 s-1, TEM bright-field images reveal the presence of small nanoscale twin lamellae within the ultrafine grains with an equivalent grain size of approximately 500 nm, as shown in Figure 8. The thickness of these twin lamellae is approximately 10 nm. The occurrence of twinning within the ultrafine grains is not widespread but rather localized, observed in certain individual grains. This localized twinning may be due to the inhomogeneous deformation during impact, which leads to highly localized stress levels that satisfy the nucleation conditions for twinning within the ultrafine grains[33,34]. The significance of this phenomenon lies in gaining a profound understanding of the fundamental reasons behind the inhibitory effect of grain size refinement on twinning. It uncovers that twinning is not completely absent within ultrafine grains but rather occurs under excessively stringent conditions.
Numerous studies have demonstrated that dislocations play a pivotal role in the initiation of twinning in pure Ti[35,36,37]. Furthermore, the Hall-Petch relationship, based on the principle of dislocation obstacle at grain boundaries, has effectively explained the origin of strength[38]. Therefore, we speculate that the relationship between the required stress for twin activation and the grain size is similar to the Hall-Petch relationship. Thus, to better understand the emergence of nanoscale twin lamellae in ultrafine grain, we propose a modified Hall-Petch relationship, which takes into account the fact that the stress required to initiate deformation twinning, σ t w i n , is inversely proportional to the square root of grain size, and the relationship can be described as:
σ t w i n = K t w i n ∗ d − 1 2
where d is the average grain size and K t w i n is a constant that represents the sensitivity of twin activation to grain size. A higher K t w i n value indicates a stronger grain size effect on twinning. The experimental results in this study demonstrate that twinning is activated at an equivalent grain size of 500 nm (the finest observable grain size where twinning is activated) when the strain rate reached 2000 s-1. Based on the stress-strain curve (Figure 2), the corresponding range of flow stress is between 0.92 GPa and 1.04 GPa. According to the Equation(4), the K t w i n can be calculated to range from 0.651 MNm-3/2 to 0.735 MNm-3/2, which is significantly larger than the K value obtained from the traditional Hall-Petch relationship (0.24 MNm-3/2)[39]. Extensive research has indicated that the critical shear stress for compression twinning in pure titanium falls within the range of 125 MPa to 255 MPa when the grain size is between 10 μm and 50 μm[40,41,42]. As a validation, by assuming values of K t w i n as 0.651 and 0.735, the critical shear stress for twinning at grain sizes ranging from 10 μm to 50 μm can be calculated as follows: 92 MPa to 203 MPa and 105 MPa to 232 MPa. These values are in good agreement with the previous studies, confirming the scientific validity of this equation. The value of K t w i n   reported in this study can be used to predict the stress required to initiate deformation twinning across a wide range of grain sizes spanning from coarse to ultrafine.
In summary, our experimental results and theoretical model greatly enhance our understanding of the twinning mechanism at ultrafine grains, as well as establish a correlation between grain size and critical shear stress. These findings also offer potential avenues for strengthening mechanisms through twinning in ultrafine-grained HCP structured materials.

4. Conclusion

This study investigates the influence of deformation rate on the microstructures and deformation mechanisms in hetero-structured pure titanium. The results can be summarized as follows:
  • The mechanical responses and deformation mechanisms of hetero-structured pure titanium samples are closely related to the strain rate. As the strain rate increases from 500 s-1 to 2000 s-1, dislocation activities are the primary deformation carrier, but the dominance of dislocation slipping reduces and the dislocation configurations undergo changes. Conversely, there is an increase in the percentage of deformation twinning with higher strain rates.
  • It has been found that under different high deformation rates (500 s-1, 1000 s-1, 2000 s-1), the changes in texture are relatively minimal,, and the degree of temperature rise is low (far lower than the recrystallization temperature). Consequently, the alterations in these two influential factors are insufficient to induce changes in the deformation mechanism.
  • When subjected to a strain rate of 2000 s-1, martensitic phase transformation is identified in the deformed Ti sample. Moreover, nanoscale twin lamellae are observed within the ultrafine grain, which can be attributed to the high flow stress. A modified Hall-Petch model is proposed, and the obtained K t w i n can be used to effectively establish the correlation between the stress required for twinning and the grain size.

Author Contributions

Shuaizhuo Wang and Yusheng Li conceived and designed the experiments; Shuaizhuo Wang, Haotian Yan, Dongmei Zhang and Jiajun Hu performed the experiments; Yusheng Li and Shuaizhuo Wang, analyzed the data; Shuaizhuo Wang and Yusheng Li wrote the paper. Each contributor was essential to the production of this work.

Acknowledgment

This work was supported by the National Key Laboratory of Transient Physics Foundation (6142604220103), the Key Program of National Natural Science Foundation of China (No. 51931003), the National Natural Science Foundation of China (No. 52071180), and the Projects in Science and Technique Plans of Ningbo City (No. 2019B10083).

Conflict of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Özcan, Mutlu, and Christoph Hämmerle. "Titanium as a Reconstruction and Implant Material in Dentistry: Advantages and Pitfalls." Materials 5, no. 9 (2012): 1528-45. [CrossRef]
  2. Konstantinov, A. S., P. M. Bazhin, A. M. Stolin, E. V. Kostitsyna, and A. S. Ignatov. "Ti-B-Based Composite Materials: Properties, Basic Fabrication Methods, and Fields of Application (Review)." Composites Part A: Applied Science and Manufacturing 108 (2018): 79-88. [CrossRef]
  3. Yan, Na, Zezhou Li, Yongbo Xu, and Marc A. Meyers. "Shear Localization in Metallic Materials at High Strain Rates." Progress in Materials Science 119 (2021). [CrossRef]
  4. Lei, Lei, Qinyang Zhao, Yongqing Zhao, Cong Wu, Shixing Huang, Weiju Jia, and Weidong Zeng. "Gradient Nanostructure, Phase Transformation, Amorphization and Enhanced Strength-Plasticity Synergy of Pure Titanium Manufactured by Ultrasonic Surface Rolling." Journal of Materials Processing Technology 299 (2022). [CrossRef]
  5. Wang, Mingsai, Yanfei Wang, Qiong He, Wei Wei, Fengjiao Guo, Wuli Su, and Chongxiang Huang. "A Strong and Ductile Pure Titanium." Materials Science and Engineering: A 833 (2022): 142534. [CrossRef]
  6. Won, Jong Woo, Seulbi Lee, Woo Chul Kim, Yong-Taek Hyun, and Dong Won Lee. "Significantly Increased Twinning Activity of Pure Titanium During Room-Temperature Tensile Deformation by Cryogenic-Deformation Treatment." Materials Science and Engineering: A 862 (2023). [CrossRef]
  7. Zhao, S., R. Zhang, Q. Yu, J. Ell, R. O. Ritchie, and A. M. Minor. "Cryoforged Nanotwinned Titanium with Ultrahigh Strength and Ductility." Science 373, no. 6561 (2021): 1363-68. [CrossRef]
  8. Huang, Zhaowen, Yang Cao, Jinfeng Nie, Hao Zhou, and Yusheng Li. "Microstructures and Mechanical Properties of Commercially Pure Ti Processed by Rotationally Accelerated Shot Peening." Materials 11, no. 3 (2018). [CrossRef]
  9. Zhou, Ping, Dawu Xiao, Chunli Jiang, Ge Sang, and Dongli Zou. "Twin Interactions in Pure Ti under High Strain Rate Compression." Metallurgical and Materials Transactions A 48, no. 1 (2016): 126-38. [CrossRef]
  10. Jia, Hailong, Knut Marthinsen, and Yanjun Li. "Revealing Abnormal {112¯1} Twins in Commercial Purity Ti Subjected to Split Hopkinson Pressure Bar." Journal of Alloys and Compounds 783 (2019): 513-23. [CrossRef]
  11. Wang, Tong Bo, Bo Long Li, Mian Li, Ying Chao Li, and Zuo Ren Nie. "The Dynamic Mechanical Behavior and Microstructural Evolution of Commercial Pure Titanium." Advanced Materials Research 968 (2014): 7-11. [CrossRef]
  12. Gurao, N. P., Rajeev Kapoor, and Satyam Suwas. "Deformation Behaviour of Commercially Pure Titanium at Extreme Strain Rates." Acta Materialia 59, no. 9 (2011): 3431-46. [CrossRef]
  13. Deguchi, Misaki, Shigeto Yamasaki, Masatoshi Mitsuhara, Hideharu Nakashima, Genki Tsukamoto, and Tomonori Kunieda. "Tensile Deformation Behaviors of Pure Ti with Different Grain Sizes under Wide-Range of Strain Rate." Materials 16, no. 2 (2023): 529. [CrossRef]
  14. Xu, Feng, Xiyan Zhang, Haitao Ni, and Qing Liu. "Deformation Twinning in Pure Ti During Dynamic Plastic Deformation." Materials Science and Engineering: A 541 (2012): 190-95. [CrossRef]
  15. Wu, X., M. Yang, F. Yuan, G. Wu, Y. Wei, X. Huang, and Y. Zhu. "Heterogeneous Lamella Structure Unites Ultrafine-Grain Strength with Coarse-Grain Ductility." Proc Natl Acad Sci U S A 112, no. 47 (2015): 14501-5. [CrossRef]
  16. Tanaka, Y., M. Kondo, N. Miyazaki, and R. Ueji. "Deformation Behavior of Pure Titanium at a Wide Range of Strain Rates." Journal of Physics: Conference Series 240 (2010). [CrossRef]
  17. Li, Qiang, Y. B. Xu, and M. N. Bassim. "Dynamic Mechanical Behavior of Pure Titanium." Journal of Materials Processing Technology 155-156 (2004): 1889-92. [CrossRef]
  18. Xu, Shun, and Jian Wang. "Deformation Twins Stimulated by {112¯2} Twinning in Adjacent Grain in Titanium." Acta Materialia 229 (2022). [CrossRef]
  19. Huang, Z. W., S. B. Jin, H. Zhou, Y. S. Li, Y. Cao, and Y. T. Zhu. "Evolution of Twinning Systems and Variants During Sequential Twinning in Cryo-Rolled Titanium." International Journal of Plasticity 112 (2019): 52-67. [CrossRef]
  20. Yu, Qian, Raja K. Mishra, and Andrew M. Minor. "The Effect of Size on the Deformation Twinning Behavior in Hexagonal Close-Packed Ti and Mg." Jom 64, no. 10 (2012): 1235-40. [CrossRef]
  21. Li, Lifei, Zheng Zhang, and Gongtian Shen. "Effect of Grain Size on the Tensile Deformation Mechanisms of Commercial Pure Titanium as Revealed by Acoustic Emission." Journal of Materials Engineering and Performance 24, no. 5 (2015): 1975-86. [CrossRef]
  22. Yu, Kehang, Xin Wang, Subhash Mahajan, Irene J. Beyerlein, Penghui Cao, Timothy J. Rupert, Julie M. Schoenung, and Enrique J. Lavernia. "Twin Nucleation from Disconnection-Dense Sites between Stacking Fault Pairs in a Random Defect Network." Materialia 30 (2023). [CrossRef]
  23. Mittemeijer, Eric J. "The Crystal Imperfection;Structure Defects." (2021).
  24. Wei, Kang, Rong Hu, Dongdi Yin, Lirong Xiao, Song Pang, Yang Cao, Hao Zhou, Yonghao Zhao, and Yuntian Zhu. "Grain Size Effect on Tensile Properties and Slip Systems of Pure Magnesium." Acta Materialia 206 (2021). [CrossRef]
  25. Huang, Zhaowen, Donghui Wen, Xiaodong Hou, Yusheng Li, Biao Wang, and Anding Wang. "Grain Size and Temperature Mediated Twinning Ability and Strength-Ductility Correlation in Pure Titanium." Materials Science and Engineering: A 849 (2022). [CrossRef]
  26. Ahmadikia, Behnam, Leyun Wang, M. Arul Kumar, and Irene J. Beyerlein. "Grain Boundary Slip – Twin Transmission in Titanium." Acta Materialia 244 (2023). [CrossRef]
  27. Zhao, Hong, Nanjie Ding, Yuping Ren, Hongbo Xie, Bo Yang, and Gaowu Qin. "Shear-Induced Hexagonal Close-Packed to Face-Centered Cubic Phase Transition in Pure Titanium Processed by Equal Channel Angular Drawing." Journal of Materials Science 54, no. 10 (2019): 7953-60. [CrossRef]
  28. Zheng, XiaodongGong, MingyuXiong, TingGe, HualongYang, LixinZhou, YangtaoZheng, ShijianWang, JianMa, Xiuliang. "Deformation Induced Fcc Lamellae and Their Interaction in Commercial Pure Ti." Scripta Materialia 162 (2019). [CrossRef]
  29. Sun, J. L., P. W. Trimby, F. K. Yan, X. Z. Liao, N. R. Tao, and J. T. Wang. "Grain Size Effect on Deformation Twinning Propensity in Ultrafine-Grained Hexagonal Close-Packed Titanium." Scripta Materialia 69, no. 5 (2013): 428-31. [CrossRef]
  30. Palán, Jan, Radek Procházka, Jan Džugan, Jan Nacházel, Michal Duchek, Gergely Németh, Kristián Máthis, Peter Minárik, and Klaudia Horváth. "Comprehensive Evaluation of the Properties of Ultrafine to Nanocrystalline Grade 2 Titanium Wires." Materials 11, no. 12 (2018): 2522. [CrossRef]
  31. Zhu, Yuntian, and Xiaolei Wu. "Heterostructured Materials." Progress in Materials Science 131 (2023). [CrossRef]
  32. Zhu, Yuntian, Kei Ameyama, Peter M. Anderson, Irene J. Beyerlein, Huajian Gao, Hyoung Seop Kim, Enrique Lavernia, Suveen Mathaudhu, Hael Mughrabi, Robert O. Ritchie, Nobuhiro Tsuji, Xiangyi Zhang, and Xiaolei Wu. "Heterostructured Materials: Superior Properties from Hetero-Zone Interaction." Materials Research Letters 9, no. 1 (2020): 1-31. [CrossRef]
  33. Xu, Shun, Ping Zhou, Guisen Liu, Dawu Xiao, Mingyu Gong, and Jian Wang. "Shock-Induced Two Types of {101¯2} Sequential Twinning in Titanium." Acta Materialia 165 (2019): 547-60. [CrossRef]
  34. He, Y., B. Li, C. Wang, and S. X. Mao. "Direct Observation of Dual-Step Twinning Nucleation in Hexagonal Close-Packed Crystals." Nat Commun 11, no. 1 (2020): 2483. [CrossRef]
  35. Kou, Zongde, Yanqing Yang, Bin Huang, Xian Luo, Pengtao Li, Guangming Zhao, and Wei Zhang. "Observing the Dynamic101¯1twining Process in Pure Ti at Atomic Resolution." Scripta Materialia 139 (2017): 139-43. [CrossRef]
  36. Liao, Xiaozhou, Jian Wang, Jianfeng Nie, Yanyao Jiang, and Peidong Wu. "Deformation Twinning in Hexagonal Materials." MRS Bulletin 41, no. 4 (2016): 314-19. [CrossRef]
  37. Paudel, YubRaj, Deepesh Giri, Matthew W. Priddy, Christopher D. Barrett, Kaan Inal, Mark A. Tschopp, Hongjoo Rhee, and Haitham El Kadiri. "A Review on Capturing Twin Nucleation in Crystal Plasticity for Hexagonal Metals." Metals 11, no. 9 (2021). [CrossRef]
  38. Ovid'ko, I. A., R. Z. Valiev, and Y. T. Zhu. "Review on Superior Strength and Enhanced Ductility of Metallic Nanomaterials." Progress in Materials Science 94 (2018): 462-540. [CrossRef]
  39. Zherebtsov, S. V., G. S. Dyakonov, A. A. Salem, V. I. Sokolenko, G. A. Salishchev, and S. L. Semiatin. "Formation of Nanostructures in Commercial-Purity Titanium Via Cryorolling." Acta Materialia 61, no. 4 (2013): 1167-78. [CrossRef]
  40. Wang, L., Z. Zheng, H. Phukan, P. Kenesei, J. S. Park, J. Lind, R. M. Suter, and T. R. Bieler. "Direct Measurement of Critical Resolved Shear Stress of Prismatic and Basal Slip in Polycrystalline Ti Using High Energy X-Ray Diffraction Microscopy." Acta Materialia 132 (2017): 598-610. [CrossRef]
  41. Cao, Yang, Song Ni, Xiaozhou Liao, Min Song, and Yuntian Zhu. "Structural Evolutions of Metallic Materials Processed by Severe Plastic Deformation." Materials Science and Engineering: R: Reports 133 (2018): 1-59. [CrossRef]
  42. Yang, H., H. Li, J. Ma, D. Wei, J. Chen, and M. W. Fu. "Temperature Dependent Evolution of Anisotropy and Asymmetry of A-Ti in Thermomechanical Working: Characterization and Modeling." International Journal of Plasticity 127 (2020). [CrossRef]
Preprints 87760 g001
Figure 1. (a-1) The schematics of the split Hopkinson pressure bar system; (a-2) specimen; b. EBSD characterization of the initial hetero-structured sample. (b-1) Inverse polar figure (IPF) map; (b-2) distribution of grain boundary orientation; (b-3) distributions of grain size.
Figure 1. (a-1) The schematics of the split Hopkinson pressure bar system; (a-2) specimen; b. EBSD characterization of the initial hetero-structured sample. (b-1) Inverse polar figure (IPF) map; (b-2) distribution of grain boundary orientation; (b-3) distributions of grain size.
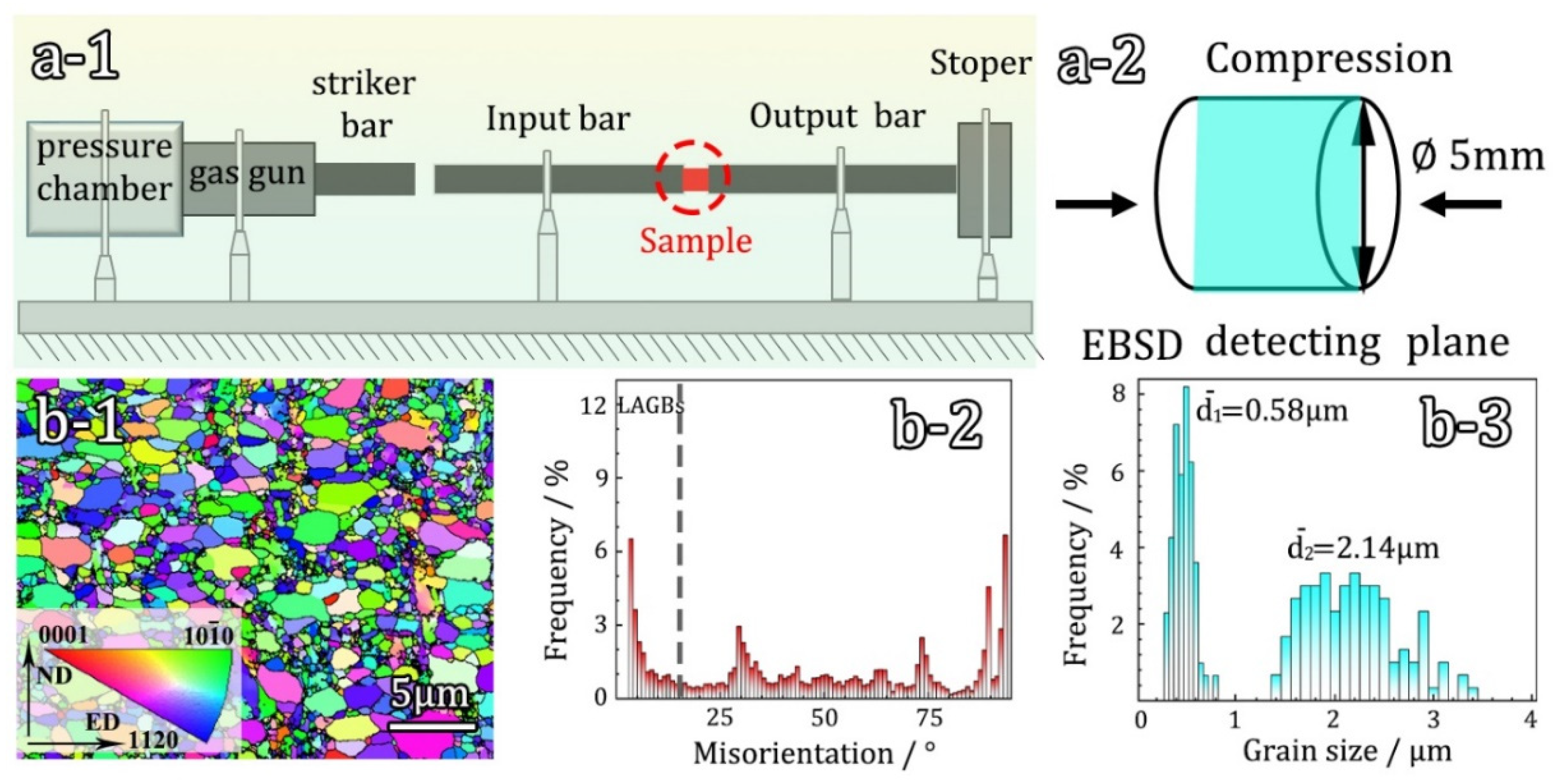
Preprints 87760 g001
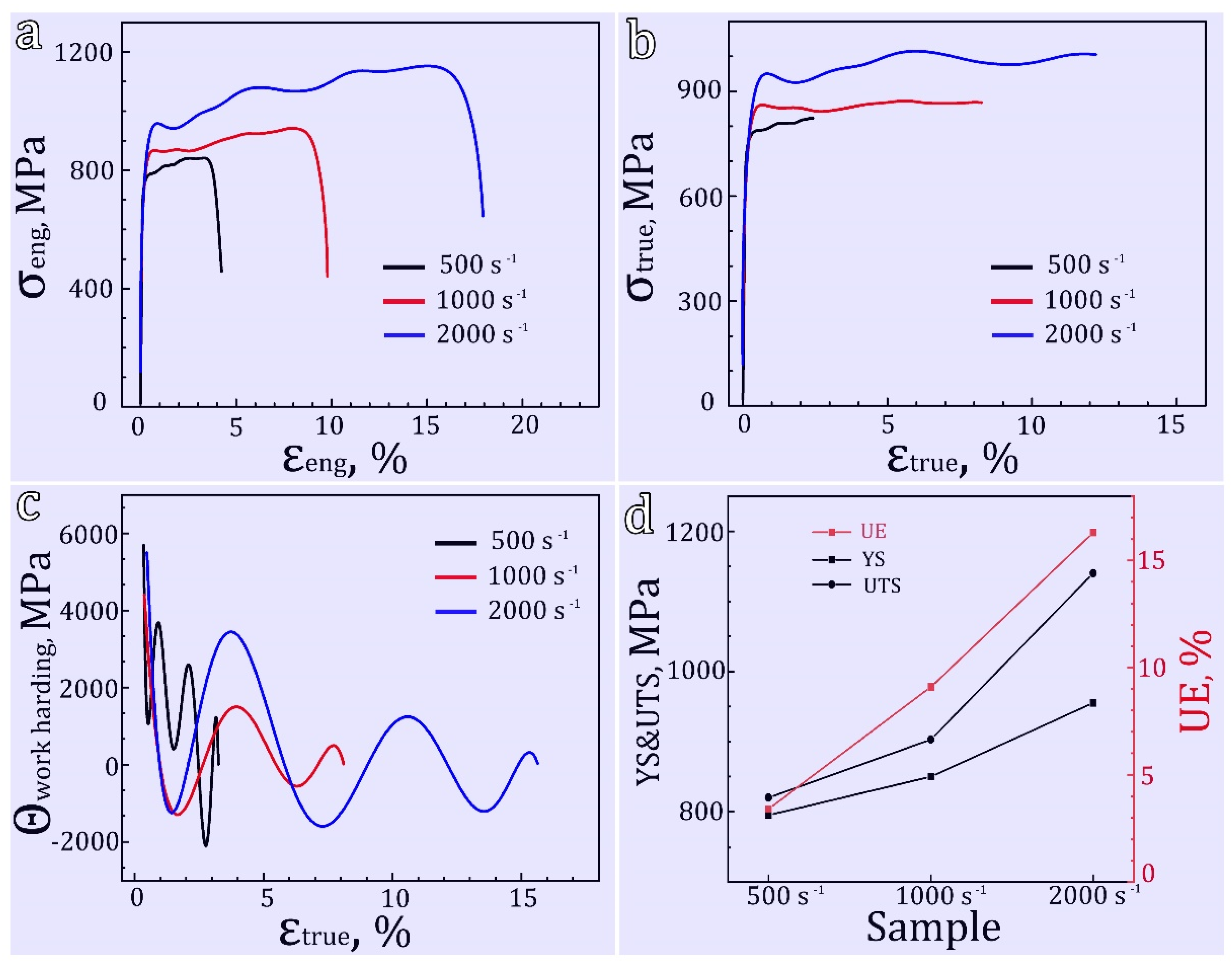
Preprints 87760 g002
Figure 2. Mechanical properties of hetero-structured samples under different strain rate: (a) compressive engineering stress-strain curves; (b) true stress-strain curves from compressive tests; (c) strain hardening rate curves; (d) corresponding yield strength (YS), ultimate compressive strength (UCS) and compression strain of the samples under different strain rate.
Figure 2. Mechanical properties of hetero-structured samples under different strain rate: (a) compressive engineering stress-strain curves; (b) true stress-strain curves from compressive tests; (c) strain hardening rate curves; (d) corresponding yield strength (YS), ultimate compressive strength (UCS) and compression strain of the samples under different strain rate.
Preprints 87760 g002
Preprints 87760 g003
Figure 3. Adiabatic temperature rise values for overall hetero-structured samples under different strain rate.
Figure 3. Adiabatic temperature rise values for overall hetero-structured samples under different strain rate.
Preprints 87760 g003
Preprints 87760 g004
Figure 4. EBSD observations of deformed hetero-structured sample under a strain rate of 500 s-1, 1000 s-1, 2000 s-1, respectively: (a-1), (b-1), (c-1) IPF map; (a-2), (b-2), (c-2) twin boundary map; (a-3), (b-3), (c-3) distribution of grain boundary orientation; (a-4), (b-4), (c-4) statistical distributions of Local Misorientation.
Figure 4. EBSD observations of deformed hetero-structured sample under a strain rate of 500 s-1, 1000 s-1, 2000 s-1, respectively: (a-1), (b-1), (c-1) IPF map; (a-2), (b-2), (c-2) twin boundary map; (a-3), (b-3), (c-3) distribution of grain boundary orientation; (a-4), (b-4), (c-4) statistical distributions of Local Misorientation.
Preprints 87760 g004
Preprints 87760 g005
Figure 5. (0001), (11 2 ¯ 0) and (10 1 ¯ 0) pole figures of deformed hetero-structured samples under different strain rate: (a) 500 s-1, (b) 1000s-1, (c) 2000 s-1.
Figure 5. (0001), (11 2 ¯ 0) and (10 1 ¯ 0) pole figures of deformed hetero-structured samples under different strain rate: (a) 500 s-1, (b) 1000s-1, (c) 2000 s-1.
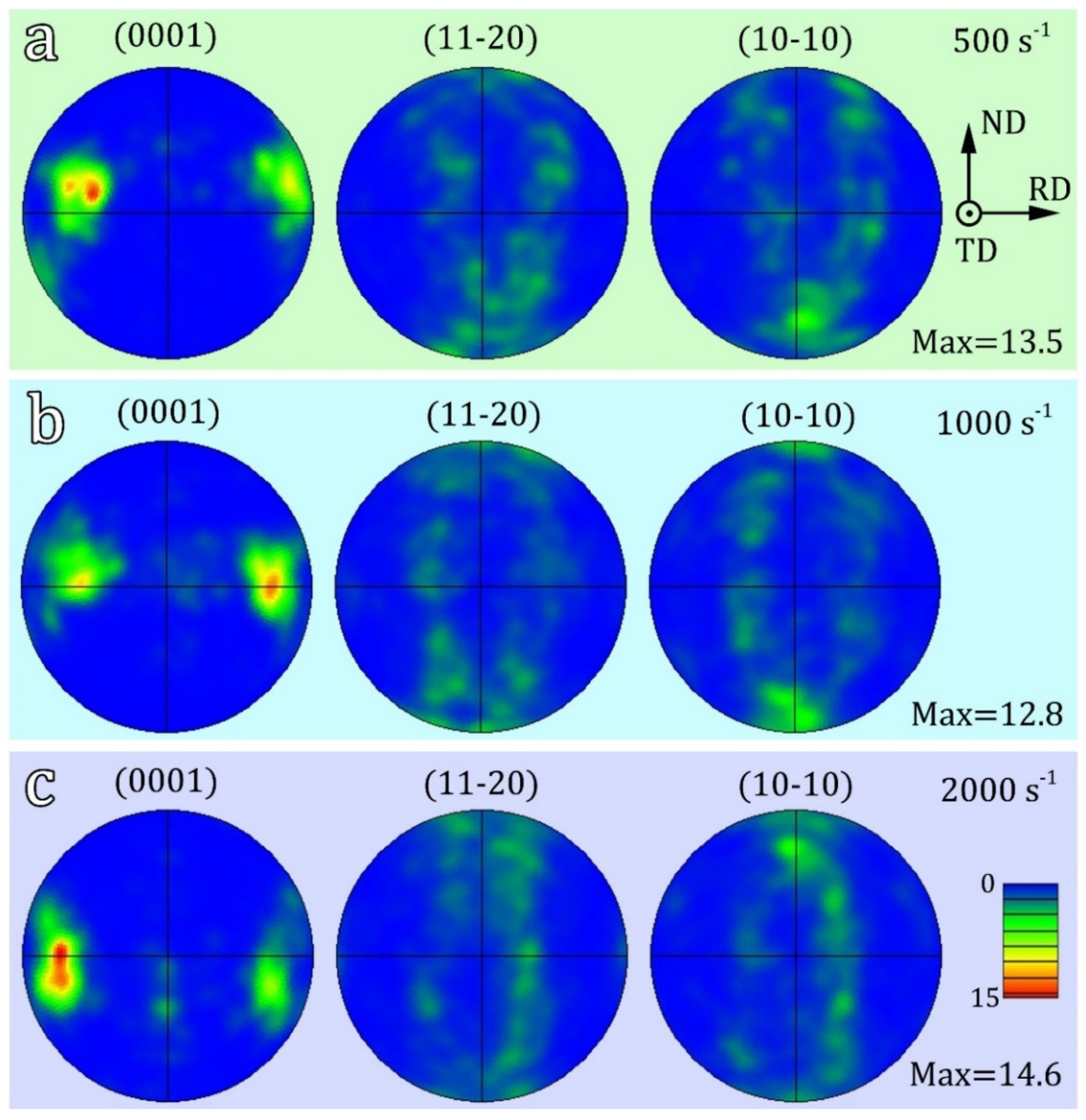
Preprints 87760 g005
Preprints 87760 g006
Figure 6. TEM images of deformed hetero-structured sample with different strain rate. (a)500 s-1; (b) 1000 s-1.
Figure 6. TEM images of deformed hetero-structured sample with different strain rate. (a)500 s-1; (b) 1000 s-1.
Preprints 87760 g006
Preprints 87760 g007
Figure 7. TEM images of deformed hetero-structured sample with a strain rate of 2000 s-1: (c-2) close-up view of the area marked by the white dash line box in (c-1).
Figure 7. TEM images of deformed hetero-structured sample with a strain rate of 2000 s-1: (c-2) close-up view of the area marked by the white dash line box in (c-1).
Preprints 87760 g007
Preprints 87760 g008
Figure 8. TEM images of ultra-fine grain of deformed hetero-structured sample under a strain rate of 2000 s-1: (b) close-up view of the area marked by the white dash line box in (a).
Figure 8. TEM images of ultra-fine grain of deformed hetero-structured sample under a strain rate of 2000 s-1: (b) close-up view of the area marked by the white dash line box in (a).
Preprints 87760 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated