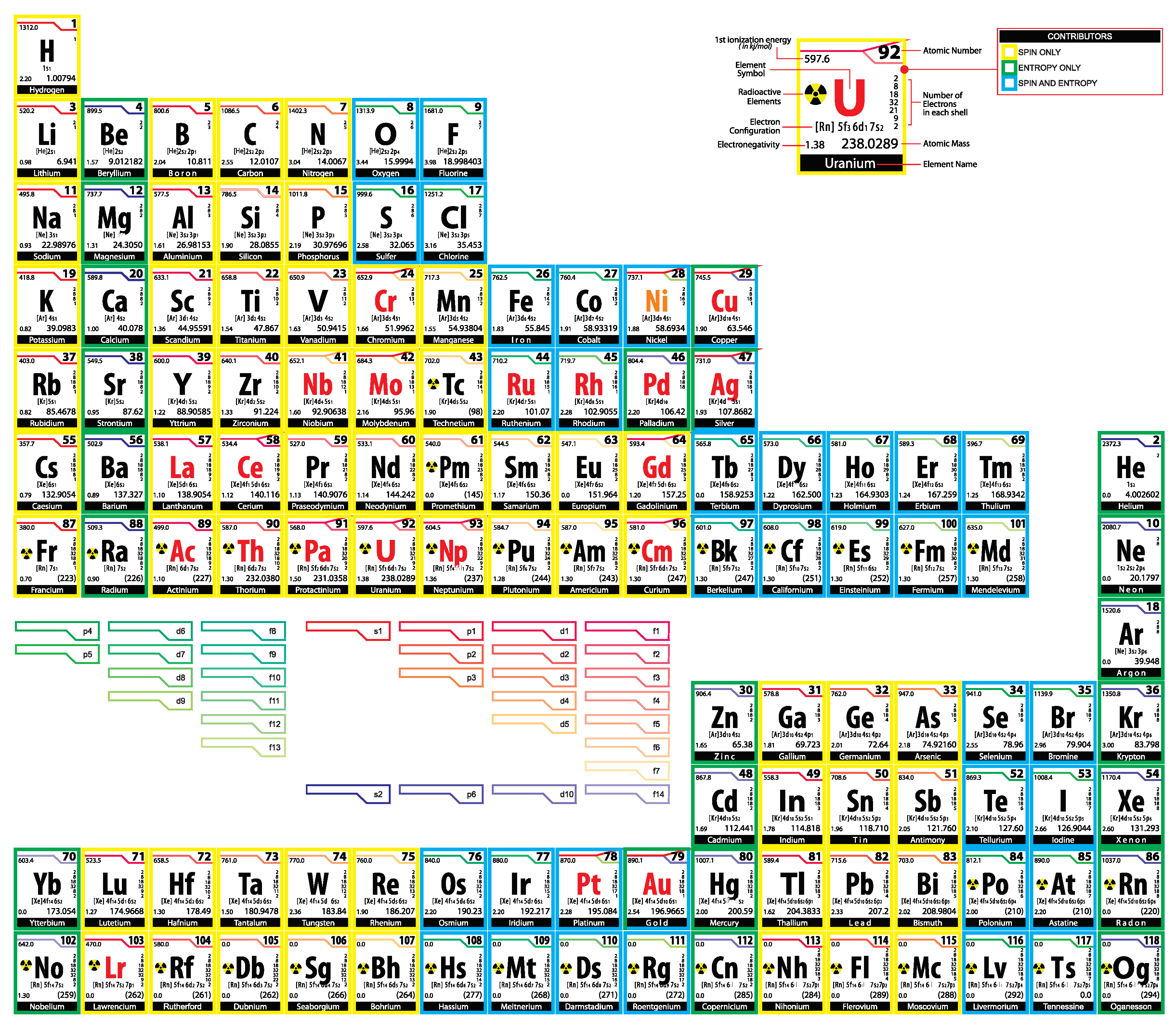
2. Hund’s rule and Shannon entropy
A simple but inventive procedure for determining Shannon entropy of an electron population was disclosed in [
1]. Any set of
N electrons satisfies
, where
and
denote, respectively, the number of up- and down-spin electrons. Thus, the probabilities of finding ↑ and ↓ electrons within the set of
N electrons are
and
.
Definition 1 (Electron set entropy).
An electron set entropy is
This definition was disclosed in [
1] but is given here for clarity Electrons are fermions, so electron sets populating chemical elements’ orbitals must satisfy the Pauli exclusion principle. For the s orbital, for example, which can accommodate a maximum of
electrons, the corresponding probabilities are
if the orbital accommodates one electron and
if the orbital accommodates two electrons. Thus, possible electron set entropies (
4) are
. The author of [
1] assumes that the electron set entropies of states s
1 and s
2 are the same, but this assumption is unjustified, as we shall discuss later.
In general, any orbital can store up to
electrons, where
is the angular momentum quantum number and
n is the principal quantum number. Thus, the situation becomes more diverse for orbitals with larger
ℓ as multiple sets with different electron set entropies and numbers of unpaired electrons are possible, as shown in
Figure 1,
Figure 2,
Figure 3 and
Figure 4. In general, the number of distinct electron sets allowed by the Pauli exclusion principle and available for an orbital is given by triangular numbers as
and therefore for
, only one distinct electron set is possible. If there is more than one electron set available, nature selects this electron set that maximizes the number of unpaired electrons, so the electron set entropy is
However, as shown in [
1], for
, nature also selects this electron population among the allowed ones, which minimizes the orbital Shannon entropy. This rule of populating the sublevels can be stated in the simple theorem illustrated in
Figure 5.
Theorem 1 (Orbital entropy).
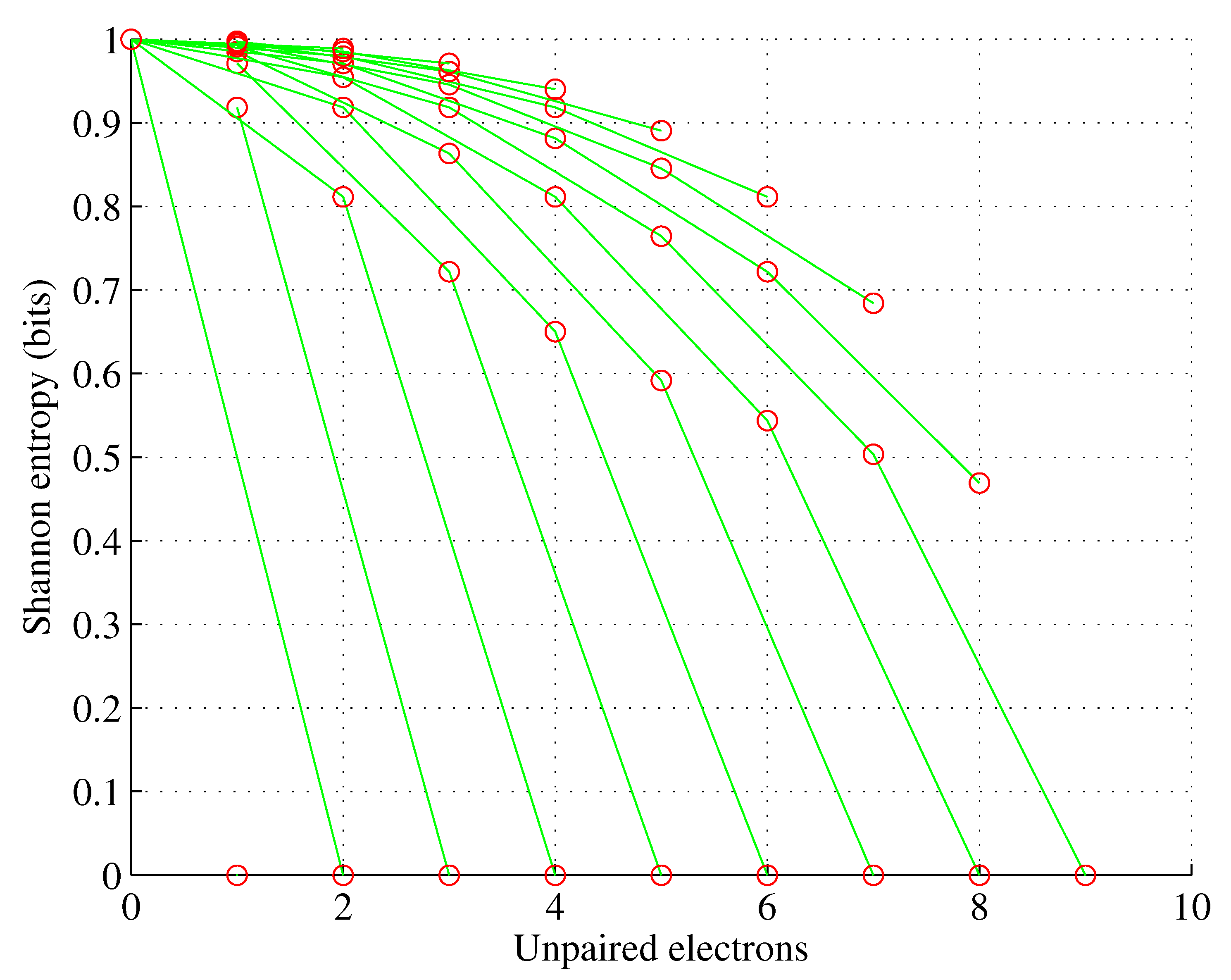
For any orbital capable of storing (5) electrons, storing N electrons, and populated to maximize the number of unpaired electrons (i.e. according to Hund’s rule), the orbital Shannon entropy amounts
where for we call the entropy intermediate and for pure.
Proof. According to Hund’s rule, for the number of unpaired electrons is equal to , while for is equal to . For electrons can freely populate available sublevels and therefore (the same for ↓). For the electrons will begin to repopulate the available sublevels following the Pauli exclusion principle up to , where . This completes the proof. □
Some researchers postulate that certain elements are exceptions to Hund’s rule. Chromium, for example, having the atomic number is between vanadium (, electron configuration [Ar]3d34s2) and manganese (, [Ar]3d54s2) within the periodic table of elements. Thus, it should have electron configuration [Ar]3d44s2, following Hund’s rule, but instead, it has [Ar]3d54s1, as one electron from 4s moves to 3d to make it more stable. But it is not Hund’s rule that is violated. It is the Aufbau rule. Hund’s rule governs the electron population of a solitary orbital only.
3. Aufbau rule and Shannon entropy
The Aufbau or Madelung energy ordering rule is another powerful empirical tool for predicting the electron configurations of chemical elements corresponding to the ground state. It correctly predicts the electron configurations of most of the elements. However, about twenty chemical elements (with only two nondoubleton sets of consecutive ones) violate the Aufbau rule, leading to intriguing exceptions and anomalies. Chromium and copper violations are attributed to a delicate balance of electron-electron repulsion and the energy gap between the 3d and 4s orbitals. Only palladium exhibits double electron promotion with all ten electrons filling the 4d orbital and therefore is often called a "double anomaly". Palladium also has the smallest differential entropy [
19]. This exceptional behavior is attributed to the compactness of 3d orbitals and complex electron interactions. Furthermore, there are no chemical elements that have orbital f
8 in their electron configurations, although the Aufbau rule predicts f8 for gadolinium and curium (
). The elements that violate the Aufbau rule are listed in
Table 1, which shows their actual electron configurations and the configurations predicted by the Aufbau rule.
We note that for , actual ground states are predicted. Thus, other elements, such as darmstadtium () and roentgenium () may also violate the Aufbau rule. Furthermore, the electron configuration of nickel () is disputed, but we included it in the list of exceptions.
Similarly to orbitals, we can calculate the number of unpaired electrons of a chemical element, as shown in
Figure 6 for
. We can also calculate the Shannon entropy of a chemical element. In two ways.
First, we can consider an element as an electron set and calculate its entropy using Definition 1, as shown in
Figure 7. For example, the electron configuration of oxygen is [He]2s
22p
4→ 2·s
2+p
4 and thus
,
,
, and
.
However, the entropy according to this definition does not increase monotonically and, in addition, palladium has a lower entropy in the Aufbau configuration. Therefore, noting that the entropies of independent systems are additive quantities, we provide another, monotonically increasing entropy.
Definition 2. An element’s Shannon entropy is the sum of the orbital entropies (8) in the electron configuration of this element, neglecting the principal quantum number n.
The principal quantum number represents the average distance of electrons from the nucleus, and therefore its meaning in the context of the emergent dimensionality is restricted. Only the Pythagorean theorem introduces negative distances (as non-principal square roots), and distance non-negativity is not an axiom of diffuse metrics [
26], such as the Łukaszyk–Karmowski metric [
9].
For example, for oxygen is [He]2s
22p
4→ s
2s
2p
4. Since
, and
is given by the relation (
8), the entropy for oxygen is equal to
and the number of unpaired electrons
. Similarly, for chromium (
)
, so its entropy is
and the number of unpaired electrons
.
Elements’ entropies
and
for
(Hassium is the heaviest element with known properties) are shown in
Figure 8 based on actual electron configurations and configurations obtained using the Aufbau rule. Furthermore,
Table 1 lists the entropies and numbers of unpaired electrons of the Aufbau rule violators.
The Aufbau rule reflects the periodicity of the elements within the windows defined by the noble gases’ atomic numbers, as shown in
Figure 6,
Figure 7 and
Figure 8. Subsequent atomic orbitals form the Janet’s sequence (OEIS A167268) that can be generated by the relation
(
5) with
given by
where
and
are floor and ceiling functions
2.
The atomic numbers of noble gases
form the sequence OEIS A018227 that can be generated using formulas
where
is the sum of the elements of a given period of the periodic table (OEIS A093907) that can be generated using formulas
Figure 9.
The periodic table of chemical elements arranged according to their entropy. The Aufbau rule violators (red symbols). Spin-only-contributors (yellow frames). Entropy-only-contributors (green frames). Spin-and-entropy-contributors (blue frames). are exceptional spin-only-contributors. are exceptional spin-and-entropy-contributors having pure entropy. is an exceptional entropy-only-contributor, which is not a spin-contributor.
Figure 9.
The periodic table of chemical elements arranged according to their entropy. The Aufbau rule violators (red symbols). Spin-only-contributors (yellow frames). Entropy-only-contributors (green frames). Spin-and-entropy-contributors (blue frames). are exceptional spin-only-contributors. are exceptional spin-and-entropy-contributors having pure entropy. is an exceptional entropy-only-contributor, which is not a spin-contributor.
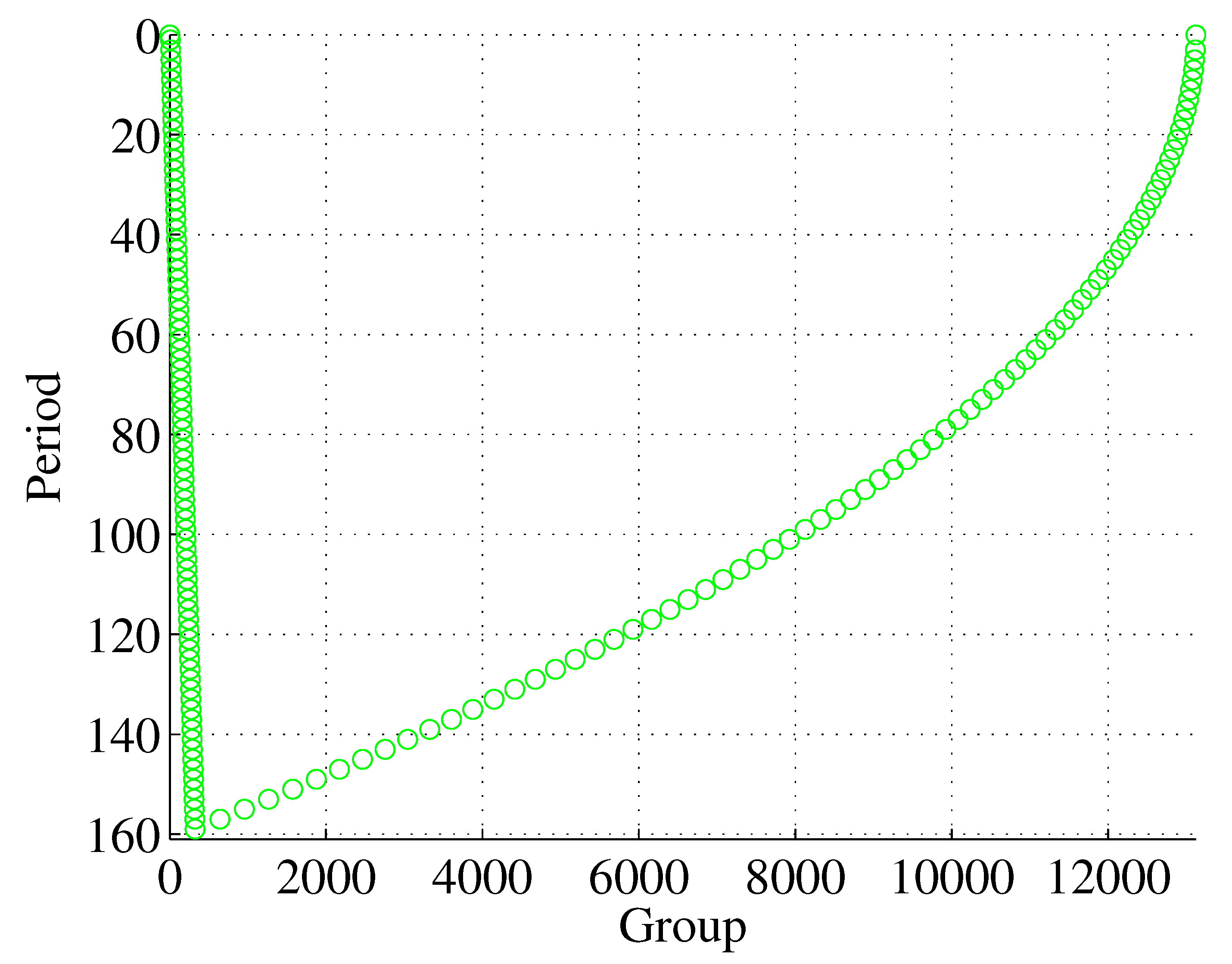
However, the sequence (
10) is also valid for
, as shown in
Table 2. In particular
for
and thus, 2’s generated by positive
l’s are denser, as these
l’s include pronic numbers (OEIS A002378) and
for
. A mirror situation occurs for imaginary
,
, in which case
for
and 2’s generated by negative
l’s are denser, as shown in
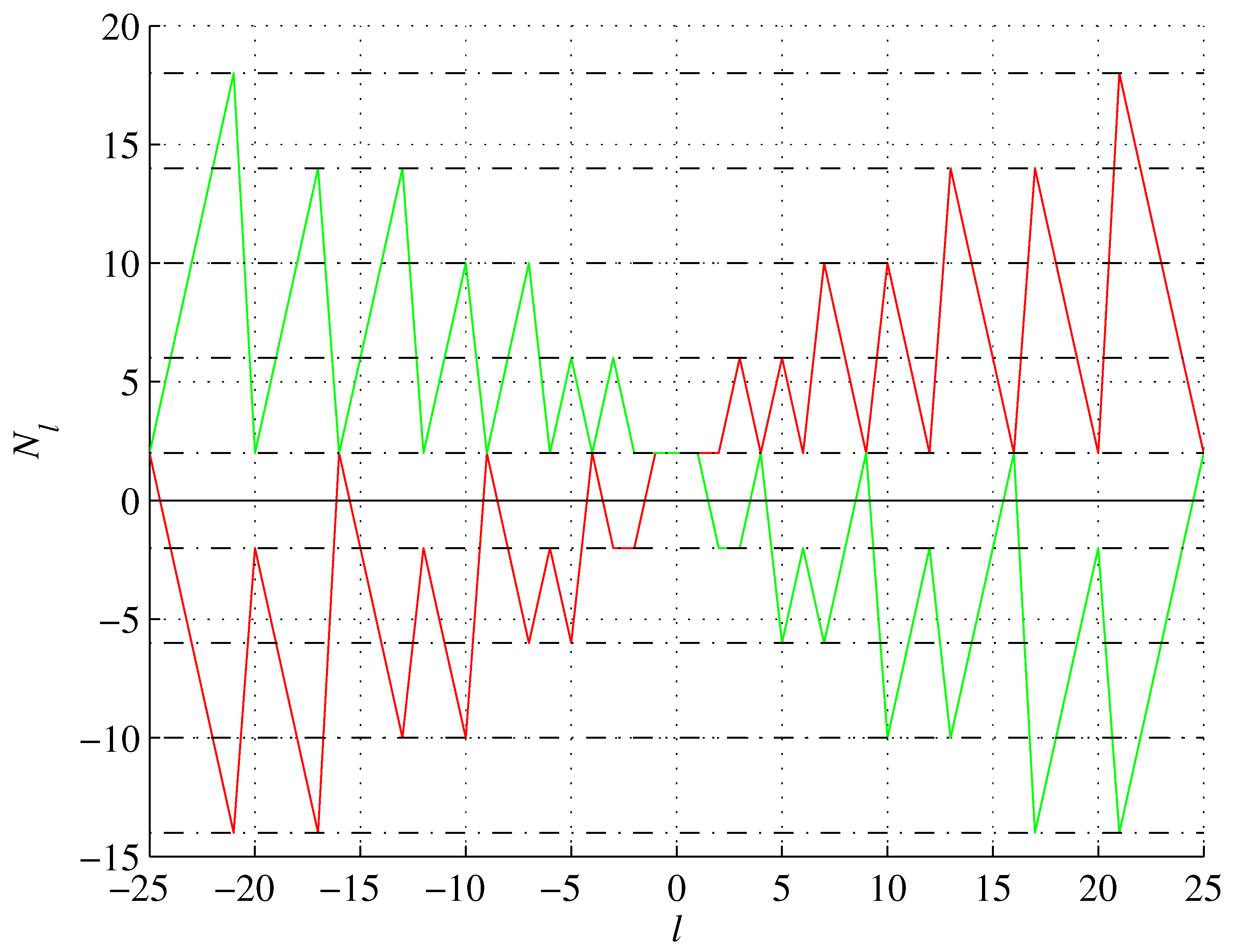
Figure 10.
Figure 10.
Janet’s sequence (red) and its reflection (green).
Figure 10.
Janet’s sequence (red) and its reflection (green).
Furthermore, although the sequences (
13) are equivalent to each other
their elements no longer represent the sums of the elements of a given period of the periodic table if
. Also, the sequences (
11) and (
12) are different for
, as shown in
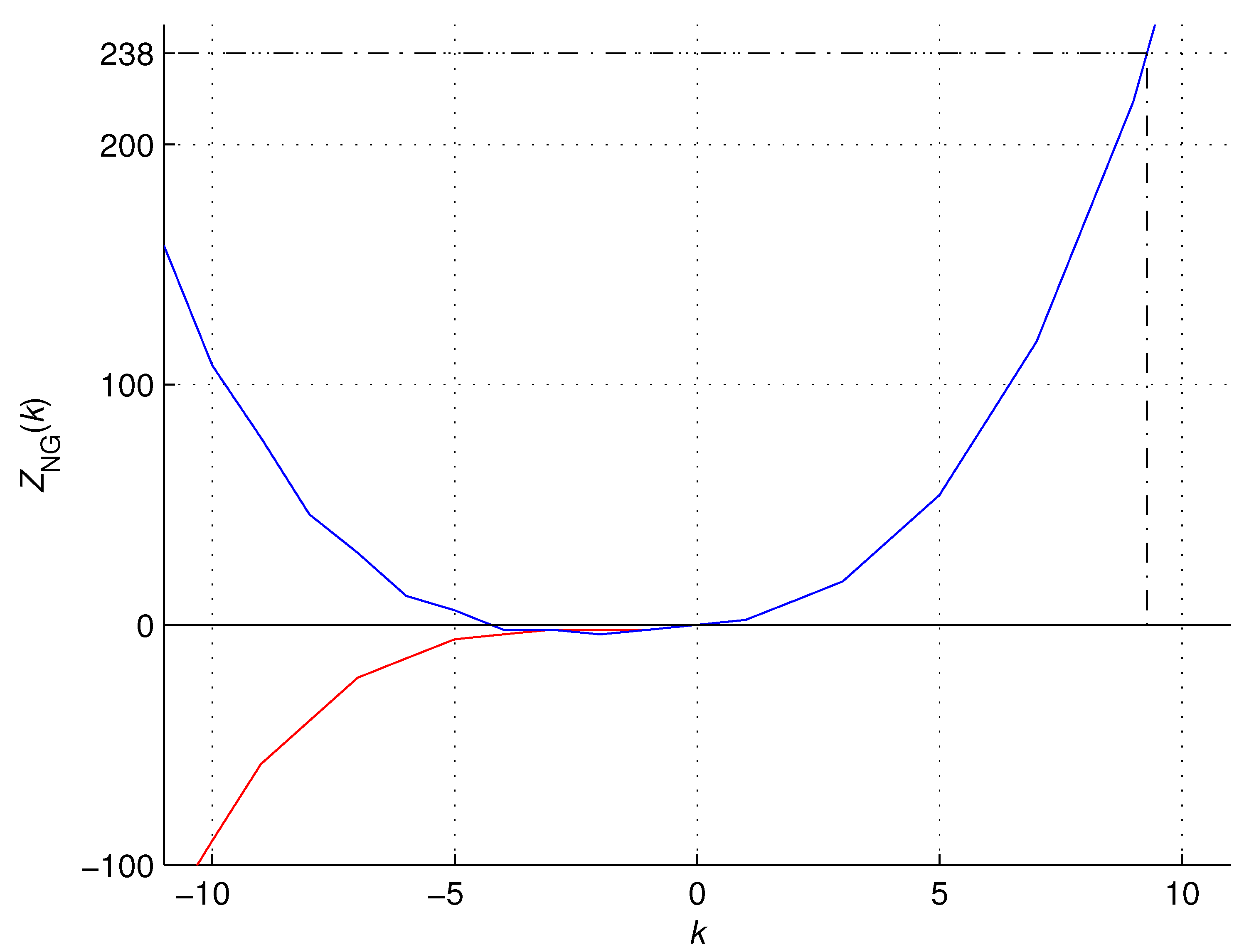
Figure 11.
Figure 11.
The atomic numbers of noble gases
generated by the OEIS formula (
12) (red) and recurrence formula (
11) (blue).
Figure 11.
The atomic numbers of noble gases
generated by the OEIS formula (
12) (red) and recurrence formula (
11) (blue).
A simple conclusion of Theorem 1 (cf.
Figure 5) is that the entries s
1, p
1-p
3, d
1-d
5, f
1-f
7, etc. of the configuration of an element do not contribute to the entropy of the element, but only to the number of unpaired electrons; entries s
2, p
6, d
10, f
14, etc., contribute with
to the entropy but do not contribute to the number of unpaired electrons; and the remaining entries contribute both to entropy and to the number of unpaired electrons. Therefore, we can introduce the following definitions.
Definition 3. An entropy-only-contributor is the element that has entropy , where and the number of unpaired electrons .
These elements are defined by
where
is given by (
10) (cf.
Figure 6) and
l increases from
for
to
for
, etc.
Definition 4. A spin-only-contributor is the element that has the number of unpaired electrons greater than the preceding element and entropy , where .
These elements range between
(
16) and
Definition 5. A spin-and-entropy-contributor is the element that has the number of unpaired electrons lower than the preceding element and entropy , where .
These elements range between
(17) and
(16) and are responsible for soft transitions between the entropy steps shown in
Figure 8 and
Figure 13.
Thus, for the Aufbau electron configurations each element is either a spin-only-contributor, an entropy-only-contributor, or a spin-and-entropy-contributor. There are only four exceptions to this rule for actual electron configurations, which occur for orbital d, namely which are spin-and-entropy-contributors having entropy equal to . For example, d10 in silver’s configuration [Kr]4d105s1 makes it entropy equal to (krypton has entropy ) and s1 makes it a spin-contributor. Furthermore, palladium is an entropy-only-contributor instead of being a spin-and-entropy-contributor and (orbitals f) are spin-only-contributors instead of being spin-and-entropy-contributors. Furthermore, all Aufbau rule non-singleton violators, have entropies higher or equal than those of the preceding exceptional elements. These results strengthen the meaning of the Aufbau rule.
The fact that hydrogen is a spin-only-contributor, while helium is an entropy-only-contributor suggests a different arrangement of the periodic table of elements shown in
Figure 9, where period terminating entropy-only-contributors define the separations of the elements. The outline of the extended periodic table is shown in
Figure 12 for
. From the 3
rd period, the left-hand rows of this periodic table increase by four every two periods
, which represents the linear part of the curve.
Figure 12.
The outline of the periodic table of elements arranged to isolate pure-entropy-contributors for
(cf.
Figure 9).
Figure 12.
The outline of the periodic table of elements arranged to isolate pure-entropy-contributors for
(cf.
Figure 9).
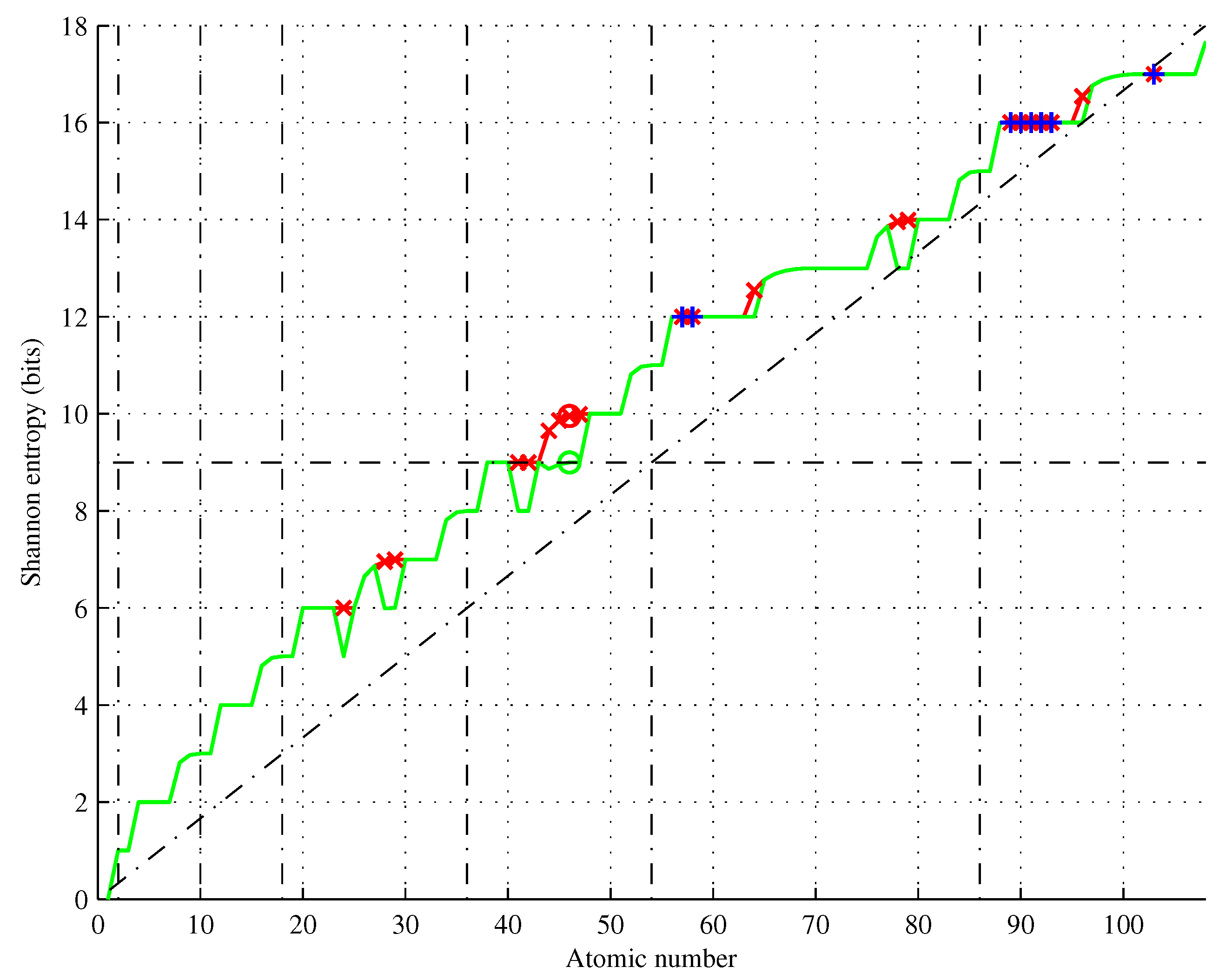
Figure 13.
Shannon entropy of elements as given by Hund’s and Aufbau rules (red), and its approximations (green) and (blue). Inset for .
Figure 13.
Shannon entropy of elements as given by Hund’s and Aufbau rules (red), and its approximations (green) and (blue). Inset for .
Figure 13 shows the element entropies for
, yielding
. This value is well beyond any considerable physical limit, although elements as heavy as
(or even
) are predicted to exist in nature [
27] due to doubly-magic nuclei [
27,
28]. However, the Compton wavelength of an atom becomes smaller than the Planck length for
[
10,
14], which is physically implausible because the Planck area is the smallest area required to encode one bit of information [
10,
29,
30,
31].
Figure 13 illustrates a trend of increasing the entropy of the elements. We conjecture that this trend continues until the element’s half-life is equal to Planck time and for
is bounded by
(cf. the blue curve in the inset of
Figure 13).
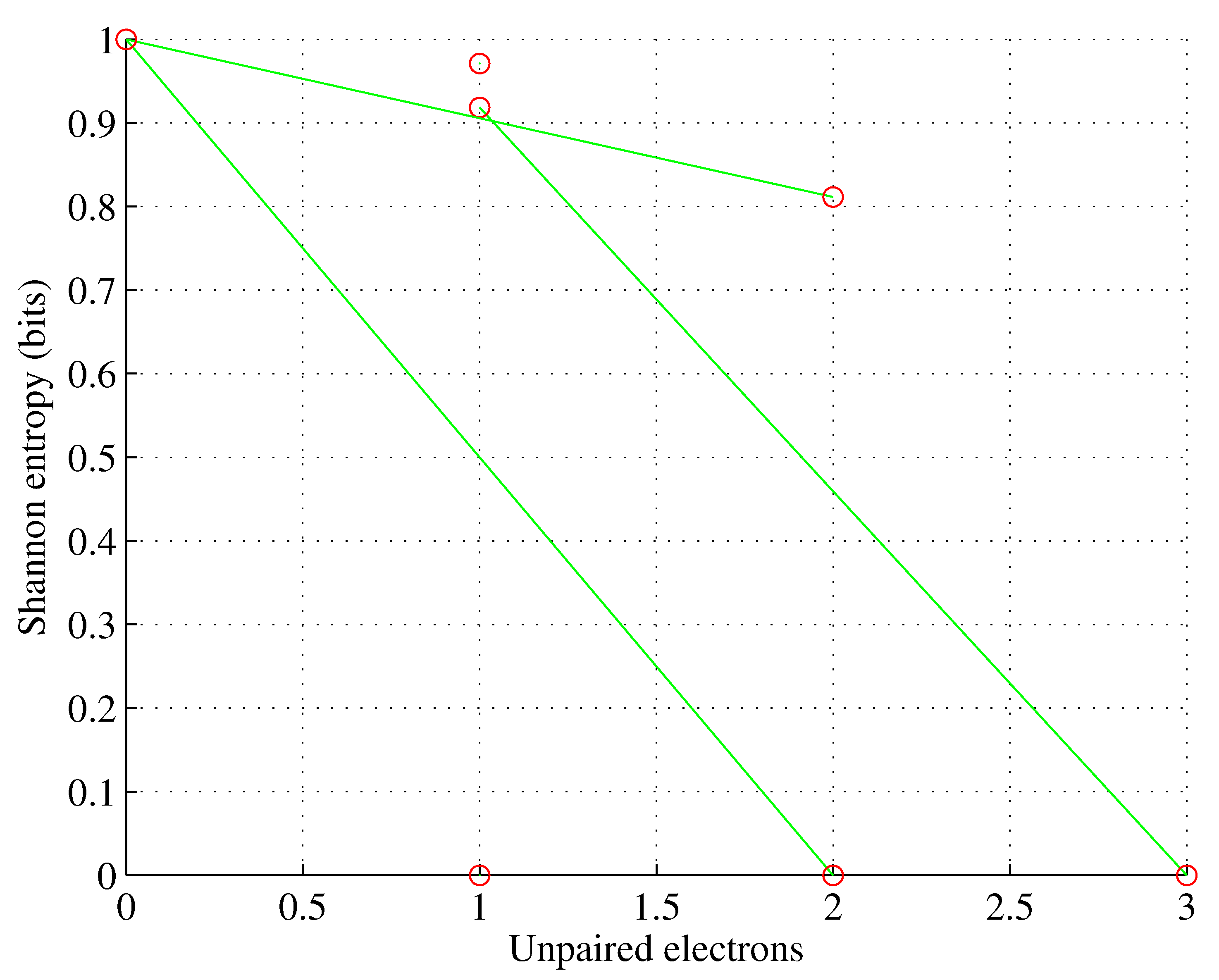
Figure 1.
Orbital p. , for , , , .
Figure 1.
Orbital p. , for , , , .
Figure 2.
Orbital d. , for , .
Figure 2.
Orbital d. , for , .
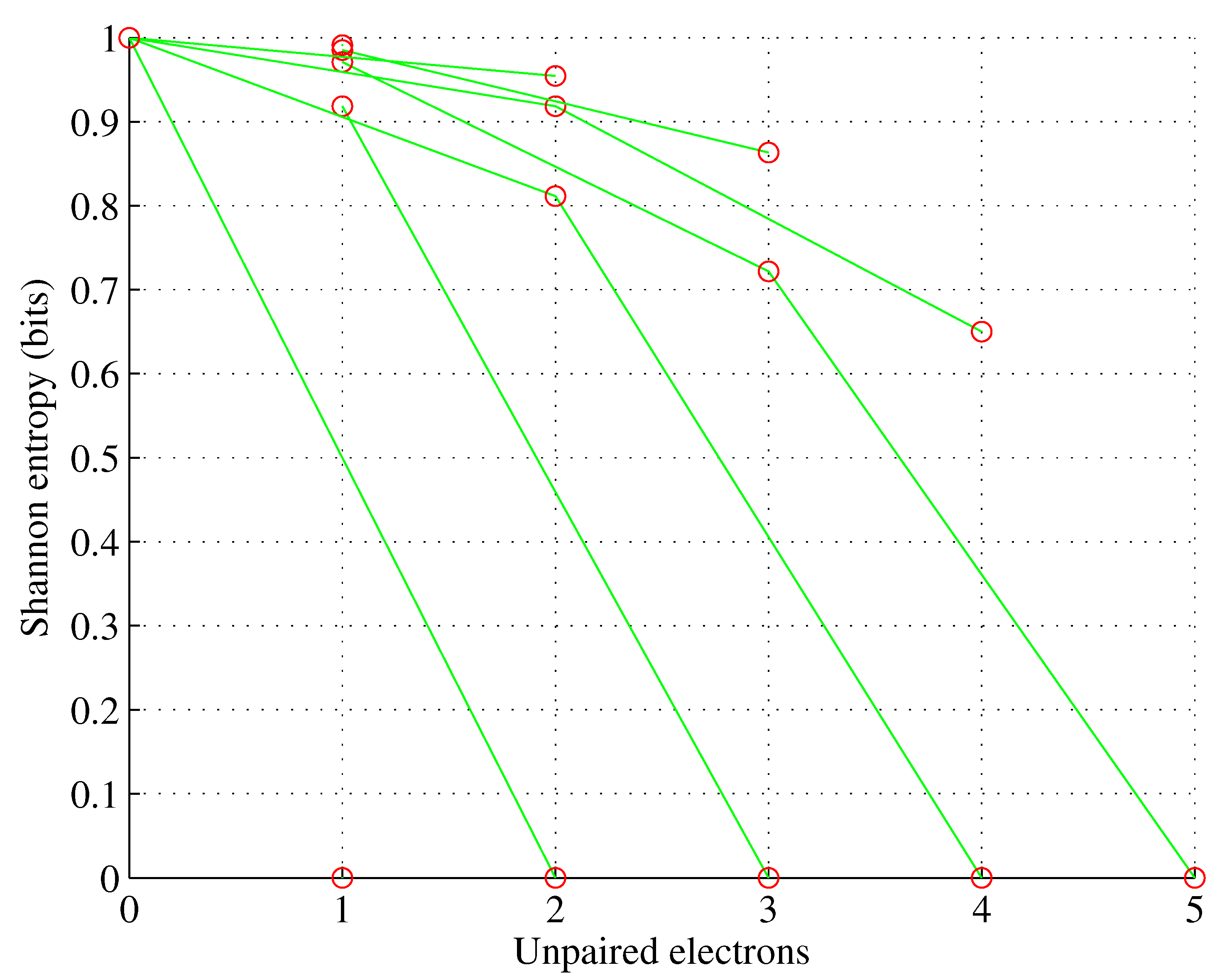
Figure 3.
Orbital f. , for , .
Figure 3.
Orbital f. , for , .
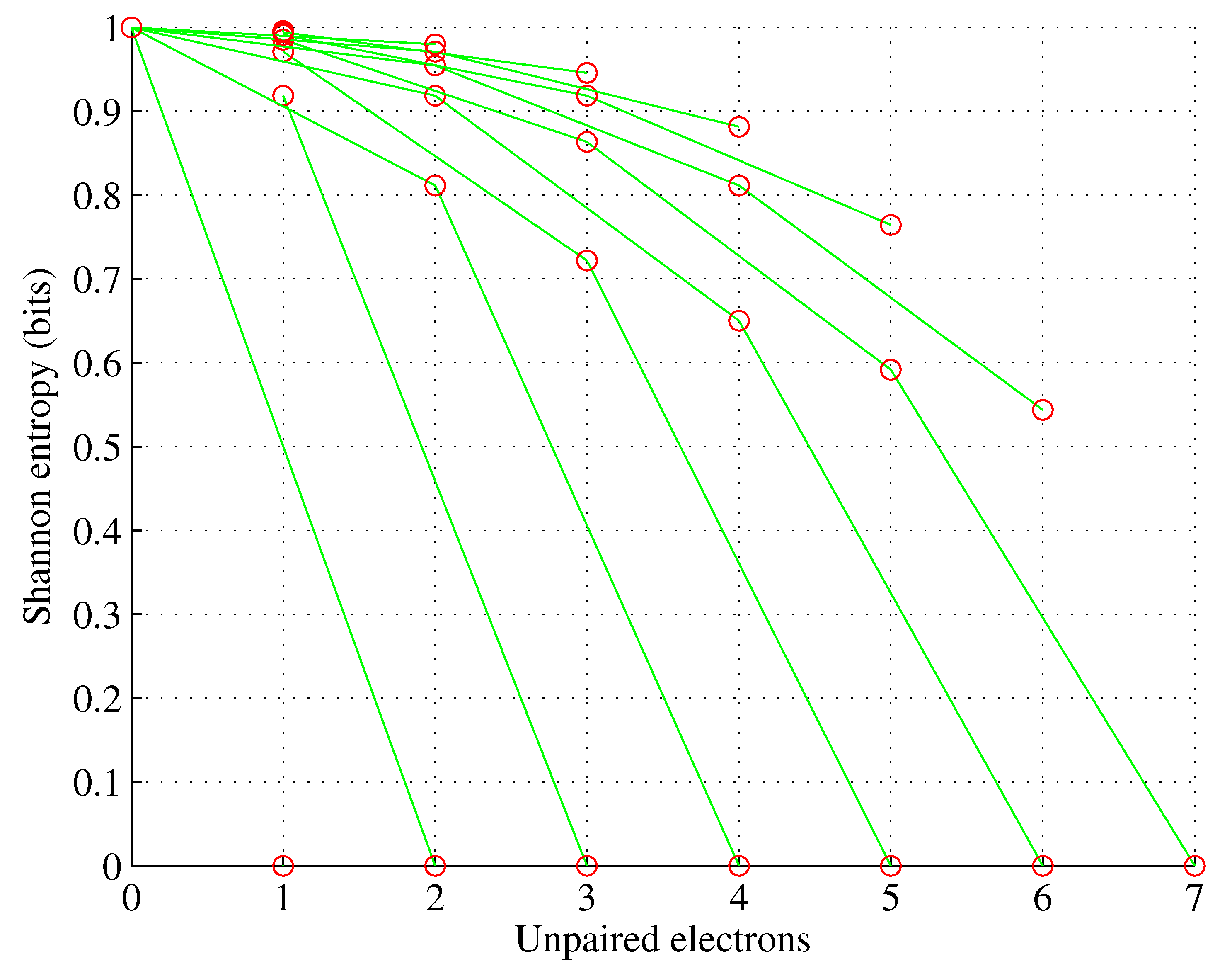
Figure 4.
Orbital g. , for , .
Figure 4.
Orbital g. , for , .
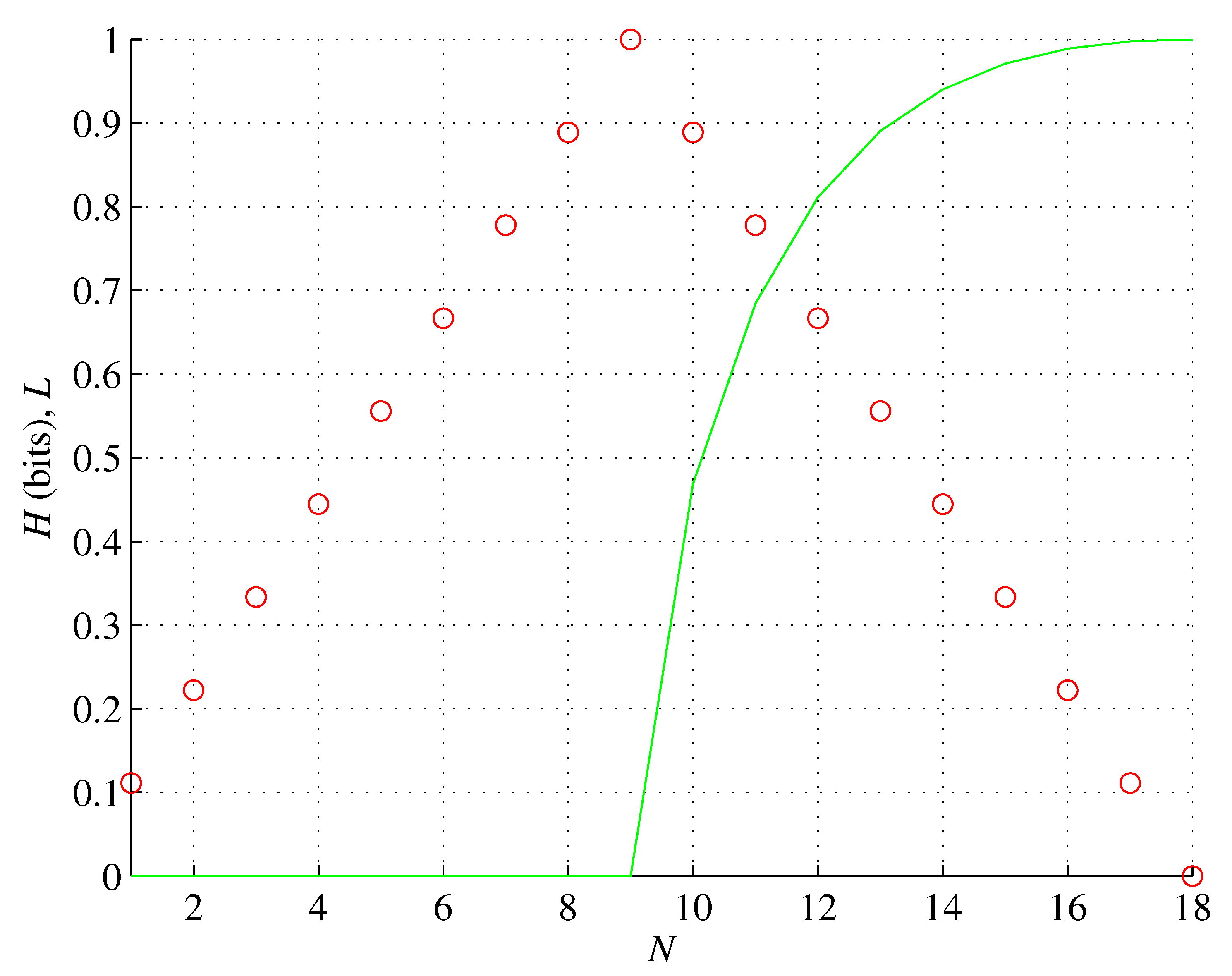
Figure 5.
Orbital g. The number of unpaired electrons L (red, rescaled) and associated orbital entropy H (green) as functions of the number of the orbital electrons N.
Figure 5.
Orbital g. The number of unpaired electrons L (red, rescaled) and associated orbital entropy H (green) as functions of the number of the orbital electrons N.
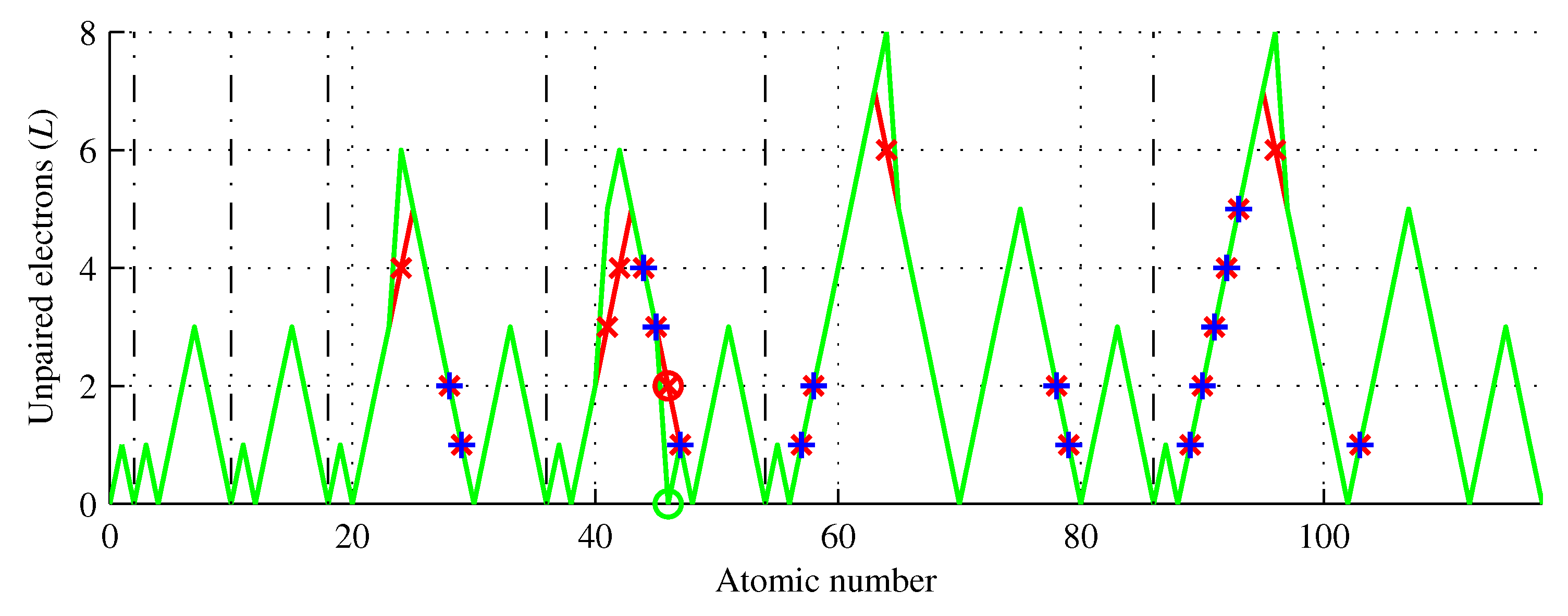
Figure 6.
Number of unpaired electrons of chemical elements (green) showing the Aufbau rule violators (red) and elements of the same L (blue). Five elements () have L higher than that predicted by the Aufbau rule. Only palladium () has a lower L.
Figure 6.
Number of unpaired electrons of chemical elements (green) showing the Aufbau rule violators (red) and elements of the same L (blue). Five elements () have L higher than that predicted by the Aufbau rule. Only palladium () has a lower L.
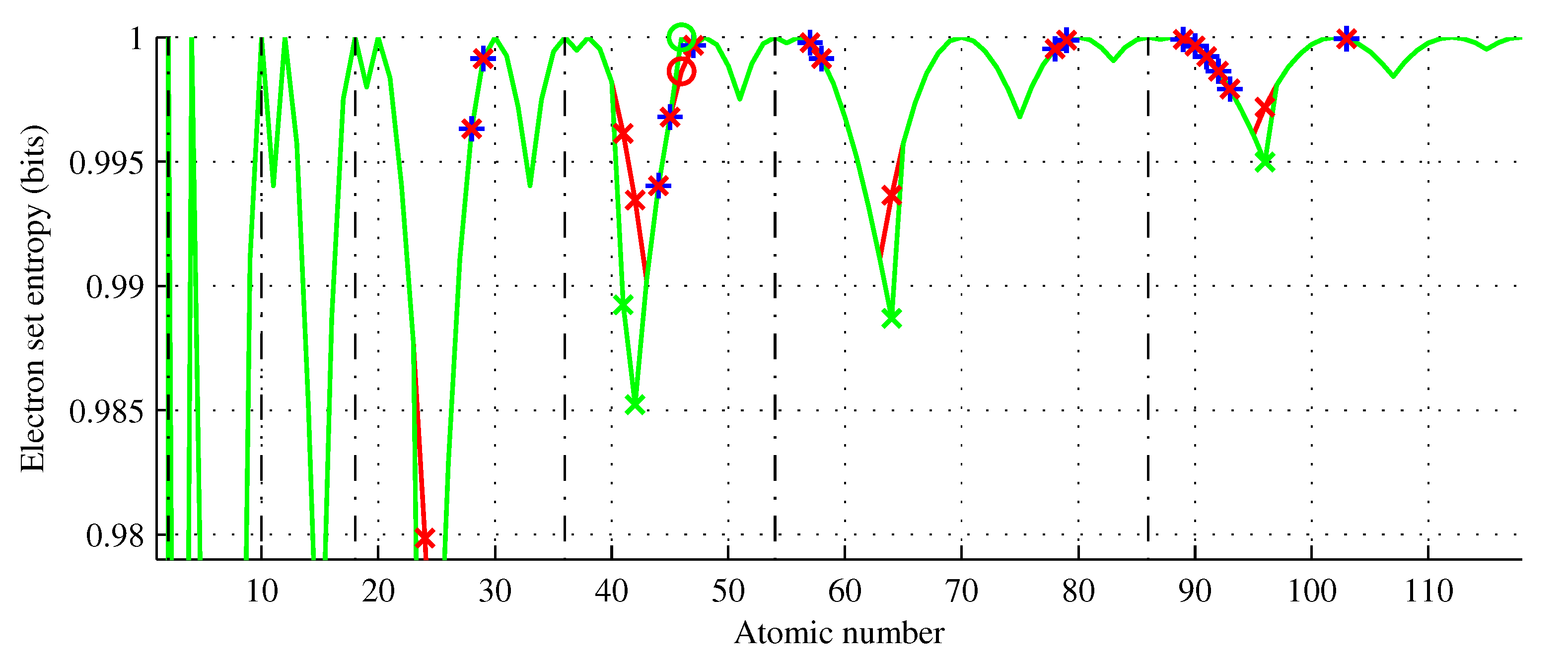
Figure 7.
Electron set entropy of chemical elements (green curve) showing the Aufbau rule violators (red x) and elements of the same entropy (blue +). Five elements () have electron entropy lower than that predicted by the Aufbau rule. This function does not increase monotonically and .
Figure 7.
Electron set entropy of chemical elements (green curve) showing the Aufbau rule violators (red x) and elements of the same entropy (blue +). Five elements () have electron entropy lower than that predicted by the Aufbau rule. This function does not increase monotonically and .
Figure 8.
Shannon entropy of chemical elements (green) showing Aufbau rule violators (red) and elements of the same entropy (blue). Thirteen elements ( including palladium) have entropy lower than that predicted by the Aufbau rule. Furthermore, .
Figure 8.
Shannon entropy of chemical elements (green) showing Aufbau rule violators (red) and elements of the same entropy (blue). Thirteen elements ( including palladium) have entropy lower than that predicted by the Aufbau rule. Furthermore, .
Table 1.
Chemical elements violating Aufbau rule.
Table 1.
Chemical elements violating Aufbau rule.
| |
|
Electron configuration |
Unpaired electrons |
Shannon entropy |
Electron set entropy |
| |
Z |
actual |
Aufbau |
|
|
|
|
|
|
| Cr |
24 |
[Ar]3d54s1
|
[Ar]3d44s2
|
6 |
4 |
|
|
0.9544 |
0.9799 |
| Ni |
28 |
[Ar]3d84s2 (or [Ar]3d94s1) |
[Ar]3d84s2
|
2 |
|
|
0.9963 |
| Cu |
29 |
[Ar]3d104s1
|
[Ar]3d94s2
|
1 |
|
|
0.9991 |
| Nb |
41 |
[Kr]4d45s1
|
[Kr]4d35s2
|
5 |
3 |
|
|
0.9892 |
0.9961 |
| Mo |
42 |
[Kr]4d55s1
|
[Kr]4d45s2
|
6 |
4 |
|
|
0.9852 |
0.9934 |
| Ru |
44 |
[Kr]4d75s1
|
[Kr]4d65s2
|
4 |
|
|
0.9940 |
| Rh |
45 |
[Kr]4d85s1
|
[Kr]4d75s2
|
3 |
|
|
0.9968 |
| Pd |
46 |
[Kr]4d10
|
[Kr]4d85s2
|
0 |
2 |
|
|
1 |
0.9986 |
| Ag |
47 |
[Kr]4d105s1
|
[Kr]4d95s2
|
1 |
|
|
0.9997 |
| La |
57 |
[Xe]5d16s2
|
[Xe]4f16s2
|
1 |
|
0.9998 |
| Ce |
58 |
[Xe]4f15d16s2
|
[Xe]4f26s2
|
2 |
|
0.9991 |
| Gd |
64 |
[Xe]4f75d16s2
|
[Xe]4f86s2
|
8 |
6 |
|
|
0.9887 |
0.9937 |
| Pt |
78 |
[Xe]4f145d96s1
|
[Xe]4f145d86s2
|
2 |
|
|
0.9995 |
| Au |
79 |
[Xe]4f145d106s1
|
[Xe]4f145d96s2
|
1 |
|
|
0.9999 |
| Ac |
89 |
[Rn]6d17s2
|
[Rn]5f17s2
|
1 |
|
0.9999 |
| Th |
90 |
[Rn]6d27s2
|
[Rn]5f27s2
|
2 |
|
0.9996 |
| Pa |
91 |
[Rn]5f26d17s2
|
[Rn]5f37s2
|
3 |
|
0.9992 |
| U |
92 |
[Rn]5f36d17s2
|
[Rn]5f47s2
|
4 |
|
0.9986 |
| Np |
93 |
[Rn]5f46d17s2
|
[Rn]5f57s2
|
5 |
|
0.9979 |
| Cm |
96 |
[Rn]5f76d17s2
|
[Rn]5f87s2
|
8 |
6 |
|
|
0.9950 |
0.9972 |
| Lf |
103 |
[Rn]5f147s27p1
|
[Rn]5f146d17s2
|
1 |
|
0.9999 |
Table 2.
Extended Aufbau rule. Periodic table for .
Table 2.
Extended Aufbau rule. Periodic table for .
| k |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
0 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
2 |
| 0 |
0 |
|
2 |
|
|
|
|
|
2 |
0 |
| 1 |
1 |
|
2 |
|
|
|
|
|
2 |
2 |
| 2 |
2 |
3 |
2 |
|
|
|
|
6 |
8 |
10 |
| 3 |
4 |
5 |
2 |
|
|
|
|
6 |
8 |
18 |
| 4 |
6 |
8 |
2 |
|
|
|
|
6 |
18 |
36 |
| 5 |
9 |
11 |
2 |
|
|
|
|
6 |
18 |
54 |
| 6 |
12 |
15 |
2 |
|
|
|
|
6 |
32 |
86 |
| 7 |
16 |
19 |
2 |
|
|
|
|
6 |
32 |
118 |
| 8 |
20 |
24 |
2 |
|
18 |
14 |
10 |
6 |
50 |
168 |
| 9 |
25 |
29 |
2 |
|
18 |
14 |
10 |
6 |
50 |
218 |
| 10 |
30 |
35 |
2 |
22 |
18 |
14 |
10 |
6 |
72 |
290 |
| 11 |
36 |
41 |
2 |
22 |
18 |
14 |
10 |
6 |
72 |
362 |