Prerpints.org logo
Preprint
Article

Filtering Methods for Biomedical Image Denoising

Altmetrics

Downloads

241

Views

158

Comments

0

This version is not peer-reviewed

Submitted:

18 October 2023

Posted:

18 October 2023

You are already at the latest version

Alerts
Abstract
In this paper, the filtering method of biomedical image denoising is described comprehensively. Firstly, it introduces the biomedical image denoising, describes the relationship between biomedical image denoising and medical care, introduces the filtering methods, the filtering methods of biomedical image denoising, the challenges encountered by the current filtering methods, and other application fields of filtering methods. Firstly, the background of biomedical image denoising is introduced. Biomedical image denoising is a challenge. Different imaging modes have different noise characteristics, and noise levels can vary greatly depending on the specific application. Secondly, it describes that biomedical image denoising plays an important role in medical care, and the biomedical image directly affects the patient's diagnosis, treatment plan and the overall quality of medical care service. Then the filtering method is introduced in detail, describing the core concepts and related features of linear filtering, nonlinear filtering and frequency domain filtering, and then focusing on the adaptive filtering method, describing the characteristics, conditions of use, common algorithms and advantages of adaptive filtering method. Then the filter methods of biomedical image denoising are introduced, and the core concepts of Gaussian filter, median filter, total variation denoising and Wiener filter are introduced respectively. Then, the challenges encountered by filtering methods are described, such as the accurate selection of filters, the balance between noise reduction and image detail preservation are introduced. Finally, the application of filtering method in other fields is mentioned, such as audio processing, speech recognition and so on. In summary, this paper comprehensively expounds the denoising and filtering methods of biomedical images, the filtering methods of medical image denoising, the relationship between medical image denoising and medical care, and the challenges encountered by filtering methods.
Keywords: 
Subject: Biology and Life Sciences  -   Life Sciences

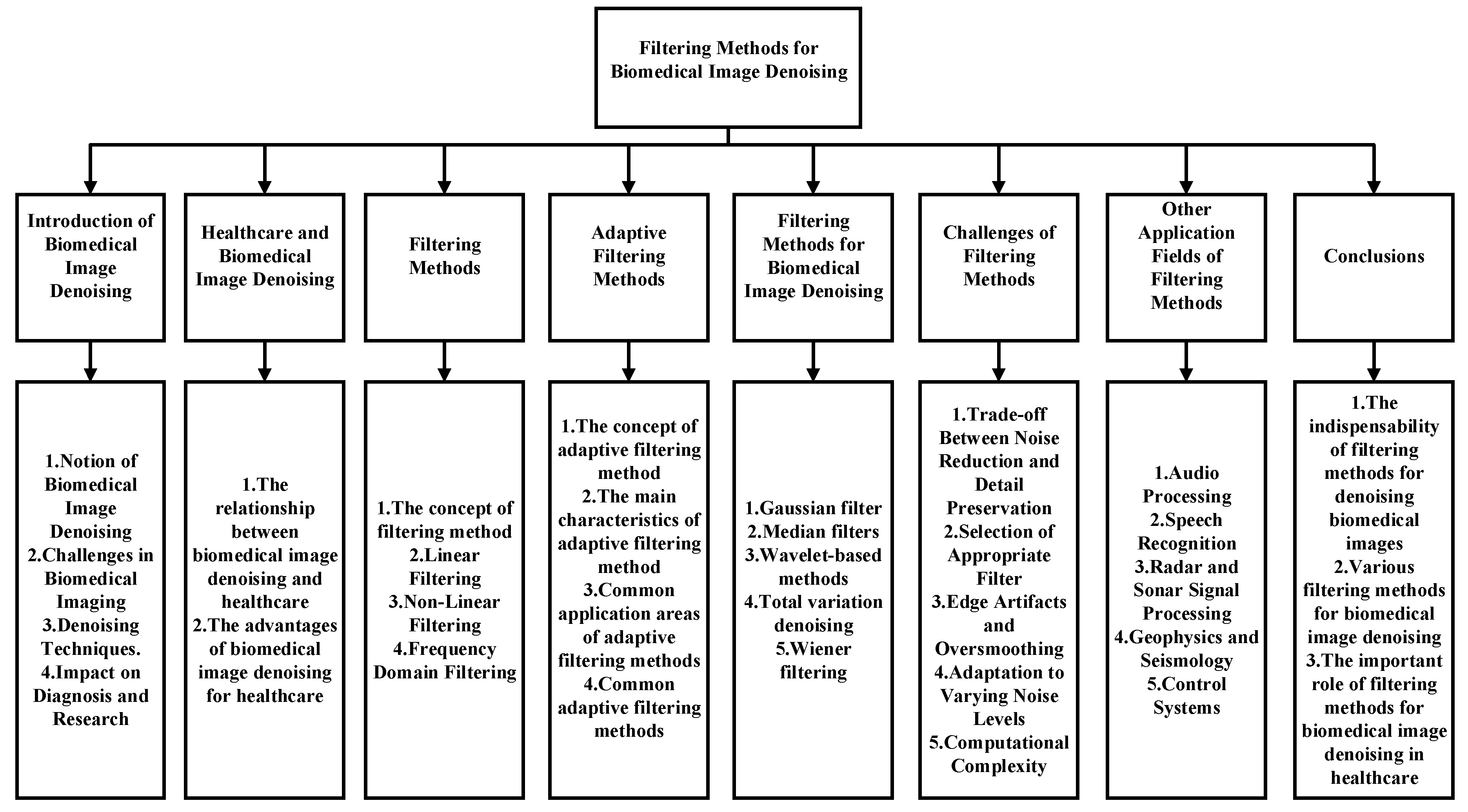
1. Introduction of Biomedical Image Denoising

Biomedical image denoising refers to the process of reducing or removing unwanted noise from images acquired in various medical imaging modalities, such as X-ray, MRI (Magnetic Resonance Imaging), CT (Computed Tomography) scans, ultrasound, and microscopy. These medical images are crucial for diagnosis, treatment planning, and research in the field of healthcare and life sciences [1]. According to Figure 1, they are often subject to noise due to various factors, including limitations in imaging equipment, patient motion, and electronic interference.
Challenges in Biomedical Imaging: Biomedical images [2] often present unique challenges for denoising. Different imaging modalities have distinct noise characteristics, and the level of noise can vary widely based on the specific application [3]. For example, MRI images may suffer from thermal noise, while ultrasound images may exhibit speckle noise [4]. Moreover, medical images frequently contain subtle details and structures that need to be preserved during denoising to ensure accurate diagnosis and research analysis [5,6].
Denoising Techniques: Various denoising techniques are applied in biomedical image processing, including traditional methods like Gaussian filtering, median filtering, and anisotropic diffusion, as well as more advanced 1.approaches like wavelet-based denoising, total variation denoising, and deep learning-based methods [7,8]. The choice of denoising method depends on the nature of the noise, the imaging modality, and the specific objectives of the medical imaging task [9].
Impact on Diagnosis and Research: The successful denoising of biomedical images has a significant impact on medical professionals and researchers. It enhances the visibility of critical structures, reduces artifacts, and improves the overall quality of images [10]. In turn, this leads to more accurate diagnoses, better treatment planning, and more reliable scientific conclusions in biomedical research. As imaging technology continues to advance, the development and application of effective denoising techniques remain critical for the progress of healthcare and medical science [11]. Paper structure is as in Figure 2:

2. Healthcare and Biomedical Image Denoising

As in Figure 3, the relationship between healthcare and biomedical image denoising is integral and highly symbiotic. Biomedical image denoising plays a crucial role in healthcare, directly impacting patient diagnosis, treatment planning, and the overall quality of healthcare services [12]. Here are several key aspects of the relationship between healthcare and biomedical image denoising:
Biomedical image denoising enhances the quality and clarity of medical images obtained through various modalities such as X-ray, MRI [13], CT scans, ultrasound, and more [14]. When medical images are less noisy and contain fewer artifacts, healthcare professionals, including radiologists, physicians, and surgeons, can make more accurate and reliable diagnoses [15]. This directly translates into better patient outcomes and informed treatment decisions.
Biomedical researchers heavily rely on high-quality images for their studies, whether they are conducting clinical trials, investigating disease mechanisms, or developing new medical technologies and treatments. Clean and denoised biomedical images are crucial for generating valid and reproducible research results, which can lead to breakthroughs in healthcare and the development of new diagnostic and therapeutic approaches [16].
In the era of precision medicine, where treatments are tailored to individual patients based on their unique genetic makeup, medical history, and disease characteristics, biomedical image denoising plays a critical role. It ensures that the images used for personalized treatment planning are as accurate and informative as possible, enabling healthcare providers to make the most appropriate choices for each patient [17].
Biomedical image denoising also contributes to patient safety and comfort. When medical imaging procedures can produce high-quality images with reduced noise, there is often less need for repeated scans or higher radiation doses [18], which can expose patients to unnecessary risks. Moreover, patients can experience less anxiety and discomfort when they have confidence in the accuracy of their diagnostic images.
In healthcare settings, time is often of the essence. Biomedical image denoising can contribute to a more efficient workflow by producing cleaner images that are easier to interpret [19]. This efficiency benefits both healthcare professionals and patients by reducing the time required for diagnosis, treatment planning, and follow-up procedures [20].
In the context of telemedicine and remote consultations, especially relevant during the COVID-19 pandemic, high-quality denoised images are essential for remote healthcare providers to make accurate assessments and recommendations without the need for in-person visits [21].

3. Filtering Methods

Filtering methods refer to a broad class of techniques used in various fields, including signal processing, image processing, and data analysis, to modify or extract specific components of a signal or data [22]. Filters are employed to enhance, suppress, or isolate certain features or information within a signal or dataset. There are several types of filtering methods, including:
Linear Filtering: (i) Linear filters, such as low-pass, high-pass, bandpass, and notch filters, operate on signals or data using linear operations like convolution [23]. (ii) Low-pass filters allow low-frequency components to pass through while attenuating high-frequency components, making them useful for smoothing or noise reduction [24]. All linear low-pass filters can be understood as integral operators acting on the space of integrable real functions. They can be expressed as integrals on the real line, involving certain kernel functions.
G x = 1 2 a 0 + ∑ n = 1 ∞ a n cos ⁡ k x + b n sin ⁡ k x
where the coefficients are given by
a n = 1 Π ∫ − Π Π d x   cos ⁡ k x   G x
b n = 1 Π ∫ − Π Π d x   sin ⁡ k x   G x
(iii) High-pass filters emphasize high-frequency components while suppressing low-frequency ones and are often used for edge detection [25]. (iv) Bandpass filters allow a specific range of frequencies to pass through, ideal for isolating a particular frequency band of interest [26]. (v) Notch filters reject a specific frequency or narrow frequency range, typically used to remove unwanted interference or noise at specific frequencies [27]. Table 1 shows the difference between them.
Non-Linear Filtering [28]: (i) Non-linear filters, unlike linear filters, apply non-linear operations to modify or process data. Examples include median filters and morphological filters [29]. (ii) Median filters replace a pixel's value with the median value of its neighborhood, effectively reducing the impact of outliers and impulse noise [30]. (iii) Morphological filters are used in image processing to perform operations like erosion and dilation, which can enhance or suppress features based on their shapes and structures [31]. From Table 2, we can see the comparison between linear filtering and nonlinear filtering.
Frequency Domain Filtering: (i) Frequency domain filtering involves transforming a signal or image into the frequency domain using techniques like the Fourier transform [32]. Filtering is then applied in the frequency domain, followed by an inverse transform to return to the time or spatial domain [33]. (ii) Frequency domain filters can be used for tasks like image enhancement and noise reduction by targeting specific frequency components [34].

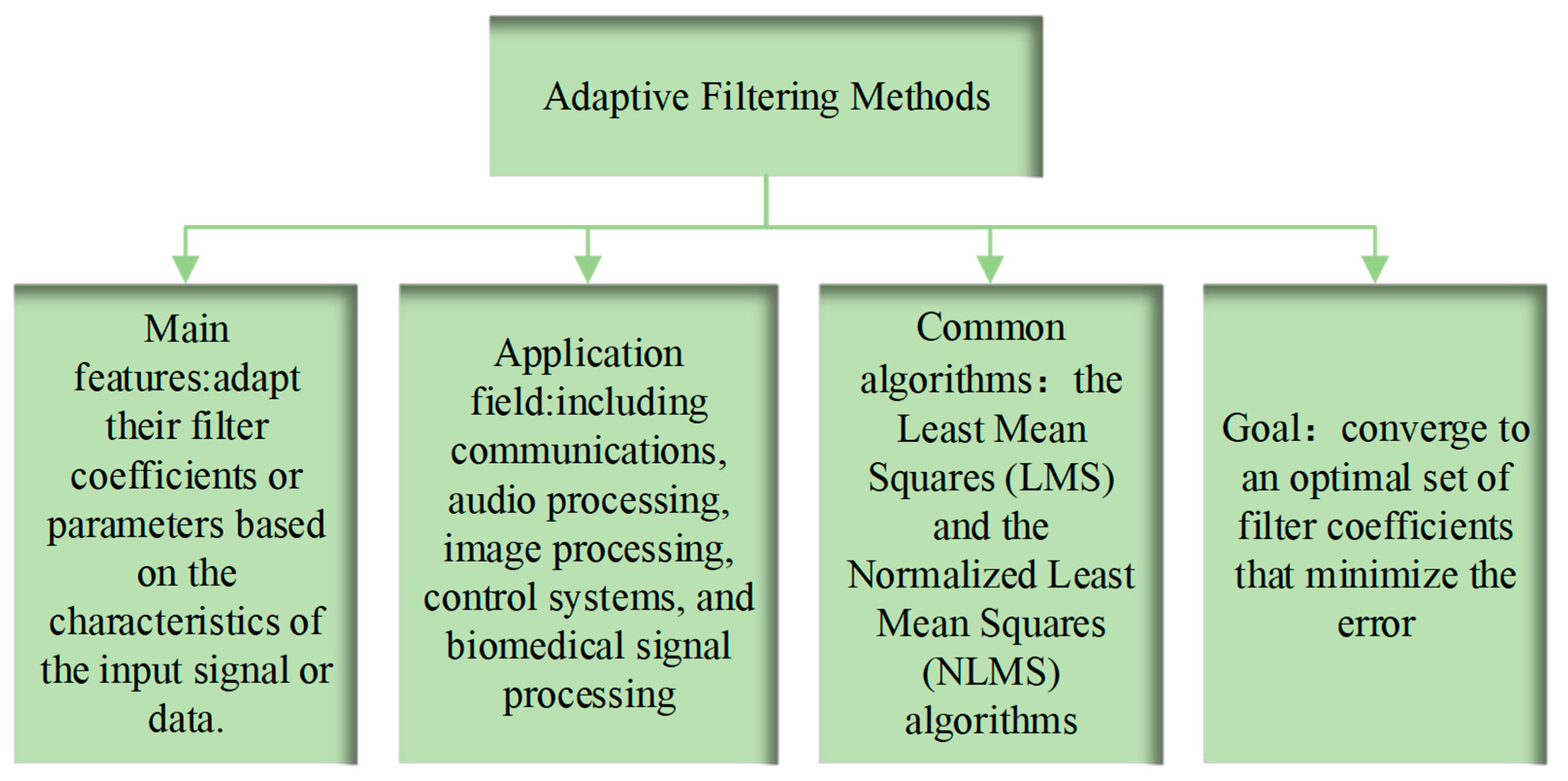
4. Adaptive Filtering Methods

Adaptive filtering methods [35] are a class of signal processing techniques that adjust the parameters of a filter or the filtering process in response to changes in the input signal or data [36]. These methods are particularly useful when the characteristics of the input signal are dynamic, unknown, or vary over time. Adaptive filters can automatically adapt to these changing conditions to optimize their performance. As shown in the Figure 4, here are some key aspects of adaptive filtering methods:
The primary feature of adaptive filters is their ability to adapt their filter coefficients or parameters based on the characteristics of the input signal or data [37]. This adaptation allows the filter to continuously modify its behavior, making it well-suited for scenarios where the signal statistics are not constant.
Adaptive filtering methods find applications in various fields, including communications, audio processing, image processing, control systems, and biomedical signal processing [38]. They are used for tasks such as noise cancellation, echo suppression, channel equalization, and adaptive beamforming in microphone arrays.
Two commonly used adaptive filtering algorithms are the Least Mean Squares (LMS) [39] and the Normalized Least Mean Squares (NLMS) algorithms [40]. Consider an image Y, the filtered value at a point p using the NLM method is calculated as a weighted average of all the pixels in the image:
N L M N P = ∑ ∀ q ∈ α Z p , q N q ,   0 ≤ Z p , q ≤ 1 , ∑ ∀ q ∈ α Z p , q = 1
where p is the point being filtered and q represents each one of the pixels in the neighbourhood n of radius .The similarity Z(p,q) is then calculated as:
Z p , q = 1 T p e − d p , q h 2
where T(p) is called normalizing constant and can be calculated as:
T p = ∑ ∀ q e − d p , q h 2
h is an exponential decay control parameter and d is a Gaussian weighted Euclidian distance of all the pixels of each neighbourhood. These algorithms iteratively adjust filter coefficients to minimize the mean squared error between the filter output and a desired signal, which is typically related to the input signal.
Adaptive filters aim to converge to an optimal set of filter coefficients that minimize the error. Convergence speed is a crucial consideration [41], as faster convergence can be desirable for real-time applications. Tracking ability is also important to ensure that the filter adapts effectively to changes in the input signal.
Some adaptive filtering algorithms employ variable step sizes, allowing the filter to adapt more quickly when the input signal changes rapidly and more slowly when it stabilizes. This helps strike a balance between adaptation speed and stability [42].
Adaptive filtering is often used for noise reduction tasks, such as echo cancellation and noise suppression in audio and communication systems. These applications benefit from the ability of adaptive filters to continuously adapt to changing noise conditions [43].
In modern machine learning [44] and neural network training [45], adaptive filtering techniques can be used as optimization algorithms for training deep learning models [46,47]. They adapt the model's parameters based on the training data and the loss function to achieve better model performance.

5. Filtering Methods for Biomedical Image Denoising

Filtering methods for biomedical image denoising are essential techniques used to enhance the quality and clarity of medical images by reducing or removing unwanted noise and artifacts [48]. Biomedical images, acquired through modalities like MRI, CT scans, ultrasound, and microscopy, often suffer from noise due to factors such as equipment limitations, patient motion, and interference [49]. Filtering methods are crucial in healthcare and life sciences for accurate diagnosis, treatment planning, and research. As shown in Table 3, here's an introduction to some of the key filtering methods used in biomedical image denoising:
Gaussian filters are commonly used in biomedical image denoising to reduce noise. They apply a weighted average to pixel values within a local neighborhood, effectively smoothing the image [50]. Gaussian filters are particularly useful for reducing Gaussian noise, which is characterized by a bell-shaped probability distribution.
Median filters are effective for removing impulse noise, such as salt-and-pepper noise, commonly seen in medical images. Instead of averaging pixel values, median filters replace each pixel with the median value within a local window. This approach is robust against outliers and preserves edges and fine details [51].
Wavelet-based methods utilize the discrete wavelet transform (DWT) to represent images at multiple scales. These methods decompose an image into different frequency components and then apply thresholding or other techniques to denoise high-frequency components while preserving low-frequency details. Wavelet denoising is well-suited for medical images with varying textures and structures [52].
Total variation denoising is a regularization technique used to reduce noise in biomedical images while preserving edges. It minimizes the total variation in pixel values within the image, effectively smoothing the image while maintaining sharp boundaries [53].
Wiener filtering is an optimal linear filter that minimizes the mean squared error between the estimated image and the true image. It is particularly useful when noise statistics are known or can be estimated accurately [54].
Deep learning techniques, particularly convolutional neural networks (CNNs), 2DCNN is composed of convolution layer and pooling layer. The m th feature map of the n th layer is obtained by the calculation of several feature maps in the upper layer, which can be calculated as
x m n = S ∑ i ∈ N m x i n − 1 * w i m n + b m n
where S() is an activation function called relu. x i n − 1 represents the pixel value of the upper feature map, N m represents the subset of the upper feature map, w i m n is the convolution kernel, b m n It's a deviation. The pooling window slides on the feature map at a certain step size and samples in the corresponding block, which is expressed as
x m n = S G x m n − 1 + b m n
where G() denotes the pooling function. The three-dimensional convolution process can be expressed as
V i m x y z = s b i m + ∑ l ∑ p = 0 P i − 1 ∑ q = 0 Q i − 1 ∑ r = 0 R i − 1 W i m l p q r V i − 1 l x + p y + q z + r V i m x y z
represents the result of the m th feature mapping pixel (x,y) in the layer i, s() represents the activation function, b i m is the deviation of the m th feature in layer i, l is the number of feature mappings in layer (i-1).They have shown remarkable success in biomedical image denoising [55]. These networks are trained on large datasets of noisy-clean image pairs and can learn complex noise patterns for effective denoising while preserving important image features.

6. Challenges of Filtering Methods

While filtering methods are powerful tools for various signal processing and image enhancement tasks. As shown in Figure 5,they also face several challenges and limitations that need to be considered during their application:
Trade-off Between Noise Reduction and Detail Preservation: One of the primary challenges of filtering methods is finding the right balance between noise reduction and detail preservation [56]. Aggressive noise reduction can result in the loss of important image features and structures, potentially impacting the accuracy of diagnostic or analytical results. Striking the optimal trade-off often requires fine-tuning filter parameters, which can be a complex and time-consuming task.
Selection of Appropriate Filter: Choosing the most suitable filter for a specific task can be challenging. Different types of noise and image characteristics may require different filtering techniques [46]. Understanding the nature of the noise in the data and the desired outcome is crucial for selecting the right filter. In some cases, a combination of filters or advanced hybrid approaches may be necessary to achieve the desired results.
Edge Artifacts and Oversmoothing: Many filtering methods, such as Gaussian or median filters, can introduce edge artifacts or oversmooth the image, particularly near sharp transitions or boundaries. These artifacts can distort the image and obscure important features [57]. Careful consideration of the filter's impact on edges and boundaries is essential to mitigate this challenge.
Adaptation to Varying Noise Levels: In real-world scenarios, noise levels may vary within an image or across different images. Standard filtering methods may not be well-equipped to handle such variations effectively. Adaptive filtering approaches, which adjust filter parameters based on local image characteristics, can address this challenge to some extent but may require complex algorithms and extensive computational resources [58].
Computational Complexity: Some advanced filtering methods, especially those based on wavelets or deep learning, can be computationally intensive. Processing large biomedical images or high-resolution data can be time-consuming and resource-intensive, which may limit their practical application in real-time or resource-constrained environments [59].

7. Other Application Fields of Filtering Methods

Filtering methods find applications in various fields beyond traditional signal processing and image enhancement. Their ability to modify or extract specific components of data or signals makes them valuable tools in a wide range of domains. As shown in Figure 6, here are some other application fields of filtering methods:
Audio Processing : Filtering methods are extensively used in audio processing for tasks such as noise reduction, equalization, and audio effects like reverb and echo removal [60].Audio equalizers employ filters to adjust the frequency response of audio signals, allowing users to enhance or attenuate specific frequency bands.
Speech Recognition: Filtering is crucial in speech recognition systems for preprocessing speech signals. Techniques like voice activity detection (VAD) and noise reduction filters help improve the accuracy of speech recognition algorithms [61].
Radar and Sonar Signal Processing: Radar and sonar systems use filtering methods to extract relevant information from complex signals. Filters help detect targets, remove clutter, and enhance signal-to-noise ratios in radar and sonar data [62].
Geophysics and Seismology: Filtering plays a critical role in the analysis of seismic data. Filters help identify earthquake events, locate underground structures, and study ground motion characteristics in geophysics and seismology [63].
Control Systems: Control systems often utilize filters for noise rejection, signal conditioning, and feedback control. Filters can improve the stability and performance of control systems in engineering applications [64].

8. Conclusions

In conclusion, filtering methods for biomedical image denoising are indispensable tools in healthcare and life sciences, playing a pivotal role in enhancing the quality and reliability of medical images. These methods address the persistent challenge of noise reduction in medical images acquired through modalities such as MRI, CT scans, ultrasound, and microscopy [48]. The effectiveness of filtering techniques is instrumental in ensuring accurate diagnoses, precise treatment planning, and scientific research in the field.
Biomedical image denoising encompasses various filtering approaches, including Gaussian filtering, median filtering, wavelet denoising, total variation denoising, non-local means (NLM) denoising, and deep learning-based methods [65]. Each of these techniques is tailored to address specific noise characteristics and image structures encountered in medical imaging.
The application of filtering methods in biomedical image denoising is guided by a deep understanding of the underlying noise sources and the need to strike a balance between noise reduction and the preservation of critical anatomical and pathological features. Challenges, such as edge artifacts, oversmoothing, and adaptability to varying noise levels, must be carefully considered and mitigated during the denoising process [66].
In healthcare, filtering methods for biomedical image denoising contribute significantly to improving patient care, enabling precise diagnoses, and advancing medical research [67]. As technology continues to evolve, these methods will play an increasingly vital role in harnessing the potential of medical imaging for better patient outcomes and deeper insights into the complexities of human health and disease.

Funding

This research did not receive any grants.

Acknowledgments

We thank all the anonymous reviewers for their hard reviewing work.

References

  1. S. Wang, "Detection of Dendritic Spines using Wavelet Packet Entropy and Fuzzy Support Vector Machine," CNS & Neurological Disorders - Drug Targets, vol. 16, pp. 116-121, 2017. [CrossRef]
  2. Y.-D. Zhang, "Advanced deep learning methods for biomedical information analysis: An editorial," Neural networks, vol. 133, pp. 101-102, 2021. [CrossRef]
  3. S. Wang, "Advances in data preprocessing for biomedical data fusion: an overview of the methods, challenges, and prospects," Information Fusion, vol. 76, pp. 376-421, 2021.
  4. C. P. Loizou and C. S. Pattichis, Despeckle filtering for ultrasound imaging and video, volume I: Algorithms and software: Springer Nature, 2022.
  5. Y. Zhang, "A Fast Document Image Denoising Method based on Packed Binary format and Source Word Accumulation," Journal of Convergence Information Technology, vol. 6, pp. 131-137, 2011.
  6. C. Huang, "Analysis methods of coronary artery intravascular images: A review," Neurocomputing, vol. 489, pp. 27-39, 2022. [CrossRef]
  7. S. V. M. Sagheer and S. N. George, "A review on medical image denoising algorithms," Biomedical signal processing and control, vol. 61, p. 102036, 2020. [CrossRef]
  8. S.-H. Wang and S. Fernandes, "AVNC: Attention-based VGG-style network for COVID-19 diagnosis by CBAM," IEEE Sensors Journal, vol. 22, pp. 17431 - 17438, 2022. [CrossRef]
  9. F. Garcea, A. Serra, F. Lamberti, and L. Morra, "Data augmentation for medical imaging: A systematic literature review," Computers in Biology and Medicine, p. 106391, 2022. [CrossRef]
  10. Z. Chen, K. Pawar, M. Ekanayake, C. Pain, S. Zhong, and G. F. Egan, "Deep learning for image enhancement and correction in magnetic resonance imaging—state-of-the-art and challenges," Journal of Digital Imaging, vol. 36, pp. 204-230, 2023. [CrossRef]
  11. K. B. Johnson, W. Q. Wei, D. Weeraratne, M. E. Frisse, K. Misulis, K. Rhee, et al., "Precision medicine, AI, and the future of personalized health care," Clinical and translational science, vol. 14, pp. 86-93, 2021. [CrossRef]
  12. J. Huang, Z. Zhao, C. Ren, Q. Teng, and X. He, "A prior-guided deep network for real image denoising and its applications," Knowledge-Based Systems, vol. 255, p. 109776, 2022. [CrossRef]
  13. S. Wang, "Magnetic resonance brain classification by a novel binary particle swarm optimization with mutation and time-varying acceleration coefficients," Biomedical Engineering-Biomedizinische Technik, vol. 61, pp. 431-441, 2016. [CrossRef]
  14. G. V. Sai, C. Seshank, P. P. S. Krishna, and J. S. Dhatterwal, "Reduction of Noise in Medical Imaging Quality," in 2023 International Conference on Disruptive Technologies (ICDT), 2023, pp. 364-368.
  15. A. Albahri, A. M. Duhaim, M. A. Fadhel, A. Alnoor, N. S. Baqer, L. Alzubaidi, et al., "A systematic review of trustworthy and explainable artificial intelligence in healthcare: Assessment of quality, bias risk, and data fusion," Information Fusion, 2023.
  16. F. A. Al-Joufi, A. Setia, M. M. Salem-Bekhit, R. K. Sahu, F. Y. Alqahtani, R. Widyowati, et al., "Molecular pathogenesis of colorectal cancer with an emphasis on recent advances in biomarkers, as well as nanotechnology-based diagnostic and therapeutic approaches," Nanomaterials, vol. 12, p. 169, 2022.
  17. A. Tariq, A. Y. Gill, and H. K. Hussain, "Evaluating the Potential of Artificial Intelligence in Orthopedic Surgery for Value-based Healthcare," International Journal of Multidisciplinary Sciences and Arts, vol. 2, pp. 27-35, 2023. [CrossRef]
  18. L. R. Koetzier, D. Mastrodicasa, T. P. Szczykutowicz, N. R. van der Werf, A. S. Wang, V. Sandfort, et al., "Deep learning image reconstruction for CT: technical principles and clinical prospects," Radiology, vol. 306, p. e221257, 2023. [CrossRef]
  19. arXiv:2309.11820.A. Ramesh, A. Nandanan, P. N. MD, and G. Gressel, "Automatic Endoscopic Ultrasound Station Recognition with Limited Data," arXiv preprint arXiv:2309.11820, 2023.
  20. M. Strunga, R. Urban, J. Surovková, and A. Thurzo, "Artificial intelligence systems assisting in the assessment of the course and retention of orthodontic treatment," in Healthcare, 2023, p. 683. [CrossRef]
  21. A. Saeed, "Improved Diagnosis of COVID-19 with CXGNet: A Deep CNN with Enhanced Grey-wolf Optimizer," 2023.
  22. D. C. Prakash, R. Narayanan, N. Ganesh, M. Ramachandran, S. Chinnasami, and R. Rajeshwari, "A study on image processing with data analysis," in AIP Conference Proceedings, 2022.
  23. D. Sen, B. B. Mishra, and P. K. Pattnaik, "A Review of the Filtering Techniques used in EEG Signal Processing," in 2023 7th International Conference on Trends in Electronics and Informatics (ICOEI), 2023, pp. 270-277.
  24. T. Yang, H. Yu, and Y. Wang, "An efficient low-pass-filtering algorithm to de-noise global GRACE data," Remote Sensing of Environment, vol. 283, p. 113303, 2022. [CrossRef]
  25. C. Tang, X. Wang, Y. Bai, Z. Wu, J. Zhang, and Y. Huang, "Learning spatial-frequency transformer for visual object tracking," IEEE Transactions on Circuits and Systems for Video Technology, 2023. [CrossRef]
  26. X. Lv, R. T. Ako, M. Bhaskaran, S. Sriram, C. Fumeaux, and W. Withayachumnankul, "Frequency-selective-surface-based mechanically reconfigurable terahertz bandpass filter," IEEE Transactions on Terahertz Science and Technology, vol. 12, pp. 257-266, 2022. [CrossRef]
  27. S. Kocoń and J. Piskorowski, "Power Line Interference Removal From Short-Latency Evoked Potentials Using Digital Time-Efficient Selective Elliptic Notch Filter," IEEE Transactions on Instrumentation and Measurement, vol. 71, pp. 1-9, 2022. [CrossRef]
  28. arXiv:2204.09302.S. Satpathy, S. Panda, K. K. Nagwanshi, S. Nayak, and C. Ardil, "Adaptive non-linear filtering technique for image restoration," arXiv preprint arXiv:2204.09302, 2022.
  29. C. S. K. Abdulah, M. N. K. H. Rohani, B. Ismail, M. A. M. Isa, A. S. Rosmi, W. A. W. Mustafa, et al., "Review Study of Image De-Noising on Digital Image Processing and Applications," Journal of Advanced Research in Applied Sciences and Engineering Technology, vol. 30, pp. 331-343, 2023. [CrossRef]
  30. S. Gantenapalli, P. Choppala, V. Gullipalli, J. Meka, and P. Teal, "A fast method for impulse noise reduction in digital color images using anomaly median filtering," in 2022 IEEE 5th International Conference on Image Processing Applications and Systems (IPAS), 2022, pp. 1-6.
  31. F. Zhang, Y. Wu, M. Xu, S. Liu, C. Peng, and Z. Gao, "A Morphological Image Segmentation Algorithm for Circular Overlapping Cells," Intelligent Automation & Soft Computing, vol. 32, 2022. [CrossRef]
  32. J. A. Stuchi, N. G. Canto, L. Boccato, and R. Attux, "A frequency-domain approach with learnable filters for image classification," Available at SSRN 4333420, 2023.
  33. H. Shuai, L. Junxia, W. Lei, and Z. Wei, "Research on acoustic fault diagnosis of bearings based on spatial filtering and time-frequency domain filtering," Measurement, p. 113533, 2023. [CrossRef]
  34. R. Al Sobbahi and J. Tekli, "Low-light homomorphic filtering network for integrating image enhancement and classification," Signal Processing: Image Communication, vol. 100, p. 116527, 2022. [CrossRef]
  35. Y. Ding, Z. Zhang, X. Zhao, D. Hong, W. Li, W. Cai, et al., "AF2GNN: Graph convolution with adaptive filters and aggregator fusion for hyperspectral image classification," Information Sciences, vol. 602, pp. 201-219, 2022.
  36. Z. Chi, J. Jiang, X. Diao, Q. Chen, L. Ni, Z. Wang, et al., "Novel leakage detection method by improved adaptive filtering and pattern recognition based on acoustic waves," International Journal of Pattern Recognition and Artificial Intelligence, vol. 36, p. 2259001, 2022. [CrossRef]
  37. X. Yan and M. Jia, "Bearing fault diagnosis via a parameter-optimized feature mode decomposition," Measurement, vol. 203, p. 112016, 2022.
  38. R. Rajalakshmi, G. Vishnupriya, R. Sudharsanan, S. Navaneethan, P. Vijayakumari, and M. Karthikeyan, "Digital Filter Design on High speed Communication with Low Power Criteria," in 2023 International Conference on Computer Communication and Informatics (ICCCI), 2023, pp. 1-5.
  39. arXiv:2209.11899.D. Alpay, K. Diki, and M. Vajiac, "Two bicomplex least mean square (BLMS) algorithms," arXiv preprint arXiv:2209.11899, 2022.
  40. A.-G. Rusu, C. Paleologu, J. Benesty, and S. Ciochină, "A variable step size normalized least-mean-square algorithm based on data reuse," Algorithms, vol. 15, p. 111, 2022. [CrossRef]
  41. J. Casebeer, N. J. Bryan, and P. Smaragdis, "Meta-af: Meta-learning for adaptive filters," IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 31, pp. 355-370, 2022. [CrossRef]
  42. H. Javaid, "Adaptive Filter Utilizing Recursive Least Squares Algorithm with Adaptive Forgetting Factor," Texas A&M University-Kingsville, 2023.
  43. K. N. Watcharasupat, T. N. T. Nguyen, W.-S. Gan, S. Zhao, and B. Ma, "End-to-end complex-valued multidilated convolutional neural network for joint acoustic echo cancellation and noise suppression," in ICASSP 2022-2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2022, pp. 656-660.
  44. Y. Zhang, "Smart detection on abnormal breasts in digital mammography based on contrast-limited adaptive histogram equalization and chaotic adaptive real-coded biogeography-based optimization," Simulation, vol. 92, pp. 873-885, 2016. [CrossRef]
  45. M. Ivanov, M. Posysoev, and A. P. Lyubartsev, "Coarse-Grained Modeling Using Neural Networks Trained on Structural Data," Journal of Chemical Theory and Computation, vol. 19, pp. 6704-6717, 2023. [CrossRef]
  46. R. Vankdothu and M. A. Hameed, "Brain tumor MRI images identification and classification based on the recurrent convolutional neural network," Measurement: Sensors, vol. 24, p. 100412, 2022. [CrossRef]
  47. Y. D. Zhang and S. Satapathy, "A seven-layer convolutional neural network for chest CT-based COVID-19 diagnosis using stochastic pooling," IEEE Sensors Journal, vol. 22, pp. 17573 - 17582, 2022.
  48. A. Kaur and G. Dong, "A Complete Review on Image Denoising Techniques for Medical Images," Neural Processing Letters, pp. 1-44, 2023. [CrossRef]
  49. A. Azarkaman, P. R. Deilamani, and N. Ghorbani, Medical Devices Engineering Textbook 1: Nobel TM, 2022.
  50. X. Zhang and C. He, "Robust double-weighted guided image filtering," Signal Processing, vol. 199, p. 108609, 2022.
  51. G. Ramesh, J. Logeshwaran, J. Gowri, and A. Mathew, "The management and reduction of digital noise in video image processing by using transmission based noise elimination scheme," ICTACT Journal on Image & Video Processing, vol. 13, 2022.
  52. A. Halidou, Y. Mohamadou, A. A. A. Ari, and E. J. G. Zacko, "Review of wavelet denoising algorithms," Multimedia Tools and Applications, pp. 1-31, 2023. [CrossRef]
  53. M. Diwakar, P. Kumar, P. Singh, A. Tripathi, and L. Singh, "An efficient reversible data hiding using SVD over a novel weighted iterative anisotropic total variation based denoised medical images," Biomedical Signal Processing and Control, vol. 82, p. 104563, 2023. [CrossRef]
  54. Y. Shi and A. Singer, "Ab-initio contrast estimation and denoising of cryo-EM images," Computer Methods and Programs in Biomedicine, vol. 224, p. 107018, 2022. [CrossRef]
  55. G. Liu, M. Dang, J. Liu, R. Xiang, Y. Tian, and N. Luo, "True wide convolutional neural network for image denoising," Information Sciences, vol. 610, pp. 171-184, 2022. [CrossRef]
  56. X. Liu, M. Pedersen, and R. Wang, "Survey of natural image enhancement techniques: Classification, evaluation, challenges, and perspectives," Digital Signal Processing, vol. 127, p. 103547, 2022.
  57. S. Kumar and Y. Kurmi, "CNN-based denoising system for the image quality enhancement," Multimedia Tools and Applications, vol. 81, pp. 20147-20174, 2022. [CrossRef]
  58. D. C. Lepcha, B. Goyal, A. Dogra, and V. Goyal, "Image super-resolution: A comprehensive review, recent trends, challenges and applications," Information Fusion, 2022.
  59. Y. Bi, B. Xue, P. Mesejo, S. Cagnoni, and M. Zhang, "A survey on evolutionary computation for computer vision and image analysis: Past, present, and future trends," IEEE Transactions on Evolutionary Computation, vol. 27, pp. 5-25, 2022.
  60. S. Chhetri, M. S. Joshi, C. V. Mahamuni, R. N. Sangeetha, and T. Roy, "Speech Enhancement: A Survey of Approaches and Applications," in 2023 2nd International Conference on Edge Computing and Applications (ICECAA), 2023, pp. 848-856.
  61. M. Labied, A. Belangour, M. Banane, and A. Erraissi, "An overview of Automatic Speech Recognition Preprocessing Techniques," in 2022 International Conference on Decision Aid Sciences and Applications (DASA), 2022, pp. 804-809.
  62. Y. Lin, L. Zhang, H. Han, Y. Li, W. Shen, and Y. Wang, "Periodic-Filtering Method for Low-SNR Vibration Radar Signal," Remote Sensing, vol. 15, p. 3461, 2023. [CrossRef]
  63. M. S. Abdalzaher, H. A. Elsayed, and M. M. Fouda, "Employing remote sensing, data communication networks, ai, and optimization methodologies in seismology," IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 15, pp. 9417-9438, 2022.
  64. X. Shen, D. Shi, W.-S. Gan, and S. Peksi, "Adaptive-gain algorithm on the fixed filters applied for active noise control headphone," Mechanical Systems and Signal Processing, vol. 169, p. 108641, 2022. [CrossRef]
  65. P. Datta and R. Rohilla, "Denoising Magnetic Resonance Images with Rician Noise Based On Deep Learning," in 2022 International Conference on Computational Intelligence and Sustainable Engineering Solutions (CISES), 2022, pp. 545-550.
  66. Z. Haider, "Deep Learning-based Image Denoising Techniques: A Survey and Comparative Study," 2023.
  67. K. S. H. Kulathilake, N. A. Abdullah, A. Q. M. Sabri, A. R. Bandara, and K. W. Lai, "A review on self-adaptation approaches and techniques in medical image denoising algorithms," Multimedia Tools and Applications, vol. 81, pp. 37591-37626, 2022. [CrossRef]
Preprints 88079 g001
Figure 1. Causes of noise in images.
Figure 1. Causes of noise in images.
Preprints 88079 g001
Preprints 88079 g002
Figure 2. Paper structure.
Figure 2. Paper structure.
Preprints 88079 g002
Preprints 88079 g003
Figure 3. The relationship between healthcare and biomedical image denoising.
Figure 3. The relationship between healthcare and biomedical image denoising.
Preprints 88079 g003
Preprints 88079 g004
Figure 4. Characteristics, application fields, common algorithms and objectives of adaptive filtering methods.
Figure 4. Characteristics, application fields, common algorithms and objectives of adaptive filtering methods.
Preprints 88079 g004
Preprints 88079 g005
Figure 5. The challenges of filtering methods.
Figure 5. The challenges of filtering methods.
Preprints 88079 g005
Preprints 88079 g006
Figure 6. Other areas where filtering methods can be applied.
Figure 6. Other areas where filtering methods can be applied.
Preprints 88079 g006
Table 1. Common linear filtering differences.
Table 1. Common linear filtering differences.
Linear Filtering Frequency Function
Low-pass filters Allow low-frequency components to pass through while attenuating high-frequency components Making them useful for smoothing or noise reduction
High-pass filters Emphasize high-frequency components while suppressing low-frequency ones Often used for edge detection
Bandpass filters Allow a specific range of frequencies Ideal for isolating a particular frequency band of interest
Notch filters Reject a specific frequency or narrow frequency range Remove unwanted interference or noise at specific frequencies
Table 2. Comparison between linear filtering and nonlinear filtering.
Table 2. Comparison between linear filtering and nonlinear filtering.
Filtering methods Relationship with filtering results Implementation method Common filter Function implementation
Linear Filtering Arithmetic operation Add, subtract, multiply, divide and so on Gaussian filter,Mean filter Definite and unique transfer function
Non-Linear Filtering Logical relation Logical operation Maximum filter,Minimum filter,Median filter Unspecified transfer function
Table 3. Key filtering methods for biomedical image denoising.
Table 3. Key filtering methods for biomedical image denoising.
Filtering methods Data processing Function
Gaussian filters Apply a weighted average to pixel values within a local neighborhood Reducing Gaussian noise, which is characterized by a bell-shaped probability distribution.
Median filters Replace each pixel with the median value within a local window Removing impulse noise
Wavelet-based methods Decompose an image into different frequency components Well-suited for medical images with varying textures and structures
Total variation denoising Regularization technique, minimizes the total variation in pixel values within the image Smoothing the image while maintaining sharp boundaries
Wiener filtering Minimizes the mean squared error between the estimated image and the true image Useful when noise statistics are known or can be estimated accurately
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated