Preprint
Article
Bilinear Interpolation of Three-Dimensional Gain-Scheduled Autopilots
Altmetrics
Downloads
113
Views
25
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
15 October 2023
Posted:
18 October 2023
You are already at the latest version
Alerts
Abstract
Gain-scheduled autopilots have emerged as a dominant strategy to achieve adaptive control of coupled, non-linear engineering complexities, owing to an ability to adapt to changing operational conditions and uncertainties. This study focuses on utilizing bilinear interpolation of gain-scheduled autopilots, emphasizing enhanced system performance and robustness. Through a comprehensive investigation and comparative analysis using three disparate cases, advantages over conventional methods are revealed. Strengths and weaknesses of both simple and specialized variants (such as linear, and real-time gain-scheduling) are introduced. Three missile guidance case–studies utilize simulation time and miss distance figures of merit. Potential to achieve precise control across various mission scenarios, while ensuring reduced computational complexity is revealed by nearly two–hundred percent improved missile miss distances with comparable distances traveled and slightly improved computational burden.
Keywords:
Subject: Engineering - Aerospace Engineering
1. Introduction
Gain-scheduled autopilots hold immense significance in the field of modern missile technology, as they address critical challenges and elevate the capabilities of guidance control in missile systems. As the complexity of military operations intensifies, the demand for highly adaptable countermeasures and precise missile guidance systems have become paramount. By providing dynamic control gains that cater to varying flight conditions, gain-scheduled autopilots offer a robust solution for missile defense. This study delves into the fundamental principles, working mechanisms, and functional advantages of various designs of gain-scheduled autopilots for missiles, highlighting the effectiveness of bilinear interpolation in control systems.
As a missile travels over vast distances, it encounters diverse atmospheric conditions that impact its aircraft stability, experiencing variations in altitude, velocity, and aerodynamic forces. Traditional fixed-gain autopilots suffer from limitations in adapting to the constantly changing environment and unexpected disturbances, leading to reduced accuracy and compromised performance. Accordingly, fixed-gain systems severely lack the ability to counter agile adversaries. Unmanned aerial systems (UAS), for instance, can exhibit unpredictable and erratic flight patterns, making them challenging targets for traditional fixed-gain autopilots.
Gain-scheduled autopilots, on the other hand, provide a dynamic and responsive solution. A gain-scheduled autopilot can tailor the control gains to suit each phase of the flight based on the real-time feedback and operational parameters. This adaptability significantly enhances the missile’s accuracy and maneuverability, increasing the chances of successful target engagement against evasive threats like UAS. Furthermore, in a mission-critical scenario where multiple missiles are employed in a salvo attack, gain-scheduled autopilots offer a crucial advantage. With the ability to dynamically adjust to surroundings, the missiles can adapt to the specific requirements of each individual missile, ensuring that the entire salvo operates cohesively. The ability to coordinate and synchronize multiple missiles makes gain-scheduled autopilots indispensable tools in modern warfare scenarios.
The study explores the advantages of bilinear interpolation of control gains in a three-dimensional lookup table for gain-scheduled autopilots, including improved robustness, reduced control effort, and enhanced adaptability to handle complex, non-linear systems. By intelligently blending discrete control gains through simple algorithms, bilinear interpolation unlocks the full potential of gain-scheduled autopilots, contributing to the overall efficiency and reliability of missile guidance.
Figure 1.
(a) Original RIM-174 Standard Extended Range Active Missile (ERAM), also known as Standard Missile-6 (SM-6) launched off the Hawaiian coast April 6-13, 2017 [1]. (b) guided-missile destroyer USS Fitzgerald (DDG 62) launches a Standard Missile-3 (SM-3) [2]. Images credit: U.S. Navy in accordance with image use policy [3]. Department of Defense photographs and imagery, unless otherwise noted, are in the public domain.
Figure 1.
(a) Original RIM-174 Standard Extended Range Active Missile (ERAM), also known as Standard Missile-6 (SM-6) launched off the Hawaiian coast April 6-13, 2017 [1]. (b) guided-missile destroyer USS Fitzgerald (DDG 62) launches a Standard Missile-3 (SM-3) [2]. Images credit: U.S. Navy in accordance with image use policy [3]. Department of Defense photographs and imagery, unless otherwise noted, are in the public domain.

1.1. Review of the literature
Current long-range missile defense systems are seemingly much less effective than believed and suffer from severe limitations [4], particularly in light of recent improvements in decoys [5], where a long list of intercept failures was published in 2021 [6], where mitigation by sensor improvements was proposed the following year [7] in a proposal to utilize space–based sensors which was reinforced by the U.S. Air Force Association the same year in [8].
1.2. State of the art benchmarks
The following list highlights the current state of the art developments for high–fidelity six degree of freedom simulation:
- In 2020, reference [9] illustrated ubiquitous use of simplified models and probabilistic assessments leading to recommendations on the number of interceptors necessary using a shoot-look-shoot mode of operations.
- Russian President Putin boasted to have developed missiles traveling at twenty times the speed of sound [10] necessitating increased confidence in engagement analysis.
- Tracy, et al. forwarded the notion that “Misperceptions of hypersonic weapon performance have arisen from social processes by which the organizations developing these weapons construct erroneous technical facts favoring continued investment”, and recommended rigorous, quantitative analysis [11].
- In 2022, Bryson, et al. published elaborated a baseline automated gain–scheduling approach for three–loop autopilots for high–speed projectiles with supersonic flight envelopes.
1.3. Novelties presented
The following proposals are developed in subsequent pages of this manuscript:
- Automatic gain scheduling is proposed and compared to index–search as the comparative benchmark.
- Bilinear interpolation is proposed and compared to index–search as the comparative benchmark.
2. Materials and Methods
2.1. Specification and Initialization
The missile for the simulation is fictional, a replica of the original RIM-174 Standard Extended Range Active Missile (ERAM), also known as Standard Missile-6 (SM-6). SM is the most reliable type of surface-to-air missile, still favored by the United States Navy [12]. This study employs the aerodynamic fundamentals organized by Raytheon Missile Systems [13,14], and thus the most accurate simulation was expected by using SM, whose primary manufacturer is Raytheon. Possibly due to security purpose, some specifications of SM are not available publicly. The parameters not listed in the table, like total thrust of the actuators, are instead computed from reference velocity (~Mach 5) using the drag equation. The bandwidth of the actuator is approximated to a realistic rate. The final specification of the missile is shown in Table 1:
Table 1.
Specifications of the missile for the simulation.
| Description | Value | Unit |
|---|---|---|
| Total Missile Mass | 160 | kg |
| Initial Missile Velocity | 1000 | |
| Maximum Axial Acceleration | 400 | |
| Reference Area | 0.050 | |
| Reference Length | 0.300 | |
| Pitch Moment of Inertia | 180 | kg |
| Actuator Bandwidth | 3.000 | deg |
| Maximum Fin Deflection | 30 | deg |
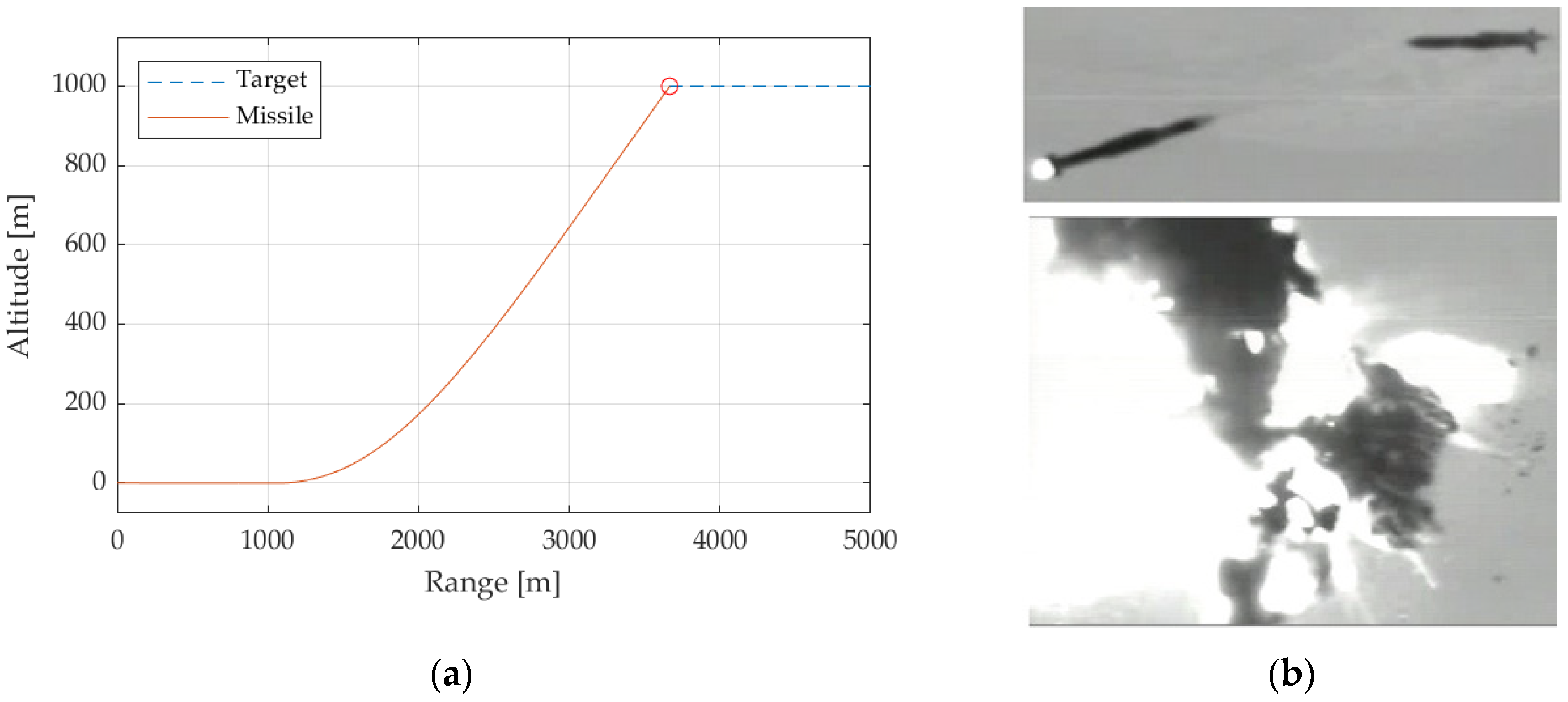
The study is focused on the relative performance of different designs of autopilots by comparing the simulation time and the miss distance. For this purpose, the target object does not require a complex, realistic geometry and it is simplified to a point mass with fixed flight coefficients. In contrast, the missile has varying flight coefficients for a more effective analysis of its aerodynamics. The initial position of the missile is defined as the origin. The missile initially travels parallel to the ground at a velocity of . To make the iteration process more efficient, the target parameters are initialized relative to those of the missile. The target is placed ahead and above the missile’s initial position, traveling at a speed half of the initial speed of the missile, in the direction parallel to the surface and towards the missile, as seen in Figure 2.
Figure 2.
(a) Flight simulation of missile and target. The red solid line represents the trajectory of the missile. The blue dotted line represents the trajectory of the target, cruising horizontally. The red circle indicates the point of impact depicted in (b) from [15] where a Standard Missile-6 successfully intercepted a mock cruise missile flying low and slow over land at White Sands Missile Range, New Mexico. (image credit: Sydney J. Freedberg Jr.).
Figure 2.
(a) Flight simulation of missile and target. The red solid line represents the trajectory of the missile. The blue dotted line represents the trajectory of the target, cruising horizontally. The red circle indicates the point of impact depicted in (b) from [15] where a Standard Missile-6 successfully intercepted a mock cruise missile flying low and slow over land at White Sands Missile Range, New Mexico. (image credit: Sydney J. Freedberg Jr.).
2.2. Airframe Dynamics: Force and Moment
First, the environmental condition is established. The study utilizes the International Standard Atmosphere (ISA) model for altitudes between 0 to 20 km. The model takes in the current altitude of the missile and returns the climatic data elements, such as temperature, speed of sound, air pressure and air density, which are used to compute the full aerodynamics in the equations of motion.
To enhance the accuracy of the simulation, the force and moment coefficients of the missile are adjusted in accordance with the current flight condition. The coefficients are stored in a linearly spaced, three-dimensional partition of angle of attack, Mach number, and flight coefficients (,,). The coefficients are parametrized as function of incidence angle and Mach number, represented as lattice points on the partition. When a flight condition is newly introduced on the grid as a nonlattice point, the simulation computes the relative position of the nonlattice point to the nearest lattice points. The new coefficient is estimated by a three-dimensional lookup table (‘3D-LUT’) using bilinear interpolation. 3D-LUT is explained with further detail in [16].
There are two major types of forces acting on the missile: axial force and normal force. The main axial force is drag acting on the missile body. The axial force coefficient is assumed to be constant, equal to that of a bullet with a spherical cap [17]. The study assumes the drag caused by the fins is negligible. The assumption is valid for fins with small effective surface area.
Table 2.
Table of proximal variables and nomenclature 1.
| Variable/acronym | Definition | Variable/acronym | Definition |
|---|---|---|---|
| Drag coefficient of fins | Lift coefficient of wings | ||
| Drag coefficient of body | Lift coefficient of fins | ||
| Total drag coefficient | Total lift coefficient |
1 Such tables are offered throughout the manuscript to aid readability.
The lift force acts in the direction normal to the direction in which the missile travels. The largest contributors to the lift force are the main wings (or angle of attack) and the missile fins. The coefficient of the lift force created by the missile fins is estimated in [13]. The lift coefficient of the main wings is estimated using the non-linear equation () introduced by Shamma, et al. [18] Fin deflection is computed using the angle of attack and the velocity at the instant, allowing the simulation to compute the actual lift force. The total lift coefficient is the sum of the two lift coefficients.
The pitch moment coefficient of the main wings is calcualted in Equation (7). [18] The pitch moment coefficient due to fin deflection is provided in [13]. The total pitch moment coefficient is the sum of the moment coefficients.
The resulting axial and normal forces are shown in equation (10) and equation (11) where and are the air density and the reference area, respectively. Since the exact dimension of the missile elements is not published, the forces are assumed to share the same reference area, provided by Mracek, et. al. [13] The equation for the moment includes the moment arm , equal to the reference length. The resulting forces and the moment are used to compute the flight metrics, such as position, velocity, acceleration, and attitude of the aircraft, in 3 degrees-of-freedom equations of motion. The metrics are fed into the autopilot, which determines the behavior of the aircraft.
Table 3.
Table of proximal variables and nomenclature 1.
| Variable/acronym | Definition | Variable/acronym | Definition |
|---|---|---|---|
| Axial force | Moment coefficient of wings | ||
| Normal force | Moment coefficient due to fins | ||
| Pitch moment | Total moment coefficient |
1 Such tables are offered throughout the manuscript to aid readability.
2.3. Proportional Navigation Guidance Law
The study utilizes proportional navigation guidance (‘PN guidance’) for the entire homing phase. [19] PN guidance is one of the simpler guidance laws to implement. It only requires rate of change of line-of-sight (LOS) and closing velocity, allowing the missile to have the minimal sensory technology onboard. [19] The relative ease of implementation, however, does not signify its lack of performance. In fact, PN guidance has proven to be the most robust guidance system assuming a no-lag missile: a system that reacts instantly and exactly as commanded. [19] The conventional PN guidance law is shown in Equation (13).
is the commanded missile acceleration normal to the LOS. and are the closing velocity and the rate of change of LOS, respectively. is equal to , where is the range between the missile and the target. Note that is a negative value during pursuit. For the system to be stable, the navigational gain must be larger than 2.
2.4. Basic Fixed Gain Three-loop Autopilot
The most basic form of autopilot is fixed gain autopilot. In fixed gain autopilot, the control gains are unchanged throughout the operation. The strength of the fixed gain autopilot is the simplicity of its structure. It neglects the change in the flight conditions and thus does not require the additional adjustments to optimize the gains during the operation. The key to the design is finding the gains that yield the desired time constant, ideally less than 0.2 seconds, and small steady-state error (~3%) prior to the main simulation.
Figure 3.
Topology of basic three-loop autopilot with fixed control gains [20].
Figure 3.
Topology of basic three-loop autopilot with fixed control gains [20].
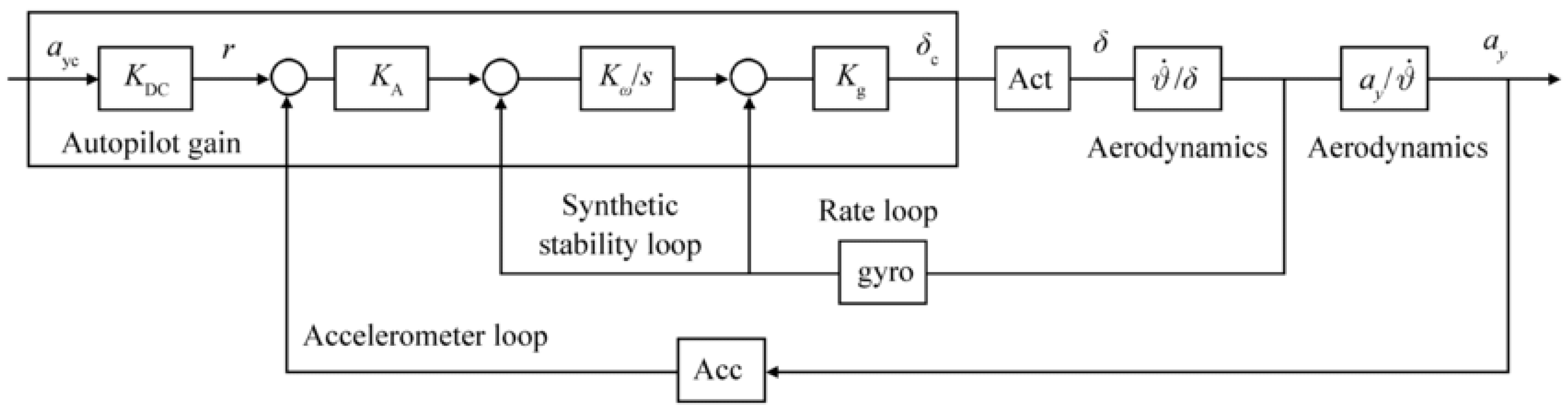
The modelling of fixed gain autopilot requires the following steps:
- Derive the nonlinear missile dynamics.
- Derive the state representation of the linearized dynamics.
- Tune the control gains for the nominal flight condition.
Nonlinear missile dynamics is derived from the longitudinal motion of the missile in the pitch plane. Specifically, the derivation of the nonlinear dynamics involves computation of the three critical angles in aerodynamics: the angle of attack, the flight-path-angle, and the pitch angle. The geometry of the angles is shown in Figure 4, the anatomy of a missile in longitudinal motion.
Figure 4.
Nomenclature of critical angles in aerodynamics [9]. is velocity vector; is normal acceleration acting on the missile body; is angle of attack; is pitch angle, γ is flight-path-angle.
Figure 4.
Nomenclature of critical angles in aerodynamics [9]. is velocity vector; is normal acceleration acting on the missile body; is angle of attack; is pitch angle, γ is flight-path-angle.
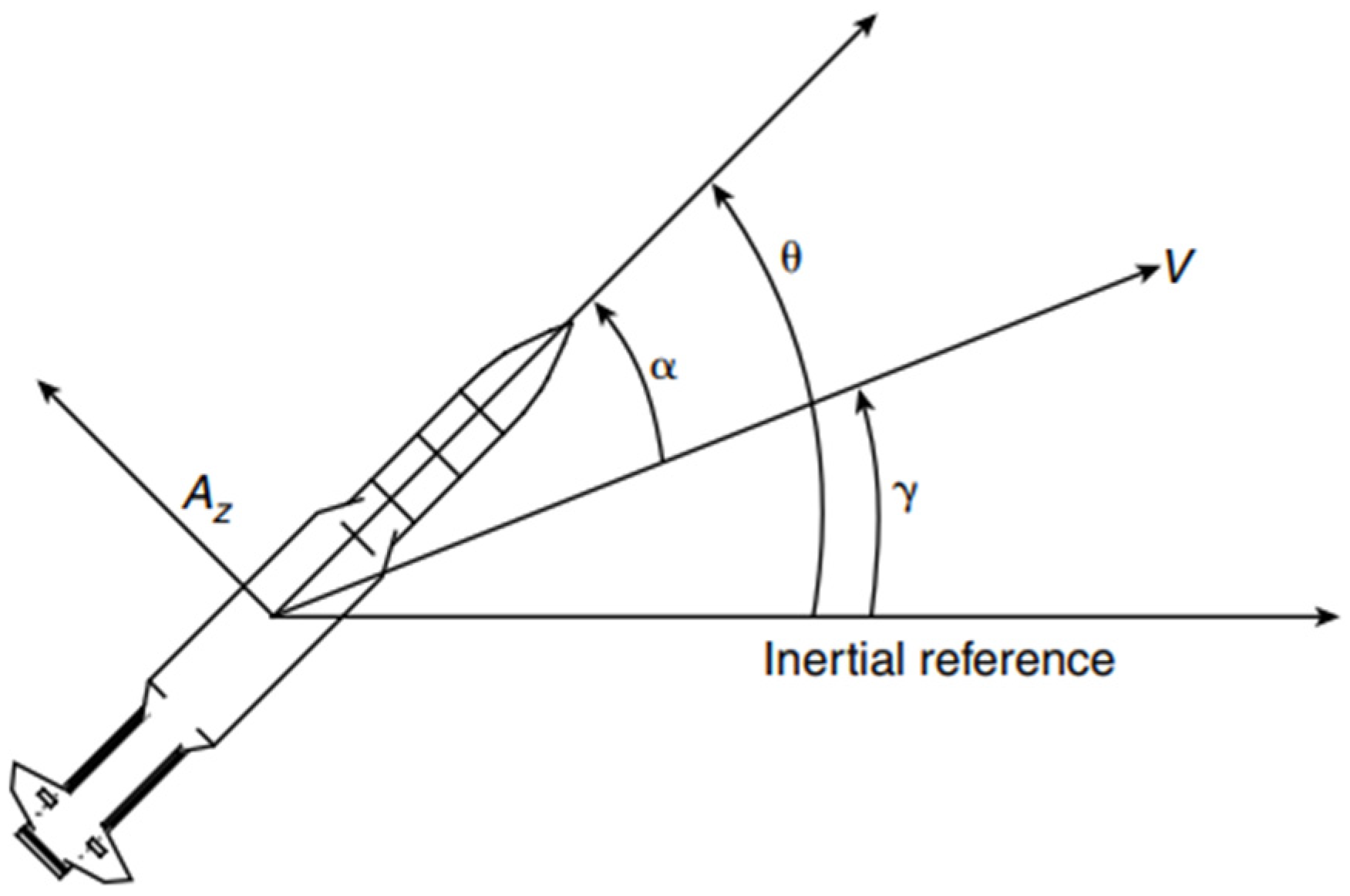
The velocity of the missile and the required normal acceleration are denoted and , respectively. is the angle of attack which describes the orientation of the missile relative to the airflow. is the flight-path-angle which describes the attitude of the missile. is the pitch angle which describes the orientation of the missile relative to the inertial reference frame. Naturally, the angle of attack is the difference between the pitch angle and the flight-path angle.
The rate of change in the flight-path-angle, , can be expressed as a function of the vertical component of the normal acceleration, relative to the longitudinal axis, and the velocity vector. When the angle of attack is sufficiently small, the vertical component of the normal acceleration is assumed to be equal to the total acceleration. For maximum accuracy of the results, the estimation is not made.
According to Newton’s 2nd law, the vertical acceleration of the missile is the vertical force applied to the missile divided by its mass. The final expression for is given in Equation (16). The nonlinear dynamics are shown in Equation (17) and Equation (18), where is the dynamic pressure, is the reference diameter, and , is the moment of inertia [13,18,19].
With short-period approximation, the speed of the missile is assumed to be constant. Due to linear systems theory, nonlinear differential equations can be approximated in a linear form. is originally a function of and . The analytical state-space model solved in the time domain is:
Table 4.
Table of proximal variables and nomenclature 1.
| Variable/acronym | Definition | Variable/acronym | Definition |
|---|---|---|---|
| Moment of inertia | Rate of change in AOA | ||
| Analytic body inertia | Rate of change in FPA | ||
| Mass of missile | Pitch acceleration |
1 Such tables are offered throughout the manuscript to aid readability.
The state-space model can be linearized via Taylor series expansion around the selected flight condition and only keeping the first-order terms. The final state-space model [13] is:
Raytheon provides a fully linearized model for both stable and unstable systems [13], well aligned with the purpose of the study. The linearized model for an unstable system is:
Refer to Equation (32)–Equation (35) in Appendix A for the stable system solution [13]. The corresponding open loop transfer functions for the actuator model are:
For simplicity of the study, the actuator model is often assumed to be a linear system due to its structural complexity and nonlinear behavior. However, unlike the popular belief, the discrepancy raised from the assumption is not significant enough to hurt the validity of a simulation [21]. Hence, the second-order approximation of the actuator model is:
Table 5.
Table of proximal variables and nomenclature 1.
| Variable/acronym | Definition | Variable/acronym | Definition |
|---|---|---|---|
| Gravitational acceleration | Fin deflection | ||
| Actuator frequency | Normal acceleration | ||
| Actuator damping ratio | Axial acceleration |
1 Such tables are offered throughout the manuscript to aid readability.
Using the linearized dynamics and the simplified actuator model, the control gains are tuned to yield the time constant less than 0.2 seconds. The fixed autopilot gains for the nominal condition are:
2.5. Various Gain-scheduled Autopilots
Gain-scheduled autopilot is an augmented version of fixed gain autopilot with the ability to optimize flight performance in the middle of operation. Unlike fixed gain autopilots which have predetermined, unchanging control gains, gain-scheduled autopilot swaps out the gain values from an index of previously stored gains, allowing the autopilot to perform optimally in the current flight condition. Particularly, the ability to adjust gain values is most highlighted at the end game of pursuit where the flight conditions are most rapidly changing.
Due to its effectiveness, gain-scheduled autopilot is widely adopted in modern systems. It is still being actively studied and thus has many variations in its design. This study analyzes the relative performance of three methods of gain-scheduled autopilots, each with a unique method of optimizing a family of linear controllers.
2.5.1. Index-search
Index-search is the simplest form of gain-scheduled autopilot. The study considers a three-loop autopilot with four control gains: , , , and . The control gains are tuned at each flight condition and stored in their respective indices. When an aircraft reaches a certain flight condition, the gain values are selected strictly from the stored gain values. The number of sets of gain values is equal to the number of available flight conditions. The design process is as following:
- Trim and linearize the nonlinear plant models for each flight condition.
- Tune the control gains for each linear mode.
- Store the linear controllers into a family of controllers.
- Swap the control gains based on the current flight condition.
The trimming and linearization process is like the process previously introduced in Section 2.4. In short, one must find steady-state values of elevator deflection and pitch rate that yield steady angle of attack at a chosen velocity. The angle of attack and the velocity are called scheduling variables, used to determine the actual flight condition. Once a family of linear controllers is established, the autopilot can swap the control gains. As the scheduling variables shift during the operation, autopilot chooses the gains from one of the pre-existing flight conditions that is in the closest vicinity to the actual flight condition. Although the method ensures a more desirable performance than a fixed-gain autopilot, it is unable to fully describe the plant behavior of controllers that are not linearized in prior and hence not included in the family.
2.5.2. Bilinear Interpolation in 3D-LUT
Bilinear interpolation allows the autopilot to estimate control gains for plant models that are unlisted in the family. Unlike index-search, the number of sets of gains is not limited to the number of linear controllers. Rather, the autopilot can generate control gains as necessary regardless of the current flight condition. Hence, the transition of control gains is much smoother in the second method than the first method.
- Trim and linearize the nonlinear plant models for each flight condition.
- Tune the control gains for each linear model.
- Create a 3D-LUT, a linearly spaced partition of , , and ;
- Store the tuned to their respective lattice points (, ) on the partition.
- When aircraft enters a new flight condition, determine the relative position of the new nonlattice point to the nearest lattice points.
- Perform bilinear interpolation (, ) to estimate the new control gain.
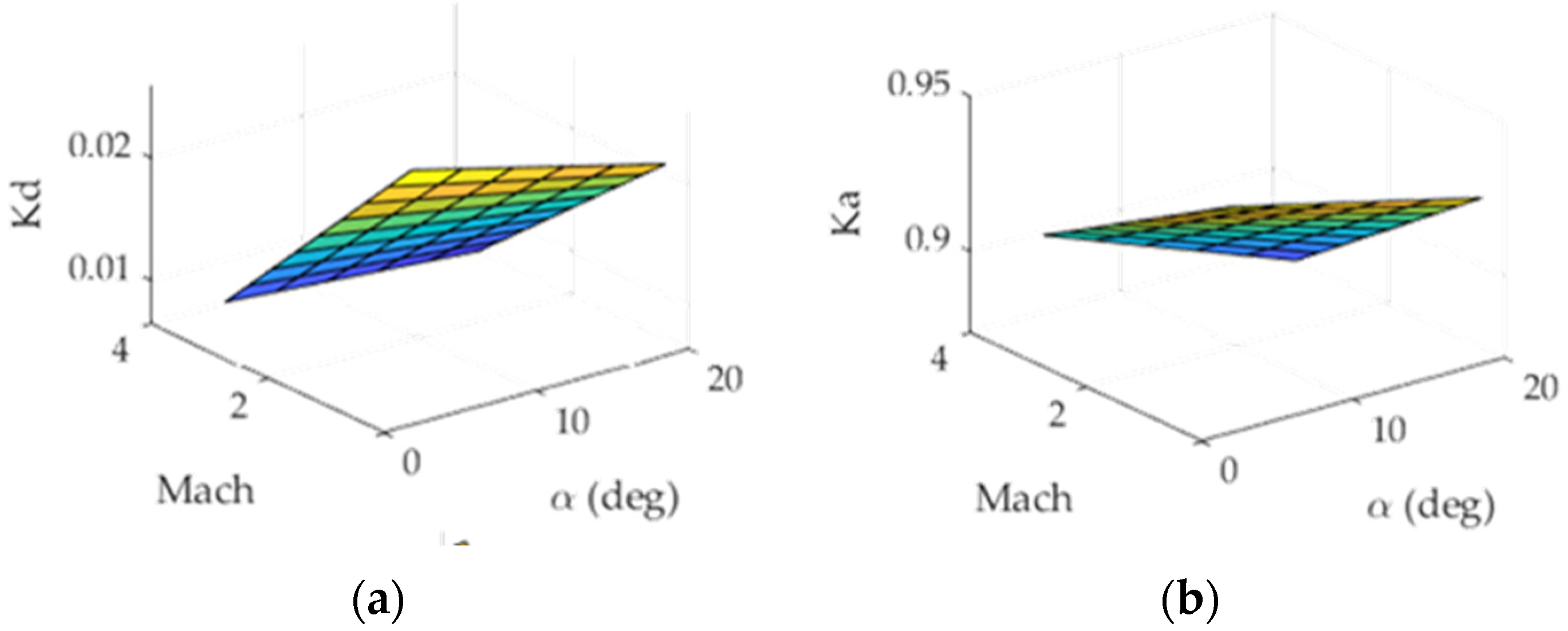
The center of the design is the estimation of the control gains via bilinear interpolation. Consider a three-dimensional lookup table (‘3D-LUT’), a partition with control gains as its lattice points whose coordinates are (, ). The autopilot determines where the new condition, represented as a nonlattice point, falls on the partition when an aircraft enters a new flight condition. Particularly, autopilot checks the position of the new point by comparing and to those of the nearest points. Using the difference in the positions of the nonlattice point and the nearest points, the new control gain is computed by performing two consecutive bilinear interpolation. However, it must be noted that the generated control gains may not work optimally with nonlinear plant models.
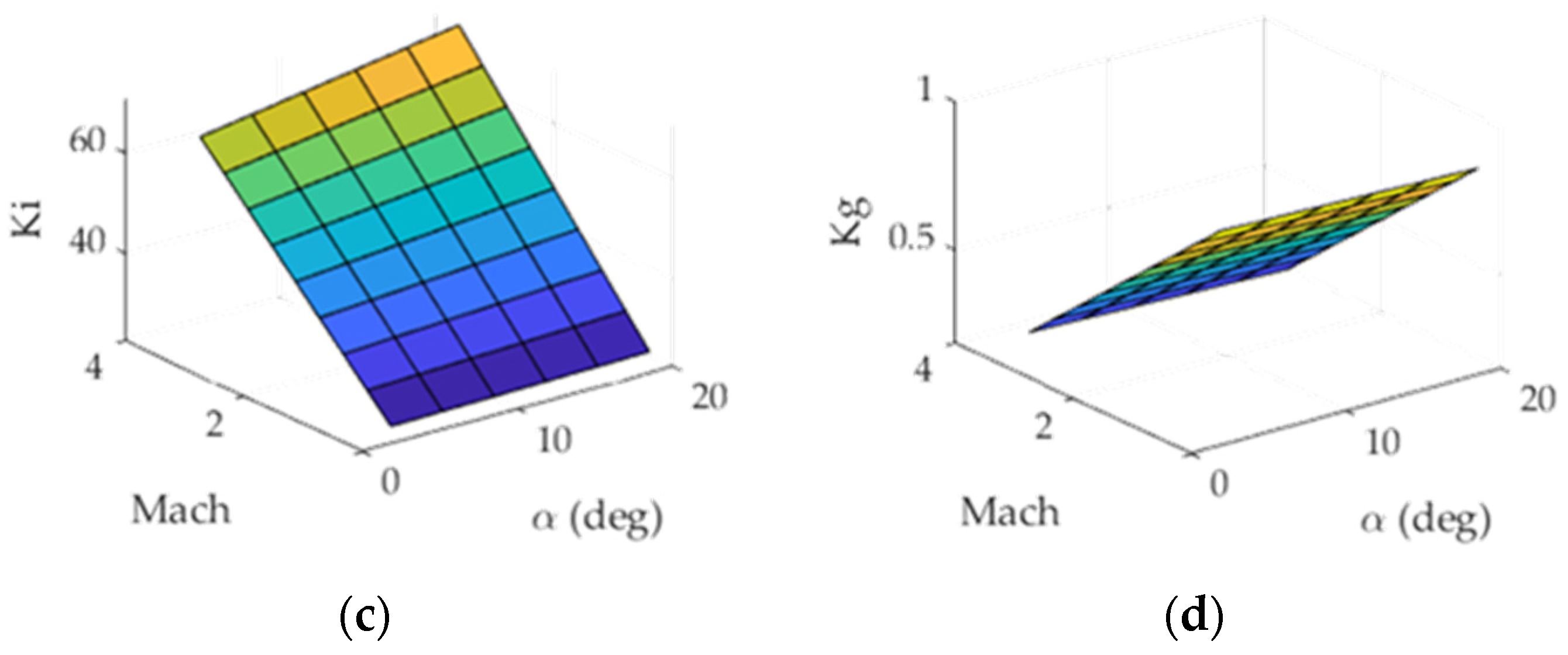
Figure 5.
Two-dimensional gain surfaces visualized in three-dimensional lookup table. (a) is , (b) is , (c) is , (d) is
Figure 5.
Two-dimensional gain surfaces visualized in three-dimensional lookup table. (a) is , (b) is , (c) is , (d) is
2.5.3. Automatic Real-time Tuning
The third method is to parametrize the control gains as first-order polynomials of the scheduling variables. A conventional method of tuning control gains involves a brutal amount of variables. This novel approach, the parametrization of gains, reduces the number of variables to four, allowing the system to compute the gains instantaneously with minimal computational burden. Consider a gain parametrized as a polynomial function of the scheduling variables. [22]
The simplest way to tune the polynomial coefficients is to convert the polynomials into tunable surfaces in MATLAB. The tunable surfaces can be tuned automatically using MATLAB functions, such as <systune> and <looptune>. The control gains must be initialized prior to the tuning. The tuning requirements, time constant and steady-state error, are equal to those introduced in Section 2.4. The detailed tutorial on the automatic tuning of tunable surfaces is included in [22]
The obvious strength of the method is that the tuned control gains are always optimal for their respective flight conditions. Unlike the previous methods, the gains are neither compromised nor estimated from linear models, allowing the autopilot to perform at utmost accuracy in nonlinear environments. However, automatic tuning requires the most computational power which raises the system requirements on board.
3. Results
The relative performance of the three methods of gain-scheduled autopilot is investigated. Each method is tested in three missile behavioral profiles. Particularly, the missile is configured to (1) stable-low-velocity profile, (2) stable-high-velocity profile, and (3) unstable-high-velocity profile. It is expected that an autopilot with a more advanced method for obtaining the control gains will deliver finer results. Respectively, a shorter simulation time and a smaller miss distance signify greater efficiency and higher accuracy.
3.1. Simulation Results
3.1.1. Simulation Time
The simulation time, or the time taken for target acquisition, varies noticeably across the autopilots. As shown in Table 2, the third autopilot exhibits the shortest simulation time while the first autopilot requires a significantly longer time on average (~5%). The second autopilot reaches the target almost simultaneously with the third autopilot, running nearly equally in efficiency. Initially, the control effort was expected to heavily affect the simulation time. Rather, it appears the simulation time is dictated by how effectively a controller commands a missile to pursue the optimal trajectory. For instance, the third autopilot has the most fluid transition in its control gains, allowing the controller to give fin demands that prevent the missile from escaping the optimal trajectory.
Table 6.
Simulation time and percent comparison.
| Case | Method | Simulation time [seconds] | Percent difference |
|---|---|---|---|
| 1 | Index-search | 4.233 | 0% |
| Bilinear interpolation | 4.071 | -3.90% | |
| Automatic | 4.063 | -4.09% | |
| 2 | Index-search | 4.192 | 0% |
| Bilinear interpolation | 3.980 | -5.19% | |
| Automatic | 3.974 | -5.34% | |
| 3 | Index-search | 4.300 | 0% |
| Bilinear interpolation | 4.016 | -6.83% | |
| Automatic | 4.001 | -7.20% |
3.1.2. Range Traveled
To help visualize the actual efficiency of each autopilot, the total range traveled by the target is collected. On the exterior, the longer the range covered by the target the more imminent the threat becomes. The difference between the range covered by the targets in the second and the third autopilots is almost negligible. The target has traveled approximately 2% longer range with the first autopilot.
Table 7.
Range traveled by target and percent comparison.
| Case | Method | Range traveled [meters] | Percent Difference |
|---|---|---|---|
| 1 | Index-search | 1352.96 | 0% |
| Bilinear Interpolation | 1341.85 | -0.82% | |
| Automatic | 1340.88 | -0.89% | |
| 2 | Index-search | 1339.31 | 0% |
| Bilinear Interpolation | 1310.77 | -2.15% | |
| Automatic | 1310.02 | -2.21% | |
| 3 | Index-search | 1362.71 | 0% |
| Bilinear Interpolation | 1324.90 | -2.81% | |
| Automatic | 1322.03 | -3.03% |
3.1.3. Miss Distance
The most important factor in determining the effectiveness of an autopilot is the miss distance. The study assumes that a missile must denotate near its target within 10 m for effective blast fragmentation. In other words, the miss distance must be smaller than 10 m for a reliable hit-to-kill. The miss distance of the first autopilot in the third case is frighteningly close to the threshold distance. In other words, the first autopilot may not be reliable in scenarios with more evasive targets. The miss distance of the second and the third autopilot is safely within the explosion radius. Particularly, both the second and third autopilots exhibit minimal miss distance, less than 1m, in all of the cases provided.
Table 8.
Miss distance and percent comparison.
| Case | Method | Miss Distance [meters] | Percent Difference |
|---|---|---|---|
| 1 | Index-search | 6.8411 | 0% |
| Bilinear Interpolation | 0.4684 | -174.37% | |
| Automatic | 0.0710 | -195.89% | |
| 2 | Index-search | 8.1884 | 0% |
| Bilinear Interpolation | 0.4552 | -178.94% | |
| Automatic | 0.0702 | -196.60% | |
| 3 | Index-search | 9.8919 | 0% |
| Bilinear Interpolation | 0.4583 | -182.29% | |
| Automatic | 0.0863 | -196.54% |
In summary, the second autopilot, which uses bilinear interpolation, demonstrates capability comparable to the third autopilot in efficiency and accuracy. The simple interpolation algorithm reduces the control effort significantly while maintaining nearly perfect guidance for interception. Owing to its simple structure, the second autopilot can be easily fitted to any system and be a compelling candidate for control engineers seeking a robust, accessible alternative to the conventional autopilots.
3.2. Validation of Results
It is crucial to examine whether the second autopilot ensures the structural integrity of the missile while pursuing a target. Most structural failures occur when the acceleration experienced by the missile is too large or when the rate of change in the fin angle is too drastic. In particular, the acceleration in the direction normal to the surface of the missile and the maximum fin demand are investigated.
Figure 6.
Acceleration acting normal to the surface of the missile. The underscore numbers represent their respective case numbers.
Figure 6.
Acceleration acting normal to the surface of the missile. The underscore numbers represent their respective case numbers.
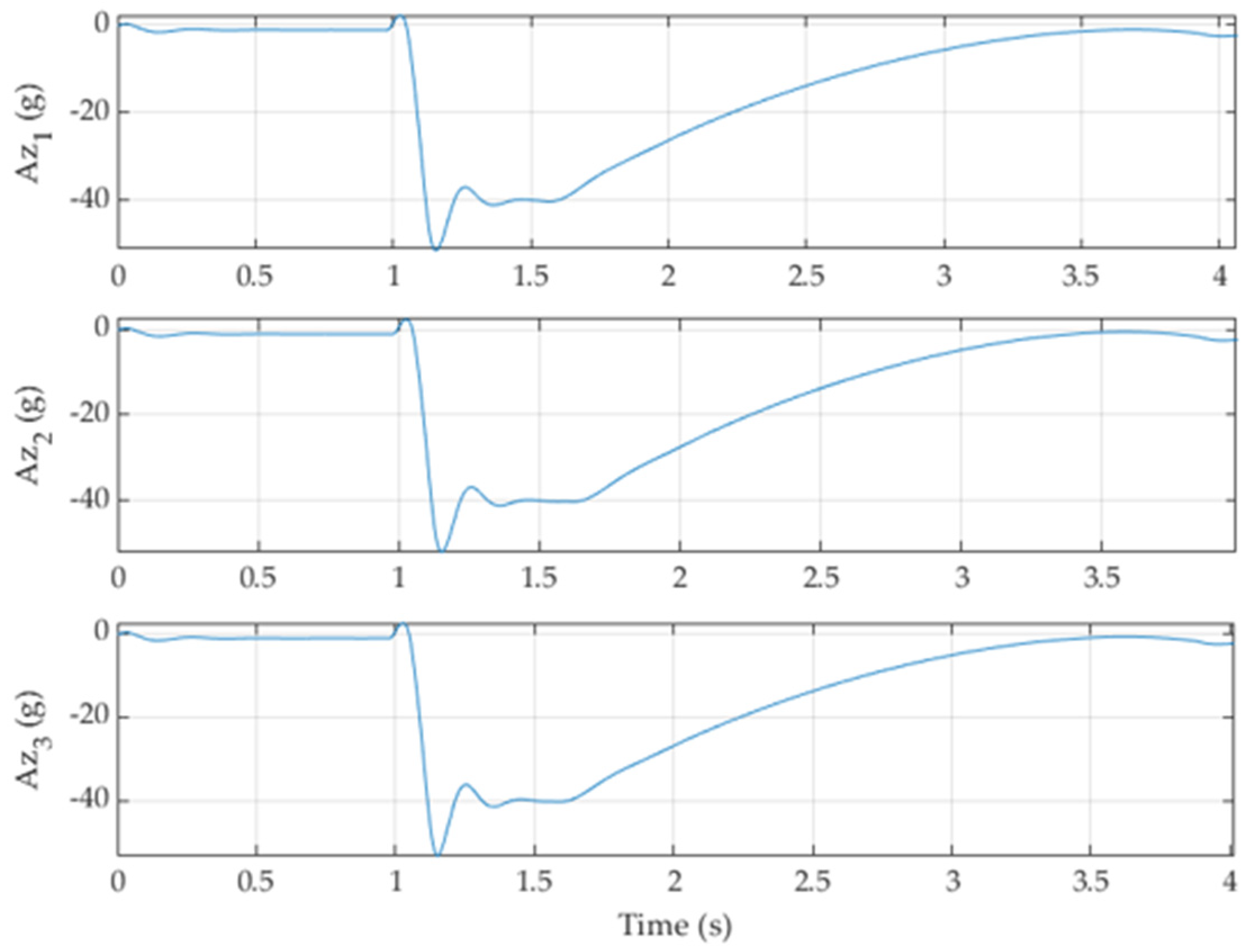
Table 9.
Inspection of aerodynamic stress on the structure of the missile.
| Case | Maximum normal acceleration [G] | Threshold margin [G] |
|---|---|---|
| 1 | 53.813 | 6.187 |
| 2 3 |
52.055 53.392 |
7.945 6.608 |
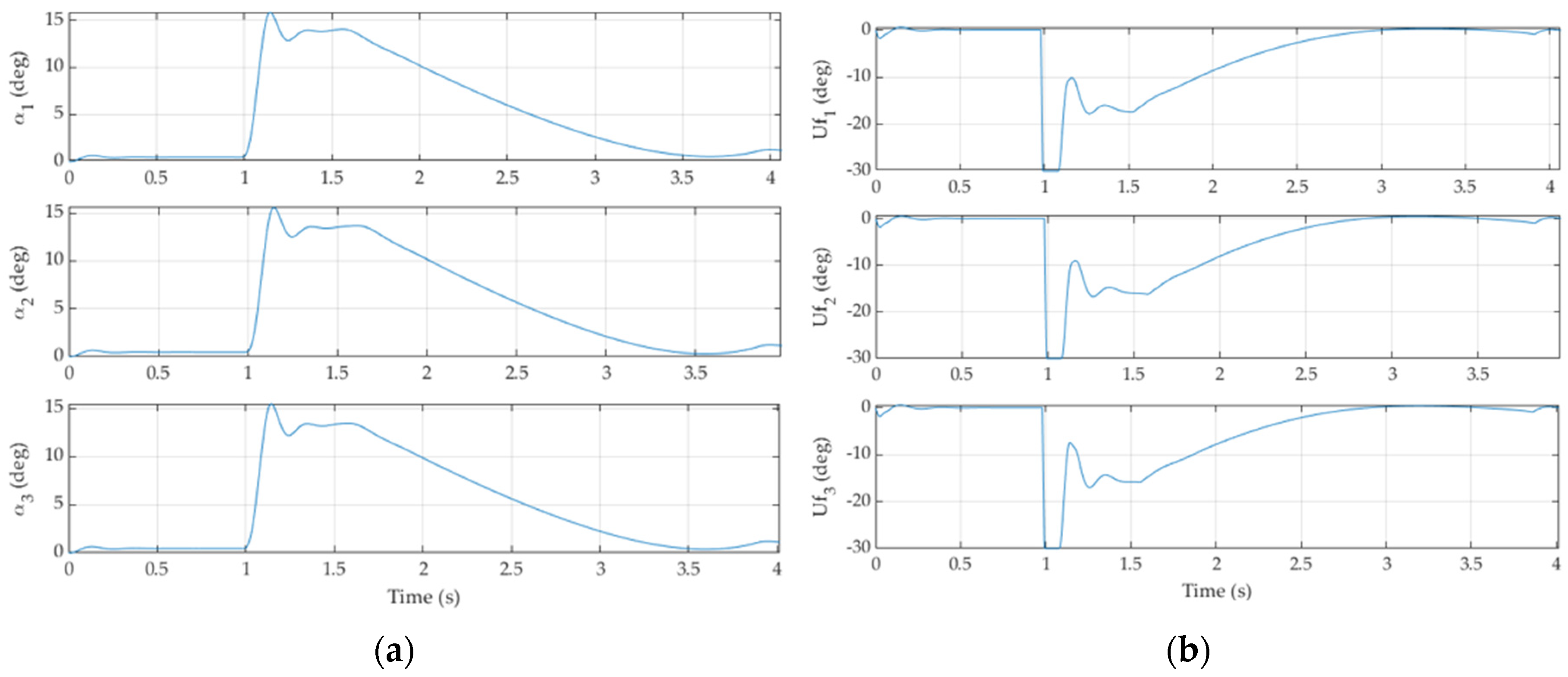
The normal acceleration must be lower than 60 G, the typical maximum acceleration experienced by an aerobatic missile. [23] The missile is most likely to suffer the largest acceleration in Case 2 and Case 3 where the missile maintains high velocity. Their respective maximum acceleration is 52.055G and 53.392G. All of the maximum accelerations are below the threshold with reasonable margin, implicating the feasibility of the selected autopilot. Moreover, angle of attack and fin deflection do not exhibit any cusp or discontinuity in their trends, as seen in Figure 7, meaning the autopilot is viable for a real mission.
Figure 7.
(a) Angle of attack; (b) Commanded fin deflection. Any discontinuity signifies the selected autopilot method may not be applicable to a real system.
Figure 7.
(a) Angle of attack; (b) Commanded fin deflection. Any discontinuity signifies the selected autopilot method may not be applicable to a real system.
4. Discussion
Bilinear interpolation of control gains in 3D-LUT provides a simple and robust solution to control design of gain-scheduled autopilot. The straightforward interpolation algorithm makes the autopilot easy to implement, thus reducing control effort and complexity of the technology onboard. In fact, the overall performance of the autopilot with bilinear interpolation is comparable to that of the state-of-the-art autopilot with severely higher computational burden. In conclusion, the study shows that bilinear interpolation of control gains offers a practical and competent way to enhance control system performance, adapt to changing conditions, and achieve robustness and stability, making it a valuable tool in the arsenal for aerospace control. Engineers and researchers can leverage the insights gained from this study to design highly efficient and robust autonomous control systems for a wide range of applications not limited to aerial guidance, accelerating advancements in adaptive control technology, and fostering the development of more sophisticated and reliable autonomous systems.
Future research could explore innovative ways of leveraging big data and machine learning algorithms to learn and adapt to system dynamics in real-time. By incorporating data-driven gain-scheduling, gain-scheduled autopilots may better address unforeseen disturbances and changing system characteristics, ultimately leading to more robust and resilient autonomous control systems.
Supplementary Materials
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy decisions.
Author Contributions
Conceptualization, S.M.K.; methodology, S.M.K.; software, S.M.K.; validation, S.M.K. and T.S.; formal analysis, S.M.K.; investigation, S.M.K.; resources, S.M.K. and T.S.; writing—original draft preparation, S.M.K.; writing—review and editing, S.M.K. and T.S.; visualization, S.M.K.; supervision, S.M.K.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data supporting reported results can be obtained by contacting the corresponding author.
Acknowledgments
Engineers from Cornell University and Naval Postgraduate School for the development of the skeleton code of 6DOF aerodynamic system.
Conflicts of Interest
The authors declare no conflict of interest. All the authors declare the work has not any kind of relation or/and conflict of interest with any military company or military project. It is solely the independent thoughts and work of the two individual authors.
Appendix A
Raytheon provides the solution to the short period dynamics of a lightly damped, fast, stable system [2]. The state space representation of a stable system is
and the corresponding open loop transfer functions are as follows:
References
- Available online: https://www.navy.mil/Press-Office/News-Stories/Article/2255644/sm-6-test-displays-range-and-versatility/(accessed August 11, 2023).
- Available online: https://www.thedrive.com/the-war-zone/sm-6-missile-used-to-strike-frigate-during-massive-sinking-exercise-in-pacific (Accessed August 11, 2023).
- Available online: https://www.defense.gov/Help-Center/Article/Article/2762906/use-of-department-of-defense-imagery/#:~:text=Department%20of%20Defense%20photographs%20and,use%2C%20subject%20to%20specific%20guidelines (accessed on August 11, 2023).
- Fontana, S.; Di Lauro, F. An Overview of Sensors for Long Range Missile Defense. Sensors 2022, 22(24). [Google Scholar] [CrossRef] [PubMed]
- Wright, D. Decoys Used in Missile Defense Intercept Tests, 1999–2018; Technical Report; Union of Concerned Scientists: Cambridge, MA, USA, 2019. [Google Scholar]
- Lewis, G.; Grego, L. Ground-Based Intercept (GBI) Intercept Tests; Technical Report; American Physical Society: Ridge, NY, USA, 2021. [Google Scholar]
- Belfadel, D.; Macwan, I. Ballistic missile tracking in the presence of decoys using space base IR sensors. In Proceedings of the Signal Processing, Sensor/Information Fusion, and Target Recognition XXXI, Orlando, FL, USA, 3 April–13 June 2022; SPIE: Bellingham, WA USA, 2022; Volume 1212209, pp. 70–77. [Google Scholar]
- Stone, C. Key Points Orbital Vigilance: The Need for Enhanced Space-Based Missile Warning and Tracking. Mitchell Institute. Policy Paper. Available online: https://mitchellaerospacepower.org/wp-content/uploads/2022/06/Space_Based_Early_Warning_Policy_Paper_36-FINAL.pdf (accessed August 12, 2023). 2022, 36, 148–152. [Google Scholar]
- Wilkening, D.A. A simple model for calculating ballistic missile defense effectiveness. Sci. Glob. Secur. 2000, 8, 183–215. [Google Scholar] [CrossRef]
- Tracy, C.L.; Wright, D.C. Overhyped. Scientific American 2021, 325(2), 64–71. [Google Scholar] [CrossRef]
- Tracy, C.L.; Wright, D. Modeling the Performance of Hypersonic Boost-Glide Missiles. Sci. Glob. Secur. 2020, 28(3), 135–170. [Google Scholar] [CrossRef]
- Missile Threat CSIS Missile Defense Project, System Component: Standard Missile-6 (SM-6). Available online: https://missilethreat.csis.org/defsys/sm-6/(accessed on 2 May 2023).
- Mracek, C.; Ridgely, D. Missile Longitudinal Autopilots: Connections Between Optimal Control and Classical Topologies. AIAA ARC 2005, 1–16. [Google Scholar] [CrossRef]
- Mracek, C.; Ridgely, D. Missile Longitudinal Autopilots: Comparison of Multiple Three Loop Topologies. AIAA ARC 2005, 1–11. [Google Scholar] [CrossRef]
- Freedberg, S. Non-Standard: Navy SM-6 Kills Cruise Missiles Deep Inland. Breaking Defense. August 19, 2014. Available online: https://breakingdefense.com/2014/08/non-standard-navy-sm-6-kills-cruise-missiles-deep-inland/(accessed August 12, 2023).
- Kang, H. Computational Computer Technology: Three-Dimensional Lookup Table with Interpolation. SPIE 2006, 159, 151–155. [Google Scholar] [CrossRef]
- NASA Shape Effects on Drag. Available online: https://www.grc.nasa.gov/www/k-12/rocket/shaped.html (accessed on 22 April 2023).
- Shamma, J.; Cloutiert, J. Gain-Scheduled Missile Autopilot Design using Linear Parameter Varying Transformation. Journal of Guidance Control and Dynamics 1993, 16, 256–262. [Google Scholar] [CrossRef]
- Palumbo, N.F.; Blauwkamp, R.A.; Lloyd, J.M. Basic Principles of Homing Guidance. Johns Hopkins Apl Technical Digest https://api.semanticscholar.org/CorpusID:1858151. 2010, 29, 25–41. [Google Scholar]
- Abd-elatif, M.A.; Qian, L.; Bo, Yu-ming. Optimization of three-loop missile autopilot gain under crossover frequency constraint. Defence Technology 2016, 12, 32–38. [CrossRef]
- Jackson, P.B. Overview of Missile Flight Control Systems. Johns Hopkins Apl Technical Digest https://api.semanticscholar.org/CorpusID:17756801. 2010, 29, 9–24. [Google Scholar]
- MathWorks, Control Systems: Tuning of Gain-Scheduled Three-Loop Autopilot. Available online: https://kr.mathworks.com/help/control/ug/tuning-of-gain-scheduled-three-loop-autopilot.html (accessed on 19 April 2023).
- The Motion of Ballistic Missiles. Available online: https://apps.dtic.mil/sti/pdfs/AD0731662.pdf (accessed on 22 April 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions, or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







