Causal Fuzzy Deep Learning Algorithm for the Differentiation of Gliosarcoma From Glioblastoma

In this paper, we introduce an innovative approach to distinguish Gliosarcoma (GSM) from Glioblastoma (GBM). Our method combines causal fuzzy logic rules with the Big Bird architecture, a Transformer-based Deep Learning algorithm. Unlike prior research, which often relied on statistical models to reduce dataset dimensions before causal analysis, our approach harnesses the complete dataset in tandem with our causal fuzzy Big Bird architecture. Additionally, we benchmark our results not only against previous Gliosarcoma/Glioblastoma studies but also against GPT-2 for a comprehensive evaluation.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Glioblastoma (GBM) is one of the most common brain cancers [1]. GBM generally happens in the glial cells [2] and has several variants. Gliosarcoma (GSM) is a cancer classified by the World Health Organization (WHO) as a variant of GBM [1,3]. It is particularly important to accurately distinguish GSM from GBM [3]. Radiomics is an emerging field for imaging data analysis. It has been successfully employed for the differentiation of the central nervous system tumors [4]. In a recent paper, Qian et al. [4] conducted a study to identify an optimal machine learning algorithm for the differentiation of GSM from GBM based on radiomics data analysis. Baldé and Ghosh [20] studied the causal effect of Edema on the differentiation of GSM from GBM by using machine learning algorithms in radiomics. To do so, the authors developed a two steps procedure: In the first step, they reduced the dataset dimension using the sure independence screening procedure [5,6]. In the second step, they employed the outcome adaptive lasso [7] or the generalized outcome adaptive lasso [8].

To find the causes of Gliosarcoma, most of the previous studies use dimension reduction and/or statistical machine learning algorithms.

In this paper, we will use the entire dataset without applying any dimension reduction algorithms. Specifically, we will use causal fuzzy logic rules from [9], combined with Transformer-based deep learning algorithms [10] to identify the possible causes of Gliosarcoma. To the best of our knowledge, we are the first to use Causal Fuzzy Deep Learning Algorithm to detect the causes of Gliosarcoma.

2. Causal reasoning

In causal reasoning, we are looking how or why something happened and the relationship between the causes and their effects. In causal reasoning, we examine the relationship between causes and effects, and we try to understand how or why something happened. To calculate the causes of an event, current causal models use Individual or Average Treatment Effect (I-ATE). For instance, Pearl [11] computes Average Causal Effect by subtracting the means of the treatment and control groups. Pearl uses Directed Acyclic Graphs (DAGs) to visualize and compute the associations or causal relationships between a set of elements. He also uses do operators, which are interventions on the nodes of DAGs, as well as probability theory, the Markov assumptions, and other concepts/methods/tools [11].

However, in [12] the authors showed that ATE describes the linear relationship between variables and in some examples cannot reflect the causality. Also, Pearl’s approach to causation does not allow reasoning in cases of degrees of uncertainty [9]. Since do operators cut the relation between two nodes, Pearl’s approach cannot answer gradient questions such as: given that you smoke a little, what is the probability that you have cancer to a certain degree? To solve Pearl’s do operator problem the authors in [9,13], used fuzzy logic rules which implement human language nuances such as “small” instead of mere zero or one. Furthermore, Janzing [14] showed that at a macro level, Pearl’s causal model works well with situations that are rare, such as rare medical conditions but, at a micro level, fails with bidirectional nodes. Authors in [12] showed that Janzing’s model [15] works well with bidirectional nodes, but fails with situations that are rare [12].

In [9] which uses fuzzy logic as the fundamental part of their causal model, there are two types of rules which we call association and causal rules. An association rule can be of type A

\to

B. A causal rule can be ~A & B. That is, tell me what happens to B when A is missing. In other words, using fuzzy logic rules, we can estimate more than fourteen values in the presence and the absence of each element (in the dataset context this becomes columns or variables).

In [9], instead of cutting the relationships between the treatment and its confounding parents, the model using fuzzification method assigns fuzzy membership values, such as very low, low, medium, and high, to the Treatment. To automatically assign membership values, the authors used fuzzy c-mean algorithm [16] which is widely used for clustering the datasets using fuzzy logic.

Once, the membership assignments step is done, the model then applies causal fuzzy interventional rules from [9] as following

m a x (1 - μ (a), μ (b))

. Doing so, it can calculates more than fourteen different possible membership degree based fuzzy counterfactual values for each variable using different causal fuzzy rules such as

m a x (1 - μ (a), μ (b))

, where

μ (a)

and

μ (b)

are the highest membership degrees of

a

and

b

among all considered fuzzy attributes for

a

and

b

, respectively [9]. We would like to put more emphasis that using the following causal rules, we are applying interventions and estimate fuzzy counterfactuals at the same time.

Here are some of our fuzzy interventional rules.

m a x (1 - μ (a), μ (b))

m i n (1 - μ (a), μ (b))

m a x (m i n (1 - μ (a), 1 - μ (b)), b)

We note that based on the model introduced in [9], each of the above rules has a meaning based on a subjective random selection. For instance,

m i n (1 - μ (b), μ (a))

could be seen as the probability of subjectively selecting

A = a

F_{A}

and

B = b

F (\neg B)

, where

F_{A}

and

F_{B}

are the fuzzy attributes that

μ (a)

and

μ (b)

come from, respectively. The model then applies defuzzification to the dataset in order to obtain the outputs. The big changes in the fuzzy output values can indicate possible causes.

3. Model description

Causal models can reason but cannot learn, and Deep Learning algorithms can learn but have limited capacity for reasonings [17]. Causal fuzzy rules for the first time were integrated with DLs such as Variational Autoencoders [17] and Big Bird architecture [10]- the latter outperformed ChatGpt 2 in reasoning [10]. To handle long sequences, Big Bird is equipped with a sparse attention mechanism which reduces the computational complexity of self-attention from quadratic to linear.

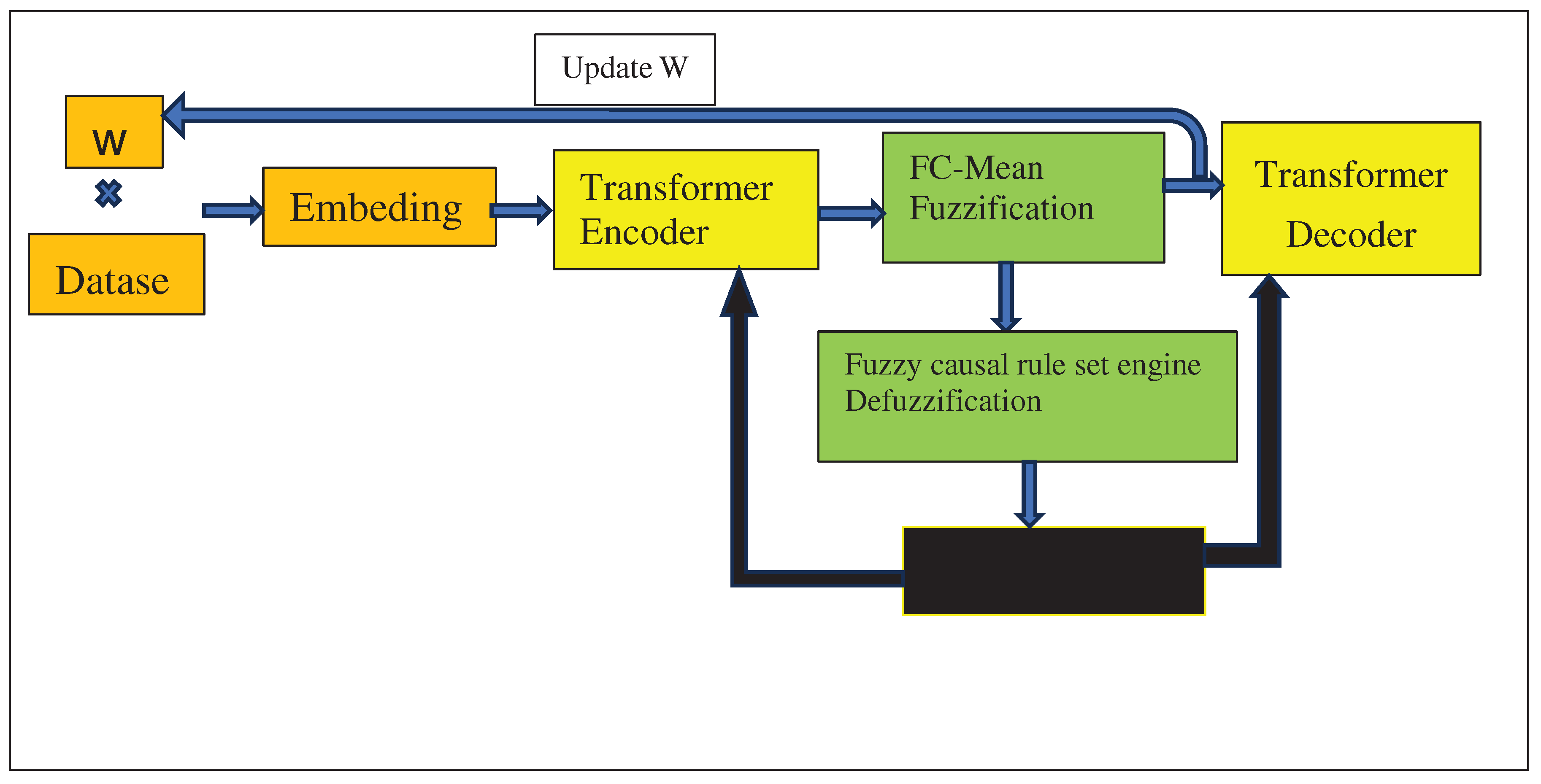
Causal fuzzy rules, fuzzification and defuzzification steps were integrated with Big Bird as follows: the model first creates a matrix W with randomly generated values between zero and one (Figure 1). W will represent the potential causal relationships between the columns of the dataset D [17]. To do this, the model first initialized matrix W with size (n*n) where n is the number of columns in D. It then multiplied W by the dataset. The result of this step was then fed into the Transformer’s Embedding module. The output of the Embedding module was then fed into the Transformer’s Encoder module which then partitioned using the Fuzzy c-means algorithm [16] (shown as FC-mean in Figure 1). This partitioning was done to automatically find fuzzy membership intervals without requiring an expert to define them. Using the output of the Fuzzy c-means algorithm, the architecture then used Fuzzification method (Figure 1) to fuzzify the dataset. In the next step, the Fuzzy causal rule set engine (Figure 1) applies the above causal fuzzy rules from [9] to each of the dataset D’s columns. Finally, the architecture applies Defuzzification (Figure 1).

The next step was to incorporate fuzzy rules into the Big Bird’s loss function. According to [5], this was done by dividing the Big Bird Loss Function by the variations of fuzzy causal reasoning rules obtained from the previous defuzzification step.

The result of the previous step was then multiplied by the original dataset before being fed into the Transformer’s Encoder module. These steps were repeated until the architecture converged. The elements of the matrix W, which resulted from the previous steps, are possible causes.

3. Dataeset Description

We used the radiomics data studied in Qian et al. [4]. The dataset contained a sample size n=183 patients including 100 with GBM and 83 with GSM with 1 303 radiomic features extracted from MRI images. In our study, we took “Edema” A (Yes: 1 / No: 0) as the exposure variable (treatment) and the outcome variable Y (Y = 1 if the patient had gliosarcoma and Y = 0 if the patient had glioblastoma. We used 1 303 radiomics features as potential confounders of the relationship between A and Y.

5. Results

In this section, we compare the Causal Fuzzy Big Bird Architecture (CFT) [10] (code on GitHub) and the GPT-2 architecture [18] in terms of features selection and accuracy. GPT-2 architecture is a powerful deep learning algorithm which is described in the following address[1]. We applied both CFT and GPT-2 to analyze the radiomics dataset. The objective was to identify the key radiomics confounders of the causal relationship of Edema and Gliosarcoma. As these confounding features can inform the distinction of GSM from GBM. Based on the analysis, the radiomics features were grouped into four categories (Please see Appendix): Group A, Group B, Group C, and Singleton D, each representing varying probabilities of being an important potential confounder of the relationship between Edema and GSM.

We added a new embedding layer of size 20K to GPT-2, a language model, so that it could learn from numerical data. We used the same embedding size for CFT. We split the dataset into 70% for training and 30% for testing. Since the dataset had only 183 rows, we augmented it by 200 folds. We trained both models for 500 epochs on a Nvidia A100 with 24 GB RAM.

Since, Big Bird and GTP-2 are both language models, we used perplexity formula [19] to to measure the accuracy of both models. As we can see, GPT-2’s perplexity score is higher than CFT. However, this cannot be considered as a good measure for causal inference.

One way to support this claim is to compare how GPT-2 and CFT performance on detecting the ‘original_shape_Sphericity’, which is the most important radiomics feature. GPT-2 fails to detect it, while CFT succeeds, even though CFT has a lower test accuracy than GPT-2.

In the following we provided the result of the CFT and GPT-2 and their comparison. Our results agree with the findings in [20], who identified the radiomics feature original_shape_Sphericity as one of the key factors informing the distinction of GSM from GBM. That is this feature is a strong potential confounder of the relationship of Edema and GSM.

Once more, we wish to underscore the methodology distinction. In prior research, including the work referenced in [20], the standard practice involved the initial application of dimension reduction techniques followed by the utilization of statistical and machine learning algorithms, such as Lasso [8], to derive their findings. In contrast, our approach for this study involved the direct utilization of the entire dataset with our architecture, without any alterations or preprocessing steps.

The Appendix shows the groups A, B, and C of variables that are most likely to contribute to the distinction of GSM from GBM by CFT and GPT-2. However, GPT-2 detected fewer variables than CFT in each group.

Conclusion:

Unlike previous studies on gliosarcoma detection that relied on statistical models to reduce the size of the dataset and then used machine learning, we used the entire dataset for causal inference. To do so, we used causal fuzzy logic rules from [9] integrated with Big Bird architecture which is a Transformer based Deep Learning algorithm [10]. Our finding is in accordance with the findings in [8]. We also compared causal fuzzy Big Bird results with GPT-2 which is one of the well-known DLs. Causal fuzzy Big Bird outperformed GPT-2 by detecting "original_shape_Sphericity," as a key potential radiomics confounder of the relationship of Edema and GSM. It is worth mentioning that DLs need lots of data to learn. However, our causal fuzzy Big Bird architecture used very small amount of data to discover the causal variables. This is because our model is equipped with casual fuzzy logic rules from [9].

Appendix

In the following list, we have enumerated the variables detected by our CFT architecture. Those variables highlighted in yellow represent cases that were not detected by GPT-2 architecture.

CFT output

Groupe D	Proportion of times each radiomics group features was selected
original_shape_Sphericity	> 95%

Groupe C

Proportion of times each radiomics group features was selected

original_shape_MajorAxis, original_shape_Maximum2DDiameterRow,
original_shape_Sphericity, original_gldm_DependenceNonUniformity,
3-0-mm-3D_glszm_GrayLevelNonUniformity,
original_shape_SurfaceVolumeRatio, log-sigma-3-0-mm-3D_glszm_SizeZoneNonUniformity,
log-sigma-3-0-mm-3D_gldm_DependenceNonUniformity,
log-sigma-5-0-mm-3D_glszm_GrayLevelNonUniformity,
LHH_glcm_ClusterShade,
waveletLHH_glcm_Idn,
wavelet-HLL_firstorder_10Percentile,
waveletHLL_firstorder_MeanAbsoluteDeviation,
wavelet-HLL_firstorder_Skewness,
waveletHLH_firstorder_Minimum, wavelet-HLH_glcm_JointAverage,
original_shape_SurfaceVolumeRatio,
waveletHLH_gldm_SmallDependenceHighGrayLevelEmphasis,
waveletHHL_gldm_LowGrayLevelEmphasis

> 85%

Groupe B

Proportion of times each radiomics group features was selected

original_shape_MajorAxis,
original_shape_Maximum2DDiameterRow,
original_shape_SurfaceVolumeRatio,
original_shape_Maximum3DDiameter,
original_shape_Sphericity,
original_glszm_SizeZoneNonUniformity,
original_gldm_DependenceNonUniformity, 3-0-mm-3D_glszm_GrayLevelNonUniformity,
logsigma-3-0-mm-3D_glszm_SizeZoneNonUniformity,
log-sigma-3-0-mm-3D_gldm_DependenceNonUniformity,
log-sigma-5-0-mm-3D_glszm_GrayLevelNonUniformity,
LHH_glcm_ClusterShade,
wavelet-LHH_glcm_Idn,
wavelet-HLL_firstorder_10Percentile,
wavelet-HLL_firstorder_MeanAbsoluteDeviation,
wavelet-HLL_firstorder_Skewness,
waveletHLH_firstorder_Minimum,
wavelet-HLH_glcm_JointAverage,
original_shape_SurfaceVolumeRatio,
waveletHLH_gldm_SmallDependenceHighGrayLevelEmphasis,
waveletHHL_gldm_LowGrayLevelEmphasis

> 75%

Groupe A

Proportion of times each radiomics group features was selected

original_shape_MajorAxis, original_shape_Maximum2DDiameterRow,
original_shape_Maximum2DDiameterSlice,
original_shape_Maximum3DDiameter,
original_shape_Sphericity, original_shape_SurfaceArea,
original_glszm_SizeZoneNonUniformity,
original_gldm_DependenceNonUniformity,
log-sigma-3-0-mm-3D_glszm_GrayLevelNonUniformity,
log-sigma-3-0-mm-3D_glszm_SizeZoneNonUniformity,
log-sigma-3-0-mm-3D_gldm_DependenceNonUniformity,
log-sigma-5-0-mm-3D_glszm_GrayLevelNonUniformity,
wavelet-LLL_glszm_LargeAreaEmphasis,
wavelet-LLL_glszm_ZoneEntropy,
wavelet-LLH_glrlm_GrayLevelNonUniformityNormalized,
wavelet-LLH_glrlm_RunEntropy,
wavelet-LHL_firstorder_Variance,
waveletLHL_glcm_Correlation, wavelet-LHL_glrlm_LowGrayLevelRunEmphasis,
waveletLHL_glrlm_RunVariance,
wavelet-LHL_glszm_SmallAreaHighGrayLevelEmphasis,
waveletLHL_glszm_ZoneVariance, wavelet-LHL_gldm_SmallDependenceLowGrayLevelEmphasis,
wavelet-LHH_firstorder_Entropy,
wavelet-LHH_firstorder_Variance,
waveletLHH_glcm_ClusterShade,
wavelet-LHH_glcm_Idn,
wavelet-HLL_firstorder_10Percentile,
wavelet-HLL_firstorder_MeanAbsoluteDeviation,
wavelet-HLL_firstorder_Skewness,
waveletHLH_firstorder_Minimum,
wavelet-HLH_glcm_JointAverage,
original_shape_SurfaceVolumeRatio,
wavelet-HLH_gldm_SmallDependenceHighGrayLevelEmphasis, waveletHHL_gldm_LowGrayLevelEmphasis

> 60%

In the following we show GPT-2’s output:

Groupe D	Proportion of times each radiomics group features was selected
Null	> 90%

Groupe C	Proportion of times each radiomics group features was selected
original_shape_MajorAxis, original_shape_Maximum2DDiameterRow, 3-0-mm-3D_glszm_GrayLevelNonUniformity, original_shape_SurfaceVolumeRatio, log-sigma-3-0-mm-3D_glszm_SizeZoneNonUniformity, waveletHLH_firstorder_Minimum, wavelet-HLH_glcm_JointAverage, original_shape_SurfaceVolumeRatio, waveletHLH_gldm_SmallDependenceHighGrayLevelEmphasis,	> 85%

Groupe B

Proportion of times each radiomics group features was selected

original_shape_SurfaceArea,
original_glszm_SizeZoneNonUniformity,
original_gldm_DependenceNonUniformity,
wavelet-LLL_glszm_ZoneEntropy,
wavelet-LLH_glrlm_GrayLevelNonUniformityNormalized,
waveletLHL_glcm_Correlation, wavelet-LHL_glrlm_LowGrayLevelRunEmphasis,
wavelet-LHL_glszm_SmallAreaHighGrayLevelEmphasis,
waveletLHL_glszm_ZoneVariance, wavelet-LHL_gldm_SmallDependenceLowGrayLevelEmphasis,
wavelet-LHH_glcm_Idn,
wavelet-HLL_firstorder_10Percentile,
wavelet-HLL_firstorder_MeanAbsoluteDeviation,
waveletHLH_firstorder_Minimum,
wavelet-HLH_gldm_SmallDependenceHighGrayLevelEmphasis,

> 75%

Note

1. https://github.com/huggingface/transformers

References

Miller, C.R.; Perry, A. Glioblastoma: morphologic and molecular genetic diversity. Archives of pathology & laboratory medicine 2007, 131, 397–406. [Google Scholar]
Ohgaki, H. Epidemiology of brain tumors. Cancer Epidemiology: Modifiable Factors 2009, 323–342. [Google Scholar]
Zaki, M.M.; et al. Genomic landscape of gliosarcoma: distinguishing features and targetable alterations. Scientific Reports 2021, 11, 18009. [Google Scholar] [CrossRef] [PubMed]
Qian, Z.; et al. Machine learning-based analysis of magnetic resonance radiomics for the classification of gliosarcoma and glioblastoma. Frontiers in Oncology 2021, 11, 699789. [Google Scholar] [CrossRef] [PubMed]
Fan, J.; Lv, J. Sure independence screening for ultrahigh dimensional feature space. Journal of the Royal Statistical Society Series B: Statistical Methodology 2008, 70, 849–911. [Google Scholar] [CrossRef] [PubMed]
Tang, D.; Kong, D.; Pan, W.; Wang, L. Ultra-high dimensional variable selection for doubly robust causal inference. Biometrics 2023, 79, 903–914. [Google Scholar] [CrossRef] [PubMed]
Shortreed, S.M.; Ertefaie, A. Outcome-adaptive lasso: variable selection for causal inference. Biometrics 2017, 73, 1111–1122. [Google Scholar] [CrossRef] [PubMed]
Baldé, I.; Yang, Y.A.; Lefebvre, G. Reader reaction to “Outcome-adaptive lasso: Variable selection for causal inference” by Shortreed and Ertefaie (2017). Biometrics 2023, 79, 514–520. [Google Scholar] [CrossRef] [PubMed]
Faghihi, U.; Robert, S.; Poirier, P.; Barkaoui, Y. From Association to Reasoning, an Alternative to Pearl’s Causal Reasoning. In Proceedings of AAAI-FLAIRS 2020. North-Miami-Beach (Florida) 2020. [Google Scholar]
Kalantarpour, C.; Faghihi, U.; Khelifi, E.; Roucaut, F.-X. Clinical Grade Prediction of Therapeutic Dosage for Electroconvulsive Therapy (ECT) Based on Patient’s Pre-Ictal EEG Using Fuzzy Causal Transformers. presented at the International Conference on Electrical, Computer, Communications and Mechatronics Engineering, Tenerife, Canary Islands, Spain, 2023., ICECCME 2023. [Google Scholar]
Pearl, J.; Mackenzie, D. The book of why: the new science of cause and effect. Basic Books, 2018.
Faghihi, U.; Saki, A. Probabilistic Variational Causal Effect as A new Theory for Causal Reasoning. arXiv arXiv:2208.06269, 2023.
Robert, S.; Faghihi, U.; Barkaoui, Y.; Ghazzali, N. Causality in Probabilistic Fuzzy Logic and Alternative Causes as Fuzzy Duals. ICCCI 2020, vol. Ngoc-Thanh Nguyen, et al, 2020.
Janzing, D.; Minorics, L. ; Blöbaum, P, Feature relevance quantification in explainable AI: A causal problem. presented at the International Conference on Artificial Intelligence and Statistics; 2020. [Google Scholar]
Janzing, D.; Balduzzi, D.; Grosse-Wentrup, M.; Schölkopf, B. Quantifying causal influences. 2013.
Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Computers & geosciences 1984, 10, 191–203. [Google Scholar]
Faghihi, U.; Kalantarpour, C.; Saki, A. Causal Probabilistic Based Variational Autoencoders Capable of Handling Noisy Inputs Using Fuzzy Logic Rules. presented at the Science and Information Conference; 2022. [Google Scholar]
Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI blog 2019, 1, 9. [Google Scholar]
Jelinek, F.; Mercer, R.L.; Bahl, L.R.; Baker, J.K. Perplexity—a measure of the difficulty of speech recognition tasks. The Journal of the Acoustical Society of America 1977, 62, S63–S63. [Google Scholar] [CrossRef]
Baldé, I.; Ghosh, D. Ultra-high dimensional confounder selection algorithms comparison with application to radiomics data. arXiv 2023, arXiv:2310.06315. [Google Scholar]

Figure 1. Causal Fuzzy Big Bird Architecture (CFT).

Table 1. Train/Test accuracy of the Architectures that we have used.

Architecture	Train Accuracy	Test Accuracy
GPT-2	96.5%	93%
CFT	95%	92%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Causal Fuzzy Deep Learning Algorithm for the Differentiation of Gliosarcoma From Glioblastoma

Abstract

1. Introduction

2. Causal reasoning

3. Model description

3. Dataeset Description

5. Results

Conclusion:

Appendix

CFT output

Note

References

MDPI Initiatives

Important Links

Subscribe