Prerpints.org logo
Preprint
Article

Foundry-processed Compact and Broadband Adiabatic Optical Power Splitters with Strong Fabrication Tolerance

Altmetrics

Downloads

147

Views

63

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

17 October 2023

Posted:

18 October 2023

You are already at the latest version

Alerts
Abstract
Optical power splitters play a crucial role as the fundamental building blocks for many integrated optical devices. They should have low losses, broad bandwidth, and a high tolerance to fabrication errors. Adiabatic optical power splitters inherently possess these qualities while being compatible with foundry processes well-suited for mass-production. The long device lengths of adiabatic power splitters, however, are a limiting factor to achieve compact device sizes, which must be reduced. Here, we use a polynomial taper profile optimization algorithm to design 1×2 and 2×2 adiabatic power splitters with significantly shorter lengths than their adiabatic counterparts. The best performing 1×2 and 2×2 power splitters have 20 μm and 16 μm coupling lengths, respectively. Our designs have minimum feature sizes ranging from 140 nm to 200 nm, and our measurements averaged across 9 different chips show excellent consistency in performance for devices with 180 nm and 200 nm minimum features. Both the 1×2 and 2×2 adiabatic optical power splitters have excess losses less than 0.7 dB over a 100 nm bandwidth, with a standard deviation lower than 0.3 dB. Furthermore, our measurements show greater than 20 dB extinction ratios over 130 nm bandwidth. We also demonstrate the design of 1×2 power splitters with arbitrary splitting ratios, where splitting ratios ranging from 50:50 to 94:6 were achieved with standard deviations between 2% and 6%.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Power splitters are among the most fundamental building blocks of complicated on-chip optical circuits. They are used in optical switches [1], modulators [2], programmable optical circuits [3], and multiplexers [4], to name a few. Ideal power splitters should have low losses, broad bandwidth, compact size, high tolerance to fabrication errors, and small deviations from the intended power splitting ratio. In addition, it is desired that the minimum feature sizes of power splitters are large (>150 nm) so that they are suitable for production at complementary metal oxide semiconductor (CMOS) foundries using mass-production. Satisfying these criteria simultaneously has proven to be challenging. There have been a wide variety of reported implementations of on-chip optical power splitters with differing strengths and weaknesses when the above-mentioned performance metrics are considered.
Among the various types of optical power splitters, directional couplers can achieve low loss and arbitrary power splitting ratios [5]. Yet, they are typically wavelength sensitive, making it difficult to realize polarization-insensitive and broadband response [6]. This problem has been partially solved by replacing the straight directional couplers with curved waveguides [1,7], which yields a broader bandwidth. The inherent strong polarization sensitivity, on the other hand, is difficult to overcome. Alternatively, power splitters based on multimode interferometers (MMIs) work using the self-imaging principle [8] and can be designed for an arbitrary number of inputs and outputs [9], as well as arbitrary splitting ratios [10]. Generally, MMI power splitters are less sensitive to wavelength than directional couplers, although the designed devices can have a large footprint. For example, as in the case of a 2×2 3 dB coupler designed to operate with the TE0 and TE1 modes, the device length of 86.5 μ m has been reported [11], whereas, in the case of 1x4 and 1x8 power splitters device lengths of 36 μ m and 47.8 μ m were achieved, respectively [12]. More compact devices and polarization-insensitive operation have been achieved by engineering the width and thickness of the MMI power splitters, which yielded a footprint of 1.5 x 1.8 μ m2 [13]. However, this device was designed for a 300 nm thick Si layer, which is not commonly used by industrial foundries. More successful implementations of MMI power splitters have been achieved by modifying the profile of the MMI region, yielding in a very compact and low-loss operation [14,15]. One downside of MMI power splitters is that the profile of the device between the MMI region and the output waveguides changes abruptly. This abrupt change constitutes a source for reflections and imbalance in the output, where a slight imbalance in the output waveguides can cause imperfect splitting or increased losses, as we have demonstrated a similar effect in previous work [16].
More recently, subwavelength gratings (SWG) have been used to improve the performance of optical power splitters. For example, the bandwidths of directional coupler-based power splitters were increased via utilizing SWGs [17,18]. A variety of designs for SWG-assisted directional couplers have been reported with low losses and broad bandwidth [19,20,21,22]. SWG-assisted MMI-based power splitters have also been designed to improve the bandwidth, losses, and footprint of traditional MMI power splitters [23,24]. Moreover, SWG-assisted Y-junctions power splitters have shown good performance [25,26,27]. However, it is important to note that the above referenced works report devices with minimum feature sizes smaller than 135 nm, making them unsuitable for large-scale fabrication at CMOS foundries.
In addition to the aforementioned approaches, various inverse design algorithms have been used to optimize the device power splitting efficiencies, where the device is divided into pixels [28,29,30,31] or subwavelength-sized stripes [32]. However, these optimization approaches yield devices that only work with the TE mode and consist of many small-sized features, which can result in fabrication intolerance [33]. When these devices are designed with considerations of foundry limitations, inverse-designed power splitters with minimum feature sizes as large as 200 nm can be achieved [34]. However, these devices suffer from high losses and large output variations. Topological photonic devices have been an alternative to inverse-designed photonic components with small features [35]. With topological optimizations, foundry-compliant designs can be achieved by putting heavy constraints on the design [36,37]. In addition, machine learning models have been used to correct photonic device design layouts prior to fabrication [38]. Yet, these devices typically suffer from over 0.5 dB losses and there is little discussion in the literature on making them polarization insensitive.
Unlike other power splitter implementations, adiabatic optical power splitters are inherently low-loss, broadband, tolerant to fabrication error, and polarization-insensitive. These advantages can be realized even with devices with large minimum feature sizes, yet the resultant adiabatic components are typically much longer than their counterparts. The long device lengths ensure that the mode evolution is slow enough to avoid radiation losses. Using small minimum feature sizes could reduce the device length, which has been demonstrated in the case of a 1×2 adiabatic power splitter with a 30 nm minimum feature size, resulting in a coupling length of 5 μ m [39].Unfortunately, such small features are well beyond fabrication limitations set by foundries. The majority of the adiabatic power splitters with larger minimum feature sizes have linear taper profiles [40,41,42,43,44,45,46]; whereas the linear taper profiles are not ideal for adiabatic transitions and using non-linear profiles can significantly reduce the device lengths even with large minimum feature sizes.
Methods such as shortcuts to adiabaticity [47,48] and quasi-adiabatic dynamics [49,50,51] have been used to design adiabatic taper profiles that resulted in 2×2 3 dB couplers with much shorter lengths as compared to the devices with linear taper profiles. Reference [51] demonstrates over an order-of-magnitude reduction in the length of a 2×2 3 dB coupler as compared to a 3 dB coupler with a linear taper profile, where a 11.7 μ m device length and a 3±0.5 dB bandwidth of 75 nm were achieved. Other methods for designing adiabatic power splitters include ensuring that the adiabatic transition losses are maintained below a certain level by engineering the rate of change of the taper width profile [52]. In Ref. [53], we have developed a different approach where the width profiles of the adiabatic tapers were expressed in terms of a polynomial function and the coefficients of the polynomial terms were optimized using numerical methods for the lowest losses for a given taper length. This method has the advantage of providing more design flexibility for the taper. Using this approach, we have shown a reduction by half in the length of an adiabatic fiber-to-chip light coupler with no additional losses. More recently, we have also applied this technique to a 1×2 Y-junction power splitter with a 120 nm minimum feature size and have shown less than 0.25 dB and 0.23 dB losses for the TE and TM modes, respectively, in the spectral range of 1500 nm and 1600 nm [54]. The polynomial taper optimization is yet to be applied for the design of adiabatic power splitters with large minimum feature sizes and the performance of these devices are to be analyzed when a CMOS-compatible fabrication process is used.
In this work, we propose and implement a polynomial-based adiabatic taper profile optimization algorithm for the design of 1×2 and 2×2 adiabatic optical power splitters. The designed 1×2 Y-Junction power splitters yielded coupling lengths ranging from 10 μ m to 30 μ m for minimum feature sizes ranging from 140 nm to 200 nm. The experimental results show that a device with 180 nm minimum feature size can have a coupling length of 20 μ m with losses lower than 0.5 dB for both the TE and TM modes between 1480 nm and 1585 nm. Besides, the 1×2 Y-Junction architecture can be modified to allow arbitrary power splitting ratios by tuning the gap between the coupling waveguides. We have designed power splitters with ratios of 50:50, 58:42, 68:32, 77:23, and 89:11. The measured standard deviations in the power splitting ratios for these 1×2 Y-Junction splitters were between two to six percent. In addition, a broadband 2×2 3 dB power splitter with a 16 μ m coupling region was measured to have 0.7 dB losses and a bandwidth of over 130 nm, where a larger bandwidth measurement was not possible due to the range of our tunable laser source. Our experiments were performed over 9 different chips and results indicate excellent consistency of performance and significantly fabrication-tolerant power splitters.

2. 1×2 Y-Junction Optical Power Splitters

In this section, we apply our polynomial-based taper profile optimization algorithm to the design of adiabatic 1×2 Y-Junction power splitters for symmetric power splitting (50:50) and arbitrary ratio power splitting. The optimization algorithm and the design procedure are defined, followed by the experimental results.

2.1. Design Methodology for 1×2 Y-Junction Power Splitters

A schematic of the 1×2 Y-Junction power splitters is shown in Figure 1(a). The width of the tips is denoted by wtip, and the gaps are denoted by wgap,1 and wgap,2. The first stage of the Y-Junction splitter is an adiabatically tapered region that gradually splits the input power from the middle waveguide to the upper and lower waveguides. The middle waveguide varies from 500 nm to wtip, while the upper and lower waveguides vary from wtip to 500 nm over the taper length (LY). The value of wtip is the smallest feature in this design. A smaller wtip results in shorter devices but it is typically limited by the minimum feature that is allowed by the foundry. The values of wgap,1 and wgap,2 are the widths of the lower and uppers gaps, respectively, and they are always chosen to be at least 20 nm wider than wtip to reduce potential reflections due to the abrupt changes at the two ends of the tapers. After the adiabatic coupling region, the waveguides are separated by 4 μ m with by using two 15 μ m-long S-bends, whose length was chosen generously to ensure the losses are predominantly due to the coupling region.
When wgap,1 and wgap,2 are equal, the Y-Junction power splitter has a 50:50 splitting ratio. An imbalance between wgap,1 and wgap,2 cause the splitting ratio to vary. Here, we design 4 devices with 50:50 splitting ratios with minimum feature sizes (i.e., wtip) of 140 nm, 160 nm, 180 nm, and 200 nm. Designs with different wtip allow us to observe the effect of minimum feature size on the performance of the Y-Junction power splitters. For these devices wgap,1 and wgap,2 are equal and they are 20 nm wider than wtip. To realize Y-Junctions with arbitrary splitting ratios, we keep wtip and wgap,1 fixed at 180 nm and 200 nm, respectively, and vary wgap,2 depending on the power splitting ratio we wish to achieve.
The width of the upper and lower tapers is defined by a polynomial function with 8 terms, given by
w u p ( z n o r m ) = ∑ ∑ n = 1 8 c n z n o r m p n ,
where pn is the power of the nth term, and cn is the coefficient of the nth term. The chosen p values are [0, 0.3, 0.5, 0.7, 1, 2, 5, 10], and cn values are to be determined by the optimization. The normalized length (znorm) is defined as znorm=z/LY, and is limited by the bounds of [0,1]. Using the polynomial function in Eq. 1 allows great freedom in modifying the shape of the taper. To satisfy the boundary conditions (i.e, w u p ( 0 ) =wtip, and w u p ( 1 ) =500 nm), we ensure that
c 1 = w t i p & p 1 = 0 & ∑ ∑ n = 1 8 c n = 500 nm .
We define the width of the middle taper in terms of the widths of the upper and lower tapers (i.e., w u p ),
w m i d ( z n o r m ) = 500 nm − ( 500 nm − w t i p ) . w u p ( z n o r m ) − w t i p 500 nm − w t i p α ,
where α is a parameter that determines the relation between the widths of the upper and middle tapers. α serves as a value that provides an additional degree of freedom in the design and causes the profile of the middle taper to vary differently from the profiles of the upper and lower tapers.
The Y-Junction power splitters were modeled with Lumerical Eigenmode Expansion (EME) solver. With the EME method, the 3-D device is divided into 2-D slices, where the finite-difference method is used to calculate eigenmodes at each slice. Once the eigenmodes are calculated, mode evolution can be calculated along the taper with great accuracy. A significant advantage of the EME method is that the distance between the cells can be modified after the calculation of eigenmodes to generate the desired taper profiles without the need for recalculating the eigenmodes. The pn values are chosen prior to the optimization, and the taper profiles are optimized by optimizing the cn values. A wide range of p values were chosen to allow for a wide range of taper shapes. Small p values (p<1) allow for rapid change of shape at the beginning of the taper, followed by a more gradual change towards the end of the taper while larger p values (p>1) cause the taper shape to vary slowly, followed by a rapid change of width. The cn values determine to what degree these shapes should be included in the optimized structure. A particle swarm optimization algorithm was used to optimize the cn values. The optimization goal was set to minimize the taper losses at the wavelength of 1550 nm for the TE, or the TM mode, whichever is higher. The number of particles was selected to be 45 and the optimization was run for 25 generations, or until the result has not improved for 3 consecutive generations, whichever happens first. After the optimization, we simulated the devices with the 3-D finite-difference time-domain (FDTD) method to ensure the accuracy of the results. The field profiles along an optimized 1×2 50:50 Y-Junction power splitter for a minimum feature size of 180 nm (i.e., wtip=180 nm, wgap,1=wgap,2=200 nm) are shown for the TE and TM modes in Figure 1(b), and (c), respectively.

2.2. Profile-optimized 1×2 Y-Junction Power Splitters

To understand the effect of the α parameter on the taper losses, we optimized a 50:50 Y-Junction power splitter with a 180 nm minimum feature size for α values ranging from 0.2 to 1. The simulated taper losses for the TE mode, as a function of the Y-Junction length, are presented in Figure 2(a). For all the α values we analyze here, the required Y-Junction lengths are drastically shorter than a linear Y-Junction, which is shown with the dashed lines. We note that for the α value of 0.5 and lower, the taper losses are minimized rapidly. Moreover, we observed that the α value of 0.5 works well for all other minimum feature sizes and hence we continue our optimizations by setting α equal to 0.5.
Figure 2(b) and (c) show the minimized taper losses for the TE and TM modes, respectively, at a wavelength of 1550 nm and for an α parameter of 0.5. For both the TE and TM modes, devices with smaller minimum feature sizes tend to require shorter Y-Junction lengths to achieve low losses (<∼0.05 dB). To ensure that the taper losses are minimal for both modes, we choose coupling lengths of 10 μ m, 15 μ m, 20 μ m, and 30 μ m for the minimum feature sizes of 140 nm, 160 nm, 180 nm, and 200 nm, respectively.
The excess losses for the optimized devices were simulated with the FDTD method and are shown in Figure 2(d) for the four minimum feature sizes. For the TE mode, all minimum feature sizes achieve very low excess losses around 1550 nm, as expected from the losses calculated with the EME solver. However, at shorter wavelengths, the excess losses increase, which is more pronounced for the TE mode and for larger minimum feature sizes. This is because at shorter wavelengths, the TE mode is more strongly confined in the Si core, hence, the Y-Junction length needs to be longer as compared to longer wavelengths for low-loss power splitting. Yet, the excess losses for the TE mode are lower than 0.2 dB for wavelengths longer than 1500 nm. For the TM mode, on the other hand, the excess losses are much less wavelength dependent and are between 0.15 dB and 0.25 dB in the whole spectrum range. These values are slightly above the taper losses estimated by the EME calculations. Further analysis showed that the abrupt changes at the beginning and end of the tapers cause an extra ∼0.1 dB loss, which was not included in the EME analysis.
To design 1×2 Y-Junctions with arbitrary power splitting ratios, we choose a minimum feature size of 180 nm and keep wtip and wgap,1 fixed at 180 nm and 200 nm, respectively, while varying wgap,2. For each value of the wgap,2, we optimize the profile of the device to minimize the taper losses for the TE mode. Although arbitrary splitting ratios are achievable for both modes, for a given wgap,2 value, Y-Junctions will have different splitting ratios for the TE and TM modes. To prove the effectiveness of this structure, we design our devices for the TE mode only, although the same optimization can be done for the TM mode. The ratio of the transmitted power to the lower arm of the Y-Junction power splitter is shown in Figure 3(a) for the TE mode as a function wgap,2. Power splitting ratios from 50:50 to 98:2 can be achieved by varying the wgap,2 from 200 nm to 520 nm.
We chose values for wgap,2 of 200 nm, 220 nm, 250 nm, 290 nm, and 355 nm, which result in power splitting ratios of 50:50, 58:42, 68:32, 77:23, and 89:11, respectively. The spectra of the power ratios at the lower arm are shown in Figure 3(b). The spectral variations in the splitting ratios are within ±1% for all the Y-Junction power splitters throughout the wavelength range of 1450 nm to 1650 nm. The excess losses for these devices are shown in Figure 3(c), where the excess losses are below 0.2 dB for wavelengths longer than 1500 nm. The electric field profiles (|E|) along the Y-Junction splitters show that the power splitting takes places with little radiation losses at 1550 nm wavelength for wgap,2 of 250 nm and 355, as shown in Figure 3(d) and (e), respectively.

2.3. Experimental Results for 1×2 Y-Junction Power Splitters

The 1×2 Y-Junction power splitters were fabricated at the Advanced Micro Foundry (AMF), in Singapore, on a 220 nm SOI platform with a 3 μ m buried oxide layer. The devices were then coated with a 2.3 μ m thick SiO2 cladding layer. The edges of the chips were deep etched to allow access to the edge couplers. Scanning electron microscope images of the resultant Y-Junctions with 50:50 and 89:11 power splitting ratios are shown in Figure 4(a) and (b), respectively, for a minimum feature size of 180 nm.
To measure the excess losses, light from a tunable laser was passed through a waveplate and a linear polarizer to control the polarization of the light. Ten percent of the light was then sampled using a fiber-based power splitter in order to measure the power of the light before the chip. The rest of the light was coupled into the chip. Light coupling into and out of the chip was performed with polarization maintaining lensed-fibers with a 5 μ m spot size. The lensed-fiber at the output was connected to a fiber-based polarization beam splitter, to ensure the measured output power belongs to either the TE or the TM mode, and any depolarization that might have occurred in the chip or in the fibers was not measured. The transmission was obtained from the ratio of the output power to the sampled input power and was normalized with a reference measurement, whose path consisted of two edge couplers and a waveguide connecting the edge couplers. Transmission through Y-Junction power splitters were then measured, and the excess losses were calculated after measuring the transmission through both arms of the devices. The excess losses were measured on 9 different chips, and the results were averaged, and standard deviations were calculated. The standard deviation in the transmission due to the variations of losses of edge couplers and waveguides were measured to be 0.1 dB for the TE mode, and 0.2 dB for the TM mode for the same chip, with nearly no wavelength sensitivity. For measurements involving Mach Zehnder interferometers (MZIs), we used a broadband superluminescent diode source centered at 1550 nm with a 3 dB bandwidth of 50 nm and measured the output power with an optical spectrum analyzer. The MZI spectra were then used to deduce the extinction ratios of the peaks and dips, which is used as a metric for how equally a 50:50 splitter splits the optical power. A good extinction ratio is typically over 20 dB, which ensures that the power splitting ratio is confined within 50±5%.
The average measured excess losses for the 50:50 Y-Junction power splitters are shown in Figure 5(a) (TE) and Figure 5(b) (TM) for the four different minimum feature sizes. The Y-Junction power splitters with 140 nm and 160 nm minimum feature sizes perform poorly, as it is evident from excess losses higher than 1 dB. The devices with larger minimum feature sizes (i.e., 180 nm and 200 nm), on the other hand, show drastically lower losses. Although features as small as 140 nm are allowed by the foundry, the significant minimum feature size dependency shows that the fabrication process is better suited for devices with larger features. Among the four minimum feature sizes, the 180 nm minimum feature size set has losses lower than 0.4 dB for both the TE and TM modes in the wavelength range of 1490 nm and 1590 nm.
Figure 5(c) and (d) show the average excess losses for the TE and TM modes, respectively, for a minimum feature size of 180 nm. The shaded regions show one standard deviation above and below the average excess losses, calculated from our measurements on nine chips. The standard deviation for the TE and TM modes are relatively constant around 0.2 and 0.3 dB, respectively, throughout the spectrum. These values are comparable to the deviations among different edge couplers on the same chip, which are 0.1 dB and 0.2 dB for the TE and TM modes, respectively. Yet, it is important to note that the standard deviations Figure 5(c) and (d) are a combination of deviations in light coupling losses, waveguide losses, and the losses of the Y-Junction power splitters.
To analyze the balance in power splitting, an MZI with a length imbalance of 204 μ m was constructed with two Y-Junction power splitters. Representative MZI transmission spectra are shown in Figure 5(e) and (f) for the TE and TM modes, respectively, for the 180 nm minimum feature sizes. The extinction ratios between the peaks and the dips are over 20 dB for the wavelength range of 1460 nm to 1610 nm for both modes. When the average of the extinction ratios is concerned, the 180 nm minimum feature size outperforms the other minimum feature sizes, as shown in Figure 5(g) and (h). The average extinction ratios are over 24 dB between 1480 nm and 1590 nm for both modes for the 180 nm minimum feature size. Although Y-Junctions with 160 nm and 200 nm minimum feature sizes have 20 dB extinction ratios over a broadband for both modes, the Y-Junction with 140 nm minimum feature size performs poorly with an extinction ratio under 20 dB for the TE mode. It is worthwhile to note that we were unable to extract the extinction ratios from some of the MZI spectra for Y-Junctions with 140 nm and 160 nm minimum feature sizes due to low extinction ratios or noisy spectrum. Hence, the extinction ratios for devices with 140 nm and 160 nm minimum feature sizes in Figure 5(g) and (h) were averaged over four and five spectra, respectively. For the devices with 180 nm and 200 nm minimum feature sizes, the average extinction ratios were calculated from all nine devices we tested. We have previously observed a similar minimum feature size dependency of splitting ratios, where devices with moderate minimum feature sizes performed better in terms of loss and splitting ratio than devices with small and large minimum feature sizes [55].
The average excess losses for the TE mode of the arbitrary ratio power splitters are shown in Figure 6(a) for varying wgap,2. All the devices we have analyzed here have excess losses lower than 0.6 dB for wavelengths longer than 1490 nm, indicating that the varying of the splitting ratio does not affect the bandwidth significantly. Figure 6(b) shows the spectra of the average power ratio at the lower arm of the Y-Junction power splitter along with the simulated results shown as dashed lines. For the power splitters with designed splitting ratios of 50:50, and 58:42, the experimental results are in excellent agreement with the simulated splitting ratios. For the splitters with designed splitting ratios of 68:32, 77:23, and 89:11, however, the differences are 3%, 7%, and 5%, respectively, in the C-band. This discrepancy might have been caused by the gaps between the waveguides being affected disproportionately by the fabrication errors. Such fabrication errors typically do not affect the results for splitting ratios close to 50:50, thanks to the inherent fabrication tolerance of the adiabatic power splitters, but they are more pronounced when the asymmetry in the structure is higher.
The standard deviations in the splitting ratios on different chips are shown in Figure 6(c) for the varying wgap,2 values. The standard deviations range between 2% and 4% with the exception of a wgap,2 of 290 nm, where the deviation is around 6%.

3. Broadband 2×2 50:50 Optical Power Splitters on 90 nm Slab

In this section, we present our 2×2 50:50 optical power splitters fabricated on a 90 nm Si slab along with the taper profile optimization. We discuss the design procedure, experimental excess losses, and splitting ratios of the devices.

3.1. Design of 2×2 50:50 Power Splitters

A schematic of the 2×2 50:50 power splitter is shown in Figure 7(a). The device architecture has been borrowed from Ref. [46]. This power splitter is designed on a 90 nm Si slab, which is a commonly offered thickness by foundries. For the TE mode, the device shows a significant reduction in the coupling length as compared to a device with linear coupling region. However, the 2×2 50:50 power splitters can also be designed (and optimized) without the 90 nm slab, and hence can be made to operate with both the TE and TM mode.
The use of a 90 nm Si slab requires conversion from the bus-waveguide to rib-waveguide modes. Prior to the conversion, the upper input waveguide was tapered down to 400 nm, while the lower input waveguide was tapered up to 600 nm, over a 1 μ m long taper. Then, 3 μ m long profile-optimized tapers on the 90 nm slab were used, while the widths of the 220 nm Si ribs remained constant. This taper was followed by 25 μ m long Bezier bends that bring the gap between the waveguides from 4 μ m down to 200 nm. Long bends are needed to ensure low losses, since rib-waveguides are typically lossy when sharp bends are used. Furthermore, when the waveguides get closer, coupling between waveguide modes become stronger, hence bends need to have a larger radius as the bends get closer to each other.
In the adiabatic coupling stage, the upper and lower waveguides are tapered from 400 nm and 600 nm, respectively, to a width of 500 nm. The mode on the upper arm is transformed into the anti-symmetric waveguide mode at the output of the adiabatic coupling stage, while the mode in the lower arm is transformed into the symmetric mode, whose profiles are shown in Figure 7(a). The width of the upper waveguide is given by
w u p ( z n o r m ) = ∑ ∑ n = 1 8 c n z n o r m p n .
The selected pn values are [0, 0.1, 0.3, 0.5, 0.7, 1, 3, 5]. The selected pn values are smaller than the ones for the 1×2 Y-Junction power splitter. This is because the 2×2 50:50 power splitters perform better with smaller p values and including 0.1 in the p values has reduced the times to find the optimal structures. To satisfy the boundary conditions (i.e., wup(0)=400 nm, and wup(1)=500 nm), we ensure that
c 1 = 400 nm & p 1 = 0 & ∑ ∑ n = 1 8 c n = 500 nm .
We define the width of the lower waveguide in terms of the width of the upper waveguide according to
w d o w n ( z n o r m ) = 600 nm − ( 600 nm − 500 nm ) . w u p ( z n o r m ) − 500 nm 600 nm − 500 nm α ,
where α is a parameter, similar to the one used in the optimization of the 1×2 Y-Junction power splitter. Since two TE mode evolutions take place in the adiabatic coupling stage, we minimize whichever transition has higher losses. The adiabatic coupler stage is followed by 11 μ m long Bezier bends, and a rib-waveguide to bus waveguide converter with a length of 2 μ m.
Figure 7(b) shows the optimized taper losses as a function of the coupler length (Lc), along with the linear taper (red solid line) for comparison. The linear taper requires approximately 60 μ m coupling length to achieve losses lower than 0.1 dB. On the other hand, profile optimized tapers can achieve 0.1 dB losses with a coupling length of approximately 12 μ m and 16 μ m, depending on the α parameter. Among the α parameters analyzed here, an α of 0.3 achieved the lowest losses with the shortest length; hence, we have used an α parameter of 0.3 and coupling length of 16 μ m. When the coupling region is simulated with the 3-D FDTD method, an excess loss of less than 0.2 dB can be achieved over a bandwidth of 200 nm, as shown in Figure 7(c). Moreover, the excess loss difference between the 2 inputs is less than 0.05 dB throughout the spectrum, indicating a balance in losses seen from both inputs. Figure 7(d) and (e) show the field profiles of the mode evolution from the inputs to the anti-symmetric and symmetric modes, respectively. The mode profiles show successful transition from inputs to the desired output modes.

3.2. Experimental Design for the 2×2 50:50 Power Splitters

A scanning electron microscope image of the 2×2 50:50 power splitter is shown in Figure 8(a). Testing for the 2×2 50:50 power splitters was done similar to that of the 1×2 Y-Junction power splitters. The transmission through the 2×2 50:50 power splitters were measured from both inputs to both outputs; hence, there are four measurements for a single device, whereas two measurements were taken for the 1×2 Y-Junction power splitters. The excess losses were obtained for each input. The average excess losses of the 2×2 50:50 power splitter are shown in Figure 8(b) and (c) when input power was launched from input 1 and input 2 of the device, respectively. The excess losses fluctuate around 0.7 dB, with a standard deviation of approximately ±0.3 dB. The excess losses demonstrate excellent wavelength insensitivity in the 1460 nm to 1590 nm wavelength range. The standard deviations for the 2×2 50:50 power splitter are higher when compared to the 1×2 Y-Junction power splitter. This could be because the 2×2 50:50 power splitter has more stages, which causes more overall deviations. The mode conversion losses from the 500 nm wide Si bus waveguide to the waveguide with 90 nm slab make up some of the excess losses and deviations in loss. Lower excess losses could be achieved if this power splitter is used along with other devices that are already on a slab, such as programmable optical meshes [3].
Transmission through MZIs, consisting of two devices connected in series with a length imbalance of 160 160 μ m, were measured from both inputs and both outputs, totaling to four measurements per interferometer – unlike the 1×2 Y-Junction power splitters, which required only one measurement per interferometer. For this measurement, one of the 2×2 50:50 power splitters was rotated by 180 along the z-axis before creating the interferometer, so that if there is an imbalance in power splitting, it would be emphasized in the output. A representative transmission spectrum of an MZI is shown in Figure 8(d). In the wavelength range of 1450 nm to 1610 nm, extinction ratios when light power is launched from both inputs are above 20 dB. The average extinction ratios, as seen in Figure 8(e) and (f) when the light is launched from the input 1 and input 2, respectively, indicate extinction ratios greater than 20 dB in the 1460 nm and 1595 nm. Hence, the designed power splitter has an excellent balance in the splitting ratio over a wide bandwidth. We have summarized the key performance metrics for the select devices in Table 1. The data shown in Figure 8(d-f) were taken from output 1 of the device, since the extinction ratios were observed to be nearly identical regardless of which output the light was collected from.

4. Conclusions

In conclusion, we have developed an adiabatic taper profile optimization algorithm for the design of 1×2 and 2×2 power splitters with low losses, broad bandwidth, balanced splitting ratios, and compact sizes. The 1×2 Y-junction power splitters with a 180 nm minimum feature size and 20 μ m coupling length showed average excess losses lower than 0.5 dB for both modes in the wavelength range of 1480 nm to 1585 nm. When the 1×2 Y-Junction power splitter geometry was modified to achieve arbitrary splitting ratios, the excess losses were maintained below 0.6 dB across the same wave-length range, while achieving splitting ratios ranging from 50% to 94% with standard deviations ranging between 2% and 6%. Similarly, 2×2 50:50 power splitters with a 16 μ m coupling length were observed to have an average excess loss of 0.7 dB. Our device designs demonstrate excellent consistency across multiple chips, while ensuring low losses and wide bandwidth. With the aforementioned power splitters, we have demonstrated the effectiveness of a polynomial-based optimization algorithm for minimization of the losses of adiabatic power splitters, which results in low-loss and highly fabrication-tolerant devices with significantly improved footprints, as compared to their adiabatic counterparts. This optimization is applicable to many other adiabatic components and can accommodate devices with a wide range of minimum feature sizes.

Author Contributions

Conceptualization, C.O.; methodology, C.O.; software, C.O.; validation, C.O.; formal analysis, C.O.; investigation, C.O.; writing—original draft preparation, C.O., J.S.A., and M.M.; writing—review and editing, C.O., J.S.A., and M.M.; visualization, C.O.; supervision, J.S.A., and M.M. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

The authors would like to thank CMC Microsystems for arranging the fabrication run at the Advanced Micro Foundry (AMF), Singapore.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table A1 shows the optimized structural parameters of the optimized devices presented throughout the paper.
Table A1. Optimized parameters of the power splitters.
Table A1. Optimized parameters of the power splitters.
Device Min. Feature Size (nm) Coupling Length ( μ m) α pn cn
1×2 50:50 Y-Junction 140 10 0.5 [0, 0.3, 0.5, 0.7, 1, 2, 5, 10] [140, 0, 0, 0, 170, 37, 153]
160 15 [160, 0, 0, 50, 68, 127, 11, 84]
180 20 [180, 0, 1, 117, 52, 57, 82, 11]
200 30 [200, 0, 7, 73, 71, 33, 16, 100]
1×2 58:42 Y-Junction 180 20 0.5 [0, 0.3, 0.5, 0.7, 1, 2, 5, 10] [180, 22, 49, 57, 8, 56, 47, 81]
1×2 68:32 Y-Junction 180 20 [180, 35, 57, 78, 5, 31, 54, 60]
1×2 78:22 Y-Junction 180 20 [180, 60, 43, 40, 33, 21, 57, 66]
1×2 89:11 Y-Junction 180 20 [180, 60, 79, 9, 13, 16, 56, 87]
2×2 50:50 200 16 0.3 [0, 0.1, 0.3, 0.5, 0.7, 1, 3, 5] [400, 14, 45, 18, 1, 10, 0, 12]

References

  1. Chen, S.; Shi, Y.; He, S.; Dai, D. Low-loss and broadband 2 ×2 silicon thermo-optic Mach–Zehnder switch with bent directional couplers. Opt. Lett. 2016, 41, 836–839. [Google Scholar] [CrossRef]
  2. He, M.; Xu, M.; Ren, Y.; Jian, J.; Ruan, Z.; Xu, Y.; Gao, S.; Sun, S.; Wen, X.; Zhou, L.; others. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit s- 1 and beyond. Nature Photonics 2019, 13, 359–364. [Google Scholar] [CrossRef]
  3. Bogaerts, W.; Pérez, D.; Capmany, J.; Miller, D.A.; Poon, J.; Englund, D.; Morichetti, F.; Melloni, A. Programmable photonic circuits. Nature 2020, 586, 207–216. [Google Scholar] [CrossRef]
  4. González-Andrade, D.; Wangüemert-Pérez, J.G.; Velasco, A.V.; Ortega-Moñux, A.; Herrero-Bermello, A.; Molina-Fernández, I.; Halir, R.; Cheben, P. Ultra-Broadband Mode Converter and Multiplexer Based on Sub-Wavelength Structures. IEEE Photonics Journal 2018, 10, 1–10. [Google Scholar] [CrossRef]
  5. Cao, G.; Gao, F.; Jiang, J.; Zhang, F. Directional couplers realized on silicon-on-insulator. IEEE Photonics Technology Letters 2005, 17, 1671–1673. [Google Scholar] [CrossRef]
  6. Campenhout, J.V.; Green, W.M.J.; Vlasov, Y.A. Design of a digital, ultra-broadband electro-optic switch for reconfigurable optical networks-on-chip. Opt. Express 2009, 17, 23793–23808. [Google Scholar] [CrossRef]
  7. Chen, G.F.; Ong, J.R.; Ang, T.Y.; Lim, S.T.; Png, C.E.; Tan, D.T. Broadband silicon-on-insulator directional couplers using a combination of straight and curved waveguide sections. Scientific reports 2017, 7, 7246. [Google Scholar] [CrossRef] [PubMed]
  8. Soldano, L.; Pennings, E. Optical multi-mode interference devices based on self-imaging: principles and applications. Journal of Lightwave Technology 1995, 13, 615–627. [Google Scholar] [CrossRef]
  9. Lagali, N.; Paiam, M.; MacDonald, R. Theory of variable-ratio power splitters using multimode interference couplers. IEEE Photonics Technology Letters 1999, 11, 665–667. [Google Scholar] [CrossRef]
  10. Deng, Q.; Liu, L.; Li, X.; Zhou, Z. Arbitrary-ratio 1 ×2 power splitter based on asymmetric multimode interference. Opt. Lett. 2014, 39, 5590–5593. [Google Scholar] [CrossRef]
  11. Liu, R.; Lu, L.; Zhang, P.; Chang, W.; Liu, D.; Zhang, M. Integrated Dual-Mode 3-dB Power Splitter Based on Multimode Interference Coupler. IEEE Photonics Technology Letters 2020, 32, 883–886. [Google Scholar] [CrossRef]
  12. Yao, R.; Li, H.; Zhang, B.; Chen, W.; Wang, P.; Dai, S.; Liu, Y.; Li, J.; Li, Y.; Fu, Q.; Dai, T.; Yu, H.; Yang, J.; Pavesi, L. Compact and Low-Insertion-Loss 1xN Power Splitter in Silicon Photonics. J. Lightwave Technol. 2021, 39, 6253–6259. [Google Scholar] [CrossRef]
  13. Xiao, Z.; Luo, X.; Lim, P.H.; Prabhathan, P.; Silalahi, S.T.H.; Liow, T.Y.; Zhang, J.; Luan, F. Ultra-compact low loss polarization insensitive silicon waveguide splitter. Opt. Express 2013, 21, 16331–16336. [Google Scholar] [CrossRef]
  14. Nair, D.P.; Ménard, M. A Compact Low-Loss Broadband Polarization Independent Silicon 50/50 Splitter. IEEE Photonics Journal 2021, 13, 1–7. [Google Scholar] [CrossRef]
  15. Zhang, Y.; Yang, S.; Lim, A.E.J.; Lo, G.Q.; Galland, C.; Baehr-Jones, T.; Hochberg, M. A compact and low loss Y-junction for submicron silicon waveguide. Opt. Express 2013, 21, 1310–1316. [Google Scholar] [CrossRef]
  16. Ozcan, C.; Mojahedi, M.; Aitchison, J.S. Optimization of Adiabatically Tapered Y-Branches for Dual Polarization Operation. 2021 IEEE Photonics Conference (IPC), 2021, pp. 1–2. [CrossRef]
  17. Halir, R.; Maese-Novo, A.; Ortega-Moñux, A.; Molina-Fernández, I.; Wangüemert-Pérez, J.G.; Cheben, P.; Xu, D.X.; Schmid, J.H.; Janz, S. Colorless directional coupler with dispersion engineered sub-wavelength structure. Opt. Express 2012, 20, 13470–13477. [Google Scholar] [CrossRef]
  18. Wang, Y.; Lu, Z.; Ma, M.; Yun, H.; Zhang, F.; Jaeger, N.A.F.; Chrostowski, L. Compact Broadband Directional Couplers Using Subwavelength Gratings. IEEE Photonics Journal 2016, 8, 1–8. [Google Scholar] [CrossRef]
  19. Zhao, S.; Liu, W.; Chen, J.; Ding, Z.; Shi, Y. Broadband Arbitrary Ratio Power Splitters Based on Directional Couplers With Subwavelength Structure. IEEE Photonics Technology Letters 2021, 33, 479–482. [Google Scholar] [CrossRef]
  20. Zhang, A.; Xia, L.; Li, T.; Chang, C.; Zhou, P.; Xu, X.; Zou, Y. Ultra-compact polarization-independent 3 dB power splitter in silicon. Opt. Lett. 2021, 46, 5000–5003. [Google Scholar] [CrossRef]
  21. Yang, N.; Xiao, J. A compact silicon-based polarization-independent power splitter using a three-guide directional coupler with subwavelength gratings. Optics Communications 2020, 459, 125095. [Google Scholar] [CrossRef]
  22. Hu, R.; Sun, L.; Zhang, Z.; Sun, Q.; Pan, Y.; Su, Y. Ultrabroadband and compact 2 ×2 3-dB coupler based on trapezoidal subwavelength gratings. Opt. Express 2023, 31, 23542–23550. [Google Scholar] [CrossRef]
  23. Zhong, W.; Xiao, J. Ultracompact polarization-insensitive power splitter using subwavelength-grating-based MMI couplers on an SOI platform. Appl. Opt. 2020, 59, 1991–1997. [Google Scholar] [CrossRef]
  24. Maese-Novo, A.; Halir, R.; Romero-García, S.; Pérez-Galacho, D.; Zavargo-Peche, L.; Ortega-Moñux, A.; Molina-Fernández, I.; Wangüemert-Pérez, J.G.; Cheben, P. Wavelength independent multimode interference coupler. Opt. Express 2013, 21, 7033–7040. [Google Scholar] [CrossRef]
  25. Wang, Z.; Liu, Y.; Wang, Z.; Liu, Y.; Du, J.; Song, Q.; Xu, K. Ultra-broadband 3 dB power splitter from 1.55 to 2 µm wave band. Opt. Lett. 2021, 46, 4232–4235. [Google Scholar] [CrossRef]
  26. Xu, Y.; Xiao, J. An Ultracompact Polarization-Insensitive Silicon-Based Strip-to-Slot Power Splitter. IEEE Photonics Technology Letters 2016, 28, 536–539. [Google Scholar] [CrossRef]
  27. Xiao, J.; Guo, Z. Ultracompact Polarization-Insensitive Power Splitter Using Subwavelength Gratings. IEEE Photonics Technology Letters 2018, 30, 529–532. [Google Scholar] [CrossRef]
  28. Chang, W.; Ren, X.; Ao, Y.; Lu, L.; Cheng, M.; Deng, L.; Liu, D.; Zhang, M. Inverse design and demonstration of an ultracompact broadband dual-mode 3 dB power splitter. Opt. Express 2018, 26, 24135–24144. [Google Scholar] [CrossRef]
  29. Xie, Y.; Huang, T.; Ji, Q.; Yang, M.; Wang, J.; Tu, X.; Cheng, Z.; Xu, G.; Wei, Q.; Wu, Y.; Shum, P.P. Design of an arbitrary ratio optical power splitter based on a discrete differential multiobjective evolutionary algorithm. Appl. Opt. 2020, 59, 1780–1785. [Google Scholar] [CrossRef] [PubMed]
  30. Xu, X.; Li, Y.; Huang, W. Inverse design of the MMI power splitter by asynchronous double deep Q-learning. Opt. Express 2021, 29, 35951–35964. [Google Scholar] [CrossRef]
  31. Tahersima, M.H.; Kojima, K.; Koike-Akino, T.; Jha, D.; Wang, B.; Lin, C.; Parsons, K. Deep neural network inverse design of integrated photonic power splitters. Scientific reports 2019, 9, 1368. [Google Scholar] [CrossRef] [PubMed]
  32. Kim, J.; Kim, J.Y.; Yoon, J.; Yoon, H.; Park, H.H.; Kurt, H. Experimental demonstration of inverse-designed silicon integrated photonic power splitters. Nanophotonics 2022, 11, 4581–4590. [Google Scholar] [CrossRef]
  33. Ma, H.; Huang, J.; Zhang, K.; Yang, J. Inverse-designed arbitrary-input and ultra-compact 1×N power splitters based on high symmetric structure. Scientific Reports 2020, 10, 11757. [Google Scholar] [CrossRef] [PubMed]
  34. Mak, J.C.C.; Sideris, C.; Jeong, J.; Hajimiri, A.; Poon, J.K.S. Binary particle swarm optimized 2 ×2 power splitters in a standard foundry silicon photonic platform. Opt. Lett. 2016, 41, 3868–3871. [Google Scholar] [CrossRef] [PubMed]
  35. Pilozzi, L.; Farrelly, F.A.; Marcucci, G.; Conti, C. Machine learning inverse problem for topological photonics. Communications Physics 2018, 1, 57. [Google Scholar] [CrossRef]
  36. Schubert, M.F.; Cheung, A.K.C.; Williamson, I.A.D.; Spyra, A.; Alexander, D.H. Inverse Design of Photonic Devices with Strict Foundry Fabrication Constraints. ACS Photonics 2022, 9, 2327–2336. [Google Scholar] [CrossRef]
  37. Hammond, A.M.; Oskooi, A.; Johnson, S.G.; Ralph, S.E. Photonic topology optimization with semiconductor-foundry design-rule constraints. Opt. Express 2021, 29, 23916–23938. [Google Scholar] [CrossRef] [PubMed]
  38. Gostimirovic, D.; Grinberg, Y.; Xu, D.X.; Liboiron-Ladouceur, O. Improving Fabrication Fidelity of Integrated Nanophotonic Devices Using Deep Learning. ACS Photonics 2023, 10, 1953–1961. [Google Scholar] [CrossRef]
  39. Wang, Y.; Gao, S.; Wang, K.; Skafidas, E. Ultra-broadband and low-loss 3 dB optical power splitter based on adiabatic tapered silicon waveguides. Opt. Lett. 2016, 41, 2053–2056. [Google Scholar] [CrossRef]
  40. Han, L.; Kuo, B.P.P.; Alic, N.; Radic, S. Ultra-broadband multimode 3dB optical power splitter using an adiabatic coupler and a Y-branch. Opt. Express 2018, 26, 14800–14809. [Google Scholar] [CrossRef]
  41. González-Andrade, D.; Lafforgue, C.; Durán-Valdeiglesias, E.; Le Roux, X.; Berciano, M.; Cassan, E.; Marris-Morini, D.; Velasco, A.V.; Cheben, P.; Vivien, L.; others. Polarization-and wavelength-agnostic nanophotonic beam splitter. Scientific reports 2019, 9, 3604. [Google Scholar] [CrossRef]
  42. Kim, H.; Shin, H. Tailorable and Broadband On-Chip Optical Power Splitter. Applied Sciences 2019, 9. [Google Scholar] [CrossRef]
  43. Sia, J.X.B.; Wang, W.; Guo, X.; Zhou, J.; Zhang, Z.; Rouifed, M.S.; Li, X.; Qiao, Z.L.; Liu, C.Y.; Littlejohns, C.; Reed, G.T.; Wang, H. Mid-Infrared, Ultra-Broadband, Low-Loss, Compact Arbitrary Power Splitter Based on Adiabatic Mode Evolution. IEEE Photonics Journal 2019, 11, 1–11. [Google Scholar] [CrossRef]
  44. Nguyen, H.V.; Kim, I.K.; Seok, T.J. Low-Loss and Broadband Silicon Photonic Y- Junction Using Tapered Rib Waveguides. 2019 International Conference on Optical MEMS and Nanophotonics (OMN), 2019, pp. 76–77. [CrossRef]
  45. Nguyen, V.H.; Kim, I.K.; Seok, T.J. Low-Loss and Broadband Silicon Photonic 3-dB Power Splitter with Enhanced Coupling of Shallow-Etched Rib Waveguides. Applied Sciences 2020, 10. [Google Scholar] [CrossRef]
  46. Yun, H.; Shi, W.; Wang, Y.; Chrostowski, L.; Jaeger, N.A.F. 2×2 adiabatic 3-dB coupler on silicon-on-insulator rib waveguides. Photonics North 2013; Cheben, P.; Schmid, J.; Boudoux, C.; Chen, L.R.; Delâge, A.; Janz, S.; Kashyap, R.; Lockwood, D.J.; Loock, H.P.; Mi, Z., Eds. International Society for Optics and Photonics, SPIE, 2013, Vol. 8915, p. 89150V. [CrossRef]
  47. Guo, D.; Chu, T. Compact broadband silicon 3 dB coupler based on shortcuts to adiabaticity. Opt. Lett. 2018, 43, 4795–4798. [Google Scholar] [CrossRef] [PubMed]
  48. Chung, H.C.; Wang, T.C.; Hung, Y.J.; Tseng, S.Y. Robust silicon arbitrary ratio power splitters using shortcuts to adiabaticity. Opt. Express 2020, 28, 10350–10362. [Google Scholar] [CrossRef]
  49. Hung, Y.J.; Li, Z.Y.; Chung, H.C.; Liang, F.C.; Jung, M.Y.; Yen, T.H.; Tseng, S.Y. Mode-evolution-based silicon-on-insulator 3 dB coupler using fast quasiadiabatic dynamics. Opt. Lett. 2019, 44, 815–818. [Google Scholar] [CrossRef] [PubMed]
  50. Hung, Y.J.; Chen, C.H.; Lu, G.X.; Liang, F.C.; Chung, H.C.; Tseng, S.Y. Compact and robust 2 ×2 fast quasi-adiabatic 3-dB couplers on SOI strip waveguides. Optics & Laser Technology 2022, 145, 107485. [Google Scholar] [CrossRef]
  51. Chung, H.C.; Chen, C.H.; Hung, Y.J.; Tseng, S.Y. Compact polarization-independent quasi-adiabatic 2×2 3 dB coupler on silicon. Opt. Express 2022, 30, 995–1002. [Google Scholar] [CrossRef]
  52. Siriani, D.F.; Tambasco, J.L. Adiabatic guided wave optics – a toolbox of generalized design and optimization methods. Opt. Express 2021, 29, 3243–3257. [Google Scholar] [CrossRef]
  53. Ozcan, C.; Aitchison, J.S.; Mojahedi, M. Adiabatic Waveguide Taper Profile Optimization on Al2O3/Si Platform for Polarization Insensitive Fiber-to-Chip Light Coupling. 2021 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference (CLEO/Europe-EQEC), 2021, pp. 1–1. [CrossRef]
  54. Ozcan, C.; Mojahedi, M.; Aitchison, J.S. Compact Adiabatic Power Splitters with Polynomial Taper Profile Optimization. CLEO 2023. Optica Publishing Group, 2023, p. JW2A.79. [CrossRef]
  55. Ozcan, C.; Mojahedi, M.; Aitchison, J.S. Short, broadband, and polarization-insensitive adiabatic Y-junction power splitters. Opt. Lett. 2023, 48, 4901–4904. [Google Scholar] [CrossRef]
Preprints 88053 g001
Figure 1. (a) Schematic of the 1×2 Y-Junction power splitters. Electric fields along the Y-Junctions for the (b) TE and (c) TM modes at 1550 nm wavelength.
Figure 1. (a) Schematic of the 1×2 Y-Junction power splitters. Electric fields along the Y-Junctions for the (b) TE and (c) TM modes at 1550 nm wavelength.
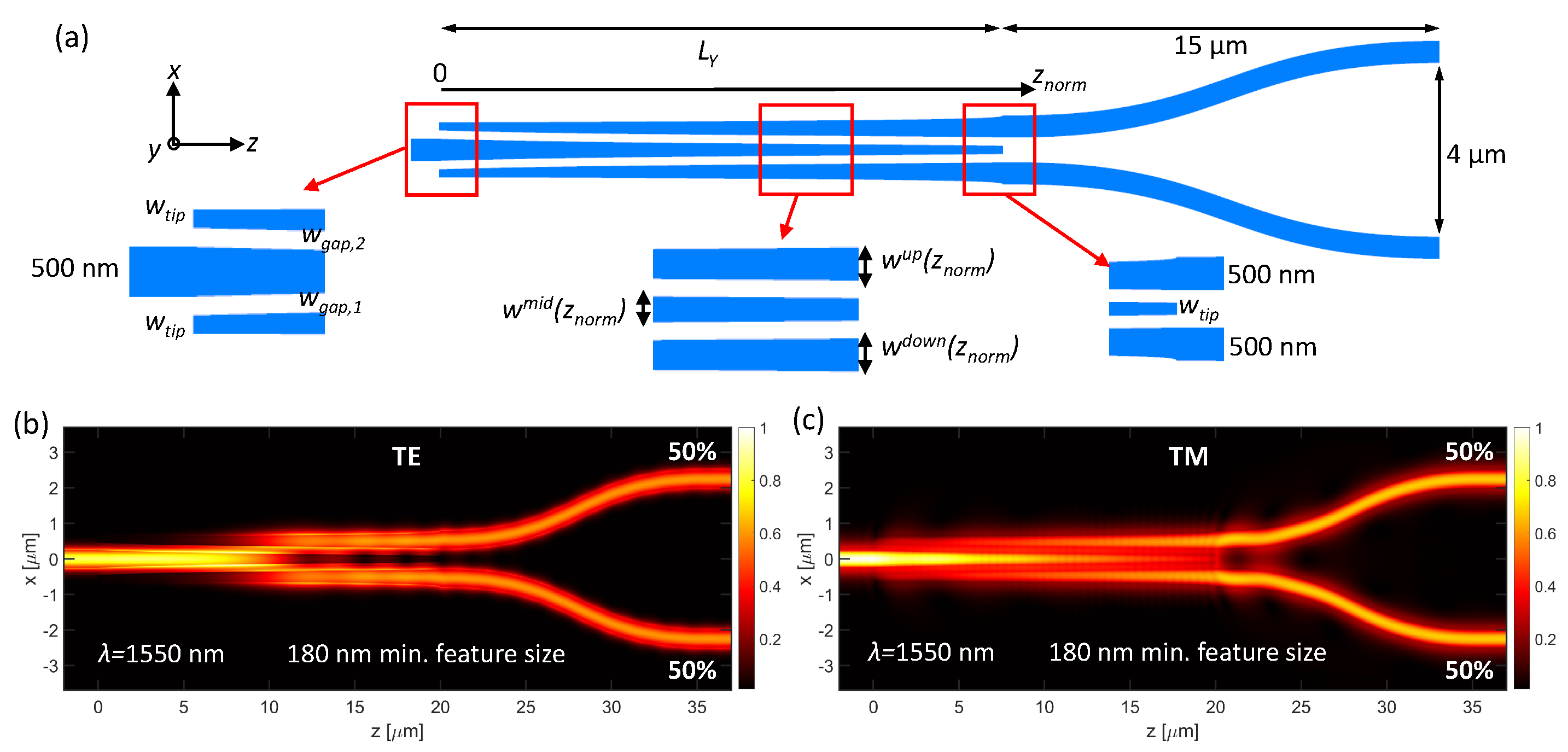
Preprints 88053 g001
Preprints 88053 g002
Figure 2. (a) Simulated taper losses for the Y-Junction power splitter with 180 nm minimum feature size for varying α for the TE mode. The optimized taper losses for the (b) TE and (c) TM modes. (d) Spectra of the excess losses for the devices with four minimum feature sizes.
Figure 2. (a) Simulated taper losses for the Y-Junction power splitter with 180 nm minimum feature size for varying α for the TE mode. The optimized taper losses for the (b) TE and (c) TM modes. (d) Spectra of the excess losses for the devices with four minimum feature sizes.
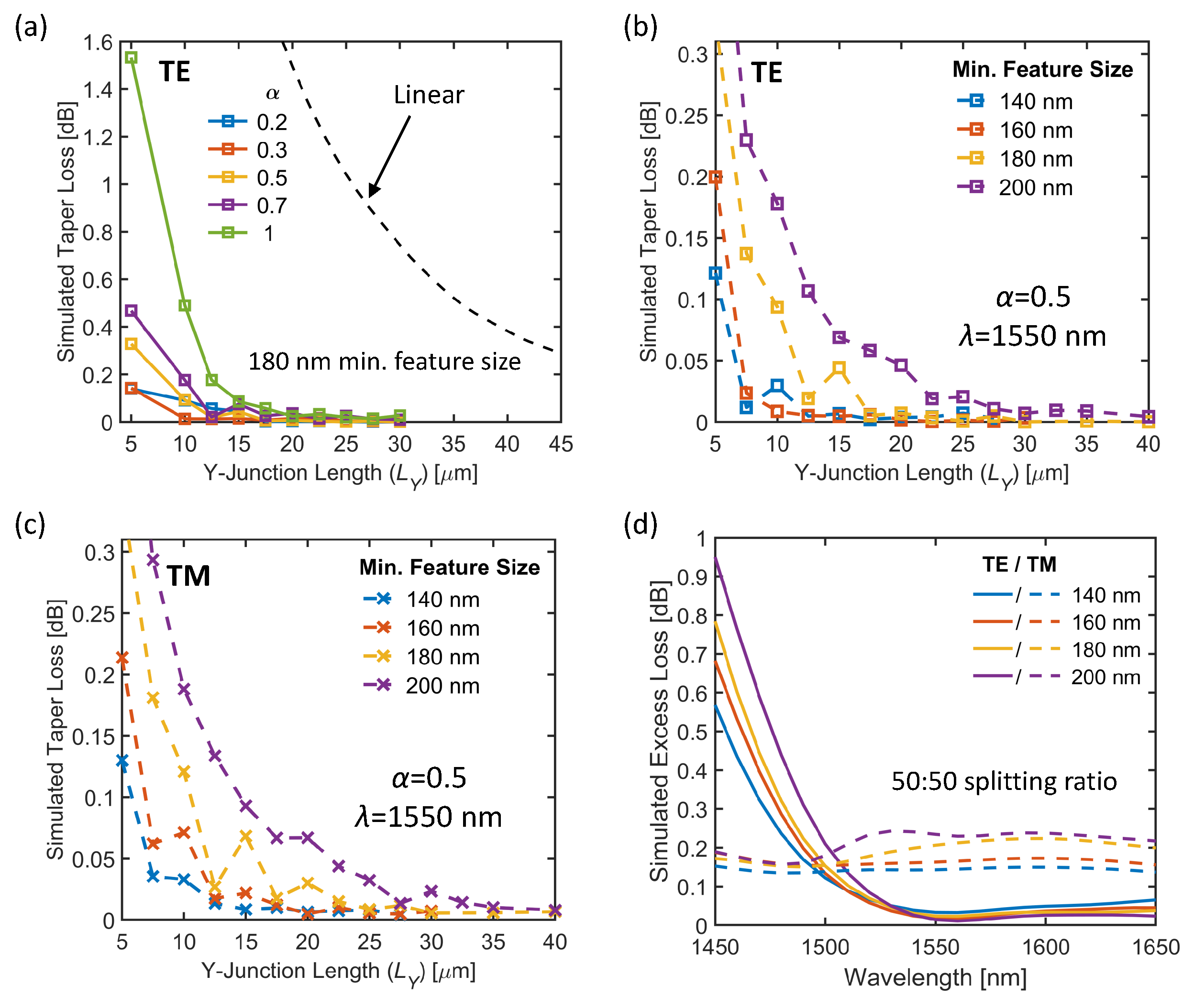
Preprints 88053 g002
Preprints 88053 g003
Figure 3. (a) Power fraction at the lower arm for varying wgap,2. (b) Spectra of the splitting ratios for the Y-Junction power splitters for varying wgap,2. (c) Spectra of the excess losses for the devices with arbitrary power splitting ratios. The magnitude of electric fields (|E|) along the Y-Junction power splitter with (d) wgap,2=250 nm and (e) wgap,2=355 nm, at 1550 nm. All figures pertain to the TE mode.
Figure 3. (a) Power fraction at the lower arm for varying wgap,2. (b) Spectra of the splitting ratios for the Y-Junction power splitters for varying wgap,2. (c) Spectra of the excess losses for the devices with arbitrary power splitting ratios. The magnitude of electric fields (|E|) along the Y-Junction power splitter with (d) wgap,2=250 nm and (e) wgap,2=355 nm, at 1550 nm. All figures pertain to the TE mode.
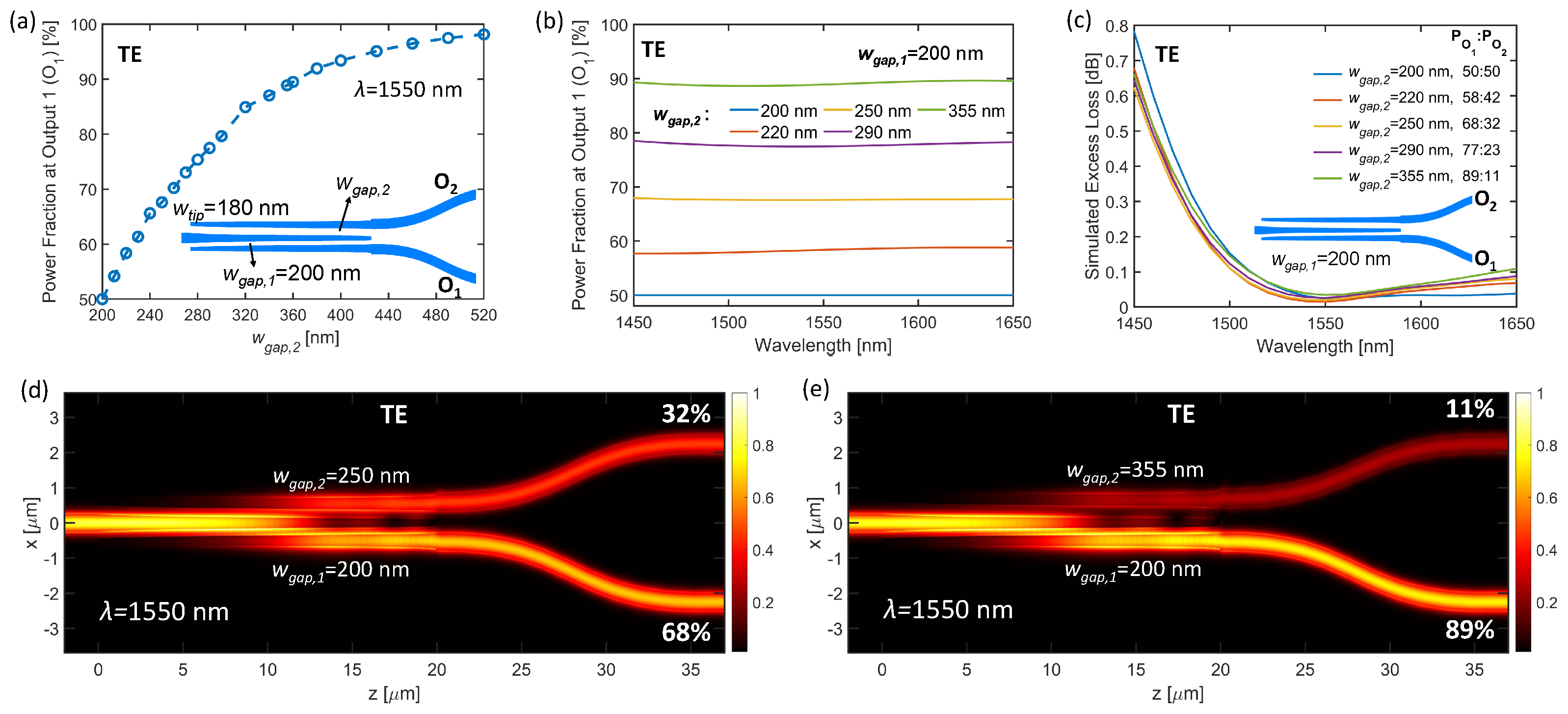
Preprints 88053 g003
Preprints 88053 g004
Figure 4. Scanning electron microscope images of the (a) 50:50 power splitter and (b) 89:11 power splitter with 180 nm minimum feature sizes.
Figure 4. Scanning electron microscope images of the (a) 50:50 power splitter and (b) 89:11 power splitter with 180 nm minimum feature sizes.
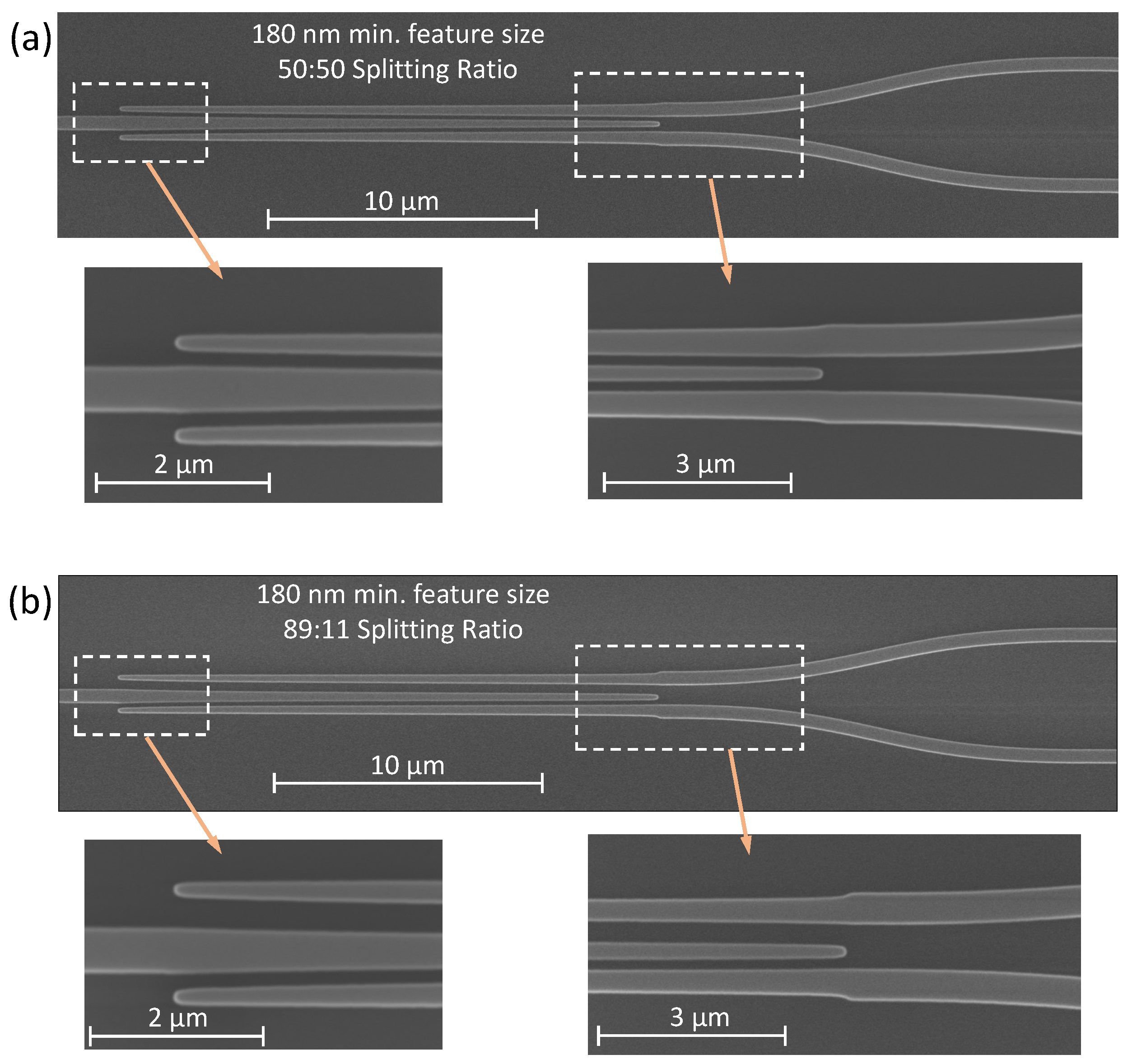
Preprints 88053 g004
Preprints 88053 g005
Figure 5. Average excess losses for the 50:50 1×2 Y-Junction for the (a) TE and (b) TM modes. Average excess losses and standard deviation in losses for the Y-Junction with 180 nm minimum feature size for the (c) TE and (d) TM modes. Transmission spectra of the Mach Zehnder interferometer for the Y-Junction with 180 nm minimum feature size for the (e) TE and (f) TM modes. Spectra of the average extinction ratios for the (g) TE and (h) TM modes.
Figure 5. Average excess losses for the 50:50 1×2 Y-Junction for the (a) TE and (b) TM modes. Average excess losses and standard deviation in losses for the Y-Junction with 180 nm minimum feature size for the (c) TE and (d) TM modes. Transmission spectra of the Mach Zehnder interferometer for the Y-Junction with 180 nm minimum feature size for the (e) TE and (f) TM modes. Spectra of the average extinction ratios for the (g) TE and (h) TM modes.
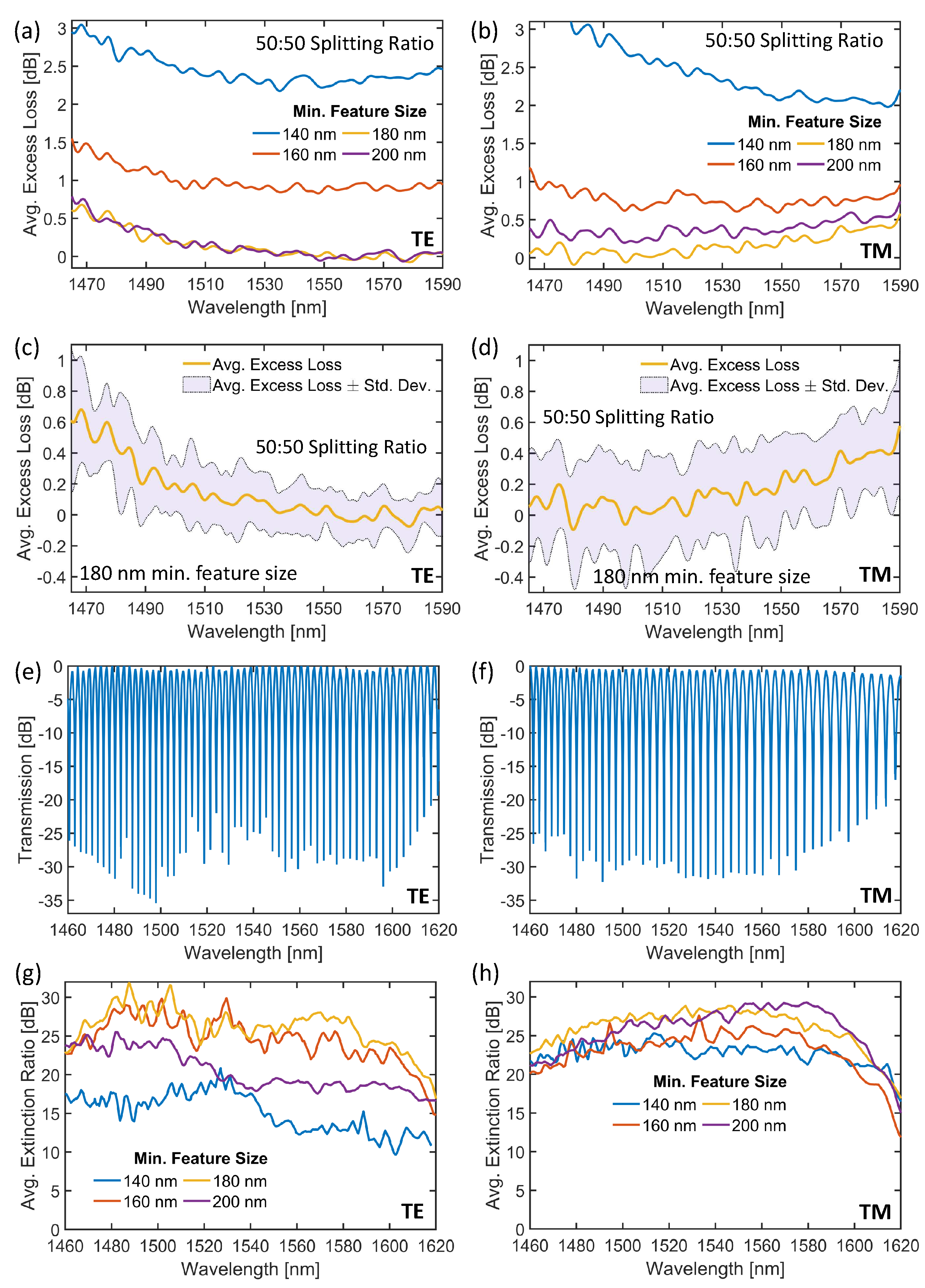
Preprints 88053 g005
Preprints 88053 g006
Figure 6. (a) Average excess losses for the 1×2 Y-Junction with arbitrary splitting ratios. (b) The average power ratio at the lower arm of the Y-Junction for the power splitters with different splitting ratios. (c) Standard deviation in the measured splitting ratios of the 1×2 Y-Junction power splitters.
Figure 6. (a) Average excess losses for the 1×2 Y-Junction with arbitrary splitting ratios. (b) The average power ratio at the lower arm of the Y-Junction for the power splitters with different splitting ratios. (c) Standard deviation in the measured splitting ratios of the 1×2 Y-Junction power splitters.
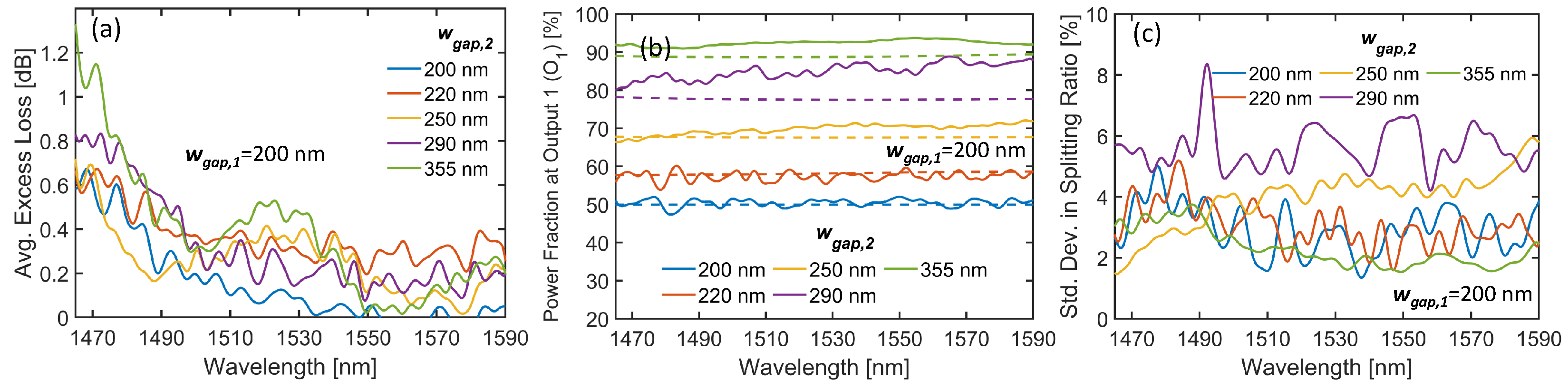
Preprints 88053 g006
Preprints 88053 g007
Figure 7. (a) Schematic of the designed 2×2 power splitter. (b) Simulated taper losses in the adiabatic coupling region. (c) Spectra of the simulated excess losses when power is launched from both inputs. The mode field profiles along the coupling region for (d) input 1 (TE1 mode) and (e) input 2 (TE2 mode).
Figure 7. (a) Schematic of the designed 2×2 power splitter. (b) Simulated taper losses in the adiabatic coupling region. (c) Spectra of the simulated excess losses when power is launched from both inputs. The mode field profiles along the coupling region for (d) input 1 (TE1 mode) and (e) input 2 (TE2 mode).
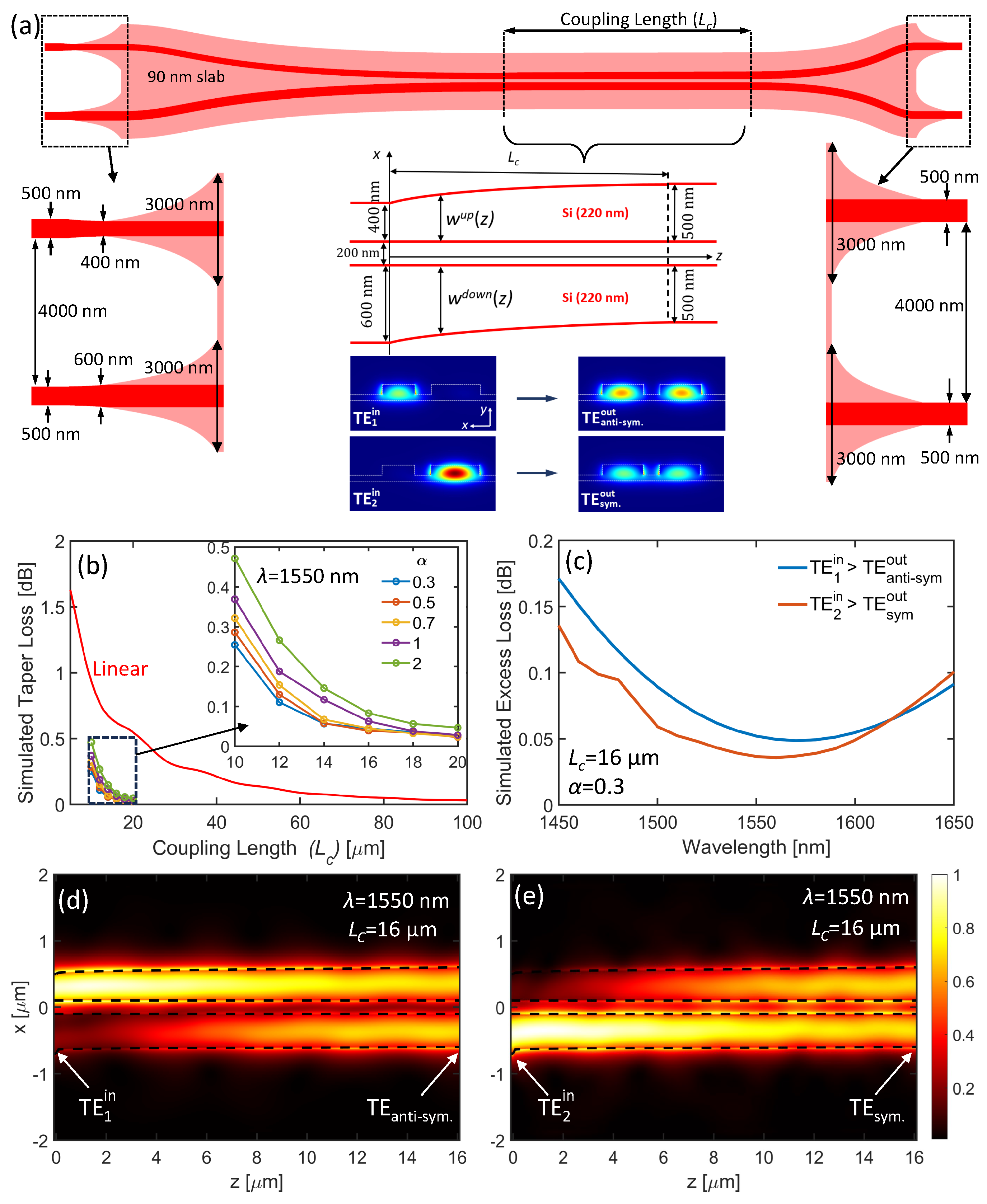
Preprints 88053 g007
Preprints 88053 g008
Figure 8. (a) Scanning electron microscope image of the 2×2 3 dB power splitter. Average excess losses and standard deviation in losses when input power is launched from (b) input 1 and (c) input 2. (d) A representative transmission spectra of the Mach Zehnder interferometer. Spectra of the average extinction ratios when input power is launched from (e) input 1 and (f) input 2.
Figure 8. (a) Scanning electron microscope image of the 2×2 3 dB power splitter. Average excess losses and standard deviation in losses when input power is launched from (b) input 1 and (c) input 2. (d) A representative transmission spectra of the Mach Zehnder interferometer. Spectra of the average extinction ratios when input power is launched from (e) input 1 and (f) input 2.
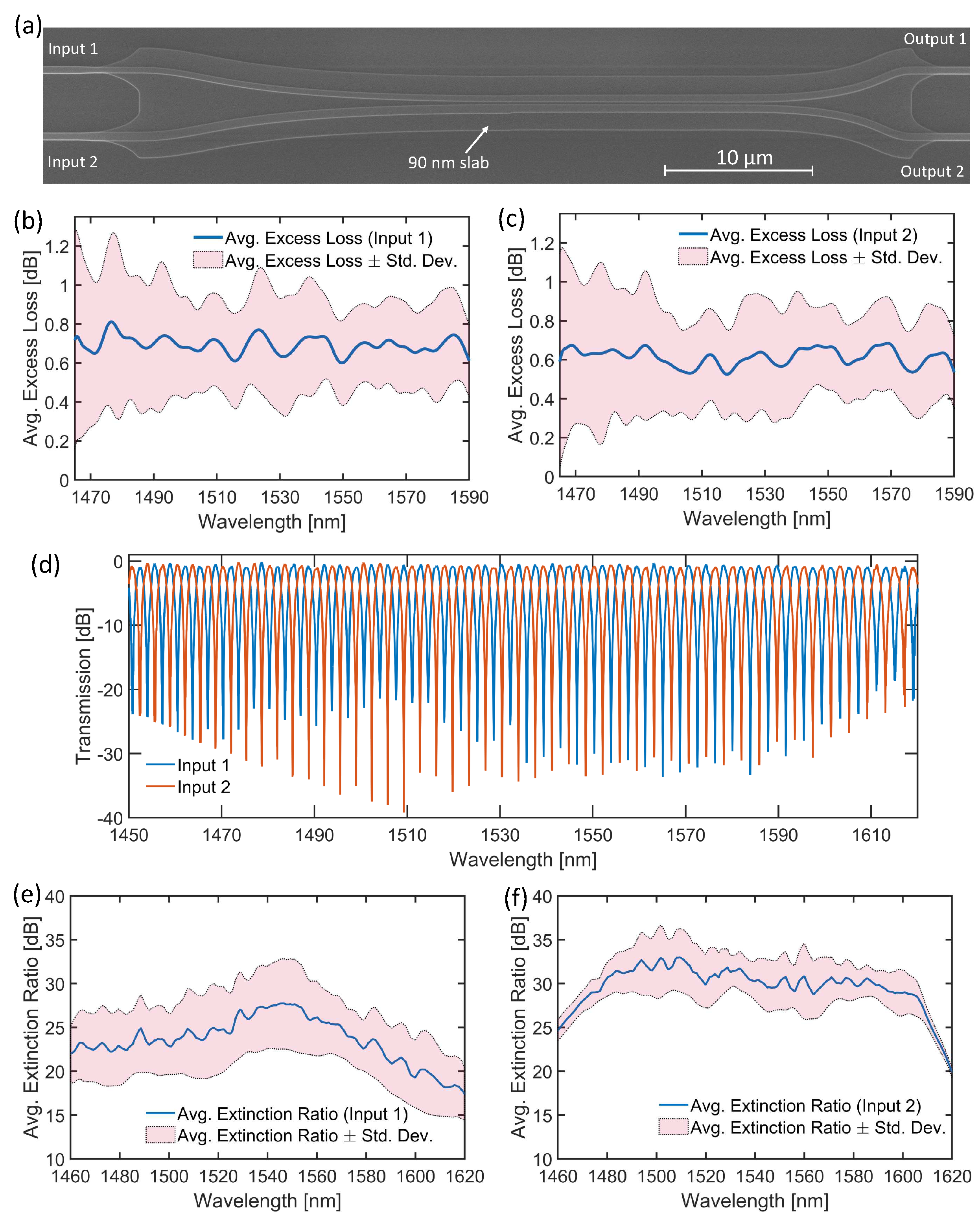
Preprints 88053 g008
Table 1. Summary of measured performance metrics of the select power splitters designed in this paper.
Table 1. Summary of measured performance metrics of the select power splitters designed in this paper.
Device Min. Feature Size (nm) ELTE1 (dB) ELTM1 (dB) SRTE2 Bandwidth (nm)
1×2 50:50 Y-Junction 180 <0.5 <0.5 50±2 1480-1585
1×2 58:42 Y-Junction 180 <0.6 - 58±2 1490-1590
1×2 68:32 Y-Junction 180 <0.5 - 71±3 1487-1590
1×2 78:22 Y-Junction 180 <0.6 - 84±5 14890-1590
1×2 89:11 Y-Junction 180 <0.6 - 94±2 1490-1590
2×2 50:50 200 <0.7 - 50±3 1465-1590
1 EL: Excess loss. 2 SR: Splitting ratio.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated