Prerpints.org logo
Preprint
Article

Measuring Absorbed Energy in the Human Auditory System Using Finite Element Models: A Comparison with Experimental Results

Altmetrics

Downloads

134

Views

78

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 January 2024

Posted:

26 January 2024

You are already at the latest version

Alerts
Abstract
There are different ways to analyse energy absorbance (EA) in the human auditory system. In previous research, we developed a complete finite element model (FEM) of the human auditory system. In this mentioned work, the external auditory canal (EAC), middle ear, and inner ear (spiral cochlea, vestibule, and semi-circular canals) were modelled based on human temporal bone histological sections. Multiple acoustic, structure and fluid-coupled analyses were conducted using the FEM to perform harmonic analyses in the 0.1–10 kHz range. Once the FEM had been validated with published experimental data, the FEM numerical results were used to calculate the EA or energy reflected (ER) by the tympanic membrane. This EA was also measured in clinical audiology tests which were used as a diagnostic parameter. A mathematical approach was developed to calculate the EA and ER, with numerical and experimental results showing adequate correlation up to 1 kHz. Another published FEM had adapted its boundary conditions to replicate experimental results. Here, we recalculated those numerical results by applying the natural boundary conditions of human hearing and found that the results almost totally agreed with our FEM. This boundary problem is frequent and problematic in experimental hearing test protocols: the more invasive they are, the more the results are affected. One of the main objectives of using FEMs is to explore how the experimental test conditions influence the results. Further work will still be required to uncover the relationship between the middle ear structure and EA to clarify how to best use FEMs. Moreover, the FEM boundary conditions must be more representative in future work to ensure their adequate interpretation.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

In recent years, numerous studies have been developed to measure acoustic impedances[1,2,3,4,5,6,7,8,9,10,11]. Moller [12] first introduced the use of ‘calibrated sound sources’ as a means for measuring impedances, a method that is now extensively used [13,14,15,16,17,18,19,20]. Norton or Thevenin equivalent sources are used for measuring device calibration, with only a single pressure measurement then being needed to calculate the external auditory canal (EAC) entrance impedance[21]. Other research has used the transfer function method, which relies on measuring the influence of the termination impedance on duct pressure [22], thereby requiring robust coupling of the device and the EAC [16,17]. Finally, Lanoye et al. [23] proposed a third method using impedance probes containing separated pressure and volume velocity sensors, although high levels of disturbance of the sound field at the measuring position are a problem when using this technique.
Most studies published to date have employed the two first methods where a sound (pressure) source and measuring device are usually placed inside the EAC. This is to avoid discontinuity between the device and the EAC to avoid exciting higher-order modes [24,25,26,27]. The frequencies of the minimum and maximum input impedances are mainly affected by the EAC length and its cross-sectional area. This means that the sound source and measurement device directly affect the impedance calculations because they change the canal length. One possible solution to this problem could be the application of inverse procedures to derive the EAC shape from its input impedance [12]. Thus, knowing the calculated cross-sectional area of the EAC allows the required eardrum impedance transformation for the energy calculations to be estimated.
To obtain middle ear diagnostics, the input impedances of the EAC measurements are transformed to represent the position of the eardrum and thus, record reflected energy (RE) and the energy absorbed, EA [5,7,8,13,14,15,16,17,18]. However, these impedance and energy results are often inaccurate. Thus, the main objective of this current work was to clarify the origin of possible errors in these measurements and their transformation as well as the consequences of these errors in terms of the impedances and energy calculated from them. In this sense, the use of finite element models (FEMs) is now widely accepted as an adequate and complementary research tool. Thus, this paper was based on several numerical simulations conducted using a FEM previously described and validated in the academic literature. This original work was first conducted for the outer and middle ear [35,36], was then applied to an inner ear FEM by employing a semiautomatic algorithm [37], and was finally coupled to the previous outer and middle ear FEMs [38]. Therefore, this FEM presents a complete fluid–structure interaction between the EAC, tympanic membrane (TM), and the oval window.
TM modelling was a crucial innovation with respect to previous models because the elements it used were better formulated and thereby eliminated problems associated with ‘shear locking’ elements used in thin membranes. Thus, together with adequate mesh convergence analysis, TM modelling provides sufficient guarantees of correct results. This means that, apart from geometric uncertainties caused by natural variability, most inaccuracy in this type of modelling comes from the difficulty of discerning the mechanical properties of some components such as the TM, tensors, and joints, among others. In this current article, we used assumed values for these components without attempting to discuss their accuracy. We simulated different combinations to discern the impact of each subsystem in the human auditory system (AS), building on a previous paper with a similar methodology [39] that determined how the AS influences pressure distribution in the EAC.
In this context, over the past century, Rong Gan has led a research group that has published several FEMs that have become an important source of inspiration for other researchers developing FEMs [40,41,42,43,44]. Gan’s work has focused on calculating EAC and eardrum impedances as well as the EA and ER from the TM [44]. Our work differs from that of Gan et al. in two clear ways. First, their main objective was to calculate the relationship between three middle ear disorders (otitis media, otosclerosis, and ossicular chain disarticulation), as simulated in their FEM, and any changes in the EA. In contrast, our objective was to determine how the AS subsystems affect EA. We employed a range of FEMs, with the most basic one comprising an EAC and eardrum, to calculate the impedances and EAs. This methodology has already been applied successfully in previous work which gave us a better understanding of the mutual influence of each part of the AS on these factors.
It is important to understand the differences in our strategic goals and those of Gan et al. because these differing objectives affect the simulation conditions employed. Gan and colleagues aimed to offer a useful tool for the diagnosis of middle ear disorders by testing EAs through pneumatic otoscopic and wideband absorbance audiometry tests. Therefore, they literally reproduced the experimental setup boundary conditions and placed the sound source 20 mm from the eardrum to simulate the experimental test conditions in the FEM (see Figure 1). They determined that this approach gave them the best correlation between their numerical and experimental results. However, this does not mean that these numerical results most closely resemble reality. Indeed, controversy remains regarding the accuracy of the experimental methods used to measure impedance and in turn, the subsequent energy calculation results [45,46,47,48,49,50]. Therefore, more theoretical background work will still be required to increase our knowledge in this area.

2. Theoretical background

The EA is calculated based on the ER. It describes the fraction of incident acoustic power reflected by the TM, where a reflective power of 1 corresponds to complete reflection of all the acoustic power and a reflectance of 0 corresponds to the condition in which all the power is absorbed by the TM [31]. First, the characteristic impedance of the EAC was calculated as:
Z c = ρ c S
where ρ is the density of the air contained in the EAC, c is the speed of sound in air, and S is the cross-sectional area of ​​the EAC. In this study, air density and sound speed values ​​of 1.21 kg/m3 and 343 m/s, were used, respectively. To calculate the TM impedance, the impedance of each of the elements of the FEM for the TM was determined as a function of the acoustic pressure p T M i ( f ) , with v T M i ( f )   being the velocity in element i of the TM, and where A T M i was the element area. Both the velocity and pressure depend on the frequency f, so we used values ​​obtained for a frequency range of 0.1–10 kHz according to the FEM:
Z T M i ( f ) = p T M i ( f ) A T M i v T M i ( f )
The total TM impedance, Z T M ( f ) , was obtained by adding the impedances of each of the elements of the TM surface in parallel:
Z T M ( f ) = 1 ∑ i [ 1 Z T M i ( f ) ]
The acoustic impedance in the EAC was calculated based on Z T M ( f ) and Z c :
Z E C ( f ) = Z c Z T M ( f ) + j Z c tan ( k L ) Z c + j Z T M ( f ) tan ( k L )
Where k is the wave number and L is the distance between the TM and the location of the measurement points in the EAC, which was at 30 mm in our study. The reflected acoustic pressure is obtained using the expression:
R P ( f ) = Z E C − Z C Z E C + Z C
Thus, the ER is calculated based on the reflected acoustic pressure   R P ( f ) :
E R ( f ) = | R P ( f ) | 2 = | Z E C − Z C Z E C + Z C | 2
Finally, the EA was obtained as a function of the frequency calculated as:
E A ( f ) = 1 − E R ( f )

3. Finite element model

The construction and validation of the FEM applied in this section, as well as its material properties, have been previously published [35,36,37,38]. However, in this current work, the EAC was re-meshed with hexahedral elements [51,52] to help improve the accuracy of the FEM post-process calculations (Figure 2).
As summarised in Table 1, three different FEM combinations were simulated to discern the impact of the different AS subsystems.

4. Results

The TM was modelled using 7,880 hexahedral elements, with each one itself comprising 8 nodes, although only the 4 that formed the surface in contact with CAE air were valid in our calculations. Thus, a total of 8,193 nodes formed the TM surface. With harmonic analysis, we obtained 16,386 real and imaginary values each for pressure and speed. Thus, when we performed the harmonic calculation for the 0.1–10 kHz range, we produced matrices comprising a total of 1,638,600 data points each for pressure and speed. In turn, the area was composed of only the 7,880 element data points. We then used ANSYS engineering simulation software to obtain a total of 3,285,080 values for use in impedance and EA calculations using MATLAB software.
A. Tympanic membrane velocity
The average of all the elements in the TM velocity module is shown in Figure 3. There were three clearly differentiated resonance zones. One was at around 800–1,000 Hz because of the eardrum itself, while the other two, located at 4 kHz and 9 kHz, were the result of the characteristic resonances of the CAE [53].
B. External auditory canal characteristic impedance.
The characteristic impedance of the EAC Zc depends on the air density, ρ, speed of sound in air, c, and cross-sectional area of ​​the canal, S. The cross-sectional area was measured at the entrance of the canal where the pressure source was located and was 89,652 mm2. The density and speed of sound values we​are 1.21 kg/m3 and 343 m/s respectively, and so the characteristic impedance of the EAC was 4.6294 ×103 Pa s/mm3. This value was used for all the FAMs and was frequency independent.
C. Tympanic membrane impedance (direct calculation)
Figure 4 represents the module and phase TM impedance in a frequency range of 0.1 to 10 kHz. Figure 4A shows a comparison of the module impedance for the three studied FEMs and showed a decrease in the impedance with frequency up to 800–1,000 Hz, after which it increased. This minimum coincided with the first eardrum resonance frequency in that range. Figure 4B shows how the system formed by the CAE and TM opposes the system of least resistance to wave propagation and so was where the highest speeds occurred. Figure 4B shows how the phase impedance started at a value of −80° for 100 Hz and increased with the frequency until it reached 0° for a range of 700–900 Hz. For frequency values ​​between 8,000 -9,000 Hz, the phase impedance reached a maximum between 60–80°. Therefore, the phase advanced until it reached the resonance frequency at around 900 Hz, with the phase also changing from lagging to leading at this point. In addition, there was a tendency towards an asymptotic phase shift at 180°, meaning that this was a second order system.
D. External auditory canal impedance (backward calculation) based on tympanic membrane impedance
Figure 5A shows the module EAC impedance for each of the studied FEMs, which strongly coincided, especially at high frequencies. The EAC curves presented two minima, one at 3,000 Hz and the other at 9,000 Hz, with a maximum at around 6,000 Hz. In turn, Figure 5B shows the phase EAC impedance curves for each FEM, which also strongly coincided at high frequencies. The WM stopped influencing the results in both the module and phase EAC impedance at around 1,000 Hz, with curve disturbances at a lower range than those present at 3,000, 6,000, or 9,000 Hz. The first and second resonance frequencies of the EAC were at 3,000 and 9,000 Hz, respectively, while the anti-resonance of the canal was at 6,000 Hz.
E. Energy absorbance at the tympanic membrane
The EA curve presented a maximum for a frequency value around 700–900 Hz in all three tested FEMs, reaching a minimum for low frequency values ​​between 100–200 Hz and a maximum at 9,000–10,000 Hz. Figure 6A shows how the maximum EA values coincided with the minimum of the MV impedance, as shown in Figure 4B.

5. Discussion

To calculate the impedances, it appears that a well-defined cochlea model is unnecessary, especially at high frequencies. To validate this finding, we compared our data with those provided in previous academic publications. As shown in Figure 8 for module (A) and phase (B) EAC impedance, the values ​​obtained with our FEMs corresponded to the data obtained by Zhang and Gan [44]. The blue curve represents the impedance of the EAC calculated according to Zhang and Gan to which a correction method [50] was applied to simulate our test condition (L = 0.03 m) and our EAC section (S), which thereby modified the value of the characteristic impedance (Zc). These results strongly concurred with the complete FEM model (CATIOSCO) for this correction.

6. Conclusions

Here we established a process for the numerical calculation of impedances and acoustic EA by the TM. This process starts with post-processing in ANSYS software followed by data exportation and processing in MATLAB.
Regarding the Impedance of the External Auditory Canal, it is worth noting the agreement of the results obtained in this study with those of GAN once the length of the canal is modified to 0.03 m, with values ranging from 10-4 to 10-1 Pa·s/mm³, with valleys at 3 and 9 kHz, and a peak at 7 kHz. The modelling of the ossicular chain, as well as the cochlea, are shown to be crucial in the impedance of the Tympanic Membrane. Without these elements, the impedance drops to 0.6·10-2 Pa·s/mm³ with the minimum around 800 Hz, while modelling the complete system reduces the minimum to 2·10-2 Pa·s/mm³, shifting the valley frequency to approximately 1 kHz. The experimental values [13,15,44] closely match those obtained in this study.
Regarding the values obtained for EA (Energy Absorption), there is a significant difference in this study when the ossicular chain and cochlea are introduced. Without these elements, EA reaches a value of almost 1 at around 900 Hz, which is quite logical as this frequency coincides with the first natural frequency of the eardrum, absorbing almost all incoming energy. When modelling the ossicular chain and cochlea, this maximum value is reduced to 0.6, and the frequency slightly increases to 1 kHz. Experimental results show discrepancies; This work [11] exhibits a similar frequency of maximum EA but with a value close to 1. Other results (15,31,33,34,44) have a first part nearly identical to that of this study, with a maximum around 1 kHz and a value of 0.6, but the significant difference is that EA continues to rise to 3-4 kHz with values between 0.7 and 1. Considering the equation used to calculate EA (Equation 7) and referring to the previous equations (Equations 4-6), it is deduced that the terms ZTM, ZC, and ZEC (Tympanic and Auditory Canal Impedances), once it has been shown that ZTM coincides between experimental work and the one presented in this study, it is deduced that ZEC is what causes the difference in results. This is due to the placement of the measuring device within the canal, considerably reducing its length, affecting the impedance values, as demonstrated in Figure 8. This may be because it is difficult to establish the conditions of a ‘normal ear’ as a FEM [31]. Therefore, it would be advisable to carry out more experiments of this type in the future to help refine these initial results.

Contributions

A. García-González and C. Castro-Egler, Developed all the FEMs in ANSYS software. J. A. Aguilera-García and P. M. Cerezo carried out all the post-processing in MATLAB software. A. García-González was the project coordinator and supervised all the processes.

References

  1. Jønsson S, Schuhmacher A, Ingerslev H. Wideband impedance measurement in the human ear canal; In vivo study on 32 subjects. Physics arXiv: Medical Physics. 2018. [CrossRef]
  2. Keefe DH, Sanford CA, Ellison JC, Fitzpatrick DF, Gorga MP. Wideband aural acoustic absorbance predicts conductive hearing loss in children. Int J Audiol. 2012 Dec;51(12):880–91. [CrossRef]
  3. Niemczyk E, Lachowska M, Tataj E, Kurczak K, Niemczyk K. Wideband acoustic immitance – Absorbance measurements in ears after stapes surgery. Auris Nasus Larynx. 2020 Dec 1;47(6):909–23. [CrossRef]
  4. Chris S., Lisa H., Patrick F., Hideko H. Wideband Acoustic Immittance: Tympanometric Measures. Ear Hear. 2013. [CrossRef]
  5. Keefe DH, Sanford CA, Ellison JC, Fitzpatrick DF, Gorga MP. Wideband aural acoustic absorbance predicts conductive hearing loss in children. Int J Audiol. 2012 Dec;51(12):880–91. [CrossRef]
  6. Frear DL, Guan X, Stieger C, Rosowski JJ, Nakajima HH. Impedances of the inner and middle ear estimated from intracochlear sound pressures in normal human temporal bones. Hear Res. 2018 Sep 1;367:17–31. [CrossRef]
  7. Doğan E, Közen MA, Mungan Durankaya S, Kenar G, Birlik AM. Evaluation of middle ear and hearing status of ankylosing spondylitis patients with wideband tympanometry and pure tone audiometry tests. European Archives of Oto-Rhino-Laryngology. 2023 May 1;280(5):2273–81. [CrossRef]
  8. Allen JB, Jeng PS, Levitt H. Evaluation of human middle ear function via an acoustic power assessment. Vol. 42, Journal of Rehabilitation Research and Development. 2005. p. 63–77. [CrossRef]
  9. Madahana MCI, Nyandoro OTC, Ekoru JED. A Human Inner Ear Model for assessment of Noise Induced Hearing Loss via energy methods. In: IFAC-PapersOnLine. Elsevier B.V.; 2020. p. 16424–9. [CrossRef]
  10. Allen JB, Jeng PS, Levitt H. Evaluation of human middle ear function via an acoustic power assessment. Vol. 42, Journal of Rehabilitation Research and Development. 2005. p. 63–77. [CrossRef]
  11. Yilmaz N, Soylemez E, Sanuc MB, Bayrak MH, Sener V. Sound energy absorbance changes in the elderly with presbycusis with normal outer and middle ear. European Archives of Oto-Rhino-Laryngology. 2023 May 1;280(5):2265–71. [CrossRef]
  12. Møller AR. Improved Technique for Detailed Measurements of the Middle Ear Impedance. J Acoust Soc Am. 1960 Feb;32(2). [CrossRef]
  13. Rabinowitz WM. Measurement of the acoustic input immittance of the human ear. J Acoust Soc Am. 1981 Oct;70(4). [CrossRef]
  14. Larson VD, Nelson JA, Cooper WA, Egolf DP. Measurements of acoustic impedance at the input to the occluded ear canal. J Rehabil Res Dev. 1993;30(1).
  15. Voss SE, Allen JB. Measurement of acoustic impedance and reflectance in the human ear canal. J Acoust Soc Am. 1994 Jan;95(1). [CrossRef]
  16. Sanborn PE. Predicting hearing aid response in real ears. J Acoust Soc Am. 1998 Jun;103(6). [CrossRef]
  17. Keefe DH, Ling R, Bulen JC. Method to measure acoustic impedance and reflection coefficient. J Acoust Soc Am. 1992 Jan;91(1). [CrossRef]
  18. Keefe DH, Sanford CA, Ellison JC, Fitzpatrick DF, Gorga MP. Wideband aural acoustic absorbance predicts conductive hearing loss in children. Int J Audiol. 2012 Dec 16;51(12). [CrossRef]
  19. Ellison JC, Gorga M, Cohn E, Fitzpatrick D, Sanford CA, Keefe DH. Wideband acoustic transfer functions predict middle-ear effusion. Laryngoscope. 2012 Apr;122(4). [CrossRef]
  20. Shahnaz N, Bork K, Polka L, Longridge N, Bell D, Westerberg BD. Energy Reflectance and Tympanometry in Normal and Otosclerotic Ears. Ear Hear. 2009 Apr;30(2). [CrossRef]
  21. Lawton BW, Shaw EAG. Estimation of acoustical energy reflectance at the eardrum from measurements of pressure distribution in the human ear canal. Journal of the Acoustical Society of America. 1982;72(3):766–73. [CrossRef]
  22. Utsuno H, Tanaka T, Fujikawa T, Seybert AF. Transfer function method for measuring characteristic impedance and propagation constant of porous materials. J Acoust Soc Am. 1989 Aug;86(2). [CrossRef]
  23. Lanoye R, Vermeir G, Lauriks W, Kruse R, Mellert V. Measuring the free field acoustic impedance and absorption coefficient of sound absorbing materials with a combined particle velocity-pressure sensor. J Acoust Soc Am. 2006 May;119(5). [CrossRef]
  24. Hudde H, Letens U. Scattering matrix of a discontinuity with a nonrigid wall in a lossless circular duct. J Acoust Soc Am. 1985 Nov;78(5). [CrossRef]
  25. Fletcher NH, Smith J, Tarnopolsky AZ, Wolfe J. Acoustic impedance measurements—correction for probe geometry mismatch. J Acoust Soc Am. 2005 May;117(5). [CrossRef]
  26. Stinson MR, Daigle GA. Transverse pressure distributions in a simple model ear canal occluded by a hearing aid test fixture. J Acoust Soc Am. 2007;121(6). [CrossRef]
  27. Brass D, Locke A. The effect of the evanescent wave upon acoustic measurements in the human ear canal. J Acoust Soc Am. 1997 Apr;101(4). [CrossRef]
  28. Rasetshwane DM, Neely ST. Inverse solution of ear-canal area function from reflectance. J Acoust Soc Am. 2011 Dec;130(6). [CrossRef]
  29. Shahnaz N, Bork K, Polka L, Longridge N, Bell D, Westerberg BD. Energy Reflectance and Tympanometry in Normal and Otosclerotic Ears. Ear Hear. 2009 Apr;30(2). [CrossRef]
  30. Allen JB, Jeng PS, Levitt H. Evaluation of human middle ear function via an acoustic power assessment. The Journal of Rehabilitation Research and Development. 2005;42(4s). [CrossRef]
  31. Rosowski JJ, Nakajima HH, Hamade MA, Mahfoud L, Merchant GR, Halpin CF, et al. Ear-Canal Reflectance, Umbo Velocity, and Tympanometry in Normal-Hearing Adults. Ear Hear. 2012 Jan;33(1). [CrossRef]
  32. Sebothoma B, Khoza-Shangase K, Mol D, Masege D. The sensitivity and specificity of wideband absorbance measure in identifying pathologic middle ears in adults living with HIV. South African Journal of Communication Disorders. 2021 Sep 30;68(1). [CrossRef]
  33. Piskorski P, Keefe DH, Simmons JL, Gorga MP. Prediction of conductive hearing loss based on acoustic ear-canal response using a multivariate clinical decision theory. J Acoust Soc Am. 1999 Mar;105(3). [CrossRef]
  34. Keefe DH, Simmons JL. Energy transmittance predicts conductive hearing loss in older children and adults. J Acoust Soc Am. 2003 Dec;114(6). [CrossRef]
  35. Garcia-Gonzalez A, Castro-Egler C, Gonzalez-Herrera A. Analysis of the mechano-acoustic influence of the tympanic cavity in the auditory system. Biomed Eng Online. 2016 Dec 31;15(1). [CrossRef]
  36. Garcia-Gonzalez A, Gonzalez-Herrera A. Effect of the middle ear cavity on the response of the human auditory system. J Acoust Soc Am. 2013 May;133(5). [CrossRef]
  37. Castro-Egler C, García-González A. Semiautomatic algorithm for 3D modelling of finite elements of the cochlea. J Med Imaging Health Inform. 2017;7(5). [CrossRef]
  38. A. García-González, A. Durán-Escalante, C. Castro-Egler. 3D Modelling and Numerical Analysis of Human Inner Ear by Means of Finite Elements Method. International Journal of Computer and Information Engineering. 2016;10(3):596–606. [CrossRef]
  39. Garcia-Gonzalez A, Castro-Egler C, Gonzalez-Herrera A. Influence of the auditory system on pressure distribution in the ear canal. J Mech Med Biol. 2018 Mar 15;18(02). [CrossRef]
  40. Gan RZ, Reeves BP, Wang X. Modeling of Sound Transmission from Ear Canal to Cochlea. Ann Biomed Eng. 2007 Nov 14;35(12). [CrossRef]
  41. Gan RZ, Sun Q, Feng B, Wood MW. Acoustic–structural coupled finite element analysis for sound transmission in human ear—Pressure distributions. Med Eng Phys. 2006 Jun;28(5). [CrossRef]
  42. Gan RZ, Feng B, Sun Q. Three-Dimensional Finite Element Modeling of Human Ear for Sound Transmission. Ann Biomed Eng. 2004 Jun;32(6). [CrossRef]
  43. Brown MA, Bradshaw JJ, Gan RZ. Three-Dimensional Finite Element Modeling of Blast Wave Transmission From the External Ear to a Spiral Cochlea. J Biomech Eng. 2022 Jan 1;144(1). [CrossRef]
  44. Zhang X, Gan RZ. Finite element modeling of energy absorbance in normal and disordered human ears. Hear Res. 2013 Jul;301. [CrossRef]
  45. Nørgaard KR, Fernandez-Grande E, Laugesen S. Compensating for oblique ear-probe insertions in ear-canal reflectance measurements. J Acoust Soc Am. 2019 Jun;145(6):3499–509. [CrossRef]
  46. Hudde H, Engel A. Measuring and Modeling Basic Properties of the Human Middle Ear and Ear Canal. Part III: Eardrum Impedances, Transfer Functions and Model Calculations. Vol. 84, ACUSTICA. acta acustica. 1998.
  47. Hudde H, Engel A. Measuring and Modeling Basic Properties of the Human Middle Ear and Ear Canal. Part II: Ear Canal, Middle Ear Cavities, Eardrum, and Ossicles. Vol. 84, ACUSTlCA· acta acustica. 1998.
  48. Hudde H, Engel A. Measuring and Modeling Basic Properties of the Human Middle Ear and Ear Canal. Part I: Model Structure and Measuring Techniques. Vol. 84. 1998.
  49. Hudde H. Measurement of the eardrum impedance of human ears. J Acoust Soc Am. 1983 Jan;73(1). [CrossRef]
  50. Fletcher NH, Smith J, Tarnopolsky AZ, Wolfe J. Acoustic impedance measurements—correction for probe geometry mismatch. J Acoust Soc Am. 2005 May;117(5). [CrossRef]
  51. Ramos Valero JP. Modelado y análisis numérico con el método de los elementos finitos del canal auditivo externo y membrana timpánica. Málaga: [s.n.]; 2013.
  52. Castro Egler C. Modelado 3D & Análisis Numérico del Oído Interno mediante Elementos Finitos. 2020 Mar 9 [cited 2022 Jul 28]; Available from: https://hdl.handle.net/10630/19420.
  53. Garcia-Gonzalez A, Castro-Egler C, Gonzalez-Herrera A. Influence of the auditory system on pressure distribution in the ear canal. J Mech Med Biol. 2018;18(2). [CrossRef]
Preprints 97351 g001
Figure 1. A cross-section of the ear illustrating the probe used to measure impedance when inserted into the ear canal. The probe emits a sound pressure wave that is incident to the tympanic membrane. Some of the incident sound pressure is reflected and this is then measured by the probe. The remaining incident sound pressure is absorbed by the tympanic membrane and the structures behind it.
Figure 1. A cross-section of the ear illustrating the probe used to measure impedance when inserted into the ear canal. The probe emits a sound pressure wave that is incident to the tympanic membrane. Some of the incident sound pressure is reflected and this is then measured by the probe. The remaining incident sound pressure is absorbed by the tympanic membrane and the structures behind it.
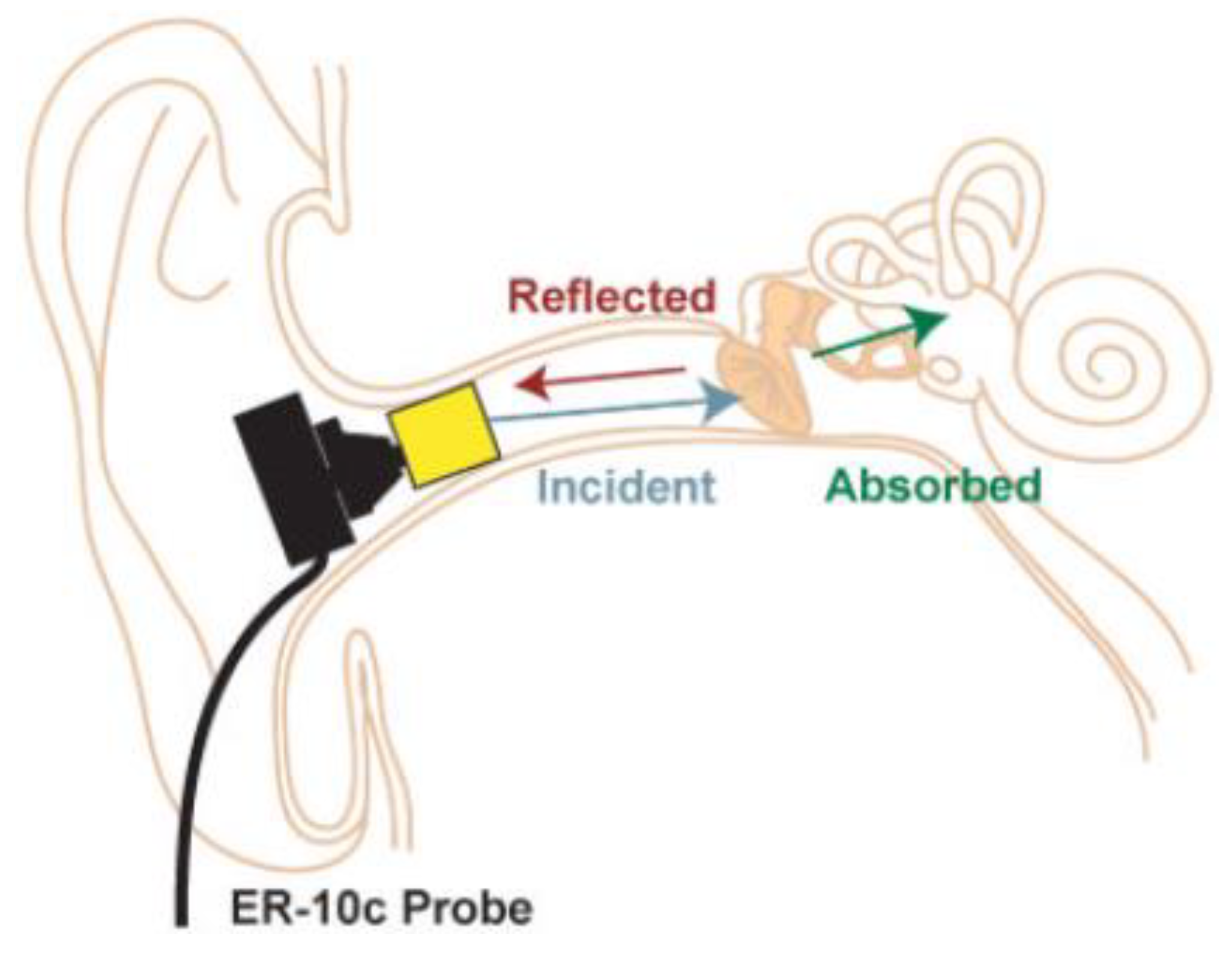
Preprints 97351 g001
Preprints 97351 g002
Figure 2. Hexahedral finite element model (FEM) for the external auditory canal based on the tympanic membrane FEM.
Figure 2. Hexahedral finite element model (FEM) for the external auditory canal based on the tympanic membrane FEM.
Preprints 97351 g002
Preprints 97351 g003
Figure 3. The means for the tympanic membrane speed module for the three finite element models studied, CATIOSCO, CATI, and CATIOS. The CATI comprised the external auditory canal (EAC) and tympanic membrane (TM); CATIOS comprised the EAC, TM, ossicular chain (OC), and simplified cochlea; and CATIOSCO comprised the EAC, TM, OC, and the entire cochlea.
Figure 3. The means for the tympanic membrane speed module for the three finite element models studied, CATIOSCO, CATI, and CATIOS. The CATI comprised the external auditory canal (EAC) and tympanic membrane (TM); CATIOS comprised the EAC, TM, ossicular chain (OC), and simplified cochlea; and CATIOSCO comprised the EAC, TM, OC, and the entire cochlea.
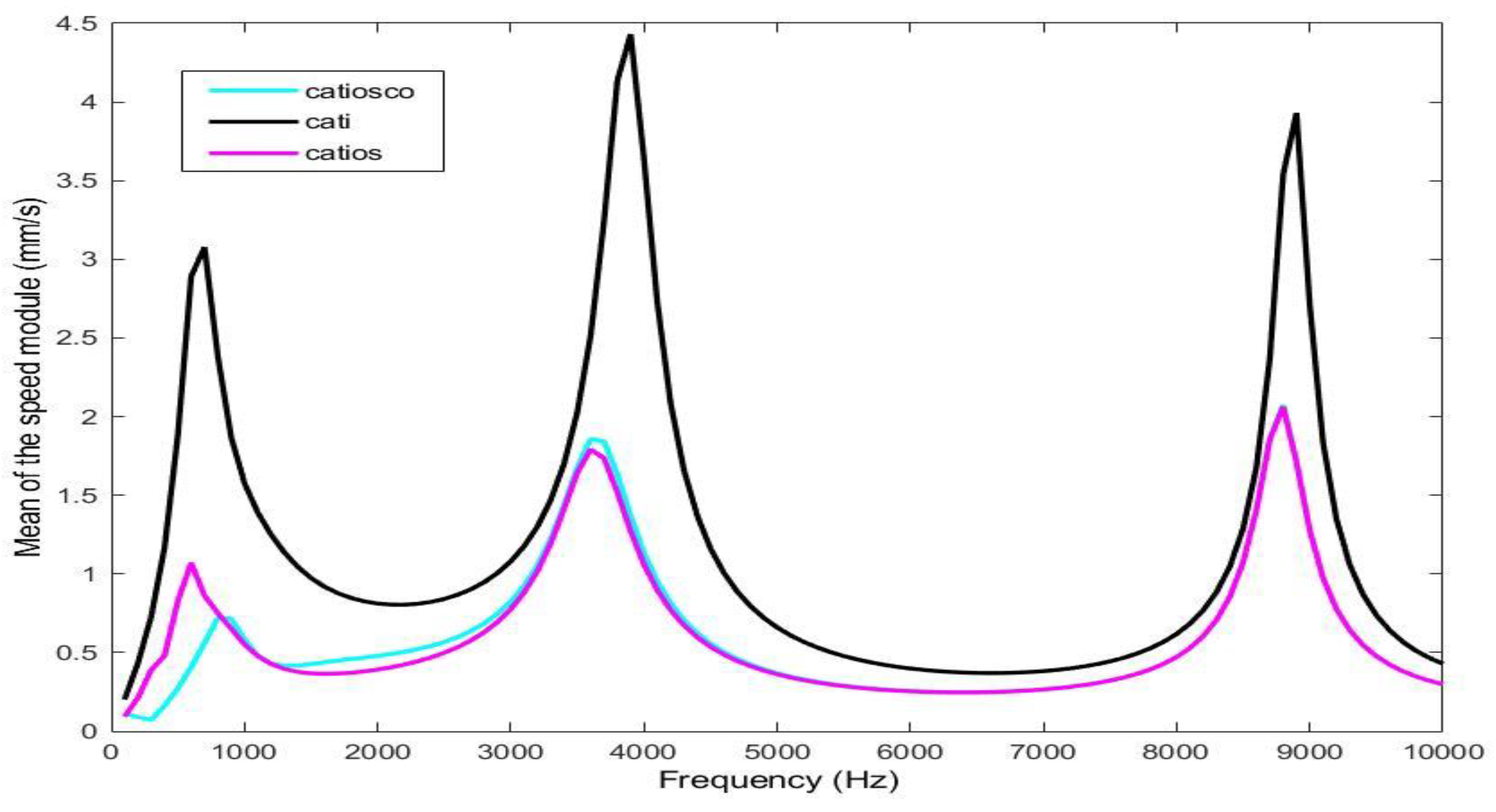
Preprints 97351 g003
Preprints 97351 g004aPreprints 97351 g004b
Figure 4. Comparison of the three studied finite element models with an experimental model by Zhang and Gan for the module (A) and phase (B) tympanic membrane impedance (ZTM).
Figure 4. Comparison of the three studied finite element models with an experimental model by Zhang and Gan for the module (A) and phase (B) tympanic membrane impedance (ZTM).
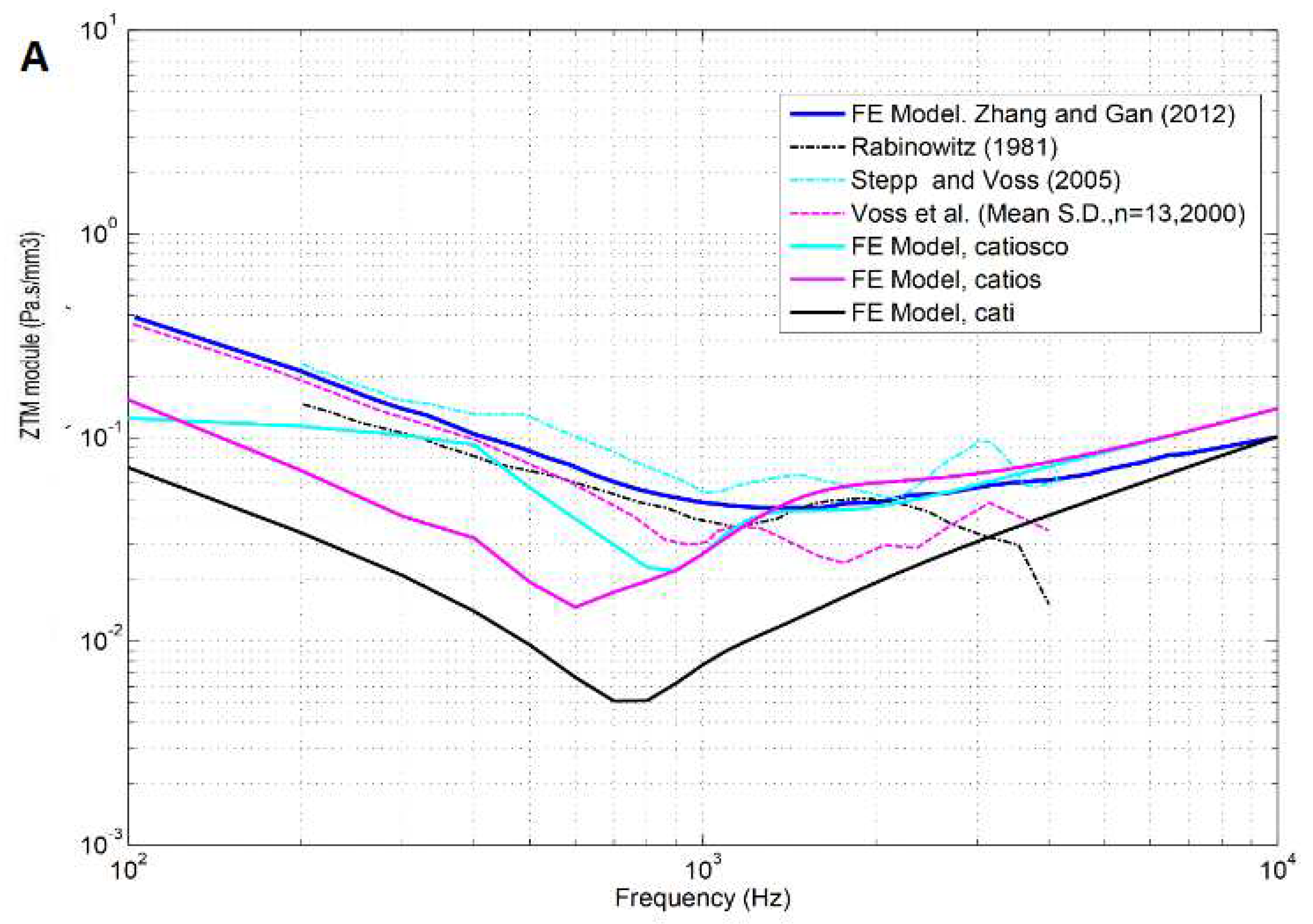
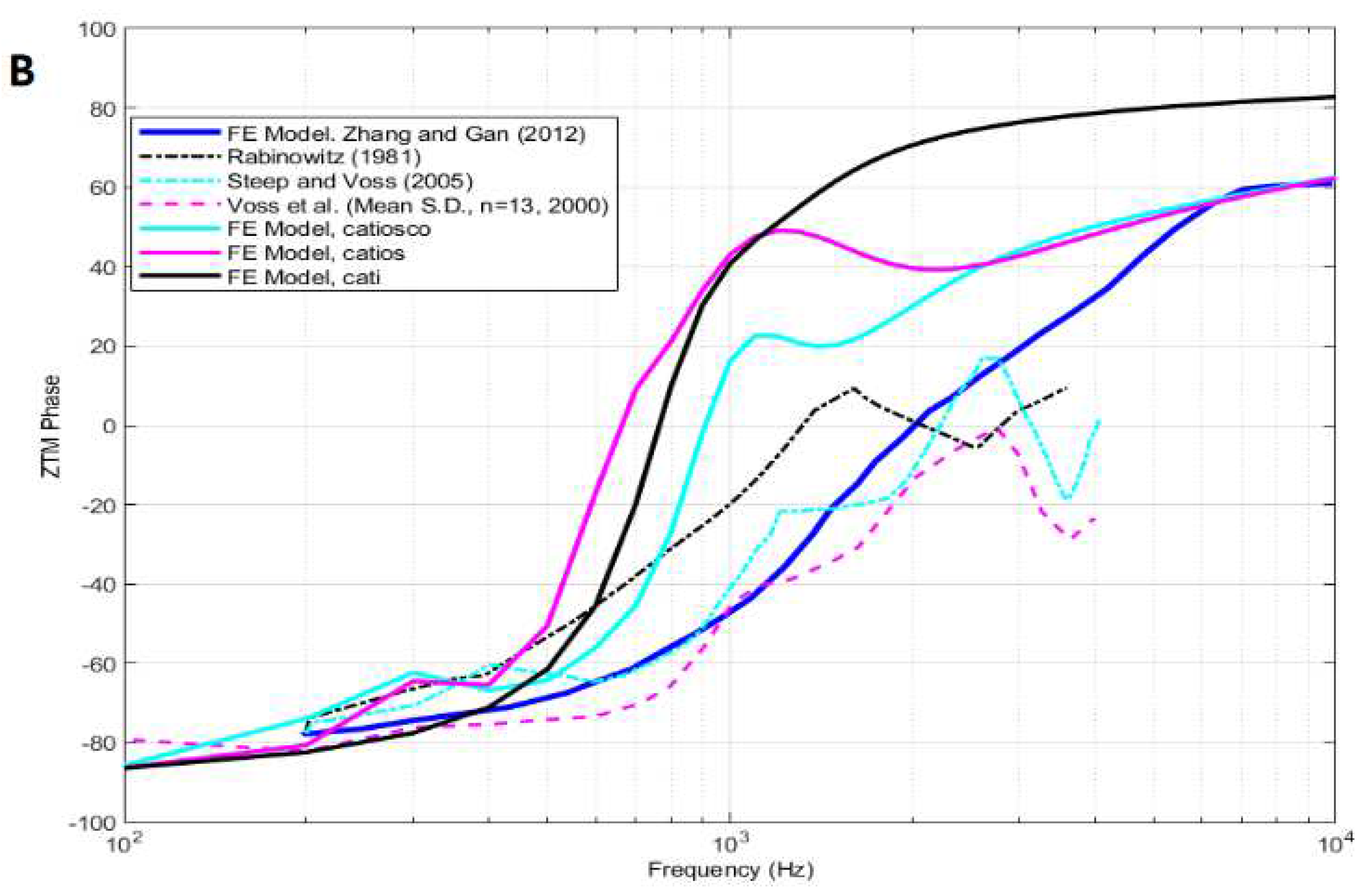
Preprints 97351 g004aPreprints 97351 g004b
Preprints 97351 g005
Figure 5. Comparison of the three studied finite element models for the module (A) and phase (B) EAC impedance (ZEC).
Figure 5. Comparison of the three studied finite element models for the module (A) and phase (B) EAC impedance (ZEC).
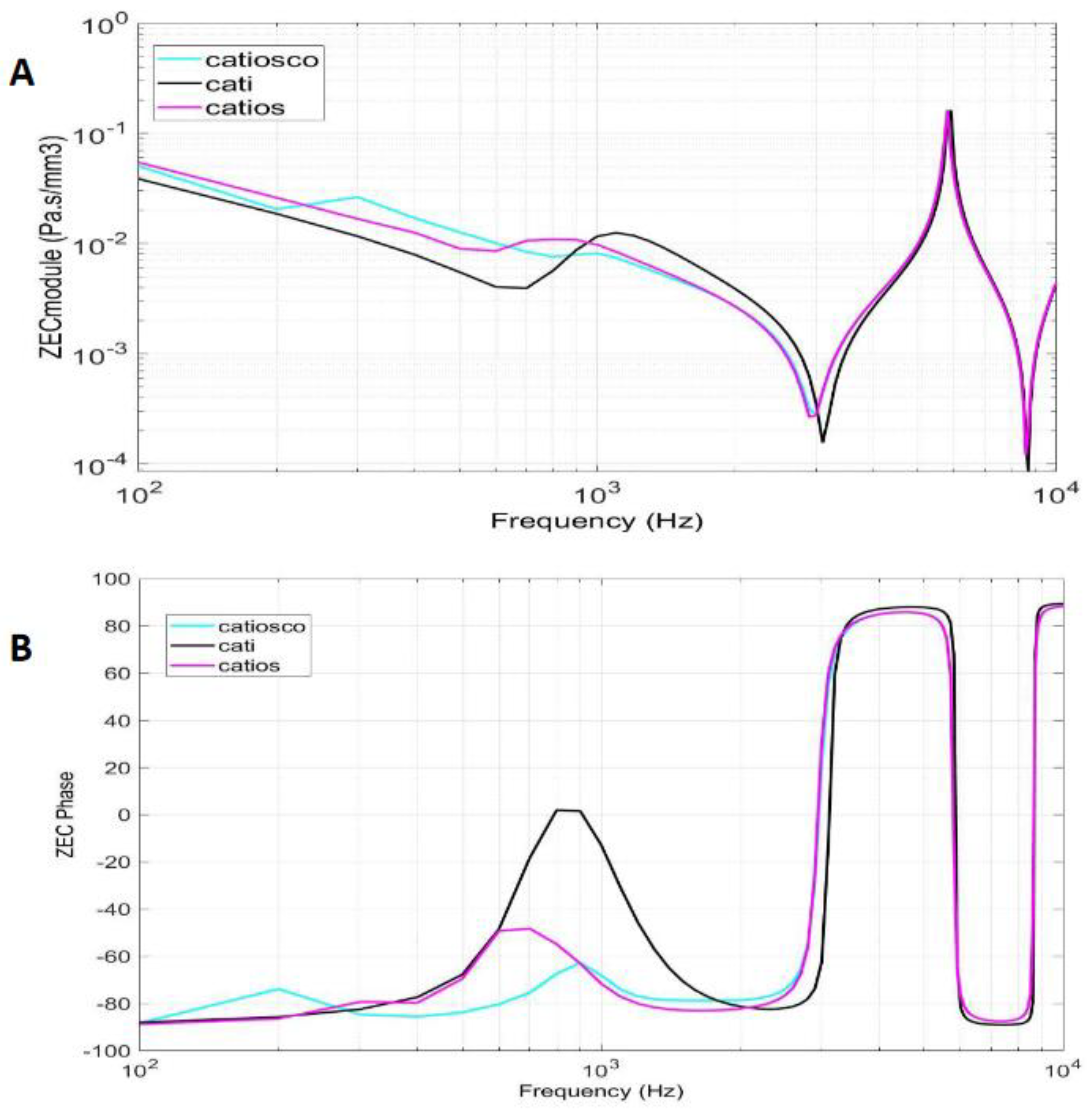
Preprints 97351 g005
Preprints 97351 g006
Figure 6. Energy absorbed by the tympanic membrane for the different finite element models studied.
Figure 6. Energy absorbed by the tympanic membrane for the different finite element models studied.
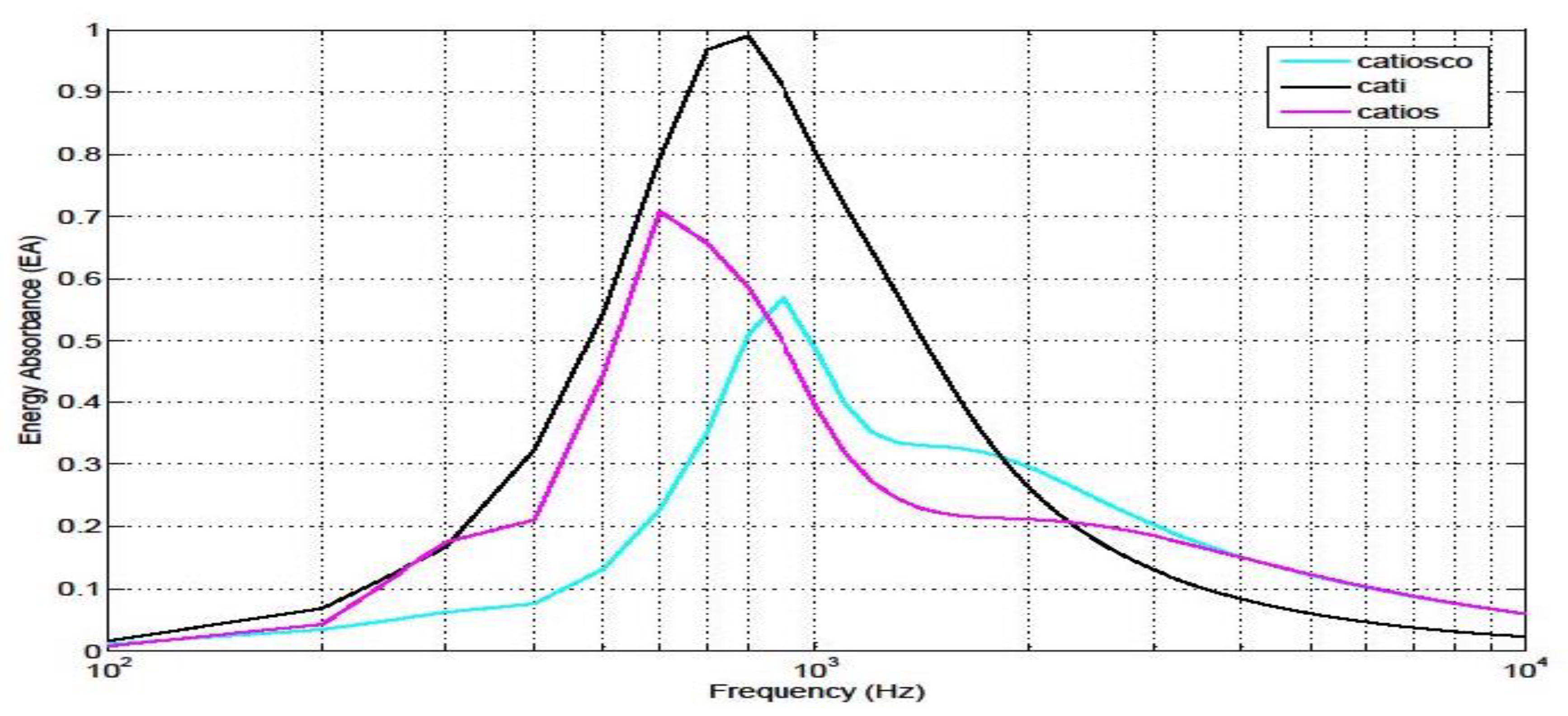
Preprints 97351 g006
Preprints 97351 g007
Figure 7. Energy absorbed by the tympanic membrane for the finite element models described in other publications.
Figure 7. Energy absorbed by the tympanic membrane for the finite element models described in other publications.
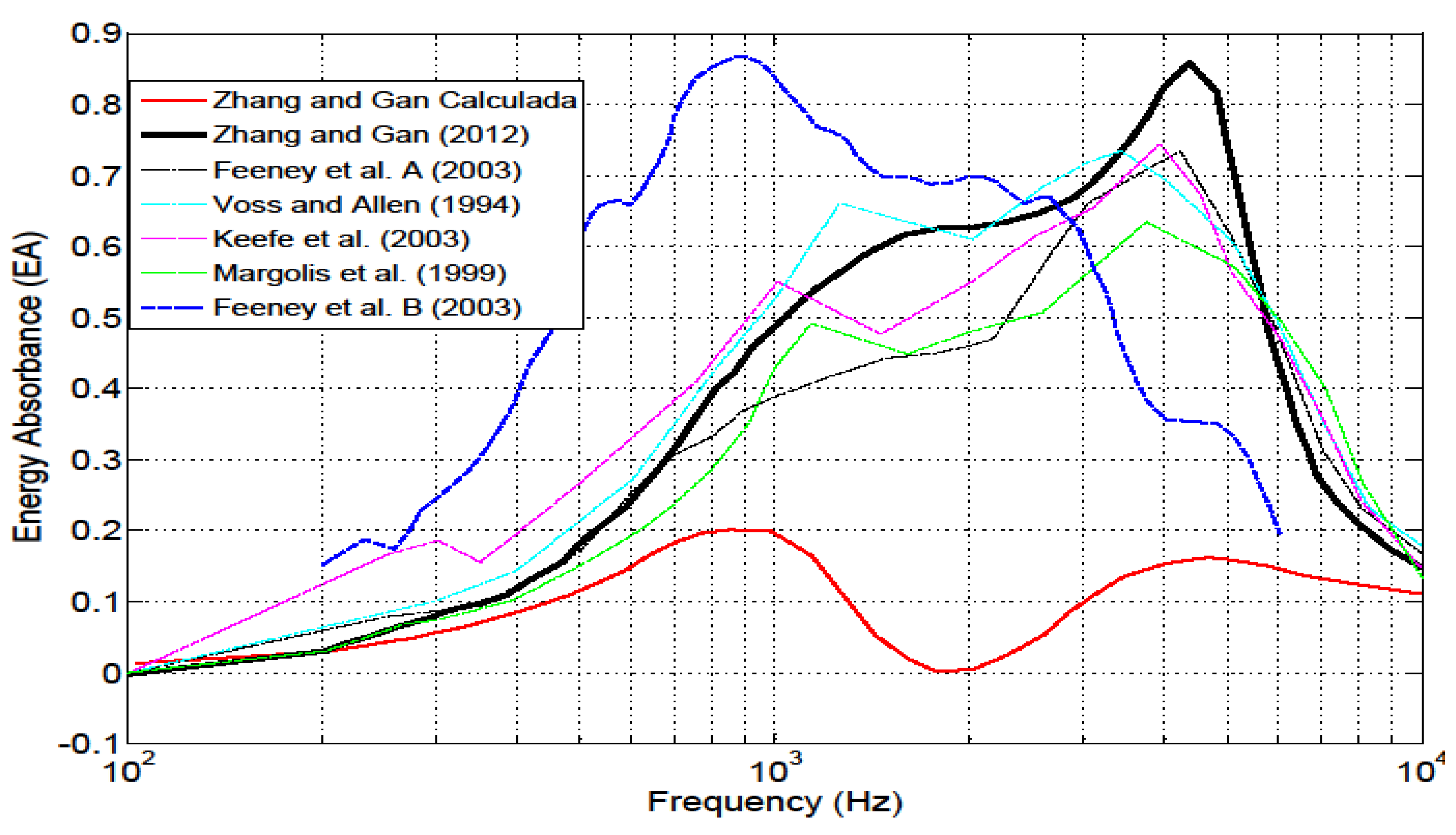
Preprints 97351 g007
Preprints 97351 g008
Figure 8. Phase comparison of the module (A) and phase (B) external auditory canal impedance with the findings published by Zhang and Gan (2012).
Figure 8. Phase comparison of the module (A) and phase (B) external auditory canal impedance with the findings published by Zhang and Gan (2012).
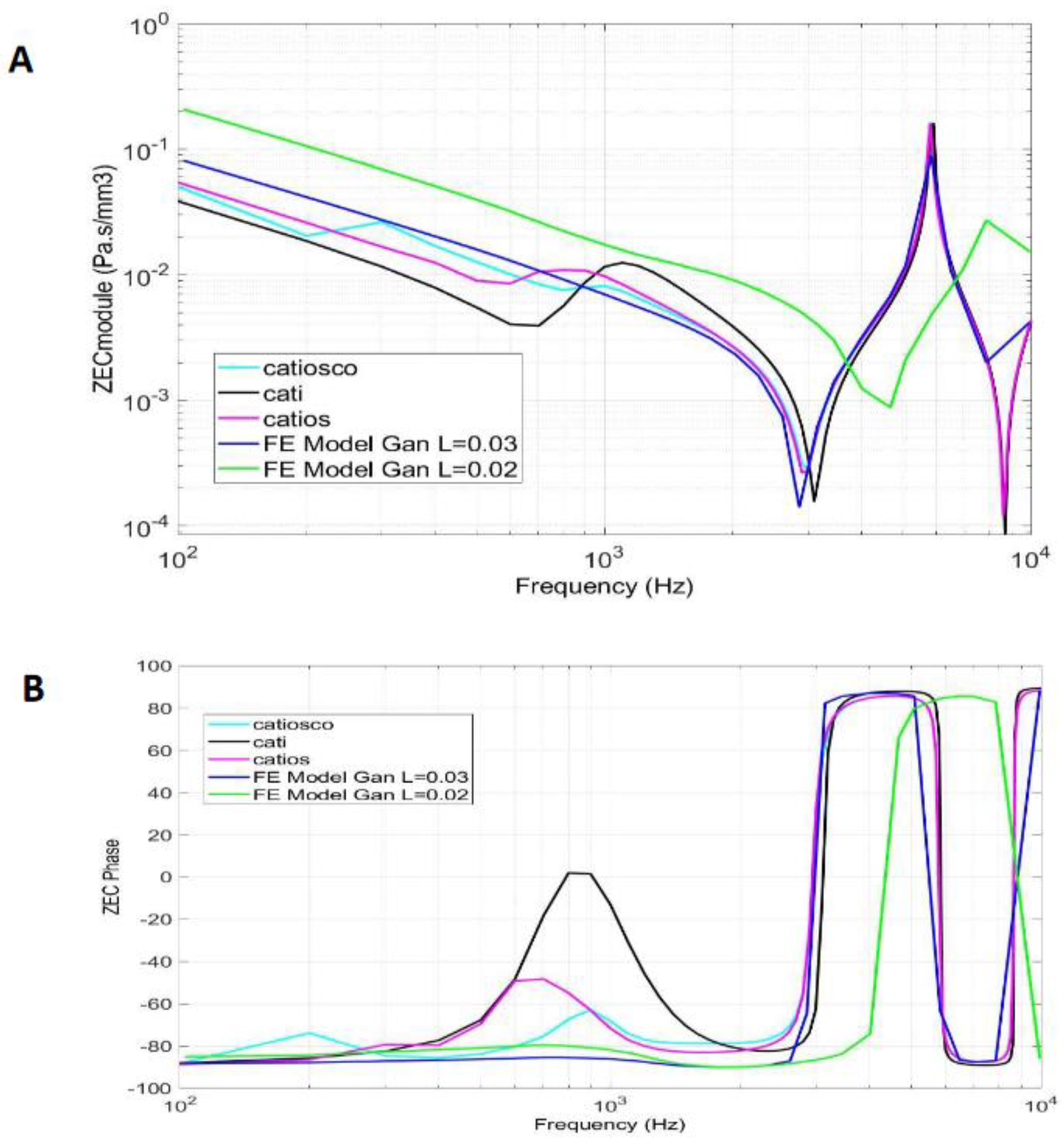
Preprints 97351 g008
Table 1. Combinations of different finite elements simulated in the CATI, CATIOS, and CATIOSCO finite element models.
Table 1. Combinations of different finite elements simulated in the CATI, CATIOS, and CATIOSCO finite element models.
Model Subsystem modelled Name
Preprints 97351 i001 External auditory canal
Tympanic membrane		 CATI
Preprints 97351 i002 External auditory canal
Tympanic membrane
Ossicular chain
Cochlea simplified		 CATIOS
Preprints 97351 i003 External auditory canal
Tympanic membrane
Ossicular chain
Choclea
Vestibuli
Semi-circular canals		 CATIOSCO
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated