Parameter-Robust Numerical Scheme for Computing Singularly Perturbed Differential Equations with Mixed Large Shifts

Preprint

Article

Parameter-Robust Numerical Scheme for Computing Singularly Perturbed Differential Equations with Mixed Large Shifts

Altmetrics

Downloads

125

Views

Comments

Ababi Hailu Ejere^*

This version is not peer-reviewed

Submitted:

18 October 2023

Posted:

19 October 2023

You are already at the latest version

Alerts

Abstract

This study focuses on the formulation and analysis of a numerical method to compute singularly perturbed functional differential equations (SP-FDEs) involving large mixed shifts. SP-FDEs are a class of differential equations with both shifts and small perturbation parameter. Such equations arise in various scientific fields to model phenomena with memory effects and perturbed dynamics. In this particular study, the considered SP-FDEs involve large negative shift (delay) and large positive shift (advance). Dealing with large mixed shifts in SP-FDEs gives rise to challenges in terms of stability analysis, numerical methods, and convergence of a solution. In this paper, the influence of the large mixed shifts is treated by choosing a uniform mesh discretized in such a way that the term with the shifts lie on the nodal points. Then, using the Numerov’s finite difference method, the continuous problem is transformed into a finite difference scheme and the influence of the perturbation parameter is handled by introducing a fitting factor in the difference scheme. Stability estimate and convergence analysis of the developed scheme are investigated and proved. Numerical experiments are carried out to demonstrate the validity and applicability of the developed scheme. It is shown that the numerical scheme obtained in this work is parameter-robust of second order convergence rate.

Keywords:

Subject: Computer Science and Mathematics - Computational Mathematics

MSC: 65L03; 65L11; 65L20; 65L70

1. Introduction

Singularly perturbed functional differential equations (SP-FDEs) are a type of differential equation that combines the features of functional differential equations (FDEs) and singularly perturbed differential equations. They involve both mixed-shift arguments and small perturbation parameters. Functional differential equations are a class of differential equations where the unknown function depends not only on the current values of its variables but also on past values. FDEs include time delays or memory effects in the equation. The solutions of FDEs often require the history of the function over a certain time interval [1]. Singularly perturbed differential equations are also a class of differential equations where a small parameter

ε

appears as a coefficient of the term with largest order of derivative. This small parameter characterizes the relative importance of the different terms in the equation [2]. The presence of the mixed-shift arguments introduces memory effects, where the solution at a given time depends not only on the current state but also on its history. The small parameter

ε

determines the relative importance of the different terms in the equation. As

ε

approaches zero, the differential equation becomes singularly perturbed (i.e. it becomes increasingly stiff) with rapid variations in some regions of the solution.

SP-FDEs are arise in many applications across different scientific disciplines. They offer a powerful framework for modeling systems with memory effects and perturbed dynamics. For instance, in control theory, the observed in modeling systems with delays, memory effects, and perturbed dynamics [3]. In population dynamics, it arise in modeling the interactions, delays, and effects of environmental changes [4]. In epidemiology, studying the spread of infectious diseases, incorporating time delays in transmission rates are modeled by SP-FDEs [5]. In biology and bio-engineering, it is frequently observed in modeling biological systems with memory effects, such as gene regulation, enzyme kinetics, or drug delivery [6].

Solving singularly perturbed functional differential equations poses several challenges due to the combined complexities of functional dependencies, delay effects, and small perturbation parameters. These problems often exhibit multi-scale behavior, where the solution varies at different rates in different regions of the domain. This can lead to sharp gradients, boundary or interior layers, and slow-fast dynamics. Capturing and resolving these variations accurately is a challenge. Obtaining analytical solutions for SP-FDEs is exceedingly difficult due to the combination of functional dependencies, delays, and perturbation parameters. Applying analytical techniques to general SP-FDEs are limited, and solving equations with specific forms or simplifying assumptions may be required. On the other hand due to the small parameter

ε

, standard numerical methods can struggle with stability and convergence issues. The presence of delays and singular perturbations requires carefully designed numerical schemes that can handle the specific characteristics of SP-FDEs. Addressing these difficulties often requires specialized knowledge of numerical analysis, stability theory, delay differential equations, and the characteristics of functional dependencies.

To overcome these challenges, various researchers have developed different numerical schemes using a combination of numerical methods, adaptive algorithms, and careful analysis of the problem’s behavior and solution properties. The choice of the most appropriate approach depends on the specific SP-FDE being solved and its unique characteristics. For instance, in [7], a singularly perturbed problems with shift is solved by formulating a fitted exponential spline method. The authors accomplished derivation of the method by including a fitted factor in the constructed numerical scheme which is based on a special type of grids, and the fitted factor is evaluated applying the theory of singular perturbation. Woldaregay [8] solved singularly perturbed differential equations with delays by developing three different schemes. The author used nonstandard mid-point upwind finite difference method on uniform grids, a standard mid-point upwind finite difference method on Shiskin’s meshes and a nonstandard mid-point upwind finite difference method on Shiskin’s meshes. Numerical analysis and results of the methods show that the third technique is more accurately convergent method.

In the work of [9] a non-polynomial cubic spline technique is devised to solve singularly perturbed delay problems having two layer regions and oscillatory characteristics in the solution. Lalu and Phaneendra [10] developed a difference scheme for nonlinear singularly perturbed differential equation using the trigonometric spline technique and obtained a uniformly convergent method. In [11], singularly perturbed differential equations involving mixed large delays of convection-diffusion type are solved by developing a fitted mesh numerical method. The authors used finite and hybrid difference schemes to treat the problem on piece-wise uniform Shishkin mesh. Elango and Unyong [12] solved singularly perturbed SP-FDEs involving mixed delays. They treated the problem by constructing fitted mesh scheme on Shishkin-type meshes and Bakhvalov-Shishkin type meshes. In the work of [13], a fitted operator scheme is constructed by decomposing the domain into inner and outer parts for singularly perturbed ordinary differential equations and obtained a second order convergent method. Wondimu et al. [14] treated singularly perturbed problems with delay and non-local boundary condition by developing an exponentially fitted finite difference scheme and obtained that the method is uniformly convergent.

Though various forms of perturbation problems have been treated in literature, very few attentions are given for singularly perturbed differential equations with mixed large shifts. In this paper, motivated by the fitted mesh methods developed in [11,12], we inspired to develop a fitted operator difference scheme for the reaction-diffusion type singularly perturbed ordinary differential equations with mixed large shifts. To tackle the influence of the shift arguments, we have chosen a special uniform mesh in which the shift arguments lie on the nodal points. On such meshes, a numerical scheme is proposed using the Numerov’s finite difference approach.The convergence analysis of the scheme shows that the method is parameter-robust numerical scheme.

The remaining sections of this work are arranged as follows: In Section 2, the continuous problem and some preliminary properties of the continuous solution are presented. The numerical formulation and analysis are presented in Section 3. Numerical examples are provided in Section 4 to confirm the theoretical findings in practice. In Section 5 some concluding remarks and future plans end the study in this paper.

Notation: In this work,

C

is taken as a generic number not depending on the mesh number and the perturbation parameter. The norm

∥ . ∥

is defined as

∥ . ∥ = {max}_{\bar{Φ}} | . |

for any function in

\bar{Φ}

2. Continuous Problem

Consider the singularly perturbed functional differential equation given by

\begin{matrix} L_{ε} ω (x) = & - ε \frac{d^{2} ω (x)}{d x^{2}} + μ (x) ω (x) + ν (x) ω (x - 1) + γ (x) ω (x + 1) = ψ (x), \end{matrix}

(1)

\begin{matrix} \{\begin{matrix} ω (x) = p (x), x \in [- 1, 0], \\ ω (x) = q (x), x \in [3, 4], \end{matrix} \end{matrix}

(2)

where

0 < ε ≪ 1

and

L_{ε}

is a differential operator. The coefficient functions

μ (x)

ν (x)

γ (x)

and the source function

ψ (x)

are assumed to be continuous on

[0, 3]

, and the history functions

p (x)

and

q (x)

are continuous on

[- 1, 0]

and

[3, 4]

, respectively. To avoid oscillations in the solution, we assumed that the coefficient functions satisfy

μ (x) + ν (x) + γ (x) \geq 2 α > 0, μ (x) > 0, ν (x) < 0 a n d γ (x) < 0, \forall x \in [0, 3] .

(3)

For simplicity, we used the notations

Φ^{-} = (0, 1)

Φ^{0} = (1, 2)

Φ^{+} = (2, 3)

Φ = (0, 3)

\bar{Φ} = [0, 3]

and

Φ^{*} = Φ^{-} \cup Φ^{0} \cup Φ^{+}

. Thus, the above assumptions hold that for

x \in \bar{Φ}

ω \in M = C^{0} (\bar{Φ}) \cap C^{1} (Φ) \cap C^{2} (Φ^{-} \cup Φ^{0} \cup Φ^{+})

Considering the interval conditions in (2), we rewrite (1) as

L_{ε} ω (x) = ℜ (x),

(4)

where

\begin{matrix} L_{ε} ω (x) = \{\begin{matrix} - ε \frac{d^{2} ω (x)}{d x^{2}} + μ (x) ω (x) + γ (x) ω (x + 1), x \in Φ^{-}, \\ - ε \frac{d^{2} ω (x)}{d x^{2}} + μ (x) ω (x) + ν (x) ω (x - 1) + γ (x) ω (x + 1), x \in Φ^{0}, \\ - ε \frac{d^{2} ω (x)}{d x^{2}} + μ (x) ω (x) + ν (x) ω (x - 1), x \in Φ^{+} \end{matrix} \\ and \\ ℜ (x) = \{\begin{matrix} ψ (x) - ν (x) p (x - 1), x \in Φ^{-}, \\ ψ (x), x \in Φ^{0}, \\ ψ (x) - ω (x) q (x + 1), x \in Φ^{+} \end{matrix} \end{matrix}

with the interval-boundary conditions given in (2).

Letting

ε = 0

yields the corresponding reduced form of (4) as

L_{ε} ω_{0} (x) = ℜ_{0} (x),

(5)

where

\begin{matrix} L_{ε} ω_{0} (x) = \{\begin{matrix} μ (x) ω_{0} (x) + γ (x) ω_{0} (x + 1), x \in Φ^{-}, \\ μ (x) ω_{0} (x) + ν (x) ω_{0} (x - 1) + γ (x) ω_{0} (x + 1), x \in Φ^{0}, \\ μ (x) ω_{0} (x) + ν (x) ω_{0} (x - 1), x \in Φ^{+} \end{matrix} \\ and \\ ℜ_{0} (x) = \{\begin{matrix} ψ (x) - ν (x) p_{0} (x - 1), x \in Φ^{-}, \\ ψ (x), x \in Φ^{0}, \\ ψ (x) - γ (x) q_{0} (x + 1), x \in Φ^{+} \end{matrix} \end{matrix}

In fact the reduced solution

ω_{0} (x)

of (5) need not satisfy

ω_{0} (0) = ω (0)

and

ω_{0} (3) = ω (3)

. As a result, the solution exhibits boundary layers at

x = 0

and

x = 3

. Moreover, at the points

x = 1

and

x = 2

, the reduced solution may not satisfy

ω (1^{-}) = ω (1^{+})

ω^{'} (1^{-}) = ω^{'} (1^{+})

ω (2^{-}) = ω (2^{+})

and

ω^{'} (2^{-}) = ω^{'} (2^{+})

, where

x^{-}

and

x^{+}

denote the left and right sides limiting value of x at 1 and 2, respectively. As a result, the solution involves strong interior layers at

x = 1

and

x = 2

[15].

Lemma 2.1

(Continuous maximum principle). Suppose

π (x) \in M

satisfying

π (x) \geq 0

for

x \in \partial Φ

and

L_{ε} π (x) \geq 0

for

x \in Φ

. Then

π (x) \geq 0

for

x \in \bar{Φ}

Proof.

Let

λ \in \bar{Φ}

and suppose that

π (λ) = {min}_{\bar{Φ}} π (x) < 0

. Then, from the given hypothesis, we observe that

λ \notin \partial Φ

, and by the extreme value theorem

π_{x} (λ) = 0

and

π_{x x} (λ) \geq 0

Case 1: On the interval

(0, 1]

, we have

\begin{matrix} L_{ε} π (λ) = & - ε \frac{d^{2} π (λ)}{d x^{2}} + μ (λ) π (λ) + γ (λ) π (λ + 1) \\ \leq & - ε \frac{d^{2} π (λ)}{d x^{2}} + μ (λ) π (λ) + γ (λ) π (λ), a s γ (λ) π (λ + 1) \leq γ (λ) π (λ) f o r γ (λ) < 0, \\ = & - ε \frac{d^{2} π (λ)}{d x^{2}} + [μ (λ) + γ (λ)] π (λ) \leq 0, a s μ (λ) + γ (λ) > 0 . \end{matrix}

Case 2: On the interval

(1, 2]

, we get

\begin{matrix} L_{ε} π (λ) = & - ε \frac{d^{2} π (λ)}{d x^{2}} + μ (λ) π (λ) + ν (λ) π (λ - 1) + γ (λ) π (λ + 1) \leq - ε \frac{d^{2} π (λ)}{d x^{2}} + μ (λ) π (λ) \\ + ν (λ) π (λ - 1) + γ (λ) π (λ), \\ = & - ε \frac{d^{2} π (λ)}{d x^{2}} + [μ (λ) + ν (λ) + γ (λ)] π (λ) + ν (λ) [π (λ - 1) - π (λ)] \\ \leq & 0, a s μ (λ) + ν (λ) + γ (λ) > 0 a n d π (λ - 1) - π (λ) \leq 0 . \end{matrix}

Case 3: On the interval

(2, 3)

, we get

\begin{matrix} L_{ε} π (λ) = & - ε \frac{d^{2} π (λ)}{d x^{2}} + μ (λ) π (λ) + ν (λ) π (λ - 1) \leq - ε \frac{d^{2} π (λ)}{d x^{2}} + μ (λ) π (λ) + ν (λ) π (λ - 1), \\ = & - ε \frac{d^{2} π (λ)}{d x^{2}} + [μ (λ) + ν (λ)] π (λ) + ν (λ) [π (λ - 1) - π (λ)] \\ \leq & 0, a s μ (λ) + ν (λ) > 0 a n d π (λ - 1) - π (λ) \leq 0 . \end{matrix}

All the above cases contradict to the hypothesis, which imply that our supposition is wrong. Thus,

π (x) \geq 0

for

x \in \bar{Φ}

. □

Lemma 2.2

(Continuous stability estimate). The continuous solution

ω (x)

of (1)-() is bounded as

| ω (x) | \leq \frac{∥ L_{ε} ω (x) ∥}{α} + max_{x \in \bar{Φ}} {| ω (0) |, | ω (3) |}

Proof.

Define barrier functions as

ϖ^{\pm} (x) = \frac{∥ L_{ε} ω (x) ∥}{α} + max_{x \in \bar{Φ}} {| ω (0) |, | ω (3) |} \pm ω (x) .

(6)

Then, we have the following results.

\begin{matrix} ϖ^{\pm} (0) = \frac{∥ L_{ε} ω (x) ∥}{α} + max_{x \in \bar{Φ}} {| ω (0) |, | ω (3) |} \pm ω (0) \geq 0 . \\ ϖ^{\pm} (3) = \frac{∥ L_{ε} ω (x) ∥}{α} + max_{x \in \bar{Φ}} {| ω (0) |, | ω (3) |} \pm ω (3) \geq 0 . \end{matrix}

For

x \in (0, 1]

, we have

\begin{matrix} L_{ε} ϖ^{\pm} (x) = & - ε \frac{d^{2} ϖ^{\pm} (x)}{d x^{2}} + μ (x) ϖ^{\pm} (x) + γ (x) ϖ^{\pm} (x + 1) \\ = & \pm ℜ (x) + [μ (x) + γ (x)] (\frac{∥ L_{ε} ω ∥}{α} + max_{x \in \bar{Φ}} {| ω (0) |, | ω (3) |}) \\ \geq & 2 α (\frac{∥ L_{ε} ω ∥}{α} + max_{x \in \bar{Φ}} {| ω (0) |, | ω (3) |}) \geq 0 . \end{matrix}

For

x \in (1, 2]

, we have

\begin{matrix} L_{ε} ϖ^{\pm} (x) = & - ε \frac{d^{2} ϖ^{\pm} (x)}{d x^{2}} + μ (x) ϖ^{\pm} (x) + ν (x) ϖ^{\pm} (x - 1) + γ (x) ϖ^{\pm} (x + 1) \\ = & \pm ℜ (x) + [μ (x) + ν (x) + γ (x)] (\frac{∥ L_{ε} ω ∥}{α} + max_{x \in \bar{Φ}} {| ω (0) |, | ω (3) |}) \\ \geq & 2 α (\frac{∥ L_{ε} ω ∥}{α} + max_{x \in \bar{Φ}} {| ω (0) |, | ω (3) |}) \geq 0 . \end{matrix}

For

x \in (2, 3]

, we have

\begin{matrix} L_{ε} ϖ^{\pm} (x) = & - ε \frac{d^{2} ϖ^{\pm} (x)}{d x^{2}} + μ (x) ϖ^{\pm} (x) + ν (x) ϖ^{\pm} (x - 1) + γ (x) ϖ^{\pm} (x + 1) \\ = & \pm ℜ (x) + [μ (x) + ν (x)] (\frac{∥ L_{ε} ω ∥}{α} + max_{x \in \bar{Φ}} {| ω (0) |, | ω (3) |}) \\ \geq & 2 α (\frac{∥ L_{ε} ω ∥}{α} + max_{x \in \bar{Φ}} {| ω (0) |, | ω (3) |}) \geq 0 . \end{matrix}

Applying Lemma 2.1, we obtain

ϖ^{\pm} (x) \geq 0

x \in \bar{Φ}

, which yields the required stability estimate. □

Lemma 2.3.

Assuming the conditions in (3) hold true, the

ℓ^{t h}

order derivative of the solution

ω (x), x \in \bar{Φ}

of (1)-(1) are bounded as

|\frac{d^{ℓ} ω (x)}{d x^{ℓ}}| \leq C (1 + ε^{- \frac{ℓ}{2}}), ℓ = 0, 1, 2, 3, 4 .

Proof.

For

ℓ = 0

, it immediately implies Lemma . For

ℓ = 1

, consider

x \in (0, 1]

and define a neighborhood

ℵ_{x} = (t, t + \sqrt{ε})

, so that

x \in ℵ_{x}

and

ℵ_{x} \subset [0, 1]

. For some

ς \in ℵ_{x}

, the mean value theorem yields

\begin{matrix} |\frac{d ω (ς)}{d x}| = |\frac{ω (t + \sqrt{ε}) - ω (t)}{(t + \sqrt{ε}) - t}| = ε^{- \frac{1}{2}} | ω (t + \sqrt{ε}) - ω (t) | \leq 2 ε^{- \frac{1}{2}} ∥ ω ∥ . \end{matrix}

(7)

For

x \in ℵ_{x}

and

s \in (ς, x)

, we can have

\begin{matrix} |\frac{d ω (x)}{d x}| = & |\frac{d ω (ς)}{d x} + \int_{ς}^{x} \frac{d^{2} ω (s)}{d x^{2}} d s| \\ = & |\frac{d ω (ς)}{d x} + ε^{- 1} \int_{ς}^{x} [μ (s) ω (s) + ν (s) p (s - 1) + γ (x) ω (s + 1) - ψ (s)] d s| \\ \leq & |\frac{d ω (ς)}{d x}| + ε^{- 1} [∥ μ ω ∥ + ∥ ν p ∥ + ∥ γ ω ∥ + ∥ ψ ∥] | \int_{ς}^{x} d s | \\ \leq & 2 ε^{- \frac{1}{2}} ∥ ω ∥ + ε^{- 1} [∥ μ ω ∥ + ∥ ν p ∥ + ∥ γ ω ∥ + ∥ ψ ∥] \sqrt{ε}, u s i n g () \\ \leq & C ε^{- \frac{1}{2}} \leq C (1 + ε^{- \frac{1}{2}}) . \end{matrix}

For

ℓ = 2

, rearrangement of (1) becomes

\frac{d^{2} ω (x)}{d x^{2}} = ε^{- 1} [μ (x) ω (x) + ν (x) p (x - 1) + γ (x) ω (x + 1) - ψ (x)],

(8)

from which we obtain

\begin{matrix} |\frac{d^{2} ω (x)}{d x^{2}}| \leq ε^{- 1} [∥ μ ω ∥ + ν p ∥ + γ ω ∥ + ∥ ψ ∥] \leq C ε^{- 1} \leq C (1 + ε^{- 1}) . \end{matrix}

For

ℓ = 3

, differentiating (8) once becomes

\frac{d^{3} ω (x)}{d x^{3}} = ε^{- 1} [{(μ ω)}^{'} (x) + {(ν (x) p (x - 1))}^{'} + {(γ (x) ω (x + 1))}^{'} - ψ^{'} (x)],

(9)

from which we obtain

|\frac{d^{3} ω (x)}{d x^{3}}| \leq ε^{- 1} [C + C ε^{- \frac{1}{2}}] \leq C ε^{- \frac{3}{2}} \leq C (1 + ε^{- \frac{3}{2}}) .

By similar procedure, for

ℓ = 4

, differentiating (9) yields

|\frac{d^{4} ω (x)}{d x^{4}}| \leq ε^{- 1} [C + C ε^{- \frac{1}{2}} + C ε^{- 1}] \leq C ε^{- 2} \leq C (1 + ε^{- 2}) .

Similar procedure hold true on the intervals

(1, 2)

and

(2, 3)

, and hence the continuous solution and its derivatives are bounded. □

3. Formulation of the Numerical Method

Let the interval

[0, 3]

be divided into

3 N

specially constructed sub-intervals, so that the terms containing the shift arguments coincide with the nodal points. Choosing h as an equal mesh size, we have

h = \frac{1}{ξ} = \frac{2}{η} = \frac{3}{3 N}

, where

ξ

and

η

are mesh numbers up to the nodal points

x_{i} = 1

and

x_{i} = 2

, respectively, and satisfying

ξ < η < 3 N

Now, rearranging the differential equation in (1) as

ε \frac{d^{2} ω (x)}{d x^{2}} = ℑ (x),

(10)

where

ℑ (x) = μ (x) ω (x) + ν (x) ω (x - 1) + γ (x) ω (x + 1) - ψ (x)

. At a mesh point

x_{i}

, we have

ε \frac{d^{2} ω (x_{i})}{d x^{2}} = ℑ (x_{i}),

(11)

where

ℑ (x_{i}) = μ (x_{i}) ω (x_{i}) + ν (x_{i}) ω (x_{i} - 1) + γ (x_{i}) ω (x_{i} + 1) - ψ (x_{i})

Applying the Nomerov’s finite difference approach [16] on to equation (11), we get

\frac{ε}{h^{2}} (ω_{i + 1} - 2 ω_{i} + ω_{i - 1}) = \frac{1}{12} (ℑ_{i + 1} + 10 ℑ_{i} + ℑ_{i - 1})

(12)

To handle the effect of

ε

in the layers, we introduce the fitting factor

σ

in (12) as

\frac{ε σ}{h^{2}} (ω_{i + 1} - 2 ω_{i} + ω_{i - 1}) = \frac{1}{12} (ℑ_{i + 1} + 10 ℑ_{i} + ℑ_{i - 1}),

which is expressed as

\begin{matrix} \frac{σ}{ρ^{2}} (ω_{i + 1} - 2 ω_{i} + ω_{i - 1}) = & \frac{1}{12} [μ_{i + 1} ω_{i + 1} + 10 μ_{i} ω_{i} + γ_{i - 1} ω_{i - 1} + ν_{i + 1} ω_{i + 1 - N} \\ + & 10 ν_{i} ω_{i - N} + ν_{i - 1} ω_{i - 1 - N}] + γ_{i + 1} ω_{i + 1 + N} + 10 γ_{i} ω_{i + N} + γ_{i - 1} ω_{i - 1 + N} \\ - \frac{1}{12} [ψ_{i + 1} + 10 ψ_{i} + ψ_{i - 1}], i = 0, 1, . . ., 3 N . \end{matrix}

(13)

Assuming uniform convergence of the solution and taking

h \to 0

, we obtain

σ = \frac{ρ^{2} μ (0) (2 cosh (\sqrt{μ (0)} ρ) + 10)}{48 {sinh}^{2} (\sqrt{μ (j)} ρ / 2)},

(14)

which is a fitting factor in the left layers for

j = 0

and in the right layers for

j = 3

. Using the fitting factor (14), we get

L_{ε}^{3 N} ω_{i} = ε σ D^{+} D^{-} ω_{i} = \frac{1}{12} [ℑ_{i + 1} + 10 ℑ_{i} + ℑ_{i - 1}],

which can be re-expressed as

\begin{matrix} (\frac{σ}{ρ^{2}} - \frac{μ_{i + 1}}{12}) ω_{i + 1} - (\frac{2 σ}{ρ^{2}} + \frac{10 μ_{i}}{12}) ω_{i} + (\frac{σ}{ρ^{2}} - \frac{μ_{i - 1}}{12}) ω_{i - 1} = \frac{1}{12} [ν_{i + 1} ω_{i + 1 - N} + 10 ν_{i} ω_{i - N} \\ + ν_{i - 1} ω_{i - 1 - N} + γ_{i + 1} ω_{i + 1 + N} + 10 γ_{i} ω_{i + N} + γ_{i - 1} ω_{i - 1 + N} - (ψ_{i + 1} + 10 ψ_{i} + ψ_{i - 1})], ρ = \frac{h}{\sqrt{ε}} . \end{matrix}

(15)

To accomplish the required discrete scheme, first we set

ε = 0

and determine the reduced problem as

μ (x_{i}) ω_{0} (x_{i}) + ν (x_{i}) ω_{0} (x_{i} - 1) + γ (x_{i}) ω_{0} (x_{i} + 1) = ψ (x_{i}) .

(16)

From the reduced scheme (16), compute the approximate values of

ω (x_{i} = 1)

and

ω (x_{i} = 2)

. Then for

i = 1, 2, \dots, N - 1

, the scheme in (15) is simplified to

℘^{+} ω_{i + 1} + ℘^{o} ω_{i} + ℘^{-} ω_{i - 1} = Ξ_{i + 1}^{-},

(17)

with the boundary conditions

ω_{0} = p (0)

and

ω_{N} = ω_{0} (1)

, where

\begin{matrix} ℘^{+} = & \frac{σ}{ρ^{2}} - \frac{μ_{i + 1}}{12}, ℘^{o} = - \frac{2 σ}{ρ^{2}} - \frac{10 μ_{i}}{12}, ℘^{-} = \frac{σ}{ρ^{2}} - \frac{μ_{i - 1}}{12} \\ Ξ_{i + 1}^{-} = & \frac{1}{12} [ν_{i + 1} p_{i + 1 - N} + 10 ν_{i} p_{i - N} + ν_{i - 1} p_{i - 1 - N} + γ_{i + 1} ω_{i + 1 + N} + 10 γ_{i} ω_{i + N} \\ + γ_{i - 1} ω_{i - 1 + N} - (ψ_{i + 1} + 10 ψ_{i} + ψ_{i - 1})], \end{matrix}

Similarly, for

i = N + 1, N + 2, \dots, 2 N - 1

, the scheme in (15) becomes

℘^{+} ω_{i + 1} + ℘^{o} ω_{i} + ℘^{-} ω_{i - 1} = Ξ_{i + 1}^{o},

(18)

with the boundary conditions

ω_{N} = ω_{0} (1)

and

ω_{2 N} = ω_{0} (2)

, where

\begin{matrix} Ξ_{i + 1}^{o} = & \frac{1}{12} [ν_{i + 1} ω_{i + 1 - N} + 10 ν_{i} ω_{i - N} + ν_{i - 1} ω_{i - 1 - N} + γ_{i + 1} ω_{i + 1 + N} + 10 γ_{i} ω_{i + N} + γ_{i - 1} ω_{i - 1 + N} \\ - (ψ_{i + 1} + 10 ψ_{i} + ψ_{i - 1})], \end{matrix}

and for

i = 2 N + 1, 2 N + 2, . . ., 3 N - 1

, the scheme in (15) becomes

℘^{+} ω_{i + 1} + ℘^{o} ω_{i} + ℘^{-} ω_{i - 1} = Ξ_{i + 1}^{+},

(19)

with the boundary conditions

ω_{2 N} = ω_{0} (2)

and

ω_{3 N} = q (x_{3 N})

, where

\begin{matrix} Ξ_{i + 1}^{+} = & \frac{1}{12} [ν_{i + 1} ω_{i + 1 - N} + 10 ν_{i} ω_{i - N} + ν_{i - 1} ω_{i - 1 - N} + γ_{i + 1} q_{i + 1 + N} + 10 γ_{i} q_{i + N} + γ_{i - 1} q_{i - 1 + N} \\ - (ψ_{i + 1} + 10 ψ_{i} + ψ_{i - 1})] . \end{matrix}

Thus, we solve the systems obtained in (17)-(19) on a uniform meshes using suitable solver of system of equations following the computational algorithm given below.

Algorithm 1:Computing the numerical solution

ω_{i + 1}, i = 0, 1, \dots, 3 N - 1

1.3

1:: On $[0, 3]$ , set a uniform mesh $x_{i} = i h$ , $i = 0, 1, 2, \dots, 3 N$ with $x_{0} = 0$ , $x_{N} = 1$ , $x_{2 N} = 2$ and $x_{3 N} = 3$ .
2:: Set $ε = 0$ and approximate $ω_{i + 1}$ from (16) at $x_{i} = 1$ and $x_{i} = 2$ .
3:: For $i = 1, 2, \dots, 3 N - 1$ ,
4:: if $i = 1, 2, \dots, N - 1$ , compute $ω_{i + 1}$ from the system (18)
5:: else if $i = N + 1, N + 2, \dots, 2 N - 1$ , compute for $ω_{i + 1}$ from the system (17)
6:: else compute for $ω_{i + 1}$ from the system (19).
7:: Simulate the solution $ω_{i + 1}$ for all i graphically.
8:: Stop

3.1. Uniform Stability and Convergence Analysis

Lemma 3.1

(Discrete maximum principle). Suppose the mesh function

ϑ_{i}

be in

L_{ε}^{3 N} (\bar{Φ})

satisfying

ϑ_{0} \geq 0

ϑ_{3 N} \geq 0

and

L_{ε}^{3 N} ϑ_{i} \geq 0

i = 1, 2, \dots, 3 N - 1

. Then,

ϑ_{i} \geq 0

i = 0, 1, \dots, 3 N

Proof.

Let

ξ \in {0, 1, \dots, 3 N}

be given such that

ϑ_{ξ} = {min}_{0 \leq i \leq 3 N} ϑ_{i} < 0

. From the given hypothesis, it is clear that

ξ \notin {0, 3 N}

. Then, we have

ϑ_{ξ} - ξ_{ξ - 1} \leq 0

and

ϑ_{ξ + 1} - ξ_{ξ} \geq 0

Case 1: For

i = 1, \dots, N

, we get

\begin{matrix} L_{ε}^{3 N} ϑ_{ξ} = & - ε σ D^{+} D^{-} ϑ_{ξ} + \frac{1}{12} [μ_{ξ + 1} ϑ_{ξ + 1} + 10 μ_{ξ} ϑ_{ξ} + μ_{ξ - 1} ϑ_{ξ - 1} + γ_{ξ + 1} ϑ_{ξ + 1 + N} \\ + 10 γ_{ξ} ϑ_{ξ} + γ_{ξ - 1} ϑ_{ξ - 1 + N}] \\ = & - \frac{ε σ}{h^{2}} [(ϑ_{ξ + 1} - ϑ_{ξ}) - (ϑ_{ξ} - ϑ_{ξ - 1})] + \frac{1}{12} [μ_{ξ + 1} ϑ_{ξ + 1} \\ + 10 μ_{ξ} ϑ_{ξ} + μ_{ξ - 1} ϑ_{ξ - 1} + γ_{ξ + 1} ϑ_{ξ + 1 + N} + 10 γ_{ξ} ϑ_{ξ} + γ_{ξ - 1} ϑ_{ξ - 1 + N}] \\ \leq & - \frac{ε σ}{h^{2}} [(ϑ_{ξ + 1} - ϑ_{ξ}) - (ϑ_{ξ} - ϑ_{ξ - 1})] + \frac{1}{12} [(μ_{ξ + 1} + γ_{ξ + 1}) ϑ_{ξ + 1} + 10 (μ_{ξ} + γ_{ξ}) ϑ_{ξ} \\ + (μ_{ξ - 1} + γ_{ξ - 1}) ϑ_{ξ - 1}] \leq 0 . \end{matrix}

Case 2: For

i = N + 1, . . ., 2 N

, we get

\begin{matrix} L_{ε}^{3 N} ϑ_{ξ} = & - ε σ D^{+} D^{-} ϑ_{ξ} + \frac{1}{12} [μ_{ξ + 1} ϑ_{ξ + 1} + 10 μ_{ξ} ϑ_{ξ} + μ_{ξ - 1} ϑ_{ξ - 1} + ν_{ξ + 1} ϑ_{ξ + 1 - N} + 10 ν_{ξ} ϑ_{ξ - N} \\ + ν_{ξ - 1} ϑ_{ξ - 1 - N} + γ_{ξ + 1} ϑ_{ξ + 1 + N} + 10 γ_{ξ} ϑ_{ξ} + γ_{ξ - 1} ϑ_{ξ - 1 + N}] \\ = & - \frac{ε σ}{h^{2}} [(ϑ_{ξ + 1} - ϑ_{ξ}) - (ϑ_{ξ} - ϑ_{ξ - 1})] + \frac{1}{12} [μ_{ξ + 1} ϑ_{ξ + 1} + 10 μ_{ξ} ϑ_{ξ} + μ_{ξ - 1} ϑ_{ξ - 1} \\ + ν_{ξ + 1} ϑ_{ξ + 1 - N} + ν_{ξ} ϑ_{ξ - N} + ν_{ξ - 1} ϑ_{ξ - 1 - N} + γ_{ξ + 1} ϑ_{ξ + 1 + N} + 10 γ_{ξ} ϑ_{ξ} + γ_{ξ - 1} ϑ_{ξ - 1 + N}] \\ \leq & - \frac{ε σ}{h^{2}} [(ϑ_{ξ + 1} - ϑ_{ξ}) - (ϑ_{ξ} - ϑ_{ξ - 1})] + \frac{1}{12} [(μ_{ξ + 1} + ν_{ξ + 1} + γ_{ξ + 1}) ϑ_{ξ + 1} \\ + 10 (μ_{ξ} + ν_{ξ} + γ_{ξ}) ϑ_{ξ} + (μ_{ξ - 1} + ν_{ξ - 1} + γ_{ξ - 1}) ϑ_{ξ - 1}] \leq 0 . \end{matrix}

Case 3: For

i = 2 N + 1, \dots, 3 N - 1

, we get

\begin{matrix} L_{ε}^{3 N} ϑ_{ξ} = & - ε σ D^{+} D^{-} ϑ_{ξ} + \frac{1}{12} [μ_{ξ + 1} ϑ_{ξ + 1} + 10 μ_{ξ} ϑ_{ξ} + μ_{ξ - 1} ϑ_{ξ - 1} + ν_{ξ + 1} ϑ_{ξ + 1 - N} \\ + 10 ν_{ξ} ϑ_{ξ - N} + ν_{ξ - 1} ϑ_{ξ - 1 - N}] \\ = & - \frac{ε σ}{h^{2}} [(ϑ_{ξ + 1} - ϑ_{ξ}) - (ϑ_{ξ} - ϑ_{ξ - 1})] + \frac{1}{12} [μ_{ξ + 1} ϑ_{ξ + 1} + 10 μ_{ξ} ϑ_{ξ} + μ_{ξ - 1} ϑ_{ξ - 1}] \\ + ν_{ξ + 1} ϑ_{ξ + 1 - N} + ν_{ξ} ϑ_{ξ - N} + ν_{ξ - 1} ϑ_{ξ - 1 - N}] \\ \leq & - \frac{ε σ}{h^{2}} [(ϑ_{ξ + 1} - ϑ_{ξ}) - (ϑ_{ξ} - ϑ_{ξ - 1})] + \frac{1}{12} [(μ_{ξ + 1} + ν_{ξ + 1}) ϑ_{ξ + 1} \\ + 10 (μ_{ξ} + ν_{ξ}) ϑ_{ξ} + (μ_{ξ - 1} + ν_{ξ - 1}) ϑ_{ξ - 1}] \leq 0 . \end{matrix}

The above three cases contradict to the hypothesis. Thus, the supposition fails, so that

ϑ_{ξ} \geq 0

ξ = 1, 2, \dots, 3 N - 1

. Thus,

ϑ_{i} \geq 0

ξ = 0, 1, \dots, 3 N

. □

Lemma 3.2.

Under the assumptions in (3), the discrete solution

ω_{i}, i = 0, 1, \dots, 3 N

of (15) is estimated as

| ω_{i} | \leq \frac{∥ L_{ε}^{3 N} ω_{i} ∥}{α} + max_{i \in [0, 3 N]} {| ω_{0} |, | ω_{3 N} |}

Proof.

Introduce two barrier functions as

ϖ_{i}^{\pm} = \frac{∥ L_{ε}^{3 N} ω_{i} ∥}{α} + max_{i \in [0, 3 N]} {| ω_{0} |, | ω_{3 N} |} \pm ω_{i}, i = 0, 1, \dots, 3 N .

Then, we obtain the following results.

For

i = 0

ϖ_{0}^{\pm} = \frac{∥ L_{ε}^{3 N} ω_{0} ∥}{α} + {max}_{i \in [0, 3 N]} {| ω_{0} |, | ω_{3 N} |} \pm ω_{0} \geq 0

For

i = 3 N

ϖ_{3 N}^{\pm} = \frac{∥ L_{ε}^{3 N} ω_{3 N} ∥}{α} + {max}_{i \in [0, 3 N]} {| ω_{3 N} |, | ω_{3 N} |} \pm ω_{3 N} \geq 0

For

i = 1, 2, \dots, N

, we have

\begin{matrix} L_{ε}^{3 N} ϖ_{i}^{\pm} = & - ε σ D^{+} D^{-} ϖ_{i}^{\pm} + \frac{1}{12} [μ_{i + 1} ϖ_{i + 1}^{\pm} + 10 μ_{i} ϖ_{i}^{\pm} + μ_{i - 1} ϖ_{i - 1}^{\pm} + γ_{i + 1} ϖ_{i + 1 + N}^{\pm} \\ + 10 γ_{i} ϖ_{i}^{\pm} + γ_{i - 1} ϖ_{i - 1 + N}^{\pm}] \\ = & \pm L_{ε}^{3 N} ω_{i} + \frac{1}{12} (μ_{i + 1} \frac{∥ L_{ε}^{3 N} ω_{i + 1} ∥}{α} + μ_{i + 1} max_{i \in [0, 3 N]} {| ω_{0} |, | ω_{3 N} |}) \\ + \frac{1}{12} (μ_{i} \frac{∥ L_{ε}^{3 N} ω_{i} ∥}{α} + μ_{i} max_{i \in [0, 3 N]} {| ω_{0} |, | ω_{3 N} |}) \\ + \frac{1}{12} (μ_{i - 1} \frac{∥ L_{ε}^{3 N} ω_{i - 1} ∥}{α} + μ_{i - 1} max_{i \in [0, 3 N]} {| ω_{0} |, | ω_{3 N} |}) \\ + \frac{1}{12} (γ_{i + 1} \frac{∥ L_{ε}^{3 N} ω_{i + 1} ∥}{α} + γ_{i + 1} max_{i \in [0, 3 N]} {| ω_{0} |, | ω_{3 N} |}) \\ + \frac{1}{12} (γ_{i} \frac{∥ L_{ε}^{3 N} ω_{i} ∥}{α} + γ_{i} max_{i \in [0, 3 N]} {| ω_{0} |, | ω_{3 N} |}) \\ + \frac{1}{12} (γ_{i - 1} \frac{∥ L_{ε}^{3 N} ω_{i - 1} ∥}{α} + γ_{i - 1} max_{i \in [0, 3 N]} {| ω_{0} |, | ω_{3 N} |}), \end{matrix}

which implies that

\begin{matrix} L_{ε}^{3 N} ϖ_{i}^{\pm} \geq & \frac{1}{12} (α \frac{∥ L_{ε}^{3 N} ω_{i + 1} ∥}{α} + α max_{i \in [0, 3 N]} {| ω_{0} |, | ω_{3 N} |}) \\ + \frac{1}{12} (α \frac{∥ L_{ε}^{3 N} ω_{i} ∥}{α} + α max_{i \in [0, 3 N]} {| ω_{0} |, | ω_{3 N} |}) \\ + \frac{1}{12} (α \frac{∥ L_{ε}^{3 N} ω_{i - 1} ∥}{α} + α max_{i \in [0, 3 N]} {| ω_{0} |, | ω_{3 N} |}), a s μ_{i} + γ_{i} \geq α \\ \geq & \frac{α}{12} max_{i \in [0, 3 N]} {| ω_{0} |, | ω_{3 N} |} \geq 0 . \end{matrix}

Applying Lemma 3.1, the result implies that

ϖ \geq 0, i = 1, 2, \dots, N - 1

, and consequently it yields the required estimate. Similar procedures hold for

i = N + 1, N + 2, \dots, 2 N - 1

and

i = 2 N + 1, 2 N + 2, \dots, 3 N - 1

. □

Theorem 3.1.

Let

ω (x_{i})

and

ω_{i}

be the solution of the prtoblem (1) and the scheme (15), respectively. Then, the truncation error is estimated as

| ω (x_{i}) - ω_{i} | \leq C N^{- 2}, i = 0, 1, \dots, 3 N,

with

C

independent of i, h and ε.

Proof.

From the definitions of truncation error [17], we have

\begin{matrix} | L_{ε}^{3 N} (ω (x_{i}) - ω_{i}) | = | L_{ε} ω (x_{i}) - L_{ε}^{3 N} ω_{i} | = |- ε \frac{d^{2} ω (x_{i})}{d x^{2}} + ε σ D^{+} D^{-} ω_{i}| . \end{matrix}

(20)

Applying Taylor’s series expansion on

ω_{i \pm 1}

, we obtain

\begin{matrix} ω_{i + 1} = ω_{i} + h \frac{d ω (x_{i})}{d x} + \frac{h^{2}}{2!} \frac{d^{2} ω (x_{i})}{d x^{2}} + \frac{h^{3}}{3!} \frac{d^{3} ω (x_{i})}{d x^{3}} + \frac{h^{4}}{4!} \frac{d^{4} ω (x_{i})}{d x^{4}} + O (h^{5}), \\ ω_{i - 1} = ω_{i} - h \frac{d ω (x_{i})}{d x} + \frac{h^{2}}{2!} \frac{d^{2} ω (x_{i})}{d x^{2}} - \frac{h^{3}}{3!} \frac{d^{3} ω (x_{i})}{d x^{3}} + \frac{h^{4}}{4!} \frac{d^{4} ω (x_{i})}{d x^{4}} + O (h^{5}) . \end{matrix}

Plugging the above expansion into (20) and simplifying gives

\begin{matrix} | L_{ε}^{3 N} (ω (x_{i}) - ω_{i}) | \leq & C | ε σ - ε | ∥\frac{d^{2} ω (t_{i})}{d x^{2}}∥ + C ε σ h^{2} ∥\frac{d^{4} ω (t_{i})}{d x^{4}}∥, t_{i} \in [x_{i - 1}, x_{i + 1}] . \end{matrix}

As it is estimated in [18], we have

| ε σ - ε | \leq C h^{2}

. Applying Taylor’s series expansion on

σ

and using Lemma 2.3, we have

| L_{ε}^{3 N} (ω (x_{i}) - ω_{i}) | \leq C h^{2} = C N^{- 2}, a s h = \frac{1}{N} .

Thus, by the discrete maximum principle, we get

| ω (x_{i}) - ω_{i} | \leq C N^{- 2}, i = 0, 1, \dots, 3 N

. □

4. Numerical Examples and Discusions

In this section, the developed finite difference scheme is validated by carrying out numerical experiments. The effect of the perturbation parameter and the mixed shift arguments on the solution is determined by computing the point wise maximum absolute errors (MAEs) and convergence rates (CRs). Since computation of the exact solution is difficult, to compute MAEs and CRs we used the double mesh principle [18] as given in Algorithm 2 below.

Algorithm 2:Computations of MAEs and corresponding CRs

1.3

1:: From (16)–(19), compute $ω_{i + 1}^{h}$ and $ω_{i + 1}^{\frac{h}{2}}$ at each mesh point.
2:: For $i = 0, 1, \dots, 3 N$ , compute
3:: $e_{ε}^{h} = max | ω_{i + 1}^{h} - ω_{i + 1}^{\frac{h}{2}} |$ , ▹ Point-wise absolute error
4:: $e^{h} = max (e_{ε}^{h})$ , ▹ Uniform absolute error
5:: $r_{ε}^{h} = {log}_{2} (e_{ε}^{h} / e_{ε}^{\frac{h}{2}})$ , ▹ Point-wise convergence rate
6:: $r^{h} = {log}_{2} (e^{h} / e^{\frac{h}{2}})$ , ▹ Uniform convergence rate.
7:: Sketch log-log plots of MAE versus N.

Example 4.1.

[12] Consider the the SP-FDE given as

\begin{matrix} - ε \frac{d^{2} ω (x)}{d x^{2}} + 5 ω (x) - ω (x - 1) - ω (x + 1) = 1, x \in M \\ \{\begin{matrix} ω (x) = 1, x \in [- 1, 0], \\ ω (x) = 1, x \in [3, 4] . \end{matrix} \end{matrix}

Example 4.2.

[12] Consider the the SP-FDE given as

\begin{matrix} - ε \frac{d^{2} ω (x)}{d x^{2}} + (5 + x^{2}) ω (x) - ω (x - 1) - ω (x + 1) = x, x \in M \\ \{\begin{matrix} ω (x) = 1, x \in [- 1, 0], \\ ω (x) = 1, x \in [3, 4] . \end{matrix} \end{matrix}

The examples are treated applying the formulated numerical method. The error analyses of the solutions are also performed by computing MAEs and CRs by using the double mesh principle as given in Algorithm 2 and the obtained results are displayed in Table 1 and Table 2. From Table 1, one can see that increasing the mesh numbers reduces the error and reducing

ε

gives a rapidly decreasing MAEs for each mesh number. The maximum errors are shown when

ε = 2^{- 1}

with the corresponding second order convergence rates. From Table 2, we observe that if the mesh number is increased, the MAE is decreasing and decreasing

ε

yields stable maximum absolute errors and corresponding second order convergence rates. The accuracy of the present method is compared with previous published work for both examples as given in Table 3 and Table 4. From these tables, it is shown that the present fitted operator difference scheme is second order convergent method and the fitted mesh method developed in [12] is almost first order convergent method.

The numerical solutions of example 4.1 and 4.2 are shown in Figure 1 and Figure 2, respectively, for different values of

ε

. From the figures, it is shown that decreasing the perturbation parameter reduces the width of the layers with more steep gradients. In Figure 3, log-log plots are given, which show that increasing the number of meshes decreases the MAEs for different value of

ε

5. Conclusion and Future Plans

In the present research work, we have developed a parameter-robust numerical for computing SP-FDEs with mixed large shifts. Such equations are a class of differential equations that incorporate shift effects and small perturbation parameters. The presence of the perturbation parameter and large mixed shifts adds complexity to the problem to be solved analytically, and applying standard numerical methods. The proposed numerical scheme tackles the challenges posed by the perturbation parameter and shift arguments yielding accurate approximate solution. We have demonstrated the effectiveness and robustness of the scheme by two numerical experiments, showing that it consistently produces accurate results across a wide range of parameter values. While this research work has provided an efficient and accurate numerical method for the considered singularly perturbed ordinary differential equations with mixed large shifts, there are several avenues for future exploration and enhancement. In the near future, the method is extended to singularly perturbed functional partial differential equations in one and two dimensions.

Funding

This research received no external funding.

Informed Consent Statement

Not applicable.

Data Availability Statement

There is no collected data used in this research work.

Acknowledgments

The author kindly acknowledge the editor receiving and handling the manuscript, and referees for their insightful review of the initial version of the paper.

Conflicts of Interest

The author declares no conflict of interest.

References

Hale, J.K.; Lunel, S.M. Introduction to Functional Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
Barbu, L.; Morosanu, G. Singularly Perturbed Boundary-Value Problems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
Naidu, D. Singular perturbations and time scales in control theory and applications: an overview. Dynam. Cont. Disc. Impul. Syst. Ser. B 2008, 9, 233–278. [Google Scholar]
Eva, S.; and Ovide, A.; Pierre, A.; de la Parra, R. A singular perturbation in an age-structured population model. Siam J. Appl. Math. 2000, 60, 408–436. [Google Scholar]
Ducrot, A.; Magal, P.; Seydi, O. A singularly perturbed Delay Differential Equation modeling nosocomial infections. Differ. Integ. Equ. 2016, 29, 21–35. [Google Scholar] [CrossRef]
Nagarajan, S.; Miller, J.; Sigamani, V. Robust numerical solutions of two singularly perturbed problems in mathematical biology. Biomath Commun. 2014, 1. [Google Scholar] [CrossRef]
Prasad, E.S.; Omkar, R.; Phaneendra, K. Fitted Parameter Exponential Spline Method for Singularly Perturbed Delay Differential Equations with a Large Delay. Comput. Math. Methods 2022, 2022. [Google Scholar] [CrossRef]
Woldaregay, M.M. Solving singularly perturbed delay differential equations via fitted mesh and exact difference method. Res. Math. 2022, 9, 2109301. [Google Scholar] [CrossRef]
Tirfesa, B.; Duressa, G.; Debela, H.G. Non-Polynomial Cubic Spline Method for Solving Singularly Perturbed Delay Reaction-Diffusion Equations. Thai J. Math. 2022, 20, 679–692. [Google Scholar]
Lalu, M.; Phaneendra, K. A numerical approach for singularly perturbed nonlinear delay differential equations using a trigonometric spline. Comput. Math. Methods 2022, 2022. [Google Scholar] [CrossRef]
Hammachukiattikul, P.; Sekar, E.; Tamilselvan, A.; Vadivel, R.; Gunasekaran, N.; Agarwal, P. Comparative study on numerical methods for singularly perturbed advanced-delay differential equations. J. Math. 2021, 2021, 1–15. [Google Scholar] [CrossRef]
Elango, S.; Unyong, B. Numerical Scheme for Singularly Perturbed Mixed Delay Differential Equation on Shishkin Type Meshes. Fractal Fract. 2022, 7, 43. [Google Scholar] [CrossRef]
Ejere, A.H.; Duressa, G.F.; Woldaregay, M.; Dinka, T. An exponentially fitted numerical scheme via domain decomposition for solving singularly perturbed differential equations with large negative shift. J. Math. 2022, 2022, 1–13. [Google Scholar] [CrossRef]
Wondimu, G.M.; Woldaregay, M.M.; Duressa, G.F.; Dinka, T.G. Exponentially fitted numerical method for solving singularly perturbed delay reaction-diffusion problem with nonlocal boundary condition. BMC Res. Notes 2023, 16, 1–10. [Google Scholar] [CrossRef] [PubMed]
Lange, C.G.; Miura, R.M. Singular perturbation analysis of boundary value problems for differential-difference equations. Siam J. Appl. Math. 1982, 42, 502–531. [Google Scholar] [CrossRef]
Chakravarthy, P.; Rao, R. A modified Numerov method for solving singularly perturbed differential–difference equations arising in science and engineering. Results Phys. 2012, 2, 100–103. [Google Scholar] [CrossRef]
Kadalbajoo, M.K.; Sharma, K.K. A numerical method based on finite difference for boundary value problems for singularly perturbed delay differential equations. Appl. Math. Comput. 2008, 197, 692–707. [Google Scholar] [CrossRef]
Doolan, E.P.; Miller, J.H.; Schilders, W.A. Uniform Numerical Methods for Problems with Initial and Boundary Layers; Boole Press: Dublin, Ireland, 1980. [Google Scholar]

Figure 1. Simulations of the numerical solution of Example 4.1 taking various value of

ε

Figure 1. Simulations of the numerical solution of Example 4.1 taking various value of

ε

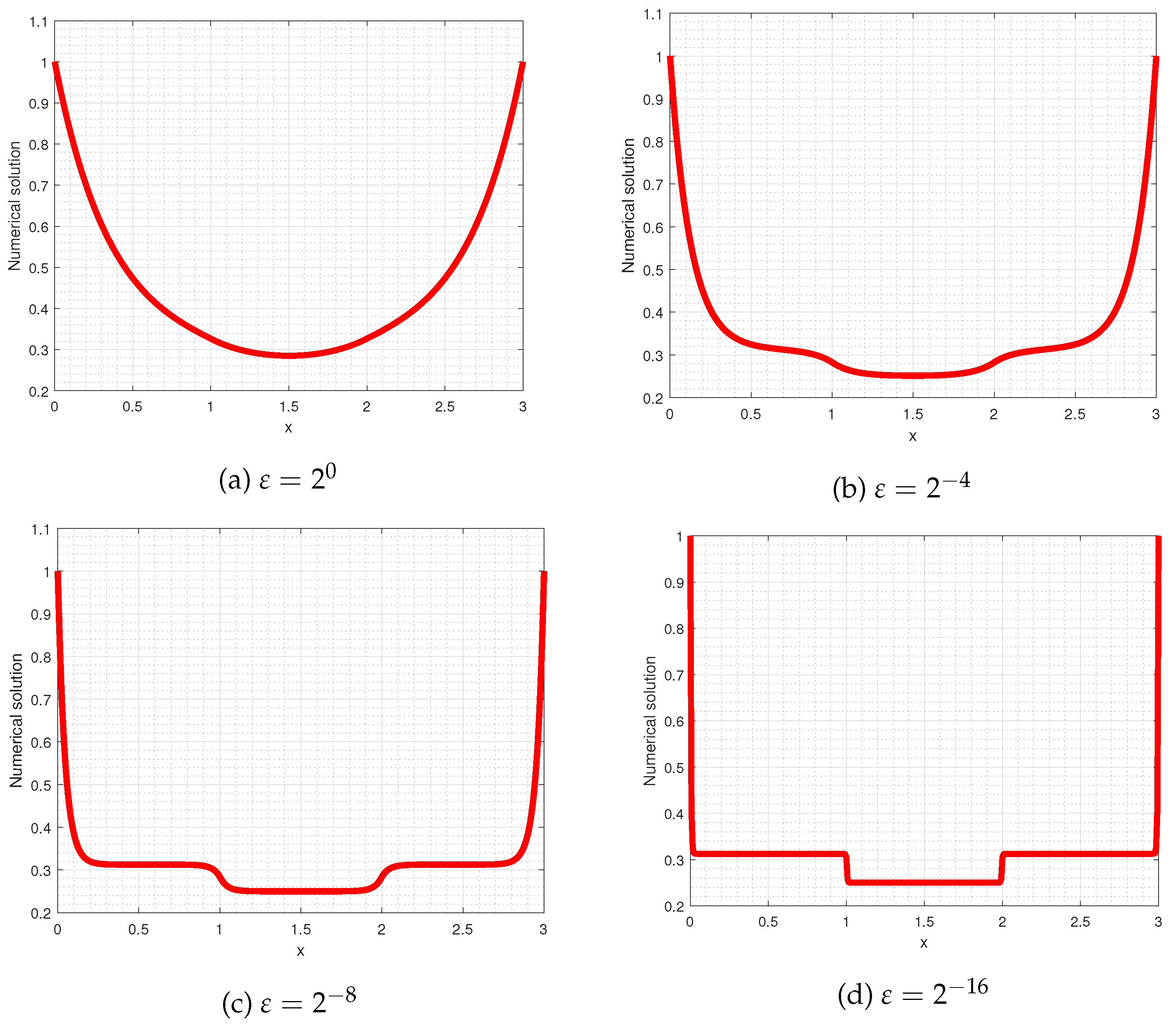
Figure 2. Simulations of the numerical solution of Example 4.2 taking various value of

ε

Figure 2. Simulations of the numerical solution of Example 4.2 taking various value of

ε

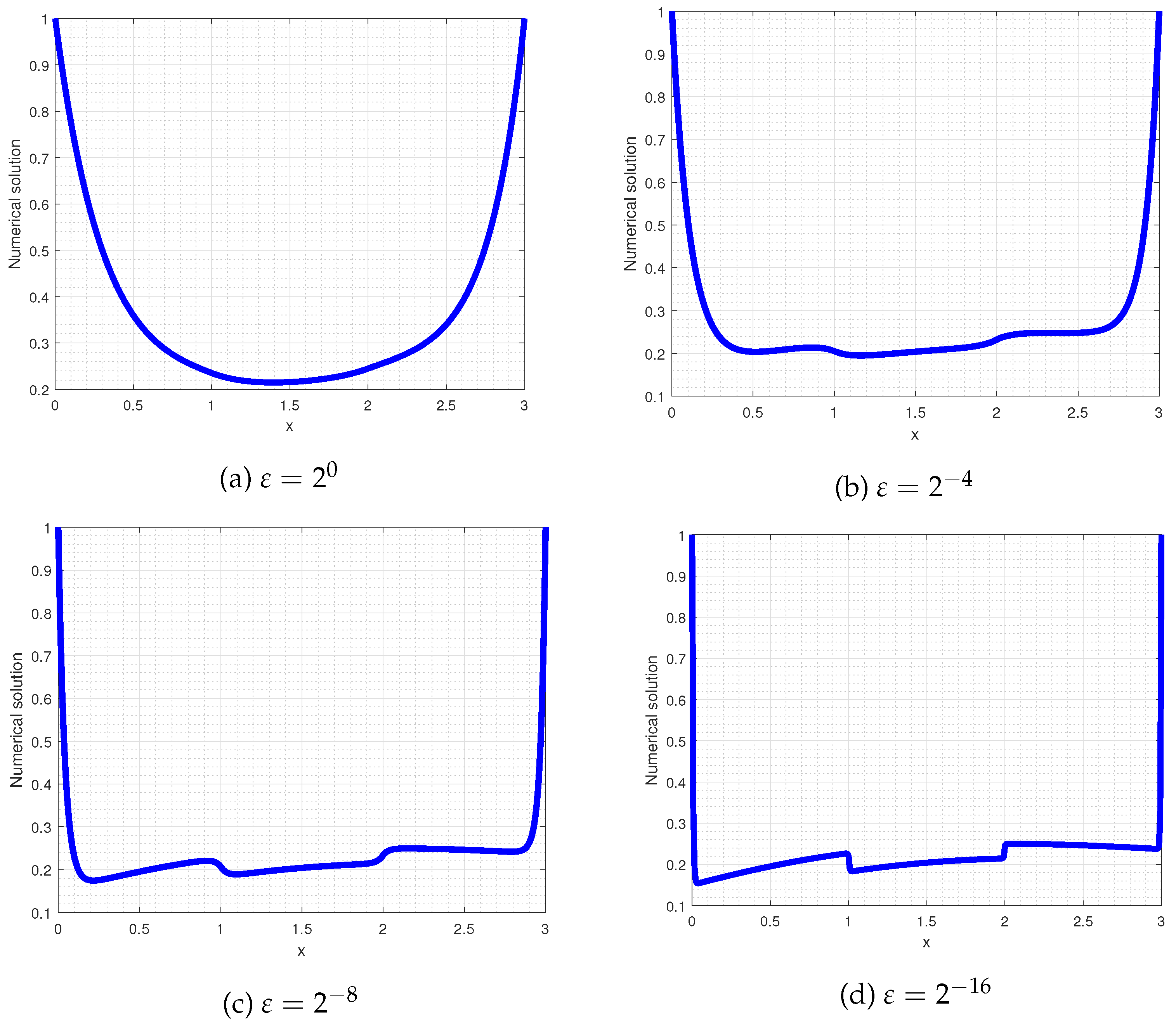
Figure 3. The logarithmic scale simulations of MAEs versus N for (a) Example 4.1 and (b) Example 4.2

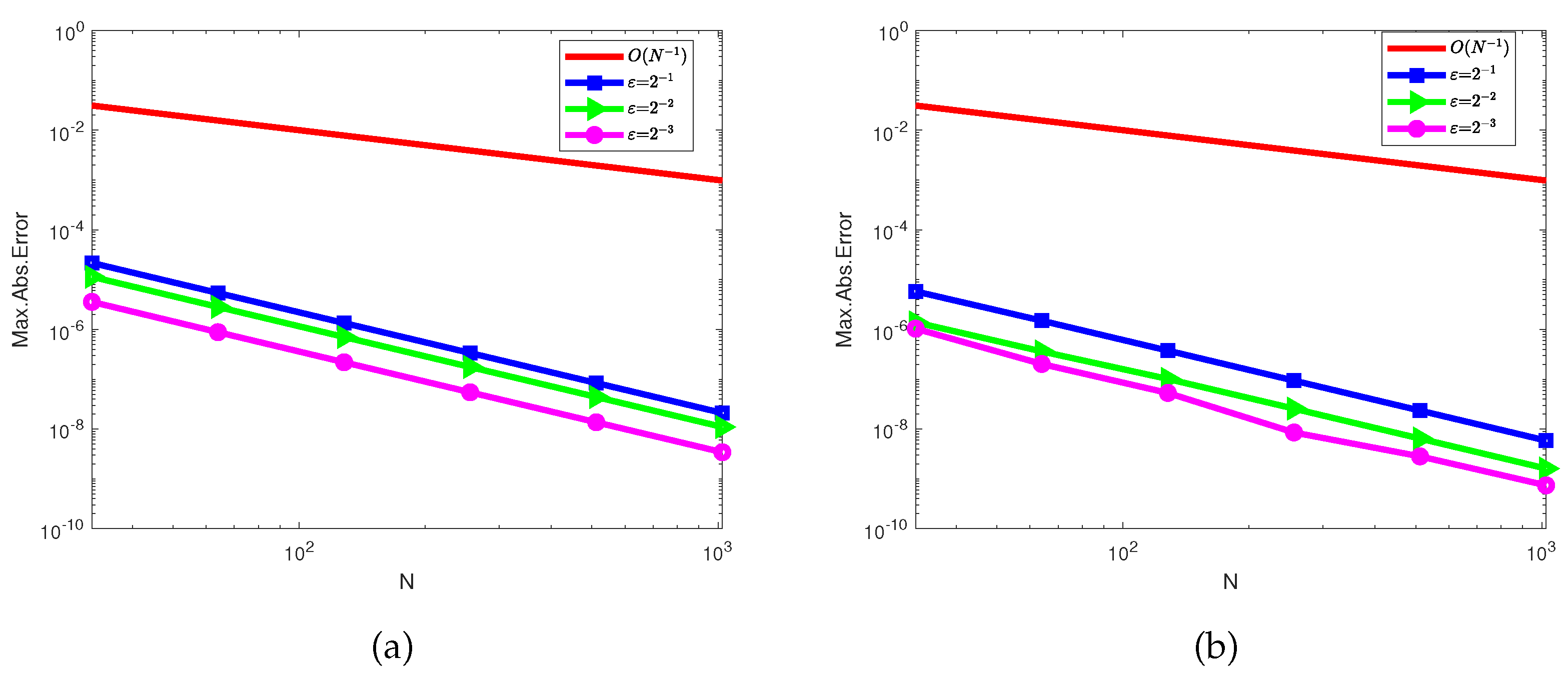
Table 1. MAEs and uniform CRs of Example 4.1 at various values of

ε

and N.

Table 1. MAEs and uniform CRs of Example 4.1 at various values of

ε

and N.

$↓ ε \| N :$	32	64	128	256	512	1024
$2^{- 1}$	2.1651e-05	5.3923e-06	1.3468e-06	3.3662e-07	8.4150e-08	2.1037e-08
$2^{- 2}$	1.1398e-05	2.8278e-06	7.0561e-07	1.7632e-07	4.4074e-08	1.1018e-08
$2^{- 3}$	3.5774e-06	8.8091e-07	2.1939e-07	5.4796e-08	1.3696e-08	3.4239e-09
$2^{- 4}$	5.3067e-07	1.2874e-07	3.1941e-08	7.9701e-09	1.9916e-09	4.9775e-10
$2^{- 5}$	2.7155e-08	6.3984e-09	1.5756e-09	3.9242e-10	9.8060e-11	2.4620e-11
$2^{- 6}$	3.1070e-10	6.9252e-11	1.6793e-11	4.1558e-12	1.0334e-12	2.3659e-13
$2^{- 7}$	4.3432e-13	8.9040e-14	2.6645e-14	1.4544e-14	1.0757e-14	5.5067e-15
$e^{N}$	2.1651e-05	5.3923e-06	1.3468e-06	3.3662e-07	8.4150e-08	2.1037e-08
$r^{N}$	2.0055	2.0014	2.0003	2.0001	2.0000	-

Table 2. MAEs and uniform CRs of Example 4.2 at various values of

ε

and N.

Table 2. MAEs and uniform CRs of Example 4.2 at various values of

ε

and N.

$↓ ε \| N :$	32	64	128	256	512	1024
$2^{- 1}$	5.8033e-06	1.4979e-06	3.7583e-07	9.3972e-08	2.3492e-08	5.8728e-09
$2^{- 2}$	1.3910e-06	3.6189e-07	1.0139e-07	2.5722e-08	6.4442e-09	1.6107e-09
$2^{- 3}$	1.0370e-06	2.0245e-07	5.3082e-08	8.5472e-09	2.8296e-09	7.4239e-10
$2^{- 4}$	2.3199e-05	1.1764e-06	4.6405e-07	1.5298e-08	4.3938e-09	1.9497e-10
$2^{- 5}$	8.4647e-05	5.2442e-06	2.3032e-07	8.5273e-8	2.8981e-09	9.3812e-10
$2^{- 6}$	2.6443e-04	5.1757e-05	1.9992e-06	4.3622e-07	1.5356e-08	5.0939e-09
$2^{- 7}$	4.5694e-04	8.0984e-05	4.9954e-06	2.1877e-07	8.0871e-08	2.7481e-08
$2^{- 8}$	1.1685e-03	3.0659e-04	7.9042e-05	2.0603e-06	4.2009e-07	1.4776e-07
$2^{- 9}$	1.2426e-03	2.5637e-04	7.9174e-05	2.1724e-05	6.1306e-06	1.8693e-06
$2^{- 10}$	1.2417e-03	2.5621e-04	7.9171e-05	2.0688e-05	6.0409e-06	1.4121e-06
$e^{N}$	1.2426e-03	3.0659e-04	7.9174e-05	2.1724e-05	6.1306e-06	1.8693e-06
$r^{N}$	2.0190	1.9532	1.8657	1.8252	1.7135	-

Table 3. Comparison of the present scheme with other published work.

	N→	32	64	128	256	512	1024
Example 4.1
Present method
	$e^{N}$	2.1651e-05	5.3923e-06	1.3468e-06	3.3662e-07	8.4150e-08	2.1037e-08
	$r^{N}$	2.0055	2.0014	2.0003	2.0001	2.0000	1.9986
Results in [12]
Shishishkin Mesh
	$e^{N}$	5.2513e-03	3.4209e-03	2.0832e-03	1.1436e-03	7.3014e-04	3.7640e-04
	$r^{N}$	0.61827	0.71558	0.86515	0.64740	0.95589	0.86652
Bakhvalov-Shishkin mesh
	$e^{N}$	2.9952e-03	1.5057e-03	7.5395e-04	3.7712e-04	1.8858e-04	9.4293e-05
	$r^{N}$	0.99221	0.99790	0.99944	0.99985	0.99995	0.99998

Table 4. Comparison of the present scheme with other published work.

	N→	32	64	128	256	512	1024
Example 4.2
Present method
	$e^{N}$	1.2426e-03	3.0590e-04	7.9174e-05	2.1724e-05	6.1306e-06	1.8693e-06
	$r^{N}$	1.7634	1.9532	1.8657	1.8252	1.7135	1.7814
Results in [12]
Shishishkin Mesh
	$e^{N}$	5.9350e-03	3.9301e-03	2.4026e-03	1.3469e-03	8.4650e-04	4.3631e-04
	$r^{N}$	0.59466	0.70994	0.83491	0.67014	0.95613	0.84693
Bakhvalov-Shishkin mesh
	$e^{N}$	3.3073e-03	1.6716e-03	8.3715e-04	4.1850e-04	2.0918e-04	1.0457e-04
	$r^{N}$	0.98440	0.99769	1.0002	1.0004	1.0003	1.0001

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Parameter-Robust Numerical Scheme for Computing Singularly Perturbed Differential Equations with Mixed Large Shifts

Abstract

1. Introduction

2. Continuous Problem

3. Formulation of the Numerical Method

3.1. Uniform Stability and Convergence Analysis

4. Numerical Examples and Discusions

5. Conclusion and Future Plans

Funding

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe