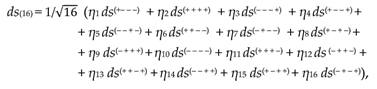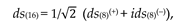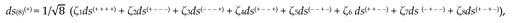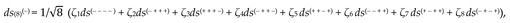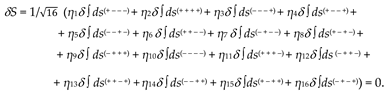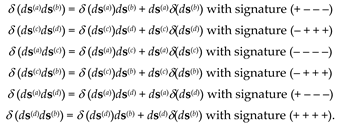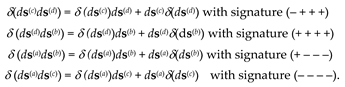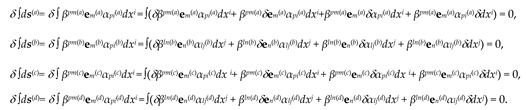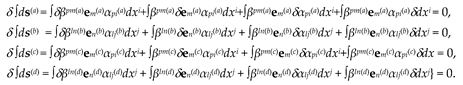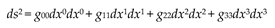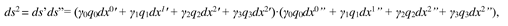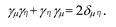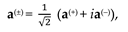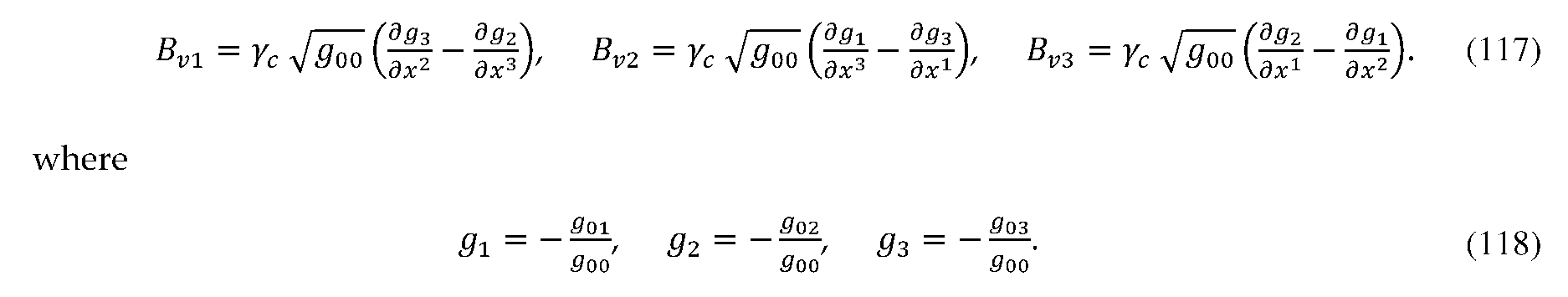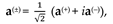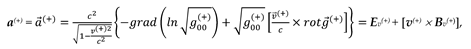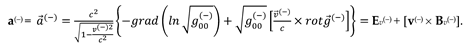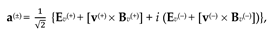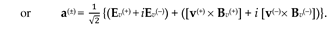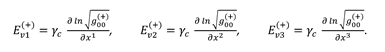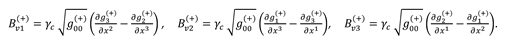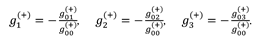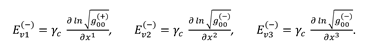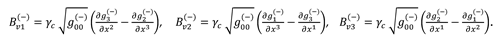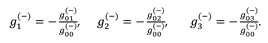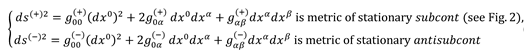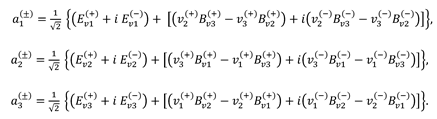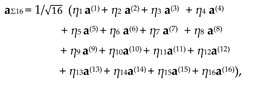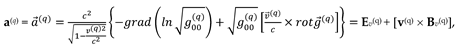Geometrized Vacuum Physics. Part IV: Dynamics of Vacuum Layers

Preprint

Article

Geometrized Vacuum Physics. Part IV: Dynamics of Vacuum Layers

Altmetrics

Downloads

156

Views

Comments

Mikhail Batanov-Gaukhman^*

This version is not peer-reviewed

Submitted:

27 October 2023

Posted:

30 October 2023

You are already at the latest version

Alerts

Abstract

This article is the fourth part of a scientific project under the general title “Geometrized vacuum physics based on the Algebra of Signatures". In the first three articles [1,2,3], the foundations of the Algebra of Stignatures were laid and the main aspects of the kinematics of vacuum layers were considered. This article continues the development of the mathematical apparatus of the proposed project, in particular, the dynamics of vacuum layers is developed based on the Algebra of Signatures. The development of this direction of research (with simplifications related to Riemann's differential geometry) led to the possibility of a geometrized representation of the electric field strength and magnetic field induction. This geometrized mathematical apparatus allows one to interpret the electromagnetic field as an interweaving of accelerated and rotational flows of the adjacent layers of vacuum. The proposed dynamic models of accelerated movements and rotations of vacuum layers can provide a theoretical basis for the development of “zero” (i.e. vacuum) technologies.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Background and Introduction

This paper is the fourth in a series of articles under the general title “Geometrized vacuum physics”. In the previous three articles [1,2,3] the basics of the Algebra of Signatures and the kinematics of vacuum layers were outlined.

Let’s recall that the subject of study of Algebra of Signatures (abbreviated as Alsigna) is the volume of the “vacuum”, i.e. local 3-dimensional area of the void [1,2,3].

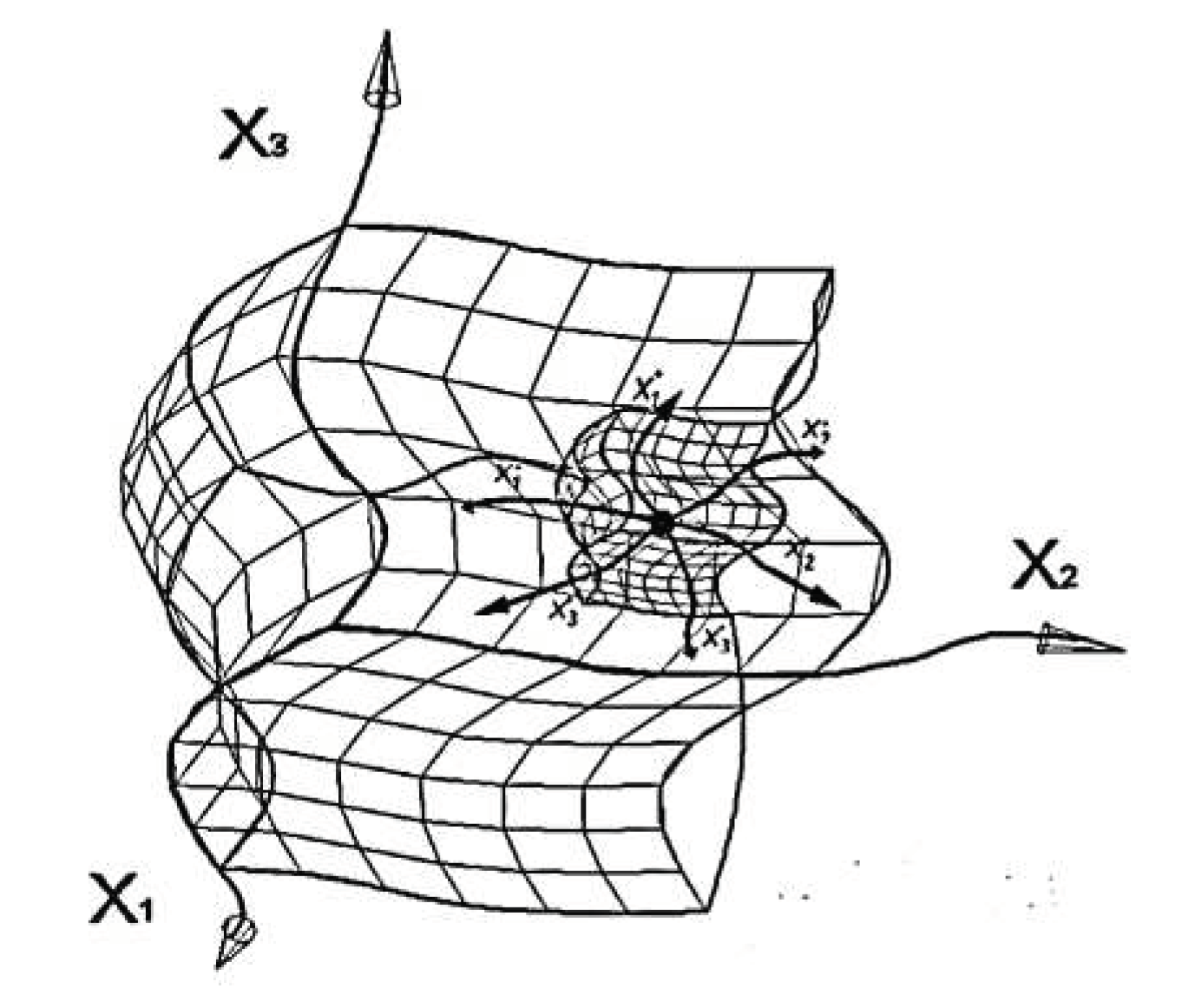
Within Alsigna, the “vacuum” is stratified into an infinite number of nested λm,n-vacuums, which are illuminated from the void by probing it with monochromatic rays of light with wavelengths λm,n from different ranges Δλ =10m ÷ 10n cm, where n = m + 1 (see §§2.1–2.2 in [1]). In this case, each λm,n-vacuum is a 3Dm,n-landscape (or 3Dm,n-lattice), the geodesic lines of which are the corresponding rays of light (see Figure 1).

This article considers the geodesic lines of only one curved region of one of the λm,n-vacuums. The geodesic lines of the remaining λm,n-vacuum are studied similarly.

Let’s recall that within the framework of the Algebra of Signature, the simplest level of research is a bilateral consideration of the uncurved local region of the 23-λm,n-vacuum (see §2.4 in [3] and Figure 2), which is specified by a set of pseudo-Euclidean metrics (83) in [3]

\{\begin{matrix} d s_{0}^{(+) 2} = c^{2} d t^{2} - d x^{2} - d y^{2} - d z^{2} = d s^{(+)} d s^{(+)} = c d t c d t - d x d x - d y d y - d z d z, \\ d s_{0}^{(-) 2} = - c^{2} d t^{2} + d x^{2} + d y^{2} + d z^{2} = d s^{(-)} d s^{(-)} = - c d t c d t + d x d x + d y d y + d z d z . \end{matrix}

(1)

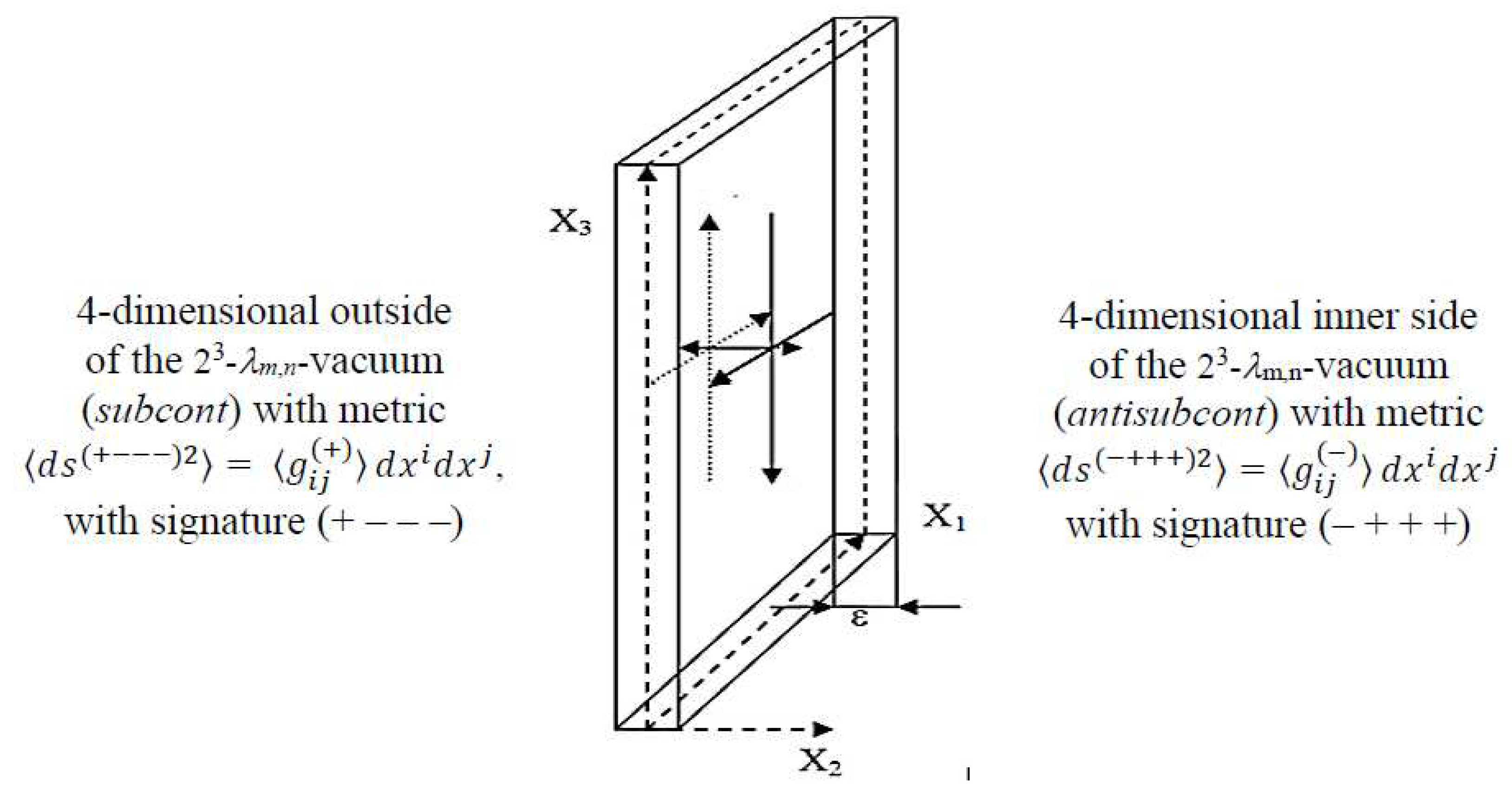
Figure 2. Simplified illustration of a two-sided section of the 23-λm÷n-vacuum, the outer side of which (subcont) is described by the averaged metric

〈d s^{(+ - - -) 2}〉

with the signature (+ – – –), and its inner side (antisubcont) is described by the metric

〈d s^{(- + + +) 2}〉

with the opposite signature (– + + +), as ε → 0 (repetition of Figure 7 in [3]).

Figure 2. Simplified illustration of a two-sided section of the 23-λm÷n-vacuum, the outer side of which (subcont) is described by the averaged metric

〈d s^{(+ - - -) 2}〉

with the signature (+ – – –), and its inner side (antisubcont) is described by the metric

〈d s^{(- + + +) 2}〉

with the opposite signature (– + + +), as ε → 0 (repetition of Figure 7 in [3]).

The metric-dynamic state of the same, but curved section of the double-sided 23-λm,n-vacuum is described by the averaged metric (61) in [3]

ds (\pm) 2 = \frac{1}{2} (ds (+ - - -) 2 + ds (- + + +) 2) = \frac{1}{2} (ds (+) 2 + ds (-) 2) = ½ (g ij (+) + g ij (-)) dxidxj,

(2)

where

ds (+ - - -) 2 = ds (+) 2 = g ij (+) dxidxj with signature (+ - - -),

(3)

g_{i j}^{(+)} = (\begin{matrix} g_{00}^{(+)} & g_{10}^{(+)} & g_{20}^{(+)} & g_{30}^{(+)} \\ g_{01}^{(+)} & g_{11}^{(+)} & g_{21}^{(+)} & g_{31}^{(+)} \\ g_{02}^{(+)} & g_{12}^{(+)} & g_{22}^{(+)} & g_{31}^{(+)} \\ g_{03}^{(+)} & g_{13}^{(+)} & g_{23}^{(+)} & g_{33}^{(+)} \end{matrix})

(4)

is metric tensor of the “outer” side of the 23-λm,n-vacuum (i.e. subcont) (see Figure 2);

ds (- + + +) 2 = ds (-) 2 = g ij (-) dxidxj with signature (- + + +),

(5)

g_{i j}^{(-)} = (\begin{matrix} g_{00}^{(-)} & g_{10}^{(-)} & g_{20}^{(-)} & g_{30}^{(-)} \\ g_{01}^{(-)} & g_{11}^{(-)} & g_{21}^{(-)} & g_{31}^{(-)} \\ g_{02}^{(-)} & g_{12}^{(-)} & g_{22}^{(-)} & g_{31}^{(-)} \\ g_{03}^{(-)} & g_{13}^{(-)} & g_{23}^{(-)} & g_{33}^{(-)} \end{matrix})

(6)

is metric tensor of the “inner” side of the 23-λm,n-vacuum (i.e. antisubcont) (see Figure 2);

Conditional concepts of "subcont" (short for "substantial continuum") and "antisubcont" (short for "antisubstantial continuum") were introduced in §2.7 in [2] to designate, respectively, the outer and inner sides of the 23-λm,n-vacuum, as well as to facilitate the visualization of intertwined intra-vacuum processes. It is conditionally assumed that the "subcont" is formed from streams (threads) of white color, and the antisubcont is formed from streams (threads) of black color (see Figure 3b and Figure 12 in [3]).

In § 2.5.2 in [3] it was shown that adjacent segments of the “white” lines ds(+) of the subcont and the “black” lines ds(–) of the antisubcont are mutually perpendicular ds(+) ⊥ ds(–) (see Figure 3a). This is possible only if they are everywhere intertwined with each other (Figure 3b), and form a 3-dimensional affine fabric of 23-λm,n-vacuum (Figure 3b,c).

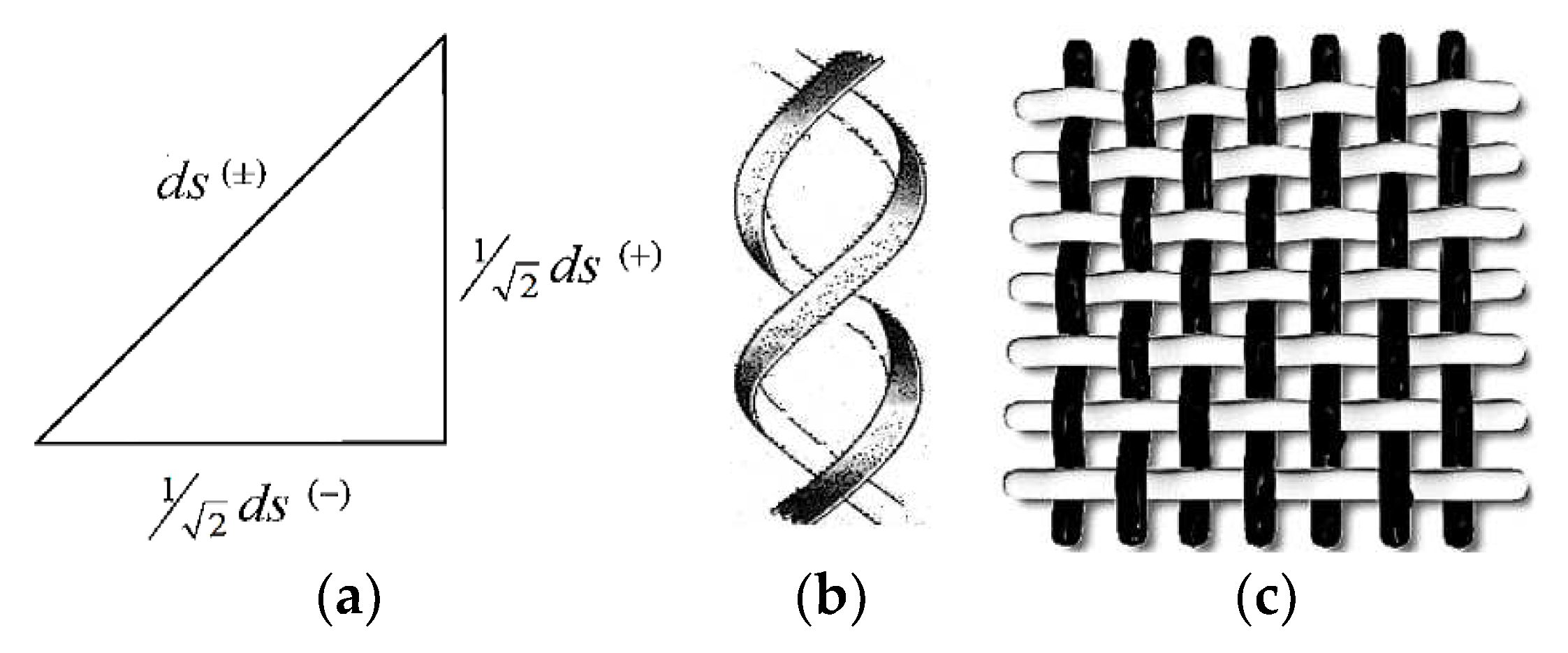
Figure 3. a) Mutually perpendicular adjacent segments (

\frac{1}{2}

)1/2ds(+) and (

\frac{1}{2}

)1/2ds(–); b) If we project a double helix onto a plane, then at the intersection of its lines ds(+) and ds(–) are always mutually perpendicular (repetition of Figure 10 in [3]); c) Conventionally, the “white” lines of the ds(+) subcont and the “black” lines of the ds(–) antisubcont form a single intertwined affine fabric of the 23-λm,n-vacuum.

Figure 3. a) Mutually perpendicular adjacent segments (

\frac{1}{2}

)1/2ds(+) and (

\frac{1}{2}

Thus, the averaged metric (2) corresponds to a segment of a 2-braid consisting of two mutually intertwined spirals s(–) and s(+) (see the definition of a k-braid in § 2.5.2 in [3]), which can be described by a complex number

ds (\pm) = \frac{1}{\sqrt{2}} (ds (-) + ids (+)),

(7)

which we will call a 2-helix. The squared modulus of a complex number (7) (i.e., a 2-helix) is equal to the length of a segment of a 2-braid (2) or expression (61) in [3].

Based on the Algebra of Signature presented in [1,2,3] and partly repeated in this introduction, this article discusses the general dynamics of vacuum layers, from which, under certain conditions, “vacuum electrodynamics” and “vacuum electrostatics” are obtained.

Like the three previous articles [1,2,3], this article is mainly of a theoretical nature and is aimed at further development of the mathematical apparatus of the Algebra of Signature (abbreviated as «Alsigna»).

It is planned that in the following articles of this series, Alsigna’s mathematical apparatus will be used for applied problems, in particular, for the development of a vacuum model of the Universe, a vacuum model of elementary particles, to explain the nature of gravity and electromagnetism, as well as for development of the “zero” (vacuum) technologies.

2. Materials and Method

2.1. Equation of the geodesic line of a two-sided 23-λm,n-vacuum

The shortest distance between two infinitely close points p1 and p2 in a curved area of a two-sided 23-λm,n-vacuum is defined as an extremal of the functional

S = \int_{p 1}^{p 2} d s^{(\pm)},

(8)

where

d s^{(\pm)}

is a 2-helix (7), integration is performed from point p1 to point p2.

We find the equation of this extremal based on the condition that the first variation is equal to zero

S = \int_{p 1}^{p 2} d s^{(\pm)} = \int_{p 1}^{p 2} \frac{1}{\sqrt{2}} (d s^{(+)} + i d s^{(-)}) = 0 .

(9)

Let’s represent expression (9) in the form

S = \frac{1}{\sqrt{2}} (\int_{p 1}^{p 2} d s^{(+)} + i \int_{p 1}^{p 2} d s^{(-)}) = 0,

(10)

or taking into account metrics (3) and (5)

S = \frac{1}{\sqrt{2}} (\sqrt{{g_{i j}}^{(+)} d x^{i} d x^{j}} + i \int_{p 1}^{p 2} \sqrt{{g_{i j}}^{(-)} d x^{i} d x^{j}}) = 0

(11)

Expression (11) is equal to zero provided that both terms are equal to zero

\int_{p 1}^{p 2} \sqrt{{g_{i j}}^{(+)} d x^{i} d x^{j}} = 0 a n d \int_{p 1}^{p 2} \sqrt{{g_{i j}}^{(-)} d x^{i} d x^{j}} = 0 .

(12)

In §2.2 in [3], it was shown that in the most general case, the metric of a local area of a curved 4-dimensional space with any of the 16 possible signatures (22) in [3], can be represented as a scalar product of two vectors given in distorted affine spaces with corresponding stignatures (see Expressions (18) – (20) in [3])

ds(q)2 = ds(a)ds(b) = gij(q)dxidxj = βpm(a)em(a)αpi(a)βln(b)en(b)αlj(b)dxidxj,

(13)

where

ds(a)=βpm(a)em(а)αpi(a)dxi and ds(b) = βln(b)en(b)αlj(b)dxj

(14)

is vectors defined respectively in the a-th and b-th curved affine space with the corresponding stignature (see §2.2 in [3]);

αij(a) =dx′i(a)/dxj(a)

(15)

is components of the elongation tensor of the axes of the curved region of the a-th affine space with the corresponding stignature from matrix (2) in [2]);

βpm(a) = (e′p(a) ⋅em(a)) = cos (e′p(a) ^em(a))

(16)

is direction cosines between the axes of the curved section of the a-th affine space with the same stignatura;

em(a) is basis vector specifying the direction of the m-th axis of the a-th affine space;

dxj(a) is an infinitesimal segment of the j-th axis of the a-th affine space.

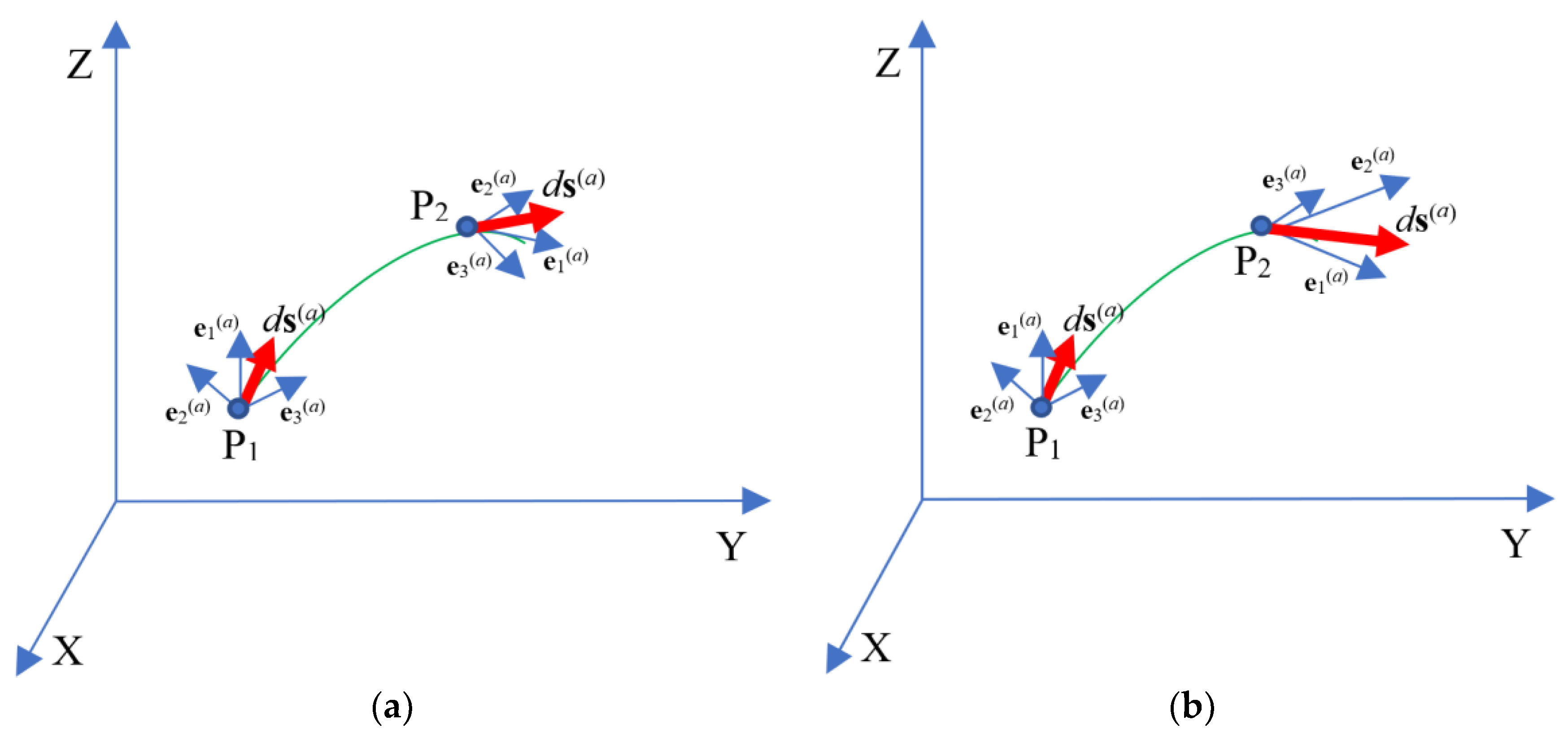
When parallel translation, for example, a vector ds(a) (or a vector ds(b)) in a complexly curved, twisted and displaced affine (i.e., vector) space along a geodesic line from point p1 to a nearby point p2 (see Figure 4b), it should be taken into account that the magnitude and direction of this vector may depend on changes in all four parameters αij(a), βpm(a), em(a), dxj(a). That is, when translating the vector ds(a from point p1 to p2, in the most complex case the following may change (see Figure 4b): 1) The length of the basis vectors αij(a); 2) angles between the basis vectors βpm(a); 3) rotation of the entire 4-basis as a whole em(a); 4) Displacement of the 4-basis in general dxj(a). This is due to the fact that the geodesic line between two points p1 and p2 of a complexly distorted space can not only be curved, but also deformed, displaced and twisted.

Figure 4. a) In Riemannian geometry, the parallel translation of the vector ds(a) from point p1 to the nearby point p2 is carried out strictly tangent to the geodesic line connecting these points. In this case, only the direction of this vector changes, and its magnitude remains unchanged. It means that the magnitude of the basis vectors em(а) and the angles between them do not change; b) In the most complexly curved, displaced and twisted space, when transferring (i.e. translation) the vector ds(a) from point p1 to the nearby point p2, its direction, magnitude and displacement may change. When transferring the vector ds(a) in such a complexly distorted space, the magnitude of the basis vectors em(a) and the angles between them can change, and the 4-basis itself as a whole can rotate and shift. In this case, all four parameters of the 4-basis αij(a), βpm(a), em(a), dxj(a) can change, which, according to expression (14), affects the change in the vector ds(a) when it is transferred.

Depending on what distortions, displacements and rotations of the vectors ds(a) and ds(b) are taken into account when considering the metric-dynamic properties of curved space, various differential geometries are obtained: for example, Riemannian geometry (see Figure 4a), Weyl geometry, affine geometry of Eddington, geometry with torsion of Cartan-Schouten, geometry of absolute parallelism of Weizenbeck-Vitali-Shipov [4], etc.

2.2. Equation of the geodesic line of a two-sided 23-λm,n-vacuum in the case of Riemannian geometry

First, let’s assume that the outer and inner 4-dimensional sides of the 23-λm,n-vacuum (i.e. subcont and antisubcont) are only curved, i.e. are described by the simplest differential Riemannian geometry (see Figure 4a). In this case, the extremals of functionals (12) are defined identically, so we introduce a generalized metric

d s^{2} = g_{i j} d x^{i} d x^{j} \leftrightarrow \{\begin{matrix} o r d s^{(+) 2} = g_{i j}^{(+)} d x^{i} d x^{j}, \\ o r d s^{(-) 2} = g_{i j}^{(-)} d x^{i} d x^{j} . \end{matrix}

We consider the general case

\int_{p 1}^{p 2} d s = \int_{p 1}^{p 2} \sqrt{g_{i j} d x^{i} d x^{j}} = 0,

(17)

provided that at the ends of the desired geodesic line ds (i.e. at points p1 and p2) the variations are zero

δ d s_{(р_{1})} = δ d s_{(р_{2})} = δ x_{(р_{1})} = δ x_{(р_{2})} = 0 .

(18)

Let's use the expression

δ d s^{2} = 2 d s δ d s,

(19)

whence it follows [5]

δ d s = \frac{1}{2 d s} δ g_{i j} d x^{i} d x^{j} = \frac{1}{2 d s} [\frac{\partial g_{i j}}{\partial x^{μ}} δ x^{μ} d x^{i} d x^{j} + g_{i j} d x^{j} d δ x^{i} + g_{i j} d x^{i} d δ x^{j}],

(20)

where the commutativity of the operations of variation and differentiation

δ (d x^{i}) = d (δ x^{i})

is used.

Let’s substitute Ex. (20) under the integral (17), and divide and multiply this expression by ds, as a result we obtain [5]

δ S = \frac{1}{2} \int_{р_{1}}^{р_{2}} \{\frac{\partial g_{i j}}{\partial x^{μ}} \frac{d x^{i}}{d s} \frac{d x^{j}}{d s} δ x^{μ} + (g_{μ j} \frac{d x^{j}}{d s} + g_{i μ} \frac{d x^{i}}{d s}) \frac{d (δ x^{μ})}{d s}\} d s = 0 .

(21)

We integrate the expression in parentheses by parts [5]:

\frac{1}{2} \int_{р_{1}}^{р_{2}} (g_{μ j} \frac{d x^{j}}{d s} + g_{i μ} \frac{d x^{i}}{d s}) \frac{d (δ x^{μ})}{d s} d s = {\frac{1}{2} (g_{μ k} \frac{d x^{k}}{d s} + g_{i μ} \frac{d x^{i}}{d s}) δ x^{μ}|}_{р_{1}}^{р_{2}} - \frac{1}{2} \int_{р_{1}}^{р_{2}} δ x^{μ} \frac{d}{d s} (g_{μ j} \frac{d x^{j}}{d s} + g_{i μ} \frac{d x^{i}}{d s}) d s .

(22)

The first term in this expression, due to conditions (18), becomes zero. Let’s substitute the remaining part of expression (22) into equation (21) and perform differentiation, as a result we obtain [5]:

δ S = \frac{1}{2} \int_{р_{1}}^{р_{2}} \{(\frac{\partial g_{i j}}{\partial x^{μ}} - \frac{\partial g_{μ j}}{\partial x^{i}} - \frac{\partial g_{i μ}}{\partial x^{j}}) \frac{d x^{i}}{d s} \frac{d x^{j}}{d s} + 2 g_{μ j} \frac{d^{2} x^{j}}{d s^{2}}\} d s δ x^{μ} = 0 .

(23)

From the fact that integral (23) vanishes for any variations of δхμ, it follows that the expression enclosed in curly brackets is equal to zero. From where, taking into account the relation

g_{i j} g^{i j} = 4

, after simple calculations we obtain the equation of the geodesic line [5]:

\frac{d^{2} x^{l}}{d s^{2}} + Г_{i j}^{l} \frac{d x^{i}}{d s} \frac{d x^{j}}{d s} = 0,

(24)

where

Г_{i j}^{l} = \frac{1}{2} g^{l μ} (\frac{\partial g_{μ i}}{\partial x^{j}} + \frac{\partial g_{μ j}}{\partial x^{i}} - \frac{\partial g_{i j}}{\partial x^{μ}}) i s C h r i s t o f f e l s y m b o l s;

(25)

x^{i}

(s) is coordinates of the curved line.

Eq. (24) is intended to determine the extremal of functional (17) with simplifications related to Riemannian geometry (Figure 4a). This equation determines the most optimal (geodesic) line connecting two close points p1 and p2 in a curved 4-dimensional space. That is, this is a line that, under the above conditions, allows you to get from point p1 to the nearby point p2 in the shortest time and with the least energy costs.

At the same time, Eq. (24) can be represented in the form

\frac{d^{2} x^{l}}{d s^{2}} = - Г_{i j}^{l} \frac{d x^{i}}{d s} \frac{d x^{j}}{d s},

(26)

this equation defines the 4-acceleration field

d^{2} x^{l} / d s^{2}

, which can be interpreted as a massless force field

f^{l}

\frac{d^{2} x^{l}}{d s^{2}} = f^{l} / m_{b},

where

m_{b}

is the mass of a body that is carried away by a continuous “medium”, which moving with acceleration

d^{2} x^{l} / d s^{2}

At this stage of research, it is difficult to explain what is meant by a force field in vacuum physics. However, it is possible to compare the acceleration of a local section of the vacuum layer with the accelerated movement of a small volume of liquid in the general flow of the river. Such an accelerated flow carries with it everything that comes in its way and makes it move with the same acceleration. From the point of view of post-Newtonian physics, if a body moves with acceleration, then a force acts on it. Therefore, the accelerated movement of the local volume of a 3-dimensional medium (in this case, subcont, or antisubcont) can be interpreted as a local force effect.

Performing separately similar operations (17) – (24) for variations (12), we obtain two equations

\frac{d^{2} x^{l}}{d s^{2}} + Г_{i j}^{l (-)} \frac{d x^{i}}{d s} \frac{d x^{j}}{d s} = 0,

(27)

\frac{d^{2} x^{l}}{d s^{2}} + Г_{i j}^{l (+)} \frac{d x^{i}}{d s} \frac{d x^{j}}{d s} = 0,

(28)

where respectively

Г_{i j}^{l (+)} = \frac{1}{2} g^{l μ (+)} (\frac{\partial g_{μ i}^{(+)}}{\partial x^{j}} + \frac{\partial g_{μ j}^{(+)}}{\partial x^{i}} - \frac{\partial g_{i j}^{(+)}}{\partial x^{μ}})

(29)

is Christoffel symbols of a subcont;

Г_{i j}^{l (-)} = \frac{1}{2} g^{l μ (-)} (\frac{\partial g_{μ i}^{(-)}}{\partial x^{j}} + \frac{\partial g_{μ j}^{(-)}}{\partial x^{i}} - \frac{\partial g_{i j}^{(-)}}{\partial x^{μ}})

(30)

is Christoffel symbols of a antisubcont;

When considering variation (11), taking into account the Christoffel symbols (29) and (30), we find that the sought-for extremal of the functional (8), with simplifications related to Riemannian geometry, is determined by the following equation of a geodesic line in a curved two-sided 23-λm,n-vacuum

\frac{d^{2} x^{l}}{d s^{2}} + \frac{1}{\sqrt{2}} (Г_{i j}^{l (+)} + i Г_{i j}^{l (-)}) \frac{d x^{i}}{d s} \frac{d x^{j}}{d s} = 0,

(31)

\frac{d^{2} x^{l}}{d s^{2}} = - \frac{1}{\sqrt{2}} (Г_{i j}^{l (+)} + i Г_{i j}^{l (-)}) \frac{d x^{i}}{d s} \frac{d x^{j}}{d s} .

(32)

Ex. (31) shows that the geodesic lines of the subcont and antisubcont, i.e. two mutually opposite sides of the local section of the two-sided 23-λm,n-vacuum is twisted into a 2-spiral. This is similar to how rivulets twist in a freely falling jet of liquid (see Figure 5).

Continuing the analogy with liquid, it should be noted that within the framework of the Algebra of Signature, a two-sided 23-λm,n-vacuum can be represented as an interweaving (mixing) of two liquids (subcont and antisubcomt), which can be conditionally “colored” in white and black colors (see Figure 6). These two conjugate “liquids” cannot separately move in a straight line; they are interconnected and can move in one direction only by twisting into a 2-helix.

2.3. Equation of the geodesic line of a 16-sided 26-λm,n-vacuum in the case of Riemannian geometry

In the previous paragraph, we considered the most simplified model representation of the interweaving of geodesic lines of a two-sided 23-λm,n-vacuum which can be interpreted as mixing and interweaving of flows of two liquids: conventionally “white” and “black”). With a more detailed examination of such conjugate “multi-colored” liquids there should be 16. With an even more detailed examination of these liquids there are already 256 and so on ad infinitum.

More in-depth and accurate is the sixteen-sided consideration of the local area of the 26-λm,n-vacuum (see §3 and §5.3 in [3]). In this case, the curved state of the 26-λm,n-vacuum is described by a superposition (averaging) not of two, as in the previous paragraph, but of sixteen 4-metrics (see Ex. (25) in [3]).

s_{(16)}^{2} = \frac{1}{16} \sum_{q = 1}^{16} g_{i j}^{(q)} d x_{i} d x_{j} = \frac{1}{16} [g_{i j}^{(1)} d x^{i} d x^{j} + g_{i j}^{(2)} d x^{i} d x^{j} + g_{i j}^{(3)} d x^{i} d x^{j} + g_{i j}^{(4)} d x^{i} d x^{j} + + g_{i j}^{(5)} d x^{i} d x^{j} + g_{i j}^{(6)} d x^{i} d x^{j} + g_{i j}^{(7)} d x^{i} d x^{j} + g_{i j}^{(8)} d x^{i} d x^{j} + + g_{i j}^{(9)} d x^{i} d x^{j} + g_{i j}^{(10)} d x^{i} d x^{j} + g_{i j}^{(11)} d x^{i} d x^{j} + g_{i j}^{(12)} d x^{i} d x^{j} + + g_{i j}^{(13)} d x^{i} d x^{j} + g_{i j}^{(14)} d x^{i} d x^{j} + g_{i j}^{(15)} d x^{i} d x^{j} + g_{i j}^{(16)} d x^{i} d x^{j}] = 0,

(33)

where

g_{i j}^{(q)} = (\begin{matrix} g_{00}^{(q)} & g_{10}^{(q)} & g_{20}^{(q)} & g_{30}^{(q)} \\ g_{01}^{(q)} & g_{11}^{(q)} & g_{21}^{(q)} & g_{31}^{(q)} \\ g_{02}^{(q)} & g_{12}^{(q)} & g_{22}^{(q)} & g_{32}^{(q)} \\ g_{03}^{(q)} & g_{13}^{(q)} & g_{23}^{(р)} & g_{33}^{(q)} \end{matrix}) .

(34)

is components of the metric tensor of the q-th metric space with a signature from the matrix (22) in [3]:

s i g n (g_{i j}^{(q)}) = \begin{matrix} {(+ + + +)}^{1} & {(+ + + -)}^{5} & {(- + + -)}^{9} & {(+ + - +)}^{13} \\ {(- - - +)}^{2} & {(- + + +)}^{6} & {(- - + +)}^{10} & {(- + - +)}^{14} \\ {(+ - - +)}^{3} & {(+ + - -)}^{7} & {(+ - - -)}^{11} & {(+ - + +)}^{15} \\ {(- - + -)}^{4} & {(+ - + -)}^{8} & {(- + - -)}^{12} & {(- - - -)}^{16} . \end{matrix} .

(35)

In the framework of the Algebra of Signature, Ex. (33) is called a 16-braid, which is formed by the additive superposition of sixteen 4-dimensional metric spaces (see §5.3 in [3]). In this case, a section of a 16-braid is formed from sixteen intertwined “colored” lines (spiral threads) ds(q), and is described by Ex. (69) in [3]

(36)

where ηm (m = 1,2,3,…,16) is an orthonormal basis of objects (similar to the imaginary unit i) satisfying the anticommutative Clifford algebra relation (68) in [3]

ηmηn + ηnηm = 2δmn ,

(37)

where δnm is the unit 16×16 matrix.

For example, let‘s imagine a segment of a 16-helix (36) as a sum of two complex conjugated 8-helices (octonions) with signatures {+ – – –} and {– + + +}

(38)

where

(39)

(40)

where the objects ζr (where r = 1, 2, 3, … ,8), as well as the objects ηm, satisfy the anticommutative relations of the Clifford algebra:

ζm ζk + ζk ζm = 2δkm ,

(41)

where δkm is the Kronecker symbol (δkm = 0 for m ≠ k and δkm = 1 for m = k).

These requirements are satisfied, for example, by a set of 8×8 matrices of type (65) in [1]:

ζ_{2} = (\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}) ζ_{2} = (\begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ - 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & - 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & - 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & - 1 & 0 \end{matrix}) ζ_{3} = (\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ - 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & - 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & - 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \end{matrix}) ζ_{4} = (\begin{matrix} 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & - 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ - 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & - 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & - 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \end{matrix}) ζ_{5} = (\begin{matrix} 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ - 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & - 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & - 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & - 1 & 0 & 0 & 0 & 0 \end{matrix}) ζ_{6} = (\begin{matrix} 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & - 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & - 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ - 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & - 1 & 0 & 0 & 0 & 0 & 0 \end{matrix}) ζ_{7} = (\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & - 1 \\ 0 & 0 & 0 & 0 & - 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & - 1 & 0 & 0 & 0 & 0 \\ - 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}) ζ_{8} = (\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & - 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & - 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & - 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ - 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix})

(42)

In this case, δkm is a unit 8×8-matrix:

δ_{k m} = (\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{matrix})

(43)

Similarly, the objects ηm can be represented by sixteen 16x16 matrices.

Let’s look at the functional

S = \int_{р_{1}}^{р_{2}} d s_{(16)},

(44)

where ds(16) is a segment of the 16-helix (36).

Let’s equate the first variation of this functional to zero

(45)

With each term ηqδ

\int_{р_{1}}^{р_{2}} d s^{(q)}

from Ex. (45) we perform operations like (17) – (24), as a result we obtain the extremal equation for a geodesic line in a curved 16-sided 26-λm,n-vacuum

\frac{d^{2} x^{l}}{d s^{2}} + 1 / \sqrt{16} (η_{1} Г_{i j}^{l (1)} + η_{2} Г_{i j}^{l (2)} + η_{3} Г_{i j}^{l (3)} + . . . + η_{15} Г_{i j}^{l (15)} + η_{16} Г_{i j}^{l (16)}) \frac{d x^{i}}{d s} \frac{d x^{j}}{d s} = 0,

(46)

\frac{d^{2} x^{l}}{d s^{2}} = - \frac{1}{\sqrt{16}} (\sum_{q = 1}^{16} η_{q} Г_{i j}^{l (q)}) \frac{d x^{i}}{d s} \frac{d x^{j}}{d s},

(47)

where

Г_{i j}^{l (q)} = \frac{1}{2} g^{l μ (q)} (\frac{\partial g_{μ i}^{(q)}}{\partial x^{j}} + \frac{\partial g_{μ j}^{(q)}}{\partial x^{i}} - \frac{\partial g_{i j}^{(q)}}{\partial x^{μ}})

(48)

is Christoffel symbols of the q-th metric space with components of the metric tensor

g_{i j}^{(q)} = (\begin{matrix} g_{00}^{(q)} & g_{10}^{(q)} & g_{20}^{(q)} & g_{30}^{(q)} \\ g_{01}^{(q)} & g_{11}^{(q)} & g_{21}^{(q)} & g_{31}^{(q)} \\ g_{02}^{(q)} & g_{12}^{(q)} & g_{22}^{(q)} & g_{32}^{(q)} \\ g_{03}^{(q)} & g_{13}^{(q)} & g_{23}^{(р)} & g_{33}^{(q)} \end{matrix})

(49)

with the corresponding signature from matrix (35).

Ex. (46) shows that at this level of consideration, the curved area of the 26-λm,n-vacuum is a complex interweaving of the 16-“colored” geodesic lines (see Figure 7). In this case, the 16-strains of the same section of the 26-λm,n-vacuum are described by the strain tensor (63) in [3].

At the same time, the equation of geodesic lines (46) can be represented in the form.

\frac{d^{2} x^{l}}{d s^{2}} = - \frac{1}{\sqrt{16}} (\sum_{q = 1}^{16} η_{q} Г_{i j}^{l (q)}) \frac{d x^{i}}{d s} \frac{d x^{j}}{d s},

(50)

which defines the field of 4-accelerations

d^{2} x^{l} / d s^{2}

, i.e. total massless force field (see Figure 7)

\frac{d^{2} x^{l}}{d s^{2}} = \frac{1}{\sqrt{16}} \sum_{q = 1}^{16} η_{q} \frac{d^{2} x^{l (q)}}{d s^{2}} {= f}^{l} / m_{b},

(51)

where

m_{b}

is the mass of the body that is carried away by the total (more precisely averaged) accelerated flow.

The next level of consideration is the 210-λm,n-vacuum, which is considered as the result of the interweaving of not 16, but 256 metric intra-vacuum layers (see §2.9 in [2] and § 2.5.3 in [3]). In this case, the curved area of 26-λm,n-vacuum is the result of averaging 265-deformations of the curved area of the 210-λm,n-vacuum, just as the curved area of the 23-λm,n-vacuum is the result of averaging 16-deformations of the curved area 26-λm,n-vacuum.

A more sophisticated consideration of the curvature of the λm,n-vacuum area can be continued to infinity by a multiple of 2k (see § 2.9 in [2]). In this case, each time the metric-dynamics of the subsequent transverse level of consideration of the 2k-λm,n-vacuum is the result of averaging (i.e., in fact, coarsening) of the metric-dynamics of the previous, much more finely and elegantly arranged level 2k+l-λm,n-vacuum.

3. Different directions of development of dynamics of a λm,n-vacuum layers

As part of the development of the general dynamics of λm,n-vacuum layers, a number of other possibilities should be considered that may be useful for solving various metric-dynamic problems of geometrized vacuum physics.

The expanded dynamics of a two-sided 23-λm,n-vacuum is based on a functional of the form (8)

S = \int_{p 1}^{p 2} d s^{(\pm)} = \frac{1}{\sqrt{2}} \int_{p 1}^{p 2} (d s^{(+)} + i d s^{(-)}),

however, the linear forms

d s^{(+)} a n d d s^{(-)}

can be represented in different ways, depending on the task and the depth of consideration. Below are several

(1). Let's return to the simplest level of consideration of the curved two-sided area of the 23-λm,n-vacuum. In this case, instead of the system of metrics (1), the outer and inner sides (i.e. subcont and antisubcont) of the curved area of the 23-λm,n-vacuum are described by conjugate metrics

\{\begin{matrix} d s^{(+) 2} = g_{i j}^{(+)} d x^{i} d x^{j} w i t h s i g n a t u r e (+ - - -), \\ d s^{(-) 2} = g_{i j}^{(-)} d x^{i} d x^{j} w i t h s i g n a t u r e (- + + +), \end{matrix}

(52)

which, according to Exs. (13) – (14), can be represented as scalar products of vectors

d s^{(a)} a n d d s^{(b)}

\{\begin{matrix} d s^{(+) 2} = d s^{(a)} d s^{(b)} w i t h s i g n a t u r e (+ - - -), \\ d s^{(-) 2} = d s^{(c)} d s^{(d)} w i t h s i g n a t u r e (- + + +), \end{matrix}

(53)

where, for example,

(54)

We find variations of all possible binary scalar products of vectors (54)

(55)

Among them there are only four variations with different signatures

(56)

We equate the variations of the following functionals to zero

(57)

Ex. (57) can be represented as

(58)

Here, all possible changes (distortions, deformations and displacements) of the 4-bases em(а), for example, those shown in Figure 4b.

Substituting variations (58) into Exs. (56), and finding equations for the extremals of these functionals, we obtain 32 types of different accelerations (or massless force effects).

(2). In §2.10 in [2], the spintensor representation of metrics with various signatures was considered. For example, let’s write the diagonal quadratic form with the signature (+ – – –) in the following form

d s^{(+) 2} = g_{00} d x^{0} d x^{0} - g_{11} d x^{1} d x^{1} - g_{22} d x^{2} d x^{2} - g_{33} d x^{3} d x^{3} = = {(\begin{matrix} q_{0} d x^{0} + q_{3} d x^{3} & q_{1} d x^{1} + i q_{2} d x^{2} \\ q_{1} d x^{1} - i q_{0} d x^{0} & q_{0} d x^{0} - q_{3} d x^{3} \end{matrix})}_{d e t},

(59)

where

q_{i} = \sqrt{g_{i i}} .

This A4 matrix can be represented as a linear form

A_{4}^{(+ - - -)} = (\begin{matrix} q_{0} d x^{0} + q_{3} d x^{3} & q_{1} d x^{1} + i q_{2} d x^{2} \\ q_{1} d x^{1} - i q_{0} d x^{0} & q_{0} d x^{0} - q_{3} d x^{3} \end{matrix}) = = q_{0} d x^{0} (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) - q_{1} d x^{1} (\begin{matrix} 0 & - 1 \\ - 1 & 0 \end{matrix}) - q_{2} {d x}^{2} (\begin{matrix} 0 & - i \\ i & 0 \end{matrix}) - q_{3} d x^{3} (\begin{matrix} - 1 & 0 \\ 0 & 1 \end{matrix}) .

(60)

In this case, the dynamics of a 23-λm,n-vacuum layer with signature (+ – – –) can be determined by the equality to zero of the first variation of the functional of the form

\int_{р_{1}}^{р_{2}} A_{4}^{(+ - - -)} = \int_{р_{1}}^{р_{2}} (q_{0} d x^{0} (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) - q_{1} d x^{1} (\begin{matrix} 0 & - 1 \\ - 1 & 0 \end{matrix}) - q_{2} {d x}^{2} (\begin{matrix} 0 & - i \\ i & 0 \end{matrix}) - q_{3} d x^{3} (\begin{matrix} - 1 & 0 \\ 0 & 1 \end{matrix})) = 0,

(61)

The dynamics of all other 23-λm,n-vacuum layers are determined similarly (see Table 1 in §10 in [2]) with all possible signatures from matrix (35).

(3). In §2.12 in [2] the Dirac representation of a diagonal quadratic form is considered, for example, with signature (+ + + +)

(62)

as a product of two affine (linear) forms

(63)

where

q_{i} = \sqrt{g_{i i}};

γμ is objects satisfying the anticommutative relation of the Clifford algebra

(64)

Condition (64) is satisfied, for example, by the following set of 4×4-Dirac matrices:

γ_{0} = (\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & - 1 \end{matrix}), γ_{1} = (\begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{matrix}), γ_{2} = (\begin{matrix} 0 & 0 & 0 & - i \\ 0 & 0 & i & 0 \\ 0 & - i & 0 & 0 \\ i & 0 & 0 & 0 \end{matrix}), γ_{3} = (\begin{matrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & - 1 \\ 1 & 0 & 0 & 0 \\ 0 & - 1 & 0 & 0 \end{matrix}), δ_{μ η} = (\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}) .

Also, the diagonal quadratic form (62) with signature (+ + + +) can be represented as

d s \equiv \sqrt{(d s_{i i}^{2})} = (\begin{matrix} \sqrt{d s_{00}^{2}} & 0 & 0 & 0 \\ 0 & \sqrt{d s_{11}^{2}} & 0 & 0 \\ 0 & 0 & \sqrt{d s_{22}^{2}} & 0 \\ 0 & 0 & 0 & \sqrt{d s_{33}^{2}} \end{matrix}) = \sqrt{\frac{1}{2} \sum_{μ = 0}^{3} \sum_{μ = 0}^{3} (γ_{μ} γ_{η} + γ_{η} γ_{μ}) d x^{μ} d x^{η}} .

(65)

The variation of the product of two linear forms (63) is equal to

δ(ds’ds”) = δ (ds’)ds”+ ds’δ(ds”).

(66)

In this case, the dynamics of a 23-λm,n-vacuum layer with signature (+ + + +) is determined by the system of equations

\{\begin{matrix} d s ’ = (γ_{0} q_{0} d x^{0} ’ + γ_{1} q_{2} d x^{1} ’ + γ_{2} q_{2} d x^{2} ’ + γ_{3} q_{3} d x^{3} ’) = 0, \\ d s ” = (γ_{0} q_{0} d x^{0} ” + γ_{1} q_{2} d x^{1} ” + γ_{2} q_{2} d x^{2} ” + γ_{3} q_{3} d x^{3} ”) = 0 . \end{matrix}

(67)

The dynamics of all other 23-λm,n-vacuum layers with all possible signatures (35) are determined similarly, see §2.12 in [2].

Further development of various options for the dynamics of vacuum layers, based on different methods of representing quadratic forms with different signatures (35) in the form of two linear forms with different signatures (3) in [1] can significantly enrich the mathematical apparatus of the Algebra of Signature for describing complex intra-vacuum structures and processes. Perhaps these areas of the calculus of variations will interest mathematicians with the hope that they will be in demand by physicists.

Looking significantly ahead, we note that for the geometrization of most branches of modern physics based on the Algebra of Signatures, simplifications related to Riemannian geometry (see Figure 4a) are sufficient. This will be shown in the following articles of this series. However, to geometrize psychophysical phenomena, it is necessary to develop the most complex version of differential geometry: – the geometry of absolute parallelism (see Figure 4b) [4,6] with using the Algebra of Signature, i.e. taking into account the totality of distortions of all 16 types of affine spaces with different stignatures (3) in [1]

s t i g n (e_{i}^{(a)}) = (\begin{matrix} \{+ + + +\} & \{+ + + -\} & \{- + + -\} & \{+ + - +\} \\ \{- - - +\} & \{- + + +\} & \{- - + +\} & \{- + - +\} \\ \{+ - - +\} & \{+ + - -\} & \{+ - - -\} & \{+ - + +\} \\ \{- - + -\} & \{+ - + -\} & \{- + - -\} & \{- - - -\} \end{matrix} .)

(68)

4. Dynamics of a two-sided 23-λm,n-vacuum in a state of constant curvature

4.1. Stationary metric in Riemannian geometry

Let's continue considering metrics (52)

\{\begin{matrix} d s^{(+) 2} = g_{i j}^{(+)} d x^{i} d x^{j} w i t h s i g n a t u r e (+ - - -) - m e t r i c o f s u b c o n t (o u t e r s i d e o f a 2^{3} -_{m, n} - v a c u u m), \\ d s^{(-) 2} = g_{i j}^{(-)} d x^{i} d x^{j} w i t h s i g n a t u r e (- + + +) - m e t r i c o f a n t i s u b c o n t (i n e r s i d e o f a 2^{3} -_{m, n} - v a c u u m) . \end{matrix}

(69)

Everything described below applies to both metrics (69) separately, so we investigate the general case

d s^{2} = g_{i j} d x^{i} d x^{j} \leftrightarrow \{\begin{matrix} o r d s^{(+) 2} = g_{i j}^{(+)} d x^{i} d x^{j}, \\ o r d s^{(-) 2} = g_{i j}^{(-)} d x^{i} d x^{j} . \end{matrix}

(70)

Further in this paragraph we will partially repeat the derivation of several equations from the classical source [5], pp. 250 – 251 due to the fact that these equations are of particular importance for the vacuum dynamics developed here. In addition, the order of presentation has been expanded and changed, and a slightly different interpretation of the results obtained has been proposed.

We assume that all components of the metric tensor in metric (70) are independent of time

g_{i j} = c o n s t .

(71)

Let’s rewrite the quadratic form (70), highlighting the components with zero indices

d s^{2} = с^{2} g_{00} d t^{2} + 2 c g_{0 α} d x^{α} d t + g_{α β} d x^{α} d x^{β} \leftrightarrow \{\begin{matrix} o r d s^{(+) 2} = {g_{00}^{(+)} (d x^{0})}^{2} + 2 g_{0 α}^{(+)} d x^{0} d x^{α} + g_{α β}^{(+)} d x^{α} d x^{β}, \\ o r d s^{(-) 2} = {g_{00}^{(-)} (d x^{0})}^{2} + 2 g_{0 α}^{(-)} d x^{0} d x^{α} + g_{α β}^{(-)} d x^{α} d x^{β}, \end{matrix}

(72)

where α, β = 1, 2, 3; dx0 = cdt.

4.2. Velocity of a local region of metric space

Let’s determine the speed of movement of a local region of the metric space (in particular, subcont or antisubcont), the metric-dynamic properties of which are determined by the stationary metric (72).

To do this, to the right side of the generalized metric (72) we add and subtract the quantity

{(\frac{g_{0 α} d x^{α}}{\sqrt{g_{00}}})}^{2} = \frac{g_{0 α} g_{0 β}}{g_{00}} d x^{α} d x^{β},

(73)

as a result, we get

d s^{2} = с^{2} {[\sqrt{g_{00}} d t + \frac{g_{0 α} d x^{α}}{c \sqrt{g_{00}}}]}^{2} - [- g_{α β} + \frac{g_{0 α} g_{0 β}}{g_{00}}] d x^{α} d x^{β},

(74)

whence for the studied area of space we have an analogue of proper time [5]

d τ = \sqrt{g_{00}} d t + \frac{g_{0 α} d x^{α}}{c \sqrt{g_{00}}} o r d τ = \frac{\sqrt{g_{00}}}{с} (d x^{0} + \frac{g_{0 α}}{g_{00}} d x^{α}) .

(75)

The second term in Ex. (74) is the square of the distance between two points in a 3-dimensional metric space (in this case, in a 3-dimensional subcount or in a 3-dimensional antisubcount)

d l^{2} = - [g_{α β} - \frac{g_{0 α} g_{0 β}}{g_{00}}] d x^{α} d x^{β} o r d l^{2} = γ_{α β} d x^{α} d x^{β},

(76)

where the 3-dimensional spatial metric tensor is introduced

{γ_{α β} = - g}_{α β} + \frac{g_{0 α} g_{0 β}}{g_{00}}

(77)

Metric (74) taking into account Exs. (75) and (76) takes the form

d s^{2} = с^{2} d τ^{2} - d l^{2},

(78)

which corresponds to the reference system in which the local area under study of one of the sides of the 23-λm,n-vacuum (in particular, subcont or antisubcont) is at rest.

Now we can introduce the 3-dimensional speed of movement of a local region of the metric space (in this case, subcont or antisubcont), the metric-dynamic properties of which are specified by the components of the metric tensor from metric (72). We divide the distance (76) by the time (75), as a result we obtain the modulus of the velocity vector

|\vec{v}| = \frac{d l}{d τ} = \frac{c d l}{\sqrt{g_{00}} (x^{0} + \frac{g_{0 α}}{g_{00}} d x^{α})} = \frac{c \sqrt{(- g_{α β} + \frac{g_{0 α} g_{0 β}}{g_{00}}) d x^{α} d x^{β}}}{\sqrt{g_{00}} (x^{0} + \frac{g_{0 α}}{g_{00}} d x^{α})}

(79)

with components [5], p. 250

v^{α} = \frac{c d x^{α}}{\sqrt{g_{00}} (x^{0} + \frac{g_{0 α}}{g_{00}} d x^{α})} .

(80)

The covariant components of the velocity vector

v_{α}

are determined by the Expressions [5], p. 250

v_{α} = γ_{α β} v^{β}

v^{2} = v_{α} v^{β}

Taking into account Ex. (79), the stationary metric (72) can be represented as [5], p. 250

d s^{2} = g_{00} {(d x^{0} - g_{α} d x^{α})}^{2} (1 - \frac{v^{2}}{с^{2}}),

(81)

where the 3-dimensional vector is introduced

g_{α} = - \frac{g_{0 α}}{g_{00}} .

(82)

The 4-speed components

u^{i} = \frac{d x^{i}}{d s}

, taking into account Ex. (81) are equal [5], p. 251

u^{0} = \frac{1}{\sqrt{g_{00}} \sqrt{1 - \frac{v^{2}}{c^{2}}}} + \frac{g_{α} v^{α}}{c \sqrt{1 - \frac{v^{2}}{c^{2}}}}, u^{α} = \frac{v^{α}}{c \sqrt{1 - \frac{v^{2}}{c^{2}}}} .

(83)

4.3. Acceleration of a local region of metric space

Let’s find the acceleration of a local region of the metric space (in particular, subcont or antisubcont), the metric-dynamic properties of which are determined by the stationary metric (72).

As was shown in §1.1, the acceleration of a local region of the metric space with simplifications related to Riemannian geometry is given by Eq. (26)

\frac{d^{2} x^{l}}{d s^{2}} = - Г_{i j}^{l} \frac{d x^{i}}{d s} \frac{d x^{j}}{d s}

(84)

We find Christoffel symbols (25)

Г_{i j}^{l} = \frac{1}{2} g^{l μ} (\frac{\partial g_{μ i}}{\partial x^{j}} + \frac{\partial g_{μ j}}{\partial x^{i}} - \frac{\partial g_{i j}}{\partial x^{μ}})

(85)

for the considered stationary case.

Let’s substitute the components of the metric tensor from the stationary metric (72) into Ex. (85). As a result, taking into account conditions (71), we obtain the following non-zero components of this pseudo-tensor [5], p. 251

Г_{00}^{α} = ½ g_{00}^{; α},

(86)

Г_{0 β}^{α} = ½ g_{00} (g_{; β}^{α} - g_{β}^{; α}) - ½ g_{β} g_{00}^{; α},

(87)

Г_{β λ}^{α} = λ_{β λ}^{α} + ½ g_{00} [g_{β} (g_{λ}^{; α} - g_{; λ}^{α}) + g_{λ} (g_{β}^{; α} - g_{; β}^{α})] + ½ g_{β} g_{λ} g_{00}^{; α},

(88)

where, for example,

g_{λ}^{; α}

is the covariant derivative, which in this case coincides with the partial derivative [5]:

g_{; γ}^{α} = \frac{\partial g^{α}}{\partial x^{γ}} + Г_{k γ}^{α} g^{k} = \frac{\partial g^{α}}{\partial x^{γ}};

(89)

λ_{β λ}^{α}

is a 3-dimensional Christoffel symbol composed of components of the metric tensor

g_{α β}

in the same way as

Г_{i j}^{l}

is composed of components

g_{i j}

In Ex. (86) – (89) all tensor actions (covariant differentiation, raising and lowering indices) are performed in a 3-dimensional space with a metric

g_{α β}

over a 3-dimensional vector

g_{α}

and a scalar

g_{00}

Let’s substitute Ex. (86) – (89) into the equation of motion (84), as a result we obtain [5], p. 251

\frac{d u^{α}}{d s} = - Г_{00}^{α} {(u^{0})}^{2} - 2 Г_{0 β}^{α} u^{0} u^{β} - Г_{β λ}^{α} u^{β} u^{λ} .

(90)

After transforming Ex. (90) using 4-speed components (83) and Christoffel symbols (86) – (89), we obtain [5], p. 251

\frac{d u^{a}}{d s} = \frac{d}{d s} \frac{ν^{α}}{с \sqrt{1 - \frac{ν^{2}}{с^{2}}}} = - \frac{g_{00}^{; α}}{2 g_{00} (1 - \frac{ν^{2}}{c^{2}})} - \frac{\sqrt{g_{00}} (g_{; β}^{α} - g_{β}^{; α}) ν^{β}}{c (1 - \frac{ν^{2}}{c^{2}})} - \frac{λ_{β γ}^{α} ν^{β} ν^{γ}}{c^{2} (1 - \frac{ν^{2}}{c^{2}})} .

(91)

In the general theory of relativity, based on Riemannian geometry, the force acting on a particle with momentum p = mv (where m is the mass of the particle, v is the speed of the flow entraining the particle) is defined as a 3-dimensional covariant differential [5], p. 251

f^{α} = c \sqrt{1 - \frac{ν^{2}}{с^{2}}} \frac{D p^{α}}{d s} = c \sqrt{1 - \frac{ν^{2}}{с^{2}}} \frac{d}{d s} \frac{{m ν}^{α}}{\sqrt{1 - \frac{ν^{2}}{с^{2}}}} + λ_{β γ}^{α} \frac{{m ν}^{β} ν^{γ}}{\sqrt{1 - \frac{ν^{2}}{с^{2}}}} .

(92)

Let’s divide the components of the force vector (92) by the particle mass m. As a result, we obtain the rooms of the acceleration vector of the local region of the metric space (in particular, subcont or antisubcont)

\frac{f^{α}}{m} = a^{α} = c \sqrt{1 - \frac{ν^{2}}{с^{2}}} \frac{d}{d s} \frac{ν^{α}}{\sqrt{1 - \frac{ν^{2}}{с^{2}}}} + \frac{λ_{β γ}^{α} ν^{β} ν^{γ}}{\sqrt{1 - \frac{ν^{2}}{с^{2}}}} .

(93)

components of the acceleration vector (93), taking into account Ex. (91), can be represented in the form (for convenience, the index α is omitted) [5], p. 252

a_{α} = \frac{c^{2}}{\sqrt{1 - \frac{ν^{2}}{c^{2}}}} \{- \frac{\partial \ln \sqrt{g_{00}}}{\partial x^{a}} + \sqrt{g_{00}} (\frac{\partial g_{β}}{\partial x^{a}} - \frac{\partial g_{α}}{\partial x^{β}}) \frac{v^{β}}{c}\},

(94)

or in conventional three-dimensional vector notation [5], p. 252

\vec{a} = \frac{c^{2}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} \{- g r a d (\ln \sqrt{g_{00}}) + \sqrt{g_{00}} [\frac{\vec{v}}{c} \times r o t \vec{g}]\},

(95)

where

\vec{g} (g_{1}, g_{2}, g_{3})

is a 3-dimensional vector with components

g_{α} = - \frac{g_{0 α}}{g_{00}} .

(96)

In the note by Landau L.D. and Lifshits E.M. noted that in three-dimensional curvilinear coordinates

r o t \vec{g}

should be understood in the same sense as the vector dual to the tensor

(\frac{\partial g_{β}}{\partial x^{a}} - \frac{\partial g_{α}}{\partial x^{β}})

, so that its contravariant components should be written in the form [5], p 252

{(r o t \vec{g})}^{γ} = \frac{1}{2 \sqrt{γ}} e^{α β γ} (\frac{\partial g_{β}}{\partial x^{a}} - \frac{\partial g_{α}}{\partial x^{β}}),

(97)

where

\sqrt{γ}

is the determinant of the spatial metric tensor (77);

e^{α β γ} = e^{123} = e_{123}

= 1, and when two symbols are rearranged, the sign changes.

\vec{v} = \frac{d \vec{l}}{d τ} = \frac{c d \vec{l}}{\sqrt{g_{00}} (d x^{0} + \frac{g_{α β}}{g_{00}} d x^{α})}

(98)

is vector of the 3-dimensional velocity of a local region of a metric space (in particular, subcont or antisubcont) with components (80)

v^{1} = \frac{c d x^{1}}{\sqrt{g_{00}} (x^{0} + \frac{g_{01}}{g_{00}} d x^{1})}, v^{2} = \frac{c d x^{2}}{\sqrt{g_{00}} (x^{0} + \frac{g_{02}}{g_{00}} d x^{2})}, v^{3} = \frac{c d x^{3}}{\sqrt{g_{00}} (x^{0} + \frac{g_{03}}{g_{00}} d x^{3})} .

(99)

We note once again that the formula for the acceleration vector (95) was borrowed from the classical source [5], pp. 250 – 251, where it was obtained within the framework of Riemannian geometry (see Figure 4a), and under the condition that the metric is stationary (72), i.e. when the components of the metric tensor are independent of time (71)

g_{i j} = c o n s t

4.4. Acceleration of a local section of 23-λm,n-vacuum

If we perform all operations (71) – (98) separately with each of the metrics (69), we obtain two acceleration vectors:

a (+) = {\vec{a}}^{(+)} = \frac{c^{2}}{\sqrt{1 - \frac{v^{(+) 2}}{c^{2}}}} \{- g r a d (\ln \sqrt{g_{00}^{(+)}}) + \sqrt{g_{00}^{(+)}} [\frac{{\vec{v}}^{(+)}}{c} \times r o t {\vec{g}}^{(+)}]\}

(100)

is acceleration vector of the local region of the subcont (i.e., the outer side of the 23-λm,n-vacuum);

a (-) = {\vec{a}}^{(-)} = \frac{c^{2}}{\sqrt{1 - \frac{v^{(-) 2}}{c^{2}}}} \{- g r a d (\ln \sqrt{g_{00}^{(-)}}) + \sqrt{g_{00}^{(-)}} [\frac{{\vec{v}}^{(-)}}{c} \times r o t {\vec{g}}^{(-)}]\}

(101)

is acceleration vector of the local region of the antisubcont (i.e., the inner side of the 23-λm,n-vacuum).

Acceleration of a local region of the 23-λm,n-vacuum (32)

\frac{d^{2} x^{l}}{d s^{2}} = - \frac{1}{\sqrt{2}} (Г_{i j}^{l (+)} \frac{d x^{i}}{d s} \frac{d x^{j}}{d s} + i Г_{i j}^{l (-)} \frac{d x^{i}}{d s} \frac{d x^{j}}{d s}),

(102)

can be represented in the form

a^{(\pm) l} = \frac{1}{\sqrt{2}} (a^{(+) l} + i a^{(-) l}),

(103)

or with indexes omitted

a_{α}^{(\pm)} = \frac{1}{\sqrt{2}} (a_{α}^{(+)} + i a_{α}^{(-)}),

(104)

where in the stationary case under consideration, according to Ex. (94),

a_{α}^{(+)} = \frac{c^{2}}{\sqrt{1 - \frac{v^{(+) 2}}{c^{2}}}} \{- \frac{\partial \ln \sqrt{g_{00}^{(+)}}}{\partial x^{a}} + \sqrt{g_{00}^{(+)}} (\frac{\partial g_{β}^{(+)}}{\partial x^{a}} - \frac{\partial g_{α}^{(+)}}{\partial x^{β}}) \frac{v^{(+) β}}{c}\},

(105)

a_{α}^{(-)} = \frac{c^{2}}{\sqrt{1 - \frac{v^{(-) 2}}{c^{2}}}} \{- \frac{\partial \ln \sqrt{g_{00}^{(-)}}}{\partial x^{a}} + \sqrt{g_{00}^{(-)}} (\frac{\partial g_{β}^{(-)}}{\partial x^{a}} - \frac{\partial g_{α}^{(-)}}{\partial x^{β}}) \frac{v^{(-) β}}{c}\} .

(106)

In this case, the acceleration vector of the local region of the 23-λm,n-vacuum, taking into account (100) – (101) has the form

(107)

where a(±) =

{\vec{a}}^{(\pm)} (\frac{1}{\sqrt{2}} (a_{1}^{(+)} + i a_{1}^{(-)}), \frac{1}{\sqrt{2}} (a_{2}^{(+)} + i a_{2}^{(-)}), \frac{1}{\sqrt{2}} (a_{3}^{(+)} + i a_{3}^{(-)})) .

5. Geometrized Lorentz force

5.1. Geometricized vectors of eclectic tension and magnetic induction

5.2. The meaning of geometrized vectors of electric field strength Ev and magnetic induction Bv

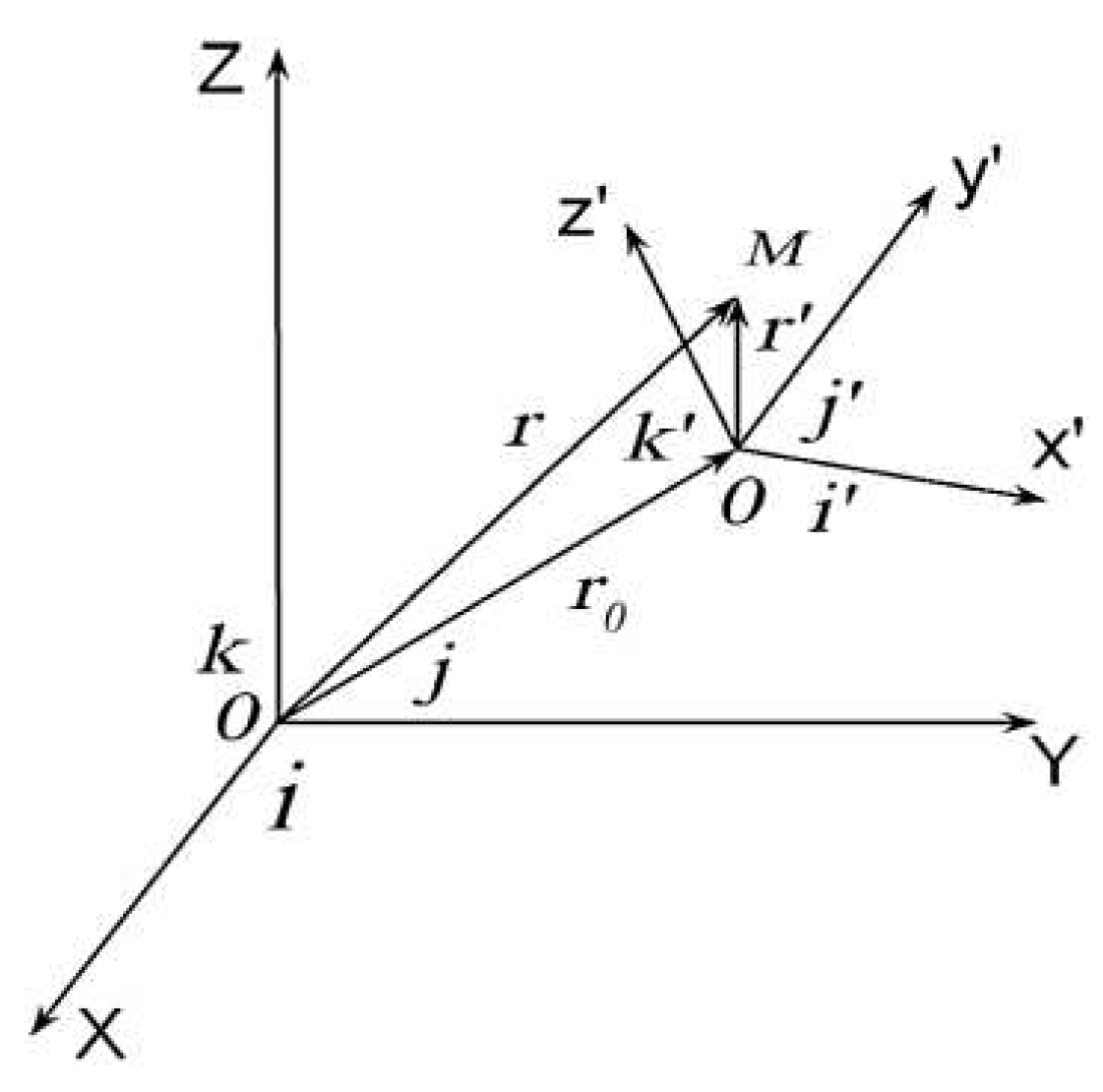
To clarify the meaning of the vectors Ev and Bv, consider the arbitrary motion of an affine space with stignature {+ + + +} (i.e., reference frame) K′ (t′,x′,y′,z′) relative to a stationary affine space with signature {+ + + +} (i.e. frame of reference) K (t,x,y,z) (see Figure 8). This well-known classical task is borrowed from [7] in full, because otherwise, establishing the meaning of the vectors Ev and Bv will be very problematic.

6. Geometricized vectors of electric field strength and magnetic induction of the 2k-λm,n-vacuum

6.1. Geometricized vectors of electric field strength and magnetic induction of the 23-λm,n-vacuum

Let‘s return to the consideration of a stationary curved area of a two-sided 23-λm,n-vacuum within the framework of the Algebra of Signature representations with simplifications related to Riemannian geometry (see Figure 4a).

In § 4.4, the acceleration vector of the stationary area of the 23-λm,n-vacuum (107) was obtained

(134)

where, according to Exs. (100) – (101) and § 5.1,

(135)

(136)

Let‘s substitute the acceleration vectors (135) and (136) into Ex. (134), as a result we obtain

(137)

(138)

where according to expressions (116) – (118):

Ev(+) is geometrized vector of the electric field strength of subcont, with components:

(139)

Bv(+) is geometrized vector of the magnetic induction with of subcont, with components:

(140)

here

(141)

Ev(−) is geometrized vector of the electric field strength of antisubcont, with components:

(142)

Bv(−) is geometrized vector of the magnetic induction with of antisubcont, with components:

(143)

here

(144)

We recall that time-independent components of the metric tensors

g_{i j}^{(+)} = c o n s t

and

g_{i j}^{(-)} = c o n s t

from the conjugate stationary metrics (72):

(145)

are substituted into Exs. (139) – (144).

Taking into account Exs. (139) – (144), the components of the 3-dimensional acceleration vector of the stationary curved local area of the two-sided 23-λm,n-vacuum a(±) (138) are equal to the modules of complex numbers: a(±)

(|a_{1}^{(\pm)}|, |a_{2}^{(\pm)}|, |a_{3}^{(\pm)}|),

where:

(146)

or according to Ex. (137)

a_{1}^{(\pm)} = \frac{1}{\sqrt{2}} \{[E_{v 1}^{(+)} + (v_{2}^{(+)} B_{v 3}^{(+)} - v_{3}^{(+)} B_{v 2}^{(+)})] + i [E_{v 1}^{(-)} + (v_{2}^{(-)} B_{v 3}^{(-)} - v_{3}^{(-)} B_{v 2}^{(-)})]\}, a_{2}^{(\pm)} = \frac{1}{\sqrt{2}} \{[E_{v 2}^{(+)} + (v_{3}^{(+)} B_{v 1}^{(+)} - v_{1}^{(+)} B_{v 3}^{(+)})] + i [E_{v 2}^{(-)} + (v_{3}^{(-)} B_{v 1}^{(-)} - v_{1}^{(-)} B_{v 3}^{(-)})]\}, a_{3}^{(\pm)} = \frac{1}{\sqrt{2}} \{[E_{v 3}^{(+)} + (v_{1}^{(+)} B_{v 2}^{(+)} - v_{2}^{(+)} B_{v 1}^{(+)})] + i [E_{v 3}^{(-)} + (v_{2}^{(-)} B_{v 1}^{(-)} - v_{1}^{(-)} B_{v 2}^{(-)})]\} .

(147)

We recall that these results were obtained for the simplest level of consideration, i.e. for a two-sided 23-λm,n-vacuum with simplifications corresponding to Riemannian geometry, and in the case of constancy of the subcont metric tensors

g_{i j}^{(+)} = c o n s t

and antisubcont

g_{i j}^{(-)} = c o n s t

6.2. Geometricized vectors of electric field strength and magnetic induction of the 26-λm,n-vacuum

At the level of considering a 16-sided 26-λm,n-vacuum with similar simplifications and stationarity conditions, based on Ex. (47), we similarly obtain

(148)

where

(149)

where

g_{α}^{(q)} = - \frac{g_{0 α}^{(q)}}{g_{00}^{(q)}},

in this case, the time-independent components of the metric tensors

g_{i j}^{(q)} = c o n s t

are taken from sixteen interconnected stationary metrics

d s^{(q) 2} = {g_{00}^{(q)} (d x^{0})}^{2} + 2 g_{0 α}^{(q)} d x^{0} d x^{α} + g_{α β}^{(q)} d x^{α} d x^{β}

(150)

with the corresponding signature from matrix (35).

The dynamics of the next deeper level of stationary 210-λm,n-vacuum and the dynamics of all subsequent deeper 2k-λm,n-vacuums (with k tending to infinity) can be developed similarly.

Conclusions

In this fourth part of the scientific project under the general title “Geometrized vacuum physics", the dynamics of vacuum layers is considered using the Algebra of Signature (Alsigna), the foundations of which are presented in [1,2,3].

This article continues the development of Alsigna’s mathematical apparatus for studying accelerated processes in λm,n-vacuum layers at the simplest levels of consideration: 23-λm,n-vacuum and 26-λm,n-vacuum. In this case, the main results were obtained with simplifications related to Riemannian geometry.

At the same time, methods are given to expand the capabilities of differential geometry by increasing the complexity of the considered types of distortions of metric spaces with different signatures (i.e., topologies), which are considered as adjacent layers of 2k-λm,n-vacuum.

At the end of the article, the acceleration of layers of a 2k-λm,n-vacuum, which is in a stationary state (i.e., unchanged with time), is considered. In this case, with simplifications related to Riemannian geometry, it was possible to show that stable intertwined, accelerated laminar and rotational flows of a 2k-λm,n-vacuum can be described in terms of vacuum electric field strength and vacuum magnetic induction.

This result may be important, since it allows us to outline ways of conscious control of intra-vacuum processes by generating electromagnetic fields of a given configuration.

Thus, the stationary dynamic models of accelerated and rotational movements of a 2k-λm,n-vacuum layers proposed in this article can serve as a theoretical basis for the development of “vacuum electromagnetic dynamics” and subsequently for increasing the capabilities of “zero” (i.e. vacuum) technologies.

In subsequent articles of the “Geometrized vacuum physics” it will be shown that Riemannian geometry, taking into account the Algebra of Signature, may be sufficient to create geometrized mathematical models of the standard Universe, all elementary particles, electromagnetic phenomena, nuclear and gravitational interactions and many others physical processes. In other words, a project aimed at the complete geometrization of inanimate physics does not require a radical complication of the original differential geometry.

However, it later became clear that it is impossible to create a completely complete mathematical model of the Universe without developing the most complex version of differential geometry, which takes into account all types of distortions (see Figure 4b) of intertwined spaces with different signatures (i.e. topologies). Some directions of development of differential geometry are indicated in §3. Many steps in this direction have already been made in the geometries of Weyl, Eddington, Lobachevsky, Klein, Cartan - Schouten, Penrose, Finsler, Weizenbeck - Vitali - Shipov, etc. However, an all-encompassing differential geometry has not yet been created, and this does not allow physicists to break out of the circle outlined by simplified versions of geometries.

References

Batanov-Gaukhman, M. “Geometrized Vacuum Physics. Part I. Algebra of Stignatures“. Preprints 2023, 2023060765. [CrossRef]
Batanov-Gaukhman, M. “Geometrized Vacuum Physics. Part II. Algebra of Signatures“. Preprints 2023, 2023070716. [CrossRef]
Batanov-Gaukhman, M. “Geometrized Vacuum Physics. Part III. Curved Vacuum Area“. Preprints 2023, 2023080570. [CrossRef]
Shipov, G. (1997). “Geometry of absolute parallelism“, – Moscow: Science, 134 р.
Landau, L.D. , & Lifshitz, E.M. (1971). “The Classical Theory of Fields“/ Course of theoretical physics, V.2. Translated from the Russian by Hamermesh M. University of Minnesota – Pergamon Press Ltd. Oxford, New York, Toronto, Sydney, Braunschwei, p. 387.
Shipov, G. (1998). ”A Theory of Physical Vacuum”. Moscow ST-Center, Russia ISBN 5 7273-0011-8.
Detlaf, A.A. , Yavorsky, B.M. (1989). “Physics Course”. – Moscow: Higher School, ISBN: 5-06-003556-5.

Figure 1. λm,n-vacuum is embedded in λf,d -vacuum, where λf,d > λm,n (repetition of Figure 3 in [3]).

Figure 5. Many streams in a freely falling stream of liquid twist into a spiral.

Figure 6. Illustrations of mixing of white and black "liquids".

Figure 7. Fractal illustration of the interweaving of 16-“colored” geodesic lines, (i.e. accelerated streams or currents) forming the fabric of the 26-λm,n-vacuum.

Figure 8. Motion of the reference frame (or affine space) К′ with signature {+ + + +}. relative the rest reference frame (or affine space) K with signature {+ + + +}.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Geometrized Vacuum Physics. Part IV: Dynamics of Vacuum Layers

Abstract

1. Background and Introduction

2. Materials and Method

2.1. Equation of the geodesic line of a two-sided 23-λm,n-vacuum

2.2. Equation of the geodesic line of a two-sided 23-λm,n-vacuum in the case of Riemannian geometry

2.3. Equation of the geodesic line of a 16-sided 26-λm,n-vacuum in the case of Riemannian geometry

3. Different directions of development of dynamics of a λm,n-vacuum layers

4. Dynamics of a two-sided 23-λm,n-vacuum in a state of constant curvature

4.1. Stationary metric in Riemannian geometry

4.2. Velocity of a local region of metric space

4.3. Acceleration of a local region of metric space

4.4. Acceleration of a local section of 23-λm,n-vacuum

5. Geometrized Lorentz force

5.1. Geometricized vectors of eclectic tension and magnetic induction

5.2. The meaning of geometrized vectors of electric field strength Ev and magnetic induction Bv

6. Geometricized vectors of electric field strength and magnetic induction of the 2k-λm,n-vacuum

6.1. Geometricized vectors of electric field strength and magnetic induction of the 23-λm,n-vacuum

6.2. Geometricized vectors of electric field strength and magnetic induction of the 26-λm,n-vacuum

Conclusions

References

MDPI Initiatives

Important Links

Subscribe