Unifying Quantum Mechanics and General Relativity: A Significant Application of Semi-Structured Complex Numbers

Preprint

Article

Unifying Quantum Mechanics and General Relativity: A Significant Application of Semi-Structured Complex Numbers

Altmetrics

Downloads

174

Views

Comments

Peter Jean Paul^*,Shanaz Wahid

This version is not peer-reviewed

Submitted:

19 October 2023

Posted:

20 October 2023

You are already at the latest version

Alerts

Abstract

Recently, a paper was written to establish semi-structured complex numbers ℍ (a new number set invented to enable division by zero) as a useful mathematical tool providing novel results from its application in engineering and science. Whilst the paper was a milestone, the application of this number set to quantum and classical physics had not been fully explored. Consequently, the aim of this research was to use semi-structured complex numbers to develop a new mathematical model for the mass of an object and in course unite classical and quantum physics in a simple yet effective manner. As its major contributions this paper: (1) develops a new mathematical model for the mass of an object called the wave-mass function using De Broglie’s mass and frequency relation and semi-structured complex numbers; (2) uses the new wave-mass function to determine what happens to an object traveling at the speed of light; (3) derives a relation between Schrödinger’s wave function and the new wave-mass function; (4) derives a relation between Einstein’s Field Equation and the new wave-mass function; (5) uses the wave-mass function to combine Einstein’s Field Equation with Schrödinger’s wave function to form a new quantum gravity equation. These results and their applications provide a firm foundation to advance the number set ℍ as a useful mathematical tool.

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

1. Introduction

1.1. Newtonian Mechanics and Einstein’s General Theory of Relativity

In the 17th Century Sir Isaac Newton discovered the Universal Law of Gravitation. This Law states that “any two bodies in the universe with mass

m_{1}

and

m_{2}

respectively attract each other with a force

F

that is directly proportional to the product of their mass and inversely proportional to the square of the distance (

r^{2}

) apart” [1]. The Law of universal gravitation can be represented by Equation (1) [1].

F = \frac{G m_{1} m_{2}}{r^{2}}

(1)

According to Newton, gravity was a force of attraction that acted instantaneously between objects. However, whilst Newton’s Universal Law of Gravity could predict the motion of an apple falling from a tree and the orbit of the moon around the earth, Newton could not explain why gravity exist nor why it acts.

To answer these questions Albert Einstein released his theory of General Relativity in 1915 [2]. In his theory he stated that the three dimensions of space and the one dimension of time are two parts of the same thing, that thing being space-time [2]. Objects exist at a given point in space at a given time.

Whilst Newton’s Law of Universal Gravity indicated that gravity was a force that acts instantaneously between objects, Einstein’s Theory of General Relativity indicated that gravity was actually the curvature of space-time that results from the presence of matter. The more matter exist the more space-time becomes warped. In turn the curvature of space-time dictates how matter moves. This is demonstrated in Figure 1a,b.

One object B in the gravitational field of another object A moves according to the curvature of the space time produced by both B and A (as shown in Figure 2) [3].

Einstein’s Theory of General Relativity agreed with Newton’s Universal Law of Gravity in situations where gravity is weak, but the two theories produce different results in cases where gravity is strong (such as in Black Holes). Nevertheless, Einstein’s theory is considered a better explanation of gravity as it not only predicts the same phenomenon that Newton’s Universal Law of Gravity predicts but also predicts other experimentally verifiable phenomenon (such as gravitational waves and gravitation lensing) that Newton’s Universal Law of Gravity fails to accurately predict [4]. Einstein’s Theory of General relativity is represented by Equation (2) [5].

R_{μ ν} - \frac{1}{2} R g_{μ ν} = \frac{8 π G}{c^{4}} T_{μ ν}

(2)

here
$R_{μ ν}$	Ricci tensor curvature. The Ricci tensor represents how a volume in a curved space differs from a volume in Euclidean space [6].
$R$	Ricci scalar curvature. This is a measure of the curvature of a Riemannian manifold. A manifold is the multidimensional analogue of a surface. A Riemannian manifold is a smooth manifold (locally Euclidean) with nicely defined structures (inner products, tangent space etc.) that allow for easy transfer of Euclidean math to the curved object.
$g_{μ ν}$	The metric tensor. This tensor is a function which tells how to compute the distance between any two points in a given space.
$T_{μ ν}$	The stress-energy tensor. The stress–energy tensor describes the flow of energy and momentum in spacetime. It is the source of gravitational fields [7].
$c$	speed of light in a vacuum
$G$	universal gravitational constant
$π$	The constant pi

The left side of the equation (

R_{μ ν} - \frac{1}{2} R g_{μ ν}

) describes the geometry of space-time and indicated how gravitational fields affects that geometry [5]. The right side of the equation contains the stress-energy tensor

T_{μ ν}

(the energy and mass terms) and is the origin of gravitational fields. As is popularly known the left side tells mass and energy how to move whilst the right side tells space-time how to curve. The expression

\frac{8 π G}{c^{4}}

is merely present for housekeeping purposes to ensure the units on either side of the expression matches correctly.

One of the most important foundational points is that the stress-energy tensor

T_{μ ν}

has 16 elements (as shown in Equation (3)).

T^{μ ν} = (\begin{matrix} \begin{matrix} T^{00} & T^{01} \\ T^{10} & T^{11} \end{matrix} & \begin{matrix} T^{02} & T^{03} \\ T^{12} & T^{13} \end{matrix} \\ \begin{matrix} T^{20} & T^{21} \\ T^{30} & T^{31} \end{matrix} & \begin{matrix} T^{22} & T^{23} \\ T^{32} & T^{33} \end{matrix} \end{matrix})

(3)

Each element or set of elements in the stress-energy tensor represents some specific quantity. These quantities, their meaning and equations are given in Table 1.

The elements of the stress-energy tensor

T_{μ ν}

are more clearly shown in Figure 3.

According to column 3 of Table 1, the elements in the stress-energy tensor are some form of energy divided by other physical quantities. This fact can become very useful in creating an equation for quantum gravity.

1.2. The Problem with Einstein’s General Theory of Relativity and Quantum Mechanics

Although valuable, General Relativity cannot ultimately be the correct theory for space-time. It an approximation that works in some circumstances but fails in others. This is known because General relativity does not fit together with another well-established theory; quantum mechanics.

Quantum mechanics is the branch of mechanics that deals with the mathematical description of the motion and interaction of subatomic particles, incorporating the concepts of quantization of energy and wave-particle duality [8]. In quantum mechanics it has been shown experimentally that quantum particles have strange properties such as being in two places at the same time and obeying the uncertainty principle [8]. For example, an electron going through a double slit. Quantum Physics indicated that the electron goes through both slits at the same time. However, an electron has mass. This begs the question to which place does the gravitational pull go if the electron travels through both slits at the same time?

Unfortunately, General Relativity is not a quantum theory. To understand how to solve this we need to understand the quantum properties of gravity and as a consequence there needs to be a theory of quantum gravity.

Quantum gravity is a field of theoretical physics that seeks to describe gravity according to the principles of quantum mechanics. It deals with environments in which neither gravitational nor quantum effects can be ignored, such as in the vicinity of black holes or similar compact astrophysical objects, such as neutron stars as well as in the early stages of the universe moments after the Big Bang.

Whilst several have tried to develop such a theory there has been no satisfactory outcome. Two primary examples are, String theory and Loop Gravity. The central idea of String Theory is to replace the classical concept of a point particle in quantum field theory with a quantum theory of one-dimensional extended objects: strings. The theory is successful in that it successfully models a graviton (the messenger particle of gravity); however, unfortunately it introduces six extra dimensions of space in addition to the usual three for space (and one for time). Loop Gravity on the other hand postulates that the structure of space and time is composed of finite loops woven into an extremely fine fabric or network. The biggest problem with Loop Gravity is that it has not yet shown that you can take a quantized space and take out a smooth space-time. Moreover, String theory and Loop Gravity adds needless complexity when attempting to combine the theories of General Relativity and Quantum Mechanics.

1.3. New Tools Required to Solve the Problem of Quantum Gravity

As a result, it has become obvious that new tools are required to solve the problem of quantum gravity. These new tools when used alongside well-established theories in classical and quantum mechanics should lead to a theory of quantum gravity that is simple to comprehend (mathematically and conceptually), well grounded in our current understanding of classical and quantum physics and does not add any needless features that would make the new theory unnecessarily complicated.

To establish a theory of quantum gravity it is first necessary to develop a basic understanding of two of the key quantities; energy and mass. To do this early work developed by Albert Einstein (Special Theory of Relativity and mass-energy equivalence), Louis De Broglie (particle-wave duality) and Erwin Schrödinger (wave function and wave equation). After developing a basic understanding of these theories one additional new tool semi-structured complex numbers (a new number set recently developed to solve the problem of division by zero) will be introduced. After this, all the tools necessary to form a new theory of quantum gravity would have been laid out and, the new theory can be developed.

1.4. Einstein’s Special Theory of Relativity and the Lorentz Factor

According to Einstein’s theory of general relativity the speed of an object affects its mass, length and time (as seen by an observer in a difference frame of reference). This can be represented mathematically using what is known as the Lorentz transformation [9]. For example, then when an object is at rest, it has a rest mass of

m_{0}

. The total energy that the object has is given by Equation (4):

E = m_{0} c^{2}

(4)

Here

c

is the speed of light and

E

is the internal energy (the sum of the potential and kinetic energy) of the object. Equation (4) is a partial representation of what is commonly known as the mass-energy equivalence equation. Note for an object in motion with momentum

\bar{p}

the complete equation becomes:

E^{2} = {(m_{0} c^{2})}^{2} + {(\bar{p} c)}^{2}

(5)

When an object begins to move with a speed

v

its mass increases. The increase mass (known as the relativistic mass

m_{r e l}

) is given by Equation (6).

m_{r e l} = \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} m_{0} = γ m_{0}

(6)

The symbol

γ

in Equation (6) is called the Lorentz factor and Equation (6) is called the Lorentz transformation.

There are two primary problems with Equation (6) that causes the equation to be subject to misinterpretation. First it implies that the increase of energy of an object with velocity appear to be connected with some change in the internal structure of the object. In reality, the greater the velocity of the object the greater the relativistic mass and the greater the object’s gravitational effect (or influence on the geometric properties of space-time). Secondly, the equation cannot give an interpretation of the relativistic mass of the object when it is moving at the speed of light. According to traditional physics, when

v = c

the Lorentz factor is undefined (which has no meaning physically), as shown in Equation (7).

γ = \frac{1}{\sqrt{1 - \frac{c^{2}}{c^{2}}}} = \frac{1}{\sqrt{1 - 1}} = \frac{1}{0} (u n d e f i n e d a c c d o r i n g t o t r a d i t i o n a l p h y s i c s)

(7)

Whilst the result in Equation (7) may appear impossible to solve, the use of semi-structured complex numbers may shade some light on a possible solution to the problem. However, this has never been attempted before. Despite these drawbacks Equation (4) did lead to other important discoveries.

1.5. Wave-Particle Duality: De Broglie’s Discoveries

In October 1925 Einstein published his thesis in which he described the photoelectric effect. The photoelectric effect essentially prove that light waves can behave like particles. Einstein called these particles photons. Louis De Broglie published his thesis a year earlier (1924) in which he explained the wave-particle duality. In his thesis he theorized that if light wavs can behave like particles then particles (like electrons) can behave like waves. De Broglie proposed that for a matter particle of mass

m

moving with velocity

v

you can associate a wave with wavelength

λ

. De Broglie showed this by simply stating that if

E = m c^{2}

and

E = h f

then the relation given in Equation (8) must be true.

E = m c^{2} and E = h f m c^{2} = h f m = \frac{h}{c^{2}} f

(8)

De Broglie also indicated that if the particle has a total energy

E

, the wave associated with the particle also has a frequency

f

given by Equation (9). Additionally, he showed that the relationship between the wavelength of the wave and the momentum of the particle (given by

m v

) is described in Equation (10). De Broglie assumed that Equation (9) and Equation (10) holds for all matter particles. At the time, even though there was no experimental evidence to support these equations, Equation (9) and Equation (10) were a landmark discovery.

f = \frac{E}{h}

(9)

λ = \frac{h}{\bar{p}} = \frac{h}{m v}

(10)

here
$E$	Energy of particle (note the particle does not have to be subatomic)
$m$	Mass of the object
$c$	Speed of light of the object
$f$	Frequency of the object
$h$	Planck’s constant
$\bar{p}$	Momentum of the particle (Note, a bar was placed over the symbol for momentum to distinguish it from the symbol for the unstructured unit $p$ for semi-structured complex numbers)

Equation (8) establishes a relationship between the mass of a body and the frequency of its associated wave (the same wave that Schrödinger developed his wave function for in 1926). Unfortunately, the mathematics at the time did not permit De Broglie to go any further in flushing out other connections and the physics community was satisfied with the result.

Nevertheless, as small reconstruction of Equation (8) using semi-structured complex numbers could possibility yield even more results, further the understanding of wave-particle duality and open the door to other discoveries particularly in the areas of general relativity and quantum mechanics. However, this has not been attempted in recent literature.

1.6. Schrödinger’s Equation and the Wave Function

Erwin Schrödinger made his contribution by developing the wave function (

Ψ

) that describes the wave associated with any matter particle. He also developed what is now called Schrödinger ‘s equation, an equation that enables one to find the wave function of the wave associated with any particle. Schrödinger ‘s equation is given by Equation (11). This equation lead to the development of quantum physics.

i ℏ \frac{\partial Ψ}{\partial t} = \frac{- ℏ^{2}}{2 m} \frac{\partial^{2} Ψ}{\partial x^{2}} + V Ψ

(11)

here
$Ψ$	The wave function and it is usually the unknown in this equation that needs to be solved
$i ℏ \frac{\partial Ψ}{\partial t}$	Describes the total energy of the system. Over time the total energy must remain the same (law of conservation of energy).
$\frac{- ℏ^{2}}{2 m} \frac{\partial^{2} Ψ}{\partial x^{2}}$	Describes the kinetic energy of the particle (or system of particles).
$V Ψ$	Describes the potential energy of the particle (or system of particles).
$ℏ$	Planck’s constant divided by $2 π$ .

The problem with the Schrödinger’s equation is the interpretation of the wave function. One of the observations made was that the wave function does not describe a physical wave and the wave function itself is not a physically measurable quantity. The reason for this observation is that a quantity containing the imaginary unit

i

(as seen on the left-hand side of Equation (11)), is not a physically measurable quantity. In 1926 the physicist Max Born stated that the modulus squared of the wave function (that is,

{|Ψ|}^{2}

) gave the probability of finding the particle at a particular point in space. Max Born stated that the

Ψ

(the wave function) is a non-physical quantity called the probability amplitude of the particle. Whilst this interpretation does have value in explaining the uncertainty that is generally found in quantum mechanics, it does not help to fully provide a workable theory of quantum gravity.

Nevertheless, Einstein’s mass energy relation, De Broglie’s wave-particle duality and Schrödinger’s wave function can all be evolved into a theory of quantum gravity with the help of one more tool; semi-structured complex numbers.

1.7. Semi-Structured Complex Numbers: A Recent Development in Division by Zero

Recently there has been a range of research involving division by zero. Table 3, Appendix 1, shows sample research conducted from 2018 to 2022 on “division by zero”.

The problem of division by zero can simply be stated as: What is

\frac{a}{0}

where “a” is any complex number. There have been several solutions to the problem the most recent being the invention of the semi-structured complex number set

H

[10]. The first attempt at creating this number set was riddled with issues [10], however, a second paper [11], written to reformulate and strengthen the theory of semi-structured complex numbers, produced several grounded and profound results. Table 2 shows the major results (pertinent to this research) developed in paper [11].

Results 1 to Result 15 in Table 2 provide some significant foundational results for semi-structured complex numbers. Nevertheless, it is necessary to go beyond just the foundational setting and look at how this new number set can be applied in a practical setting particularly in the area of physics. Incidentally, this new number set could possibly be an important tool in developing a workable theory of quantum gravity.

1.8. Major Contributions

Given the potential importance of developing a theory of quantum gravity, the aim of this paper was:

To use semi-structured complex numbers to develop a new mathematical model for the mass of an object and in course unite classical and quantum physics in a simple yet effective manner.

Based on the stated aim, this paper makes the following five major contributions:

Develops a new mathematical model for the mass of an object called the wave-mass function ( $w_{m}$ ) using De Broglie’s mass and frequency relation and semi-structured complex numbers.
Uses the new wave-mass function to determine what happens to an object traveling at the speed of light.
Derives a relation between Schrödinger’s wave function and the new wave-mass function.
Derives a relation between Einstein’s Field Equation and the new wave-mass function.
Uses the wave-mass function to combine Einstein’s Field Equation with Schrödinger’s wave function to form a new quantum gravity equation.

The rest of this paper is devoted to showing how achieving the main aim of the paper leads to the major contributions outline.

2.0. The Wave-Mass Function: A New Model for the Mass of an Object

In order the solve the issues in special and general relativity and seamlessly tie quantum and classical mechanics, it is first necessary to develop a new model for the mass of an object. Semi-structured complex numbers along with De Broglie’s discoveries can be used to do this.

According to wave-particle duality, a particle (or an object) has both a mass (

m

) and an associated wave with frequency (

f

). The mass and the frequency are related by Equation (8). It can essentially be said that mass and frequency are the same aspect of an object just in different forms. This idea can be represented mathematically using semi-structured complex number form (as suggested by Result 15 of Table 2). However, whatever representation that is contrived must agree with established physics whilst adding new knowledge to the field. This is done using the following steps.

First, start with the assumption that the wave-particle nature of a particle of mass

m

and associated wave function frequency

f

can be represented as the semi-structured complex number given in Equation (14).

w_{m} = m_{0} - p (α f)

(14)

here
$w_{m}$	Wave-mass function of the object
$m_{0}$	Rest mass of the object
$α$	mass-frequency constant given by $α = \frac{h}{c^{2}} = 7.3725 \times 10^{- 51} k g . {H z}^{- 1}$
$f$	Frequency of the associated wave function of the object
$h$	Planck’s constant
$p$	The unstructured unit for the semi-structured complex number

Equation (14) simply says that the total mass of an object

w_{m}

(referred to in this paper as the wave-mass function of the object) is given by its rest mass

m_{0}

along with the frequency

f

of its associated wave (adjust by a constant

α

that is referred to in this paper as the mass-frequency constant). From Result 13 in Table 2, the unstructured unit

- p = 0

. This is used in Equation (14) to show that when the rest mass of an object (

m_{0}

) can be measured, the frequency

f

of its associated wave cannot be measured (only calculated). This agrees with standard physics.

The second step is to justify the existence of Equation (14). This is done by simply showing that it can be used to calculate the total energy of a particle and show that this agrees with classical physics. Using Equation (14) the total energy of a particle of wave-mass

w_{m}

can be calculated as shown:

w_{m} = m_{0} - p (α f)

Multiplying by

c^{2}

w_{m} c^{2} = m_{0} c^{2} - p (α f) c^{2}

w_{m} c^{2} = m_{0} c^{2} - p h f (since α c^{2} = h)

But recall the relations

λ = \frac{h}{\bar{p}}

which implies

h = λ \bar{p}

where

\bar{p}

is the momentum of the particle. Additionally,

c = f λ w h i c h i m p l i e s t h a t f = \frac{c}{λ}

Hence

w_{m} c^{2} = m_{0} c^{2} - p h f

(15)

w_{m} c^{2} = m_{0} c^{2} - p (λ \bar{p} \times \frac{c}{λ})

(16)

w_{m} c^{2} = m_{0} c^{2} - p c \bar{p}

From there the square magnitude of

w_{m} c^{2}

(that is,

{|w_{m} c^{2}|}^{2}

) can be found. Since the square of the magnitude of a semi-structured complex number is given by the sum of the square of its components, this implies that:

{|w_{m} c^{2}|}^{2} = {(m_{0} c^{2})}^{2} + {(c \bar{p})}^{2}

However, Equation (17) looks similar to Equation (5). Therefore, it can be concluded that the square of the total energy

E

of the particle is the same as

{|w_{m} c^{2}|}^{2}

. That is:

{|w_{m} c^{2}|}^{2} = E^{2} = {(m_{0} c^{2})}^{2} + {(c \bar{p})}^{2}

|w_{m} c^{2}| = E = \sqrt{{(m_{0} c^{2})}^{2} + {(c \bar{p})}^{2}}

(17)

Incidentally, Equation (17) is the famous mass energy equivalence relation developed by Einstein in 1905. Equation (17) shows that Equation (14) agrees with well-established classical physics. Equation (17) provides justification for the existence and use of Equation (14). This new model for the mass of an object links the classical mechanics idea of mass (

m

) and quantum mechanics of frequency (

f

) of the associated wave function. Other examples of where Equation (14) agrees with well-established classical physics is given in Appendix 2.

At this point it is instructive to investigate the value of Equation (14) into gaining new insight into the importance of wave-particle duality in the area of Special Relativity.

3.0. The Wave-Mass Function and Einstein’s Special Theory of Relativity

According to Einstein’s Special Theory of Relativity, the mass of a body travelling at velocity

v

near the speed of light is given by Equation (18).

m^{'} = γ m_{0} = \frac{m_{0}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}

(18)

Using Equation (14), Equation (18) can be rewritten as shown in Equation (19). Equation (19) essentially provides a link between Einstein’s Special Theory of Relativity and quantum mechanics.

{w_{m}}^{'} = γ w_{m} γ w_{m} = \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} \times [m_{0} - p (α f)]

(19)

Rewriting Equation (19) to Equation (20) clarifies what happens to an object as it moves with speeds close to the speed of light.

{w_{m}}^{'} = γ w_{m} γ w_{m} = \frac{m_{0}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} - p α \frac{f}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}

(20)

As an object begins to move at speeds close to the speed of light the components of the object’s wave-mass function increases; that is, the objects mass increases (which agrees with Einstein’s classical observations) and the frequency of the associated wave function also increases (this makes sense since frequency and mass are directly proportional).

The strength of Equation (20) is that it can tell us what happens to an object at the speed of light (that is, at

v = c

). Using Equation (20) and the rules for semi-structured complex numbers, this gives the following result:

When

v = c

{w_{m}}^{'} = γ w_{m}

γ w_{m} = \frac{m_{0}}{\sqrt{1 - \frac{c^{2}}{c^{2}}}} - p α \frac{f}{\sqrt{1 - \frac{c^{2}}{c^{2}}}}

γ w_{m} = \frac{m_{0}}{\sqrt{1 - 1}} - p α \frac{f}{\sqrt{1 - 1}}

γ w_{m} = \frac{m_{0}}{0} - p α \frac{f}{0}

γ w_{m} = \frac{1}{0} m_{0} - p \frac{1}{0} α f

But according to semi-structured complex numbers

\frac{1}{0} = p

(Table 2, Result 2). Hence this gives

γ w_{m} = p \times m_{0} - p \times p α f

Moreover, according to the rules of semi-structured complex numbers

- p \times p = 1

. Hence this gives:

{w_{m}}^{'} = p m_{0} + α f

(21)

Equation (21) suggests that at the speed of light the frequency of the associated wave of the particle becomes a measurable quantity and the mass of the particle becomes a quantity that cannot be measured. Essentially this implies that the particle essential behaves like a wave (or more specifically an electromagnetic wave) at the speed of light. Equation (21) also implies that at the speed of light classical mechanics gives way to quantum mechanics.

Further, Equation (21) can be interpreted in terms of space-time. According to Equation (20) and Equation (21) an object traveling at the speed of light no longer disturbs space-time by curving it but rather affects space-time by producing electromagnetic disturbances in the form of electromagnetic waves. For the wave-mass function to go back to its original state (that is, back to the form of Equation (14)) the particle must come to a complete stop. Proof of this is given in Appendix 3.

4.0. Uniting Einstein’s General Theory of Relativity and Quantum Mechanics

4.1. Deriving a Relation between Schrödinger’s Wave Function and the New Wave-Mass Function

The frequency

f

in the wave-mass function (

w_{m}

) is the frequency of the wave described by Schrödinger’s wave function (

Ψ

). It therefore stands to reason that a relation can be derived linking Schrödinger’s wave function and the new wave-mass function. The relation between Schrödinger’s wave function and the new wave-mass function is given in Equation (22). Here all the symbols have their previously defined meanings.

w_{m} = \frac{α e^{p (\frac{3}{4} π)}}{\sqrt{2} π i Ψ} \times \frac{\partial Ψ}{\partial t}

(22)

Proof of the relation given by Equation (22) is given in Appendix 4. This relation forms one of the corner pieces to unifying general relativity and quantum mechanics. For this reason, we will call this relation Schrödinger’s wave-mass relation.

4.2. Deriving a Relation between Einstein’s Field Equation and the New Wave-Mass Function

To derive a relation between Einstein’s Field Equation and the new wave-mass function, it is necessary to derive an expression between the wave-mass function and the energy

E

of an object and then relate this to the stress-energy tensor

T_{μ ν}

in Einstein’s Field Equations.

First, the relation between the energy an object possesses and the wave-mass function of the object is given by Equation (23). The derivation of Equation (23) is found in Appendix 5.

{E = w}_{m} . c^{2} . e^{p (\frac{π}{4})}

(23)

Secondly, since recall that one of the most important foundational points is that the stress-energy tensor

T^{μ ν}

has 16 elements

(T^{i j})

(as shown in Equation (3)).

T^{μ ν} = (\begin{matrix} \begin{matrix} T^{00} & T^{01} \\ T^{10} & T^{11} \end{matrix} & \begin{matrix} T^{02} & T^{03} \\ T^{12} & T^{13} \end{matrix} \\ \begin{matrix} T^{20} & T^{21} \\ T^{30} & T^{31} \end{matrix} & \begin{matrix} T^{22} & T^{23} \\ T^{32} & T^{33} \end{matrix} \end{matrix})

According to column 3 of Table 1, the elements in the stress-energy tensor are some form of energy divided by other physical quantities. Therefore, the stress-energy tensor can be written generically as:

T^{μ ν} = (\begin{matrix} \begin{matrix} \frac{E^{00}}{V^{00}} & \frac{E^{01}}{{(d A \times d t)}^{01}} \\ \frac{E^{10}}{{c . V}^{10}} & \frac{E^{11}}{V^{11}} \end{matrix} & \begin{matrix} \frac{E^{02}}{{(d A \times d t)}^{02}} & \frac{E^{03}}{{(d A \times d t)}^{03}} \\ \frac{E^{12}}{V^{12}} & \frac{E^{13}}{V^{13}} \end{matrix} \\ \begin{matrix} \frac{E^{20}}{{c . V}^{20}} & \frac{E^{21}}{{c . (d A \times d t)}^{21}} \\ \frac{E^{30}}{{c . V}^{30}} & \frac{E^{31}}{{c . (d A \times d t)}^{31}} \end{matrix} & \begin{matrix} \frac{E^{22}}{V^{22}} & \frac{E^{23}}{V^{23}} \\ \frac{E^{32}}{{c . (d A \times d t)}^{32}} & \frac{E^{33}}{V^{33}} \end{matrix} \end{matrix})

(24)

Hence using the expression in Equation (23), the stress-energy tensor can be converted into a wave-mass version of itself that can be called the wave-mass stress-energy tensor given by the symbol

{T_{w_{m}}}^{μ ν}

. The wave-mass stress-energy tensor

{T_{w_{m}}}^{μ ν}

is given as

T^{μ ν} = c^{2} . e^{p (\frac{π}{4})} . (\begin{matrix} \begin{matrix} \frac{{w_{m}}^{00}}{V^{00}} & \frac{{w_{m}}^{01}}{{(d A \times d t)}^{01}} \\ \frac{{w_{m}}^{10}}{{c . V}^{10}} & \frac{{w_{m}}^{11}}{V^{11}} \end{matrix} & \begin{matrix} \frac{{w_{m}}^{02}}{{(d A \times d t)}^{02}} & \frac{{w_{m}}^{03}}{{(d A \times d t)}^{03}} \\ \frac{{w_{m}}^{12}}{V^{12}} & \frac{{w_{m}}^{13}}{V^{13}} \end{matrix} \\ \begin{matrix} \frac{{w_{m}}^{20}}{{c . V}^{20}} & \frac{{w_{m}}^{21}}{{c . (d A \times d t)}^{21}} \\ \frac{{w_{m}}^{30}}{{c . V}^{30}} & \frac{{w_{m}}^{31}}{{c . (d A \times d t)}^{31}} \end{matrix} & \begin{matrix} \frac{{w_{m}}^{22}}{V^{22}} & \frac{{w_{m}}^{23}}{V^{23}} \\ \frac{{w_{m}}^{32}}{{c . (d A \times d t)}^{32}} & \frac{{w_{m}}^{33}}{V^{33}} \end{matrix} \end{matrix}) T^{μ ν} = c^{2} . e^{p (\frac{π}{4})} . {T_{w_{m}}}^{μ ν}

(25)

Hence Einstein’s Field Equation given by Equation (2) can be rewritten as Equation (26).

R_{μ ν} - \frac{1}{2} R g_{μ ν} = \frac{8 π G}{c^{4}} T_{μ ν} R_{μ ν} - \frac{1}{2} R g_{μ ν} = \frac{8 π G}{c^{4}} (c^{2} . e^{p (\frac{π}{4})} . {T_{w_{m}}}^{μ ν})

(26)

This can be simplified to Equation (27).

R_{μ ν} - \frac{1}{2} R g_{μ ν} = \frac{8 π G e^{p (\frac{π}{4})}}{c^{2}} {T_{w_{m}}}^{μ ν}

(27)

Equation (27) essentially uses semi-structured complex numbers to rewrite Einstein’s field equation so that the geometry of space-time is now dependent on the wave-mass function of the objects that affect space-time.

4.3. Combining Einstein’s Field Equation with Schrödinger’s Wave Function to form a New Quantum Gravity Equation

Using Equation (27) and Equation (22) Einstein’s field equations can now be rewritten in terms of Schrödinger’s wave equation. This can be done as follows:

{T_{w_{m}}}^{μ ν} = (\begin{matrix} \begin{matrix} \frac{{w_{m}}^{00}}{V^{00}} & \frac{{w_{m}}^{01}}{{(d A \times d t)}^{01}} \\ \frac{{w_{m}}^{10}}{{c . V}^{10}} & \frac{{w_{m}}^{11}}{V^{11}} \end{matrix} & \begin{matrix} \frac{{w_{m}}^{02}}{{(d A \times d t)}^{02}} & \frac{{w_{m}}^{03}}{{(d A \times d t)}^{03}} \\ \frac{{w_{m}}^{12}}{V^{12}} & \frac{{w_{m}}^{13}}{V^{13}} \end{matrix} \\ \begin{matrix} \frac{{w_{m}}^{20}}{{c . V}^{20}} & \frac{{w_{m}}^{21}}{{c . (d A \times d t)}^{21}} \\ \frac{{w_{m}}^{30}}{{c . V}^{30}} & \frac{{w_{m}}^{31}}{{c . (d A \times d t)}^{31}} \end{matrix} & \begin{matrix} \frac{{w_{m}}^{22}}{V^{22}} & \frac{{w_{m}}^{23}}{V^{23}} \\ \frac{{w_{m}}^{32}}{{c . (d A \times d t)}^{32}} & \frac{{w_{m}}^{33}}{V^{33}} \end{matrix} \end{matrix})

(28)

Substituting Equation (22) into Equation (28) gives:

{T_{w_{m}}}^{μ ν} = \frac{α e^{p (\frac{3}{4} π)}}{\sqrt{2} π i} (\begin{matrix} \begin{matrix} \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{00}}{V^{00}} & \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{01}}{{(d A \times d t)}^{01}} \\ \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{10}}{{c . V}^{10}} & \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{11}}{V^{11}} \end{matrix} & \begin{matrix} \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{02}}{{(d A \times d t)}^{02}} & \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{03}}{{(d A \times d t)}^{03}} \\ \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{12}}{V^{12}} & \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{13}}{V^{13}} \end{matrix} \\ \begin{matrix} \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{20}}{{c . V}^{20}} & \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{21}}{{c . (d A \times d t)}^{21}} \\ \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{30}}{{c . V}^{30}} & \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{31}}{{c . (d A \times d t)}^{31}} \end{matrix} & \begin{matrix} \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{22}}{V^{22}} & \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{23}}{V^{23}} \\ \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{32}}{{c . (d A \times d t)}^{32}} & \frac{{(\frac{1}{Ψ} . \frac{\partial Ψ}{\partial t})}^{33}}{V^{33}} \end{matrix} \end{matrix}) {T_{w_{m}}}^{μ ν} = \frac{α e^{p (\frac{3}{4} π)}}{\sqrt{2} π i} {T_{Ψ}}^{μ ν}

(29)

Substituting Equation (29) back into Equation (27) gives the following result:

R_{μ ν} - \frac{1}{2} R g_{μ ν} = \frac{8 π G e^{p (\frac{π}{4})}}{c^{2}} ({T_{μ ν}}^{w_{m}}) R_{μ ν} - \frac{1}{2} R g_{μ ν} = \frac{8 π G e^{p (\frac{π}{4})}}{c^{2}} (\frac{α e^{p (\frac{3}{4} π)}}{\sqrt{2} π i} {T_{μ ν}}^{Ψ}) R_{μ ν} - \frac{1}{2} R g_{μ ν} = \frac{8 π G e^{p (\frac{π}{4})}}{c^{2}} (\frac{h e^{p (\frac{3}{4} π)}}{c^{2} \sqrt{2} π i} {T_{μ ν}}^{Ψ}) R_{μ ν} - \frac{1}{2} R g_{μ ν} = \frac{4 \sqrt{2} h G e^{p (π)}}{i c^{4}} ({T_{μ ν}}^{Ψ}) R_{μ ν} - \frac{1}{2} R g_{μ ν} = \frac{4 \sqrt{2} h G (- 1)}{i c^{4}} ({T_{μ ν}}^{Ψ})

R_{μ ν} - \frac{1}{2} R g_{μ ν} = i \frac{4 \sqrt{2} h G}{c^{4}} ({T_{μ ν}}^{Ψ})

(30)

Equation (30) is the new quantum version of the Einstein Field Equation. There are a few points to note about this equation. Firstly, please note that

{T_{μ ν}}^{Ψ} = {T_{Ψ}}^{μ ν}

, it is only the subscripts that have changed position (when the stress-energy tensor is used in the field equation the letters

μ ν

become subscripts).

Secondly, this equation introduces a new matrix

{T_{μ ν}}^{Ψ}

which is the stress-energy tensor written in terms of 16 different Schrödinger’s wave equations (the elements of

{T_{μ ν}}^{Ψ}

). This new matrix

{T_{μ ν}}^{Ψ}

is called the Schrödinger’s wave stress-energy Tensor. Equation (30) basically says that the Schrödinger’s waves of the stuff in the system collectively combine to influence the geometry of space-time.

Thirdly, the right-hand side of the equation has the imaginary unit

i

. This does not mean that the right-hand side of the equation is not a physically measurable quantity. This

i

is for housekeeping purposes. When the Schrödinger’s wave stress-energy Tensor

{T_{μ ν}}^{Ψ}

produces an imaginary number this

i

cancels with that imaginary number to produce a real number.

Fourthly, this quantum version of Einstein’s Field Equation is called Einstein’s Quantum Field Equation. This equation ties quantum mechanics (Schrödinger’s waves on the right) with classical mechanics (Einstein’s space-time geometry on the left hand side of the equation). It is important to note that whilst Equation (30) suggests that all the elements in the Schrödinger’s wave stress-energy Tensor (

{T_{μ ν}}^{Ψ}

) must be converted into a Schrödinger’s wave function, this may not necessarily be the case. For example, there may be situations where the elements are mixed with some elements converted into a Schrödinger’s wave function and others remaining in a classical form. In any case, the key point remains that the elements in the original stress-energy tensor can be transformed into Schrödinger’s wave function with the use of the new wave-mass function derived in this paper.

Finally, it is worth noting that even though semi-structured complex numbers were used to derive this equation, the semi-structured complex components disappear in the final answer (Equation (30)).

5.0. Discussion

At the heart of this paper is the introduction of the new wave-mass function

w_{m}

, that expresses the mass of an object in terms of its rest mass and the frequency of its associated quantum wave (Equation (14)). This wave-mass function essentially takes De Broglie’s results and combines it into one semi-structured complex function. The form of the wave-mass function was chosen to ensure that it agrees with Einstein’s Special Relativity equations whilst adding new knowledge to the field of Special Relativity. The new wave-mass function was also used to unite Einstein’s General Theory of Relativity and Quantum mechanics.

There must be further study of the wave-mass function and its applications in other areas of classical and quantum mechanics to yield new insights into lingering problems. For example, as future research the wave-mass function can possibility be used in the double slit experiment to explain the distribution of gravity from an election that goes through two slits at the same time. As another example the wave-mass function and Einstein’s Quantum Field Equations (derived in this research) can be used to explain the interaction of gravitational and quantum effects at may be experienced in the vicinity of a black hole.

6.0. Conclusions

The aim of this research was to use semi-structured complex numbers to develop a new mathematical model for the mass of an object and in course unite classical and quantum physics in a simple yet effective manner to create a new theory of quantum gravity. In the process this paper makes four major contributions: (1) develops a new mathematical model for the mass of an object called the wave-mass function using De Broglie’s mass and frequency relation and semi-structured complex numbers (2) uses the new wave-mass function to determine what happens to an object traveling at the speed of light (3) derives a relation between Schrödinger’s wave function and the new wave-mass function (4) derives a relation between Einstein’s Field Equation and the new wave-mass function (5) uses the wave-mass function to combine Einstein’s Field Equation with Schrödinger’s wave function to form a new quantum gravity equation. These results and their applications provide a firm foundation to advance the number set ℍ as a useful mathematical tool.

Author Contributions

The Author’s contribution to the wok is as follows: Peter Jean Paul conducted the research and wrote the paper; Shanaz Wahid proofread the paper correcting grammatical errors and checking for mathematical consistency. All authors have approved the final version.

Conflict of Interest

The authors declare no conflict of interest.

Appendix 1. Research Conducted from 2018 to 2022 Involving Division by Zero

Table 3. Research conducted on division by zero from 2018 to 2022.

Research	Research Aim
[12,13,14]	Explores the application of division by zero in calculus and differentiation
[15]	Uses classical logic and Boolean algebra to show the problem of division by zero can be solved using today’s mathematics
[16]	Develops an analogue to Pappus Chain theorem with Division by Zero
[17]	This paper proposes that the quantum computation being performed by the cancer cell at its most fundamental level is the division by zero. This is the reason for the insane multiplication of cancer cells at its most fundamental scale.
[18]	Explores evidence to suggest zero does divide zero
[19]	Considered using division by zero to compare incomparable abstract objects taken from two distinct algebraic spaces
[20]	Show recent attempts to divide by zero
[21]	Generalize a problem involving four circles and a triangle and consider some limiting cases of the problem by division by zero.
[22]	Paper considers computing probabilities from zero divided by itself
[23,24]	Considers how division by zero is taught on an elementary level
[25]	Develops a method to avoid division by zero in Newton’s Method
[26]	This work attempts to solve division by zero using a new form of optimization called Different-level quadratic minimization (DLQM)

Appendix 2: Other Examples of Where Equation (13) Agrees with Well-Established Classical Physics

Equation (14) can be used to find the force (F) acting on a particle of mass (

w_{m}

)

F = w_{m} . a

Substituting for

w_{m 1}

and

w_{m 2}

gives:

F = [(m - p (α f)) . (a)]

Multiplying the two brackets:

F = [m . a - p . α f . a]

Since the

- p

in the equation implies that the force from

α f . a

is not a physically measurable quantity, then Equation (31) reduces to F=ma. That is:

F = [m . a - p . α m . a] \approx m a

(31)

Equation (14) can also be used to find the gravitational force (F) acting between two particles of wave-mass (

w_{m 1}

and

w_{m 2}

)

According to Newton’s Law of Universal Gravitation (Equation (1)) the gravitational effect between Particle 1 with given wave-mass function

w_{m 1}

and Particle 2 with given wave-mass function

w_{m 2}

is given as follows:

F = \frac{G w_{m 1} . w_{m 2}}{r^{2}} = \frac{G}{r^{2}} [w_{m 1} . w_{m 2}]

Substituting for

w_{m 1}

and

w_{m 2}

gives:

F = \frac{G}{r^{2}} [(m_{01} - p (α f_{1})) . (m_{02} - p (α f_{2}))]

Multiplying the two brackets:

F = \frac{G}{r^{2}} [m_{01} . m_{02} - p m_{01} . α f_{2} - p m_{02} . α f_{1} - α^{2} f_{1} f_{2}]

F = \frac{G}{r^{2}} [m_{01} . m_{02} - p (m_{01} . α f_{2} + m_{02} . α f_{1}) - α^{2} f_{1} f_{2}]

F = \frac{G m_{01} . m_{02}}{r^{2}} - p \frac{G (m_{01} . α f_{2} + m_{02} . α f_{1})}{r^{2}} - \frac{G α^{2} f_{1} f_{2}}{r^{2}}

F = \frac{G m_{01} . m_{02}}{r^{2}} - \frac{G α^{2} f_{1} f_{2}}{r^{2}} - p \frac{G (m_{01} . α f_{2} + m_{02} . α f_{1})}{r^{2}}

(32)

Equation (32) is significant as it implies that there are three gravitational forces at work in the interaction between two particles. These three must agree with our current understanding of physics.

The first force (

\frac{G m_{01} . m_{02}}{r^{2}}

) is the normal gravitational effect between two particles as expressed by Newton’s original equation (Equation (1)). Since this force is real it can be measured. In fact, it has been measured in countless experiments in physics.

The second force (

\frac{G α^{2} f_{1} f_{2}}{r^{2}}

) is negative, implying that it is a force of repulsion (or an antigravity force) arising from the frequencies of the wave functions of the particles. This force is also real which implies that it can also be measured. However, such a force has never been measured in any physics experiments. Based on Equation (32) three possible reasons for this. Firstly, factor

G α^{2}

is in the order of

10^{- 113}

. This implies that assuming that the frequencies of the wavefunction of the particles are within the normal electromagnetic range the force of repulsion between the particles (arising from

\frac{G α^{2} f_{1} f_{2}}{r^{2}}

) would be too small to detect even with the most sensitive laboratory instruments.

Secondly, Newton’s Universal Law of Gravity was designed treating objects like point masses and not waves. Therefore, Newton’s Universal Law of Gravity does not have a wave counterpart that would take into account the distribution of energy of the object that produces the gravitational effect. Waves are essentially not stationary (like their particle counterparts) but spread out over time. Since the term

\frac{G α^{2} f_{1} f_{2}}{r^{2}}

only measures the overall gravitational repulsion between the waves for a given distance r, it does not capture the fact that, as the waves spread out, the gravitational repulsion between them per unit volume would decrease. This implies that if one is measuring the strength of gravity between the two waves at any one point, the strength of gravity at that point would decrease over time. If we assume that the waves are traveling at the speed of light this decrease per unit volume would be rapid (even though the overall gravity between the waves would remain the same). Putting it in term of Einstein’s General Theory of Relativity, the fact that the waves spread out over time and their gravitational effect per unit volume decreases implies that their effect on the curvature of space-time per unit volume also decreases.

Finally, the third reason why this force (

- \frac{G α^{2} f_{1} f_{2}}{r^{2}}

) has never been detected could simply be that no one has been looking for it.

The third force (

- p \frac{G (m_{01} . α f_{2} + m_{02} . α f_{1})}{r^{2}}

) cannot be measured since it has attached to it a

- p

. Recall that unstructured and complex components of a semi-structured complex number cannot be physically measured. However, this third force does imply that there is some interaction between the mass and the waves of the individual particles.

As an added thought, having looked at the three forces in Equation (32), it is possible that in the case where two particles interact the gravity between them is partly mechanical (

\frac{G m_{01} . m_{02}}{r^{2}}

) as a result of the rest masses of the particles and partly quantized (

\frac{G α^{2} f_{1} f_{2}}{r^{2}}

) as a result for the frequencies of the wave functions of the particles. It is also possible that the curvature of space-time produced by the mechanical part of gravity is opposite in nature to the curvature of space-time produced by the quantized part of gravity. Finally, it is possible that the curvature of space-time produced by the mechanical part of gravity is localized and constant (since the rest mass of particles is localized) and the curvature of space-time produced by the waves of the particles is decrease per unit volume as the waves spread outwards. Based on the mathematics these are significant findings worth investigation via experimentation.

Appendix 3: Wave-Mass Function Converted to Its Original State

Consider a particle that has reached the speed of light (but not currently at the speed of light). Its wave-mass function would be shown in Equation (33).

{w_{m}}^{'} = p m_{0} + α f

(33)

If Equation (33) is multiplied by velocity this equation becomes:

{v . w_{m}}^{'} = p m_{0} v + α f v

(34)

When the velocity of the object goes to zero (for example if the object hits a barrier), then Equation (34) becomes:

{0 . w_{m}}^{'} = p m_{0} . 0 + α f . 0

Since

- p = 0

, then

{- p w_{m}}^{'} = p m_{0} . - p + α f . - p {- p w_{m}}^{'} = m_{0} - p α f w_{m} = m_{0} - p α f

(35)

Equation (36) is the original wave-mass function. This means that when the velocity of the wave reaches zero (for example the wave hitting a screen or barrier) it will turn back into a particle.

Appendix 4: Proof of the Relation between Schrödinger’s Wave Function and the New Wave-Mass Function Is Given in Equation (22)

Schrödinger’s wave function (

Ψ

) is given by Equation (36)

Ψ = e^{i (k x - ω t)}

(36)

where,

k

is the wave number,

x

is the position along the wave,

ω

is the angular frequency and

t

is the time at which the wave is being examined. Now, the frequency

f

of the wave is related to the angular frequency

ω

by the expression:

f = \frac{ω}{2 π}

(37)

The angular frequency

ω

can be extracted from Schrödinger’s wave function (

Ψ

) using the following expression:

ω = \frac{1}{- i Ψ} \times \frac{\partial Ψ}{\partial t}

(38)

Combining Equation (37) and Equation (38) gives frequency f in terms of the Schrödinger’s wave function (

Ψ

f = \frac{1}{- 2 π i Ψ} \times \frac{\partial Ψ}{\partial t}

(39)

Using Equation (8) we can replace

m_{0}

and

f

in the wave-mass function with Equation (39) and simplify. This gives the following:

w_{m} = m_{0} - p (α f) w_{m} = (\frac{α}{- 2 π i Ψ} \times \frac{\partial Ψ}{\partial t}) - p (\frac{α}{- 2 π i Ψ} \times \frac{\partial Ψ}{\partial t}) w_{m} = (\frac{α}{- 2 π i Ψ} \times \frac{\partial Ψ}{\partial t}) + p (\frac{α}{2 π i Ψ} \times \frac{\partial Ψ}{\partial t}) w_{m} = (\frac{α}{2 π i Ψ} \times \frac{\partial Ψ}{\partial t}) (- 1 + p) w_{m} = (\frac{α}{2 π i Ψ} \times \frac{\partial Ψ}{\partial t}) (- 1 + p)

But

- 1 + p = \sqrt{2} (\frac{- 1}{\sqrt{2}} + \frac{1}{\sqrt{2}} p) = \sqrt{2} e^{p (\frac{3}{4} π)}

Hence:

w_{m} = (\frac{α}{2 π i Ψ} \times \frac{\partial Ψ}{\partial t}) (- 1 + p) w_{m} = (\frac{α}{2 π i Ψ} \times \frac{\partial Ψ}{\partial t}) \sqrt{2} e^{p (\frac{3}{4} π)} w_{m} = (\frac{α e^{p (\frac{3}{4} π)}}{\sqrt{2} π i Ψ} \times \frac{\partial Ψ}{\partial t})

This is the derivation of the relation given by Equation (22).

Appendix 5: Proof of Equation (23) the Relation between Energy an Object Possesses and the New Wave-Mass Function

w_{m} = m_{0} - p (α f)

Multiplying by

c^{2}

w_{m} c^{2} = m_{0} c^{2} - p (α f) c^{2}

(40)

w_{m} c^{2} = m_{0} c^{2} - p h f (\sin ce α c^{2} = h)

(41)

But recall the relations

λ = \frac{h}{\bar{p}}

which implies

h = λ \bar{p}

where

\bar{p}

is the momentum of the particle. Additionally,

c = f λ w h i c h i m p l i e s t h a t f = \frac{c}{λ}

Hence

w_{m} c^{2} = m_{0} c^{2} - p h f w_{m} c^{2} = m_{0} c^{2} - p (λ \bar{p} \times \frac{c}{λ}) w_{m} c^{2} = m_{0} c^{2} - p c \bar{p}

Now:

w_{m} c^{2} = (\sqrt{{(m_{0} c^{2})}^{2} + {(c \bar{p})}^{2}}) (\frac{m_{0} c^{2}}{\sqrt{{(m_{0} c^{2})}^{2} + {(c \bar{p})}^{2}}} - p \frac{c \bar{p}}{\sqrt{{(m_{0} c^{2})}^{2} + {(c \bar{p})}^{2}}})

But according to Equation (17):

E = \sqrt{{(m_{0} c^{2})}^{2} + {(c \bar{p})}^{2}}

Hence:

w_{m} c^{2} = E (\frac{m_{0} c^{2}}{\sqrt{{(m_{0} c^{2})}^{2} + {(c \bar{p})}^{2}}} - p \frac{c \bar{p}}{\sqrt{{(m_{0} c^{2})}^{2} + {(c \bar{p})}^{2}}})

By result 10 of Table 2

w_{m} c^{2} = E (e^{- p \frac{π}{4}}) w_{m} c^{2} (e^{p \frac{π}{4}}) = E

This is the derivation of Equation (23).

References

Afolabi, P.A. The Impact of Sir Isaac Newton’s Discoveries On 17th Century Scientific Revolution And The Implications To The Young Science Scholars. Int. J. Res. Educ. Sustain. Dev. 2021, 1, 118–127. [Google Scholar]
Soffel, M.H.; Han, W.B. Applied general relativity. In Astronomy and Astrophysics; Switzerland: Cham, Switzerland, 2019. [Google Scholar]
ScienceClic, “Youtube,” ScienceClic English, 24 January 2019. [Online]. Available online: https://www.youtube.com/watch?v=Avhs78WjhVY&list=PLu7cY2CPiRjVCbSWwSe0mXxWK0S8e8Ssx&index=19 (accessed on 16 October 2023).
Hossenfelder, S. How we know that Einstein’s General Relativity can’t be quite right,” Youtube, 17 August 2019. [Online]. Available online: https://www.youtube.com/watch?v=Ov98y_DCvRY (accessed on 16 October 2023).
Harper, T. “Stress Energy Momentum Tensor Physical Interpretation | Tensor Intuition,” The Cynical Philosopher, 7 December 2021. [Online]. Available online: https://www.youtube.com/watch?v=dHM1Azz6aVM (accessed on 16 October 2023).
Hirvonen, V. “The Ricci Tensor: A Complete Guide With Examples,” Profound Physics, 2023. [Online]. Available online: https://profoundphysics.com/the-ricci-tensor/ (accessed on 8 October 2023).
Crowell, B. “9.2: The Stress-Energy Tensor,” LibreTexts. 2023. Available online: https://phys.libretexts.org/Bookshelves/Relativity/Book%3A_Special_Relativity_(Crowell)/09%3A_Flux/9.02%3A_The_Stress-Energy_Tensor (accessed on 8 October 2023).
Tan-Holmes, J. “The Heisenberg Uncertainty Principle Explained Intuitively,” Youtube, 20 September 2018. [Online]. Available online: https://www.youtube.com/watch?v=qwt6wUUD2QI (accessed on 10 October 2023).
Osiak, Z. Energy in Special Relativity. Theor.Phys. 2019, 4, 22–25. [Google Scholar] [CrossRef]
Paul, P.J.; Wahid, S. Unstructured and Semi-structured Complex Numbers: A Solution to Division by Zero. Pure Appl. Math.J. 2021, 10, 49. [Google Scholar] [CrossRef]
Paul, P.J.; Wahid, S. Reformulating and Strengthening the theory of Semi-strucutred Complex Numbers. Int. J. Appl. Phys.Math. 2022. [Google Scholar]
Pinelas, S.; Saitoh, S. Division by Zero Calculus and Differential Equations. In Differential and Difference Equations with Applications; ICDDEA: Amadora, Portugal, 2018. [Google Scholar]
Saitoh, S. Introduction to the Division by Zero Calculus; Scientific Research Publishing, Inc.: USA, 2021. [Google Scholar]
Okumura, H. The arbelos in Wasan geometry: Atsumi’s problem with division by zero calculus. Sangaku J.Math. 2021, 5, 32–38. [Google Scholar]
Barukčić, I. Classical logic and the division by zero. Int. J. Math. Trends Technol. IJMTT 2019, 65, 31–73. [Google Scholar] [CrossRef]
Okumura, H. An Analogue to Pappus Chain theorem with Division by Zero. Forum Geom 2018, 18, 409–412. [Google Scholar]
Lobo, M.P. Cancer: Division by Zero. Open J. Math. Phys. 2020, 2, 5. [Google Scholar]
Lobo, M.P. Does zero divide zero. Open J. Math.Phys. 2020, 2, 3. [Google Scholar]
Czajko, J. On unconventional division by zero. World Sci. News 2018, 99, 133–147. [Google Scholar]
Okumura, H. Is It Really Impossible To Divide By Zero. J Appl Math 2018, 27, 191–198. [Google Scholar] [CrossRef]
Okumura, H. A four circle problem and division by zero. Sangaku J. Math. 2020, 4, 1–8. [Google Scholar]
Mwangi, W. Definite Probabilities from Division of Zero by Itself Perspective. Asian J. Probab. Stat. 2020, 6, 1–26. [Google Scholar] [CrossRef]
Dimmel, J.; Pandiscio, E. When it’s on zero, the lines become parallel: Preservice elementary teachers’ diagrammatic encounters with division by zero. J. Math. Behav. 2020, 58, 1–27. [Google Scholar] [CrossRef]
Karakus, F.; Aydin, B. Elementary Mathematics Teachers’ Specialized Content Knowledge Related to Division by Zero. Malays. Online J. Educ. Sci. 2019, 7, 25–40. [Google Scholar]
Abdulrahman, “A Method to Avoid the Division-by-Zero or Near-Zero in Newton-Raphson Method,” Feburary 2022. [Online]. Available online: https://www.researchgate.net/publication/358857049_A_Method_to_Avoid_the_Division-by-Zero_or_Near-Zero_in_Newton-Raphson_Method (accessed on 28 April 2022).
Zhang, Y.; Ling, Y.; Yang, M.; Mao, M. Exemplar Different-Level Quadratic Minimization. In Proceedings of the 2018 5th International Conference on Systems and Informatics; 2018. [Google Scholar]
Kataru, B. “Deriving the Lorentz Factor (γ) of Special Relativity,” Physics Scribbles, 30 July 2019. [Online]. Available online: https://medium.com/physics-scribbles/deriving-the-lorentz-factor-%CE%B3-of-special-relativity-d5462f3b3b91#:~:text=At%20the%20heart%20of%20special,classical%20behavior%20under%20relativistic%20conditions (accessed on 10 October 2023).
Ash, “The Crazy Mass-Giving Mechanism of the Higgs Field Simplified,” Youtube, 10 March 2023. [Online]. Available online: https://www.youtube.com/watch?v=R7dsACYTTXE (accessed on 10 September 2023).

Figure 1. (a) massive object curving space-time and (b) more massive object producing a greater curvature in space time [3].

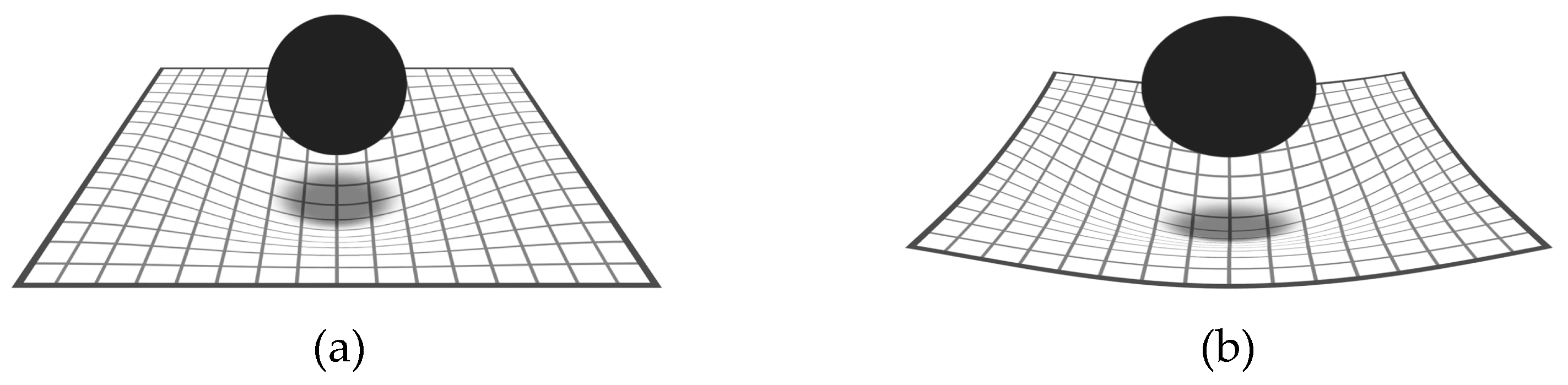
Figure 2. Curvature of space-time produced by both masses A and B.

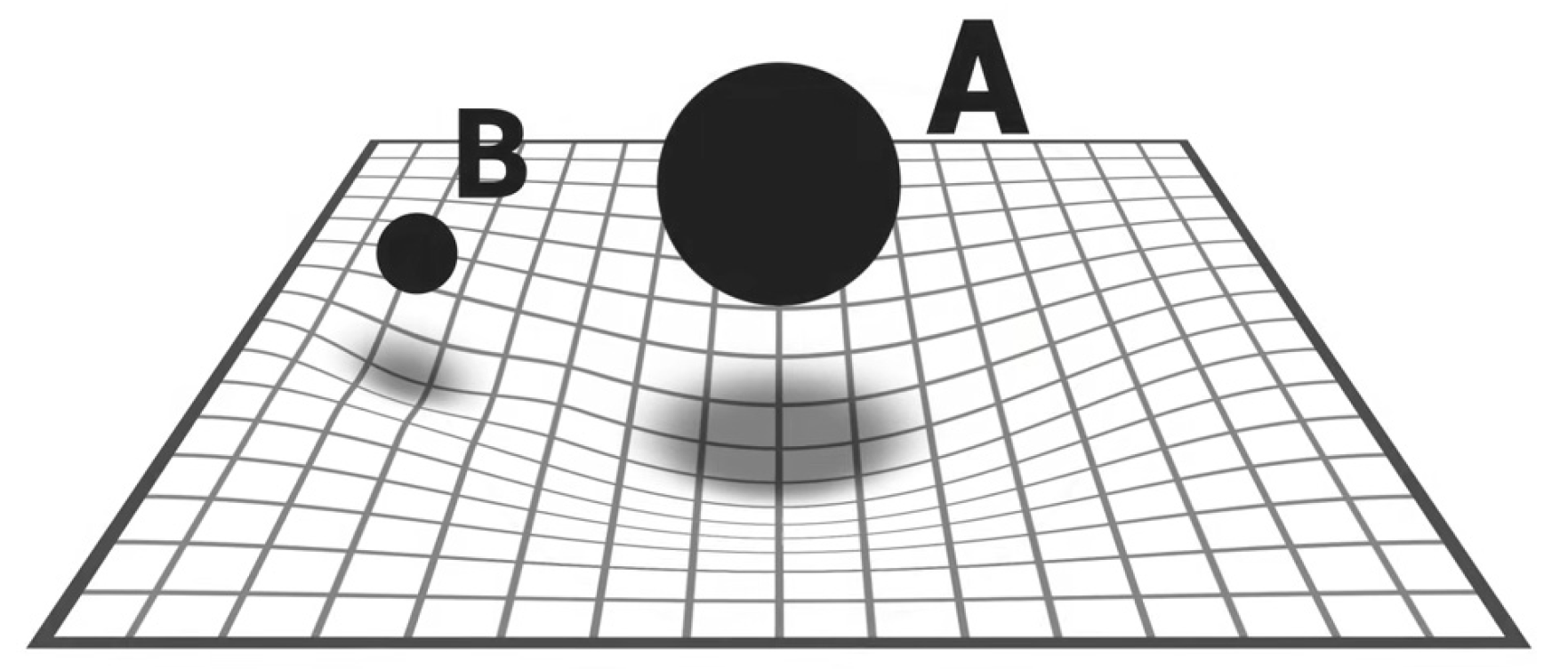
Figure 3. Elements of the stress-energy tensor

T_{μ ν}

Figure 3. Elements of the stress-energy tensor

T_{μ ν}

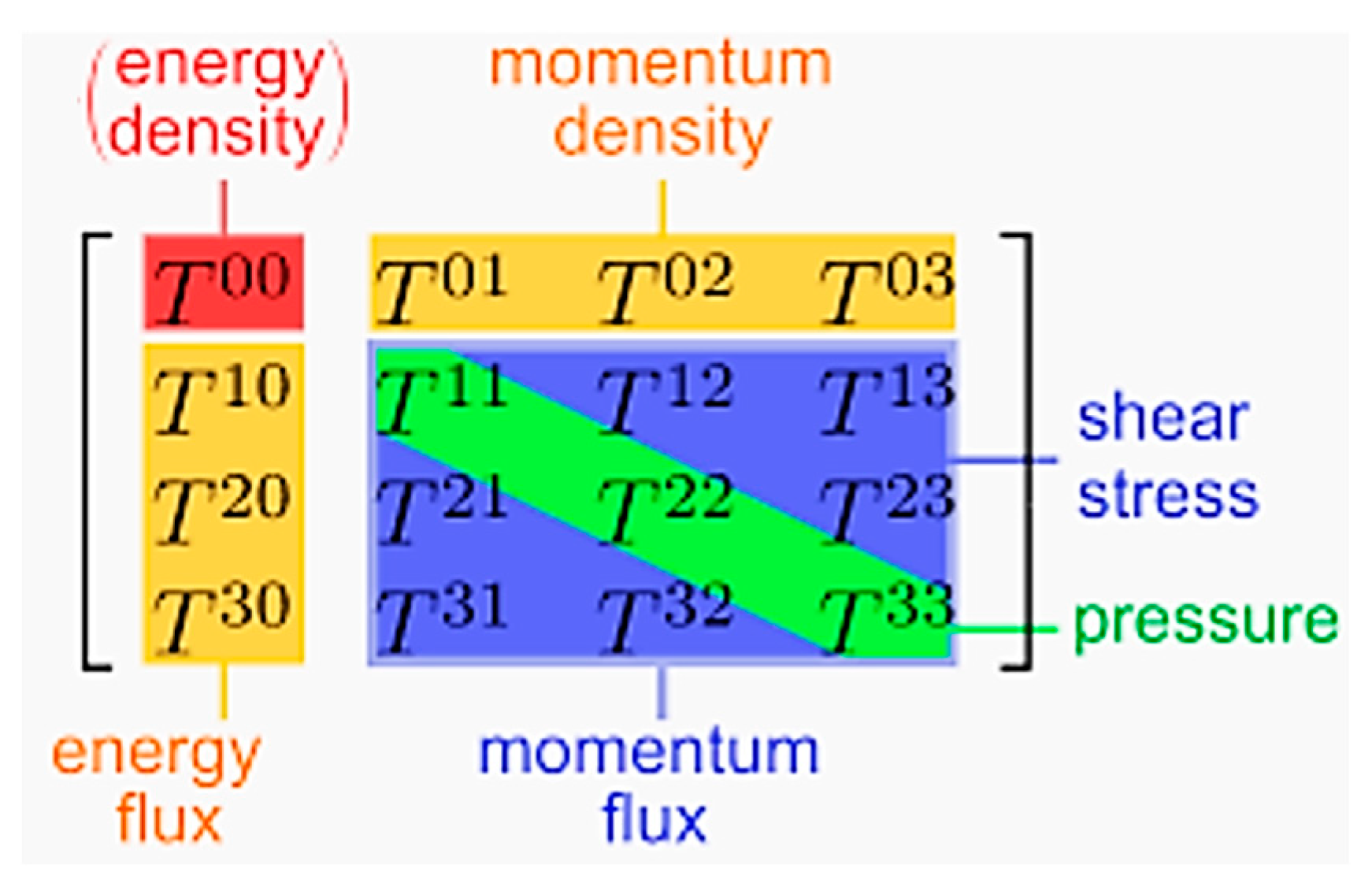
Table 1. Stress-energy tensor elements, their meaning and equations.

Element(s)	Meaning	Equation	Equivalent Equation	Units
$T^{00}$	Local energy density: including any potential contributions from forces between particles and their kinetic energy.	$\frac{E^{00}}{V^{00}}$	$\frac{E^{00}}{V^{00}}$	$J . m^{- 3}$
$T^{0 i}$	Energy flux in the i^th direction: This includes not only bulk motion but any other processes giving rise to transfer of energy as for example heat conduction	$\frac{E^{0 i}}{{(d A \times d t)}^{0 i}}$	$\frac{E^{0 i}}{{(d A \times d t)}^{0 i}}$	$J . m^{- 2} . s^{- 1}$
$T^{i 0}$	Momentum Density: Density of the momentum component in the i^th direction, (that is the 3-momentum density). This component also considers the change in momentum associated with heat transfer.	$\frac{{(m v)}^{i 0}}{V^{i 0}}$	$\frac{E^{i 0}}{{c . V}^{i 0}}$	$J . m^{- 4} . s^{- 1}$
$T^{j i}$	Shear Stress: Force tending to cause deformation of a material by slippage along a plane or planes parallel to the imposed stress.	$\frac{F^{j i}}{A^{j i}}$	$\frac{E^{j i}}{V^{j i}}$	$J . m^{- 3}$
$T^{i i}$	Pressure: Force applied perpendicular to the surface of an object per unit area over which that force is distributed	$\frac{F^{i i}}{A^{i i}}$	$\frac{E^{i i}}{V^{i i}}$	$J . m^{- 3}$
$T^{i j}$	Momentum Flux (or stress tensor): the rate of flow of the i^th component of the momentum per unit area in the plane orthogonal to the j^th direction. $T^{i j}$ can also represent the momentum of fluid passing through some area per unit time. (Note $i \neq j$ )	$\frac{{(m v)}^{i j}}{{(d A \times d t)}^{i j}}$	$\frac{E^{i j}}{{c . (d A \times d t)}^{i j}}$	$J . m^{- 3} . s^{- 1}$

c

is the speed of light;

E

is energy;

V

is volume;

d A

is area;

d t

is time;

F

is force.

Table 2. Major results from paper [11].

Result 1	Semi-structured complex number set can be defined as follows: A semi-structured complex number is a three-dimensional number of the general form $h = x + y i + z p;$ that is, a linear combination of real ( $1$ ), imaginary ( $i$ ) and unstructured ( $p$ ) units whose coefficients $x, y, z$ are real numbers. The number $h$ is called semi-structured complex because it contains a structured complex part $(x + y i)$ and an unstructured part $(z p)$ .
Result 2	The unstructured number $p$ was redefined as: $p^{n} = \frac{\sqrt{2} \times \cos (\frac{π}{2} n - \frac{π}{4})}{f^{n} (1)}$ (12) where $f^{n} (c)$ is a composite function such that $f (c) = 1 - c$ . Integer powers of $p$ yield the following cyclic results: $\begin{matrix} p^{1} = \frac{1}{0} & p^{2} = - 1 & p^{3} = - p & p^{4} = 1 & p^{5} = \frac{1}{0} & p^{6} = - 1 & p^{7} = - p & \dots \end{matrix}$
Result 3	$p$ does not belong to the set of complex numbers $C$ (that is, $p \notin C$ ), but belongs to a higher order number set $H$ called the set of semi-structured complex numbers such that the set of complex numbers is a subset of $H$ (that is, $C \subset H$ ).
Result 4	The field of semi-structured complex numbers was defined, and proof was given that this field obeys the field axioms. This implies (1) the number set can easily be used in everyday algebraic expressions and can be used to solve algebraic problems, (2) the number set can be used to form more complicated structures such as vector spaces and hence solve more complex problems that may involve “division by zero”.
Result 5	Semi-structured complex number set $H$ does not form an ordered field. For the objects in a field to have an order, operations such as greater than or less than can be applied to these objects. This is because in an ordered field the square of any non-zero number is greater than 0; this is not the case with semi-structured complex numbers.
Result 6	Semi-structured complex numbers can be represented by points in a 3-dimensional Euclidean $x y z$ -space. The xyz-space consist of three perpendicular axes: the real $x$ -axis, the imaginary y-axis, and the unstructured $z$ -axis. These axes form three perpendicular planes: the real-imaginary $x y$ -plane, the real-unstructured $x z$ -plane, and the imaginary-unstructured $y z$ -plane.
Result 7	The unit $p$ was used to find a viable solution to the logarithm of zero. The logarithm of zero was found to be: $\log 0 = - p (\frac{π}{2} + 2 k π)$ (13) where k is some integer value.
Result 8	The new definition of $p$ provided an unambiguous understanding that $\frac{0}{0} = n$ simply represents $90^{°}$ clockwise rotation of the vector $n p$ from the positive unstructured z-axis to $n$ on the positive real x-axis along the real-unstructured $x z$ -plane. Note that $n$ is any real number.
Result 9	Semi-structured complex numbers have both a 3D and 4D representation in the form: $\begin{array}{c} h = x + y i + z p & (3D form) \\ h = A + B i + C p + D i p & (4D form) \end{array}$ Where: $x, y, z, A, B, C, D$ are real numbered scalars and $i, p$ are semi-structured basis units.
Result 10	Two new Euler formulas were developed. PlaneEuler formulaReal imaginary When combined with the original Euler formula describes the relationship between trigonometric, hyperbolic, and exponential functions for the entire semi-structured complex Euclidean $x y z$ -space.
Result 11	Semi-structured complex numbers can be used to resolve singularities that may arise in engineering and science equations (because of division by zero) to develop reasonable conclusions in the absence of experimental data.
Result 12	The zeroth root of a number h can be found using the equation $\sqrt[0]{h} = h^{p} = e^{p \ln h} = \cos (\ln h) + p \sin (\ln h)$
Result 13	Since $p^{1} = \frac{1}{0}$ this implies that $\frac{1}{p} = 0$ which further implies that $- p = 0$
Result 14	Any real number with the semi-structured unit $p$ attached to it is not a physically measurable quantity. That is, $k p$ where $k$ is a real number is not physically measurable (however, $k$ can be calculated given enough information)
Result 15	If $a$ and $b$ measure different (but quantitatively related) aspects of the same object, where $a$ is physically measurable but $b$ is not, then $a$ and $b$ can be combined into one equation in the form $a + b p$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Unifying Quantum Mechanics and General Relativity: A Significant Application of Semi-Structured Complex Numbers

Abstract

1. Introduction

1.1. Newtonian Mechanics and Einstein’s General Theory of Relativity

1.2. The Problem with Einstein’s General Theory of Relativity and Quantum Mechanics

1.3. New Tools Required to Solve the Problem of Quantum Gravity

1.4. Einstein’s Special Theory of Relativity and the Lorentz Factor

1.5. Wave-Particle Duality: De Broglie’s Discoveries

1.6. Schrödinger’s Equation and the Wave Function

1.7. Semi-Structured Complex Numbers: A Recent Development in Division by Zero

1.8. Major Contributions

2.0. The Wave-Mass Function: A New Model for the Mass of an Object

3.0. The Wave-Mass Function and Einstein’s Special Theory of Relativity

4.0. Uniting Einstein’s General Theory of Relativity and Quantum Mechanics

4.1. Deriving a Relation between Schrödinger’s Wave Function and the New Wave-Mass Function

4.2. Deriving a Relation between Einstein’s Field Equation and the New Wave-Mass Function

4.3. Combining Einstein’s Field Equation with Schrödinger’s Wave Function to form a New Quantum Gravity Equation

5.0. Discussion

6.0. Conclusions

Author Contributions

Conflict of Interest

Appendix 1. Research Conducted from 2018 to 2022 Involving Division by Zero

Appendix 2: Other Examples of Where Equation (13) Agrees with Well-Established Classical Physics

Appendix 3: Wave-Mass Function Converted to Its Original State

Appendix 4: Proof of the Relation between Schrödinger’s Wave Function and the New Wave-Mass Function Is Given in Equation (22)

Appendix 5: Proof of Equation (23) the Relation between Energy an Object Possesses and the New Wave-Mass Function

References

MDPI Initiatives

Important Links

Subscribe