On the Oracle Properties of Bayesian Random Forest for Sparsed High-Dimensional Gaussian Regression

Preprint

Article

On the Oracle Properties of Bayesian Random Forest for Sparsed High-Dimensional Gaussian Regression

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Oyebayo Ridwan Olaniran^*

Ali Rashash R Alzahrani

Oyebayo Ridwan Olaniran^*

Ali Rashash R Alzahrani

This version is not peer-reviewed

Submitted:

18 October 2023

Posted:

19 October 2023

You are already at the latest version

Alerts

Abstract

Random Forest (RF) is a widely used data prediction and variable selection technique. However, the variable selection aspect of RF can become unreliable when there are more irrelevant variables than relevant ones. In response, we introduced the Bayesian Random Forest (BRF) method specifically designed for high-dimensional datasets with a sparse covariate structure. Our research demonstrates that BRF possesses the oracle property, which means it achieves strong selection consistency without compromising efficiency or bias.

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

MSC: 62F15; 62G20; 62G08

1. Introduction

Several techniques for handling high-dimensional data have been proposed from different areas of research, such as in oncology (modelling and identification of relevant genetic biomarkers for tumourous cancer cells) [1,2,3,4,5]. The methodologies of the techniques differ, but the collective standpoint is to find an efficient way to analyze high-dimensional data [6]. In a broader sense, high-dimensionality (HD) refers to a modelling situation where the number of unknown parameters p are far greater than the sample size n that’s

p ≫ n

[7]. This scenario includes supervised regression and classification with several explanatory variables or features largely greater than sample size, unsupervised learning with more attributes than samples and hypothesis testing parlance with more considered hypotheses than observations [8]. [9] identified the need for developing robust methods for high-dimensional data. Classical methods like ordinary least squares, logistic regression, and

k - N N

often break down due to an ill-conditioned design matrix when

p ≫ n

. [10] described two major approaches to analyzing high-dimensional data, namely: modification of

n > p

approaches to accommodate high-dimensional data or developing a new approach. Modifying approaches involves moving from complex to simple models by selecting relevant subsets of the p variables. This approach is widely referred to as variable selection.

Variable selection is an approach used to adapt existing low-dimensional data modeling techniques for high-dimensional data. Simultaneously, penalized regression involves imposing constraints on dimensionality to achieve a similar objective. The primary advantage of variable selection methods is their ability to preserve the desirable qualities of low-dimensional approaches like the Maximum Likelihood Estimator (MLE), even though they may struggle to address the complexity of high-dimensional datasets. Penalized methods such as LASSO [11] and SCAD [12], among others, offer a partial solution to the problem but introduce bias in estimation. Both approaches share the drawback of not fully capturing the complexities of high-dimensional datasets, including interactions, non-linearity, and non-normality [13]. One robust procedure that has been shown to overcome these challenges in both low and high-dimensional scenarios is Classification and Regression Trees (CART) [14,15]. CART is a non-parametric statistical method that relaxes dimensionality assumptions and naturally accommodates modeling of interactions and non-linearity.

The strength of CART in terms of simplicity and interpretability is offset by a significant drawback, which often leads to a loss of accuracy. In the late 20th century, a new methodological framework emerged for combining multiple models to create a more comprehensive model, known as ensemble modeling. One of the earliest ensemble techniques within the CART framework is Bagging (Bootstrap Aggregating) [16]. The Bagging process involves taking multiple versions of the bootstrap sample [17] from the training dataset and fitting an unpruned CART to each of these bootstrap samples. The final predictor is derived by averaging these different model versions. Remarkably, this procedure works well and typically outperforms its competitors in most situations. Some intuitive explanations for why and how it works were provided in [18]. This concept has spurred subsequent work, including the development of Random Forests (RF) [19], which presents a broader framework for tree ensembles. RF enhances Bagging by replacing all covariates in the CART’s splitting step with a random sub-sampling of covariates. This adjustment helps reduce the correlation between adjacent trees, thereby enhancing predictive accuracy.

The complexity of dealing with high-dimensional data has led to the development of multiple versions of Random Forest (RF) algorithms in the context of regression modeling. One prominent characteristic of high-dimensional datasets is their sparsity, which means there are relatively few relevant predictors within the predictor space. This sparsity is often observed in microarray data, where only a small number of genes are associated with a specific disease outcome [13,20]. The traditional approach of RF, which involves randomly subsampling either the square root of the predictors

\sqrt{p}

\frac{p}{3}

, fails to effectively capture this sparsity [21]. This failure arises from RF’s unrealistic assumption that the predictor space should be densely populated with relevant variables to achieve reasonable accuracy. In contrast, boosting techniques, as introduced by [20], specifically address this issue by boosting weak trees rather than averaging all the trees, as done in RF. However, boosting comes at the cost of reduced predictive accuracy compared to RF. The Bayesian modified boosting approach, known as Bayesian Additive Regression Trees (BART) proposed by [22], provides an alternative method for estimating a boosting-inspired ensemble of Classification and Regression Trees (CART) models. Nevertheless, BART does not focus on solving the problem of sparsity and is not robust to an increase in dimensionality, as reported by [23].Therefore, in this paper, we introduce a new framework for Random Forest (RF) by incorporating Bayesian estimation and a hybrid variable selection approach within the splitting step of RF. This innovation aims to enhance prediction efficiency and improve the consistency of variable selection in high-dimensional datasets.

2. Random Forest and Sum of Trees Models

Suppose we let

D = [y_{i}, x_{i 1}, x_{i 2}, \dots, x_{i p}], i = 1, 2, \dots, n

be an

n \times p

dataset with

y_{i}

assuming continuous values and

x = [x_{i 1}, x_{i 2}, \dots, x_{i p}]

be the vector of p covariates. Thus, we can define a single regression tree using the formulation of [22]

y_{i} = f (x_{i 1,}, x_{i 2}, \dots, x_{i p}) + ϵ_{i} .

(1)

where the random noise seen during estimation is denoted by the variable

e p s i l o n_{i}

, which is assumed to have an independent, identical Gaussian distribution with a mean of 0 and a constant variance of

s i g m a 2

. Consequently, in the same formulation by [22], a sum of trees model can be defined as:

y_{i} = h (x_{i 1,}, x_{i 2}, \dots, x_{i p}) + ϵ_{i} .

(2)

where

h (x_{i 1,}, x_{i 2}, \dots, x_{i p}) = \sum_{j = 1}^{J} f (x_{i 1,}, x_{i 2}, \dots, x_{i p})

and the total number of trees in the forest is J. In the notation of a tree, we have;

y = \sum_{j = 1}^{J} I_{j} (β_{m j} : x \in R_{m j})

(3)

where

β_{m}

is an estimate of y in region

R_{m}

I_{j} (β_{m j} : x \in R_{m j})

is the single regression tree.

The model’s parameters

β_{m}

and

σ^{2}

(3) are often estimated using the frequentist approach. These approaches include Bagging [16], Stacking [24], Boosting [25] and Random forest [19]. Stacking improves the performance of the single tree in the model (1) by forming a linear combination of different covariates in x. Similarly, boosting improves (1) by fitting a single tree model on data sample points not used by an earlier fitted tree. Bagging and random forest iteratively randomize the sample data D and fitting (1) on each uniquely generated sample. Random forest improves over bagging by using a random subset of p covariates, often denoted

m t r y

, to fit (1) instead of all p covariates. This procedure has been shown to dramatically lower the correlations between adjacent trees and thus reduce the overall prediction risk of (3). Freidman [26] defined the risk of using the random forest for estimating (3) as:

V a r ({\hat{y}}_{R F}) = ρ (x) σ^{2} (x)

(4)

where

ρ (x)

is the pairwise correlation between adjacent trees and

σ^{2} (x)

is the variance of any randomly selected tree from the forest. Equation (4) implies that

ρ (x)

plays a vital role in shrinking the risk towards 0 as

J \to \infty

. Achieving infinite forests is rarely possible due to computational difficulty. This drawback has necessitated the development of Bayesian [27] alternatives that are adaptive in nature in terms of averaging many posterior distributions. Chipman [22] proposed the Bayesian Additive Regression Trees (BART) that average many posterior distributions of single Bayesian Classification and Regression trees (BCART, [28]). The approach is specifically similar to a form of boosting proposed in [20]. BART boosts weak trees by placing some form of deterministic priors on them. Although the empirical bake-off results of 42 datasets used to test the BART procedure showed improved performance over RF, there is no theoretical backup on why BART is better than RF. Several authors have queried the improvement, especially in a high-dimensional setting where RF still enjoys moderate acceptance. Hernandez [13] claimed the BART algorithm implemented in R as package “bartMachine” is memory hungry even at moderate p with T the number of MCMC iterations for posterior sampling fixed at 1000.

Taddy [29] proposed the Bayesian and Empirical Bayesian Forests (BF and EBF) to maintain the structure of RF and modify the data randomisation technique using a Bayesian approach. BF replaces the uniform randomisation with the Dirichlet posterior distribution of sampled observation. Similarly, EBF considered the hierarchical parameter structure of estimating the next stage prior hyperparameters using current data. The results from the empirical analysis showed that BF and EBF are not different from RF except in the aspect of model interpretation.

2.1. Variable Selection Inconsistency and Inefficiency of Random Forest in Sparse High-Dimensional Setting

Definition 1.

Let

D_{h d} = [Y | X]

be a partitioned matrix composed of

n \times 1

response variable Y vector and X be an

n \times p

matrix with

y_{i}, x_{i k} \in ℜ

, for

i = 1, \dots, n

and

k = 1, \dots, p

then a rectangular matrix

D_{h d}

(5)

is referred to as high-dimensional data matrix if

p ≫ n

[8].

If we redefine some of the columns in

D_{h d}

such that the entries are zeros, thus truncating the matrix structure, we have a sparsed HD. Sparsity is inherent in HD where only a few of the p covariates xS are usually related to the response y.

Definition 2.

A typical sparsed HD matrix is given by

(6)

in Olaniran & Abdullah [30].

The risk of random forests (RF), as indicated in equation (4), increases in high-dimensional situations with a sparse covariate matrix. This increase is a consequence of the random selection of the variable set

m t r y

used to build equation (1). The method of hypergeometric sampling for selecting

m t r y \subset p

is notably sensitive to the mixing parameter

π

, which represents the proportion of relevant variables. Specifically, when the proportion of relevant variables (

π

) is higher, the risk associated with RF is lower, and vice versa.

It’s worth noting that many software implementations of RF regression commonly set

m t r y

p / 3

. This choice is expected to yield a satisfactory set of covariates for predicting the target variable y under two conditions: when the data matrix D is of low dimensionality or when the number of observations (n) is greater than the number of covariates (p).

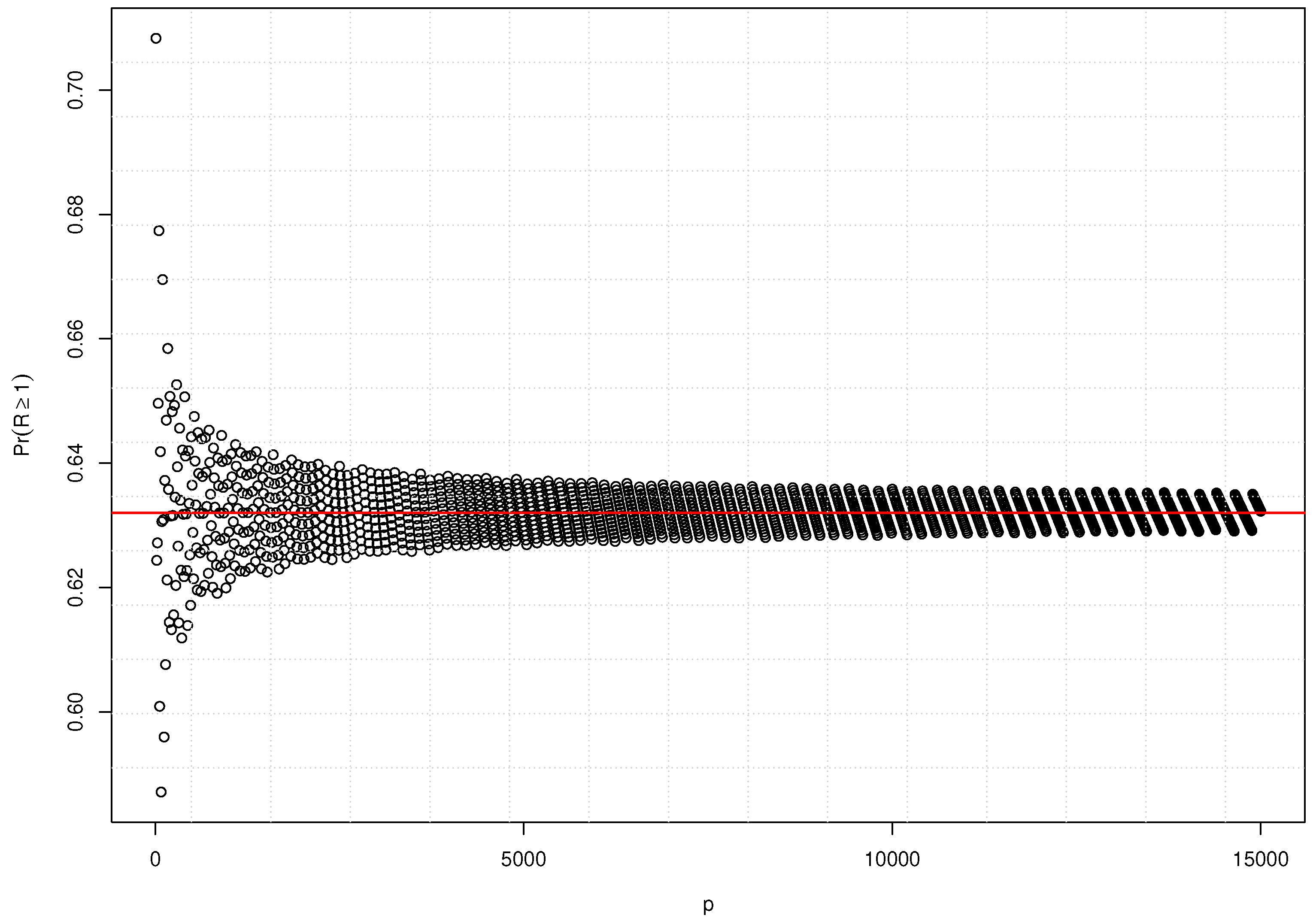
In the specific scenario where

D = D_{s h d}

, theorem (1) is employed to establish an upper bound for the probability of correctly selecting at least one relevant covariate from the set of p. This theorem is the foundation for defining the selection consistency of random forests in high-dimensional, sparse settings.

Theorem 1.

Given p covariates,

r \subset p

relevant variables, if we set the RF subsample size

m t r y = p / 3

as r, then the probability that at least one of the covariates in r is relevant converges to

1 - e^{- 1}

p \to \infty

Proof.

Proposition 1.Let

R_{1}, R_{2}, \dots R_{r}

denote the event that the

R_{k}

covariate is relevant. Then, the event that at least one covariate in r is relevant is

R_{1} \cup R_{2} \cup \dots R_{r}

, the required probability is

P (R_{1} \cup R_{2} \cup \dots R_{r})

. It is worthy of note that the subsample selection done by RF is without replacement, implying that the sample space of p covariates can be partitioned into two (R relevant covariates and

p - R

irrelevant covariates). This partitioning done without replacement is often referred to as a hypergeometric or non-mutually exclusive process [31]. Thus, by the generalization of the principle of non-mutually exclusive events, we have

\begin{matrix} P (R_{1} \cup R_{2} \cup \dots R_{r}) & = \sum_{k = 1}^{r} P (R_{k}) - \sum_{j, k = 1; k > j}^{r} P (R_{j} \cap R_{k}) + \sum_{i, j, k = 1; k > j > i}^{r} P (R_{i} \cap R_{i} \cap R_{k}) \\ - \dots + {(- 1)}^{r - 1} P (R_{1} \cap R_{2} \cap \dots \cap R_{r}) \end{matrix}

(7)

\begin{matrix} P (R_{1} \cup R_{2} \cup \dots R_{r}) & = (\binom{r}{1}) (\frac{1}{r}) - (\binom{r}{2}) (\frac{1}{r}) (\frac{1}{r - 1}) + (\binom{r}{3}) (\frac{1}{r}) (\frac{1}{r - 1}) (\frac{1}{r - 3}) \\ - \dots + {(- 1)}^{r - 1} (\binom{r}{r}) (\frac{1}{r!}) \\ = 1 - (\frac{1}{2!}) + (\frac{1}{3!}) - \dots + {(- 1)}^{r - 1} (\frac{1}{r!}) \end{matrix}

(8)

Recall that the exponential function

e^{ξ} = 1 + ξ + \frac{ξ^{2}}{2!} + \frac{ξ^{3}}{3!} + \dots + \frac{ξ^{r}}{r!}

, if

ξ = - 1

e^{- 1} = 1 - (1 - \frac{1}{2!} + \frac{1}{3!} + \dots + {(- 1)}^{r - 1} \frac{1}{r!})

(9)

Thus,

P (R_{1} \cup R_{2} \cup \dots R_{r}) = 1 - e^{- 1} = 0.6321

(10)

□

Theorem (1) implies that when p grows infinitely, the maximum proportion of relevant covariates that would be selected is

63.2 %

assuming the number of subsample

m t r y

chosen equals the number of relevant covariates in p. Figure 1 shows the convergence over varying p covariates.

Lemma 1.

RF variable selection is consistent if

{lim}_{p \to \infty} P (\hat{M} = M) = 1

Remark 1.

Lemma (1) indicates that for an RF model

\hat{M}

fitted using r subsampled covariates, RF variable selection is consistent if the fitted model converges almost surely to the true model

M

that contains all relevant variables R.

Corollary 1.

{lim}_{p \to \infty} P (⋃_{k = 1}^{r \subset p} R_{k}) = 0.6321 < 1

, then RF variable selection is inconsistent in HD with large p.

Now that we have established the inconsistency of RF in the HD setting, the following lemma presents RF variance for

D_{s h d}

matrix.

Lemma 2.

Let π be the proportion of relevant covariates and

0 \leq π \leq 1

, the variance of a single tree

σ^{2} (x)

can be decomposed into random and noise variance such that the risk of RF in a high-dimensional setting with

p ≫ n

can be defined as:

V a r ({\hat{y}}_{R F}) = ρ (x) [π σ_{1}^{2} (x) + (1 - π) σ_{2}^{2} (x)]

(11)

where

σ_{1}^{2} (x)

and

σ_{2}^{2} (x)

are the random and noise variances respectively.

Remark 2.

It is clear from lemma (2) that the risk of RF in (11) is larger than (4) when

π < 1

, thus RF violates the oracle property conditions defined by [32,33,34] among others as:

i.: Identification of the right subset model $M$ such that $P (\hat{M} = M) \to 1$ .
ii.: Achievement of the optimal estimation rate, $\sqrt{n} (\hat{M} - M) \overset{d}{\to} N (0, V a r (M))$

Many authors have argued that a good estimator

\hat{M}

should satisfy these oracle properties. However, from theorem (1) and (2), RF fails to achieve these conditions in the sparse HD setting. Thus, there is a need to propose an alternative procedure that enjoys these attractive properties.

3. Priors and Posterior Specification of Bayesian Random Forest for Sparse HD

The Bayesian Random Forest (BRF) proposed here has three major prior parameters. The first is model uncertainty prior defined over tree

I

. Here we propose a uniform prior

I \sim U (0, 1)

by [35] such that

P r (I) = 1

for any candidate tree. We used this prior specification to retain the average weighing procedure of RF so that each tree

I_{j}

has an equal voting right. The core advantage of this prior is to retain RF’s strength in correcting the over-fitting problem by averaging over all trees. The second form of prior is terminal node parameter

β_{M}

and

σ^{2}

prior, here we propose the Normal Inverse Gamma prior

N I G (μ_{M}, σ^{2} \sum, a_{0}, b_{0})

by [35], where

μ_{M}

and

Σ

are the prior mean and covariance for parameter

β_{M}

a_{0}

and

b_{0}

are the prior sample size and sum of squares for response

y_{i}

on parameter

σ^{2}

. Furthermore, we assumed a conditional prior of trees parameters

β_{M}

σ^{2}

, that’s for a single tree with M terminal nodes:

P (β_{M}, σ^{2}) = P (β_{M} | σ^{2}) P (σ^{2}) .

(12)

This can be easily extended to J trees with the assumption of constant model variance

σ^{2}

over all trees. Thus we have;

\begin{matrix} P (I_{1}, I_{2}, \dots, I_{J}) & = \prod_{j = 1}^{J} P (I_{j}, β_{M j}) P (σ^{2}) \end{matrix}

(13)

\begin{matrix} P (I_{1}, I_{2}, \dots, I_{J}) & = \prod_{j = 1}^{J} P (β_{M j} | σ^{2}) P (I_{j}) P (σ^{2}) \end{matrix}

(14)

with

P r (I_{j}) = 1

P (I_{1}, I_{2}, \dots, I_{J}) = [\prod_{j = 1}^{J} P (β_{M j} | σ^{2})] P (σ^{2})

(15)

P (β_{M j} | σ^{2}) = \frac{exp [\frac{- 1}{2 σ^{2}} {(β_{M j} - μ_{M j})}^{'} \sum_{j}^{- 1} (β_{M j} - μ_{M j})]}{{(\sqrt{2 π})}^{M} {| σ^{2} \sum_{j} |}^{\frac{1}{2}}}

(16)

If we assumed that the trees are independent and identically distributed, then,

\prod_{j = 1}^{J} P (β_{M j} | σ^{2}) \sim N (J μ_{M}, J σ^{2} Σ)

\begin{matrix} \prod_{j = 1}^{J} P (β_{M j} | σ^{2}) & = \frac{exp [\frac{- 1}{2 J σ^{2}} {(β_{M j} - J μ_{M j})}^{'} Σ_{j}^{- 1} (β_{M j} - J μ_{M j})]}{{(\sqrt{2 π})}^{J M} {| σ^{2} J \sum_{j} |}^{\frac{J}{2}}} \end{matrix}

(17)

\begin{matrix} P r (σ^{2}) & = \frac{b_{0}^{a_{0}} {(σ^{2})}^{- a_{0} - 1} exp (- b_{0} / σ^{2})}{Γ (a_{0})} \end{matrix}

(18)

\begin{matrix} P r (I_{1}, I_{2}, \dots, I_{J}) & = \frac{exp [\frac{- 1}{2 J σ^{2}} {(β_{M j} - J μ_{M j})}^{'} \sum_{j}^{- 1} (β_{M j} - J μ_{M j})]}{{(\sqrt{2 π})}^{J M} {| σ^{2} J \sum_{j} |}^{\frac{J}{2}}} \\ \times \frac{b_{0}^{a_{0}} {(σ^{2})}^{- a_{0} - 1} exp (- b_{0} / σ^{2})}{Γ (a_{0})} \end{matrix}

(19)

\begin{matrix} P r (I_{1}, I_{2}, \dots, I_{J}) & = \frac{b_{0}^{a_{0}} {(σ^{2})}^{- (a_{0} + (J / 2) + 1)}}{Γ (a_{0}) {(\sqrt{2 π})}^{J M} {| J \sum_{j} |}^{\frac{J}{2}}} \\ \times \frac{exp \{\frac{- 1}{2 σ^{2}} [{(β_{M j} - J μ_{M j})}^{'} J^{- 1} \sum_{j}^{- 1} (β_{M j} - J μ_{M j}) + 2 b_{0}]\}}{Γ (a_{0}) {(\sqrt{2 π})}^{J M} {| J \sum_{j} |}^{\frac{J}{2}}} \end{matrix}

(20)

The Bayes theorem leads to the posterior density of trees;

\begin{matrix} P r (I_{1}, \dots, I_{J} | y, x) & = \\ \frac{[\prod_{j = 1}^{J} P r (β_{M j} | σ^{2})] P r (σ^{2}) L (y, x | I_{1}, \dots, I_{J})}{\int_{β_{M j}} \int_{σ^{2}} [\prod_{j = 1}^{J} P r (β_{M j} | σ^{2})] P r (σ^{2}) L (y, x | I_{1}, \dots, I_{J}) d β_{M j} d σ^{2}} \end{matrix}

(21)

The integral at the denominator of equation (21) cannot be solved analytically thus, it is often dropped in most Bayesian analyses suggested by [35] and hence, we proceed as;

P r (I_{1}, I_{2}, \dots, I_{J} | y, x) \propto [\prod_{j = 1}^{J} P r (β_{M j} | σ^{2})] P r (σ^{2}) L (y, x | I_{1}, I_{2}, \dots, I_{J}) .

(22)

The likelihood of J trees can be defined as;

\begin{matrix} L (y, x | I_{1}, I_{2}, \dots, I_{J}) & = \prod_{j = 1}^{J} L (y, x | I_{j}) \end{matrix}

(23)

\begin{matrix} L (y, x | I_{j}) & = \frac{exp [\frac{- 1}{2 σ^{2}} {(y - β_{M j})}^{'} (y - β_{M j})]}{{(\sqrt{2 π σ^{2}})}^{n}} \end{matrix}

(24)

\begin{matrix} L (y, x | I_{1}, I_{2}, \dots, I_{J}) & = \frac{exp [\frac{- 1}{2 σ^{2}} \sum_{j = 1}^{J} {(y - β_{M j})}^{'} (y - β_{M j})]}{{(\sqrt{2 π σ^{2}})}^{J n}} . \end{matrix}

(25)

Therefore, the posterior of Bayesian Random Forest regression is;

\begin{matrix} P r (I_{1}, I_{2}, \dots, I_{J} | y, x) & \propto \frac{{(σ^{2})}^{- (a_{0} + (J / 2) + 1)}}{Γ (a_{0}) {(\sqrt{2 π})}^{J M} {| J Σ_{j} |}^{\frac{J}{2}}} \\ \times \frac{exp \{\frac{- 1}{2 σ^{2}} [{(β_{M j} - J μ_{M j})}^{'} J^{- 1} Σ_{j}^{- 1} (β_{M j} - J μ_{M j}) + 2 b_{0}]\}}{Γ (a_{0}) {(\sqrt{2 π})}^{J M} {| J Σ_{j} |}^{\frac{J}{2}}} \\ \times \frac{exp [\frac{- 1}{2 σ^{2}} \sum_{j = 1}^{J} {(y - β_{M j})}^{'} (y - β_{M j})]}{{(\sqrt{2 π σ^{2}})}^{J n}} . \end{matrix}

(26)

\begin{matrix} P r (I_{1}, I_{2}, \dots, I_{J} | y, x) & \propto {(σ^{2})}^{- (a_{1} + (J / 2) + 1)} \\ \times exp \{\frac{- 1}{2 σ^{2}} [{(β_{M j} - J μ_{M j}^{1})}^{'} {(J Σ_{j}^{1})}^{- 1} (β_{M j} - J μ_{M j}^{1}) + 2 b_{1}]\} \end{matrix}

(27)

where;

J μ_{M j}^{1} = {[{(J Σ_{j})}^{- 1} + (J V_{j})]}^{- 1} [{(J Σ_{j})}^{- 1} μ_{M j} + {(J V_{j})}^{- 1} n_{M j} {\bar{y}}_{M j}]

(28)

where

V_{j}

is an

m \times m

matrix of data information such that the diagonal of

V_{j}

σ_{m j}^{- 2}

which is defined as;

\begin{matrix} σ_{m j}^{- 2} & = \frac{n_{m j} - 1}{\sum_{i = 1}^{n_{m j}} {(y - {\bar{y}}_{m j})}^{2}} \end{matrix}

(29)

\begin{matrix} J Σ_{j}^{1} & = {[{(J Σ_{j})}^{- 1} + (J V_{j})]}^{- 1} \end{matrix}

(30)

\begin{matrix} a_{1} & = a_{0} + n / 2 \end{matrix}

(31)

\begin{matrix} b_{1} & = b_{0} + (\frac{μ_{M j}^{'} {(Σ_{j})}^{- 1} μ_{M j} + y^{'} y - μ_{M j}^{1^{'}} {(Σ_{j}^{1})}^{- 1} μ_{M j}^{1}}{2}) \end{matrix}

(32)

The marginal densities of

P r (I_{1}, I_{2}, \dots, I_{J} | y, x)

is important when performing inference about

β_{M}

and

σ^{2}

. The marginal density of

β_{M}

is given by;

P r (β_{M} | I_{1}, I_{2}, \dots, I_{J}, y, x) = \int_{σ^{2}} P r (I_{1}, I_{2}, \dots, I_{J} | y, x) d σ^{2}

(33)

\begin{matrix} P r (β_{M} | I_{1}, I_{2}, \dots, I_{J}, y, x) & = \int_{σ^{2}} {(σ^{2})}^{- (a_{1} + (J / 2) + 1)} \\ \times exp [\frac{- 1}{2 σ^{2}} {(β_{M j} - J μ_{M j}^{1})}^{'} {(J Σ_{j}^{1})}^{- 1} \\ \times (β_{M j} - J μ_{M j}^{1}) + 2 b_{1}] d σ^{2} \end{matrix}

(34)

According to [36], the marginal distribution is identical to the

s t u d e n t - t

distribution defined as:

P r (β_{M} | I_{1}, I_{2}, \dots, I_{J}, y, x) \sim t (μ_{M j}^{1}, s^{2} Σ_{j}^{1}, 2 a_{1})

where,

s^{2} = \frac{b_{1}}{a_{1} - 1} = \frac{b_{0} + (\frac{μ_{M j}^{'} {(Σ_{j})}^{- 1} μ_{M j} + y^{'} y - μ_{M j}^{1^{'}} {(Σ_{j}^{1})}^{- 1} μ_{M j}^{1}}{2})}{a_{0} + n / 2 - 1}

(35)

Therefore, the posterior mean for

β_{M}

is;

{\hat{β}}_{M} = J^{- 1} \{{[{(J Σ_{j})}^{- 1} + (J V_{j})]}^{- 1} ({(J Σ_{j})}^{- 1} μ_{M j} + {(J V_{j})}^{- 1} n_{M j} {\bar{y}}_{M j})\}

(36)

and the posterior variance for

β_{M}

is;

v a r (β_{M}) = J^{- 1} \{\frac{2 a_{1} s^{2}}{2 a_{1} - 2} {[{(J Σ_{j})}^{- 1} + (J V_{j})]}^{- 1}\}

(37)

The posterior mean of

β_{M}

can be interpreted as the weighted average of prior mean

μ_{M}

and data mean

{\bar{y}}_{M}

. The scaling factor is the joint contribution of prior and data information. Similarly, the posterior variance of

β_{M}

is the scaled form of the joint contribution of data and prior information matrix. The parameters

β_{M}

and

σ^{2}

can be extracted from their posterior density using a hybrid of Metropolis-Hastings and Gibbs sampler algorithms described as follows:

3.0.1. Hybrid Gibbs and MH procedure for extracting posterior information from Bayesian Random Regression Forest with Gaussian Response

Step 0: Define initial values for $β_{M j}^{0}$ and ${(σ^{2})}^{0}$ such that $P r (β_{M j}^{0} | y, x) > 0$ and $P r [{(σ^{2})}^{0}] > 0$ .
Step 1: For $v = 1, 2, \dots, V$
Step 2: Sample ${\tilde{σ}}^{2}$ from lognormal distribution; $q_{1} ({\tilde{σ}}^{2}, ν_{1}) = L N [{({\tilde{σ}}^{2})}^{v - 1}, ν_{1}]$ .
Step 3: For $j = 1, 2, \dots, J$ trees
Step 4: Sample ${\tilde{β}}_{M j}$ from independent multivariate normal distribution $q_{2} ({\tilde{β}}_{M j}, ν_{2}) = I N M (β_{M j}^{v - 1}, ν_{2})$ .
Step 5: Calculate the moving probability for $β_{M j}$ by;

$π_{1} (β_{M j}^{v}, {\tilde{β}}_{M j}) = min [\frac{P r ({\tilde{β^{v}}}_{M j} | y, x)}{P r (β_{M j}^{v} | y, x)}, 1]$
Step 6: Sample $U_{1} \sim U (0, 1)$ ; then

$β_{M j}^{v} = \{\begin{matrix} {\tilde{β}}_{M j} & i f U_{1} \leq π_{1} (β_{M j}^{v}, {\tilde{β}}_{M j}); \\ β_{M j}^{v - 1} & i f U_{1} > π_{1} (β_{M j}^{v - 1}, {\tilde{β}}_{M j}) . \end{matrix}$
Step 7: Compute the residuals $ϵ_{i} = y_{i} - J^{- 1} \sum_{j = 1}^{J} I_{j} (β_{M j}^{v} : x \in R_{M j})$
Step 8: Calculate the moving probability for $σ^{2}$ by;

$π_{2} [{(σ^{2})}^{v}, {\tilde{σ}}^{2}] = min \{\frac{P r ({\tilde{σ}}^{2} | ϵ_{i}) q_{1} [{(σ^{2})}^{v - 1} | {\tilde{σ}}^{2}, ν_{1}]}{P r [{(σ^{2})}^{v - 1} | ϵ_{i}] q_{1} [{\tilde{σ}}^{2} | {(σ^{2})}^{v - 1}, ν_{1}]}, 1\}$
Step 9: Sample $U_{2} \sim U (0, 1)$ ; then

${(σ^{2})}^{v} = \{\begin{matrix} {\tilde{σ}}^{2} & i f U_{2} \leq π_{2} [{(σ^{2})}^{v}, {\tilde{σ}}^{2}]; \\ {(σ^{2})}^{v - 1} & i f U_{2} > π_{2} [{(σ^{2})}^{v}, {\tilde{σ}}^{2}] . \end{matrix}$

The proposed algorithm is a combination of the Metropolis-hasting algorithm and Gibbs sampler. It is a Metropolis Hasting algorithm with further updates on

σ^{2}

using Gibbs sampler. The algorithm’s validity was demonstrated with a simulated response variable y scenario with no predictor variable. A regression tree with three terminal nodes was assumed. Each terminal node of the regression tree consists of 5 observations with mean

β_{m} = 10

; variance

σ_{m}^{2} = 4

;

m = 1, 2, 3

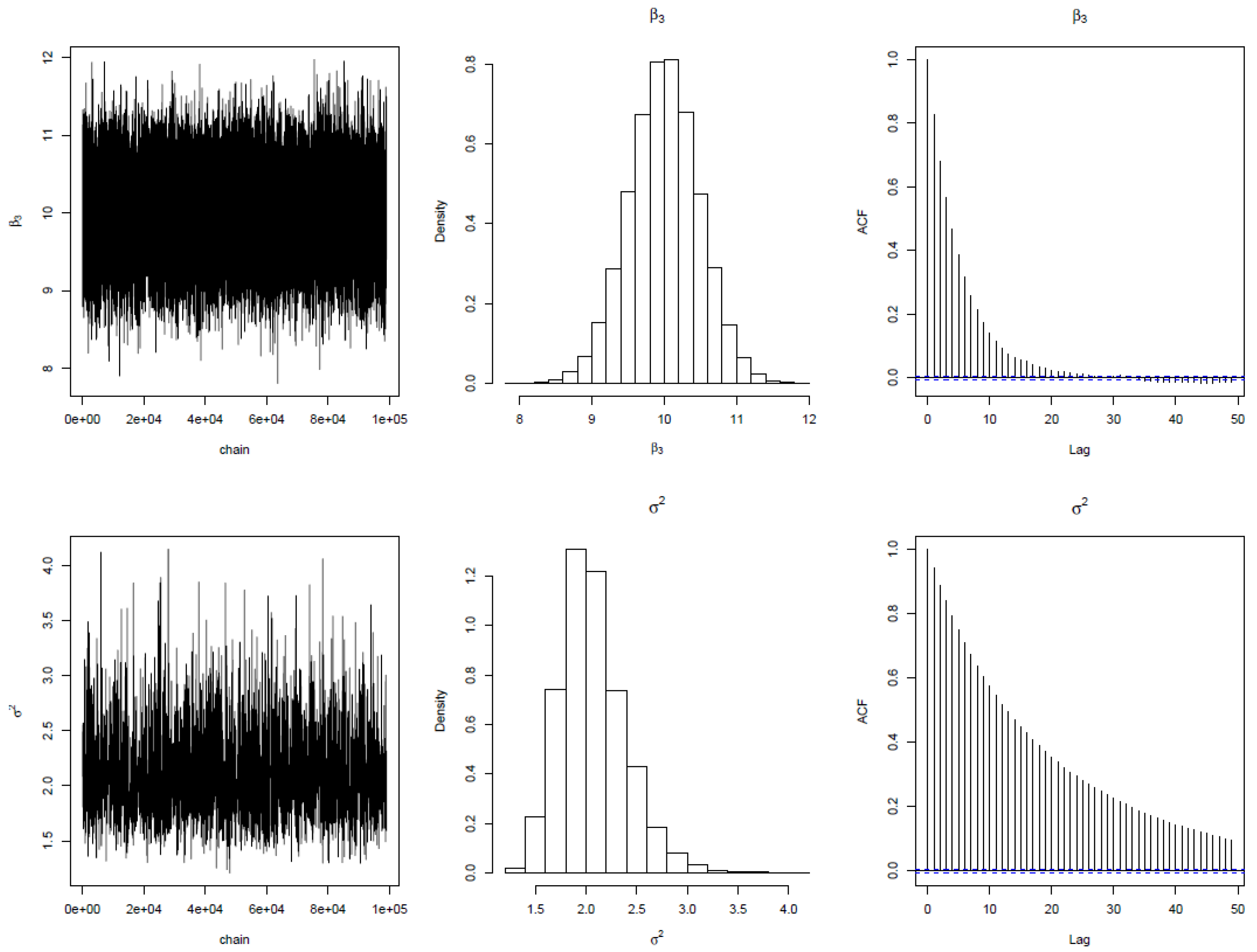
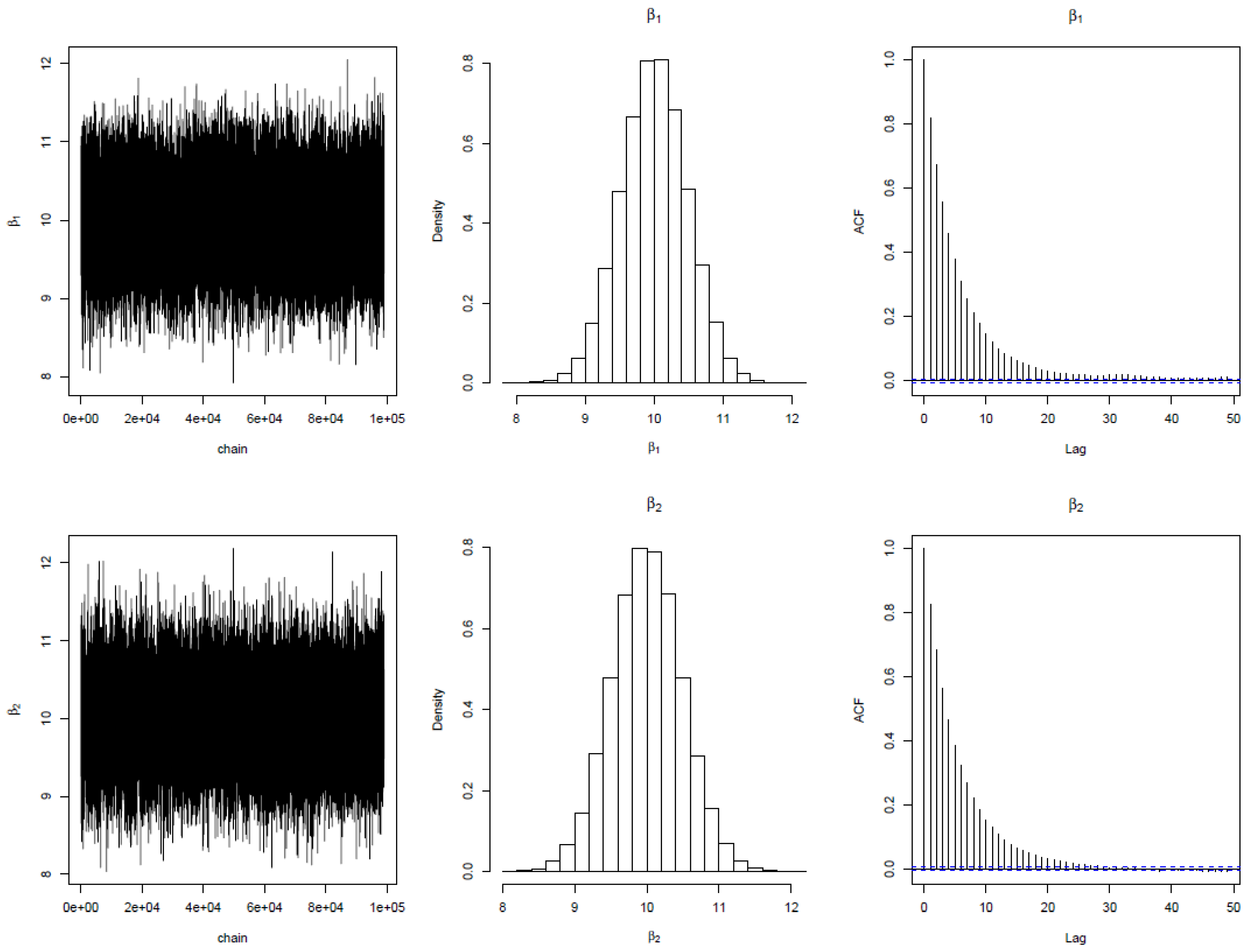
. The regression tree was replicated 5 times using bootstrapping to make a forest. The MCMC iteration results are shown below. The first column shows the trace plot of the parameter for each node over the trees. The trace plot for the four parameters shows that the iterations converge very sharply at 10000. The autocorrelation plots show an exponential decay, suggesting independent MCMC chains. The acceptance rate lies within the tolerable range of 20%

- 40

% as suggested by [35]. These features established the validity of the algorithm. In addition, the histogram supports the analytical densities proposed for the posterior distribution of parameters. The posterior densities for

β_{m}

is very much closer to student t distribution with values at the tail end while

σ^{2}

density is very much closer to Gamma. The overall model standard error estimate using the Bayesian Random Forest (BRF) algorithm is

σ_{b r f} = 1.42

while that of frequentist estimate is

σ_{r f} = 2.04

. This established that empirically, BRF is more efficient than the frequentist RF method.

Figure 3. Simulation plot 2 of the hybrid algorithm for Bayesian Random Forest regression.

The performance of the BRF procedure was also examined for predicting response y given three covariates that correspond to genes. The three covariates are denoted as

G e n e 1

G e n e 2

G e n e 3

. The functional relation between the response and genes was defined as:

y_{i} = 5 + 10 \times G e n e 1 + 20 \times G e n e 2 + 30 \times G e n e 3 + ϵ_{i}

where

i = 1, 2, \dots, 30

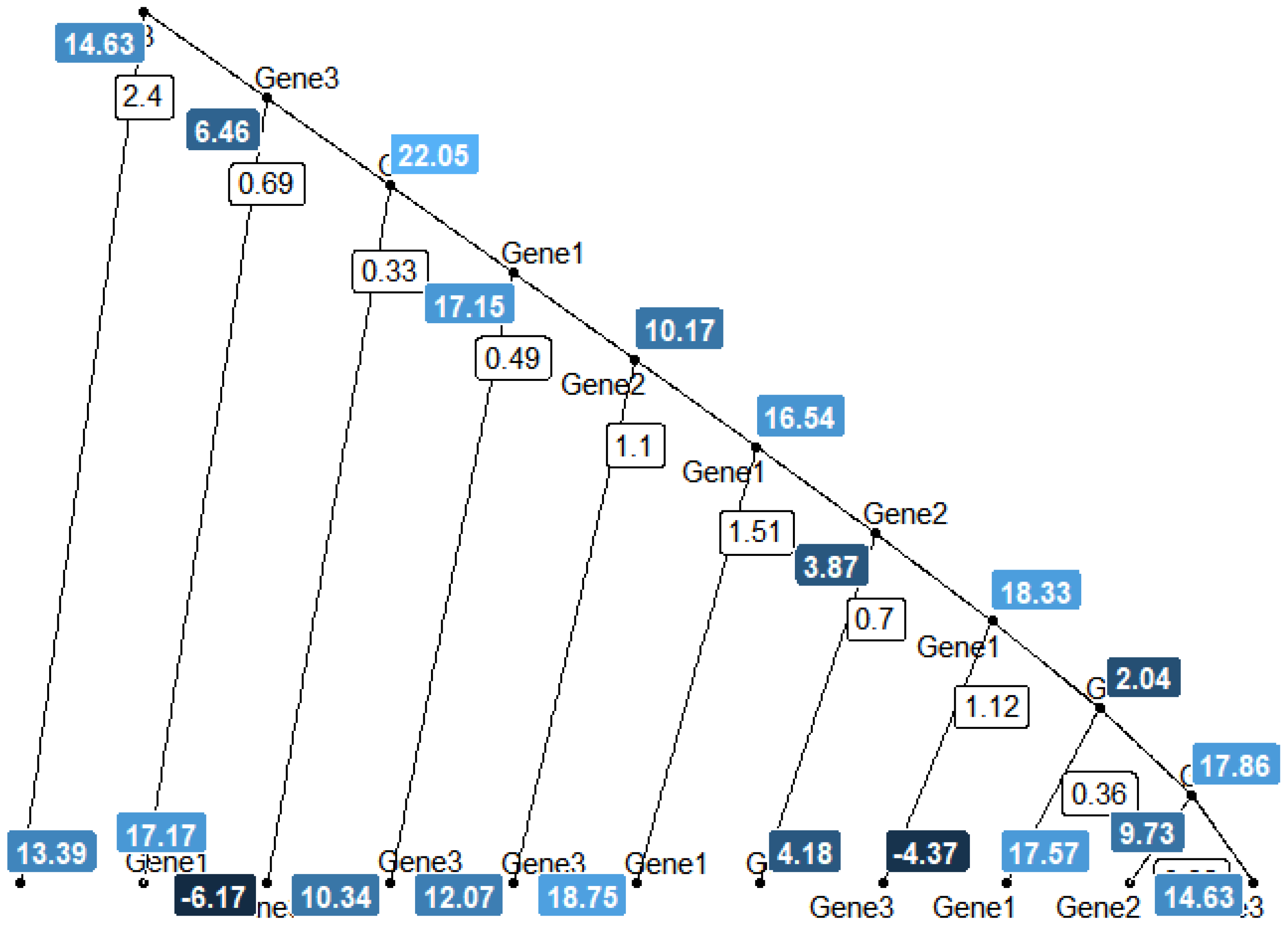
. Figure 4 and 5 shows a single tree diagram from a Bayesian random forest consisting of 5 trees. The plot shows simulated 20 terminal nodes.

The first white box in Figure 4 housed value

2.4

, corresponding to the split decision value. Variable Gene3 split into two daughter nodes with the left node terminating on predicted

\hat{y} = 13.39

based on the condition that

G e n e 3 < 2.4

. Subsequently, the right node further splits into another two daughter nodes using condition

G e n e 3 < 0.69

. Again, the left daughter node terminates on predicted

\hat{y} = 17.17

. The process continues until the maximum number of nodes set to be 20 is reached. The number of nodes condition is also referred to as maximal tree depth by [6]. The reason for more splits on

G e n e 3

can be easily observed from how the response was simulated such that

G e n e 3

is the most relevant in terms of weights. If the variable importance score is desired,

G e n e 3

will be the most important variable since it occurs more frequently than others in the predictor set. The posterior estimates in equations (36) and (37) obtained earlier rely on the accuracy of prior parameter values assumed. In most occasions, searching for appropriate prior parameters may be difficult, especially in the case of the sum of trees model. A data-driven approach is often used, such as those used in [22,28]. Another alternative is the Empirical Bayes. Empirical Bayes [37,38,39] allows the experimenter to estimate the prior hyperparameter values from the data. It is a hierarchical modelling approach where the parameter of a second stage or later model depends on initial stage data. The empirical Bayes approach is often used when hierarchical data are available. However, it can also be applied for non-hierarchical situations as extended by [40] using bootstrapped data to construct confidence intervals. The sum of trees modelling strategy is thus further simplified using the bootstrap prior technique. The approach was used to obtain the prior hyperparameters

μ_{M}

Σ

for each tree. The major advantage of bootstrap prior is that it guarantees an unbiased estimate of

β_{M}

for each tree. To achieve a fast grasp of the approach, we consider Bayesian inference of a single tree j with one of the terminal node parameters defined by

β_{m}

and

λ_{m}

. The likelihood of a single tree

I_{j} (β_{m} : x \in R_{m})

L [y, x | I_{j} (β_{m} : x \in R_{m})]

can be written as;

L [y, x | I_{j} (β_{m} : x \in R_{m})] = {(\frac{λ_{m j}^{\frac{1}{2}}}{\sqrt{2 π}})}^{n_{m j}} exp [- \frac{λ_{m j}}{2} \sum_{i : x \in R_{m j}}^{n_{m j}} {(y_{i} - β_{m j})}^{2}]

(38)

where

λ_{m j} = σ_{m j}^{- 2}

interpreted as precision for node m. Correspondingly, we can write the prior density for the parameters of a single tree as;

\begin{matrix} P r (β_{m j}, λ_{m j} | n_{0}, a_{0}, b_{0}) & = \frac{{(λ_{m j} n_{0})}^{1 / 2}}{\sqrt{2 π}} exp [- \frac{λ_{m j}}{2} {(β_{m j} - μ_{0})}^{2}] \\ \times \frac{b_{0}^{a_{0}} λ_{m j}^{a_{0} - 1} exp (- λ_{m j} b_{0})}{Γ (a_{0})} \end{matrix}

(39)

where

n_{0}

is the prior sample size for terminal node m,

μ_{0}

is the prior mean obtained from

n_{0}

a_{0}

is the prior sample size for the precision

λ_{m j}

and

b_{0}

is the prior sum of squares deviation from prior mean

μ_{0}

. The posterior distribution of a single tree thus follows from the Bayes theorem:

\begin{matrix} P r (β_{m j}, λ_{m j} | y, x) & = \\ \frac{P r (β_{m j}, λ_{m j}) \times L [y, x | I_{j} (β_{m} : x \in R_{m})]}{\int_{β_{m j}} \int_{λ_{m j}} P r (β_{m j}, λ_{m j}) \times L [y, x | I_{j} (β_{m} : x \in R_{m})] d β_{m j} d λ_{m j}} . \end{matrix}

(40)

After a little arrangement, the posterior distribution can be defined as:

\begin{matrix} P r (β_{m j}, λ_{m j} | y, x) & = \frac{{(λ_{m j} n_{1})}^{1 / 2}}{\sqrt{2 π}} exp [- \frac{λ_{m j}}{2} {(β_{m j} - μ_{1})}^{2}] \\ \times \frac{b_{1}^{a_{1}} λ_{m j}^{a_{1} - 1} exp (- λ_{m j} b_{1})}{Γ (a_{1})} \end{matrix}

(41)

where

μ_{1} m = (n_{0} μ_{0} + n_{m} {\bar{y}}_{m}) / (n_{0} + n_{m})

is the posterior estimate of

β_{m}

n_{1} = n_{0} + n_{m}

is the posterior sample size for which

μ_{1} m

can be estimated,

a_{1} = a_{0} + n_{m} / 2

is the posterior sample size for which

λ_{m}

can be estimated and

b_{1} = b_{0} + 1 / 2 \sum_{i = 1}^{n_{m}} {(y_{i} - {\bar{y}}_{m})}^{2} + \frac{n_{0} n_{m} {({\bar{y}}_{m} - μ_{0})}^{2}}{2 (n_{0} + n_{m})}

. The terminal node estimate

{\bar{y}}_{m}

is defined as;

{\bar{y}}_{m} = {(n_{m})}^{- 1} \sum_{i = 1}^{n_{m}} (y_{i} | x_{i} \in R_{m})

(42)

is the maximum likelihood estimate of

E (y_{i} | x_{i} \in R_{m})

. The estimate is unbiased and that is used in RF algorithms. The variance of the estimate followed as;

v a r ({\bar{y}}_{m}) = n_{m}^{- 1} σ_{m}^{2}

(43)

The corresponding empirical bayes estimate for equations (42) and (43) are;

\begin{matrix} {\hat{μ}}_{[E B] m} & = ({\hat{n}}_{0} {\hat{μ}}_{0} + n_{m} {\bar{y}}_{m}) / ({\hat{n}}_{0} + n_{m}) \end{matrix}

(44)

\begin{matrix} {\hat{σ}}_{[E B] m}^{2} & = \frac{{\hat{b}}_{0} + 1 / 2 \sum_{i = 1}^{n_{m}} {(y_{i} - {\bar{y}}_{m})}^{2} + \frac{{\hat{n}}_{0} n_{m} {({\bar{y}}_{m} - {\hat{μ}}_{0})}^{2}}{2 ({\hat{n}}_{0} + n_{m})}}{{\hat{a}}_{0} + n_{m} / 2} \end{matrix}

(45)

As a further update on the empirical Bayes procedure, the prior hyperparameters are estimated from a bootstrapped sample by following the procedure below:

Creating B bootstrap samples $y_{b}$ from the initial sample $y_{m}$ in the terminal node m,
Estimating the hyperparameters (prior parameters) each time the samples are generated using the Maximum Likelihood (ML) method,
Updating the posterior estimates using the hyperparameters in step (2) above using equations (44) and (),
Then obtaining the bootstrap empirical Bayesian estimates ${\hat{μ}}_{B T}$ and ${\hat{σ}}_{B T}^{2}$ using;

\begin{matrix} {\hat{μ}}_{B T} & = B^{- 1} \sum_{b = 1}^{B} {\hat{μ}}_{[E B] m_{b}} \end{matrix}

(46)

\begin{matrix} {\hat{σ}}_{B T}^{2} & = B^{- 1} \sum_{b = 1}^{B} {\hat{σ}}_{[E B] m_{b}}^{2} \end{matrix}

(47)

Theorem 2.

The bootstrap prior estimate

{\hat{μ}}_{B T}

is a uniformly minimum variance unbiased estimator of

β_{m} = E (y_{i} | x_{i} \in R_{m})

under mild regularity conditions.

Proof.

\begin{matrix} {\hat{μ}}_{B T} & = B^{- 1} \sum_{b = 1}^{B} \frac{{\hat{n}}_{0} {\hat{μ}}_{0} + n_{m} {\bar{y}}_{m}}{{\hat{n}}_{0} + n_{m}} \end{matrix}

(48)

\begin{matrix} {\hat{μ}}_{B T} & = B^{- 1} \sum_{b = 1}^{B} [\frac{{\hat{n}}_{0} {\hat{μ}}_{0}}{{\hat{n}}_{0} + n_{m}} + \frac{n_{m} {\bar{y}}_{m}}{{\hat{n}}_{0} + n_{m}}] \end{matrix}

(49)

Suppose we fix the prior parameters as;

{\hat{n}}_{0 b} = B

and

{\hat{μ}}_{0 b} = {\bar{y}}_{m b}

, where

\bar{(} {y)}_{m b}

is the ML estimate based on a bootstrap sample selected from

y_{b}

. That is,

{\bar{y}}_{m b} = {(n_{m})}^{- 1} \sum_{i = 1}^{n_{m}} (y_{b i} | x_{i} \in R_{m})

Then,

\begin{matrix} {\hat{μ}}_{B T} & = B^{- 1} \sum_{b = 1}^{B} [\frac{B {\bar{y}}_{m b}}{B + n_{m}} + \frac{n_{m} {\bar{y}}_{m}}{B + n_{m}}] \end{matrix}

(50)

\begin{matrix} {\hat{μ}}_{B T} & = \frac{\sum_{b = 1}^{B} {\bar{y}}_{m b}}{B + n_{m}} + \frac{n_{m} {\bar{y}}_{m}}{B + n_{m}} \end{matrix}

(51)

\begin{matrix} E [{\hat{μ}}_{B T}] & = E [\frac{\sum_{b = 1}^{B} {\bar{y}}_{m b}}{B + n_{m}} + \frac{n_{m} {\bar{y}}_{m}}{B + n_{m}}] \end{matrix}

(52)

\begin{matrix} E [{\hat{μ}}_{B T}] & = \frac{\sum_{b = 1}^{B} E [{\bar{y}}_{m b}]}{B + n_{m}} + \frac{n_{m} E [{\bar{y}}_{m}]}{B + n_{m}} \end{matrix}

(53)

Since

{\bar{y}}_{m}

and

{\bar{y}}_{m b}

are known unbiased estimates of

β_{m}

, →

\begin{matrix} E [{\hat{μ}}_{B T}] & = \frac{\sum_{b = 1}^{B} β_{m}}{B + n_{m}} + \frac{n_{m} β_{m}}{B + n_{m}} \end{matrix}

(54)

\begin{matrix} = \frac{1}{B + n_{m}} [B β_{m} + n_{m} β_{m}] \end{matrix}

(55)

\begin{matrix} E [{\hat{μ}}_{B T}] & = β_{m} \end{matrix}

(56)

Therefore,

{\hat{μ}}_{B T}

is unbiased for estimating

β_{m}

. Also, the MSE is the combination of the square of bias and variance of the estimate, then following from the above derivation the MSE is just the variance of the estimate. Thus,

\begin{matrix} v a r [{\hat{μ}}_{B T}] & = v a r [\frac{\sum_{b = 1}^{B} {\bar{y}}_{m b}}{B + n_{m}} + \frac{n_{m} {\bar{y}}_{m}}{B + n_{m}}] \end{matrix}

(57)

\begin{matrix} = \frac{\sum_{b = 1}^{B} v a r [{\bar{y}}_{m b}]}{{(B + n_{m})}^{2}} + \frac{n_{m}^{2} v a r [{\bar{y}}_{m}]}{{(B + n_{m})}^{2}} \end{matrix}

(58)

\begin{matrix} = \frac{\sum_{b = 1}^{B} [n_{m}^{- 1} σ_{m}^{2}]}{{(B + n_{m})}^{2}} + \frac{n_{m}^{2} [n_{m}^{- 1} σ_{m}^{2}]}{{(B + n_{m})}^{2}} \end{matrix}

(59)

\begin{matrix} v a r [{\hat{μ}}_{B T}] & = [\frac{n_{m}^{2} + B}{{(B + n_{m})}^{2}}] n_{m}^{- 1} σ_{m}^{2} \end{matrix}

(60)

Hence, it can be shown that the limiting form of

[\frac{n_{m}^{2} + B}{{(B + n_{m})}^{2}}]

is 0, by applying L’hospital rule:

\begin{matrix} lim_{B \to \infty} [\frac{n_{m}^{2} + B}{{(B + n_{m})}^{2}}] & = lim_{B \to \infty} [\frac{\frac{d (n_{m}^{2} + B)}{d B}}{\frac{d {(B + n_{m})}^{2}}{d B}}] \end{matrix}

(61)

\begin{matrix} lim_{B \to \infty} [\frac{n_{m}^{2} + B}{{(B + n_{m})}^{2}}] & = lim_{B \to \infty} [\frac{1}{2 (B + n_{m})}] \end{matrix}

(62)

\begin{matrix} lim_{B \to \infty} [\frac{n_{m}^{2} + B}{{(B + n_{m})}^{2}}] & = \frac{1}{\infty} \end{matrix}

(63)

\begin{matrix} lim_{B \to \infty} [\frac{n_{m}^{2} + B}{{(B + n_{m})}^{2}}] & = 0 \end{matrix}

(64)

□

The derivation above implies that at sample size

n_{m}

, the

{lim}_{B \to \infty} v a r [{\hat{μ}}_{B T}] = 0

. This affirms that the experimenter can control the stability of the estimator by increasing the number of bootstrap samples B. In addition,

v a r [{\hat{μ}}_{B T}] = [\frac{n_{m}^{2} + B}{{(B + n_{m})}^{2}}] n_{m}^{- 1} σ_{m}^{2} < v a r [{\hat{μ}}_{M L}] = n_{m}^{- 1} σ_{m}^{2}

, by a factor

[\frac{n_{m}^{2} + B}{{(B + n_{m})}^{2}}]

that converges faster to zero with increasing B. Therefore, the frequentist estimator (ML) is less efficient than the estimator

{\hat{μ}}_{B T}

, which is more efficient. Because they are both unbiased, this comparison is valid. Since this proposed estimator reduces the MSE in terms of bias and variance reduction, it is additionally more efficient within the Bayesian framework. By only lowering the variance, the conventional Bayesian estimator reduces the MSE.. Therefore,

{\hat{μ}}_{B T}

is a minimum variance unbiased estimator for estimating the population mean

β_{m}

. The proof established here serves as a baseline for using bootstrapped prior with the sum of trees model.

3.1. A New Weighted Splitting for Bayesian Random Forest in Sparse High-Dimensional Setting

Apart from the probabilistic interpretation update on random forest regression achieved using Bayesian modelling, we also dealt with the variable selection principle used during splitting. Tree-based methods use a greedy approach to build trees. In a high-dimensional setting with a large number of covariates, modelling with all the covariates increases the computational time and thus subsampling variables randomly or using a deterministic approach is suitable for tree-based methods. There are two popular approaches for handling high-dimensional data;

Greedy search: Identifying the relevant subset of variables and fitting the desired model on them.
Random search: Randomly selecting subset (whether relevant or irrelevant) and fitting the desired model on them.

The two approaches are not

100 %

perfect in variable selection, greedy search fails to capture the interaction effect between variables and sometimes overfits while random search does not overfit if replicated a large number of times but tends to suffer the loss of efficiency when the variable space is populated with irrelevant variables. The RF regression algorithm randomly selects variables from the predictor space by selecting a fixed number

p / 3

irrespective of their predictive interaction with the response variable. This subsample size does not take into account the number of relevant predictors in the entire predictor space, thus the chance of selecting irrelevant features increases with increased p. Therefore, using the same data configuration, the predictive performance of RF reduces with increasing p.

The weakness of RF can be attributed to its random subset selection mechanism. Updating the subset selection with a data-driven approach such that predictors are ranked in the order of relative correlation with response y will be fruitful. The motivation behind this idea follows from a greedy background, by trying to build a sum of tree models with only a relevant subset of predictors. However, this will affect the interaction modelling strength of RF which might further lead to a reduction in predictive power. In addition, we intend to update and not modify RF so as to maintain all its strength. Based on this fact, we developed a new framework that combines the strength of greedy search as well as random search by ranking the variables based on their initially computed importance.

Let

T_{1}, T_{2}, T_{3}, \dots, T_{p}

be p independent t statistics with cumulative distribution function

F (t)

. Here,

T_{k}

corresponds to the t statistic for each covariate

x_{k}

after fitting a Bayesian simple linear regression model of the response y on

x_{k}

. Specifically,

T_{k}

can be defined as follows:

T_{k} = \frac{{\hat{θ}}_{k}}{S D ({\hat{θ}}_{k})}

(65)

where

{\hat{θ}}_{k}

is the Bayesian estimated weight of

x_{k}

in the simple linear regression model:

y = θ_{0} + θ_{k} x_{k} + ϵ

(66)

θ_{0}

is the bias of estimating y using

x_{k}

and

ϵ

is the random noise that arises during the estimation of y with the linear model; it is considered to be independent, identical, Gaussian-distributed noise with a mean of zero and a constant variance

δ^{2}

S D ({\hat{θ}}_{k})

is the posterior standard deviation of

θ_{k}

. The t- statistics

T_{k}

are then ranked in the increasing order of magnitude as;

T_{(1)} \leq T_{(2)} \leq T_{(3)} \leq \dots \leq T_{(p)}

. The

T_{(k)}

is the

k t h

order statistic

(k = 1, 2, \dots, p)

. Then, the cumulative distribution function

(C D F)

of the largest order statistic

T_{(p)}

is given by;

\begin{matrix} F_{p} (t) & = P r (T_{(p)} \leq t) \end{matrix}

(67)

\begin{matrix} F_{p} (t) & = P r (a l l T_{(k)} \leq t) = F^{p} (t) \end{matrix}

(68)

Also, we can see that

P r (T_{(k)} \geq a l l T_{(p - k)}) \equiv P r (a l l T_{(p - k)} \leq T_{(k)})

; thus

F_{p - k} (t) = P r (a l l T_{(p - k)} \leq T_{(k)}) .

(69)

Equation (69) can be interpreted as the probability that at least

p - k

of the

T_{(k)}

are less than or equal to t. This also implies that all other

(p - k)

variables are less relevant to response y than

X_{k}

\begin{matrix} P r (a l l T_{(p - k)} \leq T_{(k)}) & = \sum_{k = (p - k)}^{p} (\binom{p}{k}) F^{(k)} (t) {[1 - F (t)]}^{p - k} \end{matrix}

(70)

\begin{matrix} F^{(p - k)} (t) & = \sum_{k = (p - k)}^{p} (\binom{p}{k}) F^{(k)} (t) {[1 - F (t)]}^{p - k} . \end{matrix}

(71)

We now refer to

F^{(p - k)} (t)

as weight

w_{k}

which is the probability that each

x_{p - k}

variable is less important to y than

x_{k}

. A binary regression tree’s splitting mechanism is then updated using this weight in the following ways:

Q_{m}^{w} (T) = (1 - w_{k}) [\sum_{i : x_{k} \in R_{1} (j, s)}^{n_{1 m}} {(y_{i} - {\hat{β}}_{1 m})}^{2} + \sum_{i : x_{k} \in R_{2} (j, s)}^{n_{2 m}} {(y_{i} - {\hat{β}}_{2 m})}^{2}]

(72)

If a variable

x_{k}

is important and subsequent splitting on it will have significance, the weighted deviation

Q_{m}^{w} (T)

reduces to zero (since

w_{k} \to 1

). Due to the fact that variables with lower weights w won’t be further divided in the tree-building algorithm, this strategy helps to speed up the algorithm and improve the variable selection component of random forest regression. The procedure below summarizes BRF for a Gaussian response.

Step 0: Start with input data $D = [x; y]$
Step 1: Analyze each variable $x_{k} \in x$ individually by running a univariate analysis and save the bootstrap Bayesian t statistic $t^{B P}$ .
Step 2: Calculate the probability of maximal weight $w_{k}$ for each variable $x_{k} \in x$ .
Step 3: For each of the J trees, where $j = 1, 2, \dots, J$ :
Step 4: Compute the bootstrap prior predictive density weights $ω_{i}$ from a Normal-Inverse $(N I G)$ distribution with parameters $μ_{M}^{B P}, σ^{2} Σ_{M}^{B P}, a_{B P}, b_{B P}$ .
Step 5: Generate a Bayesian weighted simple random sample $D^{*}$ of size N with replacement from the training data D using the weights $ω_{i}$ .
Step 6: Generate a Bayesian weighted simple random sample:
Step 7: Grow a weighted predictors CART tree $I_{j}$ , by iteratively repeating the following steps for each terminal node m, until the minimum node size $n_{m i n}$ is reached:

(a)

Randomly select $m t r y = ⌊ p / 3 ⌋$ variables without replacement from the pavailable variables.

(b)

Choose the best variable and split-point from the selected variables.

(c)

Divide the node into two daughter nodes.

(d)

Compute weighted splitting criterion $Q_{m}^{w} (T)$ and identify the node with the minimum deviance $Q_{m}^{w} (T)$ .
Step 8: Print the ensemble of trees $I_{j}$ over J iterations.
Step 10: To predict test data $x_{t e}$ , apply:

${\hat{y}}_{b r f}^{J} = \frac{1}{J} \sum_{j = 1}^{J} I_{j} (x_{t e})$

3.2. Oracle Properties of Bayesian Random Forest

In this section, we show that if the Bayesian bootstrap prior estimator

{\hat{μ}}_{B T}

is used for estimating

β_{M}

and the weighted splitting approach is utilized, the Bayesian Random Forest (BRF) enjoys the oracle properties.

Theorem 3.

Suppose

{\hat{β}}_{M} = {\hat{μ}}_{B T}

and

F^{(p - k)} (t) \to 1

, then the Bayesian Random Forest (BRF) satisfy the following:

i.: Identification of the right subset model $M$ such that $P (\hat{M} = M) \to 1$ .
ii.: Achievement of the optimal estimation rate, $\sqrt{n} (\hat{M} - M) \overset{d}{\to} N (0, V a r (M))$

Proof.

From theorem (1), we know that the probability of selecting at least one relevant subset R from the set p using RF is

\begin{matrix} P (R_{1} \cup R_{2} \cup \dots R_{r}) & = \sum_{k = 1}^{r} P (R_{k}) - \sum_{j, k = 1; k > j}^{r} P (R_{j} \cap R_{k}) + \sum_{i, j, k = 1; k > j > i}^{r} P (R_{i} \cap R_{i} \cap R_{k}) \\ - \dots + {(- 1)}^{r - 1} P (R_{1} \cap R_{2} \cap \dots \cap R_{r}) . \end{matrix}

Now using the weighted splitting, there is assurance that the selected variable

x_{k}

is relevant provided

F^{(p - k)} (t) \to 1

. This implies that the random selection of variables for splitting in BRF is a mutually exclusive process that is

P (R_{i} \cap R_{j}) = 0 \forall i \neq j

. Thus, the probability of selecting at least one relevant subset R from the set p using BRF is

\begin{matrix} P (R_{1} \cup R_{2} \cup \dots R_{r}) & = \sum_{k = 1}^{r} P (R_{k}) \\ = (\binom{r}{1}) (\frac{1}{r}) \\ = 1 \end{matrix}

(73)

Lemma 3.BRF variable selection is consistent if

{lim}_{p \to \infty} P (\hat{M} = M) = 1

Corollary 2.From equation (73)

{lim}_{p \to \infty} P (⋃_{k = 1}^{r \subset p} R_{k}) = 1

, then BRF variable selection is consistent in HD with large p.

Theorem (2) revealed that the Bayesian estimator

{\hat{μ}}_{B T}

is a uniformly minimum variance unbiased estimator for the parameter

β_{M}

under mild regularity conditions. This implies

\begin{matrix} v a r ({\hat{y}}_{b r f}) & = v a r ({\hat{μ}}_{B T}) \\ v a r ({\hat{y}}_{b r f}) & = [\frac{n_{m}^{2} + B}{{(B + n_{m})}^{2}}] n_{m}^{- 1} σ_{m}^{2} < v a r [{\hat{y}}_{r f}] = n_{m}^{- 1} σ_{m}^{2} \end{matrix}

(74)

Remark 3.Equation (74) implies that BRF is more efficient than RF when the bootstrap size

B \to \infty

. □

4. Simulation and Results

In this section, we conducted an empirical evaluation of BRF in comparison to its major competitors using both simulation and real-life data. The analyses were performed through 10-fold cross-validations on the datasets. All the analyses were executed in the R statistical package. We utilized the newly built-in function

b r f

for BRF,

g l m n e t

function [26] for LASSO,

g b m

for Gradient Boosting [20],

r f s r c

for Random Forest,

w b a r t

for BART1 as described in [22], and

b a r t M a c h i n e

for BART2 [41].

To implement the Bayesian Forest method (BF), we modified the

c a s e . w t

parameter of

r f s r c

from [42], introducing random weights distributed exponentially with a rate parameter of 1. It’s worth noting that we employed two different R packages for BART due to observed discrepancies in the results produced by these packages. Detailed information regarding the setup of tuning parameters can be found in Table 1.

Two simulation scenarios were created based on the problem we intend to tackle in this paper. The simulation scenarios were adapted from the works of [22] and [13]. In each of the scenarios, six levels of low and high-dimensional settings were defined as

p = 50, 100, 500, 1000, 5000, 10000

and used so as to mimic realistic gene expression datasets. The sample size corresponding to the number of patients n which is usually far smaller than p was fixed at 200 in all the scenarios. Here, the Root Mean Square Error

(R M S E)

and Average Root Mean Square

(A R M S E)

were used as performance measures over the 10-folds. Note

p = 50 & 100

were used to examine the behaviour of the methods in low dimensional data situations.

R M S E = \sqrt{\frac{\sum_{i = 1}^{n_{t e s t}} {(y_{i} - \hat{y_{i}})}^{2}}{n_{t e s t}}}

A R M S E = \frac{\sum_{e = 1}^{10} R M S E_{e}}{10}

Scenario 1: Linear Case; Set

x_{1}, \dots, x_{p}

as multivariate standard normal

N (0, 1)

random variables with associated covariance structure define as;

Σ = b l o c k d i a g (Σ_{1}^{1}, \dots, Σ_{G}^{1}) = I_{G} \otimes Σ^{1}

, where ⊗ is the kronecker product. Here we assume that the first five predictors

[x_{1}, \dots, x_{5}]

are relevant and the associated covariance structure is defined as

Σ^{1} = \{\begin{matrix} ρ & i f i \neq j; \\ 1 & i f i = j . \end{matrix}

, such that the first five variables have pairwise correlation value

ρ = 0.9

and likewise the other blocks of size five variables have the same correlation structure. The response is then simulated as

y = x_{1} + 2 x_{2} + 3 x_{3} + 4 x_{4} + 5 x_{5} + ϵ

, where

[x_{6}, \dots, x_{p}]

are the irrelevant predictor set. Note, with the covariance structure

Σ

defined, the

p - 5

variables are independent and identically distributed and

ϵ \sim N (0, 1)

Scenario 2: Nonlinear Case; This follows the same structure as in scenario one except for the simulation of the response which is defined as

y = 10 s i n (x_{1} x_{2}) + 20 {(x_{3} - 0.5)}^{2} + 10 | x_{4} - 0.5 | + 5 {(x_{5} - 0.5)}^{3} + ϵ

and

ρ = 0.2

4.1. Simulation Results

Table 2 summarizes the 10-fold cross-validation simulation of a Gaussian response for the seven methods. As expected for scenario 1 with the linearity assumption, LASSO takes the lead followed by the new method BRF. Also, the ARMSE increases with an increase in p for most of the methods except GBM which is unaffected by the increase in p. RF also performs much better than other ensemble methods like BF, BART1 and BART2 and most especially GBM. Although an increase in p affects the performance of RF significantly, the situation is different for BRF as the increase in p does not correspond to an increase in the ARMSE. BART2 performance tends to be better than BART1 for the low-dimensional case than the high-dimensional situation. BF performance is better than BART1 and BART2 but, BRF still takes the lead within the Bayesian class of models. 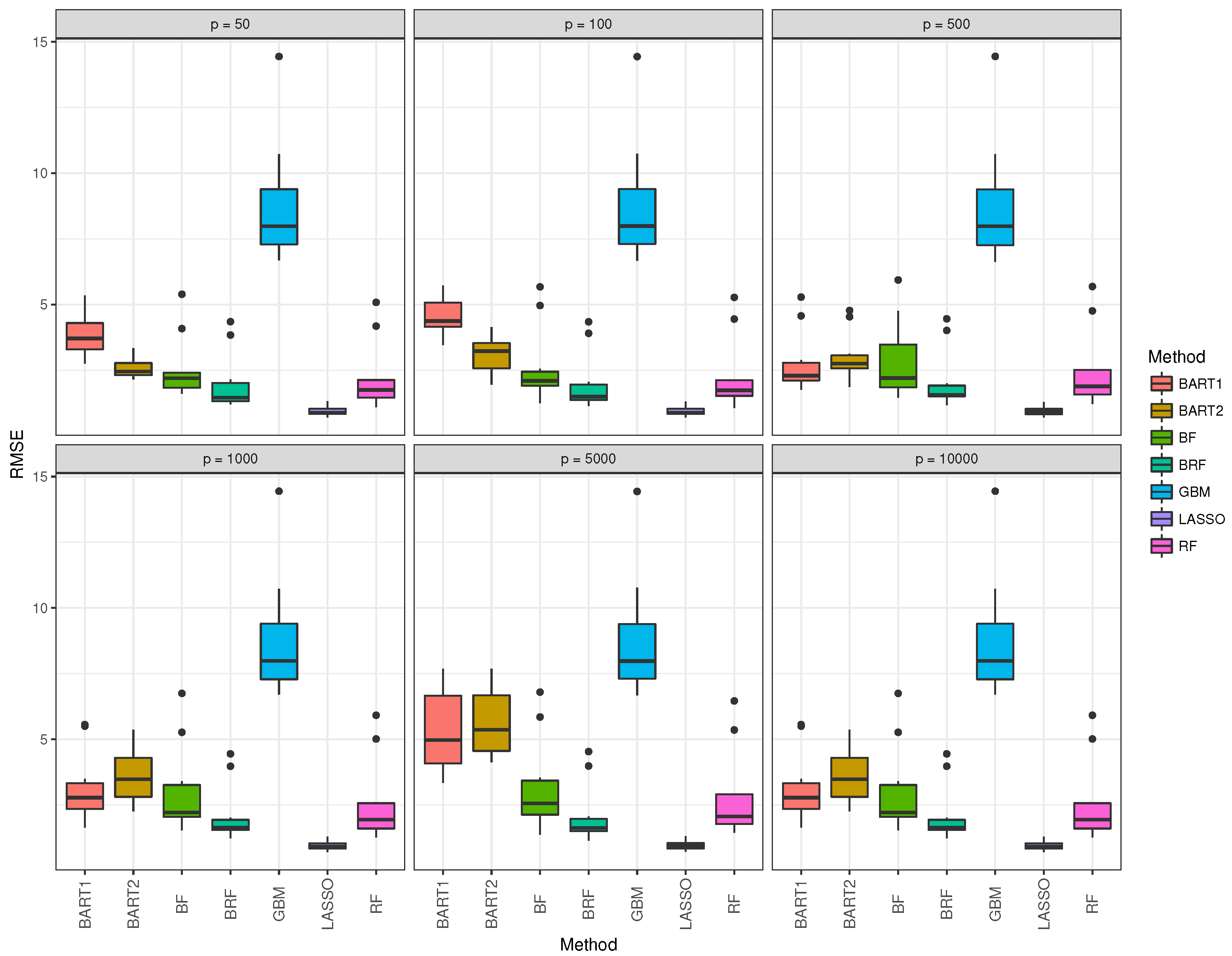The boxplot in Figure 5 corroborates the findings in Table 2 with the median RMSE of BRF and LASSO being the lowest over the different data dimensions.

The box and whisker plot for GBM (blue) was observed to be the highest in all data dimension situations. Table 3 summarizes the 10-fold cross-validation simulation for Gaussian response for the seven methods when the nonlinear model is assumed. The performance of all methods degrades drastically when compared to the linear case in Table 2. LASSO performs worse as expected in this situation. BART1 and BART2 performance are again better for the low dimensional situation when

p < n

, precisely for

p = 50, 100

. However, their performances depreciate faster as p approaches 500 and in fact worse than LASSO as p approaches 10000. GBM performance is again unaffected with the increase in p but the performance is not different from LASSO. RF and likewise BF perform moderately better than BART1 and BART2 for

p > 1000

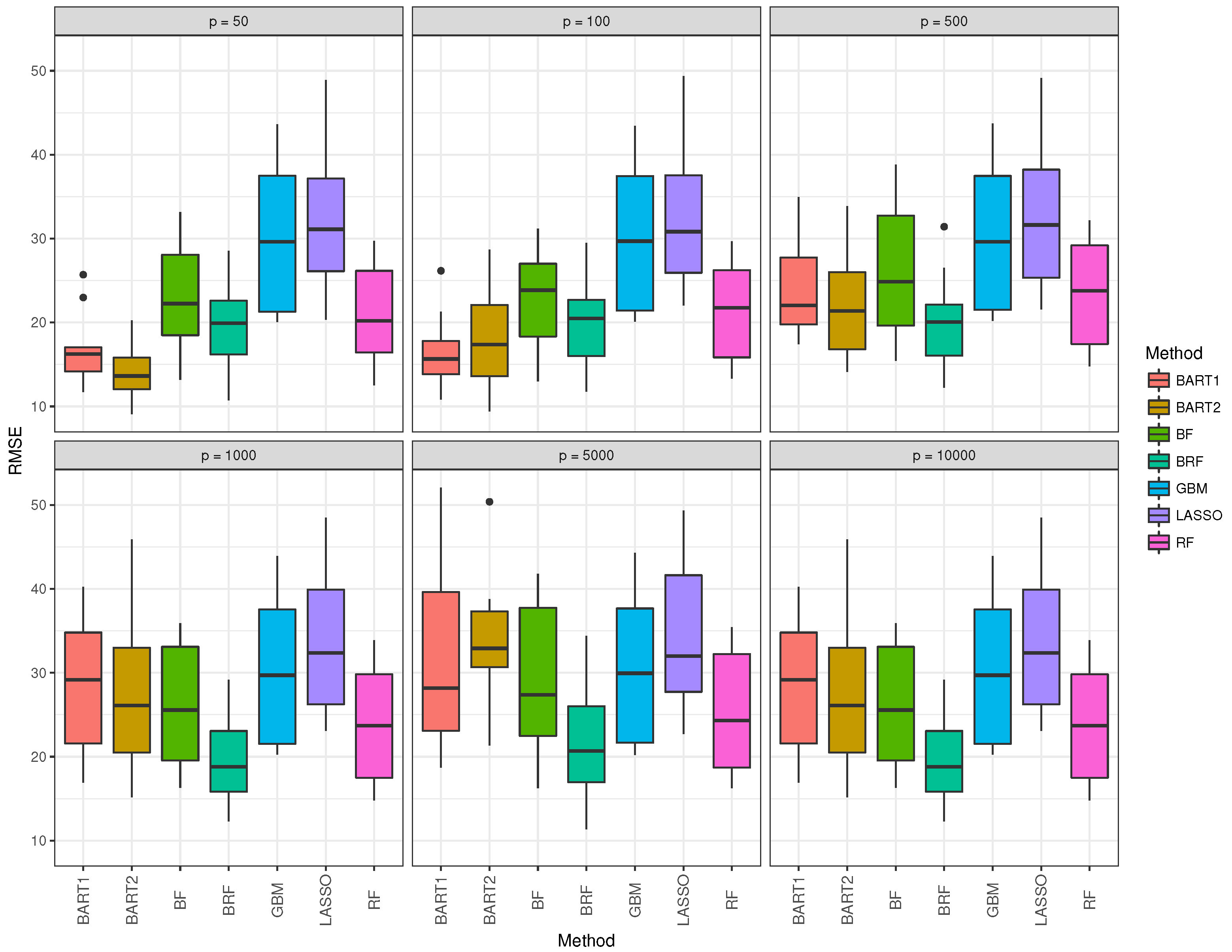
. BRF simultaneously achieves robustness to increase in p as well as maintaining the lowest RMSE for low and high dimensional settings when compared with the six other competing methods. The boxplot in Figure 6 corroborates the findings in Table 3, with the median RMSE of BRF being the lowest for

p > 500

Table 3. Average test Root Mean Square Error (ARMSE) over 10-fold cross-validation for scenario 2.

Scenario 2: Nonlinear
	p
Method	50	100	500	1000	5000	10000
BRF	19.498	19.896	19.889	19.906	21.637	22.543
GBM	30.355	30.352	30.444	30.551	30.708	30.964
LASSO	32.404	32.453	32.585	33.526	34.626	35.230
RF	20.664	21.264	23.266	23.742	25.043	25.954
BF	23.288	22.993	26.062	26.095	29.121	28.210
BART1	16.844	16.493	24.151	28.180	31.917	38.156
BART2	14.037	18.071	22.193	27.450	33.522	37.932

4.2. Variable Selection

The two scenario models (Linear and Non-linear) were investigated to determine the best method in terms of the selection of the five relevant variables imposed. Table 4 presents the results of the variable selection performance of BRF alongside competing methods. For the linear model, the average proportion of relevant variables identified using LASSO is 1 and constant over all the six datasets used. This result corroborates the findings in Table 2 where LASSO was found to be the best in terms of lowest ARMSE. The entire five relevant variables were correctly identified with LASSO under the linearity assumption. BRF competes favourably with LASSO with the identification of about

4 / 5

relevant variables up to

p = 5000

. BRF also consistently identified all the relevant variables in low dimensional conditions with

p = 50 & 100

. The performances of RF, BF and GBM are very similar with GBM slightly above RF and BF. BART2 also consistently identified about

4 / 5

relevant variables up till

p = 1000

. However, the performance at

p = 5000 & 10000

is not presented due to computational difficulty while computing the probability of inclusion for

p > 1000

. The lowest performance was observed with BART1 over all the dimensions of datasets used.

For the non-linear condition, none of the methods could achieve

100 %

identification as the functional path is now rough but BRF is still the best for

p = 50

, and it converges to

2 / 5

from

p = 1000

. LASSO performance is not consistent here and it also corroborates the high ARMSE observed in Table 3. BART2 competes with BRF at various levels of p and in fact the highest for

p \leq 1000

. A similar worse performance was observed for BART1 under the non-linear condition.

Table 4. Average proportion of relevant variables selected in 10 folds cross validation.

	p
Method	50	100	500	1000	5000	10000
			Linear
BRF	1.00	0.98	0.90	0.84	0.76	0.68
RF	0.96	0.84	0.80	0.78	0.68	0.64
BF	0.98	0.84	0.76	0.68	0.64	0.64
GBM	0.96	0.84	0.82	0.80	0.76	0.76
LASSO	1.00	1.00	1.00	1.00	1.00	1.00
BART1	0.76	0.86	0.82	0.80	0.48	0.24
BART2	0.88	0.88	0.84	0.80	-	-
			Non-linear
BRF	0.66	0.58	0.44	0.40	0.40	0.40
RF	0.60	0.60	0.44	0.42	0.40	0.38
BF	0.58	0.58	0.40	0.36	0.36	0.26
GBM	0.58	0.56	0.40	0.40	0.38	0.34
LASSO	0.62	0.72	0.42	0.40	0.40	0.40
BART1	0.54	0.56	0.40	0.30	0.14	0.10
BART2	0.62	0.64	0.52	0.44	-	-

4.3. Predicting Tumour Size and Biomarker Score

Three real-life cancer datasets on the prediction of tumour size and biomarker score. The two breast cancer datasets were used to predict the size of tumour before the patients underwent chemotherapy. The other dataset was used to predict the biomarker score of lung cancer for patients with smoking history. The dataset’s detailed description can be found below:

Breast1 Cancer: [43] obtained 22,283 gene expression profiles using Affymetrix Human Genome U133A Array on 61 patients prior to chemotherapy. The pre-chemotherapy size of tumours was recorded for both negative Estrogen Receptor (ER-) and positive Estrogen Receptor (ER+). A preliminary analysis carried out on the dataset using a Bayesian t-test revealed that only 7903 genes are relevant at some specific threshold.
Breast2 Cancer: [44] obtained 22,575 gene expression profiles using 60mer oligonucleotide array from 60 patients with ER-positive primary breast cancer and treated with tamoxifen monotherapy for 5 years. Data were generated from whole tissue sections of breast cancers. The pre-chemotherapy size of tumours was recorded for both negative Estrogen Receptor (ER-) and positive Estrogen Receptor (ER+). A preliminary analysis carried out on the dataset using a Bayesian t-test revealed that only 4808 genes are relevant at some specific threshold.
Lung Cancer: [45] obtained 22,215 gene expression profiles using Affymetrix Suggested Protocol on 163 patients. The biomarker score to detect the presence or absence of lung cancer was recorded alongside the gene expression profile. A preliminary analysis carried out on the dataset using a Bayesian t-test revealed that only 7187 genes are relevant at some specific threshold.

The RMSE of the methods were obtained for the test dataset that arose from ten-fold cross-validation. Table 5 shows the summary of ARMSE for the test dataset over the ten-fold cross-validation. For Breast1 and Breast2, BRF was found to be the best with the lowest ARMSE. In terms of ranking, RF was found to be in the second position in terms of performance when compared with other methods. For the prediction of biomarker score, the best is LASSO with the lowest ARMSE. On average, BRF has the lowest ARMSE over the three datasets. The Standard Error of Mean (SEM) estimates measure the relative spread of RMSE for each dataset. The SEM results show that the most stable method is BRF with least SEM over most datasets except Lung.

Table 5. Average test RMSE and (Standard error) over 10-fold cross-validation for regression cancer datasets.

				Method
Dataset	BRF	GBM	LASSO	RF	BF	BART1	BART2
Breast1	1.014	1.131	1.283	1.117	1.120	1.128	1.123
	(0.071)	(1.086)	(0.258)	(0.673)	(0.749)	(0.661)	(1.380)
Breast2	0.347	0.450	0.458	0.448	0.449	0.456	0.452
	(0.048)	(0.352)	(0.246)	(0.298)	(0.576)	(0.139)	(0.239)
Lung	1.099	5.243	0.825	2.287	2.420	1.589	1.934
	(0.243)	(1.125)	(0.309)	(0.162)	(0.298)	(0.717)	(0.255)

5. Discussion of Results

BRF achieves impressive results because it employs Bayesian estimation at the tree node parameter stage and combines a greedy and random search to select splitting variables. In contrast, RF fails since it randomly selects variables without considering their importance. Random search is adequate for low-dimensional cases, as seen in various simulation conditions. However, as the number of irrelevant variables increases, the performance of random search significantly deteriorates. For example, in a five-dimensional simulation with five relevant variables, the probabilities of selecting at least one relevant variable when

m t r y = ⌊ \sqrt{p} ⌋

are as follows

0.546, 0.416, 0.202, 0.150, 0.06, 0.05, 0.04

for different values of

p = 50, 100, 500, 1000, 5000, 10000

. This demonstrates that as the data dimension grows with a fixed sample size n, more irrelevant variables are selected, resulting in a poor model fit.

The new approach, BRF, directly addresses this issue by ensuring the use of only relevant variables, regardless of the dataset’s dimension. This approach is akin to what GBM does, as it assesses the influence of each variable on the response. However, BRF surpasses GBM due to its application of Bayesian estimation methods and robust data-driven prior techniques. Moreover, it’s clear that BRF’s performance relies on correctly identifying variables during the greedy search. If irrelevant variables are ranked higher than relevant ones, it will affect performance, emphasizing the need for a robust procedure for preliminary variable ranking. While the bootstrap prior technique performed reasonably well in both linear and non-linear scenarios, the accuracy of BRF can also be improved by introducing a more effective subset selection procedure.

6. Conclusion

This paper investigated the strengths and flaws of Random Forest (RF) for modelling high-dimensional data. The major weakness of RF methods is that they are not governed by any statistical model, and thus, they cannot provide probabilistic results as in the Bayesian setting. Another critical issue with the RF methods occurs in high-dimensional data with a large number of predictors but a small number of relevant ones. The performance of RF tends to depreciate as the dimension of the data grows infinitely under this condition. These two issues motivated the development of Bayesian Random Forests (BRF) presented in this paper. The theoretical results revealed that BRF satisfies the oracle properties under mild regularity conditions. Furthermore, the various empirical results from the simulation and real-life data analysis established that BRF is more consistent and efficient than other competing methods for modelling non-linear functional relationships in low and high-dimensional situations. Also, BRF was found to be better than the competing Bayesian methods, especially in high-dimensional settings.

Author Contributions

“Conceptualization, O.R.O. and A.R.A.; methodology, O.R.O; software, O.R.O.; validation, O.R.O, and A.R.A; formal analysis, O.R.O; investigation, O.R.O; resources, A.R.A; data curation, O.R.O; writing—original draft preparation, O.R.O; writing—review and editing, O.R.O; visualization, A.R.A; supervision, O.R.O; project administration, O.R.O. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The authors confirm that the data supporting the findings of this study are available within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

Gohil, S.H.; Iorgulescu, J.B.; Braun, D.A.; Keskin, D.B.; Livak, K.J. Applying high-dimensional single-cell technologies to the analysis of cancer immunotherapy. Nature Reviews Clinical Oncology 2021, 18, 244–256. [Google Scholar] [CrossRef]
Quist, J.; Taylor, L.; Staaf, J.; Grigoriadis, A. Random forest modelling of high-dimensional mixed-type data for breast cancer classification. Cancers 2021, 13, 991. [Google Scholar] [CrossRef]
Nederlof, I.; Horlings, H.M.; Curtis, C.; Kok, M. A high-dimensional window into the micro-environment of triple negative breast cancer. Cancers 2021, 13, 316. [Google Scholar] [CrossRef]
Olaniran, O.R.; Olaniran, S.F.; Popoola, J.; Omekam, I.V. Bayesian Additive Regression Trees for Predicting Colon Cancer: Methodological Study (Validity Study). Turkiye Klinikleri J Biostat. 2022, 14, 103–109. [Google Scholar] [CrossRef]
Olaniran, O.R.; Abdullah, M.A.A. Bayesian weighted random forest for classification of high-dimensional genomics data. Kuwait Journal of Science 2023, 50, 477–484. [Google Scholar] [CrossRef]
Hastie, T.; Tibshirani, R.; Friedman, J. The elements of statistical learning; Springer, New York, 2009.
Olaniran, O.R. Shrinkage based variable selection techniques for the sparse Gaussian regression model: A Monte-Carlo simulation comparative study. In Proceedings of the AIP Conference Proceedings. AIP Publishing LLC, Vol. 2423; 2021; p. 070014. [Google Scholar]
Bühlmann, P.; Van De Geer, S. Statistics for high-dimensional data: methods, theory and applications; Springer Science & Business Media, 2011.
Gündüz, N.; Fokoue, E. Predictive performances of implicitly and explicitly robust classifiers on high dimensional data. Communications Faculty of Sciences University of Ankara-Series A1 Mathematics And Statistics 2017, 66, 14–36. [Google Scholar]
Vapnik, V. The nature of statistical learning theory; Springer science & business media, 2013.
Tibshirani, R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological) 1996, 58, 267–288. [Google Scholar] [CrossRef]
Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American statistical Association 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
Hernández, B.; Raftery, A.E.; Pennington, S.R.; Parnell, A.C. Bayesian additive regression trees using Bayesian model averaging. Statistics and Computing 2018, 28, 869–890. [Google Scholar] [CrossRef]
Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and regression trees; 1984.
Hwang, K.; Lee, K.; Park, S. Variable selection methods for multi-class classification using signomial function. Journal of the Operational Research Society 2017, 68, 1117–1130. [Google Scholar] [CrossRef]
Breiman, L. Bagging predictors. Machine learning 1996, 24, 123–140. [Google Scholar] [CrossRef]
Efron, B.; Tibshirani, R.J. An introduction to the bootstrap; CRC press: Florida, 1994. [Google Scholar]
Breiman, L.; et al. Arcing classifier (with discussion and a rejoinder by the author). The annals of statistics 1998, 26, 801–849. [Google Scholar] [CrossRef]
Breiman, L. Random forests. Machine learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
Friedman, J.H. Greedy function approximation: a gradient boosting machine. The Annals of Statistics 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
Hastie, T.; Friedman, J.; Tibshirani, R. Overview of supervised learning; Springer: New York City, 2010. [Google Scholar]
Chipman, H.A.; George, E.I.; McCulloch, R.E.; et al. BART: Bayesian additive regression trees. The Annals of Applied Statistics 2010, 4, 266–298. [Google Scholar] [CrossRef]
Linero, A.R. Bayesian regression trees for high-dimensional prediction and variable selection. Journal of the American Statistical Association, 2018, pp. 1–11.
Breiman, L. Stacked regressions. Machine learning 1996, 24, 49–64. [Google Scholar] [CrossRef]
Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. Journal of computer and system sciences 1997, 55, 119–139. [Google Scholar] [CrossRef]
Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software 2010, 33, 1. [Google Scholar] [CrossRef]
Olaniran, O.R.; Olaniran, S.F.; Popoola, J. Bayesian Regularized Neural Network for Forecasting Naira-USD Exchange Rate. In Proceedings of the International Conference on Soft Computing and Data Mining. Springer; 2022; pp. 213–222. [Google Scholar]
Chipman, H.A.; George, E.I.; McCulloch, R.E. Bayesian CART model search. Journal of the American Statistical Association 1998, 93, 935–948. [Google Scholar] [CrossRef]
Taddy, M.A.; Gramacy, R.B.; Polson, N.G. Dynamic trees for learning and design. Journal of the American Statistical Association 2011, 106, 109–123. [Google Scholar] [CrossRef]
Olaniran, O.R.; Abdullah, M.A.A.B.; Affendi, M.A. BayesRandomForest: An R implementation of Bayesian Random Forest for Regression Analysis of High-dimensional Data. Romanian Statistical Review 2018, 66, 95–102. [Google Scholar]
Johnson, N.L.; Kemp, A.W.; Kotz, S. Univariate discrete distributions; John Wiley & Sons: New York City, 2005. [Google Scholar]
Zou, H. The adaptive lasso and its oracle properties. Journal of the American statistical association 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
Shi, G.; Lim, C.Y.; Maiti, T. High-dimensional Bayesian Variable Selection Methods: A Comparison Study. Calcutta Statistical Association Bulletin 2016, 68, 16–32. [Google Scholar] [CrossRef]
Heinze, G.; Wallisch, C.; Dunkler, D. Variable selection–A review and recommendations for the practicing statistician. Biometrical Journal 2018, 60, 431–449. [Google Scholar] [CrossRef] [PubMed]
Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian data analysis; CRC press: Florida, 2013. [Google Scholar]
Denison, D.G.; Holmes, C.C.; Mallick, B.K.; Smith, A.F. Bayesian methods for nonlinear classification and regression; John Wiley & Sons, 2002.
Olaniran, O.R.; Yahya, W.B. Bayesian Hypothesis Testing of Two Normal Samples using Bootstrap Prior Technique. Journal of Modern Applied Statistical Methods 2017, 16, 34. [Google Scholar] [CrossRef]
Olaniran, O.R.; Abdullah, M.A.A. Bayesian variable selection for multiclass classification using Bootstrap Prior Technique. Austrian Journal of Statistics 2019, 48, 63–72. [Google Scholar] [CrossRef]
Olaniran, O.R.; Abdullah, M.A.A. Bayesian analysis of extended cox model with time-varying covariates using bootstrap prior. Journal of Modern Applied Statistical Methods 2020, 18, 7. [Google Scholar] [CrossRef]
Laird, N.M.; Louis, T.A. Empirical Bayes confidence intervals based on bootstrap samples. Journal of the American Statistical Association 1987, 82, 739–750. [Google Scholar] [CrossRef]
Bleich, J.; Kapelner, A.; George, E.I.; Jensen, S.T. Variable selection for BART: an application to gene regulation. The Annals of Applied Statistics 2014, pp. 1750–1781.
Ishwaran, H.; Kogalur, U.B.; Blackstone, E.H.; Lauer, M.S. Random survival forests. The Annals of Applied Statistics 2008, pp. 841–860.
Iwamoto, T.; Bianchini, G.; Booser, D.; Qi, Y.; Coutant, C.; Ya-Hui Shiang, C.; et al. Gene pathways associated with prognosis and chemotherapy sensitivity in molecular subtypes of breast cancer. Journal of the National Cancer Institute 2010, 103, 264–272. [Google Scholar] [CrossRef]
Ma, X.J.; Wang, Z.; Ryan, P.D.; Isakoff, S.J.; Barmettler, A.; Fuller, A.; Muir, B.; et al. A two-gene expression ratio predicts clinical outcome in breast cancer patients treated with tamoxifen. Cancer Cell 2004, 5, 607–616. [Google Scholar] [CrossRef]
Gustafson, A.M.; Soldi, R.; Anderlind, C.; Scholand, M.B.; Qian, J.; Zhang, X.; Cooper, K.; et al. Airway PI3K pathway activation is an early and reversible event in lung cancer development. Science Translational Medicine 2010, 2, 1–25. [Google Scholar] [CrossRef] [PubMed]

Figure 1. Probability of selecting relevant variables for RF at varying dimensionality p.

Figure 2. Simulation plot 1 of the hybrid algorithm for Bayesian Random Forest regression.

Figure 4. Single regression tree plot from forest of five trees using Bayesian Random Forest (BRF) hybrid Gibbs and MH procedure. The coloured box corresponds to the terminal node or final prediction, and the white box corresponds to the decision node or split point.

Figure 5. Boxplot of test 10-folds cross-validation RMSE of Scenario 1. The black middle line in each box represents the median. The dots represent outliers in RMSE results. The outliers in GBM is the highest.

Figure 6. Boxplot of test 10 folds cross-validation RMSE of Scenario 2 for Gaussian response. The black middle line in each box represents the median.

Table 1. Tuning parameters set-up for the various methods used in data analysis.

Method	Tuning Parameter Set-up
LASSO	$λ \in [0, 1]$ is selected via 10 folds cross validation. Other settings are default as in $g l m n e t$ .
GBM	Number of trees is fixed at 1000 and all other settings are default.
RF	$m t r y$ settings are default $p / 3$ , number of trees is fixed at 1000. Other settings are default.
BART1	All settings are default.
BART2	All settings are default
BF	$m t r y$ settings are default, number of trees is fixed at 1000. $c a s e . w t \sim e x p (1)$ . Other settings are default.
BRF	$m t r y$ settings are default $p / 3$ , number of trees is fixed at 1000, search type is random, split weight is obtained using $F^{(p - k)} (t)$ .

Table 2. Average test Root Mean Square Error (ARMSE) over 10-fold cross-validation for scenario 1.

Scenario 1: Linear
	p
Method	50	100	500	1000	5000	10000
BRF	2.005	2.012	2.084	2.113	2.114	2.156
GBM	8.853	8.861	8.843	8.854	8.854	8.847
LASSO	0.950	0.949	0.952	0.958	0.967	0.977
RF	2.247	2.296	2.513	2.603	2.824	2.947
BF	2.568	2.627	2.855	3.022	3.185	3.590
BART1	3.843	4.521	2.763	3.126	5.364	7.210
BART2	2.596	3.113	3.007	3.621	5.658	8.395

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On the Oracle Properties of Bayesian Random Forest for Sparsed High-Dimensional Gaussian Regression

Abstract

1. Introduction

2. Random Forest and Sum of Trees Models

2.1. Variable Selection Inconsistency and Inefficiency of Random Forest in Sparse High-Dimensional Setting

3. Priors and Posterior Specification of Bayesian Random Forest for Sparse HD

3.0.1. Hybrid Gibbs and MH procedure for extracting posterior information from Bayesian Random Regression Forest with Gaussian Response

3.1. A New Weighted Splitting for Bayesian Random Forest in Sparse High-Dimensional Setting

3.2. Oracle Properties of Bayesian Random Forest

4. Simulation and Results

4.1. Simulation Results

4.2. Variable Selection

4.3. Predicting Tumour Size and Biomarker Score

5. Discussion of Results

6. Conclusion

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe