1. Introduction
Both, linear and non-linear response spectroscopies provide valuable and complementary information on the excitations of high-temperature superconductors. Since the discovery of these materials optical conductivity measurements have been central in advancing our understanding of the unusual electronic properties, including e.g. the superconducting gap, pseudogap or the transition from a Mott-insulating state to a (non-) Fermi liquid (for a review see e.g. [
1]).
On the other hand, the development of non-equilibrium spectroscopies has significantly put forward our understanding of complex materials, due to the possibility of disentangling different dynamical processes via their different relaxation times. [
2] With regard to superconducting materials, measurements of the non-linear current response have been recently been applied in order to elucidate the order parameter dynamics which, as a scalar quantity, is not visible in the equilibrium response. Corresponding experiments have been conducted in NbN [
3,
4,
5], MgB
2 [
6,
7], pnictides [
8] and cuprate superconductors [
9,
10,
11,
12] whereas the theoretical understanding of these studies has been advanced in Refs. [
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24]. Basically, the current density in response to an applied vector potential
can be expanded up to third order as
where
is the linear response which is related to the optical conductivity. On the other hand,
incorporates processes where the (scalar) order parameter fluctuations
are driven by terms quadratic in
so that the third harmonic generation (THG) is expected to be enhanced at twice the frequency of the incoming field
corresponding to the spectral gap
of the superconductor (SC). However, it has been shown [
13] that for clean single-band s-wave SC’s these amplitude (’Higgs’) excitations yield only a minor contribution to the THG which instead is dominated by the BCS quasiparticle excitations across the SC spectral gap. For a square lattice, the amplitude excitations only become visible when the THG is measured at an angle of
with respect to the bond direction which suppresses the QP contribution. For a clean system the response is only due to the diamagnetic current while disorder induces also a paramagnetic contribution [
4,
15,
16,
19]. It has been shown [
19] that at moderate disorder the response is still dominated by the BCS part while collective modes may yield comparable contributions only in the limit of strong disorder.
In this context various approximations for the theoretical description of disorder within the BCS theory have been considered. In the weakly disordered limit
previous work [
16,
21] is either based on the Mattis-Bardeen model [
25] or on the self-consistent Born approximation [
4]. The summation of diagrams with impurity ladders, equivalent to the solution of quasiclassical Eilenberger equations and formally valid for arbitrary scattering rate, has been accomplished in Ref. [
15]. In our previous work [
19,
26] we have treated the influence of disorder on the THG
exactly by solving the time-dependent Bogoljubov-de Gennes equations on finite lattices with local Anderson-type disorder. Formally this has been achieved by adding a time-dependent vector potential to the hamiltonian and by computing the resulting dynamics from the equation of motion for the time-dependent density matrix. This formalism can be accomplished in two different ways which have been used in Ref. [
19] and Ref. [
26], respectively. First, the dynamics of the full density matrix can be computed from the equation of motion and at the end the various harmonic contributions, proportional to the corresponding power in the amplitude of the applied vector potential
, have to be extracted numerically, see [
19]. This is a rather flexible approach, which allows to consider the influence of collective modes (amplitude, phase, charge) and in principle also allows to incorporate different pump-probe protocols. However, for a lattice with
N sites, the density matrix for a superconductor has dimensions
so that the formalism is restricted to small lattices only. Second, as outlined in Ref. [
26], the density matrix can be expanded from the beginning in powers of the applied vector potential. The equations of motion can be immediately formulated in frequency space for the individual components and allow for the computation of the current response at the respective order. This approach is less flexible in the time domain but can be applied to much larger lattices as relevant for the investigation of d-wave superconductors, at least on the BCS level, as has been demonstrated in Ref. [
26].
Here we compare in detail both formalisms and also discuss how collective modes can be incorporated into the second approach.
Section 2 introduces the model and we will analyze the two different approaches for the computation of the THG in disordered tight-binding lattices in
Section 3. In the same section we also compare the outcome of both procedures for the case of a disordered s-wave system. We conclude our discussion in
Section 4.
2. Model
We illustrate our formalism within the attractive Hubbard model on a square lattice plus local on-site disorder (cf. e.g., [
19,
27,
28,
29,
30,
31])
where the local potential
is taken from a flat distribution
.
To describe the SC state Equation (
1) is solved in mean-field using the BdG transformation
which yields the eigenvalue equations
and the SC order parameter is defined as
.
From the eigenvalue problem Equations (
2,
3) one can iteratively determine the ground state density matrix
with the elements
and which in compact notation can be written as
The BdG approximated energy can then be expressed via the density matrix as
and the BdG-hamiltonian matrix is defined as
In the absence of an external field the density matrix
and the Hamiltonian
commute, so that the density matrix has no time evolution. The dynamics of
is induced via the coupling to the electromagnetic field
. Let us consider e.g the case of a (spatially constant) field along the
x direction.
is coupled to the system via the Peierls substitution
, where for simplicity we will drop from the equations all the constant by putting the lattice spacing, the electronic charge
e, the light velocity
c and the Planck constant
ℏ equal to one. The Peierls substitution, modifies the kinetic-energy part, leading to the following contribution to
:
where we have included a nearest (
) and next-nearest (
) neighbor hopping into the hamiltonian.
3. Computation of the Dynamics
The equation of motion for the density matrix reads
with the BdG hamiltonian matrix given by Equation (
4).
Solving Equation (
6) yields a time-dependent BdG energy
and thus a time-dependent current density which is obtained from
with
N denoting the number of sites. The task is now to evaluate the current reponse for a given order in the amplitude of the applied vector potential. As a first step we expand Equation (
5) up to third order in
which yields
with
Here the subscript
and
refer to the usual identification of the leading terms coupling the gauge field to the fermionic operators in the Hamiltonian, i.e. the linear coupling between the paramagnetic term and
, and a quadratic coupling between the electronic density and
, that leads to the standard diamagnetic contribution to the current in linear response. However, both
and
still contain the vector potential to all orders in
.
Writing
we can expand the currents in a power series in
which upon inserting into Equation (
8) allows us to extract the various current contributions to order
n,
. In particular, the 3rd harmonic contribution to the current density reads
where we find that the dominant para- and diamagnetic contributions are given by
and
. On the other hand,
and
also enter the calculation of the optical conductivity in first order.
In Ref. [
19] we have numerically integrated Equation (
6) using an Adams-Bashforth algorithm and an initializing 4th order Runge-Kutta method. The resulting time-dependent currents
and
then have been separated numerically into the individual components
and
from which, after Fourier transformation, the frequency dependent third harmonic response Equation (
9) has been evaluated. In particular at low energies, this procedure is rather time consuming since the integration has to be performed over several periods of the incoming field.
Here we compare this approach with a different strategy where from the beginning we expand the density matrix in powers of the applied vector potential
Here
is the equilibrium density matrix for which
as we already emphasized above.
According to Equation (
9) higher order contributions to the density matrix
allow for the computation of the non-harmonic current responses
and
which, as we will show in the following, can be directly obtained in frequency space. The next subsections will address in detail the evaluation of current responses up to 3rd order including the contribution from collective mode via the random phase approximation (RPA).
3.1. First order
The first order current contribution, relevant for the evaluation of the optical conductivity, is given by
which requires evaluation of the density matrix up to order
.
By selecting all terms
in the equation of motion Equation (
6) one obtains
with
and
The matrix
is defined as
and the subscript
D indicates that it only contains the diagonal elements of the respective matrices, e.g.
which are part of
.
The non-perturbed hamiltonian
(i.e. for
) can be diagonalized
and the same transformation also diagonalizes the non-perturbed density matrix
With this transformation Equation (
13) can be written as
where
and
denote the transformed matrices Equations (
14,
15).
We now perform a Fourier transformation
so that Equation (
16) reads
On the BCS level (
) the density matrix is now obtained by transforming back to
in the original site representation. For the practical computation,
should be shifted into the complex plane in order to avoid singularities.
Including fluctuations means to include the corrections due to the matrix . In the original site representation and in case of local interactions (as in the present case of the attractive Hubbard model) has only diagonal elements in and which in the following we denote by greek letters, i.e. refers to a non-zero element of the matrix . The case of intersite interactions, as e.g. relevant for the description of d-wave superconductivity requires a corresponding modification of the following discussion.
However, in the present case the elements
are related to diagonal elements of the density matrix which we obtain by backtransforming Equation (
17)
where we have used the following identity for the diagonal elements of the density matrix
with
Equation (
18) can be solved for
as
where in the last step we have transformed back
into the original site representation.
We now define
so that the equation for
is given by
or
and therefore
Inserting the transformed solution of Equation (
25) into Equation (
17) yields the transformed solution for the density matrix.
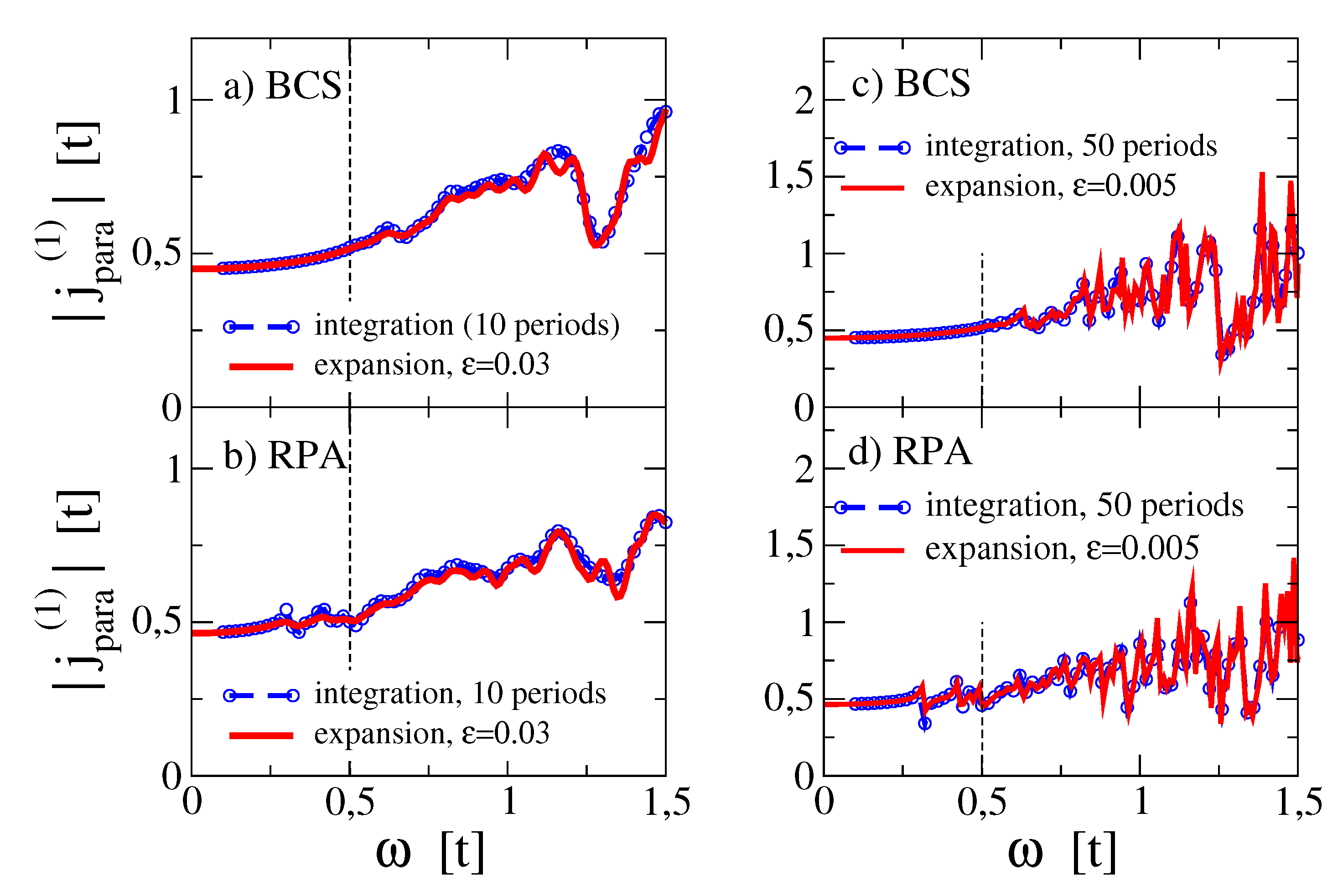
Figure 1 shows the magnitude of the first harmonic response for a particular disorder configuration (
) on a
square lattice. We compare the current, obtained from the direct time integration of Equation (
6) with the result from Equation (
17). For the BCS result, we have neglected the time evolution of local charge densities and anomalous correlations in the BdG hamiltonian Equation (
4). This amounts to neglect the contribution of
in Eq. (
17) which instead is relevant for the inclusion of collective modes within the RPA. In particular phase modes are responsible for the excitations (peaky structures in
Figure 1b,d) below the optical gap
, cf. Ref. [
19]. Note that
Figure 1 reports the
magnitude of the first order current response so that the finite BCS response below
is due to the real part of the current-current correlations. Obviously the energy resolution in the direct time integration (blue dotted lines) depends on the time interval over which the time integration is performed. In the expansion approach, Equation (
17) this resolution can be mimicked by using different values for the parameter
which shifts the energy into the complex plane. However, a finite
describes an exponential damping of the time dependent density matrix over a time scale
. On the other hand, there is no damping in the time integration method but the integration is simply performed over a fixed time interval. In
Figure 1 we use 10 (panels a,b) and 50 (panels c,d) periods of the applied vector potential as time interval for the integration. Note that for each frequency point a separate time integration is required.
3.2. Second order
We proceed by evaluating the diamagnetic contribution to the third harmonic current
, cf. Equation (
9). Collecting all term
we find for the correction to the density matrix in second order
where we have defined the matrix
and
Fourier transformation yields
which upon applying the transformation to diagonal states can be written as
Here we have defined
We can now follow the same procedure than in case of the 1st order RPA calculation. By transforming to the real space representation, where
is again diagonal (similar to Equation (
15)), one obtains
where the matrix
is the same than in Equation (
24) and we have defined
Then by solving Equation (
30) and plugging the transformed result into Equation (
29) one obtains the second order frequency dependent contribution to the density matrix in response to an external field
.
We exemplify the result for a harmonic external field with
. Then from Equation (
9) it turns out that the diamagnetic contribution to
is given by
which upon Fourier transformation implies that
is given by
. Thus the diamagnetic response at
is determined by the density matrix
. From Equations (
29,
30) one finds
with
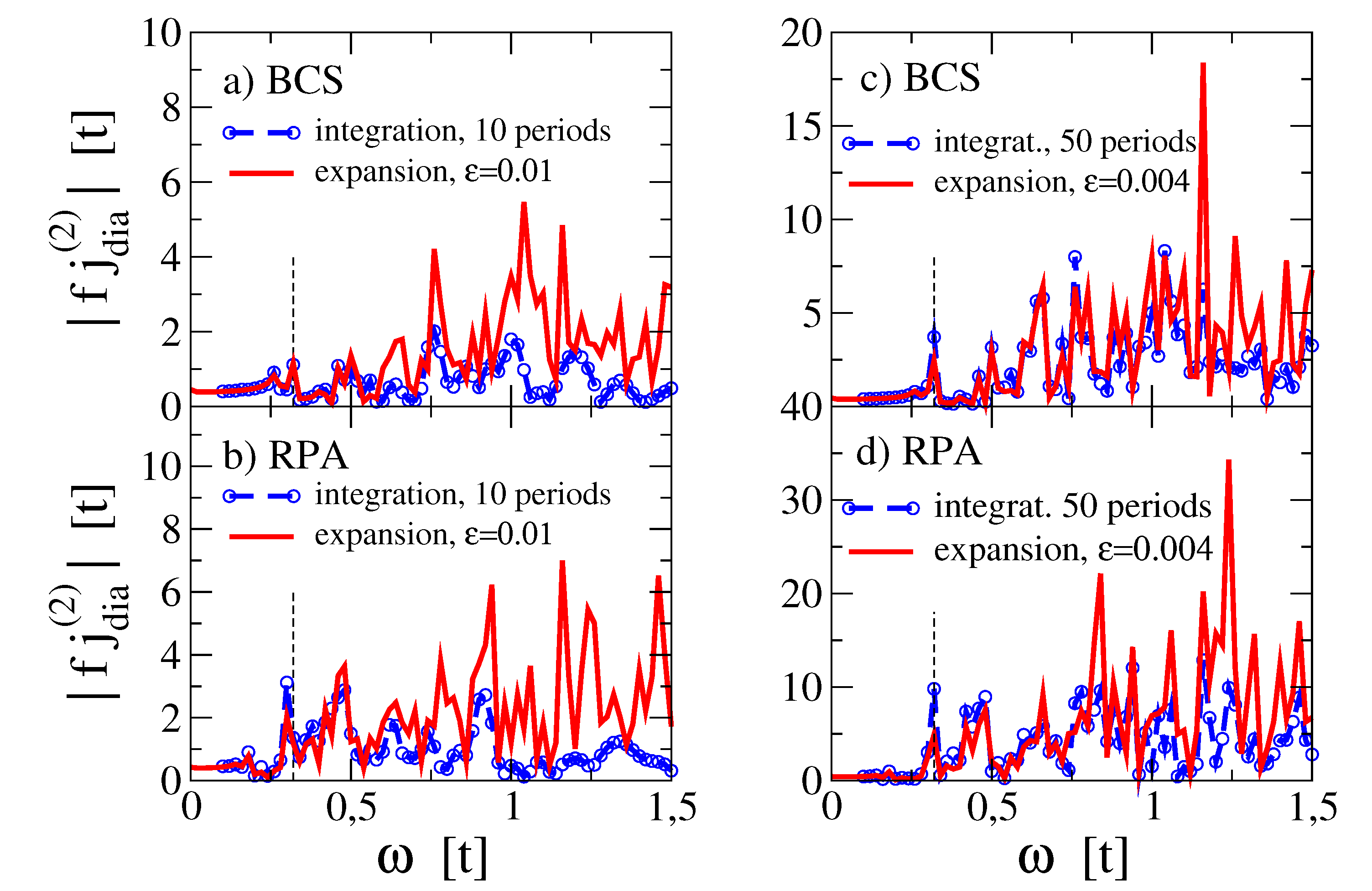
Figure 2 compares the second harmonic response from the direct time integration of Equation (
6) with the expansion from Equations (
32,
33) for a particular disorder realization. As discussed in Ref. [
19] disorder washes out the resonance at
and collective modes only slightly increase the intensity of the diamagnetic response. One can also observe that a single parameter
allows to adjust the response, evaluated from the expansion (red line) to the time integrated result (blue dotted line) at low energy, however, the agreement in intensity gets lost at larger values of
. For larger time integration intervals (cf. panels c,d) the agreement is pushed to higher energies.
3.3. Third order
Finally, we evaluate the paramagnetic contribution to the third harmonic current
. Collecting all terms
in the equation of motion Equation (
6) results in the following equation for the third order correction to the density matrix
Fourier transformation yields
Defining
and transforming to diagonal states, Equation (
35) becomes
Now we follow the usual procedure and write Equation (
38) in terms of the diagonal elements, i.e.
which yields
and which upon inserting into Equation (
38) yields the 3rd order correction to the density matrix.
We consider again a harmonic external field with
. The contribution of
is then given by
with
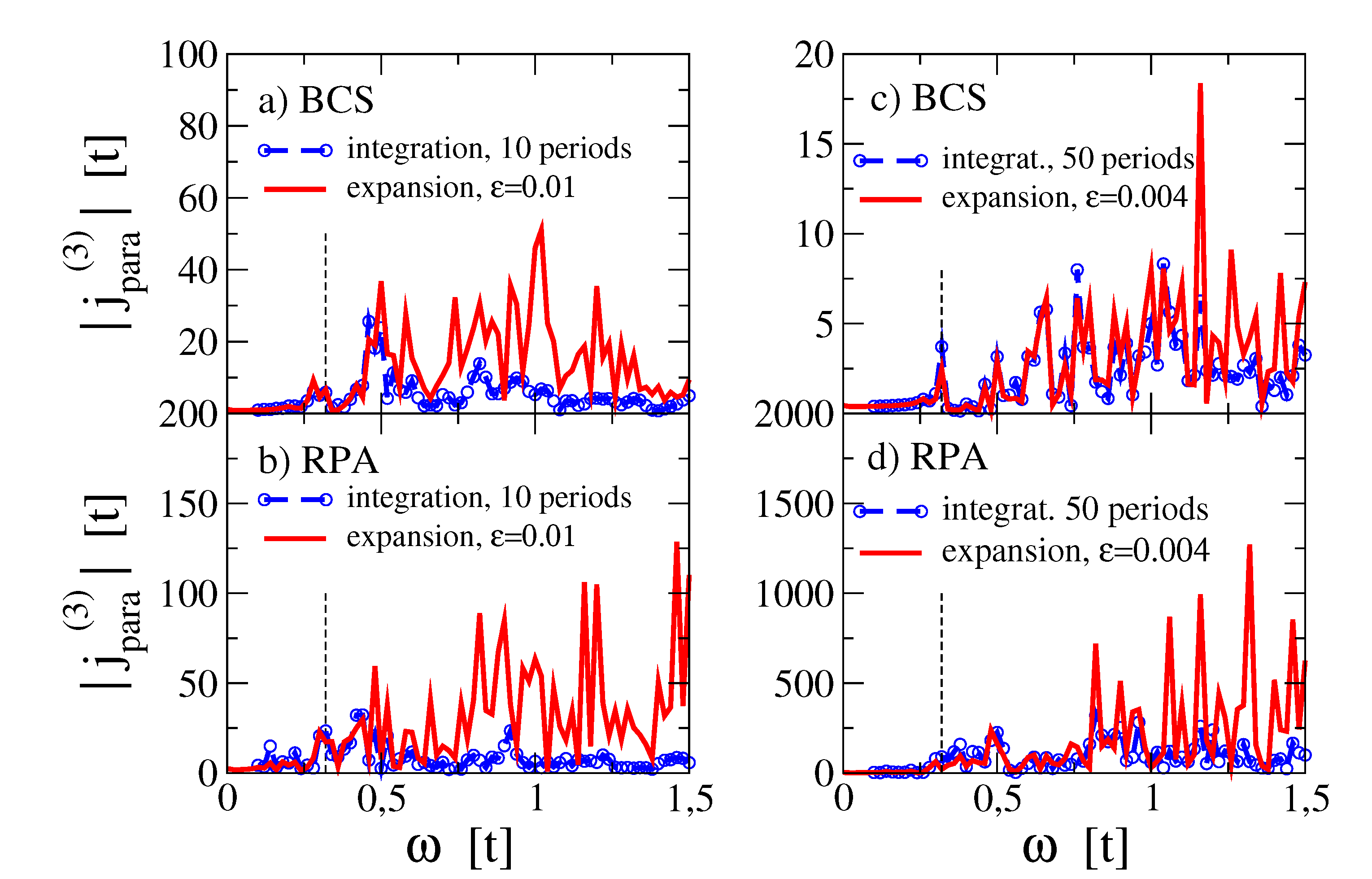
For the same disorder configuration as has been used for
Figure 1,
Figure 2 we show in
Figure 3 third harmonic response from Equations (
17,
25) as compared to the direct time integration of Equation (
6). Consistent with our previous results [
19] the strongly disordered ordered sample displays a low paramagnetic energy response at
, both in BCS and RPA, where the latter is enhanced by the contribution from collective modes. As in case of the diamagnetic contribution, cf.
Figure 2, the ’expansion result’ (red) for a fixed
parameter can be adjusted to the time integrated spectrum (blue dotted line) at low energies, but with decreasing number of periods in the time integration the agreement in intensity gets lost at higher energies. This is particularly visible in
Figure 3d where the contribution from band excitations leads to significantly larger intensities for the small
as compared to the time integration over 50 periods of the applied vector potential.
4. Conclusions
We have presented a detailed comparison of two approaches to evaluate the higher harmonic current response to an applied electromagnetic field for disordered and superconducting systems on a lattice. The first method is based on the direct time integration of the equation of motion Equation (
6) as has been used in Ref. [
19] for the investigation of the influence of collective modes in disordered s-wave superconductors. Since in this case the higher harmonic contribution has to be extracted numerically from the total response, the calculation has to be performed for at least three different magnitudes of the vector potential for each frequency. Together with the fact, that in order to obtain a reasonable frequency resolution, the integration has to be performed over a significant number of periods of the applied vector potential, this method is limited to a small number of lattice sites. On the other hand, it is rather flexible with regard to the simulation of different pump-probe protocols which can be easily implemented into the formalism.
Alternatively, one can compute the THG from an expansion of the density matrix in powers of the applied vector potential. As we have demonstrated in the present paper, the equations of motion for the individual components can be directly solved in frequency space from which the currents in the various orders are obtained. In Ref. [
26] this approach has been applied to the evaluation of the third harmonic response in d-wave superconductors, where at least in the BCS limit one could treat much larger systems than via the direct time integration of the density matrix. In this paper we have shown how RPA corrections can be included into the formalism. An open issue is the problem, how these RPA corrections can be separated into contributions from amplitude, phase and charge modes, which, on the other hand, can be easily accomplished within the time integration method.