Prerpints.org logo
Preprint
Article

Mine Productivity Upper Bounds and Truck Dispatch Rules

This version is not peer-reviewed.

Submitted:

19 October 2023

Posted:

23 October 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
This paper proposes an upper bound for mine productivity and also a simple truck dispatch rule that demonstrates how tight the upper bound can be using simulation. It also proposes a greedy search to approximate the productivity upper bound, which is faster and often exact. Uncertainty is added to the simulation in order to verify how the productivity responds to it. Typically, the productivity upper bound is less tight close to its saturation point as a function of the number of trucks, where adding more trucks only increases queues. Furthermore, more uncertainty in the model typically leads to a less tight upper bound. The results are conducted using real data from an open pit mine in Brazil.
Keywords: 
Subject: 
Engineering  -   Mining and Mineral Processing

1. Introduction

Mining is a process of extracting valuable materials from underground and open pit mines. These materials, known as ores, are typically a combination of minerals, natural rocks or sediments, which have economic value when refined. Since the last few decades, mining has always played an important role in the economic development of several countries, especially in the emerging ones [1]. However, mining is a very complex industrial operation and its project must contain several planning stages, starting with prospecting for ore bodies and ending with the final reclamation of the land after mine is closed. In addition, a mining project must maximize net present value (NPV), extracting the ore at the lowest possible cost over the mine’s life-cycle and, therefore, making the effort of such labor worthwhile.
In open pit mines, where operating costs are very high, it is even more essential to maximize productivity with minimum cost. Among the most expensive open pit mine operations, haulage and materials handling stand out, accounting for 50%-60% of the total operating costs [2]. In order to reduce this cost and thereby maximize NPV of the mining project, a fleet management system (FMS) is required, whose goal is to solve two problems: (i) find the shortest path to travel between each pair of locations (loading and dumping sites) in the mine (shortest path problem) and (ii) determine the number of truck trips required for each path and then dispatch the trucks to the locations in real-time, which is the focus of this paper.
Hence, an FMS can be a single-stage or a multi-stage. The single-stage approaches dispatch trucks without considering any production targets or constraints and typically consist of heuristics based on rules of thumb [3,4]. However, multistage approaches have a great advantage over single stage approaches by dividing problem (ii) into two sequential sub-problems [5,6]. This division into stages introduces a level of knowledge to the FMS that improves the quality of the solutions, as well as better adapting them to real scenario with uncertainties. The first sub-problem consists of efficiently allocating haulage resources for excavation activities based on truck loads and aiming to maximize truck productivity (truck and shovel allocation problem - upper stage), and the second sub-problem consists of dispatching trucks to a loading or a dumping site (truck dispatching problem - lower stage) [7].
Although it has not been extensively investigated as the upper stage sub-problem, the truck dispatching problem is essential for the fleet management system. It is by solving the lower stage sub-problem that the planning come into operation to achieve the production targets defined in the previous stage. Formally, the truck dispatching problem, which can be treated as an assignment problem [5,8] or a transportation problem [9,10,11], is a real-time decision making on the destination of trucks to satisfy production requirements in a mining operation. To achieve these requirements, one or more objectives are usually defined, such as maximizing mine productivity or minimizing truck inactivity (whether through idle time, waiting time, loading/dumping time). Therefore, several formulations of this optimization problem have already been proposed, as well as different solutions for these formulations.
Since the truck dispatch problem also occurs in fuel and package deliveries, taxis and ride-hailing services and any other industry that has to manage a fleet of vehicles, some approaches used to solve the dispatch problem in other contexts were naturally adopted for the problem applied in the mining industry. However, the transition of approaches in different contexts can be inappropriate. In open pit mines, some important particularities must be considered in the optimization problem. For example, the travel distance between two locations is usually short, the time for the truck to load or dump is often longer than usual and the frequency of demand at each location is often higher [2].
Therefore, the efficiency of a solution to the truck dispatch problem aimed at maximizing the mine’s productivity is strictly related to the fleet size and the haulage distances. A fleet with an insufficient number of trucks (under-truck) will result in substantially unproductive periods and a fleet with a high number of trucks (over-truck) may lead to queues for loading or dumping. Thus, several methods have been proposed to select the optimal size of the truck fleet in the truck dispatching problem, i.e. consider the number of trucks as a decision variable, which would avoid the aforementioned problems. Generally, these methods are based on match factor [12,13,14,15], artificial intelligence [16,17,18], operations research [19,20], life cycle cost analysis [21,22] or discrete event simulation [23,24,25]. However, the major drawback of these works is that they were developed to address only the equipment selection and sizing problem, in particular, the size of the haulage fleet handling the dump materials, and typically disregard the truck dispatch rules [15]. On the other hand, dispatching rules have been studied apart from fleet sizing, based on optimization models with dynamic truck allocation [26], heuristics with real-time data [27,28], simulation [29], or artificial intelligence [30].
From this perspective, we define a linear programming model that derives the upper bound for mine productivity by considering trucks of a heterogeneous fleet allocated in cycles (pairs of loading-dumping sites). In addition, we propose a simple truck dispatch rule that leads to a mine productivity, found in a discrete event simulation, close to this upper bound. Through a case study in an open pit mine in Brazil, we also show that the simulation takes into account fleet size problems and the results obtained are feasible to be implemented in the real world.

2. Mine model

The mine model used in this paper consider a productive cycle of individual trucks in a mine which are dispatched to a loading site, displaced to the chosen loading site where they are loaded, dispatched to a dumping site, displaced to the chosen dumping site where they are finally dumped and start the cycle all over again, as shown in Figure 1. The degree of freedom lies on where to dispatch the trucks to load or dump at each moment, which must maximize the mine productivity in long term. In the next section, an upper bound for mine productivity is proposed using linear programming, which is latter approximated by a greedy search. The mine productivity is physically realized by a discrete event simulation using a simple truck dispatch rule.

2.1. Optimization problem

In order to derive an upper bound for mine productivity, trucks are considered to be allocated in cycles defined by pairs of loading-dumping sites, where the cycle times are given by
t c , i u , i ℓ , i m = 2 d i u , i ℓ v i m + t u , i u , i m + t ℓ , i ℓ , i m , ∀ i u , i ℓ , i m
where d i u , i ℓ is the distance between dumping site i u and loading site i ℓ , v i m is the truck speed for model i m , t u , i u , i m is the dumping time at dumping site i u for truck model i m , t ℓ , i ℓ , i m is the loading time at loading site i ℓ for truck model i m . The trucks are allowed to change loading and dumping sites after each load or dump operation. Hence, in order to derive an upper bound for productivity, the number of trucks of model i m allocated in the cycle defined by loading site i ℓ and dumping site i u is a non negative real number N i u , i ℓ , i m , where fractions denote the truck relative time-slice in each cycle. The resulting productivity of this allocation is given by
N i u , i ℓ , i m L i m t c , i u , i ℓ , i m
where L i m is the load of truck model i m and t c , i u , i ℓ , i m is the respective cycle time.
The maximum number of trucks that a resource (e.g. loading or dumping site) can support in a cycle without queues is given by
t c , i u , i ℓ , i m t u , i u , i m or t c , i u , i ℓ , i m t ℓ , i ℓ , i m
so that each truck occupies a cycle time slice of length given by the service time and will be serviced in a continuous way without queue. Hence, the occupation due to an allocated number of trucks N i u , i ℓ , i m is given by
N i u , i ℓ , i m t u , i u , i m t c , i u , i ℓ , i m or N i u , i ℓ , i m t ℓ , i ℓ , i m t c , i u , i ℓ , i m
which must be at most 1 to not generate queues.
The linear optimization problem for maximum productivity can be written as
maximize ∑ i u = 1 n u ∑ i ℓ = 1 n ℓ ∑ i m = 1 n m N i u , i ℓ , i m L i m t c , i u , i ℓ , i m
subject to ∑ i ℓ = 1 n ℓ ∑ i m = 1 n m N i u , i ℓ , i m t u , i u , i m t c , i u , i ℓ , i m ≤ 1 , ∀ i u
∑ i u = 1 n u ∑ i m = 1 n m N i u , i ℓ , i m t ℓ , i ℓ , i m t c , i u , i ℓ , i m ≤ 1 , ∀ i ℓ
∑ i u = 1 n u ∑ i ℓ = 1 n ℓ N i u , i ℓ , i m ≤ n t , i m , ∀ i m
0 ≤ N i u , i ℓ , i m ≤ n t , i m , ∀ i u , i ℓ , i m
where N i u , i ℓ , i m (design variable) is the number of trucks of model i m allocated in the cycle between dumping site i u and loading site i ℓ , n t , i m is the number of available trucks of model i m , n u is the number of dumping sites, n ℓ is the number of loading sites, n m is the number of truck models. The problem is basically a productivity maximization (5) subject to resources constraints (6)-(8).

2.1.1. Greedy search

A greedy search may be applied to find an approximate solution to the linear problem (5)-(9) by allocating trucks to the most productive cycles first.
Algorithm 1 depicts this greedy search. Lines 1 and 2 initialise the output parameters. Lines 3 and 4 initialise cycle time and cycle productivity. Lines 5-7 initialise resource (dumping sites, loading sites and trucks) allocation. Line 8 initialises remaining cycle indicator. Line 10 finds the most productive remaining cycle. Line 11 allocates truck according to resource availability. Lines 12-14 update resource availability. Lines 15 and 16 update output parameters. Lines 17-26 update remaining cycle indicator.
Algorithm 1 Greedy search for mine productivity.
Preprints 88257 i001

2.2. Simulation

The truck cycles can be simulated using discrete event system simulation considering a dispatch rule, as depicted in Figure 2. Initially, one event is scheduled in the event calendar for each truck. In order to improve the simulation warming up, the trucks are distributed on dumping sites according to their respective cycle capacity obtained from the optimization model (5)-(9). The simulator then basically fires the next event in the calendar at each time, until the time horizon is reached. Each fired event schedules a new event in the calendar and changes the respective truck state. The scheduled times may follow a particular probability distribution, leading to a stochastic simulation. Despite simple, this computational model may be extended to consider further model details as needed.
The proposed dispatch rule is to route trucks to services (i.e. loading or dumping) which will finish first in a prediction at dispatch moment, as depicted in Algorithm 2 to dispatch to a loading site. The algorithm to dispatch to a dumping site is analogous. This dispatch rule is easy to implement and, as shown in the result section of this paper, it leads to an almost optimal solution when compared to the productivity upper bounds provided by the optimization model (5)-(9),
Algorithm 2 Dispatch rule to a loading site.
Preprints 88257 i002
Following Algorithm 2, the predicted service (i.e. dumping and loading) finish time is tracked in a variable t ˜ q . During the dispatch, the predicted service finish time t ˜ j s + t ˜ s , j s , s ∈ { u , ℓ } , is calculated for each destination server j s , considering the service time t s , j s and the predicted service starting time t ˜ j s , which in turn depends on the transit time t h , j s , the current time t, and the predicted last finish time of the respective server t ˜ q , j s . The truck is then dispatched to the server i s with the earliest predicted service finish time, which is set to the respective service finish time in t ˜ q , i s . For stochastic simulations, the mean value of respective probability distributions are considered in the prediction.

3. Results

The main objective of the tests in the next subsections is to show how tight the proposed upper bound for productivity can be, verified by a physical realization obtained from simulation using the simple proposed truck dispatch rule.

3.1. Simulated productivity convergence and its upper bound

Figure 3 shows the productivity convergence for a discrete event system simulation for
d = 4095 3427 2700 5200 5394 5189 4617 4615 2293 2617 2816 3135 3242 3587 3862 4198 3029 2770 5300 5400 6626 4800 4800 3325 3516 3374 3436 3210 2638 4000 3554 2907 2704 5509 5736 5534 4985 4995 1607 1932 2212 2475 2529 2926 4248 m ,
n u = 3 dumping sites, n ℓ = 15 loading sites, n m = 2 truck models, dumping time t u given in Table 1, loading time t ℓ in Table 2, truck speed v given in Table 3, truck load L given in Table 4 and truck number n t = ( 12 , 9 ) . These data were obtained from 7 months of real operation in mine Pico in Brazil, whose truck models are respectively CAT-785C and CAT-789D. Notice that one day of simulation is enough for a long term productivity estimation, and also that the simulated productivity never gets larger than the upper bound. The gap between the simulated steady state productivity and its upper bound is majorly explained by the heterogeneous fleet. A queue priority for more productive models would make the gap smaller, but it is beyond the scope of this paper and it could be a research theme for further investigation.

3.2. Fleet sizing

Figure 4 shows the mine productivity increasing with the number of available trucks of model CAT-789D until a saturation point where more trucks will only generate queues. Notice that the greedy search solution matches the optimal solution, which is typical but does not happen always (sometimes the greedy search productivity is a little smaller just before the saturation point). This quantifies the optimality of the greedy search. Notice also that the simulated productivity, which is a feasible realization of trucks in the mine, starts close to the optimal productivity upper bound given by the solution of (5)-(9), gradually gets smaller because of queues as the number of trucks increases, and ends close to the upper bound again as the number of trucks is large enough to occupy all loading and dumping services without gaps. This quantifies the optimality of the dispatch rule and also quantifies how tight the upper bound can be. Finally, notice also that a greater uncertainty in simulation leads to less productivity due to unforeseen queues, whose gap becomes smaller as the number of trucks gets farther from saturation point. For 50% of uncertainty (i.e. triangular distribution with mean c = μ , minimum a = 0.5 μ and maximum b = 1.5 μ ), the gap between the simulated productivity and its upper bound can get as large as 25%.

4. Conclusions

The mine productivity upper bound proposed in this paper is considerably tight when the number of trucks get large and it can be quickly obtained. This makes it suitable for long term planning of a mine (e.g. truck and shovel allocation problem). On the other hand, the simulation is slower, but it provides a physical realization of the mine operation. Furthermore, more details can be added to the simulation, making it suitable for short term planning (e.g. truck dispatch problem).
The simple dispatch rule proposed in this paper leads to a productivity close the its upper bound for homogeneous fleets, which indicates how good it is. When queues in the mine are small or when there are too many trucks in the mine, the proposed dispatch rule tends to provide a productivity close to its upper bound. Considering that the dispatch rule is greedy, the good agreement between the greedy search and the linear programming productivity upper bound supports the good performance of the dispatch rule.

Acknowledgments

This work was supported by CNPq, CAPES and FAPEMIG, Brazil.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Humphreys, D. The mining industry after the boom. Mineral Economics 2019, 32, 145–151. [Google Scholar] [CrossRef]
  2. Alarie, S.; Gamache, M. Overview of solution strategies used in truck dispatching systems for open pit mines. International Journal of Surface Mining, Reclamation and Environment 2002, 16, 59–76. [Google Scholar] [CrossRef]
  3. Hauck, R.F. A real-time dispatching algorithm for maximizing open-pit mine production under processing and blending requirements. Seminar on Scheduling in Mining, Smelting and Metallurgy 1973, pp. 1–10.
  4. Hauck, R.F. Computer-controlled truck dispatching in open-pit mines. Computer Methods for the 80’s in the Mineral Industry 1979, pp. 735–742.
  5. Li, Z. A methodology for the optimum control of shovel and truck operations in open-pit mining. Mining Science and Technology 1990, 10, 337–340. [Google Scholar] [CrossRef]
  6. Subtil, R.F.; Silva, D.M.; Alves, J.C. A practical approach to truck dispatch for open pit mines. 35Th APCOM Symposium, 2011.
  7. Moradi Afrapoli, A.; Askari-Nasab, H. Mining fleet management systems: a review of models and algorithms. International Journal of Mining, Reclamation and Environment 2019, 33, 42–60. [Google Scholar] [CrossRef]
  8. Lizotte, Y.; Bonates, E. Truck and shovel dispatching rules assessment using simulation. Mining Science and Technology 1987, 5, 45–58. [Google Scholar] [CrossRef]
  9. Temeng, V.A.; Otuonye, F.O.; Frendewey Jr, J.O. Real-time truck dispatching using a transportation algorithm. International Journal of Surface Mining, Reclamation and Environment 1997, 11, 203–207. [Google Scholar] [CrossRef]
  10. Afrapoli, A.M.; Tabesh, M.; Askari-Nasab, H. A multiple objective transportation problem approach to dynamic truck dispatching in surface mines. European Journal of Operational Research 2019, 276, 331–342. [Google Scholar] [CrossRef]
  11. Afrapoli, A.M.; Tabesh, M.; Askari-Nasab, H. A transportation problem-based stochastic integer programming model to dispatch surface mining trucks under uncertainty. Proceedings of the 27th International Symposium on Mine Planning and Equipment Selection-MPES 2018. Springer, 2019, pp. 255–264. [CrossRef]
  12. Maran, J. Study of truck allocation and truck dispatching problems in open pit mines. Master’s thesis, Virginia Tech, 1987.
  13. Burt, C.N.; Caccetta, L. Match factor for heterogeneous truck and loader fleets. International Journal of Mining, Reclamation and Environment 2007, 21, 262–270. [Google Scholar] [CrossRef]
  14. Dabbagh, A.; Bagherpour, R. Development of a match factor and comparison of its applicability with ant-colony algorithm in a heterogeneous transportation fleet in an open-pit mine. Journal of Mining Science 2019, 55, 45–56. [Google Scholar] [CrossRef]
  15. Mohtasham, M.; Mirzaei-Nasirabad, H.; Askari-Nasab, H.; Alizadeh, B. Truck fleet size selection in open-pit mines based on the match factor using a MINLP model. Mining Technology, 2021; 1–17. [Google Scholar] [CrossRef]
  16. Ercelebi, S.G.; Bascetin, A. Optimization of shovel-truck system for surface mining. Journal of the Southern African Institute of Mining and Metallurgy 2009, 109, 433–439. [Google Scholar]
  17. Ganguli, R.; Bandopadhyay, S. Expert system for equipment selection. International Journal of Surface Mining, Reclamation and Environment 2002, 16, 163–170. [Google Scholar] [CrossRef]
  18. Lashgari, A.; Yazdani-Chamzini, A.; Fouladgar, M.M.; Zavadskas, E.K.; Shafiee, S.; Abbate, N. Equipment selection using fuzzy multi criteria decision making model: key study of Gole Gohar iron min. Engineering Economics 2012, 23, 125–136. [Google Scholar] [CrossRef]
  19. Edwards, D.J.; Malekzadeh, H.; Yisa, S.B. A linear programming decision tool for selecting the optimum excavator. Structural Survey 2001. [Google Scholar] [CrossRef]
  20. Fu, Z.; Topal, E.; Erten, O. Optimisation of a mixed truck fleet schedule through a mathematical model considering a new truck-purchase option. Mining Technology 2014, 123, 30–35. [Google Scholar] [CrossRef]
  21. Samanta, B.; Sarkar, B.; Mukherjee, S. Selection of opencast mining equipment by a multi-criteria decision-making process. Mining Technology 2002, 111, 136–142. [Google Scholar] [CrossRef]
  22. Markeset, T.; Kumar, U. Application of LCC techniques in selection of mining equipment and technology. In Mine Planning and Equipment Selection 2000; Routledge, 2018; pp. 635–640.
  23. Que, S.; Anani, A.; Awuah-Offei, K. Effect of ignoring input correlation on truck–shovel simulation. International Journal of Mining, Reclamation and Environment 2016, 30, 405–421. [Google Scholar] [CrossRef]
  24. Chaowasakoo, P.; Seppälä, H.; Koivo, H.; Zhou, Q. Digitalization of mine operations: Scenarios to benefit in real-time truck dispatching. International Journal of Mining Science and Technology 2017, 27, 229–236. [Google Scholar] [CrossRef]
  25. Chaowasakoo, P.; Seppälä, H.; Koivo, H.; Zhou, Q. Improving fleet management in mines: The benefit of heterogeneous match factor. European Journal of Operational Research 2017, 261, 1052–1065. [Google Scholar] [CrossRef]
  26. Mirzaei-Nasirabad, H.; Mohtasham, M.; Askari-Nasab, H.; Alizadeh, B. An optimization model for the real-time truck dispatching problem in open-pit mining operations. Optimization and Engineering 2023. [Google Scholar] [CrossRef]
  27. Yao, J.; Wang, Z.; Chen, H.; Hou, W.; Zhang, X.; Li, X.; Yuan, W. Open-Pit Mine Truck Dispatching System Based on Dynamic Ore Blending Decisions. Sustainability 2023, 15, 3399. [Google Scholar] [CrossRef]
  28. Arelovich, A.; Masson, F.; Agamennoni, O.; Worrall, S.; Nebot, E. Heuristic rule for truck dispatching in open-pit mines with local information-based decisions. 13th International IEEE Conference on Intelligent Transportation Systems 2010, pp. 1408–1414. [CrossRef]
  29. Forsman, B.; Rönnkvist, E.; Vagenas, N. Truck dispatch computer simulation in Aitik open pit mine. International Journal of Surface Mining 1993, 7, 117–120. [Google Scholar] [CrossRef]
  30. de Carvalho, J.P.; Dimitrakopoulos, R. Integrating Production Planning with Truck-Dispatching Decisions through Reinforcement Learning While Managing Uncertainty. Minerals 2021, 11, 1–17. [Google Scholar] [CrossRef]
Preprints 88257 g001
Figure 1. Truck cycle with its four states.
Figure 1. Truck cycle with its four states.
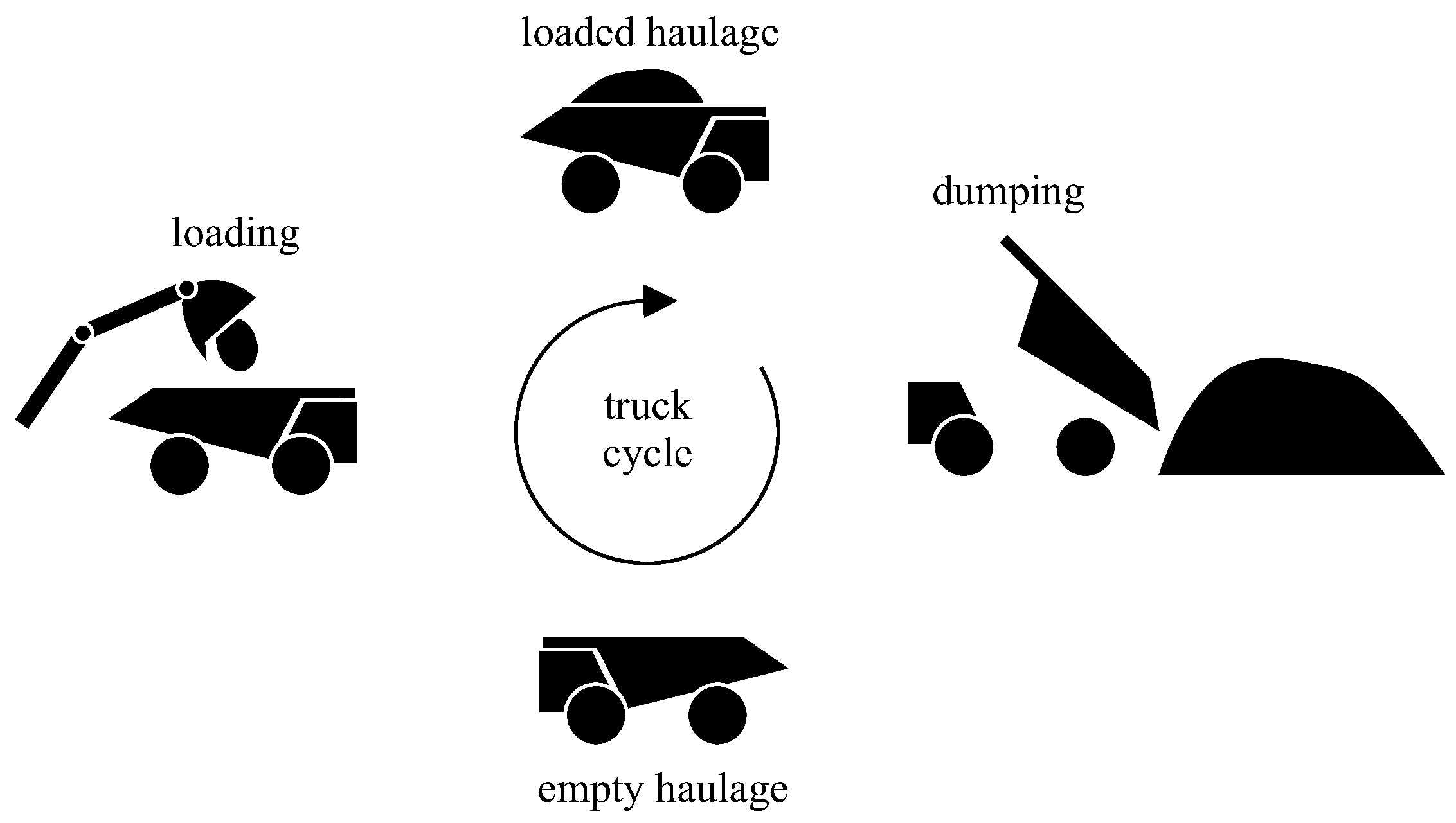
Preprints 88257 g001
Preprints 88257 g002
Figure 2. Discrete event simulator for mining truck cycles in a time horizon.
Figure 2. Discrete event simulator for mining truck cycles in a time horizon.
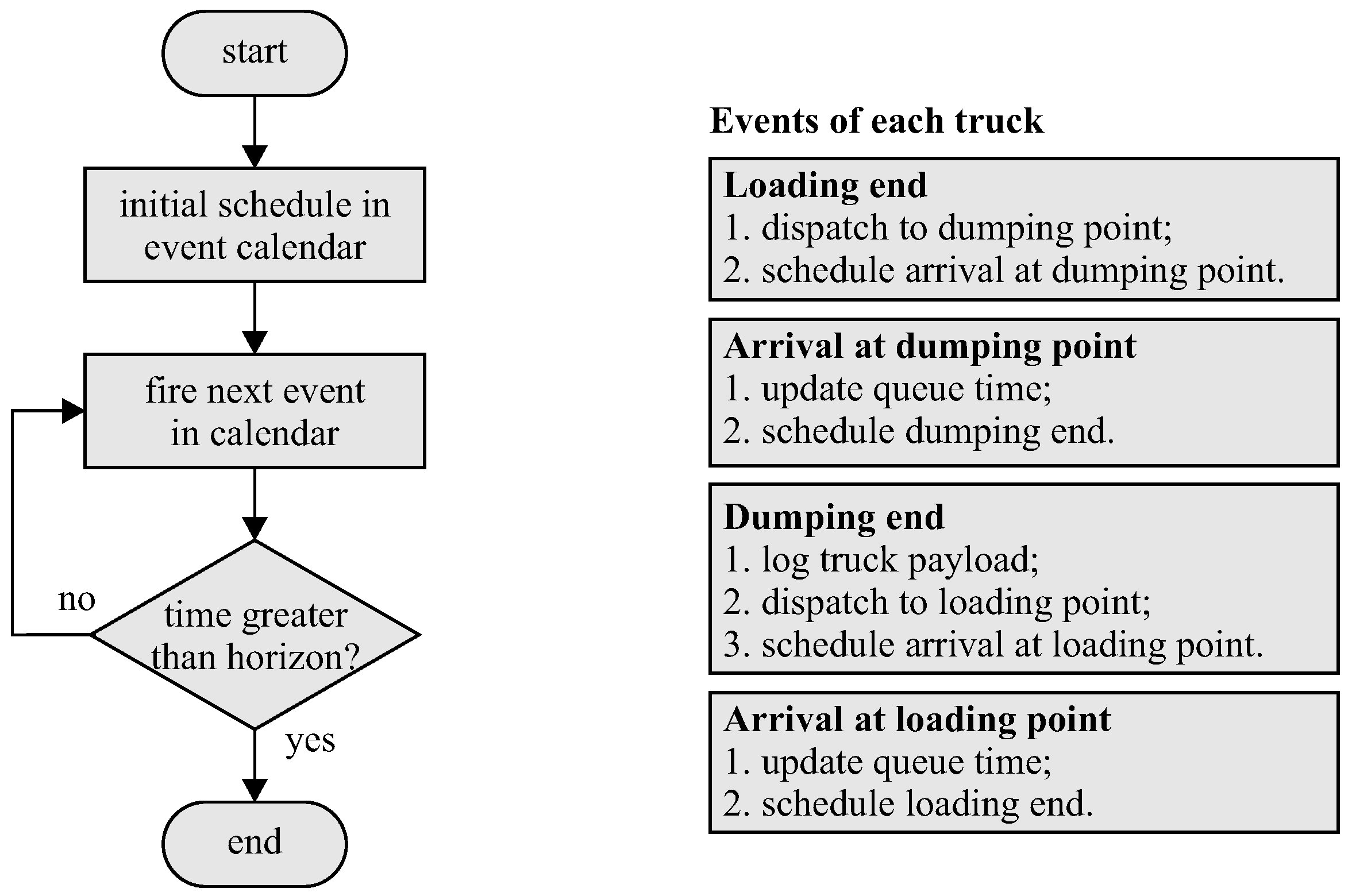
Preprints 88257 g002
Preprints 88257 g003
Figure 3. Productive convergence using a discrete event system simulation for the mine, which must be bellow the upper bound given by the linear optimization problem (5)-(9)
Figure 3. Productive convergence using a discrete event system simulation for the mine, which must be bellow the upper bound given by the linear optimization problem (5)-(9)
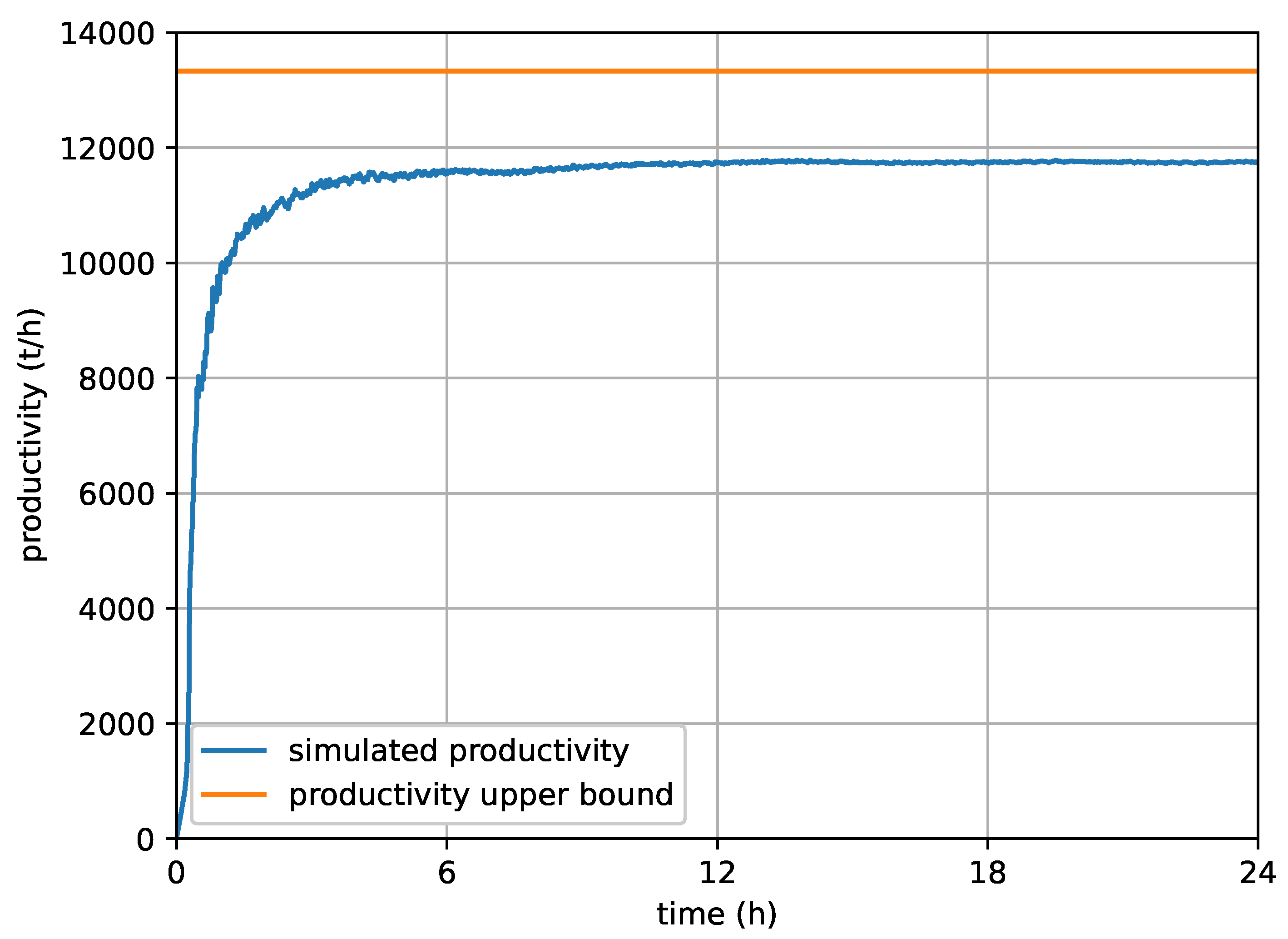
Preprints 88257 g003
Preprints 88257 g004
Figure 4. Mine productivity as a function of number of trucks available in the mine. Models with uncertainty p ∈ { 20 % , 50 % } consider the average productivity of 30 runs using symmetric triangular distributions with mean at μ , whose minimum and maximum are at ( 1 − p ) μ and ( 1 + p ) μ respectively.
Figure 4. Mine productivity as a function of number of trucks available in the mine. Models with uncertainty p ∈ { 20 % , 50 % } consider the average productivity of 30 runs using symmetric triangular distributions with mean at μ , whose minimum and maximum are at ( 1 − p ) μ and ( 1 + p ) μ respectively.
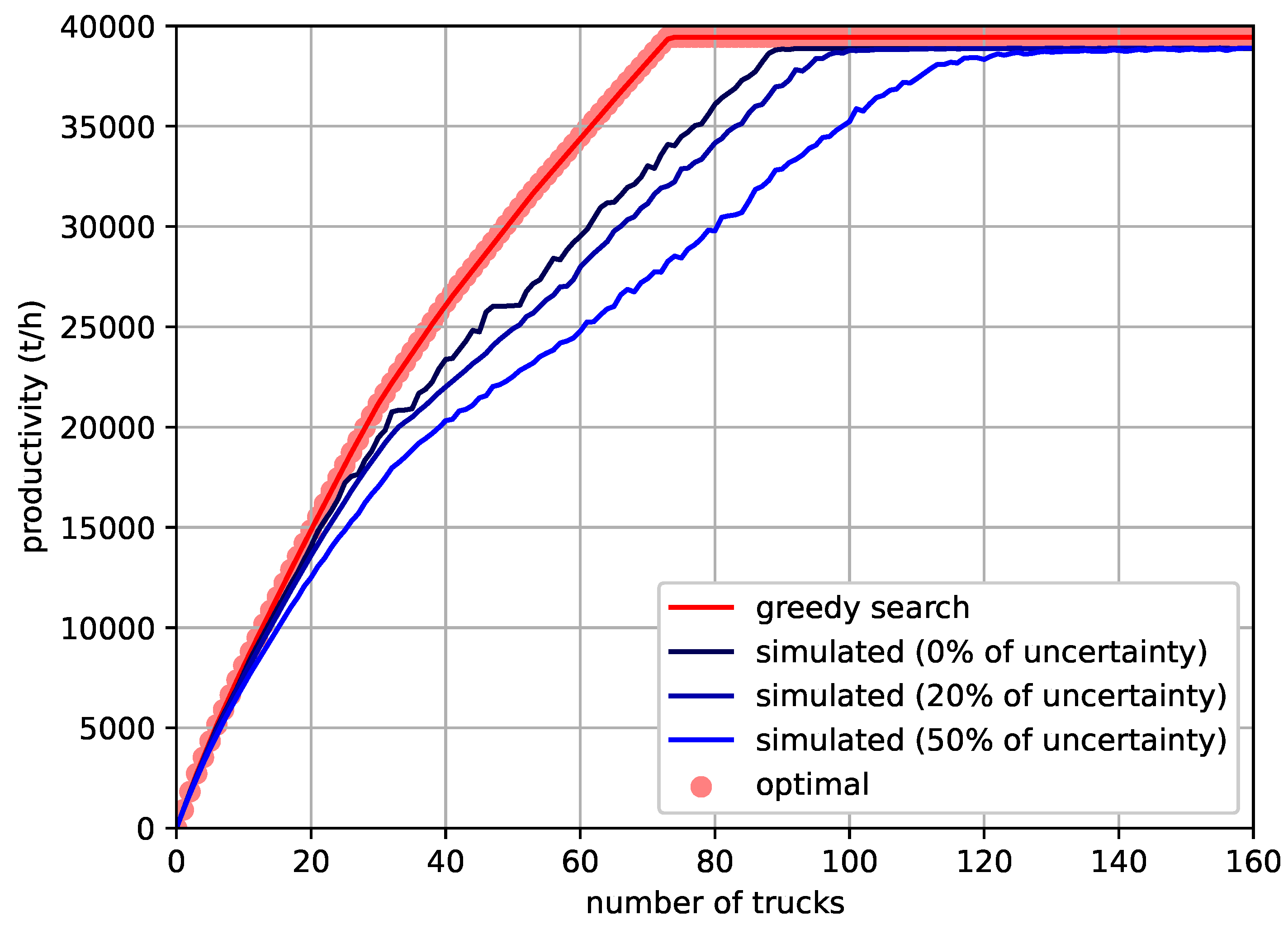
Preprints 88257 g004
Table 1. Dumping time t u for each truck model (i.e. they are the same for every dumping site) following a triangular distribution in interval [ a , b ] with mode at c.
Table 1. Dumping time t u for each truck model (i.e. they are the same for every dumping site) following a triangular distribution in interval [ a , b ] with mode at c.
Truck model i m Minimum a (s) Maximum b (s) Mode c (s)
1 23 47 35
2 30 54 42
Table 2. Loading time t ℓ for each truck model (i.e. they are the same for every loading site) following a triangular distribution in interval [ a , b ] with mode at c.
Table 2. Loading time t ℓ for each truck model (i.e. they are the same for every loading site) following a triangular distribution in interval [ a , b ] with mode at c.
Truck model i m Minimum a (s) Maximum b (s) Mode c (s)
1 146 298 222
2 185 349 267
Table 3. Truck speed v for each truck model following a triangular distribution in interval [ a , b ] with mode at c.
Table 3. Truck speed v for each truck model following a triangular distribution in interval [ a , b ] with mode at c.
Truck model i m Minimum a (km/h) Maximum b (km/h) Mode c (km/h)
1 15 31 23
2 17 33 25
Table 4. Truck load L for each truck model following a triangular distribution in interval [ a , b ] with mode at c.
Table 4. Truck load L for each truck model following a triangular distribution in interval [ a , b ] with mode at c.
Truck model i m Minimum a (t) Maximum b (t) Mode c (t)
1 138 148 143
2 189 201 195
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated