Preprint
Article
A Multispectral Camera Suite for the Observation of Earth’s Outgoing Radiative Energy
Altmetrics
Downloads
98
Views
35
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
20 October 2023
Posted:
20 October 2023
You are already at the latest version
Alerts
Abstract
As part of the Earth Climate Observatory space mission concept for the direct observation from space of the Earth Energy Imbalance, we propose an advanced camera suite for the high resolution observation of the Total Outgoing Radiation of the Earth. For the observation of the Reflected Solar Radiation, we propose the use of two multispectral cameras covering the range from 400 to 950 nm, with a nadir resolution of 1.7 km, combined with a high resolution RGB camera, with a nadir resolution of 0.57 km. For the observation of the Outgoing Longwave Radiation, we propose the use of 6 microbolometer cameras, with each a spectral bandwidth of 1 μm in the range from 8 to 14 μm, and with a nadir resolution of 2.2 km.
Keywords:
Subject: Environmental and Earth Sciences - Remote Sensing
Introduction
The Earth Energy Imbalance (EEI) is defined as the small difference between the incoming energy received by the Earth from the Sun, and the outgoing energy lost by the Earth to space. Both the incoming solar and the terrestrial outgoing energy are of the order of 340 W/m2 at the global annual mean level [1], while the EEI is of the order of 0.9 W/m2 [2,3]. The EEI is accumulated in the Earth climate system, particularly in the oceans which have a high heat capacity, and results in global temperature rise.
The monitoring of the EEI is of prime importance for a predictive understanding of climate change [4,5]. In particular, monitoring of the EEI gives an early indication on how well mankind is doing in implementing the Paris Climate Agreement.
Despite its fundamental importance, the EEI is currently poorly measured from space, due to two fundamental challenges.
The first fundamental challenge is that the EEI is the difference between two opposite terms with nearly equal amplitude. Currently the incoming solar radiation and outgoing terrestrial radiation are measured with separate instruments, which means that their calibration errors are added, and overwhelm the signal to be measured. The current error on the direct measurement of the EEI is of the order of 5 W/m2 [1], significantly larger than the signal to be measured of the order of 0.9 W/m2. In order to make significant progress in this challenge, a differential measurement using identically designed, intercalibrated instruments - so-called Wide Field Of View (WFOV) radiometers - to measure both the incoming solar radiation and the outgoing terrestrial radiation, is needed [6].
The second fundamental challenge, is that the outgoing terrestrial radiation has a systematic diurnal and annual cycle. From 2003 to 2023, the diurnal cycle of the outgoing terrestrial radiation was sampled from the so-called morning and afternoon Sun synchronous orbits, complemented by geostationary imagers [7,8]; recently the sampling from the morning orbit had to be abandonned [9]. The sampling of the diurnal cycle can be improved, by using two orthogonal inclined orbits [10] which provide both global coverage, and a statistical sampling of the full diurnal cycle at the seasonal (3 month) time scale.
The wide field of view radiometer will make accurate low resolution measurements of the Total Outgoing Radiation (TOR) of the Earth. Auxiliary visible and thermal imagers will be used to increase the spatial resolution of the radiometer observations, and to separate the TOR spectrally in the Reflected Solar Radiation (RSR) and the Outgoing Longwave Radiation (OLR). Figure 1 shows a multi-annual mean TOR at resolution, Figure 2 shows the corresponding RSR, and Figure 3 shows the corresponding OLR.
A reference design of the visible imager is described in [11].
A reference design of the thermal imager is described in [12].
A new space mission concept, called the Earth Climate Observatory (ECO) for the accurate and stable monitoring of the EEI, is currently elaborated , building further on the basic concepts of [6,11,12].
In this paper we describe an advanced multispectral camera suite with performance that goes beyond the [11,12] reference designs in terms of spectral information content. In Section 1, we describe the advanced shortwave camera suite. In Section 2, we describe the optical design for a new visible high resolution camera used in the advanced shortwave camera suite. In Section 3 we develop the advanced longwave camera suite. We discuss our results in Section 4, and provide our conclusions in Section 5.
1. Shortwave camera suite
In the [11] reference design, the ShortWave (SW) camera - also called solar camera - consists of an RGB CMOS detector array with a wide field of view lens allowing to view the Earth from limb to limb. The field of view is . The Wide Field Of View (WFOV) lens design is illustrated in Figure 4. The nadir resolution is 2.2 km. The f-number is 3. The used RGB CMOS spectral responses are illustrated in Figure 5. On a stand alone basis the RSR can be estimated from an RGB CMOS imager through spectral regression with a noise level of 3 %.
The only on-board calibration source for the SW camera suite will be a shutter, allowing to verify the dark current, and also allowing to shield the camera from direct solar illumination during solar pointing. The camera spectral gains and dark current will be determined pre-flight during ground calibration. The stability of the RGB spectral responses and the gains will be monitored, and if needed adjusted in-flight through vicarious calibration monitoring stable Earth targets similar to [13,14,15].
The spectral regression noise level by which the RSR broadbance radiance can be estimated, can be improved by increasing the number of narrowband spectral channels used as input for the regression. In [16] a commercially available CMOS sensor with 4x4 filter bands in the VIS (470-620nm) is described. Also a commercially available CMOS sensor with 5x5 filter bands in the VIS-NIR (650-975nm) is described.
The newly proposed ECO Shortwave Camera Suite (SCS) consists of 3 separate ShortWave (SW) cameras. Camera 2 and 3 can be based on the same CMOSIS CMV2000 sensor array. Since the size of the detector is comparable to the detector used in [11], the reference wide field of view lens from Figure 4 can be re-used. Camera 1 can be realized using the higher resolution CMOSIS CMV12000 sensor array. Since the size of the CMV12000 sensor is about 3 times larger than the detector size used in [11], a new lense design is appropriate, and will be presented in Section 2.The 3 shortwave cameras, have different spectral responses, by using different filters directly integrated on the CMOS chip, with spatial patterns illustrated in Figure 6.
The 3 ECO SW cameras are the following:
- ECO SW Camera 1 will be the RGB high-resolution SW camera, formed by a CMOS sensor, with spectral response between 400 and 1000 nm, with standard ’RGGB’ Bayer pattern. The active area of the CMOS sensor will be 3000*3000 pixels, yielding a nadir resolution for a single pixel of 0.57 km, and a nadir resolution for the 2x2 RGGB pixels of 1.1 km. The pixel pattern of SW camera 1 is illustrated in the left part of Figure 6.
2. Optical design high-resolution SW camera
The SW camera uses the CMOSIS CMV12000 4K CMOS detector with pixel size 5.5 . For the envisioned FOV of , we use a circular area of 16.5 mm diameter, corresponding to 3000 pixels. For a WFOV lens with field angle observing the Earth from an altitude of 700 km, the size of the nadir pixel is 0.57 km. Considering that the sensor is used with a Bayer color filter, the RMS spot size we require should be smaller than 2 pixels - corresponding to 11 . The barrel distortion is considered to be corrected in post processing.
2.1. The Design parameters
The lens train - illustrated in Figure 7 - consist of 6 lenses, two of which form an achromatic doublet. The doublet along with the third lens works as a chromatic aberration correction system along with focusing the image on the image plane. The main lens properties are summarised in Table 1. The Lens materials were selected from the SCHOTT ® catalog. The LAK14 is a crown glass with relatively high refractive index and SF6 is a flint glass with high refractive index as well.
There are 3 aspherical surfaces on the system. the first surface, the last surface and the final surface of the achromatic doublet. This is done to ensure increased light collection and to reduce spherical aberrations. The initial reference design for this lens train was the one shown in Figure 4 [11].
The system was designed and optimised using the Zemax OpticStudio® software. Only a few parameters were constrained, namely, the ’Effective focal length’, at 15.6 mm, the lens thickness minimum being 2 mm. The initial merit function for spot size was done through the ’Quick focus’ function provided by Zemax. Once a substantial percentage of criteria is fulfilled during optimization and satisfactory RMS values along with a good relative illumination were achieved, further optimization was done using the ’Hammer optimization’ function provided by Zemax.
2.2. Optical performance
2.2.1. RMS error
The RMS error - see Figure 8 - shows the root mean square deviation of a bunch of rays of light from its intended spot of incidence. This value is supposed to be below approximately. This is widely true for the said lens train and only reaches for the 400 nm wavelength at the extreme incidence angle. This can be considered sufficient for our purposes.
2.2.2. Seidel aberrations
The Seidel aberrations - see Figure 9 - apart from distortion have been optimized and kept low. The distortion/ barrel distortion is to be corrected on ground as post-processing.
2.2.3. Point Spread Function (PSF)
The optical PSF is the characterization of how a point of light is transformed when passing through an optical system. The optical PSF is related to the RMS spot size as shown in Figure 8, which mostly lies below the desired 11 m. The average optical PSF of all wavelengths is given in Figure 10.
To evaluate the joint effect of the optical PSF, and the pixel shape, we calculate the convolution op the optical PSF with the detector pixel shape. We use a layer of fixed size containing several pixels of the same type, either Red/Blue active pixels or Green-Green active pixels. The two types of pixels exist due to the presence of the Bayer filter. The individual pixels have sizes of but to emulate real pixels, we use an active area of 80% of the nominal pixel size as shown in Figure 11. We assume the variation of the optical PSF is negligeable within the layer of pixels.
The convolution of these pixel layers with the optical PSF for the incidence angle, is shown in Figure 12. It can be seen that, after the convolution, individual pixels are still recognisable.
From the RMS Figure 8, we see that the 400 nm wavelength at incidence angle and 500 nm at incidence angles have high RMS spot radius. We therefore examine in detail the PSFs and convolutions at these particular wavelengths and angles.
The optical PSF for light with a wavelength of 400 nm incident at , is shown in the left of Figure 10. The convolution of this optical PSF with the blue-type active pixel layer is shown in the right of Figure 10.
Figure 13.
Left : The PSF of 400 nm wavelength for incidence angle. Image size 53.236 by 53.236 . Right: The convolution of active pixel layer of blue-type with the PSF of incident light of 400 nm wavelength, where individual pixels are overlaid over the convolution.
Figure 13.
Left : The PSF of 400 nm wavelength for incidence angle. Image size 53.236 by 53.236 . Right: The convolution of active pixel layer of blue-type with the PSF of incident light of 400 nm wavelength, where individual pixels are overlaid over the convolution.
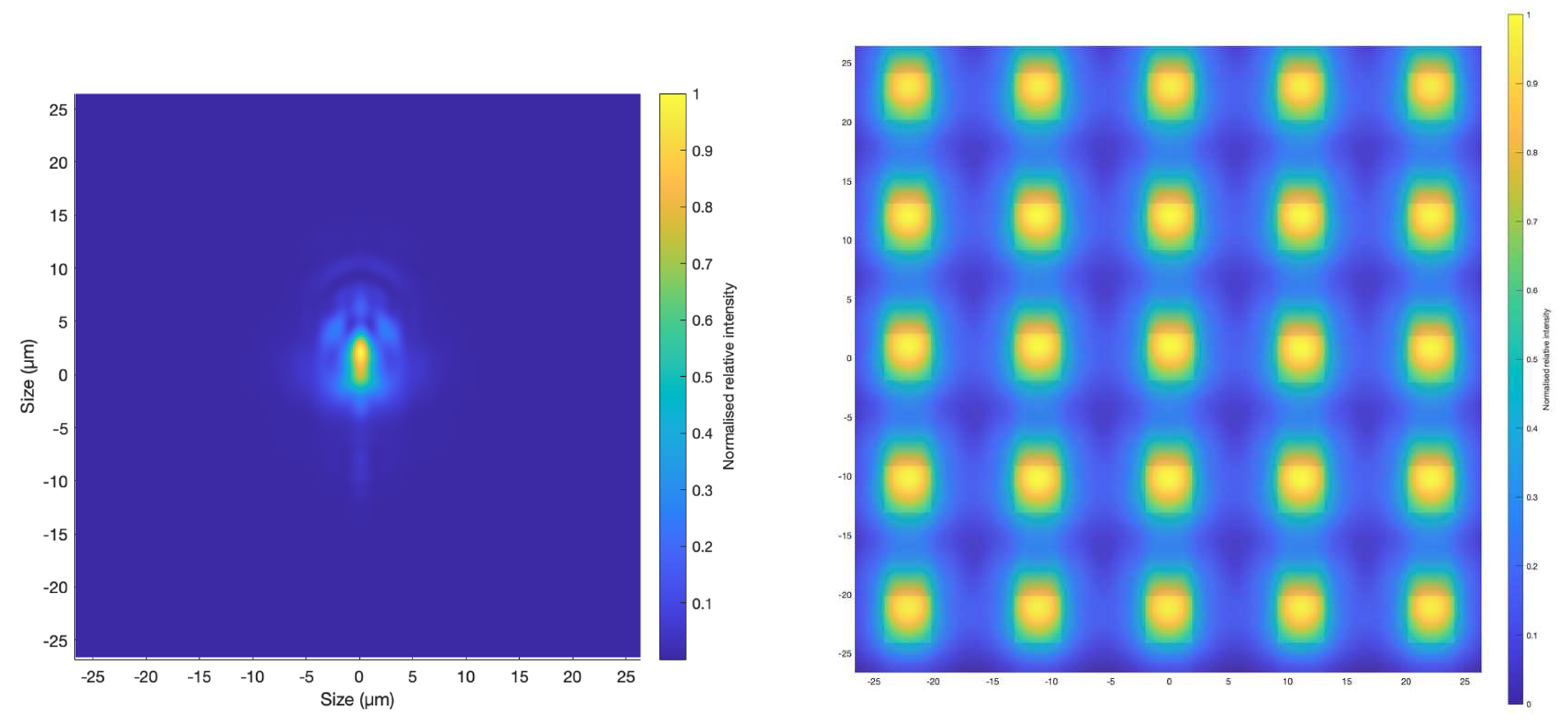
2.2.4. Relative intensity
The relative intensity of light as a function of angle of incidence is shown in Figure 15.
2.2.5. Chromatic aberration
The chromatic aberration of the system is that of a compensated system as shown in Figure 16.
2.3. Simulated Performance for Earth observation
2.3.1. SNR High-resolution 4K-RGB camera
For camera 1, with a nadir resolution of 570 m, and a nominal satellite altitude of 700 km, Lambertian Earth leaving flux is attenuated towards the entrance of the camera by a factor . Within the optical system, with a radiometric aperture diameter of 5.38 mm, and a detector pixel size of 5.5 micron, the entrance flux is amplified towards the detector by a factor . Assuming no light loss, the ratio between the detector flux and the Earth flux is then . Assuming a 50 % light loss, the ratio becomes .
The detector for camera 1, is the CMOSIS CMV12000 CMOS detector array, with pixels, and a full well capacity of 1485 counts, corresponding to approximately 10.5 bit per pixel. For a pixel subarray, it can be read out at a maximum frame rate of 400 fps, corresponding to a minimum readout time for a single frame of 2.5 ms. We calculate the maximum integration time before saturation occurs for the theoretical case of 100 % diffuse reflection for an incident solar irradiance of 1500 W/m2. The wavelength dependent saturation time for Red, Green and Blue wavelengths with peaks at 634 nm, 547 nm, 453 nm respectively, are 16.7 s, 18.9 s , 26 s respectively. An average Quantum efficiency of 0.45 is assumed.
Before motion blurring occurs, a further time averaging is allowed within a time period of 0.57 km / (7 km/s)= 81.4 ms, so over frames. The SNR as a function of wavelength for 32 integrations of 15 s each for red, green and blue wavelengths are , and respectively. If we follow the procedure of [11] to estimate the RSR from the RGB camera measurements, the quantisation errors corresponding to these SNR values cause an error on the RSR of 0.04 W/m2. This 0.04 W/m2 quantisation error, is small compared to the [11] spectral regression error of 3 %, which for the reference scene of 1500 W/m2 corresponds to 3 % × 1500 W/m2 = 45 W/m2.
2.3.2. SNR multispectral cameras
For cameras 2 and 3, with a nadir resolution of 1.71 km, and a nominal satellite altitude of 700 km, Lambertian Earth leaving flux is attenuated towards the entrance of the camera by a factor . Within the optical system, with a radiometric aperture diameter of 1.14 mm, and a detector pixel size of 5.5 micron, the entrance flux is amplified towards the detector by a factor . The ratio between the detector flux and the Earth flux is then without light loss, and with 50 % light loss.
The detector for camera 2 and 3 is the CMOSIS CMV2000 CMOS detector array, with 1024×2048 pixels, and a full well capacity of 1012.5 counts, corresponding to bit per pixel. For a 1000×1000 pixel subarray, it can be read out at a maximum frame rate of 680 fps, corresponding to a minimum readout time for a single frame of 1.47 ms. Before motion blurring occurs, a further time averaging is allowed within a time period of 1.71 km / 7 km/s = 243 ms, so over 166 frames. The Signal to Noise Ratio (SNR) as a function of wavelength for 166 readouts of 400 s each is illustrated in Figure 17. For the least sensitive wavelength at 950 nm, the SNR for a single readout is 771, the SNR for 166 readouts is .
3. Longwave camera suite
3.1. Multispectral thermal cameras
A reference design of the thermal imager is described in [12]. The thermal imager consists of a microbolometer detector array with a WFOV lens allowing to view the Earth from limb to limb. The WFOV lens design is illustrated in Figure 18. The nadir sampling distance is 2.2 km, and the nadir effective resolution is 4.4 km. Using a single wavelength band of 8-14 micron, on a stand alone basis the OLR can be estimated from the thermal imager with an accuracy of 5 %.
The LongWave (LW) cameras will be equipped with a shutter with known temperature and known high emissivity. This shutter will act as a flat blackbody. Combined with the deep space view a two-point in-flight calibration for the longwave cameras will be implemented. The shutter view will be used for the characterization of the thermal offset as a function of the lens temperature. The deep space view will be used for an in-flight verification of the gain, that will also be measured on the ground before flight.
For improving the spectral regression OLR noise level, the number of ECO LW channels can be increased. This will be done by using multiple cameras, with filters inserted in front of the microbolometer detector array. In [19], the TIRI/HERA space instrument is described using the same detector as in [12], and a filter wheel with 6 filters each having a bandwidth of approximately 1 m. For ECO we will adopt similar filters, listed in Table 2.
The 6 ECO filter spectral responses are also similar to filter responses used for the SEVIRI/MSG [20] and FCI/MTG [21] instruments.
The ECO LW Camera Suite (LCS) will be formed by 6 separate LW cameras, each consisting of the same microbolometer array and WFOV lens, and each equiped with a different filter realising the spectral responses from Table 2. For the microbolometer array, the Lynred 1024x768 array with 17 m pixel pitch [22] can be used.
The LW spectral responses are illustrated in Figure 19.
3.2. Noise Equivalent Differential Temperature (NEDT)
For the thermal cameras, with a nadir sampling distance of 2 km, and a nominal satellite altitude of 700 km, Lambertian Earth leaving flux is attenuated towards the entrance of the camera by a factor (2/700)2=8.2. Within the optical system, with a radiometric aperture diameter of 6.61 mm, and a detector pixel size of 17 micron, the entrance flux is amplified towards the detector by a factor /4*(6.61/17)2 = 119. Asssuming no light loss, the ratio between the detector flux and the Earth flux is then 8.2 * 119 = 0.97. Assuming 50 % light loss, the ratio becomes 0.97 * 0.5 = 0.49.
The Lynred 1024x768 microbolometer detector array has an NEDT of 50 mK for a f/1 optics at 300 K and at 30 Hz. For the above calculated optical magnification of 0.49, the NEDT will be increased to 50 mK / = 72 mK. Before motion blurring occurs, the microbolometer signal can be integrated during 4.4 km / 7 km/s = 0.63 s. After 0.63 s averaging, the NEDT will be reduced to 72 mK / = 17 mK for a hypothetical microbolometer without spectral filter. From the ECO spectral filters - illustrated in Figure 19 and quantised by equations 3 - the fractions measured for an ideal black body at 300 K are calculated, and the respective resulting NEDTs are calculated and listed in Table 3.
3.3. Longwave spectral regression
In [12], the OLR was estimated from a single narrowband irradiance measurement, by the following steps:
- conversion of the narrowband irradiance to a narrowband brightness temperature
- conversion of the narrowband brightness temperature to a broadband brightness temperature
- conversion of the broadband brightness temperature to the OLR
Here we will generalise this approach using 6 narrowband irradiances , for i=1,...,6. The 6 narrowband irradiances are obtained from the 6 thermal cameras with spectral response illustrated in Figure 19. Using the sigmoid function , with
we define the synthetic microbolometer spectral response
with the wavelength, and we define the synthetic narrowband spectral responses , for i=1,...,6 as
For a given general spectral irradiance distribution , the narrowband irradiance is given by
and the broadband irradiance, also known as the OLR, is given by
For the specific case of blackbody radiation, the irradiance distribution is given by the Planck curve and depends only on the temperature T of the blackbody, . We define the brightness temperature from an exponential fit to this blackbody radiation:
and we define the broadband brightness temperature from Planck’s law:
For the general narrowband radiance - given by equation 4, the narrowband brightness temperature is obtained by inverting the exponential fit from equation 6:
and the broadband brightness temperature is obtained by inverting Planck’s law:
Similar to [12], we use the libradtran radiative transfer simulation tool, to simulate the narrowband irradiances and OLR for 15 reference scenes, listed in column 1 of Table 4.
For the ensemble of these 15 reference scenes, we regress as a linear function of :
next we evaluate the OLR from using Planck’s law - using equation 9. The resulting OLR regression error is given as column 3 of Table 4. It lies within the range +/- 0.61 %.
The general recipee for estimating the OLR from measured narrowband irradiances , for i=1,...,6 is:
4. Discussion
The monitoring of the Earth Energy imbalance is one of the most critical aspects of mastering our planet’s climate change [4,5], and is the main mission objective of the Earth Climate Observatory (ECO) space mission concept. The ECO payload concept consists of four WFOV radiometers as main instruments, targeting an accurate differential measurement of the EEI as the difference of the ISR and the TOR, at a low spatial resolution of approximately 6000 km for a single measurement of the TOR. As auxiliary ECO instruments, cameras are proposed, allowing to spectrally separate the TOR into RSR and OLR, and to resolve the RSR and the OLR at a spatial resolution of at least 5 km at nadir, allowing to distinguish clear-sky from cloudy scenes. In [11] a 1500x1500 RGB CMOS camera was proposed, providing a nadir resolution of approximately 1 km for a single pixel, and allowing to estimate the RSR with a spectral regression error of 3 % at the 2x2 pixel level. In [12] a 750x750 microbolometer camera was proposed, providing a nadir resolution of approximately 2 km, and allowing to estimate the OLR with a spectral regression error of 5 % at the pixel level. In this paper we are introducing some improvements in the ECO camera concept, building further on the [11,12] baseline designs.
For the SW camera, in [11] a single RGB camera - with pixel size of 3.2 m, and image diameter of 1536 pixels, corresponding to 1536*3.2 m = 4.9 mm - was used. The accuracy by which the high resolution RSR radiance can be estimated from this camera, is limited to 3 % by the information contained in the three spectral channels, the Red, Green and Blue channels with typical spectral responses shown in Figure 5.
Here we have proposed a dramatic improvement in the number of spectral channels by adopting the IMEC multispectral cameras described in [16], which we adopt as our SW cameras 2 and 3. Camera 2 and 3 provide a total of 31 spectral channels, in the form of a 4x4 VIS and 5x5 VIS-NIR MultiSpectral Filter Array (MSFA) respectively, as illustrated in Figure 6. The IMEC multispectral detectors are based on the CMOSIS CMV2000 detector, with a pixel size of 5.5 m, and image diameter of 1000 pixels, corresponding to 1000*5.5 m = 5.5 mm. For the SW camera lense we can use the optical design of [11], with a scaling of 5.5/4.9 = 1.1.
The use MSFA based cameras requires a demosaicing algorithm, for which Deep Learning (DL) based methods are currently an active area of research [23,24]. The quality of the demosaicing will improve if we can provide additional high resolution input information. For this purpose we propose to include SW camera 1, a high resolution RGB camera, based on the CMOSIS CMV12000 detector, with a pixel size of 5.5 m, and image diameter of 3000 pixels, corresponding to 3000*5.5 m = 16.5 mm. For this camera, we need a new optical design, which is presented in Section 2 and Figure 7.
For the thermal or LongWave (LW) camera, in [12] a single ’broadband’ microbolometer camera with spectral response between 8 and 14 m - see the purple curve in Figure 19 - is proposed. The corresponding OLR spectral regression error is 5 %. Here we propose to use 6 different copies of this basic camera - using the same microbolometer detector array and WFOV LW lense, see Figure 18 - with 6 different filters in front of it. Inspired by the TIRI instrument [19] to be launched as part of the Hera mission [18], we choose 6 adjacent filters with a width of 1 m, with spectral responses illustrated in Figure 19.
Extending the methodology of [12], with the newly proposed 6 channel LW camera concept, in Section 3.3 we evaluate the OLR radiance spectral regression error to be 0.6 %. Thus, comparing our newly proposed LW camera design to the one of [12], by going from 1 to 6 channels, we reduce the OLR spectral regression error from 5 % to 0.6 %.
A detailed analysis of the optical performance of the newly designed high-resolution SW camera, as well as an evaluation of the SNR of all SW cameras and the NEDT of all LW cameras is given in Section 2.2. The optical performance is well above what is required for the ECO mission scientific objectives.
5. Conclusions
We propose in this work, an update to the work previously done for the ECO space mission to measure what can be considered as the most essential of all climate variables: the Earth energy imbalance. The proposed payload consists of a combination of highly accurate, but low resolution radiometers measuring the incoming solar radiation and the total outgoing terrestrial radiation in a differential way, enhanced with lightweight uncooled camera systems aiming to separate the total outgoing terrestrial radiation spectrally in reflected solar - or shortwave, and emitted thermal - or longwave radiation, and to increase the spatial resolution to 5 km at nadir or better. Compared to our earlier proposal for the camera system, which consisted of a single SW camera and a single LW camera, we now propose a suite of 3 SW cameras and 6 LW cameras, with strongly improved spectral information content, and with an optical performance that is largely sufficient for the intended application.
Acknowledgments
The work performed by Y.Z was supported by the China Scholarship Council, funding a one year stay of Y.Z at the Royal Observatory of Belgium.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EEI | Earth energy Imbalance |
| FWHM | Full Width at Half Maximum |
| OLR | Outgoing Longwave Radiation |
| RSR | Reflected Solar Radiation |
| WFOV | Wide Field of View |
| VIS | Visible |
| VIS-NIR | Visible and Near-infrared |
| CMOS | Complementary metal oxide semiconductor |
| FOV | Field of View |
| RMS | Root-Mean Square |
| PSF | Point Spread Function |
| SNR | Signal to Noise Ratio |
| LSB | Least significant Bit |
| NEDT | Noise Equivalent Differential Temperature |
References
- Dewitte, S.; Clerbaux, N. Measurement of the Earth radiation budget at the top of the atmosphere—A review. Remote Sensing 2017, 9, 1143. [Google Scholar] [CrossRef]
- Trenberth, K.; Fasullo, J.; Von Schuckmann, K.; Cheng, L. Insights into Earth’s energy imbalance from multiple sources. Journal of Climate 2016, 29, 7495–7505. [Google Scholar] [CrossRef]
- Von Schuckmann, K.; Cheng, L.; Palmer, M.; Hansen, J.; Tassone, C.; Aich, V.; Adusumilli, S.; Beltrami, H.; Boyer, T.; Cuesta-Valero, F.; Desbruyères, D. Heat stored in the Earth system: where does the energy go? Earth System Science Data 2020, 12, 2013–2041. [Google Scholar] [CrossRef]
- Hansen, J.; Nazarenko, L.; Ruedy, R.; Sato, M.; Willis, J.; Del Genio, A.; Koch, D.; Lacis, A.; Lo, K.; Menon, S.; Novakov, T. Earth’s energy imbalance: Confirmation and implications. Science 2005, 308, 1431–1435. [Google Scholar] [CrossRef]
- Von Schuckmann, K.; Palmer, M.; Trenberth, K.; Cazenave, A.; Chambers, D.; Champollion, N.; Hansen, J.; Josey, S.; Loeb, N.; Mathieu, P.; Meyssignac, B. An imperative to monitor Earth’s energy imbalance. Nature Climate Change 2016, 6, 138–144. [Google Scholar]
- Schifano, L.; Smeesters, L.; Geernaert, T.; Berghmans, F.; Dewitte, S. Design and analysis of a next-generation wide field-of-view earth radiation budget radiometer. Remote Sensing 2020, 12, 425. [Google Scholar] [CrossRef]
- Doelling, D.; Keyes, D.; Nordeen, M.; Morstad, D.; Nguyen, C.; Wielicki, B.; Young, D.; Sun, M. Geostationary enhanced temporal interpolation for CERES flux products. J. Atmos. Oceanic Technol. 2013, 30, 1072–1090. [Google Scholar] [CrossRef]
- Loeb, N.; Doelling, D.; Wang, H.; Su, W.; Nguyen, C.; Corbett, J.; Liang, L.; Mitrescu, C.; Rose, F.; Kato, S. Clouds and the earth’s radiant energy system (CERES) energy balanced and filled (EBAF) top-of-atmosphere (TOA) edition-4.0 data product. Journal of Climate 2018, 31(2), 895–918. [Google Scholar] [CrossRef]
- S. Kato, N. S. Kato, N. Loeb, F.R.T.T.D.R.S.H.D.D. Earth radiation budget climate record composed of multiple satellite observations. 2023, pp. IUGG23–4506.
- Hocking, T.; Mauritsen, T.; Megner, L. Sampling strategies for Earth Energy Imbalance measurements using a satellite radiometer; Earth Energy Imbalance Assessment Workshop,, 2023.
- Schifano, L.; Smeesters, L.; Berghmans, F.; Dewitte, S. Optical system design of a wide field-of-view camera for the characterization of earth’s reflected solar radiation. Remote Sensing 2020, 12, 2556. [Google Scholar] [CrossRef]
- Schifano, L.; Smeesters, L.; Berghmans, F.; Dewitte, S. Wide-field-of-view longwave camera for the characterization of the earth’s outgoing longwave radiation. Sensors 2020, 21, 4444. [Google Scholar] [CrossRef]
- Wu, A.; Xiong, X.; Doelling, D.; Morstad, D.; Angal, A.; Bhatt, R. Characterization of Terra and Aqua MODIS VIS, NIR, and SWIR spectral bands’ calibration stability. IEEE Transactions on Geoscience and Remote Sensing 2012, 51, 4330–4338. [Google Scholar] [CrossRef]
- Decoster, I.; Clerbaux, N.; Baudrez, E.; Dewitte, S.; Ipe, A.; Nevens, S.; Blazquez, A.; Cornelis, J. Spectral aging model applied to meteosat first generation visible band. Remote Sensing 2014, 6, 2534–2571. [Google Scholar] [CrossRef]
- Sterckx, S.; Adriaensen, S.; Dierckx, W.; Bouvet, M. In-orbit radiometric calibration and stability monitoring of the PROBA-V instrument. Remote Sensing 2016, 8, 546. [Google Scholar] [CrossRef]
- Geelen, B.; Blanch, C.; Gonzalez, P.; Tack, N.; Lambrechts, A. A tiny VIS-NIR snapshot multispectral camera. SPIE Advanced Fabrication Technologies for Micro/Nano Optics and Photonics VIII 2015, 9374, 194–201. [Google Scholar]
- Weidmann, D.; Antonini, K.; Pino, D.; Brodersen, B.; Patel, G.; Hegglin, M.; Sioris, C.; Bell, W.; Miyazaki, K.; Alminde, L.; Gabriele, A. Cubesats for monitoring atmospheric processes (CubeMAP): a constellation mission to study the middle atmosphere. SPIE. In Sensors, Systems, and Next-Generation Satellites XXIV 2020, 11530, 141–159. [Google Scholar]
- Michel, P.; Küppers, M.; Bagatin, A.; Carry, B.; Charnoz, S.; De Leon, J.; Fitzsimmons, A.; Gordo, P.; Green, S.; Hérique, A.; Juzi, M. The ESA Hera mission: detailed characterization of the DART impact outcome and of the binary asteroid (65803) Didymos. The Planetary Science Journal 2022, 3(7), 160. [Google Scholar] [CrossRef]
- Okada, T.; Tanaka, S.; Sakatani, N.; Shimaki, Y.; Arai, T.; Senshu, H.; Demura, H.; Sekiguchi, T.; Kouyama, T.; Kanamaru, M.; Ishizaki, T. Calibration of the Thermal Infrared Imager TIRI onboard Hera. In European Planetary Science Congress; 2022; p. EPSC2022–1191. [Google Scholar]
- Schmetz, J.; Pili, P.; Tjemkes, S.; Just, D.; Kerkmann, J.; Rota, S.; Ratier, A. An introduction to Meteosat second generation (MSG). Bulletin of the American Meteorological Society 2002, 83(7), 977–992. [Google Scholar] [CrossRef]
- Ouaknine, J. The FCI on board MTG: optical design and performances. 2017, Vol. SPIE Vol. 10563, pp. 617–625. Riguet, F. The FCI on board MTG: optical design and performances. 2017.
- Tissot, J.; Tinnes, S.; Durand, A.; Minassian, C.; Robert, P.; Vilain, M. High-performance uncooled amorphous silicon VGA and XGA IRFPA with 17µm pixel-pitch. SPIE. In Electro-optical and infrared systems: Technology and applications VII 2010, 7834, 147–154. [Google Scholar]
- Arad, B. R.Y.R.M.N.B.A.W.Y.W.X.F.Z.X.C.Z.F.; Liu, S. NTIRE 2022 spectral demosaicing challenge and data set. 2022, pp. 882–896.
- Zeng, H.; Feng, K.; Huang, S.; Cao, J.; Chen, Y.; Zhang, H.; Luong, H.; Philips, W. MSFA-Frequency-Aware Transformer for Hyperspectral Images Demosaicing, 2023, [arXiv:eess.IV/2303.13404].
Figure 1.
Multi-annual mean Total Outgoing Radiation at resolution. Unit: W/m2. Reproduced from [1].
Figure 1.
Multi-annual mean Total Outgoing Radiation at resolution. Unit: W/m2. Reproduced from [1].
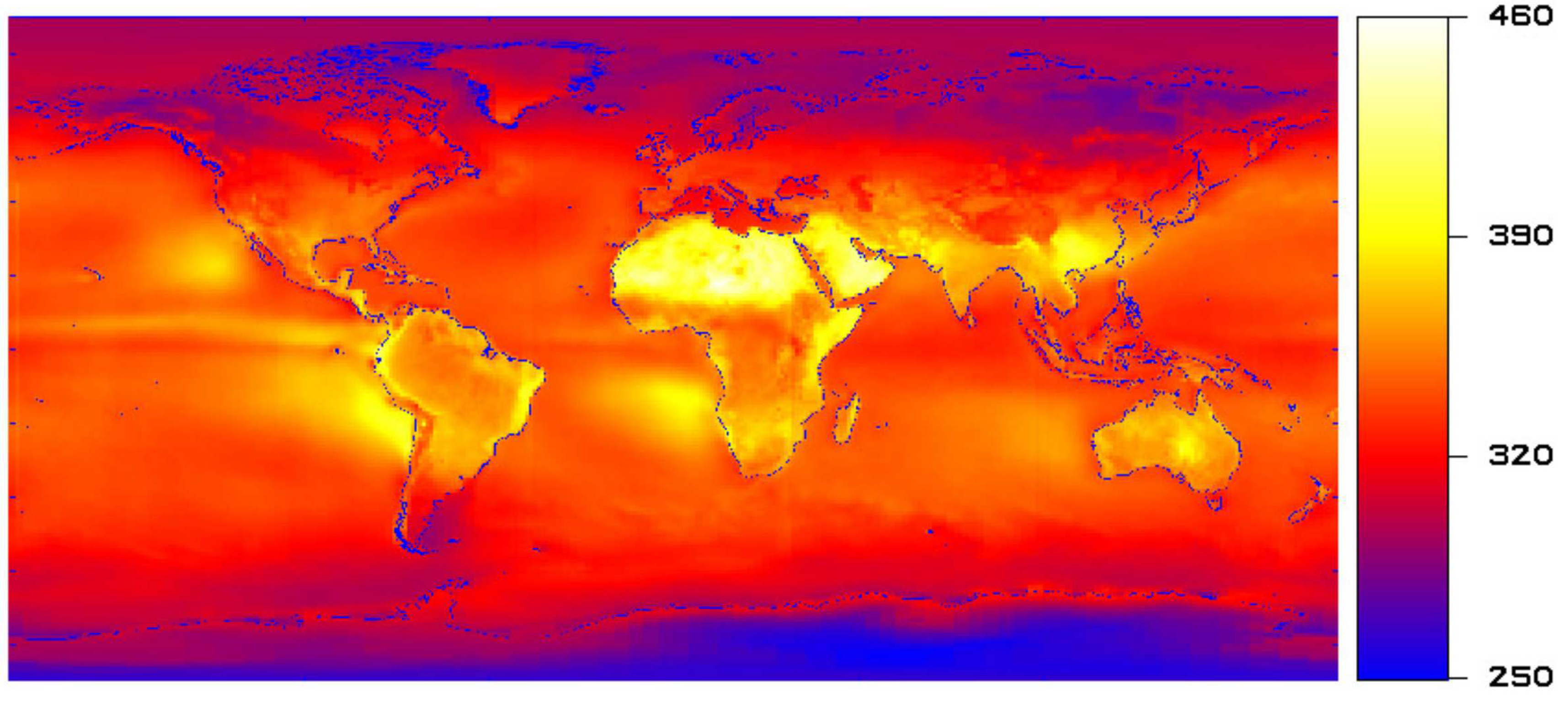
Figure 2.
Multi-annual mean Reflected Solar Radiation at resolution. Unit: W/m2. Reproduced from [1].
Figure 2.
Multi-annual mean Reflected Solar Radiation at resolution. Unit: W/m2. Reproduced from [1].
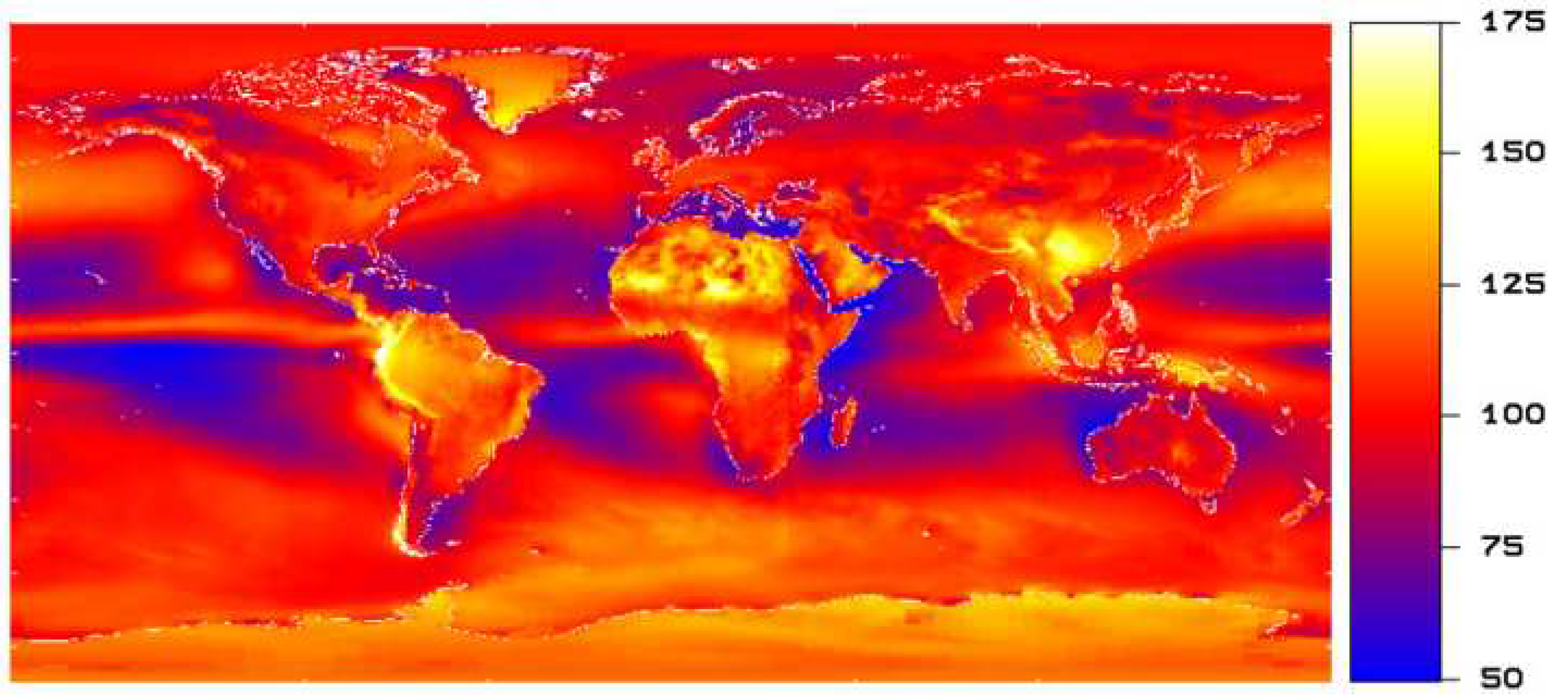
Figure 3.
Multi-annual mean Outgoing Longwave Radiation at resolution. Unit: W/m2. Reproduced from [1].
Figure 3.
Multi-annual mean Outgoing Longwave Radiation at resolution. Unit: W/m2. Reproduced from [1].
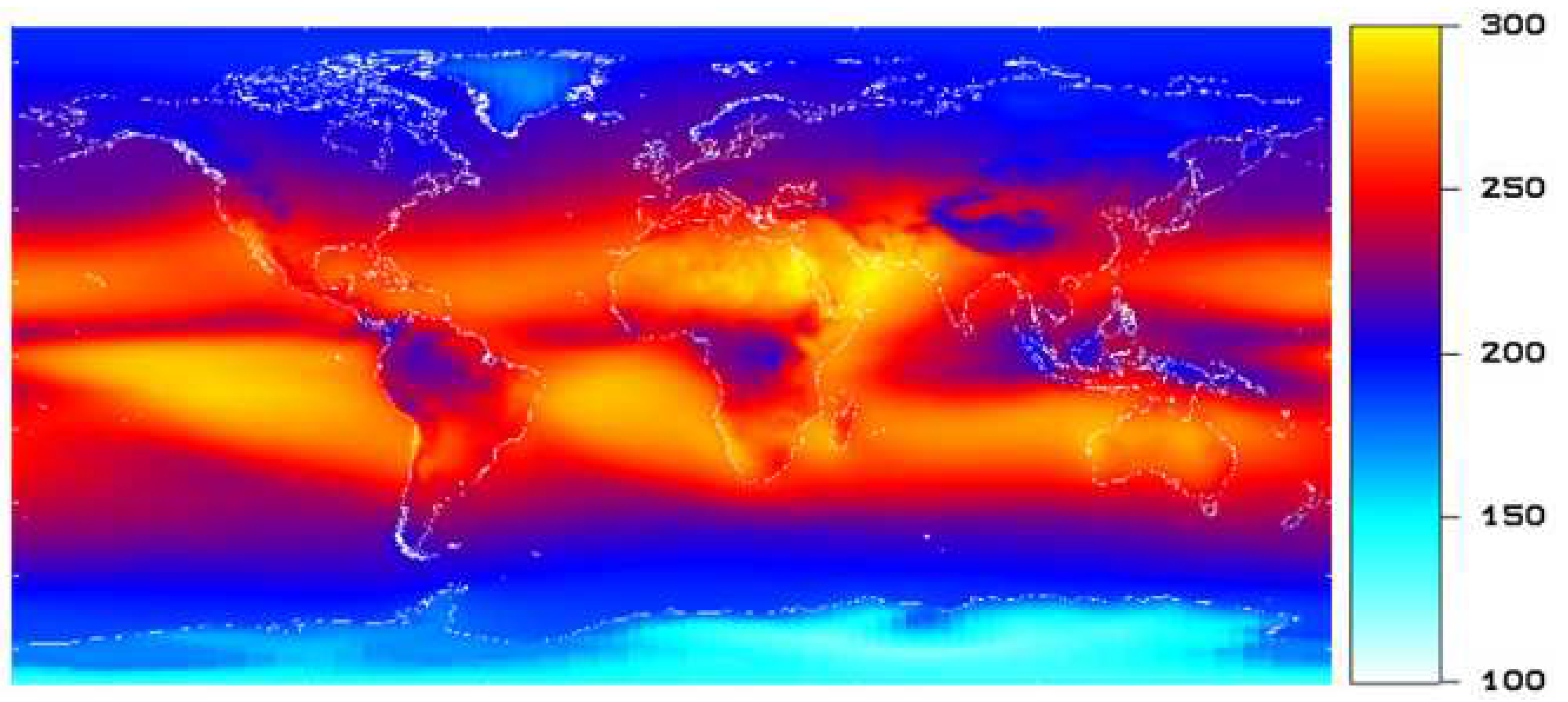
Figure 4.
Wide field of view reference lens design for the SW camera. Reproduced from [11].
Figure 4.
Wide field of view reference lens design for the SW camera. Reproduced from [11].

Figure 5.
RGB CMOS spectral responses used in [11].
Figure 5.
RGB CMOS spectral responses used in [11].
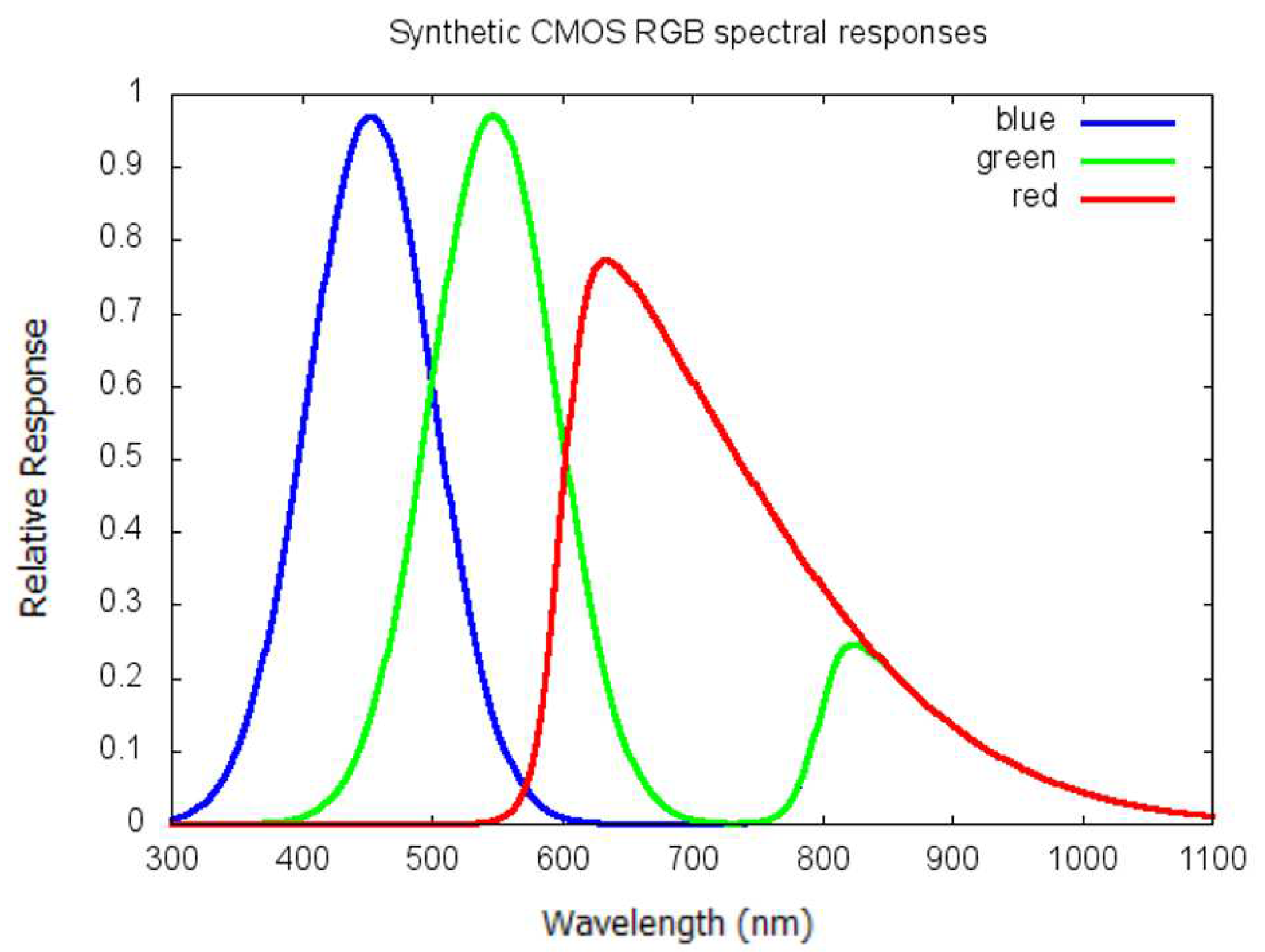
Figure 6.
Realization of the ECO SW camera suite, using 3 separate cameras.
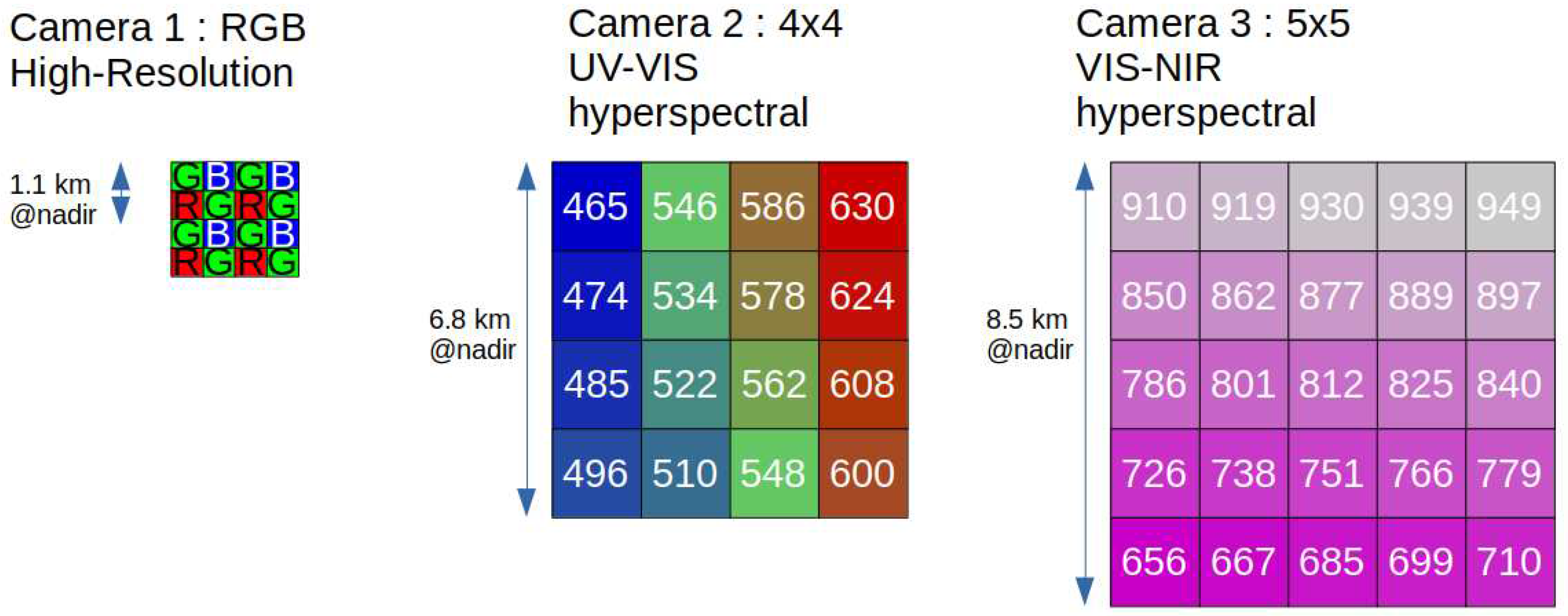
Figure 7.
Optical design of the SW camera. The total axial length equals 50.6 mm. The lens train consists of 4 singlet (s) lenses and an acromatic doublet (d) arranged in a s-s-s-d-s format. The detector has a size of 16.5 × 16.5 mm. The FOV is . The 12 different colors pertain to 12 different angles between and with a step of .
Figure 7.
Optical design of the SW camera. The total axial length equals 50.6 mm. The lens train consists of 4 singlet (s) lenses and an acromatic doublet (d) arranged in a s-s-s-d-s format. The detector has a size of 16.5 × 16.5 mm. The FOV is . The 12 different colors pertain to 12 different angles between and with a step of .
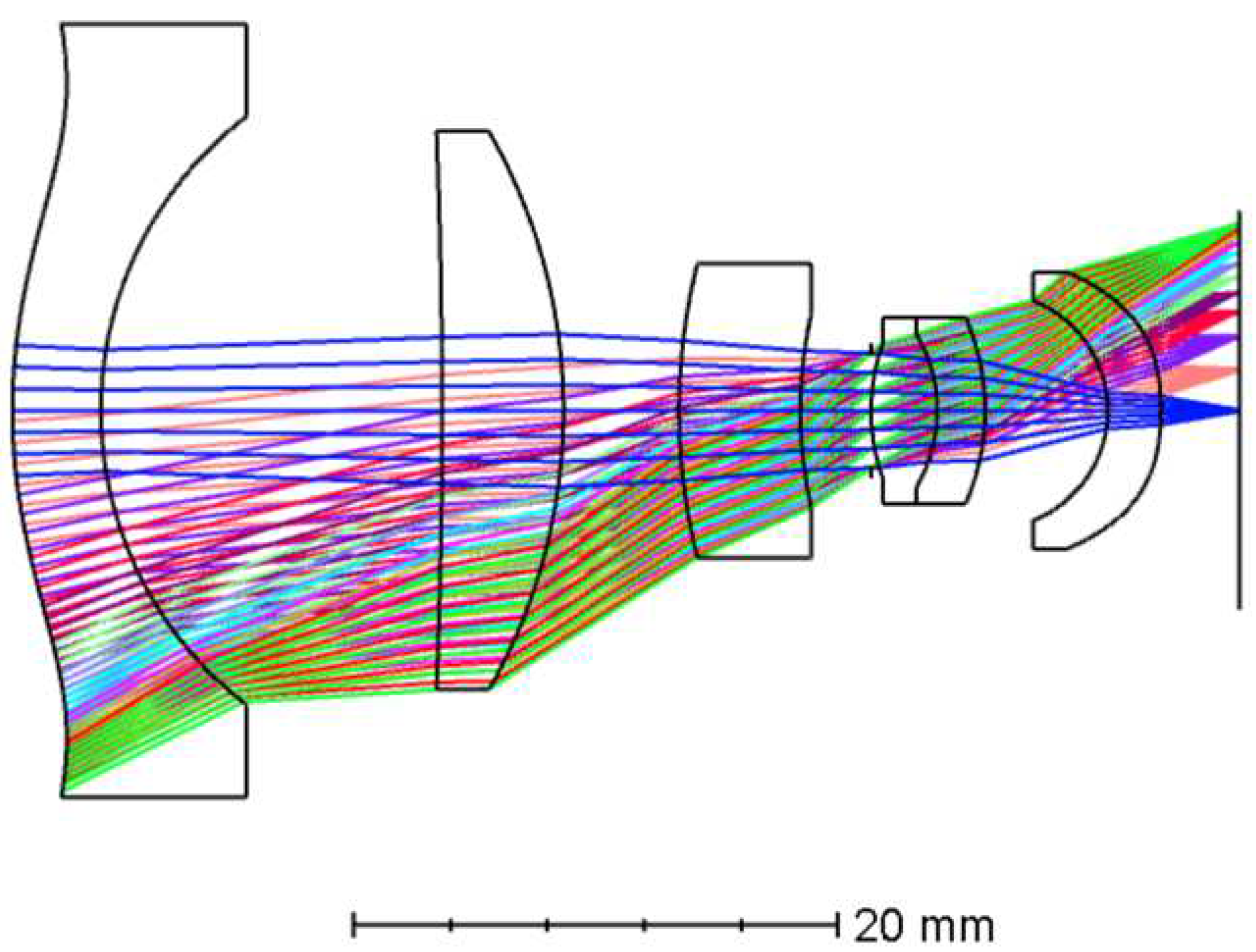
Figure 8.
The RMS error shown in m versus incidence angle of the light on the first surface of the lens. the colors depict various wavelengths of light (in m).
Figure 8.
The RMS error shown in m versus incidence angle of the light on the first surface of the lens. the colors depict various wavelengths of light (in m).
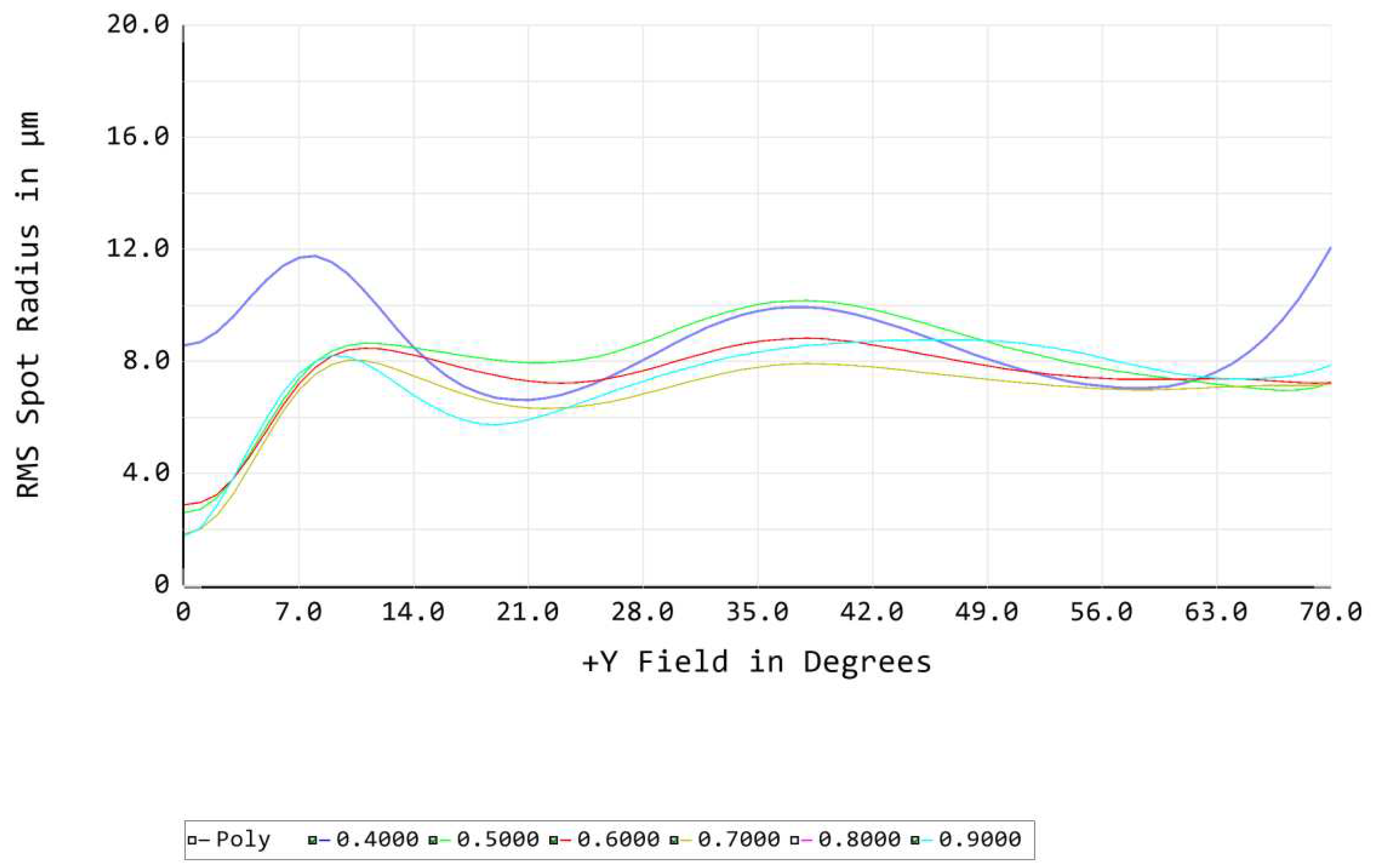
Figure 9.
The five different Seidel aberrations and chromatic aberrations.The largest contributor being the barrel distortion.
Figure 9.
The five different Seidel aberrations and chromatic aberrations.The largest contributor being the barrel distortion.

Figure 10.
The average optical PSF of all simulated wavelengths for the incidence angle. Image size 53.236 by 53.236 .
Figure 10.
The average optical PSF of all simulated wavelengths for the incidence angle. Image size 53.236 by 53.236 .
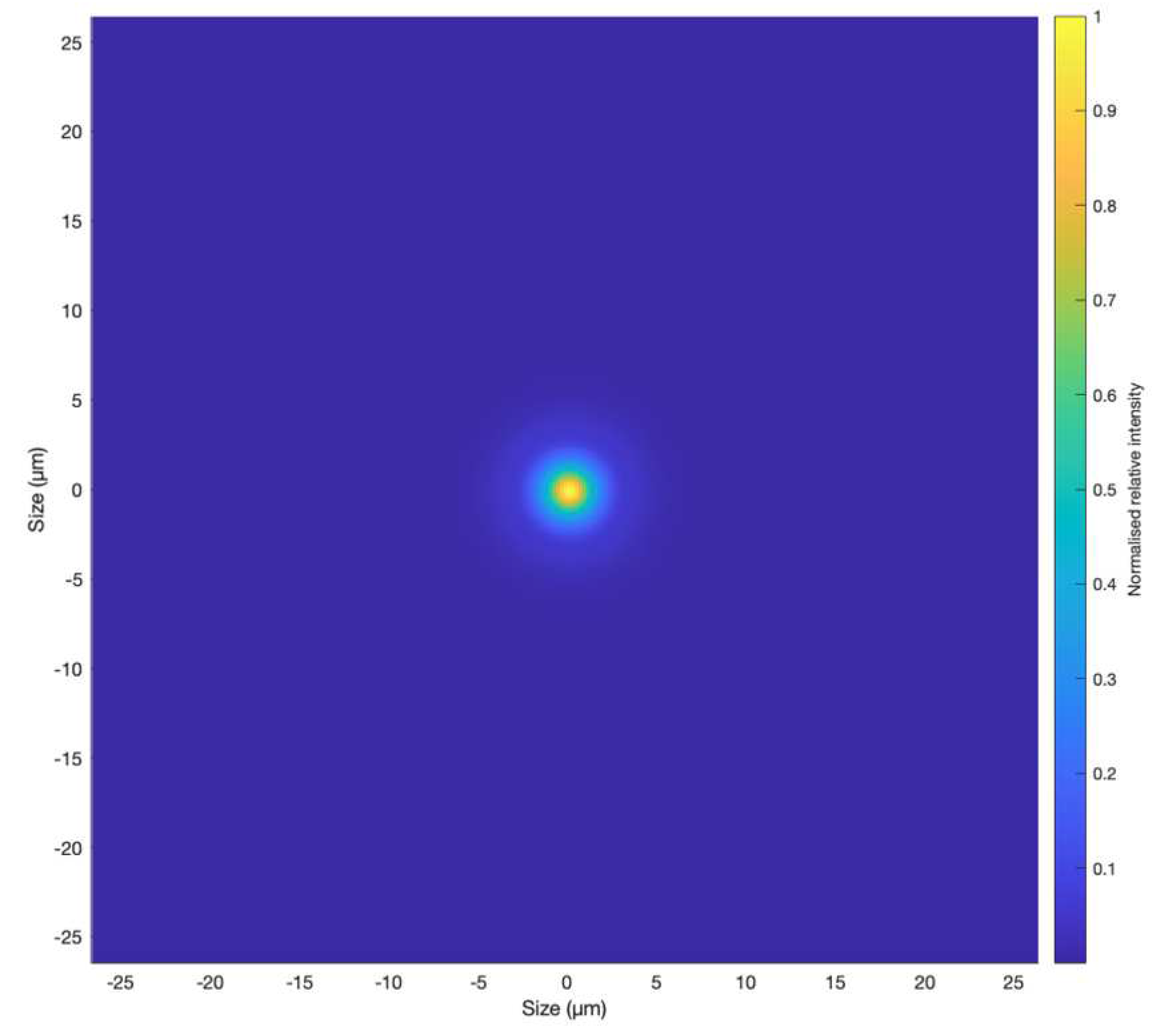
Figure 11.
The active pixel layer of type (a)Red/Blue pixels, (b) Green-Green pixels, for a fixed detector area of 53.236 by 53.236 , where individual pixels cover 80% of a nominal square area.
Figure 11.
The active pixel layer of type (a)Red/Blue pixels, (b) Green-Green pixels, for a fixed detector area of 53.236 by 53.236 , where individual pixels cover 80% of a nominal square area.
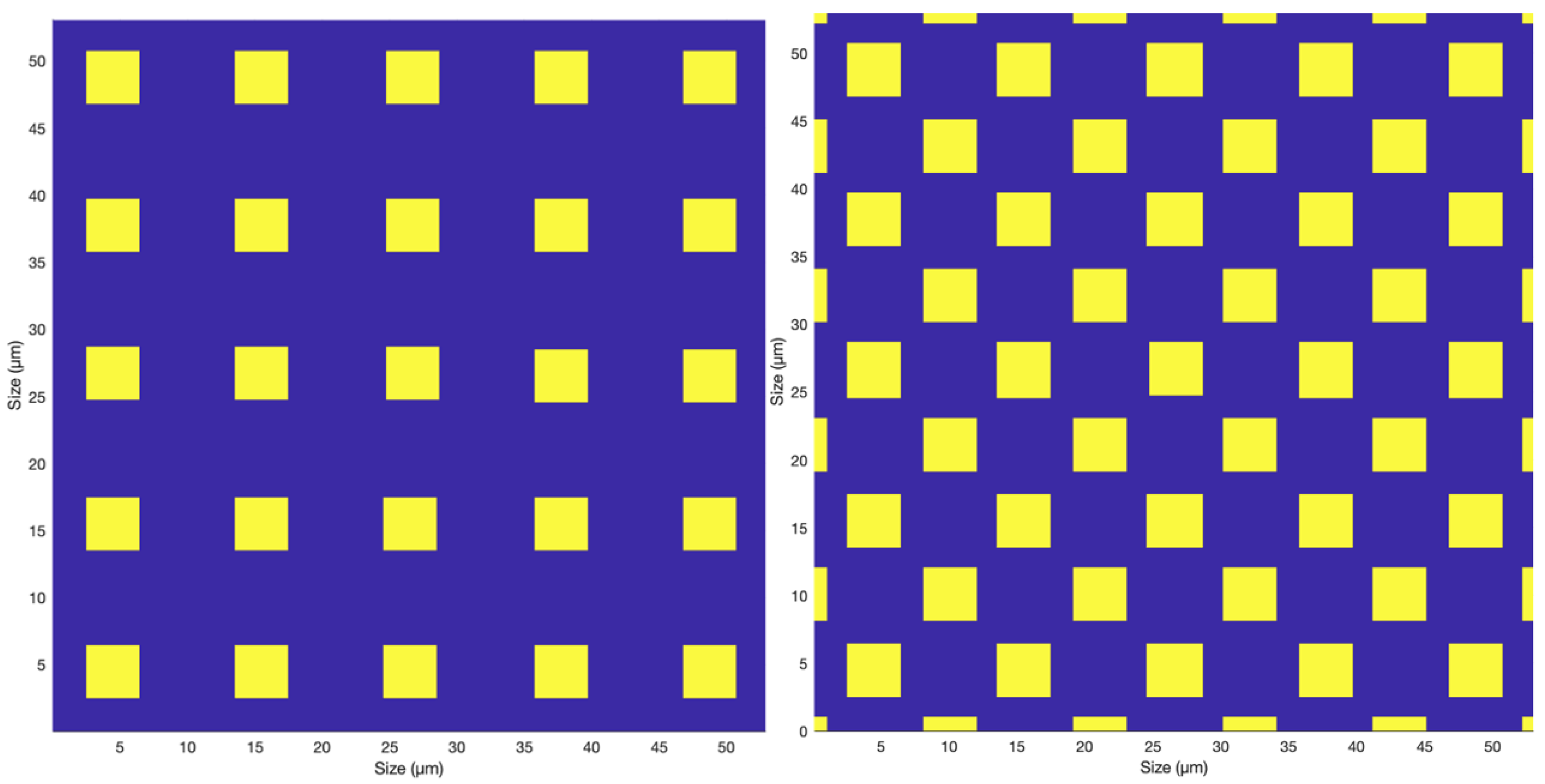
Figure 12.
The convolution of active pixel layer of type (a)Red/Blue, (b) Green-Green with the PSF of incident light, where individual pixels are overlaid over the convolution.
Figure 12.
The convolution of active pixel layer of type (a)Red/Blue, (b) Green-Green with the PSF of incident light, where individual pixels are overlaid over the convolution.
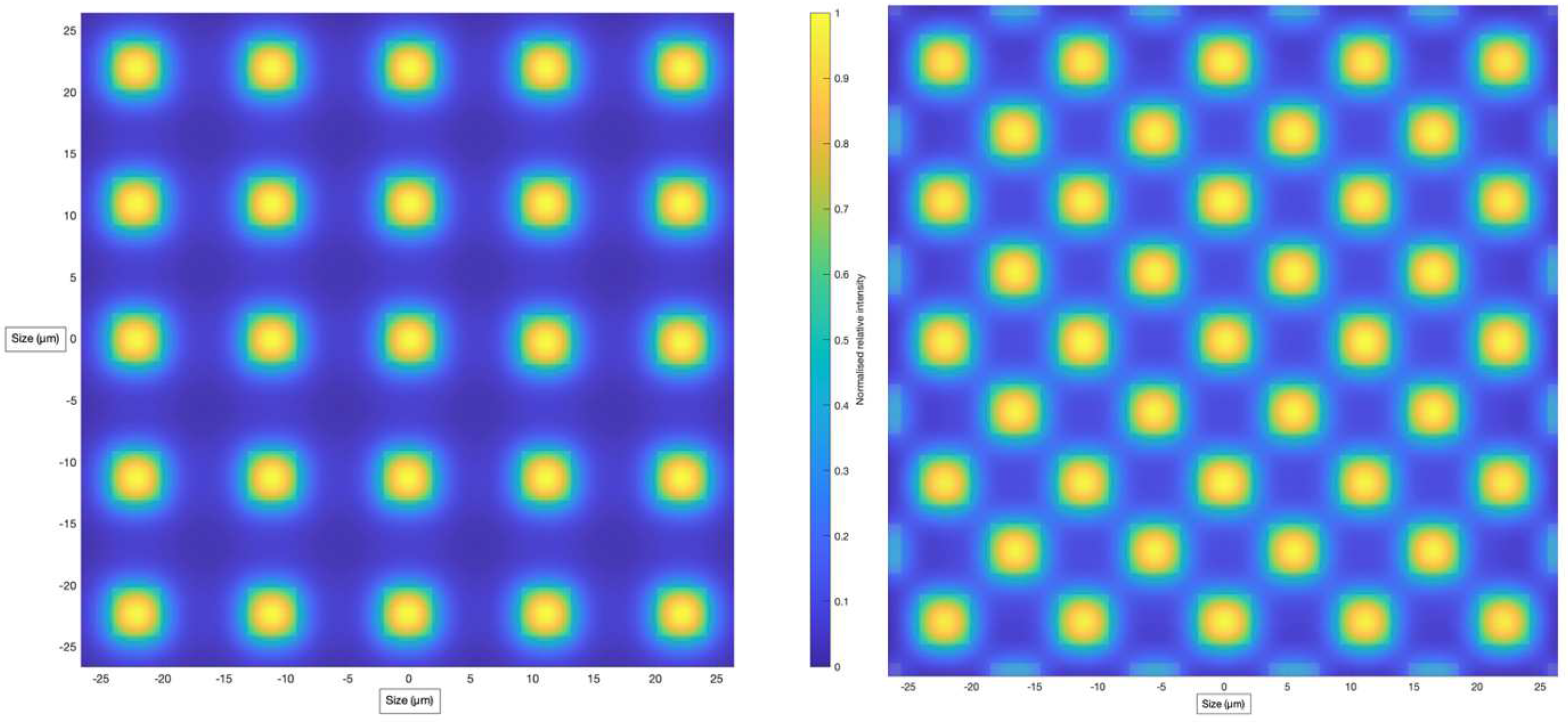
Figure 14.
Left: The PSF of 500 nm wavelength for incidence angle. Image size 66.545 by 66.545 . Right: The convolution of active pixel layer of green-type with the PSF of incident light of 500 nm wavelength, where individual pixels are overlaid over the convolution.
Figure 14.
Left: The PSF of 500 nm wavelength for incidence angle. Image size 66.545 by 66.545 . Right: The convolution of active pixel layer of green-type with the PSF of incident light of 500 nm wavelength, where individual pixels are overlaid over the convolution.

Figure 15.
The relative intensity versus the angle of incidence.
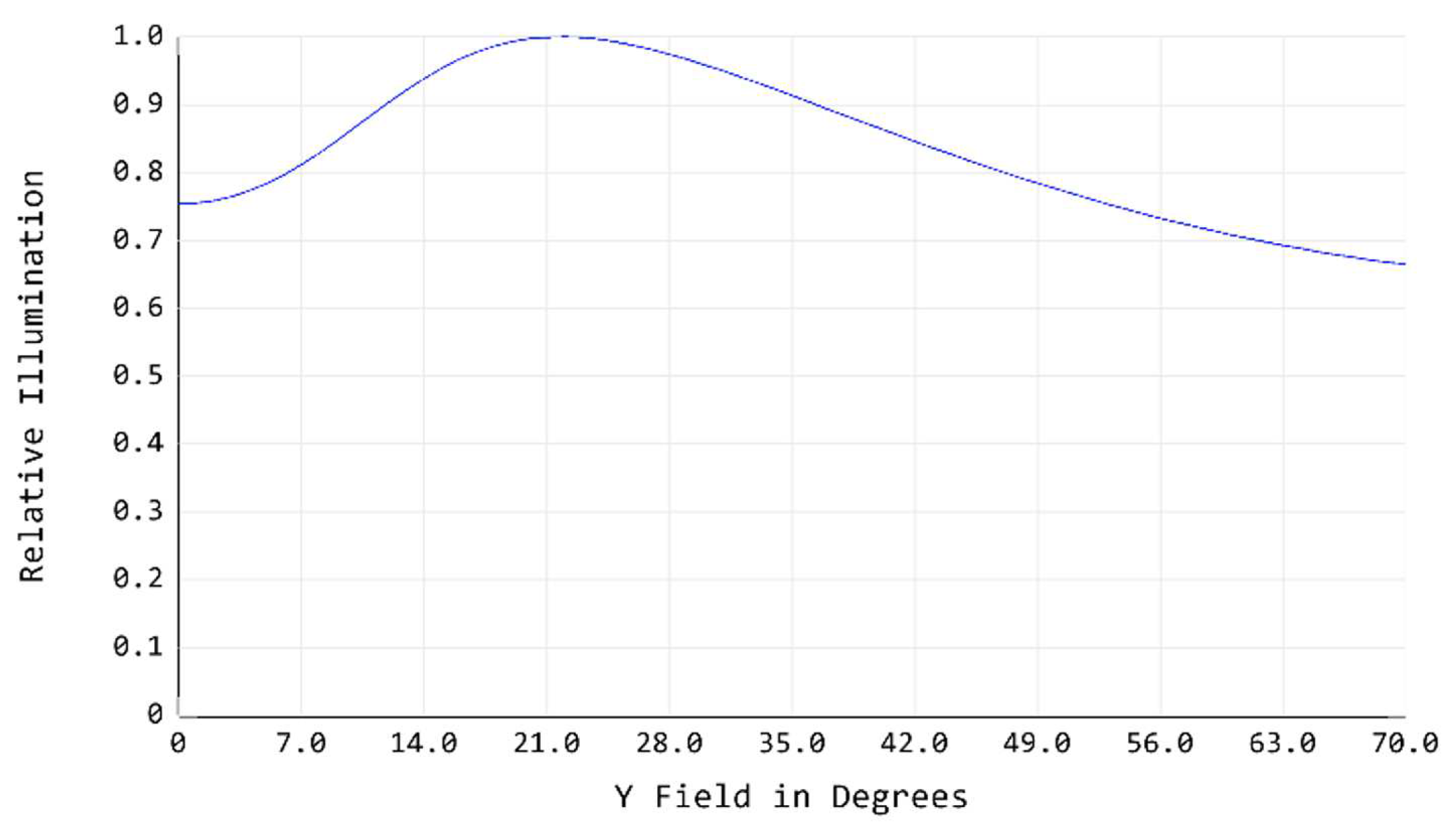
Figure 16.
Chromatic aberration of the entire optical system.
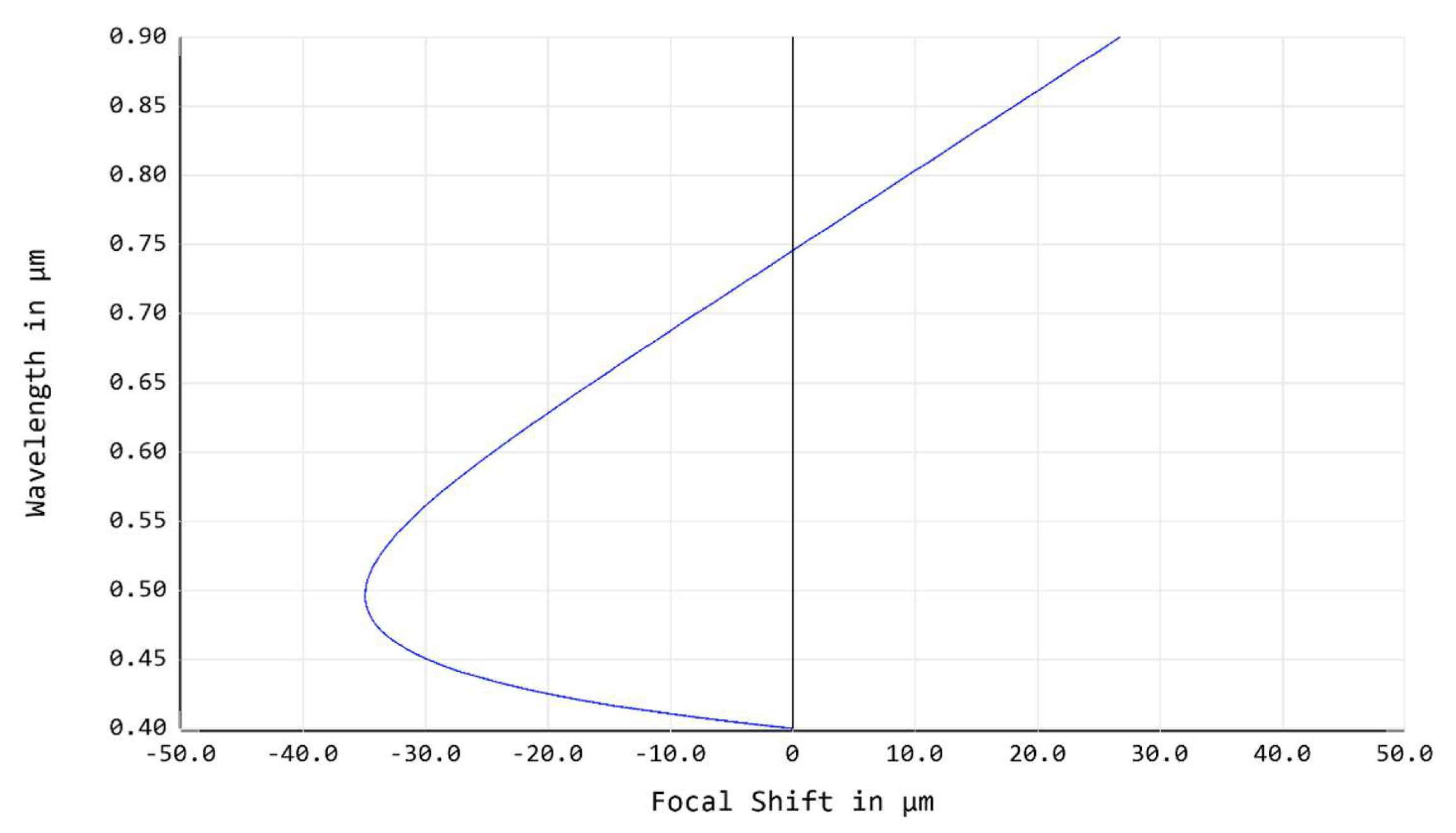
Figure 17.
166 integration signal to Noise ratio versus wavelength of multispectral cameras.
Figure 18.
Wide field of view reference lens design for the thermal camera.

Figure 19.
Longwave spectral responses.
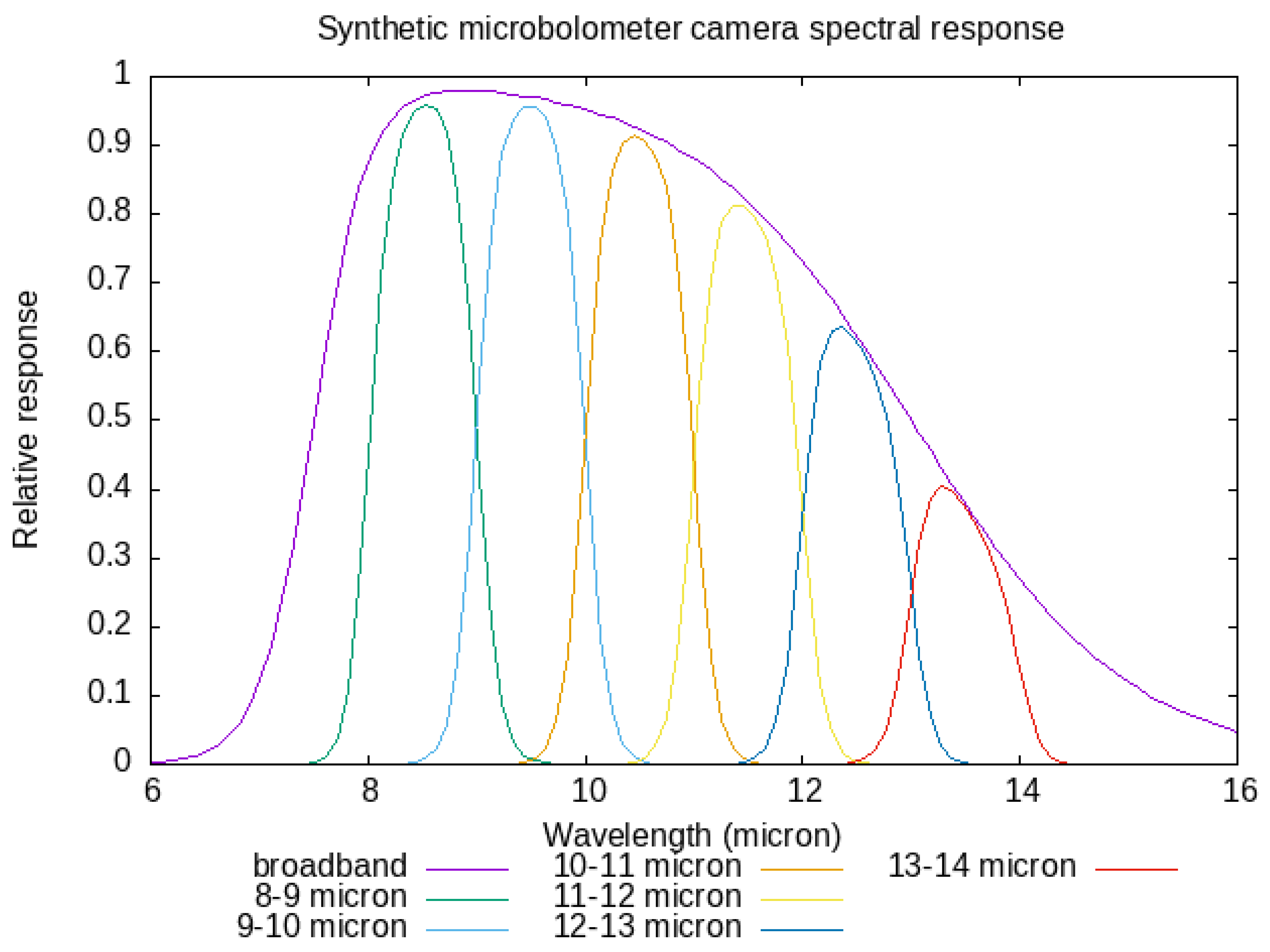
Table 1.
Lens data: Surface type, Material, thickness and diameters. Three aspherical surfaces. s-s-s-d-s format.
Table 1.
Lens data: Surface type, Material, thickness and diameters. Three aspherical surfaces. s-s-s-d-s format.
| Lens order (singlet/doublet) | Front surface type | Rear surface type | Material | Thickness | Diameter |
|---|---|---|---|---|---|
| First lens (s: singlet) | Aspherical | Spherical | LAK14 | 3.7 | 32 |
| Second lens (s) | Spherical | Spherical | LAK14 | 5 | 23 |
| Third lens (s) | Spherical | Spherical | SF6 | 5 | 12 |
| Fourth lens (d: doublet) | Spherical | Spherical | N-FK51A | 2.7 | 7.6 |
| Fifth lens (d) | Spherical | Aspherical | N-SF6 | 2 | 7.6 |
| Sixth lens (s) | Spherical | Aspherical | LAK14 | 2.2 | 11.4 |
Table 2.
ECO longwave spectral bands. The limits are defined at the FWHM (Full Width at Half Maximum) of the spectral bands.
Table 2.
ECO longwave spectral bands. The limits are defined at the FWHM (Full Width at Half Maximum) of the spectral bands.
| Band | Limits |
|---|---|
| LW-1 | 8-9 m |
| LW-2 | 9-10 m |
| LW-3 | 10-11 m |
| LW-4 | 11-12 m |
| LW-5 | 12-13 m |
| LW-6 | 13-14 m |
Table 3.
Long-wave Filter fraction and NEDT.
| Band 1 | Band 2 | Band 3 | Band 4 | Band 5 | Band 6 | |
|---|---|---|---|---|---|---|
| Fraction of Black body radiation | 0.1087 | 0.1155 | 0.1083 | 0.0908 | 0.0643 | 0.0362 |
| NEDT per band (mK) | 51.55 | 50.03 | 51.66 | 56.40 | 67.02 | 89.3785 |
Table 4.
Longwave reference scenes, OLR, and OLR regression error.
| Scene | OLR (W/m2) | OLR error (%) |
|---|---|---|
| US standard - clear sky | 257.59 | 0.21 |
| Tropical - clear sky | 284.46 | -0.44 |
| Midlatitude summer - clear sky | 277.87 | -0.25 |
| Midlatitude winter - clear sky | 227.95 | -0.46 |
| Subarctic summer - clear sky | 260.81 | -0.11 |
| Subarctic winter - clear sky | 197.04 | -0.17 |
| US standard - water cloud | 214.31 | 0.61 |
| US standard - thin ice cloud | 184.32 | 0.04 |
| US standard - thick ice cloud | 124.75 | -0.61 |
| Midlatitude winter - water cloud | 200.64 | -0.52 |
| Midlatitude winter - thin ice cloud | 171.44 | -0.49 |
| Midlatitude winter - thick ice cloud | 125.25 | 0.23 |
| Subarctic summer - water cloud | 227.57 | -0.42 |
| Subarctic summer - thin ice cloud | 196.57 | -0.07 |
| Subarctic summer - thick ice cloud | 142.98 | -0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






