Prerpints.org logo
Preprint
Article

A Computational Study of Hydrogen Dispersion and Explosion after Large-Scale Leakage of Liquid Hydrogen

Altmetrics

Downloads

144

Views

55

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

23 October 2023

Posted:

23 October 2023

You are already at the latest version

Alerts
Abstract
This study employs the FLACS code to analyze hydrogen leakage, vapor dispersion, and subsequent explosions. Utilizing pseudo-source models, a liquid pool model, and a hybrid model combining both, we investigate dispersion processes for varying leak mass flow rates (0.225 kg/s and 0.73 kg/s) in a large open space. We also evaluate explosion hazards based on overpressure and impulse effects on humans. The computational results, compared with experimental data, demonstrated reasonable hydrogen vapor cloud concentration predictions, especially aligned with the wind direction. For higher mass flow rate of 0.73 kg/s, the pseudo-source model and hybrid model proved appropriate, while the liquid pool model was more suitable for lower mass flow rate of 0.225 kg/s. Regarding explosion analyses using overpressure-impulse diagram, higher mass flow rates leaded to potentially fatal overpressure and impulse effects on humans. However, lower mass flow rates may cause severe eardrum damage at the maximum overpressure point.
Keywords: 
Subject: Engineering  -   Chemical Engineering

1. Introduction

Hydrogen has been widely touted as a future, clean energy resource to replace fossil fuels; it has been used in various energy facilities [1,2,3,4,5]. However, to utilize hydrogen as a viable energy source, further studies are needed to address various aspects related to its production, transportation, and storage; safety issues require attention.
Hydrogen is stored as high-pressure gas, liquid, and solids that exhibit chemical and physical hydrogen bonds (metal hydrides and carbon-based materials) [6,7]. High-pressure gas is stored in the tanks of fuel cell vehicles and the tubes of hydrogen-charging stations. Large-scale storage is inappropriate; leakage and explosions are notable concerns [8,9,10]. Hydrogen is a liquid at 20K and atmospheric pressure. The density is approximately 70.8 kg/m3, which is approximately 1.8-fold higher than the 39 kg/m3 of a high-pressure (700-bar) tank [7]. Thus, liquid hydrogen storage requires less volume and is safer than gaseous storage. Long-distance hydrogen transportation uses the liquid form [11,12].
To address the safety issues and behavior of liquid hydrogen, extensive research has been conducted through both experimental [13,14,15,16,17,18] and computational studies [18,19,20,21,22,23,24] focused on dispersion and explosions resulting from liquid hydrogen leakage. A NASA study explored a significant liquid hydrogen leakage, simulating an accident in a large reservoir [13]. In total, 5.7 m3 (~400 kg) of liquid hydrogen leaked; the effects were observed over time. A longer leakage time (i.e., lower leakage rate) was associated with slower combustible vapor cloud spread along the ground.
HSL (Health and Safety Laboratory) conducted experiments on the behavior of liquid hydrogen when released at a rate of 60 L/min [14]. This study provided quantitative data on hydrogen concentration, liquid pool formation, and temperatures within the pool. The visible results of the hydrogen plumes demonstrated buoyant or non-buoyant behaviors of liquid and vapor phases of hydrogen based on the release conditions.
Experiments were conducted to investigate the spreading and vaporization of liquid hydrogen, as well as the transient behavior of cryogenic liquids such as nitrogen and hydrogen after release onto water or solid ground [15]. The pool radius of these liquids after release was compared with a computer model, LAUV, developed based on shallow-layer differential equations of mass and momentum conservation. The simple computer model reasonably predicted the pool radius of liquid hydrogen. However, it did not solve all the governing equations related to liquid hydrogen leakage, resulting in limitations in predicting the concentration distribution of liquid hydrogen.
The BAM (Federal Institute for Materials Research and Testing) conducted experiments to investigate the spread and evaporation of cryogenic hydrogen pools resulting from liquid hydrogen leakage, as well as the formation and dispersion of vapor clouds between buildings [16]. Additional computation was also conducted to investigate the behaviors of cryogenic hydrogen pools for the BAM’s experiments. The size of the hydrogen pool, the ground temperature, and the evaporation rate were measured when liquid hydrogen leaked from one corner of two buildings 23.9 m apart at approximately 0.4 kg/s for 2 min. The computations were qualitatively and quantitatively compared with the experimental behavior of the condensed cold vapor cloud near the leakage source, as well as the effect of buoyancy on the cloud at distant sites. The buildings blocked the wind; the wind direction had an important role in vapor cloud spread.
An experimental study of liquid hydrogen leakage was recently conducted by the FFI (Norwegian Defense Research Establishment) [17,18]. Liquid pool formation and evaporation, vapor cloud dispersion, and hydrogen concentrations in vapor clouds were investigated when liquid hydrogen leaked into an external space through a 1-inch-diameter pipe. Explosion tests were conducted in the open under defined conditions. Liquid hydrogen leakage and explosions in a machine room were also evaluated. The hydrogen vapor concentrations after leakage were measured at various locations and times. Explosion overpressures were also assessed for the explosion in a closed space.
Additionally, computational studies are important; liquid hydrogen evaporation has not been adequately explored. The experiment of NASA was computationally analyzed in terms of the leakage rate and duration, as well as the wind speed [19]. In their study, a liquid pool model was employed in FLACS computations for simulating large-scale liquid hydrogen pool leakages, considering pool size. The computations were conducted for leakage rates of 1.67, 9.5, and 10.3 kg/s. They investigated the downwind hazardous distance and the distribution of flammable concentrations in the hydrogen-air clouds formed under different leakage rate conditions. The results indicated that the leakage rate, duration, and wind speed all influence the distribution of hydrogen vapor clouds. Moreover, the release rate and duration had a greater impact on the shape of the flammable concentration distribution compared to wind speed.
The dynamics of liquid hydrogen release were computationally investigated, and the modeling process for liquid hydrogen release was described [20]. The study demonstrated that the pseudo-source approach for liquid hydrogen release yielded reasonable predictions for the temperature near the jet exit by appropriately selecting the release velocity. However, it overestimated the distance to reach a 15% hydrogen concentration compared to the experimental results.
A computational study was conducted on the leakage and explosion in a liquid hydrogen refueling station in China [21]. A pseudo-source model was established to compute the liquid hydrogen leakage. The optimal mass fractions for the pseudo-source model at the leakage exit boundary in the computations were determined by comparing them with the experimental temperature distribution. The distributions of hydrogen concentration, temperature, and overpressure during the explosion were investigated using the optimized pseudo-source model.
CFD was is employed to simulate the dispersion of liquid hydrogen for the experiment conducted by HSL [22]. This study investigated several factors that greatly influence modeling of the dispersion from the leaked liquid hydrogen. The computations with a homogeneous equilibrium model (HEM) was compared with those with a non-homogeneous equilibrium model (NHEM) to consider the slip effects of the non-vapor phase. The prediction performance for the steady temperatures around the leakage source obtained by those two models was evaluated by comparing with the HSL experiments.
A different HEM for handling liquid hydrogen release through two-phase flashing jets and pool spills has been developed as part of the FLACS model [23]. The model treats the liquid hydrogen release as two-phase flows in local thermal and kinematic equilibrium. The prediction performance for temperatures using the HEM was validated by comparing them with previous experiments. However, the HEM for the FLACS code is not yet available.
Recently, CFD studies were conducted for large-scale liquid hydrogen release [18,24]. In these studies, a pseudo-source model with limited air entrainment was utilized in the computations, and the distributions of hydrogen concentration and explosion overpressure were compared with selected FFI experiments [17]. The computational approach represented the very cold liquid hydrogen leak scenarios properly in the near field, and reproduced concentrations and temperatures observed in the experiments reasonably.
It has been acknowledged that achieving a precise model for the detailed near-field dynamics of liquid hydrogen release in CFD is impractical. Furthermore, the implementation of such a model cannot guarantee accuracy due to the highly complex nature of the phenomena, and there are too few proper experiments with low uncertainties available for validation [20]. Therefore, at this stage, it seems more appropriate to employ a simplified approach that can simulate the characteristics of liquid hydrogen release, rather than rigorously considering two-phase behaviors when analyzing the release of liquid hydrogen.
Here, we conducted a computational analysis of evaporation and dispersion following a liquid hydrogen leak from a storage tank using a previously established pseudo-source model, liquid pool model, and a hybrid model combining both. The prediction performance of each model for hydrogen concentration and temperature was evaluated by comparing the results with those from previous experiments [17]. Furthermore, we analyzed the effects of explosions on humans using an overpressure-impulse diagram when the released liquid hydrogen was ignited.

2. Numerical Methods

2.1. Numerical Methods and Conditions

We used the FLACS code ver. 20.2 of Gexcon [25]. We applied an unsteady, Reynolds-averaged Navier-Stokes (RANS) approach to the analysis of turbulent flow in a large space. The governing equations were the Favre-averaged mass conservation, momentum, energy, and species equations. The governing equations are solved with a finite volume method (FVM). The pressure and velocity are corrected by the SIMPLE method and this can be applicable for compressible flows. The FLACS adopts the standard k-ε turbulence model for the simulation of turbulent flows; the details have been published [25]. The simulated conditions were the same as those of the experimental TEST 1 and TEST 3 in terms of liquid hydrogen leakage, evaporation, and dispersion in the FFI report [17]. Liquid hydrogen was released vertically onto the ground at a height of 0.5 m with mass flow rates of 0.225 and 0.73 kg/s for 13 and 15 mins, respectively, from a 1-inch-diameter pipe of a liquid hydrogen storage tank. Table 1 shows the release and weather conditions for each leakage case in the experiments. The computations were conducted using identical release and weather conditions to simulate the leakage of liquid hydrogen.
Figure 1 shows a schematic of the computational domain, the location of leakage source, and the surroundings. The wind direction was defined by an angle θ measured counterclockwise from the east. In Figure 1, x indicates the location of hydrogen leakage; an ISO container of dimensions 13 × 2.5 × 5.2 -m3 served as an obstacle. The atmospheric pressures, ambient temperatures, and dry air consists of 21% oxygen and 79% nitrogen by volume were preset for the entire solution domain and Boundaries A to D. The wind speed and direction shown in Table 1 were also imposed to the Boundaries A to D. The temperature of ground surface was set to be the same as the ambient temperature. Apart from the initial state, there was no change in hydrogen concentration and vapor cloud temperature in the computational results as time progressed, and the computations were carried out up to 800 s for each leakage case.
Liquid hydrogen was tank-stored at approximately 20 K; after leakage, it rapidly vaporized and dispersed. Thus, the phases of leaked hydrogen can be gas and liquid. The FLACS code simulates gaseous flow and liquid pool with pseudo-source model and liquid pool model, separately when hydrogen is released [25]. After the release of liquid hydrogen, a portion rapidly vaporizes, and the remaining liquid hydrogen forms a pool from which vapor emanates. To date, the physical models for gaseous release and liquid pool formation used in FLACS have not been rigorously validated for liquid hydrogen. Even models that can consider two-phase behavior, such as HEM, have been tested for liquid hydrogen leakage [22,23], but they have not been implemented in FLACS. Thus, we utilized two distinct models: the pseudo-source model and the liquid pool model, as well as a hybrid model that considers both simultaneously, to simulate liquid hydrogen leaks. When using the pure pseudo-source model, all leaked hydrogen was assumed to be in a gaseous state.
We further compared the predictive performance of the pseudo-source model and the pool model for liquid hydrogen leaks by varying the fraction parameter χ. χ represents the ratio of utilizing the pseudo-source model to the liquid pool model based on the leaked mass flow rate. Specifically, χ = 1.0 indicates that the pseudo-source model is applied to the entire mass flow rate of leaked liquid hydrogen, while χ = 0.0 implies the use of the liquid pool model for the entire mass flow rate. Likewise, χ = 0.6 signifies that the pseudo-source model was applied to only 60% of the mass flow rate of leaked liquid hydrogen. When applying the pure pseudo-source model (χ = 1.0) for liquid hydrogen leakage, the temperature of released hydrogen was set to 20.5 K slightly above the boiling point of hydrogen.
In this study, we opted for 60% utilization of the pseudo-source model (χ = 0.6), considering previous research [20,21] that achieved reasonable results using the pseudo-source model to simulate the dispersion resulting from liquid hydrogen leaks. The equations and numerical procedures for these models can be found in the referenced publications [19,25].
Gas dispersion into the atmosphere is substantially affected by turbulence. Pasquill identified atmospheric stabilities ranging from Class A (very unstable) to Class F (stable); stability is affected by wind speed, cloud cover, and solar radiation [26]. This classification is now standard when assessing material dispersions [27]. Table 2 lists the Pasquill stability classes according to weather conditions. Both the computational and experimental wind speeds for cases 1 and 2 were 3.2 and 5.8 m/s, respectively as shown in Table 1. As a result, we applied the Pasquill Class C and D criteria (Day, moderate sun), respectively, to represent the stability conditions in the FLACS computations, taking into account the weather conditions on the experimental days.

2.2. Grid System and the measurement locations

Figure 2 shows a schematic of the three-dimensional computational grid. The +X-axis runs east and the +Y-axis runs north. The FLACS code uses Cartesian coordinates; the pipe must be rectangular. If a 1-inch-diameter leakage source is rendered square, the length of a side is 2.25 cm. During FLACS computation, the grid size should be set so that the leakage source area does not exceed 1.25-fold of grid area. Because the pipe diameter is very small compared with the computational domain, grid sides of 2.25 cm in all directions were used to divide a 1 × 1 × 1-m3 region near the source of leakage, but the size was extended to 10 m in more remote regions. The stretched grid system is shown in Figure 2 (b).
Parallel computation was conducted using a message-passing interface with 40 cores running on a PC with an Intel Xeon Silver 4214 CPU @ 2.20 GHz. The computation time, depending on the number of grids, was approximately 48-76 hours of wall clock time for each case based on the optimized grid system.
Figure 3 shows the locations where hydrogen concentrations were measured numerically based on the radius (R) from the leakage point. The angle (θ) represents the counterclockwise rotation angle in reference to the eastward direction. The wind is blowing from the southwest, corresponding to 259 and 246° counterclockwise from the east, respectively, as shown in Table 1. Specifically, hydrogen concentrations were measured at radii of 30, 50, and 100 m, and at heights (H) of 0.1, 1.0, and 1.8 m above the ground. The sensing locations were categorized based on radius, height, and angle.

3. Results and Discussion

3.1. Results and Discussion

Prior to computation, we explored the grid sensitivity of the results. The minimum grid size was 2.25 cm in the 1 × 1 × 1-m3 region (Region I) near the leakage source, considering the small pipe diameter. For the 20 × 20 × 20-m3 space of the intermediate Region II (outside of Region I), around the leakage source, the grid size was gradually enlarged from 2.25 cm to 0.2, 0.3, 0.5, and 1.0 m. In the outermost Region III, the grid size gradually increased to a maximum of 10 m. Table 3 lists the grid sizes and numbers for Region II, as well as the computation times necessary for each grid system. These times were 132 h for the smallest grid (0.2 m) and 48 h for the largest grid (1.0 m).
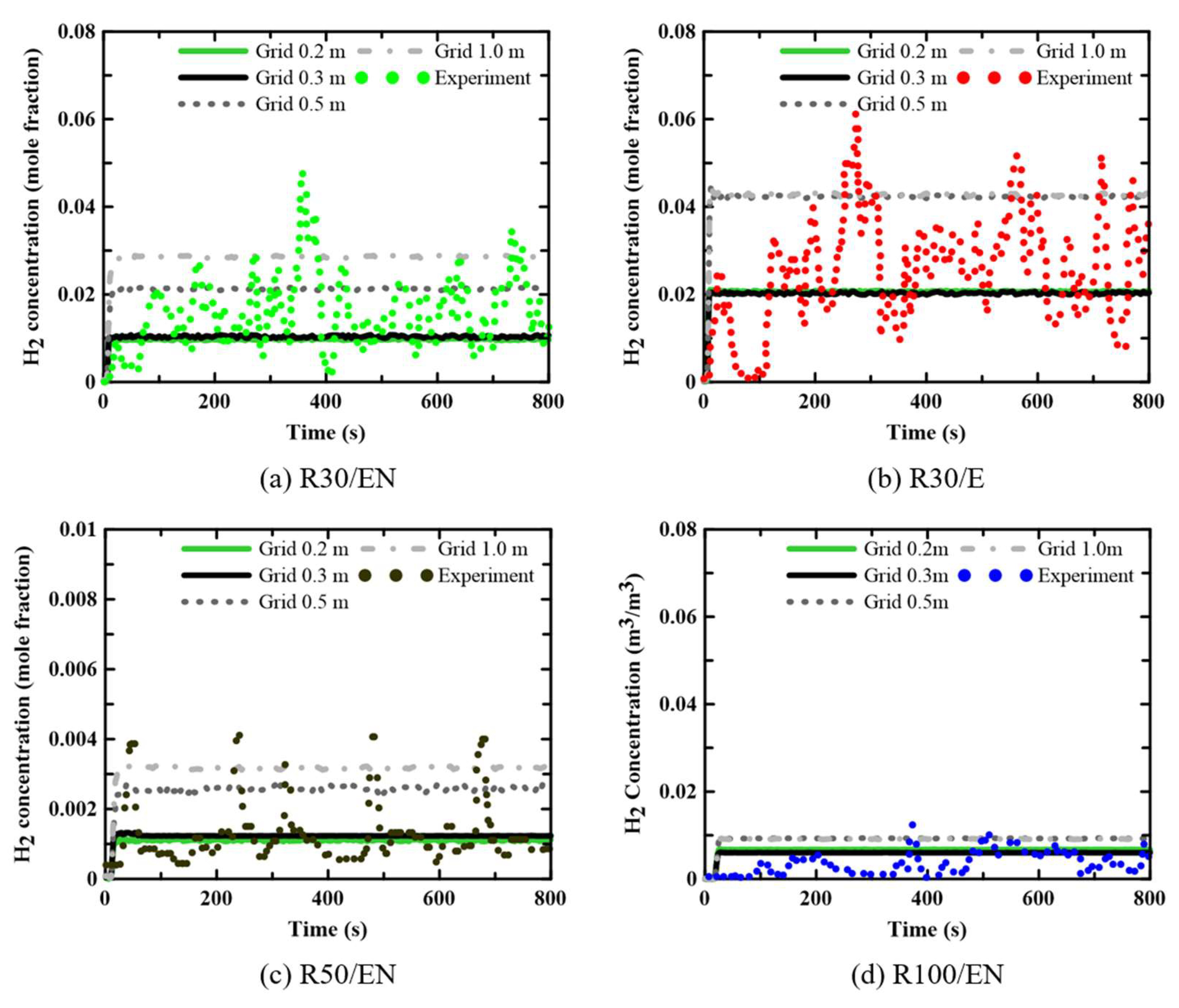
Figure 4 shows the computed and experimental variations in hydrogen concentration (the mole fractions) at radii of 30 and 50 m for a leaked mass flow rate (ṁ) of 0.73 kg/s. Although the experimental concentrations considerably changed over time, the computed concentrations were nearly constant except initially. The computational trend toward a constant hydrogen concentration over time reflects the RANS approach toward turbulent flow simulation. For grid sizes of 0.2 and 0.3 m for Region II, the computational results were similar, and the hydrogen concentrations were within the experimental ranges. Considering these data and the computation times shown in Table 3, a grid of 0.3 m for Region II was appropriate; we used this grid in subsequent analyses. Although not shown here, it was confirmed that the computational results were not significantly affected by the grid size in the outermost Region III.

3.2. Prediction performance of three models for the liquid hydrogen release

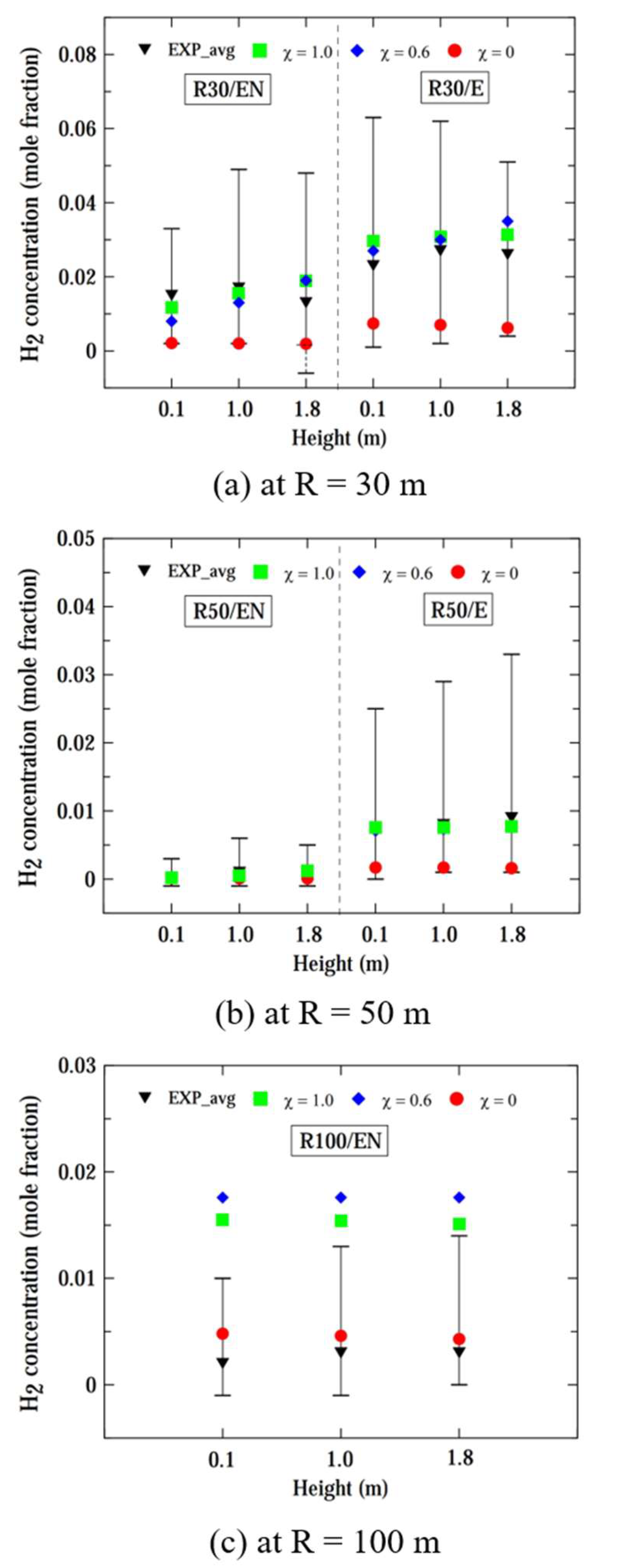
Figure 5 shows the computed and experimental hydrogen concentrations at radii of 30, 50, and 100 m, and heights of 0.1, 1.0, and 1.8 m, considering a smaller leaked mass flow rate (ṁ) of 0.225 kg/s. The black inverted triangular symbol represents the experimentally obtained time-averaged hydrogen concentration and the fluctuation bar indicates the maximum and minimum limits of concentration variation over time for the experimental concentration. The computed concentrations remained relatively constant, while the experimental concentrations exhibited significant fluctuations over time, as previously mentioned in Figure 4.
For the locations of R30/E and R50/E, slightly offset from the wind direction, it can be observed that the computed values from all models were nearly identical and these computed values were close to the lower limits of experimental concentrations. For the R30/EN location, the pseudo-source model (χ = 1.0) and hybrid model (χ = 0.6) overestimated the experimental concentration, while the computed concentration by the liquid pool model (χ = 0.0) relatively well matched the experimental values. For the R50/EN location, the results from the three models were in the range of experimental fluctuations, but the pseudo-source model predicts the highest hydrogen concentration, while the liquid pool model predicts the lowest. For R = 100 m, the computed results were similar to each other, and fell within the fluctuation limits of experimental concentrations.
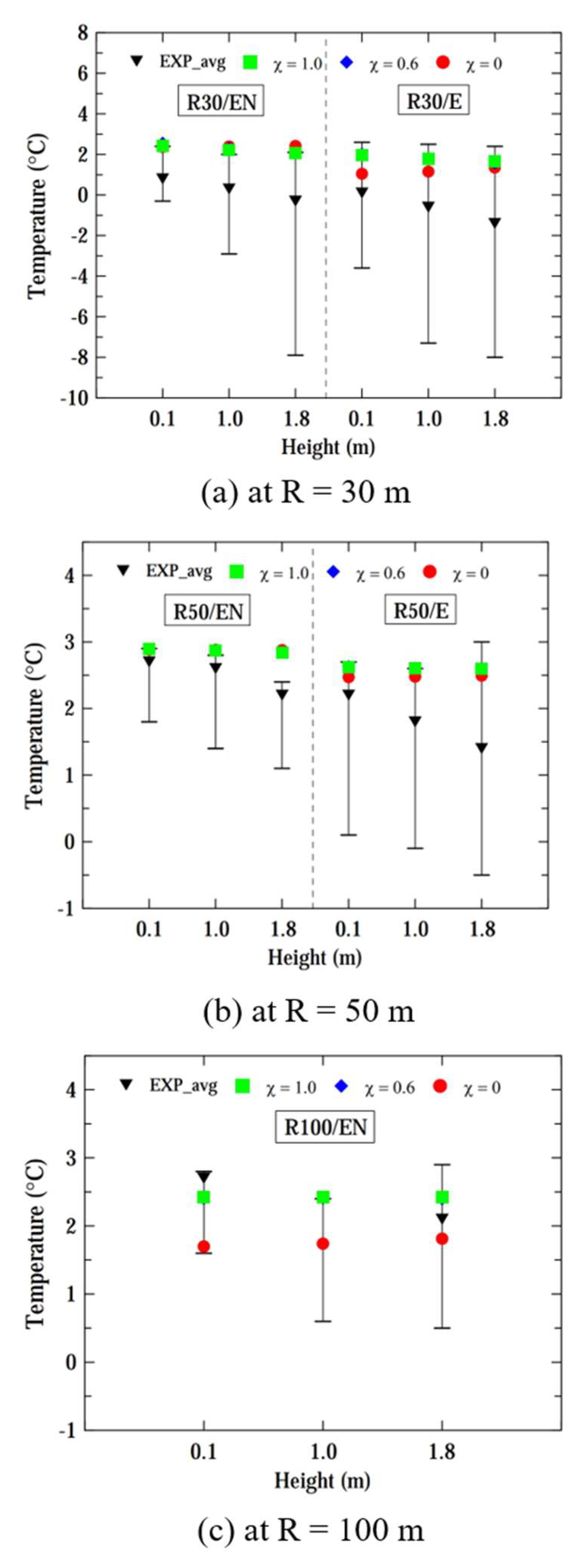
Figure 6 shows the computed and experimental temperatures of vapor clouds at radii of 30, 50 and 100 m for a case of ṁ = 0.225 kg/s. For all locations, the temperatures computed by three models fell within the fluctuation limits of experimental temperatures. The computed results from the three models were very similar for all locations, except that the temperature computed by the liquid pool model was slightly lower than those from the other two models for the R30/EN location. Considering the results of Figure 5 and Figure 6, it can be concluded that the liquid pool model performs better than the other two models for a smaller mass flow rate of ṁ = 0.225 kg/s.
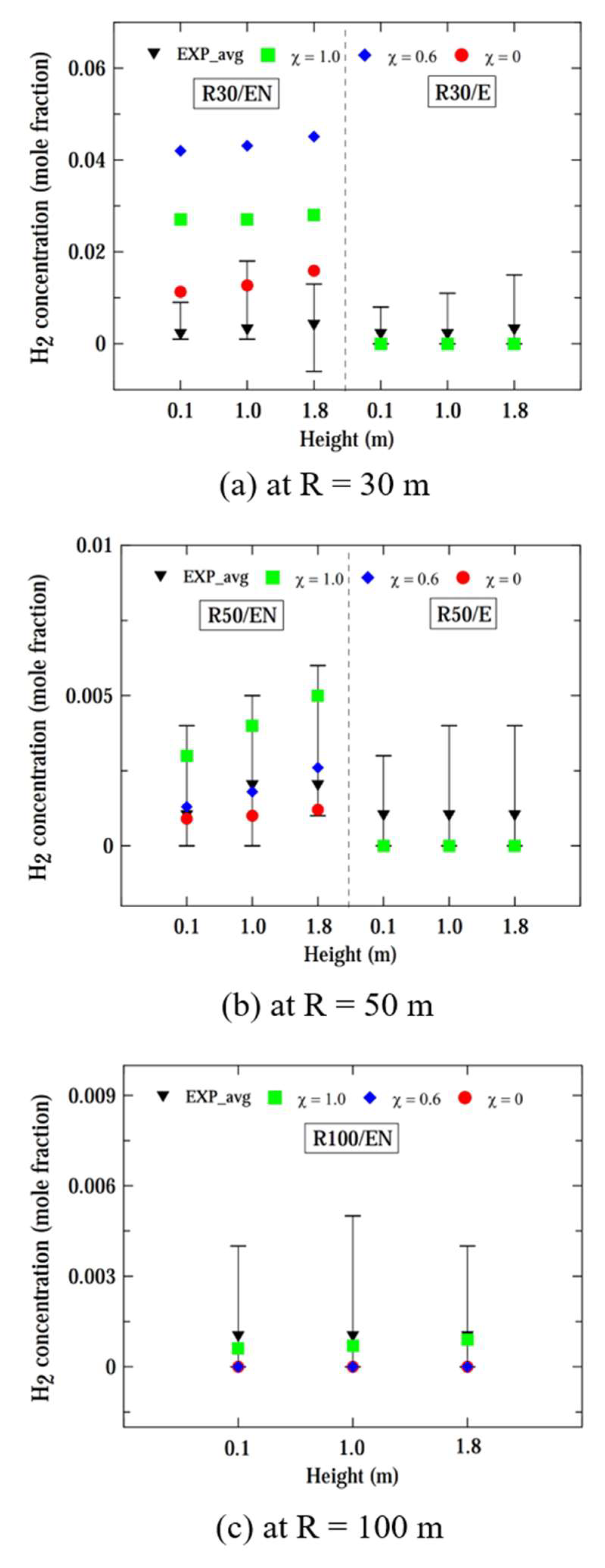
Figure 7 shows the computed and experimental hydrogen concentrations at radii of 30, 50, and 100 m, and heights of 0.1, 1.0, and 1.8 m, considering a leaked mass flow rate of 0.73 kg/s. For all radii and heights, the hydrogen concentrations were similar for χ = 1.0 and 0.6, whereas the concentration for χ = 0.0 was lower than the results predicted by the other two models. At radii of 30 and 50 m from the leak source, the simulation results of the pseudo-source model and hybrid model closely matched the experimental concentration near the time-average value. However, the computed concentrations for χ = 0.0 were closer to the minimum limits of experimental concentrations at distances of R ≤ 50 m. When considering locations at R ≤ 50 m with various directions, the results computed by all three models demonstrated reasonable prediction performance.
At location R50/EN aligned with the wind direction, the computed concentration more closely aligned with the experimental data compared to location R50/E. It is presumed that at a farther radial distance of R = 50 m, the location R50/EN is more directly influenced by the wind, resulting in a narrow range of fluctuations in hydrogen concentration compared to location R50/E.
At locations with R = 100 m, the concentrations for χ = 0.0 closely matched those of the experiment. Consequently, it was observed that the pseudo-source model and hybrid model provided better predictions for the experimental hydrogen concentration within a radial distance of 50 m. However, at a larger distance of R = 100 m, the prediction performance of both the pseudo-source model and hybrid model decreased compared to that at distances closer to the source of the leak.
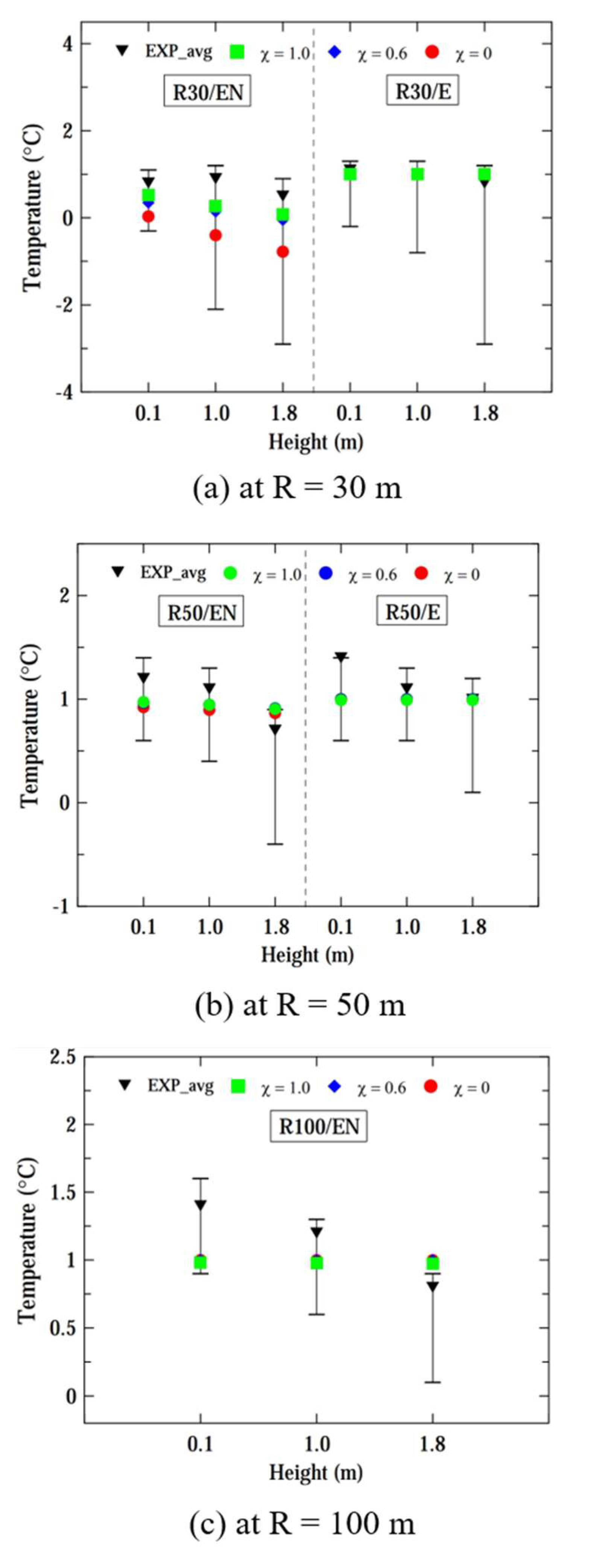
Figure 8 shows the computed and experimental temperatures of vapor clouds at radii of 30, 50, and 100 m, considering a case of ṁ = 0.73 kg/s. Across all locations, the disparity in the prediction performance for temperatures computed by the three models was not significant within a distance of R ≤ 50 m. Overall, the computed temperatures fell within the range of experimental temperature fluctuations, but the computed results were closer to the upper limits of the fluctuation ranges. However, the computed temperatures computed by the liquid pool model were lower than those obtained by the other two models at R = 100 m.
Considering both the hydrogen concentration and ground temperature computed by the three models, the pseudo-source model and hybrid model appear to be more suitable for computing the dispersion for ṁ = 0.73 kg/s, except at R = 100 m, which is far from the source of the leak.
Hereinafter, considering the prediction performances for hydrogen concentration and vapor clouds temperature, we will describe the results using the pseudo-source model for a case of ṁ = 0.73 kg/s and the liquid pool model for a smaller mass flow rate case of ṁ = 0.225 kg/s.
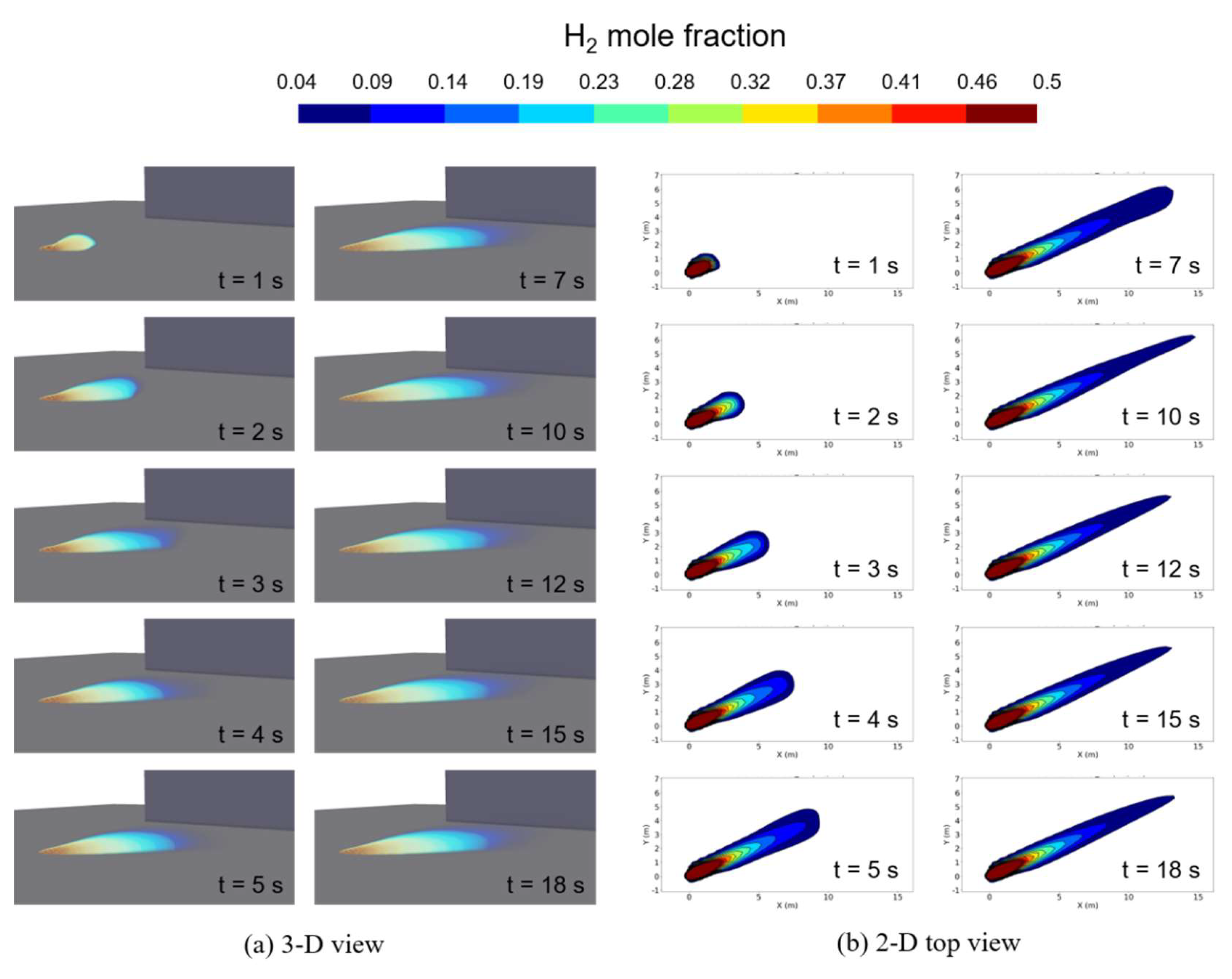
Figure 9 shows the 3-D and 2-D top views of the hydrogen concentration distribution on the ground obtained from the computation with the pseudo-source model for a case of ṁ = 0.225 kg/s. These visualizations effectively illustrate the process of hydrogen vapor dispersion as time progresses from the moment of leakage. From the initiation of the leak, hydrogen vapor dispersed mainly in the direction of the wind. However, comparing with the case of ṁ = 0.73 kg/s (shown in Figure 10), the shape of hydrogen vapor clouds in the wind direction was narrower, and a V-shaped hydrogen vapor distribution was not observed from the 3-D and 2-D views.
From the 3-D distribution of hydrogen concentration, it became apparent that the approximate shape of hydrogen vapor clouds remained relatively unchanged after about 18 s from the start of the leak. This shape was also identifiable in the 2-D top view. Additionally, the distribution of hydrogen vapor plumes does not exhibit a shape with a noticeable end due to buoyancy effects. The wind speed for this condition was set to be 3.2 m/s. From the previous work, the hydrogen vapor cloud becomes buoyant at wind speed of 3.0 m/s or less [11,19]. While the wind speed meets the conditions for hydrogen vapor clouds to become buoyant, it is presumed that the reason hydrogen vapor clouds do not exhibit buoyancy characteristics is due to the very small amount of leaked liquid hydrogen.
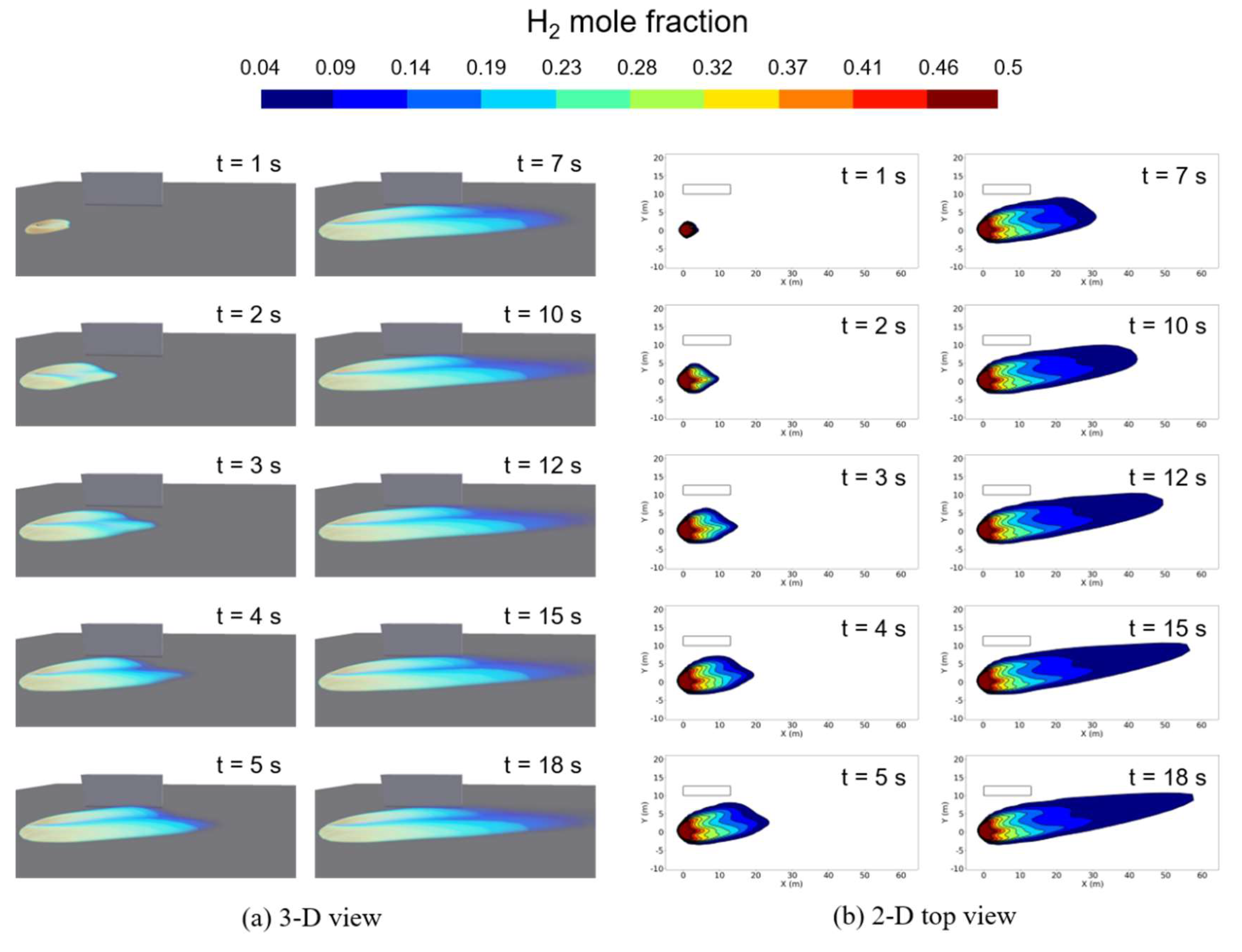
Figure 10 shows the 3-D and 2-D top view of the hydrogen concentration distribution on the ground obtained from the computation with the liquid pool model for a case of ṁ = 0.73 kg/s. The figures also effectively illustrate the process of hydrogen vapor dispersion for a larger leaked mass flow rate condition. From the initiation of the leak, hydrogen vapor dispersed mainly in the direction of the wind. In the 3-D view, it can be observed that hydrogen vapor clouds form a V-shaped distribution above the elliptical flat distribution along the wind direction. Furthermore, even as hydrogen dispersed after the leak, the vapor cloud's shape displayed minimal vertical dispersion due to buoyancy. The wind speed for this condition was set to be 5.2 m/s. This observation aligns well with previous findings [11,19], indicating that as wind speeds exceed 5.0 m/s, the vapor cloud dispersion tend to stay close to the ground.

3.3. Explosion of hydrogen vapor clouds

In this section, we investigated the explosion characteristics in cases where the vapor cloud, generated from the leaked liquid hydrogen, was ignited even though no ignition was introduced in the experiment. The ignition source was applied at a location where the equivalence ratio was approximately 0.8 to initiate the vapor cloud explosion since the hydrogen concentration was excessively high near the leak source of liquid hydrogen. For both hydrogen leakage flow conditions of ṁ = 0.225 and 0.73 kg/s, the ignition source was introduced 20 s after the liquid hydrogen began to leak.
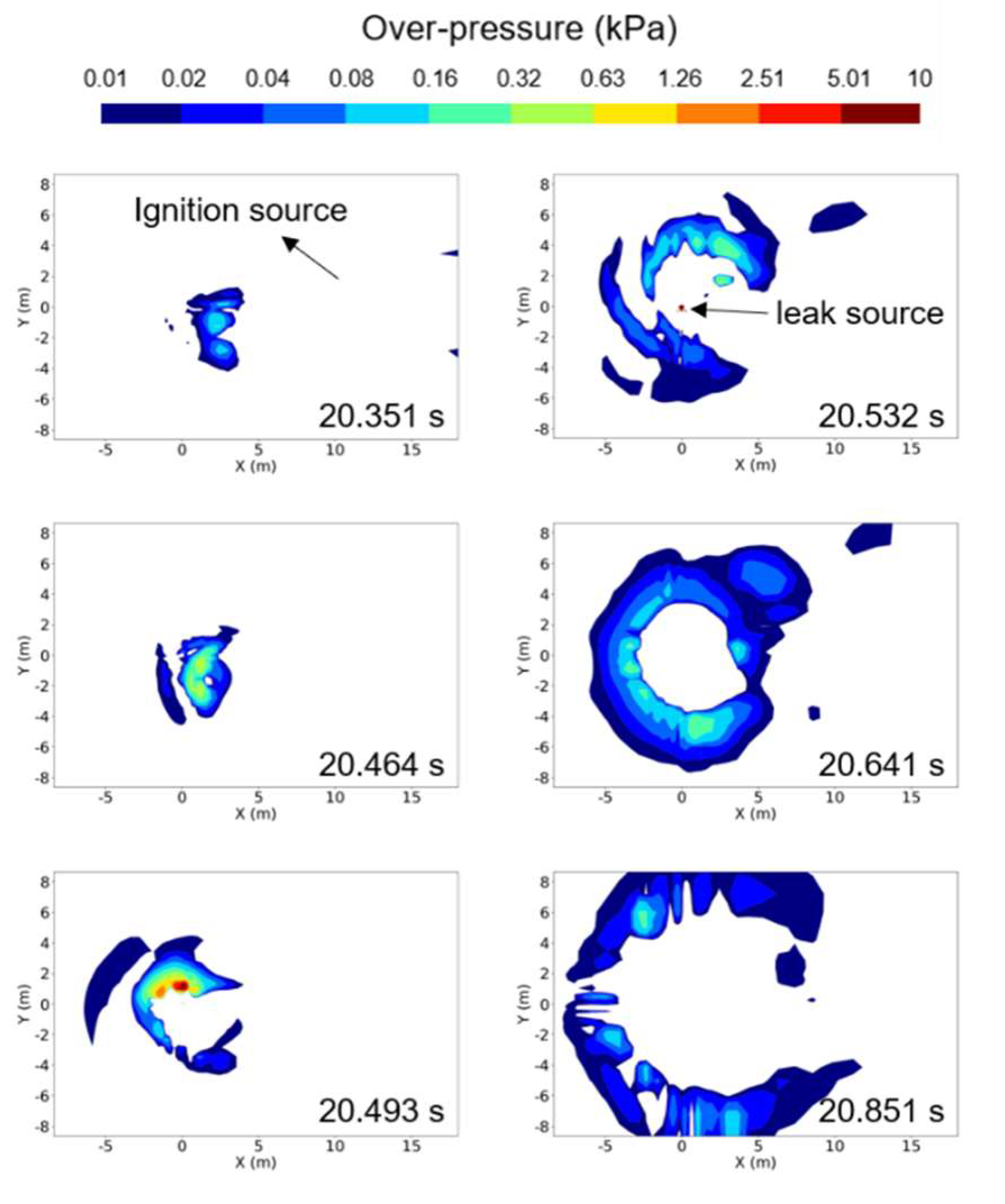
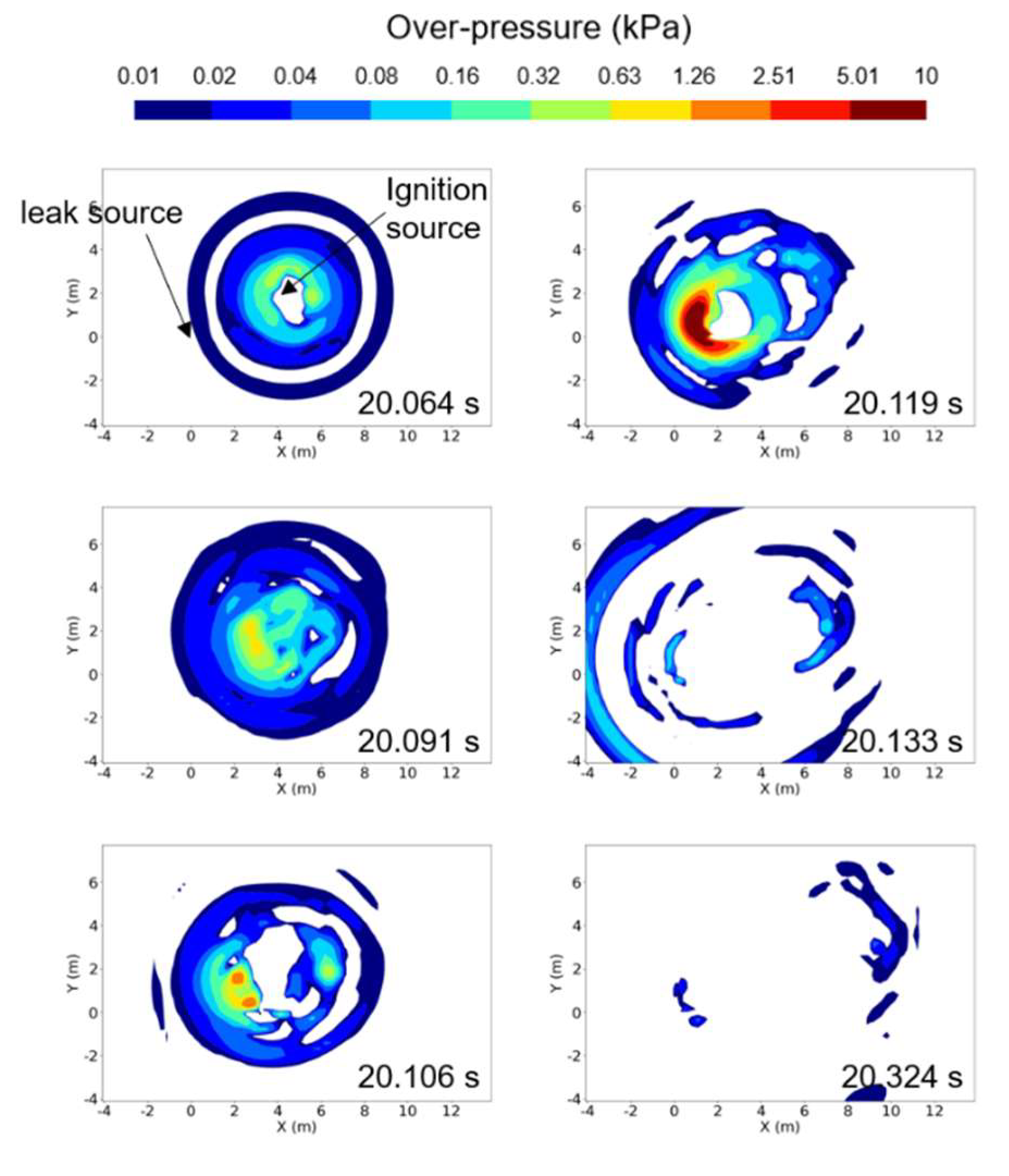
Figure 11 shows the overpressure distribution within a cross section of Z = 0.4 m during the explosion of a hydrogen vapor cloud, for a case of ṁ = 0.225 kg/s. In the figure, the coordinates (X, Y) with a position of (0 m, 0 m) represent the origin of the leak. For this condition, the ignition source was located at coordinates (4.0 m, 2.0 m) at the cross section of Z = 0.2 m. The highest overpressure was observed in the cross section of Z = 0.4 m, despite the ignition source being positioned at Z = 0.2 m. High overpressure began to generate near the ignition source and propagated in all directions, forming a maximum overpressure region near the leak source at approximately 20.119 s. At this time, the maximum overpressure recorded was 38.3 kPa, which was lower than that for a case of ṁ = 0.73 kg/s with a larger leakage mass flow rate. After the maximum overpressure was reached, it rapidly propagated in all directions and dissipated.
12 shows the overpressure distribution in a cross section of Z = 0.2 m. The highest overpressure was recorded in this section when the vapor cloud, resulting from a leak in liquid hydrogen, exploded for the case of ṁ = 0.73 kg/s. Similar to Figure 11, the coordinates (X, Y) with a position of (0 m, 0 m) represent the origin of the leak, while the coordinates (6.5 m, 4.2 m) denote the position of the ignition source. Following ignition, the explosion rapidly progressed, and at approximately 20.493 s after the onset of leakage, the maximum overpressure region was identified near the leak source, reaching a peak overpressure of 428 kPa. Subsequently, the overpressure rapidly propagated in all directions for a brief duration and gradually decreased.
Preprints 88468 g012
Figure 12. Computed overpressure distributions at the cross section of Z = 0.2 m, for a case of ṁ = 0.73 kg/s.
Figure 12. Computed overpressure distributions at the cross section of Z = 0.2 m, for a case of ṁ = 0.73 kg/s.
Preprints 88468 g012
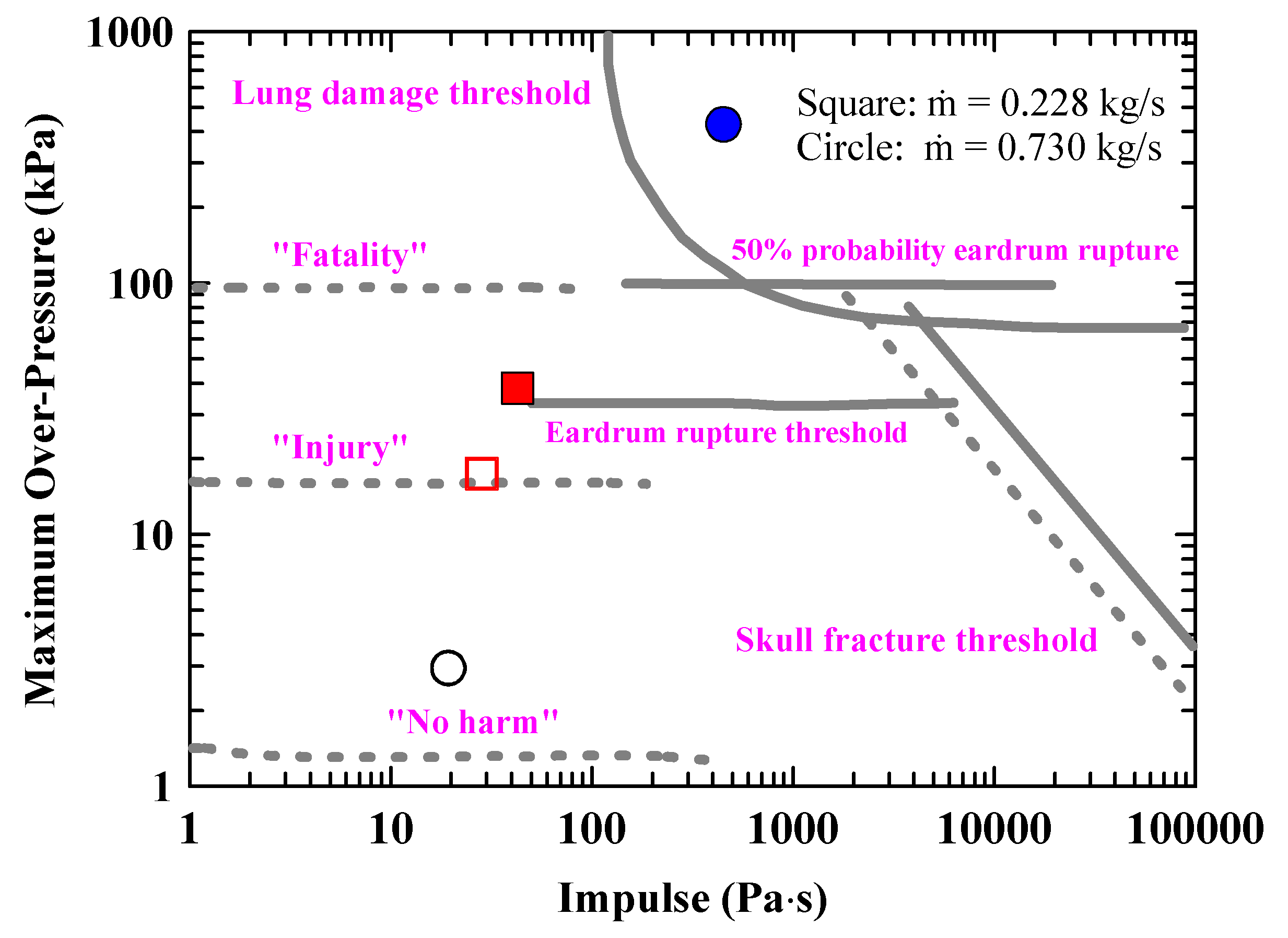
Figure 13 shows the overpressure-impulse diagram and damage thresholds for human by explosion [28]. The overpressures and impulses were recorded at the locations of the maximum overpressure point and ignition point to assess the hazards to humans resulting from the explosions for the cases of ṁ = 0.225 and 0.73 kg/s. When an explosion occurs under the condition of a larger leaked mass flow rate, ṁ = 0.73 kg/s, the impact of the explosion is not severe enough to cause significant injuries near the ignition source. However, humans can still be strongly affected by the maximum overpressure and impulse, potentially resulting in fatal outcomes. Furthermore, in the case of a smaller leaked mass flow rate, ṁ = 0.225 kg/s, injuries can occur near the ignition source, and at the point of maximum overpressure, the damage can be severe enough to rupture the eardrum. As confirmed by the results, it is important to note that the damage caused by the explosion varies depending on the mass flow rate of the leaked liquid hydrogen. However, the magnitude and distribution of the explosion overpressure may vary depending on the location of the ignition source. In this study, the hydrogen vapor cloud was ignited 20 s after the liquid hydrogen began to leak, inducing the explosion. However, if the duration of the liquid hydrogen leakage is longer before ignition, resulting in a larger amount of leaked hydrogen, it is estimated that the overpressure caused by the explosion would increase further.

5. Conclusions

We utilized the FLACS code to computationally analyze the dispersion of a hydrogen vapor cloud resulting from liquid hydrogen leakage in an FFI experiments. The dispersion process was investigated using a pseudo-source model, a liquid pool model, and a hybrid model that combines both. We compared the computational results with experimental data regarding hydrogen vapor cloud concentration and temperatures to evaluate the prediction performance of each model. Additionally, we explored the potential impact of the explosion on humans when the leaked liquid hydrogen was ignited. Here are the key findings:
Hydrogen concentrations computed were relatively constant at all tested locations, except initially, while the experimental data showed significant variation over time. Predicted hydrogen concentrations were most accurate in the wind direction.
For a leaked mass flow rate of 0.73 kg/s, computational results closely matched experimental concentrations at a distance of 30 m from the leak source. Predictions were reasonable even at a distance of 50 m. The pseudo-source model and hybrid model performed similarly at distances of 30 and 50 m. However, at a distance of 100 m, these models slightly overpredicted, whereas the liquid pool model provided a more accurate prediction. The computed temperatures for each distance demonstrated good prediction, roughly within the range of experimental variations.
For a smaller leaked mass flow rate of 0.225 kg/s, the computations by pseudo-source model and hybrid model overestimated the experimental concentrations while the liquid pool model predicted the hydrogen concentration reasonably at a distance of 30 m from the leak source. Predictions by three models were generally reasonably for distances of 50 and 100 m. The computations also demonstrated reasonably prediction of the experimental temperatures for all locations.
In summary, for relatively large leaked mass flow rate conditions, the pseudo-source model or hybrid model appeared more appropriate for computation. Conversely, for small leaked mass flow rate conditions, the liquid pool model seemed more suitable.
Regarding explosion analyses, it is evident that larger mass flow rates (ṁ = 0.73 kg/s) can lead to maximum overpressure and impulse, potentially resulting in fatal outcomes. The impact of the explosion near the ignition source is less severe in this scenario. On the other hand, for lower mass flow rates (ṁ = 0.225 kg/s), injuries near the ignition source are possible, and severe eardrum damage can occur at the maximum overpressure point.

Author Contributions

Conceptualization, S.Y.C. and C.B.O.; methodology, S.Y.C.; validation, S.Y.C. and C.B.O.; investigation, K.H.D. and B.I.C.; writing—original draft preparation, S.Y.C. and C.B.O.; writing—review and editing, C.B.O.; project administration, K.H.D. and B.I.C.; funding acquisition, C.B.O.; All authors have read and agreed to the published version of the manuscript.

Funding

Please add: This work was supported by the principal research programs funded by the Korea Institute of Machinery and Materials (KIMM) of Korea (Development of the core equipment for liquid hydrogen supply systems).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The manuscript was prepared by revising and improving the contents of the first author’s thesis.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Alazemi, J.; Andrews, J. Automotive hydrogen fueling stations. Int. Rev. 2015, 48, 483–499. [Google Scholar]
  2. Apostolou, D.; Xydis, G. A literature reciew on hydrogen refueling stations and infrastructure. Current status and future prospects., Renew. Sust. Energy. Rev. 2019, 113, 109292. [Google Scholar] [CrossRef]
  3. Maus, S.; Hapke, J.; Ranong, C.N.; Wüchner, E.; Friedlmeier, G.; Wenger, D. Filling procedure for vehicles with compressed hydrogen tanks. Int. J. Hydrogen Energy 2008, 38, 4612–4621. [Google Scholar] [CrossRef]
  4. Li, Z.; Gao, D.; Chang, L.; Liu, P.; Pistikopoulos, E.N. Hydrogen infrastructure design and optimization: A case study of China. , Int. J. Hydrogen Energy 2008, 33, 5875–5286. [Google Scholar] [CrossRef]
  5. Miguel, N.; Acosta, B.; Baraldi, D.; Melideo, R.; Cebolla, R.O.; Moretto, P. The role of initial tank temperature on refueling of on-board hydrogen tanks. , Int. J. Hydrogen Energy 2016, 41, 8606–8615. [Google Scholar] [CrossRef]
  6. Barthelemy, H.; Weber, M.; Barbier, F. Hydrogen storage: Recent improvements and industrial perspectives. Int. J. Hydrogen Energy 2017, 42, 7254–7262. [Google Scholar] [CrossRef]
  7. Satyapal, S.; Petrovic, J.; Read, C.; Thomas, G.; Ordaz, G. The U.S. department of energy’s national hydrogen storage project: Progress towards meeting hydrogen-powered vehicle requirements. Cata. Today 2007, 120, 246–256. [Google Scholar] [CrossRef]
  8. Zheng, J.; Liu, X.; Xu, P.; Liu, P.; Zhao, Y.; Yang, J. Development of high pressure gaseous hydrogen storage technologies. Int. J. Hydrogen Energy 2012, 37, 1048–1057. [Google Scholar] [CrossRef]
  9. Zheng, J.; Guo, J.; Yang, J.; Zhao, Y.; Zhao, L.; Pan, X.; Ma, J.; Zhang, L. Experimental and numerical study on temperature rise within a 70 MPa type III cylinder during fast refueling. Int. J. Hydrogen Energy 2013, 38, 10956–10962. [Google Scholar] [CrossRef]
  10. Gentilleau, B.; Touchard, F.; Grandidier, J.C. Numerical study of influence of temperature and matrix cracking on type IV hydrogen high pressure storage vessel behavior. Compos. Struct. 2014, 111, 98–110. [Google Scholar] [CrossRef]
  11. Wijayanya, A.T.; Oda, T.; Purnomo, C.W.; Kashiwagi, T.; Aziz, M. Liquid hydrogen, nethylcyclohexane, and ammonia as potential hydrogen storage: Comparison review. Int. J. Hydrogen Energy 2019, 44, 15026–15044. [Google Scholar] [CrossRef]
  12. Mori, D.; Hirose, K. Recent challenges of hydrogen storage technologies for fuel cell vehicles. Int. J. Hydrogen Energy 2009, 34, 4569–4574. [Google Scholar] [CrossRef]
  13. Witcofski, R.D.; Chirivella, J.E. Experimental and analytical analysis of the mechanisms governing the dispersion of flammable clouds formed by liquid hydrogen spills. Int. J. Hydrogen Energy 1984, 9, 425–435. [Google Scholar] [CrossRef]
  14. Royle, M.; Willoughby, D. Release of unignited liquid hydrogen. RR986; HSE Report; Health and Safety Lab., 2014. [Google Scholar]
  15. Veffondern, K.; Dienhart, B. Pool spreading and vaporization of liquid hydrogen. Int. J. Hydrogen Energy 2007, 32, 2106–2119. [Google Scholar] [CrossRef]
  16. Stathatas, J.C.; Venetsanos, A.G.; Bartzis, J.G.; Würtz, J.; Schmidtcehn, U. Analysis of data from spilling experiments performed with liquid hydrogen. J. Hazard. Mat. 2000, 77, 57–75. [Google Scholar] [CrossRef] [PubMed]
  17. Anaeby, J.; Gjesdal, T.; Voie, Ø. Large scale leakage of liquid hydrogen (LH2) – tests related to bunkering and maritime use of liquid hydrogen; Norwegian Defence Research Establishment (FFI), 2021; 20/03101. [Google Scholar]
  18. Hansen, O. R.; Hansen, E. S. CFD-modelling of large-scale LH2 release Experiments. Chem. Eng. Trans. 2022, 90, 619–624. [Google Scholar]
  19. Holborn, P.G.; Benson, C.M.; Ingram, J.M. Modelling hazardous distances for large-scale liquid hydrogen pool releases. Int. J. Hydrogen Energy 2020, 45, 23851–23871. [Google Scholar] [CrossRef]
  20. Hansen, O. R. Liquid hydrogen releases show dense gas behavior. Int. J. Hydrogen Energy 2020, 45, 1343–1358. [Google Scholar] [CrossRef]
  21. Yuan, W.; Li, J.; Zhang, R.; Li, X.; Xie, J.; Chen, J. Numerical investigation of the leakage and explosion scenarios in China’s first liquid hydrogen refueling station. Int. J. Hydrogen Energy 2022, 47, 18786–18798. [Google Scholar] [CrossRef]
  22. Giannissi, S.G.; Venetsanos, A.G. Study of key parameters in modeling liquid hydrogen release and dispersion in open environment. Int. J. Hydrogen Energy 2018, 43, 455–467. [Google Scholar] [CrossRef]
  23. Ichard, M.; Hansen, O. R.; Middha, P.; Willoughby, D. CFD computations of liquid hydrogen releases. Int. J. Hydrogen Energy 2012, 37, 17380–17389. [Google Scholar] [CrossRef]
  24. Hansen, O. R.; Hansen, E. S. CFD-modelling of large-scale LH2 release and explosion experiments. Proc. Safety Environ. Protec. 2023, 174, 376–390. [Google Scholar] [CrossRef]
  25. Gexcon AS, Co. FLACS-CFD v20.1 User’s Manual; 2020. [Google Scholar]
  26. Pasquill, F. The estimation of the dispersion of windborne material. Meteorol. Magaz. 1961, 90, 33–49. [Google Scholar]
  27. Sutherland, R.A.; Hansen, F.V.; Bach, W.D. A quantitative method for estimating pasquill stability class from windspeed and sensible heat flux density. Boundary-Layer Meteorol. 1986, 37, 357–369. [Google Scholar] [CrossRef]
  28. Molkov, V.; Kashkarov, S. Blast wave from a high-pressure gas tank rupture in a fire: Stand-alone and under-vehicle hydrogen tanks. Int. J. Hydrogen Energy 2015, 40, 12581–12603. [Google Scholar] [CrossRef]
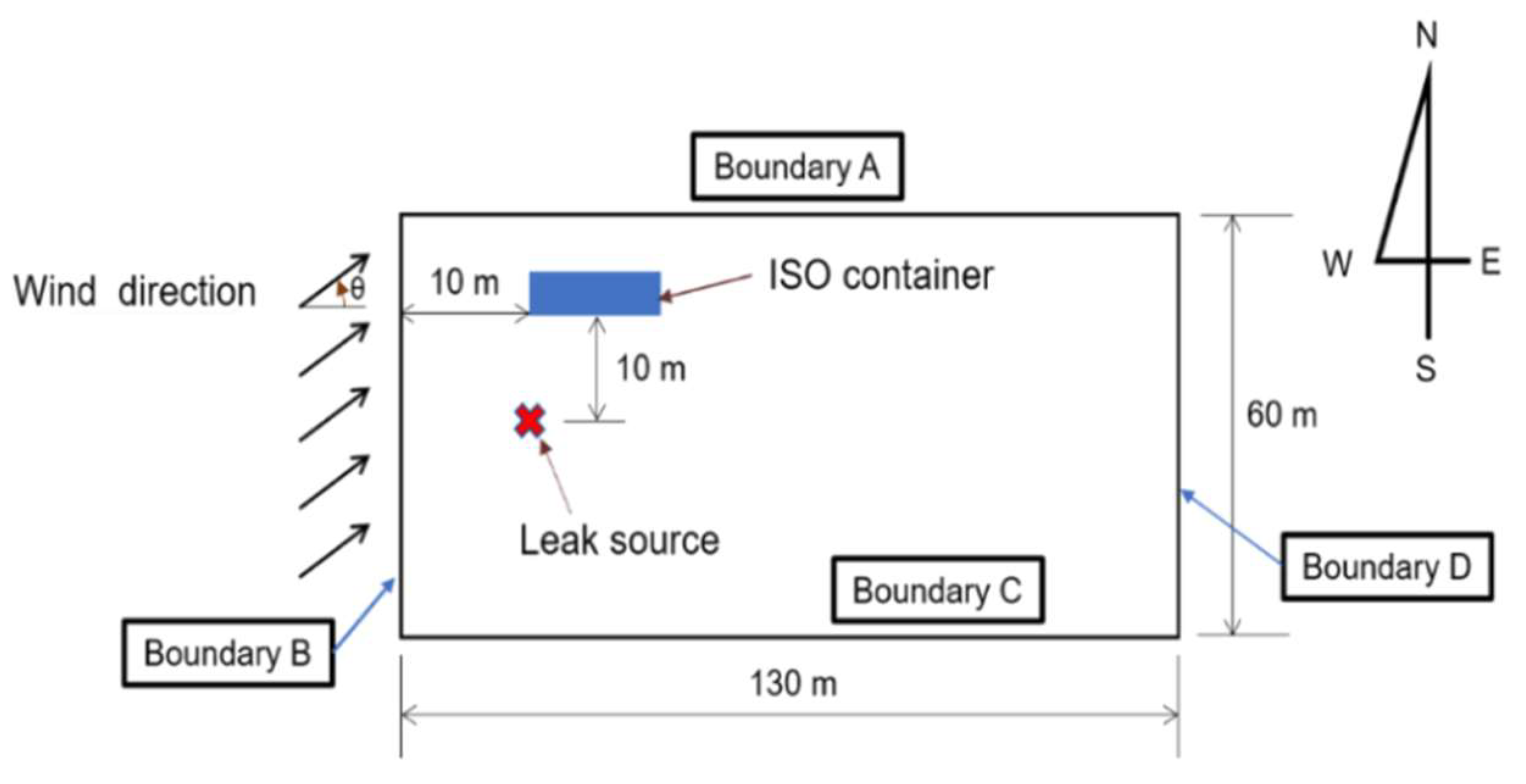
Preprints 88468 g001
Figure 1. Schematic of the computational domain showing the geometries of the leak source, obstacle and the surrounding environment.
Figure 1. Schematic of the computational domain showing the geometries of the leak source, obstacle and the surrounding environment.
Preprints 88468 g001
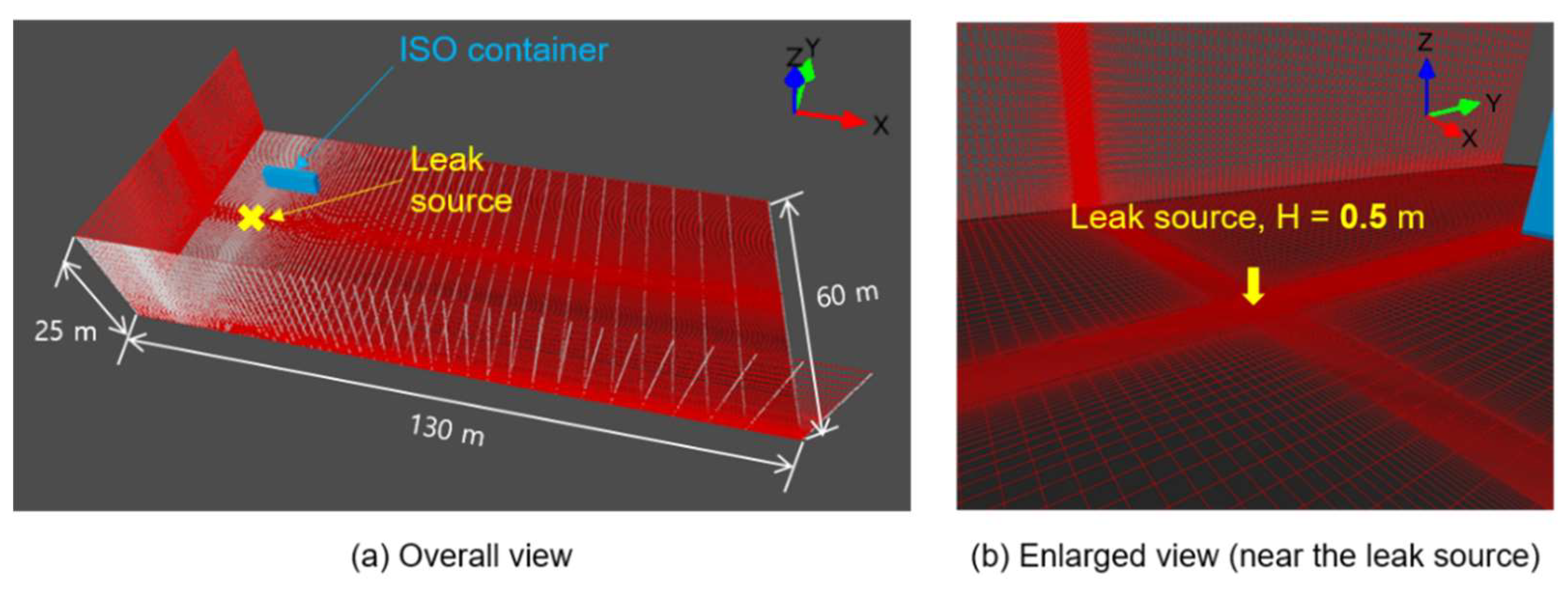
Preprints 88468 g002
Figure 2. The computational domain and the grid system.
Figure 2. The computational domain and the grid system.
Preprints 88468 g002
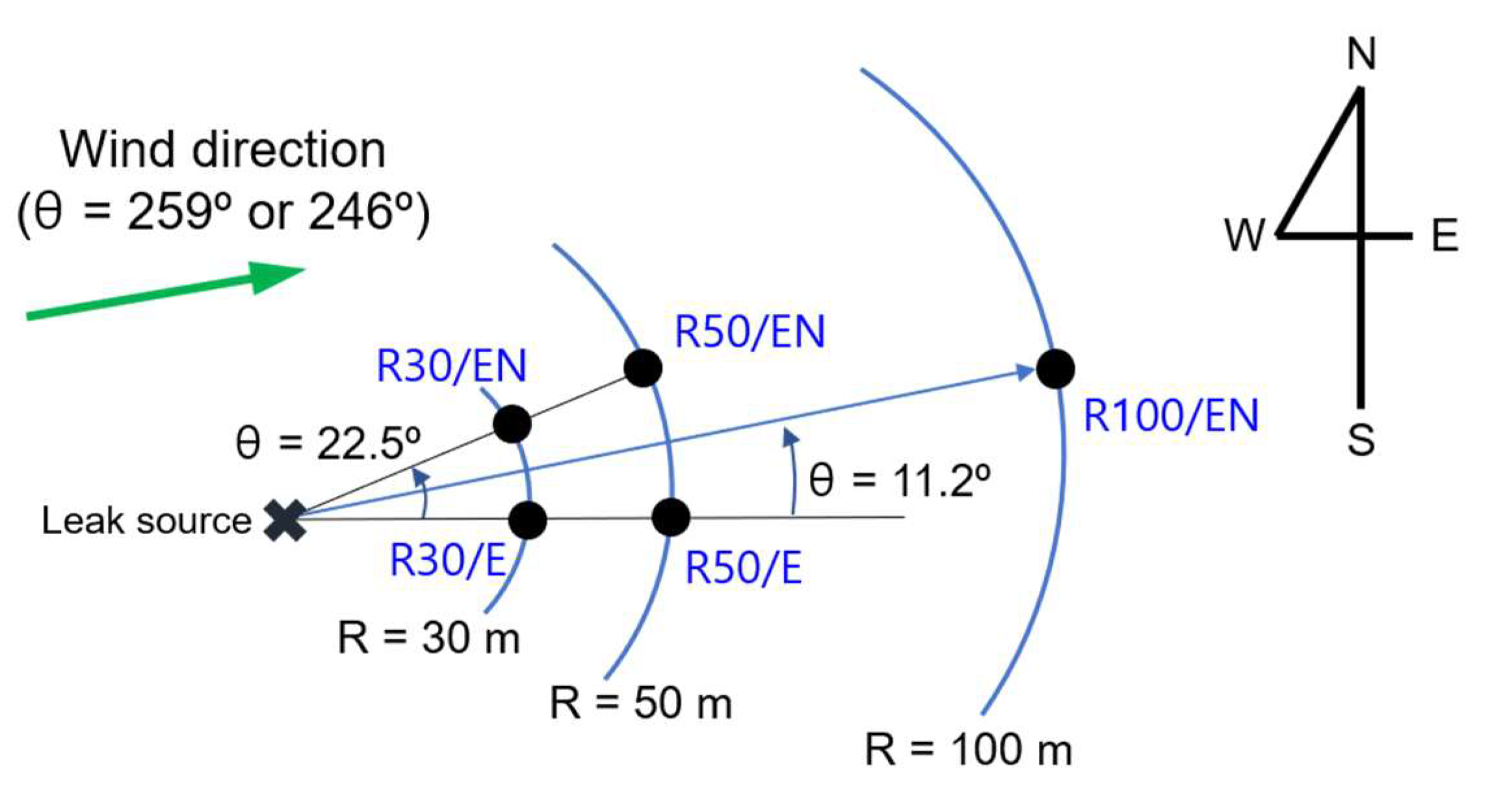
Preprints 88468 g003
Figure 3. Schematic of locations where hydrogen concentrations were measured.
Figure 3. Schematic of locations where hydrogen concentrations were measured.
Preprints 88468 g003
Preprints 88468 g004
Figure 4. Hydrogen mole fractions for different grid sizes at selected locations (grid sizes of 0.2, 0.3, 0.5, and 1.0 m for Region II, and at H = 1.0 m).
Figure 4. Hydrogen mole fractions for different grid sizes at selected locations (grid sizes of 0.2, 0.3, 0.5, and 1.0 m for Region II, and at H = 1.0 m).
Preprints 88468 g004
Preprints 88468 g005
Figure 5. Comparison of hydrogen concentrations computed by three models and those measured in the experiment at various locations for a case of ṁ = 0.225 kg/s.
Figure 5. Comparison of hydrogen concentrations computed by three models and those measured in the experiment at various locations for a case of ṁ = 0.225 kg/s.
Preprints 88468 g005
Preprints 88468 g006
Figure 6. Comparison of temperatrue computed by three models and those measured in the experiment at various locations for a case of ṁ = 0.225 kg/s.
Figure 6. Comparison of temperatrue computed by three models and those measured in the experiment at various locations for a case of ṁ = 0.225 kg/s.
Preprints 88468 g006
Preprints 88468 g007
Figure 7. Comparison of hydrogen concentrations computed by three models and those measured in the experiment at various locations for a case of ṁ = 0.73 kg/s.
Figure 7. Comparison of hydrogen concentrations computed by three models and those measured in the experiment at various locations for a case of ṁ = 0.73 kg/s.
Preprints 88468 g007
Preprints 88468 g008
Figure 8. Comparison of temperatrue computed by three models and those measured in the experiment at various locations for a case of ṁ = 0.73 kg/s.
Figure 8. Comparison of temperatrue computed by three models and those measured in the experiment at various locations for a case of ṁ = 0.73 kg/s.
Preprints 88468 g008
Preprints 88468 g009
Figure 9. Computed hydrogen concentration distributions for a case of ṁ = 0.225 kg/s.
Figure 9. Computed hydrogen concentration distributions for a case of ṁ = 0.225 kg/s.
Preprints 88468 g009
Preprints 88468 g010
Figure 10. Computed hydrogen concentration distributions for a case of ṁ = 0.73 kg/s.
Figure 10. Computed hydrogen concentration distributions for a case of ṁ = 0.73 kg/s.
Preprints 88468 g010
Preprints 88468 g011
Figure 11. Computed overpressure distributions at the cross section of Z = 0.4 m, for a case of ṁ = 0.225 kg/s.
Figure 11. Computed overpressure distributions at the cross section of Z = 0.4 m, for a case of ṁ = 0.225 kg/s.
Preprints 88468 g011
Preprints 88468 g013
Figure 13. Computed overpressures and impulses at selected locations for ṁ = 0.225and 0.73 kg/s (filled symbol: at the maximum overpressure point, vacant symbol: at the ignition point).
Figure 13. Computed overpressures and impulses at selected locations for ṁ = 0.225and 0.73 kg/s (filled symbol: at the maximum overpressure point, vacant symbol: at the ignition point).
Preprints 88468 g013
Table 1. Conditions for liquid hydrogen release and weather [17].
Table 1. Conditions for liquid hydrogen release and weather [17].
case leaked outflow rate (kg/s) tank pressure (barg) wind speed (m/s) wind direction, θ (deg) ambient temperature (oC) weather conditions
1 0.225 2 3.2 246 1.0 overcast, rain prior to test
2 0.730 10 5.8 259 2.9 overcast, rain prior to test
Table 2. The Pasquill stability classes.
Table 2. The Pasquill stability classes.
Wind speed Day, strong sun Day, moderate sun Night, clouds (> 50%) Night, clouds (< 50%)
< 2 m/s A B E F
2–3 m/s A-B B-C E F
3–5 m/s B B-C D E
5–6 m/s C C-D D D
> 6 m/s C D D D
Table 3. Grid sizes and computation times.
Table 3. Grid sizes and computation times.
Grid for Region II 0.2 m 0.3 m 0.5 m 1.0 m
Total number of grids 1,576,440 713,934 328,328 150,144
Computation time (wall clock time) 132 h 76 h 52 h 48 h
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated