The $k$-set tree connectivity, as a natural extension of classical connectivity, is a very important index to evaluate the fault-tolerance of interconnection networks. Let $G=(V, E)$ be a connected graph and a subset $S\subseteq V$, an $S$-tree of graph $G$ is a tree $T=(V',E')$ that contains all the vertices of $S$. Two $S$-trees $T$ and $T'$ are internally disjoint if and only if $E(T)\cap E(T')=\varnothing$ and $V(T)\cap V(T')=S$. The cardinality of maximum internally disjoint $S$-trees is defined as $\kappa_{G}(S)$, and the $k$-set tree connectivity is defined by $\kappa_{k}(G)=\min\{\kappa_{G}(S)|S\subseteq V(G)\ \text{and} \ |S|=k\}$. In this paper, we show that the $k$-set tree connectivity of hierarchical folded hypercube when $k=4$, that is, $\kappa_{4}(HFQ_{n})=n+1$, where $HFQ_{n}$ is hierarchical folded hypercube for $n\geq 7$.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

All graphs in this paper are finite simple and undirected. For more terminology and notation that are used but not described here, refer to reference [1]. A network is commonly molded by a graph

G = (V, E)

, where vertices correspond to processors and edges correspond communication links. For any vertex

x \in V

, let

N_{G} (x) = {y \in V (G) ∖ x | x y \in E}

be the neighbour set of x in the graph G, and

N_{G} [x] = N_{G} (x) \cup {x}

. Let

d_{G} (x) = | N_{G} (x) |

be the degree of x in G. Besides, we use

δ (G)

and

Δ (G)

to denote the minimum degree and maximum degree of G, respectively. If

δ (G) = Δ (G)

, then G is called a regular graph. For any

a, b \in V

, an

(a, b)

-path is a simple graph whose vertices begin with a and end with b. Any two

(a, b)

-paths A and B are internally disjoint if and only if

V (A) \cap V (B) = {a, b}

. For any vertex set

S \subseteq V

, let

G_{[S]}

be the induced subgraph of G that contains all the vertices of S. For convenience sake, let

[n + 1] = {1, 2, \dots, n + 1}

and use “

w . l . o . g .

” to express “Without loss of generality”. Let

x = x_{1} x_{2} \dots x_{n}

be n-bit binary string and

x_{i}

be the i-th bit of x. Denotes

H (x, y)

by the Hamming distance of two distinct n-bit binary strings of x and y is that the number of positions where they differ.

With the rise and rapid development of high-performance parallel computer science, more and more attention is being paid to interconnection networks with excellent performance. An eminent topological structure can significantly improve the reliability of a network. Therefore, it is essential to consider the fault tolerance of the network while designing the topology of the network. This means that the interconnection network should be able to operate effectively even when certain nodes and edges fail, ensuring that it retains specific network properties. In fact, the topological structure of an interconnection network commonly modeled by an undirected simple graph

G = (V, E)

, where every vertex corresponds to a processor, and each edge corresponds to a communication link. Then many computer scientists and engineers use some parameters of graph theory to design and analyzing topological structures of interconnection networks, for instance the connectivity.

The connectivity

κ (G)

of a connected graph G is the minimum cardinality of vertices whose removed to obtain a disconnected graph or only a vertex. A famous theorem that we know of Whitney [2] gives another equivalent definition of connectivity. For any vertex set

S = {x, y}

, let

κ_{G} (S)

be the maximum cardinality of internally disjoint paths joining x and y in G. Then

κ (G) = min {κ_{G} (S) | S \subseteq V

and

| S | = 2}

. However, the connectivity has an evident drawback that in the practical application of interconnection networks, the probability of all neighbours adjacent to a vertex failing at the same time is extremely small. Therefore, it is not precise enough to measure the fault tolerance of a network by the parameter of connectivity.

In order to better evaluate the fault tolerance level of a network, Chartrand et al. [3] extended the connectivity and came up with the concept of the k-set tree connectivity. For any vertex set

S \subseteq V

G_{[S]}

as the induced subgraph of G is actually a tree. An S-tree

T = (V^{'}, E^{'})

of a connected graph G is a tree that contains the subset S. Two S-trees T and

T^{'}

are internally disjoint if and only if

E (T) \cap E (T^{'}) = ⌀

and

V (T) \cap V (T^{'}) = S

. Let

κ_{G} (S)

be the maximum number of internally disjoint S-trees in graph G. The k-set tree connectivity is denoted by

κ_{k} (G) = min {κ_{G} (S) | S \subseteq V

and

| S | = k}

The relation between the tree connectivity and the connectivity and the bounds of the tree connectivity have been extensively investigated [4,5,6]. Furthermore, the 3-set tree connectivity of some networks have been studied. Such as, Chartrand ea al. explored the 3-set tree connectivity of complete graphs [7]. Li ea al. derived the 3-set tree connectivity of card product graphs [8]. Li et al. determined product graphs [9]. Li et al. evaluated the 3-set tree connectivity of complete bipartite graph [10]. Zhao et al. investigated the 3-set tree connectivity of star graphs and alternating group graphs [11]. However, there are few results about 4-set tree connectivity. The results known about 4-set tree connectivity of networks so far, are hypercubes [12], exchanged hypercubes [13] and dual cube [14] and hierarchical cubic networks [15]. For more researches and results about the k-set tree connectivity, refer to [16,17,18,19,22,23].

In this paper, we study the 4-set tree connectivity of the hierarchical folded hypercube.

2. Preliminaries

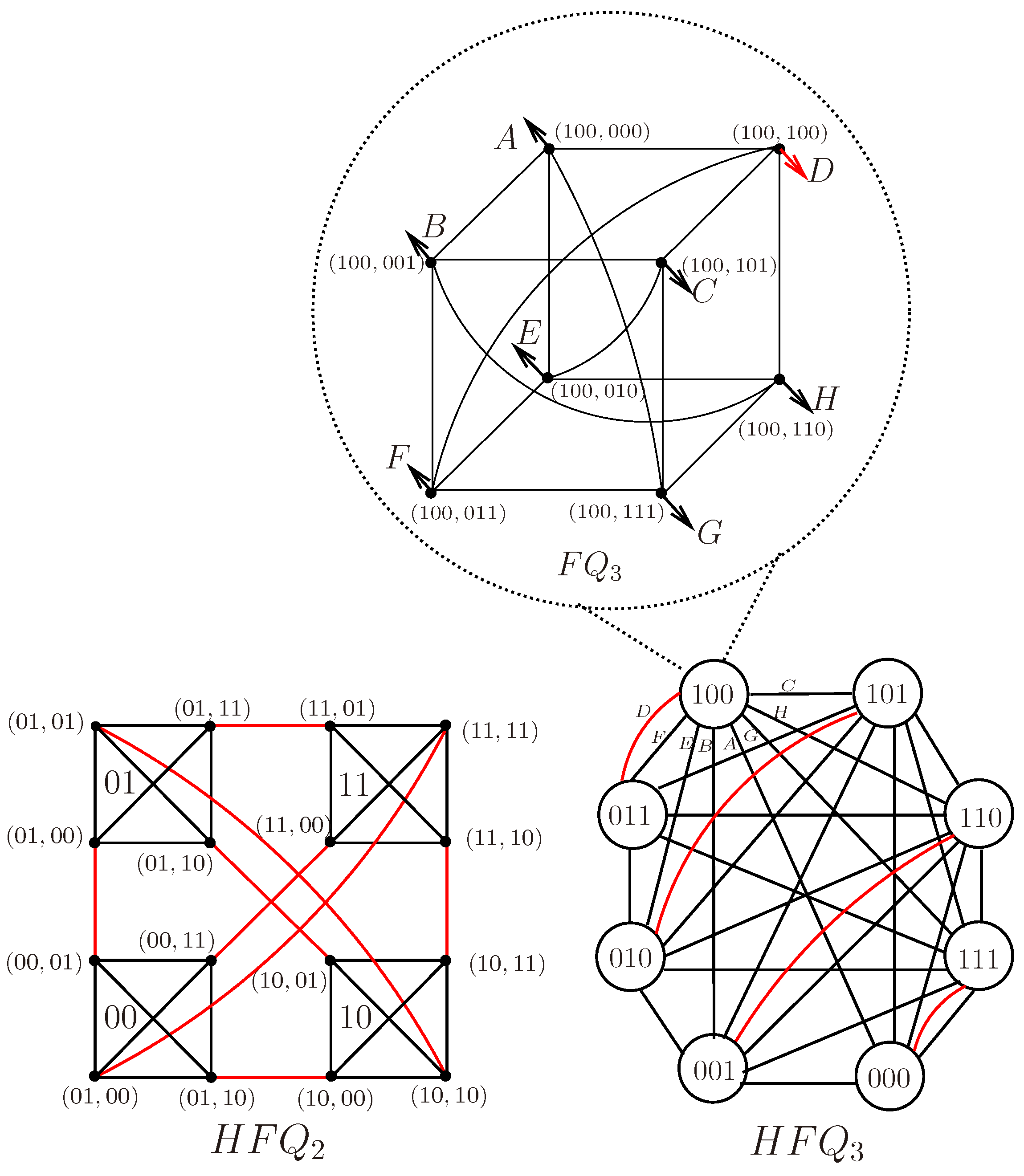
An n-dimensional hierarchical folded hypercube

H F Q_{n}

can be divided into

2^{n}

clusters, say

C_{1}

C_{2}

, …,

C_{2^{n}}

and every cluster is isomorphic to the n-dimensional folded hypercube

F Q_{n}

. Any vertex

a \in V (H F Q_{n})

can be denoted by a two-tuple address

a = (c (a), p (a))

, where both

c (a)

and

p (a)

are n-bit binary strings. The first binary string

c (a)

identifies the cluster the vertex a belong to and the second binary string

p (a)

identifies the vertex within the cluster. Two vertices

a = (c (a), p (a))

and

b = (c (b), p (b))

are adjacent in

H F Q_{n}

if and only if one of the following two prerequisites holds:

E_{c u} (H F Q_{n}) = {a b | H (P (a), P (b)) = 1}

E_{c r} (H F Q_{n}) = {a b |

c (a) = P (a)

, then

c (b) = p (b) = \bar{c (a)}

otherwise,

c (a) = P (b)

and

p (a) = c (b)}

Where

E_{c u} (H F Q_{n})

is called cube edge, which in a cluster of

H F Q_{n}

and

E_{c r} (H F Q_{n})

is called cross edge, which connecting two vertices in two distinct clusters of

H F Q_{n}

Figure 1. The

2, 3

-dimension hierarchical folded hypercube.

Figure 1. The

2, 3

-dimension hierarchical folded hypercube.

Lemma 2.1.

Let

C_{1}

C_{2}

, …,

C_{2^{n}}

be the

2^{n}

clusters of

H F Q_{n}

for

n \geq 7

, we have

(1)

For

i \in [2^{n}]

, let

b \in V (C_{i})

with

c (b) = p (b)

. The external neighbors of different vertices in

V (C_{i}) ∖ {b}

distributes in distinct clusters of

H F Q_{n}

. Besides, if

a \in V (C_{i}) ∖ {b}

with

p (a) = \bar{p (b)}

, the external neighbor of a distributes in the same cluster with b.

(2)

For

a \in V (C_{i})

and

b \in V (C_{j})

, there exist two cross edges between

C_{i}

and

C_{j}

for

i \neq j

and

i, j \in [2^{n}]

if and only if

c (a) = \bar{c (b)}

; otherwise there is just one cross edge.

(3)

For any two vertices

a, b \in V (C_{i})

H F Q_{n}

for

i \in [2^{n}]

, the external neighbor of a and b can not be the same vertex.

Proof.

(1)

Let

b_{1}, b_{2} \in V (C_{i}) ∖ {b}

and

b_{1} \neq b_{2}

. By the definition of

H F Q_{n}

c (b_{1}) \neq p (b_{1})

c (b_{2}) \neq p (b_{2})

and

p (b_{1}) \neq p (b_{2})

. Therefore, the external neighbors of

b_{1}

and

b_{2}

are

(p (b_{1}), c (b_{1}))

and

(p (b_{2}), c (b_{2}))

, respectively. Since

p (b_{1}) \neq p (b_{2})

, the external neighbor of

b_{1}

and

b_{2}

distribute in different clusters of

H F Q_{n}

. In view of

b \in V (C_{i})

and

c (b) = p (b)

, the external neighbor of b is

\bar{c (b)} = \bar{p (b)}

. Let

a \in V (C_{i}) ∖ {b}

, then

c (a) \neq p (a)

and the external neighbor of a is

(p (a), c (a))

. When

(p (a) = \bar{p (b)})

, the external neighbors of a and b belong to the same cluster of

H F Q_{n}

(2)

By (1), it is clear that the result holds.

(3)

Let

a, b \in V (C_{i})

for

i \in [2^{n}]

and suppose that a and b have a same external neighbor, denote by x, then a and b are the two external neighbors of x, a contradiction.□

Lemma 2.2.

Let

C_{1}, C_{2}, \dots, C_{2^{n}}

be the

2^{n}

clusters of

H F Q_{n}

for

n \geq 7

. Then, arbitrary vertex

b = (c (b), p (b)) \in V (C_{i})

for

i \in [2^{n}]

| N_{C_{i}} (b) | = n + 1

, we have

(1)

The external neighbors of the distinct vertices in

N_{C_{i}} (b)

distribute in different clusters of

H F Q_{n}

(2)

When

c (b) = p (b) (c (b) = \bar{p (b)})

, there is one and only one vertex

b_{i}

N_{C_{i}} (b)

with the external neighbor belongs to the same cluster with the vertex v and

b_{i} = (c (b), \bar{p (b)}) (c (b), p (b))

. Otherwise, all the vertices in

N_{C_{i}} (b)

with the external neighbors distribute in different clusters with the vertex b.

Proof.

(1)

w.l.o.g., let

b \in V (C_{1})

. Recall that

C_{1} ≅ F Q_{n}

, which is

(n + 1)

-regular, therefore

| N_{C_{1}} (v) | = n + 1

. As

n \geq 7

, for any

b_{1}, b_{2} \in N_{C_{1}} (b)

p (b_{1}) \neq \bar{p (b_{2})}

. By (1) of Lemma 1, the external neighbors of vertices in

N_{C_{1}} (b)

distribute in different clusters of

H F Q_{n}

(2)

By the definition of

H F Q_{n}

, the result can be obtained directly.□

Lemma 2.3.

Let

C_{1}, C_{2}, \dots, C_{2^{n}}

be the

2^{n}

clusters of

H F Q_{n}

and

N = H F Q_{n} [⋃_{j = 1}^{k} V (C_{i_{j}})]

for

i_{j} \in V (2^{n})

, where

k \geq 1

and

n \geq 7

, then N is connected.

Proof.

w.l.o.g., let

N = H F Q_{n} [⋃_{j = 1}^{k} V (C_{j})]

. By (2) of Lemma 1, there exists at least one cross edge between arbitrary two different clusters of

H F Q_{n}

. Therefore, N is connected.□

Lemma 2.4.

[20] The folded hypercube

F Q_{n}

(n + 1)

-regular and

κ (F Q_{n}) = n + 1

for

n \geq 2

Lemma 2.5.

[21] The hierarchical folded hypercube

H F Q_{n}

(n + 2)

-regular and

κ (H F Q_{n}) = n + 2

for

n \geq 2

3. The 4-set tree connectivity of hierarchical folded hypercube

In this part, we determine the k-set tree connectivity of folded hypercubes

H F Q_{n}

, when

k = 4

. That is,

κ_{4} (H F Q_{n}) = n + 1

where

n \geq 7

The following lemma provides a sharp upper bound for our main result.

Lemma 3.1.

[5] Let G be a connected graph of order

| V (G) |

with minimum degree

δ (G)

. Then

κ_{k} (G) \leq δ (G)

for

3 \leq k \leq | V (G) |

. In addition, if there exist two adjacent vertices of degree

δ (G)

, then

κ_{k} (G) \leq δ (G) - 1

for

3 \leq k \leq | V (G) |

The following three Lemmas describe several clear and crucial properties on k-connected graphs, which provide great convenience when we construct internally disjoint paths.

Lemma 3.2.

[1] Let G be a k-connected graph and u and v be arbitrary two distinct vertices of G. Then there are k internally disjoint paths joining x and y in G.

Lemma 3.3.

[1] Let

G = (V, E)

be a k-connected graph, arbitrary vertex

u \in V

, let

Y \subseteq V ∖ {u}

be a vertex subset of V and

| Y | \geq k

. Then, there exists a k-fan in G from u to Y.

Lemma 3.4.

[1] Let

G = (V, E)

be a k-connected graph and

U, W \subseteq V

be two disjoint vertex subsets with

| U | \geq k

and

| W | \geq k

. Then, there exist k disjoint

(U, W)

-paths in G.

The following two Theorems on the folded hypercube

F Q_{n}

are very beneficial to our proof of the main result.

Theorem 3.1.

[25]

κ_{3} (F Q_{n}) = n

, where

n \geq 2

Theorem 3.2.

[26]

κ_{4} (F Q_{n}) = n

, where

n \geq 7

Lemma 3.5.

Let

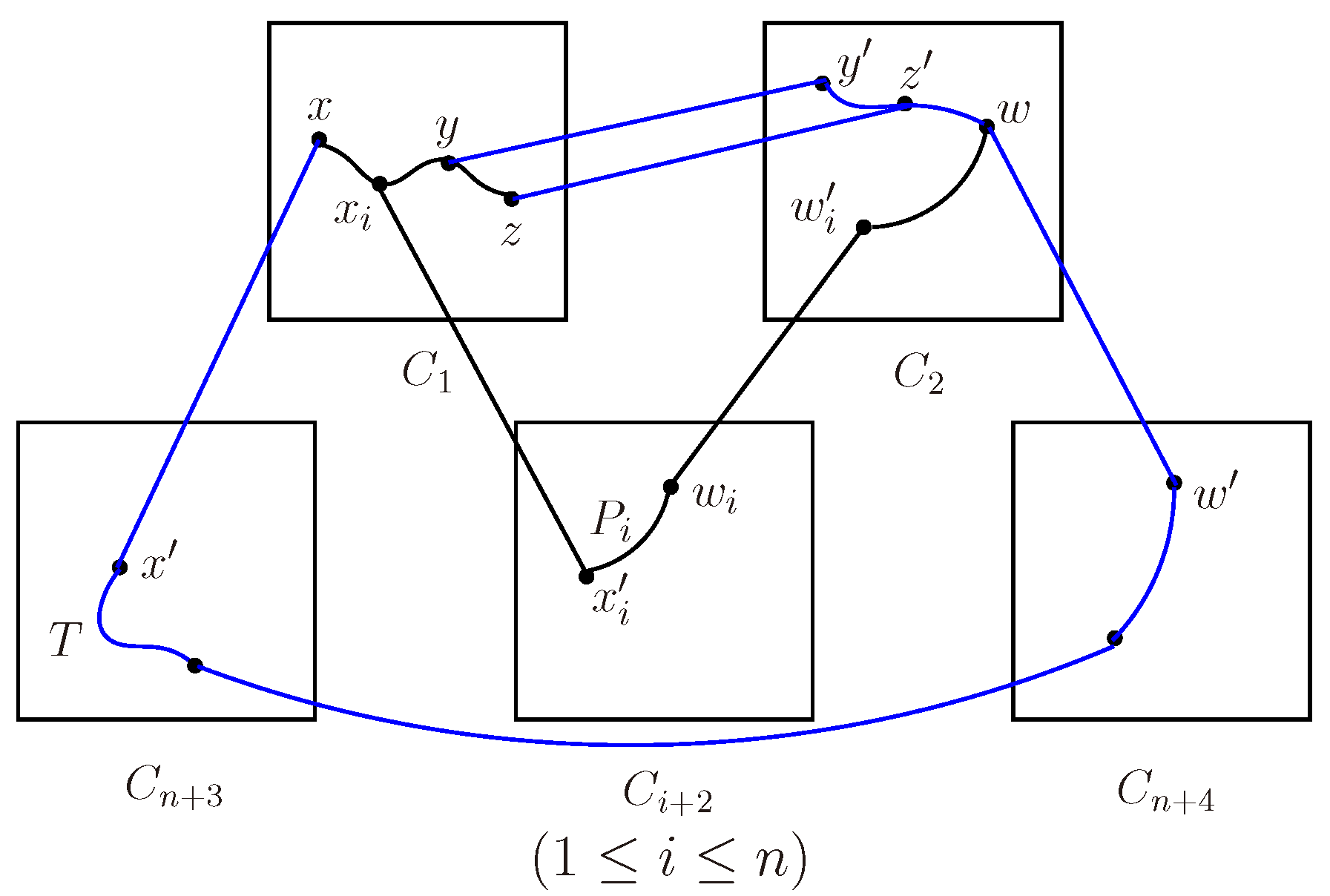
C_{1}, C_{2}, \dots, C_{2^{n}}

be the

2^{n}

clusters of

H F Q_{n}

for

n \geq 7

and

S = {x, y, z, w} \subseteq V (H F Q_{n})

. Let

| S \cap V (C_{i}) | = 3

and

| S \cap V (C_{j}) | = 1

for different

i, j \in [2^{n}]

, then there exist

n + 1

internally disjoint S-trees in

H F Q_{n}

Proof.

w.l.o.g., suppose that

| S \cap V (C_{1}) | = 3

and

| S \cap V (C_{2}) | = 1

. Let

{x, y, z} \subseteq V (C_{1})

and

w \in V (C_{2})

. See Figure 2. By Theorem 3.1, there are n internally disjoint trees

{\hat{T}}_{1}, {\hat{T}}_{2}, \dots, {\hat{T}}_{n}

connecting

x, y, z

. Recall that

C_{i} ≅ F Q_{n}

, for each

i \in [2^{n}]

. By Lemma 2.4,

κ (F Q_{n}) = n + 1

, there are

n + 1

neighbors

x_{1}, x_{2}, \dots, x_{n + 1}

of x in

C_{1}

. Let

x_{i} \in V ({\hat{T}}_{i})

for

i \in [n]

and

X = {x_{1}, x_{2}, \dots, x_{n + 1}, x}

Note that

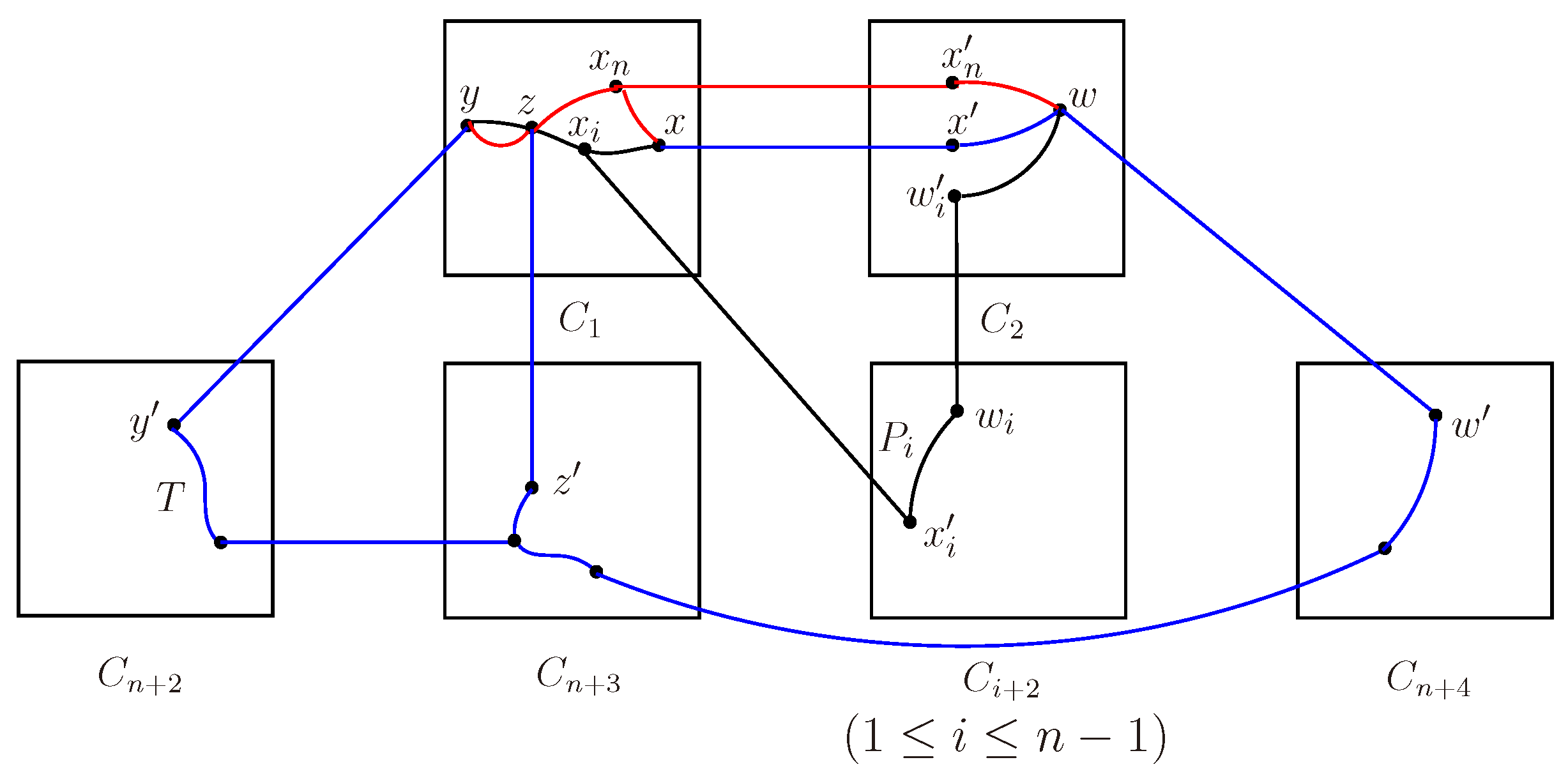
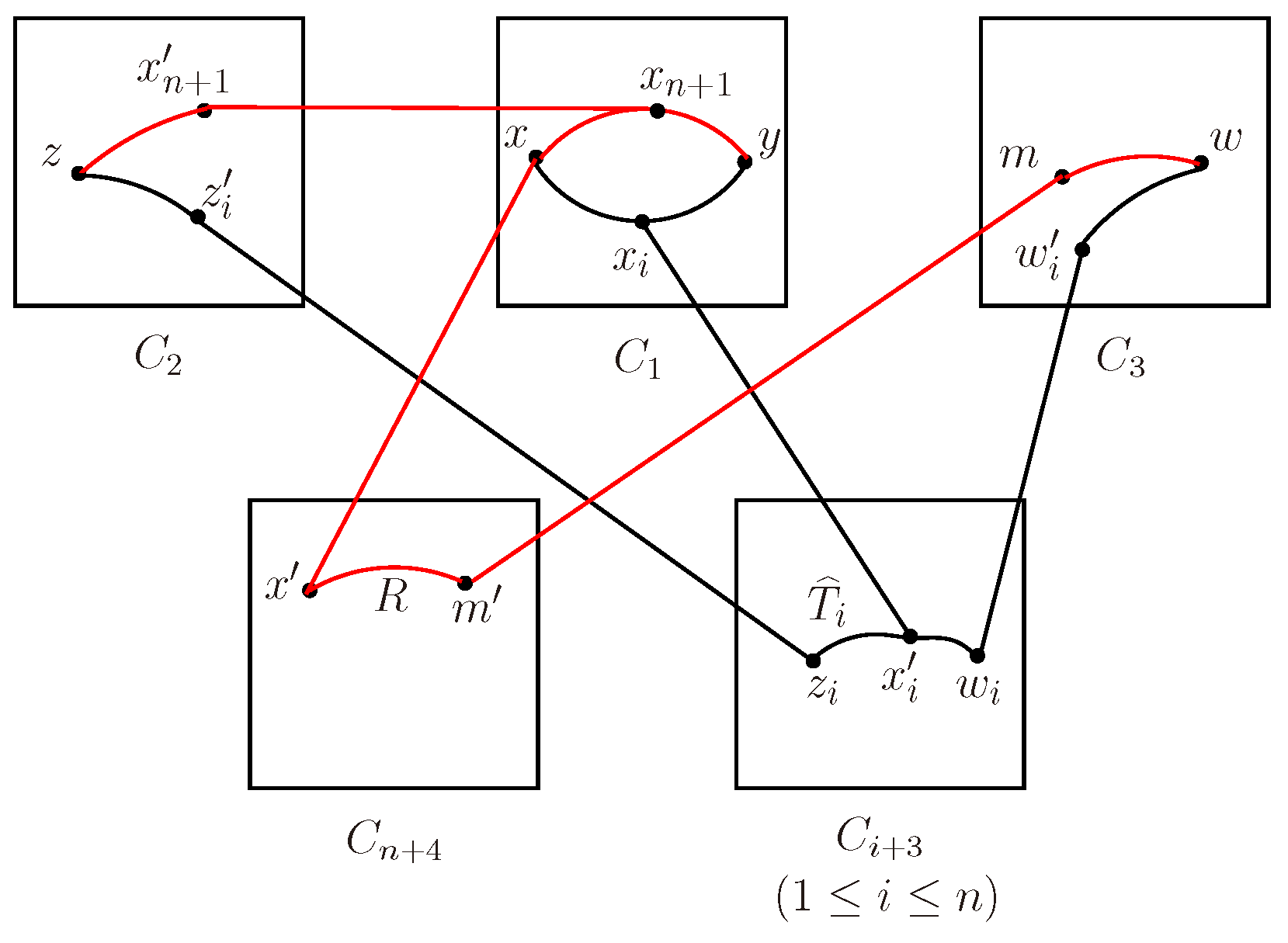
X = {x_{1}, x_{2}, \dots, x_{n + 1}, x}

, it is potential that

y \in X

z \in X

. To avoid repetition, we only consider the case of

y \notin X

and

z \notin X

, as the discussion about

y \in X

z \in X

is similar. By

(2)

of Lemma 2.2, there are at most two vertices of X with the external neighbors belonging to

C_{2}

, and the two vertices must be x and

x_{i}

, for some

i \in [n + 1]

. To obtain the main result, we need two consider following three cases.

Case 1. There are two vertices in X with the external neighbors belonging to

C_{2}

Figure 2. The explanation of Case 1.

w.l.o.g., assume that the two vertices are x and

x_{n}

, that is

x^{'}, x_{n}^{'} \in V (C_{2})

. Let

x_{i} \in V (C_{i + 2})

and there exists a vertex

w_{i} \in V (C_{i + 2})

and such that

w_{i}^{'} \in V (C_{2})

for

i \in [n - 1]

. Since

C_{i + 2}

is connected, there exists a path

P_{i}

joining

x_{i}^{'}

and

w_{i}

C_{i + 2}

, for

i \in [n - 1]

. Let

W = {w_{1}^{'}, \dots, w_{n - 1}^{'}, x_{n}^{'}, x^{'}}

. By Lemma 3.3, there are

n + 1

disjoint paths

P_{1}^{'}, P_{2}^{'}, \dots, P_{n + 1}^{'}

from w to W, and such that

x_{i}^{'} \in V (P_{i}^{'})

x_{n}^{'} \in V (P_{n}^{'})

x^{'} \in V (P_{n + 1}^{'})

for

i \in [n - 1]

. w.l.o.g., suppose that

y^{'} \in V (C_{n + 2})

z^{'} \in V (C_{n + 3})

w^{'} \in V (C_{n + 4})

. By Lemma 2.3,

H F Q_{n} [\cup_{i = n + 2}^{n + 4} V (C_{i})]

is connected, then there is a tree T connecting

y^{'}, z^{'}

and

w^{'}

. Let

T_{i} = {\hat{T}}_{i} \cup x_{i} x_{i}^{'} \cup P_{i} \cup w_{i} w_{i}^{'} \cup P_{i}^{'}

for

i \in [n - 1]

T_{n} = {\hat{T}}_{n} \cup x_{n} x_{n}^{'} \cup P_{n}^{'}

and

T_{n + 1} = x x^{'} \cup P_{n + 1}^{'} \cup y y^{'} \cup z z^{'} \cup w w^{'} \cup T

, then

T_{1}, T_{2}, \dots, T_{n + 1}

are

n + 1

internally disjoint S-trees.

Case 2. There is only one vertex in X with the external neighbor belonging to

C_{2}

Case 2.1.

x^{'} \in V (C_{2})

Figure 3. The explanation of Case

2.1

Figure 3. The explanation of Case

2.1

Recall that, we consider that

y, z \notin X

, by

(2)

of Lemma 2.2,

y^{'}, z^{'} \notin V (C_{2})

. Let

x_{i}^{'} \in V (C_{i + 2})

for

i \in [n]

. Since

C_{i + 2}

is connected, there is a path

P_{i}

joining

x_{i}^{'}

and

w_{i}

C_{i + 2}

, and such that

w_{i}^{'} \in V (C_{2})

for

i \in [n]

. Let

W = {w_{1}^{'}, \dots, w_{n}^{'}, x^{'}}

. By Lemma 3.3, there are

n + 1

disjoint paths

P_{1}^{'}, P_{2}^{'}, \dots, P_{n + 1}^{'}

between w and W, and subject to

x_{i}^{'} \in V (P_{i}^{'})

x^{'} \in V (P_{n + 1}^{'})

for

i \in [n]

. w.l.o.g., assume that

y^{'} \in V (C_{n + 3})

z^{'} \in V (C_{n + 4})

w^{'} \in V (C_{n + 5})

. By Lemma 2.3,

H F Q_{n} [\cup_{i = n + 3}^{n + 5} V (C_{i})]

is connected, then there is a tree T connecting

y^{'}, z^{'}

and

w^{'}

. Let

T_{i} = {\hat{T}}_{i} \cup x_{i} x_{i}^{'} \cup P_{i} \cup w_{i} w_{i}^{'} \cup P_{i}^{'}

for

i \in [n]

and

T_{n + 1} = x x^{'} \cup P_{n + 1}^{'} \cup y y^{'} \cup z z^{'} \cup w w^{'} \cup T

, then

T_{1}, T_{2}, \dots, T_{n + 1}

are

n + 1

internally disjoint S-trees.

Case 2.2.

x_{i}^{'} \in V (C_{2})

for certain

i \in [n + 1]

w.l.o.g., suppose that

x_{n}^{'} \in V (C_{2})

. By Lemma 2.1, at most one vertex of

y^{'}

and

z^{'}

belongs to

C_{2}

Case 2.2.1.

y^{'}, z^{'} \notin V (C_{2})

Let

x_{i}^{'} \in V (C_{i + 2})

for

i \in [n - 1]

. Since

C_{i + 2}

is connected, there exists a path

P_{i}

joining

x_{i}^{'}

and

w_{i}

C_{i + 2}

, and such that

w_{i}^{'} \in V (C_{2})

for

i \in [n - 1]

. w.l.o.g., assume that

x^{'} \in V (C_{n + 2})

. Note that,

y^{'}

z^{'}

may belongs to the same cluster

C_{i + 2}

with some

x_{i}^{'}

for some

i \in [n - 1]

. We need to discuss the following two situations.

Figure 4. The explanation about

y^{'}, z^{'} \notin V (C_{i + 2})

for

i \in [n - 1]

of Case

2 . 2.1

Figure 4. The explanation about

y^{'}, z^{'} \notin V (C_{i + 2})

for

i \in [n - 1]

of Case

2 . 2.1

When

y^{'}, z^{'} \notin V (C_{i + 2})

for

i \in [n - 1]

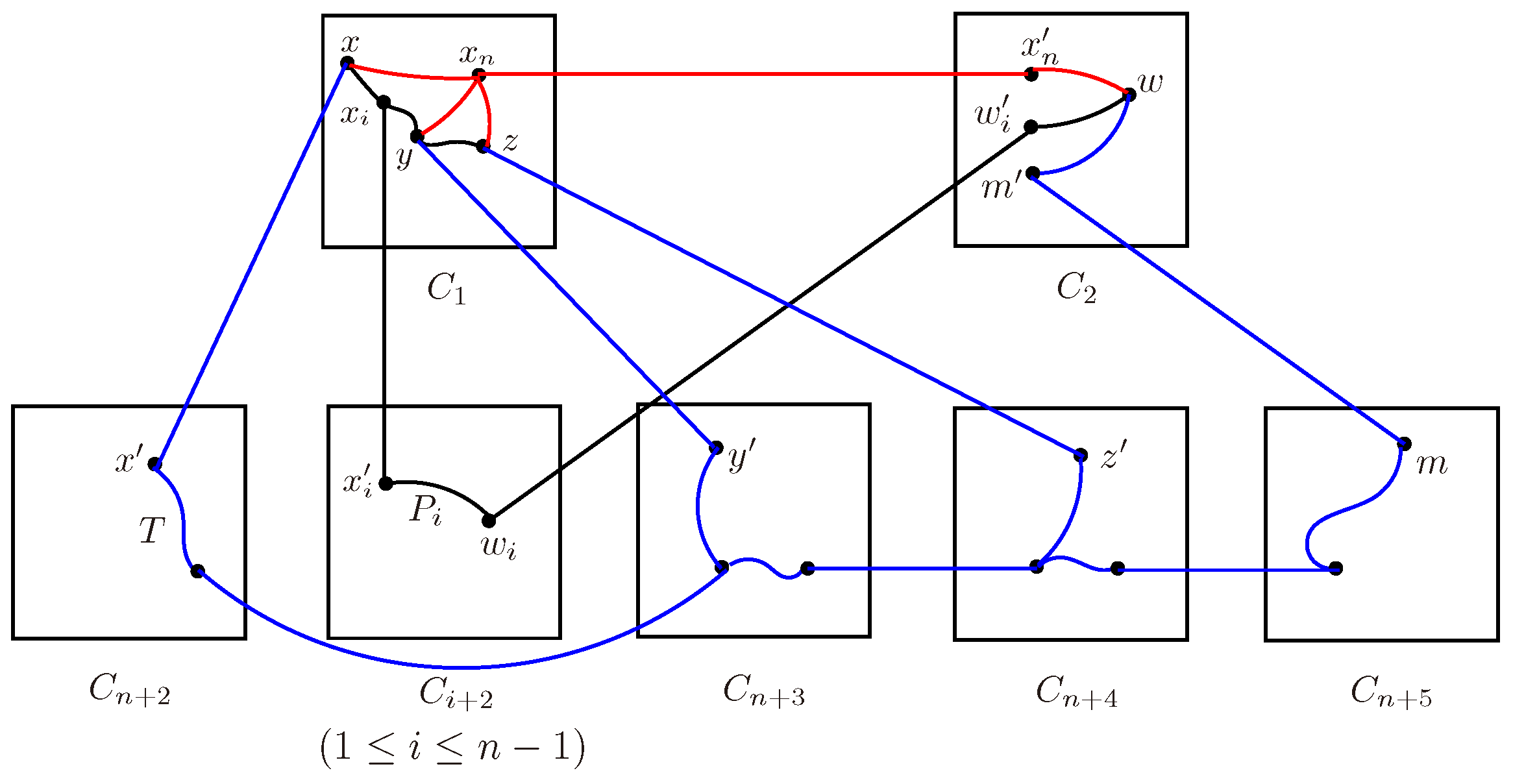
. w.l.o.g., suppose that

y^{'} \in V (C_{n + 3})

z^{'} \in V (C_{n + 3})

m \in V (C_{n + 5})

and such that

m^{'} \in V (C_{2})

. Let

W = {w_{1}^{'}, w_{2}^{'}, \dots, w_{n}^{'}, m^{'}}

. By Lemma 3.3, there exist

n + 1

disjoint paths

P_{1}^{'}, P_{2}^{'}, \dots, P_{n + 1}^{'}

from w to W, and such that

P_{n + 1}^{'}

be the path joining w and

m^{'}

. By Lemma 2.3,

H F Q_{n} [\cup_{i = n + 2}^{n + 5} V (C_{i})]

is connected, then there exists a tree T connecting

x^{'}, y^{'}, z^{'}

and m. Let

T_{i} = {\hat{T}}_{i} \cup x_{i} x_{i}^{'} \cup P_{i} \cup w_{i} w_{i}^{'} \cup P_{i}^{'}

for

i \in [n - 1]

T_{n} = {\hat{T}}_{n} \cup x_{n} x_{n}^{'} \cup P_{n}^{'}

and

T_{n + 1} = x x^{'} \cup y y^{'} \cup z z^{'} \cup P_{n + 1}^{'} \cup m m^{'} \cup T

, then

T_{1}, T_{2}, \dots, T_{n + 1}

are

n + 1

internally disjoint S-trees.

When

y^{'} \in V (C_{i + 2})

z^{'} \in V (C_{i + 2})

for certain

i \in [n - 1]

w.l.o.g., suppose that

y^{'} \in V (C_{n + 1})

and

z^{'} \in V (C_{n + 3})

. That is,

x_{n - 1}^{'}, y^{'} \in V (C_{n + 1})

. Let

w_{n - 1}, g \in V (C_{n + 1})

and

w_{n - 1}^{'} \in V (C_{2})

g^{'} \in V (C_{n + 3})

. Let

A = {x_{n - 1}^{'}, y^{'}}

B = {w_{n - 1}, g}

and

A, B \subseteq V (C_{n + 1})

. By Lemma 3.4, there exist two internally disjoint

(A, B)

-paths, saying

P_{n - 1}

and Q, subject to

P_{n - 1}

be the path from

x_{n - 1}^{'}

w_{n - 1}

and P be the path from

y^{'}

to g. Similar to the case of

y^{'}, z^{'} \notin V (C_{i + 2})

for

i \in [n - 1]

, we get n internally disjoint S-trees

T_{1}, T_{2}, \dots, T_{n}

. Let

m \in V (C_{n + 4})

and

m^{'} \in V (C_{2})

. By Lemma 2.3,

H F Q_{n} [\cup_{i = n + 2}^{n + 5} V (C_{i})]

is connected, then there exists a tree T connecting

y^{'}, z^{'}, g^{'}

and m. Let

T_{n + 1} = x x^{'} \cup y y^{'} \cup z z^{'} \cup Q \cup g g^{'} \cup P_{n + 1}^{'} \cup m m^{'} \cup T

Figure 5. The explanation about

y^{'} \in V (C_{i + 2})

for some

i \in [n - 1]

of Case

2 . 2.1

Figure 5. The explanation about

y^{'} \in V (C_{i + 2})

for some

i \in [n - 1]

of Case

2 . 2.1

Case 2.2.2.

y^{'} \in V (C_{2})

z^{'} \in V (C_{2})

w.l.o.g., assume that

y^{'} \in V (C_{2})

, by

(2)

of Lemma 2.2, y must be the neighbor of

x_{n}

C_{1}

. Then The proof is similar to that of Case 1.

Case 3. None of the vertex in X with their external neighbor belongs to

C_{2}

(2)

of Lemma 2.1,

y^{'}

and

z^{'}

may belong to

C_{2}

. We consider the following three subcases to obtain the result.

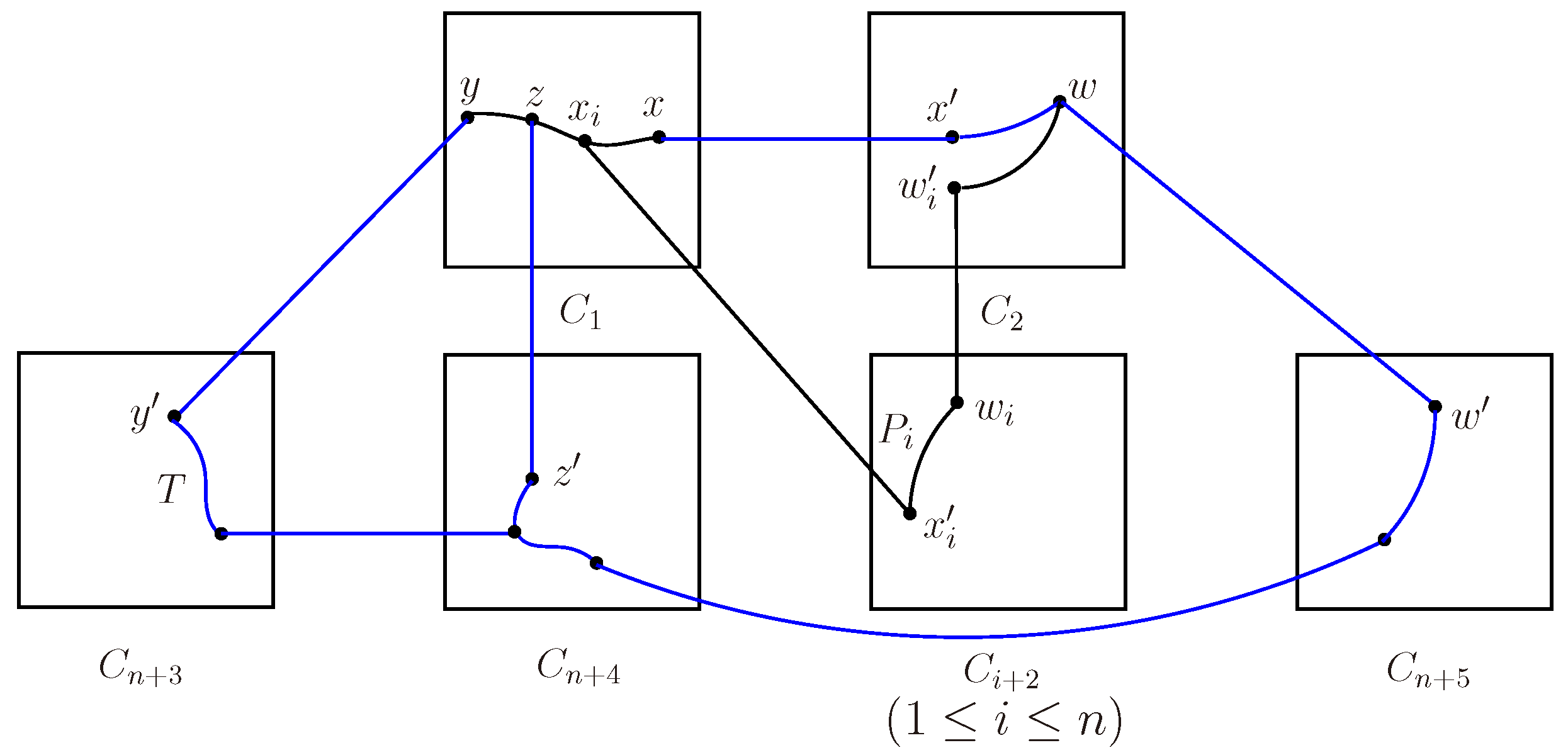
Case 3.1.

y^{'}, z^{'} \in V (C_{2})

(2)

of Lemma 2.2, y is adjacent to z in

C_{1}

and

y^{'}

is adjacent to

z^{'}

C_{2}

. Let

x_{i}^{'} \in V (C_{i + 2})

for

i \in [n - 1]

. Since

C_{i + 2}

is connected, there is a path

P_{i}

joining

x_{i}^{'}

and

w_{i}

C_{i + 2}

, and subject to

w_{i}^{'} \in V (C_{2})

for

i \in [n]

. w.l.o.g., assume that

x^{'} \in V (C_{n + 3})

w^{'} \in V (C_{n + 4})

. By Lemma 2.3,

H F Q_{n} [\cup_{i = n + 3}^{n + 4} V (C_{i})]

is connected, then there exists a tree T connecting

x^{'}

and

w^{'}

. Let

W = {w_{1}^{'}, w_{2}^{'}, \dots, w_{n}^{'}, y^{'}}

. By Lemma 3.3, there exist

n + 1

disjoint paths

P_{1}^{'}, P_{2}^{'}, \dots, P_{n + 1}^{'}

from w to W, and such that

P_{n + 1}^{'}

is the path joining

y^{'}

and w. Let

T_{i} = {\hat{T}}_{i} \cup x_{i} x_{i}^{'} \cup P_{i} \cup w_{i} w_{i}^{'} \cup P_{i}^{'}

for

i \in [n]

When

z^{'} \in V (P_{i}^{'})

, for certain

i \in [n + 1]

. w.l.o.g., suppose that

z^{'} \in V (P_{n + 1}^{'})

. Let

T_{n + 1} = x x^{'} \cup y y^{'} \cup z z^{'} \cup w w^{'} \cup P_{n + 1}^{'} \cup T

Figure 6. The explanation about

z^{'} \in V (p_{n + 1}^{'})

of Case

3.1

Figure 6. The explanation about

z^{'} \in V (p_{n + 1}^{'})

of Case

3.1

When

z^{'} \notin V (P_{i}^{'})

, for

i \in [n + 1]

. Since

y^{'}

is adjacent to

z^{'}

, let

R = P_{n + 1}^{'} \cup y^{'} z^{'}

. Obviously,

P_{1}^{'}, P_{2}^{'}, \dots, P_{n}^{'}, R

are disjoint paths. Let

T_{n + 1} = T \cup x x^{'} \cup y y^{'} \cup z z^{'} \cup w w^{'} \cup R

Case 3.2.

y^{'} \in V (C_{2})

z^{'} \in V (C_{2})

Is clear that, similar to that of Case

2.1

, we can get

n + 1

internally disjoint S-trees.

Case 3.3.

y^{'} \notin V (C_{2})

and

z^{'} \notin V (C_{2})

Note that,

y^{'}

z^{'}

may belongs to the same cluster

C_{i + 2}

with

x_{i}^{'}

for some

i \in [n]

When

y^{'}, z^{'} \notin V (C_{i + 2})

for

i \in [n]

. w.l.o.g., assume that

y^{'} \in V (C_{n + 4})

and

z^{'} \in V (C_{n + 5})

. Similar to that of Case

3.1

, we get n internally disjoint S-trees. By Lemma 2.3,

H F Q_{n} [\cup_{i = n + 3}^{n + 5} V (C_{i})]

is connected, then there exists a tree T connecting

x^{'}, y^{'}, z^{'}

and m. Let

T_{n + 1} = x x^{'} \cup y y^{'} \cup z z^{'} \cup m m^{'} \cup P_{n + 1}^{'} \cup T

Figure 7. The explanation of Case

3.3

Figure 7. The explanation of Case

3.3

When

y^{'} \in V (C_{i + 2})

z^{'} \in V (C_{i + 2})

for certain

i \in [n]

. w.l.o.g., suppose that

y^{'} \in V (C_{n + 2})

and

z^{'} \in V (C_{n + 4})

. That is,

x_{n}^{'}, y^{'} \in V (C_{n + 2})

. Let

w_{n}, f \in V (C_{n + 2})

and

w_{n}^{'} \in V (C_{2})

f^{'} \in V (C_{n + 4})

. Let

C = {x_{n}^{'}, y^{'}}

D = {w_{n}, f}

and

C, D \subseteq V (C_{n})

. By Lemma 3.4, there exist two internally disjoint

(C, D)

-paths, saying

P_{n}

and R, subject to

P_{n}

be the path joining

x_{n}^{'}

and

w_{n}

, subject to R be the path joining

y^{'}

and f. Similar to the subcase of

y^{'}, z^{'} \notin V (C_{i + 2})

for

i \in [n]

, we get

T_{1}, T_{2}, \dots, T_{n}

n internally disjoint S-trees. Let

m, z^{'} \in V (C_{n + 4})

and

m^{'} \in V (C_{2})

. By Lemma 2.3,

H F Q_{n} [\cup_{i = n + 3}^{n + 5} V (C_{i})]

is connected, then there exists a tree T connecting

x^{'}, z^{'}, f^{'}

and m. Let

T_{n + 1} = x x^{'} \cup y y^{'} \cup z z^{'} \cup R \cup f f^{'} \cup P_{n + 1}^{'} \cup m m^{'} \cup T

.□

Lemma 3.6.

Let

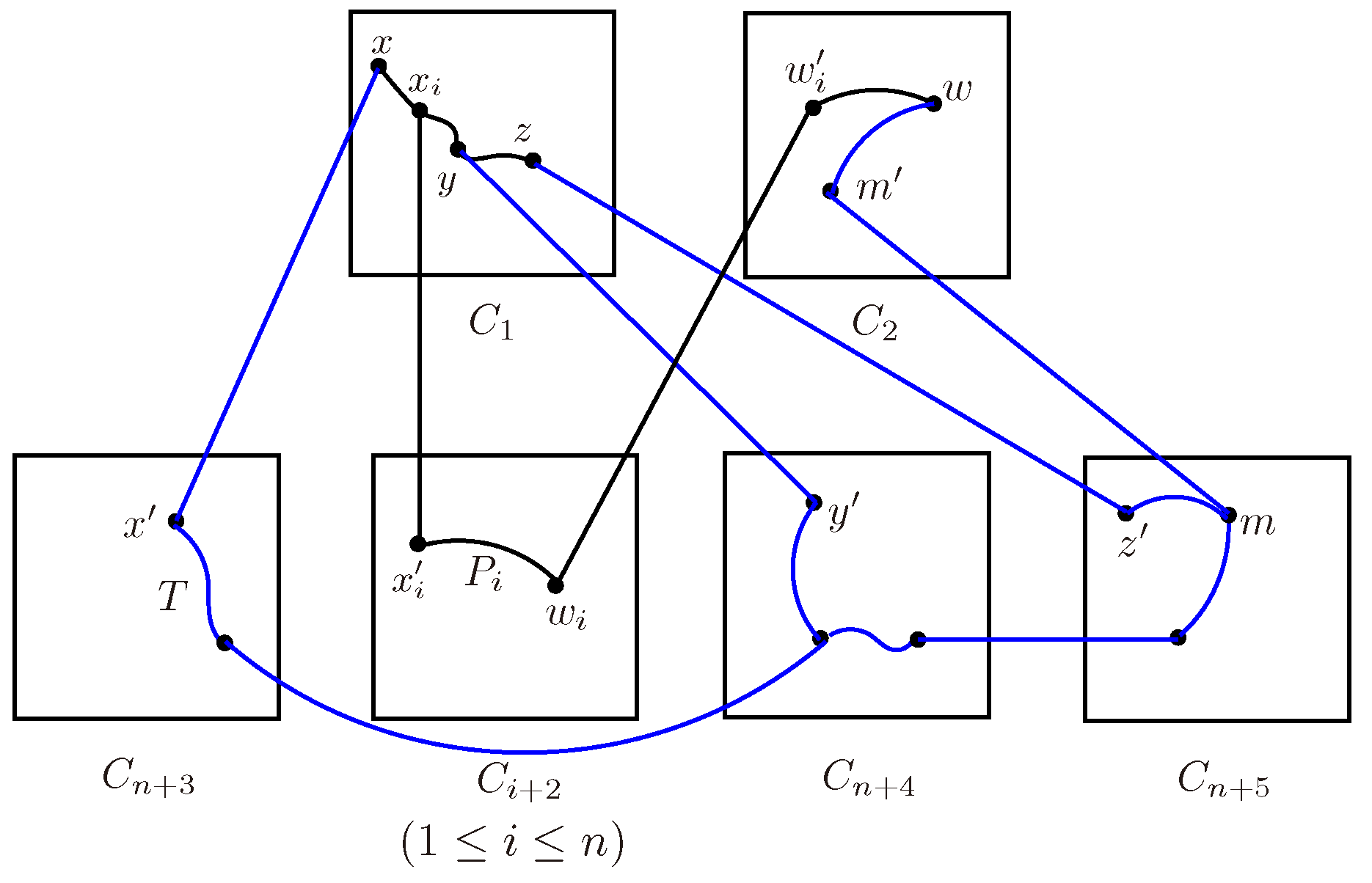
C_{1}, C_{2}, \dots, C_{2^{n}}

be the

2^{n}

clusters of

H F Q_{n}

for

n \geq 7

and

S = {x, y, z, w} \subseteq V (H F Q_{n})

. Let

| S \cap V (C_{i}) | = 2

and

| S \cap V (C_{j}) | = 2

for different

i, j \in [2^{n}]

, then there exist

n + 1

internally disjoint S-trees in

H F Q_{n}

Proof.

w.l.o.g., suppose that

| S \cap V (C_{1}) | = 2

| S \cap V (C_{2}) | = 2

. Let

x, y \in V (C_{1})

and

z, w \in V (C_{2})

. By Lemma 2.5,

κ (C_{1}) = κ (C_{2}) = n + 1

, then there exist

n + 1

internally disjoint paths

P_{1}, P_{2}, \dots, P_{n + 1}

joining x and y in

C_{1}

and

n + 1

internally disjoint paths

P_{1}^{'}, P_{2}^{'}, \dots, P_{n + 1}^{'}

joining z and w in

C_{2}

. Let

x_{i} \in V (P_{i}) \cap N (x)

and

z_{i} \in V (P_{i}^{'}) \cap N (z)

for

i \in [n + 1]

. Let

\hat{X} = {x, x_{1}, x_{2}, \dots, x_{n + 1}}

and

\hat{Z} = {z, z_{1}, z_{2}, \dots, z_{n + 1}}

. Select n vertices from

\hat{X}

, namely X, subject to the external neighbor of arbitrary vertex in X doesn’t distribute in

C_{2}

. As the same way, select n vertices from

\hat{Z}

, namely Z, subject to the external neighbor of arbitrary vertex in Z doesn’t distribute in

C_{1}

. By Lemma 2.2, it can be done. w.l.o.g., suppose that

X = {x_{1}, x_{2}, \dots, x_{n}}

and

Z = {z_{1}, z_{2}, \dots, z_{n}}

. By

(1)

of Lemma 2.2, any vertex in

X (r e s p . Z)

with its external neighbor belongs to different clusters. Let vertex subset

X^{'} = {x_{1}^{'}, x_{2}^{'}, \dots, x_{n + 1}^{'}}

and vertex subset

Z^{'} = {z_{1}^{'}, z_{2}^{'}, \dots, z_{n + 1}^{'}}

Case 1. There are two vertices in

\hat{X}

with the external neighbors distribute in

C_{2}

By (2) of Lemma 2.2, two vertices

x^{'}, x_{n + 1}^{'} \in V (C_{2})

. By (1) of Lemma 2.2, any vertex in

X (r e s p . Z)

with its external neighbor belongs to different clusters. To avoid repetition, we just consider the vertices in

X^{'} \cup Z^{'}

distribute in distinct clusters, as the discussion of some vertex

x_{i}^{'}

belongs to the same cluster with

z_{i}^{'}

is similar. Let

x_{i}^{'} \in V (C_{i + 2})

and

z_{i}^{'} \in V (C_{n + i + 2})

for

i \in [n]

. By Lemma 2.3,

H F Q_{n} [\cup_{j = i + 2}^{n + i + 2} V (C_{j})]

is connected, then there exists a tree

{\hat{T}}_{i}

connecting

x_{i}^{'}

and

z_{i}^{'}

. Let

T_{i} = P_{i} \cup x_{i} x_{i}^{'} \cup {\hat{T}}_{i} \cup P_{i}^{'} \cup z_{i} z_{i}^{'}

for

i \in [n]

When

x^{'}

x_{n + 1}^{'}

distributes in

V (P_{i}^{'})

for some

i \in [n + 1]

. w.l.o.g., assume that

x_{n + 1}^{'} \in V (P_{n + 1}^{'})

. Let

T_{n + 1} = P_{n + 1} \cup x_{n + 1} x_{n + 1}^{'} \cup P_{n + 1}^{'}

Figure 8. The explanation about

x^{'}

x_{n + 1}^{'}

distributes in

V (P_{i}^{'})

of Case 1.

Figure 8. The explanation about

x^{'}

x_{n + 1}^{'}

distributes in

V (P_{i}^{'})

of Case 1.

When

x^{'}

and

x_{n + 1}^{'}

don’t belong to

V (P_{i}^{'})

for

i \in [n + 1]

. Since

C_{2}

is connected, there is a path R joining

x^{'}

and z, that is

R \cap N_{C_{2}} (z) \neq ⊘

. w.l.o.g., let

R \cap N_{C_{2}} (z) = {z_{n + 1}}

. Let

T_{n + 1} = P_{n + 1} \cup x x^{'} \cup R \cup P_{n + 1}^{'}

Case 2. There is only one vertex in

\hat{X}

with the external neighbor distributing in

C_{2}

The proof is similar to that of Case 1.

Case 3. None of the vertex in

\hat{X}

with their external neighbor distributes in

C_{2}

To avoid repetition, we just consider the vertices in

X^{'} \cup Z^{'}

distribute in distinct clusters, as the discussion of some vertex

x_{i}^{'}

belongs to the same cluster with

z_{i}^{'}

is similar. This can be done for

n \geq 7

. Let

x_{i}^{'} \in V (C_{i + 2})

and

z_{i}^{'} \in V (C_{n + i + 3})

for

i \in [n + 1]

. By 2 of Lemma 2.1,

C_{i + 2}

is connected to

C_{n + i + 3}

, then there is a tree

{\hat{T}}_{i}

connecting

x_{i}^{'}

and

z_{i}^{'}

. Let

T_{i} = P_{i} \cup x_{i} x_{i}^{'} \cup {\hat{T}}_{i} \cup z_{i} z_{i}^{'}

for

i \in [n + 1]

.□

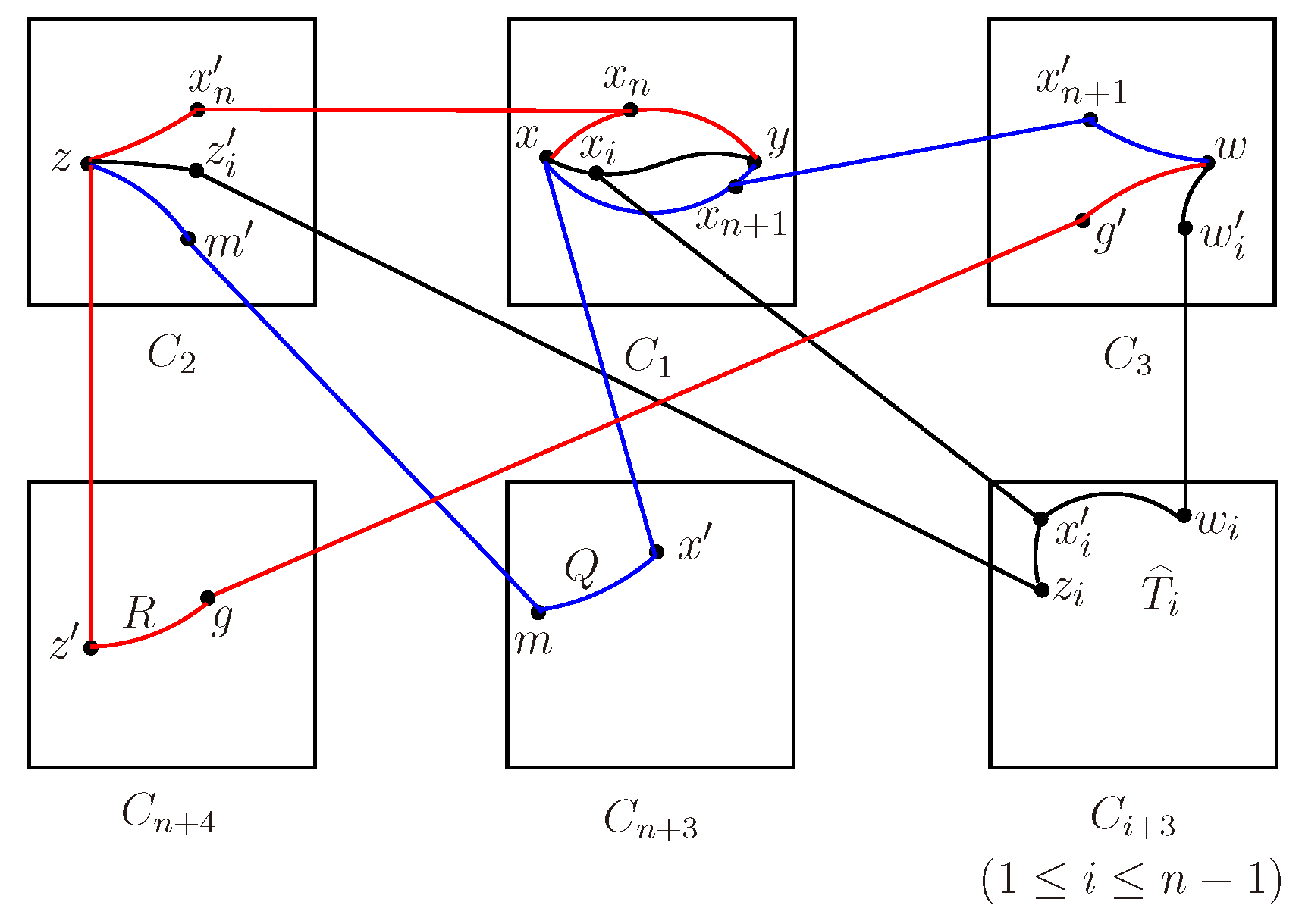
Lemma 3.7.

Let

C_{1}, C_{2}, \dots, C_{2^{n}}

be the

2^{n}

clusters of

H F Q_{n}

for

n \geq 7

and

S = {x, y, z, w} \subseteq V (H F Q_{n})

. Let

| S \cap V (C_{i}) | = 2

| S \cap V (C_{j}) | = 1

and

| S \cap V (C_{k}) | = 1

for different

i, j, k \in [2^{n}]

, then there exist

n + 1

internally disjoint S-trees in

H F Q_{n}

Proof.

w.l.o.g., suppose that

| S \cap V (C_{1}) | = 2

| S \cap V (C_{2}) | = 1

and

| S \cap V (C_{3}) | = 1

. Let

{x, y} \subseteq V (C_{1})

z \in V (C_{2})

and

w \in V (C_{3})

. By Lemma 2.5,

κ (C_{1}) = n + 1

, then there are

n + 1

internally disjoint paths

P_{1}, P_{2}, \dots, P_{n + 1}

joining x and y in

C_{1}

. Let

x_{i} \in V (P_{i}) \cap N (x)

for

i \in [n + 1]

and

X = {x_{1}, x_{2}, \dots, x_{n + 1}, x}

. Note that, it is possible that

y \in X

. In fact, to avoid repetition, we only consider the case of

y \notin X

Case 1. There exist three cross edges between X and

V (C_{2} \cup C_{3})

Figure 9. The explanation of Case 1.

w.l.o.g., assume that there are two cross edges between X and

C_{2}

and one cross edge between X and

C_{3}

. By Lemma 2.2, suppose that

x^{'}, x_{n + 1}^{'} \in V (C_{2})

and

x_{n}^{'} \in V (C_{3})

. Let

x_{i}^{'} \in V (C_{i + 3})

, where

i \in [n - 1]

. Since

C_{i + 3}

is connected, there is a tree

{\hat{T}}_{i}

connecting

z_{i}, w_{i}

and

x_{i}^{'}

C_{i + 3}

and such that

z_{i}^{'} \in V (C_{2})

w_{i}^{'} \in V (C_{3})

. There are two cross edges between

C_{1}

and

C_{2}

, then

z^{'} \notin H F Q_{n} [V (C_{1} \cup C_{2} \cup C_{i + 3})]

for

i \in [n - 1]

. w.l.o.g., let

z^{'} \in V (C_{n + 3})

. Since

C_{n + 3}

is connected, there is a path R joining

z^{'}

and m in

C_{n + 3}

and such that

m^{'} \in V (C_{3})

. Let

Z = {z_{1}^{'}, z_{2}^{'}, \dots, z_{n - 1}^{'}, x^{'}, x_{n + 1}^{'}}

and

W = {w_{1}^{'}, w_{2}^{'}, \dots, w_{n - 1}^{'}, x_{n}^{'}, m^{'}}

. By Lemma 3.3, there exist

n + 1

internally disjoint paths

P_{1}^{'}, P_{2}^{'}, \dots, P_{n + 1}^{'}

between z and Z, subject to

z_{i}^{'} \in V (P_{i}^{'})

x^{'} \in V (P_{n}^{'})

and

x_{n + 1}^{'} \in V ((P_{n + 1}^{'})

for

i \in [n - 1]

. Similarly, there are

n + 1

internally disjoint paths

{\hat{P}}_{1}, {\hat{P}}_{2}, \dots, {\hat{P}}_{n + 1}

from w to W, such that

w_{i}^{'} \in V ({\hat{P}}_{i})

x_{n}^{'} \in V ({\hat{P}}_{n})

and

m^{'} \in V ({\hat{P}}_{n + 1})

for

i \in [n - 1]

. Let

T_{i} = P_{i} \cup x_{i} x_{i}^{'} \cup {\hat{T}}_{i} \cup z_{i} z_{i}^{'} \cup P_{i}^{'} \cup w_{i} w_{i}^{'} \cup {\hat{P}}_{i}

for

i \in [n - 1]

T_{n} = P_{n} \cup x x^{'} \cup P_{n}^{'} \cup x_{n} x_{n}^{'} \cup {\hat{P}}_{n}

and

T_{n + 1} = P_{n + 1} \cup x_{n + 1} x_{n + 1}^{'} \cup P_{n + 1}^{'} \cup z z^{'} \cup R \cup m m^{'} \cup {\hat{P}}_{n + 1}

Case 2. There exist two cross edges between X and

V (C_{2} \cup C_{3})

Case 2.1. There are two cross edges between X and

C_{2}

w.l.o.g., suppose that

x^{'}, x_{n + 1}^{'} \in V (C_{2})

. Similar to Case 1, we by replacing subset

Z = {z_{1}^{'}, z_{2}^{'}, \dots, z_{n - 1}^{'}, x^{'}, x_{n + 1}^{'}}

to subset

Z = {z_{1}^{'}, z_{2}^{'}, \dots, z_{n}^{'}, x_{n + 1}^{'}}

and replacing subset

W = {w_{1}^{'}, w_{2}^{'}, \dots, w_{n - 1}^{'}, x_{n}^{'}, m^{'}}

to subset

W = {w_{1}^{'}, w_{2}^{'}, \dots, w_{n}^{'}, m^{'}}

, we get

T_{1}, T_{2}, T_{n - 1}, T_{n + 1}

n internally disjoint S-trees. As for the n-th S-tree, we changed

T_{n} = P_{n} \cup x x^{'} \cup P_{n}^{'} \cup x_{n} x_{n}^{'} \cup {\hat{P}}_{n}

into

T_{n} = P_{i} \cup x_{n} x_{n}^{'} \cup {\hat{T}}_{n} \cup z_{n} z_{n}^{'} \cup P_{n}^{'} \cup w_{n} w_{n}^{'} \cup {\hat{P}}_{n}

Figure 10. The explanation of Case

2.1

Figure 10. The explanation of Case

2.1

Case 2.2. There is one cross edge between X and

C_{2}

, the other between X and

C_{3}

Case 2.2.1.

x^{'}, x_{i}^{'} \in V (C_{2} \cup C_{3})

for certain

i \in [n + 1]

w.l.o.g., assume that

x^{'} \in V (C_{2})

x_{n + 1}^{'} \in V (C_{3})

. By Lemma 2.2, the vertices in

{x_{1}^{'}, x_{2}^{'}, \dots, x_{n}^{'}}

distribute in different clusters. Let

x_{i}^{'} \in V (C_{i + 3})

for

i \in [n]

. Since

C_{i + 3}

is connected, there exists a tree

{\hat{T}}_{i}

connecting

x_{i}^{'}, z_{i}, w_{i}

and such that

z_{i}^{'} \in V (C_{2})

w_{i}^{'} \in V (C_{3})

. Let

Z = {z_{1}^{'}, z_{2}^{'}, \dots, z_{n}^{'}, x^{'}}

and

W = {w_{1}^{'}, w_{2}^{'}, \dots, w_{n}^{'}, x_{n + 1}^{'}}

. By Lemma 3.3, there exist

n + 1

internally disjoint paths

P_{1}^{'}, P_{2}^{'}, \dots, P_{n + 1}^{'}

from z and Z,

n + 1

internally disjoint paths

{\hat{P}}_{1}, {\hat{P}}_{2}, \dots, {\hat{P}}_{n + 1}

from w to W and subject to

z_{i}^{'} \in V (P_{i}^{'})

x^{'} \in V (P_{n + 1}^{'})

w_{i}^{'} \in V ({\hat{P}}_{i})

x_{n + 1}^{'} \in V ({\hat{P}}_{n + 1})

, where

i \in [n]

. Let

T_{i} = P_{i} \cup x_{i} x_{i}^{'} \cup {\hat{T}}_{i} \cup z_{i} z_{i}^{'} \cup P_{i}^{'} \cup w_{i} w_{i}^{'} \cup {\hat{P}}_{i}

, where

i \in [n]

. Let

T_{n + 1} = P_{n + 1} \cup x x^{'} \cup P_{n + 1}^{'} \cup x_{n + 1} x_{n + 1}^{'} \cup {\hat{P}}_{n + 1}

Case 2.2.2.

x_{i}^{'}, x_{j}^{'} \in V (C_{2} \cup C_{3})

, for

i \neq j

and

i, j \in [n + 1]

w.l.o.g., suppose that

x_{n}^{'} \in V (C_{2})

x_{n + 1}^{'} \in V (C_{3})

and

x_{i}^{'} \in V (C_{i + 3})

, where

i \in [n - 1]

When

y^{'} \in V (C_{2})

, by 2 of Lemma 2.1,

x^{'} \notin V (C_{1} \cup C_{2} \cup \dots \cup C_{n + 2})

. w.l.o.g., assume that

x^{'} \in V (C_{n + 3})

. As

C_{n + 3}

is connected, there is a path Q joining

x^{'}

and m, subject to

m^{'} \in V (C_{2})

. Let

Z = {z_{1}^{'}, z_{2}^{'}, \dots, z_{n - 1}^{'}, x_{n}^{'}, m^{'}}

. Note that, it is possible that

z \in Z

. To avoid repetition, we just consider the case of

z \notin Z

, as the discussion of

z \in Z

is similar. By

(2)

of Lemma 2.1,

z^{'} \notin V (C_{1} \cup C_{2} \cup \dots \cup C_{n + 3})

. w.l.o.g., let

z^{'} \in V (C_{n + 4})

. As

C_{n + 4}

is connected, there is a path R joining

z^{'}

and g and subject to

g^{'} \in V (C_{3})

. Let

W = {w_{1}^{'}, w_{2}^{'}, \dots, w_{n - 1}^{'}, x_{n + 1}^{'}, g^{'}}

. By the Lemma 2.4,

κ (C_{2}) = κ (C_{3}) = n + 1

. By the Lemma 3.3, there are

P_{1}^{'}, P_{2}^{'}, \dots, P_{n + 1}^{'}

n + 1

internally disjoint paths between z and Z and

{\hat{P}}_{1}, {\hat{P}}_{2}, \dots, {\hat{P}}_{n + 1}

n + 1

internally disjoint paths between w and W such that

z_{i}^{'} \in V (P_{i}^{'})

x_{n}^{'} \in V (P_{n}^{'})

m^{'} \in V (P_{n + 1}^{'})

and

w_{i}^{'} \in V ({\hat{P}}_{i})

g^{'} \in V ({\hat{P}}_{n})

x_{n + 1}^{'} \in V ({\hat{P}}_{n + 1})

for

i \in [n - 1]

. Let

T_{i} = P_{i} \cup x_{i} x_{i}^{'} \cup {\hat{T}}_{i} \cup z_{i} z_{i}^{'} \cup P_{i}^{'} \cup w_{i} w_{i}^{'} \cup {\hat{P}}_{i}

, where

i \in [n - 1]

T_{n} = P_{n} \cup x_{n} x_{n}^{'} \cup P_{n}^{'} \cup z z^{'} \cup R \cup g g^{'} \cup {\hat{P}}_{n}

and

T_{n + 1} = P_{n + 1} \cup x_{n + 1} x_{n + 1}^{'} \cup {\hat{P}}_{n + 1} \cup x x^{'} \cup Q \cup m m^{'} \cup P_{n + 1}^{'}

Figure 11. The explanation of

y^{'} \in V (C_{2})

of Case

2.2 . 2

Figure 11. The explanation of

y^{'} \in V (C_{2})

of Case

2.2 . 2

When

y^{'} \in V (C_{3})

, similar to the situation of

y^{'} \in V (C_{2})

, we obtain

n + 1

internally disjoint S-trees.

When

y^{'} \in V (C_{i + 3})

, for certain

i \in [n - 1]

. Similar to the situation of

y^{'} \in V (C_{2})

, we obtain

n + 1

internally disjoint S-trees.

When

y^{'} \notin V (H F Q_{n}) ∖ \cup_{i = 1}^{n + 2} V (C_{i})

. w.l.o.g., assume that

y^{'} \in V (C_{n + 3})

. Since

C_{n + 3}

is connected, there is a path M joining

y^{'}

and m, subject to

m^{'} \in V (C_{2})

. Let

Z = {z_{1}^{'}, z_{2}^{'}, \dots, z_{n - 1}^{'}, x_{n}^{'}, m^{'}}

and

W = {w_{1}^{'}, w_{2}^{'}, \dots, w_{n - 1}^{'}, g, x_{n + 1}^{'}}

and subject to

g^{'} \in V (C_{2})

. By the Lemma 2.4,

κ (C_{2}) = κ (C_{3}) = n + 1

. By the Lemma 3.3, there are

P_{1}^{'}, P_{2}^{'}, \dots, P_{n + 1}^{'}

n + 1

internally disjoint paths between z and Z,

{\hat{P}}_{1}, {\hat{P}}_{2}, \dots, {\hat{P}}_{n + 1}

n + 1

internally disjoint paths from w to W such that

z_{i}^{'} \in V (P_{i}^{'})

x_{n}^{'} \in V (P_{n}^{'})

m^{'} \in V (P_{n + 1}^{'})

and

w_{i}^{'} \in V ({\hat{P}}_{i})

g^{'} \in V ({\hat{P}}_{n})

x_{n + 1}^{'} \in V ({\hat{P}}_{n + 1})

, where

i \in [n - 1]

. We obtain

T_{1}, T_{2}, \dots, T_{n - 1}

n - 1

internally disjoint S-trees, similar to the situation of

y^{'} \in V (C_{2})

. Let

T_{n + 1} = P_{n + 1} \cup x_{n + 1} x_{n + 1}^{'} \cup {\hat{P}}_{n + 1} \cup y y^{'} \cup M \cup m m^{'} \cup P_{n + 1}^{'}

. For the n-th tree, we consider the following two situations. First, assume that

m^{'} \in V (P_{i}^{'})

for certain

i \in [n + 1]

. w.l.o.g., suppose that

g^{'} \in V (P_{n}^{'})

. Let

T_{n} = P_{n} \cup x_{n} x_{n}^{'} \cup P_{n}^{'} \cup g g^{'} \cup {\hat{P}}_{n}

. Next, suppose that

g^{'} \notin V (P_{i}^{'})

for

i \in [n + 1]

. As

C_{2}

is connected, there is a path Q joining z and

g^{'}

. That is,

R \cap N (z) \neq ⊘

. w.l.o.g., let

R \cap N (z) = {z_{n}}

, that is

R \cap V (P_{n}^{'}) = {z_{n}}

. Let

T_{n} = P_{n} \cup x_{n} x_{n}^{'} \cup P_{n}^{'} \cup R \cup g g^{'} \cup {\hat{P}}_{n}

Case 3. There exist one cross edge between X and

V (C_{2} \cup C_{3})

Suppose that the cross edge is between X and

V (C_{2})

Case 3.1.

x^{'} \in V (C_{2})

By Lemma 2.2, the vertices in

{x_{1}^{'}, x_{2}^{'}, \dots, x_{n + 1}^{'}}

distribute in distinct clusters of

H F Q_{n}

. Let

x_{i}^{'} \in V (C_{i + 3})

, where

i \in [n + 1]

. Since

C_{i + 3}

is connected, there is a tree

{\hat{T}}_{i}

connecting

x_{i}^{'}, z_{i}, w_{i}

and subject to

z_{i}^{'} \in V (C_{2})

w_{i}^{'} \in V (C_{3})

, where

i \in [n + 1]

. Let subset

Z = {z_{1}^{'}, z_{2}^{'}, \dots, z_{n + 1}^{'}}

and subset

W = {w_{1}^{'}, w_{2}^{'}, \dots, w_{n + 1}^{'}}

. By Lemma 2.4,

κ (C_{2}) = κ (C_{3}) = n + 1

. By Lemma 3.3, there are

P_{1}^{'}, P_{2}^{'}, \dots, P_{n + 1}^{'}

n + 1

internally disjoint paths between z and Z,

{\hat{P}}_{1}, {\hat{P}}_{2}, \dots, {\hat{P}}_{n + 1}

n + 1

internally disjoint paths between w and W. Let

T_{i} = P_{i} \cup x_{i} x_{i}^{'} \cup {\hat{T}}_{i} \cup z_{i} z_{i}^{'} \cup P_{i}^{'} \cup w_{i} w_{i}^{'} \cup {\hat{P}}_{i}

for

i \in [n + 1]

Figure 12. The explanation of Case

3.1

Figure 12. The explanation of Case

3.1

Case 3.2.

x_{i}^{'} \in V (C_{2})

for some

i \in [n + 1]

w.l.o.g., suppose that

x_{n + 1}^{'} \in V (C_{2})

and

x_{i}^{'} \in V (C_{i + 3})

for

i \in [n]

When

x^{'} \in V (C_{n + 4})

. By Lemma 2.2, the vertices in

{x_{1}^{'}, x_{2}^{'}, \dots, x_{n}^{'}}

distribute in different clusters of

H F Q_{n}

. Let

x_{i}^{'} \in V (C_{i + 3})

for

i \in [n]

. Since

C_{i + 3}

is connected, then there is a tree

{\hat{T}}_{i}

connecting

x_{i}^{'}, z_{i}, w_{i}

and subject to

z_{i}^{'} \in V (C_{2})

w_{i}^{'} \in V (C_{3})

, where

i \in [n]

. Let

Z = {z_{1}^{'}, z_{2}^{'}, \dots, z_{n}^{'}, x_{n + 1}^{'}}

W = {w_{1}^{'}, w_{2}^{'}, \dots, w_{n}^{'}, m}

and subject to

m^{'} \in V (C_{n + 4})

. By Lemma 2.4,

κ (C_{2}) = κ (C_{3}) = n + 1

. By Lemma 3.3, there are

P_{1}^{'}, P_{2}^{'}, \dots, P_{n + 1}^{'}

n + 1

internally disjoint paths between z and Z subject to

z_{i}^{'} \in V (P_{i}^{'})

x_{n + 1}^{'} \in V (P_{n + 1}^{'})

n + 1

internally disjoint paths

{\hat{P}}_{1}, {\hat{P}}_{2}, \dots, {\hat{P}}_{n + 1}

from w to W subject to

w_{i}^{'} \in V ({\hat{P}}_{i})

m^{'} \in V ({\hat{P}}_{n + 1})

for

i \in [n]

. Since

C_{n + 4}

is connected, then there exist a path R joining

x^{'}

and

m^{'}

. Let

T_{i} = P_{i} \cup x_{i} x_{i}^{'} \cup {\hat{T}}_{i} \cup z_{i} z_{i}^{'} \cup P_{i}^{'} \cup w_{i} w_{i}^{'} \cup {\hat{P}}_{i}

, where

i \in [n]

. Let

T_{n + 1} = P_{n + 1} \cup x_{n + 1} x_{n + 1}^{'} \cup P_{n + 1}^{'} \cup x x^{'} \cup R \cup m m^{'} \cup {\hat{P}}_{n + 1}

Figure 13. The explanation of

x^{'} \in V (C_{n + 4})

of Case

3.2

Figure 13. The explanation of

x^{'} \in V (C_{n + 4})

of Case

3.2

When

x^{'} \in V (C_{i + 3})

, by Lemma 2.2,

y^{'} \in V (C_{3})

y^{'} \in H F Q_{n} [⋃_{i = n + 4}^{2^{n}} V (C_{i})]

, similar to the case of

x^{'} \in V (C_{n + 4})

, we get

n + 1

internally disjoint S-trees.

Case 4. There is no cross edge between X and

V (C_{2} \cup C_{3})

Similar to that of Case

3.1

, we get

n + 1

internally disjoint S-trees.□

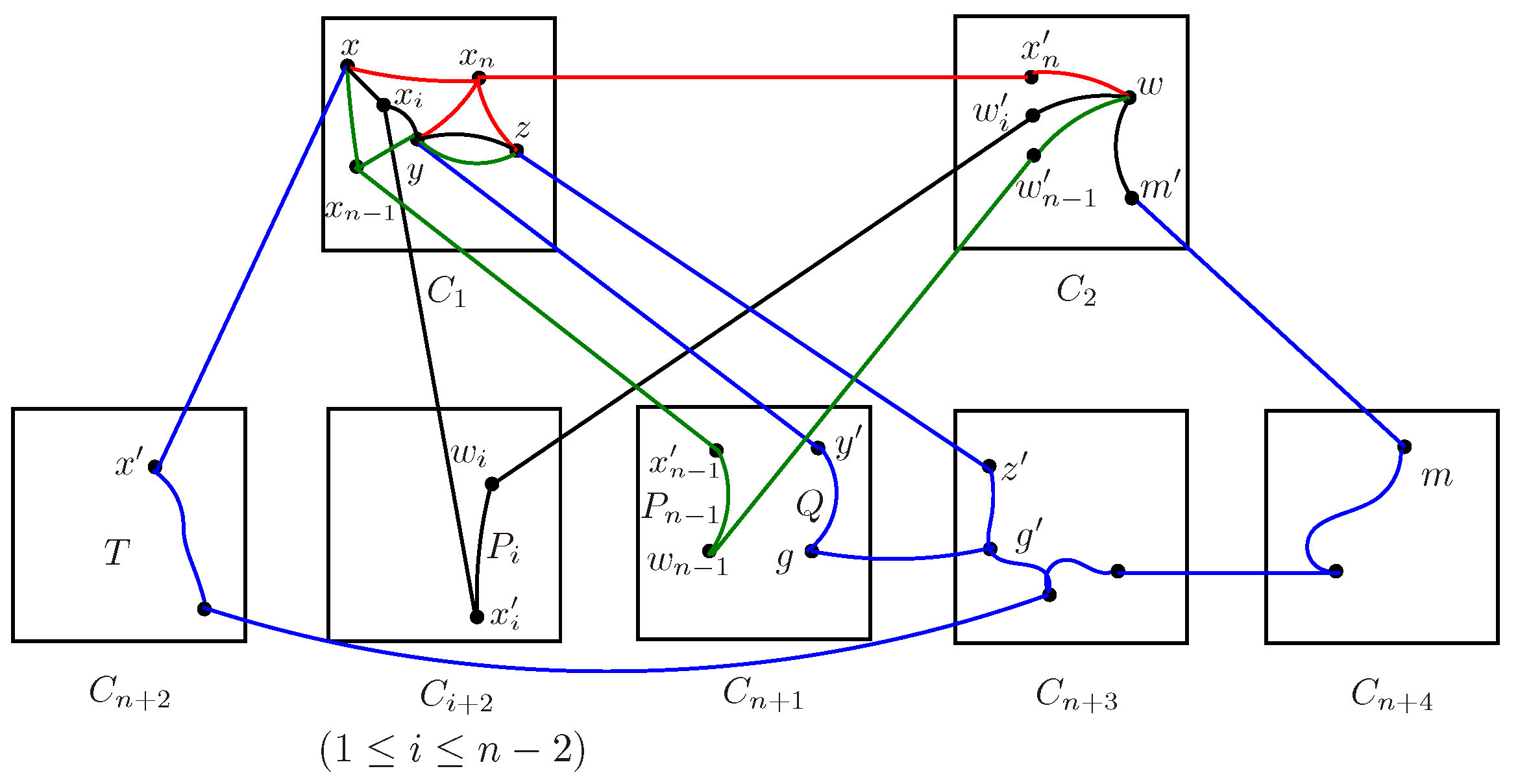
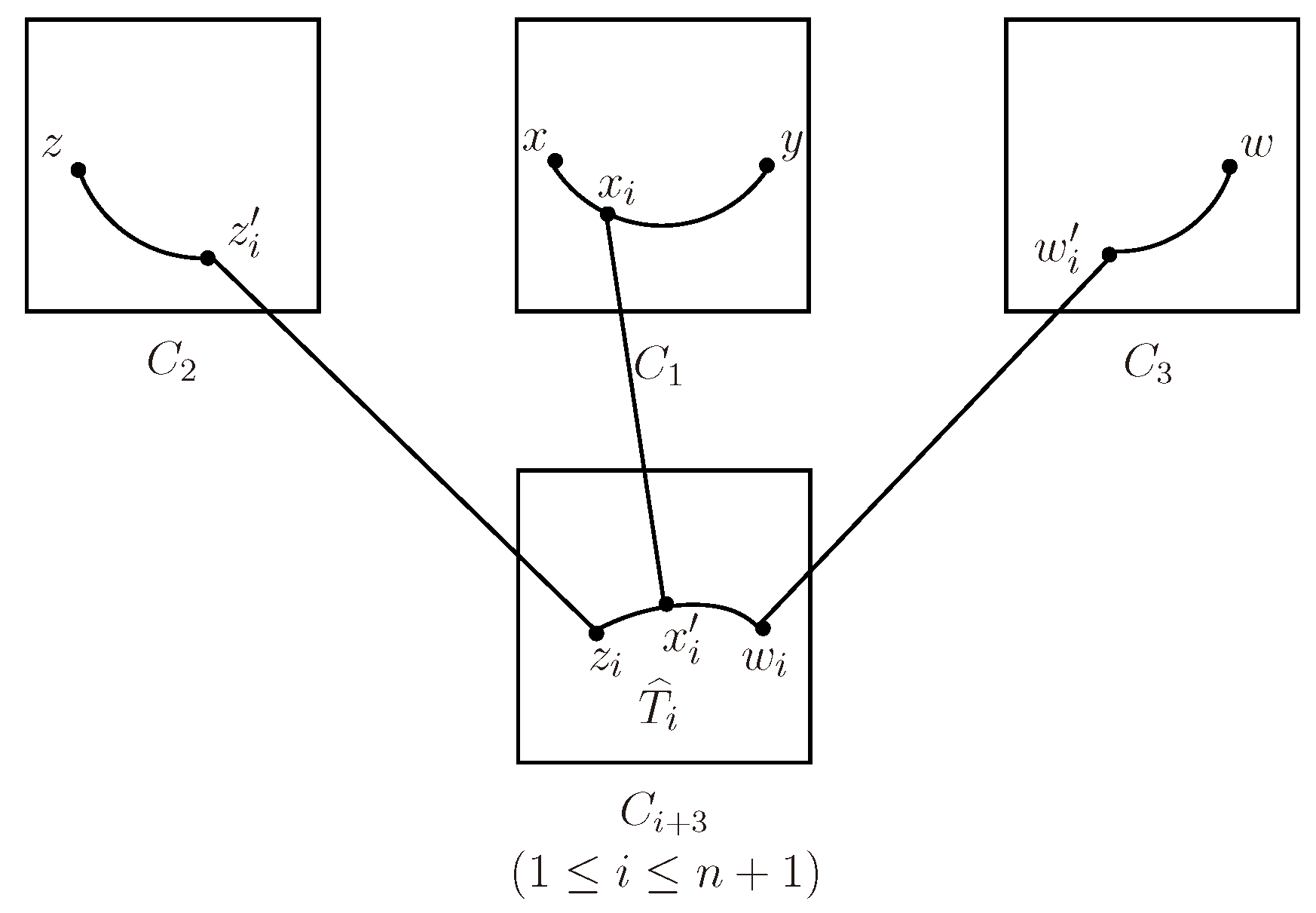
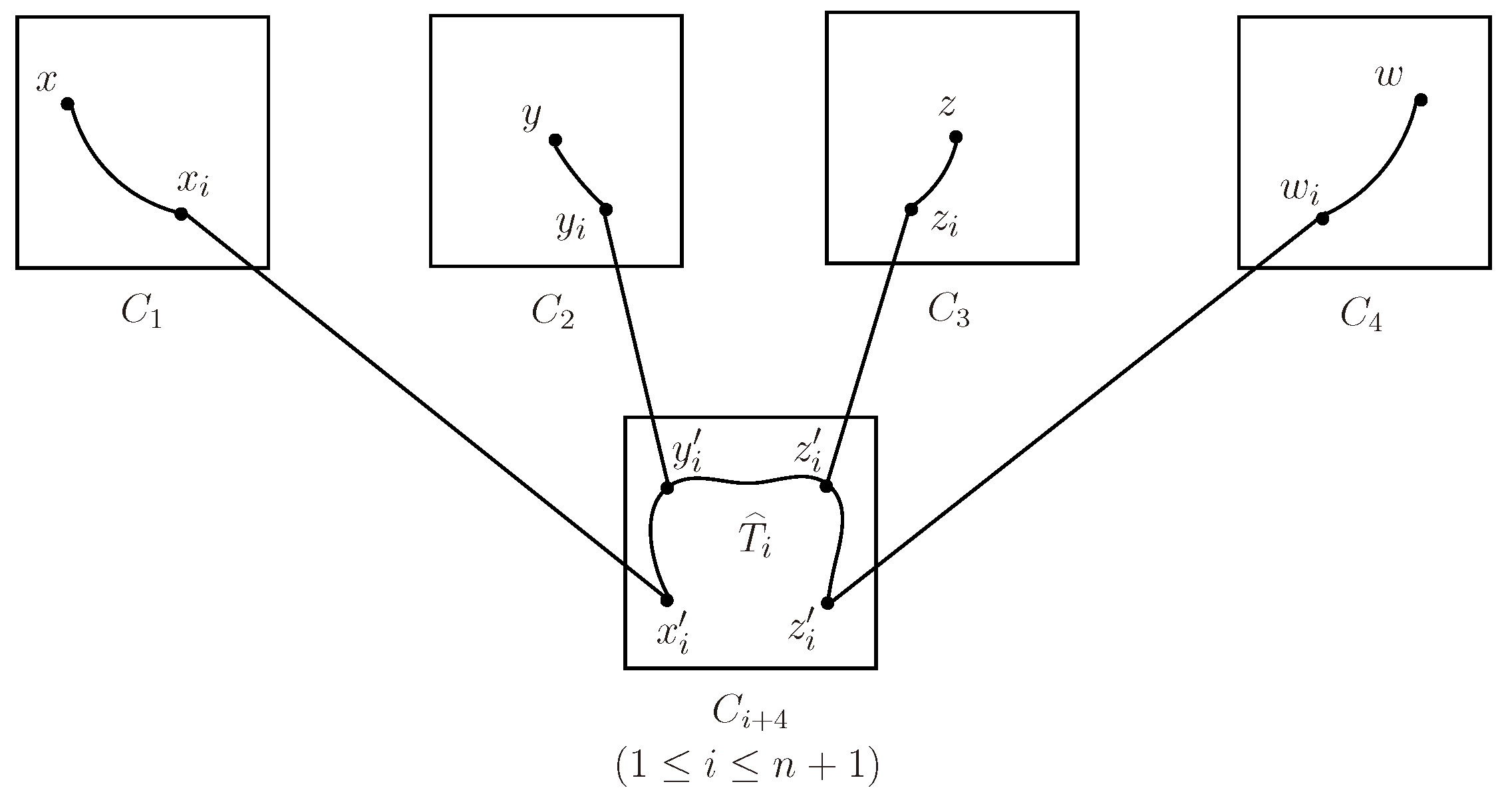
Lemma 3.8.

Let

C_{1}, C_{2}, \dots, C_{2^{n}}

be the

2^{n}

clusters of

H F Q_{n}

for

n \geq 7

and

S = {x, y, z, w} \subseteq V (H F Q_{n})

. Let

| S \cap V (C_{i}) | = 1

| S \cap V (C_{j}) | = 1

| S \cap V (C_{k}) | = 1

and

| S \cap V (C_{l}) | = 1

for different

i, j, k, l \in [2^{n}]

, then there exist

n + 1

internally disjoint S-trees in

H F Q_{n}

Figure 14. The explanation of Lemma 3.8.

Proof.

w.l.o.g., suppose that

| S \cap V (C_{1}) | = 1

| S \cap V (C_{2}) | = 1

| S \cap V (C_{3}) | = 1

and

| S \cap V (C_{4}) | = 1

. Let

x \in V (C_{1})

y \in V (C_{2})

z \in V (C_{3})

and

w \in V (C_{4})

. Let

X = {x_{1}, x_{2}, \dots, x_{n + 1}} \subseteq V (C_{1})

Y = {y_{1}, y_{2}, \dots, y_{n + 1}} \subseteq V (C_{2})

Z = {z_{1}, z_{2}, \dots, z_{n + 1}} \subseteq V (C_{3})

W = {w_{1}, w_{2}, \dots, w_{n + 1}} \subseteq V (C_{4})

. By Lemma 2.5,

κ (C_{1}) = κ (C_{2}) = κ (C_{3}) = κ (C_{4}) = n + 1

, then there are

n + 1

internally disjoint paths

P_{1}, P_{2}, \dots, P_{n + 1}

from x and X in

C_{1}

n + 1

internally disjoint paths

P_{1}^{'}, P_{2}^{'}, \dots, P_{n + 1}^{'}

from y and Y in

C_{2}

n + 1

internally disjoint paths

{\hat{P}}_{1}, {\hat{P}}_{2}, \dots, {\hat{P}}_{n + 1}

from z and Z in

C_{3}

n + 1

internally disjoint paths

{\tilde{P}}_{1}, {\tilde{P}}_{2}, \dots, {\tilde{P}}_{n + 1}

from z and Z in

C_{4}

, such that

x_{i} \in V (P_{i})

y_{i} \in V (P_{i}^{'})

z_{i} \in V ({\hat{P}}_{i})

z_{i} \in V ({\tilde{P}}_{i})

and such that

{x_{i}^{'}, y_{i}^{'}, z_{i}^{'}, w_{i}^{'}} \subseteq V (C_{i + 4})

for

i \in [n + 1]

. Since

C_{i + 4}

is connected, there exists a tree

{\hat{T}}_{i}

connecting

x_{i}^{'}, y_{i}^{'}, z_{i}^{'}, w_{i}^{'}

C_{i + 4}

for

i \in [n + 1]

. Let

T_{i} = {\hat{T}}_{i} \cup x_{i} x_{i}^{'} \cup y_{i} y_{i}^{'} \cup z_{i} z_{i}^{'} \cup w_{i} w_{i}^{'} \cup P_{i} \cup P_{i}^{'} \cup {\hat{P}}_{i} \cup {\tilde{P}}_{i}

for

i \in [n + 1]

.□

Theorem 3.3.

κ_{4} (H F Q_{n}) = n + 1

, for

n \geq 7

Proof.

By Lemma 2.5,

κ (H F Q_{n}) = n + 2

. By Lemma 3.1,

κ_{4} (H F Q_{n}) \leq δ (H F Q_{n}) - 1 = n + 1

. By Lemma 3.5, Lemma 3.6, Lemma 3.7, Lemma 3.8, we obtain that

κ_{4} (H F Q_{n}) \geq n + 1

. Thus, the result holds.□

4. Concluding remarks

The hierarchical folded hypercube

H F Q_{n}

is a more popular topology for designing the internetworks due to its regularity, symmetry and many other unique properties. As one of the important variants of the hypercube, hierarchical folded hypercube has received more attention and many research results on hierarchical folded hypercube have emerged. We mainly study the 4-set tree connectivity of hierarchical folded hypercube and obtain that

κ_{4} (H F Q_{n}) = n + 1

for

n \geq 7

. Currently, there are few results about k-set tree connectivity of networks when

k = 4

and most of the results are about

k = 3

. Our future work would like to consider the k-set tree connectivity of some network for

k \geq 5

and it will be a great challenge.

Funding

Supported by Qinghai University Science Foundation of China (No. 2023-QGY-6), the National Science Foundation of China (Nos. 12261074, 12201335 and 11661068)

References

Bondy, J.A.; Murty, U.S.R. Graph Theory; Springer: New York, 2008. [Google Scholar]
Whitney, H. Congruent graphs and connectivity of graphs. J. Amer Math Soc. 1932, 54, 150–168. [Google Scholar] [CrossRef]
Chartrand, G.; Kappor, S.; Lesniak, L. Generalized connectivity in graphs. Bombay Math 1984, 2, 1–6. [Google Scholar]
Li, H.; Li, X.; Mao, Y.; Sun, Y. Note on the generalized connectivity. Ars Combin 2014, 114, 193–202. [Google Scholar]
Li, S.; Li, X.; Zhou, W. Sharp bounds for the generalized connectivity. Discrete Math 2010, 310, 2147–2163. [Google Scholar] [CrossRef]
Li, H.; Wu, B.; Meng, J.; Mao, Y. Steiner tree packing number and tree connectivity. Discrete Math 2018, 341, 1945–1951. [Google Scholar] [CrossRef]
Chartrand, G.; Okamoto, F.; Zhang, P. Rainbow trees in graphs and generalized connectivity. Networks 2010, 55, 360–367. [Google Scholar] [CrossRef]
Li, H.; Li, X.; Sun, Y. The generalized 3-connectivity of Cartesian product graphs. Discrete Math Theor Comput Sci 2012, 14, 43–54. [Google Scholar] [CrossRef]
Li, H.; Ma, Y.; Yang, W.; Wang, Y. The generalized 3-connectivity of graph products. Appl Math Comput 2017, 295, 77–83. [Google Scholar] [CrossRef]
Li, S.; Li, W.; Li, X. The generalized connectivity of complete bipartite graphs. Ars Combin 2012, 104, 65–79. [Google Scholar] [CrossRef]
Zhao, S.; Hao, R. The generalized connectivity of alternating group graphs and (n,k)-star graphs. Discrete Appl Math 2018, 251, 310–321. [Google Scholar] [CrossRef]
Lin, S.; Zhang, Q. The generalized 4-connectivity of hypercubes. Discret Appl Math 2017, 220, 60–67. [Google Scholar] [CrossRef]
Zhao, S.; Hao, R. The generalized 4-connectivity of exchanged hypercubes. Appl Math Comput 2019, 347, 342–353. [Google Scholar] [CrossRef]
Zhao, S.; Hao, R.; Cheng, E. Two kinds of generalized connectivity of dual cubes. Discret Appl Math 2019, 257, 306–316. [Google Scholar] [CrossRef]
Zhao, S.; Hao, R.; Wu, J. The generalized 4-connectivity of hierarchical cubic networks. Discret Appl Math 2021, 289, 194–206. [Google Scholar] [CrossRef]
Li, X.; Mao, Y. Generalized Connectivity of Graphs; Springer Cham Publishing, 2016. [Google Scholar]
Sun, Y.; Li, X. On the difference of two generalized connectivities of a graph. J Combin Optim 2017, 33, 283–291. [Google Scholar] [CrossRef]
Sun, Y.; Li, F.; Jin, Z. On two generalized connectivities of graphs. Disc Math Theo 2018, 38, 245–261. [Google Scholar]
Li, X.; Mao, Y. A survey on the generalized connectivity of graphs. Comput Sci 2012. [CrossRef]
EL-Amawy, A.; Latifi, S. Properties and performance of folded hypercubes. IEEE Trans. Parallel Distrib. Syst. 1991, 2, 31–42. [Google Scholar] [CrossRef]
Sun, X.; Dong, Q.; Zhou, S.; et al. Fault tolerance analysis of hierarchical folded cube. Theor Comput Sci 2019, 790, 117–130. [Google Scholar] [CrossRef]
Li, S.; Tu, J.; Yu, C. The generalized 3-connectivity of star graphs and bubble-sort graphs. Appl Math Comput 2016, 274, 41–46. [Google Scholar] [CrossRef]
Li, C.; Lin, S.; Li, S. The 4-set tree connectivity of (n,k)-star networks. Theor Comput Sci 2020, 844, 81–86. [Google Scholar] [CrossRef]
Wang, J.; Zou, J.; Zhang, S. The generalized 4-connectivity of hierarchical star networks. Open Math 2022, 20, 1261–1275. [Google Scholar] [CrossRef]
Wang, J.; Zhang, S.; Ge, H. The generalized 3-connectivity of folded hypercubes. Journal of Shandong Univerdity 2022, 27, 42–49. [Google Scholar] [CrossRef]
Li, H.; Cheng, D. The generalized 4-connectivty of folded hypercube. International Journal of Computer Mathematics: Computer Systems Theory 2022, 7, 235–245. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.