Research on Two-Layer Optimal Dispatching Method Considering Mutual Aid of Peak Regulation Resources in Regional Power Grid

Preprint

Article

Research on Two-Layer Optimal Dispatching Method Considering Mutual Aid of Peak Regulation Resources in Regional Power Grid

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Tianmeng Yang^*,

Suhua Lou,Meng Zhang,Yanchun Li,Wei Feng,Jicheng Liu

Tianmeng Yang^*,

Suhua Lou,Meng Zhang,Yanchun Li,Wei Feng,Jicheng Liu

This version is not peer-reviewed

Submitted:

09 October 2023

Posted:

24 October 2023

You are already at the latest version

Alerts

Abstract

The power generation structure and load characteristics in different provinces are quite different in China, and the distribution of peak regulating resources and demands is extremely unbalanced. Due to many factors such as low power marketization degree, shortage of peak regulating resources and block of transmission channels, the consumption of new energy is facing greater pressure. In order to improve the mutual aids in regional power grid, this paper proposes a two-layer optimization dispatching model considering the mutual aids of peak regulation resources between each province, and determines the optimal units startup mode and power output in each provinces, thus obtaining all the power supply output arrangements and the technical and economic indicators. Finally, take the actual regional power grid in China as an example, the simulation results show that the proposed model can significantly improve the new energy utilization rate, which verified the effectiveness and feasibility of the proposed model and methods in this paper.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

With the proposal of the goal of "carbon peak and carbon neutral", the power generation structure is undergoing a low-carbon transformation in China, and renewable energy power generation is developing rapidly[1]. In order to make full use of zero-carbon renewable energy, the government has put forward high requirements of the consumption and utilization rate of renewable energy[2]. Therefore, how to scientifically plan the power grid development, optimize the operation mode of the power grid, make fully use of the limited flexible regulating resources in the regional power grid, maximize the consumption and utilization rate of renewable energy, and reduce the peak regulation costs have become critical problems which need to be solved in the current process of renewable energy development in China[3,4,5].

Currently, there are papers have studied the optimal dispatching operation method of power grid on the basis of considering the full utilization of peak regulation resources, but most of the research objects are provincial power grid. In [6], the multi-objective optimal scheduling model comprehensively considering the economy and flexibility of deep peak regulation is constructed, and the random characteristics of new energy power output is considered in the optimal model. In [7], by establishing the peak regulation right transaction of wind power and thermal power units, the combined thermoelectric economic dispatching model with the largest profits in the scheduling cycle is established, so as to stimulate the enthusiasm of thermoelectric units to participate in peak regulation, reduce the wind abandon power and improve the overall economic benefits of the system. In [8], based on the peak-regulating energy consumption costs model of different stages of thermal power units, the economic dispatching model which give priority to wind power utilization is established. In [9], based on the Manson-Coffin formula, the loss costs model of thermal power units under variable load is established, and on the basis of full acceptance of wind power, the economic dispatching model of power system based on hierarchical deep peak regulation is established with the goal of minimizing the total power generation costs of generating units.

In the study of the optimization dispatching method of the regional power grid, in [10,11,12], the feasibility and effectiveness of regional power grid peak regulation are verified. In [10], in view of the possible shortages of peak regulation resources in each provincial power grid, the transaction mechanism of peak regulation auxiliary service between regional power grid is proposed, and the clearing pricing model of peak regulation auxiliary services market is constructed. In [11], based on the analysis of power source and load characteristics in multiple regions, the typical peak-valley mutual aid operation scheme is given, and the typical operation mode and economic evaluation results of the multi-region power grid are optimized. In [12], a two-stage iterative power exchange optimization method based on marginal power generation costs is put forward. However, this method only aims at getting the minimum power grid operation costs, which can’t fully utilize of regional peak regulating resources. In [13], the environmental economy dispatching model of the regional power grid considering the inter-provincial power balance is established. However, only the actual power limit of the power grid is taken into consideration, and the influence of the actual electricity trading of the inter-provincial connection line is not considered. In [14], by studying the peak regulating characteristics of different power sources, the optimal dispatching method of regional power grid which considers peak regulating resources is studied. However, only the deep peak regulating operation costs of thermal power units is considered, and the influence of other peak regulating power sources in the current system is not considered.

In summary, the provincial power grid in China can exchange peak regulation resources through inter-provincial transmission lines, so as to make full use of peak regulating resources in the regional power grid. Based on this, on the basis of analyzing the peak regulation characteristics of different power sources, this paper fully considers the difference of surplus and gap of peak regulation power in different provinces in the region, and put forward a two-layer optimized dispatching model with the lowest operation costs and the highest utilization rate of renewable power in the regional power grid. The upper layer takes the lowest operation costs of each province in the region as the objective function, and the lower layer takes the highest utilization rate of renewable energy in the region as the objective function. Base on this, the inter-provincial transmission curve with the lowest costs and the highest renewable power utilization rate and the optimized operation results of the whole region are obtained. At last, take the actual regional power grid as an example, the feasibility and high efficiency of the proposed model and optimization method are verified.

2. System Peak-Regulating Resource Analysis

2.1. Analysis of Different Types of Power Supply

The power grid peak regulation scale of active power and quantity of electricity is large in China. Now the main resources that can effectively participate in the peak regulation are coal-fired units, gas units, cascade hydro-power units (non-runoff), pumped storage and other types of large capacity power storage. Among them, coal-fired units are non-stop peaking units, and gas units and cascade hydro-power units can be used as stop peaking units because of their rapid start and stop characteristics[15,16]. The peaking regulating characteristics of each power generation is shown in Table 1.

2.2. Analysis of Energy Consumption Costs of Coal-Fired Units

Based on the current power structure of power system, the function of coal-fired units gradually changes from the main source of electricity to the role of regularity and guaranteed power supply. When the coal-fired generation plays the regulatory function, the operating states of the unit changes frequently, and the technical and economic costs characteristics of the power generation have changed significantly.

According to the operating states and energy consumption characteristics of coal-fired units, the peak regulation process of coal-fired units can be divided into three stages: basic peak regulation(RPR), non-oil supply peak regulation(DPR) and oil supply peak regulation(DPRO). The peak regulation process and the corresponding energy consumption costs characteristic curves are shown in Figure 1.

P_{\max}^{G}

represents the rated power output of the coal-fired unit,

P_{a}^{G}

represents minimum technical power output of the unit in the RPR stage,

P_{b}^{G}

represents minimum technical power output in the DPR stage,

P_{c}^{G}

represents minimum technical power output in the DPRO stage.

In recent years, with the design and technical progress of thermal units, the minimum stable combustion load of the 200MW and 300MW low parameter units can be reduced to 45% after transforming. And minimum stable combustion load of the 600MW and 1000MW high-parameter units can be reduced to 30%~35% after transforming. The energy consumption costs of the thermal power unit are shown below.

F_{peak}^{G} = \{\begin{cases} F_{coal} (P_{peak}^{G}) P_{a}^{G} < P_{peak}^{G} \leq P_{a}^{\max} \\ F_{coal} (P_{peak}^{G}) + F_{loss} (P_{peak}^{G}) P_{b}^{G} < P_{peak}^{G} \leq P_{a}^{G} \\ F_{coal} (P_{peak}^{G}) + F_{loss} (P_{peak}^{G}) + F_{oil} (P_{peak}^{G}) \\ + F_{en} (P_{peak}^{G}) P_{c}^{G} < P_{peak}^{G} \leq P_{b}^{G} \end{cases}

(1)

In the formula, F_coal(

P_{peak}^{G}

) represents the operating coal consumption costs of the thermal power units, which is described by the second order consumption characteristics in (2).

F_{coal} (P_{peak}^{G}) = k_{coal} \cdot (α {P_{peak}^{G}}^{2} + β P_{peak}^{G} + γ)

(2)

In the formula, k_coal represents the price of coal,

α

、

β

、

γ

represent the consumption characteristic coefficients of thermal power units.

F_loss(

P_{peak}^{G}

) represent the unit loss costs caused by the excessive thermal stress of the rotor shaft system in the DPR and DPRO stage. The unit loss costs is mainly determined by the cracking cycle of the rotor as shown in (3).

F_{loss} (P_{peak}^{G}) = \frac{1}{2 N_{T} (P_{peak}^{G})} τ k_{unit}

(3)

In the formula, N_T(

P_{peak}^{G}

) represents the cracking cycle of the rotor, which is interrelated with the power output of units.

τ

represents the actual operating loss coefficient of the thermal power unit,

τ_{1}

is in DPR stage and

τ_{2}

is in DPRO stage, and

τ_{2}

is larger than

τ_{1}

. k_unit represents purchase costs of thermal power units.

F_oil(

P_{peak}^{G}

) represents the fuel consumption costs in the DPRO stage, which is mainly determined by the fuel consumption quantity and oil price of the unit invested in the DPRO stage as is shown in (4).

F_{oil} (P_{peak}^{G}) = k_{oil} \cdot E_{oil}

(4)

In the formula, k_oil represents the price of oil, E_oil represents fuel consumption in the DPRO stage.

F_en(

P_{peak}^{G}

) represents the additional environmental penalties caused by the excessive discharge of pollutants since the reduction of desulfidation efficiency in the DPRO stage, which is shown in (5).

F_{en} (P_{peak}^{G}) = k_{punish} \cdot λ_{S}

(5)

In the formula, k_punish represents the penalty costs coefficient of pollutant discharge exceeding the standard, λ_S represents the excessive discharge of pollutants.

2.3. Peak Regulation Costs of Pumped Storage Units

As the main tool for peak regulating, the pumped storage power station has the functions concluding peak load shifting and valley filling, frequency modulation and phase modulation, rotary reserve and black start. On the one hand, pumped storage units adopt reversible pump turbine units with flexible operation modes; on the other hand, pumped storage units have specific operating characteristics and constraints limited by their own characteristics and operating conditions.

The pumped storage unit is similar to the conventional generator at generating state. At the pumping state, it absorbs power from the power grid. According to the working principle of the pumped storage units, the operation costs generated by the pumped storage units in the process of operation is mainly the costs generated by the conversion between the two working states of pumping and power generation, which is formed by the start-up costs of generator and motor.

F_{peak, j, t}^{PH} = F_{j, t}^{PH - G} + F_{j, t}^{PH - P}

(6)

In the formula,

F_{j, t}^{PH - G}

and

F_{j, t}^{PH - P}

represents the starting cost at tth period when the jth pumped storage unit is at the generating state and the starting costs at the pumping state at tth period respectively.

3. Two-Layer Optimization Dispatching Model of the Regional Power Grid

3.1. Two-Layer Optimization Dispatching Model of Regional Power Grid

Considering the differences of power structure and load characteristics of each province in the regional power grid, the peak regulation margin and demands is in large distribution imbalance. Therefore, the regional provincial peak regulation resources should be fully utilized, which can improve the new energy utilization rate of regional power grid.

Thus, on the basic of principles of provincial power balance and dispatching management in China, a two-layer optimal dispatching model of regional power grid is constructed in this paper, the core of which is to divide the optimal dispatching problem of regional power grid into two parts: units optimal dispatching of each province and optimization of inter-provincial power transmission plan. The flow chart of two-layer optimization scheduling is shown in Figure 2.

3.2. Two-Layer Optimization Dispatching Model of the Regional Power Grid

3.2.1. Objective Function

The optimal scheduling of units is to optimize the startup mode and output power in each province on the basis of the given power transmission plan curves, so that the overall operation costs of units in each province is the lowest. Take one province as an example, its objective function is shown in Equation (7).

\min F = \min (α_{1} \cdot F_{oper} + α_{2} \cdot F_{dep})

(7)

In the formula, α₁ and α₂ represents the weight coefficient of the system unit operation costs and new energy power abandonment costs respectively. F_oper represents the operating costs of all units in the system, which includes the operating costs of thermal power units and pumped storage units in the system. F_dep represents the penalty costs of new energy abandonment.

\begin{array}{l} F_{oper} = F_{peak}^{G} + F_{peak}^{PH} \\ \{\begin{cases} F_{peak}^{G} = \sum_{t = 1}^{T} \sum_{i = 1}^{N_{G}} F_{peak, i, t}^{G} \\ F_{peak}^{PH} = \sum_{t = 1}^{T} \sum_{j = 1}^{N_{PH}} F_{peak, j, t}^{PH} \end{cases} \end{array}

(8)

F_{dep} = k_{dep} \cdot E_{dep}

(9)

In the formula,

F_{peak, i, t}^{G}

、

F_{peak, i, t}^{PH}

represents the peaking operation costs of ith thermal power unit and jth pumped storage unit respectively, k_dep represents penalty costs of abandoned power, E_dep represents the abandonment power of new energy power.

In which, the peak regulating operation costs of thermal power units are mainly obtained according to formula (1), and the peak regulating operation costs of pumped storage units are mainly obtained according to formula (6).

3.2.2. Constraints

System power balance constraints

P_{t}^{L} + P_{t}^{C} = P_{t}^{N} + \sum_{i = 1}^{N_{G}} P_{peak, i, t}^{G} + \sum_{j = 1}^{N_{PH}} P_{j, t}^{PH} - P_{dep, t}

(10)

In the formula,

P_{t}^{L}

represents the system load at tth period,

P_{t}^{C}

represents the reserve capacity of the system at tth period,

P_{t}^{N}

represents the new energy output of system,

P_{peak, i, t}^{G}

represents the power output of ith unit at tth period,

P_{j, t}^{PH}

represents the power output of jth unit at tth period, and positive value represents generate state, negative value represents pumping state, P_dep,t represents the abandon power output at tth period.

Thermal power unit climbing constraints

{DP}_{i}^{G} \leq P_{peak . i, t}^{G} - P_{peak, i, t - 1}^{G} \leq {UP}_{i}^{G}

(11)

In the formula,

{DP}_{i}^{G}

and

{UP}_{i}^{G}

represents the climbing up and down the floor.

Pumped storage operation constraints

According to the actual operation situation of the pumped storage unit, the pumped storage unit pumps with the rated power during the pumping state, the power is within the maximum and minimum technical output range, pumped power generation should meet the storage capacity constraints, its power output and storage capacity constraints are shown below.

P_{j, t}^{PH - P} = u_{j, t}^{PH - P} \cdot P_{j, \max}^{PH}

(12)

0 \leq P_{j, t}^{PH - G} \leq u_{j, t}^{PH - G} P_{j, \max}^{PH}

(13)

E_{PH, \min} \leq E_{PH, t} \leq E_{PH, \max}

(14)

E_{PH, t} = E_{PH, t - 1} + Δ T \cdot (\sum_{j = 1}^{N_{PH}} η_{PH - P} \cdot P_{j, t}^{PH - P} - \sum_{j = 1}^{N_{PH}} \frac{P_{j, t}^{PH - G}}{η_{PH - G}})

(15)

In the formula,

P_{j, \max}^{PH}

represents the rated power output of the jth pumped storage unit,

u_{j, t}^{PH - P}

and

u_{j, t}^{PH - G}

represents the state variables of power pumping and generating, which satisfied

u_{j, t}^{PH - P} + u_{j, t}^{PH - G} \leq 1

P_{j, t}^{PH - P}

and

P_{j, t}^{PH - G}

represents the pumping power and generating power of jth unit at tth period respectively.

E_{PH ， \max}

represents the rated storage capacity of pumped storage energy,

E_{PH ， \min}

represents the minimum storage capacity of pumped storage energy,

η_{PH - P}

and

η_{PH - G}

represents pumping and generating efficiency of pumped storage units.

Upper and lower limits of thermal power units

P_{c, i}^{G} \leq P_{peak, i, t}^{G} \leq P_{i, \max}^{G}

(16)

In the formula,

P_{c, i}^{G}

represents the minimum technical power output lower limit of thermal power unit.

3.3. Analysis of Peak Regulation Margin and Gap between Provinces in the Regional Power Grid

By solving the provincial unit coordination optimization model in Section 2.2, the startup plan and power output arrangements of each unit under the initial inter-provincial power transmission plan can be obtained. The index of peak regulation resource margin and gap of each province can be calculated, which can provide a basis of the subsequent optimization of the transmission curve between provinces.

\{\begin{cases} P_{t}^{margin} = \sum_{i = 1}^{N_{G}} (P_{peak, i, t}^{G} - P_{c, i}^{G}) \\ P_{t}^{insuff} = P_{dep, t} \end{cases}

(17)

In the formula,

P_{t}^{margin}

and

P_{t}^{insuff}

represents the value of peak regulation resource margin and peak regulation gap at tth period.

3.4. Optimized Scheduling Model of Inter-Provincial Transmission Plan Curve

Based on the margin and gap of peak regulation resource of each province in the region calculated in Section 2.3, the initial setting of inter-provincial transmission curves can be optimized and adjusted. Under the condition that the physical power constraints of the provincial transmission lines are satisfied, the optimal transmission curve with the highest new energy utilization rate in the whole region can be calculated, which can realize the most balanced peak regulation resource call of the regional power grid.

3.4.1. Objective Function

The objective function of the inter-provincial transmission curve optimization model mainly considers two aspects, which are the highest new energy utilization rate and the least system peak regulation costs in the whole region. The objective function is shown as below.

\min E_{dep} = \min (β_{1} \cdot k_{dep} \cdot \sum_{t = 1}^{T} P_{dep, t}^{'} + β_{2} \cdot k_{peak} \cdot \sum_{l = 1}^{N_{L}} \sum_{t = 1}^{T} Δ P_{l, t}^{D})

(18)

In the formula, β₁ and β₂ represents weight coefficients of the new energy power abandoned punishment costs and system peak regulation costs, k_peak is the system peak regulation cost coefficient,

P_{dep, t}^{'}

represents the new energy power abandoned power at tth period after optimizing the inter-provincial transmission line,

Δ P_{l, t}^{D}

represents the power difference of lth inter-provincial transmission lines at tth period.

Thus, the calculation of new energy abandon power before and after optimizing the inter-provincial transmission line is as follows,

\{\begin{cases} P_{dep, t}^{'} = P_{dep, t} + \sum_{l = 1}^{N_{L}} Δ P_{l, t}^{D} \\ \sum_{l = 1}^{N_{L}} Δ P_{l, t}^{D} \leq P_{t}^{insuff} \end{cases}

(19)

3.4.2. Constraints

Transmission limit constraints

\begin{array}{l} P_{l, t}^{' D} = P_{l, t}^{D} + Δ P_{l, t}^{D} \\ \{\begin{cases} P_{l, t}^{' D} \leq P_{l, N}^{Pos} ， P_{l, t}^{' D} \geq 0 \\ P_{l, t}^{' D} \geq P_{l, N}^{Neg} ， P_{l, t}^{' D} < 0 \end{cases} \end{array}

(20)

In the formula,

P_{l, t}^{D}

and

P_{l, t}^{' D}

represents power of lth transmission line at tth period before and after optimization,

P_{l, N}^{Pos}

and

P_{l, N}^{Neg}

represents the positive and negative limitation of lth connection line.

Constraints of transmission power limitation

E_{l}^{D} = \sum_{t = 1}^{T} \sum_{l = 1}^{N_{L}} P_{l, t}^{' D}

(21)

E_{l}^{\min} \leq E_{l}^{D} \leq E_{l}^{\max}

(22)

In the formula,

E_{l}^{D}

represents the transmission power of lth transmission line after optimization,

E_{l}^{\max}

and

E_{l}^{\min}

represents the upper and lower transmission power limitation of lth transmission line.

4. Case Study

In order to fully verify the effectiveness and feasibility of the proposed model and method, the IEEE RTS-96 system and a regional power grid in China are used as examples for simulation and analysis. The optimization of all regional power grid units and the transmission lines mainly use Matlab Software with CPLEX and Yalmip optimization engine.

4.1. Test System Analysis Based on IEEE RTS-96

4.1.1. Overview of the Test System

Based on a modified IEEE RTS-96 system as an example analysis, the system can be divided into three sub-regional power grids. Each Region is connected through DC transmission line. The load characteristics of the three sub-regions are shown in Figure 3, the load level of region 1 and region 2 power grids is lower than region 3, the load in region 1 is stable with the smallest peak-valley difference, the system thermal power peak regulating abilities in each region are shown in Table 2. The wind power capacities are 1300MW, and the wind power output characteristics in each region are shown in Figure 4. The peak regulation characteristics of wind power output in region 1 is positive, which can reduce the peak regulation pressure. The peak regulation characteristics of wind power output in region 2 is negative, which aggravate the peak regulation pressure. The characteristics of wind power output in region 3 is stable, which has small influence to peak regulation.

The value of weight coefficient α₁ and α₂ is 0.7 and 0.3, and the value of weight coefficient β1 and β2 is 0.8 and 0.2.

4.1.2. Analytical Calculation

The region 1 and 2 are the main power transmission areas with large units capacity and low load level, while the region 3 is the main power receiving area with small units capacity and high load level. The initial transmission curve between regions takes the constant mode. The operating costs results in each region before and after the optimization are shown in Table 3, the regional daily transmission curves before and after optimization are shown in Figure 5.

As can be shown in Figure 5, the power transmission curves after optimization of region 1 and 2 show great differences, since there exist extreme differences between peak regulation capacities and demands in different regions. Due to the load peak and valley differences in region 1 is small, the peak regulation demand is the minimum. While the load peak and valley differences in region 2 is large, the peak regulation demand is the maximum, and the support ability of peak regulation is the minimum. Therefore, in order to fully call up the peak regulation resources of the three regions and reduce the system operating costs and power abandonment penalty costs, and raise the operation efficiency of each regional power grid, region 2 transmission power to region 3 during low load periods, and region 2 transmission power mainly at high load periods.

4.2. Analysis of an Actual Regional Power Grid in China

4.2.1. Overview of the Regional System

In this part, a regional power grid in China is taken as an example for analysis and calculation, and this region consists 4 provincial power grid. In this region, province A,B,C have surplus electricity and province D mainly accept electricity from B and C. The actual power flows are shown in Figure 6. And the actual power flow direction main be opposite with the what is shown in Figure 6.

Since this region is located with a high latitude, the load demands and the peak regulation demands are large in winter. Therefore, take winter load characteristics as an example, the load characteristics of the four provinces are shown in Figure 7. The load demands of province A,B,C are small and the load peak valley difference is small of province B. The power output characteristics of each province are shown in Figure 8.

4.2.2. Analytical Calculation

Before optimization, the DC power transmission curve outside the region and the initial transmission power curve between provinces in the region are based on the historical annual transmission curves. The results of the operating costs of each regional power grid before and after the optimization are shown in Table 4. The regional daily power curves before and after optimization are shown in Figure 9.

As can be seen from Figure 9, the differences of the transmission curves of C between D and B between D provinces before and after optimization are the largest. The main reason is that the peak regulation capacity and margin of D province is the largest. After optimizing the curves of C between D and B between D provinces, the peak regulation resources can be supported to B and C provinces, which can maximize the new energy utilization rate of the whole region grid.

According to the calculation results in Table 4, after the unit combination optimization of the whole grid and the optimization of the power transmission curves between provinces, the total costs of the regional power grid has descended 7.6%, the operation costs has descended 5.2%, the new energy power abandonment penalty costs has descended 20.4%. After optimization, the utilization rate of new energy in the whole region raised 3.2%. And the utilization rate of new energy of B province has maximum improvement, which is 3.5%.

Comparison and Analysis

In order to further verify the effectiveness and feasibility of the proposed optimization model and algorithm, based on the actual power grid in section 3.2, the traditional optimization method based on equal peak regulating rate was used for comparison. In the traditional equal peak regulating rate mode, it is required for all thermal power units in each province in the region to share the peak regulation demand equally in accordance with the principle of equal peak regulation depth. However, the model proposed in this paper focuses on the whole region, which can maximize the mutual aid and sharing of peak regulation resources of the whole region power grid.

The calculation results of the two models are shown in Table 5. As can be seen from the comparison results, the total costs by using the equal peak rate optimization model is higher than the proposed model in this paper, and the new energy utilization rate is lower, the solution time of the two models is relatively similar. As can be seen from the above comparison results, the proposed optimization model and method in this paper has higher calculation accuracy and solution efficiency, which can fully consider the mutual aids of peak regulating resources, and can achieve the highest new energy power utilization rate and operation costs in the region, and it is more suitable to solve the actual optimization dispatching problems of regional power grid in China.

5. Conclusions

Based on deeply studying the peak regulation characteristics of different types power supplies in this paper, a two-layer optimal dispatching model considering the resources aiding in regional power grid is established. The upper layer is mainly the units startup coordination and optimization scheduling model of each province in the region. The lower layer is mainly the optimal scheduling model of the transmission curve of each province in the region. By solving the two-layer optimization model, the lowest operation costs and the highest new energy utilization rate of the regional power grid can be obtained, which can realize the full aids and sharing of peak regulation resources in the whole region. At last, based on the simulation and analysis of the IEEE RTS-96 power system and an actual regional power grid, the feasibility and effectiveness of the proposed model and optimization method are verified.

References

Zhang, N.; Zhou, T.; Duan, C. Impact of large-scale wind farm connecting with power grid on peak load regulation demand. Power Syst. Technol. 2010, 34, 152–158. [Google Scholar]
Zhu, L.; Chen, N.; Han, H. Key problems and solutions of wind power accommodation. Autom. Electr. Power Syst. 2011, 35, 29–34. [Google Scholar]
Jiang, P.; Yang, S.; Huo, Y. Static security analysis of power systems considering randomness of wind farm output. Autom. Electr. Power Syst. 2013, 37, 35–40. [Google Scholar]
Zhang, H.; Yin, Y.; Shen, H. Peak-load regulating adequacy evaluation associated with large-scale wind power integration. Proc. CSEE 2011, 31, 26–31. [Google Scholar]
Kabouris, J.; Kanellos F, D. Impacts of large-scale wind penetration on designing and operation of electric power systems. IEEE Trans. Sustain. Energy 2010, 1, 107–114. [Google Scholar] [CrossRef]
Ying, Y.; Wang, Z.; Wu, X. Multi-objective strategy for deep peak shaving of power grid considering uncertainty of new energy. Power Syst. Prot. Control 2020, 48, 34–42. [Google Scholar]
Yang, L.; Liang, X.; Wang, X. Combined heat and power economic dispatching considering peak regulation right trading to improve secondary accommodation capability of wind power. Power Syst. Technol. 2020, 44, 1872–1880. [Google Scholar]
Lin, L.; Zou, L.; Zhou, P. Multi-angle economic analysis on deep peak regulation of thermal power units with large-scale wind power integration. Autom. Electr. Power Syst. 2017, 41, 21–27. [Google Scholar]
Lin, L.; Tian, X. Analysis of deep peak regulation and its benefit of thermal units in power system with large scale wind power integrated. Power Syst. Technol. 2017, 41, 2255–2263. [Google Scholar]
Huang, H.; Xiong, H.; Jiang, B. Design of day-ahead trading mechanism for trans-province peak-shaving auxiliary service of regional power grid. Smart Power 2020, 48, 119–124. [Google Scholar]
Xu, Z.; Zhang, F.; Chen, S. Design of day-ahead trading mechanism for trans-province peak-shaving auxiliary service of regional power grid. Electric Power 2018, 51, 64–69. [Google Scholar]
Lu, S.; Zhang, X.; Xu, Y. Two-stage iterative method to optimize tie-line exchange power based on marginal power generation cost. Power Syst. Prot. Control 2021, 49, 77–88. [Google Scholar]
Zhang, Y.; Hou, Y.; Hu, T. Regional power network environment/economic power dispatching considering balance of power between provinces. Eng. J. Wuhan Univ. 2017, 50, 548–555. [Google Scholar]
Fang, B.; Xiao, L.; Sun, C.; et al. An optimization dispatch method for regional power grid considering peaking resource mutual support. Electr. Drive 2022, 52, 54–60. [Google Scholar]
Liu, D.; Huang, Y.; Wang, W. Analysis on provincial system available capability of accommodating wind power considering peak load dispatch and transmission constraints. Autom. Electr. Power Syst. 2011, 35, 77–81. [Google Scholar]
Zhuo, Z.; Zhang, N.; Xie, X. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Autom. ELectric Power Syst. 2021, 45, 171–191. [Google Scholar]

Figure 1. Peak regulation costs of fuel units.

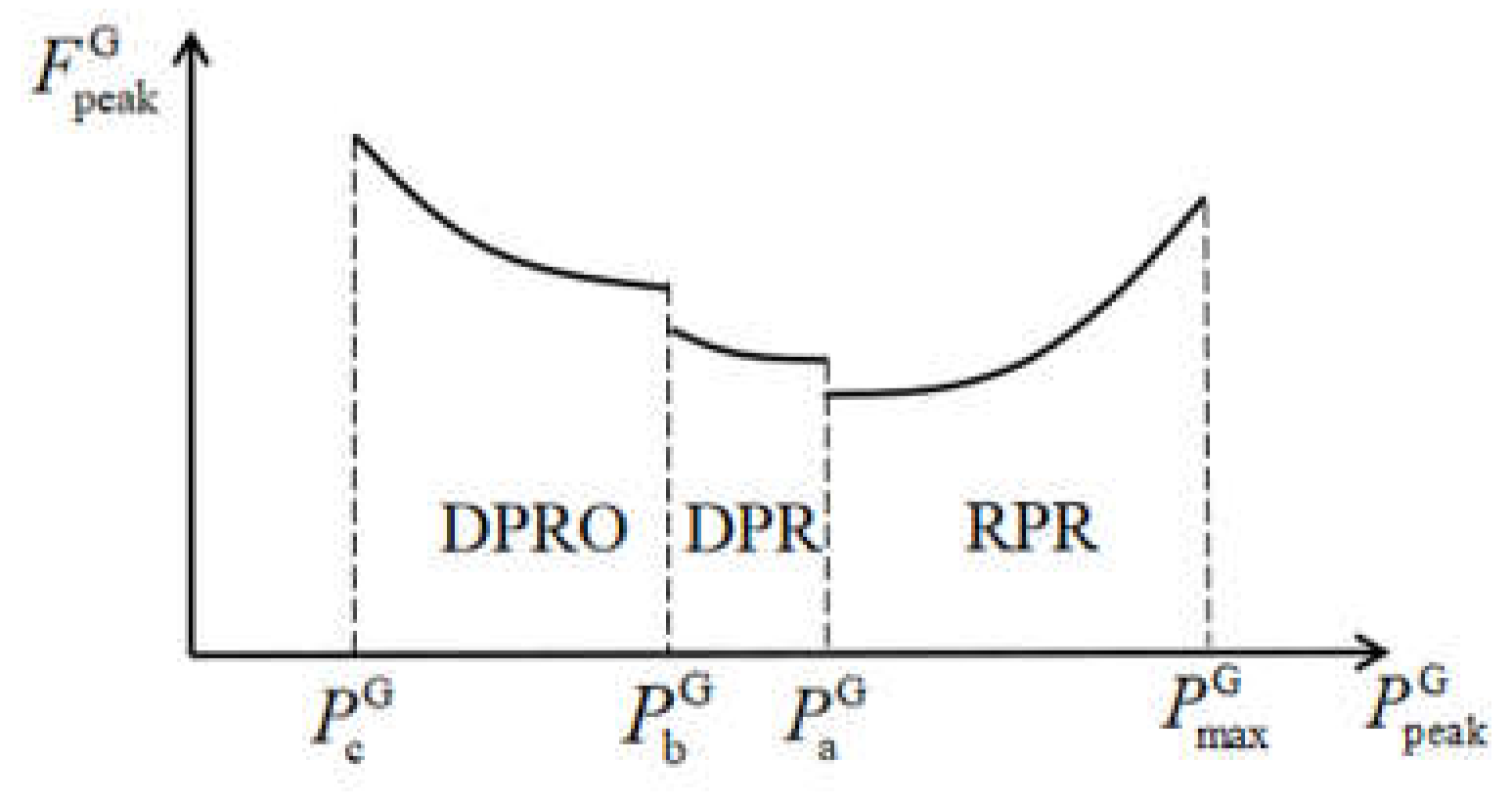
Figure 2. Two layer optimal dispatching process of regional power grid.

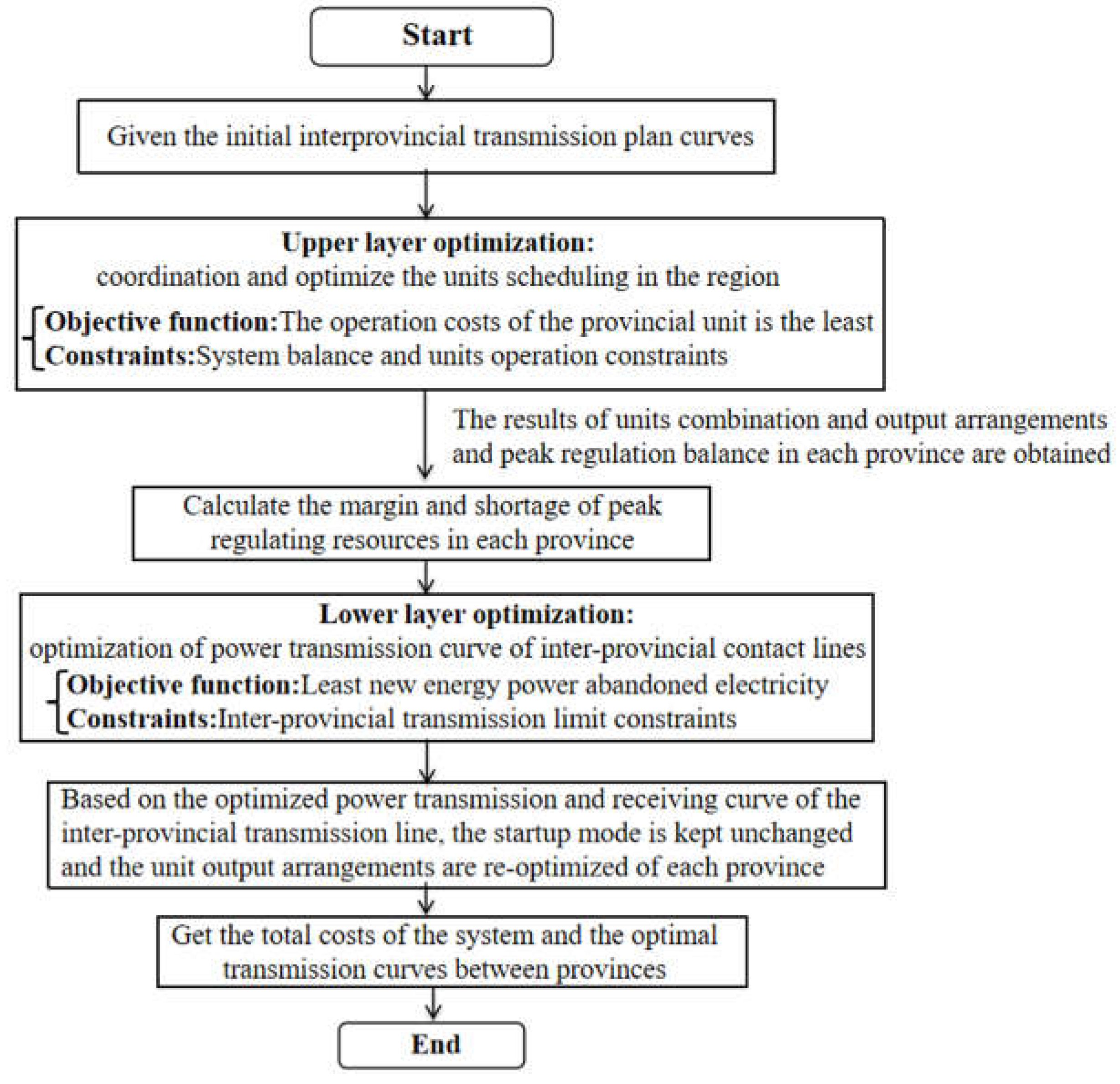
Figure 3. Load characteristics of regional power grid.

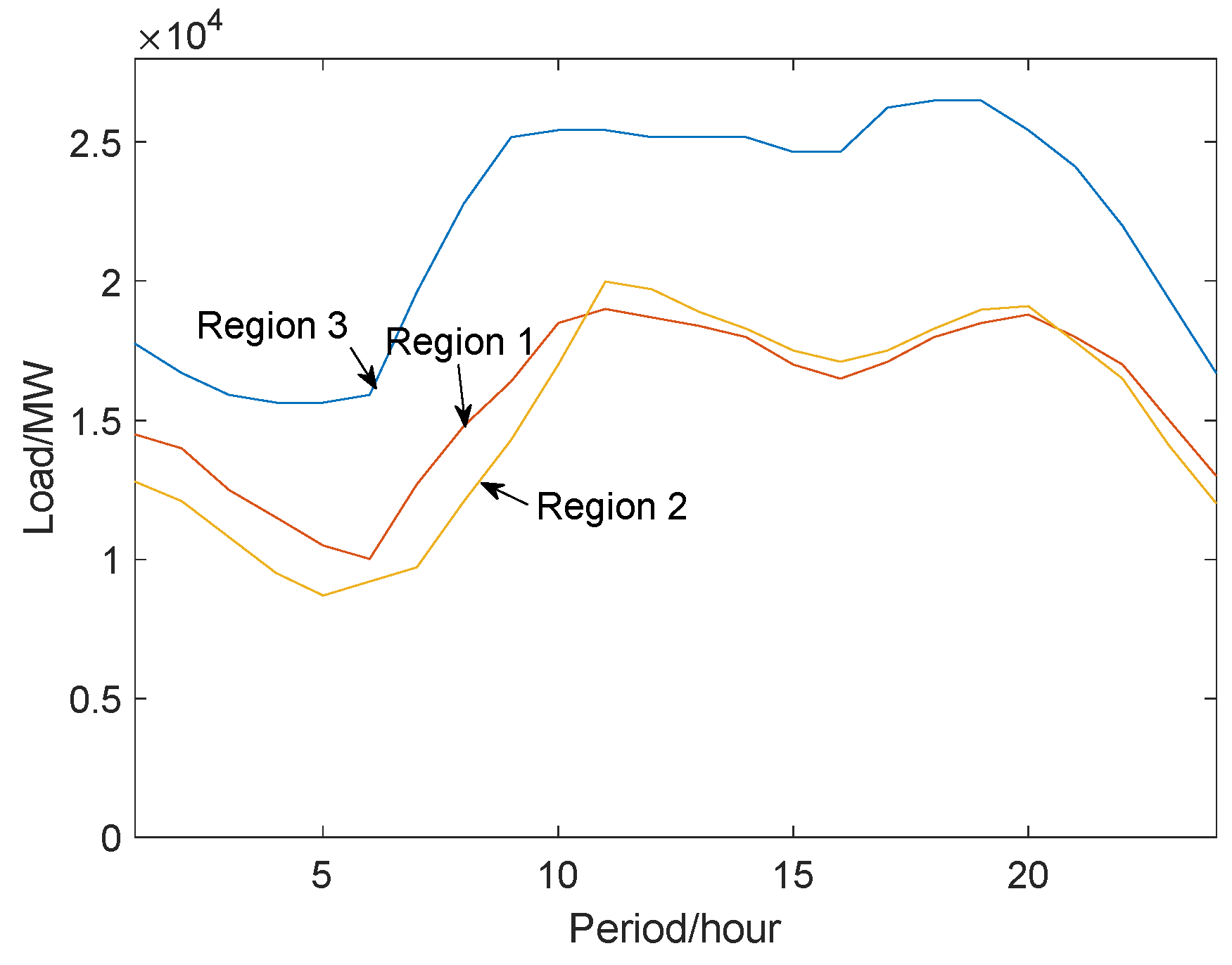
Figure 4. Wind power characteristics of regional power grid.

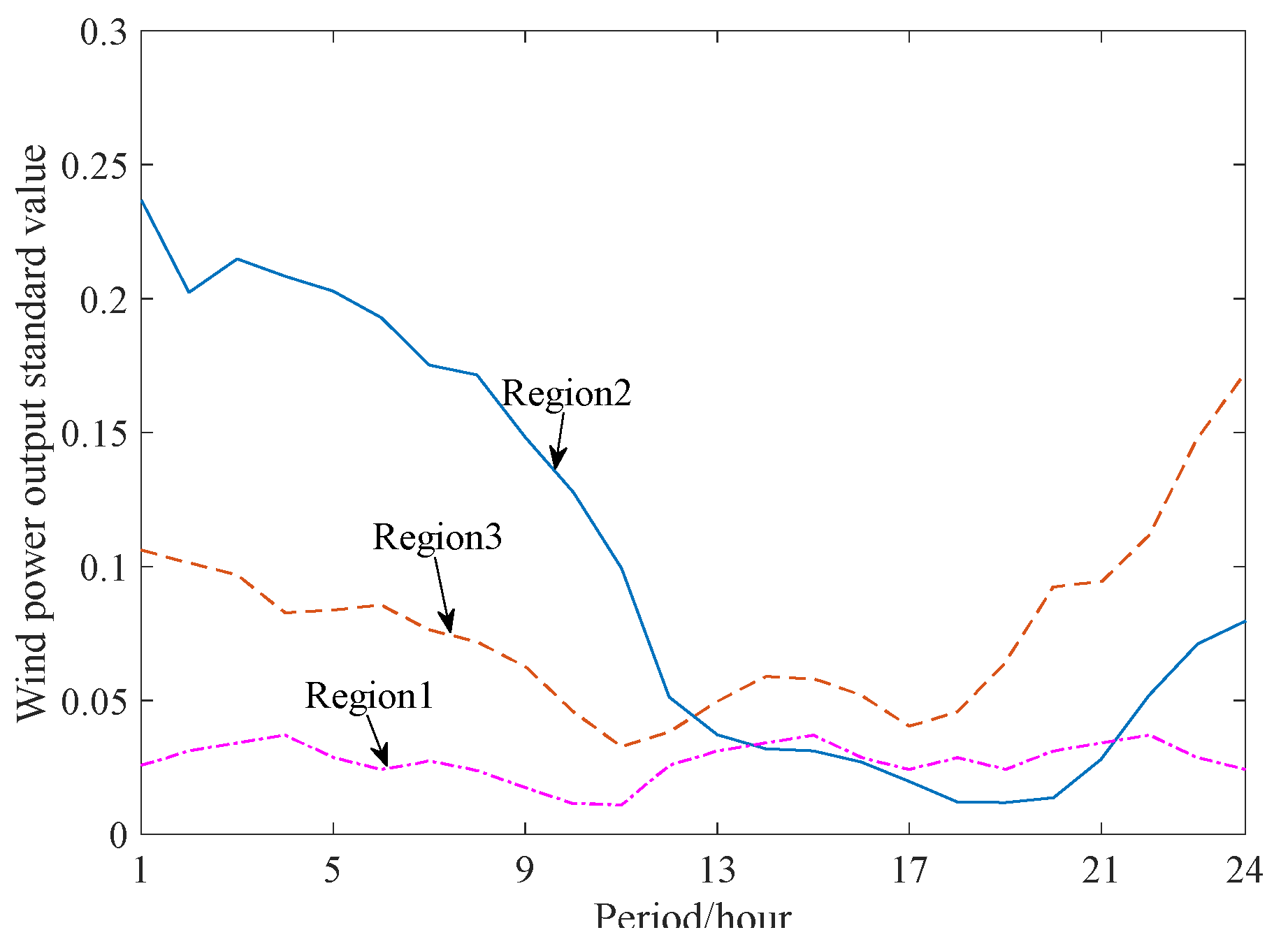
Figure 5. Daily power transmission curve between each region power grid before and after inter-provincial transmission plan curve optimization.

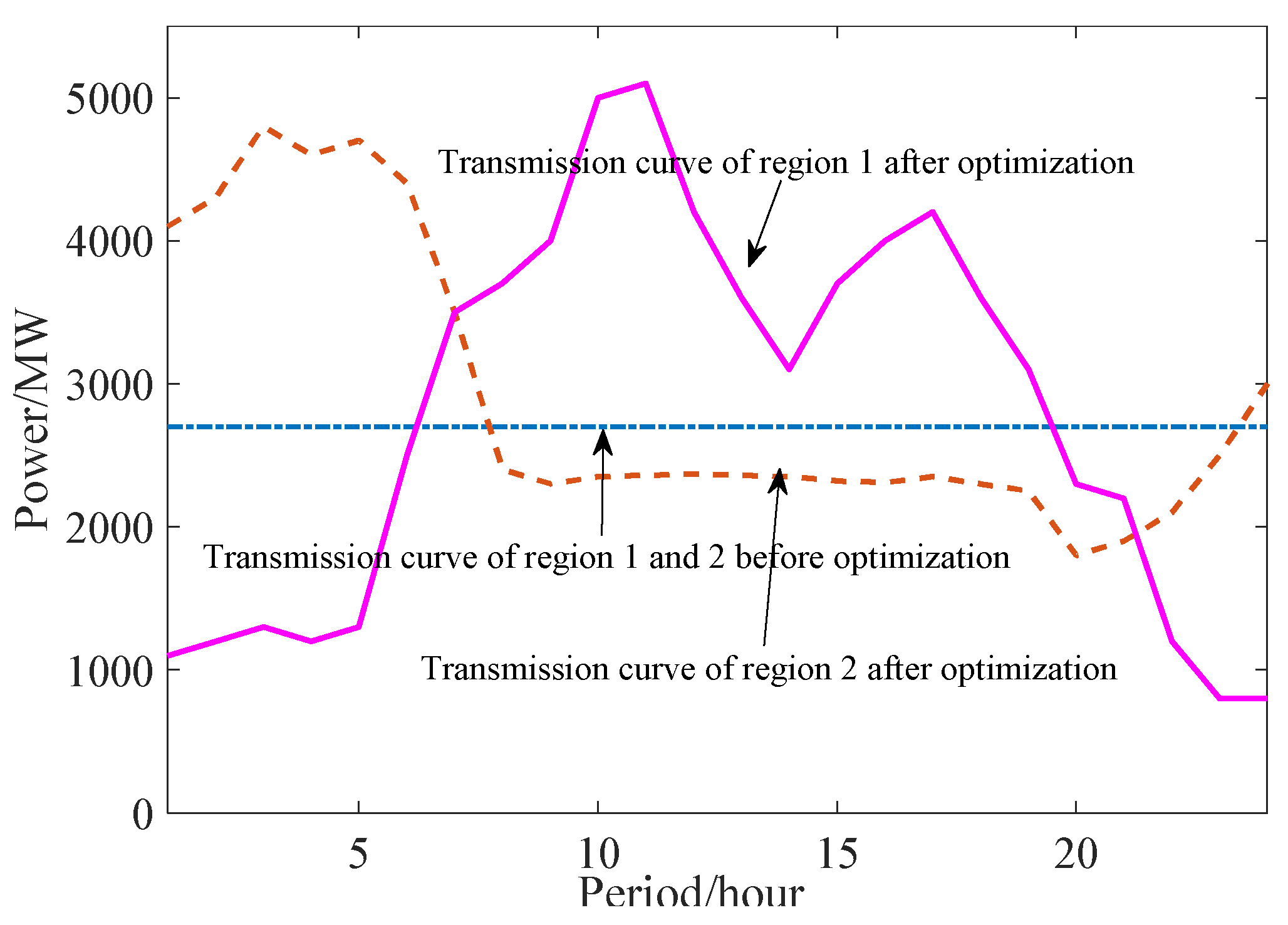
Figure 6. Schematic diagram of power transmission and reception of regional power grid.

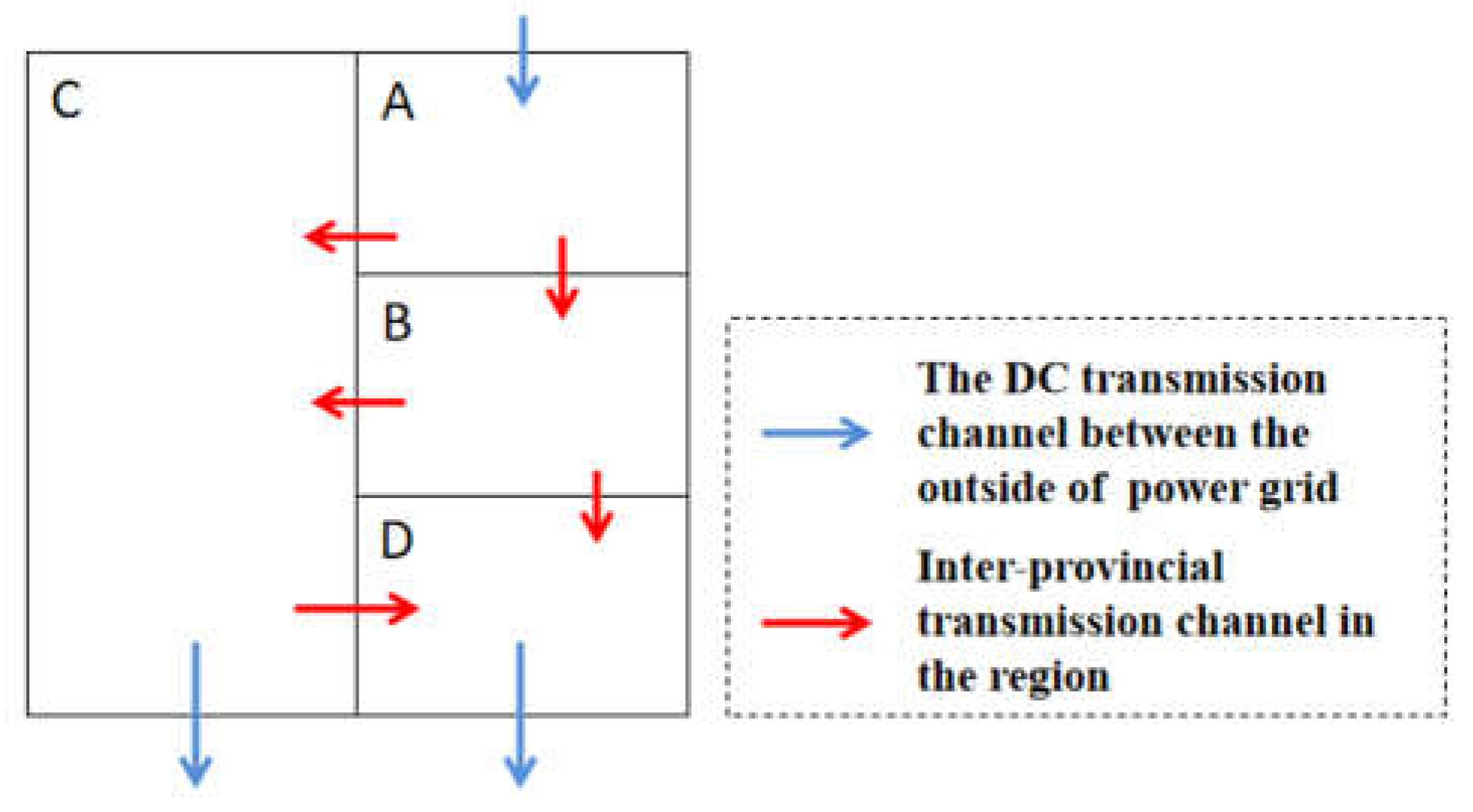
Figure 7. Load characteristics of each province in regional power grid.

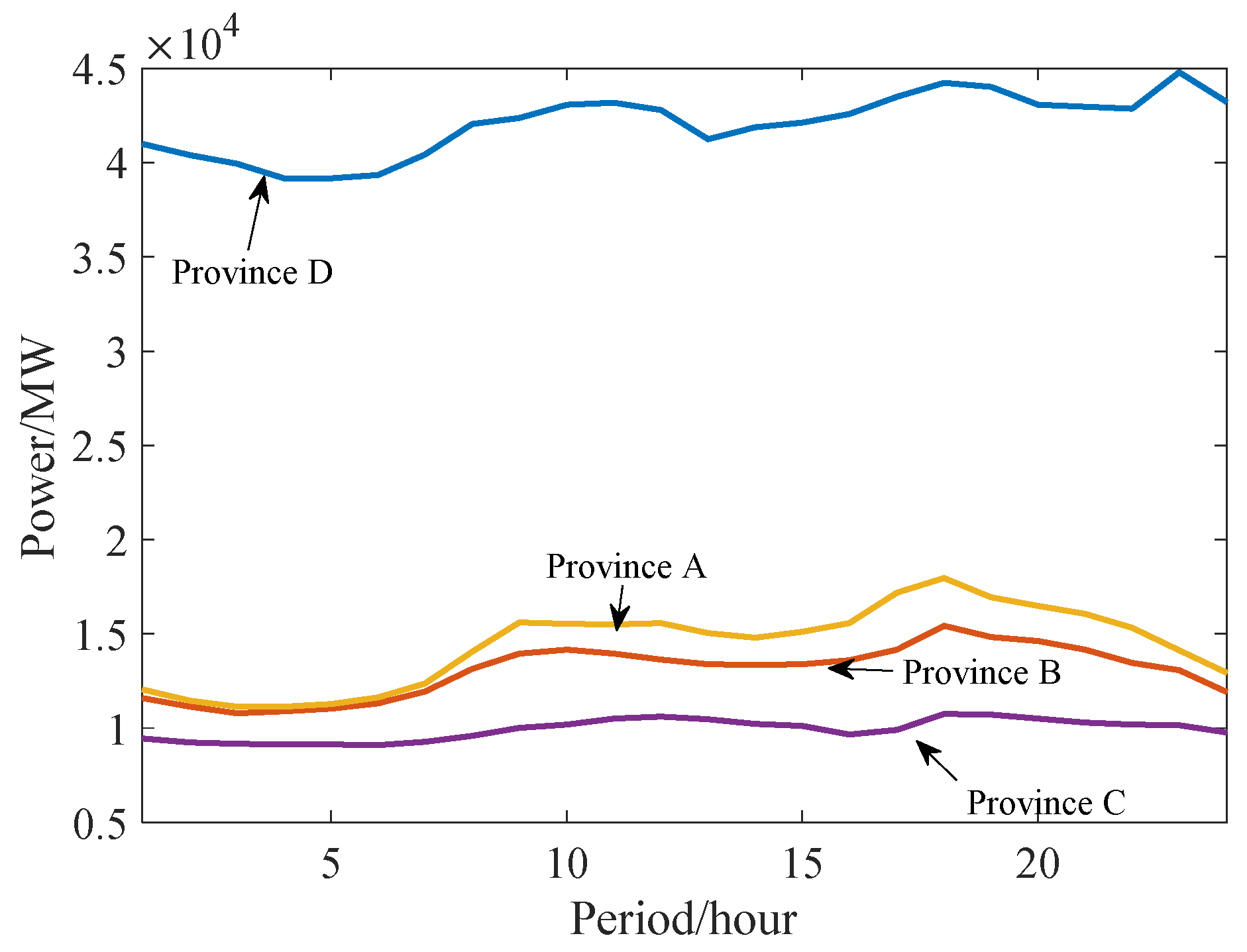
Figure 8. Wind power output characteristics of each province in regional power grid. PV power output characteristic of each province in regional power grid.

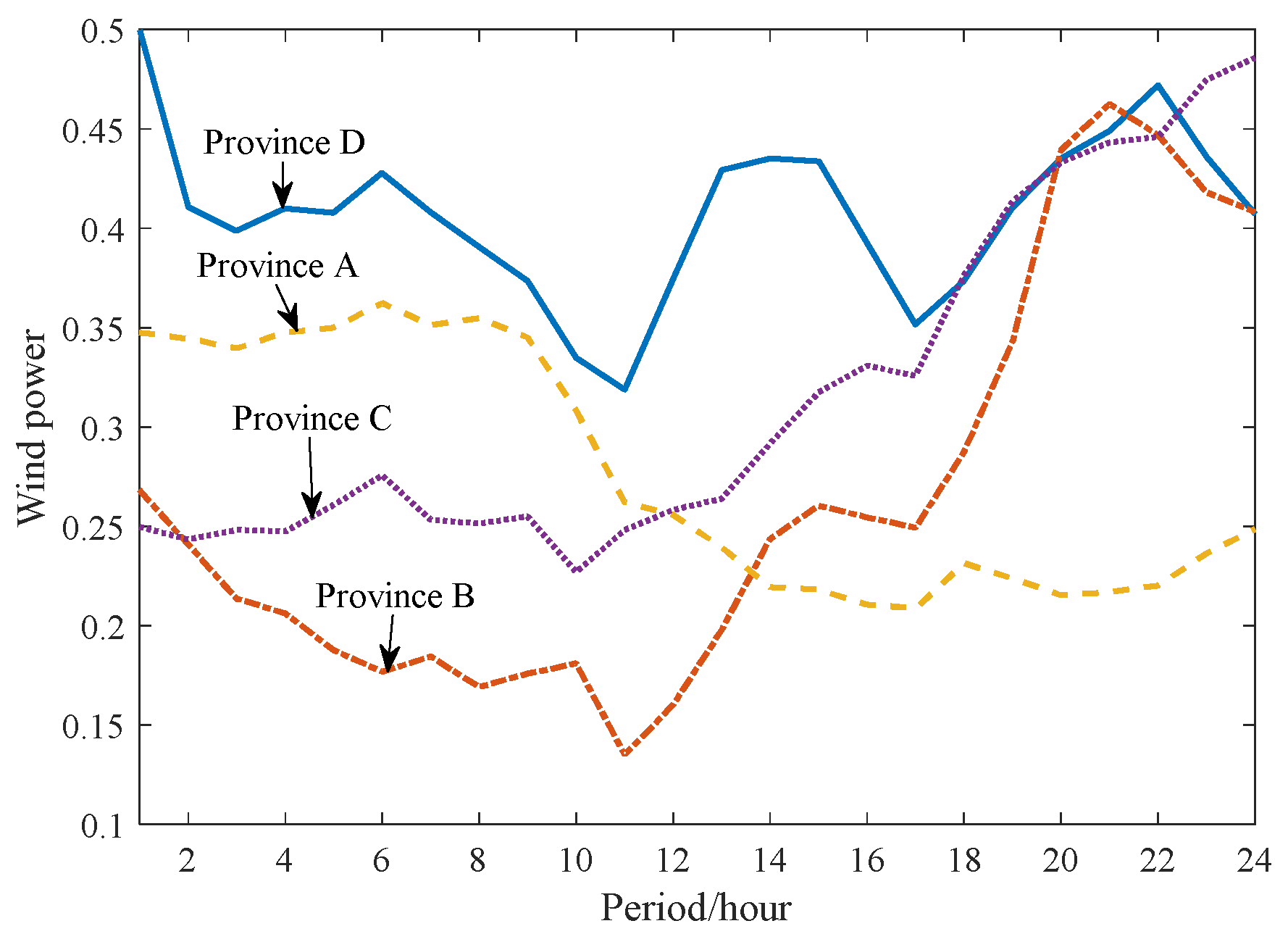
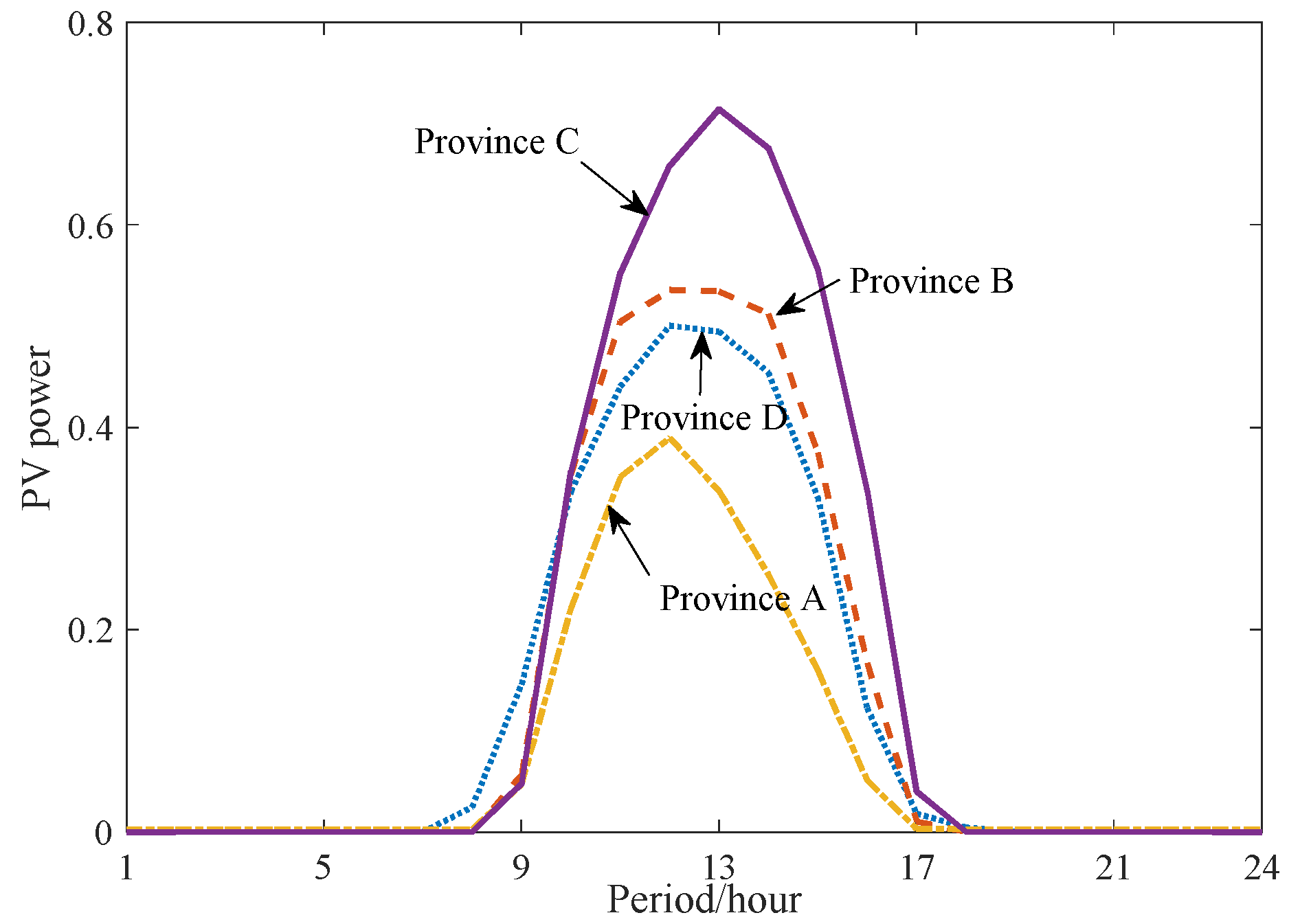
Figure 9. Daily power transmission curves between each region power grid before and after transmission line optimization.

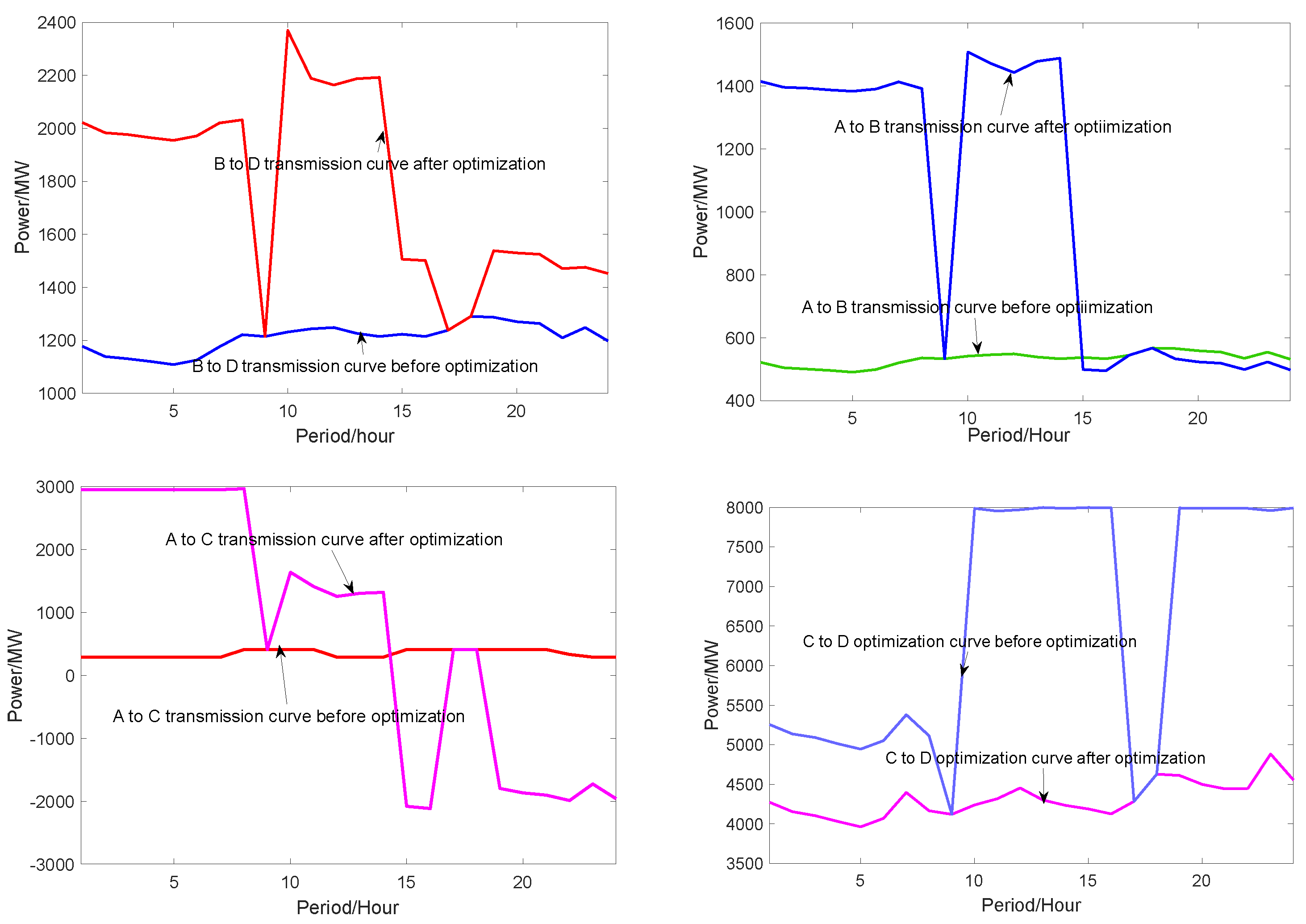
Table 1. Peak regulation characteristics of different types power generation.

Power Generation	Peak regulation ability
Coal-fired units	Conventional traditional units: 40%~50% After the flexibility transformation: 55%~70%
Gas unit	Have the ability of shutdown and peak regulation:100%
Cascade hydro-power unit (non-runoff)	Have the ability of shutdown and peak regulation:100%
pump storage units	200%
Other energy storage units	160%
small hydro-power stations (Radial flow)	No peak regulation ability
Wind	No peak regulation ability
photovoltaic	No peak regulation ability

Table 2. Peak regulation capacity of thermal units in each sub-region

Region	Units capacities /MW	Wind power capacities/MW	Peak regulation capacities	Peak regulating capacities without oil	Peak regulating capacities with oil
Region 1	29410	1300	50%	40%	35%
Region 2	29410	1300	50%	45%	40%
Region 3	21100	1300	50%	43%	38%

Table 3. Operation costs of each region before and after inter-provincial transmission plan curve optimization.

	Before optimization			After optimization
Region	Total costs/100 million $	Operation costs/100 million $	Abandon punishment costs/100 million $	Total costs/100 million $	Operation costs/100 million $	Abandon punishment costs/100 million $
1	0.28	0.23	0.05	0.24	0.22	0.02
2	0.27	0.23	0.03	0.25	0.23	0.02
3	0.25	0.2	0.04	0.22	0.19	0.02
Total	0.79	0.66	0.12	0.7	0.64	0.06

Table 4. Operation costs of each region power grid before and after inter-provincial transmission plan curve optimization.

	Before optimization				After optimization
Province	Total costs/100 million $	Operation costs/100 million $	Abandon punishment costs/100 million $	New energy utilization rate%	Total costs/100 million $	Operation costs/100 million $	Abandon punishment costs/100 million $	New energy utilization rate%
A	0.46	0.396	0.064	87.9	0.419	0.377	0.042	89.9
B	0.545	0.452	0.092	84.8	0.495	0.433	0.061	88.3
C	0.455	0.335	0.121	89.6	0.423	0.315	0.108	90.7
D	0.653	0.599	0.053	93.3	0.617	0.565	0.052	93.5
Total	2.113	1.782	0.33	87.7	1.941	1.69	0.263	90.9

Table 5. Comparison of calculation results by two optimization models.

Model	Optimization Results
Model	Total costs/100 million $	New energy utilization rate%
1	1.953	9.1
2	2.116	12.9

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Research on Two-Layer Optimal Dispatching Method Considering Mutual Aid of Peak Regulation Resources in Regional Power Grid

Abstract

1. Introduction

2. System Peak-Regulating Resource Analysis

2.1. Analysis of Different Types of Power Supply

2.2. Analysis of Energy Consumption Costs of Coal-Fired Units

2.3. Peak Regulation Costs of Pumped Storage Units

3. Two-Layer Optimization Dispatching Model of the Regional Power Grid

3.1. Two-Layer Optimization Dispatching Model of Regional Power Grid

3.2. Two-Layer Optimization Dispatching Model of the Regional Power Grid

3.2.1. Objective Function

3.2.2. Constraints

3.3. Analysis of Peak Regulation Margin and Gap between Provinces in the Regional Power Grid

3.4. Optimized Scheduling Model of Inter-Provincial Transmission Plan Curve

3.4.1. Objective Function

3.4.2. Constraints

4. Case Study

4.1. Test System Analysis Based on IEEE RTS-96

4.1.1. Overview of the Test System

4.1.2. Analytical Calculation

4.2. Analysis of an Actual Regional Power Grid in China

4.2.1. Overview of the Regional System

4.2.2. Analytical Calculation

Comparison and Analysis

5. Conclusions

References

MDPI Initiatives

Important Links

Subscribe